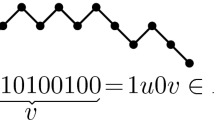Counting Hamiltonian Cycles in the Matroid Basis Graph

Abstract

We present superfactorial and exponential lower bounds on the number of Hamiltonian cycles passing through any edge of the basis graph of generalized Catalan, uniform, and graphic matroids. All lower bounds were obtained by a common general strategy based on counting appropriated cycles of length four in the corresponding matroid basis graph.

1 Introduction

Basis graphs of matroids have been extensively studied. Gel$'$fand and Serganova [11] proved that basis graphs are 1-skeletons of basis polytopes [6, 7]. Maurer [15] gave a characterization of basis graphs, Liu [12,13,14] investigated their connectivity, and Donald, Holzmann, and Tobey [9] gave a characterization of basis graphs of uniform matroids.

A graph is edge-Hamiltonian if it has at least three vertices and every edge is in a Hamiltonian cycle. According to Bondy and Ingleton [2], Haff (unpublished) showed that every basis graph is edge-Hamiltonian, unless it is $K_1$ or $K_2$, generalizing a result due to Cummins [8] and Shank [17] for graphic matroids. So, basis graphs with at least three vertices are edge-Hamiltonian. In fact, the work of Bondy and Ingleton  [2, Theorems 1 and 2] implies the edge-Hamiltonicity proved by Haff. Alspach and Liu [1] proved that basis graphs are Hamilton-connected and edge-pancyclic. In this paper, we investigate further the edge-Hamiltonicity of basis graphs.

A matroid${M = (E,\mathscr {B})}$ of rank$r=r(M)$ is a finite set E together with a nonempty collection $\mathscr {B}=\mathscr {B}(M)$ of r-subsets of E, called the bases of M, satisfying the following basis exchange axiom:

(BEA):

If $B_1$ and $B_2$ are members of $\mathscr {B}$ and $e\in B_1\setminus B_2$,

then there is an element $g\in B_2\setminus B_1$ such that $(B_1-e)+g \in \mathscr {B}$.

A loop is an element that does not belong to any basis and an isthmus is an element that belongs to all bases. For general background in matroid theory, we refer the reader to Oxley [16] and Welsh [19].

The basis graph${\text {BG}}(M)$of a matroidM is the graph having as vertex set the bases of M and two vertices (bases) $B_1$ and $B_2$ are adjacent if and only if the symmetric difference of $B_1$ and $B_2$ has cardinality two. A graph is a basis graph if it can be labeled to become the basis graph of some matroid. We make no distinction between a basis of M and a vertex of ${\text {BG}}(M)$.

For a given matroid M let ${\text {HC}}^*(M)=\min \{{\text {HC}}_e(M) : e \in E({\text {BG}}(M)) \}$, where ${\text {HC}}_e(M)$ denotes the number of Hamiltonian cycles in ${\text {BG}}(M)$ containing edge ${e\in E({\text {BG}}(M))}$. Bondy and Ingleton state that ${\text {HC}}^*(M)\ge 1$ for every matroid M with at least three bases.

We start, in Sect. 2, by presenting the general strategy we use. In Sect. 3, we investigate ${\text {HC}}^*(M)$ when M is in the class of lattice path matroids. We present a lower bound on ${\text {HC}}_e(M)$ when M is a generalized Catalan matroid (Theorem 1). In particular, the derived lower bound for the k-Catalan matroid is superfactorial on k. In Sect. 4, we give lower bounds on ${\text {HC}}^*(M_G)$ where $M_G$ is the cycle matroid obtained from a k-edge-connected graph G. The lower bound for $k = 2$ is exponential on the number of vertices of G (Theorem 3). The lower bound for $k \ge 3$ is exponential on both k and the number of vertices of G (Theorem 4). Section 5 presents some concluding remarks.

2 General Strategy

In order to give a lower bound on ${\text {HC}}^*(M)$, we follow the strategy described below, which has the same spirit as the one used by Bondy and Ingleton [2].

Let M be a matroid and ${\text {BG}}(M)$ be its basis graph. Let $B_1$ and $B_2$ be adjacent vertices (bases) in ${\text {BG}}(M)$. By (BEA), there exist elements e and g of M, with ${e \in B_1\setminus B_2}$ and ${g \in B_2\setminus B_1}$, such that $B_2= B_1-e+g$. We define an (X, Y)-bipartition (determined by e) of the bases of M, with

$$\begin{aligned} X = \{ B\in \mathscr {B}(M) :\, e \in B \} \hbox { and }{Y = \{B \in \mathscr {B}(M) :\, e \not \in B \}}. \end{aligned}$$

The bases in X (Y, respectively) correspond exactly to the bases of the matroid $M' = M/e$ obtained by contractinge ($M'' = M\setminus e$, obtained by deleting e, respectively). Moreover, ${\text {BG}}(M')$ is ${\text {BG}}(M)[X]$ (${\text {BG}}(M'')$ is ${\text {BG}}(M)[Y]$, respectively), which is the subgraph of ${\text {BG}}(M)$ induced by X (Y, respectively). We do not distinguish between ${\text {BG}}(M')$ and ${\text {BG}}(M)[X]$ (${\text {BG}}(M'')$ and ${\text {BG}}(M)[Y]$, respectively).

A basis sequence $B_1B_2B_3B_4$ is a good cycle for $B_1B_2$ if it is a cycle in ${\text {BG}}(M)$, each of $B_1$ and $B_4$ contains e, and none of $B_2$ and $B_3$ contains e (Fig. 1).

Fig. 1

A good cycle $C=B_1B_2B_3B_4$ for $B_1B_2$

The symmetric difference between two cycles $C_1$ and $C_2$ is the graph induced by the edges in the symmetric difference of $E(C_1)$ and $E(C_2)$.

If $C=B_1B_2B_3B_4$ is good, then the symmetric difference of a Hamiltonian cycle of ${\text {BG}}(M')$ passing through the edge $B_1B_4$, the good cycle C, and a Hamiltonian cycle of ${\text {BG}}(M'')$ passing through the edge $B_2B_3$ is a Hamiltonian cycle of ${\text {BG}}(M)$.

So, if $\mathscr {C}(B_1,B_2)$ is the set of good cycles for $B_1B_2$, then

$$\begin{aligned} {\text {HC}}_{B_1B_2}(M) \ge {\text {HC}}^*(M') \cdot |\mathscr {C}(B_1,B_2)| \cdot {\text {HC}}^*(M''). \end{aligned}$$

This inequality suggests an inductive way to achieve a lower bound on ${\text {HC}}^*(M)$. A key part in this approach involves proving a lower bound on the number of good cycles for any edge of ${\text {BG}}(M)$.

3 Generalized Catalan Matroids

In this section we address a special class of transversal matroids introduced by Bonin, de Mier, and Noy [5]. We specialize the description of Bonin and de Mier [4] and Stanley [18].

A lattice pathL in $\mathbb {Z}^2$ is a sequence $v_0, \ldots , v_k \in \mathbb {Z}^2$ such that each consecutive difference $s_j = v_j - v_{j-1}$ lies in $\{(1,0), (0,1)\}$. We say that L goes from $v_0$ to $v_k$ and call $s_j$ the jth step of L. All lattice paths we consider go from (0, 0) to a certain (m, r). If we write East (E) for (1, 0) and North (N) for (0, 1), then L can be represented by a word of length $m+r$ on the alphabet $\{E,N\}$ or by the subset $\{ j :\, j\text {th step of }L\text { is } N \}$ of $\{1, \ldots , m+r\} = [m{+}r]$.

Let Q be a lattice path from (0, 0) to (m, r) and $\mathscr {P}$ be the set of all lattice paths from (0, 0) to (m, r) that do not go above Q. For each i with $1 \le i \le r$, let $A_i = \left\{ j :\, j\text {th step is the }i\text {th North}\right.$$\left. \text {for some path in } \mathscr {P}\right\}$. Each $A_i$ is the interval $[a_i, m+i]$ in $[m{+}r]$ where $a_i$ is the position of the ith North step of Q (Fig. 2).

Fig. 2

Lattice path Q from (0, 0) to (10, 8) and the corresponding sets $A_1,\ldots ,A_8$. Representation of Q as a subset of $[10+8]$ and as a word of length $10 + 8$ in the alphabet $\{E,N\}$. Lattice paths $B_1$ and $B_2$ that do not go above Q and their representations as a subset and as a word

Let $M_Q$ be the transversal matroid on the set $[m{+}r]$ with standard presentation $(A_1,\ldots ,A_r)$. Note that $M_Q$ has rank r and corank (or nullity) m. The bases of $M_Q$ are the subsets of $[m{+}r]$ that represent lattice paths in $\mathscr {P}$. A generalized Catalan matroid is a matroid $M_Q$ for some lattice path Q. The class of generalized Catalan matroids is minor-closed [4, Theorem 4.2]. The k-Catalan matroid is the generalized Catalan matroid $M_Q$ with $Q=( N E )^{k}$.

Lemma 1

Let $M_Q$ be a generalized Catalan matroid of rank r and corank m with neither a loop nor an isthmus, for $m \ge r \ge 2$. Then every edge of ${\text {BG}}(M_Q)$ is in ${r-1}$ good cycles.

Proof

As $M_Q$ has neither a loop nor an isthmus, the first step of Q is North and the last one is East. Let $B_1B_2$ be an edge of ${\text {BG}}(M_Q)$. Say $B_1= x_1 \ldots x_{m+r}$ and $B_2= y_1 \ldots y_{m+r}$, with $x_i$, $y_i \in \{ N , E \}$ for $i\in [m{+}r]$. There exist indices e and g such that $x_e = y_g = N$, $x_g = y_e = E$, and $x_{\ell } = y_{\ell }$ for $\ell \ne e$, g. So $B_2= B_1- e + g$. We may assume that $e < g$.

If there exists an index $f < e$ such that $x_f = y_f = N$, let f be as small as possible. For every index w such that $x_w = y_w = E$, basis $B_4$ rises by switching $x_w$ for $N$ and $x_f$ for $E$ in $B_1$ and basis $B_3$ rises by switching $y_w$ for $N$ and $y_f$ for $E$ in $B_2$; that is, $B_4= B_1- f + w$ and $B_3= B_2- f + w$ (Fig. 3). Since the first step of Q is North and the last one is East, the paths corresponding to the words $B_3$ and $B_4$ are in $M[Q]$. Thus, for every common $E$ step of $B_1$ and $B_2$, we obtain a good cycle. Therefore, there are $m-1$ good cycles passing through the edge $B_1B_2$. Similarly, if there exists an index $f > g$ such that ${x_f = y_f = E }$, by replacing North by East and vice-versa in the previsous argument, one can conclude that there are $r-1$ good cycles passing through the edge $B_1B_2$.

Fig. 3

$B_3$ and $B_4$ for $w=3,9,17$ and $B_1$ and $B_2$ as in Fig. 2, with $e = 6$, $g = 13$, and $f=5$

Otherwise $x_e$ is the first $N$ in $B_1$ and $x_g$ is the last $E$. Let $x_h$ be the penultimate $E$ in $B_1$. Such $x_h$ exists because $m \ge r \ge 2$. As $y_g = N$, $y_h$ is the last $E$ in $B_2$. We will obtain a good cycle for each $N$ in $B_1$, except for $x_e$, proving that there are $r-1$ good cycles passing through $B_1B_2$.

We partition $B_1-e$ in maximal blocks$x_i \cdots x_{w-1}$ such that $x_i = \cdots = x_{w-1} = N$ with $i>e$ and consider three cases:

$w < g$::

For every $f \in \{i, \ldots , w-1\}$, basis $B_4$ rises by switching $x_f$ for $E$ and $x_{w}$ for $N$ in $B_1$ and basis $B_3$ rises by switching $y_f$ for $E$ and $y_{w}$ for $N$ in $B_2$; that is, $B_4= B_1- f + w$ and $B_3= B_2- f + w$.

$w = g$::

Let $x_h$ be the penultimate $E$ in $B_1$. As $y_w = y_g = N$, $y_h$ is the last $E$ in $B_2$. For every $f \in \{i, \ldots , g-1\}$, basis $B_4$ rises by switching $x_f$ for $E$ and $x_g$ for $N$ in $B_1$, and basis $B_3$ rises by switching $y_f$ for $E$ and $y_h$ for $N$ in $B_2$; that is, $B_4= B_1- f + g$ and $B_3= B_2- f + h$.

$i = g+1$::

For every element $f~\in ~\{{g+1}, \ldots , {m+r}\}$, basis $B_4$ rises by switching $x_f$ for $E$ and $x_g$ for $N$ in $B_1$, and basis $B_3$ rises by switching $y_f$ for $E$ and $y_h$ for $N$ in $B_2$; that is, $B_4= B_1- f + g$ and $B_3= B_2- f + h$.

$\square$

Bonin and de Mier [4] observed that the class of all generalized Catalan matroids is closed under duals. In particular, a basis $B^*$ of the dual of $M_Q$ corresponds to the $E$ steps of the basis B in $M_Q$. Therefore, the following is a consequence of this fact and Lemma 1.

Corollary 1

For r, $m \ge 2$, let $M_Q$ be a generalized Catalan matroid of rank r and corank m, with neither a loop nor an isthmus. Then every edge of ${\text {BG}}(M_Q)$ is in $\min \{r-1, m-1\}$ good cycles.

Let $M_Q$ be a generalized Catalan matroid and e be an element of $M_Q$. From an observation of Bonin and de Mier [4], if e is neither a loop nor an isthmus, then $M_Q \setminus e$ is the matroid $M_{Q'}$ where $Q'$ is formed by deleting from Q the first $E$ step that is at or after step e, and $M_Q / e$ is the matroid $M_{Q''}$ where $Q''$ is formed by deleting from Q the last $N$ step that is at or before step e.

Remark 1

If the k-Catalan matroid is a minor of the generalized Catalan matroid $M_Q$, then the ${(k-1)}$-Catalan matroid is a minor of both $M_Q \backslash e$ and $M_Q \slash e$ for every element e of $M_Q$.

For the class of generalized Catalan matroids, we define the function

$$\begin{aligned} {\text {hc}}(k) = \min \left\{ {\text {HC}}^*(M_Q) :\, M_Q \text { has a }k\text {-Catalan matroid as a minor} \right\} . \end{aligned}$$

Proposition 1

For $k \ge 2$, ${\text {hc}}(k) \ge (k-1)\big ({\text {hc}}(k-1) \big )^2$.

Proof

Let $M_Q$ be a generalized Catalan matroid such that ${\text {HC}}^*(M_Q) = {\text {hc}}(k)$. We may assume that $M_Q$ has neither a loop nor an isthmus. Thus, both the rank and corank of M are at least k. By Corollary 1, there are $\min \left\{ r-1,m-1 \right\} \ge k-1$ good cycles for every edge of ${\text {BG}}(M_Q)$. Let $B_1B_2$ be an edge of ${\text {BG}}(M_Q)$, say $B_1= B_2- e + g$, and let $M' = M_Q \backslash e$ and $M'' = M_Q \slash e$. It follows from Remark 1 that both $M'$ and $M''$ contain a $(k-1)$-Catalan matroid as a minor. Thus ${\text {HC}}^*(M')\ge {\text {hc}}(k-1)$ and ${\text {HC}}^*(M'') \ge {\text {hc}}(k-1)$. Therefore we conclude that ${\text {hc}}(k) \ge (k-1) \big ({\text {hc}}(k-1) \big )^2$. $\square$

For a nonnegative integer x, we denote by ${\text {sf}}(x)$ the superfactorial$x!(x-1)!\cdots 0!$ of x.

Theorem 1

For $k \ge 2$, ${\text {hc}}(k) \ge {\text {sf}}(k-1){\text {sf}}(k-2)$.

Proof

The proof is by induction on k. Let $M_Q$ be a generalized Catalan matroid such that ${\text {HC}}^*(M_Q) = {\text {hc}}(k)$. We may assume that $M_Q$ has neither a loop nor a isthmus. In particular, $M_Q$ has both rank and corank at least k. Let $k = 2$. Then ${\text {BG}}(M_Q)$ has at least three vertices and is edge-Hamiltonian. Thus ${{\text {hc}}(2) \ge 1 = {\text {sf}}(1){\text {sf}}(0)}$.

Now let $k \ge 3$. Let $B_1B_2$ be an edge of ${\text {BG}}(M_Q)$, say $B_2= B_1- e + g$. By Corollary 1, the edge $B_1B_2$ is in $\min \{r-1,m-1\} \ge k-1$ good cycles. Consider $M' = M_Q \backslash e$ and ${M'' = M_Q \slash e}$. By Remark 1, the $(k-1)$-Catalan matroid is a minor of both $M'$ and $M''$. Thus, by the induction hypothesis,

$$\begin{aligned} {\text {HC}}^*(M'), {\text {HC}}^*(M'') \ge {\text {hc}}(k-1) \ge {\text {sf}}(k-2){\text {sf}}(k-3). \end{aligned}$$

So, every edge of ${\text {BG}}(M_Q)$ is in $(k-1)\bigl ({\text {sf}}(k-2){\text {sf}}(k-3)\bigr )^2 \ge {\text {sf}}(k-1){\text {sf}}(k-2)$ Hamiltonian cycles. $\square$

The uniform matroid $U_{r,n}$ is a lattice path matroid $M_Q$, where $Q = N^r E^{n-r}$. By applying the same techniques, we can achieve better lower bounds for them [10].

Theorem 2

Every edge of ${\text {BG}}(U_{r,n})$ is in $\bigl ((n-r-1)!(r-1)!\bigr )^{\min \{n-r-1, r-1\}}$ Hamiltonian cycles, for $n > r \ge 1$.

4 Graphic Matroids

In this section, we consider a graphic matroid $M_G$ where G is a loopless k-edge-connected multigraph of order n; that is, the elements of $M_G$ are the edges of G and a basis of $M_G$ corresponds to a spanning tree of G. We refer to G as a graph instead of a loopless multigraph.

For readability, we do not distinguish between a basis of $M_G$ and a spanning tree of G. If B is a basis of $M_G$ and g is an edge of G not in B, then $B+g$ induces a unique cycle (circuit) C(g, B) in G (in $M_G$, respectively) called the fundamental cycle (circuit, respectively) with respect to g and B [16].

Let X and Y be disjoint subsets of the vertex set V(G). We denote by E[X, Y] ($= E[Y,X]$) the set of edges of G with one end in X and the other end in Y, and by e(X, Y) the number of edges in E[X, Y].

4.1 General Structure of Good Cycles

Here we fix the structure that we will use in the rest of Sect. 4.

Let G be a connected graph and $B_1$ and $B_2$ be bases of $M_G$ such that $B_2= B_1-e +g$. Let f be an edge of $B_1-e$. Let X be the vertex set of the component of $B_1-e$ that contains no end of f. Let Z be the vertex set of the component of $B_1-f$ that contains no end of e. Let $Y = V(G) \setminus (X \cup Z)$.

Fig. 4

Components X, Y, Z provided by the edges e and f in $B_1$, and possible positions for the edge g

Let $\mathscr {C}= \mathscr {C}(B_1B_2)$ be the set of good cycles for $B_1B_2$. An arbitrary element of $\mathscr {C}$ is represented as $B_1B_2B_3B_4$. For $f \in B_1-e$, let $\mathscr {C}(f)$ be the set of good cycles $B_1B_2B_3B_4$ in $\mathscr {C}$ for which $f \not \in B_4$. For every ${f' \in B_1- e}$ with $f'\ne f$, if $B_1B_2B_3B_4\in \mathscr {C}(f)$, then $f'$ belongs to $B_4$, and so $B_1B_2B_3B_4\not \in \mathscr {C}(f')$. Thus ${\mathscr {C}(f) \cap \mathscr {C}(f') = \emptyset }$. For every ${w \not \in B_1+ g = B_2+ e}$, we denote by $\mathscr {C}(f,w)$ the set of cycles in $\mathscr {C}(f)$ such that $w \in B_3$. Similarly, ${\mathscr {C}(f,w) \cap \mathscr {C}(f,w') = \emptyset }$ for every $w' \not \in B_1+ g$ with $w' \ne w$. Therefore

$$\begin{aligned} \mathscr {C}&= \mathscr {C}(B_1B_2) \nonumber \\&= \dot{\bigcup } \big \{\mathscr {C}(f) : f \in B_1- e \big \}\nonumber \\&= \dot{\bigcup } \big \{\mathscr {C}(f,w) : f \in B_1- e, \ w \not \in B_1+ g \big \}. \end{aligned}$$

(1)

4.2 2-Edge-Connected Graphs

We give a lower bound on ${\text {HC}}^*(M_G)$ where $M_G$ is the cycle matroid obtained from a 2-edge-connected graph G. This bound will be used in the next subsection to achieve a lower bound for k-edge-connected graphs with $k \ge 3$.

Lemma 2

If G is a 2-edge-connected graph of order $n \ge 4$ and size at least $n+2$, then every edge of ${\text {BG}}(M_G)$ is in two good cycles.

Proof

Let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$. Suppose e and g are parallel edges. As $n \ge 4$, there are edges f and $f'$ in $B_1-e$ not in $C(g,B_1)$ with $f \ne f'$. Consider the edge f and let X, Y, and Z be as in Fig. 4a. Since G is 2-edge-connected, there is at least one edge $w \in E[X \cup Y, Z] \setminus \{f\}$, and a good cycle in $\mathscr {C}(f,w)$ (Fig. 5a). Similarly, there is a good cycle in $\mathscr {C}(f',w')$ for some $w'$. By (1), these two good cycles are distinct and we are done. So we may assume that e and g are not parallel edges and $C(g,B_1)$ has at least three edges. For each edge w not in $B_1+g$, if w has its two ends in $C(g,B_1)$, then there is an $f \in C(g,B_1)$ with $f \not \in \{e, g\}$. Let X, Y, and Z be as in Fig. 4b. Edge w is as edge $\ell$ in Fig. 5b or as edges h or j in Fig. 5c. In each of these cases, there is a good cycle in $\mathscr {C}(f,w)$. On the other hand, if w has at most one end in $C(g,B_1)$, there is an edge $f \in B_1$ not in $C(g,B_1)$ such that $f \in C(w,B_1)$, and there is a good cycle in $\mathscr {C}(f,w)$ as in Fig. 5a. Since G has size at least $n+2$, there are at least two edges not in $B_1+ g$ and, by (1), the corresponding good cycles are distinct and we are done. $\square$

Fig. 5

The bold edges are in $B_1$. a For $f \not \in C(g,B_1)$ and $w = w_1$ or $w = w_2$ in $E[X \cup Y, Z]$, the table shows a good cycle in $\mathscr {C}(f,w)$. b For $f \in C(g,B_1)$ and $\ell$ in E[Y, Z], the table shows two good cycles in $\mathscr {C}(f,\ell )$. c For $f \in C(g,B_1)$ and h in E[X, Y] or j in E[X, Z], the table shows a good cycle in $\mathscr {C}(f,h)$ and one in $\mathscr {C}(f,j)$

The 1-sum$C \oplus _1 C'$ of two cycles C and $C'$ is the graph obtained from identifying a vertex of C with a vertex of $C'$.

Lemma 3

Let G be a 2-edge-connected graph of order $n \ge 4$. There exists an edge in ${\text {BG}}(M_G)$ not in two good cycles if and only if G is either $C_n$ or $C_2 \oplus _1 C_{n-1}$.

Proof

Let m denote the number of edges of G. Since G is 2-edge-connected, every edge is in a cycle, so $m \ge n$. If $m = n$, then G is the n-cycle $C_n$ and no edge of ${\text {BG}}(M_G)$ is in a good cycle. For $m \ge n+2$, Lemma 2 implies that every edge of ${\text {BG}}(M_G)$ is in two good cycles. So, we may assume that $m = n+1$. Because every 2-edge-connected graph has a closed ear-decomposition [3] and G has exactly $n+1$ edges, the closed ear-decomposition of G consists of exactly two ears. Thus, G is either the 1-sum of two cycles, or the union of three internally disjoint paths that have the same two end vertices.

First, suppose that G is the 1-sum of two cycles. Since we only consider graphs with no loops, the length of both of these cycles is at least two. If G is $C_2 \oplus _1 C_{n-1}$, then it can be verified that there are adjacent bases in ${\text {BG}}(M_{G})$ for which there is only one good cycle (Fig. 6). So assume the length of both cycles is at least three, and let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$. For each edge $f \in B_1$ not in $C(g,B_1)$, let X, Y, and Z be as in Fig. 4a. Since G is 2-edge-connected, there is at least a $w \in E[X \cup Y, Z] \setminus \{f\}$ and such w corresponds to a good cycle in $\mathscr {C}(f,w)$ as shown in Fig. 5a. As both cycles in G have length at least three, there are at least two such edges f and, by (1), the corresponding good cycles are distinct.

Fig. 6

A 2-edge-connected graph G whose basis graph ${\text {BG}}(M_{G})$ has an edge $B_1B_2$ with no two good cycles. The basis $B_1$ is the spanning tree in thick edges and $B_2= B_1- e + g$

Now, suppose that G is the union of three internally disjoint paths $P_1$, $P_2$, $P_3$ with the same two end vertices. In this case, every edge of ${\text {BG}}(M_G)$ is in two good cycles. Indeed, let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$. First, suppose that e and g are in the same path, say $P_1$. We may assume that all edges of $P_2$ are in $B_1$ and that there exists an edge w in $P_3$ not in $B_1$. Let f be an edge of $P_2$ (and thus of $B_1$). For X, Y, and Z as in Fig. 4b, edge w is in E[Y, Z] as $\ell$ in Fig. 5b, so there are two good cycles in $\mathscr {C}(f,w)$. Finally, suppose that e and g are in different paths; say e belongs to $P_1$ and g belongs to $P_2$. Hence all edges of $P_1$ are in $B_1$, and there exists an edge w in $P_3$ not in $B_1$. If there is an $f \in B_1-e$ in $P_1$, then w is in E[X, Z] as j in Fig. 5c. If there is an $f \in B_1$ in $P_2$, then w is in E[X, Y] as h in Fig. 5c. If there is an $f \in B_1$ in $P_3$, then w is in $E[X\cup Y,Z]$ as $w_1$ or $w_2$ in Fig. 5a. In any case we get a good cycle in $\mathscr {C}(f,w)$. Since $n \ge 4$, there are two edges $f, f' \in B_1$ other than e. Therefore, by (1), there are two good cycles, one in $\mathscr {C}(f,w)$ and the other in $\mathscr {C}(f',w)$. $\square$

Theorem 3

If G is a 2-edge-connected graph of order $n \ge 3$, then every edge of ${\text {BG}}(M_G)$ is in $2^{n-3}$ Hamiltonian cycles.

Proof

The proof is by induction on n. If $n = 3$, then $2^{n-3} = 1$ and the theorem follows from the edge-Hamiltonicity of ${\text {BG}}(M_G)$. So we may assume that $n \ge 4$.

By Lemma 3, if there exists an edge in ${\text {BG}}(M_G)$ not in two good cycles, then G is either $C_n$ or $C_2 \oplus _1 C_{n-1}$. If $G=C_n$, then ${\text {BG}}(M_G) = K_n$ and every edge of ${\text {BG}}(M_G)$ is in ${(n-2)! \ge 2^{n-3}}$ Hamiltonian cycles. If $G = C_2 \oplus _1 C_{n-1}$, then ${\text {BG}}(M_G)$ is the cartesian product of $K_2$ and $K_{n-1}$, that is, the graph whose vertex set is $V(K_2) \times V(K_{n-1})$ and whose edge set consists of all pairs $(u_1,v_1)(u_2,v_2)$ such that either $u_1u_2 \in E(K_2)$ and $v_1 = v_2$, or ${v_1v_2 \in E(K_{n-1})}$ and $u_1 = u_2$. In this case, every edge of ${\text {BG}}(M_G)$ is in ${(n-2)!(n-3)! \ge 2^{n-3}}$ Hamiltonian cycles. Therefore, we may assume that G has at least $n+1$ edges and every edge of ${\text {BG}}(M_G)$ is in two good cycles.

Let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$. Let $G' = G / e$ and ${G'' = G \setminus e}$. As $G'$ is 2-edge-connected of order $n-1 \ge 3$, by the induction hypothesis, every edge of ${\text {BG}}(M_{G'})$ is in $2^{n-4}$ Hamiltonian cycles in ${\text {BG}}(M_{G'})$. As $G''$ has $n \ge 4$ vertices and at least n edges, $G''$ has at least two spanning trees, and therefore ${\text {BG}}(M_{G''})$ is either $K_2$ or edge-Hamiltonian. Let $C=B_1B_2B_3B_4$ be a good cycle. If ${\text {BG}}(M_{G''})$ is $K_2$, then the symmetric difference of $C$ and a Hamiltonian cycle of ${\text {BG}}(M_{G'})$ containing $B_1B_4$ is a Hamiltonian cycle of ${\text {BG}}(M_G)$. On the other hand, if ${\text {BG}}(M_{G''})$ is edge-Hamiltonian, then the symmetric difference of $C$, a Hamiltonian cycle of ${\text {BG}}(M_{G'})$ containing $B_1B_4$, and a Hamiltonian cycle of ${\text {BG}}(M_{G''})$ containing $B_2B_3$ is a Hamiltonian cycle of ${\text {BG}}(M_G)$. As every edge of ${\text {BG}}(M_G)$ is in two good cycles, in either case we conclude that every edge of ${\text {BG}}(M_G)$ is in ${2^{n-4}\cdot 2 \cdot 1 = 2^{n-3}}$ Hamiltonian cycles. $\square$

4.3 k-Edge-Connected Graphs

Now, we turn our attention to k-edge-connected graphs for $k \ge 3$.

Lemma 4

If G is a k-edge-connected graph of order $n \ge 3$ for $k \ge 3$, then every edge of ${\text {BG}}(M_G)$ is in ${(n-2)(k-1)}$ good cycles.

Proof

Let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$ and $f \in B_1-e$. We shall prove that there are $k-1$ good cycles in $\mathscr {C}(f)$. By (1) and as there are $n-2$ choices for f, there are $(n-2)(k-1)$ good cycles for every edge of ${\text {BG}}(M_G)$ and we are done.

Let X, Y, and Z be as in Fig. 4. If $f \not \in C(g,B_1)$, as G is k-edge-connected, there are distinct edges $w_1,\ldots ,w_{k-1}$ in $E[X \cup Y, Z]$ and a distinct good cycle in each $\mathscr {C}(f,w_i)$ for $i=1,\ldots ,k-1$ (Fig. 5a). If $f \in C(g,B_1)$, there is a good cycle in $\mathscr {C}(f,w)$ for each $w \in (E[X,Y] \cup E[X,Z] \cup E[Y,Z]) \setminus \{e, f, g\}$ (Fig. 5b, c). As G is k-edge-connected and $k \ge 3$, there are at least

$$\begin{aligned} \left\lceil \frac{e(X,Y) + e(X,Z) + e(Y,Z)}{2}\right\rceil - 3 \ge \left\lceil \frac{3k}{2}\right\rceil -3 \ge k-1, \end{aligned}$$

choices for w. $\square$

In order to give a bound on ${\text {HC}}^*(M_G)$, we define the function

$$\begin{aligned} {\text {hc}}(n,k) =\min \left\{ {\text {HC}}^*(M_G) :\, G\text { is a }k\text {-edge-connected graph of order }n \right\} . \end{aligned}$$

Proposition 2

For k, $n \ge 3$, ${\text {hc}}(n,k) \ge (n-2)(k-1){\text {hc}}(n-1,k){\text {hc}}(n,k-1)$.

Proof

Let G be a k-edge-connected graph of order n such that ${\text {HC}}^*(M_G) = {\text {hc}}(n,k)$. By Lemma 4, there are $(n-2)(k-1)$ good cycles for every edge of ${\text {BG}}(M_{G})$. Let $B_1$ and $B_2= B_1- e + g$ be adjacent bases of ${\text {BG}}(M_G)$ and let $G' = G / e$ and $G'' = G \setminus e$. The symmetric difference of a good cycle $C=B_1B_2B_3B_4$, a Hamiltonian cycle of ${\text {BG}}(M_{G'})$ containing $B_1B_4$, and a Hamiltonian cycle of ${\text {BG}}(M_{G''})$ containing $B_2B_3$ is a Hamiltonian cycle of ${\text {BG}}(M_{G})$ containing $B_1B_2$. Hence, $B_1B_2$ is in ${(n-2)(k-1){\text {HC}}^*(M_{G'}){\text {HC}}^*(M_{G''})}$ Hamiltonian cycles of ${\text {BG}}(M_{G})$. Now, as $G'$ is k-edge-connected of order $n-1$, we have that ${{\text {HC}}^*(M_{G'}) \ge {\text {hc}}(n-1,k)}$ and, as $G''$ is $(k-1)$-edge-connected of order n, we have that ${{\text {HC}}^*(M_{G''}) \ge {\text {hc}}(n,k-1)}$. Therefore we conclude that ${\text {hc}}(n,k) = {\text {HC}}^*(M_G) \ge (n-2)(k-1) {\text {hc}}(n-1,k) {\text {hc}}(n,k-1).$$\square$

Theorem 4

For n, $k \ge 2$ with $n+k \ge 5$, ${\text {hc}}(n,k) \ \ge \ (2^{n-2}(n-2)!)^{k-2}.$

Proof

The proof is by induction on $n+k$. If $k=2$ or $n=2$, then the theorem follows from the edge-Hamiltonicity of ${\text {BG}}(M_{G})$. Now assume that $n \ge 3$ and $k \ge 3$. By applying Proposition 2 and the induction hypothesis on both ${\text {hc}}(n-1,k)$ and ${\text {hc}}(n,k-1)$, we have that

$$\begin{aligned} {\text {hc}}(n,k)&\ge (n-2)(k-1){\text {hc}}(n-1,k){\text {hc}}(n,k-1) \\&\ge (n-2)(k-1) (2^{n-3}(n-3)!)^{k-2} (2^{n-2}(n-2)!)^{k-3} \\&= (n-2)(k-1) 2^{(n-3)(k-2)+(n-2)(k-3)} ((n-3)!)^{k-2} ((n-2)!)^{k-3} \\&\ge 2^{(n-3)(k-2)+(n-2)(k-3)+1} (n-2)(n-3)! ((n-2)!)^{k-3} \\&\ge (2^{n-2}(n-2)!)^{k-2}, \end{aligned}$$

where the last inequality holds because $(n-3)(k-2)+(n-2)(k-3)+1 \ge (n-2)(k-2)$ for $k \ge 3$ and $n \ge 3$. This completes the proof of the theorem. $\square$

5 Concluding Remarks

The general strategy (Sect. 2) used in order to give a lower bound on ${\text {HC}}^*(M_G)$ takes into account only Hamiltonian cycles that cross some particular cuts exactly twice. Using the same strategy and doing some tedious computation, the lower bound presented for 2-edge-connected graphs can be improved to a superfactorial one for k-edge-connected graphs, by proving specific lower bounds on both ${\text {hc}}(3,k)$ and ${\text {hc}}(n,3)$ [10]. Namely, one can prove the following theorems.

Theorem 5

(Theorem 13 [10]) For $k \ge 3$, ${\text {hc}}(3,k) \ge {\text {sf}}(k-1)$.

Theorem 6

(Theorem 14 [10]) For $n \ge 3$, ${\text {hc}}(n,3) \ge (n-2)!\,2^{\left( {\begin{array}{c}n-1\\ 2\end{array}}\right) }$.

Theorem 7

(Theorem 15 [10]) For n, $k \ge 4$,

$$\begin{aligned} {\text {hc}}(n,k) \ \ge \ \frac{2^{\left( {\begin{array}{c}n+k-4\\ n-3\end{array}}\right) } \cdot 3^{\left( {\begin{array}{c}n+k-7\\ k-3\end{array}}\right) }}{(n-1)k}\, \prod \limits ^{k}_{r = 4} \bigl (r{\text {sf}}(r-1)\bigr )^{\left( {\begin{array}{c}n+k-4-r\\ n-4\end{array}}\right) } \cdot \prod \limits ^{n}_{s = 4} (s-1)!^{\left( {\begin{array}{c}n+k-4-s\\ k-4\end{array}}\right) }. \end{aligned}$$

The bound given by Theorem 7 is best possible using the general strategy. For the sake of comparison, the bound on ${\text {hc}}(10,4)$ provided by Theorem 4 is a number with 15 digits, while the bound provided by Theorem 7 is a number with 61 digits.

The following corollary follows from mathematical manipulations on the right side of the inequality given by Theorem 7 and it gives a more explicit and concise expression.

Corollary 2

(Corollary 16 [10]) For $n > k \ge 5$,

$$\begin{aligned} {\text {hc}}(n,k) > \prod \limits ^{n}_{r=3} ({\text {sf}}(r-1))^{\left( {\begin{array}{c}n+k-5-r\\ n-6\end{array}}\right) +\left( {\begin{array}{c}n+k-4-r\\ n-4\end{array}}\right) +\left( {\begin{array}{c}n+k-5-r\\ k-5\end{array}}\right) }. \end{aligned}$$

As our last remark, we point out that the function ${\text {hc}}(n,k)$ is monotonically increasing.

Lemma 5

(Lemma 11 [10]) Let G be a 3-edge-connected graph of order $n \ge 3$ and let e be an edge of G. Then ${\text {HC}}^*(M_G) \ge {\text {HC}}^*(M_{G / e})$ and ${\text {HC}}^*(M_G) \ge {\text {HC}}^*(M_{G \setminus e})$.