Spanning Eulerian Subgraphs of Large Size

Abstract

A graph $G=(V(G), E(G))$ is supereulerian if it has a spanning Eulerian subgraph. Let $\ell (G)$ be the maximum number of edges of spanning Eulerian subgraphs of a graph G. Motivated by a conjecture due to Catlin on supereulerian graphs, it was shown that if G is an r-regular supereulerian graph, then $\ell (G)\ge \frac{2}{3}|E(G)|$ when $r\ne 5$, and $\ell (G)> \frac{3}{5}|E(G)|$ when $r=5$. In this paper we improve the coefficient and prove that if G is a 5-regular supereulerian graph, then $\ell (G)\ge \frac{19}{30}|E(G)|+\frac{4}{3}$. For this, we first show that each graph G with maximum degree at most 3 has a matching with at least $\frac{2}{7}|E(G)|$ edges and this bound is sharp. Moreover, we show that Catlin’s conjecture holds for claw-free graphs having no vertex of degree 4. Indeed, Catlin’s conjecture does not hold for claw-free graphs in general.

1 Introduction

In this paper we consider simple graphs and all concepts not defined can be found in [2]. A spanning subgraph of a graph G is called an even factor if the degree of each vertex of it is a positive and even number. A connected even factor of G is called an Eulerian subgraph of G. A graph G is supereulerian if it has a spanning Eulerian subgraph. We denote the maximum number of edges of the spanning Eulerian subgraphs of G by $\ell (G)$. The maximum and minimum degree of the vertices of G are denoted by $\varDelta (G)$ and $\delta (G)$, respectively. Also the number of vertices and edges of a graph G are denoted by $n_G$ and |G|, respectively and $n_G$ is called the order of G. The size of maximum matching of G and the set of vertices which are joined to v are denoted by $\alpha '(G)$ and $N_G(v)$, respectively. The symmetric difference of two subgraphs H and K of G is denoted by $H\triangle K$ and is the subgraph of G such that $E(H\triangle K)=(E(H)\cup E(K))-(E(H)\cap E(K))$ and $V(H\triangle K)=V(H)\cup V(K)$. For a subset $X \subseteq V (G)$, an induced subgraph by X is the subgraph of G whose vertex set is X and whose edges are the edges of G joining vertices of X. A graph which has no $K_{1, 3}$ as an induced subgraph is called a claw-free graph.

In 1999, Lai and Chen [5] showed that if G is a bridgeless graph with $\delta (G)\ge 3$, then G has an even factor F with $|F|\ge \frac{2}{3}|G|$. Let $V_2(G)$ be the set of vertices with degree 2 of G. Recently, in [3] it was proved that if G has an even factor, then it has an even factor F with $|F|\ge \frac{4}{7}(|G|+1)+\frac{1}{7}|V_2(G)|$.

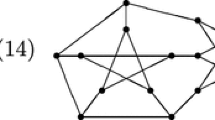
Determining whether or not a graph is supereulerian is NP-complete [7] (Fig. 1). In 1996, Catlin [4] conjectured that if G is a supereulerian graph and $G\ne K_1$, then $\ell (G)\ge \frac{2}{3}|G|$. In 2003, infinite counterexamples were found for Catlin’s conjecture [6]. All these counterexamples have at least a vertex of degree 2. We construct an infinite family of counterexamples with minimum degree 3, which are in particular bipartite. Consider the graph G in Fig. 2. If G consists of t subgraphs isomorphic to $G_0$, then we have $|G|=14t+2$ and maximum spanning Eulerian subgraph of G is a Hamiltonian cycle and we have $l(G)=9t+2$. It is obvious that if $t\ge 1$, then $9t+2<\frac{2}{3}(14t+2)=\frac{2}{3}|G|$.

Fig. 1

Graph G, a bipartite counterexample with minimum degree 3

Fig. 2

Graph $G_0$

Verifying Catlin’s conjecture for graphs with higher minimum degrees could be still an interesting problem. In particular, the conjecture holds in the case of $\delta (G)\ge 6$. Indeed, let F be a maximum spanning Eulerian subgraph of G. Then $G-E(F)$ is a forest and $|G-E(F)|\le n_G-1$. Also, $|F|\ge |G|-n_G+1\ge |G|-\frac{2}{6}|G|+1=\frac{2}{3}|G|+1$. Therefore, the graphs having $\delta (G)\le 5$ are considered hereinafter.

Moreover, it is not difficult to see that this conjecture is valid for r-regular supereulerian graphs with $r\ne 5$ (see [6]), while in the case of $r=5$, it is still widely open. In [6], it was also mentioned that for a 5-regular supereulerian graph G, $\ell (G)> \frac{3}{5}|G|$. In this paper, as our main result in Theorem 3, we improve the coefficient $\frac{3}{5}$ to $\frac{19}{30}$ for 5-regular supereulerian graphs. For this, we present a lower bound on the size of maximum matching in the graphs with $\varDelta (G)\le 3$, which is a sharp bound.

In Sect. 3, we discuss Catlin’s conjecture in the case of claw-free graphs . In fact, we show that this conjecture holds for claw-free graphs with no vertex of degree 4. In additional, we provide examples which show that this conjecture is not valid for claw-free graphs in general.

2 Spanning Eulerian Subgraphs of 5-Regular Graphs

In this section we prove our main results conserning supereulerian 5-regular graphs. For this purpose, first we provide a lower bound for $\alpha '(G)$ in the case of graphs with $\varDelta (G)\le 3$.

Theorem 1

If G is a graph with $\varDelta (G)\le 3$, then $\alpha '(G)\ge \frac{2}{7}|G|$.

Note that this bound is best possible and there is a graph G with $\varDelta (G)= 3$ and maximum matching of size $\frac{2}{7}|G|$ (Fig. 3).

Fig. 3

A graph G with $\varDelta (G)= 3$ and $\alpha '(G)=\frac{2}{7}|G|$

To prove Theorem 1 we need the next theorem from [1].

Theorem 2

([1, Theorem 13]) Any connected 3-regular graph G of order $n_G$ has a matching of size $\frac{4n_G-1}{9}$.

Now, we prove Theorem 1.

Proof of Theorem 1

If G is a 3-regular graph and $|G|\ge 11$, then by Theorem 2, $\alpha '(G)\ge \frac{4n_G-1}{9}=\frac{8|G|-3}{27}\ge \frac{2}{7}|G|$. If G is a 3-regular graph with $|G|\le 10$, then $\frac{3n_G}{2}\le 10$ and $n_G\in \{4, 6\}$. Therefore it is easy to see that $\alpha '(G)\ge \frac{2}{7}|G|$. Hence, the assertion holds for 3-regular graphs.

Now, assume on the contrary that G is a counterexample to the statement such that $n_G$ is minimized. First, suppose that G has a vertex u with degree 1, and let $N_G(u)=\{v\}$ and $e=uv$. In this case let $G'=G-\{u,v\}$. Since $n_{G'}< n_G$, we have $\alpha '(G')\ge \frac{2}{7}|G'|$. We have $|G'|\ge |G|-3$, since $\varDelta (G)\le 3$. By adding the edge e to the maximum matching of $G'$, it follows that $\alpha '(G)\ge \frac{2}{7}|G'|+1\ge \frac{2(|G|-3)}{7}+1> \frac{2}{7}|G|$.

Now, assume that $\delta (G)\ge 2$. Hence, there is a vertex x with degree 2. Let $N_G(x)=\{y, z\}$ and $d_G(y)=2$. We set $G'=G-\{x,y\}$. Since $n_{G'}< n_G$, similar to the above discussion, it follows that $\alpha '(G)>\frac{2}{7}|G|$. Therefore, $d_G(y)=3$ and similarly $d_G(z)=3$. Now, we consider the following two cases:

$\mathbf Case 1$$|N_G(y)\cap N_G(z)|>1$.

Assume that $w\ne x$ such that $w\in N_G(y)\cap N_G(z)$ and $G'=G-\{x, y, z, w\}$. Since $n_{G'}< n_G$ and $\varDelta (G)\le 3$, we have $\alpha '(G')\ge \frac{2}{7}|G'|$ and $|G'|\ge |G|-7$. Adding the edges xy and wz to the maximum matching of $G'$ implies that $\alpha '(G)\ge \frac{2}{7}|G'|+2\ge \frac{2(|G|-7)}{7}+2= \frac{2}{7}|G|$.

$\mathbf Case 2$$|N_G(y)\cap N_G(z)|=1$.

There are two subcases:

$\mathbf (2a)$$yz\in E(G)$. In this case suppose that $N_G(z)=\{x, y, s\}$ and $G'=G-\{x, y, z, s\}$. Similarly, Since $n_{G'}\le n_G$ we have $\alpha '(G')\ge \frac{2}{7}|G'|$. Also, $|G'|\ge |G|-7$, since $\varDelta (G)\le 3$. The addition of the edges xy and zs to the maximum matching of $G'$ implies that $\alpha '(G)\ge \frac{2}{7}|G'|+2\ge \frac{2(|G|-7)}{7}+2= \frac{2}{7}|G|$.

$\mathbf (2b)$$yz\notin E(G)$. According to the above cases, $|N_G(y)\cup N_G(z)|=5$. Let $N_G(y)=\{p, q, x\}$ and $N_G(z)=\{s, t, x\}$. It is obvious that $ys\notin E(G)$. Let $G'=(G-\{x, z\}) + ys$. Similarly, $\alpha '(G')\ge \frac{2}{7}|G'|$ and $|G'|=|G|-3$. Suppose that $M'$ is a maximum matching of $G'$. If $ys\in E(M)$, then $M= M'- ys + xy + zs$ is a matching of G. Therefore, $\alpha '(G)\ge (\frac{2}{7}|G'|-1)+2= \frac{2(|G|-3)}{7}+1> \frac{2}{7}|G|$. Otherwise, $ys\notin M$ and $M= M'+xz$ is a matching of G. Thus, $\alpha '(G)\ge \frac{2}{7}|G'|+1= \frac{2(|G|-3)}{7}+1> \frac{2}{7}|G|$, as desired.

Now, we are ready to present our main theorem:

Theorem 3

Let G be a 5-regular supereulerian graph. Then $\ell (G)\ge \frac{19}{30}|G|+\frac{4}{3}$.

Proof

Let F be a spanning Eulerian subgraph of G such that |F| is maximum and $R=G-E(F)$. Since |F| is maximum, the graph R is a forest. Let T be a spanning tree of F, and M be a maximum matching of $F-E(T)$. If C is a cycle of $R\cup M$, then $C\triangle F$ does not have any isolated vertex and it is an spanning Eulerian subgraph, since $T\subset C\triangle F$. We have $|C\triangle F|\le |F|$. Therefore, $|((E(C)\cap E(R))\cup E(F))-(E(C)\cap E(M))| \le |F|$ and so $|E(C)\cap E(R)|\le |E(C)\cap E(M)|$. Now, since M is a matching, the edges of each cycle of $R\cup M$ belong to R and M, alternately. Thus, each cycle of $R\cup M$ has at least two edges of M. Moreover, the cycles in $R\cup M$ are pairwise vertex-disjoint. Let k be the number of cycles of $R\cup M$. We have $k\le \frac{|M|}{2}$. If we remove one edge from each cycle of $R\cup M$, then we get a forest and $|R\cup M|-k\le n_G-1$. Thus, $|R|\le n_G -1+k-|M|\le n_G-1-\frac{|M|}{2}$. We have $\varDelta (F-E(T))\le 3$, since T is a tree. Now, by Theorem 1, $|M|\ge \frac{2(|F|-(n_G-1))}{7}$, and so $|R|\le n_G-\frac{|F|-n_G}{7}-\frac{8}{7}$. Consequently, $|F|=|G|-|R|\ge \frac{19n_G}{14}+\frac{|F|}{7}+\frac{8}{7}$. Also, $|F|\ge \frac{19}{30}|G|+\frac{4}{3}$, and we are done. $\square$

3 Even Factor of Claw-Free Graphs

In this section, we study Catlin’s Conjecture for claw-free graphs. Indeed, we have the following theorem:

Theorem 4

If G is a claw-free supereulerian graph having no vertex with degree 4, then $\ell (G)\ge \frac{2}{3}|E(G)|$.

Proof

Let F be a maximum spanning Eulerian subgraph of G. Then $R=G-E(F)$ is a forest. Let C be a component of R and $e=uv$ be an edge of $G-E(R)$ such that $u, v\in V(C)$. Since C is a tree, there is a path $P_{uv}$ in C between u and v. Therefore, $F-e+P_{uv}$ is a spanning Eulerian subgraph of G and $|F-e+P_{uv}|> |F|$. This is a contradiction. Hence, each component of R is an induced subgraph of G, and so for each vertex $v\in V(G)$ we have $d_R(v)\le 2$ and $d_F(v)\ge d_G(v)-2$, since G is a claw-free graph. Let $Odd(G)=\{v\in V(G)|d_G(v)$ is odd$\}$, $Even(G)=\{v\in V(G)|d_G(v)$ is even and is not equal to 2 $\}$ and $t=|\{v\in V(G)|d_G(v)=2\}|$. Also, $d_R(v)=1$ for $v\in Odd(G)$. Since G does not have any vertex with degree 4, we have

$$\begin{aligned} 2|G|=\sum _{v\in Odd(G)}d_G(v)+\sum _{v\in Even(G)}d_G(v)+2t\ge 3|Odd(G)|+6|Even(G)|+2t. \end{aligned}$$

Therefore,

$$\begin{aligned}&3 \left( \sum _{v\in Odd(G)}d_G(v)-|Odd(G)|+\sum _{v\in Even(G)}d_G(v)-2|Even(G)|+2t\right) \\&\quad \ge 2\left( \sum _{v\in Odd(G)}d_G(v)+\sum _{v\in Even(G)}d_G(v)+2t\right) . \end{aligned}$$

Now, we have

$$\begin{aligned} 3|F|= & {} 3\frac{\sum _{v\in V(F)}D_F(v)}{2}\ge 3\frac{\left( \sum _{v\in Odd(G)}(d_G(v)-1)\right) + \left( \sum _{v\in Even(G)}(d_G(v)-2)\right) +2t}{2}\\= & {} \frac{3}{2}\left( \sum _{v\in Odd(G)}d_G(v)-|Odd(G)|+\sum _{v\in Even(G)}d_G(v)-2|Even(G)|+2t\right) \\\ge & {} \sum _{v\in Odd(G)}d_G(v)+\sum _{v\in Even(G)}d_G(v)+2t=2|G|. \end{aligned}$$

Thus, $|F|\ge \frac{2}{3}|G|$. $\square$

We would like to remark that the graph in Fig. 4, shows that the condition of having no vertex of degree 4, in Theorem 4, is crucial and could not be canceled. This, indeed, implies that Catlin’s conjecture does not hold for claw-free graph in general.

Fig. 4

A counterexample with minimum degree 3

According to the proof of Theorem 4 we have the following theorem.

Theorem 5

If G is a claw-free graph having no vertex with degree 4 and G has an even factor, then G has an even factor of size at least $\frac{2}{3}|G|$.

Note that the above theorem is not satisfied for each claw-free graph having even factor (see Fig. 5).

Fig. 5

A claw-free graph with an even factor

The claw-free graph G has an even factor and number of edges of every even factor of G is less than $\frac{2}{3}|G|$.