1 Introduction and motivation

In the past decades, computer animation is becoming prevalently popular with the rapid technical advancement in movie and game industry. A digital computer animation is usually generated by means of driving a character mesh created by designer using 3D modeling software, and stored as a sequence of dynamic meshes with fixed connectivity and time-varying geometry. Such dynamic meshes, especially those with complex geometric details, require large storage space and transmission bandwidth in practical computer graphics applications. Therefore, high-fidelity compression of dynamic meshes with fine details has gained increasing attention during the past decades.

In technical essence, the goal of compressing dynamic meshes is to find a compact representation of the sequence under a controllable distortion, and the most intuitive way is to pursue a set of bases that can well character geometry of the meshes. Principle Component Analysis (PCA) has been reused frequently in combination with other compression techniques [1, 18, 36], wherein the meshes are projected onto a few principal orthogonal bases and the compression is achieved by removing the bases whose influence is negligible compared with others. Nonetheless, these bases take up to 50% of the encoded data size [37] and inevitably limit the compression ratio of these methods when being applied to meshes with a lot of geometric details or a large number of vertices, so it is necessary to find a compression method which does not need to store bases explicitly; on the other hand, even though these methods achieve high compression rate under traditional limited vertex-based error measurement, the removal of bases inevitably cause information loss and consequently affect the quality of reconstructed meshes from the perceptual aspect. We shall explore a high-fidelity way for dynamic meshes compression, whose reconstructed meshes should not only be statistical precise but also visually plausible which can be evaluated under perceptual metric such as our newly proposed local rigidity (LR) error .

Manifold harmonic transform [33] projects a 3D mesh onto several Fourier-like function bases derived as eigenfunctions of the Laplace–Beltrami operator and converts the mesh from geometry domain into frequency domain. Some static mesh compression methods [15, 41] showed that they can reconstruct a static mesh with a small number of low-frequency bases according to the assumption that low-frequency coefficients contribute more to the mesh than the high-frequency ones. In addition, these bases can be obtained by solving an eigenvalue problem of the Laplace–Beltrami operator defined on the mesh itself without the need for explicit storage. However, simply ignoring the high-frequency bases certainly loses geometric details and causes errors similar to those in PCA-based methods. Nonetheless, how to apply the manifold harmonic bases (MHBs) to high-fidelity dynamic meshes compression still remains challenging.

Traditional vertex-based error metric, such as Karni–Gotsman (KG) error [16], tends to evaluate the accuracy of geometry information of the reconstructed mesh sequence. However, simply treating the meshes as coordinates data and calculate the error ignoring the geometric structure of each mesh are obviously not suitable for validation on dynamic meshes compression methods. Because, on the one hand, small translation or rotation on meshes will result in large quantization of KG error, but these kinds of global motion can be easily removed when generating animations and is not a big deal; on the other hand, even though many methods can achieve high compression ratio under this kind of metric, the reconstructed mesh still has visually obvious artifacts, as shown in Fig. 1. Thus, how to define a perceptual metric that measures the visual plausibility need to be further studied.

Fig. 1
figure 1

Comparison with CoDDyaC under the same compression ratio. From left to right: the original frame (a), reconstructed frame using CoDDyaC (b), reconstructed frame using our newly proposed method (c)

Full size image
Fig. 2
figure 2

Reconstructed low-frequency parts with different bases. From left to right: SamBa sequence’s original frame 28 (a), frame 30 (b), reconstructed low-frequency part of frame 30 using 400 MHBs of frame 28 (c), and using 400 MHBs of frame 30 itself (d). The reconstructed meshes using different bases are almost the same

Full size image

In this paper, we propose a key-frame-based framework for dynamic meshes compression with manifold harmonic bases, in which we decompose the sequence into low-frequency primary poses and high-frequency geometric details and compress them separately. We first partition the sequence by the notion of pose similarity into several small fragments and observe that in each fragment, low-frequency parts of all meshes can be well described by manifold harmonic bases derived from one single mesh within this fragment, as shown in Fig. 2. So we can compress the low-frequency part in this fragment by storing one representative key-frame and a few coefficients instead of many large bases to reduce the spatial redundancy. For high-frequency part, we find that geometric details of the meshes within one fragment are almost unchanged, because a mesh sequence is usually created by deforming one static mesh along time axis and geometric details of meshes should be similar to those with similar poses. So we can just store the details of one representative key-frame to remove redundant information. Furthermore, we use state-of-the-art static mesh compression method to store the key-frames and apply a second-order linear prediction coding to the harmonic coefficients to further reduce the spatial-temporal redundancy. To validate the ability of our method when compressing meshes with limited distortion, we also introduce a new perceptual metric based on as-rigid-as-possible definition which measures distortion as the variation of local rigidity. In particular, the primary contributions of this paper can be summarized as follows:

  • We devise a hierarchical framework in which we decompose the mesh sequence into high-frequency part and low-frequency part and compress them separately to reduce the geometric redundancy in space.

  • We apply the notion of pose similarity to extract the key-frames and define the piece-wise manifold harmonic bases to compress the primary poses.

  • We apply deformation transfer techniques to preserve the geometry details in order to reconstruct high-quality mesh sequence.

  • We apply the notion of as-rigid-as-possible energy to define local rigidity (LR) error metric to evaluate the spatial and temporal reconstruction errors, which measures the precision both in statistical and perceptual perspectives.

Fig. 3
figure 3

Flowchart of the proposed compression algorithm (encoder)

Full size image

2 Related works

All compression schemes aim at exploiting correlations among mesh sequence. In terms of de-correlation techniques, the existing compression methods can be roughly classified into two categories [19]: spatial de-correlation methods and temporal de-correlation methods. Actually most methods explore both temporal and spatial redundancy, the two categories are roughly classified according to whether the core idea is benefited more from spatial de-correlation or temporal de-correlation.

2.1 Spatial de-correlation

The most commonly used method to exploit spatial correlations is principal component analysis (PCA) which was firstly introduced to mesh sequence compression by Alexa and Müller [1] in which they projected the sequence data onto a few principal orthogonal bases to represent each frame as a linear combination of these bases. The approach was improved by Lee et al. [17] who described how to determine the optimal number of PCA bases. Then Karni et al. [16] applied linear prediction coding to further compress PCA coefficients.

Some authors proposed methods that segmented frames into meaningful clusters to exploit spatial correlation. Sattler et al. [25] first clustered the vertex trajectories and applied PCA to the trajectories of all vertices of a cluster. Mamou et al. [20] proposed a skinning approach based on segmentation. The mesh vertices were partitioned into patches whose motion can be accurately described by a 3D affine transform. Then an affine motion model was defined to estimate the frame-wise motion of each patch. Hou et al. [11] proposed learned spatial de-correlation transform to transform each frame into a sparse vector to reduce the spatial redundancy, then they [12] used low-rank matrix approximation for data compression and in 2014 they [13] use the near-isometric property of human facial expressions to parameterize the 3-D dynamic faces into an expression-invariant 2-D canonical domain to compress 3-D time-varying meshes.

Some methods encoded only a set of key-information and used them to predict the missing information with some spatial predictors. Stefanoski et al. [28] proposed a linear predictive compression approach in which patch-based mesh simplification algorithms were applied to derive spatially decomposed layers of each frame to support spatial scalability. Then scalable predictive coding (SPC) [30] was proposed to support spatial-temporal scalability by decomposing animated meshes in spatial and temporal layers and predicting these layers using the already encoded spatio-temporal neighborhood. It was then improved by Bici et al. [3], who proposed three novel prediction structures based on weighted spatial prediction with its weighted refinement and angular relations of triangles between current and previous frames. Hajizadeh et al. [8] proposed a key-frame-based technique in which extracted key-frames were then linearly combined using blending weights to predict the vertex locations of the other frames. Hou et al. [10] extracts key-frames and produces a reconstruction matrix to compress 3D human motion data using geometry video format.

2.2 Temporal de-correlation

PCA can be also used to exploit temporal coherence by applying it to the space of vertex trajectories rather than shapes. Váša and Skala [36] proposed CoDDyaC algorithm in which they applied PCA to the vertex trajectories to find a minimal number of significant trajectories characterizing the motion of the shape over the sequence. Compared with PCA on shape space, it involved the eigenvalues decomposition of a covariance matrix of \(3F\times 3F\) instead of \(3V\times 3V\), where F, V is the number of frames and vertices of the mesh, respectively. Improved results were obtained by predicting PCA bases with an efficient mechanism [37]. Then in [35] they combined CoDDyaC with a novel spatio-temporal predictor and used a discrete geometric Laplacian of average surface to encode the coefficients to achieve a good compression rate. Luo et al. [18] applied PCA to temporal clusters based on pose similarity to extend the notion of temporal coherence to postural coherence.

Payan and Antonini [24] exploited the temporal coherence by using a temporal wavelet filtering and using a bit allocation process to optimize the resulting wavelet coefficients. A signal-to-noise ratio (SNR) and temporal scalable coding algorithm for 3D mesh sequences using singular value decomposition (SVD) was proposed by Heu et al. [9]. They developed a temporal prediction mode to improve the rate-distortion performance which also supports temporal scalability. In 2003, Ibarria et al. [14] introduced two extrapolating space-time predictors: the ELP extension of the Lorenzo predictor and the Replica predictor. With these two predictors they predicted the position of each vertex v of frame f from three of its neighbors in frame f and from the positions of v and of these neighbors in the previous frame.

2.3 Spectral analysis

Researchers have been looking for spectral geometric processing methods [40] for spectral geometry filtering [33], compression [15, 41], and surface editing [33]. Manifold Harmonics constitute a compact and elegant basis for spectral shape processing that is independent of the actual shape representation and parameterization. Due to their compactness, encoding efficiency, isometric invariance, and computational efficiency, manifold harmonics can be found in countless applications in computer graphics. The proposed functional map framework [23] used maps between functions on shapes, for example to transfer segmentations or to estimate correspondences between deformed shapes. Various point signatures based on Laplace–Beltrami eigenfunctions were successfully used in shape matching [32]. Other applications included mesh parametrization [21] and shape segmentation [5]. In this paper, we employ spectral analysis for dynamic meshes compression for its general ability of representing shapes in reduced space, which greatly improves the performance of compression.

3 Dynamic meshes compression based on local spectral analysis and deformation transfer method

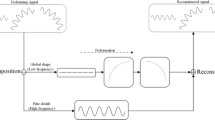
Given a sequence of F triangular meshes \(\mathbf {f}_i\), \(i = 1,\ldots ,F\) with fixed connectivity of N vertices in each frame, a frame \(\mathbf {f}_i\) is composed of the vertex coordinates of the mesh which we represent as a column vector: \(\mathbf {f}_i=[x_{i,1} \ldots x_{i,N}\ y_{i,1} \ldots y_{i,N}\ z_{i,1} \ldots z_{i,N}]^T\). The mesh sequence is then represented with a matrix \(\mathbf {A}\) whose columns are the frames of the animation, \(\mathbf {A}=[\mathbf {f}_i \ldots \mathbf {f}_F]\), we assume that the connectivity is encoded once using any state-of-the-art algorithm. The purpose of our method is to compress the time-varying coordinate data only. Our method can also be briefly summarized as an encoder shown in Fig. 3 and a decoder shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the proposed decompression algorithm (decoder)

Full size image

3.1 Key-frame extraction based on pose similarity

As shown in Fig. 3, the first step of the encoder is to group the frames into clusters in which poses are similar to each other and then extract one key-frame in each cluster. Geometry of the frames with similar posture within one cluster lies in a space with much lower dimensionality than the whole sequence. Compressing each cluster separately enables us to reduce the temporal redundancy in order to achieve a higher compression rate and retain a reasonable reconstruction quality at the same time. Note that, the frames belonging to the same cluster may not be contiguous.

3.1.1 Global rotation and translation elimination

As we know, an animation character usually not only deforms as different poses, but also moves or rotates in or along certain direction. And such global motion will of course affect the mesh clustering step, because the global translation and rotation will result in significant difference in geometry coordinates even though the poses are similar. However, we want to put meshes with similar poses into one cluster despite the global location and orientation, so we first apply frame alignment to align all the poses to a reference (the first mesh we used in this paper) using the method by Paul and Neil [2]. For each vertex \(\mathbf {v}_i\) on frame \(\mathbf {f}_t\), we solve for the optimal rotation \(\mathbf {R}_t\) and translation \(\mathbf {t}_t\) that will align this frame to the reference frame \(\mathbf {f}_r\) as follows:

$$\begin{aligned} \mathbf {v}_t^i=\mathbf {R}_t*\mathbf {v}_r^i+\mathbf {t}_t. \end{aligned}$$
(1)

The rotation matrix can be calculated by solving an SVD problem of the coordinates’ covariance matrix, and the translation can be obtained by subtracting the rotated frame from the reference. The global motion can be represented with three coefficients for rotation and three for translation which can be compressed separately.

3.1.2 Pose similarity-based frames clustering

After frame alignment, we employ K-medoids clustering to cluster the sequence. Given a mesh sequence \(\mathbf {A}\) with dimension \(3N\times F\), K-medoids clusters the F frames into J (\(J<F\)) clusters (\(\mathbf {S}_1,\mathbf {S}_2,\ldots ,\mathbf {S}_J\)):

$$\begin{aligned} \arg \min _\mathbf {S} \sum _{i=1}^{J}\sum _{\mathbf {f} \in \mathbf {S}}\Vert \mathbf {f}_j-{\mu }_i\Vert _1, \end{aligned}$$
(2)

where \({\mu }_i\) is one frame which has the smallest distance to all other frames in the current cluster. The choice of the number of clusters is an important factor of the compression ratio which will be explained in the next section. Note that we choose K-medoids clustering rather than K-means clustering because in contrast to the latter, K-medoids chooses one of frames as center frame (medoid) rather than the mean of frame vectors in \(\mathbf {S}_i\) which may produce artifacts, and works with a generalization of the Manhattan Norm to define distance between frames instead of L2 which is gainful for the key-frame extraction.

Fig. 5
figure 5

Extracted key-frames of the Walk dataset from [38]. Left: Cluster centers of K-medoids as key-frames; Right: Average shapes in edge space as key-frames

Full size image

3.1.3 Key-frame extraction within clusters

After the clustering, it is vital to extract the key-frame in each cluster, in this paper we offer two methods to extract key-frames. In the first method, we select the medoid frame in each K-medoids clusters as the key-frames directly. It is noteworthy that key-frame, which is not only applied to compute the piece-wise MHB but also applied to recover the high-frequency part of non-key-frames in the decoded processing, should be the one that obtains significant posture and representative high-frequency geometry information. So in the second method, we compute the average mesh which captures the common inter-vertex relationships as the key-frame in each cluster separately. We first compute the average mesh in the edge shape space [39], where each frame is expressed by edges lengths and dihedral angles between adjacent faces. Then we project the average mesh back to the original Euclidean space by solving a global nonlinear system via Gauss–Newton algorithm [6]. The key-frame extraction results of the two methods for Walk dataset are shown in Fig. 5. Experiments show that there is only a very little difference on these two methods, and we use the first convenient method for most sequence. We then store the key-frames using any state-of-the-art static mesh compression methods [27, 34].

3.2 Intra-cluster compression with piece-wise MHBs

Now we have segmented the mesh sequence into clusters such that frames within a cluster share similar postures and extracted one key-frame for each cluster. We now apply piece-wise manifold harmonic bases to compress the subsequence. As mentioned above, geometric details of the frames within one cluster are almost unchanged and the geometric primaries lie in a very low-dimensional space as the result of pose similarity clustering. So we devise a hierarchical framework in which we convert the mesh from geometry domain into frequency domain and then the shape space is decomposed into high-frequency and low-frequency domains. We compress these two part separately to reduce spatial redundancy.

3.2.1 Piece-wise MHBs for geometry compression

In the low-frequency domain, meshes are treated as primary poses, and then we project these meshes onto a few manifold harmonic bases derived from the key-frame in each cluster. These bases of the key-frame are derived as eigenvectors of the Laplace–Beltrami operator, which can be computed by solving the following eigenvalue problem [33]:

$$\begin{aligned} -\mathbf {L}{\varvec{\Phi }}_k=\lambda \mathbf {M}{\varvec{\Phi }}_k, \end{aligned}$$
(3)

where \(\mathbf {M}\) is an \(N \times N\) mass matrix of the key-frame and \(\mathbf {L}\) is an \(N \times N\) matrix which is so-called cotangent weight:

$$\begin{aligned} \mathbf {L}_{ij}=\left\{ \begin{array}{lll} &{}{cot \alpha _{ij}+cot \beta _{ij},} &{}\quad j \in \mathbf {N}(i)\\ &{}{0,} &{}\quad j\notin \mathbf {N}(i)\\ &{}{- \sum \limits _{k \ne i} L_{ik},} &{}\quad i=j \\ \end{array} \right. , \end{aligned}$$
(4)

where \(\mathbf {N}(i)\) are the vertices adjacent to (neighboring) vertex i, and \(\alpha _{ij}\), \(\beta _{ij}\) are the angles opposite to edge ij. We assemble the first K eigenvectors into a basis matrix \(\mathbf {U} \in R^{N \times K}\), where each column \({\varvec{\Phi }}_k\) is one eigenvector. After performing MHBs for all J clusters, we get J new basis matrices \(\{\mathbf {U}_1,\ldots ,\mathbf {U}_J\}\) which we call piece-wise manifold harmonic bases. Low-frequency part of original frame \(\mathbf {f}_j\), reshaped as \(\mathbf {f}_j' \in R^{N\times 3}\), from \(\mathbf {S}_i\) is then represented by MHB coefficients:

$$\begin{aligned} \mathbf {c}_j=\mathbf {U}_i^T*\mathbf {f}_j' \in R^{K\times 3}. \end{aligned}$$
(5)

Combining the coefficients of frames in each cluster into \(\mathbf {C}_i\), we can get coefficient matrices \(\{\mathbf {C}_1,\ldots ,\mathbf {C}_J\}\) for all clusters. One clear advantage of MHBs is that we can just store or transmit the key-frames and re-compute MHBs in the decompressing process which saves a lot of storage space compared with other PCA-based methods in which they store the PCA bases directly. In addition, manifold harmonic basis captures all the intrinsic properties of the mesh and is invariant to extrinsic shape transformations such as isometric deformations so that the reconstructed meshes have a better shape fidelity. Note that increasing the number of eigenvectors reduces the distortion, while the total code size might increase due to the additional coefficients as shown in Fig. 6.

Fig. 6
figure 6

Compression with different number of bases. From left to right: Low-frequency part of Frame 134 (yellow) of Samba with 200, 400, 600 bases (a, c, e) with the corresponding reconstruction errors (blue, b, d, f) mapped to blue-red color map

Full size image

3.2.2 Geometric details preserving and linear predictive encoding

In the high-frequency domain, as geometric details of the frames within one cluster are almost unchanged, we can just store the details once to reduce the spatial redundant information. Actually we store full geometry of key-frames which has included the representative geometric details for each cluster in the previous section, so there is no more effort for storing geometric details. A further compression improvement can be achieved by efficiently encoding the coefficient matrix \(\mathbf {C}\). In this paper we follow [16] by applying linear predictive coding to compress the MHB coefficient matrix.

Linear prediction coding (LPC) predicts coefficients of the t-th frame in a sequence as a linear function of the preceding m frames’ coefficients:

$$\begin{aligned} \qquad \mathbf {c}_t=a_0+\sum _{j=1}^{m}a_j\mathbf {c}_{t-j} \quad \quad \forall k<t\le F. \end{aligned}$$
(6)

As many physics-based animations may be represented by second-order PDEs, second-order LPC (\(m=2\)) will probably suffice to capture the temporal correlation. So given the coefficient matrix \(\mathbf {C}\) with dimension \(3K\times F\) where K is the number of MHBs and F is the number of frames, we solve 3K second-order LPC problems each of size F. To make the coefficients compression lossless, the residuals \(\Delta c_t\) must be encoded as

$$\begin{aligned} \qquad \Delta c_t=\mathbf {c}_t-\left( a_0+\sum _{j=1}^{m}a_{j}\mathbf {c}_{t-j}\right) . \end{aligned}$$
(7)

We need to encode 3K triples of LPC coefficients and the \(3K\times (F-2)\) LPC residuals. After LPC, we apply quantization and arithmetic coder to the LPC coefficients and residuals as other compression methods do in order to further reduce the data size. After LPC, we apply quantization and arithmetic coder to the LPC coefficients and residuals as other compression methods do in order to further reduce the data size.

In summary, the compressed information we should store in our method only includes the following two parts:

  • the compressed geometry and connectivity of key-frames, which can be efficiently stored by any state-of-the-art static mesh compression method;

  • the quantized integers of LPC coefficients and residuals, which only takes up a small fraction of storage comparing to the meshes themselves.

Fig. 7
figure 7

Illustration of transferring the high-frequency part of key-frame to the low-frequency parts of non-key-frames. The left and middle top row are the decompressed low-frequency parts. The left and middle bottom row are the reconstructed full frames. The right are reconstruction errors mapped to blue-red color map

Full size image

3.3 Decompression with deformation transfer method

In the decompressing process, we firstly use the LPC coefficients and residuals to retrieve the MHB coefficient matrix \(\mathbf {C}\) (lossless up to quantization). Then with the decompressed key-frames, we re-compute the manifold harmonic bases \(\mathbf {U}_i\) for each cluster. Low-frequency part of frame \(\mathbf {f}_i'\) is reconstructed using corresponding bases and coefficients:

$$\begin{aligned} \mathbf {f}_i'=\mathbf {U}_i*\mathbf {c}_i. \end{aligned}$$
(8)

As mentioned above, we only store the geometry of key-frames and low-frequency parts of non-key-frames represented by MHB coefficients, so the last step of decompression is to transfer the high-frequency geometric details of key-frames to the low-frequency primary poses of non-key-frames to recover high-quality mesh sequence via deformation transfer techniques [31]. We first take the low-frequency part of key-frame as source mesh and the full key-frame as target mesh. Then the source and target deformations are represented as affine transformations and a correspondence is built here between them. Finally we use this correspondence to map geometry details of key-frames to low-frequency parts of non-key-frames by solving a constrained optimization as shown in Fig. 7.

Multi-resolution technique for performance improvement Even though we have proposed a key-frame-based compression scheme with piece-wise manifold harmonic bases; however, computing the spectral bases involves computing the eigenvectors of an \(N \times N\) matrix which will cost much time. Thus, we need a multi-resolution scheme to reduce the space complexities of the sequence to reduce the decompression time. We firstly use an edge-collapse [7] scheme to coarsen the given mesh sequence with exactly same rule to keep topology consistent across coarse meshes (Ghost) which have around 10000 vertices (actual number depends on mesh complexity), explicitly reducing the information present in the data set. Note that there is a trade-off between space complexities and time, reconstruction error. Then we apply the proposed scheme on the ghost sequence. In the decompressing process, as the topology is modified, we need to build a corresponding relationship between the source and target mesh. Fortunately edge-collapse schemes simplify a mesh by collapsing a few vertices into one. For a vertex on the ghost mesh, we choose the nearest one of these vertices as its corresponding vertex on the original mesh. The multi-resolution scheme is shown in Fig. 8.

Fig. 8
figure 8

Flowchart of the proposed multi-resolution scheme. a Original mesh (165954 vertices). b Ghost mesh (10002 vertices). c Low-frequency part of decompressed mesh. d Reconstructed mesh

Full size image

4 Statistical and perceptual metrics for comprehensive evaluations

For any compression method, the most importation metric that measures the compression quality is the distortion between decompressed data and its original counterpart using limited storage. In compression community, researchers tend to develop techniques where decompressed data are as-close-as-possible to the uncompressed data, and for dynamic meshes compression researchers also inherit this intuitive metric. However, simply forcing the decompressed meshes to be close to the uncompressed sequence in statistics of vertex coordinates is usually not enough for dynamic meshes compression, the decompressed mesh should also look like its uncompressed counterpart one in a perceptual view.

4.1 Measuring statistical errors for dynamic meshes compression

Statistical error is to measure the compressing distortion between decompressed and uncompressed sequences by treating the meshes as simple data and computing the difference of their vertex coordinates. Karni–Gotsman (KG) error [16] is one of the most popular metric used for dynamic meshes compression, which measures the difference between a mesh sequence and its decompressed one and defined as follows,

$$\begin{aligned} \hbox {KG}_\mathrm{error}=100*\frac{\Vert \mathbf {A}-\mathbf {A}'\Vert }{\Vert \mathbf {A}-\mathbf {E(A)}\Vert }, \end{aligned}$$
(9)

where \(\mathbf {A}\) is a \(3n\times F\) matrix containing the original animation sequence. \(\mathbf {A}'\) is the same animation after the compression and reconstruction stages. \(\mathbf {E(A)}\) is an average matrix.

However, even though this metric has been used for years in dynamic meshes compression, it still has obvious limitation that simply consider the meshes of coordinates as normal data inevitably ignoring the geometric structure of meshes themselves. It may occur as visual artifacts even under a very small error in statistical view, as shown in Fig. 1. Statistical error works well only as long as the property being preserved is vertices located near their original location; however, we will show that visual similarity with the original is a different property and it should be therefore evaluated by a different measurement.

4.2 Perceptual local rigidity error

We believe that visual shape fidelity is more important than the accuracy of geometric coordinates. Traditional statistical metrics such as KG error are unable to distinguish between smooth error and random error even though intuitively there is a big perceptual difference between these two, as these metrics explore just the accuracy of data and ignore the intrinsic properties of the geometric structure. If we take the decompressed mesh as the deformation of source model, shape fidelity expects the deformation to preserve the shape of the object locally which can be called detail-preserving deformation. In other words, if the deformation is greater, the distortion rate is higher and the shape fidelity is lower. Here we apply the famous as-rigid-as-possible energy [26] between source mesh \(\mathbf {f}_i\) and decompressed mesh \(\mathbf {f}_i'\) to measure the distortion:

$$\begin{aligned} E_{\mathbf {V}}(\mathbf {V}')= \sum _{\mathbf {v}_i \in \mathbf {V}} \min _{c_i}\sum _{j \in \mathbf {N}_i} w_{ij}\Vert c_i \times (\mathbf {v}_i-\mathbf {v}_j)-\mathbf {v}_i'+\mathbf {v}_j'\Vert ^2, \end{aligned}$$
(10)

where \(\mathbf {V} = \{\mathbf {v}_i, i = 1,2,\ldots ,N\}\) is a set of all vertices of frame \(\mathbf {f}_i\) and \(\mathbf {V}'\) is of frame \(\mathbf {f}_i'\). Here, \(\mathbf {N}_i=\mathbf {N}(\mathbf {v}_i)=\{j:\Vert \mathbf {v}_j-\mathbf {v}_i\Vert <\epsilon \}\) is a set of indices of neighboring points for each point \(\mathbf {v}_i\), and the weights are simple symmetric \(w_{ij} = (|\mathbf {N}_i|+|\mathbf {N}_j|)^{-1}\) . As we can see, as-rigid-as-possible energy only measures the variation of shape local rigidity and ignores the difference in coordinates, which is very suitable for quantify the precision of the reconstructed mesh in a perceptual view. That means small as-rigid-as-possible energy between two meshes indicates small visual shape fidelity difference. With the energy \(E_{\mathbf {V}}(\mathbf {V}')\) between two frames, we can define the LR error of the whole sequence as the average as-rigid-as-possible energy between all decompressed meshes and their corresponding references as follows:

$$\begin{aligned} \hbox {Error}_\mathrm{LR}=\frac{\alpha }{F}\sum _{i=0}^{F}\Vert E_{\mathbf {V_i}}(\mathbf {V_i}')\Vert _1. \end{aligned}$$
(11)

where \(\alpha \) is the corresponding coefficient taking different values depending on the sequence. The LR error is affected by the size of sequence and the number of frames so that comparison of errors between different sequences is not advisable. We use \(\alpha \) to limit the error to a certain range to compare the relative errors of different algorithms in the same sequence.

Fig. 9
figure 9

Map LR error to blue-red color map. From left to right: Reconstructed meshes using 200, 400, 600, 800 bases

Full size image

Figure 9 shows the result of mapping LR error to blue-red color map, it is obvious that there is a big error at the bottom of skirt, hands and shoulder which corresponds to the error on the reconstructed mesh observed by the human vision. That is because these parts are all high-frequency parts which are recovered from key-frames that have some differences and lose local rigidity. As the number of MHBs increases, the error becomes very small and concentrates on the skirt. Figure 6 shows the result of mapping KG error to blue-red color map, there is a little error in these parts while there is a big perceptual difference between these parts that verifies that KG error cannot be used to measure human visual errors.

5 Experimental results and comparisons

In this section, we show the experiments of our compression scheme with different mesh sequences which are shown in Table 1. We use bit per vertex per frame (bvpf) to represent the size of data after compression. The overall sequence distortion is measured by the traditional vertex-based error: Karni–Gotsman (KG) error [16] and the Local Rigidity (LR) error for measuring visual discrepancy between two dynamic meshes.

Table 1 Mesh sequence
Full size table
Table 2 Compression performance with different number of clusters
Full size table
Table 3 Compression performance with different number of MHB
Full size table

Choice of compression parameters The encoding performance of our scheme is mainly affected by 2 parameters: (1) the number of clusters, (2) the number of manifold harmonic basis. Table 2 shows the compression and distortion results with different numbers of clusters. The optimal number of clusters cannot be defined as a priori, but we can roughly estimate a general range according to the pose changing. When the similarity of each frame in one cluster is higher, the representation ability of embedded space of MHBs of key-frames is stronger and the compression performance is better. Taking into the key-postures in the test sequences, experiments show that there is a significant reduction in reconstruction errors with just 2 or 4 clusters for sequences with a few key-postures such as Horse and Humanoid, while the complicated sequences such as Samba and Walk need more clusters. It is obvious that the number of extracted key-frames increases, the error reduces while the bvpf increases. Therefore, there is a trade-off between compression ratio and reconstruction error. Table 3 shows the compression and distortion results with different numbers of manifold harmonic bases which determines the threshold of high-frequency domain and low-frequency domain. As the number of MHBs increases, bvpf increases very little, because we just store key-frames and the growing number of MHBs only affects coefficient matrix. It is obvious that the number of bases increases, the error reduces which is because more information of low-frequency part has transmitted to the decompressing process by embedding the space with more MHBs as shown in Figs. 6 and 10. However, it needs more time to re-compute MHBs in decompressing process, so there is a trade-off between compression ratio and decompressing time.

Fig. 10
figure 10

Frame-wise LR error for Cloth sequence under the same compression ratio. Blue: Ours; Red: CdmGL; Yellow: CoDDyaC

Full size image
Fig. 11
figure 11

R-D curves for all test sequences measured in KG error

Full size image
Fig. 12
figure 12

Multi-resolution scheme for Armadillo. Top row from left to right: Original frame with 165954 vertices, edge collapse to 10002 vertices, edge collapse to 5002 vertices. Middle row are the corresponding reconstruction errors. Bottom row are the corresponding reconstruction LR errors

Full size image
Table 4 Encoding computation times (in seconds) of the proposed method for different test sequences
Full size table

Performance with different datasets Figure 11 shows typical rate-distortion (R-D) curves under the KG error on all test sequence. It is obvious that the reconstructed error decreases as the data rate increases. As we just store key-frames, our method reduces the required data rate to 0.5 bpfv at 1% distortion rate compared to other traditional PCA-based methods and predictive methods. Our results are seen to be excellent for relatively smooth sequence like Cloth and Jump. This is due to the low frequencies present the geometry primary more than the sharp parts like fingers or horseshoe. Note that combination of different numbers of bases and clusters may result in different reconstruction errors with the same bpvf. Figure 12 shows the results of multi-resolution scheme. With the edge-collapse scheme, the reconstruction error increases while the encoding time decreases obviously shown in Table 4, so there is a trade-off between distortion rate and decompression time for complex sequence. Table 4 shows the timing cost for the encoding process implemented with MATLAB on a PC with Intel Core i7-3770 CPU @ 2.40 GHz. Note that the most time-consuming steps are computing MHBs of key-frames and encoding coefficients which is dependent on the number of vertices.

Comparison with other methods We compare the reconstruction accuracy measured by KG error with previous techniques, namely SPC [28], improved SPC (im-SPC) [3] and MPEG-4 FAMC [29] using data from their papers. Figure 13 shows the comparison results of Horse and Jump. As observed from this figure our algorithm performs better than others in low data rate. That means that inter-frame redundancy can be captured with fewer cluster centers and manifold harmonic bases. With the data rate increases, the KG error decreases more slowly and becomes almost constant, since we recover the geometry details of the non-key-frames via deformation transfer which inevitably lose certain information during transfer process. However, we concentrate on obtaining a high compression rate with a limited distortion rate for complicated dynamic mesh sequences, and the results seem satisfactory for this.

Fig. 13
figure 13

R-D curves comparison of the proposed method with previous techniques measured by KG error. Left: Horse sequence. Right: Jump sequence

Full size image
Fig. 14
figure 14

R-D curves comparison of the proposed method with previous techniques measured by LR error. Left: Samba sequence. Right: Cloth sequence

Full size image

As said earlier, KG error only measures the precision of coordinates data and low KG error do not means the visual shape fidelity is also good enough. So we also quantify our compression method using newly introduced LR error in a perceptual view. Figure 14 shows typical rate-distortion(R-D) curves for our algorithm as well as CoDDyaC [36] and CdmGL [35]. It shows that our method performs much better than CoDDyaC which is a traditional PCA-based method. That is because we can reconstruct the perfect geometry primary with MHBs which occupy an important component in terms of human vision while CoDDyaC just uses PCA in vertex space which can not keep the high shape fidelity making the reconstructed model not smooth which is also shown in Fig. 1. CdmGL which uses Laplacian weights of average shape to encode the delta trajectories is better than us in low data rate. However, our scheme is better than CdmGL in higher data rate. That is because we use more Laplacian matrix of key-frames to capture the intrinsic properties of sequence while CdmGL just store one average shape. As our aim is to achieve a very high compression rate with limited distortion, it is obviously our method is better than the others in this case. Figure 10 shows the frame-wise LR error for the three algorithms. As we store six frames directly, so there are six zero-points on the energy curve making the overall LR error smaller than the state-of-the-art algorithm CdmGL.

6 Conclusion and discussion

In this paper, we have presented a key-frame-based method with piece-wise manifold harmonic bases to compress complex mesh sequence and a perceptual error metric LR error. We explored intrinsic geometry properties of sequence with MHBs to reduce spatial redundancy by decomposing the shape space into high-frequency part and low-frequency part and compressing them separately. Then we applied the notion of pose similarity to reduce the geometric redundancy along the time axis. We extended the traditional spectral methods to piece-wise manifold harmonic bases to compress the low-frequency part of non-key-frames and applied the deformation transfer techniques to recover geometry details of non-key-frames. Compared with PCA-based methods and other predictive methods, we not only eliminated the need for an explicit storage bases to improve the compression radio, but also achieved better shape fidelity which we strongly believe is more important than the accuracy of geometric coordinates by way of a piece-wise MHBs.

Limitations and future works A possible limitation arises when dealing with frames which have many sharp protrusions, which means we need more bases to reconstruct even the low-frequency part subject to a limited reconstruction error and of course the computation cost and compression rate will increase in such cases. One possible solution is to partition the meshes into a few patches with simpler structure and compress these patches separately, or replace the globally defined manifold harominic bases with the compressed manifold modes (CMM) [22] which has local support in contrast. However, the feasibility and the broader impacts of these solutions will need further investigation in the future. In addition, the parameters in our framework, such as the number of clusters and the number of harmonic bases, are all empirically set according to adequate experiments. Adaptively determining these parameters based on the sequence itself will make our method more practical and adaptable in a wider range of graphics applications.