Point sets joint registration and co-segmentation

Abstract

We present a novel approach of joint registration and co-segmentation for point sets where objects move in different ways. We consider joint registration and co-segmentation as two problems that are heavily entangled with each other; thus, we represent the input point sets as samples from a generative model and bring up with a novel formulation based on Gaussian mixture model. By maximizing the posterior probability of the samples, we gradually recover the latent object models as well as an object-level segmentation and simultaneously align the segmented points to the latent object models. Along with the formulation, we design an interactive tool that helps users intuitively intervene the process to optimize the registration and segmentation results. The experiment results on a group of synthetic and scanned point clouds demonstrate that our method is powerful and effective for joint registration and co-segmentation on point sets of multiple objects.

1 Introduction

Many research projects and applications of indoor scenes require segmented and even annotated 3D databases [5, 8, 10, 11, 20]. One way to build such databases is to interactively compose scenes using 3D meshes for objects, which yields natural object segmentation and annotation. An alternative method for database building is to segment and annotate existing 3D scenes manually. This procedure is tedious and time-consuming, despite many efforts of improving the interaction experience [18, 28]. Another way is to automatically compose a scene model from an image based on existing 3D shape models [5, 17]. In the aforementioned methods, a retrieval procedure is usually needed, which inevitably limits the results to a particular set of 3D models. However, the actual 3D shapes that appear in the input image may still not be produced.

Generating scene models directly from captured point clouds will significantly facilitate dataset construction and increase the variety of the dataset. However, there is a large gap between the desired 3D model dataset and available scene capturing tools. Typically, clean, complete and separated models for objects are desired to construct a scene database. By contrast, a noisy and incomplete point set of different objects all in one is usually obtained with available consumer-level scene capturing frameworks [7, 13, 21]. Thus, a general object-level segmentation and modeling method from scanned point sets is a strong demand to fill the gap.

A general object-level segmentation is not equivalent to a multi-label classification problem since segmentation is not limited to a fixed number of object categories predefined in the training data. Existing approaches for segmenting scanned 3D data require additional knowledge, such as a block-based stability [14], or motion consistency of rigid objects [29]. While a robot is employed to do proactive pushes, movement tracking is used to verify and iteratively improve the object-level segmentation result [29]. However, it remains significantly challenging to recover the motion consistency in a noninvasive way.

In this paper, we explore the motion consistency of rigid objects from a new perspective. While the motion consistency of objects in indoor scenes is naturally revealed by human activities over time, we expect the scanned point sets at different times to be segmented into objects based on their motions. With these concepts in mind, one must choose an appropriate scanning scheme. One way is to record the change of a scene along with human activities. Another option is to schedule a periodic sweep that only records the result of human activities without capturing human motion. In both schemes, it is non-trivial to recover object correspondences in different point sets due to occlusions. In the former scheme, the occlusions are probably caused by human bodies; in the latter scheme, they are likely caused by sparse sampling times. In the former scheme, extra challenging processing may be required such as tracking objects with severe occlusions by human bodies. Therefore, we choose the latter scanning scheme.

Thus, our original intention of building 3D scene datasets from scanned point sets leads us to the problem of coupled joint registration and co-segmentation. By solving the problem of coupled joint registration and co-segmentation, we not only partition point sets into objects, but also recover the rigid object motions among different point sets. In this problem, registration and segmentation are entangled with each other. On the one hand, the segmentation problem depends on the registration to connect the point clouds into a series of rigid movement so that the object-level segmentation can be done based on the motion consistency. On the other hand, the registration problem relies on the segmentation to break the problem into a series of rigid joint registration of objects. Otherwise, the registration of multiple scenes is a non-rigid joint registration with non-coherent point drift. Non-coherent point drift means that a pair of points are close to each other in one point set, but their corresponding pair of points in another point set are far from each other. This happens when two points actually belong to different objects. This makes a big difference from non-rigid registration problems where point motions are smooth everywhere (such as the problem studied in [19]). Solving such a non-coherent non-rigid joint registration is non-trivial. Consequently, breaking it up into a series of rigid joint registration with object-level segmentation makes it possible to tackle the problem.

In our method, we employ a group of Gaussian mixture models (GMM) and each of these Gaussian mixture models represents a potential object. This representation unentangles the registration and segmentation in the way that the segmentation can be done by evaluating the probability of belonging to the Gaussian mixture models for each point, while the registration can be done by evaluating a rigid registration in different point sets against each Gaussian mixture model.

In summary, our work makes the following contributions:

• 1. To the best of our knowledge, we first put forward the problem of object-level joint registration and co-segmentation of multiple point sets.

• 2. We propose a generative model to simultaneously solve the joint registration and co-segmentation of point sets.

• 3. We design an interactive tool for joint registration and co-segmentation based on the generative model.

2 Related work

In this section, we review a series of techniques on point set registration and segmentation that are related to our method.

2.1 Point set registration with GMM representation

Gaussian mixture models are widely used for point set registration problems due to their general ability of representing point sets for both rigid and non-rigid registrations and their robustness against noise. A comprehensive survey about point set registration approaches using Gaussian mixture models can be found in [15]. They also present a unified framework for rigid and non-rigid registration problems. These methods select one of the point sets as the “template model” and fit the other point sets to this “template model”. Myronenko and Song consider the registration of two point sets as a probability density estimation problem [19]. They use GMM to represent the geometry and force the GMM centroids to move coherently as a group to preserve the topological structure of the point sets. This method is applicable to both rigid registration and non-rigid registration. Unlike the above approaches, [9] treats all point sets equally as the realizations of a GMM and the registration is cast into a clustering problem. A more recent method pushes this idea to the application on a large-scale dataset [2]. Compared to these methods, our method can be seen as an extension of the formulation of [9] to simultaneously handle joint registration and co-segmentation. The difference between our method and non-rigid registration techniques is that we handle the non-coherent point drift by estimating independent transformation for each object.

2.2 Interactive segmentation and co-segmentation of images

Many interactive methods have been proposed to leverage human interaction on high-level hints and the powerful computational ability of computers. An influential technique for interactive image segmentation is GrabCut [22]. It uses two GMMs for foreground and background, respectively. To initialize these two Gaussian mixture models, a rectangle is manually placed to contain the foreground. Our user interaction design draws on the experience from [22]. The difference is that our tool is designed for 3D space and handles multi-object segmentation rather than binary segmentation. Dating back to 2006, extensive research has been done on image co-segmentation [23]. These works are based on the basic idea of exploring inter-image consistent information to extract common objects from multiple images. A more recent approach of [25] jointly recovers co-segmentation and dense per-pixel correspondences in two images. Though our input and output are totally different from [25], we share with [25] the idea of jointly recovering co-segmentation and point-to-point correspondences (by registration).

2.3 Segmentation and motion

Object motion, as a strong hint for object segmentation, is widely used in many approaches. [29] employs a robot to do proactive pushes and tracks the motion to learn prior knowledge about object segmentation on the fly. [16] exploits motions in a video and uses the motion edges as training data to learn an edge detector for images. These methods lean on the motion that is continuous over time and can be tracked. In comparison, our method handles motion that is non-continuous over time. [24] solves the object-level segmentation along with the SLAM problem. However, its object-level segmentation depends on retrieval from an existing object database. Neither a database nor prior knowledge is required in our method.

2.4 3D object recognition based on correspondence grouping

By interactively inputting the scene layout, the joint registration and co-segmentation problem can be treated as a series of 3D object recognition problems in point sets. Our method should be classified as one of the correspondence grouping methods. Compared to previous methods [4, 26], our method simultaneously solves the problem for multiple target models in multiple scenes.

3 Problem definition

In this section, we introduce our formulation of the joint registration and co-segmentation problem for point sets. The input of our problem is a group of 3D point sets $\mathscr {V}=\{\mathbf {V}_m\}^{M}_{m=1}$ that are captured at M different times in a scene, where objects move in different ways. Each point set $\mathbf {V}_m=[\mathbf {v}_{m1},\mathbf {v}_{m2},\ldots ,\mathbf {v}_{m{L_m}}]$ contains $L_m$ 3D points. Our target is to simultaneously partition the point sets into N objects and figure out the transformations from objects to each point set. For partitioning, we assign point-wise label vectors $\{\mathbf {y}_m\}$ for each input point set to indicate its object partition. For registration, we compute $\{\mathbf {R}_{mn},\mathbf {t}_{mn}\}$ to indicate the transformations from N objects to M point sets, respectively.

3.1 Basic formulation

For robustness, we do not model a point set as a simple composition of transformed 3D points in each object model. Instead, we model each point set as a realization of several unknown central Gaussian mixture models (GMMs) of the transformed objects. In other words, we explicitly separate the total $K_{\mathrm{all}}$ Gaussian models to N groups to represent N objects $\{O_n\}_{n=1}^N$ as

$$\begin{aligned}&\left\{ \underbrace{ \{\mathbf {x}_{1},\varSigma _{1}\}, \ldots , \{\mathbf {x}_{K_1},\varSigma _{K_1}\} }_{O_1},\right. \nonumber \\&\quad \left. \underbrace{ \{\mathbf {x}_{K_1+1},\varSigma _{K_1+1}\}, \ldots , \{\mathbf {x}_{K_1+K_2},\varSigma _{K_1+K_2}\} }_{O_2},\nonumber \right. \\&\quad \left. \ldots , \underbrace{ \{\mathbf {x}_{K_S+1},\varSigma _{K_S+1}\},\ldots ,\{\mathbf {x}_{K_S+K_n},\varSigma _{K_S+K_n}\} }_{O_n},\ldots \right\} ,\nonumber \\ \end{aligned}$$

(1)

where $K_S = \sum _{i=1}^{n-1}K_i$.

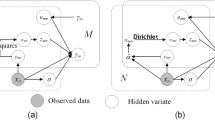
The Gaussian centroids $\{\mathbf {x}_{k}\}$ represent the point positions in objects. $\{\varSigma _{k}\}$ represents the variance of point positions in objects. $O_n$ has $K_n$ Gaussian models and $\{K_n\}_{n=1}^N$ are predefined, as described in Sec. 4. The total number of Gaussian centroids is denoted as $K_{\mathrm{all}} = \sum _{n=1}^{N}K_n$. Each object $O_{n}$ is rigidly transformed to each point set $\mathbf {V}_m$ with a transformation $\phi _{mn}(\mathbf {x}_{k})=\mathbf {R}_{mn}\mathbf {x}_{k}+\mathbf {t}_{mn}$ for $\mathbf {x}_{k} \in O_n$. Figure 1 shows a simple illustration for this formulation. Hence, for each point $\mathbf {v}_{mi}$ in a point set $\mathbf {V}_m$, given object models $\{O_{n}\}$ and their rigid transformations $\{\phi _{mn}\}$ to the point sets, we can write:

$$\begin{aligned} P(\mathbf {v}_{mi})=\sum ^{K_{\mathrm{all}}}_{k=1}p_k\mathscr {N}(\mathbf {v}_{mi} |\phi _{mn}(\mathbf {x}_k),\varSigma _k), \end{aligned}$$

(2)

where the observed point $\mathbf {v}_{mi}$ is a sampling point from a large Gaussian mixture model that represents N objects together. $\{p_k\}_{k=1}^{K_{\mathrm{all}}}$ are weights for $K_{\mathrm{all}}$ Gaussian models. Given the generative representation, the unknown parameters of our joint registration and segmentation problem are:

$$\begin{aligned} \varTheta =\left\{ \{p_k,\mathbf {x}_{k},\varSigma _k\}_{k=1}^{K_{\mathrm{all}}}, \{\phi _{mn}\}_{m=1,n=1}^{M,N}\right\} . \end{aligned}$$

(3)

Fig. 1

Our generative model for joint registration and co-segmentation (left) and its associated graphical model (right). The left figure illustrates 7 Gaussian models $\{\mathbf {x}_i, \varSigma _i\}^{7}_{i=1}$ are grouped into two object models $O_1$ and $O_2$. Each object is transformed to a point set $\mathbf {V}_i$ by $\phi _{mi}$. A 3D point in a point set $\mathbf {V}_m$ is a sampling point from a Gaussian mixture model composed of the 7 transformed Gaussian models

Once we estimate these parameters, each point in all input point sets can be assigned to one of the Gaussian models according to the largest sampling probability. Since the Gaussian models are simply predefined to be one of the N objects, we can further deduce the $\{\mathbf {y}_m\}_{m=1}^M$ indicating vectors of object-level co-segmentation for each input point set based on such assignment. To estimate the parameters $\varTheta$ to fit all the input point sets without knowing object labels for all 3D points, the problem can be solved in an Expectation–Maximization (EM) framework. In particular, we bring in hidden variables as:

$$\begin{aligned} \mathscr {Z}=\{z_{mi}|m=1,\ldots ,M,~i=1,\ldots ,L_m\}, \end{aligned}$$

(4)

such that $z_{mi}=k$, $k \in \{1,2,\ldots ,K_{\mathrm{all}}\}$ assigns the observed point $\mathbf {v}_{mi}$ to the kth Gaussian model $\mathbf {x}_k, \varSigma _k$. We aim to maximize the expected complete-data log-likelihood:

$$\begin{aligned} \begin{aligned} \mathscr {E}(\varTheta |\mathscr {V},\mathscr {Z})&=\mathbb {E}_{\mathscr {Z}}[\ln P(\mathscr {V},\mathscr {Z};\varTheta )|\mathscr {V}]\\&={\sum _{\mathscr {Z}}P(\mathscr {Z}|\mathscr {V},\varTheta )\ln {P(\mathscr {V},\mathscr {Z};\varTheta )}}. \end{aligned} \end{aligned}$$

(5)

This formulation can be seen as an adaption of the joint registration formulation in [9], upon which we separate Gaussian models into groups to express multiple objects. Under the assumption that the input points are independent and identically distributed, we can rewrite the objective defined in Eq. (5) into:

$$\begin{aligned} \varTheta =\arg \max \sum _{m,i,k}\alpha _{\mathrm{mik}}\big (\ln p_k + \ln P(\mathbf {v}_{mi}|z_{mi}=k;\varTheta )\big ), \end{aligned}$$

(6)

where $\alpha _{\mathrm{mik}} = P( z_{mi} = k | \mathbf {v}_{mi} ; \varTheta )$. By bringing in Eq. (2) and ignoring constant terms, we can rewrite the objective as:

$$\begin{aligned} \begin{aligned} \varTheta =&\arg \max \Big (-\frac{1}{2}\sum _{m,i,k}\alpha _{\mathrm{mik}}\big (||\mathbf {v}_{mi}-\phi _{mn}(\mathbf {x}_k)||_{\varSigma _k}^2 \\&+ \ln |\varSigma _k| - 2\ln p_k\big )\Big ), \end{aligned} \end{aligned}$$

(7)

where the $|\cdot |$ denotes the determinant and $||\mathbf {x}||_{\mathbf {A}}^2= \mathbf {x}^T\mathbf {A}^{-1}\mathbf {x}$. It is predefined that $\mathbf {x}_k$ is one of the Gaussian centroids used to represent the nth object, which is why we apply the transformation $\phi _{mn}$ on $\mathbf {x}_k$. For the convenience of computation, we restrict the model to isotropic covariances, i.e., $\varSigma _k=\sigma ^2\mathbf {I}$ and $\mathbf {I}$ is an identity matrix. Next, we can optimize the objective through iterating between estimating $\alpha _{\mathrm{mik}}$ (Expectation-step) and maximizing $\mathscr {E}(\varTheta |\mathscr {V},\mathscr {Z})$ with respect to each parameter in $\varTheta$ (Maximization-step).

E-step this step estimates the posterior probability $\alpha _{\mathrm{mik}}$ of $\mathbf v_{mi}$ to be a point generated by the kth Gaussian model.

$$\begin{aligned} \alpha _{\mathrm{mik}}=\frac{p_k\sigma _k^{-3}\exp \left( -\frac{1}{2\sigma _k^2}||\mathbf v_{mi}-\phi _{mn}(\mathbf x_k)||^2\right) }{\sum _s^{K_{\mathrm{all}}}p_s\sigma _s^{-3}\exp \left( -\frac{1}{2\sigma _s^2}||\mathbf v_{mi}-\phi _{mn}(\mathbf x_s)||^2\right) }. \end{aligned}$$

(8)

M-step-a: this step updates the transformations $\phi _{mn}$ that maximize $\mathscr {E}(\varTheta )$, given instant values for $\alpha _{\mathrm{mik}}$, $\mathbf {x}_k$, $\sigma _k$. We only consider rigid transformations, making $\phi _{mn}(\mathbf {x})=\mathbf {R}_{mn}\mathbf {x}+\mathbf {t}_{mn}$. The maximizer $\mathbf {R}_{mn}^*,\mathbf {t}_{mn}^*$ of $\mathscr {E}(\varTheta )$ is the same as the minimizers of the following constrained optimization problems:

$$\begin{aligned} \left\{ \begin{array}{ll} \min _{\mathbf {R}_{mn},\mathbf {t}_{mn}}&{} \left\| \left( \mathbf {W}_{mn}-\mathbf {R}_{mn}\mathbf {X}_n-\mathbf t_{mn}\mathbf {e}^T\right) \varLambda _{mn}\right\| _F^2\\ \hbox {s.t.}&{} \mathbf {R}_{mn}^T\mathbf {R}_{mn}=\mathbf {I}, |\mathbf {R}_{mn}|=1\\ \end{array} \right. , \end{aligned}$$

(9)

where $\varLambda _{mn}$ is a $K_n \times K_n$ diagonal matrix with elements $\lambda _{mnk}=\frac{1}{\sigma _k}\sqrt{\sum _i^{L_{m}}\alpha _{\mathrm{mik}}}$, $L_m$ is the number of points in the mth input point set, $\mathbf {X}_n = [\mathbf {x}_{K_S+1}, \mathbf {x}_{K_S+2},\ldots , \mathbf {x}_{K_S+K_n}]$ is the matrix stacked by the centroids of Gaussian models that are predefined to represent the nth object. $\mathbf {e}^T$ is a vector of ones, and $||\cdot ||_F$ denotes the Frobenius norm. $\mathbf {W}_{mn}=[\mathbf {w}_{m(K_S+1)}, \mathbf {w}_{m(K_S+2)},\ldots , \mathbf {w}_{mk},\ldots ,\mathbf {w}_{m(K_S+K_n)}]$ where $\mathbf {w}_{mk}$ is a weighted average point as:

$$\begin{aligned} \mathbf {w}_{mk}=\frac{\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}} \mathbf {v}_{mi}}{\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}}. \end{aligned}$$

(10)

This problem has a similar solution with [9]. The only difference is that we are estimating the transformation from Gaussian models to the input point sets instead of the transformation from input point sets to Gaussian models, since there are multiple groups of $\mathbf {x}_k$ corresponding to multiple objects in our Gaussian models. The optimal can be given by:

$$\begin{aligned} \mathbf {R}_{mn}^*= & {} \mathbf {U}_{mn}\mathbf {C}_{mn}\mathbf {V}_{mn}^T, \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {t}_{mn}^*= & {} \frac{1}{tr(\varLambda _{mn}^2)}(\mathbf {W}_{mn}-\mathbf {R}_{mn}X_n)\varLambda _{mn}^2\mathbf {e}, \end{aligned}$$

(12)

where $[\mathbf {U}_{mn},\mathbf {S},\mathbf {V}_{mn}]=\hbox {svd}\left( \mathbf {W}_{mn}\varLambda _{mn}\mathbf {P}_{mn}\varLambda _{mn}\mathbf {X}_{n}^T \right)$ and $\mathbf {P}_{mn}=\mathbf {I}-\frac{\varLambda _{mn}\mathbf {e}(\varLambda _{mn}\mathbf {e})^T}{(\varLambda _{mn}\mathbf {e})^T\varLambda _{mn}\mathbf {e}}$, $\mathbf {I}$ is identity matrix.

$$\begin{aligned} \mathbf {C}_{mn}=\hbox {diag}(1,1,|\mathbf {U}_{mn}||\mathbf {V}_{mn}|). \end{aligned}$$

(13)

M-step-b: in this step, we update the parameters related to the Gaussian mixture model and the indicating vector for object segmentation:

$$\begin{aligned} \mathbf x_k^*=\frac{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}\left( \mathbf {R}_{mn}^{-1}\mathbf {v}_{mi}-\mathbf t_{mn}\right) }{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}}, \end{aligned}$$

(14)

where $\mathbf {x}_k$ is one of the Gaussian centroids that is predefined to represent the nth object.

$$\begin{aligned} \sigma _k^{*2}= & {} \frac{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}\left\| \left( \mathbf {v}_{mi}-\mathbf t_{mn}-\mathbf {R}_{mn}^*\mathbf x_k^*\right) \right\| _2^2}{3\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}} \end{aligned}$$

(15)

$$\begin{aligned} p_k^*= & {} \frac{\sum _{m,i}\alpha _{\mathrm{mik}}}{M} \end{aligned}$$

(16)

$$\begin{aligned} y_{mi}^*= & {} \arg \max _n \sum _{k=\sum _{s=1}^{n-1}K_S+1}^{\sum _{s=1}^{n}K_S} \alpha _{\mathrm{mik}}, \end{aligned}$$

(17)

where $y_{mi}$ is the ith entry of the indicate vector $\mathbf {y}_{m}$ and it assigns the ith point of the mth point set to one of the N objects.

3.2 Bilateral formulation

In the basic formulation, only position information is used in Gaussian models. When considering point-wise features (such as color, texture, or other more complicated features like the ones discussed in [12, 27]), we can add bilateral terms into the generative model.

$$\begin{aligned} P(\mathbf {v}_{mi},\mathbf {f}_{mi})=\sum ^{K_{\mathrm{all}}}_{k=1}p_k\mathscr {N}\left( \mathbf {v}_{mi}|\phi _{mn}\left( \mathbf {x}^v_k\right) ,\sigma v_k\right) \mathscr {N}\left( \mathbf {f}_{mi}|\mathbf {x}^f_k,\sigma ^f_k\right) , \end{aligned}$$

(18)

where $\mathbf {f}_{mi}$ is the feature vector for point $\mathbf {v}_{mi}$, and $\mathbf {x}_k^f$ is the feature vector for kth point in object model. As shown in the formulation, there is no transformation applied onto $\mathbf {x}_k^f$, which means that this formulation is only suitable to the feature that is rotation and translation invariant. For example, we use the point color as a 3D feature vector in this paper. In this formulation $\mathscr {N}(v_{mi}|\phi _{mn}(xv_k),\sigma v_k)$ is the spatial term and $\mathscr {N}(\mathbf {f}_{mi}|\mathbf {x}^f_k,\sigma ^f_k)$ is the feature term. For the bilateral formulation, iteration steps will be as follows:

E-step: in this step, the posterior probability calculation consider both the spatial terms and the feature terms:

$$\begin{aligned} \alpha _{\mathrm{mik}}=\frac{p_kP_v\left( \mathbf {v}_{mi},\phi _{mn}\left( \mathbf {x}^v_k\right) ,\sigma v_k\right) P_f\left( \mathbf f_{mi},\mathbf x^f_k,\sigma ^f_k\right) }{\sum _s^{K_{\mathrm{all}}}p_sP_v\left( \mathbf v_{mi},\phi _{mn}\left( \mathbf {x}^v_s\right) ,\sigma ^v_s\right) P_f\left( \mathbf f_{mi},\mathbf {x}^f_k,\sigma ^f_s\right) }, \end{aligned}$$

(19)

where $P_v(\mathbf {x},\mathbf {y},\sigma )=\sigma ^{-3}\hbox {exp}\left( -\frac{1}{2\sigma ^2}||\mathbf {x}-\mathbf {y}||^2\right)$$P_f(\mathbf {x},\mathbf {y},\sigma )=\sigma ^{-D(\mathbf {x})}\hbox {exp}\left( -\frac{1}{2\sigma ^2}||\mathbf {x}-\mathbf {y}||^2\right)$ and $D(\mathbf {x})$ means the dimension of the vector $\mathbf x$.

M-step-a: for bilateral formulation, this step is the same with the basic formulation and the update can be done as Eqs. (11) and (12).

M-step-b: for bilateral formulation, this step not only updates model centroids and variance for the spatial term as Eqs. (14) and (15) but also updates the centroids and variance for the feature term as in Eqs. (20) and (21).

$$\begin{aligned} \mathbf {x}_k^{f*}= & {} \frac{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}\mathbf {f}_{mi}}{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}}, \end{aligned}$$

(20)

$$\begin{aligned} \sigma _k^{f*2}= & {} \frac{\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}\left\| \mathbf {f}_{mi}-\mathbf {x}_k^{f*}\right\| _2^2}{D(\mathbf {f})\sum _{m=1}^M\sum _{i=1}^{L_m}\alpha _{\mathrm{mik}}}, \end{aligned}$$

(21)

where $D(\mathbf {f})$ is the feature dimension. The update of $p_k$ for bilateral formulation is the same as the basic formulation in Eq. (16).

4 Initialization and optimization

Based on our formulation, as described in Sect. 3, our method for joint registration and co-segmentation can be summarized in Algorithm 1. In this section, we will explain in detail the parameter initialization and the user-guided optimization of our algorithm.

4.1 Initialization

In our formulation, there are a large number of parameters that can not be easily initialized. We provide an interactive tool to help with the initialization, as shown in Fig. 2. A set of boxes can be manually placed to indicate a rough segmentation of different objects in one point set. Each object can be roughly indicated by multiple boxes. Based on the roughly placed boxes, we can initialize the parameters in our formulation.

Fig. 2

The procedure of interaction: a load all the input point sets into the system. Our system shows these point sets in multiple sub-windows. These point sets record the same scene at different time. The objects inside the scene have been moved. b Pick one point set (by picking one sub-window) to add boxes to indicate the object layout. The box in white is the box currently under editing. c Add boxes to represent each object inside the scene. One color represents one object. The interaction allows multiple boxes to represent same object (e.g., the desk is represented by three boxes in same color). d The interaction is finished

Number of objectsN: N is naturally determined as the number of box groups placed in the point set.

Number of Gaussian models in each object$\{K_n\}^N_{n=1}$: While objects in an indoor scene have varying volumes, we use different numbers of Gaussian models for objects according to their volumes. We set $K_n$ as:

$$\begin{aligned} K_n=\frac{\hbox {vol}(O_n)}{\sum \hbox {vol}(O_n)}K_{\mathrm{all}}, \end{aligned}$$

(22)

where $\hbox {vol}(O_n)$ represents the total volume of the boxes for $O_n$. The total number of Gaussian models $K_{\mathrm{all}}$ in the scene is initialized as $\frac{1}{2}\big (\hbox {median}(\{L_m\}^M_{m=1}\big )$, where $L_m$ is the number of points in $\mathbf {V}_m$. This is an empirical choice borrowed from [9].

Gaussian parameters$\{p_k,\mathbf {x}_k,\varSigma _k\}_{k=1}^{K_{\mathrm{all}}}$: We initially set $p_k=\frac{1}{K_{\mathrm{all}}}$, which means each Gaussian model is equally weighted at the beginning. For object $O_n$, we initialize its $K_n$ Gaussian centroids $\{\mathbf {x}_k\}_{K_S+1}^{K_S+K_n}$ as random positions uniformly distributed on the surface of a sphere, whose radius r is chosen as the median of the radius of the input point sets. The radius of a point set is defined as half of the length of diagonal line of its axis-aligned bounding box.

The center of the nth sphere is $\mathbf {c}_n=(0,0,z_n)$, where $z_n\in \{-(N-1)r,-(N-3)r,\ldots ,(N-1)r\}$. This means that the object models are vertically arranged as shown in Fig. 3b. We choose vertical arrangement for groups of objects merely for the convenience of visualization. Figure 4b E00 shows an example of the initial Gaussian centroids of a scene with three objects. The variance $\{\varSigma _k\}$ is all initialized as $\varSigma _k=\sigma ^2 \mathbf {I}$ in which $\sigma =r$. Without any prior knowledge, such initialization for Gaussian parameters puts all the objects at similar starting points and they can compete fairly to group points in the input point sets. If we set r differently for each object based on the size of input boxes, it could be easily stuck to a local minimum that all the points are assigned to the largest object.

Transformations$\{\phi _{mn}\}_{m=1,n=1}^{M,N}=\{\mathbf {R}_{mn},\mathbf {t}_{mn}\}_{m=1,n=1}^{M,N}$: Since we have chosen spheres as the initial shapes, we can initialize all the $\mathbf {R}_{mn}$ to an identity matrix. For translations, we initialize them as $\mathbf {t}_{mn}=- \mathbf {c}_n$ so that all the object models start with position at the origin point when they are transformed to the space of each input set. However, if boxes are manually placed in the point set $\mathbf {V}_m$, we treat the associated $\mathbf {t}_{mn}$ differently:

$$\begin{aligned} \mathbf {t}_{mn}=\frac{\sum _{\mathbf {v}_{mi} \in B_n}\mathbf {v}_{mi}}{N(B_n)}-\mathbf {c}_n, \end{aligned}$$

(23)

where $N(B_n)$ here is the number of points enclosed by the manually placed boxes indicating object $O_n$.

Fig. 3

An example result when our algorithm converges to a local optimal with bad initialization. a The segmentation result in six point sets. The algorithm gets stuck at a local optimal wherein a part of the table and a part of the chair are segmented into one combined object. b The same result as a, but in the view of Gaussian centroids. It shows three groups of Gaussian centroids vertically arranged. Each row shows one group of Gaussian centroids representing one object. It shows that the chair and the table are not perfectly segmented

4.2 Layout constrained optimization

Our formulation inherits the disadvantage of easily getting stuck at a local optimal from the EM framework. Without further constraint, the EM framework usually fails to get a globally optimal solution. This is shown in Fig. 3 wherein the chair and the table are not perfectly segmented. To cope with this problem, we adopt the user placed boxes as soft constraints to guide the optimization and confine the shapes of generated object models. Such constraints are enforced by altering the posterior probability as

$$\begin{aligned} \alpha _{\mathrm{mik}}^*=\frac{\alpha _{\mathrm{mik}}\beta _{\mathrm{mik}}}{\sum _{i,k}\alpha _{\mathrm{mik}}\beta _{\mathrm{mik}}}, \end{aligned}$$

(24)

where $\beta _{\mathrm{mik}}$ is the prior probability according to the boxes, defined as:

$$\begin{aligned} \beta _{\mathrm{mik}}=\left\{ \begin{array}{ll} 1,&{}\quad \mathbf v_{mi} \in B_n\\ \exp \left( -\frac{\min _{\mathbf v_{mj}}|| \mathbf v_{mi} - \mathbf v_{mj} ||_2^2}{ 2r^2}\right) ,&{}\quad \mathbf v_{mi} \notin B_n~\hbox {and}~\mathbf v_{mj} \in B_n\\ \end{array} \right. \end{aligned}$$

(25)

where $B_n$ is a set of points that are enclosed by the boxes used to represent object $O_{n}$. $\min _{\mathbf {v}_{mj}}|| \mathbf {v}_{mi} - \mathbf {v}_{mj} ||_2^2$ is the minimum distance from a point $\mathbf {v}_{mi}$ to the points $\{\mathbf {v}_{mj}\}$ in object $O_n$. r is the median of the radius of input point sets. This alteration on posterior probability is only done for the points in the point set where boxes are manually placed.

Fig. 4

The convergence process of our algorithm. a Objective w.r.t. iteration number. The objective value is calculated according to (7). Note that the curve is not monotonic increasing, which makes it difficult to set a stop condition based on our objective. b Segmentation results of three points sets (12 point sets are used in total). Column “00” shows the input point sets and the initial Gaussian centroids, among which “B00” has two images: the left one is the input layout (boxes) which is only placed in the first point set. The column “01”–“08” shows result of segmentation (in row “B”–“D”) and Gaussian centroids (in row ”E”) at different iteration numbers q. The q is shown at top of each column. The row “A” shows highlighted areas of “B01”–“B08”

This alteration prevent object models from deforming into arbitrary shape. Figure 4 demonstrates the converging procedure with box constraints. We can see that with the boxes placed in one point set as constraints, our framework converges to a good segmentation result. The point sets are finally segmented to three objects, and the object models develop from an initial sphere shape at $q=1$ to a dense point cloud which fits the input point sets well. However, in Fig. 4a, the objective function is not monotonically increasing. This is due to our alteration on the posterior probability in Eq. (24). This alteration is quite a brutal solution to enforce the shape constraint, and it will interfere with the convergence of EM algorithms. This makes it difficult to set a stop criterion based on the objective value. We simply stop the iteration when the maximum iteration number $q_{\mathrm{max}}$ is reached.

As highlighted in Fig. 4b “A01”–“A08”, the segmentation in the first point set seldom changes until the last few iterations. This is due to the alteration in Eq. (24) as well. In order to constrain the object shape, we do alteration on the posterior probability of the point set where boxes are placed. This alteration is only done in $q_{\mathrm{alt}}$ iterations, as described in the step 4 in Algorithm 1. However, the initial segmentation based on the boxes is not accurate. Therefore, we no longer do such alteration in the last few iterations and let the algorithm to refine the segmentation based on the result of registration. We set $q_{\mathrm{alt}}=q_{\mathrm{max}}-10$ for all experiments in this paper.

For initialization and object shape constraint, the boxes are first roughly placed in one point set only. In more challenging cases, if the user is not satisfied with the segmentation and registration results, we also allow the user to add more box-shape constraints in different point sets to refine the results. The same alteration as Eq. (24) is performed in the optimization. We will discuss an example of such case later in Sect. 5.4.

5 Experiment and discussion

In this section, we will show a series of experimental results including evaluation for co-segmentation and joint registration on synthetic data for quantitative analysis, investigation on the robustness of our method on point completeness and amount of user interaction, and testing on one group of real data.

5.1 Synthetic data collection

We generate a group of synthetic datasets ( synthetic point sets) to quantitatively evaluate our algorithm. For each dataset, we model a 3D scene using object models from 3D Warehouse. We convert the mesh model of the scene into a point set using the Poisson sampling method [6]. Then, we manually move the objects according to their functions and generate multiple point sets.

5.2 Co-segmentation on synthetic data

Table 1 The means and standard deviations of IOU scores on two synthetic datasets

Fig. 5

Segmentation evaluations on two groups of synthetic data (study room and office desk). Three examples of point set from each group are shown

From the perspective of co-segmentation, we quantitatively evaluate our algorithm on two groups of synthetic data of indoor scenes. To estimate the power of the proposed algorithm, the interaction of placing boxes is only performed at one point set. No further interaction is required. For numerical estimation, we calculate the intersection over union (IOU) scores for the induced segmentation against the ground-truth segmentation. We compare our results with the state-of-the-art semantic segmentation method, PointNet [3], which trains a network using a large-scale database. Table 1 shows the numeric result, and Fig. 5 shows visual results of three input point sets including the one that is equipped with input layout. For the object class that is not annotated in the training data, PointNet [3] treats it as a special class of ”clutter” (the black points in Fig. 5). This is why we have different ground truth for our method and PointNet. As shown in Fig. 5, we have “GT” as ground truth used to evaluate our method and “GT for PointNet” as ground truth used to evaluate PointNet. Comparing our method to PointNet is not an exact fair comparison in the following aspects:

• 1. Our method allows user interaction, while PointNet is fully automatic in the test phase.

• 2. Our synthetic data are quite different from the data in Stanford 3D semantic parsing dataset [1], which is used to train the semantic segmentation network of PointNet.

• 3. Our method generates object-level segmentation without semantic label, while PointNet generates semantic labels.

However, by comparison, the generalization ability of current learning-based methods is still far from enough to be used as tool to prepare data and build dataset. The semantic segmentation method is limited to certain set of object classes (13 classes for PointNet) and cannot be used to carry on our task.

5.3 Joint registration on synthetic data

From the perspective of joint registration, we first evaluate the result by transferring the point cloud of objects to each input point set based on the estimated results $\{\phi _{mn}\}$ and calculating the average distance from a point to its true correspondent point for each input point set. We use this average distance as the fitness error to evaluate the registration quality with respect to each input set.

Table 2 Registration errors of the three groups of synthetic data in Fig. 5

Table 2 shows the evaluation results. The Maximum, Median and Minimum of the fitness error across input sets are reported. We find that even the input set with high IOU scores in segmentation can result in high fitness error. We believe this is due to the symmetric and near-symmetric objects in the scene. For symmetric objects, even if the registration is correct, the distance from one point to its true corresponding point may still be high. This distance is due to the fact that the registration result’s rotation may differ from the one used to generate the synthetic data. For near-symmetric objects, the registration often gets stuck in a local optimal and results in a high IOU score but a high fitness error. In Fig. 6, the registration of the round carpet is correct, but its point-wise correspondences do not follow an identity transformation due to its symmetry, while the shelf corner highlighted in the red rectangles is not correctly aligned and it gets stuck at a local minimum that maps its left part to the right part.

Fig. 6

Joint registration results on two scenes using two variants of our method. Point-wise correspondences are color-coded. The three rows show three point clouds captured at different times in the same scene, respectively. Columns A and B show results of JRCS-Basic and JRCS-Bilateral for study room. Columns C and D show results of JRCS-Basic and JRCS-Bilateral for the office desk

We then compare our method (JRCS-Basic) with [9] (JRMPC) on the synthetic point sets released by [9]. These data contain four point sets of Stanford Bunny with different noise and outliers. The experiment results in Table 3 and Fig. 7 show that our method generates similar results with [9] when dealing with a single object.

Table 3 RMSE of joint registration on 4 point sets of Stanford Bunny by two methods

Fig. 7

Joint registration results on 4 point sets of Stanford Bunny by JRMPC [9] (left) and our JRCS-Basic (right)

5.4 Amount of interaction

For parameter initialization and object shape constraint, we only need the user to input layout (boxes) in one of the input point sets. However, our algorithm sometimes gets stuck at a local minimum on handling non-local motion of objects. In such challenging cases, more user input is desired to further guide the optimization. Figure 8 shows how the IOU score increases along with the amount of interaction. In this experiment, we use JRCS-Basic. In Fig. 8, the Minimum IOU curve does not monotonically increase with the amount of manual input, which means more interaction does not guarantee improvement of the segmentation results in all point sets. When the initial correspondences in most point sets are far from correct, our method loses its ability to transfer the information among different point sets. The further interaction only improves the segmentation in the point set which the user adds layout into and barely improves the segmentation in other point sets. From Fig. 9, we can see that actually quite a lot of interactions are needed for the overall segmentation result to be visually satisfying for the dataset in this experiment.

Fig. 8

IOU scores of co-segmentation results based on different amount of user interaction. The X axis is the ratio: $x=\frac{\text {Input Box Number}}{\text {Total Object Number}}$. $x=1.0$ means that the user places one box for each object in all point sets

Fig. 9

Given the same input point sets, more accurate segmentation results can be obtained with more interaction. From left to right: 3 out of 16 input point sets, the ground-truth segmentation, our result when only one point set is equipped with manual input layout, and our result when 11 out of 16 point sets are equipped with manual input layout

5.5 Influence of point incompleteness

In the previous evaluations on the synthetic data, the point sets are sampled as the objects in the scene are completely covered. In this subsection, we investigate how the point set incompleteness affects the result of our algorithm. To test this, we pick a group of point sets and gradually remove certain percentage (0–30%) of points from each point set. Using a simple method to simulate the occlusion-induced point incompleteness, we generate the incomplete point sets with incompleteness of $p\%$ as follows:

• 1. Randomly pick one point from each complete point set.

• 2. For one point set, sort all points in ascending order according to their Euclidean distances to the picked point.

• 3. Remove the first $p\%$ points from the point set to generate a point set with incompleteness of $p\%$.

Figure 10 shows the IOU scores with three levels of incompleteness $p={0.0, 14.0, 30.0}$, and Fig. 11 shows the test data and segmentation results. Some objects in the scene are occluded severely, and over half of the points are missing (Fig. 11 A09-E09). Even with serious incompleteness on some objects, our algorithm converges to a relative good result.

Fig. 10

IOU scores of co-segmentation with different data incompleteness. The test data are partially shown in Fig. 11

Fig. 11

Experiments on data incompleteness. This figure shows results at three different levels of incompleteness which are 0.0% at row 01–04, 14% at row 05–08 and 30% at row 09–12. Each column shows the information of the same point set. Rows 01, 05, 09 show the inputs. Column A shows one point set and the manual input for initialization. The initial segmentation and final segmentation of this point set are shown in column A as well. Rows 02, 06, 10 are ground-truth segmentation. Rows 03, 07, 11 are our segmentation results. Rows 04, 08, 12 show the point-wise correspondences of joint registration by color-coding

Fig. 12

Common challenges in scanned data

Fig. 13

Segmentation and registration on the scanned data of a kid’s table. a Scanned mesh using method in voxel hashing [21]. b Remove walls and floors by plane fitting. c Sampled point set using [6]. d With roughly placed boxes on only one point set, the points are initially segmented in this one point set. Note that parts of the chair legs are segmented to the table due to the rough box placement by users. e Pairs of input point sets and corresponding segmentation results. f The final Gaussian centroids for the five objects in the scene. g Verification of the registration result by aligning all point sets with respect to each object in f. The light blue rectangle highlights the object that is aligned together. Except the aligned object, the other objects are placed quite messy since they came from different point sets and have different arrangement relative to the aligned object

5.6 Test on real data

To capture real data, we employ the voxel hashing method [21] and use plane fitting to remove walls and floors. The meshes are transferred into point sets using a Poisson sampling process [6]. Figure 12 shows a scanned point set, where we can see that, there are noised and blurred color, shape distortion, partial scanning and outliers in real data. Figure 13 shows the segmentation and registration results on a group of scanned point sets of a kid’s table. We use JRCS-Bilateral in this test, and Fig. 13d shows the only point set that is equipped with layout in this test. From Fig. 13e, we can see that all input point sets are partitioned into objects. In Fig. 13g, we align the point sets all together respective to each of the objects. There are four objects in the scene, so there are four different aligned results in Fig. 13g. The light blue rectangle highlights the object that is used to align the point sets. We can verify that the objects from each input set are aligned together by the result transformation. Figure 14 shows the results on another group of scanned point sets of an office desk.

Fig. 14

Segmentation and registration on the scanned data of an office desk. a Scanned mesh using method in [21]. b Remove walls and floors by plane fitting. c Sampled point set using [6]. d With roughly placed boxes on one point set, the points are initially segmented in this one point set. Note that parts of the chair legs are segmented to the table due to the rough box placement by users. e Pairs of input point sets and corresponding segmentation results. f The final Gaussian centroids for the nine objects in the scene. g Verification of the registration result by aligning all point sets with respect to each object in f. The light blue rectangle highlights the object that is aligned together. Except the aligned object, the other objects are placed quite messy since they came from different point sets and have different arrangement relative to the aligned object

5.7 Limitations and future work

With all the experiments above, we now summarize the limitations and discuss possible future directions of our work.

A major limitation holding us back is the time performance of our current implementation, which prevents us from going over more initialization and optimization strategies. For a group of 11 point sets with about 9K points in each point set, our current implementation will take about 110 min to run 100 iterations. Our algorithm could be sped up with a parallelized implementation in the future.

The requirement of human input is another major limitation, though our solution is already better than manually segmenting each point set. For this matter, we believe integrating learning-based method is necessary. However, a semantic segmentation method as [3] will lead to a loss of generality. It is better to lean on methods that predict general object boundaries, so that we could use them to initialize segmentation for general objects.

For now our method uses fused scanned data (the result of [21]) as input, it is more attempting to develop a method that accepts a set of single view scans as input and do joint registration and co-segmentation. To work on this direction, we need improve out current approach to handle much more severe data incompletion respecting to each object.

6 Conclusion

For the challenging problem of point set joint registration and co-segmentation, we come up with a formulation that simultaneously models the two entangled subproblems. For the difficult initialization and optimization of this formulation, we provide a strategy that leans on a few manual inputs. In the evaluation, we thoroughly investigate the performance of our algorithm. Our algorithm presents a series of successful cases on both synthetic and real data. We also summarize the limitations of the current solution and discuss possible future solutions for these issues.