1 Introduction

Metal additive manufacturing (AM) is an advanced fabrication technology broadly applied in industry because of its ability to produce complex structural components [1, 2]. Directed energy deposition (DED) is one of the most promising AM techniques due to its high deposition efficiency suitable for manufacturing large-scale components [3]. However, AM is a complicated multi-physics and multi-scale process characterized by several thermal cycles with large temperature gradients as well as melting and solidification phase changes. As a consequence, AM-built products typically show non-uniform microstructure distribution, large residual stresses, thermal distortions, cracks and unsatisfactory mechanical properties [4,5,6,7,8,9,10]. Such drawbacks significantly prevent the extensive application of AM technologies in high-end manufacturing industry.

Taking into account the large number of variables (process parameters, material data, etc.) involved in AM, the use of numerical methods is generally employed to optimize the AM process. To date, several numerical models for AM have been developed to investigate the thermal, mechanical and microstructure evolutions [9,10,11,12,13]. Among them, Smith et al. [11] utilized the FE simulation coupled with the computational phase diagram thermodynamics to predict both the thermo-mechanical and the microstructural behavior. Denlinger et al. [12] developed a FE model to simulate the thermo-mechanical responses of Ti–6Al–4V and Inconel® 625 during DED; they found that only in Ti–6Al–4V it is possible to reduce both residual stress and distortion induced by solid-state phase-transformation (SSPT). Furthermore, Wang et al. [13] utilized compression tests at 600 °C and 700 °C with in-situ neutron diffraction analysis to investigate the stress relief of Ti-6Al-4V using AM and conventional processing; their results showed that stresses are faster relaxed with the temperature rise.

The influence of different AM variables is investigated to try to reduce both residual stresses and part warpage [14,15,16,17,18,19]. In this sense, Mukherjee et al. [14] illustrated that the part warpage is dependent on the scanning strategy, the preheating and cooling conditions, the material properties and the printing parameters. Usually, residual stresses and warpage can be mitigated by preheating the substrate before AM, optimizing the deposition sequence and/or the process parameters [15,16,17]. It must be noted that the effect of different AM variables on the material behavior is not fully understood yet, especially for large-scale AM parts adopting complex scanning sequences.

On the other hand, the homogenization of the final microstructure is also a challenge in AM because of the temperature histories experienced at any location of the AM builds [20,21,22]. For instance, the lower part of the builds often undergoes a larger number of subsequent thermal cycles during the DED process than the top of the metal deposition. Consequently, the microstructure initially formed is generally coarsened and the martensitic phase (α′ in AM titanium alloy) is decomposed because of an intrinsic heat treatment (IHT) [21, 22]. In addition, AM titanium alloys also present regularly distributed layer-bands along the building direction [23]. By modifying the scanning patterns (i.e. the induced thermal history), it is possible to tailor the microstructure and, thus, the final material properties. Kürnsteiner et al. [24] demonstrated that adopting a periodic interlayer dwell-time produce martensite and, thus, the yield strength and ductility of a maraging steel by DED can be increased.

Generally, most of the reported studies are focused on either the microstructural control or the reduction of residual stresses and part warpage. Controlling both of them is a complex task even if it is mandatory to satisfy the fabrication requirements for high-quality AM parts. Thus, the main objective of this work is to propose a fabrication strategy able to deal with both issues: the mitigation of the residual stresses and the homogenization of the resulting microstructure. In AM, this can be achieved by optimizing the temperature field and its evolution during the printing process allowing for the IHT effect on the microstructural transformation and stress relaxation.

It has been also observed that the mechanical response of the AM builds is closely related to the mechanical constraining with the baseplate. This is especially true when large/thick baseplate are utilized to avoid the part warpage. Nevertheless, such rigid baseplates easily yield high residual stresses that transform into part-distortion after the baseplate removal [9]. Therefore, the optimization of the baseplate stiffness is key to mitigate residual stresses and warpage. Figure 1 presents the diagram for the simultaneous control of residual stresses and microstructure evolution by optimizing both the temperature histories (i.e. thermal cycles) and the mechanical constraints (baseplate geometry) during DED processes.

Fig. 1
figure 1

Concurring control of residual stress and microstructure in AM

Full size image

To this end, an in-house 3D thermo-mechanical FE model is first calibrated adopting in-situ temperature and displacement measurements from two part-scale Ti–6Al–4V blocks by DED. Next, the validated model is employed to investigate the influence of the baseplate size and the laser energy density on the thermal, metallurgical and mechanical responses. Finally, two strategies are proposed to effectively reduce both the stress accumulation and the microstructural coarsening in DED components: (i) the use of a forced cooling suitable for small baseplates and, (ii) the adoption of grooves when large baseplates are used.

2 Experimental campaign

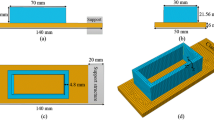
Until now, the influence of the processes parameters on AM process has been often reported, while the effect of the baseplate size has seldom been studied. Thereby, two baseplates annealed Ti–6Al–4V of different sizes and, thus, characterized by different heat-retaining capability and structural stiffness were investigated to assess their respective thermomechanical behavior. As shown in Fig. 2, the larger baseplate (200 × 100 × 25 mm3) is fixed as a cantilever while the smaller one (140 × 50 × 6 mm3) is clamped at both ends because of its reduced bending stiffness. These two baseplates are used to manufacture the same multi-layer multi-pass blocks by DED technology. The DED system used consists of a semiconductor laser diode with a maximum output power of 6 kW, a five-axis numerical control workbench, a DPSF-2 high-accuracy adjustable automatic power feeder and an argon purged processing chamber with very low oxygen content. The material used to deposit the blocks is spherical Ti–6Al–4V powder with 53–325 μm diameter and low oxygen, produced by a plasma electrode process. The powder is dried in a vacuum oven at 125 °C for 3 h before the DED.

Fig. 2
figure 2

Experimental equipment of in-situ temperature and displacement measurement during the DED process: a the large baseplate is clamped as a cantilever, b the small baseplate is fixed at both ends

Full size image

Figure 3 shows the baseplates and the corresponding location of both the thermocouples (TC1–TC6) and the displacement sensors (DS1–DS2) used to record the temperature and displacement evolutions of the bottom surface of the baseplates, respectively. Six Omaga GG-K-30 type thermocouples with a measurement uncertainty of 2.2 °C (± 7.5%) and two WXXY PM11-R1-20L displacement sensors with a maximum range of 20 mm and an accuracy of 0.02% were employed. All the temperature and displacement signals during the DED process are recorded via a Graphtec GL-900 8 high-speed data-logger.

Fig. 3
figure 3

Part sizes and the locations of the six thermocouples (TC1–TC6) and two displacement sensors (DS1–DS2) on the bottom surface of the baseplates

Full size image

Figure 4 shows the printing path defined by four different sequences repeated every 4-layers. Table 1 displays the DED process parameters. Case-1 setting is used to fabricate two 40-layers blocks with the same dimension of 125 × 35 × 20 mm3. The other settings in Table 1 are used for the sensitivity analysis of the volumetric energy density, \(E=P/\left(\mathrm{VHD}\right)\), on the thermo-metallurgical-mechanical responses.

Fig. 4
figure 4

Schematic of scanning strategy used to build the two blocks

Full size image
Table 1 DED processing parameters utilized for printing the blocks
Full size table

To examine the microstructure, the samples extracted from the mid-YZ plane are firstly etched using Kroll’s solution (1 ml HF, 3 ml HNO3 and 46 ml H2O) and then featured by optical microscopy (Keyence VH-Z50L). Next, the α-lath width is measured from 5 photographs with a magnification of 2000. In each case the number of measures is higher than 100. Finally, the average value of the α-lath size is calculated. Additionally, the Vickers hardness corresponding to the above microstructure is tested using a Duranmin-A300 micro-hardness tester with a load of 2000 g and an acting time of 15 s. Twenty different points are chosen to measure the mean hardness at each position.

3 Numerical simulation

In this work, an in-house 3D thermo-mechanical FE software, COMET, is used to perform high-fidelity modelling of the AM process. The sequential thermo-mechanical coupling is undertaken as follows: (i) for each time-step, the transient thermal analysis is firstly carried out; next (ii) the stress analysis is solved adopting to the obtained thermal field. The details of this thermo-mechanical model in terms of both the governing equations and the constitutive laws can be found in previous works [25,26,27].

3.1 Thermal analysis for AM

The governing equation for the transient thermal analysis is the balance of energy equation:

$$\dot{H}=-\nabla \cdot \mathbf{q}+\dot{Q},$$
(1)

where \(\dot{H}\) and \(\dot{Q}\) are the enthalpy rate and the heat source (per unit of volume), respectively. The latter is defined in terms of the total laser input, \(\dot{P}\), the laser absorption efficiency, \({\eta }_{\mathrm{p}}\), and the volume of the melt pool, \({V}_{\mathrm{pool}}^{\Delta t}\), as:

$$\dot{Q}=\frac{{\eta }_{\mathrm{p}}\dot{P}}{{V}_{\mathrm{pool}}^{\Delta t}}.$$
(2)

The heat flux \(\mathbf{q}\) is defined according to Fourier’s law

$$\mathbf{q}=-k\nabla T,$$
(3)

where \(k\) and \(\nabla T\) are the (temperature-dependent) thermal conductivity and the thermal gradient, respectively.

The heat dissipation due to convection is defined through Newton’s law:

$${q}_{\mathrm{conv}}={h}_{c\mathrm{onv}}\left(T-{T}_{\mathrm{room}}\right),$$
(4)

where \({h}_{\mathrm{conv}}\) is the convective Heat Transfer Coefficient (HTC), \(T\) is the surface temperature of the workpiece and \({T}_{\mathrm{room}}\) is the room temperature.

The heat loss by the radiation, \({q}_{\mathrm{rad}}\), is computed by Stefan-Boltzmann’s law:

$${q}_{\mathrm{rad}}={\varepsilon }_{\mathrm{rad}}{\sigma }_{\mathrm{rad}}\left({T}^{4}-{T}_{\mathrm{room}}^{4}\right),$$
(5)

where \({\varepsilon }_{\mathrm{rad}}\) and \({\sigma }_{\mathrm{rad}}\) are the surface emissivity and the Stefan–Boltzmann constant, respectively.

3.2 Mechanical analysis

The stress analysis is governed by the balance of momentum and the continuity equations:

$$\nabla \cdot \mathbf{s}+\nabla p+\mathbf{b}=0,$$
(6)
$$\left(\nabla \cdot \mathbf{u}-{e}^{T}\right)-\frac{p}{K}=0,$$
(7)

where the Cauchy stress tensor \({\varvec{\sigma}}\) is split into its spherical (pressure) \(p\) and deviatoric \(\mathbf{s}\) parts, respectively, as:

$${\varvec{\sigma}}=p{\varvec{I}}+ \mathbf{s}\left(\mathbf{u}\right),$$
(8)

\(\mathbf{b}\) and \(K(T)\) are the body force (per unit of volume) and the (temperature-dependent) bulk modulus, respectively. The thermal deformation \({e}^{\mathrm{T}}\) is determined as

$${e}^{\mathrm{T}}\left(T,{f}_{S}\right)={e}^{\mathrm{cool}}\left(T\right)+{e}^{\mathrm{pc}}\left({f}_{\mathrm{S}}\right),$$
(9)

where \({e}^{\mathrm{cool}}\left(T\right)\) and \({e}^{\mathrm{pc}}({f}_{\mathrm{S}})\) are the thermal expansion/contraction and thermal shrinkage in the liquid-to-solid phase transformation, as a function of the initial temperature \({T}_{0}\) and the solid fraction \({f}_{\mathrm{S}}\), respectively and expressed as

$${e}^{\mathrm{cool}}\left(T\right)=\alpha \left(T\right)\left(T-{T}_{0}\right),$$
(10)
$${e}^{\mathrm{pc}}\left({f}_{\mathrm{S}}\right)=\beta {f}_{\mathrm{S}},$$
(11)

where \(\alpha\) and \(\beta\) are the (temperature-dependent) thermal expansion and the shrinkage coefficients, respectively.

Note that the mechanical problem defined by Eqs. (6), (7) is dependent on both the displacement \(\mathbf{u}\) and the pressure field \(p\), and it is suitable for both compressible and the fully incompressible (isochoric) material behavior.

In AM, the temperature fluctuates between \({T}_{\mathrm{room}}\) and temperatures above the melting point (\({T}_{\mathrm{melt}}\)). Thus, the materials must be featured in its solid, mushy and liquid phases.

A J2-thermo-elasto-visco-plastic model is adopted in the solid phase, thus from \({T}_{\mathrm{room}}\) to the annealing temperature \({T}_{\mathrm{anneal}}\). All the material properties are assumed as temperature-dependent. The von-Mises yield surface is determined as

$$\Phi \left(\mathbf{s},{q}_{\mathrm{h}},T\right)=\Vert \mathbf{s}\Vert -\sqrt{\frac{2}{3}} \left[{\sigma }_{\mathrm{y}}\left(T\right)-{q}_{\mathrm{h}}\right],$$
(12)

where \({\sigma }_{y}\) is the (temperature-dependent) yield stress accounting for the thermal softening while \({q}_{\mathrm{h}}\) is the stress-like variable controlling the isotropic strain-hardening, defined as

$${q}_{\mathrm{h}}\left(\xi ,T\right)=-\left[{\sigma }_{\infty }\left(T\right)-{\sigma }_{\mathrm{y}}\left(T\right)\right]\left[1-{e}^{-\delta \left(T\right)\xi }\right]-h\left(T\right)\xi ,$$
(13)

where \(\xi\) and \({\sigma }_{\infty }\) are the isotropic strain-hardening variable and the (temperature-dependent) saturation flow stress, respectively, while \(\delta\) and \(h\) are the (temperature-dependent) parameters to model the exponential and linear hardening laws, respectively.

The deviatoric counterpart of Cauchy’s stress tensor is expressed as

$$\mathbf{s}=2G\left(\mathbf{e}-{\mathbf{e}}^{\mathrm{vp}}\right),$$
(14)

where \(G\) is the (temperature-dependent) shear modulus, while \(\mathbf{e}\) and \({\mathbf{e}}^{\mathrm{vp}}\) are the total (deviatoric) strain and the visco-plastic strain, respectively. The former is obtained from the total strain tensor \({\varvec{\varepsilon}}\left(\mathbf{u}\right)={\nabla }^{\mathrm{sym}}\left(\mathbf{u}\right)\), while the evolution laws of both the visco-plastic strain tensor and the isotropic strain-hardening variable are obtained from the principle of maximum plastic dissipation as

$${\dot{\mathbf{e}}}^{\mathrm{vp}}={\dot{\gamma }}^{\mathrm{vp}}\frac{\partial \Phi \left(\mathbf{s},{q}_{\mathrm{h}}\right)}{\partial \mathbf{s}}={\dot{\gamma }}^{\mathrm{vp}}\frac{\mathbf{s}}{\| \mathbf{s}\| }={\dot{\gamma }}^{\mathrm{vp}}\mathbf{n},$$
(15)
$$\dot{\xi }={\dot{\gamma }}^{\mathrm{vp}}\frac{\partial \Phi \left(\mathbf{s},{q}_{\mathrm{h}}\right)}{\partial {q}_{\mathrm{h}}}=\sqrt{\frac{2}{3}} {\dot{\gamma }}^{\mathrm{vp}},$$
(16)

where \(\mathbf{n}\) stands for the normal to the yield surface, and \({\dot{\gamma }}^{\mathrm{vp}}\) is the visco-plastic multiplier, expressed as.

$${\dot{\gamma }}^{\mathrm{vp}}={\left\langle \frac{\partial \Phi \left(\mathbf{s},{q}_{\mathrm{h}}\right)}{\eta }\right\rangle }^\frac{1}{m},$$
(17)

where \(\langle \dot \rangle\) is the Macaulay bracket, while \(m\) and \(\eta\) are the temperature-dependent rate sensitivity and plastic viscosity, respectively.

Note that, when the temperature gets close to \({T}_{\mathrm{anneal}}\), the yield limit \({\sigma }_{\mathrm{y}}\) tends to 0. Thereby, the deviatoric Cauchy stress reduces to

$$\mathbf{s}=\eta {\left({\dot{\gamma }}^{\mathrm{vp}}\right)}^{m}\mathbf{n}={\eta }_{\mathrm{eff}}{\dot{\mathbf{e}}}^{\mathrm{vp}},$$
(18)

where \({\eta }_{\mathrm{eff}}=\eta {\left({\dot{\gamma }}^{\mathrm{vp}}\right)}^{m-1}\) is the effective viscosity. Thus, above \({T}_{\mathrm{anneal}}\) the material is featured by a purely viscous law [28]. A non-Newtonian behavior with \(m>1\) is adopted for the mushy phase (from \({T}_{\mathrm{anneal}}\) to \({T}_{\mathrm{melt}}\)), while a Newtonian law, \(m=1\), features the liquid phase (for \({T>T}_{\mathrm{melt}}\)).

3.3 FE modelling of AM

To model the advance of the AM process, a time discretization procedure is needed. The time-marching scheme is characterized by a time step, \(\Delta t={t}^{n+1}-{t}^{n}\). Thereby, the melt pool is allowed to move step-by-step according to the printing pattern from the current location defined at time \({t}^{n}\) to that at time \({t}^{n+1}\). Within this interval, the heat is input to the elements belonging to the melt-pool volume and, at the same time, the feeding powder conforms the AM deposit.

Hereby, the software parses the same input file (CLI format) following the actual building sequence as adopted to inform the AM printer. The birth–death-element technique is utilized to activate the elements corresponding to each new layer. Therefore, the numerical strategy for the AM process requires an ad-hoc procedure to categorize the elements into: active, inactive and activated elements. At each time step, an octree-based searching algorithm is employed to search the elements belonging to the melt pool (active) and to the new deposit (activated). The current computational domain consists of both active and activated elements, while the inactive elements are neither assembled nor computed into the global matrix of the analysis [29].

3.4 Geometrical model and mesh generation

In this work, the generation of the CAD geometries and the FE meshing, as well as the results post-processing are carried out through the pre–post-processor GiD [30]. Figure 5 presents different 3D geometries of DED parts and the corresponding generated meshes. Figure 5a, b show the same multi-layer multi-pass block deposited on the large and small baseplates, respectively. Figure 5c depicts an optimized baseplate with some grooves to control the stress development. Table 2 summarizes the geometrical dimensions of all the samples shown in Fig. 5 and the corresponding numbers of elements and nodes. According to the mesh convergence investigations [16], the mesh size is set to 1.25 × 1.25 × 0.5 mm3 for the build, while a coarser mesh is used for the baseplate, balancing the computing cost and an acceptable simulation accuracy.

Fig. 5
figure 5

3D FE meshes of the blocks deposited on the: a large baseplate, b small baseplate, c large baseplate with grooves

Full size image
Table 2 Baseplate dimensions and the numbers of FE elements and nodes
Full size table

3.5 Material properties and boundary conditions

Table 3 shows the values of the temperature-dependent thermal and mechanical properties of Ti–6Al–4V titanium alloy used for the material characterization of both the metal depositions and the baseplates in all the numerical predictions [9]. A higher heat conductivity of 83.5 W/(m °C) is assumed when the temperatures is above \({T}_{\mathrm{melt}}\), to account for the convective flow inside the melt pool [31].

Table 3 Temperature-dependent material properties of Ti–6Al–4V [8]
Full size table

The heat transfer by convection and radiation between the DED parts and the surrounding is considered for all the free surfaces of the workpiece. The calibrated value of the HTC by convection and emissivity are hconv = 5 W/m2 °C and \({\varepsilon }_{\mathrm{rad}}=0.45\), respectively. Also, an HTC of 40 W/(m2 °C) is adopted to account for the heat conduction at the interface between the fixture and the baseplate. The room temperature, Troom = 25 °C, is assumed for all thermal analyses. The laser efficiency is set as \(\eta =0.37\).

4 Calibration of the thermo-mechanical FE model

In previous works, the coupled thermomechanical model adopted was validated to optimize both material properties and processing parameters for the AM analysis with Ti–6Al–4V [7]. Here, to guarantee the accuracy of the simulation, the FE model is calibrated by in-situ temperature and displacement measurements. Figure 6 compares the predicted and experimental temperature histories at different points (see Fig. 3). Note that a remarkable agreement between numerical (dash lines) and experimental (solid lines) results is achieved, as reported in reference [21]. Also, the average numerical error during the entire processing is calculated, resulting in less than 3% for each thermocouple.

Fig. 6
figure 6

Comparison between the predicted and measured temperature histories at the bottom of a the large baseplate, b the small baseplate

Full size image

Based on this calibrated thermal model, the mechanical response induced by the DED process is predicted by the fully coupled thermo-mechanical analysis. To assess the model precision, Fig. 7 compares the computed and measured vertical displacements of points DS1 and DS2 at the baseplate bottom along the deposition direction. Also in this case, the numerical results agree with the experimental evidence. A slight discrepancy is due to the simplification of the boundary conditions used and the possible experimental uncertainties.

Fig. 7
figure 7

Large baseplate comparison between the simulated and the experimental results of the vertical displacement of points DS1 and DS2 at the bottom of the baseplate

Full size image

5 Thermo-metallurgical–mechanical responses

In this section, the baseplate size and the sensitivity to the energy density input are analyzed in terms of thermal, metallurgical and mechanical responses during the AM process. Thereby, their influence is evaluated to deepen the understanding of AM processes and to improve the metal printing process.

5.1 Effect of the baseplate size

First, the evolution of the temperature field for two different baseplates is simulated and shown in Fig. 8. Note that when the laser beam crosses the center of the building region during the fabrication of the 1st layer, the large baseplate yields sharp thermal gradients (up to 8E + 6 °C/m) around the melt pool, while the maximum thermal gradient is lower than 5E + 5 °C/m for the small baseplate. After finishing the deposition of the 2nd layer, the average temperature of the small baseplate reaches about 800 °C, but it is less than 400 °C for the larger one. During the subsequent printing process (3rd–40th layers), the small baseplate holds the high-temperature field (Fig. 6b). However, the heat is slowly accumulated in the larger baseplate during the initial building stage and the quasi-steady state occurs after completing the deposition of more than 10 layers when the temperature field is of approximately 500 °C (Fig. 8a). Thus, the level of the heat accumulation is closely related with the baseplate size.

Fig. 8
figure 8

Temperature filed evolution in DED process in the cases of a the large baseplate, b the small baseplate

Full size image

The microstructure and the microhardness at different building heights of the two manufactured blocks are shown in Fig. 9. Figure 9a schematically presents the locations of interest. Figure 9b, c show the microstructures and the statistically averaged values in terms of α-lath width and the corresponding microhardness. Observe that the large baseplate achieves a relatively homogenous microstructural distribution (\(\overline{{W }_{\alpha }}\approx 1.15 \, \mathrm{\mu m}\)) and a consistent microhardness (\(\overline{H}\approx 330 \, \mathrm{ HV }\)) along the building direction. This is not the case for the small baseplate, in which the α-lath at the lower part of the build experiences a remarkable coarsening by IHT (\({W}_{\alpha }=2.21\pm 0.27 \, \mathrm{\mu m}\)) due to the high-temperature field which is above α dissolution temperature \({T}_{\mathrm{diss}}=747 \, ^\circ \mathrm{C}\) [23] (see Fig. 8b). As a result, the related microhardness decreases to about \(H=266\pm 8 \, \mathrm{ HV}\) (Fig. 9c). This is because by increasing the particle (α-lath) size the amount of sub-structure boundaries is reduced and, thus, hinders the dislocation slipping as the material deforms under loading. Therefore, the large baseplate is preferable from the metallurgical point of view.

Fig. 9
figure 9

Comparison of the metallurgical response at different deposit heights for different baseplates: a locations of interest, b microstructure images, c α-lath width and the microhardness as a function of the deposition height

Full size image

Finally, the evolution of the stress field is analyzed for the two baseplates. Figure 10 shows the development of the von Mises stresses in the case of the large baseplate. Observe that during the printing of the 1st layer, the large thermal gradients lead to high thermal stress of approximately 700 MPa as the metal deposition cools down and shrinks. The deposition of the 2nd layer uses the shorter scan pattern which favors the heat concentration (Fig. 8a), relaxing the large stresses previously triggered, down to about 300 MPa (Fig. 10c, d). Nevertheless, the stresses resurge up to 500 MPa when the longer scan pattern is used to print the 3rd layer. This proves how reducing the scan length can mitigate residual stresses of AM parts, as reported in the literature [17, 32]. As the number of deposited layer increases, the stresses of the build gradually decrease because the overall temperature is higher and the temperature gradients are lower (Fig. 8a). When the buildup is finished, the maximum residual stresses appear at the build–baseplate interface, especially at the corners where the material suffers the highest thermal gradients and the strongest mechanical constraining from the baseplate. Figure 10j shows some details of the residual stress field for the large baseplate. Note that the tensile stresses in all the three directions are higher than to 700 MPa at the basement of the build, while the compressive stresses (above 250 MPa) exist at the upper part of the baseplate beneath the deposit. Such stress distribution is quite typical as reported in the literature [12, 33].

Fig. 10
figure 10

Large baseplate: a–i the evolution of Von Mises stress field, j the inside residual stresses in the three components

Full size image

Figure 11 shows the evolution of the von Mises stresses when the small baseplate is used. Unlike the large baseplate, the small one achieves a pronounced stress reduction as the first two layers are built. During the subsequent printing process, the stresses in the part are lower than 150 MPa. Two reasons can justify this stress-relief: the weaker stiffness and the higher heat accumulation (annealing) in this baseplate (Fig. 8b). Hence, the small baseplate favors the stress mitigation in spite of yielding microstructural inhomogeneity.

Fig. 11
figure 11

Small baseplate: the evolution of the von Mises stress field in DED process

Full size image

Finally, Fig. 12 displays the part warpage at the end of the AM process for the two different baseplates. Observe that the maximum displacements of the blocks manufactured on the large and small baseplates are approximately 0.9 mm at the free end and about 0.6 mm at the deposition top, respectively.

Fig. 12
figure 12

Final distortion (displacement norm) for a the large baseplate, b the small baseplate

Full size image

5.2 Effect of the energy density

To mitigate the residual stress, especially for a thicker baseplate characterized by a higher stiffness, it is possible to play with the process parameters [34,35,36,37]. Thus, the influence of different input energy densities E (see Table 1) on the mechanical behavior of large-scale AM blocks is studied in this section.

Figures 13 and 14 show the thermo-mechanical evolution in terms of temperature, thermal gradient and von Mises stresses at the center (point P) and corner (point Q) of the deposits, respectively. Note that as E increases, the thermal gradients rise during the deposition of the first few layers, while all of them reduce to a lower level (< 5E + 4 °C/m) in the second half of the building process due to increased heat accumulation. On the one hand, higher energy density E tends to produce larger thermal stresses; but, on the other hand, favors the stress mitigation by annealing because of the elevated-temperature over a long duration of time. Especially at the center of the block, the residual stress level reduces from 340 MPa for \(E=27 \, \mathrm{J}/{\mathrm{mm}}^{3}\) to 70 MPa for \(E=80 \, \mathrm{J}/{\mathrm{mm}}^{3}\) (see Fig. 13). Unlike the center, during the DED process the stresses notoriously fluctuate at the corner, where higher cooling rates exist. Notably, higher E promotes the stress relief during the printing process, but triggers remarkable stress increments in the final cooling stage, and consequently, the residual stresses at point Q are very similar (495–545 MPa) for different E (see Fig. 14). Note that the thermo-mechanical behaviors for the two points are not the same even for the same E (see Figs. 13c, d and 14c, d). The reason for this is that the cooling time varies when using different scanning speeds, influencing the level of the heat accumulation and the stress annealing.

Fig. 13
figure 13

Evolution of temperature, von Mises stress and temperature gradient at point P at the center/bottom of the blocks for different energy densities

Full size image
Fig. 14
figure 14

Evolution of temperature, von Mises stress and temperature gradient at point Q at the corner/bottom of the blocks for different energy densities

Full size image

Figure 15a shows the residual von Mises stress fields for different energy densities E. Increasing E reduces the stress accumulation at the basement of the large blocks due to the stress annealing. This is not the case for small AM parts that do not experience annealing temperatures [38, 39]. Figure 15b, c show the displacement field and the evolution of the vertical displacement at point M at the free end of the baseplate, respectively. It can be seen from Fig. 15b that the smallest E leads to the largest displacement whereas the smallest value appears in the case of the moderate \(E=53 \, \mathrm{J}/{\mathrm{mm}}^{3}\). Such result can be explained as follows: increasing E, the displacements significantly grow in the initial deposition phase (Fig. 15c) due to the high thermal gradients (see Fig. 13). During the subsequent building process, the displacements gradually increase for \(E=27 \, \mathrm{J}/{\mathrm{mm}}^{3}\), but reduces for E = 80 J/mm3. In the final cooling process, higher E results in a larger displacement, up to 0.674 mm for E = 80 J/mm3 (\(V=15 \,\mathrm{ mm}/\mathrm{s}\)), increasing the final warpage. Even though the residual stresses are mitigated by rising E, they are still high at the build–baseplate interface. Thus, the optimization of process parameters alone has a limited effect for controlling the residual stress in DED.

Fig. 15
figure 15

Mechanical response of the blocks for different energy densities: a residual von Mises stresses, b final vertical displacement distribution, c evolution of vertical displacement of point M at the free end of the baseplate

Full size image

6 Strategies for the concurrent control of microstructure and residual stresses

As concluded above, the small baseplate favors the reduction of the residual stresses but causes a non-uniform microstructure, and contrariwise for the large one. To achieve the control of both the residual stresses and the metallurgical quality, two strategies are proposed in the following, based on the thermo-mechanical response of the two baseplates used.

6.1 Structural optimization of the thick baseplates

Using a thick baseplate, a better homogeneity of the final metallurgy can be guaranteed in DED because of the high heat absorption which allows for a fast cooling of the melt pool. Thereby, only the mechanical response is analyzed in this section. Particularly, to mitigate the residual stresses due to the strong constraining (stiff baseplate) of the AM-build, several grooves are added in the baseplates, as shown in Fig. 16.

Fig. 16
figure 16

Baseplates with different groove settings

Full size image

Two types of groove settings are analyzed: the first proposal assumes the division of the baseplate into different smaller 1 × 4, 2 × 7 and 3 × 10 regions, respectively, with a uniform cutting depth of 10 mm. A second proposal considers an increasing cut depth of 5 mm, 10 mm and 15 mm, respectively, for a fix baseplate division into 3 × 10 regions.

In both cases, the two ends of all baseplates are clamped.

Figures 17a and 18a show the contour fills of residual von Mises stresses and the stress distributions at the deposit-baseplate interface for different baseplate structures, respectively. Observe that the original residual stresses, up to about 640 MPa of the reference configuration, are systematically mitigated by adding the grooves and especially at the block-baseplate interface. By increasing the layout density or the cut depth of the grooves, the residual stresses gradually reduce because of the higher flexibility of the baseplate. Note that increasing the cut depth results in a more pronounced influence on the residual stresses mitigation than increasing the density of the groves pattern. Notably, the residual stresses for a cut depth of 15 mm are the lowest. The stress value is further reduced after the baseplate removal.

Fig. 17
figure 17

Stress analysis of the AM-blocks deposited on different baseplate structures: a residual von Mises stresses, b displacement norm

Full size image
Fig. 18
figure 18

Distributions of a the residual von Mises stresses along the AB line at the baseplate top, b the final distortions (displacement norm) along the CD line at the deposit top

Full size image

Figures 17b and 18b display the final displacements contour fills and the displacement evolution on the top surface of the baseplate for different baseplate geometries. It can be observed the clear mitigation of the residual stresses compared to the reference configuration as well as the sensitivity to both the grooves density and the cutting depth.

6.2 Forced cooling for the thin baseplate

When adopting a thin baseplate, the heat accumulation during the DED process allows for the microstructural coarsening. Moreover, the reduced stiffness of the support induces lower residual stresses. Hence, the proposed strategy consists of using a forced cooling to increase the heat loss (see Fig. 19a).

Fig. 19
figure 19

Forced cooling used to control the heat accumulation in the block: a experimental setup, b CAD geometrical models

Full size image

Highly purified argon with a flow rate of 50 L/min is used as cooling gas. Figure 19b shows the corresponding CAD models used in the simulation. The forced cooling is modelled assuming an increased HTC by convection of 95 W/(m2 °C) at the bottom surface of the baseplate.

Figure 20a compares the in-situ measurements and temperature evolution as predicted by the thermal analysis at point N, located at the bottom/center of the baseplate 1 (see Fig. 19b). A remarkable agreement between them is obtained.

Fig. 20
figure 20

a Comparison between the measured and numerical thermal histories of point N at the bottom/center of the baseplate, b comparison of the temperature evolutions at the bottom/center of the blocks printed on the large and thin baseplates

Full size image

Based on this calibration, the thermal model is used to predict the temperature evolution at the bottom/center of the blocks (see Fig. 9a) for the thick and the thin baseplates, respectively, as shown Fig. 20b. Note that: (i) for AM Ti–6Al–4V, the microstructures formed in the initial stage can be wiped out if the subsequent temperature field is above the β-transus temperature (\({T}_{\beta }\approx 1000 \, ^\circ \mathrm{C}\)); and (ii) the α structures do not change (freezed) once the temperature is kept below \({T}_{\mathrm{diss}}\) [23]. Thereby, only the thermal cycles in the yellow region are responsible for the final microstructural characterization. Thus, by applying the forced cooling to the thin baseplate it is possible to obtain a microstructure very similar to the one of the large baseplate.

In our previous work [21], an Integral Area (IA) index (the area colored in green in Fig. 20b) has been proposed to assess the α coarsening during DED process. The calculated IA are 1.11E + 5 °C s for the large baseplate (Fig. 5a) and 1.18E + 5 °C s for the thin baseplate with forced cooling, respectively. Such values are much lower than 1.19E + 6 °C s when the forced cooling is not adopted (see Fig. 9b). Hence, the forced cooling limits the microstructural coarsening induced by IHT during the whole printing process. Figure 21 shows the microstructures at different printing heights at the center of the block over the thin baseplate 1. Remarkably, a homogenous microstructural distribution is achieved, and the average width of α-lamellar is \(\overline{{W }_{\alpha }}\approx 1.12 \, \mathrm{ \mu m}\), similar to the one (\(\overline{{W }_{\alpha }}\approx 1.15 \, \mathrm{ \mu m}\)) observed in the case of the large baseplate (see Fig. 9b).

Fig. 21
figure 21

Microstructures at different building heights in the center of the block deposited on the thin baseplate 1 with forced cooling

Full size image

Figure 22a shows the residual stress field of the block printed on the thin baseplate 1 (see Fig. 19b) with forced cooling. Observe that the basement near the clamp presents high residual stresses (up to 500 MPa) while the stress values in the inner zone are smaller. This is because after printing the last layer, the metal deposition quickly cools and shrinks but such contraction is constrained by the baseplate clamping. Figure 22b, c show the predicted vertical displacement and the corresponding experimental result. It can be seen that a longitudinal bending is produced, leading to an unacceptable deformation (up to 1.4 mm) at the bottom/middle of the fabricated block.

Fig. 22
figure 22

Thin baseplate-1 with forced cooling: simulated results of a the residual stress field and b the vertical displacements of the block part before releasing the clamping, c experimental result of distortion after releasing the clamping

Full size image

To reduce this distortion, the geometry of the baseplate is further optimized to achieve the final design of baseplate 2 (see Fig. 19b). Figure 23 shows the results of the block fabricated on the baseplate 2 with forced cooling. In this case both the residual stresses and the part warpage are smaller. Thus, the proposed cooling strategy and the new baseplate design can accomplish with the microstructure control without a significant increase of the residual stresses and warpages of the AM part.

Fig. 23
figure 23

Thin baseplate 2 with forced cooling a residual stresses, b the final distortion (displacement norm) of the block

Full size image

7 Conclusions

In this study, different strategies for the simultaneous control of the residual stress accumulation and the microstructural evolution during the DED process are proposed.

A 3D thermo-mechanical FE model suitable for DED processes is first calibrated by in-situ temperature and displacement measurements. The validated model is used to analyze the influence of the baseplate size and the energy density input on both the microstructure evolution and the induced residual stresses.

The main conclusions drawn are as follows:

  1. (1)

    The simulation software is a powerful tool to simulate the DED process as confirmed by the remarkable agreement with the in-situ experimental evidence. Thus, the software can be used to optimize the DED processes by modifying the baseplate design, the process parameters (e.g. the energy density) or the boundary conditions (e.g. forced cooling).

  2. (2)

    The size of the baseplate influences the whole thermo-mechanical behavior of the AM components: the temperature field, the heat capacity and the actual stiffness (constraining) depend on the baseplate thickness. Thicker baseplates are able to faster dissipate the power input allowing for a finer and more uniform microstructure. However, the higher stiffness produces higher residual stresses; contrariwise for thinner baseplate.

  3. (3)

    To simultaneously mitigate the residual stresses while controlling the microstructural evolution in DED, two strategies are proposed. On the one hand, when a thick baseplate is adopted, it is possible to introduce a groove pattern to split the surface of the baseplate into smaller regions offering a reduced constraining to the metal deposition and avoiding stress concentrations. Hence, the final residual stresses can be effectively mitigated. On the other hand, a forced cooling under the bottom surface of thin baseplates can increase the heat dissipation favoring the formation of more uniform and finer microstructures. Moreover, the higher flexibility of the thin baseplate avoids stress accumulation but the warpage must be monitored.