1 Introduction

The boundary layer flow over a moving surface occurs in many industrial and manufacturing processes such as polymer extrusion, wire-drawing, metal forming, fibre processing, magnetic tape production, etc., and is used for understanding the aerodynamical properties of the fluids, for example, the wall friction, drag, etc. The fluid surrounding a moving surface plays a significant role in controlling its behaviour while it is in motion. When the surface or polymer sheet is stretched in a non-Newtonian fluid from the fixed point, sufficient care has to be taken in stretching/moving rate so that the surface should not break, and the desired properties are achieved. Moreover, the surface has to be flat throughout the process. In this case, the non-Newtonian fluid that is surrounded the surface plays a prominent role because the Newtonian fluid fails to provide adequate results. Accordingly, the non-Newtonian fluid (generalized Newtonian fluid) gives satisfactory results in most of the engineering applications. On the other hand, also the viscosity of non-Newtonian fluid depends on the shear rate. Particulate slurries, sewage sludge, inks, oil–water emulsion, butter, paints, synovial fluids, etc. are treated as non-Newtonian fluids. The power-law, Ellis, Carreau–Yasuda, Cross, Jeffrey fluids are some of the non-Newtonian fluids (Bird et al. [1]). Amongst these fluids, the power-law (Ostwal de Waele) fluid is studied extensively in the literature due to its simple mathematical equations and ample applications (Acrivos et al. [2]; Denier and Dabrowski [3]; Ishak et al. [4]). However, the power-law rheology predicts an infinite viscosity in the confinement of boundary layer for very high or small shear rates.

Nevertheless, the addition of a small amount of long-chain polymers such as 1% methylcellulose tylose in glycerol solution, 0.3% hydroxyethyle-cellulose Natrosol HHX in glycerol solution and pure polyethylene oxide, etc. to the Newtonian fluid has a beneficial effect in reducing frictional drag and enhancing effective viscosity (Metzner and Arthur [5]; Nouar et al. [6]; Nouar and Frigaard [7]). This addition constitutes the Carreau fluid model which necessarily predicts the finite viscosity in the boundary layer. The Carreau fluid model is also simultaneously valid for both low and high shear rates. The Carreau fluid is a particular class of generalized Newtonian fluids and characterizes shear thickening and shear thinning nature of fluids. Therefore, many researchers have used Carreau fluid to simulate its non-Newtonian characteristics in many aspects such as the flow around spheres (Chhabra et al. [8]; Lee et al. [9], Hsu and Yeh [10]; Uddin et al. [11] over cylinders and disks (Khellaf and Lauriat [12]; Coelho and Pinho [13]; Lashgari et al. [14]; Alqarni et al. [15]), in boundary layers of stretching surfaces (Hayat et al. [16]; Khan et al. [17]; Khan and Azam [18]; Khan et al. [19]; Ellahi et al. [20]), heat and mass transfer (Mohamed et al. [21], Hayat et al. [22], Hayat et al. [23], Muhammad et al. [24], Mohamed et al. [25]). The linear stability of shear-thinning Carreau fluids in channel flow is studied by Nouar et al. [6] and it is shown that it is possible to maintain laminarity by delaying the transition to turbulence. Griffiths et al. [26] have addressed the stability of Carreau fluid over a flat plate using triple-deck structure to show that the onset of instability can be significantly advanced in the case of shear-thinning Carreau fluids. Khan et al. [27] have studied the flow of Carreau–Yasuda fluid in the porous medium in which the heat transfer is subjected to Soret and Dufour effects and have shown that the permeability and heat transfer characterized by Prandtl number enhance wall shear stress and heat transfer rate in the boundary layer.

On the other hand, when the free-stream flow is approximated in the form \(x^m\) (where x is a measure of the distance from the leading boundary layer edge and m is some constant), the two-dimensional boundary-layer flow for the Newtonian fluid over a moving wedge admits a class of self-similar solutions (Riley and Weidman [28]; Sachdev et al. [29]) generally known as Falkner–Skan solutions. Even dual solutions for \(m>0\) are possible for the same Falkner–Skan model (Hartree [30]) who also discovered that every second solution describes the reverse flow in the boundary layer. Riley and Weidman [28] have reported multiple solutions for \(m>0\) when the wedge is considered to be moving in the same and opposite direction to the mainstream. Sachdev et al. [29] have reproduced these double solutions using exact analytical method. However, the stability of these dual solutions is not addressed in either case as to which of these dual solutions may be observed experimentally.

In the present paper, when the mainstream flow for the Carreau fluid also approximated in a similar manner, the boundary-layer flow over a wedge admits self-similar solutions including the reverse flow situations. One aim of the present paper was to extend the rich structure of dual solutions when the Carreau fluid is considered in the boundary-layer. The additional solution in the non-Newtonian rheology of Carreau fluid significantly alters the nature of the flow response and leads naturally to an algebraic/or exponential growth in the boundary-layer. Numerical solution of the boundary layer problem for Carreau fluid shows that there are dual solutions for both shear-thinning and shear-thickening for an accelerated flow. The first and second solutions thus obtained essentially form a tongue-like structure. This intriguing tongue-like structure is reported for the first in the literature. Performing the unsteady perturbations on the basic steady flow, the linear eigenvalue problem identifies as to which of these dual solutions is stable and physically realizable.

Rest of the paper is organized as follows: Mathematical formulation of the problem under discussion is derived along with physical boundary conditions and is given in Sect. 2. Suitable similarity transformations are also given in the same section. Section 3 contributes to the details of the Chebyshev collocation and shooting methods used along with detailed discussion on steady solutions. In Sect. 4 we give the linear stability analysis of the solutions obtained in Sect. 3. We perform an asymptotic analysis of the governing equation in the limit of velocity ratio parameter \(\lambda\) as \(\lambda \rightarrow \infty\) and given in Sect. 4. The final section concludes the important results and discussions.

2 Flow theory

The motion of a viscous and incompressible non-Newtonian fluid is considered in which the free stream flow is supposed to have a very large Reynolds number. The fundamental governing equations for a non-Newtonian fluid are

$$\begin{aligned} \nabla \cdot \mathbf {q}= & {} 0, \end{aligned}$$
(1)
$$\begin{aligned} \rho \left( \frac{\partial }{\partial t} + \mathbf {q} \cdot \nabla \right) \mathbf {q}= & {} -\nabla p + \nabla \cdot \tau , \end{aligned}$$
(2)

where \(\mathbf {q}\) is the velocity vector, \(\rho\) is the density of fluid, p is the pressure and \(\tau\) is the deviatoric stress tensor which is defined as

$$\begin{aligned} \tau = \mu (\dot{q})\dot{\mathbf {q}}. \end{aligned}$$
(3)

Here \(\mu\) is the non-Newtonian viscosity, and the second invariant \(\dot{q}\) of the strain-rate \(\dot{\mathbf {q}}\)  is given by

$$\begin{aligned} \dot{q} = \sqrt{\frac{1}{2} \dot{\mathbf {q}}.\dot{\mathbf {q}}} \end{aligned}$$
(4)

with

$$\begin{aligned} \dot{\mathbf {q}} = \nabla {\mathbf {q}} + \nabla {\mathbf {q}}^T \end{aligned}$$
(5)

since the first and third invariants are identically zero. In the present problem, we consider the Carreau fluid flow as a non-Newtonian fluid model which takes the following form:

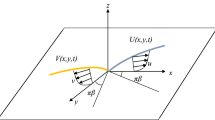
$$\begin{aligned} \tau = \mu _\infty + (\mu _0 - \mu _\infty )[1 + (\hat{\alpha } \dot{q} )^2]^{\frac{n-1}{2}} \dot{\mathbf {q}}, \end{aligned}$$
(6)

where \(\mu _0\) is the zero shear-rate viscosity, \(\mu _\infty\) is the infinite shear-rate viscosity, \(\hat{\alpha }\) is the relaxation time, and n is the fluid index in which the fluid is the shear-thinning when \(n<1\) (the effective viscosity decreases with an increasing shear) and the shear- thickening when \(n>1\) (the effective viscosity increases with an increasing shear). The infinite-shear-rate viscosity \(\mu _\infty\), which is always associated with inviscid flows is considered to be negligible (Bird et al. [1]) compared to the zero-shear rate viscosity \(\mu _0\). Accordingly, \(\mu _\infty\) will thus be neglected in (6), that is, \(\mu _0 \gg \mu _\infty\). Note that when \(n=1\) or \(\alpha = 0\), the Newtonian viscosity is recovered. Although the other non-Newtonian fluids are available, we consider Carreau fluid in the present study, since it has a sound theoretical basis, capable of modelling complex viscosities and also predicts the finite viscosity even for large or small shear rates. For the two-dimensional incompressible Carreau fluid model, the velocity field is given by

$$\begin{aligned} \mathbf {q} = (u,v,0)(x,y,t), \end{aligned}$$
(7a)

where u and v are velocity components in the x- and y- directions. Accordingly, from (4), we have that

$$\begin{aligned} \dot{q} = \bigg [2 \bigg (\frac{\partial u}{\partial x} \bigg )^2 + 2 \bigg (\frac{\partial v}{\partial y} \bigg )^2 + \bigg (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \bigg )^2 \bigg ] ^{\frac{1}{2}}. \end{aligned}$$
(7b)

Thus, the deviatoric stress tensor for the Carreau fluid model takes the following form:

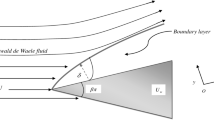
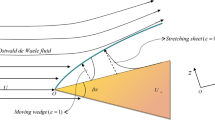
$$\begin{aligned} \tau = \mu _0[1 + (\hat{\alpha }\dot{q})^2] ^{\frac{n-1}{2}} \dot{\mathbf {q}}. \end{aligned}$$
(8)

To this end, we consider the unsteady two-dimensional boundary-layer flow of Carreau fluid over a moving wedge in which x and y axes are measured along the wall of wedge and normal to it, respectively. Figure 1 gives the flow configuration of the problem in which the flow is from left to right.

Fig. 1
figure 1

The flow configuration of the boundary layer in the Carreau fluid. The wedge is considered to be moving upstream and downstream while the fluid flow is from left to right

Full size image

The mainstream flow U of the Carreau fluid outside the boundary-layer flow is approximated by the power of distance along x-direction at any given time, i.e. U = \(U_\infty x^m\), where \(U_\infty >0\) and m are constants. Due to this assumption, the boundary-layer thickness is expected to grow along the wedge of the wall from the leading boundary-layer edge. Also, the motion of wedge is approximated in a similar manner as \(U_w\) = \(U_0 x^m\) (\(U_0\) is constant). It is further assumed that the Reynolds number for Carreau fluid

$$\begin{aligned} Re = \frac{\rho U L}{\mu } \end{aligned}$$

is asymptotically large in the boundary-layer which leads to \(\delta \approx O(Re^{-\frac{1}{2}})\) where \(\delta\) is the thickness of boundary-layer and L is the length of the wedge wall. When Re is large, the flow field divides into two regions: near-field where the viscosity effects are considered to be dominant and in the far-field the viscosity effects are completely negligible. Along with other assumptions on boundary-layers, (2), (7), (8) reduce to

$$\begin{aligned}&\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}= -\frac{1}{\rho } \frac{\mathrm{d}p}{\mathrm{d}x}\nonumber \\&\quad +\nu \bigg (1 + \hat{\alpha }^2 \bigg (\frac{\partial u}{\partial y} \bigg ) ^2 \bigg ) ^{\frac{n-3}{2}} \bigg (1 + n\hat{\alpha }^2 \bigg (\frac{\partial u}{\partial y} \bigg ) ^2 \bigg ) \frac{\partial ^2 u}{\partial y^2}, \end{aligned}$$
(9)

where \(\nu\) is the kinematic viscosity. To obtain the stability of steady solutions obtained from the system (9) for both shear-thinning and shear-thickening Carreau fluids, we first consider the basic state which can be obtained simply by dropping unsteady dependency on the flow. Further, the pressure variation along the normal direction is uniform but varies along the stream-wise direction, i.e. p = p(x). Thus, with \(u=U(x)\) from Bernoulli’s theorem, we have that

$$\begin{aligned} -\frac{1}{\rho } \frac{\mathrm{d}p}{\mathrm{d}x} = U\frac{\mathrm{d}U}{\mathrm{d}x}. \end{aligned}$$
(10)

The relevant physical boundary conditions are

$$\begin{aligned} \begin{aligned}&y=0:~~~~u=U_w(x),~~v=0 \\&\quad y\rightarrow \infty :~~~~u=U(x). \end{aligned} \end{aligned}$$
(11)

The conditions for u essentially describe that the velocity on the wedge surface in the boundary-layer will decay onto the mainstream flow far away from the wedge. The forms for \(U_w(x)\) and U(x) that have been discussed previously obviously do encompass a wide range boundary layer self-similar solutions even for Carreau fluid model. Following Sachdev et al. [29], we introduce similarity transformations

$$\begin{aligned} \psi (x,y) = \sqrt{\frac{2 \nu x U}{m+1}} \phi (\zeta ),~~\zeta = \sqrt{\frac{(m+1)U}{2 \nu x}} y, \end{aligned}$$
(12)

where \(\psi (x,y)\) is the stream function defined as

$$\begin{aligned} u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x} \end{aligned}$$

which identically satisfy the continuity equation. Substitution of (12) in (9) gives

$$\begin{aligned} \mu _\mathrm{CF}(\zeta ) \phi '''(\zeta ) + \phi (\zeta )\phi ''(\zeta ) + \beta (1 - (\phi '(\zeta ))^2) = 0, \end{aligned}$$
(13)

where

$$\begin{aligned} \mu _\mathrm{CF}(\zeta ) = [1 + n(\alpha \phi ''(\zeta ))^2][1 + (\alpha \phi ''(\zeta ))^2] ^{\frac{n-3}{2}}, \end{aligned}$$
(14)

where \(\beta = \frac{2m}{m+1}\) is the pressure gradient parameter with \(\beta >0\) and \(\beta <0\), respectively, correspond to accelerated and decelerated flows in the boundary-layer, while \(\beta = 0\) case corresponds to the flow of Carreau fluid over a moving flat plate. The fluid index parameter n is such that for \(n<1\) and \(n>1\) the fluid becomes shear-thinning and shear-thickening fluid, while when \(n=1\) or \(\alpha =0\), the system (13) reduces to the case of Newtonian fluid. Also, at lower shear rate \(\phi ''(\zeta )\ll \frac{1}{\alpha }\), a Carreau fluid behaves as a Newtonian fluid and intermediate shear rates \(\phi ''(\zeta )\approx \frac{1}{\alpha }\) the Carreau fluid behaves as a power-law fluid. While (14) gives an expression for the viscosity which exists for all parameters where \(\alpha = \hat{\alpha } \sqrt{\frac{(m+1) U_\infty ^3 x^{3m-1}}{2 \nu }}\) is the Weissenberg number (Khan and Azam [18]; Khan and Hashim [31]; Hashim et al. [32]). It is emphasized that \(\alpha\) is scaled by the streamwise coordinate, x, which essentially restricts the attention to a strictly local analysis whereby the required value for \(\alpha\) is evaluated at a specific location along the wedge surface (Griffiths et al. [26]). The physical boundary conditions in view of similarity transformations take the following form:

$$\begin{aligned} \phi (0) = 0,~~~~\phi '(0) = \lambda ,~~~~\phi '(\infty ) = 1, \end{aligned}$$
(15)

where \(\lambda = \frac{U_0}{U_\infty }\) is the ratio of wedge velocity to the mainstream velocity. When \(\lambda >1\)(\(\lambda <1\)), the wedge is moving faster (slower) than the mainstream flow, while for \(\lambda =1\) both have the same speed. Further, when \(\lambda >0\) and \(\lambda <0\), the wedge moves in the same and opposite direction to that of the mainstream. The derivative boundary conditions in (15) state that the non-dimensional velocity profile \(\phi '(\zeta )\) at the surface (\(\zeta =0\)) in the boundary layer decays into the mainstream at edge of the boundary-layer (\(\zeta \rightarrow \infty\)). Note that Griffiths [33] has derived the same problem (13)–(15) for an angle \(45^\circ\) (\(\beta = 0.5\)) and \(\lambda = 0\) and has shown that for moderate values of \(\alpha\) shear-thinning flows (\(n<1\)) will be more stable than their Newtonian equivalents.

3 Numerical procedure

3.1 Chebyshev collocation method

Numerical solution of the Carreau fluid Falkner–Skan equation (13), (14) with boundary conditions (15) for various \(\beta\), \(\alpha\) and n is performed using the Chebyshev collocation method (CCM) and the shooting technique. As the system (13), (14) is highly nonlinear, we, therefore, resort to seek an approximate solution by well-known spectral method using the Chebyshev polynomials as basis functions. The solution is expressed in terms of the truncated Chebyshev series of the functions in the given equation and these are evaluated at the root of Chebyshev polynomials, also known as Gauss-Lobatto points to obtain their respective matrix forms. This procedure reduces the differential equation into a algebraic system of equations with unknown Chebyshev coefficients. Given below is a brief procedure to employ CCM to a differential equation of Jth order. A nonlinear ordinary differential equation of Jth order can be expressed in the following form:

$$\begin{aligned}&\sum _{j=0}^{J}\sum _{k=0}^{K} {A}_{j,k} v^{k}(x)v^{(j)}(x) + \sum _{j=1}^{J}\sum _{k=1}^{K} \ {B}_{j,k} v^{(j)}(x)v^{(k)}(x)\nonumber \\&\quad +\sum _{j=1}^{J}\sum _{k=1}^{K} \ {C}_{j,k} (v^{(j)}(x))^{r}(v^{(k)}(x))^{s} = \ {D}(x). \end{aligned}$$
(16)

Here \(\ {A}(x)\), \(\ {B}(x)\), \(\ {C}(x)\) and \(\ {D}(x)\) are known functions that are well-defined in the domain [a, b] of the differential equation enclosing necessary boundary conditions. The given domain of boundary conditions [a, b] should be transformed into \([-1,1]\) the domain of Chebyshev polynomials \(P_n(x)\) using appropriate mapping. Further, v(x) and its derivatives are expressed as a truncated Chebyshev series of the following form:

$$\begin{aligned} v(x) = \sum _{n=0}^{N} c_n P_n(x), \end{aligned}$$
(17)

and

$$\begin{aligned} v^{(j)}(x) = \sum _{n=0}^{N} c_n^{(j)} P_n(x), \end{aligned}$$
(18)

where \(c_n\) and \(c_n^{(j)}\) are unknown Chebyshev coefficients of v(x) and its derivatives. The Chebyshev collocation points \(x_j\) are defined as

$$\begin{aligned} x_j = -\cos \left( \frac{i \pi }{N}\right) ,\quad i=0,1,2,\ldots ,N, \end{aligned}$$

where N is any positive integer. The above Eqs. (17) and (18) have a matrix representation as follows:

$$\begin{aligned} v(x) = P(x)~ Z \end{aligned}$$
(19)

with

$$\begin{aligned} v(x)= & {} \left[ \begin{array}{c} v(x_0)\\ v(x_1)\\ \vdots \\ v(x_N) \end{array} \right] ,\nonumber \\ P(x)= & {} \left[ \begin{array}{cccc} P_0(x_0) &{} P_1(x_0) &{} \cdots &{} P_N(x_0)\\ P_0(x_1) &{} P_1(x_1) &{} \cdots &{} P_N(x_1)\\ \vdots &{} \vdots &{}\ddots &{}\cdots \\ P_0(x_N) &{} P_1(x_N) &{} \cdots &{} P_N(x_N) \end{array}\right] , \nonumber \\ Z= & {} \left[ \begin{array}{c} c_0\\ c_1\\ \vdots \\ c_N \end{array}\right] . \end{aligned}$$
(20)

Thus, (18) takes the form

$$\begin{aligned} v^{(j)}(x) = P(x)~ Z^{(j)}. \end{aligned}$$
(21)

Using the relation by coefficient matrix of v(x) and its derivative (Sezer and Kaynak [34]),

$$\begin{aligned} Z^{(j)} = 2^j \ {Q}^j Z \end{aligned}$$
(22)

Equation (21) can be written as

$$\begin{aligned} v^{(j)}(x) = 2^j~ P(x) \ {Q}^j Z, \end{aligned}$$
(23)

where \(\ {Q}\) (Sezer and Kaynak [34], Kudenatti et al.[35, 36]) is given by

$$\begin{aligned} \ {Q} = \left[ \begin{array}{cccccccc} 0 &{} \frac{ 1}{2 } &{} 0 &{} \frac{3 }{ 2} &{} 0 &{} \frac{5 }{ 2} &{} \cdots &{}q_1 \\ 0 &{} 0 &{} 2 &{} 0 &{} 4 &{} 0 &{} \cdots &{} q_2 \\ 0 &{} 0 &{} 0 &{} 3 &{} 0 &{} 5 &{} \cdots &{} q_3 \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}N\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array} \right] \end{aligned}$$

with

$$\begin{aligned} q_1&= \frac{N}{2},~ q_2 = 0,~ q_3 = N \quad \text {for odd}~ N\\ q_1&= 0,~ q_2 = N,~ q_3 =0 \quad \text {for even}~ N. \end{aligned}$$

Similarly, the algebraic powers of v(x) can be computed as follows:

$$\begin{aligned}{}[v(x)]^{k}=[\bar{v}(x)]^{k-1} v(x); \end{aligned}$$
(24)

here

$$\begin{aligned} \bar{v} = \bar{P}\bar{Z},\quad \bar{P} = \left[ \begin{array}{cccc} P(x_0) &{} 0 &{} \cdots &{} 0\\ 0 &{} P(x_1) &{} \cdots &{}0\\ \vdots &{} \vdots &{}\ddots &{}\vdots \\ 0 &{} 0&{} \cdots &{} P(x_N) \end{array}\right] \quad \text {and} \quad \mathrm{diag}(\bar{Z}) = ,Z \end{aligned}$$

in which the Chebyshev polynomials are evaluated at each collocation point and then simplified using (23)

$$\begin{aligned} (\bar{v}(x))^{(k)}v(x)^{(j)} = 2^{^{k+j}} \bar{P}(\bar{\ {Q}})^k \bar{Z} P \ {Q}^j Z, \end{aligned}$$
(25)

where \(\mathrm{diag}(\bar{\ {Q}}) = \ {Q}.\) Accordingly, Eq. (16) takes the matrix form

$$\begin{aligned}&\sum _{j=0}^{J}\sum _{k=0}^{K} 2^j\ {A}_{j,k} (\bar{P}\bar{Z})^k P\ {Q}^{(j)}Z\nonumber \\&\quad + \sum _{j=1}^{J}\sum _{k=1}^{K} 2^{(j+k)} \ {B}_{j,k} \bar{P}\bar{\ {Q}}^k\bar{Z} P\ {Q}^jZ\nonumber \\&\quad +\sum _{j=1}^{J}\sum _{k=1}^{K} 2^{(jr+ks)} \ {C}_{j,k} (\bar{P}\bar{\ {Q}}^j\bar{Z})^{r}(P\ {Q}^kZ)^{s} = \ {D}, \end{aligned}$$
(26)

where \(\mathrm{diag}(\ {A}_{j,k}) = \ {A}_{j,k}(x)\), \(\mathrm{diag}(\ {B}_{j,k}) = \ {B}_{j,k}(x)\), \(diag(\ {C}_{j,k}) = \ {C}_{j,k}(x)\) and \(\ {D} =[\ {D}(x_0), \ {D}(x_1), \ldots , \ {D}(x_N)]'\); here \('\) represents transpose of the matrix. Concisely (26) takes the following form:

$$\begin{aligned} {W}Z = {D}. \end{aligned}$$
(27)

Equation (27) corresponds to a system of \((N+1)\) nonlinear algebraic equations with the Chebyshev coefficients Z that are to be determined. The boundary conditions are now incorporated to obtain the modified augmented matrix

$$\begin{aligned} \tilde{\ {W}}Z = \tilde{\ {D}}. \end{aligned}$$
(28)

3.2 Application of CCM to present flow problem

For the application of CCM technique to the present problem, we convert the semi-infinite flow domain of the problem into the domain of Chebyshev polynomial \([-1,1]\) by employing suitable transformations

$$\begin{aligned} \phi (\zeta ) = \frac{\zeta _\infty }{2} F(\eta )~~\text {with}~~\eta = \frac{2\zeta }{\zeta _\infty }-1, \end{aligned}$$
(29)

where \(\zeta _\infty\) truncates an infinite boundary layer domain at some value of \(\zeta\) at which the inviscid core of the flow is met. Solution of this transformed differential equation

$$\begin{aligned} \mu ^*_\mathrm{CF}(\eta ) F'''(\eta ) + F(\eta )F''(\eta ) + \beta (1 - (F'(\eta ))^2) = 0 \end{aligned}$$
(30)

with

$$\begin{aligned} \mu ^*_\mathrm{CF}(\eta ) = \left[ 1 + n\left( \dfrac{2\alpha }{\zeta _\infty } F''(\eta )\right) ^2\right] \left[ 1 + \left( \dfrac{2\alpha }{\zeta _\infty }F''(\eta )\right) ^2\right] ^{\frac{n-3}{2}} \end{aligned}$$

along with the boundary conditions

$$\begin{aligned} F(-1) = 0, ~~~~ F'(-1) = \lambda ,~~ F'(1) = 1 \end{aligned}$$
(31)

is expressed in terms of truncated Chebyshev series as

$$\begin{aligned} F(\eta ) = \sum _{n=0}^{N} c_n \ {P}_n(\eta ). \end{aligned}$$
(32)

Following (23), (24) and (25), we write the matrix representation of Eq. (30) as

$$\begin{aligned}&\left[ \bar{\mu }^*_\mathrm{CF}(\eta ) \left( \frac{2}{\zeta _\infty }\right) ^2(2^3 PQ^3)\right. \nonumber \\&\quad \left. +(\bar{P}\bar{Z})(2^2 P Q^2)- 4\beta (\bar{P}\bar{Q}\bar{Z}PQ) \right] Z =-\beta O \end{aligned}$$
(33)
$$\begin{aligned} \bar{\mu }^*_\mathrm{CF}(\eta )= & {} \left[ 1 + n\left( \dfrac{2\alpha }{\zeta _\infty } (2^2\bar{P}\bar{Q^2}\bar{Z})\right) ^2\right] \nonumber \\&\quad \left[ 1 + \left( \dfrac{2\alpha }{\zeta _\infty }(2^2\bar{P}\bar{Q^2}\bar{Z})\right) ^2\right] ^{\frac{n-3}{2}}, \end{aligned}$$
(34)

where O denotes the vector of ones of order \(( N+1)\times 1\). The computation of the solution with CCM procedure becomes quite challenging at this point, because the evaluation of \(\bar{\mu }^*_\mathrm{CF}\) becomes unpleasant owing to the fact that evaluation of matrices of order \(( N+1)\times ( N+1)\) for fractional powers is troublesome, especially when these are negative; henceforth, computational linear algebraic comes to our rescue. A close examination reveals that the matrix which is obtained as a product form of \(\left[ 1 + \left( \dfrac{2\alpha }{\zeta _\infty }(2^2\bar{P}\bar{Q^2}\bar{Z})\right) ^2\right]^\frac{n-3}{2}\) is diagonalizable. Hence, it can be written in a product form of its eigenvalues E and corresponding eigenvectors V as \(VE V^{-1}\). Hence, Eq. (34) takes the following form:

$$\begin{aligned} \bar{\mu }^*_\mathrm{CF}(\eta ) = \left[ 1 + n\left( \dfrac{2\alpha }{\zeta _\infty } (2^2\bar{P}\bar{Q^2}\bar{Z})\right) ^2\right] VE ^{\frac{n-3}{2}}V^{-1}. \end{aligned}$$
(35)

Compactly, (33) can be written as

$$\begin{aligned} W Z = R, \end{aligned}$$
(36)

where

$$\begin{aligned} W&= \left[ \bar{\mu }^*_\mathrm{CF}(\eta ) \left( \frac{2}{\zeta _\infty }\right) ^2(2^3 PQ^3)\right. \nonumber \\&\quad \left. +(\bar{P}\bar{Z})(2^2 P Q^2)- 4\beta (\bar{P}\bar{Q}\bar{Z}PQ)\right] \end{aligned}$$
(37)
$$\begin{aligned} R&= -\beta O. \end{aligned}$$
(38)

We then modify the matrix, to employ the transformed boundary conditions

$$\begin{aligned} P(-1) Z= 0,\quad 2P(-1)QZ = \lambda , \quad 2P(1)QZ = 1 \end{aligned}$$
(39)

at first, second and last row, respectively. Thus the system of modified augmented equations is solved for unknown Chebyshev coefficient vector Z as

$$\begin{aligned} \tilde{W}Z = \tilde{R}. \end{aligned}$$
(40)

As one can observe, Eq. (37) denotes the nonlinear algebraic equations in unknown Z; to overcome the difficulty in obtaining the solution of this equation we take an initial approximation to Z (in the present computations, we have chosen Z as a zero vector of order \(({N}+1,1)\) at the initial phase of computation) and then we update this at a further stage of calculation until the desired tolerance of \(10^{-6}\) is achieved and all the results provided below are tested for their convergence criteria. In most of the simulations, 43 terms are utilized in the Chebyshev series at which the required solutions are accurate enough. On the other hand, we also checked with 50 terms in the series, but the results are unaltered.

3.3 Shooting technique

We also performed the shooting technique to the Carreau fluid Falkner–Skan equation (13)–(15) in which the system is integrated using Runge–Kutta method and the missing condition \(\phi ''(0)\) is located using the secant method. The system is converted into three first-order differential equations by introducing some additional unknown functions. The Runge-Kutta twinned with the secant method is applied for their integration. The error-tolerance is set to \(10^{-6}\) and step-size \(\Delta \zeta = 0.01\) is taken. The integration procedure is repeated with \(10^{-8}\) and \(\Delta \zeta = 0.001\). However, the results from both cases are indistinguishable. We, therefore, took the former values for all our numerical simulations. Note that the solutions for \(n=1\) (Newtonian fluid) always serve as benchmark results for all our simulations.

The results for \(n=1\), as suggested by Riley and Weidman [28] and Sachdev et al. [29], have double solutions for some range of \(\beta\) and \(\lambda\). For \(n\ne 1\) case, the Carreau fluid Falkner–Skan problem also produces the double solutions for different \(\alpha\) and \(\lambda\) keeping the same typical trend as \(n=1\) case. We call the first and second solutions as the upper and lower branch solutions, and \(\lambda _c\) as a critical value where the second solutions start to appear and the first solution terminates. The significance of these additional second solutions will be explained in Sect. 4, but at this junction, they serve as useful means of correlating them to the stability analysis. At this point of time, it is appropriate to discuss the stability of dual solutions as to which of two solutions is physically realizable when the long-time asymptotics is sought. Note that the inclusion of unsteadiness term inevitably results in temporal variation in the system on account of the addition of it with convective terms. The similarity forms still exist as of the steady flow and lead to the linear stability analysis in terms of the eigenvalue problem. In the following section, we give the details of the eigenvalue problem analysis.

4 Linear stability analysis

The stability of the dual solutions can be concluded perhaps more easily by including the unsteady term \(\frac{\partial u}{\partial t}\) in (9) and then investigating the resulting eigenvalue problem for the large time. The resulting system is solved using the same shooting procedure(discussed in the Sect. 3) for an eigenvalue. It is to note that the dual solutions exist for both shear-thinning and shear-thickening fluids, and in each case, it is reasonable to expect the basic state disturbance to vary exponentially with time as \(\mathrm {e}^{-\gamma t}\), (\(\gamma\) is an unknown eigenvalue). Now setting

$$\begin{aligned}&\xi = \frac{m+1}{2} U_\infty x^{m-1} t,~~\psi (x,y) = \sqrt{\frac{2 \nu x U}{m+1}} \phi (\zeta ,\xi ),\nonumber \\&\zeta = \sqrt{\frac{(m+1)U}{2 \nu x}} y. \end{aligned}$$
(41)

The above transformations are similar to Sharma et al. [37] who certainly adopted for Newtonian fluid to assess the stability of dual solutions. Substituting (41) in (9) to get

$$\begin{aligned} \begin{aligned}&\left( 1+n\alpha ^2 \bigg (\frac{\partial ^2 \phi }{\partial \zeta ^2} \bigg )^2\right) \bigg (1+\alpha ^2 \bigg (\frac{\partial ^2 \phi }{\partial \zeta ^2}\bigg )^2\bigg )^{\frac{n-3}{2}} \frac{\partial ^3 \phi }{\partial \zeta ^3}\\&\quad + \phi \frac{\partial ^2 \phi }{\partial \zeta ^2}+ \beta \bigg (1 - \bigg (\frac{\partial \phi }{\partial \zeta }\bigg )^2\bigg )\\&\quad +2 (\beta - 1)\xi \left( \frac{\partial \phi }{\partial \xi } \frac{\partial ^2 \phi }{\partial \zeta ^2}-\frac{\partial \phi }{\partial \zeta } \frac{\partial ^2 \phi }{\partial \xi \partial \zeta }\right) - \frac{\partial ^2 \phi }{\partial \xi \partial \zeta }=0, \end{aligned} \end{aligned}$$
(42)

which is a weakly nonlinear partial differential equation. Since we are interested in stability of basic states \(\phi (\zeta )\) = \(\widehat{\phi }(\zeta )\), we perturb (42) about \(\widehat{\phi }(\zeta )\) as

$$\begin{aligned} \phi (\zeta ,\xi ) = \widehat{\phi }(\zeta ) + \mathrm {e}^{-\gamma \xi } F(\zeta ,\xi ), \end{aligned}$$
(43)

where \(\gamma\) is a real eigenvalue to be determined such that when \(\xi\) tends to infinity, the basic state \(\widehat{\phi }(\zeta )\) is stable for \(+\gamma\) and unstable for \(-\gamma\). From (42) and (43), we have

$$\begin{aligned}&\bigg [ \widehat{\mu }_\mathrm{CF} \frac{\partial ^3 F}{\partial \zeta ^3} + \widehat{\phi } \frac{\partial ^2 F}{\partial \zeta ^2} + F \widehat{\phi }'' - 2 \beta \widehat{\phi }' \frac{\partial F}{\partial \zeta }\nonumber \\&\quad + 2 (\beta - 1) \xi \bigg (\widehat{\phi }'' \bigg (\frac{\partial F}{\partial \xi } - \gamma F \bigg )\nonumber \\&\quad -\widehat{\phi }' \bigg ( \frac{\partial F}{\partial \zeta \partial \xi } - \gamma \frac{\partial F}{\partial \zeta } \bigg ) \bigg ) + \gamma \frac{\partial F}{\partial \zeta } - \frac{\partial ^2 F}{\partial \zeta \partial \xi }\bigg ] \mathrm {e}^{- \gamma \xi } = 0, \end{aligned}$$
(44)

where

$$\begin{aligned} \widehat{\mu }_\mathrm{CF} = \bigg [1 + n\alpha ^2 \bigg (\frac{\partial ^2 \widehat{\phi }}{\partial \zeta ^2}\bigg )^2\bigg ]\bigg [1 + \alpha ^2 \bigg (\frac{\partial ^2 \widehat{\phi }}{\partial \zeta ^2}\bigg )^2 \bigg ]^{\frac{n-3}{2}}. \end{aligned}$$

Now by setting \(\xi\) = 0 and \(F(\zeta ,\xi )\) = \(F(\zeta )\) in (44) leads to

$$\begin{aligned}&\widehat{\mu }_\mathrm{CF} F{'''}(\zeta ) + \widehat{\phi }(\zeta ) F{''}(\zeta )\nonumber \\&\quad + \left[ -2\beta \widehat{\phi }'(\zeta ) + \gamma \right] F'(\zeta )+ \widehat{\phi }{''} F(\zeta )= 0, \end{aligned}$$
(45)

where

$$\begin{aligned} \widehat{\mu }_\mathrm{CF} = \left[ 1 + n(\alpha \widehat{\phi }'')^2\right] \left[ 1+(\alpha \widehat{\phi }'')^2\right] ^{\frac{n-3}{2}}. \end{aligned}$$

Equation (45) can be solved using the following transformed boundary conditions:

$$\begin{aligned} F(0) = 0,~~~~F'(0) = 0,~~~~F'(\infty ) = 0. \end{aligned}$$
(46)

The above system (45)–(46) is a linearized eigenvalue problem for two unknowns: an eigenvalue \(\gamma\) and eigenfunction \(F(\zeta )\). The system requires an additional condition. We, therefore, set \(F''(0)=1\) such that the system can be solved as an initial value problem for \(\gamma\) for which \(F'(\infty )\rightarrow 0\) is satisfied. However, other choices of \(F''(0)\) is also possible but the system gives the same unique solution. Many authors (Sharma et al. [37], Harris et al. [38], Mishra et al. [39]) have used, for Newtonian fluid, the similar procedure to identify precisely the unique eigenvalue.

5 Asymptotic analysis for large \(\lambda\)

On the other hand, we perform an asymptotic analysis with the object of comparing the numerical solutions obtained for various system parameters. The two-dimensional boundary layer flow over a moving wedge is studied when the velocity ratio parameter \(\lambda\) is taken to be sufficiently large and positive such that the mainstream velocity becomes negligible, that is \(U_0 \gg U_\infty\). In this case, the boundary layer forms due to movement of the wedge in a still Carreau fluid. For Newtonian fluid, Kudenatti et al. [40] have performed the similar asymptotics in the two-dimensional boundary-layer flow. We follow the similar transformations for the Carreau fluid model, i.e,

$$\begin{aligned} \phi (\zeta ) = \lambda ^{\frac{2n-1}{n+1}} H(z),~~z = \lambda ^{\frac{2-n}{n+1}} \zeta \end{aligned}$$
(47)

for \(\lambda \rightarrow \infty\). Plugging (47) in (13)–(15) to get

$$\begin{aligned} \mu _\mathrm{CF} H'''(z) + H(z) H''(z) - \beta (H'(z))^2 = 0 \end{aligned}$$
(48a)

with

$$\begin{aligned} H(0) = 0,~~~~H'(0) = 1,~~~~H'(\infty ) = 0, \end{aligned}$$
(48b)

which is independent of \(\lambda\), where

$$\begin{aligned} \mu _\mathrm{CF}(z) = [n(\alpha H''(z))^2][(\alpha H''(z))^2] ^{\frac{n-3}{2}}, \end{aligned}$$

and \(\beta = \frac{2m}{m+1}\) is now read as the nonlinear stretching rate parameter. We again apply the shooting technique to solve the nonlinear ordinary differential equation for various \(\beta\) and n and the corresponding results for \(H''(0)\) are presented in Fig. 2 along with at \(\phi ''(0)\) obtained from (13)–(15) for the same parameters. Incidentally, the results from (48) also support and compliment those of (13)–(15). It is observed that both results compare well particularly when \(\lambda\) is quite large, thereby validating the transformations made in (47) for Carreau fluid. Also, it is noticed that each result represents the velocity profile in the boundary layer that decays to zero far away from the surface.

Fig. 2
figure 2

Comparison of the wall shear stress values obtained from the full system (13)–(15) and asymptotic system (48) for \(\lambda\)

Full size image

6 Results and discussion

Two-dimensional boundary layer flow of Carreau fluid over a moving wedge has been solved numerically using the Chebyshev collocation and shooting techniques. We shall now give various significant results in terms of the velocity profiles and the wall shear stress for the pressure gradient \(\beta\), the fluid index n, the Weissenberg number \(\alpha\) and the velocity ratio \(\lambda\). To compare the various results obtained from both methods, we present \(\phi ''(0)\) values in Table 1 for some chosen parameters. The solutions that represent the wall shear stress compare well to each other up to the desired accuracy. We note that the velocity shapes correspond to \(\phi ''(0)\) are surely indistinguishable and have not shown for the brevity of space.

Table 1 Comparison of the wall shear stress \(\phi ''(0)\) values obtained by CCM and shooting methods for \(\lambda =1.5\)
Full size table

Numerical simulations of the non-Newtonian Carreau fluid in the two-dimensional boundary layer flow over are studied when the fluid index n is varied. The velocity in the boundary layer takes different shapes in response to the modification of viscosity due to the Carreau fluid. It is shown in Fig. 3 that the velocity for the Newtonian fluid (\(n=1\)) is clearly demarcated from the shear-thinning and shear-thickening fluid. The boundary layer thickness for the shear-thinning is small compared to the Newtonian and shear-thickening fluids. For shear-thinning fluids, the viscosity decreases for large shear rate and as a result the wall shear stress is found to be smaller. An opposite trend is noticed for the shear-thickening fluids. Similar results are observed for the imposed pressure gradient due to the mainstream in Fig. 4. The very similar velocity profiles are obtained for Weissenberg number \(\alpha\) though not shown here. In both cases, the wall shear stress \(\phi ''(0)\) values are all positive since the velocity ratio \(\lambda\) is less than unity. However, when \(\lambda >1\), these wall shear stresses are all negative.

Fig. 3
figure 3

Illustration of the effects of the Carreau fluid on the boundary while keeping \(\beta =0.5\) and \(\alpha =1\) fixed

Full size image
Fig. 4
figure 4

Variation of the velocity profiles in response to the pressure gradient parameter \(\beta\) for \(n=1.4\) and \(\alpha =1\)

Full size image

We now discuss the various results in terms of \(\phi ''(0)\) which give the broader structure of the model under consideration. Additionally, since the mathematical equation is highly nonlinear because of the Carreau fluid model, we expect the solution to be non-unique in some range of the parameter space. We discuss such results in the following section with more emphasis given to the nature of double solutions and their stability

Numerical solution of the accelerated Falkner–Skan flow problem for the Newtonian fluid shows that the solutions are not unique, i.e. a new family of solutions exists for the same physical parameters (Riley and Weidman [28]). This is evidently linked to the nonlinearity of the problem under question. Incidentally, the numerical solution of the Falkner–Skan problem for non-Newtonian Carreau fluid and accelerated flow also produces a similar set of double solutions for the same physical parameters. For different values of n that were considered in the present work, there does seem to be a correlation between Newtonian and non-Newtonian Carreau fluid. When n is taken to be 1 in (13)–(15) both velocity profiles \(\phi '(\zeta )\) and the wall shear stress \(\phi ''(0)\) reduce to those of Riley and Weidman [28]. Let us now consider base flows which do possess the double solutions; the first(upper branch) and second(lower branch) solutions. It is worth mentioning that these results are produced for the same parameter and using the same numerical technique. When \(\lambda =\pm 1\), the system produces an exact solution \(\phi (\zeta )=\zeta\) at which \(\phi ''(0)\) vanishes identically.

Fig. 5
figure 5

Illustration of wall shear stress as a function of \(\lambda\) and existence of additional solutions for different \(\beta\) and n when \(\alpha =1\) is held constant

Full size image

The various wall shear stress \(\phi ''(0)\) are presented in Fig. 5 for different n, \(\alpha\) and \(\beta\). For each value of \(\phi ''(0)\) shown in Fig. 5, there is a velocity profile in the boundary layer which is benign in nature. It also predicts a finite viscosity. From Fig. 2, it is clear that when \(\lambda\) is decreased from 1, \(\phi ''(0)\) is found to be increasing and attains its maximum at some \(\lambda\). For example, for \(\beta =0\), it occurs at \(\lambda =0\) and \(\beta =1\), it is \(\lambda =-0.6\) when \(n=0.8\) and \(\alpha =1\), etc.. Then, it gradually decreases until \(\lambda\) meets \(\lambda _c\) where \(\lambda _c\) is critical value at which a breakdown of the solution occurs, seemingly similar to that of the Newtonian case. Beyond \(\lambda _c\) value, the Falkner–Skan problem for Carreau fluid fails to produce any solutions. We tried with different initial conditions but model shows no solutions. The solution structure until \(\lambda _c\) and also vanishing of \(\phi ''(0)\) at \(\lambda =-1\) hint that there is an additional solution when \(\lambda\) is increased from \(\lambda _c\). Thus, we tried with different boundary layer domain which essentially produces the second solution. Further, when \(\lambda\) is increased from a critical value \(\lambda _c\), the wall shear stress \(\phi ''(0)\) starts to decrease to zero and again vanishes at \(\lambda =-1\). Thus, the results for \(\phi ''(0)\) from \(\lambda (=1)\) to \(\lambda _c\) and \(\lambda _c\) to \(\lambda (=-1)\) are termed as the first and second solution, respectively. The prominent feature of the breakdown event at \(\lambda _c\) can be linked to the non-existence of the solution. It is also noted that the Newtonian fluid \(n=1\) clearly demarcates the shear-thinning solution structure from that of shear-thickening. For \(\phi ''(0)\) values for \(n<1\) are larger than these of \(n \ge 1\) which are clearly seen from the figures. Also, for increasing \(\beta\) the wall shear stress increases for all n tested. It is also observed that higher the \(\beta\) value larger the critical value \(\lambda _c\).

Table 2 Critical values for \(\beta\) and n
Full size table

The various critical values \(\lambda _c\) are presented in Table 2 along with Newtonian case \(n=1\). It is observed clearly that for increasing n and \(\beta\), \(|\lambda _c|\) is also increasing. Except \(\beta \ne 0\), \(|\lambda _c|\) is always greater than 1. However, for \(\beta =0\), the critical values are less than 1 as shown in Table 2 and wall shear stress \(\phi ''(0)\) is shown in Fig. 5. Figure 6 presents the structure of the double solutions for different Carreau fluid parameter n when the Weissenberg number \(\alpha =2\) is held constant. The results are analogous to those produced in Fig. 5 for \(\alpha = 1\) and the critical values \(\lambda _c\) for \(\alpha = 1\) with, in fact, slight variation. Hence, no discussion is required.

Fig. 6
figure 6

Illustration of wall shear stress for various \(\lambda\) and existence of additional solutions for different \(\beta\) and n when \(\alpha =2\) is held constant

Full size image

To visualize \(\phi (\zeta )\) the nature of the double solutions in the two-dimensional boundary-layer, we intentionally plot the velocity profiles \(\phi '(\zeta )\) in Fig. 7 for \(n= 0.8,1.2\) and \(\beta =0.6\) and \(\alpha =1\). These profiles are drawn for \(\lambda =-1.06\) which is near to the critical value \(\lambda _c= -1.06156\) so that nature can be seen clearly. It is noticed that the boundary layer thickness is found to be thinner for the first solutions and thicker for the second solutions. But in both cases they decay to the mainstream flows asymptotically satisfying the end condition.

Fig. 7
figure 7

Illustration of the velocity profiles \(\phi '(\zeta )\) for the first and second solutions. Here \(\lambda =-1.06\)

Full size image

We now discuss the stability of the double solutions that are presented in Figs. 5 and 6. The stability of the double solutions can easily be assessed perhaps in an easier way by perturbing the base flow shown in (43) and then studying the resulting linear eigenvalue problem for \(\gamma\). This eigenvalue problem is again solved using the shooting method as discussed before. The required basic states \(\phi (\zeta )\) and its derivatives are obtained by solving (13), (14) for various parameters. The shooting method is implemented twice: first to obtain the basic states form (13), (14) and second, the system (45), (46) is modified such that it can be treated as an IVP by setting \(F''(0)=1\) so that it searches for a real eigenvalue \(\gamma\). The error tolerance and step length for the eigenvalue problem are also set as discussed before. The various eigenvalues are presented Figs. 8 and 9.

Fig. 8
figure 8

Existence of eigenvalues in the (\(\gamma\), \(\lambda\))- space for \(\alpha = 1\). The solid and dashed lines in each curve represent the eigenvalues which are stable and unstable

Full size image

Figures 8 and 9 present the eigenvalues for various values of the Carreau fluid parameter n and the pressure gradient parameter \(\beta\) when \(\lambda\) is varied. The results presented in Figs. 8 and 9 correspond to those produced in Figs. 5 and 6 for the double solutions. When the first solution \(\phi (\zeta )\) is considered as basic state in (45)–(46) for selected physical parameters, say \(n=0.6\), \(\beta =0\), \(\alpha =1\), the numerical solution of (45), (46) determines an eigenvalue to be positive. It is larger for higher values of \(\lambda\). When \(\lambda\) is decreased from 1, real eigenvalue also decreases and changes its sign at \(\lambda _c=-0.35257\) (see Table 2). Note that with the first solution branch as a basic state, either beyond \(\lambda _c\) or vanishing of the positive eigenvalue, the shooting technique never converges. We tried with different initial conditions but ended without success. Thus, the first solution is always stable for large time and can be encountered practically. On the other hand, the similar procedure is repeated with the second set of solutions. When \(\lambda\) is decreased from 1, the shooting technique did not converge for any choice of the initial condition. When \(\lambda\) is increased from \(\lambda _c\), the eigenvalue starts to appear with a negative sign. This indicates that the perturbed basic state for second solution branch is always unstable and deviates from the basic state for large time. The dashed lines in each curve corresponds to the eigenvalue changing its sign. At this stage, two points of detail are worth making. First, whenever the first solution is taken to be a basic state, it is found that the flow is always eventually reverted to the original state. Second, with the first solution and \(\lambda\) increased from \(\lambda _c\) or with the second solution and \(\lambda\) decreased from \(\lambda _c\), the eigenvalue does not exist, i.e, no solution exists to the system for any choice of parameters.

Fig. 9
figure 9

Existence of eigenvalues in the (\(\gamma\), \(\lambda\))- space for \(\alpha = 2\). The solid and dashed lines in each curve represent the eigenvalues which are stable and unstable

Full size image
Fig. 10
figure 10

The viscosity profiles \(\mu _\mathrm{CF}(\zeta )\) for various \(\beta\), n and \(\alpha\)

Full size image

We now discuss our results on viscosity function \(\mu _\mathrm{CF}\) given by (14). In fact, for each parameter tested in the figures, it is to note that there is a viscosity profile. Some of the viscosity profiles \(\mu _\mathrm{CF}(\zeta )\) are given in Fig. 10 for various combinations of \(\beta\) and n. It is immediately clear that for shear thinning Carreau fluids, the profiles approach the unity from below for any \(\beta\) and \(\alpha\). This means that the viscosity is always finite within the confinement of the boundary layer which is in contrast to the power-law(Ostwald-de Waele) fluid that predicts an infinite viscosity in the boundary-layer for shear-thinning fluids (Griffiths [33]). Since the shear flow \(\phi ''(\zeta )\) approaches zero away from the surface, the model predicts finite viscosity. On the other hand, the opposite results are observed for the shear-thickening fluids (\(n\ge 1\)) and the viscosity profiles are approaching unity from the above, thereby again predicting the finite viscosity. These results for \(n\ge 1\) are consistent with the power-law fluids. In both cases, the viscosity profiles have an algebraic approach when shear-rate decreases away from the wedge surface.

7 Concluding remarks

Two-dimensional non-Newtonian boundary layer flow over a moving wedge is studied in which the Carreau fluid is allowed to flow with a large Reynolds number. The forms of the velocity of the wedge and mainstream flows, which are assumed in terms of power of distance, exhibit the self-similar solutions to the boundary layer equations. Numerical solutions show that the pressure gradient and shear-thinning fluid promote an enhancement in the fluid velocity, thereby thinning the boundary layer thickness. These together again show that there are dual solutions to the same parameters. The motivation for obtaining double solutions comes possibly from the corresponding Newtonian fluid analysis. These solutions for the Carreau fluid flow over a wedge are noticed for the first time in the literature. The two solutions which are defined as the upper and lower branch results form a tongue-like structure due to the presence of critical point beyond which no solution exists and hence these results need special attention as to which of these solutions is physically realizable. The stability analysis through the eigenvalue approach shows that the upper branch solutions are always stable when the large-time is considered, and the other solutions cannot be practically encountered. A natural extension of the present study is to obtain by enforcing an external force so that the unique solution is possible and hence practically encountered. The possible ways are to consider an applied magnetic field, allow the Carreau fluid to flow through a porous medium, etc. This study certainly would reveal significant flow phenomena including stabilizing effects.