Optimal design of large-scale frames with an advanced charged system search algorithm using box-shaped sections

Abstract

In the present article, an advanced charged system search (ACSS) algorithm is designed for optimizing the large-scale frame structures using box-shaped sections for columns. The proposed ACSS is an extended version of the charged system search (CSS) which is a metaheuristic algorithm that uses the electrostatics and Newtonian laws of mechanics under the conditions of the Coulomb law. Two large-scale 3D frames with 1026 and 1935 components are optimized using AISC-LRFD to show the efficiency of using the box-shaped sections. Overall performance of the ACSS algorithm with box-shaped sections is compared to those of the upper bound strategy for integrated versions of the standard Big Bang Big Church algorithm and two of its newly developed variants. The results show the successful performance of using steel box-shaped columns in comparison to the frames with I-shaped sections. The numerical results show that the ACSS is efficient and robust compared to its standard version.

1 Introduction

A steel frame is a structure in which vertical steel columns and horizontal beams are connected in the form of rectangular grids. Generally, the members are selected from I-shaped steel sections, to sustain vertical and lateral loads. The flexural stiffness of the beams and columns ensures lateral stability of such structures if these are rigidly linked at joints. For moment-free connection, the frame should be strengthened by a full-bracing system all over the height of the construction, so that lateral force can be transmitted to the ground. In such systems, different types of floor slabs in composite and non-composite forms can be adopted. A composite floor is made up of a high-strength profiled steel ceiling with concrete cast, and due to its high speed of construction, it is suitable for multi-story structures. The design of a structure with steel must take into account both safety and economy. Structural safety is always the main priority of an engineer to consider, while the economical design should also be taken into account relying on a trial and error approach. However, using such methods, an optimum design can only occasionally be achieved resulting in minimum structural weight or cost. Also, such methods sometimes lead to highly uneconomic solution, particularly when the design is controlled by displacement limitations. Structural optimization comprises the design of structures with best use of the available resources. Recently, this subject has attracted many scientists as a challenging topic.

Nowadays, metaheuristic algorithms are proposed as powerful means to deal with optimization problems. Many of these algorithms are inspired by natural systems [1]. Genetic algorithm (GA) emanated from Darwin’s hypothesis of biological evolution was developed by Goldberg [2]. Eberhart and Kennedy [3] suggested particle swarm optimization (PSO) which mimics birds flock and fish training social interaction behavior. Dorigo et al. [4] developed optimization of the ant colony (ACO) that simulates real-life colonial hunting behaviors for identifying the shortest path from nutrition supply to their nests. Harmony search [5] is the approach used by Geem et al. This algorithm imitates the performance process that occurs when a musician searches for a better harmony.

Metaheuristic algorithms generally focus on naturally monitorable events and are no exceptions to those used in the optimal design of steel frames [6]. Simulated annealing is mainly based on conduct of cooling and was used by balling to optimize steel structures [7]. Genetic algorithms (GA) are pure genetically engineered pursuit methods and have been modified by Rajeev and Krishnamoorthy to improve the optimal design of the steel frame [8]. Harmony search (HS) is focused on the ability of several musicians to contribute to a harmony and Saka optimized steel frame structures using this method [9]. The optimization of the ant colony (ACO), tailored by Camp et al. [10], is mainly based on the observed capacity of ant colonies to find the optimal path to the food supply for optimal design of steel frame structures. The particle swarm optimization (PSO) was first performed by Perez and Behdinan [11] to optimize steel frame structures and reflects the ability of a big number of swarms to travel jointly to a point. Charged system search (CSS) is a physical and mechanical optimization algorithm used by Kaveh and Talatahari for the design of steel frames [12]. Colliding bodies optimization (CBO) consists of a single dimension collision between bodies and is considered as mass object or a body for each agent solution. This algorithm was used for steel frame structure optimization by Kaveh and Ghazaan [13]. Very recently, an improved grey wolf optimizer (GWO) was proposed for optimization, which was improved to handle structural optimization in an efficient manner by Kaveh and Zakian [14]. Kaveh and Mahjoubi [15] suggested a new optimization method which is named as hypotrochoid spiral optimization algorithm (HSPO), the movement operation of search points is redesigned, and mechanisms are utilized to boost the potency of the method in escaping from local optima and improving the accuracy of the results. Kaveh et al. [16] suggested an efficient hybrid optimization algorithm based on invasive weed optimization algorithm and shuffled frog-leaping algorithm for optimum design of skeletal frame structures. Another metaheuristic optimization technique based on the idea of universe evolution is the Big Bang–Big Crunch (BB–BC) algorithm [17]. Tang et al. [18] have used the algorithm in structural systems for parameter calculation. The BB–BC method was first used in the optimal design of structural constructions by Camp [19]. In the optimization of planner steel sway frames, Kaveh and Abbasgholiha [20] have utilized the BB–BC algorithm. The efficiency of this algorithm in finding benchmark optimization instances was lately assessed by [21]. One of the latest researches corresponds to the charged system search [22]. The method is centered on ideas from physics and mechanics that use the rules of physics of Coulomb and Gauss and the motion of Newtonian mechanics. CSS has various agents known as charged particles (CP). Each CP may be regarded as a charged sphere of radius $a$, which has a uniform charge density and can impose electric force on other CPs under the Coulomb legislation. This force for the CP positioned within the sphere is proportional to the separation distance among the CPs and for the CP positioned outside the sphere is reciprocally proportional to the square of these parathion distances among the charged particles [23]. The superimposed pressures and the motion regulations define the new position of the CPs. In this stage, the following forces and their prior velocity are moved by every CP. To optimize this method, the exploring and the exploitation paradigms of the algorithm are very well balanced and improve the effectiveness of this algorithm.

The efficiency of the ACSS algorithm in structures with new shaped sections (box-shaped) columns is considered. The remaining document is structured accordingly: Sect. 2 describes an optimal steel frame design issue employing the AISC-LRFD [24] regulations. The ACSS algorithm is presented in Sect. 3 after a brief introduction to CSS. Section 4 comprises the design of two steel frame structures. This paper ends with a concluding section.

2 Optimal design of steel frames by AISC-LRFD

The frame columns are selected from the box-shaped sections for practical applications that are made using plates that satisfy the limitations on strength and displacement based on AISC-LRFD [24] code and other members are selected from the existing steel sections which results in a discrete size optimization problem. For a structure consisting of $N_{\text{m}}$. members, decomposed into $N_{\text{d}}$. design groups, the objective function of layout optimization is defined by Eq. (1) to minimize the weight of the frame:

$${\text{Weight}} = \mathop \sum \limits_{i = 1}^{{N_{\text{d}} }} \rho_{i} \cdot A_{i} \mathop \sum \limits_{j = 1}^{{N_{t} }} L_{j}$$

(1)

where $\rho_{i}$ is the steel section unit weight, $A_{i}$ and $L_{j}$ are the steel section area and length, and $N_{t}$ is the members’ number [25]. In this respect, several construction limitations, including strength and serviceability constraints, are required to determine the minimum weight of the structure. The following design constraints ($C_{\text{IEL}}^{i}$ and $C_{\text{IEL}}^{v}$) must be met for strength necessity, by following the AISC-LRFD [24] practice code.

$$C_{\text{IEL}}^{i} = \left[ {\frac{{P_{uJ} }}{{\phi P_{n} }}} \right]_{\text{IEL}} + \frac{8}{9}\left( {\frac{{M_{uxJ} }}{{\phi_{\text{b}} M_{nx} }} + \frac{{M_{uyJ} }}{{\phi_{b} M_{ny} }}} \right)_{\text{IEL}} - 1 \le 0\quad {\text{for}}\quad \left[ {\frac{{P_{uJ} }}{{\phi P_{n} }}} \right]_{\text{IEL}} \ge 0.2$$

(2)

$$C_{\text{IEL}}^{i} = \left[ {\frac{{P_{uJ} }}{{2\phi P_{n} }}} \right]_{\text{IEL}} + \left( {\frac{{M_{uxJ} }}{{\phi_{b} M_{nx} }} + \frac{{M_{uyJ} }}{{\phi_{b} M_{ny} }}} \right)_{\text{IEL}} - 1 \le 0{\kern 1pt} \quad {\text{for}}\quad \left[ {\frac{{P_{uJ} }}{{\phi P_{n} }}} \right]_{IEL} < 0.2$$

(3)

$$C_{\text{IEL}}^{i} = \left( {V_{uj} } \right)_{\text{IEL}} - \left( {\phi_{v} V_{n} } \right) \le 0$$

(4)

In Eqs. (2)–(4),${\text{IEL}} = 1,2, \ldots ,{\text{NEL}}$ is the element number,${\text{NEL}}$ is the entire number of the components, $J = 1,2, \ldots ,N$ is the number for the load combination and $N$ is the entire number of load design combinations. $P_{uj}$ is the necessary axial (tensile or compressive) strength, under $j{\text{th}}$ design load combination. $M_{uxj}$ and $M_{uyj}$ are the required flexural strengths for bending about $x$ and $y$, under the $j{\text{th}}$ layout load combination, severally, where subscripts x and y are the relating symbols for strong and weak axes bending, severally. Then again, $P_{n},$ $M_{nx}$ and $M_{ny}$ are the nominal axial (tensile or compressive) and flexural strengths of the ${\text{IELth}}$ member under evaluation (for bending about x- and y-axes). $\phi$ is the resistance factor for axial strength, which is $0.9$ for compression and $0.9$ for tension (based on yielding in the gross section). Here, $\phi_{b}$ is the resistance factor for flexure that is equal to $0.9$. Here, Eq. (4) is utilized for checking members’ shear capacity wherein $V_{uj}$ is the required shear strength under the $j{\text{th}}$ load combination and $V_{n}$. is the nominal shear strength of the ${\text{IELth }}$ member under evaluation. The nominal shear strength is multiplied by a resistance variable in an attempt to calculate the construction shear strength $\phi_{b}$ of 0.9 [24].

The serviceability restrictions should be incorporated in the design process in addition to the resistance requirements. This study formulates the following serviceability criteria ($C_{D}^{t}$ and $C_{F}^{d}$):

$$C_{D}^{t} = \Delta_{{{\text{Max}}J}} - \Delta_{\text{Max}}^{a} \le 0$$

(5)

$$C_{F}^{d} = \left[ {\delta_{J} } \right]_{F} - \left[ {\delta^{a} } \right]_{F} \le 0$$

(6)

The lateral structure maximum displacement in the $D{\text{th}}$ direction ($D = 1, \ldots ,ND$.) under the $j{\text{th}}$ load combination $\Delta_{{{\text{Max}}J}}$. with maximum permissible lateral displacements $\Delta_{\text{Max}}^{a}$ is compared by Eq. (5). Likewise, Eq. (6) controls the inter-story drift of the $h$ story ($F = 1,2, \ldots ,NF$. under the $j{\text{th}}$ load combination $\left[ {\delta_{J} } \right]_{s}$ against the associated authorized val $\left[ {\delta^{a} } \right]_{s}$. Here, the number of the frame storeys is shown by $NF$.

2.1 Using box-shaped sections for columns

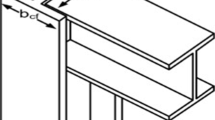
The W-shaped cross-sections are the commonly used sections for steel frame design optimization in previous studies. However, in this research, the advanced charged system search algorithm is used to specify the optimum design of steel frames with the box-shaped sections. The details of examples are depicted in Fig. 1. In other words, box-shaped sections are used for columns and W-shaped sections are used for beams and bracing. Nowadays, the demand of using box-shaped sections for columns is increasing especially for the structures with high-rise buildings. In practice, box-shaped sections might be more easily constructed especially in areas less technologically advanced. One of the merits of box-shaped sections is that it will have the same moment capacity in both directions, needless to say, the moment capacity will almost be the same. In the current work, the objective function is the weight of the structure, and the design is founded on AISC-LRFD [24].

Fig. 1

The 1026 and 1935 members sections detailed at a specific point

2.2 Nominal strengths

The nominal tensile strength of an element, based on yielding within gross section output, is the same according to AISC-LRFD [24] specification:

$$P_{\text{no}} = F_{y} A_{\text{gr}}$$

(7)

where $F_{y}$ is the member’s specified yield stress and $A_{\text{gr}}$ is the member’s gross cross-section. A member’s nominal strength of compression is the smallest from the restricted states of flexural buckling, torsional buckling, and flexural–torsional buckling, bending, torsional and bending torsional states. For members with compact and/or non-compact members, a member’s nominal strength of compression for the restricted state of flexural buckling is as below:

$$P_{\text{no}} = F_{\text{cr}} A_{\text{gr}}$$

(8)

where $F_{\text{cr}}$ is the critical stress depending on a member’s flexural buckling, so the simplified procedure is as follows:

$${\text{for}}\quad \frac{kl}{r\pi }\sqrt {\frac{{F_{y} }}{E}} \le 1.5 \Rightarrow F_{\text{cr}} = \left( {0.658^{{\lambda_{c}^{2} }} } \right)F_{y}$$

(9)

$${\text{for}}\quad \frac{kl}{r\pi }\sqrt {\frac{{F_{y} }}{E}} > 1.5 \Rightarrow F_{cr} = \left( {\frac{0.877}{{\lambda_{c}^{2} }}} \right)F_{y}$$

(10)

In the relationships mentioned above, l the unbraced lateral length of the member is defined by $l$, the effective length factor is defined by $K$, $r$ is the governing radius of gyration about the axis of buckling and the modulus of elasticity is defined by $E$.

The code of the AISC-LRFD deals with the nominal compressive strength based on the limited state of the torsional and flexural–torsional buckling, for doubly symmetric component with compact and/or non-compact elements. Equation (8) with the following modifications still applies to this limited state:

$${\text{for}}\quad \lambda_{e} > 1.5 \Rightarrow F_{\text{cr}} = \left( {\frac{0.877}{{\lambda_{e}^{2} }}} \right)F_{y}$$

(11)

$${\text{for}}\quad \lambda_{e} \le 1.5 \Rightarrow F_{\text{cr}} = \left( {0.658^{{\lambda_{e}^{2} }} } \right)F_{y}$$

(12)

where

$$\lambda_{e} = \sqrt {\frac{{F_{y} }}{{F_{e} }}}$$

(13)

$$F_{e} = \left[ {\frac{{\pi^{2} EC_{\text{w}} }}{{\left( {K_{z} l_{z} } \right)^{2} }} + GJ} \right]\frac{1}{{I_{x} + I_{y} }}$$

(14)

In Eq. (14), the warping constant is described by $C_{\text{w }}$, the shear modulus is defined by $G$, the torsional constant is described by $J$, the moments of inertia on the main axes are defineby $I_{x}$. and $I_{y}$, the unbraced length is described by $l_{z}$ for torsional buckling, and the effective length factor is defined by $K_{z}$ for the torsional buckling. In the current rearch, $K_{z}$ is considered as conservative unity.

The nominal flexural force of doubly symmetric I-shaped components and channels bent over their main axis, the minimum size achieved with compact webs and flanges is the limited yield states, lateral-torsional buckling, flange local buckling, and web local buckling. The flexing capability is as follows based on the limited yield state:

$$M_{n} = M_{p} = Z_{x} F_{y}$$

(15)

where the plastic modulus is defined by $Z$. The bending capability of doubly symmetrical segments is as follows, given the limited state of lateral-torsional buckling:

$$M_{n} = \left\{ {\begin{array}{*{20}l} {M_{p} } \hfill & {{\text{if}}\;L_{b} \le L_{p} } \hfill \\ {C_{b} \left[ {M_{p} - \left( {M_{p} - 0.7F_{y} S_{x} } \right)\left( {\frac{{L_{b} - L_{p} }}{{L_{r} - L_{p} }}} \right)} \right] \le M_{p} } \hfill & {{\text{if}}\;L_{p} < L_{b} \le L_{r} } \hfill \\ {M_{n} = F_{{cr}} S_{x} = M_{p} } \hfill & {{\text{if}}\;L_{b} > L_{r} } \hfill \\ \end{array} } \right.$$

(16)

where the length between points is $L_{b}$, which is either tied to the side of the compression flanges or twisted against the cross-section, $L_{p}$ is the laterally unbraced limited length for complete plastic bendg potential (Eq. 18), $L_{r}$ is the unbraced inelastic lateral-torsional buckling limited length prescribed by Eq. (19), $C_{\text{w}}$ and $r_{\text{ts}}$ are described through Eqs. (21) and (22), for dual symmetrical I-shaped components with rectangular flanges. Equation (22) defined the modifying factor for $C_{b}$, a non-uniform moment diagram:

$$L_{p} = 1.76r_{y} \sqrt {\frac{E}{{F_{y} }}}$$

(17)

$$L_{r} = 1.95r_{\text{ts}} \frac{E}{{0.7F_{y} }}\sqrt {\frac{Jc}{{S_{x} h_{z} }}} \sqrt {1 + \sqrt {16.76\left( {\frac{{0.7F_{y} }}{E} + \frac{{S_{x} h_{z} }}{Jc}} \right)^{2} } }$$

(18)

where

$$r_{\text{ts}}^{2} = \frac{{\sqrt {I_{y} C_{\text{w}} } }}{{S_{x} }}$$

(19)

$$C_{\text{w}} = \frac{{I_{y} h_{z}^{2} }}{4}$$

(20)

$$C_{b} = \frac{{12.5M_{\text{Max}} }}{{2.5M_{\text{Max}} + 3M_{A} + 4M_{B} + 3M_{C} }}$$

(21)

For a doubly symmetric I-shaped component, $c$ = 1 and the $h_{z}$ is the distance from the flange center when the maximum moment, the quarter-point, the centerline and the three-quarter-point of the unbraced sections are prescribed for $M_{ \hbox{max} }$, $M_{A}$, $M_{B}$ and $M_{C}.$

The nominal flexural strength, $M_{n}$, of members with doubly symmetric box-shaped sections bent about either axis, having compact or non-compact webs and compact, non-compact or slender flanges, is the smallest value achieved by the yield limit states (plastic moment), flange local buckling and web local buckling under pure flexure. The bending capability depending on the limited yield is the following:

$$M_{n} = M_{p} = Z_{x} F_{y}$$

(22)

where $Z$ is the plastic section modulus about the axis of bending. The bending capacity, given the restricted lateral-torsional buckling status, is as follows for box-shaped sections:

$$M_{n} = \left\{ {\begin{array}{*{20}l} {M_{p} } \hfill & {{\text{for}}\;{\text{compact}}} \hfill \\ {\left[ {M_{p} - \left( {M_{p} - F_{y} S} \right)\left( {3.57\frac{b}{t}\sqrt {\frac{{F_{y} }}{E}} - 4} \right)} \right] \le M_{p} } \hfill & {{\text{for}}\;{\text{noncompact}}\;{\text{flanges}}} \hfill \\ {M_{n} = {\text{F}}_{y} S_{{{\text{eff}}}} } \hfill & {{\text{for}}\;{\text{slender}}\;{\text{flanges}}} \hfill \\ \end{array} } \right.$$

(23)

where $S_{\text{eff}}$ the efficient sectional modulus with an effective width is defined as $S_{\text{eff}}$, $b_{e}$, so the flange of compression is considered as:

$$b_{e} = 1.92t\sqrt {\frac{E}{{F_{y} }}} \left[ {1 - \frac{0.38}{b/t}\sqrt {\frac{E}{{F_{y} }}} } \right] \le b_{ }$$

(24)

The bending capacity of the box-shaped sections is as follows, considering the limited state of the web:

$$M_{n} = \left\{ {\begin{array}{*{20}l} {M_{p} } \hfill & {{\text{for}}\;{\text{compact}}} \hfill \\ {\left[ {M_{p} - \left( {M_{p} - F_{y} S_{x} } \right)\left( {0.305\frac{h}{{t_{w} }}\sqrt {\frac{{F_{y} }}{E}} - 0.738} \right)} \right] \le M_{p} } \hfill & {{\text{for}}\;{\text{noncompact}}\;{\text{flanges}}} \hfill \\ \end{array} } \right.$$

(25)

The nominal shear strength $V_{n}$ for unstiffened or stiffened webs is written according to the restriction conditions of shear yield and shear buckling as:

$$V_{n} = 0.6F_{y} A_{w} C_{w}$$

(26)

The following is used for the webs of rolled I-shaped

$${\text{for}}\quad h_{s} /t_{w} \le 2.24\sqrt {E/F_{y} } \quad C_{v} = 1$$

(27)

The web shear coefficient $C_{v}$ is determined as follows for webs with any other single symmetric shapes, double symmetric and channels except round HSS.

$${\text{for}}\quad h_{s} /t_{w} \le 1.10\sqrt {K_{v} E/F_{y} } \quad C_{v} = 1$$

(28)

$${\text{for}}\quad 1.10\sqrt {K_{v} E/F_{y} } < h_{s} /t_{w} \le 1.37\sqrt {K_{v} E/F_{y} } \quad C_{v} = \frac{{1.10\sqrt {K_{v} E/F_{y} } }}{{h_{s} /t_{w} }}$$

(29)

$${\text{for}}\quad h_{s} /t_{w} > 1.37\sqrt {K_{v} E/F_{y} } \quad C_{v} = \frac{{1.51EK_{v} }}{{\left( {h_{s} /t_{w} } \right)^{2} F_{y} }}$$

(30)

where the web thickness is defined by $t_{w}$. The web plate’s coefficient,$K_{v}$, is determined as follows:

For not stiffed web with $h_{s} /t_{w} < 260$, $K_{v} = 5$ except for the stem of tee shapes where $k_{v} = 1.2$ and for the stiffed web we have:

$$K_{v} = 5 + \frac{5}{{(a/h)^{2} }} = 5\quad {\text{when}}\quad a/h > 3\quad {\text{or}}\quad a/h > \left[ {\frac{260}{{h_{s} /t_{w} }}} \right]^{2}$$

(31)

where the clear distance between transverse stiffeners is prescribed by $a$ and the clear distance between flanges without the fillet or corner for rolled shapes is defined by $h$.

2.3 Effective length factor $K$

The efficient length factor K must be determined for each member to calculate the nominal compressive strength. This factor can be calculated using the Jackson and Moreland frame buckling monograph, Ref. [26]. The effective column length factor is calculated as follows for the sway frames:

$$\frac{{ \alpha^{2} G_{i} G_{j} - 36}}{{6\left( {G_{i} + Gj} \right)}} = \frac{\alpha }{\tan \alpha }$$

(32)

$$G_{i} = \frac{{\sum I_{ci} /l_{ci} }}{{\sum I_{bi} /l_{bi} }},\quad G_{j} = \frac{{\sum I_{cj} /l_{cj} }}{{\sum I_{bj} /l_{bj} }}$$

(33)

where $\alpha = \pi /K$, $i$ and $j$ are subscripts corresponding to end-$i$ and end-$j$ of the member in compression, and subscripts $c$ and $b$ refer, respectively, to the beams and columns connected to the joint being considered. In those equations’ parameters, I and l represent, respectively, the moment of inertia and the unbraced distance of the member. The $K$ factor is taken here for components of the beams, bracings and non-sway columns as 1.$1$.

3 The CSS optimization algorithm

The charged search system is based on the electrostatic and Newtonian mechanics laws [22]. Inside and outside the electric field $\left( {E_{ij} } \right)$ of the charged insulating solid sphere, the Coulomb and Gauss law provide the magnitude of the electric field as follows:

$$E_{{ij}} = \left\{ {\begin{array}{*{20}l} {\frac{{K_{e} q_{i} }}{{a^{3} }}r_{{ij}} } \hfill &\quad {{\text{if}}\;r_{{ij}} < a} \hfill \\ {\frac{{K_{e} q_{i} }}{{r_{{ij}}^{2} }}} \hfill &\quad {{\text{if}}\;r_{{ij}} > a} \hfill \\ \end{array} } \right.$$

(34)

where the constant known as the Coulomb constant is defined by $K_{e}$, the sphere center separation and the chosen point is described by $r_{ij}$, the magnitude of the charge is described as $q_{i}$, and the radius of the charged sphere is defined by $a$. Using the superimposition principle, the resulting electric force thanks to $N$ charged spheres ($F_{j}$) is equal to:

$$F_{j} = k_{e} q_{j} \mathop \sum \limits_{i,j \ne i} \left( {\frac{{q_{i} }}{{a^{3} }}r_{ij} \cdot i_{1} + \frac{{q_{i} }}{{r_{ij}^{2} }} \cdot i_{2} } \right)\frac{{r_{i} - r_{j} }}{{r_{i} - r_{j} }} \quad \left\{ {\begin{array}{*{20}l} {i_{1} = 1, } \\ {i_{1} = 0, } \\ \end{array} } \right.\begin{array}{*{20}c} {i_{2} = 0 \; \Leftrightarrow \;r_{ij} < a} \\ {i_{2} = 1\; \Leftrightarrow \;r_{ij} \ge a} \\ \end{array}$$

(35)

Also, we have based on the mechanics of Newtonian:

$$\Delta r = r_{\text{new}} - r_{\text{old}}$$

(36)

$$v = \frac{{r_{\text{new}} - r_{\text{old}} }}{{t_{\text{new}} - t_{\text{old}} }} = \frac{{r_{\text{new}} - r_{\text{old}} }}{\Delta t}$$

(37)

$$a = \frac{{v_{\text{new}} - v_{\text{old}} }}{\Delta t}$$

(38)

where $r_{\text{old}}$ and $r_{\text{new}}$ are a particle’s first and last place, respectively; The particle velocity is described as $v$ and a is the particle acceleration. Using Newton’s second law, the displacement of any object in the function of time is achieved by combining the above equations:

$$r_{\text{new}} = \frac{1}{2}\frac{F}{m} \cdot \Delta t^{2} + v_{\text{old}} \cdot \Delta t + r_{\text{old}}$$

(39)

The following are the pseudo-codes in the CSS algorithm based on the above electrostatic and Newtonian mechanical laws [22].

3.1 Level 1: Initialization

Step 1:

Initialization. Allocate an initial CSS algorithm parameter. Set up an array of randomly located charged particles (CPs). The CPs’ starting velocity is zero. Each CP has the magnitude charge $\left( q \right)$ achieved by taking into account the quality of its solution:

$$q_{i} = \frac{{{\text{fit}}\left( i \right) - {\text{fitworst}}}}{{{\text{fitbest}} - {\text{fitworst}}}}\quad i = 1, 2, 3, \ldots , N$$

(40)

where ${\text{fit}}_{\text{best}}$ and ${\text{fit}}_{\text{worst}}$ are all the best and worst particle fitness; ${\text{fit}}\left( i \right)$. is the agent’s fitness $i$. $r_{ij}$ is prescribed for separation between two charged particles as:

$$r_{ij} = \frac{{X_{i} - X_{j} }}{{\left( {X_{i} - X_{j} } \right)/2 - X_{\text{best}} + \varepsilon }}$$

(41)

where $X_{i}$ and $X_{j}$, the positions are, respectively, the $i{\text{th}}$ and $j{\text{th}}$ CPs, $X_{\text{best}}$ is the best current CP’s position, and ε is a little positive number to avoid singularities.

Step 2:

CP Ranking. Measure the magnitude of the fitness function for the CPs. Compare and arrange in ascending order with one another.

Step 3:

CM Creation. Save the first CPs number equal to the memory charged size (CMS) and their related magnitude of the fitness functions in the charged memory (CM).

3.2 Level 2: Searching

Step 1:

Attracting force determination. Indicate the probability that each CP moves to the other in the following probability function:

$$P_{{ij}} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\frac{{{\text{fit}}\left( i \right) - {\text{fitbest}}}}{{{\text{fit}}\left( j \right) - {\text{fit}}\left( i \right)}} > {\text{rand}} \vee {\text{fit}}\left( j \right) > {\text{fit}}\left( i \right)} \hfill \\ 0 \hfill & {{\text{else}}} \hfill \\ \end{array} } \right.$$

(42)

and measure the vector of force attraction of each CP as follows:

$$F_{j} = q_{j} \mathop \sum \limits_{i,j \ne i} \left( {\frac{{q_{i} }}{{a^{3} }}r_{ij} \cdot i_{1} + \frac{{q_{i} }}{{r_{ij}^{2} }} \cdot i_{2} } \right)P_{ij} \left( {X_{i} - X_{j} } \right) \quad \left\{ {\begin{array}{*{20}l} { j = 1, 2, \ldots , N } \\ {i_{1} = 1, \;i_{2} = 0\; \Leftrightarrow \;r_{ij} < a} \\ {i_{1} = 0, \;i_{2} = 1 \Leftrightarrow \;r_{ij} \ge a} \\ \end{array} } \right.$$

(43)

where $F_{j}$. is defined as the resultant force affecting the $j{\text{th}}$ CP.

Step 2:

Solution construction. Depart each CP to the new place with the following equations and detect its velocity:

$$X_{{j,{\text{new}}}} = {\text{rand}}_{j1} \cdot k_{a} \cdot \frac{{F_{j} }}{{m_{j} }} \cdot \Delta t^{2} + {\text{rand}}_{j2} \cdot k_{v} \cdot v_{{j,{\text{old}}}} \cdot \Delta t + X_{{j,{\text{old}}}}$$

(44)

$$v_{{j,{\text{new}}}} = \frac{{X_{{j,{\text{new}}}} - X_{{j,{\text{old}}}} }}{\Delta t}$$

(45)

where ${\text{rand}}_{j1}$. and ${\text{rand}}_{j2}$. are the two uniformly scattered random numbers in the range. In the current study, $m_{j}$ is the mass of the CPs, equaling to $q_{j}$. Time step is defined as $t$, setting to $1$. The acceleration coefficient is described as k_a; $k_{v}$ is the coefficient of velocity to regulate the impact of the prior velocity. Here, $k_{a}$ and $k_{v}$ are considered as $0.5$.

Step 3:

CP PositioCorrection. Rectify its situation with the harmony search-based managementrocedure when each CP lees the allowed search area

$$\left\{ {\begin{array}{*{20}l} {w.p.\;{\text{CMCR}}} \hfill & {\begin{array}{*{20}l} { \Rightarrow {\text{select}}\;{\text{a}}\;{\text{new}}\;{\text{value}}\;{\text{for}}\;{\text{variable}}\;{\text{form}}\;CM} \\ { \Rightarrow w.p.\;(1 - {\text{PAR}})\;{\text{do}}\;{\text{nothing}}} \\ { \Rightarrow w.p.\;{\text{PAR}}\;{\text{choose}}\;{\text{a}}\;{\text{neighnoring}}\;{\text{value}}} \\ \end{array} } \hfill \\ {w.p.\;(1 - {\text{CMCR}})} \hfill & { \Rightarrow {\text{select}}\;{\text{a}}\;{\text{new}}\;{\text{value}}\;{\text{randomly}}} \hfill \\ \end{array} } \right.$$

(46)

where “w.p.” stands for “with the probability” and $x_{i,j }$. is the $i{\text{th}}$ member of the $j$ th CP. The charged memory considering rate (CMCR), which varies from 0 to 1, sets the rate of selection in the new vector of the historical magnitude saved in the CM, and (1 − CMCR) sets the rate at which a value from possible value is randomly selected. The pitch adjustment is done only after CM selects a value. The value (1 − PAR) defines the rate of nothing being done, and PAR sets the rate at which a value is selected from the nearest CP. The reader may refer to Ref. [22] for more information.

Step 4:

CP ranking. Calculate and compare the fitness values for the current CPs, and arrange them in the ascending order.

Step 5:

CM updating. If some of new CP vectors are better than the worst in the CM, add better vectors to the CM and exclude the worse ones from CM as regards their objective functional values.

3.3 Level 3: controlling the terminating criterion

Repeat the steps in the search level until a final criterion is met.

3.4 Advanced charged system search algorithm

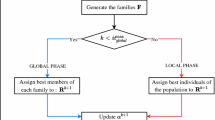
In this section, a new hybrid algorithm ACSS is suggested to enhance the performance of the CSS. In this work, three effective strategies are considered to design the new ACSS. The fit one is an improved initialization based on opposite-based learning and subspacing techniques. The second one uses previous information indirectly after their generation. The third one is Levy flight random walk for enriching the updating process of the algorithm. By enhancing the optimization process, the power of rules proliferates, and the power of randomization diminishes.

3.4.1 Basic steps of the ACSS algorithm

The following steps are summarized:

Step 1:

Initialization:

CP arrays or initial positions are randomly determined in the search area, while initial CP speed assumption is zero. The fitness magnitudes for the CPs are calculated and the CP is classified ascending. The best CP in the entire group of CPs is considered $X{\text{best}}$ with the best fitness (${\text{fitbest}}$). Similarly, the worst CP is considered as ${\text{fitworst}}$.

The problem independence and weak reliance on initialization are two main features of metaheuristics. However, some algorithms like CSS and harmony search use storage to store the finest results from the start. An improved initialization can, therefore, be helpful in the process, especially in large search spaces that exist in optimization issues. On the other hand, the CSS, which uses an initializing search space, uses fourfold initialization space as the CSS space and to the CSS three new spaces will be added [27]. First, the ACSS is started as a CSS. Next, the concept of opposition-based learning (OBL) is used to initialize space two. OBL, the latest idea in soft computing to speed up convergences between diverse optimizers, has been created by Tizhoosh et al. [28]. The OBL employs population and its opposite counterparts to develop better potential solutions. Many studies have shown that OBL offers the opportunity to find the global best [29]. Optimal solutions tend to be near domain borders and therefore a domain may be segregated to the upper and lower bound subdomains to meet these conditions. The third and fourth spaces are initialized from the lower and upper limited subdomains. As a consequence, the following four spaces are presented as part of the initialization of the ACSS:

Space 1:

$$x_{i,j}^{{{\text{Initial}}1}} = x_{{i,{ \hbox{min} }}} + {\text{rand}} \cdot \left( {x_{{i,{ \hbox{max} }}} - x_{{i,{ \hbox{min} }}} } \right)\quad i = 1,2,3, \ldots ,nv$$

(47)

Space 2:

$$x_{i,j}^{{{\text{Initial}}2}} = x_{{i,{ \hbox{max} }}} + x_{{i,{ \hbox{min} }}} - x _{i,j}^{{{\text{Initial}}1}} \quad i = 1,2,3, \ldots ,nv$$

(48)

Space 3:

$$x_{i,j}^{{{\text{Initial}}3}} = x_{{i,{ \hbox{min} }}} + {\text{rand}} \cdot \left( {\frac{{x_{{i,{ \hbox{max} }}} + x_{{i,{ \hbox{min} }}} }}{2} - x_{{i,{ \hbox{min} }}} } \right)\quad i = 1,2,3, \ldots ,nv$$

(49)

Space 4:

$$x_{i,j}^{{{\text{Initial}}4}} = \frac{{x_{{i,{ \hbox{max} }}} + x_{{i,{ \hbox{min} }}} }}{2} + {\text{rand}} \cdot \left( {x_{{i,{ \hbox{max} }}} - \frac{{x_{{i,{ \hbox{max} }}} + x_{{i,{ \hbox{min} }}} }}{2}} \right)\quad i = 1,2,3, \ldots ,nv$$

(50)

In the charged memory (CM), the best solutions from the four spaces are now saved without changing the CM size of the CSS. During the iterative procedure, no further calculation effort has been introduced to the algorithm. This means that all four spaces are only used to initialize. CM is a matrix in which several of the best CPs and their associated fitness values are saved. In this case, the rand is the random number uniformly distributed from [0,1].

Step 2:

Solution construction:

• Forces determination The force vector is calculated as Eq. (39) for the $j{\text{th}}$ CP.

• Creation of a new position. As specified by Eqs. (39) and (40), each CP has moved to the new situation. It should be observed that the location of each CP should be determined by Eq. (40), instead of the previous agents the last position is used and this contributes to the use of the previous data. The objective function is calculated after shifting the CP to its new position. Iteration changes continuously in the current algorithm and all updating processes take place after the creation of just one solution. The new position of each agent using ACSS algorithm can influence the movements of the subsequent CPs, while the new positions in the standard CSS will not be utilized unless an iteration is completed. Thus, the current location of each agent is used in the ACSS algorithm for the subsequent search, which improves not only the optimization of the current algorithm but also the velocity of the convergence [30].

Step 3:

Using Levy flight for updating

The Levy flight algorithm is suggested to improve a random exploration, as earlier stated. Levy flight is an effective random track that has lately effectively been introduced in optimization methods [31]. Levy movement is a non-Gaussian discrete method based on Levy as a power-law formulation:

$$L\left( s \right) \approx \left| s \right|^{ - 1 - \beta }$$

(51)

where the stability parameter is described as $\beta$ in the range (0, 2). A simple version of Levy distribution can be ruled out in the mathematical example:

$$L\left( {s,\gamma ,\mu } \right) = \left\{ {\begin{array}{*{20}l} {\sqrt {\frac{\gamma }{{2\pi }}} \exp \left[ { - \frac{\gamma }{{2\left( {s - \mu } \right)}}} \right]\frac{1}{{(s - \mu )^{{\frac{3}{2}}} }}} \hfill & {{\text{if}}\;0 < \mu < s < \infty } \hfill \\ 0 \hfill & {{\text{if}}\;s \le 0} \hfill \\ \end{array} } \right.$$

(52)

in which $\mu$ is the shift parameter, $\gamma > 0$ parameter is the distribution control scale and the skewness parameter is prescribed by $\alpha$ within the interval [− 1,1].

In this context, Levy flight is incorporating the influence of the best local best solution, $X_{\text{best}}$, to improve the algorithm. By incorporating Levy flight to the updated procedure, ACSS will have a new particle location as follows [27]:

$$X_{{j,{\text{new}}}} = {\text{rand}}_{j1} \cdot F_{j} + {\text{rand}}_{j2} \cdot k_{v} \cdot V_{{j,{\text{old}}}} + {\text{rand}}_{j3} \cdot \alpha \cdot {\text{Levy}}\left( \beta \right) + X_{{j,{\text{old}}}}$$

(53)

where the new speed is defined as:

$$V_{{j,{\text{new}}}} = X_{{j,{\text{new}}}} - X_{{j,{\text{old}}}}$$

(54)

The step size is the scale of the problem and the non-trivial step forming scheme is defined as:

$${\text{rand}}_{j3} \cdot \alpha \cdot {\text{Levy}}\left( \beta \right) \approx 0.01\frac{u}{{\left| \nu \right|^{{\frac{1}{\beta }}} }}\left( {X_{\text{best}} - X_{{j,{\text{old}}}} } \right)$$

(55)

When u and μ with normal distribution are selected randomly:

$$u \approx N\left( {0,\sigma_{u}^{2} } \right),\quad \nu \approx N\left( {0,\sigma_{v}^{2} } \right)$$

(56)

in which ${\text{rand}}_{j1}$, ${\text{rand}}_{j2 }$ and ${\text{rand}}_{j3}$ are uniformly distributed random numbers in the domain [0,1]. This method immediately implements the impact of the best particles during the update procedure. Furthermore, the ACSS has no acceleration coefficient $k_{a}$, and it only has the same CSS’s $k_{v}$ but with values $c_{v}$ equal or less than those of the CSS. $k_{v}$ is known as a decreasing function for stabilizing the effects of the previous speed and controlling the exploration procedure. The function is therefore described as:

$$k_{v} = c_{v} \times \left[ {1 - \left( {\frac{\text{iter}}{{{\text{iter}}_{ \hbox{max} } }}} \right)} \right]$$

(57)

where ${\text{iter}}$ is the current iteration number and ${\text{iter}}_{ \hbox{max} }$ is the maximum iteration numbers. cv has steady values to adapt to the problem of optimization. Exploration is the ability of an algorithm for searching during iterations and should be reduced for two reasons by increasing the iterations [27]. The first is to use the algorithm’s ability (exploitation) to further improve the alternatives that have been achieved. Convergence is the second reason. So, Eq. (53) offers for a decrease in searchability, whereas the ACSS sees a change in the solution as an exploitation ability during iterations, and such changes shall be made by the first term and the new term described in Eq. (49). When the new CP exits the allowed search space during the updating process, similar to the CSS, a harmonious search-based handling may be employed when a new CP exits the permitted search zone, to rectify its position oriented on the search space of the issue conducted. This strategy requires the regeneration of any solution vector component violating the variable borders from a CM or a random value that is selected for the possible range. Besides, if some new CP vectors are better than those of the CM, the worst ones in CM are replaced and the worst vectors are removed.

Step 4:

Terminating criterion control:

• Terminating criterion control. Steps 2 and 3 are repeated until a final criterion has been fulfilled.

4 Numerical examples

In this paper, the efficiency of using the steel box-shaped instead of I-shaped sections for columns based on AISC-LRFD [24] is compared. The optimization is carried out with ACSS algorithm and tested with three layout optimization examples of real structures. The outcomes are compared with those of the UBS (upper bound strategy) unified versions of the BB–BC algorithms [32]. It is important to emphasize that an enhancement of the algorithm in terms of weight with the new shaped sections of the columns is intended in this paper. Each issue is solved 30 times independently for a more accurate study. The algorithm used in MATLAB 2018 has been coded and structures are analyzed using a direct stiffness method in combination with the structural evaluation package SAP2000 v16 for analysis and designing sampled structural systems, using an application programming interface (API), throughout the optimization process. The current work is done with the following features on the computer: CPU 2.3 GHZ (an Intel Core i9 computer platform), Ram 16 GB and MATLAB 2018 running on a computer with Macintosh (macOS Mojave).

The wide-flange $\left( W \right)$ profile and steel box-shaped columns are used to size the structural members. Steel’s material properties are modulus of elasticity $\left( E \right) = 200\;{\text{GPa}}$, yield stress $\left( {F_{y} } \right) = 248.2$ MPa, and unit weight of the steel $\left( q \right) = 7.85\;{\text{ton}}/{\text{m}}^{3}$. Many examples should be carried out with an independent population initialization to get the output of the strategy to be successful. These problems include a ten-story frame with 1026 members and a 19-story frame with 1935 members to demonstrate the effectiveness of the ACSS algorithm. Results of each problem are then taken into account by some other optimization methods compared with available solutions. In each instance, both CSS and ACSS employ the same number of analyses and agents to compete reasonably.

4.1 Example 1: The 10-story frame with 1026 members

The frame with ten storeys depicted in Fig. 2 has been considered for the first instance [32]. This structure has 1026 members, including 580 beams, 96 bracing elements, and 350 columns. Besides inverted X-type bracing systems next to the x-direction, the stability of the structure is ensured by the use of moment-resistant connections. The 1026 frame members are collected in 32 member groups for requirements of practical manufacturing. The group of members is conducted in plan and level. The structural members in elevation are divided into three stories except the first. On the plan level, columns in five groups as shown in Fig. 3 are examined. The beams are classified as outer and inner beams in two groups; bracings are supposed to be in one group. Thus, there are a total of 20 column groups, eight beam groups, and four bracing groups, which are examined in this instance as 32 design variables, based on groupings of elevation and plan level. It should be noted that in the stage of analysis the floor plates are not modeled.

Fig. 2

The 10-story steel frame with 1026 members, a 3D view b side view of frames 2, 3 and 4 c side view of frames 1 and 5 d side view of frames A, B, C, D, E, F and G e plan view

Fig. 3

Columns grouping of the 10-story steel frame with 1026 members in plan level

The ten load combinations are designed as shown in Table 1. There are live loads of $12$ and $7\;{\text{kN}}/{\text{m}}$, respectively, on the floor and on the roof beams. In addition to loads that are distributed uniformly on floor and roof beams with a load of $20$ and $15\;{\text{kN}}/{\text{m}}$, respectively, the structural weight is also taken into account. The earthquake loads are calculated based on AISC [24] lateral force equivalent. Here, the earthquake base shear $\left( {V_{b} } \right)$ that is obtained here is taken as where $V_{b} = 0.1 W_{s}$ the entire dead load of the structure is $W_{s}$. On each floor, the base shear is calculated based using the following equation:

$$f_{x} = \frac{{W_{x} H_{i}^{k} V_{b} }}{{\mathop \sum \nolimits_{i = 1}^{n} W_{i} H_{i}^{k} }}$$

(58)

where $f_{x}$ is the earthquake force of the side at the height of $x$; $W$ is an entire gravity portion of the corresponding level allocated (i.e., level $i$ or $x$); and $H$ is the height from base to the corresponding level. Here, $k$ is indicated according to the period of the structure. Structures with a $0.5\;{\text{s}}$ or less period, the value is equivalent to $1$ and with a period of $2.5\;{\text{s}}$ or more, it equals $2$. $k$ is determined by linear interpolation for structures with the period between $0.5\;{\text{and}}\;2.5 {\text{s}}$. It should be pointed out that the period of the frame shall be calculated using the following equation with AISC [24]:

$$T = C_{T} H_{n}^{3/4}$$

(59)

where $C_{T}$ is considered to be $0.0853$ and $H_{n}$ is the structure’s height, $36.5\;{\text{m}}$ for this particular instance. Hence, the structure’s period, $T$, is taken as $1.267 {\text{s}}$. The parameter $k$ value in Eq. (54) is considered for this structure as 1.025 depending on the period achieved. All of the beam elements are set to unbraced lengths at one-fifth of its length. The floor system constantly braced its beam elements along its lengths and columns and bracing are supposed to be unbraced along its lengths. For all beams and bracings, the effective length factor K is considered to be 1. For the buckling of columns around their minor (weak) direction, the K factor is carefully considered as 1 too, because the frame is not moving in that direction due to X-type bracing systems. However, the $K$ factor is determined by Sect. 2.2 for buckling of the columns in their main direction. The maximum lateral movement of the top level is restricted to $0.1$ ${\text{m}}$, and the upper drift is considered as $h_{t} /400$, where $h_{t}$ is story’s height. The optimal structural weight with W-shaped sections is accomplished using the UBB–BC [32], UMBB–BC [32] and UEBB–BC [32] algorithms. In the current study, the optimum design of the frame with box-shaped columns and I-shaped sections for other members is performed using the CSS and ACSS algorithms. The ten-story frame with 1026 members is optimized to compare with other methods. Convergence curves are indicated in Fig. 4 for these algorithms. It is obvious that 25,000 analyses are needed for other algorithms to converge, while 20,000 analyses are sufficient for the CSS and ACSS algorithms.

Table 1 Load combinations

Fig. 4

Convergence histories of the 10-story steel frame with 1026-member using box-shaped sections

The minimum weight obtained by CSS and ACSS with box-shaped sections is compared to those of some other studies. The element stress ratio of the inter-story drift to the permissible inter-story drift in an optimized frame is shown in Fig. 5. Comprising other algorithms, the ACSS algorithm was better than those. It is important to note that the best solution achieved by this method and using box-shaped sections for column instead of I-shaped sections are 16.58%, 13.58%, 9.57% lighter than those of UBB–BC [32], UMBB–BC [32], UEBB–BC [32], respectively. The optimized ACSS results are given in Table 2. The ratio of the inter-story drift with the allowable inter-story drift, which is calculated for the best design, is shown in the Fig. 6. It is observed from Table 3 that the standard deviation and average of the ACSS are less than those of the standard basic algorithm, showing lower scattering of the ACSS solution and it can also be seen that the ACSS can find the better design.

Fig. 5

The element stress ratio in the optimum frame design of the 10-story steel frame with 1026 members using box-shaped sections

Table 2 Comparison of the optimized 10-story steel frame with 1026 members obtained by CSS and ACS

Fig. 6

The ratio of the inter-story drift to the allowable inter-story drift in the optimum frame design for the 10-story steel frame with 1026 members using box-shaped sections

Table 3 Comparison of the ACSS and CSS for box-shaped sections

4.2 Example 2: The 19-story frame with 1935 members

The frame with 19 stories depicted in Fig. 7 has been considered for the second instance. Besides inverted X-type bracing systems next to the x-direction, the stability of the structure is ensured by the use of moment-resistant connections. The 1935 frame members are collected in 56 member groups for requirements of practical manufacturing. The group of members is conducted in plan and level. The structural members in elevation are divided into three stories except the first. On the plan level, columns in five groups as shown in Fig. 8 are examined. The beams are classified as outer and inner beams in two groups; bracings are supposed to be in one group. Thus, there are a total of 35 column groups, 14 beam groups, and seven bracing groups, which are examined in this instance as 56 design variables, based on groupings of elevation and plan level. It should be noted that in the stage of analysis the floor plates are not modeled.

Fig. 7

The 19-story steel frame with 1935 members, a 3D view b side view of frames 2, 3 and 4 c side view of frames 1 and 5 d side view of frames A, B, C, D, E, F and G e plan view

Fig. 8

Columns grouping of the 19-story steel frame with 1935 members in plan level

The ten load combinations are designed as shown in Table 1. There are live loads of $12$ and $7 {\text{kN}}/{\text{m}}$, respectively, on the floor and on the roof beams. In addition to loads that are distributed uniformly on floor and roof beams with a load of $20$ and $15\;{\text{kN}}/{\text{m}}$, respectively, the structural weight is also taken into account. The earthquake loads are computed based on the same procedure described in the first example. Here, the earthquake base shear $\left( {V_{b} } \right)$ that is obtained here is taken as where $V_{b} = 0.1 W_{s}$ the entire dead load of the structure is $W_{s}$. Further, in Eq. (55), $C_{T}$ is considered $0.0853$ and $H_{n}$ is structure’s height, $68 {\text{m}}$ for this particular instance. Hence, structure’s period, $T$, is taken as $2.019 {\text{s}}$. The parameter $k$ value in Eq. (54) is considered for this structure as $1.7595$ depending on the period achieved. All of the beam elements are set to unbraced lengths at one-fifth of its length. The floor system constantly braced its beam elements along its lengths and columns and bracing are supposed to be unbraced along its lengths. For all beams and bracings, the effective length factor K is considered to be 1. For the buckling of columns around their minor (weak) direction, the K factor is carefully considered as 1 too because the frame is not moving in that direction due to X-type bracing systems. However, the $K$ factor is calculated according to Sect. 2.2 for buckling of the columns in their main direction. The maximum lateral movement of the top level is restricted to $0.1$ ${\text{m}}$, and the upper drift is considered as $h_{t} /400$, where $h_{t}$ is the story’s height.

First, the optimal frame design is performed using CSS and ACSS with ready sections (I-shaped) for all members. The optimization histories for ACSS and CSS are shown in Fig. 9. The ratio of the inter-story drift to the allowable inter-story drift and stress ratio of members evaluated at the best design optimized by the proposed method are illustrated in Figs. 10 and 11. Then, the design of this frame is carried out using box-shaped sections for columns with the same algorithms and the results obtained by CSS and ACSS methods in the literature are given in Table 4. Following 60,000 evaluations, the ACSS method was successful, and an optimum weight of $1951.701\;{\text{ton}}$ with box-shaped sections and $2362.733\;{\text{ton}}$ with I-shaped section columns was found. Convergence curves for these algorithms are displayed in Fig. 12. Results of the standard deviation and average of ACSS are reported in Table 5, being less than those of the CSS, and showing lower scattering of the ACSS solution. This is an improvement on the optimum design using the proposed algorithm. It should be noted that, for this large-scale frame problem, the structure with the box-shaped columns obtained the best results. According to Figs. 13 and 14, stress and displacement constraints are active in this example with new sections.

Fig. 9

Convergence of the 19-story steel frame with 1935 members using I-shaped sections

Fig. 10

The elements stress ratio in the optimum frame design of the 19-story steel frame with 1935 members using I-shaped sections

Fig. 11

The ratio of the inter-story drift to the allowable inter-story drift in the optimum frame design for the 19-story steel frame with 1935 members using I-shaped sections

Table 4 Comparison of the optimized 19-story steel frame with 1935 members obtained by CSS and ACSS

Fig. 12

Convergence histories of the 19-story steel frame with 1935 members using box-shaped sections

Table 5 Comparison of the ACSS and CSS for BOX -shaped sections

Fig. 13

The elements stress ratio in the optimum frame design of the 19-story steel frame with 1935 members using box-shaped sections

Fig. 14

The ratio of the inter-story drift to the allowable inter-story drift in the optimum frame design for the 19-story steel frame with 1935 members using box-shaped sections

5 Concluding remarks

In the current study, a new advance charged system search (ACSS) is proposed for the optimal design of real-size structures using new type of sections for columns. To improve the ACSS, several internal parameters have been introduced to give the algorithm the flexibility to solve complicated problems of optimization and this improves the equilibrium between exploitation and exploration. The added parameters are iteration numbers features, which can accelerate the operation and improve solution performance to achieve better alternatives with a decent computer attempt. Two real-scale structures are investigated to show the performance of the presented ACSS with new type of sections for columns. Numerical outcomes achieved by optimizing the practical design of two real-size structures clearly reveal that the box-shaped sections used for columns are capable of reducing the weight of frames. In particular, for frame examples with 1026 and 1935 members, the corresponding reductions are $9.57\%$, $7.16\%$, and $17.39\%$,$18.10\%$ for ACSS and CSS algorithms. Performance using box-shaped sections for columns is much better than I-shaped sections for large-scale frames with a high number of members. The convergence speed comparisons also show that the utilized algorithm rapidly converges. It is observed from Tables 3 and 5 that the standard deviation and average of the ACSS are less than those of the standard basic algorithm, showing lower scattering of the ACSS solution.

As regards future research, there are many works to be done. To name a few, the presented ACSS with new type of sections can be applied to other structures than 3D frames.