Expanding the Class of Global Objective Functions for Dissimilarity-Based Hierarchical Clustering

Abstract

Recent work on dissimilarity-based hierarchical clustering has led to the introduction of global objective functions for this classical problem. Several standard approaches, such as average linkage clustering, as well as some new heuristics have been shown to provide approximation guarantees. Here, we introduce a broad new class of objective functions which satisfy desirable properties studied in prior work. Many common agglomerative and divisive clustering methods are shown to be greedy algorithms for these objectives, which are inspired by related concepts in phylogenetics.

1 Introduction

Background

In hierarchical clustering, one seeks a recursive partitioning of the data that captures clustering information at different levels of granularity. Classical work on the subject takes an algorithmic perspective. In particular various iterative methods are widely used, including the well-known bottom-up approaches based on single, complete and average linkage schemes, and other variations (see, e.g., [Murphy , 2012 Chapter 25] or [Hastie et al. , 2009 Chapter 14]). Recent work on dissimilarity-based hierarchical clustering in the theoretical computer science literature has emphasized an alternative, optimization-based perspective. It has led to the introduction of global objective functions for this problem (Dasgupta, 2016). Some standard approaches as well as new heuristics have been shown to provide approximation guarantees (Dasgupta, 2016; Roy and Pokutta, 2016; Charikar and Chatziafratis, 2017; Cohen-Addad et al., 2018; Chatziafratis et al., 2018; Charikar te al., 2019; Alon et al., 2020). These new objective functions have also been justified through their behavior on random or structured input models (Dasgupta, 2016; Cohen–Addad et al., 2017; Cohen-Addad et al., 2018; Manghiuc and Sun, 2021). This perspective provides a principled framework to design improved clustering methods and assess them rigorously.

Here, we introduce a broad new class of objective functions which satisfy natural, desirable properties considered in these previous works. As explained in Sect. 2, our work establishes a connection between Dasgupta’s cost function approach (Dasgupta, 2016) and an important class of methods in the phylogenetic reconstruction literature. We show that several common agglomerative and divisive clustering methods, including average linkage clustering and recursive sparsest cut, can be interpreted as greedy algorithms for these objectives, potentially providing new insights into these well-known methods. This observation mirrors related results on the popular Neighbor-Joining method in phylogenetics (see Sect. 2).

Definitions and main results

Our input data is a collection of n objects to be clustered, which we denote without loss of generality $L:= \{1,\ldots ,n\}$, together with a dissimilarity map.¹

Definition 1

(Dissimilarity). A dissimilarity on L is a map $\delta :\, L\times L \rightarrow [0,+\infty )$ which satisfies: $\delta (x,x) = 0$ for all x and $\delta (x,y) = \delta (y,x) > 0$ for all $x\ne y$.

For disjoint subsets $A, B \subseteq L$, we set $\delta (A,B):= \sum _{x\in A, y\in B} \delta (x,y)$ and define

$$\begin{aligned} \bar{\delta }(A,B) = \frac{\delta (A,B)}{|A| |B|}. \end{aligned}$$

As in Dasgupta (2016); Cohen-Addad et al. (2018), we encode a hierarchical clustering as a rooted binary tree whose leaves are the objects to be clustered.

Definition 2

(Hierarchy). A hierarchy on L is a rooted binary tree $T = (V,E)$ with n leaves, which we identify with the set L.

We will need some notation. The leaves below $v \in V$, i.e., of the subtree T[v] rooted at v, are denoted by $L_T[v] \subseteq L$. We let $S_T$ be the internal vertices of T, that is, its non-leaf vertices. For $s \in S_T$, we denote by $s_-$ and $s_+$ the children of s in T. For a pair of leaves $x\ne y \in L$, the most recent common ancestor of x and y in T, denoted $x\wedge _T y$, is the internal vertex s furthest from the root (in graph distance) such that $x, y \in L_T[s]$.

In our setting, the goal of hierarchical clustering is to map dissimilarities to hierarchies. As a principled way to accomplish this, a global objective function over hierarchies was proposed in Dasgupta (2016). It was generalized in Cohen-Addad et al. (2018) to objectives of the form:

$$\begin{aligned} \Gamma (T;\delta ) = \sum _{s \in S_T} \gamma (|L_T[s_-]|,|L_T[s_+]|) \,\delta (L_T[s_-],L_T[s_+]), \end{aligned}$$

(1)

where $\gamma$ is a given real-valued function and |A| is the number of elements in A. One then seeks a hierarchy T which minimizes $\Gamma ( \,\cdot ;\delta )$ under input $\delta$.² For instance, the choice $\gamma (a,b) = \gamma _\textrm{D}(a,b):= n-a-b$ is equivalent to that made in Dasgupta (2016). Heuristically, one way to interpret the objective $\Gamma$ is in terms of “merging cost”: each internal node s corresponds to the merging of two clusters $L_T[s_-]$ and $L_T[s_+]$ into a super-cluster $L_T[s]$ in the hierarchy T; the cost $\gamma (|L_T[s_-]|,|L_T[s_+]|) \,\delta (L_T[s_-],L_T[s_+])$ is associated to this operation; and we seek to minimize the total cost over all hierarchies. See Sect. 2 for more discussion.

It was shown in Dasgupta (2016); Cohen-Addad et al. (2018) that, for $\gamma _\textrm{D}$, the objective $\Gamma$ satisfies several natural conditions. In particular, it satisfies the following.

Definition 3

(Unit neutrality). An objective $\Gamma$ is unit neutral if all hierarchies have the same cost under the unit dissimilarity $\delta (x,y) = 1$ for all $x\ne y$.

Moreover, this $\Gamma$ behaves well on ultrametric inputs. Formally, a dissimilarity $\delta$ on L is an ultrametric if for all $x,y,z \in L$, it holds that

$$\begin{aligned} \delta (x,y) \le \max \{\delta (x,z),\delta (y,z)\}. \end{aligned}$$

(2)

Ultrametrics are naturally associated to hierarchies in the following sense. If $\delta$ is an ultrametric, then there is a (not necessarily unique) hierarchy T together with a height function $h: S_T \rightarrow (0,+\infty )$ such that, for all $x\ne y \in L$, it holds that

$$\begin{aligned} \delta (x,y) = h(x\wedge _T y). \end{aligned}$$

(3)

See e.g. Semple and Steel (2003) for details. We say that such a hierarchy T is associated to ultrametric $\delta$.

Definition 4

(Consistency on ultrametrics³). The objective function $\Gamma$ is consistent on ultrametrics if the following holds for any ultrametric $\delta$ and associated hierarchy T. For any hierarchy $T'$, we have the inequality

$$\begin{aligned} \Gamma (T;\delta ) \le \Gamma (T';\delta ). \end{aligned}$$

In other words, a hierarchy associated to an ultrametric $\delta$ is a global minimum under input $\delta$.

Observe that unit neutrality in fact follows from consistency on ultrametrics as the unit dissimilarity on L is an ultrametric that can be realized on any hierarchy by assigning height 1 to all internal vertices.

Here we introduce a broad new class of global objective functions for dissimilarity-based hierarchical clustering. For a subset of pairs $M \subseteq L\times L$, let $\delta |_M:M \rightarrow [0,+\infty )$ denote the dissimilarity $\delta$ restricted to M, i.e., $\delta |_M(x,y) = \delta (x,y)$ for all $(x, y) \in M$. Let also $\min \delta |_M$ and $\max \delta |_M$ be respectively the minimum and maximum value of $\delta$ over pairs in M. We consider objective functions of the form

$$\begin{aligned} \Gamma (T;\delta ) = \sum _{s \in S_T} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}). \end{aligned}$$

(4)

This form generalizes Eq. 1 as we can take

$$\hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \gamma (|L_T[s_-]|,|L_T[s_+]|) \,\delta (L_T[s_-],L_T[s_+]), $$

which is indeed a function of only T[s] (through the sizes $|L_T[s_-]|,|L_T[s_+]|$) and $\delta |_{L_T[s_-]\times L_T[s_+]}$ (through a sum over all pairs). We refer to such an objective function as a length-based objective, a name which will be explained in Sect. 2 along with a discusssion of its interpretation.

We will require moreover that the function $\hat{h}$ satisfy the condition

$$\begin{aligned} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) \in \left[ \min \delta |_{L_T[s_-]\times L_T[s_+]}, \max \delta |_{L_T[s_-]\times L_T[s_+]} \right] , \end{aligned}$$

(5)

for any hierarchy T, any $s \in S_T$ and any dissimilarity $\delta$. This is satisfied for instance with the choice

$$\begin{aligned} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \bar{\delta }(L_T[s_-],L_T[s_+]) = \frac{\delta (L_T[s_-],L_T[s_+])}{|L_T(s_-)|\,|L_T(s_+)|}, \end{aligned}$$

(6)

a special case of Eq. 1 with

$$\begin{aligned} \gamma (|L_T[s_-]|,|L_T[s_+]|) = \frac{1}{|L_T[s_-]|\,|L_T[s_+]|}. \end{aligned}$$

We show in Sect. 2 that there are many other natural possibilities that do not fit in the framework Eq. 1, including more “non-linear” choices. Our main result is that, under condition Eq. 5, our new objectives are unit neutral and consistent on ultrametrics and therefore provide sound global objectives for hierarchical clustering.

Theorem 1

(Length-based objectives). Any length-based objective satisfying Eq. 5 is unit neutral and consistent on ultrametrics.

Organization

The rest of the paper is organized as follows. Theorem 1 is proved in Sect. 3. Motivation and further related work is provided in Sect. 2.

2 Motivation

To motivate our class of objectives for hierarchical clustering, we first give a heuristic derivation of the choice Eq. 6, which is inspired by the concept of minimum evolution (see e.g. Gascuel and Steel , 2006 and references therein). In phylogenetics, one collects molecular sequences from extant species with the goal of reconstructing a phylogenetic tree representing the evolution of these species (together with edge lengths which roughly measure the amount of evolution on the edges). One popular approach is to estimate a distance between each pair of species by comparing their molecular sequences. Various distance-based methods have been developed (see, e.g., [Warnow , 2017 Chapter 5]). One such class of methods relies on the concept of minimum evolution, which in a nutshell stipulates that the best tree is the shortest one (i.e., the one with the minimum sum of edge lengths). Put differently, in the spirit of Occam’s razor, the solution involving the least amount of evolution to explain the data should be preferred. Without going into details (see, e.g., Semple and Steel , 2003; Steel 2016; Warnow , 2017 for comprehensive introductions to phylogenetic reconstruction methods), we point out that methods based on minimum evolution are widely used in practice. In particular one of the most popular methods in this area is Neighbor-Joining (NJ) (Saitou and Nei, 1987), which has been “revealed” to be a greedy method (Gascuel and Steel, 2006) for a variant of minimum evolution called balanced minimum evolution (which is itself an NP-hard problem (Fiorini and Joret, 2012)). See also Mihaescu and Pachter (2008); Eickmeyer et al. (2008); Pardi and Gascuel (2012) for related work, as well as Atteson (1999); Bryant (2005); Willson (2005); Lacey and Chang (2006); Mihaescu et al. (2009) for further theoretical analyses of NJ.

Total Length

Inspired by the concept of minimum evolution, we reformulate the length-based objective with choice Eq. 6, i.e.,

$$\begin{aligned} \Gamma (T;\delta ) = \sum _{s \in S_T} \bar{\delta }(L_T[s_-],L_T[s_+]), \end{aligned}$$

(7)

as a measure of the “total length of the hierarchy T under $\delta$.” To explain, w e start with the ultrametric case. If $\delta$ is ultrametric and T is associated to $\delta$ with height function h then, for any $s \in S_T$, $x\in L_T[s_-]$ and $y \in L_T[s_+]$, we have

$$\begin{aligned} \bar{\delta }(L_T[s_-],L_T[s_+]) = \delta (x,y) = h(s). \end{aligned}$$

(8)

Moreover, letting $M = \max \delta + 1$, consider a modified rooted tree $\tilde{T} = (\tilde{V},\tilde{E})$ with an extra edge connected to the root of T and associate height M to the new root so created. Then assign to each edge $e = (s_0,s_1)$ of $\tilde{T}$ a length equal to $h(s_0) - h(s_1)$, where $s_0$ is closer to the root than $s_1$. Then the total length of $\tilde{T}$ is

$$\begin{aligned} \sum _{e = (s_0,s_1) \in \tilde{E}} [h(s_0) - h(s_1)] = M + \sum _{s \in S_T} h(s) = M + \sum _{s \in S_T} \bar{\delta }(L_T[s_-],L_T[s_+]) = M + \Gamma (T;\delta ), \end{aligned}$$

where we used the fact that each non-root internal vertex of $\tilde{T}$ is counted twice positively and once negatively (since it has two immediate children and one immediate parent), while the root of $\tilde{T}$ is counted once. In other words, up to translation by M, $\Gamma (T;\delta )$ measures the total length of hierarchy T associated to ultrametric $\delta$.

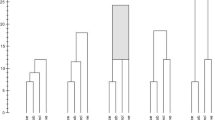
Example 1

Consider the ultrametric $\delta$ over $\{1,\ldots ,6\}$, with $D = (\delta (i,j))_{i,j\in [6]}$ and

$$ D = \begin{pmatrix} 0 &{} 2 &{} 4 &{} 4 &{} 6 &{} 6\\ 2 &{} 0 &{} 4 &{} 4 &{} 6 &{} 6\\ 4 &{} 4 &{} 0 &{} 2 &{} 6 &{} 6\\ 4 &{} 4 &{} 2 &{} 0 &{} 6 &{} 6\\ 6 &{} 6 &{} 6 &{} 6 &{} 0 &{} 2\\ 6 &{} 6 &{} 6 &{} 6 &{} 2 &{} 0 \end{pmatrix}. $$

An associated hierarchy T is depicted in Fig. 1. Here $M = 7$. The total length of the modified tree $\tilde{T}$ is

$$ 6 \times (2-0) + 2 \times (4-2) + 1 \times (6-2) + 1 \times (7-6) = 23, $$

which coincides with

$$ M + \Gamma (T;\delta ) = 7 + 3 \times 2 + 1 \times 4 + 1 \times 6. $$

Fig. 1

A hierarchy associated to $\delta$ (without the dotted edge). Adding the dotted edge produces the modified rooted tree $\tilde{T}$

More generally, on a heuristic level, if $\delta$ is not ultrametric (but perhaps close to one) and T is any hierarchy we interpret $\bar{\delta }(L_T[s_-],L_T[s_+])$ as a measure of the height of s on T based on the values $\delta |_{L_T[s_-]\times L_T[s_+]}$. Then, as above, we see $\Gamma (T;\delta )$ as the total length⁴ of T under $\delta$ (up to translation by M). Minimizing $\Gamma$ hence corresponds roughly speaking to finding a hierarchy whose total length is minimum under a fit to the input $\delta$. In addition to its connection to the fruitful concept of minimum evolution in phylogenetics, as pointed out in Sect. 1 this objective has the desirable property of being consistent on ultrametrics.

Other Choices for

$\hat{h}$ Interpreting $\hat{h}$ as a measure of height suggests many more natural choices. For instance, one can take a model-based approach such as the one advocated in the related work of Degens (1983); Castro et al. (2004). There, a simple error model is assumed (adapted to our setting): the dissimilarity $\delta$ is in fact an ultrametric $\delta ^*$ plus an entrywise additive noise that is i.i.d. If T is associated to $\delta ^*$ and $s \in S_T$, then a likelihood-based estimate of h(s) can be obtained from the values $\delta |_{L_T[s_-]\times L_T[s_+]}$, which all share the same mean h(s) and are independent. Under the assumption that the additive noise is Gaussian for instance, one recovers the least-squares estimate Eq. 6. Taking the noise to be Laplace leads to the median.⁵ As pointed out by Degens (1983), other choices of noise distribution in the simple error model above also lead to estimates that arise naturally in the hierarchical clustering context. For instance, if the probability density function of the additive noise is assumed to be 0 below 0 and non-increasing above 0 (with a discontinuous positive jump at 0), then the maximum likelihood estimate is the minimum of the observed values $\delta |_{L_T[s_-]\times L_T[s_+]}$. Note that all these examples satisfy  Eq. 5 and therefore Theorem 1 implies that they produce length-based objectives

$$\begin{aligned} \Gamma (T;\delta ) = \sum _{s \in S_T} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}), \end{aligned}$$

that are consistent on ultrametrics.

We note further that we allow in general the function $\hat{h}$ to depend on the structure of the subtree rooted at the corresponding internal vertex. For instance, one could consider a weighted average of the quantities $\delta |_{L_T[s_-]\times L_T[s_+]}$ where the weights depend on the graph distance between the leaves. In the phylogenetic context, the choice

$$\begin{aligned} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \sum _{x\in L_T[s_-], y\in L_T[s_+]} 2^{-|x|_{L_T[s_-]}} 2^{-|y|_{L_T[s_+]}} \delta (x,y), \end{aligned}$$

(9)

where $|x|_{L_T[s_-]}$ denotes the graph distance between $s_-$ and x in T[s] (i.e., the number of edges on the unique path between $s_-$ and x), is used in some distance-based phylogeny reconstruction methods and was shown rigorously to lead to significantly improved theoretical guarantees in certain regimes of parameters for standard models of sequence evolution (Roch, 2010). The analysis of Eq. 9 accounts for the fact that the dissimilarities in $\delta |_{L_T[s_-]\times L_T[s_+]}$ are not independent—but in fact highly correlated—under these models. It can be shown (by induction on the size of the hierarchy) that $\sum _{x\in L_T[s_-], y\in L_T[s_+]} 2^{-|x|_{T[s]}} 2^{-|y|_{T[s]}} = 1$, and therefore Theorem 1 applies in this case as well.

Greedy Algorithms

Finally, following (Gascuel and Steel, 2006) where NJ is interpreted as a greedy method, we connect our class of objectives to standard myopic approaches to hierarchical clustering. The first clustering approach we consider, average linkage, is an agglomerative method.

• 0. Average linkage

• 1. Input: dissimilarity $\delta$ on $L = \{1,\ldots ,n\}$.

• 2. Create n singleton trees with leaves respectively $1,\ldots , n$.

• 3. While there are at least two trees left:

  • a- Pick two trees $T_1, T_2$ with leaves $A_1, A_2$ minimizing $\bar{\delta }(A_1,A_2)$.

  • b- Merge $T_1$ and $T_2$ through a new common root adjacent to their roots.

• 4. Return the resulting tree.

The second method we consider, recursive sparsest cut, is a divisive method.

• 0. Recursive sparsest cut

• 1. Input: dissimilarity $\delta$ on $L = \{1,\ldots ,n\}$.

• 2. Find a partition $\{A_1, A_2\}$ of L maximizing $\bar{\delta }(A_1,A_2)$.

• 3. Recurse on $\delta |_{A_1 \times A_1}$ and $\delta |_{A_2 \times A_2}$ to obtain trees $T_{A_1}$ and $T_{A_2}$.

• 4. Merge $T_{A_1}$ and $T_{A_2}$ through a new common root adjacent to their roots.

• 5. Return the resulting tree.

Note that Step (2) is NP-hard and one typically resorts to approximation algorithms (Dasgupta, 2016).

From an algorithmic point of view, these methods proceed in an intuitive manner: average linkage starts from the bottom and iteratively merges clusters that are as similar as possible according to $\bar{\delta }$; recursive sparsest cut starts from the top and iteratively splits clusters that are as different as possible according to $\bar{\delta }$. From an optimization point of view, both methods seemingly use the same local criterion: $\bar{\delta }$. But, given that at each iteration one minimizes while the other maximizes this criterion, it is natural to wonder whether they share a common global objective?

Heuristically, one can think of Eq. 7 as such an objective. At each iteration, average linkage forms a new cluster whose contribution to Eq. 7 is minimized among all possible merging choices. As for recursive sparsest cut: when splitting $A_1$ and $A_2$, the value $\bar{\delta }(A_1,A_2)$ is (in the interpretation above) the height of the parent $s_{A_1,A_2}$ of the two corresponding subtrees; by maximizing $\bar{\delta }(A_1,A_2)$, one then greedily minimizes the length of the newly added edge above $s_{A_1,A_2}$ and, hence, the contribution of that edge to the total length.

Other choices of $\hat{h}$ lead to single linkage, complete linkage and median linkage as well as the more general agglomerative approach of Castro et al. (2004). For instance, single linkage greedily minimizes the total length of a hierarchy whose heights are “fitted” using maximum likelihood assuming the additive noise has any density that is 0 below 0 and is non-increasing above 0. The choice Eq. 9 on the other hand leads to WPGMA (Weighted Pair Group Method with Arithmetic Mean) (Sokal, 1958).

3 Proof of Theorem 1

In this section, we prove Theorem 1. As we noted above, it suffices to prove consistency on ultrametrics, as it implies unit neutrality.

Proof of Theorem

1 We first reduce the proof to a special $\hat{h}$.

Claim 1

(Reduction to minimum). It suffices to prove Theorem 1 for the choice $\hat{h} = \hat{h}_m$ where

$$\begin{aligned} \hat{h}_m(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \min \delta |_{L_T[s_-]\times L_T[s_+]}. \end{aligned}$$

(10)

Proof

Let $\hat{h}$ be an arbitrary choice of a function satisfying Eq. 5 and let $\delta$ be an ultrametric with associated hierarchy T. Recall that we seek to show that $\Gamma (T;\delta ) \le \Gamma (T';\delta )$ for any hierarchy $T'$.

By Eq. 3, for any $s \in S_T$ and for any $x, x' \in L_T[s_-]$ and $y, y' \in L_T[s_+]$, we have

$$\begin{aligned} \delta (x,y) = \delta (x',y') = \min \delta |_{L_T[s_-]\times L_T[s_+]} = \max \delta |_{L_T[s_-]\times L_T[s_+]}, \end{aligned}$$

since $x\wedge _T y = x' \wedge _T y' = s$, where the first equality over all choices of $x,x'y,y'$ implies the other two. Therefore, under the ultrametric associated to T, this arbitrary $\hat{h}$ in fact satisfies

$$\begin{aligned} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \min \delta |_{L_T[s_-]\times L_T[s_+]}, \end{aligned}$$

by Eq. 5. This holds for all $s \in S_T$, so that

$$\begin{aligned} \Gamma (T;\delta ) = \sum _{s \in S_T} \hat{h}(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) = \sum _{s \in S_T} \hat{h}_m(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}), \end{aligned}$$

(11)

takes the same value for any $\hat{h}$.

On the other hand, for any other hierarchy $T'$ and for any internal vertex $s' \in S_{T'}$ it holds that

$$\begin{aligned} \hat{h}(T'[s'],\delta |_{L_{T'}[s'_-]\times L_{T'}[s'_+]}) \ge \min \delta |_{L_{T'}[s'_-]\times L_{T'}[s'_+]}, \end{aligned}$$

by Eq. 5. Hence,

$$\begin{aligned} \Gamma (T';\delta ) = \sum _{s' \in S_{T'}} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]}) \ge \sum _{s' \in S_{T'}} \hat{h}_m(T'[s'],\delta |_{L_{T'}[s'_-]\times L_{T'}[s'_+]}). \end{aligned}$$

(12)

Combining Eqs. 11 and 12, we see that establishing the desired inequality under the choice Eq. 10

$$ \sum _{s \in S_T} \hat{h}_m(T[s],\delta |_{L_T[s_-]\times L_T[s_+]}) \le \sum _{s' \in S_{T'}} \hat{h}_m(T'[s'],\delta |_{L_{T'}[s'_-]\times L_{T'}[s'_+]}), $$

implies that the desired inequality $\Gamma (T;\delta ) \le \Gamma (T';\delta )$ holds under $\hat{h}$. That proves the claim.$\square$

For the rest of the proof, we assume that $\hat{h} = \hat{h}_m$. We prove the result by induction on the number of leaves. The proof proceeds by considering the two subtrees hanging from the root in the hierarchy associated to the ultrametric $\delta$ and comparing their respective costs to that of the subtrees of any other hierarchy on the same sets of leaves.

Let $\delta$ be an ultrametric dissimilarity on $L = [n]$. Let T be an associated hierarchy on L with height function h. We start with the base of the induction argument.

Claim 2

(Base case). If $n=2$, then $\Gamma (T;\delta ) \le \Gamma (T':\delta )$ for any hierarchy $T'$ on L.

Proof

When $n=2$, there is only one hierarchy, so the statement is vacuous.$\square$

Now suppose $n > 2$ and assume that the result holds by induction for all hierarchies with less than n leaves. Before we begin, it will be convenient to define a notion of hierarchy allowing degree 2 vertices.

Definition 5

(Generalized hierarchy). A generalized hierarchy on L is a rooted tree $T''$ with n leaves, which we identify with the set L, such that all internal vertices have degree at most 3 and the root has degree 2.

We generalize the objective function to generalized hierarchies $T''$ by letting

$$\begin{aligned} \Gamma (T'';\delta ) = \sum _{s \in S_{T''}^2} \hat{h}(T''[s],\delta |_{L[s_-]\times L[s_+]}), \end{aligned}$$

where $S_{T''}^2$ is the set of internal vertices of $T''$ with exactly two immediate descendants. That is, we ignore the degree 2 vertices in the objective, except for the root. We refer to these ignored vertices as muted. We also trivially extend to generalized hierarchies the notion of an associated ultrametric. We observe that the induction hypothesis holds for generalized hierarchies as well. Indeed, the internal vertices of degree 2 (except the root) are ignored in the objective, which is equivalent to suppressing those vertices in the generalized hierarchy and computing the objective over the resulting (non-generalized) hierarchy.

The presence of degree 2 vertices will arise as a by-product of the following definition.

Definition 6

(Restriction). Let $T''$ be a hierarchy on $L''$ and let $A'' \subseteq L''$. The restriction of $T''$ to $A''$, denoted $T''_{A''}$, is the generalized hierarchy obtained from $T''$ by keeping only those edges and vertices lying on a path between two leaves in $A''$.

Note that applying the restriction procedure to a hierarchy can indeed produce degree 2 vertices and that the root of a restriction has degree 2 by definition.

We are now ready to proceed with the induction. Let $\rho$ be the root of T and let $T_- = T[\rho _-]$, $T_+ = T[\rho _+]$, $L_- = L_T[\rho _-]$ and $L_+ = L_T[\rho _+]$. We note that $T_- = T_{L_-}$ and $T_+ = T_{L_+}$. Let $T'$ be a distinct hierarchy on L. Note that, for any subset $A \subseteq L$, the dissimilarity $\delta |_{A\times A}$ is an ultrametric on A as it continues to satisfy Eq. 2. Note, moreover, that $T_A$ is a generalized hierarchy associated with $\delta |_{A\times A}$, as the same heights can be used on the restriction. Hence, we can apply the induction hypothesis to $L_-$ and $L_+$. That is, we have by induction that:

Claim 3

(Induction on the subtrees hanging from the root).

$$\begin{aligned} \Gamma (T_-;\delta |_{L_-\times L_-}) \le \Gamma (T'_{L_-};\delta |_{L_-\times L_-}) \quad \text {and}\quad \Gamma (T_+;\delta |_{L_+\times L_+}) \le \Gamma (T'_{L_+};\delta |_{L_+\times L_+}). \end{aligned}$$

We now relate the quantities in the previous claim to the objective values on T and $T'$. Let $\Delta := \max \delta$.

Claim 4

(Relating T and $T'$: Applying induction). It holds that

$$\begin{aligned} \Gamma (T;\delta ) \le \Delta + \Gamma (T'_{L_-};\delta |_{L_-\times L_-}) + \Gamma (T'_{L_+};\delta |_{L_+\times L_+}). \end{aligned}$$

Proof

Because T is associated to ultrametric $\delta$, the corresponding height of the root of T is also the largest height on T and, hence,

$$\begin{aligned} \hat{h}(T[\rho ],\delta |_{L[\rho _-]\times L[\rho _+]}) = \min \delta |_{L[\rho _-]\times L[\rho _+]} = \max \delta = \Delta . \end{aligned}$$

Therefore, adding up the contributions to $\Gamma (T;\delta )$ of the root and of the two subtrees hanging from the root, we get

$$\begin{aligned} \Gamma (T;\delta ) = \Delta + \Gamma (T_-;\delta |_{L_-\times L_-}) + \Gamma (T_+;\delta |_{L_+\times L_+}). \end{aligned}$$

We use Claim 3 to conclude.$\square$

So it remains to relate the RHS in the previous claim to the objective value of $T'$. This involves a case analysis. We start with a simple case.

Claim 5

(Relating T and $T'$: Equality case). If there is $s \in S_{T'}$ such that $L_{T'}[s] = L_-$ or $L_{T'}[s] = L_+$, then it holds that

$$\begin{aligned} \Gamma (T';\delta ) = \Delta + \Gamma (T'_{L_-};\delta |_{L_-\times L_-}) + \Gamma (T'_{L_+};\delta |_{L_+\times L_+}). \end{aligned}$$

(13)

Proof

Observe that s cannot be the root of $T'$ as otherwise we would have $L_- = \emptyset$. So s has a parent. Let $\tilde{s}$ be the parent of s with descendants $\tilde{s}_-$ and $\tilde{s}_+$, and assume without loss of generality that $L_{T'}[\tilde{s}_-] \subseteq L_-$ and $L_{T'}[\tilde{s}_+] = L_+$ (i.e., $\tilde{s}_+ = s$). Then the contribution to $\Gamma (T';\delta )$ of $\tilde{s}$ is $\Delta$. Furthermore, the contribution to $\Gamma (T';\delta )$ of those vertices in $T'_{L_+}$ is $\Gamma (T'_{L_+};\delta |_{L_+\times L_+})$. Finally, in $T'_{L_-}$ vertex s has degree 2 and so is muted. The remaining vertices of $T'_{L_-}$ contribute $\Gamma (T'_{L_-};\delta |_{L_-\times L_-})$ to both sides of Eq. 13.$\square$

The general case analysis follows. We assume for the rest of the proof that:

$$\begin{aligned} \not \exists s \in S_{T'}, L_{T'}[s] = L_- \text { or } L_{T'}[s] = L_+. \end{aligned}$$

(14)

Claim 6

(Relating T and $T'$: Case analysis). Under Eq. 14, it holds that

$$\begin{aligned} \Gamma (T';\delta ) \ge \Delta + \Gamma (T'_{L_-};\delta |_{L_-\times L_-}) + \Gamma (T'_{L_+};\delta |_{L_+\times L_+}). \end{aligned}$$

(15)

Proof

Recall that $\Gamma (T';\delta )$ is a sum over internal vertices of $T'$. We divide up those vertices into several classes. Below, we identify the vertices in the restrictions to the original vertices and we write $s \in T''$ to indicate that s is a vertex of $T''$. Observe that, by definition, $T_- = T_{L_-}$ and $T_+ = T_{L_+}$ do not share vertices—but that $T'_{L_-}$ and $T'_{L_+}$ might. Recall that, for $s \in S_{T'}$, we denote by $s_-$ and $s_+$ the immediate descendants of s in $T'$.

• 1. Appears in one subtree: Let $R_1$ be the elements s of $S_{T'}$ such that either (i) $s \in T'_{L_-}$ but $s \notin T'_{L_+}$, or (ii) $s \in T'_{L_+}$ but $s \notin T'_{L_-}$. It will be important below whether or not s is muted. Case (i) means that there is a path on $T'$ between two leaves in $L_-$ that goes through s—but not between two leaves in $L_+$. Note that a path going through s necessarily has an endpoint in $L_{T'}[s_-]$ or $L_{T'}[s_+]$, or both. We claim that, for such an s, we have that both $L_{T'}[s_-]$ and $L_{T'}[s_+]$ have a non-empty intersection with $L_-$. Indeed assume that, say, $L_{T'}[s_+]$ contains only leaves from $L_+$. Because there is no path between two leaves in $L_+$ going through s in $T'$, it must be that actually $L_{T'}[s_+] = L_+$. But that contradicts Eq. (14), and proves the claim. Moreover one of $L_{T'}[s_-]$ or $L_{T'}[s_+]$ (or both) is a subset of $L_-$, as otherwise there would be a path between two leaves in $L_+$ going through s and we would have that $s \in T'_{L_+}$, a contradiction. In case (ii), the same holds with the roles of $L_-$ and $L_+$ interchanged. That implies further that s is not muted in the restriction it belongs to. However it is muted in the restriction it does not belong to. Let $r_1 = |R_1|$.

• 2. Appears in both, twice muted: Let $R_{2,tm}$ be the elements s of $S_{T'}$ such that $s \in T'_{L_-}$ and $s \in T'_{L_+}$ and s is muted in both restrictions. That arises precisely when $L_{T'}[s_-]$ and $L_{T'}[s_+]$ each belong to a different subset among $L_-$ and $L_+$. Let $r_{2,tm} = |R_{2,tm}|$.

• 3. Appears in both, once muted: Let $R_{2,om}$ be the elements s of $S_{T'}$ such that $s \in T'_{L_-}$ and $s \in T'_{L_+}$ and s is muted in exactly one restriction. That arises precisely when one of $L_{T'}[s_-]$ and $L_{T'}[s_+]$ has a non-empty intersection with exactly one of $L_-$ and $L_+$, and the other has a non-empty intersection with both $L_-$ and $L_+$. Let $r_{2,om} = |R_{2,om}|$.

• 4. Appears in both, neither muted: Let $R_{2,nm}$ be the elements s of $S_{T'}$ such that $s \in T'_{L_-}$ and $s \in T'_{L_+}$ and s is muted in neither restriction. That arises precisely when both $L_{T'}[s_-]$ and $L_{T'}[s_+]$ have a non-empty intersection with both $L_-$ and $L_+$. Let $r_{2,nm} = |R_{2,nm}|$.

Because the sets above form a partition of $S_{T'}$ and that any hierarchy on n leaves has exactly $n-1$ internal vertices, it follows that

$$\begin{aligned} r_1 + r_{2,tm} + r_{2,om} + r_{2,nm} = n-1. \end{aligned}$$

Moreover, on a generalized hierarchy with $n' < n$ leaves, the number of internal non-muted vertices is $n'-1$ (which can be seen by collapsing the muted vertices). Hence, counting non-muted vertices on each restriction with multiplicity, we get the relation

$$\begin{aligned} 1\cdot r_1 + 0\cdot r_{2,tm} + 1\cdot r_{2,om} + 2 \cdot r_{2,nm} = (|L_-| - 1) + (|L_+| - 1) = n-2. \end{aligned}$$

Combining the last two displays gives

$$\begin{aligned} r_{2,tm} = 1 + r_{2,nm}. \end{aligned}$$

(16)

This last equality is the key to comparing the two sides of Eq. 15: the twice muted vertices which contribute $\max \delta$ to the LHS are in one-to-one correspondence with terms on the RHS whose contributions are smaller or equal.

We expand on this last point. To simplify the notation, we let $\delta _- = \delta |_{L_-\times L_-}$ and $\delta _+ = \delta |_{L_+\times L_+}$. By the observations above, we have the following. Recall that $\hat{h} = \hat{h}_m$.

• 1. $R_1$: Each $s \in R_1$ is muted in the restriction it does not belong to but it is not in the restriction it belongs to, so that it contributed to exactly one term on the RHS, say $\Gamma (T'_{L_-};\delta |_{L_-\times L_-})$. In that case, we have shown that both $L_{T'}[s_-]$ and $L_{T'}[s_+]$ have a non-empty intersection with $L_-$. The RHS term $\hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]})$ differs from the corresponding LHS term $\hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]})$ only in that pairs $(x,y) \in L_{T'}[s_-]\times L_{T'}[s_+]$ with $(x,y) \in L_- \times L_+$ or $L_+\times L_-$ are removed (which we refer to below as being suppressed by restriction) from the minimum defining $\hat{h} = \hat{h}_m$—but such pairs contribute $\Delta = \max \delta$ and therefore do not affect the minimum on the LHS. We have also shown that none of these pairs can be in $L_+ \times L_+$. As a result, we have

  $$\begin{aligned}{} & {} \sum _{s \in R_1} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]})\\{} & {} = \sum _{s \in R_1\cap S_{T'_{L_-}}} \hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]}) + \sum _{s \in R_1\cap S_{T'_{L_+}}} \hat{h}(T'_{L_+},\delta _+|_{L_{T'}[s_-]\times L_{T'}[s_+]}). \end{aligned}$$

• 2. $R_{2,tm}$: Each $s \in R_{2,tm}$ contributes to neither term on the RHS, as it is muted in both restriction. On the other hand, we have argued that $L_{T'}[s_-]$ and $L_{T'}[s_+]$ each belong to a different subset among $L_-$ and $L_+$. Hence we have

  $$\begin{aligned}{} & {} \sum _{s \in R_{2,tm}} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]}) = \Delta \cdot r_{2,tm}, \end{aligned}$$

  while

  $$\begin{aligned}{} & {} \sum _{s \in R_{2,tm}} \hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]}) + \sum _{s \in R_{2,tm}} \hat{h}(T'_{L_+},\delta _+|_{L_{T'}[s_-]\times L_{T'}[s_+]}) = 0\cdot 2r_{2,tm}. \end{aligned}$$

• 3. $R_{2,om}$: In this case, we have that

  $$\begin{aligned}{} & {} \sum _{s \in R_{2,om}} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]})\\{} & {} = \sum _{s \in R_{2,om}} \hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]}) + \sum _{s \in R_{2,om}} \hat{h}(T'_{L_+},\delta _+|_{L_{T'}[s_-]\times L_{T'}[s_+]}), \end{aligned}$$

  where we used that (1) each s in $R_{2,om}$ is muted in exactly one of the sums on the second line and that (2) the pairs of leaves suppressed by restriction in the non-muted terms on the second line correspond to pairs on opposite sides of the root in T, which contribute $\Delta = \max \delta$ and therefore do not affect the minimum defining $\hat{h}$.

• 4. $R_{2,nm}$: Each $s \in R_{2,nm}$ contributes to both terms $\Gamma (T'_{L_-};\delta |_{L_-\times L_-})$ and $\Gamma (T'_{L_+};\delta |_{L_+\times L_+})$ on the RHS of Eq. 15, once with the same value as the corresponding term on the LHS and once with a larger value. Indeed, because both $L_{T'}[s_-]$ and $L_{T'}[s_+]$ have a non-empty intersection with both $L_-$ and $L_+$ and pairs $(x,y) \in L_- \times L_+$ or $L_+\times L_-$ have dissimilarity $\Delta$, it follows that the minimum

  $$\begin{aligned} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]}) = \min \delta |_{L_{T'}[s_-]\times L_{T'}[s_+]}, \end{aligned}$$

  (17)

  is achieved for a pair $(x,y) \in L_- \times L_-$ or $L_+\times L_+$. The claim then follows by noticing that restriction increases the minimum. Let $R_{2,nm}^{-,=}$ be the set of all $s \in R_{2,nm}$ such that the minimum in Eq. 17 is achieved for a pair in $L_- \times L_-$ and $R_{2,nm}^{+,=} = R_{2,nm} \setminus R_{2,nm}^{-,=}$. Then

  $$\begin{aligned}{} & {} \sum _{s \in R_{2,nm}} \hat{h}(T'[s],\delta |_{L_{T'}[s_-]\times L_{T'}[s_+]})\\{} & {} = \sum _{s \in R_{2,nm}^{-,=}} \hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]}) + \sum _{s \in R_{2,nm}^{+,=}} \hat{h}(T'_{L_+},\delta _+|_{L_{T'}[s_-]\times L_{T'}[s_+]}), \end{aligned}$$

  while

  $$\begin{aligned}{} & {} \sum _{s \in R_{2,nm}^{+,=}} \hat{h}(T'_{L_-},\delta _-|_{L_{T'}[s_-]\times L_{T'}[s_+]}) + \sum _{s \in R_{2,nm}^{-,=}} \hat{h}(T'_{L_+},\delta _+|_{L_{T'}[s_-]\times L_{T'}[s_+]})\\{} & {} \le \Delta \cdot r_{2,nm}. \end{aligned}$$

To sum up, the contributions of $R_1$ and $R_{2,om}$ are the same on both sides of Eq. 15. The contributions of $R_{2,nm}$ on the LHS are canceled out by the contributions of $R_{2,nm}^{-,=}$ and $R_{2,nm}^{+,=}$ on the RHS. The remaining terms are: on the LHS, $\Delta \cdot r_{2,tm}$; and on the RHS, $\le \Delta \cdot (1 + r_{2,nm})$. Using Eq. 16 concludes the proof.$\square$

That concludes the induction and the proof of the theorem.$\square$