Vortex-induced sound prediction of slat noise from time-resolved particle image velocimetry data

Abstract

A data-driven method for predicting the vortex-induced sound from time-resolved velocimetry data is presented and applied to the sound generated by flow passing through the slat in a multi-element high-lift airfoil. The time-dependent velocity fields in the slat-cove region of the 30P30N multi-element airfoil are obtained from time-resolved particle image velocimetry measurements, and a low-order reconstruction is achieved by using the rank-one vbnm modes from spectral proper orthogonal decomposition. The pressure force and associated dipole sound are then computed via the application of the force and acoustic partitioning methods (Seo et al. in Phys Fluids 34(5):053607, 2002) which involve volume integrals of the product of the second invariant of the velocity gradient tensor and geometry-dependent influence fields. The method enables estimation of the dipole sound generated by local flow structures, and the results are shown to be consistent with theory of vortex sound. Comparison with the measured sound data suggests that while the shear layer modes are responsible for the tonal noise, the interactions between the shear layer modes and other parts of the wing also generate a substantial level of flow noise.

1 Introduction

Understanding noise generation mechanisms is crucial for the accurate prediction of aeroacoustic noise as well as the effective mitigation of it. The investigation of noise generation mechanisms may start from the localization of noise sources, and then, the aerodynamic flow structures responsible for the noise generation can be further investigated in that source vicinity. Acoustic measurements employing microphone phased array can be used for beamforming to obtain the sound source distribution (Dougherty 2002; Brooks and Humphreys 2006). However, beamforming does not provide any physical insight about the generation mechanisms of the noise. On the other hand, recent development in particle image velocimetry (PIV) enables the measurements of time-resolved velocity fields, which can be used to identify the dynamically dominant flow features generating the sound in a conjunction with theoretical and numerical methods. For the airframe noise at low Mach numbers, dipole sound, generated by the time-varying pressure forces on the surface, is a dominant aeroacoustic sound (Zawodny and Boyd 2020; Lilley 2001; Dobrzynski et al. 2008). Curle’s acoustic analogy (Curle 1955) clearly describes the relation between the surface pressure and the radiated sound, and it can be used to localize the surface region responsible for the dipole sound generation when the surface pressure data are available. Analyzing the influence of the various flow features on the surface pressure is, however, still difficult especially at low Mach numbers, where the surface pressure is mainly governed by incompressible flow dynamics. The pressure in an incompressible flow is an elliptic variable and is simultaneously influenced by all features such as vortices, viscous diffusion, and boundary motions. This also makes the evaluation of surface pressure data by using the PIV measurements a non-trivial task. One approach to analyze the aeroacoustic sound by using the PIV measurements is obtaining the pressure field by solving the pressure Poisson equation numerically with the source term reconstructed from the PIV data (Koschatzky et al. 2011; Pascioni and Cattafesta 2018). The sound is then predicted by using Curle’s analogy. The other approach is by using the vortex sound theory derived by Powell (1964) and developed by Howe and Howe (2003). It is a different form of the Lighthill’s analogy, and the Lamb vector is considered as the aerodynamic sound source. This method requires a tailored Green’s function for a given body shape to predict the radiated dipole sound. Both methods have been employed in previous studies, and the advantages and disadvantages of each method are discussed in Koschatzky et al. (2011).

In this paper, we present a new approach to predict aeroacoustic noise from time-resolved PIV measurements by using the force and acoustic partitioning methods. The force partitioning method (FPM) and its extension to aeroacoustics—acoustic partitioning method (APM)—are recently proposed versatile data-enabled methods for the analysis of pressure forces and dipole sounds. The FPM enables the partitioning of aerodynamic pressure forces on the surface into physically distinct components, and it establishes the relation between the pressure force and the field data such as velocity fields and body motions (Zhang et al. 2015; Menon and Mittal 2021a, 2021b, 2021c). The method, therefore, can also be used to estimate the pressure force by using the available field data. Since the dipole sound is directly generated by the pressure force on the surface, the APM has been developed by combining the FPM and an acoustic analogy for the partitioning of dipole sound at low Mach numbers (Seo et al. 2022). By applying the APM, dipole sound attributed to surface pressure force can be partitioned into components associated with unsteady body motion, viscous diffusion, and vortices. The APM also decomposes the sound to the level of individual vortex contributions (Seo et al. 2022). Like the FPM, the APM can be used to evaluate the dipole sound using the available field data, and this enables us to predict the aeroacoustic noise by using the PIV measurements. Predictions of surface pressure force and resulting dipole sound by delineating the contribution of various flow features would provide useful insights into the noise-source mechanisms and could lead to effective strategies for mitigating or controlling noise generation by complex flow interactions.

The proposed approach is applied to a multi-element airfoil (30P30N) in a high-lift configuration to assess the noise prediction by using the F/APM. The high-lift airfoil geometry known as the 30P30N configuration consists of a leading-edge slat, main wing, and a trailing edge flap (see Fig. 2). This geometry has been employed in many previous studies including the High-Lift CFD Challenge Workshop (Klausmeyer and Lin 1997) and the AIAA Benchmark problems for Airframe Noise Computations (BANC) workshops (Choudhari and Lockard 2015). Once deployed, the high-lift elements generate several unsteady flow processes that can dominate the airframe noise signature. In particular, the slat flow exhibits a large separation due to the geometric cove behind the slat. As the flow passes the slat cusp, a Kelvin–Helmholtz instability develops in the initial shear layer of the separating flow, which grows into coherent structures and rolls into large vortices. These vortices eventually impinge and interact with the slat-cove surface to form a fluid-acoustic feedback loop. Along with the vortex shedding occurring at the slat trailing edge, these complex flow features produce a significant part of the acoustic energy. The sound generation by the slat flow has been investigated extensively in the literature, demonstrating there are lots of different flow mechanisms involved in the sound generation process: coherent structure in the shear layer, impingement of the shear layer on the trailing edge of the slat, vortex shedding at the slat trailing edge, vortex shedding/distortion by the mean flow through the gap, and so on. Dissection of the sound generation for each mechanism would still be necessary to identify the dominant source mechanism.

In the present study, the sound generated by the vortices in the shear layer of the slat-cove separating flow is predicted by using the PIV measurement data. The velocity fields are reconstructed by the rank-1 modes of spectral POD analysis of time-resolved PIV data to suppress high-wave number errors. The dipole sound at the far field is then predicted by applying the F/APM, and the sound pressure level (SPL) is corrected by considering the spanwise coherence length scale. The predicted SPL spectrum is then compared to the vortex sound theory and the phased array microphone measurement for further discussions.

Fig. 1

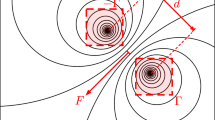
Schematic of the domain for force and acoustic partitioning method. B: Surface of the body of interest, $\Sigma$: surface of the domain boundary, $V_f$: fluid volume, $\vec n$: surface normal unit vector, $\vec v$: body velocity, $\vec x_p$: sound pressure monitoring point, $\vec r$: a vector from the source to the monitoring point

2 Methodologies

2.1 Force partitioning method

The FPM is based on the projection of the incompressible momentum equation,

$$\begin{aligned} \rho \frac{\partial {\vec {U}}}{\partial {t}}+\rho \vec {U} \cdot \nabla U + \nabla P = \mu \nabla ^2 U, \end{aligned}$$

(1)

onto a set of influence potential fields $\phi _i, i=1,2,3$, which are the solutions of the Laplace equation,

$$\begin{aligned} \nabla ^2 \phi _i = 0, \end{aligned}$$

(2)

with the boundary conditions

$$\begin{aligned} \nabla \phi _i\cdot \vec {n} = \left\{ \begin{matrix} n_i &{}\text {on}~B\\ 0 &{}\text {on}~\Sigma \end{matrix}\right. , \end{aligned}$$

(3)

where $\vec {n}$ is the surface normal unit vector, B is the control surface on which the pressure forces to be partitioned, and $\Sigma$ are all other surfaces including the outer boundaries of the domain (see Fig. 1). Subscript $i=1,2,3$ denotes the direction of the force, x, y, and z, respectively. Integrating the projection of the incompressible momentum equation onto the gradient of the potential field, $\nabla \phi _i$, over the fluid volume enclosed by B and $\Sigma$, and by using the divergence theorem, one can get

$$\begin{aligned} \begin{aligned}&\underset{F_{B,i}}{\underbrace{\int _B Pn_i\mathrm{{d}}S}} = \underset{F_{k,i}}{\underbrace{\int _{B+\Sigma }\left( -\phi _i\rho \frac{D\vec {U}}{Dt}\cdot \vec {n} \right) \mathrm{{d}}S}}+ \\&\underset{F_{\mu ,i}}{\underbrace{\int _{B+\Sigma }\left( \phi _i\mu \nabla ^2\vec {U}\cdot \vec {n} \right) \mathrm{{d}}S}} + \underset{F_{Q,i}}{\underbrace{\int _{V_f}\left( -\phi _i2\rho Q \right) \mathrm{{d}}S}}, \end{aligned} \end{aligned}$$

(4)

where Q is the second invariant of velocity gradient tensor, $Q=0.5(|\Omega _{ij}|^2-|S_{ij}|^2)$ (Jeong and Hussain 1995), in which $\Omega _{ij}$ and $S_{ij}$ are the vorticity and strain rate tensors, respectively. The left-hand side of Eq. 4 is the pressure force in the i-direction on the surface, $F_{B,i}$ , and the right-hand side terms are the decomposed forces based on the features: $F_{k,i}$ is the kinematic force due to the acceleration of the body surface (B) as well as the flow acceleration at the outer boundary ($\Sigma$), $F_{\mu ,i}$ is the pressure force due to the viscous diffusion on the surface, and $F_{Q,i}$ is the pressure force due to the interaction with nearby vortices. Since $F_{Q,i}$ is given by the volume integral, if one limits the region of volume integral, it is possible to evaluate the pressure force caused by that particular vortex. The integrand of $F_{Q,i}$ represents the vortex-induced force density which can be defined by

$$\begin{aligned} {f_{Q,i}} = - 2{\phi _i}\rho Q. \end{aligned}$$

(5)

When evaluating the vortex-induced force by performing the volume integral for a local region, the influence potential field value may need to be adjusted by subtracting its volume average, $\frac{1}{V}\int \limits _V {{\phi _i}} \mathrm{{d}}V$, to avoid the issue of solution non-uniqueness. More detailed analysis and discussion for the FPM can be found in Refs. (Zhang et al. 2015; Menon and Mittal 2021a, 2021b, 2021c).

2.2 Acoustic partitioning method

In low Mach number aeroacoustics, the dipole sound generated by the surface pressure can be predicted by an acoustic analogy-based formulation. The most well-known formulation is the Ffowcs Williams and Hawkings (FW–H) equation (Ffowcs Williams and Hawkings 1969). For the acoustically compact source and if the Mach number for the surface velocity is low enough ($M=v/c<<1$), the FW–H equation can be approximated by the compact source form (Zorumski 1982):

$$\begin{aligned} p'=\left\{ \frac{r_i}{4\pi r^2}\left( \frac{1}{c}\frac{\partial }{\partial t}+\frac{1}{r} \right) F_{B,i} \right\} _{t-r/c}. \end{aligned}$$

(6)

In the above equations, $p'$ is the sound pressure, c is the speed of sound, r is the distance from the source to the sound pressure monitoring point ($x_p$), $r_i$ is the component of the vector from the source to the monitoring point, $F_{B,i}$ is the aerodynamic pressure force vector (see Eq. 4), and $(t-r/c)$ denotes the evaluation at the retarded time. The compact source form of the FW–H equation (Eq. 6) allows us to relate the dipole sound to the unsteady aerodynamic forces on the surface and serves as a basis for the APM. Substituting Eq. 4 into Eq. 6 gives

$$\begin{aligned} \begin{aligned} p'=&\underbrace{\left[ \frac{r_i}{4\pi r^2}\left( \frac{1}{c}\frac{\partial }{\partial t}+\frac{1}{r} \right) F_{k,i} \right] _{t-r/c}}_{p'_k}+\\&\underbrace{ \left[ \frac{r_i}{4\pi r^2}\left( \frac{1}{c}\frac{\partial }{\partial t}+\frac{1}{r} \right) F_{\mu ,i} \right] _{t-r/c}}_{p'_\mu }+\\&\underbrace{ \left[ \frac{r_i}{4\pi r^2}\left( \frac{1}{c}\frac{\partial }{\partial t}+\frac{1}{r} \right) F_{Q,i} \right] _{t-r/c}}_{p'_Q}, \end{aligned} \end{aligned}$$

(7)

which represents a partitioning of the total dipole sound into a component due to surface acceleration, $p'_k$, a component due to viscous diffusion, $p'_{\mu }$, and a contribution due to the vortex-induced force, $p'_Q$. Like for the FPM, $p'_Q$ can be further partitioned into sound associated with individual vortices or groups of vortices. For a stationary body at high Reynolds numbers, the vortex-induced dipole sound ($p'_Q$) is the most dominant component. The F/APM formulation describes the vortex-induced dipole sound at the far field by

$$\begin{aligned} p{'_Q} = - \frac{{{r_i}}}{{4\pi c{r^2}}}{\left[ {\frac{\partial }{{\partial t}}\left( {\int {2{\phi _i}\rho Q} \,\mathrm{{d}}V} \right) } \right] _{t - r/c}}. \end{aligned}$$

(8)

Thus, one can predict the vortex-induced dipole sound from the Q field by using Eq. 8. Since the dipole sound source is given by the volume integral in Eq. 8, one can predict the sound generated by a particular vortical structure by limiting the region of volume integral. In the present study, Eq. 8 is used to compute the dipole sound at the far field using the time-resolved PIV measurements.

2.3 Relation to the vortex sound theory

For the incompressible flow, Q is given by

$$\begin{aligned} 2Q = - \nabla \cdot \left( {\vec U \cdot \nabla \vec U} \right) \end{aligned},$$

(9)

and thus, the source term of Eq. 8 can be rewritten as

$$\begin{aligned} \begin{aligned}&2{\phi _i}\rho Q = - \rho \nabla \cdot \left( {\vec U \cdot \nabla \vec U} \right) {\phi _i} \\&= \rho \left( {\vec U \cdot \nabla \vec U} \right) \cdot \nabla {\phi _i} - \rho \nabla \cdot \left( {\vec U \cdot \nabla \vec U{\phi _i}} \right) . \end{aligned} \end{aligned}$$

(10)

By using the vector identity, the nonlinear convection term can be separated into:

$$\begin{aligned} \vec U \cdot \nabla \vec U = \vec \omega \times \vec U + \frac{1}{2}\nabla \cdot \left( {\vec U \cdot \vec U} \right) , \end{aligned}$$

(11)

where $\vec \omega = \nabla \times \vec U$ is the vorticity. Substituting Eq. 11 into Eq. 10 yields

$$\begin{aligned} \begin{aligned} 2{\phi _i}\rho Q&= \rho \left( {\vec \omega \times \vec U} \right) \cdot \nabla {\phi _i}\\&\quad + \frac{1}{2}\rho \nabla \cdot \left( {\vec U \cdot \vec U} \right) \cdot \nabla {\phi _i} - \rho \nabla \cdot \left( {\vec U \cdot \nabla \vec U{\phi _i}} \right) . \end{aligned} \end{aligned}$$

(12)

The second term on the right-hand side can be rewritten as

$$\begin{aligned} \begin{aligned} \frac{1}{2}\rho \nabla \cdot \left( {\vec U \cdot \vec U} \right) \cdot \nabla {\phi _i}&=\frac{1}{2}\rho \nabla \cdot \left( {\vec U \cdot \vec U\nabla {\phi _i}} \right) \\&\quad - \frac{1}{2}\rho \left( {\vec U \cdot \vec U} \right) {\nabla ^2}{\phi _i}. \end{aligned} \end{aligned}$$

(13)

The last term in Eq. 13 is 0 by the definition of $\phi _i$, and one can get

$$\begin{aligned} \begin{aligned} 2{\phi _i}\rho Q&= \rho \left( {\vec \omega \times \vec U} \right) \cdot \nabla {\phi _i}\\&\quad + \frac{1}{2}\rho \nabla \cdot \left( {\vec U \cdot \vec U\nabla {\phi _i}} \right) - \rho \nabla \cdot \left( {\vec U \cdot \nabla \vec U{\phi _i}} \right) . \end{aligned} \end{aligned}$$

(14)

Taking the volume integral of Eq. 14 yields

$$\begin{aligned} \begin{aligned} \underbrace{ - \int \limits _V {2{\phi _i}\rho Q} \,\mathrm{{d}}V}_{{F_{Q,i}}} = \underbrace{ - \int \limits _V {\rho \left( {\vec \omega \times \vec U} \right) \cdot \nabla {\phi _i}} \mathrm{{d}}V}_{{F_{\omega ,i}}}\\ - \underbrace{\frac{1}{2}\int \limits _S {\rho \left( {\vec U \cdot \vec U\nabla {\phi _i}} \right) \cdot \vec n} \mathrm{{d}}S}_{II} \\ + \underbrace{\int \limits _S {\rho \left( {\vec U \cdot \nabla \vec U{\phi _i}} \right) \cdot \vec n} \mathrm{{d}}S}_{III}. \end{aligned} \end{aligned}$$

(15)

The divergence theorem is also used to derive Eq. 15. The left-hand side is the aforementioned vortex-induced force, ${F_{Q,i}}$ derived from the FPM. The first term on the right-hand side can be considered as the vortex-generated force by the Lamb vector, $\vec \omega \times \vec U$, and we denote this force by ${F_{\omega ,i}}$. The terms II and III are given by the surface integral over the boundary of the volume. For a stationary, solid body, if the volume integral is applied to the entire flow domain (e.g., $V_f$ in Fig. 1), terms II and III are vanished, and ${F_{Q,i}}$ becomes equal to ${F_{\omega ,i}}$. If the domain of volume integral is set to a truncated local region, terms II and III may not be zero and ${F_{Q,i}}$ is potentially different from ${F_{\omega ,i}}$, while ${F_{\omega ,i}}$ is the dominant vortex-generated force among the terms on the right-hand side of Eq. 15. The force density for ${F_{\omega ,i}}$ can be defined by

$$\begin{aligned} {f_{\omega ,i}} = - \rho \left( {\vec \omega \times \vec U} \right) \cdot \nabla {\phi _i}. \end{aligned}$$

(16)

Using Eq. 6, the dipole sound generated by ${F_{\omega ,i}}$ can be computed by

$$\begin{aligned} p{'_\omega } = - \frac{{{r_i}}}{{4\pi c{r^2}}}{\left[ {\frac{\partial }{{\partial t}}\left( {\int {\rho \left( {\vec \omega \times \vec U} \right) \cdot \nabla {\phi _i}} \,\mathrm{{d}}V} \right) } \right] _{t - r/c}}. \end{aligned}$$

(17)

Eq. 17 is identical to the vortex sound formulation proposed by Takaishi and Ikeda (2005) for a compact source in a finite domain. In the present study, the dipole sound based on the vortex sound theory, $p'_\omega$ , is also computed by using Eq. 17 for a comparison.

2.4 TR-PIV measurements

The 30P30N multi-element high-lift model in the current study has been used in our previous extensive investigations on the slat noise and conceptual passive noise control (Pascioni and Cattafesta 2018; Zhang et al. 2020; Zhang et al. 2021; Zhang et al. 2022). The slat and flap are in the deployed configuration. The stowed chord length of the two dimensional multi-element airfoil is $C=0.457$ m with the slat chord length being $S=0.15C$, and the spanwise dimension is 0.914 m. The time-resolved PIV data used in the current study are essentially from our previous work (Zhang et al. 2020). The experimental arrangement is briefly provided for completeness. High-speed stereo PIV measurements have been performed to investigate the flow fields at ${\text {Re}}_C=1.71 \times {10^6}$ and Mach number at ${M_\infty } = 0.17$, and the experimental arrangement is shown in Fig. 2. The geometric angle of attack of the model is set to $5.5^\circ$. The laser beam generated by a Photonics DM dual-head Nd:YAG laser passes through a series of optics before forming a laser sheet with a thickness of approximately 1.6 mm. Two Phantom V2012 high-speed cameras equipped with 180-mm Tamron SP Di Macro lenses, Scheimpflug adapters, and 532-nm band-pass filters are used for image acquisition. Tracing particles are introduced at the inlet of the wind tunnel by a TSI 9307-6 seed particle generator using olive oil. Calibration is performed by using a LaVision Type 106-10 calibration plate, which is followed by a self-calibration procedure to correct for potential misalignment between the laser sheet and image plane. The sampling rate is 11 kHz, which is sufficient to resolve the shedding of vortical flow structures by the slat-cove shear layer. A total number of 11000 snapshots are used for data reduction.

Fig. 2

Arrangement of PIV setup (not to scale)

In the processing, the background noise is subtracted using a moving average of 49 snapshots to enhance the contrast of particles. Geometric and algorithmic mask functions are used to mask out the no and low seeding regions, respectively. A 128 $\times$ 128 to 24 $\times$ 24 multipass scheme with a $75\%$ overlap is used to calculate the velocity fields. Universal outlier detection (Westerweel and Scarano 2005) is used to filter the spatially spurious outliers in the post-processing. The multivariate outlier detection (Griffin et al. 2010) is applied in MATLAB to remove statistically spurious data. The final resulting vector resolution is approximately 2.2 vectors/mm.

2.5 Velocity field reconstruction

Due to the nonuniform seeding in the flow field and inevitable outliers in the PIV results, there are random blank regions (gaps) in each snapshot of velocity field. To complete the velocity fields, the missing data are first reconstructed using a spectral POD (SPOD)-based data completion method (Schmidt and Nekkanti 2022). This algorithm leverages the temporal correlation of the SPOD modes with preceding and succeeding snapshots, and their spatial correlation with the surrounding data in the flow field. The SPOD modes are first calculated from the unaffected data, and then, gappy data are projected onto the basis of the SPOD modes. Details regarding this reconstruction method are referred to Schmidt and Nekkanti (2022). An original gappy PIV snapshot and the corresponding completed version are compared in Fig. 3. It should be noted that the 30P30N sketches in all of the figures are set at 0-degree angle of attack, which means the x-direction is not in the streamwise direction. From the comparison, the missing velocity data from the PIV measurements are well approximated using this reconstruction method.

Fig. 3

Example of the gappy and complete PIV snapshot showing contour of v-component of the flow field with vectors overlaid

Then, the spectra of SPOD modes of the complete velocity fields are calculated as shown in Fig. 4, where narrow-band peaks are clearly observed in the rank-1 modes. The frequency is normalized to the Strouhal number based on the slat length, ${\text {St}}_S=fS/u_{\infty }$, where $S=0.15C$ is the slat chord length and $u_\infty =58$ m/s. Throughout the paper, ${\text {St}}_S$ is used as a non-dimensional frequency. The mid-range (${\text {St}}_S\in (1-5)$) narrow-band peaks of the slat noise from a scaled model in wind tunnel tests are mainly attributed to the slat-cove shear layer, which contains most of the turbulent kinetic energy. In the calculation of vorticity and Q, the velocity gradient tensor is very sensitive to the small structures/noise due to the limited spatial resolution of PIV. The current resolution of PIV measurement is about 0.5 mm. In the analysis, the velocity gradient is calculated by the second-order central finite difference approximation and this introduces substantial numerical errors for the structures of which wavelength is shorter than about 2 mm. Because of this, in the spectrum of Q calculated with the raw PIV data, the peaks corresponding to the slat-cove shear layer modes are barely observed. In the spectra of SPOD modes of the velocity fields, the rank-1 modes are significantly more energetic than the higher-rank modes, especially at the slat-cove shear layer frequencies. Therefore, the flow fields are reconstructed using only the rank-1 SPOD modes to filter out the smaller-scale structures that sensitively affect the calculation of velocity gradients. Using this method, the resulting spectrum of Q obtained from the low-order reconstruction shows clear peaks at the slat-cove shear layer frequencies.

Fig. 4

Spectra of first five ranked modes for the completed velocity fields

3 Results

3.1 Flow field

The time-averaged spanwise vorticity field with vectors overlaid is shown in Fig. 5. The incoming flow separates at the slat cusp and forms a shear layer that impinges on the cove surface near the slat trailing edge, which is depicted by the high level of spanwise vorticity. The impingement generates an acoustic source that radiates acoustic waves to interact with the shear layer forming a feedback loop, which is analogous to the classic cavity flow oscillations (Roger and Perennes 2000). The narrow-band peaks (${\text {St}}_S \in (1-5)$) in the pressure/velocity spectra are attributed to these vortex shedding from the slat cusp with different time scales and wavelengths. Then, a comparison of Q fields from the complete velocity field and the low-order reconstruction is shown in Fig. 6. The high level of Q is mainly located along the slat-cove shear layer and inside the slat-cove in the original flow field. The low-order reconstruction preserves the main features of the Q in the slat-cove shear layer, with noise and small-scale structures filtered. As we only focus on the noise generation from the dominant vortex interactions, the low-order reconstruction using the rank-1 SPOD modes suffice.

Fig. 5

Contour of time-averaged non-dimensional spanwise vorticity with vectors overlaid

Fig. 6

Example snapshot of Q calculated from original flow field and low-order reconstruction

3.2 Influence potential

The F/APM requires the influence potential field, $\phi _i$ , to predict and analyze the force and dipole sound. The potential field is obtained by solving the Laplace equation, Eq. 2, with the boundary conditions given by Eq. 3. For the complex geometry, the solution can be obtained numerically. In the present study, the potential fields around the 30P30N high-lift configuration are obtained by solving Eq. 2 on the Cartesian grid by using the sharp interface immersed boundary method (Mittal et al. 2008). The control surface B is set on the surface of the airfoil, and the domain size is set to $2C\times 2C$, where C is the chord length of the airfoil. Equation 2 is discretized by the second-order central finite difference scheme and the minimum grid spacing used is 0.002C. The Laplace equation is solved by a bi-conjugate gradient method. The potential fields, $\phi _1$ (x-direction, drag component) and $\phi _2$ (y-direction, lift component), are shown in Fig. 7.

Fig. 7

Influence potential fields, $\phi _1$ (x-direction, drag component) and $\phi _2$ (y-direction, lift component). Top: potential fields over the entire wing. Bottom: zoomed-in views around the slat-cove region

The computed potential fields are then interpolated on to the PIV grid for the calculation of vortex-induced pressure force and dipole sound. The potential $\phi _i$ has a unit of length, and the local value represents the influence of the local flow structure on the corresponding pressure force. For example, Fig. 7 shows the higher value of $\phi _2$ than $\phi _1$ in the slat-cove region. This means that the vortical structures in that region have more influence on the pressure lift than drag.

3.3 Vortex-induced sound prediction

The vortex-induced pressure force, $F_Q$ , and dipole sound, $p'_Q$ , are predicted by using the F/APM formulations, Eqs. 4 and 7. The time-resolved velocity fields are reconstructed by using the rank-1 SPOD modes only, and the Q fields are computed on the cross section of measurement. An instantaneous Q field is shown in Fig. 8, where strong vortical structures along the shear layer in the slat-cove region are clearly visible. As mentioned above, we are particularly interested in the vortex-induced sound from the slat-cove shear layer, and thus, the pressure force and sound are predicted by performing the volume integral over the region indicated by the dotted box in Fig. 8.

Fig. 8

Instantaneous Q field computed from the reconstructed velocity fields. The volume inside the dotted box is used for the prediction of vortex-induced pressure force and dipole sound

The instantaneous distributions of the vortex-induced force densities for the drag ($f_{Q,1}$) and lift ($f_{Q,2}$) components are plotted in Fig. 9. As one can expect, the vortex-induced forces are generated by the strong vortical structures along the shear layer in the slat-cove region. However, due to the different magnitudes of the influence potential fields (see Fig. 7), they generate stronger lift component than drag.

Fig. 9

Instantaneous vortex-induced pressure force densities. $f_{Q,1}$: drag (horizontal) component. $f_{Q,2}$: lift (vertical) component

The vortex-induced dipole sound is then predicted by using Eq. 8. For the sound prediction, the span length, $L_s$ , is assumed to be 1 m, and a spanwise coherence length, $L_c$ (Pascioni and Cattafesta 2018), is used to correct the sound pressure level (SPL). The corrected sound pressure level in dB is calculated by

$$\begin{aligned} SPL = 20 \log (p'_{rms}/p_{\text {ref}})-10\log (L_s/L_c), \end{aligned}$$

(18)

where $p'_{\text {rms}}$ is the root-mean-squared sound pressure predicted for the span length of $L_s$ by assuming full spanwise correlation, $L_c$ is the spanwise coherence length scale, $p_{\text {ref}} = 2e-5$ Pa, and $L_s=1$ m. Note that $L_c$ is the function of frequency, and we use the coherence length scale data presented in the previous study (Pascioni and Cattafesta 2018). The SPL spectrum at 1-m distance below the airfoil is shown in Fig. 10a. The spectrum exhibits tonal peaks at ${\text {St}}_S=1.5$, 2.3, and 3.1 that are corresponding to the first, second, and third shear layer modes, respectively. The directivity patterns for two major peaks at ${\text {St}}_S$=1.5 and 2.3 are plotted in Fig. 10b at 1-m distance from the airfoil. The directivity plot shows a clear dipole sound pattern. The peak sound angles are $104^\circ$ and $106^\circ$ for ${\text {St}}_S$=1.5 and 2.3, respectively. As a reference, the sound pressure level measured by a single microphone at those two frequencies is marked in the plot. Note that, however, the measurement was for the sound generated by the entire multi-element airfoil including sounds from other sources. The measured SPL is also scaled for the 1-m span.

Fig. 10

Vortex-induced sound, $p'_Q$ predicted by F /APM formulation. a Sound pressure level spectrum at 1-m distance below the airfoil. b SPL directivity patterns at 1-m distance. Symbols: Measurements by the single microphone. Circle: ${\text {St}}_S=1.5$. Square: ${\text {St}}_S$=2.3

The vortex-generated force derived from the vortex sound theory, $F_\omega$ , and the associated dipole sound, $p'_\omega$ , are also examined. An instantaneous vorticity and vortex-generated force densities, $f_\omega$ , are plotted in Figs. 11 and 12, respectively. While the force density distributions shown in Fig. 12 also clearly indicate the forces generated by the shear layer in the slat-cove region, they look slightly more diffused than the ones based on the FPM shown in Fig. 9.

Fig. 11

Instantaneous spanwise vorticity computed from the reconstructed velocity fields

Fig. 12

Instantaneous vortex-generated force densities. $f_{\omega ,1}$: drag (horizontal) component. $f_{\omega ,2}$: lift (vertical) component

The dipole sound based on the vortex sound theory, $p'_\omega$ , is then computed by Eq. 17 and the SPL is corrected by Eq. 18. The SPL spectrum and directivity patterns for $p'_\omega$ are shown in Fig. 13. The SPL spectrum exhibits the tonal peaks at ${\text {St}}_S$=1.5 and 2.3 as well as the one at ${\text {St}}_S$=3.1 very clearly. The sound pressure levels at those tonal peaks are higher than the ones predicted by the APM ($p'_Q$) by a few decibels, especially at ${\text {St}}_S=2.3$, while the broad-banded floor of $p'_\omega$ is slightly lower than $p'_Q$. The directivity patterns at the tonal peak frequencies (${\text {St}}_S$=1.6 and 2.3) are quite similar to the ones for $p'_Q$. The peak sound angles are slightly different from the predictions by the APM, and they are at $108^\circ$ and $106^\circ$ for ${\text {St}}_S$=1.5 and 2.3, respectively.

Fig. 13

Vortex-generated sound, $p'_\omega$ , based on the vortex sound theory formulation. a Sound pressure level spectrum at 1-m distance below the airfoil. b SPL directivity patterns at 1-m distance. Symbols: Measurements by the single microphone. Circle: ${\text {St}}_S=1.5$. Square: ${\text {St}}_S$=2.3

Fig. 14

Sound pressure level spectra at 1-m distance below the airfoil. Measurement: Single microphone measurement of the sound from the entire multi-element airfoil including the slat, main wing, and flap. Data from Pascioni and Cattafesta (2018). APM: $p'_Q$ predicted by the APM formulation. Vortex sound: $p'_\omega$ based on the vortex sound theory formulation

4 Discussion

In the present study, we reconstructed the time-dependent velocity fields in the slat-cove region of the 30P30N multi-element airfoil by using the SPOD of the time-resolved PIV measurements. The reconstructed velocity fields showed the flow separation at the slat cusp and the formation of shear layer. The energy spectra of SPOD modes showed the narrow-band peaks at ${\text {St}}_S$=1.5, 2.3, and 3.1, which are corresponding to the shear layer oscillations due to the vortex roll-up. Those narrow-band peaks are almost completely resolved by the rank-1 SPOD mode only, indicating that the rank-1 SPOD modes are enough to represent the dominant vortex interactions. To predict the vortex-induced force and sound, therefore, we reconstructed the velocity fields by using the rank-1 SPOD mode only. This was also necessary to suppress high-wave number errors in the PIV measurements, which are readily amplified in the calculation of velocity gradients.

By applying the force partitioning method (FPM), the vortex-induced force densities, $f_{Q,i}$ , are computed and examined. As expected, high level of force densities is observed along the shear layer in the slat-cove region. For a comparison, the vortex-generated force densities based on the vortex sound theory, $f_{\omega ,i}$ , are also computed and examined. While $f_{Q,i}$ are proportional to the local value of Q, $f_{\omega ,i}$ depend on the Lamb vector and thus are proportional to the local vorticity. $f_{\omega ,i}$ are concentrating on the shear layer like $f_{Q,i}$; however, the actual distributions look quite different. This is because $f_{\omega ,i}$ represents the force based on the momentum balance, while $f_{Q,i}$ is directly related to the force due to the surface pressure. Taking the divergence of the momentum equation for the incompressible flow gives the pressure Poisson equation:

$$\begin{aligned} {\nabla ^2}p = 2\rho Q, \end{aligned}$$

(19)

and this clearly shows the connection between the Q and pressure. As discussed in the previous study of Menon and Mittal (2021c), $f_Q$ represents the forces due to vortex cores $(Q>0)$ as well as strain dominated flow $(Q<0)$, and it shows more complex structures.

The dipole sound by the vortex-induced force is then predicted by applying the acoustic partitioning method (APM). The sound is also predicted by the vortex sound theory formulation (Eq. 17) for a comparison. In this study, we limit the source region to the shear layer in the slat-cove to estimate the sound generated by this particular flow structure. The predicted sound pressure level spectra at the 1-m distance directly below the airfoil are plotted in Fig. 14 along with the experimental measurement presented in Pascioni and Cattafesta (2018). Note that the measurement is for the entire multi-element airfoil, and it includes the sounds from other sources such as the vortex shedding at the trailing edge of the slat and its interaction with the leading edge of the main wing. As expected, the shear layer modes identified in the SPOD energy spectra generate tonal noise and those tonal peaks are captured well by both the APM and vortex sound theory.

It is interesting to note the slight differences between the sound spectra predicted by the APM and vortex sound theory. It is shown that the APM is mathematically consistent to the vortex sound theory, especially when they are applied to the entire flow domain. If one applies the APM or vortex sound theory formulation given by Eq. 17 to the truncated flow volume locally, the terms II and III in Eq. 15 are nonzero and thus the sound prediction by the APM ($p'_Q$) is not equal to the one by the vortex sound theory ($p'_\omega$). This is primarily due to the boundary effects as shown in Eq. 15. In Takaishi and Ikeda (2005), the vortex sound formulation, Eq. 17 was derived with the boundary conditions for the potential field, ${\phi _i} = 0$ and $\nabla {\phi _i} = 0$ , to drop the terms II and III. These two boundary conditions can only be satisfied if the boundaries of the flow domain are placed very far from the body. For the locally truncated volume, therefore, terms II and III need to be considered. The effects of these terms are already included in the F/APM formulation, and it could be more useful to estimate the vortex-induced sound from the local flow structures. As shown in Fig. 14, however, the possible effects of the terms II and III are not significant especially on the dominant vortical fluctuation modes, and it can be confirmed that the vortex sound prediction by the APM is consistent to the vortex sound theory. Further investigations may be required though to see whether the more detailed source structures represented by $f_Q$ provide additional information about the sound generation mechanism.

The differences between the measured and predicted sound spectra shown in Fig. 14 suggest that the flow structures other than the flow fluctuations at the shear layer frequencies generate substantial noise as well. It has to be noted that the cut-off frequency of the measurement chamber is approximately 200 Hz, which corresponds to ${\text {St}}_S$=0.23, and the acoustic measurements below this frequency are probably corrupted. Nonetheless, the big difference in the sound pressure level around ${\text {St}}_S\sim 1$ is presumably due to the truncated SPOD modes. To check this, sound prediction by the APM formulation is performed with the velocity field reconstruction using the ranks 1–5 SPOD modes (see Fig. 4). The results are plotted in Fig. 15 along with the measured SPL spectrum. Inclusion of the higher-rank modes in the prediction increases the sound pressure level, and the predicted SPL spectrum becomes more comparable to the measured one especially in the low frequency region. As discussed above, however, the higher-rank modes bring the high-wave number errors associated with the PIV resolution, which are then amplified in the calculation of velocity gradients. As a result, the higher-rank modes introduce a significant error in the sound pressure level in the high-frequency region (${\text {St}}_S>2$). A way to suppress or filter out those high-wave number, high-frequency error will be pursued in future study. Nevertheless, the sound prediction using the rank-1 SPOD mode informs the contribution of the slat-cove shear layer itself on the overall sound generation.

Fig. 15

Sound pressure level spectra at 1-m distance below the airfoil. Measurement: Single microphone measurement of the sound from the entire multi-element airfoil including the slat, main wing, and flap. Data from Pascioni and Cattafesta (2018). APM (rank 1): $p'_Q$ predicted by the APM formulation using the velocity field reconstructed with the rank-1 SPOD mode. APM (ranks 1–5): $p'_Q$ using the reconstruction with the ranks 1–5 SPOD modes