Spectrally-resolved Rayleigh scattering to measure velocity, temperature, density, and density fluctuations in high-speed flows

Abstract

A new spectroscopic setup to analyze Rayleigh-scattered light from a high-speed jet was created at the NASA Ames Research Center for simultaneous measurement of velocity, temperature, and density. The point-measurement arrangement uses a narrow-linewidth continuous-wave laser and a stabilized, air-spaced, Fabry–Perot etalon to resolve the Rayleigh–Brillouin (RB) spectrum. Light scattered from a 0.4 mm-long and 0.15 mm-diameter probe volume was collected and 10% of the light was split to measure the scattering intensity via a photo-multiplier tube, which provided a measure of the gas density and density fluctuation spectra. The rest was directly imaged through the Fabry–Perot interferometer to an EMCCD camera. A new software program was developed in the Matlab^® platform to model the fringes seen in the camera image. At first, a small part of the incident laser light was analyzed to find the instrument function. When Rayleigh-scattered light was passed, a change in the fringe diameter corresponding to the Doppler shift from the air velocity and a thickening of the fringe corresponding to the thermal broadening were observed. A least-squares fit utilizing Tenti’s S6 model of the RB scattering provided velocity and temperature at the probe volume. A high-speed, clean-air jet, operated in the Mach range of 0 ≤ M ≤ 1.2 provided validation of the technique, and demonstrated applicability in shock-containing flows. The compact, transportable, efficient, and affordable setup was fairly accurate: uncertainties were < 7 m/s in velocity, < 5 K in temperature, and < 1% in density. Spectra of density fluctuations were measured over a frequency range of 50 kHz.

Graphic abstract

Principle of Rayleigh scattering technique, (a) schematic representation; (b) superimposed Fabry–Perot images from the present setup, U = 323 m/s, T = 249 K.

1 Introduction

Although many aircraft and spacecraft fly at supersonic-to-hypersonic velocities, experimental tools that measure gas properties and turbulence quantities around such vehicles are very few or nonexistent. Making such vehicles affordable and accessible to many requires making them safer and more efficient by better understanding and manipulating the flow-field around them. The lack of experimental data makes computational fluid dynamics (CFD) simulations as the sole provider of many critical aerodynamic information. However, CFD cannot fill the gap in knowledge alone as the computational codes require experimental data for validation. In addition to velocity, compressible flows require measurement of scalar parameters, such as density and temperature for validation. Specification of the turbulence statistics requires time-resolved measurement of velocity, temperature, and density, which are very difficult to obtain. Out of the many emerging optical techniques for aerodynamic applications that can provide this information, molecular Rayleigh scattering is the most promising due to the relatively large signal levels, the appeal of a complete measurement of kinematic and thermodynamic properties, and the affordability of the opto-electronics. While commercially available, particle-based optical techniques such as LDV and PIV have become ubiquitous in small facilities, large test facilities dislike the wide-spread particle contamination. Additionally, particle-based techniques are incapable of providing the thermodynamic parameters essential in high-speed and high-temperature flows. This Rayleigh scattering-based technique is non-intrusive, does not require injection of seed particles, and is capable of measuring gas temperature and density. Velocity and temperature values are deduced from intrinsic molecular properties—no calibration is needed.

A simplistic description of the measurement process using spontaneous Rayleigh scattering is schematically shown in Fig. 1a. The electric field of the incident laser light polarizes individual gas molecules, which in turn scatter a very small part of that light. The total scattering intensity is directly related to the number of gas molecules in the probe volume, and, thus, to the bulk density of the flow. In the present setup, air density is measured by splitting off a small part of the scattered light and measuring its intensity through a photo-multiplier tube (PMT). The moving gas molecules also create a Doppler shift in the scattered light. Airflow, such as that in a wind tunnel, can be thought of as a combination of a bulk motion at the measured Mach number plus a superimposed random velocity of the individual molecules. Therefore, the Doppler-shifted scattered light is spectrally broadened with a distinct peak. The separation between the peak of the incident laser line and the peak of the Rayleigh spectrum provides a measure of the bulk velocity. The full width at half maximum (FWHM) depends on the spread of molecular motion and, therefore, is a measure of gas temperature. Because the Doppler shift is of the order of 10⁹ Hz (2.66 MHz per m/s of flow velocity for 90° scattering using 532 nm light), which is far smaller than the optical frequency (5.6 × 10¹⁴ Hz for 532 nm light in air), there is a need to use a narrow-linewidth laser source and a hyperfine spectroscope, such as a Fabry–Perot interferometer. Figure 1b, obtained from the present work, succinctly describes the “spectrally resolved” technique. The narrow linewidth of the incident beam created the bright Airy ring—seen as white concentric circles—after passing through a Fabry–Perot interferometer (FPI). An FPI radially (angularly) distributes light based on its frequency. When the Rayleigh-scattered light is passed through the interferometer, the thermal broadening manifests as radial smearing, and the Doppler shift from the bulk velocity manifests as a radial shift from the laser line. In Fig. 1b, the Rayleigh image is in false color—white–orange as the max intensity falling to green–blue and the minimum is in black. When compared with the Airy rings, the Rayleigh image shows the Doppler shift in the peak frequency and the thermal broadening of the spectrum. The present work reports a setup to collect such images, followed by an analysis to determine local velocity and temperature inside a jet. A second part of the setup is to measure the intensity of scattering to determine air density.

Fig. 1

Principle of Rayleigh scattering technique: a schematic representation; b superimposed Fabry–Perot images from the present setup: U = 323 m/s and T = 249 K

In the last 3 decades, a number of optical flow diagnostic techniques based on Rayleigh scattering have emerged. These techniques can be broadly divided into two categories based on the laser source: continuous-wave (CW) vs pulsed or pulse-burst lasers. Each of these categories can be further divided into two categories based on the means of resolving the Rayleigh spectrum—use of an interferometer, such as a Fabry–Perot (Seasholtz 1991; Pitz et al.1976; Seasholtz and Lock 1992; Panda and Seasholtz 1999a; Fagan et al.2005; Bivolaru et al.2011), or a molecular absorption filter, such as the hyperfine absorption lines of iodine vapors (Miles et al.1991; Forkey et al.1996; George et al.2017; Doll et al.2017). A pulsed-laser based technique can be used for planar measurement, while a CW-laser based technique can take advantage of a very narrow linewidth, which, in turn, promises a better accuracy. The present work follows the combination of a CW-laser and a Fabry–Perot interferometer mainly due to the past demonstration of this combination’s capabilities to measure unsteady fluctuations (Seasholtz et al.2002; Panda et al.2005). Another reason is the affordability of such a setup: due to its use in various industries, the narrow-linewidth, CW lasers have become more affordable and have improved frequency stability.

Advancements of optical diagnostic techniques are closely tied to improvements in the laser sources and opto-electronics on which they depend. In the past (Seasholtz 1991; Seasholtz and Lock 1992; Panda and Seasholtz 1999a), large Argon-ion lasers with an inter-cavity etalon barely produced 1 W of power in single frequency. Frequent mode hopping created an additional challenge for accurate measurements. That has all changed—one can currently buy affordable lasers that produce up to 18 W of power and maintain stability over hours of operation. The bulky FPIs, which were prone to drift and hard to align, can be replaced by compact, electronically stabilized versions that are commercially available. Similarly, the advent of the EMCCD cameras has improved the ability to measure low levels of light. A goal of the present work is to take advantage of such improvements. The setup also needs to be compact for easy transportation to large testing facilities. To create a compact, affordable, and efficient Rayleigh setup that is easier to setup and can be easily transported to a large facility, such as the unitary plan transonic and supersonic wind tunnels of NASA Ames Research Center is the purpose of the present work.

1.1 Rayleigh–Brillouin (RB) spectrum

We start here with the fundamentals of measuring velocity and temperature by resolving the RB spectrum. Measurement of air density is straightforward and is presented later in Sect. 1.3. When light is passed through a gas media, the frequencies of the light scattered elastically by the very large number of molecules, which are moving over a wide range of velocities, are described by the Rayleigh–Brillouin spectrum. Figure 2 shows a scattering diagram. To scatter incident photons of wave number k_i towards the direction of the collection lens, oriented at the scattering angle θ_s, a momentum transfer needs to occur. If the scattered vector pointing towards the collection optics is k_s, then k = k_s− k_i, is the interaction (also called scattering) vector, indicating the direction of the momentum transfer. Because the wave number change is miniscule for elastic scattering |k_s| ≈ |k_i|, the magnitude of the scattering vector becomes the following:

$$\left| {\mathbf{k}} \right| = k = 2 k_{{\text{i}}} \sin \left( {\frac{{\theta_{{\text{s}}} }}{2}} \right) ,$$

(1)

and the associated wavelength Λ = 2π/k is longer than that of the incident light. A rigorous analysis of light scattering by a large number of molecules attributes the source of the momentum transfer to fluctuations of refractive index of the media, which in turn is related to the fluctuations in the number density of gas molecules, or more accurately the two-point space–time correlation of such micro-scale fluctuations (Berne and Pecora 2000; Tenti et al. 1974; Boley et al. 1972). At high pressure and low temperature when the number density is large, or at very shallow scattering angles when the light scattering is caused by an effectively large number of molecules, a part of the number density fluctuations can be seen as very-high-frequency (order of GHz) sound waves that are constantly generated and dissipated while propagating at the most-expected speed in the media. Light scattering from such sound waves is called the Brillouin scattering and is described through the hydrodynamic equation (Navier–Stokes), which gives it the name hydrodynamic regime. At the other extreme when the molecular number density is low or at very large scattering angles, there is no propagating part of the micro-scale correlation function, and the spectrum can be explained via the dilute-gas approximation. For most aerodynamic applications, the situation is somewhat in between—called the kinetic regime, which requires a full-blown description of the correlation function through the Boltzmann equation.

Fig. 2

Scattering diagram

Even at ambient conditions, gas molecules that make up air move with a wide range of velocity, some higher than the local sound speed c. In gas kinetic theories, the commonly used term is the “most probable sound speed”:

$$a = \sqrt {\left( {2k_{{\text{B}}} T/m} \right)} .$$

(2)

Note that a is related to the local sound speed c_s via the ratio of specific heats: a = c_s√(γ/2). For a moving stream of air, the random fluctuations are superimposed on the “bulk velocity” U. Due to these motions of the molecules (V: combined velocity), the scattered light is Doppler shifted to a frequency ω from that of the incident frequency of ω₀, and can be expressed by the following:

$$\omega - \omega_{0} = {\mathbf{k}} \cdot {\mathbf{V}}.$$

(3)

The two extreme cases of elastic molecular scattering described above are described by the ratio of the scattering wavelength Λ to the molecular mean-free-path ℓ. The ratio is more succinctly described by the y-parameter. Because the molecular free path relates to the local pressure P and gas viscosity η, the ratio is expressed as the following:

$$y = \frac{P}{\eta ka} \propto \frac{\Lambda }{\ell }.$$

(4)

For low density and/or large angle scattering when ℓ >> Λ (implying y << 1), the dilute-gas limit occurs. In this limit, the organized, high-frequency sound waves play little role and the spectrum of the scattered light is built up by the individual molecules moving with the velocity f(V)dV. By analyzing the frequency spectrum of the scattered light relative to the incident laser frequency, one can extract information that is proportional to the number of molecules moving in various velocity ranges. The distribution of the molecular velocity follows the Maxwellian distribution:

$$f\left( V \right) {\text{d}}^{3} V = \frac{n}{{\pi^{1.5} a^{3} }} \exp \left[ { - \frac{{\left( {V - U} \right)^{2} }}{{a^{2} }}} \right]{\text{d}}^{3} V.$$

(5)

The spectrum of the scattered light can be expressed by the following:

$$S_{{\text{R}}} \left( {{\mathbf{k}},\omega } \right) = \frac{2\sqrt \pi }{{ak}}\exp \left[ { - \frac{{\left( {\omega - \omega_{0} - {\mathbf{U}} \cdot {\mathbf{k}}} \right)^{2} }}{{a^{2} k^{2} }}} \right].$$

(6)

An examination of the above expression shows that the bandwidth (i.e., FWHM) of the Rayleigh spectrum is related to the most-probable sound speed, which in turn relates to √T. This √T dependence causes the temperature measurement to be particularly error prone and means that ultimate accuracy depends on correct modeling of instrument function (which includes frequency stability of the incident laser), the particle contamination, and efficient suppression of the background scattered light.

In typical scattering problems, the Doppler-shifted frequency is normalized by a frequency associated with the scattering by the most-probable sound speed a: ka, leading to the parameter x:

$$x = \frac{\omega }{ka}.$$

(7)

Therefore, the Rayleigh spectrum calculated in Eq. (6) becomes a function of x: S_R(x). Returning back to the other extreme of high gas density and/or shallow angle scattering ℓ << Λ (implying y >> 1), the high-frequency acoustic fluctuations from the correlated motion of the gas molecules take up a prominent role. These sound waves (phonons) moving either along or opposite to the scattering vector k cause momentum transfer to the incident photons leading to either an increase or a decrease of the frequency of the scattered light (similar to the Stokes and anti-Stokes lines of Raman scattering). Additionally, the thermal fluctuations present in the molecules, i.e., entropy waves, make a contribution that lies at the center of the spectrum. A detailed hydrodynamic analysis shows a triplet in the spectrum, which, neglecting the weaker terms, can be expressed by the following (Berne and Pecora 2000):

$$S_{{\text{B}}} \left( {k,\omega } \right) = \left| S \right|\left\{ {\left( {1 - \frac{1}{\gamma }} \right)\left[ {\frac{{D_{{\text{T}}} k^{2} }}{{\omega^{2} + \left( {D_{{\text{T}}} k^{2} } \right)^{2} }}} \right] + \frac{1}{\gamma }\left[ {\frac{{\Gamma k^{2} }}{{\left( {\omega + ka} \right)^{2} + \left( {\Gamma k^{2} } \right)^{2} }} + \frac{{\Gamma k^{2} }}{{\left( {\omega - ka} \right)^{2} + \left( {\Gamma k^{2} } \right)^{2} }}} \right]} \right\}.$$

(8)

The first term is the central, un-shifted lobe that arises from entropy fluctuations and the second term is the Brillouin doublet from acoustic fluctuations.

The expression for the light spectrum of the intermediate kinetic region, y ~ 1, which is of current interest, is complex. Like many other works before, the present paper uses Tenti’s S6 model (Tenti et al.1974; Boley et al.1972), whose claim is that Rayleigh–Brillouin spectra can be completely expressed by the non-dimensional frequency, x, and the y-parameter. Therefore, the final Rayleigh–Brillouin spectrum used is expressed as S_R(x, y). Figure 3 shows a typical Rayleigh–Brillouin spectrum used to model the experimental data. The effect of the Brillouin doublet is small yet significant enough to give the sharper rise of the two edges of the spectrum. The central hump is related to the decay of the entropy waves, while the overall shape is mostly provided by the Gaussian distribution of the dilute-gas spectrum.

Fig. 3

Rayleigh spectrum calculated from Tenti model for dry air with bulk velocity of 290 m/s, static temperature of 260 K, static pressure of 0.1 MPa, and 90° scattering from 532 nm laser

1.2 Fabry–Perot interferometer

In this experiment, the fine resolution needed to resolve the Doppler-broadened Rayleigh spectrum necessitated the use of a Fabry–Perot interferometer (FPI). There are many textbooks which describe the principle of operation (for example, Vaughan 1989). Fundamentally, an FPI acts as a light filter whose transmittance is dependent on the frequency f of the incident light, the angle θ of the incident light with respect to the optical axis, the refractive index μ in the medium between the two reflective surfaces, and the separation d between the surfaces (Fig. 4). The latter two are fixed for the imaging mode of operation used in this work, leaving angle θ and frequency f as the dependent variables. Because frequency is defined via the x parameter (Eq. 7), the following discussion is to establish the light intensity distribution (the instrument function) as functions of θ and x: I_FP(θ, x). Like many other optical calculations, the clue needed to model the instrument function is to follow the phase of the light waves. For a fixed-frequency light arriving at an incident angle of θ (Fig. 4), the successive reflection in the two mirrored surfaces creates a phase difference ψ, which, using the small angle approximation, can be expressed by the following:

$$\psi = \frac{4\pi \mu d}{\lambda }\cos \theta \approx \frac{4\pi \mu d}{\lambda }\left( {1 - \frac{{\theta^{2} }}{2}} \right).$$

(9)

Fig. 4

Schematic of imaging through a Fabry–Perot interferometer

When transmitted light of all different phase angles are summed via the fringe-forming lens, the intensity pattern of the camera image is the Airy function:

$$I_{{{\text{FP}}}} \left( \psi \right) = \left[ {1 + \left( {\frac{2N}{\pi }} \right)^{2} \sin^{2} \frac{\psi }{2}} \right]^{ - 1} ,$$

(10)

where N is the interferometer finesse that determines the sharpness of the filter roll-off (a higher finesse translates into a sharper roll-off). For an ideal interferometer, finesse is a function of the mirror reflectance only; however, in reality factors such as imperfections in the mirror coating, misalignment of the optical train, vibration, and noise (both acoustic and electronic) degrade the finesse. An incorrect finesse value affects the measurement accuracy; therefore, finesse needs to be continuously monitored during the course of an experiment.

An examination of Eq. 9 above shows that for a fixed setup and a fixed optical frequency (wavelength), the optical phase ψ varies with the angle θ of the incident light. The incidence angle θ for a point at a radial distance of r from the center of the image can be determined by an accurate knowledge of the focal length f_f of the fringe forming lens and the refractive index μ of the etalon or the gas medium in between the reflecting surfaces:

$$\theta \approx \frac{r}{{f_{{\text{f}}} \mu }}.$$

(11)

Because light from different parts of the imaging area make different θ angle with the optical axis, the variation in θ, and in turn ψ, occurs concentrically from the optical axis. Therefore, by Eq. 10, a single frequency light is imaged as concentric rings at the image plane. Consecutive bright rings represent a phase change of 2π. Also note that the optical phase ψ varies non-linearly with the incidence angle: θ² dependence in Eq. 9. Although θ varies linearly (small angle approximation) from the center of the image, the non-linear dependence of the optical phase makes fringes of higher order to form at closer spacing.

The first step in modelling the measured image is identifying the phase ψ distribution. The absolute value of phase change ψ through successive reflections in the FPI cavity is very large, which necessitates a description based on a relative phase change. Note that the peak locations of the interference patterns correspond to a phase change of 2π. If the phase of the innermost ring corresponds to an incidence angle of θ_p, then the relative phase variation over the image can be written as follows:

$$\psi = \frac{4\pi \mu d}{\lambda }\cos \theta \approx \frac{4\pi \mu d}{\lambda }\left( {\frac{{\theta_{{\text{p}}}^{2} - \theta^{2} }}{2}} \right) .$$

(12)

Another important parameter that affects the accuracy of the calculated phase angle distribution is the air gap of the planar mirrors. Typically, this thickness can be measured within an accuracy of 0.1 mm. However, the radial distance of the peak of, say, the first fringe can be used to make a correction δ to this measurement. At the interference peak, the phase change should be a multiple of 2π, and any discrepancy is due to the error in the measurement of the thickness of the air gap. The fringe order Π at the location of the incidence angle of θ_p is the following:

$$\Pi = \frac{2\mu d}{\lambda }\left( {1 - \frac{{\theta_{{\text{p}}}^{2} }}{2}} \right).$$

(13)

The correction δ in the thickness can be written as:

$$\delta = - \frac{\lambda }{2\mu }\left( {1 - \frac{{\theta_{{\text{p}}}^{2} }}{2}} \right)^{ - 1} {\text{Frac}}\left( \Pi \right),$$

(14)

where Frac(Π) is the fractional part of the fringe order. The corrected thickness then becomes d + δ which will be referred as d for simplicity.

An important parameter of an interferometer is the free-spectral range (FSR). In the present setup, the air-spaced FPI was operated in the imaging mode, that is, the mirror separation d was kept fixed to 18.8 mm. The fixed separation between the reflective surfaces, in turn, fixed the free-spectral range (FSR) of the interferometer to 8 GHz:

$${\text{FSR}} = \frac{c}{2d}.$$

(15)

The discussion so far described the filtering characteristics based on the angularity of a fixed-frequency, incident light. Light waves with frequencies different from the incident beam introduce additional phase change. This change is measured as a relative change from that of the incident light and is expressed through the x parameter described earlier (Eq. 7). The phase change due to the combined angularity and frequency difference is ultimately the relationship of interest:

$$\psi \left( {x,\theta } \right) = \frac{4\pi \mu d}{\lambda }\left( {\frac{{\theta_{{\text{p}}}^{2} - \theta^{2} }}{2} + \frac{\lambda ax}{{c\Lambda }}} \right).$$

(16)

The resulting intensity distribution used for modelling the Fabry–Perot images is stated earlier in Eq. (10).

1.3 Measurement of air density

Because density measurement requires no spectroscopic analysis, it is the simplest of all measurements. The simplicity of this measurement means that it has been used for many applications in the past—the author and others wrote reports (Panda and Seasholtz 2002; Panda 2016; Mercier et al. 2018) describing the fundamentals, which are summarized in brief below. The local density at the probe volume V_sc is determined via a measurement of the power P_s of the Rayleigh-scattered light using a set of lenses that collects light from a solid angle dΩ:

$$P_{{\text{s}}} = nI_{0} V_{{{\text{SC}}}} \left( {\frac{\partial \sigma }{{\partial \Omega }}} \right)\sin^{2} \chi {\text{d}}\Omega = nC .$$

(17)

Here, ∂σ/∂Ω is the Rayleigh scattering cross section of the gas mixture. The Rayleigh scattering cross section depends on the refractive index of the particular species and is constant for a fixed wavelength laser and a fixed gas mixture (air for this work). For a fixed optical setup, the scattered laser power is directly proportional to the molecular number density, which is related to the bulk density, ρ through the Avogadro constant N_A (6.022 × 10²⁶ kmol⁻¹), and molecular weight W of the gas mixture n = ρ N_A/W. Typically, a photo-electron counting process is employed to measure the scattered power, making the rate of photon arrival, or alternatively the photon count p over a fixed time interval Δt, directly proportional to the gas density within the probe volume. The proportionality constants C₁ and C₂ of Eq. 18 have to be determined through a calibration process. The additional constant C₂ is required to account for the contamination from the background light. Evaluation of these constants will be discussed later in Sect. 4.2:

$$p = \left( {C_{1} \rho + C_{2} } \right)\Delta t.$$

(18)

The Mie scattering signatures from the passage of dust particles need to be removed from the PMT data to improve the accuracy of measuring both the time-averaged density and the spectral estimates of density fluctuations. This is accomplished by performing photo-electron counting in a series of contiguous gates of very short time-duration (typically 1–10 μs). The passage of particles is identified by a sharp rise in counts over the average value. Replacement of the high counts is an effective means of removing the particle signature. An in-depth discussion of removing the particle signature from the PMT data can be found in Panda (2016) and Mercier et al. (2018).

2 Experimental setup

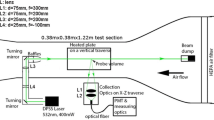
The central element of the optical setup (Fig. 5) was a CW laser beam that passed through the clean-air stream. The 532 nm, single-mode, incident laser beam for the optical setup was produced from a frequency-doubled, Nd:YVO₄ solid-state source that emitted a maximum of 6.5 W power. The vendor provided a specification of 5 MHz for the linewidth. The laser beam was focused to a 0.15 mm waist at the probe volume. Because Rayleigh scattering is strongly dependent on the polarization direction, the axis of the plane polarized incident beam was set vertical for maximum scattering towards the collection lens, which was collecting light in the horizontal direction, i.e., the angle χ of Eq. 17 was set at 90°. The molecular scattered light from a small region on the beam was collected for spectral analysis. The collection optics were made of a pair of 75 mm-diameter achromatic lenses that focused the scattered light on a 0.67 mm-wide slit. The slit also blocked stray scattered light from entering into the spectroscopic part of the setup. Baffles and curtains were placed around the PMT and the spectroscopic setup to further reduce contamination from stray light.

Fig. 5

Schematic of the directly imaged, spectrally resolved Rayleigh setup

The scattered light imaged through the slit was first collimated by a 50 mm f/2 achromatic lens. Subsequently, a small amount, ~ 10%, of the collected light was split and focused onto the photo-cathode of a PMT. The photo-electron counting was performed by a commercially available discriminator–timer–counter board and software (P7882 Multiscaler by Fastcomtec). To measure the time-evolution of the density fluctuations, counting was performed on contagious gates, each typically of 10 µs duration. Because the absolute magnitude of the density fluctuations was small < 4% of mean density in M 0.98 jet—and only ~ 10% of the scattered light was used for density measurement, a long (50 s) time record of data was needed to sufficiently reduce the shot-noise floor in the measured spectra of air-density fluctuations. Time-averaged measurements can be performed from a shorter, 1 s duration of counting.

The majority (~ 90%) of the collected light was passed through air-spaced, planar, 30 mm diameter, 90% reflectivity FPI mirrors with a free-spectral range of 8 GHz. The optical cavity of the stabilized Fabry–Perot, supplied by Lightmachinery, was actively controlled by three piezo-scanned support points and three strain gauges that provided position sensing. Once aligned, the closed-loop control maintained the parallelism of the two mirrors through extraneous environmental factors such as thermal drift. This was particularly beneficial for long-duration data collection and eliminated the need for any manual adjustment. The actively controlled interferometer simplified the day-to-day alignment so much that the laser can be turned on any day, and nicely formed fringes with no degradation of the finesse can be readily visible. Finally, the interferometer output was imaged through a 300 mm focal length fringe-forming lens on a low-light, cooled, EMCCD camera.

For the alignment of the spectroscopic setup and for determining the instrument function, a small part of the incident laser light needed to be passed through the interferometer. To achieve this goal, a small fraction of the incident light was separated out via an anti-reflection coated window placed before the primary beam dump. The intensity of the light was further reduced via a polarizer (see the part of the setup around the beam dumps in Fig. 5) and then coupled to an optical fiber, which passed it to an integrating sphere (IS). The IS was mounted on a linear actuator, which allowed placement of an opening of the IS in front of the slit. When the IS was placed in front of the slit, the Rayleigh-scattered light was blocked and the reference light from the incident beam passed through the interferometric setup. The polarizer placed on the path of the reference light allowed variation in the amount of light transmitted to the FPI setup. A relatively larger amount of light was needed for the alignment of the FPI, while a much lower intensity light was needed to determine the instrument function. The latter was set from the exposure time of the EMCCD camera, which could be easily saturated. This was accomplished by rotating the polarizer (PR of Fig. 5), which varied the amount of light transmitted to the fiber coupler. The light out of the IS needed to be converged and focused at the slit. The converging angle, i.e., the numerical aperture, needed to approximately match that of the collection lens L3. This necessitated the use of two lenses L7 and L8, which were placed after the IS opening.

All optical components were placed on axial and vertical traversing stages for alignment. The Fabry–Perot and the EMCCD camera had to be placed on additional two-axis rotation stages (pitch and yaw) for alignment. The collection lens L2 and L3 were also placed on a micrometer-controlled vertical stage for precisely placing the Rayleigh fringe through the center of the reference image produced by the camera. The setup was for a point measurement, i.e., light from a very small, ~ 0.4 mm long, part of the incident beam was used to measure velocity and temperature. This will be further discussed in the next section. The length of the probe volume for density measurements was fixed by the slit width: 0.67 mm. The direct-imaging setup made efficient use of the scattered light, such that high-quality Rayleigh images were obtained from < 0.5 s exposure.

2.1 Flow facility

A small, supersonic jet facility was built to validate the Rayleigh setup. The 10 mm-diameter convergent nozzle was supplied with clean, oil-, and particle-free air. A compressed air supply was connected to a settling chamber where four sets of perforated plates and screens were used to improve the flow quality. A large contraction section further improved the flow quality. The supply pressure was sufficient to operate the nozzle up to a fully expanded Mach number of 1.5. The 50 mm-diameter plenum chamber was equipped with a static pressure port to measure the plenum pressure and a thermocouple to measure the total temperature. The nozzle facility was mounted on an X–Y traverse. The probe location was kept fixed, while the nozzle was moved for plume survey.

A special requirement for a Rayleigh system to measure the scalar parameters, temperature and density, is the minimization of Mie scattering from particles present in the air stream. For velocity measurement, which depends on the identification of the spectral peak, the presence of the particles in fact greatly improves the signal-to-noise ratio. However, temperature values, related to the spectral broadening, become difficult to determine when too many particles pass through the probe volume. Therefore, in addition to a clean primary flow, a clean, co-flowing stream was created via a second blower connected to an HEPA^® filtration system. The low-speed, co-flowing, clean air kept the entrainment air to the primary stream particle-free and allowed for measurement over a longer region of the plume.

3 Modelling of the Fabry–Perot fringes

The interferometric measurement was a two-step process. The first step involved characterizing the instrument function, for which the Rayleigh-scattered light was blocked, and a tiny amount of the incident laser light (reference light) was passed through the FPI setup via actuating the IS. This provided the reference image I^ref (Fig. 6a). During the next step, the IS was moved out and the Rayleigh-scattered light was imaged through the FPI, providing the Rayleigh image I^Ral (Fig. 7a). Accordingly, there were two parts to the modelling: extracting the instrument function I_FP (Eq. 10) from the reference image and using the instrument function to extract the Rayleigh–Brillouin spectra S_R(x, y) from the Rayleigh image. Each step was performed via non-linear least-square curve fits that minimized the difference between the measured image and the modelled image for a selected set of parameters. Figure 8 shows a schematic of the processing steps. Because the images were made up of a set of pixels i = 1, 2, 3, … npix, the modeling was performed for all such pixels, and the least-square was calculated as the norm of the differences between the measured and the modelled images. To determine the angle θ_i created by each pixel to the optical axis, the center of the fringes in Cartesian coordinate (χ_c, ζ_c), and the radius r_p of the innermost fringe needed to be determined. Therefore, parameters extracted from the reference image are χ_c, ζ_c, r_p, and the finesse (N) of the interferometer. Notice that this combination also fixes the incidence angle θ_p (Eq. 12) at the fringe location, and ultimately specifies the variation of the phase ψ over the entire image plane for the incident light frequency. The model for the reference image included the magnitude of the peak transmission I₀ multiplied by the transmission function of Eq. (10), a constant background I_B to account for the camera read noise, and noise from spurious sources:

$$I^{{\text{FP } - \text{ mod}}} \left( {\chi_{{\text{c}}} ,\zeta_{{\text{c}}} ,r_{{\text{p}}} , N} \right) = I_{0} I_{{{\text{FP}}}} \left( {x = 0,\theta } \right) + I_{{\text{B}}} .$$

(19)

Fig. 6

a Fabry–Perot fringe due to the incident laser beam—part of the image used for model fit is shown by the chained line; b horizontal and vertical cut-outs through the measured (symbols) and modelled (line) images; finesse: 24

Fig. 7

a Fabry–Perot fringe due to the Rayleigh-scattered light—part of the image used for model fit is shown by the chained line; b horizontal cut-out through the measured (symbols) and modelled (line) images. U: 313 m/s, T: 247 K

Fig. 8

Flow diagram of the processing steps used to process the reference image (left column) followed by the Rayleigh image (right column)

The least-square minimization was performed via the Matlab^® routine “lsqnonlin” applying the ‘Levenberg–Marquardt’ algorithm. The iterative procedure minimized the difference between the measured and the modelled intensity distribution for six parameters, χ_c, ζ_c, r_p, N, I_B, and I₀:

$$\mathop {\min }\limits_{{\chi_{{\text{c}}} ,\zeta_{{\text{c}}} ,r_{{\text{p}}} , N, I_{0} , I_{{\text{B}}} }} \left( {\mathop \sum \limits_{i = 1}^{{n{\text{pix}}}} \left( {I_{i}^{{{\text{ref}}}} - I_{i}^{{\text{FP } - \text{ mod}}} } \right)^{2} } \right).$$

(20)

The iterations started with a set of initial guesses. Convergence was found to be particularly sensitive to the initial choice of the image center: χ_cand ζ_c, which were prescribed after an examination of the camera image. Figure 6 shows a reference image and the model fit to determine the instrument function. The combination of the slit width and the focal length of the fringe-forming lens fixed the range of optical frequencies covered by the FPI. The multiple fringes seen in the image of Fig. 6a are indicative of phase angle ψ variation by multiples of 2π. However; only a small, circularly cropped region around the central fringe, shown by the dotted circle, was used to determine the instrument function. The use of the small region limited the length of the probe volume, and also provided a higher value of finesse. The measured finesse was as expected from the manufacturer’s specification. A reference image was collected before every Rayleigh image to account for any drift in the laser frequency.

After the reference image, the Rayleigh image was analyzed. Note that the frequency spectrum measured by the FPI was a convolution of the actual Rayleigh scattering spectrum S_R(x,y) and the characteristics of the FPI filter represented by the instrument function I_FP(x, θ) determined above. In the absence of all extraneous light and noise sources, the light intensity measured by the ith pixel in the image can be expressed by the following expression where I_R(θ_i) is the intensity due to the Rayleigh-scattered part of the light:

$$I^{{\text{Ral } - \text{ mod}}} \left( {\theta_{i} } \right) = I_{{\text{R}}} \mathop \int \limits_{ - \infty }^{\infty } S_{{\text{R}}} \left( {x,y} \right) I_{{{\text{FP}}}} \left( {x,\theta_{i} } \right) {\text{d}}x.$$

(21)

In reality, other sources contributed to the measured intensity. These sources included particle-scattered light I_p (because complete cleaning of dust particles in realistic flows was very difficult), background scattering at the incident laser frequency I₀, and broadband noise I_B from camera read noise, etc. The particle-scattered light is expected to occur at the Doppler shift frequency, x = x_D, of the bulk flow and is expected to be slightly broadened by the turbulent fluctuations (Fagan et al. 2005); however, such broadening was not modelled in the current work. The background illumination occurred from the stray scattering of the primary laser beam and was significantly attenuated by the baffles and the beam stop. For the present setup, stray scattering at laser frequency and particle contamination were small and typically not modelled. Nevertheless, the following represents a complete model of the intensity level by the ith pixel:

$$I^{{\text{Ral } - \text{ mod}}} \left( {\theta_{i} } \right) = I_{{\text{R}}} \mathop \int \limits_{ - \infty }^{\infty } S_{{\text{R}}} \left( {x,y} \right) I_{{{\text{FP}}}} \left( {x,\theta_{i} } \right) {\text{d}}x + I_{{\text{P}}} I_{{{\text{FP}}}} \left( {x = x_{{\text{D}}} ,\theta_{i} } \right) + I_{0} I_{{{\text{FP}}}} \left( {x = 0,\theta_{i} } \right) + I_{{\text{B}}} .$$

(22)

Note that the above equation is different from and simpler than that of Fagan et al. (2005), who performed an inter-pixel integration to account for the optical phase variation within the individual pixels. The added integration may be required for a relatively large pixel size or for a small image covering a fewer number of pixels on the CCD camera. For the present combination of large magnification of the probe volume and smaller sized camera pixels, the increased computation from such a procedure was found to provide only small refinement and was not used. Because particle contamination was very low, Eq. 22 also does not include turbulence broadening of the particle spectrum. Nonetheless, the Rayleigh spectrum S_R(x) for a fixed composition of gas is a function of the flow velocity U and temperature T, which, in addition to the various intensity levels in the above equation, were iteratively adjusted to minimize the difference between the measured and the modelled images. Once again, the Matlab^® routine “lsqnonlin” with the option of the ‘Levenberg–Marquardt’ algorithm was used for this purpose:

$$\mathop {\min }\limits_{{U, T, I_{{\text{R}}} , I_{{\text{P}}} ,I_{0} , I_{{\text{B}}} }} \left( {\mathop \sum \limits_{i = 1}^{{n{\text{pix}}}} \left( {I_{i}^{{{\text{Ral}}}} - I_{i}^{{\text{Ral } - \text{ mod}}} } \right)^{2} } \right).$$

(23)

A typical Rayleigh image is shown in Fig. 7. While the reference image of Fig. 6a was made of concentric circles, the Rayleigh image appeared as fragmented parts of a line. Light from the integration sphere, used for the former, made a circular spot on the slit, while that from the Rayleigh-scattered light was imaged as a line that corresponded to the shape of the incident beam. Each spot of the Rayleigh image corresponded to an arc of the reference fringes. A superimposition of the two is shown earlier in Fig. 1b. Note that each bright spot in the Rayleigh image corresponded to a particular location on the incident beam, and could have been analyzed separately to obtain independent measures of velocity and temperature from each location. Hence, multiple-point measurements can be performed from a single image. To improve accuracy, a region around the two central spots was analyzed in the present work. The length of the analysis region (= number of pixels n_p times the size of a pixel l_p) and the magnification through the optical train dictated the length of the probe volume l_sc:

$$l_{{{\text{sc}}}} = \frac{{n_{{\text{p}}} l_{{\text{p}}} f_{{\text{c}}} }}{{f_{{\text{f}}} m_{{\text{g}}} }}.$$

(24)

Here, f_c and f_f are the focal lengths of the collimating and focusing lenses, and m_g is the magnification factor of the collection lens pair (L2, L3 of Fig. 5). When the model function (Eq. 22) was fitted to the intensity distribution of the analysis region (Fig. 7b), velocity and temperature values were extracted.

The non-linear fitting was found to be robust and quick (a few seconds for each image on a personal computer), providing a reasonable estimation of velocity and temperature. Note that such measurements were obtained from fundamental properties (such as the molecular weight, coefficients of bulk, and shear viscosity) of the gas mixture and some parameters of the optical system including the wavelength of the light, the focal length of lens, etc. This system is by far simpler than other systems used to gather identical data. The Rayleigh-based technique is so remarkable, because there is no need of calibration (except for density), or insertion of a probe, or seeding via particles or fluorescent die, or ionization by a large power laser. Finally, the presence of dust particles is expected to increase the accuracy of velocity measurement, since particles mostly follow the bulk velocity and accentuates the spectral peak. However, the accuracy of the temperature measurement is expected to diminish.

4 Results and discussion

4.1 Validation of velocity and temperature measurements

Figure 9 shows a comparison between the measured and expected velocity and temperature values over the subsonic Mach number range 0 < M < 1. In this range, the velocity, temperature, and density values inside the potential core of the jet can be calculated from the isentropic relations and by knowing the plenum pressure P₀, plenum temperature T₀, and the ambient pressure P_amb. The probe volume was positioned at the jet centerline and 1.5D away from the nozzle exit. The jet core is particularly suitable for validation as the flow properties remain uniform. The jet Mach number M was changed by changing the plenum pressure. The axial component of velocity U, temperature, and density at the core of a free jet emitting from a convergent nozzle can be determined easily using isentropic relations until a choked condition (M ≥ 1) is reached:

$$\begin{aligned} \frac{{P_{0} }}{{P_{{{\text{amb}}}} }} & = \left( {1 + \frac{\gamma - 1}{2}M^{2} } \right)^{{\frac{\gamma }{\gamma - 1}}} , \frac{T}{{T_{0} }} = 1 + \frac{\gamma - 1}{2}M^{2} , \\ U & = M\sqrt {\gamma RT} , \rho = \frac{{P_{0} }}{{RT_{0} }}\left( {\frac{{P_{0} }}{{P_{{{\text{amb}}}} }}} \right)^{{\frac{ - 1}{\gamma }}} . \\ \end{aligned}$$

(25)

Fig. 9

a Comparison between the true and measured velocity. The line corresponds to the perfect match between the two; b same for temperature

Data taken from two different days of operations are shown in Fig. 9. The comparisons in both velocity and temperature were found to be excellent. The average bias errors in velocity and temperature were 3 m/s and 2 K respectively. The standard deviation from the ideal values, indicative of random error, were 5 m/s and 2 K respectively. The fundamental source of uncertainty is the electronic shot-noise (Seasholtz 1991; Seasholtz and Lock 1992). However, the very high rate of photon arrival in this directly imaged setup is expected to create very small random error from shot noise. The primary sources of the bias error are believed to be the uncertainty in the measurement of the focal length of the fringe-forming lens (within ± 0.5 mm) and the scattering angle (within ± 0.25°). In addition, the limitation in the application of the Tenti model adds to the error as various properties of pure nitrogen are used in this work, even though oxygen and other gases are present in air. In addition to the shot noise, the sources of the random error were believed to be the convergence error with the numerical fit, passage of particles, and the small jitter in the Fabry–Perot etalon from vibration and noise created by the air flow. Such sources are difficult to quantify, yet worthy of investigation in the future. Nonetheless, error levels are deemed to be exceptionally small for a non-intrusive, particle-free, non-fluorescence, spontaneous scattering-based method.

4.2 Density and spectra of density fluctuations:

Unlike velocity and temperature, measurement of bulk density requires calibration. In this experiment, the constants C₁ and C₂ of Eq. 18 were determined through an in-situ calibration. The jet was operated in the subsonic M < 1 range, while a photo-electron count was performed over a second duration for each Mach condition. The air density was determined from the application of the isentropic relations. Subsequently, a straight line was fitted through the data (Fig. 10) to determine the calibration constants. The time-averaged data were quite accurate: absolute density numbers were found to be repeatable within ± 1% of quoted values.

Fig. 10

Variations of the photo-electron count rates with air density used for calibration

To measure the time-evolution of the air density fluctuations, the photo-electron counting needs to be performed on a series of short-duration contiguous gates. The duration time of such gates represents the effective sampling rate. To get a reasonable frequency resolution, the gate duration needs to be short, which, in turn, leads to fewer number of photo-electron count and the associated increase of the shot-noise contribution. In other words, the individual measurement of density time history is subjected to large random error due to the shot noise contribution. However, when spectrum of fluctuations is created from such a time-series, the associated averaging process reduces the noise. Furthermore, Panda and Seasholtz (2002) introduced a 2-PMT technique where the scattered light was split into two parts and measured separately by two PMT. When the two time-series were cross-correlated, the resulting cross-spectrum was found to significantly lower the impact of the electronic shot noise. Recently, Mercier et al. (2018) and Mercier (2017) simplified the process and demonstrated that a single PMT can be used to achieve the same end. The time-series data from the single PMT were split into two parts by separating every other data point, and then, a cross-spectrum was calculated from the two parts. The present paper followed this approach which required fewer opto-electronic components and reduced the cost of the setup. The photo-electron counting over contiguous gates of duration Δt (typically 5–10 μs) produced a time-series p_i, i = 0, 1, …, 2n. A pulse pile-up correction was applied to individual data points, followed by a procedure to remove particle traces (Panda 2016; Mercier et al. 2018). The odd and the even number of points in this series were split to create two series: p_1i and p_2i (i = 0, 1, 2, …. n − 1). The average values from each of the time-series were subtracted: p^/_1i = p_1i − p_1av, p^/_2i = p_2i − p_2av, and a cross spectral density ${S}_{{p}_{1}^{/}{p}_{2}^{/}}$ was calculated from individual Fourier transform, ${F}_{{p}_{1}^{/}}, {F}_{{p}_{2}^{/}}$ at discrete frequency bands ${f}_{\mathrm{l}}$:

$$\left| {S_{{p_{1}^{/} p_{2}^{/} }} \left( {f_{l} } \right)} \right| = \frac{2}{{n^{2} }}\left| {F_{{p_{1}^{/} }} \left( l \right) \cdot F_{{p_{2}^{/} }}^{*} \left( l \right) } \right|.$$

(26)

The superscript * in the above equation indicates complex conjugate. Note that the effective sampling rate is reduced by a factor of two, because the two time-series were created by choosing alternate data points from the same time-series. The density fluctuation spectra are calculated using the slope of the calibration curve C₁:

$$S_{{\rho^{/2} }} \left( {f_{l} } \right) = \frac{{S_{{p_{1}^{/} p_{2}^{/} }} \left( {f_{l} } \right)}}{{\left( {2C_{1} \Delta t} \right)^{2} }}.$$

(27)

Various details of the spectral calculation procedures are identical to that presented earlier (Panda 2016; Mercier 2017) and are not repeated for the sake of conciseness. Panda and Seasholtz (2002) also describe the reduction of aliasing error due to the photo-electron counting procedure. Figure 11 demonstrates the wide dynamic range achievable with the setup. The signal-to-noise floor ratio was ~ 50 for the unheated M 0.98 jet (Fig. 11a) where the signal part, i.e., the turbulent density fluctuations was small—only about 4% of the mean density. The signal-to-noise ratio increases by two orders of magnitude in the screeching jet of Fig. 11b where turbulence fluctuations mostly lock to the screech frequencies seen in the superposed spectra from a microphone. That the screech frequencies coincide with the tones found in the spectra of density fluctuations provides validation of the present method. In the past, Panda and Seasholtz (1999b) and, more recently, Mercier (2017) used Rayleigh scattering to determine the mechanism of sound generation from screeching jets. Note that there is no upper limit on the frequency range for which the spectrum of density fluctuations can be measured. Practically, the usable range depends on the residual noise floor of the cross-spectrum. The noise floor can be lowered by increasing the laser power or by taking a longer sample.

Fig. 11

Spectra of density fluctuations measured at the indicated locations a along the centerline of M 0.98 jet; b along lip shear layer of M = 1.2 under-expanded screeching jet; also comparison with sound spectra from a microphone kept 90° to jet axis

4.3 Centerline surveys of M0.98 and M1.2 jets

Figure 12a–c shows the centerline decay of velocity, temperature, and density measured in an M 0.98 jet. The variations are as expected in a high-speed jet. The axial component of velocity remained nearly constant until x/D ~ 4.5, the end of the potential core, and then fell farther downstream. The good comparison with data from a Pitot probe survey further validates the technique. The slight deviation is believed to be due to the error in positioning the large 3.5 mm-diameter Pitot probe at the Rayleigh probe volume in this small 10 mm-diameter jet. The temperature and density profiles also followed the expected trends. In the present, unheated jet isentropic expansion through the nozzle cooled the core flow at temperatures below the ambient value. Because the static pressure inside a subsonic jet is the same as that of the ambient, the cooling caused an increase in air density. Mixing with the ambient air slowed down the jet farther from the nozzle, and in turn caused a rise in temperature and a fall in density, both of which were expected to approach the ambient level farther downstream. The velocity data measured from the Pitot tube survey are used to estimate the temperature profile along the jet centerline using isentropic relationship and total temperature. The latter was measured in the plenum using a thermocouple. Figure 12b shows a comparison between the directly measured and the isentropically estimated temperature variations. The difference is due to error in temperature measurement, plus the departure from isentropic behavior in the jet mixing. The latter is expected to cause an increase in the local temperature, which is seen in the data points obtained beyond the end of the potential core.

Fig. 12

Centerline profiles of a velocity, b temperature, c density, and d rms of density fluctuations from a nominal M 0.98 jet

Figure 12d shows the root mean square of the density fluctuations along the jet axis. The rms values are calculated from the cross spectra by noting that the total spectral energy is a sum of mean-square of density fluctuations $\rho_{{{\text{rms}}}}^{/2}$ and the residual shot noise σ²_shot:

$$\int S_{{\rho^{/2} }} {\text{d}}f = \rho_{{{\text{rms}}}}^{/2} + \sigma_{{{\text{shot}}}}^{2} .$$

(28)

The cross-correlation process reduced the shot-noise floor; yet, convergence was slow and dependent on the signal level. An examination of the spectra shown in Fig. 11 shows that closest to the nozzle exit at x/D = 2, and at the centerline, where the level of turbulence fluctuations is very small a flat spectral floor of nominally 1 × 10^–8 (kg/m³)²/Hz is reached. At the highest resolved frequency, psd levels from all other axial stations approach this floor, which is identified as the residual contribution from the shot noise. An estimation of the true rms value from the density fluctuations alone requires a subtraction of this floor. Shot noise is known to produce a frequency-independent white-noise level in the spectrum. This constant level was estimated as the spectral density value at the highest resolved frequency of 25 kHz: $\sigma_{{{\text{shot}}}}^{2} = \left( {S_{{\rho^{/2} }} } \right)_{f = 25,000}$ where it was known that the energy from turbulent fluctuations was small:

$$\rho_{{{\text{rms}}}}^{/} = \sqrt {\left[ {S_{{\rho^{/2} }} - \left( {S_{{\rho^{/2} }} } \right)_{f = 25,000} } \right]\Delta f} .$$

(29)

The rms values measured by this subtraction process were found to be reasonable. The root-mean-square density fluctuations of Fig. 12d show that the turbulent fluctuations remained low inside the potential core x/D < 4.5, and then grew exponentially before slowly tapering down. The relative uncertainty level in the fluctuation data is higher due to the shot noise subtraction process described in the earlier section. Various features of density fluctuations are similar to that published earlier from extensive surveys (Panda and Seasholtz 2002; Mercier 2017).

As the plenum pressure increased beyond the choked flow condition, a series of shock cells formed in the jet plume. The inset Schlieren photograph of Fig. 13 shows the quasi-periodic shock-diamond pattern. An outstanding difficulty of the particle-based techniques is the inability of the seed particles to follow the fast acceleration and deceleration of the air stream. The Rayleigh scattering technique does not suffer from such limitations and provides high-accuracy measurements of velocity, temperature, and density. In a shock cell, air velocity at first increases in the expansion region and then falls as the shock-induced compression zone is approached. Temperature variation, on the other hand, takes an opposite trend: an increase in velocity accompanied by a drop in temperature and vice versa. The oscillation pattern ultimately ends in a general decay as the shock cells dissipate due to the entrainment of the ambient air. Figure 13 correctly demonstrates these flow physics.

Fig. 13

a Velocity and b temperature surveys along the centerline of an under-expanded M 1.2 jet. Inset is a Schlieren photograph

5 Summary and conclusion

A new optical arrangement developed to spectrally analyze Rayleigh-scattered light from a point probe in a high-speed air stream was built from the ground up at NASA Ames Research Center. The setup takes advantage of advancements in laser technology (stable, very-narrow-linewidth CW laser), camera technology (EMCCD camera), and commercially available stabilized Fabry–Perot interferometer to improve accuracy, reliability, and the ease of operation at a lower cost. The directly imaged arrangement makes efficient use of the Rayleigh-scattered light, and is suitable for future extension to measure spectra generated by velocity and temperature fluctuations. In addition, the compact setup can be easily transferred to large test facilities.

A new set of software programs was created to resolve the RB spectrum from the measured fringe patterns. At first, the incident light is analyzed to determine the instrument function, which is followed by an analysis of the Rayleigh-scattered light to obtain the measurements of velocity and temperature from a small, 0.4 mm-long probe volume. A remarkable feature of the Rayleigh setup is that the velocity and temperature can be measured with high accuracy, using the fundamental molecular properties, without any calibration. Air density and spectrum of density fluctuations were measured by splitting a small part of the Rayleigh-scattered light and then passing it to a PMT. A photo-electron counting process using commercially available hardware and software produced a long time-series of data that ultimately provided the fluctuation spectra in density. This paper describes the optical arrangement and the modelling steps in sufficient detail for a new user to create a similar setup. The data collected from the potential core of a subsonic M < 1 jet validated the technique. Surveys made along the centerline of an under-expanded, supersonic M 1.2 jet clearly showed the periodic modulations in the velocity and temperature due to the presence of the shock-diamond pattern. Such data show the suitability of the technique in shocked flows over other techniques such as PIV.