Measurements of freestream density fluctuations in a hypersonic wind tunnel

Abstract

Density disturbances in the freestream of the University of Southern Queensland’s Mach 6 wind tunnel ($\rho _{\infty } \approx {34\, \hbox {gm}^{-3}}$) have been measured using a focused laser differential interferometer (FLDI). The direct contribution of the turbulent shear layer from the Mach 6 nozzle to the FLDI signal was largely eliminated by mechanically shielding the FLDI beams from these effects. This improvement significantly enhanced the low wavenumber FLDI spectra which allowed a von Kármán spectrum fit and demonstrated a $-5/3$ roll-off in the inertial subrange and enabled the identification of the integral length scale (28–29 mm). The normalised root-mean-square density fluctuations were found to change over the flow duration (typically between 0.4 and $0.6\%$) for the 1–250 kHz frequency range which corresponds to the wavenumber range of 6– 1600  ${\mathrm{m}}^{-1}$ in this Mach 6 flow. Previous disturbance measurements using intrusive methods have identified a narrowband 3–4 kHz disturbance that is first measured in the core flow about 65 ms after the flow begins and remains until the flow terminates. The onset of this narrowband disturbance was previously correlated with transition-to-turbulence in the subsonic test gas supply to the nozzle. This correlation was investigated further herein, and the 3–4 kHz feature was inferred to be entropy mode disturbances by showing the departure of the FLDI measurements from Pitot pressure measurements. Through the comparison of FLDI and Pitot pressure data, Pitot pressure probes were demonstrated to produce a poor estimate of the static pressure fluctuations when non-isentropic disturbances are non-negligible.

Graphic abstract

1 Introduction

Hypersonic ground testing can make significant contributions to the development process for hypersonic vehicles. However, experimentation in conventional hypersonic ground testing facilities is complicated by the high levels of freestream fluctuations which are typically one-to-two orders of magnitude greater than in flight (Schneider 2008). This elevated noise environment can have significant impacts on flow phenomena, such as boundary layer transition, and this leads to uncertainties in the prediction of essential hypersonic vehicle design parameters. Because of this, there has been a significant worldwide effort to characterise hypersonic tunnel noise using a number of methods (Wagner et al. 2018).

Fig. 1

General arrangement of TUSQ

Hot-wire anemometry is widely used to quantify the disturbance environment for up to 100 kHz, however, these devices are very fragile and, therefore, are regarded as unsuitable for application to impulsive or high-enthalpy flows (Wagner et al. 2018). Another widely used diagnostic is the Pitot pressure gauge, which requires the freestream conditions to be inferred from measurements behind a bow shock. The response of Pitot pressure gauges are known to be influenced by the probe forebody geometry, while protective cavities also lead to corruption of the signal through damping and resonance effects (Duan et al. 2019; Wagner et al. 2018). The technique of focused laser differential interferometry (FLDI) is a non-instrusive method, which can be designed to have a frequency response of the order of tens of megahertz, for measuring density fluctuations (Parziale et al. 2013). FLDI has a streamwise spatial resolution of the order of hundreds of microns, and tens of millimetres in the spanwise direction. FLDI has been used for facility characterisation via freestream density fluctuation measurements in a reflected shock tunnel (Parziale et al. 2014) and in blowdown facilities (Fulghum 2014; Chou et al. 2018). FLDI has also been used to investigate boundary layer instabilities in hypervelocity flows (Jewell et al. 2016) owing to its high bandwidth and high streamwise spatial resolution.

The University of Southern Queensland’s hypersonic Ludwieg tube facility (TUSQ) is a conventional ground testing facility that differs from the aforementioned types of facilities where FLDI has been used. In TUSQ, the test gas is directly heated via free piston compression in a cold barrel and through the use of the free piston, longer test flow durations can be achieved relative to a standard Ludwieg tube of the same dimensions. However, with this style of operation thermal inhomogeneities which develop in the barrel will be ejected through the nozzle and could impact the quality of the the core flow region.

Prior facility characterisation via Pitot surveys (Birch et al. 2018) identified that a narrowband disturbance (3–4 kHz), beginning approximately 65 ms after flow initiation, is superimposed on a broadband acoustic environment ($f < {25}\,\hbox {kHz}$) within the flow produced by the Mach 6 nozzle. Fast-response thermocouple measurements and facility simulations indicate a correlation in time of the onset of the narrowband frequency content and the laminar-turbulent transition of the flow in the barrel. This change of the flow disturbance environment may have significant impacts on the fluid-thermal-structure and boundary layer experiments conducted in TUSQ and therefore requires further investigation.

The application of FLDI in TUSQ is an effort to resolve the disturbance environment without interfering with the flow, including the extension to significantly higher frequencies than previously measured in TUSQ via Pitot pressure surveys (25 kHz). The results of this research can inform not only the researchers that use the TUSQ facility, but also researchers operating facilities which use the free piston compression heating method.

2 Facility

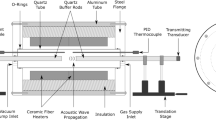
The University of Southern Queensland’s Ludwieg tube with free piston compression heating (TUSQ, Fig. 1) is used to generate quasi-steady cold flows of hypersonic air for approximately 200 ms (Buttsworth 2010). Prior to firing, the facility comprises of three discrete volumes of gas: (1) the 350 L high pressure air reservoir; (2) the air in the Ludwieg tube (or barrel); and (3) the low pressure ($< {1}\,\hbox {kPa}$) region within the nozzle, test section and dump tanks. A 350 g piston is positioned in the barrel immediately downstream of the primary valve and a light Mylar diaphragm separates the barrel and nozzle inlet.

For the condition analysed herein (Table 1), the test gas initially residing in the barrel is at the local atmospheric pressure and ambient temperature (approximately 94 kPa and 24 °C, respectively, in Toowoomba). A run is initiated by opening the primary valve which causes the piston to be driven along the barrel by the flow of high pressure air from the reservoir, compressing the test gas. The pressure in the barrel is measured by a PCB113A03 piezoelectric pressure transducer positioned 225 mm upstream of the nozzle entrance. The controlled primary valve opening speed nearly eliminates the occurrence of compression waves during the nominally isentropic compression process (Birch et al. 2018). Compression continues until the pressure ruptures the diaphragm which then allows gas to leave the barrel and accelerate through the nozzle.

Table 1 Nominal test conditions

3 FLDI diagnostic

3.1 Description of the TUSQ FLDI system

Fig. 2

Layout of the TUSQ FLDI instrument. i Laser; ii diverging lens; iii pinhole; iv variable iris; v Sanderson prism 1; vi field lens 1; vii field lens 2; viii Sanderson prism 2; ix collimating lens; x berek compensator; xi polarising beam splitting cube; xii photodetectors

The FLDI instrument at USQ (presented schematically in Fig. 2) is a two-photodetector arrangement based on the Fulghum (2014) design that uses the individual components listed in Table 2. In this research, the FLDI beams were focused on the nozzle centreline 25 mm downstream of the nozzle exit plane.

This FLDI system differs from the more widely used design based on Parziale et al. ’s (2012) implementation, which uses a single photodetector to measure beam interference. By implementing a second photodetector, it is possible to discriminate coherent turbulence from other signal noise sources, such as laser power fluctuations which has a direct effect on the quality of the FLDI spectra produced (Settles and Fulghum 2016).

Table 2 FLDI instrument components

The laser (i) provides a high quality ($\text{TEM}_{00}$) 2 mW collimated beam that is linearly polarised at 45° relative to the axis of beam separation. This beam is expanded by the lens (ii), and the expanded beam is then spatially filtered at (iii) and (iv). When the beam reaches the first Sanderson prism at (v) it is split into two narrowly diverging orthogonally polarised beams (blue and yellow in Fig. 2). These two beams continue to diverge until the first field lens at (vi) which sets the beam separation ($\varDelta x$) and focuses the FLDI beams to a point. The second field lens (vii) is used to refocus the two FLDI beams. When refocusing, these two beams pass through the second Sanderson prism (viii) which is loaded in the same state as (v). The second Sanderson prism recombines the two beams to an elliptical polarisation state, and this beam is collimated at (ix). There is a small difference in optical path length for the two beams when they pass through the Sanderson prisms due to the difference in extra-ordinary and ordinary refractive indices for the prism material. This change of optical path length is compensated for by a phase shift using a Berek compensator (x). The beam is split again at (xi) and the intensity of the two subsequent beams measured at detectors (xii). These two beams represent the two beams that propagate between the two Sanderson prisms, which are 180° out of phase. As each beam propagates across the flow they encounter slightly different refractive index fields, and when recombined the relative phase differences result in an elliptically polarised output beam. The ellipticity of the output beam is measured by the two photodetectors as a measurement of the phase difference.

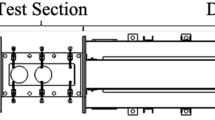
All optical components were placed outside the test section, and mounted independent of the facility and the facility framework. By not connecting the optics to the test section, the capability to open and close the test section was maintained which is beneficial for future projects where models require mounting in the test section, and for the measurement of the beam location. The TUSQ test section is a generic one-size-fits-all component common to all available nozzles and experiment types (free flight, fixed and heated models). Unfortunately, this versatility means that the test section is not optimally designed for implementation of FLDI. The test section windows are 1028 mm apart, compared to an exit diameter of 217.5 mm for the Mach 6 nozzle. This geometry effectively reduces the focusing ability of FLDI as the beam is relatively small by the time reaches the flow field. Best practice for FLDI is to place the field lenses as close to the flow-field as possible, but this can not always be achieved.

Preliminary testing showed that because of the reduced focusing ability of the FLDI instrument due to the facility geometry constraints, the spatial resolution of the FLDI instrument along the laser beam axis was large enough that the turbulent shear layer (TSL), which originates as the boundary layer (BL) on the nozzle wall, contributed significantly to the overall signal. Therefore, two ‘beam shrouds’ were positioned on either side of the flow to allow the FLDI beams to pass unperturbed through the TSL. One of these devices is represented schematically in Fig. 3. These devices forced the boundary layer on the nozzle wall and the turbulent shear layer to pass around the path of the FLDI beams, and therefore, the direct contribution of these flow features to the overall FLDI signal is largely eliminated. The effects of the beam shrouds are quantified in Sect. 4.2.1.

3.2 Sensitivity and transfer functions

Fig. 3

Schematic of a beam shroud for the beams entering the flow

The most thorough description of FLDI to date was completed by Fulghum (2014), containing derivation of system transfer functions for simple flow geometries and an analysis of the optical components. The FLDI turbulence spectra are convolved with transfer functions which are related to the separation of the beams and their convergence angle. The measured phase difference signal ($\varDelta \varphi _A - \varDelta \varphi _B$) is related to the density fluctuations ($\rho ^{\prime }$) by:

$$\begin{aligned} \rho ^{\prime }\left( t\right) = \frac{\lambda }{2 \, \pi \, K_{\mathrm{GD}} \, \varDelta x} \mathcal {F}^{-1}\left\{ \frac{\mathcal {F} \left\{ \varDelta \varphi _a - \varDelta \varphi _B \right\} }{H_{\varDelta x}\left( k\right) \, H_z\left( k\right) } \right\} , \end{aligned}$$

(1)

where $\lambda$ is the wavelength of the laser, $K_{\mathrm{GD}}$ is the Gladstone–Dale coefficient, $\varDelta x$ is the beam separation, $H_{\varDelta x}(k)$ is the transfer function due to finite beam separation and $H_z(k)$ is the transfer function due to beam width along the beam path (Fulghum 2014).

It is useful to briefly compare Eq. (1) to the equivalent post-processing equation for the Parziale et al. (2012) FLDI system which is,

$$\begin{aligned} \varDelta \rho =\frac{\lambda _0}{2\pi K_{\mathrm{GD}} L} \sin ^{-1}\left( \frac{V}{V_0} -1 \right) , \end{aligned}$$

(2)

where L is the experimentally determined integration length which is much greater than $\varDelta x$. For the same data, Parziale et al. (2012) first reports $L = {15}\,\hbox {mm}$ and then later as $L = {10}\,\hbox {mm}$ (Parziale et al. 2014). Since $L>> \varDelta x$, it appears that the post-processing using Eq. (1) will result in orders of magnitude higher density fluctuations than when using Eq. (2). However, the commonly expressed form of Eq. (2) does not show the response coefficient $c\left( k\right)$ which represents the sensitivity of the FLDI measurement to the wavenumber, and therefore, direct comparison of Eqs. (1) and (2) cannot be made. The values of the response coefficient for the Parziale et al. (2014) instrument are between ${c\left( k={10}\,\hbox {m}^{-1} \right) \approx 0.01}$ and $c\left( k={1400}\,\hbox {m}^{-1} \right) \approx 0.9$ which, if neglected, can result in orders of magnitude errors in $\varDelta \rho$.

Four transfer functions were used to transform the FLDI phase difference signal and account for the attenuation of high frequency content:

• 1. $H_{\varDelta x}(k)$, spatial filtering due to finite beam separation;

• 2. $H_z(k)$, path integrated spatial filtering due to beam size and turbulence profile;

• 3. $H_{\mathrm{PD}}(f)$, attenuation of high frequency content due to termination resistance $R_T$ at the photodetectors; and

• 4. $H_{\mathrm{Amp}}(f)$, attenuation of high frequency content due to the amplifier performance.

$H_{\varDelta x}$ is a function of the flow direction relative to the axis of beam separation and is defined as:

$$\begin{aligned} H_{\varDelta x}\left( k\right) = \left( 1+ \left[ k/k_c\right] ^2\right) ^{-1/2}, \end{aligned}$$

(3)

where k is the wavenumber of the disturbance which is given by $k = 2 \pi f / u_c$, where f is the frequency and $u_c$ is the convective velocity. The cut-off wavenumber ($k_c$) is dependent on the orientation of the flow relative to the axis of beam separation. For the TUSQ FLDI instrument the flow is perpendicular to the axis of beam separation to provide the maximum frequency response, and thus $k_c = 1.10 / \varDelta x$ (Settles and Fulghum 2016). For the investigation of freestream nozzle flow disturbances where the FLDI beams are focused at the nozzle centreline, some assumptions regarding the structure of the disturbance field are necessary. The common approach is to assume that the disturbance field is uniform for the finite width of the nozzle flow (Fulghum 2014; Settles and Fulghum 2016; Schmidt and Shepherd 2015), in which case the transfer function $H_z\left( k \right)$ is:

$$\begin{aligned} H_z\left( k\right) = \frac{\pi \, w_o \, \sqrt{2\,\pi }}{k \, L \, {\lambda }} \, \mathrm{erf}\,{\left( \frac{k \, L \, \lambda }{2\sqrt{2}\, \pi \, w_0}\right) } \, \mathrm{exp}\,{\left( -\frac{w_0^2 \, k^2}{8}\right) }, \end{aligned}$$

(4)

where L is the half-width of the flow and $w_0$ is the beam waist radius (Schmidt and Shepherd 2015). The phase difference signal is calculated from the signals of the two photodetectors (A and B) using,

$$\begin{aligned} \varDelta \varphi _A - \varDelta \varphi _B = \sin ^{-1}\left[ 2\left( \frac{F_{AB} - F_{AB,\mathrm{MIN}}}{F_{AB,\mathrm{MAX}} - F_{AB,\mathrm{MIN}}}\right) -1 \right] , \end{aligned}$$

(5)

where $F_{AB} = \left( A - B\right) / \left( A + B\right)$ (Fulghum 2014). The designation of the detector signals A and B is arbitrary.

The transfer functions are presented in Fig. 4 for a typical configuration of the TUSQ FLDI instrument, with ($L = {77}\,{\mathrm{mm}}$) and without ($L = {109}\,{\mathrm{mm}}$) the beam shrouds fitted. The convective velocity of a turbulent disturbance may be a non-trivial function of its wavenumber, however, in the absence of wavenumber resolved velocity measurements a constant $u_c$ is assumed. Settles and Fulghum (2016) assumed that the small-scale turbulent structures are convected at close to the freestream velocity for measurements in the Mach 3 PSUSWT¹ facility, which was verified using cross beam correlation Fulghum (2014). Again using $u_c \approx u_\infty$, Settles and Fulghum (2016) presents power spectral data for a Mach 10 flow in AEDC9² which produces an excellent fit to the von Kármán spectrum, which is discussed in Sect. 4.2.3. Additionally, Jewell et al. (2016) measured the convective velocity to be near to the freestream velocity in a Mach 4.5 shock tube. From these successes, the convective velocity in TUSQ was set to the average freestream velocity of the flow (980 ${\hbox {ms}^{-1}}$) for the analysis herein.

Fig. 4

Magnitude of transfer functions for $\varDelta x = {83}\,\upmu {\mathrm{m}}$, $R_{T} = {660}\,{\Omega }$, and $u_{c} =$${980}\,{\hbox {ms}}^{-1}$

The frequency response of the instrument is dominated by the path integrated spatial filtering and beam overlap due to beam size and turbulence profile, $H_z(k)$, which is independent of $\varDelta x$ and $R_T$. The filtering due to finite beam separation is dependent on the beam separation set for each test, however $H_{\varDelta _x}(k)$ always has a lesser impact on the attenuation of the frequency content than $H_z\left( k\right)$ for this TUSQ implementation of FLDI.

The attenuation of the photodetector output is dependent on the terminating resistor used. The transfer function $H_{\mathrm{PD}}$ was identified experimentally by exposing the photodiode-resistor pairs to repeated nominally square pulses of light provided by an LED. In theory, for an infinite bandwidth photodetector the output will perfectly match the applied optical input. As the bandwidth reduces, the reduced frequency response is visible as rounded corners on the photodiode output signal. The Fourier transform of a sequence of nominally square pulses is an infinite series of odd multiples of the square wave fundamental frequency. As the bandwidth of the photodetector reduces, the amplitude of high frequency harmonics of the fundamental pulse frequency reduces. By determining the ratio of the input and output amplitude at each harmonic, a transfer function can be identified for each termination resistance. The experimentally identified $H_{\mathrm{PD}}$ confirmed that the manufacturer-provided form of the equation was correct, but that the nominated junction capacitance was incorrect (Birch 2019). The amplifier transfer function ($H_{\mathrm{Amp}}$) was identified using a similar technique where the the input sequence of square pulses was supplied by a function generator.

3.3 Berek compensator calibration

The function of the Berek compensator in the TUSQ FLDI system is to compensate for the small difference in optical path length that the two FLDI beams travel because of the Sanderson prisms, and it does not require calibration for this application. However, the Berek compensator can be used in the calibration of the Sanderson prisms (Sect. 3.4) if the phase retardance ($\theta _R$) of the compensator is known.

The manufacturer-supplied calibration of the Berek compensator is:

$$\begin{aligned} \theta _R = \frac{\pi }{4} - \sin ^{-1}\left( \frac{50.22-I}{71} \right), \end{aligned}$$

(6)

where I is the indicator setting of the Berek compensator. Eq. (6) has been reported to be a poor fit to the actual performance of the device ‘for unknown reasons’ (Fulghum 2014), so it was considered prudent to check the supplied calibration. The Berek compensator was calibrated by passing a collimated linearly polarised laser beam through the compensator. This beam was then split using a polarised beam splitter where one axis of the polarising beam splitter was aligned with the original polarisation state. The intensity of the two beams was subsequently measured using the two photodetectors. This process was repeated for the full range of indicator settings of I = 0–17. Initial calibrations did not match the supplied calibration. An optical post was then fitted to the second mounting hole of the Berek compensator, and a micrometer head arrangement installed for fine adjustment of the Berek compensator angle relative to the incident beam ($\beta$). When $\beta$ = 90° (incident radiation normal to the compensator) the manufacturer-supplied calibration was confirmed as shown in Fig. 5, demonstrating that the performance of the Berek compensator is highly sensitive to its alignment.

Fig. 5

Calibration of the Berek compensator demonstrating that proper alignment is required to match the calibration provided by the manufacturer

3.4 Sanderson prism design and calibration

Two Sanderson prisms were used as adjustable inexpensive beam splitting and beam polarising elements. When a stress birefringent prismatic bar is loaded in four point bending it polarises and diverges the incident beam, providing a first order approximation of the Wollaston prism (Sanderson 2005).

The Sanderson prisms were calibrated using the grid sampling technique described in Fulghum (2014) which uses a reference refraction supplied by a meniscus lens that is traversed along the axis of beam separation and the phase retardance of the Berek compensator is measured at various settings. The results of the Sanderson prism calibration are presented in Fig. 6 with a comparison to the theoretical performance of the Sanderson prism. The maximum/minimum theory lines were set using the manufacturer-provided limits of the modulus of elasticity for the prisma material, Makrolon, of  2300 and 2400 MPa. The experimental calibration of the Sanderson prism shows excellent agreement with the theoretical performance. A small offset at $X_L= 0$ indicates the presence of residual stresses in the prism.

Fig. 6

Sanderson prism calibration with the theoretical results offset to the zero-load beam displacement due to pre-strain in the prism

4 Results and discussion

4.1 Time-resolved FLDI measurements

The FLDI instrument was used to measure the freestream density fluctuations present in the Mach 6 flow generated in TUSQ. Raw barrel pressure and photodetector data from $\hbox {Run}~{829}$ where $\varDelta {x} = {169}\,{\upmu }\hbox {m}$ is shown in Fig. 7. For clarity the signals have been offset along the ordinate, and the data arranged such that flow initiation occurs at $t = 0$. The barrel pressure trace shows that the test flow terminates at $t \approx {210}\,\hbox {ms}$. A high signal-to-noise ratio (SNR) for the photodetector signals is evident during the test time, and upon flow termination the SNR reduces to pre-flow levels. At $t \approx {220}\,\hbox {ms}$ the results show that the photodetectors measured significant density fluctuations, and this is because the gas is subjected to pressure wave disturbances as the test section pressure equilibrates with the dump tank pressure on nozzle flow termination.

Fig. 7

Raw FLDI photodetector voltage data for Run 829 with $\varDelta {x} = {169} \, {{{\upmu }}\hbox {m}}$ and comparison to the barrel pressure signal. Data offset vertically for clarity

The amplitude and frequency response of the FLDI instrument are functions of $\varDelta x$ and $R_{T}$, and the combination of these two parameters impacts the SNR. The amplitude of the density fluctuations measured by the FLDI instrument are determined using Eq. (1). For the analysis of the effect that varying the beam separation and termination resistance has on the amplitude of the fluctuations measured, it is useful to analyse Eq. (1) further. The same laser was used for all testing, and the same test gas was used. Therefore, $\lambda / 2\pi K_{\mathrm{GD}}$ has a constant value throughout all tests. The transfer function $H_{\varDelta x}$ is approximately unity for $k< {3}\,{\hbox {mm}^{-1}}$ (Fig. 4) for the beam separations possible with the TUSQ FLDI instrument, and the structures greater than this size were found to dominate the turbulent energy spectrum (Sect. 4). Thus, for comparison of the time-resolved density fluctuations at different beam separations, the assumption $H_{\varDelta x} \approx 1$ is made. The transfer function $H_{z(k)}$ is unaffected by changes to the beam separation and termination resistance and is therefore constant for all tests, assuming that the radius of the flow-field, the beam waist radius, and the convective velocity can be treated as constant across all runs. The termination resistance transfer function $H_{\mathrm{PD}}$ potentially affects the results, but similar to $H_{\varDelta x}$, it is unity for the energy containing eddies.

Therefore Eq. (1) can be reduced to:

$$\begin{aligned} \rho _{\infty }^{\prime }\left( t\right) \underset{\sim}{\propto} \frac{\varDelta \varphi _{A}-\varDelta \varphi _{B}}{\varDelta x}, \end{aligned}$$

(7)

where the normalisation of phase difference signal $\left( \varDelta \varphi _{A}-\varDelta \varphi _{\text {B}}\right)$ by beam separation $\left( \varDelta {x}\right)$ is convenient for comparison of raw phase difference data in the time, frequency and wavenumber domains.

Using this normalisation technique, the amplitude of the normalised phase difference signal was found to be similar for $R_{T} = 180$–${660}\,{\Omega }$ and $\varDelta {x} = 85$–${170}\,{{\upmu }}\mathrm{m}$. However, as $R_{T}$ decreases the SNR also decreases. The maximum sample rate of the data acquisition system is ${4}\,{\hbox {MSs}^{-1}}$ and therefore, there is no benefit in using terminating resistors that result in a bandwidth $>~{2}\,{\hbox {MHz}}$, which occurs for $R_{T} < ~{530}\,{\Omega }$. Consequently termination resistors of $R_{T} = ~{660}\,{\Omega }$ were used for most runs.

4.2 Analysis in the wavenumber domain

4.2.1 Raw spectra

To apply the transfer functions $H_{\mathrm{Amp}}(f)$ and $H_{\mathrm{PD}}(f)$ the FLDI signal in the time domain must be transformed into the frequency domain, and then into the wavenumber domain to apply $H_{\varDelta x}(k)$ and $H_z(k)$. Although the SNR was found to be high in the time domain, in the wavenumber domain the SNR of the FLDI signal is wavenumber dependent, and therefore an important step is to assess the noise baseline across the wavenumber range. Immediately prior to a run a baseline measurement of the photodetector voltages is recorded, and these signals can be used to calculate the baseline phase difference signal. Using a power spectral density (PSD) estimate of this signal, the baseline noise in the frequency and wavenumber domains is shown in Fig. 8, and compared to the spectral content for the period of 1–200 ms relative to flow initialisation.

Fig. 8

Comparison of normalised phase difference spectra for runs with and without the beam shrouds installed

Relatively high amplitude, low frequency noise is present in the baseline signal which can result from 50 Hz electrical line noise, variations in laser power intensity and slow convective currents in the laboratory environment passing across the beam. For ${\hbox {300}\,\hbox {Hz} \lesssim f \lesssim {700}\,\hbox {kHz}}$ the measured phase difference during a run is significantly above the baseline noise level, while for frequency content in the order of 1 MHz there is little-to-no useful flow information. The baseline and run spectra both exhibit many strong narrowband peaks bound between 600 kHz and 2 MHz which is interference from local AM and amateur radio broadcasts.

The effect of the beam shrouds on the measured phase difference signal is also shown in Fig. 8. The similarity of the baseline noise signals demonstrates that the FLDI beams were not clipped by the beam shrouds, nor were any stray reflections significant. During the flow, there is a significant difference between the measured phase difference signal for $k \lesssim {1000}\,{\hbox {m}^{-1}}$ when the beam shrouds are fitted and removed. This shows the improvement in the measurement due to the removal of the direct TSL signal by the beam shrouds. The distance from the FLDI best focus where a given wavenumber will no longer contribute to the overall signal is given by Schmidt and Shepherd (2015) as:

$$\begin{aligned} z_{\mathrm{neg}} = \frac{\omega _0^2 \pi }{\lambda } \sqrt{\frac{8 \log 10}{\omega _0^2 k^2} - 1}, \end{aligned}$$

(8)

which can be used to validate the experimental finding that the phase difference spectra for runs with and without the beam shrouds converge for $k > {1000}\,{\hbox {m}^{-1}}$. By fitting the beam shrouds to the Mach 6 nozzle, $z_{\mathrm{neg}}$ is forced to be 76.8 mm. Therefore the disturbances in the TSL of $k < {1800}\,{\hbox {m}^{-1}}$ will no longer contribute to the overall FLDI signal, which would have been measured had the beam shrouds not been used. Therefore, the spectra for runs with and without the beam shrouds installed should agree for $k > {1800}\,{\hbox {m}^{-1}}$, which is demonstrated in Fig. 8.

Both of the FLDI spectra shown in Fig. 8 exhibit a peak in content during the flow at  3–4 kHz, but because of the improved rejection of the TSL this feature is much more prominent in Run 843. The  3–4 kHz peak has been previously identified by Pitot pressure surveys (Birch et al. 2018) and by fast-response stagnation temperature measurements (Birch 2019) and is consistent with the laminar to turbulent transition of the test flow in the barrel which first occurs at about 65 ms after hypersonic flow initialisation. In subsequent sections of this paper, the data are analysed for smaller time periods within the overall flow duration so that the temporal development of this frequency content can be better analysed to confirm that this is the same feature previously observed.

4.2.2 Signal coherence

By using the two photodetector FLDI system the turbulence signal can be discriminated from background noise by analysing the magnitude squared coherence of the photodetector output signals given by:

$$\begin{aligned} C_{AB}\left( f\right) = \frac{\left| P_{AB}\left( f\right) \right| ^2}{P_{AA}\left( f\right) P_{BB}\left( f\right) }. \end{aligned}$$

(9)

Here $P_{AB}(f)$ is the cross-spectral density of the voltage output signals from photodetectors A and B, and $P_{AA}(f)$ and $P_{BB}(f)$ are the autocorrelations of signals A and B respectively. The magnitude squared coherence is bound in the range $0 \le C_{AB}(f) \le 1$, where  1 indicates a perfectly coherent signal and  0 that the signals are unrelated.

Segments of the spectra dominated by the density fluctuations present in the TUSQ flow have a high coherence. These segments can be consistently identified by setting a minimum coherence cutoff value. Coherence thresholds of 0.75 and 0.85 have been used for freestream FLDI measurements in a Mach 3 blowdown facility, an 0.9 for a benchtop free-space turbulent jet (Fulghum 2014). For the analysis of the experimental data obtained in TUSQ, the coherence threshold was set as 0.8.

4.2.3 von Kármán turbulence spectrum

Turbulence is a complicated broadband phenomenon, however by discussing turbulence spectra models the turbulent density spectra measured by the focused laser differential interferometer can be better understood. The turbulent kinetic energy is transferred from large eddies to smaller eddies such that the three dimensional energy spectrum, E(k), is proportional to $k^{-5/3}$ in the inertial subrange (Kolmogorov 1941).

The von Kármán spectrum can be used to predict the turbulence spectrum for the inertial subrange, small and large wavenumbers, and is defined as:

$$\begin{aligned} \varPhi _n^V \left( k \right) = \frac{0.033 \, C_n\left( z\right) ^2}{\left( k^2 - k_0^2 \right) ^{11/6}} \exp \left( -\frac{k^2}{k_m^2} \right) , \end{aligned}$$

(10)

where $k_0 = 2\pi / L_0$, $k_m = 5.92 / l_0$ and $L_0$ and $l_0$ are the integral and dissipative length scales respectively. The exponential term of Eq. (10) has the effect of rapidly rolling off the spectrum for $k>k_m$, and for a spectral fit to the data can be neglected without introducing significant error.

A $-11/3$ rolloff of the turbulent field $\varPhi _n^V \left( k \right)$ corresponds to a $-5/3$ rolloff of the 3D kinetic energy spectrum E(k) (Fulghum 2014). Therefore, Eq. (10) can be approximated as:

$$\begin{aligned} \varPhi _n^V \left( k \right) \approx \frac{A^2}{\left( k^2 + k_0^2 \right) ^{-B/2}}, \end{aligned}$$

(11)

where A and B are constants representing the amplitude and slope of the energy decay respectively. In the case of $B = -5/3$, the fit is identical to the 3D von Kármán spectrum of turbulence (Fulghum 2014).

4.3 Density based turbulence intensity

Using FLDI measurements from runs where the beam shrouds were installed, a von Kármán turbulence spectrum can be fitted to the experimental data. Recalling that the coherence spectrum of the two photodetector signals can be used to identify the regions dominated by the density fluctuations close to the FLDI best focus, the spectral fit is only to this region of data. The coherence spectrum was found to be a function of the duration of time examined. Too long of a window tended to result in reduced coherence, especially at higher wavenumbers. Shorter windows, by definition, use less data from the time domain. This reduction in the available data results in a ‘noisier’ power spectrum, but this data tends to be more coherent than for longer windows. Windows of 20 ms duration were found to preserve a high signal coherence, and to be sufficiently long for the frequency content to be clear.

A power spectral density analysis of Run  843 for $t =$  1030 ms after diaphragm rupture is presented in Fig. 9. The power spectral density for the run and baseline were calculated using Blackman windows of $2^{14}$ points wide with 90% overlap, and the signal coherence and SNR found for every frequency examined. The overlap and window lengths were selected such that the presented spectra were clear, but still preserved the information about the flow. The SNR was defined as:

$$\begin{aligned} \mathrm {SNR} = \frac{\mathrm {PSD}\left\{ \left( \varDelta \varphi _{A}-\varDelta \varphi _{B}\right) _{\mathrm{run}}\right\} }{\mathrm {PSD}\left\{ \left( \varDelta \varphi _{A}-\varDelta \varphi _{B}\right) _{\mathrm{baseline}}\right\} }, \end{aligned}$$

(12)

such that the signal-noise-ratio considered the raw data, not the signals that had been processed by the FLDI transfer functions.

Fig. 9

Spectrum of density fluctuations for Run 843, $t = 10$–${30}\,\hbox {ms}$ with a von Kármán spectrum fit to the coherent portion of the experimental spectrum

The power spectral density of the turbulent density fluctuations $\left| \rho _{\infty }^{\prime }\right| ^2$ is well above the baseline noise level for ${4}\,{\hbox {m}^{-1}} \lesssim k \lesssim {2000}\,{\hbox {m}^{-1}}$ (Fig. 9b). For $k \gtrsim {3000}\,{\hbox {m}^{-1}}$, the SNR is low and this is manifested in the PSD of density fluctuations. Because the intensity of density fluctuations is of the order of, or less than, the baseline noise level, the turbulent density fluctuations cannot be determined for $k > {3000}\,{\hbox {m}^{-1}}$. At these high wavenumbers this results in the transfer functions modulating a small signal embedded in the baseline noise which results in the increase of $\left| \rho _{\infty }^{\prime }\right| ^2$ for $k \gtrsim {3000}\,{\hbox {m}^{-1}}$ in Fig. 9a which is a non-physical behaviour.

The coherence spectrum is very noisy at high wavenumbers, and a low coherence is observed at low wavenumbers. The noise at high wavenumbers is at least in part attributable to differences in sensitivity of the photodetectors at high wavenumbers, but this region was found to have a SNR of approximately unity.

Two von Kármán spectrum fits are shown on Fig. 9a, the first where the constants A, B and C of Eq. (11) are all determined from the fitting process, and the second where B was fixed to $-5/3$ corresponding to the Kolmogorov spectrum rolloff. The free fit and the $B = -5/3$ fit are in strong agreement with the experimental spectrum for the region ${4}\,{\hbox {m}^{-1}} \lesssim k \lesssim {2000}\,{\hbox {m}^{-1}}$ where $C_{AB} \ge 0.8$. The strong agreement with the $-5/3$ von Kármán spectrum rolloff gives confidence that the selected transfer function $H_z(k)$ was appropriate. Because of the low SNR at high wavenumbers, the dissipation scale could not be resolved. Therefore, the approximate von Kármán spectrum fit (Eq. 11) was used for the analysis of all spectra.

Past freestream noise measurements via Pitot surveys revealed that the frequency content of the freestream disturbances changes during the flow time (Birch et al. 2018). Therefore, to confirm that this is a true property of the flow and not a function of the Pitot pressure measurement technique, a spectrogram analysis of the FLDI data was conducted which is shown as Fig. 10. The spectrogram was created using Blackman windows of 5 ms width using 90 % overlap evaluated every 5 ms and windowed to the wavenumber range where greater than 80 % coherence was observed. Since this is plotted in the wavenumber domain, not the frequency domain, the  3–4 kHz content appears at 20–25 ${\hbox {m}^{-1}}$. This narrowband content begins at approximately 60 ms and is superimposed on a consistent background of broadband noise which is consistent with the Pitot pressure surveys of Birch et al. (2018).

Fig. 10

Spectrogram of density fluctuations showing how the disturbances change throughout the flow

To better view the frequency content of the spectrogram, power spectral density estimates using Welch’s method for three selected 20 ms segments of flow data from Run  843 are presented in Fig. 11. In Fig. 11a the coherent segment of the spectra closely follows the von Kármán spectrum and no peaks in energy are observed. For the spectra presented in Fig. 11b and c, a strong peak is observed between  3 and 4 kHz, and a first harmonic of this content is also visible in Fig. 11b which was not always clear in Fig. 10, nor in the Pitot pressure data presented in Birch et al. (2018). This first harmonic was observed in the barrel pressure data by Birch et al. (2018). Because these peaks have a significant impact on the von Kármán fit, the peaks were excluded from the fitting routine. The amplitude of the von Kármán spectra fit is higher for Fig. 11b and c than in Fig. 11a which indicates an increase in density perturbations at later flow times.

The integral scale of turbulence was identified as $L_ 0$ = 28–29 mm from the von Kármán spectrum fit and using $L_0 = 2\pi /k_0$. Furthermore, the transfer of energy from the energetic eddies ($k < 2\pi /L_0$) to successively smaller scales followed the classic $-5/3$ energy cascade. However, from these measurements alone, the origin of the integral length scale cannot be determined with certainty. Two possible sources for this scale are: (1) the nozzle throat which has a diameter of ${28.8}\,{\hbox {mm}}$; and (2) the boundary layer on the nozzle wall which, based on Pitot pressure surveys, is up to ${30}~\hbox {mm}$ thick at the nozzle exit plane (Birch et al. 2018). For the isentropic disturbances which originate in the boundary layer on the nozzle wall to reach the probed location in the flow, they must originate upstream of the nozzle exit, where the boundary layer is thinner. For further investigation of the source of the integral length scale, other TUSQ nozzles can by studied. For example, the Mach 2 nozzle has a throat diameter of ${30.3}\,\mathrm{mm}$, which is comparable to the Mach 6 nozzle throat diameter (${28.8}\,{\hbox {mm}}$), but it has much thinner boundary layers. The Mach 7 nozzle has a nozzle exit diameter just ${0.1}\,{\hbox {mm}}$ larger than the Mach 6 nozzle and a comparable boundary layer thickness on the nozzle wall.

Fig. 11

Power spectral density plots of the density fluctuations for three periods of flow

Because there is a change of the intensity and frequency content of turbulent density fluctuations with time, and because the data is coherent in only a portion of the energy spectrum, defining the root-mean-square (denoted using a tilde) turbulent density fluctuations such that they can be identified from a frequency analysis is useful. The density-based turbulence intensity is calculable from a frequency analysis using:

$$\begin{aligned} T I_{\rho _{\infty }}&= \widetilde{\rho _{\infty }^{\prime }} / \overline{\rho _{\infty }} = \langle \rho _\infty ^\prime \rangle , \end{aligned}$$

(13)

$$\begin{aligned}&=\frac{1}{\overline{\rho _{\infty }}} \sqrt{\frac{1}{N^{2}} \sum _{N}\left| \frac{\lambda }{2 \pi K_{G D} \varDelta x} \frac{\mathcal {F}\left\{ \varDelta \varphi _{A}-\varDelta \varphi _{B}\right\} }{H_{\varDelta \mathrm {x}}(k) H_{z}(k)}\right| ^{2}}. \end{aligned}$$

(14)

Evaluating Eq. (14) in the range $1 \le f \le {250}\,\hbox {kHz}$ for 5 ms periods every 5 ms, the root-mean-square turbulent density fluctuations can be shown to change over the run duration as illustrated by Fig. 12a. The RMS density fluctuations were repeatable across each run and all followed the same trends over time. The time-resolved density fluctuations for 1–250 kHz are shown in Fig. 12b. A high amplitude density fluctuation is apparent at $t = \hbox {{0}\,{s}}$ due to the nozzle starting effects. Following the start of the flow, $\langle \rho _\infty ^\prime \rangle$ increases with time to $t \approx {60}\,$ ms and remains relatively constant until $t \approx {180}\,$ ms where a sudden increase in the amplitude of the turbulent density fluctuations is observed. The change in intensity of $\left| \rho _\infty ^\prime \right|$ at $t = 0$ on Fig. 12b shows the high SNR of the FLDI instrument for the measurement of density fluctuations in the low density ($\rho \approx {34}\,{\hbox {gm}^{-3}}$) freestream flow. At $t = {180}\,{\hbox {ms}}$ there is a sudden increase of the RMS density fluctuations in Fig. 12a.

Fig. 12

Comparison of density fluctuations (f = 1–250 kHz), barrel pressure and total temperature measurements from Birch (2019)

A sudden increase of $\rho ^\prime$ at $t \approx {180}\,\hbox {ms}$ is visible in Fig. 12a which is marked as (i), and the timing of this change is consistent with the colder gas in the barrel being expelled through the nozzle (Fig. 12c, feature (iv)), and with the reflected expansion wave arriving at the nozzle inlet for the second time (Fig. 12c, feature (iii)). However, because no similar sudden increase of density fluctuations occurred when the reflected expansion wave arrives at the nozzle inlet for the first time, it is concluded that the sudden increase in density fluctuations was actually due to the cold vortices being expelled through the nozzle. Note that the rate of temperature drop of an individual run is significantly more rapid than shown in Fig. 12c, which was calculated from the average of eight runs (Birch 2019).

4.4 Properties of the disturbance field

A complete modal analysis is only possible with data obtained from hot wire anemometry measurements. However, sensible conclusions can be made about the fluctuations present in the flow in this work through comparison to the Pitot pressure fluctuation measurements made in an earlier study (Birch et al. 2018). Isentropic sound mode disturbances are expected to dominate the fluctuations present in hypersonic ground test facilities. Under the assumption of isentropic disturbances, the density fluctuations which were measured using FLDI can be related to static pressure fluctuations using:

$$\begin{aligned} \frac{P^\prime }{\overline{P}} = \gamma \frac{\rho ^\prime }{\overline{\rho }}, \end{aligned}$$

(15)

and, for $M > 2.5$, Pitot pressure fluctuation measurements can be equated to static pressure fluctuations using the relation developed by Stainback and Wagner (1972):

$$\begin{aligned} \frac{\tilde{P}}{\overline{P}} = \frac{\gamma }{2} \left( \frac{\tilde{P}_{\mathrm{pit}}}{\overline{P}_{\mathrm{pit}}}\right) \left[ 1 - \frac{4 n_x}{M} + 4 \left( \frac{n_x}{M}\right) ^2 \right] ^{-1/2}, \end{aligned}$$

(16)

where,

$$\begin{aligned} n_x = \left( \frac{u_s - u_\infty }{u_\infty }\right) ^{-1} M^{-1}, \end{aligned}$$

(17)

and the sound source velocity us is expected to be about 60 % of the freestream velocity $u_{\infty }$ (Wagner et al. 2018).

The FLDI and Pitot pressure measurements have very different useful frequency ranges, however the interesting 3–4 kHz disturbance is common to both measurements. To ensure that bandpass filters applied to both FLDI and Pitot pressure measurements do not attenuate any of this content and that any broadening of this peak is measured, the bandwidth analysed was 2–5 kHz.

The normalised RMS static pressure fluctuations $\langle P_\infty ^\prime \rangle$ that are present in the TUSQ freestream, under the assumption that the disturbance field is dominated by isentropic sound waves, is shown in Fig. 13. For the first approximately 75 ms of flow there is an excellent agreement for the amplitude of static pressure fluctuations when inferred from the FLDI and Pitot pressure measurements. Because of this agreement, for the first 75 ms of hypersonic flow the  2–5 kHz frequency band can be confidently stated as being dominated by isentropic sound wave disturbances.

At $t \approx {75}\,\hbox {ms}$ the Pitot-based static pressure calculation diverges from the FLDI-based values, and the disturbance field is no longer dominated by isentropic waves. There are two other disturbance fields: (1) the vorticity mode; and (2) the entropy mode (Kovásznay 1953). Pure vorticity mode disturbances arise from the variation of the rotational field of velocity in a flow field with no pressure, temperature or density fluctuations. Entropy mode disturbances are the non-isentropic, isobaric variation of entropy, density and temperature.

Fig. 13

Normalised root-mean-square fluctuations of static pressure in TUSQ assuming the disturbance field is dominated by isentropic sound waves, evaluated in 5 ms bins for $f =$ 2–5 kHz. Error bars on the Pitot pressure data represent one standard deviation from the mean

Through linearisation of the equation of state, the nondimensional density fluctuations are (Kovásznay 1953):

$$\begin{aligned} \frac{\rho _\infty ^\prime }{\overline{\rho _\infty }} = \frac{P_\infty ^\prime }{\overline{P_\infty }} - \frac{T_\infty ^\prime }{\overline{T_\infty }} = P - s. \end{aligned}$$

(18)

Because FLDI measures density fluctuations, the difference between the non-dimensional pressure (P) and non-dimensional temperature (s) fluctuations is measured. The Pitot probe measurements include information about the acoustic and entropy fluctuations (Duan et al. 2019), and therefore can result in a poor estimate of the static pressure fluctuations when non-isentropic disturbances are non-negligible. Therefore the FLDI-based static pressure fluctuations are less than the Pitot-based values when the entropy mode disturbances are significant. The 3–4 kHz disturbances that were first reported by Birch et al. (2018) are therefore identified as entropy mode disturbances. These disturbances are generated in the barrel and are consistent with the laminar-turbulent transition of the gas in the barrel (Birch 2019).

Towards the end of the flow at $t \approx {175}\,\hbox {ms}$ the static pressure fluctuations that are inferred from the Pitot pressure and FLDI measurements converge. It is possible that the disturbance field is again dominated by isentropic disturbances, however further experimental investigation is required to confirm this. For $t > {175}\,\hbox {ms}$ the flow is of reduced experimental quality as the stagnation temperature of the flow is known to be significantly reduced relative to the earlier flow (Fig. 12c). It is unlikely that the data generated in this late nozzle flow is of interest for experiments that are sensitive to the freestream disturbance environment.

5 Conclusion

A focused laser differential interferometer has been designed and built for the investigation of freestream disturbances in the University of Southern Queensland’s hypersonic wind tunnel. The contribution of the turbulent shear layer from the Mach 6 nozzle to the overall FLDI signal was largely eliminated by forcing the boundary layer on the nozzle wall and the turbulent shear layer around the path of the FLDI beams, which significantly improved the low-wavenumber measurements. Without the beam shrouds, the measured density fluctuations for $k < {1000}\,{\hbox {m}^{-1}}$ were up to an order of magnitude higher than when the beam shrouds were fitted because of the direct contribution of the turbulent shear layer, for the application of the TUSQ FLDI instrument. By improving the low-wavenumber spectrum, where significant contribution from the turbulent shear layer was present, the narrowband  3–4 kHz disturbance was more pronounced. Through a comparison to previous Pitot surveys, this  34 kHz feature was found to be primarily entropy fluctuations that originate in the barrel. The intensity of the normalised root-mean-square (NRMS) density fluctuation was consistent across the three runs. However, the intensity is time-varying and it is therefore inappropriate to specify a single value. For the first 180 ms of flow the NRMS density fluctuations are bound between 0.4 and 0.6%. Since the freestream disturbance environment is known to influence the results generated in hypersonic ground test facilities, this quantification of the TUSQ flow can be used to better inform the interpretation of the data generated in TUSQ.