Entrainment in pulsing plumes

Abstract

Turbulent axisymmetric lazy plumes produced by discharging saline fluid downwards into a less dense uniform environment from a round pipe are examined experimentally. The plume development is controlled by the source flow rate $Q_0$, momentum $M_0$ and buoyancy $F_0$. This study investigated plumes where the source flow rate, momentum and buoyancy are sinusoidal functions of time. The pulsing flow is generated by a programmable ISMATEC gear pump. The maximum frequency f of this pulsing plume is of $\mathcal {O}(U_0/D)$, where $D/U_0$ is the eddy turnover time scale at the source, D is the source diameter, and $U_0$ is the average velocity at the source. Experiments with pulsing plumes were carried out with a flow rate amplitude A of up to $80\%$ and with Strouhal number $St=fD/U_0$ ranging from 0.012 to 1.2. The bulk dilution and entrainment measurements were made using the experimental approach of Hunt and Kaye (J Fluid Mech 435:377–396, 2001). Average entrainment is obtained via the integral relationship for Q(z) and M(z) from the model established by Morton et al. (Proc R Soc Lond A 234(1196):1–23, 1956) for continuous sources. The influence of the amplitude and Strouhal number St on the entrainment coefficient $\alpha$ is examined, which was found to be very small over the entire range of source conditions considered.

Graphic abstract

1 Introduction

Plumes are widely occurring free shear flows which are driven by buoyancy. Morton et al. (1956) developed an integral model for this flow based on the conservation equations for mass, momentum and buoyancy, which is referred to hereafter as the MTT model. In this model, flow is assumed self-similar and turbulent entrainment of the ambient fluid into the plume is modelled using a constant entrainment coefficient $\alpha$, which is the ratio of the radial velocity of the ambient fluid into the plume, to the plume axial velocity. For axisymmetric turbulent plumes with constant source conditions, typical values for $\alpha$ are in the range $0.10< \alpha < 0.16$ for ‘top-hat’ velocity profiles (van Reeuwijk and Craske 2015). The $\alpha$ for axisymmetric turbulent plumes with a Gaussian velocity profile is $1/ \sqrt{2}$ times that of a ‘top-hat’ velocity profile, which corresponds to $0.071< \alpha < 0.11$.

Plumes with time-varying source conditions, where flow rate, momentum and buoyancy are functions of time, have received some attention. Scase et al. (2006, 2009) and Scase and Hewitt (2012) investigated turbulent plumes where the source was suddenly changed from one constant condition to another constant condition. A general constant entrainment coefficient $\alpha$ was used in their model. The comparison between their simulations and experiments showed good agreement. Woodhouse et al. (2016) proposed an unsteady integral plume model. A non-constant entrainment coefficient was introduced by combining the constant entrainment coefficient with shape factors for momentum, buoyancy and energy. They showed the non-constant entrainment coefficient does not change the power law solution of the MTT model (Morton et al. 1956) except introducing the prefactors.

Plumes with time variation in source conditions were investigated experimentally and numerically in flows where the timescale for the source oscillation is much larger than the eddy turnover time. The ‘filling box’ problem (Baines and Turner 1969) is a flow where a plume issues from a point source at the base of a rectangular cavity. The plume rises to the ceiling of the cavity forming an intrusion which then fills the cavity, displacing the ambient fluid. Killworth and Turner (1982) studied the development of the ambient stratification numerically and analytically in a ‘filling box’ with plumes with source buoyancy fluxes that are time dependent, including sinusoidal, square wave and sawtooth functions. The forcing frequency was close to the box filling time, which is the time taken by the plume to modify its surroundings and establish a stratified environment in the cavity. Only positive (i.e. half-cycle) buoyancy fluxes at the source were considered in their study and the entrainment coefficient $\alpha$ was assumed to be constant. The authors compared the flow under pulsing and constant source conditions throughout the box and found that the time-averaged vertical velocity profile and time-averaged density profile in the box were very similar in both cases. The ‘emptying filling box’ problem, with vents in the top and base of the box, was proposed by Linden et al. (1990) to investigate the transient behaviour of a naturally ventilated space. Bolster and Caulfield (2008) performed laboratory experiments of the ‘emptying filling box’ problem, where the plume buoyancy flux was forced with a square wave function at a frequency close to the box filling time. They investigated the transient response of three-layer stratification in the box to the time-varying buoyancy flux and the change of the average flow rate through the box driven by hydrostatic pressure associated with the upper layer. Their results showed a higher forcing frequency results in a larger average flow rate. In the studies of Killworth and Turner (1982) and Bolster and Caulfield (2008), the forcing frequency was low compared with the timescale of turbulence in plumes. Entrainment measurements at higher forcing frequency have not been reported for plumes.

There have been a number of studies examining how jet development is modified by periodic forcing at the source. Crow and Champagne (1971) and Solero and Coghe (2002) placed a loudspeaker at the source of an air jet to perturb the flow. Marzouk et al. (2003) and Choutapalli et al. (2009) investigated pulsing jets by oscillating the source flow rate sinusoidally. These studies showed that the entrainment rate of pulsing jets is increased in the initial potential core region. This behaviour was observed over $z/D<10$ where z denotes the axial distance downstream of the nozzle (Crow and Champagne 1971; Solero and Coghe 2002). The maximum increase in entrainment occurs when the jets are forced at close to their natural dimensionless puffing frequency, Strouhal number $St \sim 0.30$ (Crow and Champagne 1971). The source Strouhal number is $St = fD/U_0$ where f represents the forcing frequency, D the diameter of the source and $U_0$ the average velocity at the source. Crow and Champagne (1971) show that the entrained volume flow of pulsing jets was increased by $32\%$ at $St=0.30$ compared with the constant source case and Solero and Coghe (2002) found the maximum increase of the entrained flow rate reached $25\%$ at a relatively low $St=0.033$. Jets with constant source conditions have been shown to have the ‘top-hat’ entrainment coefficient $0.065<\alpha <0.080$ (van Reeuwijk and Craske 2015). When a Gaussian self-similar profile is adopted, the values of $\alpha$ are scaled by $1/ \sqrt{2}$, and are then in the range of $0.046<\alpha <0.059$. Fully pulsing jets, where the minimum flow rate is zero, were examined experimentally by Bremhorst and Hollis (1990), who found that $\alpha$ was not constant for $z/D<10$, varying from 0.07 to 0.09, with the larger values at smaller z/D.

To our knowledge, there is no previous work showing what influence forcing frequency and amplitude have on pulsing plumes and how the effects vary with distance z/D from the source. We have conducted experiments on a pulsing flow, whose flow rate, momentum and buoyancy are sinusoidal functions of time. The effect of the dimensionless forcing frequency St and amplitude A upon the entrainment coefficient $\alpha$ of the pulsing plume are considered. The forcing frequency f is of ${\mathcal {O}}(U_0/D)$ where $D/U_0$ is the eddy turnover timescale at the source.

The paper is organised as follows. The experimental setup and the instruments are described in Sect. 2. In Sect. 3, the pure plume model with a point source established by Morton et al. (1956) and the virtual correction method for lazy plumes of Hunt and Kaye (2001) are applied. Time-varying source conditions are discussed in Sect. 4. Experimental results are presented in Sect. 5. The results for constant source plumes are shown as benchmarks in Sect. 5.1. The results for pulsing plumes with multiple St and amplitude A are presented and compared with constant source plumes in Sect. 5.2. In Sect. 5.3, the comparison is made over a wider range of St and A. Sect. 6 briefly summarises the findings in this paper.

2 Experimental setup

Fig. 1

Schematic of the experimental setup

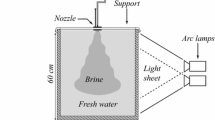
A schematic representation of our laboratory setup is shown in Fig. 1. The experiments were conducted in a $1\,\,\hbox {m}^3$ transparent Perspex tank. The tank was filled with freshwater and plumes were generated by discharging the saline source fluid downwards from a round pipe located in the upper region at the horizontal centre of the tank. The ISMATEC MCP-Z Standard gear pump, which is programmed using a Moxa C168 card and a LabVIEW driver, was used to pump the saline source fluid into the round pipe. In this setup, plumes develop downwards until reaching the bottom of the tank where a saline intrusion forms. The intrusion grows and eventually partially fills the tank resulting in a two-layer stratification with a well-defined interface. Dye was added to the saline source to visualise the behaviour of the plume and indicate the location of the interface. This interface was tracked by a Basler camera pilot piA640-210gc during the experiments. Fluid was drained continuously from the bottom of the tank, where the drainage flow rate $Q_\mathrm{d}$ was adjustable via an outlet valve and measured by the outlet MESLCD5 flow meter.

The distance between the outlet of the pipe and the interface is Z, which is determined by the source flow rate $Q_0$, drainage flow rate $Q_\mathrm{d}$ and entrained flow rate $Q_\mathrm{e}$. Decreasing the value of $Q_\mathrm{d}$ will result in a deeper intrusion and a shorter plume length Z for entrainment. For each experiment, a fixed source flow rate $Q_0$ and a drainage flow rate $Q_\mathrm{d}$ are applied. During an experiment at full development, the interface height achieves a steady value for these settings. Steady conditions were verified by monitoring both the interface height and also by monitoring the outlet fluid salinity c, which was determined with an Anton Paar Snap 50 ($\pm \,\,5 \times 10^{-4}\hbox { g/cm}^3$). The interface is considered steady when the change of its height is less than $\pm \,\, 2\,\,\hbox {mm}$ over 15 min. The error in the measurement of the interface was estimated as being less than $\pm \,\,2\,\,\hbox {mm}$; however, we have adopted the thickness of the interface as a more conservative measure of the uncertainty. The interface thickness is a function of the interface stability controlled by the balance between entrainment and diffusion through it (Kaye et al. 2010), which increases with decreasing the density difference across the interface. The density difference across the interface decreases with increasing Z as the plume source is increasingly diluted by entrainment. The thickness of the interface is analysed from the images taken by the camera. Using the light attenuation method of Allgayer and Hunt (2012), the upper and lower extents of the interface were chosen as between 90 and 10% of the saline intrusion layer concentration. The maximum value of uncertainty was $\pm \,\, 10\,\,\hbox {mm}$ for $Z = 400\,\,\hbox {mm}$.

A freshwater make up flow was introduced at the top of the tank with the make up flow rate $Q_\mathrm{s}$. Taking the whole tank as a control volume gives $Q_\mathrm{s} +Q_0 = Q_\mathrm{d}$. The make up flow rate $Q_\mathrm{s}$ was made equal to $Q_\mathrm{d}$ as $Q_0$ is very small compared with $Q_\mathrm{s}$. This ensures that the water-free surface level in the tank is approximately constant during the experiments. The makeup flow is released from four diffusers each with $250\,\,\hbox {mm }\times 250\,\,\hbox {mm}$ outlets that are suspended 80  mm above two layers of perforated plates with 3.5-mm holes. These plates are 100  mm above the source outlet. Dye flow visualisation was used to ensure the flow was supplied uniformly into the tank. The magnitude of the make up flow velocity was less than $4\%$ of the average source velocity $U_0$. As shown in Fig. 1, taking a control volume over the plume region from the source to the interface (i.e. over Z) enables the entrained volume flux $Q_\mathrm{e}$ to be determined as $Q_\mathrm{e} = Q_\mathrm{z} - Q_0$, where $Q_\mathrm{z}$ denotes the local volume flux of the plume at the interface. The depth of the lower saline layer was constant when a steady state was reached and $Q_\mathrm{z} = Q_\mathrm{d}$. The approach was first described by Baines (1983) and was later used by Hunt and Kaye (2001) to measure entrainment in plumes with constant sources.

3 MTT model

In this study, the power law solution of the MTT model (Morton et al. 1956) is adopted, which is applicable to pure turbulent axisymmetric plumes issuing from a point source into an unstratified environment. For an axisymmetric plume, with a self-similar Gaussian velocity profile, the actual mean fluxes of volume ${\hat{Q}}$, momentum ${\hat{M}}$ and buoyancy ${\hat{F}}$ are defined as

$$\begin{aligned} {\hat{Q}}=\pi u_\mathrm{m}b^2, {\hat{M}}=\frac{1}{2}\pi u_\mathrm{m}^2 b^2 , {\hat{F}}=\frac{1}{2}\pi u_\mathrm{m}b^2g', \end{aligned}$$

(1)

where b(z) denotes the characteristic radius of the plume in a Gaussian profile (Morton et al. 1956), $u_\mathrm{m}(0, z)$ the vertical centre line velocity, $g'=g(\rho _0 - \rho _\mathrm{a})/\rho _a$ the reduced gravity, and $\rho _0$ and $\rho _\mathrm{a}$ the densities of the saline source and ambient fluid, respectively. Source conditions are represented by $(Q_0, M_0, F_0)$, where $\;Q_0={\hat{Q}}_0/\pi$, $\;M_0=2{\hat{M}}_0/\pi$ and $F_0=2{\hat{F}}_0/\pi$ are proportional to actual mean fluxes of volume $\hat{Q_0}$, momentum $\hat{M_0}$ and buoyancy $\hat{F_0}$ at the source (i.e. $z = 0$).

Table 1 Source conditions of all constant source plumes. Pulsing plumes experiments are only shown for $St = 0.080$, $St = 0.30$ and $St = 1.0$. The jet length $L_\mathrm{m}$, the source length scale $L_\mathrm{Q}$ and the virtual origin correction $Z_\mathrm{v}$ are scaled on pipe diameter D, $\mu$ represents the dynamic viscosity of the saline source, $St_\mathrm{z}$ the Strouhal number at the maximum plume length Z achieved in each experiment, $D_\mathrm{z}$ the estimated diameter of the plume at Z, $u_\mathrm{z}$ the estimated average centre line velocity at Z based on the power law solution of the MTT model (Morton et al. 1956)

The virtual origin correction method developed by Hunt and Kaye (2001) for lazy plumes was used as the saline source was discharged from a pipe with a finite area in the experiments. Following the power law solution of the MTT model (Morton et al. 1956) and the virtual origin correction (Hunt and Kaye 2001)

$$\begin{aligned} z+Z_\mathrm{v} = C^{-3/5}Q_\mathrm{z}^{3/5}{F_0}^{-1/5}, \end{aligned}$$

(2)

where

$$\begin{aligned} Z_\mathrm{v}= & {} \frac{5\varGamma ^{-1/5}Q_0(1-\delta )}{6\alpha M_0^{1/2}}, \end{aligned}$$

(3)

$$\begin{aligned} C= & {} \frac{6\alpha }{5}\left( \frac{9\alpha }{5}\right) ^{1/3} \end{aligned}$$

(4)

and

$$\begin{aligned} \delta = \frac{3}{5}\sum _{n=1}^\infty \left( \frac{(1-\frac{1}{\varGamma })^n}{ {5^{n-1}n! (10n-3)}}\prod _{j=1}^n\left( 1+5(j-1)\right) \right) , \end{aligned}$$

(5)

where $Z_\mathrm{v}$ denotes the distance from the actual source to the virtual origin with zero volume flux and zero momentum flux, $\delta$ is given by Eq. 5, C is a function of $\alpha$ and $\varGamma$ is the flux-balance parameter at the source, expressed as

$$\begin{aligned} \varGamma =5Q_0^2F_0/4\alpha M_0^{5/2}. \end{aligned}$$

(6)

Pure jets have $\varGamma =0$ and are dependent on momentum only (i.e. $F_0 = 0$); pure plumes have $\varGamma =1$. Forced plumes, whose initial momentum flux $M_0$ is greater than that of an equivalent pure plume of the same initial buoyancy flux $F_0$, have $0<\varGamma <1$. Lazy plumes whose initial momentum flux $M_0$ is less than that of an equivalent pure plume of the same initial buoyancy flux $F_0$, have $\varGamma >1$. As the flows develop downstream, all plumes will eventually achieve the pure plume characteristic of $\varGamma _z =1$, where $\varGamma _z$ is the local $\varGamma$ at different z. Hunt and Kaye (2005) showed ${\mathrm{d} \varGamma _z}/{\mathrm{d} (z/L_Q)}$ can be estimated with

$$\begin{aligned} \frac{\mathrm{d} \varGamma _z}{\mathrm{d} (z/L_Q)}={\left\{ \begin{array}{ll} \frac{10}{3}\varGamma ^{1/2}(1-\varGamma )^{3/10} \varGamma _z^{1/2}(1-\varGamma _z)^{7/10} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \varGamma <1\\ -\frac{10}{3}\varGamma ^{1/2}(\varGamma -1)^{13/10} \varGamma _z^{1/2}(\varGamma _z-1)^{13/10}&{} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \varGamma >1,\\ \end{array}\right. } \end{aligned}$$

(7)

where $L_\mathrm{Q} = 5Q_0/6\alpha M_0^{1/2}$ denotes the source length scale. The location at which pure plume characteristics of $\varGamma _z = 1$ are reached can be determined by integrating Eq. 7 numerically. For lazy plumes with initial source condition $\varGamma > 1$, $\varGamma _z = 1$ is achieved at $z/L_\mathrm{Q} \sim 1$, this distance is shorter than that of forced plumes. In our experiments, plumes are formed by releasing saline fluid from a finite source with initial source conditions $Q_0$, $M_0$, $F_0$. To attain pure plume characteristics as close to the source as possible, all source conditions in our experiments have $\varGamma >1$ and so are lazy plumes (see Table 1). In all experiments, $L_Q$ ranged from 2D to 3D and Z ranged from 10D to 40D, so the flows achieved pure plume characteristics over most of their height.

4 Time-varying source

Plumes with time-varying sources are the focus of this study. We investigate the case where the source volume flux $\overset{\sim }{Q_0}(t)$ and buoyancy flux ${\overset{\sim }{F_0}(t)}$ are sinusoidal functions of time which are expressed as

$$\begin{aligned} \overset{\sim }{Q_0}(t) = Q_0\left( 1+ A \mathrm{sin}(2 \pi ft)\right) \end{aligned}$$

(8)

and

$$\begin{aligned} \overset{\sim }{F_0}(t) = F_0\left( 1+ A \mathrm{sin}(2 \pi ft)\right) , \end{aligned}$$

(9)

where $\sim$ denotes it is a function of time t, f denotes the forcing frequency at the source and the maximum frequency f is of ${\mathcal {O}}(U_0/D)$, where $D/U_0$ is the eddy turnover time scale at the source. The momentum flux $\overset{\sim }{M_0}(t)$ at the source of pulsing plumes is also a function of time, given as

$$\begin{aligned} \overset{\sim }{M_0}(t) = M_0\left( 1+ A \mathrm{sin}(2 \pi ft)\right) ^2. \end{aligned}$$

(10)

The time-averaged ${\overline{\varGamma }}$, determined by ${\overline{\varGamma }} = \int \overset{\sim }{\varGamma }(t) \mathrm{d}t /T$ over one sinusoidal period, is a function of $\varGamma$ (Eq. 6), and the amplitude A, as the momentum flux $\overline{M_0} = \int \overset{\sim }{M_0}(t) \mathrm{d}t /T = M_0\left( 1+ A^2/2\right)$ increases slightly compared with $M_0$, where $M_0$ is estimated at $\overline{Q_0}$. The time-averaged volume flux $\overline{Q_0} = Q_0$ and buoyancy flux $\overline{F_0} =F_0$ remain unchanged. The time-averaged $\overline{Z_\mathrm{v}}$ is calculated with $\overline{Z_\mathrm{v}} =(5{\overline{\varGamma }}^{-1/5}\overline{Q_0}(1-{\overline{\delta }}))/{6\alpha \overline{M_0}^{1/2}}$, which is less than 1% difference from $\overline{Z_\mathrm{v}}=\int \overset{\sim }{Z_\mathrm{v}}(t) \mathrm{d}t /T$, where ${\overline{\delta }}$ is estimated using ${\overline{\varGamma }}$ in Eq. 5. The overbar is omitted for the remainder of this article.

5 Results

5.1 Constant source plume experiments

Fig. 2

Images show turbulent plumes formed by saline fluid with dye issuing downwards from a round pipe: a constant source plumes and b pulsing plumes with the amplitude of the source flow $A = 50\%$. In both cases, the Reynolds number $Re = 300$ is based on the average conditions at the source. The downstream distance from the source to the point where the plumes become turbulent is approximately one diameter in both a and b

Our approach follows that of Hunt and Kaye (2001). We first conducted a series of experiments for plumes with constant source conditions corresponding to $\varGamma = 1.95$, $\varGamma = 5.16$, $\varGamma = 22.9$ and $\varGamma = 106$. The left side of the Table 1 shows the source conditions of these constant source plume experiments. The jet length $L_\mathrm{m} = 2^{3/2}M_0^{3/4}/\alpha ^{1/2}F_0^{1/2}$ in Table 1 represents the distance after which the source buoyancy flux plays a significant role in the plume dynamics. The Reynolds number Re at the source ranged between 160 and 520, so a parabolic velocity profile at the source was assumed. Plumes issued from one of the following two pipes: one with diameter 10.15  mm and 700  mm in length, the other with diameter 17.1  mm and 700  mm in length. Both constant source plumes and pulsing plumes became turbulent approximately one source diameter downstream. This can be seen from the flow visualisation shown in Fig. 2.

Fig. 3

The interface height and drainage flow rate measurements with error bars for constant source plumes. The solid straight line represents the linear fit to $\varGamma =22.9$ is $(Z+Z_\mathrm{v})/D=5.29Q_\mathrm{z}^{3/5}F_0^{-1/5}/D+0.91$. The subplot shows all experimental results with error bars

To commence the experiments, the Perspex tank was filled with freshwater and the fresh makeup flow was discharged from the top of the tank uniformly at the flow rate $Q_\mathrm{s}$. Simultaneously, fluid was drained from the base of the tank at the flow rate $Q_\mathrm{d} = Q_\mathrm{s}$. The plume was then injected from the top of the tank by the gear pump at the flow rate $Q_0$. A saline intrusion rises from the base of the tank, eventually reaching the steady condition where the distance Z is constant and is recorded by the camera. For each source condition $\varGamma$ tested, 4–7 experiments were performed, each with different Z, which were obtained by changing the drainage flow rate $Q_\mathrm{d}$. The distance Z was tracked by the camera and was recorded when the steady conditions were established during each experiment at a corresponding drainage flow rate $Q_\mathrm{d}$.

The results for the interface height Z and the drainage flow rate $Q_\mathrm{d}$ measured for constant source plume experiments are presented in Fig. 3. The horizontal and vertical axis scales are based on Eq. 2 scaled on the source diameter D. The local volume flux of plumes at the interface $Q_\mathrm{z} = Q_\mathrm{d}$ is used in the horizontal axis. From Eq. 2, we expect the data to be well approximated by a linear relationship between $(Z+Z_\mathrm{v})/D$ and $Q_\mathrm{z}^{3/5}F_0^{-1/5}/D$ with a constant of proportionality of $C^{-3/5}$. In Fig. 3, a regression fit is obtained for each series of data. Over all data, the regression fit is excellent. The bulk entrainment coefficient $\alpha$ for each source condition is obtained by solving Eq. 4. Applying a linear regression fit to the $\varGamma = 22.9$ data gives $\alpha = 0.094$, which is within the range of entrainment coefficients $\alpha$ reported in the literature (van Reeuwijk and Craske 2015). The plume length Z plotted in Fig. 3 is adjusted by the virtual origin method of Hunt and Kaye (2005) and the virtual origin correction $Z_\mathrm{v}$ is estimated by Eq. 3 based on the source condition $\varGamma$. After applying $Z_\mathrm{v}$, the linear regression fit is expected to cross the origin. The vertical intercept of the regression fit at $Q_\mathrm{z} = 0$ is $Z_\varepsilon /D = (Z+Z_\mathrm{v})/D$, which is the error in the Eq. 3 prediction of the location of the virtual origin. The error $Z_\varepsilon > 0$ indicates the prediction of $Z_\mathrm{v}$ is too large, and $Z_\varepsilon < 0$ denotes the prediction of $Z_\mathrm{v}$ is not enough to correct the virtual origin. The intercept of the regression curve for the $\varGamma = 22.9$ data presented in Fig. 3 is $Z_\varepsilon = 0.91D$. The intercepts of the linear regression curves for each constant source condition are shown in Fig. 4 by the round markers. The values of $Z_\varepsilon$ range from $-\,1.7D$ to 0.9D, which is small, supporting the application of the virtual origin correction of Hunt and Kaye (2001) for lazy plumes.

Fig. 4

The vertical intercepts of the linear regression fit $Z_\varepsilon = (Z+Z_\mathrm{v})/D$ at $Q_\mathrm{z} = 0$ for constant source plumes and pulsing plumes after applying the virtual origin correction method of Hunt and Kaye (2001). The round markers denote constant source plumes, the square and triangular markers represent pulsing plumes with $A = 33\%$ and $A = 50\%$, respectively. The shaded area encloses the range of $Z_\varepsilon$ for constant source plume in our experiments

The insert plot in Fig. 3 shows that our experimental results are in a good agreement with results presented by Hunt and Kaye (2001). Here, horizontal error bars are estimated by the accuracy of the MESLCD5 flow meter ($\pm \,\, 1.5\%$) and the gear pump, which was determined to be accurate to $\pm \,\,3\%$. Vertical error bars represent the combination of the measurement error and experimental uncertainties in the thickness of the interface. The density ratio $(\rho _0 - \rho _\mathrm{a})/\rho _\mathrm{a}$ was $< 5\%$ in all experiments, providing Boussinesq conditions.

5.2 Pulsing plume experiments

Fig. 5

The interface height and drainage flow rate measurements with error bars for pulsing plumes. The solid straight line represents the linear fit to $\varGamma =23.0$ is $(Z+Z_v)/D=5.64Q_z^{3/5}F_0^{-1/5}/D-0.35$. The subplot shows 12 experimental results with error bars, where the hollow markers correspond to the experiments at $A = 33\%$ and the solid markers correspond to the experiments at $A = 50\%$

The pulsing plume experiments were performed with 15 average source conditions $\varGamma$ ranging from 6.66 to 153, Strouhal number St from 0.080 to 1.0 and two amplitudes $A=33\%$ and $A=50\%$. Due to space constraints, only five initial source conditions of the pulsing plumes experiments at $St=0.080$, $St = 0.30$ and $St = 1.0$ are shown in Table 1. These three St values are of particular interest, as $St = 0.30$ has been shown to increase the entrainment rate in pulsing jets (Crow and Champagne 1971), and $St = 0.080$ and $St = 1.0$ are the lowest and highest St, respectively, for which experiments were performed in this study. The experimental process is the same as that for the constant source plume investigation. Figure 2b shows the development of the pulsing plume with $A = 50\%$ at $Re = 300$, where two distinct pulses can be seen. In all experiments, the plumes maintained morphology similar to that of a continuous plume. No pinch-off or complete separation of the pulses occurs at the source or at any location in the plume development for any of the tests performed.

The results for the interface height Z and the drainage flow rate $Q_\mathrm{d}$ are shown in the subplot of Fig. 5 for pulsing plumes at $St = 0.15, 0.20, 0.30, 0.60, 0.80\hbox { and }1.0$. The local volume flux of plumes at the interface $Q_\mathrm{z} = Q_\mathrm{d}$ is used in the horizontal axis. Error bars shown in Fig. 5 are estimated the same way as that for Fig. 3. These results show that $Z+Z_v$ is proportional to $Q_z^{3/5}{F_0^{-1/5}}$, the same result for constant source plumes. The average bulk entrainment coefficient $\alpha$ is deduced in the same way as for constant source plumes. The $\varGamma = 23.0$, $A = 50\%$ and $St = 0.30$ result, shown in the main plot, has similar average source conditions as the constant source plume with $\varGamma = 22.9$ shown in Fig. 3. The entrainment coefficient is $\alpha = 0.089$, $4.4\%$ lower than the $\alpha = 0.094$ of the constant source plume with $\varGamma = 22.9$. The decrease of $\alpha$ here is within the experimental error of $\pm 6.5 \%$. The intercept $Z_\varepsilon$ of the linear regression fit shown in Fig. 5 is within 0.35D of the origin, which suggests for time-averaged source conditions, the virtual origin correction method of Hunt and Kaye (2001) gives a reasonable correction for pulsing plumes.

The values of $\alpha$ are presented in Fig. 6 for all results. Error bars represent the experimental error of $\alpha$ estimated by the law of propagation of uncertainty using the experimental error and uncertainty of Z, $Q_\mathrm{z}$ and $F_0$ in Eq. 2. The round markers denote $\alpha$ for constant source plumes, and the square and triangular markers represent $\alpha$ for pulsing plumes at $A = 33\%$ and $A = 50\%$, respectively. The constant source plume results are at $St = 0$ while St ranges from 0.080 to 1.0 for the pulsing plumes. The $\alpha$ for constant source plumes is in the range 0.088–0.10, which is in line with earlier experimental outcomes for constant source plumes of 0.071–0.11(van Reeuwijk and Craske 2015), where a Gaussian self-similar velocity profile is assumed. The $\alpha$ for pulsing plumes is in the range 0.080–0.095, all within the range of $\alpha$ reported for constant source plumes. The characteristic timescale for turbulence in plumes at the downstream distance z is $D_{z}/u_{z}$, which increases with z, where $D_{z}$ denotes the estimated diameter of the plume at z and $u_z$ is the estimated average centre line velocity at z based on the power law solution of the MTT model. In our experiments, the local Strouhal number at the maximum plume length Z is represented by $St_{z}= fD_{z}/u_{z}$, which is 2–3 orders of magnitude larger than the St number at the source. So while St at the source ranges from 0.080 to 1.0, the St number at all downstream locations varies from 0.080 to 88. The linearity between $Z+Z_\mathrm{v}$ and $Q_{z}^{3/5}{F_0^{-1/5}}$ shown in Fig. 5 suggests the bulk entrainment coefficient $\alpha$ is not sensitive to forcing over this larger range of local St.

The results of $Z+Z_\mathrm{v}$ in Fig. 5 are found to be linear with $Q_\mathrm{z}^{3/5}{F_0^{-1/5}}$ and the entrainment coefficient $\alpha$ for pulsing plumes deduced by the MTT model is similar to that of constant source plumes, as shown in Fig. 6. These findings suggest the entrainment coefficient $\alpha$ is constant over the length of pulsing plumes, and also imply that the local entrainment velocity is proportional to the local plume velocity even in pulsing plumes where the local velocity is varying with time. Over a sinusoidal period, pulsing plumes apparently have a similar time-averaged behaviour as plumes with constant source conditions.

Fig. 6

The entrainment coefficient $\alpha$ with error bars for constant source plumes, and pulsing plumes at $A = 33\%$ and $A = 50\%$. The round markers correspond to $\alpha$ for constant source plumes, the square and triangular markers correspond to $\alpha$ values for pulsing plumes at $A = 33\%$ and $A = 50\%$, respectively. The shaded area encloses the range of $0.071<\alpha <0.11$, which is the range of $\alpha$ reported by van Reeuwijk and Craske (2015) for constant source plumes

We tested the sensitivity of the entrainment to the amplitude A by conducting experiments at $St = 0.15, 0.20, 0.30, 0.60, 0.80\hbox { and }1.0$ in pulsing plumes with $A = 33\%$ and $A = 50\%$. The results in Fig. 6 show the differences between $\alpha$ for $A = 33\%$ and $A = 50\%$ range between $3.1\%$ for $St = 0.20$ and $8.9\%$ for $St = 0.80$. The entrainment coefficient $\alpha$ for source conditions with $A = 33\%$ is higher than that of $A = 50\%$ at $St = 0.60$ and $St = 0.80$, and lower in other cases. There is no apparent bias towards increasing or decreasing $\alpha$. These values are within the experimental error in these tests and also within the range of values reported for constant source plumes, which implies $\alpha$ is not sensitive to the amplitude A over our entire experimental range. This is in contrast to results for pure jets, reported by Hirata et al. (2009) where it was found that entrainment in pure jets was increased by forcing the jets at a higher amplitude.

The experiment at $St=0.15$ is the only result where source conditions with both $A = 33\%$ and $A = 50\%$ decrease $\alpha$, compared with the lowest $\alpha$ reported for constant source plumes. Other experiments have at least one $\alpha$ within the range of $\alpha$ of constant source plumes measured in this study. These two decreases, however, are close to or within the experimental error of $\alpha$, being $8.8\%$ and $5.0\%$, respectively.

Hirata et al. (2009) and Crow and Champagne (1971) show that forcing jets at $St = 0.20$ and $St = 0.30$ can significantly increase the entrainment of jets, respectively. In our experiments, the $\alpha$ values obtained by forcing plumes at $St = 0.20$ and $St = 0.30$ are within the range of $\alpha$ values reported for constant source plumes.

Fig. 7

The interface height and drainage flow rate measurements for constant source plumes and pulsing plumes with similar source conditions. The round marker denotes the constant source plume $\varGamma = 106$, the square and triangular markers represent pulsing plumes with $\varGamma = 98.0$ and $A = 33\%$, $St = 0.80$ and $\varGamma = 108$, $A = 50\%$, $St = 0.80$, respectively, $D = 17.1\hbox { mm}$, $Q_0 = 7.80 \times 10^{-7}\hbox { m}^3/\hbox {s}$, $F_0 = (8.89-9.02) \times 10^{-7}$ $\hbox {m}^4/\hbox {s}^2$

In Fig. 7, values of $Q_z^{3/5}F_0^{-1/5}$ are plotted as a function of the normalised downstream distance for a constant source plume with $\varGamma = 106$ and for pulsing plumes with similar $\varGamma$. For all results, $Q_z^{3/5}F_0^{-1/5}$ is proportional to $Z+Z_\mathrm{v}$. The data for pulsing plumes collapse well with the constant source plume results, which indicates entrainment is similar for pulsing plumes and constant source plumes for $Z/D > 10$. The study conducted by Solero and Coghe (2002) on forcing jets found the entrained flow rate increased, primarily for $z/D < 10$. Our measurements do not extend this close to the outlet of the pipe; however, the coincidence of data at $Z/D \sim 10$ shown in Fig. 7 indicates that by extrapolation the entrainment for $Z/D < 10$ is also similar.

In early studies, the virtual origin $Z_\mathrm{v}$ of pulsing jets was shown to be shifted upstream by approximately two source diameters (2D) compared with constant source jets as a result of increased entrainment (Crow and Champagne 1971; Solero and Coghe 2002). Figure 4 shows the intercept $Z_\varepsilon$ for constant source plumes and pulsing plumes obtained in our study, after applying the virtual origin correction method of Hunt and Kaye (2001). Note that $Z_\varepsilon < 0$ indicates virtual origins are shifted upstream. The data show 93.3% of the shifts of the virtual origin for pulsing plumes are within the range of those of constant source plumes, $-\,1.7\hbox {D}$ to 0.9D.

5.3 Amplitude and Strouhal number influence

We do not observe a significant change in the entrainment coefficient $\alpha$ by forcing plumes at $A = 33\%$ and $A = 50\%$ over St ranges from 0.080 to 1.0. To investigate if there is any specific amplitude and Strouhal number which causes a significant change in $\alpha$, a different experimental approach was used to test a larger range of source conditions. A constant source plume experiment was performed initially and Z was measured. The source flow was then forced sinusoidally with amplitude A and St while maintaining a constant drainage flow rate $Q_\mathrm{d}$. The variation of the distance $\varDelta Z$ was measured for the new, pulsing plumes, source conditions. The pulsing amplitude A was set at 40% and nine tests were performed with St increasing from 0.012 to 1.1. The amplitude A was then set at 50%, three tests were performed with $0.016<St<0.16$. Another series of tests was carried out by setting $St = 1.2$, $A = 50\%, 66\%$ and $80\%$. Our measurements show that over all the tests, the ratio $\varDelta Z/Z$ varies from $-\,1.5$ to 2.4 $\%$.

The change of entrainment coefficient $\alpha$ is obtained from Eq. 2, replacing $Z + Z_\mathrm{v}$ on the left side of Eq. 2 with $Z + Z_\mathrm{v} + \varDelta Z$. The change of $\alpha$ was found to vary from $-\,2.9$ to $2.6\%$, which is within the experimental error for $\alpha$. Over the entire range, no noticeable change of $\alpha$ is observed.

Crow and Champagne (1971) showed that the increase in entrainment observed in pulsing jets at $St = 0.30$ is a result of a reinforcement of the natural puffing frequency, which is determined by Reynolds number Re at the source. Bharadwaj and Das (2017) showed plumes also have a natural puffing frequency St using global stability analysis and experiments. The natural St has been shown to scale with the source Richardson number $Ri = (\rho _0 - \rho _\mathrm{a})gD/\rho _\mathrm{a}U_0^2$ as $St = 0.82Ri^{0.39}$. They found the stability of plumes is determined by the density ratio, Richardson number (which is proportional to source conditions $\varGamma$) and Reynolds number at the source. At low density ratio, such as for our Boussinesq plumes, puffing is confined to very lazy plumes where $\varGamma \sim 10^4$ with high $Re> 400$, where the effects of buoyancy are still dominant. All source conditions in our pulsing experiments are outside the neutral curve for Ri and Re obtained in their stability analysis for Boussinesq plumes. This suggests that the natural puffing frequencies are not contributing to behaviours observed in our results.

Forcing jets periodically has been shown to increase entrainment in the near-source region over $z/D<10$ (Crow and Champagne 1971; Solero and Coghe 2002). No increase was observed in the far field in these studies. In pulsing plumes, our measurements show no significant increase of entrainment even in the near-source region, as shown in Fig. 7. It is not clear why pulsing increases entrainment in jets but not plumes. One contributing factor may be that the flow stability of jets and lazy plumes is different as discussed above. The two flows also have different sensitivities to time-averaged source pulsing conditions. The time-averaged momentum flux $M_0$ is the only parameter that is increased at the source under pulsing conditions, while the time-averaged volume flux $Q_0$ and buoyancy flux $F_0$ remain the same. Plumes and jets are expected to respond to the change in average source conditions in different ways. Jets are driven by initial momentum provided by the source. Slightly increasing the time-averaged momentum flux $M_0$ has a direct effect on the velocity scale $M_0/Q_0$ near the source. Hence, increasing the momentum flux $M_0$ by forcing may have a more observable effect on jets, such as the increased entrainment rate reported. Plumes are driven by the source buoyancy, with the flow accelerating from the source. A change in the source momentum is expected to have less impact on plumes. The plumes in this study are lazy over $z/D<3$ where the momentum flux is less than a pure plume with the same buoyancy flux. Slightly increasing the time-averaged momentum flux $M_0$ is expected to have a minimal impact on the flow at the source, which may explain the observed insensitivity of entrainment to forcing in this flow.

The pluses formed in flows with time-varying source conditions, like the ones shown in Fig. 2b, will dissipate downstream as a result of the longitudinal (vertical) dispersion. Craske and van Reeuwijk (2015) found the sharp fronts formed by an instantaneous step change of the source buoyancy flux are smoothed by longitudinal mixing in their numerical study of jets, implying the effect of the longitudinal dispersion is non-negligible in flows with time-varying source conditions. We do not measure dispersion in pulsing plumes in this study, so are unable to quantify the difference between dispersion in jets and plumes. We note, however, from the dye visualisation that the pulses are clearly visible to $Z/D \sim 20$. Differences in longitudinal dispersion between jets and plumes are unlikely to explain the different sensitivities of entrainment near the source to pulsing. A comparison of dispersion between pulsing jets and plumes needs further investigation.

6 Conclusion

Turbulent axisymmetric lazy plumes and pulsing plumes with sinusoidal source conditions were investigated experimentally in a laboratory rig. As shown in Fig. 5, the relationship between $Z+Z_v$ and $Q_z^{3/5}F_0^{-1/5}$ for pulsing plumes with different source conditions is well represented by a linear fit, which suggests that the entrainment assumption and MTT model of Morton et al. (1956) are applicable for pulsing plumes forced at timescales close to the eddy turnover time at the source. The location of the virtual origin for constant source plumes and pulsing plumes is shifted between 1.9 source diameters upstream and 0.9 source diameter downstream (see Fig. 4), which implies our results for constant source plumes and time-averaged source conditions for pulsing plumes support the virtual origin correction method proposed by Hunt and Kaye (2001). The values of $\alpha$ for pulsing plumes range over 0.080–0.095, which is close to our experiment results of $0.081<\alpha <0.10$ for constant source plume and within the range of $0.071<\alpha <0.11$ reported (van Reeuwijk and Craske 2015). Forcing jets at $St = 0.20$ (Hirata et al. 2009) and $St=0.30$ (Crow and Champagne 1971) has been shown to increase entrained flow rates. Our experiments, however, show that forcing plumes at $St = 0.20$ does achieve the highest $\alpha$ for pulsing plumes, but still within the range of $\alpha$ reported for constant source plumes. We found that the entrainment coefficient $\alpha$ does not change substantially when forcing plumes from low frequency to a frequency of the order of the eddy turnover time, $D/U_0$, at the source.