Dissipation rate estimation in the turbulent boundary layer using high-speed planar particle image velocimetry

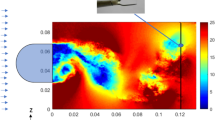
Abstract

The challenge of turbulent kinetic energy dissipation rate estimation, in general, is associated with errors embedded in measured velocity vectors and spatial resolution of appropriate optical method. Different optical methods together with different filtering procedures may yield completely different estimations. To evaluate the sources for such discrepancies, key parameters and factors which directly affect the accuracy of the dissipation rate estimation are briefly discussed. A joint effect of random error, velocity vector spacing, IW size and IW overlap on the dissipation rate estimation is theoretically and experimentally shown. In the present study, we demonstrate that high-speed planar particle image velocimetry (PIV) enables accurate estimation of the dissipation rate if high spatiotemporal resolution and appropriate local temporal filtering procedure are utilized. We consider a synthetic linear shear flow and a turbulent boundary layer flow using an assumption of locally axisymmetric turbulence when estimating the dissipation rate. The calculated dissipation rate profiles are compared with measurements by the state-of-the-art optical methods such as planar smoke image velocimetry (SIV), Stereo PIV, Tomo PIV, Tomo PTV–VIC+, and DNS results. The advantages of the implemented technique compared to others and the temporal filtering procedure are discussed.

Graphical abstract

1 Introduction

The challenge of the dissipation rate calculation by optical methods has been set by several authors (Sheng et al. 2000; Saarenrinne and Piirto 2000; Piirto et al. 2003; Tokgoz et al. 2012; Foucaut et al. 2016; Schneiders et al. 2017; Mikheev et al. 2017). The complete equation for the dissipation rate, ε, is

$$\varepsilon =\nu \overline {{\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}}+\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_j}}}{{\partial {x_i}}}}} ,$$

(1)

where ν is the kinematic viscosity of the fluid, u is the fluctuating component of the velocity vector, the subscripts i and j have values 1, 2, and 3 for the streamwise, x₁, wall-normal, x₂, and spanwise, x₃, directions, respectively. Below, we briefly discuss the key parameters and factors which directly affect the accuracy of the dissipation rate estimation.

1.1 The role of measurement error, velocity vector spacing, and IW overlap

Compared to the other terms of turbulent kinetic energy transport equation, for the dissipation rate, the derivatives have to be calculated for the instantaneous velocity field. Thus, the errors embedded in the velocity directly affect the accuracy of these derivatives. The measured instantaneous velocity component, $\tilde {u}$, can be expressed as the sum of three terms: true value of measured velocity component consisting, in turn, of its time-average, $\bar {u}$, and fluctuating component, u, associated with turbulence; bias measurement error; random measurement error, e. If multipass algorithms with discrete interrogation window (IW) offset are used, the bias error can be considered small enough (McKenna and McGillis 2002; Piirto et al. 2003; Kim and Sung 2006). Thus, the following can be written as:

$${\hat {u}_{i;k}}={u_{i,k}}+{e_{i;k}},$$

(2)

where $k=\overline {{1,K}}$ denotes a measurement time sample, ${\hat {u}_i}={\tilde {u}_i} - \bar {u}$. Following the discussions by Saarenrinne and Piirto (2000), for the first-order finite-difference scheme, the effect of the random error on the dissipation rate can be estimated by the following:

$$\overline {{{{\left( {\frac{{\partial {{\hat {u}}_i}}}{{\partial {x_j}}}} \right)}^2}}} =\frac{1}{K}\sum\limits_{{k=1}}^{K} {{{\left[ {\frac{{\Delta {u_{i;k}}}}{{\Delta {x_j}}}+\Delta {x_j}\Re +\frac{{\Delta {e_{i;k}}}}{{\Delta {x_j}}}} \right]}^2}} ,$$

(3)

where $\Re$ is the truncation error associated with the finite-difference scheme, ∆x_j is the velocity vector spacing, $\Delta {u_{i;k}}={u_k}(x+\Delta x) - {u_k}(x)$ and $\Delta {e_{i;k}}={e_k}(x+\Delta x) - {e_k}(x)$.

Expression (3) takes into account velocity vector spacing and random error. However, experience shows that the accuracy of the dissipation rate estimation also depends on IW size (Piirto et al. 2003; Shah et al. 2008; Tokgoz et al. 2012) and IW overlap (Piirto et al. 2003; Shah et al. 2008). Let us illustrate how these parameters are interrelated. Since the random error of any velocity component depends only on individual IW used for its calculation, the random errors incorporated in the velocities calculated from two non-overlapping neighboring IWs do not correlate with each other. However, if two neighboring IWs overlap, the corresponding errors may correlate which can be expressed in the following manner:

$$\frac{{\sum\nolimits_{{k=1}}^{K} {{e_k}(x+\Delta x) \cdot {e_k}(x)} }}{{K{\sigma _e}(x+\Delta x) \cdot {\sigma _e}(x)}}={F_e}(\overline {{\Delta x}} ),$$

(4)

where ${\sigma _e}(x+\Delta x)=\sqrt {\frac{1}{K}\sum\nolimits_{{k=1}}^{K} {{{[{e_k}(x+\Delta x)]}^2}} }$, ${\sigma _e}(x)=\sqrt {\frac{1}{K}\sum\nolimits_{{k=1}}^{K} {{{[{e_k}(x)]}^2}} }$, ${F_e}(\overline {{\Delta x}} )$ is some function depending on the $\overline {{\Delta x}} =\Delta x/l$ associated with IW overlap, l is the IW size. The shape of ${F_e}(\overline {{\Delta x}} )$ is not so evident and requires additional study; however, it is obviously equal to unity when neighboring IWs overlap entirely, i.e., $\overline {{\Delta x}} =0$, and tends to zero when the distance between neighboring IWs is more than IW size, i.e., $\overline {{\Delta x}}>1$. For convenience of further discussion, let us assume that the root-mean-square of the random error fluctuation is independent of location in space, i.e., ${\sigma _e}(x+\Delta x)={\sigma _e}(x)={\sigma _e}$. Taking this into account and substituting (4) into (3), the formula (3) can be expanded as:

$$\overline {{{{\left( {\frac{{\partial {{\hat {u}}_i}}}{{\partial {x_j}}}} \right)}^2}}} =\frac{1}{K}\sum\limits_{{k=1}}^{K} {{{\left[ {\frac{{\Delta {u_{i;k}}}}{{\Delta {x_j}}}+\Delta {x_j}\Re } \right]}^2}} +\frac{{2\sigma _{e}^{2}}}{{\Delta x_{j}^{2}}}\left[ {1 - {F_e}(\overline {{\Delta x}} )} \right].$$

(5)

Thus, there are three key variables which directly affect the accuracy of the measured dissipation rate, which are random error, velocity vector spacing, and IW overlap. The first term in the sum on the right side of (5) tends to a constant value and the second term diminishes when the velocity vector spacing is reduced. The behavior of the last term in (5) is not so evident when the velocity vector spacing tends to zero due to unknown shape of ${F_e}\left( {\overline {{\Delta x}} } \right)$ in the vicinity of $\overline {{\Delta x}} =0$. Both terms on the right side of (5) can have the same order of magnitude depending on the flow type and measurement technique. Moreover, the last term may be many times greater than the first term resulting in significant overestimation of the dissipation rate compared to its true value. The effect of the last term in (5) on the dissipation rate estimation can be mitigated by decreasing ${\sigma _e}$ associated with the random error. That is why, the application of an efficient filtering procedure can play a crucial role in accurate estimation of the dissipation rate.

1.2 The role of spatial resolution

One should differentiate spatial resolution associated with relative IW size, $l/{\lambda _{\text{K}}}$, from spatial resolution associated with relative velocity vector spacing, $\Delta x/{\lambda _{\text{K}}}$, where ${\lambda _{\text{K}}}={({\nu ^3}/\varepsilon )^{0.25}}$ is the Kolmogorov length scale. Both are important to resolve the smallest spatial scales in turbulence and to accurately capture the velocity gradients. In theory, in order to resolve the smallest spatial scales in turbulence, both of them should not exceed the Kolmogorov length, i.e., $l/{\lambda _{\text{K}}}<1$ and $\Delta x/{\lambda _{\text{K}}}<1$ (Sharp and Adrian 2001; Tokgoz et al. 2012). In practice, reliable results can be obtained fulfilling the criteria $1.5 < \Delta x/\lambda _{{\underline{{\text{K}}} }} < 2$ (Tokgoz et al. 2012) and $1.5 < \Delta x/\lambda _{{\underline{{\text{K}}} }} < 3$ (Saarenrinne and Piirto 2000). For different image sizes, Saarenrinne and Piirto (2000) have shown rapid nonlinear increase of the dissipation rate when $\Delta x/{\lambda _{\text{K}}}<10$. They could not find the explanation for such behavior and they have just associated it with both high number of spurious vectors and absolute errors embedded in measured velocity vectors. Since optimal value of the velocity vector spacing is not obvious, Saarenrinne and Piirto (2000) have recommended to keep the balance between the velocity vector spacing and the absolute error. However, in fact, this recommendation is simply fitting the obtained data to a reference one. According to the results of previous subsection, the increase of the estimated dissipation rate is associated with both the reduction of velocity vector spacing and increase of random error. Theoretically, the velocity vector spacing should be as large as possible to diminish the effect of the last term in (5); however, in real-world experiments, the velocity vector spacing should be of the order of the Kolmogorov length scale (Sharp and Adrian 2001; Tokgoz et al. 2012) to resolve the smallest scales in turbulence. Thus, one should use the velocity vector spacing as large as Kolmogorov length scale. Reducing the velocity vector spacing down to $\Delta x/{\lambda _{\text{K}}} \approx 1$, Tokgoz et al. (2012) have estimated the dissipation rate quite accurately compared to torque measurements, showing that the dissipation rate may be slightly underestimated as well as overestimated. This positive result is likely due to the spatial filtering procedure applied to velocity fields. Nevertheless, the effect of the filtering procedure on the estimates has not been properly analyzed and requires additional study.

1.3 The role of measurement technique and the aspects of their implementation

To directly calculate all the derivatives included in (1), one needs to know all three velocity components in space which can be calculated by volumetric PIV/PTV (Tokgoz et al. 2012; Schneiders et al. 2017). However, volumetric measurements are often limited by spatial resolution because of low seeding density required to achieve a high quality in the tomography reconstruction (Elsinga et al. 2006). To achieve higher spatial resolution, one can use higher seeding density that is the case for planar (Saarenrinne and Piirto 2000; Shah et al. 2008) or Stereo (Piirto et al. 2003) PIV. However, not all velocity components and their spatial derivatives are known in this case, and, thus, one needs to use some turbulence hypothesis (Sheng et al. 2000; Saarenrinne and Piirto 2000; Shah et al. 2008; Djenidi and Antonia 2012; Foucaut et al. 2016; Mikheev et al. 2017). Furthermore, the use of the turbulence model should be justified in one or another flow case.

It has been concluded by Tokgoz et al. (2012) that Tomo PIV has a similar order of error as for corrected planar PIV estimations; however, the role of measurement error in their estimates has not been analyzed. It should be noted that they have applied spatial filter to their velocity fields which may have played a decisive role. Similarly, in the recent study by Schneiders et al. (2017), a spatiotemporal filtering procedure based on second-order polynomial regression over time and space has been applied to reach more or less satisfactory results in turbulent boundary layer (TBL) when using Tomo PIV. Despite the complicated filtering procedure used by Schneiders et al. (2017), the dissipation rate has been still underestimated twice along the entire considered range of y⁺. The application of PTV–VIC+ has allowed Schneiders et al. (2017) to improve their results in the outer region of TBL; however, the dissipation rate has been still underestimated by 20% in the near-wall region.

Considering planar flow visualization by smoke, Mikheev et al. (2017) have proposed to use the sum of absolute difference function instead of cross correlation in order to improve the spatial resolution. On the example of TBL flow, they have shown that the dissipation rate can be estimated using fairly small IW size of 16 × 10 pix. Compared to others, Mikheev et al. (2017) have used local temporal filtering procedure with constant value of cut-off frequency that has been possible because of high-speed imaging. Thus, the question arises, does this positive outcome result from different image matching techniques or appropriate filtering procedure? Despite the fact that Mikheev et al. (2017) have been able to properly estimate the dissipation rate in outer region of TBL, it still suffered from the measurement error in the near-wall region (y⁺ < 20) yielding overestimated dissipation rate.

To directly determine the dissipation rate from the spectra of longitudinal velocity component, Djenidi and Antonia (2012) have introduced a spectral chart method, which relies on the validity of the first similarity hypothesis of Kolmogorov. Similar idea has been presented by Lavoie et al. (2007) when considering the errors due to poor spatial resolution. The key idea of both techniques is to estimate the required dissipation rate fitting experimental spectrum to a reference one. As the reference spectrum, one can use a spectrum obtained from DNS if it is available or analytical expressions such as those of Pope (2000). In the latter case, the final result depends on constants included in the model. Djenidi and Antonia (2012) used the constants that differed by several times from those presented by Pope (2000) demonstrating, in turn, that a model should also be tested beforehand. Nevertheless, we show the performance of this method for TBL flow case in the last section. If the Kolmogorov microscale cannot be resolved in certain experiment, which is the case for, e.g., higher Reynolds numbers or poor optical system, it is proposed to apply above correction methods or consider a large eddy PIV by Sheng et al. (2000). By the way, the filtering procedure introduced in the present research can be applied together with these methods prior to the dissipation rate estimation as recommended by Hearst et al. (2012) when dealing with high-speed PIV.

1.4 The problem statement

Thus, many authors (Foucaut et al. 2016; Schneiders et al. 2017; Mikheev et al. 2017) have faced the problem of either underestimated or overestimated dissipation rate in the near-wall region of TBL. All of them have associated these contradictory results with insufficient spatial resolution and the measurement error. Many of those possible sources such as IW size (Piirto et al. 2003; Shah et al. 2008; Tokgoz et al. 2012), IW overlap (Piirto et al. 2003; Shah et al. 2008), velocity vector spacing (Saarenrinne and Piirto 2000; Tokgoz et al. 2012), finite-difference scheme used for velocity gradient computation (Fouras and Soria 1998; Foucaut and Stanislas 2002; Hearst et al. 2012; Mikheev et al. 2017), image-processing method, and finally, experimental parameters (particle image density and diameter, image noise, etc.) have been discussed and appropriate recommendations have been proposed to minimize the effect of the measurement error.

Summarizing the above, there are two fundamental problems in accurate estimation of the dissipation rate that are spatial resolution and measurement error. As discussed above, planar measurement techniques are more preferable compared to volumetric ones in terms of spatial resolution. However, the problem of turbulence model arises in this case. Fortunately, some turbulence models yield fairly good results in some particular flow cases, e.g., isotropic turbulence for grid flow (Djenidi and Antonia 2012) and locally axisymmetric turbulence for TBL flow (Foucaut et al. 2016). Thus, if high spatial resolution is achieved and turbulence model is chosen correctly, the only problem is the measurement error suppression. In the present research, we show the possibility to use high-speed planar PIV technique for accurate estimation of the dissipation rate in TBL. Since, in practice, the level of measurement error varies in space, we propose to use local temporal filtering procedure which automatically takes into account both the measurement error and turbulent fluctuation level for each individual velocity component.

To directly compare our experimental results with the literature, we use the same data that have been previously used by Mikheev et al. (2017). Unlike traditional PIV, they consider the frames which show the fields of continuous image intensity instead of separate particle images. Owing to better reflectivity of smoke, they obtain higher spatial resolution in the case of light sheet generated by a relatively low-power continuous laser at high frame rate.

2 Local temporal filtering procedure

Let us briefly introduce the filtering procedure implemented in the present research. Raising the expression (2) to the square and then integrating it over the measured period T, it can be written as

$$\int\limits_{0}^{T} {{{[\hat {u}(t)]}^2}{\text{d}}t} =\int\limits_{0}^{T} {{{[u(t)]}^2}{\text{d}}t} +\int\limits_{0}^{T} {{{[e(t)]}^2}{\text{d}}t} +2\int\limits_{0}^{T} {u(t)e(t){\text{d}}t} .$$

(6)

According to Foucaut et al. (2004) and Hearst et al. (2012), the velocity signal in time is affected by “white” noise associated with the random error. Thus, if the measured period is long enough to ensure the statistical independence, the last term in (6) is equal to zero. Then, taking into account Parseval’s theorem, the formula (6) can be expressed as

$$\int\limits_{{ - \infty }}^{\infty } {|\hat {U}(f){|^2}{\text{d}}f} =\int\limits_{{ - \infty }}^{\infty } {|U(f){|^2}{\text{d}}f} +\int\limits_{{ - \infty }}^{\infty } {|E(f){|^2}{\text{d}}f} ,$$

(7)

where $\hat {U}(f) = {\mathcal {F}} [\hat {u}(t)]$, $U(f) = {\mathcal {F}}[u(t)]$ and $E(f)={\mathcal {F}}[e(t)]$ represent continuous Fourier transform of $\hat {u}(t)$, u (t) and e (t), respectively, and f is the frequency. Since “white” noise is characterized by the same amplitude of fluctuations for all considered harmonics, the integrant in the last term in (7) is constant and takes the value of |E|². Thus, for any harmonic, the following can be written as

$$\frac{{|\hat {U}(f){|^2}}}{{{{\left| E \right|}^2}}}=\frac{{|U(f){|^2}}}{{{{\left| E \right|}^2}}}+1.$$

(8)

To partially eliminate the random error, let us define a cut-off frequency, f_cut, wherein the measurement noise energy, ${\left| E \right|^2}$, begins dominating over fluid energy, ${\left| {U(f)} \right|^2}$ (see Fig. 1, where schematic diagrams of energy spectra are shown). In other words, the cut-off frequency is defined by ${\left| {U({f_{{\text{cut}}}})} \right|^2}={\left| E \right|^2}$ or, taking into account the formula (8), by

$$\,\frac{{|\hat {U}({f_{{\text{cut}}}}){|^2}}}{{|E{|^2}}}=2,$$

(9)

which can be used to define the cut-off frequency, f_cut, in real experiments.

Fig. 1

Schematic diagram of energy spectra

3 Synthetic test case

3.1 Synthetic images generation

To show the role of spatial resolution and measurement error in the dissipation rate estimation as well as the performance of the proposed filtering procedure, let us consider a synthetic test case of one-dimensional linear shear flow schematically illustrated in Fig. 2. In this case, 2049 consecutive images with the sizes of 192 × 272 pix are generated. Such an image size allows the use of 5 × 5 non-overlapping IWs with sizes up to 32 × 32 pix arranged, as shown in Fig. 2. The total number of IWs placed in each image is 17 × 17 with 75% overlap. The total number of statistically analyzed displacement vectors is 2048 calculated from 2049 consecutive images which contain only one vector placed in the middle windows, as shown in Fig. 2, by dark IWs, even though 17 × 17 × 2048 displacement vectors are calculated.

Fig. 2

One-dimensional linear shear flow (top) schematically depicted by blue vectors and sample of synthetic images (bottom). White squares denote 17 × 17 × 2049 IWs used for displacement vectors calculation (here, we show only non-overlapped IWs). Dark squares denote 1 × 2049 IWs used for statistical analysis of displacement vectors. Set of 3 × 3 IWs with vectors at their centres denote the stencil of local median filter (Westerweel and Scarano 2005): red vector placed in the dark square represents possible erroneous vector

Synthetic images are generated using conventional approach to PIV image generation (Raffel et al. 2007; Scharnowski and Kähler 2016). Particle images with diameters d_p = 2 pix are uniformly distributed over the whole image area with average concentrations C = 0.076 particles/pix², and coordinates of their center points are defined in a random way. To obtain the explicit dependence of the dissipation rate on the flow conditions, noise is not added to the images. When simulating shear flow, to provide statistically independent data “in time”, the particle images are displaced superposing uniform and linear gradient shifts, ${v_0}+(x - {x_0}){\text{d}}{v_0}/{\text{d}}x$, where x₀ is the coordinate of images’ centerline, v₀ = 32 pix as the maximum IW size considered in the present test case. For the sake of simplicity, we present the results of two flow cases, where dv₀/dx = 0.01 and 0.3 pix/pix correspond to low-gradient and high-gradient shear flows, respectively. In both cases, mean displacement is equal to IW size for statistically analyzed vectors placed in the middle, as shown in Fig. 2 (top picture).

3.2 Description of evaluation technique

The challenges of this test case are the high value of velocity gradient and high level of the out-of-plane motion. To take into account the first one, we apply an iterative window-deformation method (WIDIM) proposed by Scarano and Riethmuller (2000) as one of the state-of-the-art methods that produces less noise when considering high-gradient flow (Westerweel et al. 2013). A common feature of this iterative approach is that the velocity field is initially unknown and supposed to be equal to zero (Discetti and Astarita 2012). As a consequence, the first iteration involves the use of equal and not deformed IWs that are equally located in two consecutive images (Huang et al. 1993a). Moreover, this approach imposes constraints on IW size when considering gradient flow: typical IW size is 32 × 32 pix. The further increase of IW size leads to large random errors in determining particle images displacements, even though a low-gradient shear flow is considered (Raffel et al. 2007). To improve the spatial resolution and accuracy of the velocity vectors, the interrogation windows matching is conducted in spatial domain over a region of interest (ROI). This method is called the digital image correlation (DIC) method (Huang et al. 1993b), direct correlation PIV (DCPIV) method (Nogueira et al. 2001) or correlation imaging velocimetry (CIV) method (Nogueira et al. 2001). The abbreviation DIC will be used in this study for the reference. The idea of DIC is that IW fixed in the first image is matched with IW sliding over ROI of the second image. Thus, in contrast to WIDIM, DIC theoretically has no limitation for maximum measurable velocity (Huang et al. 1993b).

To achieve steady-state solution, ten iterations are executed: DIC at the first iteration and WIDIM at the rest ones. At the first iteration, IW_k (placed in the image k) centered at ($\xi ,\eta$) is matched with IW_k + 1 (placed in the subsequent image k + 1) displaced in the range of ξ − 6 to ξ + 6 in x-direction and η to η + 64 in y-direction. Such an ROI size covers the whole range of measured displacements. When applying WIDIM, the first-order window-deformation approach is used. A symmetric shift of both interrogation windows with respect to corresponding grid node is applied to obtain the displacement vector (Wereley and Meinhart 2001). The cardinal sine (sinc) function with kernel size of 6 × 6 pix is chosen to interpolate the images according to recommendation given by Kim and Sung (2006). The obtained displacements are defined with sub-pixel accuracy using three point parabolic peak fit. When cross-correlating, FFT-based normalized cross correlation is applied which is computed with the help of open-source FFTW library (Frigo and Johnson 2005).

In the present study, spurious displacement vectors are detected using a local median test proposed by Westerweel and Scarano (2005) and replaced by the local average of the (accepted) neighbor vectors (Westerweel et al. 1996). No additional filtering procedure has been applied, except for the specific case in which the effect of temporal filtering on the dissipation rate estimation is discussed. In these specific cases, the temporal filter is applied after each iteration; however, the dissipation rate is calculated before it.

In two-dimensional approximation, the dissipation rate (1) consists of the sum of five terms containing $\overline {{{{\left( {{{\partial \hat {u}} \mathord{\left/ {\vphantom {{\partial \hat {u}} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)}^2}}}$, $\overline {{{{\left( {{{\partial \hat {v}} \mathord{\left/ {\vphantom {{\partial \hat {v}} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)}^2}}}$, $\overline {{{{\left( {{{\partial \hat {u}} \mathord{\left/ {\vphantom {{\partial \hat {u}} {\partial y}}} \right. \kern-0pt} {\partial y}}} \right)}^2}}}$, $\overline {{{{\left( {{{\partial \hat {v}} \mathord{\left/ {\vphantom {{\partial \hat {v}} {\partial y}}} \right. \kern-0pt} {\partial y}}} \right)}^2}}}$, and $\overline {{\left( {{{\partial \hat {u}} \mathord{\left/ {\vphantom {{\partial \hat {u}} {\partial y}}} \right. \kern-0pt} {\partial y}}} \right)\left( {{{\partial \hat {v}} \mathord{\left/ {\vphantom {{\partial \hat {v}} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)}}$. To quantitatively analyze the effect of measurement error, velocity vector spacing and IW overlap on the dissipation rate estimation, let us consider the term $\overline {{{{\left( {{{\partial \hat {v}} \mathord{\left/ {\vphantom {{\partial \hat {v}} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)}^2}}}$. The other terms can be estimated similarly. Since we simulate pure one-dimensional linear shear flow without any fluctuations, the true value of this term is equal to zero, i.e., $\overline {{{{\left( {{{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)}^2}}} =0$. Accordingly, the first two terms on the right side of (5) are equal to zero, so that the following can be written as

$$\overline {{{{\left( {\frac{{\partial \hat {v}}}{{\partial x}}} \right)}^2}}} =\frac{{2\sigma _{e}^{2}}}{{\Delta {x^2}}}[1 - {F_e}(\overline {{\Delta x}} )],$$

(10)

where $\hat {v}$, x, and ${\sigma _e}$ are in pix, and ${\sigma _e}$ and ${F_e}(\overline {{\Delta x}} )$ are associated with vertical velocity component, $\hat {v}$. In the next subsection, we will refer to the left and right terms in (10) as the measured, ${\hat {\varepsilon }_{vv}}$, and estimated, ${\varepsilon _{vv}}$, values of the dissipation rate, respectively.

One special aspect should be noted regarding temporal filtering procedure applied in the synthetic test case. Since we consider the ideal linear shear flow without any additional superimposed oscillations, the true values of measured velocities of statistically analyzed vectors are equal to v₀ = 32 pix, so that the measured fluctuating velocity components consist only of random error. This results in spectra of velocity fluctuations which are very close to the spectrum of “white” noise, as it is shown below. In this case, the application of the proposed filtering procedure cuts all the harmonics leaving only mean value of the velocity components and, consequently, resulting in a zero dissipation rate. From this point of view, the proposed filtering procedure is an ideal one among others which, in one way or another, filter only a certain frequency range. For this reason, in the next subsection, to show the performance of the proposed filtering procedure, we present the estimates obtained before applying the temporal filter, even though it is applied after each iteration.

3.3 Results of synthetic test case

Figure 3 illustrates the dependence of the dissipation rate on the flow condition (velocity gradient), processing parameters (IW size, IW overlap, and number of iterations), and filtering procedure. The first thing that should be noted is a very good agreement between measured and estimated dissipation rates for all the considered cases. This shows the validity of the assumptions made in Sect. 1.1. In particular, all the lines and symbols for certain IW size and velocity gradient are equidistant showing the inverse proportional dependence of the dissipation rate on the squared velocity vector spacing: the larger the velocity vector spacing is, the better the dissipation rate estimation is. However, in real-world experiments, the velocity vector spacing should exceed the Kolmogorov length scale; otherwise, the dissipation rate may be underestimated for larger velocity vector spacing. Thus, the optimal value of the velocity vector spacing is equal to Kolmogorov length scale.

Fig. 3

Measured (lines) and estimated (symbols) dissipation rates calculated according to formula (10) for synthetic test case

Unlike the velocity vector spacing, the role of IW size in accurate estimation of the dissipation rate is associated with the random error produced by different IW sizes. Figure 3 illustrates that the larger the IW size is, the better the dissipation rate estimation is when we reach steady-state solution after iterative process. However, IW size has the same restriction on its maximum size as the velocity vector spacing does: it should be of the order of the Kolmogorov length scale as well.

As it is seen from Fig. 3, the dissipation rate has a strong dependence on the velocity gradient: higher velocity gradient leads to higher values of random error, as it is well-known from the literature (Raffel et al. 2007; Scarano and Riethmuller 2000) as well. In fairness, it must be noted that the effect of the velocity gradient can be significantly softened thanks to iterative process which is generally intended to reduce the measurement error. On the other hand, the local temporal filter allows one to greatly reduce the effect of the random error as well, resulting in good dissipation rate estimation even at the early iterations. It is essential to remind that the dissipation rates illustrated in Fig. 3 by dashed lines and open symbols are calculated before filtering the corresponding oscillograms: if we calculated the dissipation rate after filtering procedure, both the measured and estimated dissipation rates were equal to zero which, incidentally, exactly corresponds to their theoretical values.

To show the random error level for different processing and flow parameters, in Fig. 4, we illustrate the power spectra of velocity fluctuations for the first and the last iterations. For the sake of simplicity, we do not present the spectra for other iterations and only mention that all of them gradually decrease down to their steady-state conditions. From Fig. 4, one can make sure that the spectra are very close to the “white” noise spectrum and that the level of random error decreases when increasing IW size. One can also see the positive effect of iterative and filtering procedures in terms of random error reduction.

Fig. 4

Power spectra of y-components of velocity fluctuations for synthetic test case. n is the number of harmonic

Summarizing the above, we have demonstrated the role of velocity vector spacing and random error in accurate estimation of the dissipation rate on the example of the synthetic test case. To accurately estimate the dissipation rate, both the velocity vector spacing and IW size should be as large as Kolmogorov length scale. The proposed temporal filtering procedure allows one to drastically reduce the effect of the random error yielding accurate estimation of the dissipation rate at the initial iterations.

4 Dissipation rate estimation in TBL

4.1 Experimental facility

Some details of the TBL flow measurements can be found in (Mikheev et al. 2017). Schematic diagram of experimental facility is given in Fig. 5. Measurement area is 800 mm downstream of contraction inlet in the vertical symmetry plane of the rectangular 150 × 75 mm² test section made of transparent polycarbonate. To provide uniform smoke seeding, the test section inlet is mounted in a smoke-conditioning chamber (0.6 × 0.6 × 2.4 m³). This chamber together with a screen mounted at its inlet and a contraction inlet (Bernoulli lemniscate shaped) of the test section provides the required flow conditioning. Uniformity of the oncoming flow velocity profile and proper turbulent flow parameters in the test section boundary layer are provided by a turbulence grid made of metal rods with the diameter of 1.4 mm and grid spacing of 6 mm mounted at the test section inlet.

Fig. 5

Schematic diagram of experimental facility

Videos are taken by a high-speed camera Fastec HiSpec with the frame rate of 7083 fps, resolution of 654 × 110 pix, and video duration of 3.53 s (spatial resolution of CCD image sensor is 14 × 14 µm²/pix²). Exposure time of the camera is 37 µm. The camera is equipped with Nikon Micro-Nikkor 60 mm/f 2.8 lens. Magnification is 16.8 pix/mm. Images are captured in 8-bit format. Prior to the experiment, the smoke-conditioning chamber is filled with smoke containing glycerin particles with the diameter of about 1 µm. Safex F2010 Plus smoke generator is used for this purpose. The light sheet is generated by a DPSS laser KLM-532\h-5000 with adjusted power of 1–5 W. A diverging lens with a ray angle of 12° is mounted at the laser output. Figure 6 shows a typical image obtained by visualization.

Fig. 6

Typical image obtained by visualization

Experiments are conducted at the Reynolds number Re_δ = 4230 based on the boundary layer thickness δ₉₉ = 15.88 mm (204 pix). This corresponds to the air-flow velocity at the channel axis U_c = 4.06 m/s. It should be noted that at the specified mean flow velocity, the smoke-conditioning chamber is discharged in 19 s, which means that the smoke concentration is constant throughout the experiment lasting 3.53 s. Experiment parameters are summarized in Table 1.

Table 1 Experiment parameters

Measurements are performed in a 2.5 W laser light sheet with the width of about 25 mm and thickness of 1 mm. Thus, the fluence is 0.1 W/mm², which is 33 times less than the one in the paper by Willert (2015), for example, who used continuous laser as well. It should be noted that such low fluence results from smoke with reflectivity better than tracer particles’ one. Along with the reduction of the laser power, application of smoke allows reduction of the camera’s exposure time, hence reducing the image blurring.

4.2 Experimental technique and description of the dissipation rate estimation

The same processing technique and filtering procedure as used in synthetic test case are applied in the current section, but with the following settings. To achieve steady-state solution, five iterations are executed: DIC at the first iteration and WIDIM at the rest ones. At the first iteration, IW_k (placed in the image k) centered at (ξ, η) is matched with IW_k+1 (placed in the subsequent image k + 1) displaced in the range of ξ − 3.5 to ξ + 14.5 in x-direction and η − 3.5 to η + 3.5 in y-direction. Since the expected maximum values of particle image displacement in x- and y-directions are approximately 10 and 2 pix, respectively, such an ROI size covers the whole range of measured displacements.

To achieve high spatial resolution, the images are processed using elongated constant IW sizes l_x × l_y = 8 × 8, 16 × 8, and 32 × 8 pix. Following previous studies, it is useful to estimate the ratio of IW size to both wall units, ν/u_τ, and Kolmogorov length scale, λ_K, which, in general, varies in space. In the present study, IW height of 8 pix corresponds to l⁺_y = 6.12, and l_y/λ_K = 3.66 in the near-wall region (y⁺ = 15) and l_y/λ_K = 2.38 at the outer edge of the boundary layer (y⁺ = 100), where y⁺ = yu_τ/ν, u_τ = 0.194 m/s is the dynamic velocity estimated from mean streamwise velocity within the viscous sublayer, ${u_\tau}={\left[ {\nu {{\left( {\partial u/\partial y} \right)}_{y=0}}} \right]^{0.{\text{5}}}}$. As noted above, in theory, in order to resolve the smallest spatial scales in turbulence, IW size should not exceed the Kolmogorov length, i.e., l/λ_K < 1. However, this is the case only for not distorted IWs. If IWs are deformed according to flow motion, this criterion can be softened by increasing the spatial resolution at the same time (see PIV Challenges 2001, 2003, 2005; http://www.pivchallenge.org). Thus, notwithstanding the average value of l/λ_K is about three times higher in the wall-normal direction, the first-order window-deformation algorithm used in the present study is supposed to be enough to resolve the smallest structures in TBL.

Since planar PIV allows us to measure only two out of three components of velocity vector, the dissipation rate is estimated using the locally axisymmetric turbulence hypothesis (George and Hussein 1991):

$$\varepsilon =\nu \left[ { - \overline {{{{\left( {\frac{{\partial {u_1}}}{{\partial {x_1}}}} \right)}^2}}} +2\overline {{{{\left( {\frac{{\partial {u_1}}}{{\partial {x_2}}}} \right)}^2}}} +2\overline {{{{\left( {\frac{{\partial {u_2}}}{{\partial {x_1}}}} \right)}^2}}} +8\overline {{{{\left( {\frac{{\partial {u_2}}}{{\partial {x_2}}}} \right)}^2}}} } \right].$$

(11)

According to comparative analysis made by Foucaut et al. (2016), this hypothesis seems to be the most robust compared to homogeneous or isotropic ones when considering the TBL flow.

The derivatives included in (11) are computed numerically using central difference scheme as the best choice among other schemes (Fouras and Soria 1998; Foucaut and Stanislas 2002; Hearst et al. 2012; Mikheev et al. 2017). The velocity vectors are defined on a regular mesh grid with node-to-node spacing ∆x_1,2 = 2 × 2 pix which corresponds to 75% overlap in y-direction. It allows us to use different velocity vector spacing 2∆x_1,2 = 4, 8, and 16 pix when calculating the gradients in (11). To capture the velocity gradients accurately, the spatial resolution (velocity vector spacing) should not exceed the Kolmogorov microscale, i.e. 2∆x_1,2/λ_K < 1 (Sharp and Adrian 2001; Tokgoz et al. 2012). In the present study, the finest achievable spatial resolution is 2∆x_1,2/λ_K = 1.83 in the near-wall region (y⁺ = 15) and 2∆x_1,2/λ_K = 1.19 at the outer edge of the boundary layer (y⁺ = 100), which is in accord with recommendations by Tokgoz et al. (2012) and Saarenrinne and Piirto (2000) who obtained reliable results fulfilling the criteria 1.5 < 2∆x/λ_K < 2 and 1.5 < 2∆x/λ_K < 3, respectively.

4.3 Results and discussion

Figures 7 and 8 show distributions of mean streamwise velocity U⁺ and turbulent fluctuations ‹u₁′u₁′›⁺, ‹u₂′u₂′›⁺ and ‹u₁′u₂′›⁺ along y⁺, respectively, obtained by different IW sizes of 8 × 8, 16 × 8 and 32 × 8 pix. Comparison with corresponding profiles obtained numerically by DNS (Schlatter et al. 2009; Re_θ = 590; Re_τ = 255) and experimentally by PIV (Willert 2015; Re_θ = 518; Re_τ = 241; IW = 64 × 6) and SIV (Mikheev et al. 2017; Re_θ = 425; Re_τ = 214; IW = 16 × 10) is conducted. These results are chosen for comparison, because they are obtained for Reynolds numbers close to our case. Solid black lines in Fig. 7 describe theoretical profiles U⁺ = y⁺ and U⁺ = 5.5 + 5.75 lgy⁺ corresponding to viscous sublayer and boundary layer, respectively. Figures 7 and 8 demonstrate the difference in mean streamwise velocity and turbulent pulsations, respectively, along y⁺ for different IW sizes: IW size of 8 × 8 pix yields higher values compared with 16 × 8 and 32 × 8 pix. This deviation is associated with different dynamic velocities u_τ = 0.188, 0.194, and 0.194 m/s calculated by IW sizes of 8 × 8, 16 × 8, and 32 × 8 pix, respectively. Small IW size overestimates mean streamwise velocity in the wall region resulting in lower value of dynamic velocity. It is noteworthy that if the same value of dynamic velocity (u_τ = 0.194) is used for all cases, all the profiles completely coincide with each other at all y⁺ except the near-wall region. Larger inclination of mean velocity profiles in the logarithmic region is attributed to a small favorable pressure gradient dp/dx ≈ − 2 Pa/m. This gradient corresponds to acceleration parameter $K~=~ - (\nu /\rho u_{\infty }^{3})({\text{d}}p/{\text{d}}x)$ ≈ 0.38 × 10⁻⁶, which, according to Finnicum and Hanratty (1988), is fairly small to cause relaminarization of the boundary layer. In general, the mean streamwise velocities and turbulent fluctuations have the same pattern and agree well with the literature (see Figs. 7, 8), indicating that the flow is completely turbulent.

Fig. 7

Wall-normal profiles of mean streamwise velocity

Fig. 8

Wall-normal profiles of turbulent fluctuations of velocity

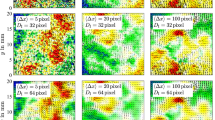
As mentioned above, the dissipation rate estimates mainly depend on velocity vector spacing, random error, and IW overlap. Figure 9 demonstrates that the less velocity vector spacing is, the higher the dissipation rate is. This behavior is in accord with the results of the synthetic test case and the literature (Saarenrinne and Piirto 2000; Tokgoz et al. 2012). However, as expected, the decrease of the velocity vector spacing down to 4 pix (which is of the order of Kolmogorov length scale) does not lead the dissipation rate to its true value, but significantly overestimates the latter compared to the DNS results calculated at Re_θ = 2000 by Schlatter and Orlu (2010). As can be seen from Fig. 9, this overestimation is the greater, the smaller IW size is, which agrees with the observations by Piirto et al. (2003), Shah et al. (2008), and Tokgoz et al. (2012). Obviously, this is because small IW size produces higher random error than larger ones as concluded above when considering synthetic test case. It can be observed in Fig. 10, where power spectra of the velocity fluctuations computed from window of 25,000 samples using a Hunning window function are plotted. It is seen from a high-frequency region of spectra that the smaller IW size is, the higher the noise level is. The spectra in Fig. 10 are normalized by Kolmogorov scales and compared to well-known power-law spectrum with exponent − 5/3 as well as the ones obtained experimentally by Willert (2015) for similar flow conditions and measurement parameters (Re_θ = 518; Re_τ = 241; IW = 64 × 6) at the same y⁺. Willert (2015), in turn, validated his results using DNS data by Wu and Moin (2009). Rapid decrease of spectra by Willert (2015) in the dissipation region is attributed to the application of Gaussian filtering procedure to PIV data in time.

Fig. 9

Wall-normal profiles of turbulent kinetic energy dissipation rate for different IW sizes and velocity vector spacings

Fig. 10

Normalized power spectra of streamwise (a) and wall-normal (b) components of velocity fluctuations

Due to turbulent kinetic energy dissipation, the power spectra must tend to zero when frequency tends to infinity. However, Fig. 10 shows nearly constant value at the high-frequency region that is associated with the “white” noise (Foucaut et al. 2004; Hearst et al. 2012; Oxlade et al. 2012). To partially eliminate the effect of “white” noise on the final results, Mikheev et al. (2017) have applied high-frequency filtering. They have defined a cut-off frequency from the spectrum of streamwise velocity component: it is equal to the frequency, where the amplitude of velocity fluctuations has approximately constant value in the high-frequency spectrum region. Note that, in order to define the cut-off frequency, they have used the formula ${\left| {\hat {U}({f_{{\text{cut}}}})} \right|^2}/{\left| E \right|^2}=1$ compared to (9), so that the noise energy might still dominate over the fluid energy in the high-frequency region, where energy dissipation occurs. Moreover, the cut-off frequency has been constant for both velocity components at any measurement place in space. Although, in general, the cut-off frequency should be defined according to the associated noise level for each individual velocity component. This is illustrated in Fig. 11, where the cut-off frequency distribution calculated using the formula (9) is shown. Similar to turbulent fluctuation profiles shown in Fig. 8, the cut-off frequency, first, grows with wall-normal distance and, then, decreases for both velocity components. Thus, the cut-off frequency depends on both the measurement noise magnitude, i.e., the random error, and turbulent fluctuation level: the lower the measurement noise and the higher the turbulent fluctuations are, the higher the cut-off frequency is.

Fig. 11

Cut-off frequency distribution for different IW sizes and velocity components. Dashed vertical lines indicate the sections, where the dissipation rate has been calculated

The dissipation rate calculated after appropriate temporal filtering procedure is demonstrated in Fig. 12. The same tendency of the dissipation rate reduction with velocity vector spacing growth is observed as in the synthetic test case and the literature (Saarenrinne and Piirto 2000; Tokgoz et al. 2012). However, the dissipation rate calculated using IW of sizes of 8 × 8 and 16 × 8 pix and velocity vector spacing of 4 pix still suffers from the measurement error. This is explained by the random error, which is still present in the high-frequency region below f_cut (see Fig. 10), as well as different dynamic velocity values for IW size of 8 × 8 pix. Since the use of IW size of 32 × 8 pix produces less noise (see Fig. 10), it yields better estimation of the dissipation rate coinciding with the curve by DNS (Schlatter and Orlu 2010) without additional correction procedures (Lavoie et al. 2007; Tanaka and Eaton 2007; Djenidi and Antonia 2012).

Fig. 12

Wall-normal profiles of turbulent kinetic energy dissipation rate after the temporal filtering procedure

Similar to the discussion on spatial resolution (IW size and velocity vector spacing), one should follow the same rule when using the temporal information. Thus, the maximum period, T_cut, associated with f_cut should not exceed the Kolmogorov time scale, τ_K = (ν/ε)^0.5, i.e., one should fulfill the following criteria of T_cut/τ_K < 1 or f_cut/f_K > 1 that has the same meaning. Corresponding normalized Kolmogorov scales, k_Kλ_K = 2πf_Kλ_K/U, are shown in Fig. 10 by vertical straight and dashed lines for y⁺ = 15 and 100, respectively.

The ratio of f_cut/f_K for two wall-normal distances, y⁺, is shown in Table 2. It is seen that, in our case, f_cut/f_K < 1 in the near-wall region (y⁺ = 15) and f_cut/f_K > 1 at the outer edge of the boundary layer (y⁺ = 100) for all considered IW sizes and both velocity components. Despite the fact that f_cut/f_K < 1 in the near-wall region (y⁺ = 15), the dissipation rate is estimated accurately enough for larger IW sizes (see Fig. 12), provided that Kolmogorov scale is resolved. This is due to the fact that larger IW size produces less random error resulting in higher value of cut-off frequency. This, in turn, enables one to resolve small-scale turbulence required for accurate estimation of the dissipation rate. On the other hand, one should note that even though the criterion of f_cut/f_K > 1 is fulfilled for y⁺ = 100, the dissipation rate is still slightly overestimated for IW sizes of 8 × 8 and 16 × 8 pix. This is explained by low turbulent fluctuations level compared to relatively high random error (see Fig. 10) which, as mentioned above, directly influences the cut-off frequency definition. It is noteworthy that lower cut-off frequency in this region yields more accurate estimation of the dissipation rate. However, it cannot be performed automatically within the framework of the proposed filtering procedure.

Table 2 Ratio of f_cut/f_K and associated values of f_cut

The comparison of the dissipation rate in the turbulent boundary layer with appropriate data obtained by SIV (Mikheev et al. 2017), Tomo PIV (Schneiders et al. 2017), Tomo PTV–VIC+ (Schneiders et al. 2017), Stereo PIV (Foucaut et al. 2016) and DNS (Schlatter and Orlu 2010) can be seen in Fig. 13. We also show the results of the spectral chart method (Djenidi and Antonia 2012). In this case, we take into account that low wavenumber range of the spectrum does not affect the dissipation rate, and high wavenumber range of the spectrum is affected by “white” noise, as shown above. Thus, the dissipation rate, ε, is estimated by fitting an experimental spectrum to an isotropic flow model of E₁₁ (k₁) = C₁ε^2/3k₁^−5/3 in the inertial subrange 0.01 < kλ_K < 0.1 using a constant C₁ = 0.49 (Pope 2000) for all considered y⁺. As can be seen from Fig. 13, the spectral chart method yields relatively good results for y⁺ > 70 but incorrect results in the near-wall region, as Djenidi and Antonia (2012) warned. The latter is associated with large anisotropy in the near-wall region. Mikheev et al. (2017) have shown the best fit of the dissipation rate to DNS curve when using IW size of 16 × 10 pix. However, they used constant value of cut-off frequency of 800 Hz defined by using the formula ${\left| {\hat {U}({f_{{\text{cut}}}})} \right|^2}/{\left| E \right|^2}=1$. This means that true value of velocity vector could still be affected by the random error in the high-frequency region, where the dissipation occurs. When using Tomo PIV, Schneiders et al. (2017) have applied complicated spatiotemporal filtering procedure based on second-order polynomial regression over a time period corresponding to f_K/f_cut ≈ 0.7 near the wall and 0.27 at the outer edge of the boundary layer in a filter volume containing 7 × 7 × 7 velocity vectors that corresponds to ∆x₁/λ_K × ∆x₂/λ_K × ∆x₃/λ_K = 29 × 7 × 15 near the wall and 9 × 9 × 9 at the outer edge of the boundary layer. Despite the fact that Schneiders et al. (2017) satisfied the assumption of f_cut/f_K > 1, they used fairly large spatial filter volume that does not satisfy the recommendation of ∆x/λ_K ≈ 1.5–2 or 1.5–3 proposed by Tokgoz et al. (2012) and Saarenrinne and Piirto (2000), respectively, to fully resolve the turbulent dissipation scales. This explains dissipation rate underestimation along the entire range of y⁺. Note that the profile obtained by elongated IW coincides with our results obtained using velocity vector spacing 2∆x_1,2 = 16 pix which corresponded to about 7 Kolmogorov length scale (compare Figs. 12, 13). The application of Tomo PTV–VIC+ to dissipation rate estimation allowed Schneiders et al. (2017) to significantly improve their results in the range of y⁺ > 25. However, Tomo PTV–VIC+ could not properly estimate the dissipation rate in the near-wall region, as can be seen from Fig. 13. Unfortunately, Foucaut et al. (2016) showed their results only for y⁺ > 16, so that the performance of Stereo PIV, in terms of the accuracy of dissipation rate estimation, which they used, is not evident in the near-wall region. Nevertheless, they showed relatively good agreement of the dissipation rate with the DNS for y⁺ > 16 with its slight underestimation, which has been explained by the filtering of the small-scale structures by Stereo PIV. In general, all the reference experimental data agree well with each other and DNS for y⁺ > 25, and are contradictory for y⁺ < 25. It is interesting that if high-speed planar PIV with high spatiotemporal resolution is applied together with temporal filtering procedure proposed in the present research, the dissipation rate is estimated quite accurately along the entire considered range of y⁺ including the near-wall region (see Fig. 13) even when using the locally axisymmetric turbulence hypothesis. Moreover, the implemented technique allows one to detect correctly the inflection point of the dissipation rate at y⁺ ≈ 10 predicted by DNS which can be attributed to the peculiarities of high-speed planar PIV implemented together with appropriate temporal filtering procedure. This event has also been detected by PTV–VIC+; however, the dissipation rate level has been underestimated by about 20%.

Fig. 13

Comparison of wall-normal profiles of turbulent kinetic energy dissipation rate estimated by different techniques

5 Conclusions

A problem of accurate estimation of the dissipation rate by PIV has been considered in the present research. Key parameters and factors which directly affect the accuracy of the dissipation rate estimation have been briefly discussed. A joint effect of random error, velocity vector spacing, IW size and IW overlap on the dissipation rate estimation has been theoretically shown. Using the example of the synthetic test case of linear shear flow, it has been demonstrated that both the velocity vector spacing and IW size should be as large as Kolmogorov length scale for accurate estimation of the dissipation rate. Simple local temporal filtering procedure has been proposed to partially eliminate the impact of the measurement random error on the dissipation rate estimation. This procedure enables to exclude the frequency region in which the measurement noise energy dominates over the fluid energy. The results of the synthetic test case have demonstrated high efficiency of the proposed filtering procedure which allows the reduction of the random error and, subsequently, accurate estimation of the dissipation rate at the initial iterations.

The results of the dissipation rate estimation in TBL have been presented as well. To achieve high spatiotemporal resolution, a high-speed planar PIV technique has been considered. Since planar PIV allows one to measure only two out of three components of velocity vector, the dissipation rate has been estimated using the locally axisymmetric turbulence hypothesis. However, as shown in the present research, it yields incorrect estimates because of large velocity vector spacing and random errors embedded in measured velocity vectors. It has been demonstrated that when the velocity vector spacing is decreased down to Kolmogorov length scale (2∆x_1,2 = 4 pix which satisfies the recommendations by Tokgoz et al. 2012, as well), the dissipation rate becomes overestimated for all considered IW sizes unless the developed filtering procedure is used. Moreover, the larger the IW size is, the lower the overestimation is since the larger IW size produces less measurement random error. This tendency agrees with the literature (Piirto et al. 2003; Shah et al. 2008; Tokgoz et al. 2012) and the results of the synthetic test case. The effect of these errors has been reduced owing to the proposed filtering procedure which in this case automatically takes into account both the random error and turbulent fluctuation levels for each individual velocity component. The best results have been obtained when using IW size of 32 × 8 pix. Increasing IW size in streamwise direction from 8 to 32 pix allowed us to reduce the random measurement error while maintaining high spatial resolution in the wall-normal direction (8 pix).

The chosen strategy, i.e., the use of high-speed planar PIV together with the developed temporal filter under the assumption of locally axisymmetric turbulence for TBL flow, has demonstrated the best performance in terms of accuracy of the dissipation rate compared to strategies based on other state-of-the-art techniques such as planar SIV, Stereo PIV, Tomo PIV, and Tomo PTV–VIC+ as well as spectral chart method. The implemented technique has detected the inflection point of the dissipation rate at y⁺ ≈ 10 predicted by DNS. This event has not been correctly detected by any other state-of-the-art technique described above, and thus, it can be attributed to the peculiarities of the high-speed planar PIV implemented together with appropriate temporal filtering procedure.