1 Introduction

Impinging jets are found in many engineering fields requiring high levels of surface heat and mass transfer, including cooling systems of turbine blades (Han and Goldstein 2001) and electronic chips (Lasance and Simons 2005), textile drying (Sarkar et al. 2004), food processing (Sarkar et al. 2004), and ground vehicle deicing (Kaplan 2003). As a result, investigations of impinging jets have been motivated by various industrial applications for the past five decades, focusing on enhancing the relevant transfer properties (Carlomagno and Ianiro 2014). Flow and geometric parameters that influence heat and mass transfer rates have been investigated extensively, including jet Reynolds number (Popiel and Trass 1991; Cornaro et al. 1999; Pieris et al. 2017), nozzle-to-plate spacing (Popiel and Trass 1991; Angioletti et al. 2003; Narayanan et al. 2004; Tummers et al. 2011), jet obliqueness (Beltaos 1976; Chin and Agarwal 1991; O’Donovan 2005), acoustic excitation (Fox et al. 1993; Roux et al. 2011), jet swirling (Ahmed et al. 2015; Ianiro et al. 2012), target wall temperature (Kalifa et al. 2016), target wall in motion (Astarita and Cardone 2008), nozzle exit geometry (Lee and Lee 2000; Gao et al. 2003; Martin and Buchlin 2011; Violato et al. 2012; Kristiawan et al. 2012; Sodjavi et al. 2016), and curvature (Popiel and Trass 1991; Cornaro et al. 1999) and roughness (Rajaratnam and Mazurek 2005) of the target surface.

As the impinging jet approaches the target surface, its axial velocity decreases, forming a time-averaged ‘stagnation zone’ of low velocity and high pressure (Schrader 1961). The flow then reorients to become aligned with the surface, after which a wall jet develops. The mean flow field formed by an impinging jet hence consists of the following three regions with distinctively different flow features (Carlomagno and Ianiro 2014) (Fig. 1): (i) the free jet region, characterized by a potential core surrounded by mixing layers formed between the jet and ambient air; (ii) the reorientation region, in which flow decelerates and deflects towards the wall-tangential direction; and (iii) the wall jet region, where the reoriented flow gradually develops into a turbulent wall jet.

The previous studies have largely focused on normal jet impingement and their heat transfer properties. A free jet without confinement typically features a potential core that extends 4.7–7.7 slot widths downstream of the nozzle exit (Livingood and Hrycak 1973). For impinging jets with a nozzle-to-plate spacing larger than the potential-core length of an unconfined jet (transitional impingement), Gardon and Akfirat (1965) and Yokobori et al. (1978) found the maximum surface heat transfer rate in the stagnation zone. For impinging jets with a nozzle-to-plate spacing smaller than the potential-core length (potential-core impingement), in contrast, Hoogendoorn (1977) and Lytle and Webb (1994) found a non-monotonic trend in heat transfer rate, exhibiting two peaks downstream of the stagnation region. Yokobori et al. (1979) and Goldstein et al. (1986) emphasized large scale, coherent structures in the flow play a predominant role in surface heat transfer for transitional and potential-core impingement. Kataoka et al. (1987) confirmed the influence of Kelvin–Helmholtz (K–H) vortices forming in the free jet region at moderate Reynolds number on the surface heat transfer enhancement. A surface-renewal parameter was found to be proportional to the Strouhal number and magnitude of the impinging K–H vortices, in the range of nozzle-to-plate spacing ratios from 2 to 10.

The interaction of K–H vortices with the target surface also plays a role in the laminar-to-turbulent transition in the wall jet region. In transitional impingement, high velocity and pressure fluctuations are observed in the direct vicinity of the stagnation point. Narayanan et al. (2004) showed that these fluctuations result in strong turbulent transport from the mixing layer in the free jet region to the jet centreline, and trigger turbulent transition in the wall jet region. Potential-core impingement, in contrast, is not associated with strong flow fluctuations along the stagnation streamline. Instead, the impinging K–H vortices enhance the entrainment in the reorientation region (Kataoka et al. 1987). Flow visualization by Popiel and Trass (1991) suggested the deformation and breakdown of K–H vortices as they are convected downstream promotes transition to a turbulent wall jet. In addition, Didden and Ho (1985) showed that the passage of K–H vortices along the wall causes the roll-up of vorticity in the near-wall region, and leads to the shedding of boundary layer vorticity into the flow, forming wall vortices. Hadžiabdić and Hanjalić (2008) showed that the instantaneous flow reversals that occur in the thin region near the wall just ahead of the roll-up of wall vortices contribute to the enhancement of the local heat and mass transfer rate.

Most of the aforementioned studies are focused on heat transfer and/or fluid mechanics of axisymmetric normal impingement. In contrast, fewer investigations have focused on fluid mechanics of slot jet impingement or oblique jet impingement. To the best knowledge of the authors, very few have reported on both aspects. Beltaos (1976) established models for oblique impinging jets; however, the derivations were based on measurements of transitional impingement of axisymmetric jets. Experiments on potential-core impingement of slot jets carried out by Chin and Agarwal (1991) were focused on surface heat and mass transfer, where velocity field information was lacking. O’Donovan (2005) extensively characterized the flow fields of oblique jet impingement using particle image velocimetry, but the investigations were limited to axisymmetric jets. Although Pieris et al. (2017) detailed the spatio-temporal behaviour of impinging slot jets, their characterization was restricted to normal impingement.

The present study is motivated by the need for a detailed characterization of the flow field formed by oblique slot impinging jets in the regime of potential-core impingement, and serves two main purposes. The first is to characterize the influence of jet Reynolds number (Re) and jet orientation angle (\(\theta\)) on the time-averaged near-wall flow development. The second is to reveal the relation between the development of dominant coherent structures and time-averaged flow characteristics.

2 Problem Definition

Figure 1 shows a schematic of an oblique impinging slot jet considered in this study, along with pertinent variable and coordinate system definitions. The intersection of the jet geometric centreline and the target surface is defined as the geometric centre, which serves as the origin of a Cartesian coordinate system, with the x-axis oriented along the target surface, and the y-axis normal to the target plate pointing towards the nozzle. Due to stagnation point eccentricity with jet angle, the actual stagnation point is defined at \(x_0\). The velocity components in the x, y, and z directions are denoted as u, v, and w, respectively. The jet orientation angle \(\theta\) is the angle formed by the jet geometric centreline and the target surface (negative x-axis). An air jet of kinematic viscosity \(\nu\) exits from a slot of width B at a centreline velocity \(U_\mathrm{j}\). The nozzle-to-plate spacing H is the distance between the slot exit plane and the origin (0, 0). The flow physics is governed by the following dimensionless parameters: Reynolds number \({Re} = U_\mathrm{j} B/\nu\), the nozzle-to-plate spacing ratio H / B, and the jet orientation angle \(\theta\).

The velocity profile in the wall jet region consists of two self-similar layers, namely, the top layer and the wall layer, which are bridged by a middle layer, thus forming a triple-layered structure (Barenblatt et al. 2005), see Fig. 1. Following (Barenblatt et al. 2005), the middle layer, which bridges the top and wall layers, is loosely defined as the region in the vicinity of \(u_\mathrm {max}\). To facilitate discussion, the y location, where u reaches a maximum is defined as the geometric boundary layer thickness \(\delta\); the y locations, where \(u = u_\mathrm {max}/2\) are defined as the local jet half-widths, \(y_{1/2, {i}}\) (\({i=T, W}\) for top and wall layer, respectively); the y location, where \(u = 0.01u_\mathrm {max}\) with \(y>y_\mathrm {max}\) is defined as the wall jet thickness \(y_\mathrm {b}\). Due to the measurement uncertainty limitations, the wall layer half-width \(y_{1/2, \mathrm {W}}\) is estimated as half the thickness of geometric boundary layer thickness, i.e., \(y_{1/2, \mathrm {W}} = \delta /2\).

Fig. 1
figure 1

Schematic of oblique impinging jet flows. The inset shows a cartoon of the wall jet velocity profile with the three layers demarcated by long dashed lines

Full size image

3 Experimental setup

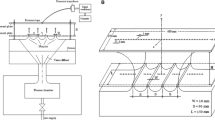
Figure 2a shows a schematic of the experimental facility and the measurement apparatus employed in this study. The flow from a blower was first conditioned by passing it through honeycomb (nominal cell diameter of 5 mm), one coarse screen (porosity of \(82.3\%\)), and three fine screens (porosities of \(64.7\%\)). The conditioned flow was then accelerated through a 9:1 two-dimensional contraction. Flow exited from a rectangular nozzle of span \(L = 200~\mathrm {mm}\) and width \(B = 10~\mathrm {mm}\). An anodized aluminium plate with dimensions of \(60\,B\times 80\,B\) served as the impingement target.

Slot jets with nominal centreline velocity \(U_\mathrm{j} = 5\) and \(10~\mathrm {m/s}\), equivalent to jet Reynolds numbers of \({Re} = 3000\) and 6000, were investigated. At the nozzle exit, the velocity profile was uniform, with maximum deviation of less than \(\pm \,1\%\) across \(95\%\) of the span. Mean flow properties were measured for the two jet Reynolds numbers at four jet orientation angles \(\theta = 90^\circ\), \(60^\circ\), \(45^\circ\), and \(30^\circ\). Reynolds number effects on the vortex dynamics were investigated for both Reynolds numbers at \(\theta = 90^\circ\). In all cases, the nozzle-to-plate spacing ratio was fixed at \(H/B = 4\). The experimental conditions are summarized in Table 1. Statistical flow field characterization was performed using a non-time-resolved, two-dimensional, two-component (2D-2C) particle image velocimetry (PIV) system. A single Imager ProX camera was equipped with a \(105~\mathrm {mm}\) Nikon lens to capture a field of view (FOV) of \(60\times 48 \, {\mathrm {mm}}^2\) with a sensor size of \(1200\times 960 ~\mathrm {px}\). Light provided by an Evergreen 70 Nd-YAG laser was conditioned into a light sheet of approximately \(1~\mathrm {mm}\) thickness to illuminate the flow at the mid-span location to guarantee the two-dimensionality of the measurements. The flow was seeded with water-glycol-based fog particles with a mean diameter of around \(1~\upmu \mathrm {m}\), corresponding to a Stokes number of \({Sk} = 0.003\) for jet flow at \({Re} = 6000\). While the particle size distribution was not assessed, larger seed particles potentially generated by the fog machine were naturally filtered out by virtue of navigating the flow facility upstream of the nozzle exit. This was confirmed by visual inspection of the impingement plate, which showed virtually no fog fluid residue in the stagnation region after multiple runs. The numerical aperture and magnification factor were \(f_\# = 2.8\) and \(M = 0.148\), respectively. The illumination and imaging systems were synchronized by the LaVision high-speed controller and DaVis 8 program, with the latter also used for image processing. Three FOVs, as shown in Fig. 2b, ranging from \(-\,4\leqslant x/B\leqslant 2\) (FOV 1), \(-\,1\leqslant x/B\leqslant 5\) (FOV 2), and \(4\leqslant x/B\leqslant 10\) (FOV 3), were investigated consecutively. A total of 1200 particle image pairs were acquired in double-frame mode at \(15~\mathrm {Hz}\) for each FOV. A sequential cross-correlation algorithm with multi-pass iterations of decreasing window sizes was used to process the images. The final interrogation window size was \(48\times 48~\mathrm {px}\), with an overlap of \(75\%\), resulting in a vector pitch of 0.6 mm. An elliptical Gaussian weighting with an aspect ratio of 2:1 was used for the final interrogation. Flow statistics retrieved from the three FOVs were stitched by blending the measurements in the overlapping regions of different cameras with a cosine weighting function. The combined FOV spans \(-\,4\leqslant x/B\leqslant 10\). The estimation calibration error of \(x-y\) coordinate was half of the pixel size. The estimated uncertainty in instantaneous velocity fields was estimated to be less than \(1\%\) of the jet exit velocity with \(95\%\) confidence limit. With uncorrelated samples, the uncertainty of mean velocity is minuscule. The uncertainty associated with turbulence statistics was quantified based on Sciacchitano and Wieneke (2016).

Fig. 2
figure 2

a Experimental setup of PIV measurements of oblique impinging jet flows. Schematics of field of view (FOV) for b mean flow measurement and c vortex dynamic investigation

Full size image
Table 1 Jet configurations for PIV measurements
Full size table

A high-speed, two-component PIV system was used to obtain time-resolved (TR) velocity measurements. Two photron SA4 high-speed cameras were used simultaneously. The cameras were equipped with \(200~{\rm {mm}}\) Nikon lenses to capture a combined FOV of \(25\times 45~{\rm {mm}}^2\) (\(25\times 25~{\rm {mm}}^2\); \(1024\times 1024~\rm {px}\) for each camera), as shown in Fig. 2c. Light provided by a Photonics DM20-527 Nd-YLF laser was conditioned and synchronized with the cameras in the same manner as for non-time-resolved PIV measurements described earlier. The numerical aperture and magnification factor were \(f_\# = 4\) and \(M = 0.819\), respectively. A total of 2728 particle image pairs were acquired in double-frame mode at \(500~\mathrm {Hz}\) and \(1950~\mathrm {Hz}\) for \({Re} = 3000\) and 6000, respectively. A sequential cross-correlation algorithm with multi-pass iterations of decreasing window sizes was used to process the images. The final interrogation window size was \(24\times 24~\mathrm {px}\), with an overlap of \(75\%\), resulting in a vector pitch of 0.15 mm. An elliptical Gaussian weighting with an aspect ratio of 2:1 was used for the final interrogation. The essential PIV parameters for both non-time-resolved and time-resolved measurements are summarized in Table 2.

Table 2 Recording parameters for PIV measurements
Full size table

4 Results

The results are divided into two sections: Sect. 4.1 analyses the effect of Re and \(\theta\) on time-averaged flow field characteristics and Sect. 4.2 presents a quantitative analysis of the development of dominant coherent structures, which provides insight into the link between the coherent structures and the salient statistical flow field characteristics.

4.1 Time-averaged flow field characteristics

The mean velocity fields for varying \(\theta\) at both Reynolds numbers investigated are presented in Fig. 3. Locations of \(\delta\) and \(y_{1/2, {i}}\), defined in Fig. 1, are shown by solid and dash–dotted lines, respectively. In all cases considered, the nozzle-to-plate spacing H is smaller than the potential-core length of a free jet, resulting in potential-core impingement. The jet exiting the nozzle experiences a sudden deceleration at approximately \(0.5\,B\) above the target surface, as a stagnation zone forms for all cases. Oblique impingement cases exhibit bias of the stagnation point towards the nozzle due to the Coandă effect (Reba 1966). That is, the jet centreline in the free jet region skews from the nozzle centreline and the stagnation point shifts towards the nozzle. With decreasing \(\theta\), the stagnation point eccentricity increases, agreeing with previous results (Chin and Agarwal 1991). Stagnation point eccentricity can be affected by aspect ratio of slot jet exit for values under 4 (Fernholz 1964); the results of the current study are expected to hold well for larger aspect ratios. In the stagnation zone, the flow bifurcates into two fractions, one reoriented towards the positive x direction and the other towards the negative x direction. At smaller jet orientation angles, a higher percentage of the incoming flow is reoriented towards the positive x direction. Downstream of the stagnation region, the reoriented flow first accelerates, and then decelerates as the jet spreads in the wall-normal direction, eventually forming a wall jet. Noticeably, for \({Re} = 3000\) at orientation angles of \(\theta = 90^\circ\) and \(60^\circ\), the wall jets are deflected away from the wall at around \(x/B = 3\). This deflection diminishes at lower \(\theta\) and is not observed at all at the higher Reynolds number.

Fig. 3
figure 3

Contours of mean velocity magnitude at four oblique angles for \({Re} = 3000\) (left column) and \({Re} = 6000\) (right column) for \(\theta = 90^\circ\), \(60^\circ\), \(45^\circ\) and \(30^\circ\). Locations of \(\delta\) and \(y_{1/2, {i}}\) are marked by solid and dash–dotted lines, respectively

Full size image

The stagnation point locations for the cases presented in Fig. 3 are at \(x_0/B =0\), \(-0.54\), \(-1.01\), and \(-2.12\) for \(\theta = 90^\circ\), \(60^\circ\), \(45^\circ\), and \(30^\circ\), respectively, for both Reynolds numbers. Based on potential flow theory, Schauer and Eustis (1963) proposed Eq. (1) for predicting the eccentricity of transitional oblique jet impingement for \(\theta \ge 30^\circ\):

$$\begin{aligned} x_0/H = -\,0.154 \mathrm {cot}\theta . \end{aligned}$$
(1)

Beltaos (1976) generalized the model by taking into account the skewness of velocity profile in the free jet region due to the presence of the target wall, predicting

$$\begin{aligned} \frac{x_0}{H} = \frac{1-\theta /90}{8\mathrm {sin}\theta }. \end{aligned}$$
(2)
Fig. 4
figure 4

Eccentricity of stagnation point from geometric centre versus \(\theta\) normalized by a nozzle-to-plate spacing ratio H, and b nozzle width B. The uncertainty of the measurement is smaller than the size of the symbols

Full size image

Figure 4a shows \(x_0\) measured in the present study compared with Eqs. 1 and 2, as well as the data from other studies, as summarized in Table 3. The figure shows that \(x_0/H\) deviates from the proposed models, as H / B decreases. This discrepancy is due to the change from the transitional impingement regime to the potential-core impingement regime, since both models were derived based on the assumption of a self-similar velocity profile in a fully developed jet prior to impingement. The strength of entrainment in the reorientation region of potential-core impingement is higher than transitional impingement, and consequently, the pressure difference impressed on both sides of the stagnation point in the near-wall region is more significant, leading to larger stagnation point eccentricity. Figure 4b shows the eccentricity normalized by nozzle width B, which exhibits better collapse of the present data and that of O’Donovan (2005). This indicates that within the regime of potential-core impingement, when normalized by nozzle exit width (diameter), a universal scaling can be attained for the \(x_0/B\) with \(\theta\) despite of the differences in H/B and jet nozzle geometry.

Table 3 Eccentricity of stagnation point from geometric centre: \(x_0\) values reported in the literature
Full size table

The flow development of the wall jet that reorients towards the positive x direction is quantified in terms of the decay of the maximum wall-tangential velocity \(u_\mathrm {max}\) and the growth of jet half-width \(y_{1/2, {i}}\), with respect to the actual stagnation point \(x_0\). Barenblatt et al. (2005) proposed incomplete self-similarity for \(u_\mathrm {max}\) and \(y_{1/2, {i}}\) in the following form:

$$\begin{aligned} \frac{u_\mathrm {max}}{U_j} \propto \left( \frac{x-x_0}{B}\right) ^\zeta \end{aligned}$$
(3)

and

$$\begin{aligned} \frac{y_{1/2,{i}}}{B} \propto \left( \frac{x-x_0}{B}\right) ^\gamma _{i} ,\quad \mathrm {where}\quad {i} = {T, W} \end{aligned}$$
(4)
Table 4 Decay rate of \(u_{max}\) for wall jets: \(\zeta\) values reported in the literature
Full size table
Table 5 Growth rate of \(y_{1/2}\) for wall jets: \(\gamma _\mathrm {T}\) values reported in the literature
Full size table

For traditional 2D turbulent wall jets, van der Hegge Zijnen (1924) suggested a decay rate of \(\zeta = -\,0.5\), which was validated by experimental measurements in the far-field of wall jets (Glauert 1956; Sigalla 1958; Seban and Back 1961; Schwarz and Cosart 1961; Bradshaw and Gee 1962; Myers et al. 1963). Launder and Rodi (1981) suggested a linear wall-normal growth rate \(\gamma _\mathrm {T} = 1\), with \(\mathrm {d}y_{1/2, \mathrm {T}}/\mathrm {d}x = 0.073\). These values are also applicable in the far-field (\(x/B\geqslant 20\)) of impinging jets of high Reynolds number, where the flow fully develops into turbulent wall jet. In the near field (\((x-x_0)/B <20\)), where flow goes through laminar-to-turbulent transition; however, Cartwright and Russell (1967) found a much lower decay rate of \(-\,0.39\) in the near-field wall jet formed by a 2D normal impinging jet (see Table 4). Furthermore, the near-field wall jet growth rate follows the power law \(y \propto x^\gamma\), with \(\gamma\) values scattering over a range of 0.78–1.34 (Bakke 1957; Tanaka and Tanaka 1977; Knowles and Myszko 1998; Barenblatt et al. 2005; Tang et al. 2015; Gao et al. 2003) (see Table 5), indicating that the value of \(\gamma _\mathrm {T}\) is not a single valued function of Re, H / B, and jet nozzle geometry.

Fig. 5
figure 5

Decay of \(u_\mathrm {max}\) in wall jet middle layer and its power-law regression for a \({Re} = 3000\) and b \({Re} = 6000\). c The trend of decay rate \(\zeta\) with jet orientation angles for \({Re} = 3000\) and 6000. The gray bar indicates the range of \(\zeta = -\,0.34\pm 0.04\)

Full size image
Fig. 6
figure 6

Growth of \(y_{1/2}\) top layer and wall layer and its power-law regression for a \({Re} = 3000\) and b \({Re} = 6000\). c The trends of growth rate \(\gamma _\mathrm {W}\) and \(\gamma _\mathrm {T}\) with jet orientation angles for \({Re} = 3000\) and 6000. The gray bar indicates the range of \(\gamma _{i} = 0.70\pm 0.11\)

Full size image

In the present study, the decay rate \(\zeta\) and the growth rate \(\gamma _{i}\) are calculated from power-law regressions of Eqs. 3 and 4, respectively, as shown in Figs. 5 and 6. Specifically, as mentioned in Sect. 2, the geometric boundary layer thickness \(\delta\) is in effect the maximum wall-tangential velocity location, and the wall layer jet half-width \(y_{1/2, \mathrm {W}}\) is approximated by \(\delta /2\). The top layer jet half-width \(y_{1/2, \mathrm {T}}\) is calculated from the PIV measurements by linear interpolation between \(u \ge u_\mathrm {max}/2\) location and the neighboring y location, where \(u \le u_\mathrm {max}/2\). Figure 5a, b shows the curve fit for \(\zeta\) values on a logarithmic scale for \({Re} = 3000\) and 6000, respectively, with hatch-filled markers indicating data used in the curve fit, and red lines indicating the fitted curves. In a similar fashion, curve fits for \(\gamma _\mathrm {T}\) and \(\gamma _\mathrm {W}\) at \({Re} = 3000\) are shown in Fig. 6a, b, respectively. The choice of data used for the estimation of these parameters is based on the onset of self-similarity in the wall jet velocity profiles, as shown in Fig. 7a, c, for \({Re} = 3000\) and 6000, respectively. For \({Re} = 3000\) (Fig. 7a), at a given \(\theta\), the velocity profiles collapse onto each other starting from \((x-x_0)/B = 5\), while for \({Re} = 6000\) (Fig. 7c), the middle and wall layer profiles collapse from \((x-x_0)/B = 5\), and the top layer profiles collapse from \((x-x_0)/B = 7\).

Fig. 7
figure 7

Measured velocity profiles in range of \((x-x_0)/B = 5\)–9 for a \({Re} = 3000\) and c \({Re} = 6000\); Collapsing of velocity profiles across four oblique angles and five sampling locations in the near-wall region for b \({Re} = 3000\) and d \({Re} = 6000\)

Full size image

The effects of Re and \(\theta\) on \(\zeta\) and \(\gamma _{i}\) are summarized in Figs. 5c and 6c, respectively. In general, for \(\theta \le 45^\circ\), there is minimal effect of Reynolds number and \(\theta\) on both \(\zeta\) and \(\gamma _{i}\), with the values falling in the range of \(\zeta = -\,0.34\pm 0.04\) and \(\gamma _{i} = 0.70\pm 0.11\) (\({i} = {T}, \, {W}\)). At larger jet orientation angles (\(\theta \ge 60^\circ\)), however, both \(\zeta\) and \(\gamma _{i}\) are influenced significantly by jet Reynolds number. Specifically, as shown in Fig. 5c, \(u_\mathrm {max}\) decays faster when Re decreases, or when \(\theta\) increases. Different trends are followed by \(\gamma _\mathrm {T}\) and \(\gamma _\mathrm {W}\) with Re, as shown in Fig. 6c. For \({Re} = 3000\) at \(\theta = 90^\circ\), with \(\gamma _\mathrm {T} = 1.45\) and \(\gamma _\mathrm {W} = 1.42\), both values are much higher than 0.70. These faster growth rates in both top and wall layers are attributed to lifting of the wall jet observed in Fig. 3a, b. For \({Re} = 6000\), while the top layer features a high growth rate of \(\gamma _\mathrm {T} = 0.98\), \(\gamma _\mathrm {W} = 0.14\) is much lower than 0.70, indicating rapid spreading of the top layer, while the wall layer remains attached to the wall, as also observed the in the mean velocity fields (see Fig. 3e, f).

Self-similarity in the wall jet velocity profile is eventually expected as the flow develops along the surface. Selected non-dimensional profiles of the u-component of velocity at \((x-x_0)/B = 5,~6,~7,~8,\) and 9 for \({Re} = 3000\) and 6000 at the four orientation angles are presented in Fig. 7. The velocity profiles defined by Schlichting’s formula for self-similar, semi-bounded turbulent jets (Yakovlevskii and Krasheninnikov 1966), given by Eq. 5, are plotted with dashed lines for each \(\theta\) (Figs. 7b, d):

$$\begin{aligned} \begin{aligned} \frac{u}{u_\mathrm {max}}&= (1-\varepsilon ^{3/2})^2 \quad \mathrm {for}\quad y\geqslant \delta ,\\ \frac{u}{u_\mathrm {max}}&= (y/\delta )^{1/n} \quad \mathrm {for}\quad y\leqslant \delta . \end{aligned} \end{aligned}$$
(5)

In Eq. 5, \(\varepsilon = (y-\delta )/(y_b-\delta )\), and \(n\approx 10\) are based on experimental data of Sakipov (1964). For \({Re} = 3000\), the near-wall velocity profiles for \(\theta = 90^\circ\) differ significantly from the profiles at smaller \(\theta\). For \(\theta <90^\circ\), the velocity profiles tend to collapse and show better agreement with Schlichting’s formula. For \({Re} = 6000\), all near-wall velocity profiles collapse onto one curve and agree well with Eq. 5. These results suggest that, for \({Re} = 3000\), the wall jet region undergoes laminar-to-turbulent transition in the range \(5<(x-x_0)/B<9\), while for \({Re} = 6000\), transition to turbulence occurs upstream of \((x-x_0)/B = 5\).

Fig. 8
figure 8

Contours of turbulent kinetic energy at four oblique angles for \({Re} = 3000\) (left column) and \({Re} = 6000\) (right column). Locations of \(\delta\) and \(y_{1/2, {i}}\) are marked by solid and dash–dotted lines, respectively

Full size image
Fig. 9
figure 9

Contours of turbulence production at four oblique angles for \({Re} = 3000\) (left column) and \({Re} = 6000\) (right column). Locations of \(\delta\) and \(y_{1/2, {i}}\) are marked by solid and dash–dotted lines, respectively

Full size image
Fig. 10
figure 10

Trend of maximum a turbulent kinetic energy and b turbulence production magnitude of the wall layer as jet orientation angle decreases from \(\theta = 90^\circ\) to \(30^\circ\)

Full size image

To gain further insight into the flow characteristics, turbulent kinetic energy (TKE) and turbulence production \({\mathscr {P}}\) are presented in Figs. 8 and 9, respectively. These parameters are defined by Eqs. 6 and. 7 based on two-component velocity measurements:

$$\begin{aligned} \mathrm {TKE}= & {} \overline{u'u'}+\overline{v'v'}, \end{aligned}$$
(6)
$$\begin{aligned} {\mathscr {P}}= & {} \overline{u'u'}\frac{\partial {\overline{u}}}{\partial x} + \overline{u'v'} \left( \frac{\partial {\overline{u}}}{\partial y}+\frac{\partial {\overline{v}}}{\partial x}\right) + \overline{v'v'}\frac{\partial {\overline{v}}}{\partial y}, \end{aligned}$$
(7)

where the prime symbol indicates a fluctuating velocity component, and the overbar indicates a time-averaged quantity. For reference, locations of \(\delta\) and \(y_{1/2, {i}}\) are marked by solid and dash–dotted lines in both field plots. In general, high TKE is observed in the wall jet top layer, where strong turbulence production takes place in the top layer around \(y_{1/2, \mathrm {T}}\), due to the K–H vortices. The primary region of turbulence destruction is confined to the wall layer, around \(y_{1/2, \mathrm {W}}\), where the presence of the wall limits the length scale of vortical structures. In the middle layer, turbulence production is nearly zero as expected, since the flow in the reoriented potential core is laminar for potential-core impingement. For all cases except \({Re} = 3000\), \(\theta = 90^\circ\) and \(60^\circ\) (Fig. 8c–h), maximum TKE occurs along \(y_{1/2, \mathrm {T}}\). TKE values quickly drop close to the middle layer. For the two exceptional cases (Fig. 8a, b), maximum TKE occurs in the middle layer around \(\delta\), and significant levels of TKE are also observed in the wall layer. These differences in the distribution of planar TKE for \({Re} = 3000\), \(\theta = 90^\circ\) and \(60^\circ\) will later be shown to stem from differences in vortex dynamics observed for these flow conditions (Sect. 4.2).

Figure 10a, b shows, respectively, the maximum TKE and turbulence production values sampled along \(y_{1/2, \mathrm {W}}\) for \((x-x_0)/B>5\) at each jet orientation angle. In general, the wall layers for the \({Re} = 3000\) cases feature higher maximum TKE than those of \({Re} = 6000\). At the same time, turbulence destruction in the wall layers is also stronger for the \({Re} = 3000\) cases. For a fixed Reynolds number, the maximum TKE in the wall layer decreases with decreasing \(\theta\). Quantitatively, for \({Re} = 3000\), as \(\theta\) decreases from \(90^\circ\) to \(30^\circ\), the maximum value of TKE in the wall layer decreases from 0.122 to 0.057, while the maximum turbulence production remains constant around \({\mathscr {P}} =0.063\) within the range of \(\theta\) investigated. For \({Re} = 6000\), as \(\theta\) decreases from \(90^\circ\) to \(30^\circ\), the maximum values of TKE in the wall layer decreases from 0.073 to 0.049. At the same time, maximum turbulence production remains constant around \({\mathscr {P}} =0.034\) within \(60^\circ \le \theta \le 90^\circ\), and increases from 0.034 to 0.054 when \(\theta\) decreases from \(60^\circ\) to \(30^\circ\). Considering the TKE budget, this indicates that around the wall-normal location of \(y_{1/2, \mathrm {W}}\), at larger \(\theta\), turbulence destruction and viscous dissipation play equal roles in balancing the TKE influx due to advection and turbulent transport, while at smaller \(\theta\), turbulence destruction dominates.

4.2 Vortex dynamics

As observed in the mean flow fields for \({Re} = 3000\), deflection of the wall jet from the wall is observed around \((x-x_0)/B = 3\) (Fig. 3a–d), especially at large orientation angles; for \({Re} = 6000\), \(\theta = 90^\circ\), the wall jet spreads faster in the y-direction than all the other cases investigated (Fig. 3e). Anomalous behaviour in in-plane TKE is also observed for \({Re} = 3000\) at \(\theta = 90^\circ\), where significant TKE is present not only in the top layer, where turbulence is produced, but also in the middle layer, and the upper part of the wall layer. To shed light on the observed variations in the time-averaged flow characteristics, the development of dominant coherent structures is considered in this section.

Fig. 11
figure 11

Two non-sequential instances of flow visualization for \({Re} = 3000\) and \(\theta = 90^\circ\) showing a intact K–H vortex impingement and b vortex merging events prior to flow reorientation

Full size image

As a precursor of quantitative measurements, flow visualization was performed by overseeding the quiescent fluid. Figure 11 shows two non-sequential snapshots of the normal impinging jet at \({Re} = 3000\). Figure 11a shows the formation of a primary vortex (‘a’) at around 1.5B downstream of the nozzle exit due to the K–H instability (Popiel and Trass 1991; Cornaro et al. 1999). Further shear layer roll-up is observed downstream as an increase in vortex diameter (‘b’). Upon impact (‘c’) and passage along the wall these vortices can induce the roll-up of wall vorticity that can act to entrain the quiescent flow (Didden and Ho 1985; Hadžiabdić and Hanjalić 2008), as observed between ‘c’ and ‘d’. Merging of primary vortices when they convect along the wall is also observed ‘d’. Figure 11b shows another scenario when merging events take place prior to flow reorientation (‘e’). The spatial extent of merging events is due to the small variability in shedding frequency as reported in (Pieris et al. 2017). This cycle-to-cycle variability leads to difference in intra-vortex spacing. As a result, merging of primary K–H vortices sometimes occur in the free jet region of the flow, leading to the advection of a merged pair through the reorientation and wall jet regions, while at other times primary vortices persist unmerged throughout the observed domain. Triple merging was also observed on occasion for \({Re} = 3000\). Figure 11b, ‘g’ shows the precursor of such an event.

The development of dominant coherent structures is illustrated in Fig. 12 using a series of instantaneous vorticity contours of spanwise vorticity (\(\omega\)) at five consecutive time instants \(t^*= t u_j/B\) for both Reynolds numbers at \(\theta = 90^\circ\). Vortical structures were identified using the \(\lambda _2\) criterion (Jeong and Hussain 1995). To reduce the effects of the PIV measurement noise, thresholds for \(\lambda _2\) and connectivity of identified structures were set to \(\lambda _2\le -\,0.5\) and \(conn>50\), respectively. The vortex core locations were defined as the centroid of the identified structures, which are marked by the gray contour lines of \(\lambda _2 = -\,0.5\) in Fig. 12. The circulation of each vortex is calculated by integrating the vorticity over the area of the identified structure, which is delineated by the contour of \(\lambda _2 = -\,0.5\), as shown in Fig. 12. Sliding windows of \({\varDelta }x/B = 0.3\) were used to reconstruct the principal trajectories of K–H vortices and to compute the mean circulation of vortices convecting along the principal trajectory. As examples, Fig. 13 shows histograms of vortex core wall-normal coordinates at three streamwise locations. Two principal trajectories were identified from the dual-peak distributions observed in the histograms. For the trajectory at the top, vortices with core locations falling in the bin of primary peak and four bins to the right were used for the calculation of statistics. Similarly, for the trajectory at the bottom, vortices with core locations falling in the secondary peak and four bins to the left were used. In this way, wall-normal statistics are calculated with windows of \({\varDelta }y/B = 0.3\), the same width as the horizontal sliding windows. The range of bins used for statistics and the averaged vortex core location are marked by gray dashed lines and red dash-dotted lines, respectively. The presence of two distinct trajectories, one for merged vortices and one for individual vortices, arises due to spatial extent over which K–H merging events occur in the flow configuration, as shown in Fig. 11. The two trajectories correspond to the mean path of individual K–H vortices and that of merged pairs. These are marked by dashed and dotted lines in Fig. 12.

Fig. 12
figure 12

Instantaneous vorticity contours overlayed with contour lines of \(\lambda _2 = -\,0.5\) and the two principal trajectories, at five consecutive snapshots at time instant \(t^*= t u_j/B = 0,~ 1,~2,~3\) and 4 for \({Re} = 3000\) (left column), and \({Re} = 6000\) (right column) at \(\theta = 90^\circ\)

Full size image

As can be observed from Fig. 12a–e, the merged vortices follow the upper trajectory, while the intact K–H vortices tend to penetrate deeper towards the wall, following the lower trajectory (Fig. 14a, b, \({{P}}_1\)). This is corroborated by the mean circulation estimates along the two trajectories, as shown in Fig. 14c, wherein the upper trajectory associates with a higher mean circulation, as expected for merged vortices. Merging events of K–H vortices at \({Re} = 3000\) occur in both the reorientation region and the wall jet region. When a merging event occurs, the two merging vortices migrate their centre of rotation from the lower trajectory to the upper (Fig. 14a, b, \({{P}}_2 + {{P}}_3\)). The vortex merging and migration result in the significant increase in mean circulation sampled along the lower trajectory (Fig. 14a) for \({Re} = 3000\). Figure 14a, b shows the locations of the principal K–H vortex trajectories with respect to the locations of \(y_{1/2, \mathrm {T}}\) and \(\delta\). The principal trajectories for both Reynolds numbers are located in the top layer as expected for shear layer vortices.

Fig. 13
figure 13

Histograms of vortex core locations within different x / B regions for \({Re} = 3000\), \(\theta = 90^\circ\). Gray dashed lines mark the bins used to calculate the vortex statistics along the trajectories. Red dash-dotted lines mark the averaged y / B of vortex cores falling in the range of calculation

Full size image
Fig. 14
figure 14

Location of the two principal trajectories with respect to jet half-width for a \({Re} = 3000\), and b 6000. c Evolution of vortex circulation along the principal trajectories of the K–H vortices. The uncertainty of the principal trajectory is bounded by \({\varDelta }y/B= \pm\, 0.03\). The maximum uncertainty of mean circulation is \(30\%\)

Full size image

For \({Re} = 3000\), when a K–H vortex formed in the free jet region convects towards the target surface, its induced velocity at the wall increases local vorticity production. As a result, the vorticity in the boundary layer rolls up into a wall vortex of opposite rotation to the K–H vortex at its direct downstream location (Fig. 12b, c, \({{S}}_2\)). The K–H vortex and its induced wall vortex pair up, and as they move downstream together, the wall vortex sources vorticity from the local boundary layer until it eventually sheds from the wall (Fig. 12d, e). After ejection, the paired vortices mutually advect, with the higher circulation K–H vortex causing the pair to move away from the wall. An inflexion in the mean K–H trajectory occurs at around \((x-x_0)/B = 3\), marking the mean shedding location of wall vortices. At the same location, wall jet deflection is observed in the time-averaged velocity field of \({Re} = 3000\), \(\theta = 90^\circ\) (Fig. 3a), indicating that the shedding of wall vortices leads to a higher growth rate in both \(y_{1/2, \mathrm {T}}\) and \(y_{1/2, \mathrm {W}}\) (Fig. 6c). Both single and merged K–H vortices remain coherent until around \((x-x_0)/B = 4.5\). These persistent large eddies drain kinetic energy from the mean flow into their circulating motion, leading to a higher decay rate of \(u_\mathrm {max}\) for \({Re} = 3000\) than \({Re} = 6000\) (Fig. 5c). The intermittent shedding of large-scale wall vortices leads to strong wall-normal velocity fluctuations, which contribute to the high TKE values in the middle and wall layers (Fig. 8a). Starting at around \((x-x_0)/B = 4.5\), interactions with the shed wall vortices become significant (Fig. 12a, b, \({{P}}_1\) and \({S_1}\)), leading to annihilation of circulation. In addition, around this location, sudden breakdown events of merged vortices are observed. Vortex breakdown and cross diffusion of vorticity both contribute to the decrease in mean circulation (Fig. 14c). In addition, the cross diffusion in the near-wall region accounts for the wall layer turbulence destruction. At the same time, the breakdown of merged vortices cascades the kinetic energy to smaller eddies, contributing to the viscous diffusion. Both mechanisms attribute to the low TKE values in the near-wall region of \((x-x_0)/B>7\) (Fig. 8a).

For \({Re} = 6000\), the breakdown of the K–H vortices starts in the flow reorientation region (Fig. 12g, h). The earlier breakdown inhibits the penetration of primary K–H vortices towards the wall and reduces the induced wall-normal velocity in the wall layer. As a result, strong shedding events of wall vortices are not detected and the wall layer remains attached to the surface within the FOV. This leads to the moderate growth rate in \(y_{1/2, \mathrm {W}}\) (Fig. 6c), and the steep near-wall velocity gradient (Fig. 7d). Breakdown events occur along the entire vortex trajectory in the range \((x-x_0)/B\ge 1.5\), resulting in the gradual decrease in mean vortex circulation (Fig. 14c). At the same time, vortex breakdown leads to earlier transition into turbulence, resulting in the quick growth in \(y_{1/2, \mathrm {T}}\). The steep near-wall velocity gradient (Fig. 7d) limits the length scale of eddies and thus suppresses the energy cascade, resulting in turbulence destruction and viscous dissipation in the near-wall region.

5 Conclusion

Mean flow development of impinging jets was characterized using non-time-resolved PIV at four jet orientation angles \(\theta = 90^\circ\), \(60^\circ\), \(45^\circ\), and \(30^\circ\). In all cases, stagnation point eccentricity increases with decreasing \(\theta\), and is insensitive to Re within the range investigated. The reoriented flow develops along the wall, and eventually forms a self-similar wall jet.

At larger orientation angles, the wall jet development is influenced significantly by the jet Reynolds number. Specifically, for \({Re} = 3000\), \(\theta \ge 60^\circ\), significant deflection of wall jet from the surface is observed. The wall jet deflection results in higher growth rates of the wall jet top and wall layers, as well as faster decay in the maximum wall-tangential velocity. For \({Re} = 6000\), on the other hand, within the range of orientation angles investigated, the wall jet remains attached to the wall. In contrast, at smaller angles, there is minimal Reynolds number effect on both wall jet growth and velocity decay.

In this study, 2D–2C PIV measurements of high spatial resolution establishes the causal relation between vortex–wall interaction and time-averaged statistics for impinging jets at \(\theta = 90^\circ\). At lower Reynolds number, the observed wall jet deflection is attributed to the interactions between the K–H vortices formed in the jet shear layer and the target surface. The impinging K–H vortices remain coherent along the wall and induce strong shedding of wall-bounded vorticity. The shed vorticity pairs with the K–H vortices and ejects from the wall, resulting in the deflection of the wall jet from the surface. The sudden breakdown of these vortical structures further downstream cascades turbulent kinetic energy to smaller scales, marking the last stages of the laminar-to-turbulent flow transition. At higher Reynolds number, on the other hand, K–H vortices experience breakdown further upstream in the reorientation region, resulting in earlier flow transition. The roll-up of wall-bounded vorticity is less significant, and consequentially, the wall layer remains attached to the surface. The energy cascade in the near-wall region is suppressed by the steep velocity gradient at the wall, resulting in turbulence destruction.