Signatures of shear-layer unsteadiness in proper orthogonal decomposition

Abstract

Proper orthogonal decomposition can be used to determine the dominant coherent structures present within a turbulent flow. In many flows, these structures are well represented by only a few high-energy modes. However, additional modes with clear spatial structure, but low-energy contribution can often be present in the proper orthogonal decomposition analysis, even for flows with a high degree of periodicity. One such mode has been observed in both free and impinging jets determined from particle image velocimetry. Both experimental and synthetic data are used to investigate the role of this particular mode, linking its existence to the unsteadiness of shear-layer large-scale coherent structures.

Graphical abstract

1 Introduction

Turbulent flows are difficult to characterize due to the large range of spatial and temporal scales. For this reason, researchers often focus on the larger scale, coherent components, which are often responsible for the dynamics of most interest. The difficulty in this type of analysis starts with isolating these larger scale dynamics. Whilst several techniques are capable of achieving this separation, proper orthogonal decomposition (POD) is perhaps the most appropriate (Berkooz et al. 1993).

The use of POD to identify coherent structures in turbulent flows dates back more than 50 years, stemming from the seminal work of Lumley (1967) on atmospheric flows. Since then, its use has spread to include boundary layers (Liu et al. 1994; Adrian et al. 2000; Podvin and Fraigneau 2017), wake flows  (Johansson et al. 2002; Kostas et al. 2005; Tang et al. 2015), and both subsonic (Glauser et al. 1987; Meyer et al. 2007; Gudmundsson and Colonius 2011; Cavalieri et al. 2013), and supersonic jets (Alkislar et al. 2003; Edgington-Mitchell et al. 2014b; Jaunet et al. 2016; Weightman et al. 2017a).

POD is ideal for identifying the large-scale coherent flow structures as the resultant modes are ranked by their relative energy contribution. Though there is no strict definition of a coherent structure, the name itself suggests a flow structure with coherence in both space and time (Robinson 1991). This means that the fluctuations associated with a coherent structure are large relative to other, random fluctuations and more persistent, usually making them among the highest energy modes of the POD analysis (Sirovich 1987). Many turbulent flows exhibit the generation of these large-scale structures at a fixed frequency. This fixed frequency results in a spatial periodicity of the structures. One class of flows that display such behaviour is aeroacoustic resonance (Powell 1953). This periodicity can often result in the fluctuations associated with the coherent structures being contained in a single pair of high-energy POD modes (Oberleithner et al. 2011).

In many shear flows, the large-scale coherent structures dominate the mixing and aeroacoustic dynamics. Consequently, researchers often restrict their analysis to a single-mode pair, or to a number of modes that contains a certain percentage of the total energy for flows with strong spatial or temporal periodicity (Tinney et al. 2008). Attempts to encapsulate important flow physics have been made by measuring a flow parameter and increasing the number of modes until a notable change in that parameter occurs (Tan et al. 2017). However, even in periodic flows, where a single-mode pair may capture the large-scale fluctuations, important flow information may be contained in relatively low-energy modes.

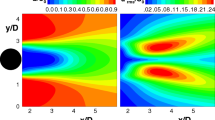
A particular POD mode, recognizable by its spatial structure, is shown in Fig. 1 and has been observed in several particle image velocimetry (PIV) data sets across various conditions and facilities. Whilst not always present, flows containing this particular mode structure include supersonic free and impinging jets, with both flat and curved impingement surfaces. When present, the relative energy contribution of this mode is often small, but within the top 10 most energetic modes. Due to variations in the flow structure, this mode can be difficult to determine based purely on the spatial mode shape, as illustrated in Fig. 1. However, looking at just the region outlined by the black box, the mode shape is similar, suggesting that even in these very different flows, the phenomenon being described by the modes is the same. An improved method for finding such a mode is presented in a later section

Fig. 1

Top: axial and bottom: transverse components of a POD mode 2 in an underexpanded free jet at an NPR of 3.4 and b POD mode 10 in an underexpanded jet at an NPR of 3.6 impinging on a cylindrical section of radius 2.5D with a plate spacing of $z/D = 3.5$

In this paper, the phenomenon underpinning the mode highlighted in Fig. 1 is investigated using PIV measurements of an impinging supersonic jet (case 1), as well as a synthetic vortex-laden shear layer (case 2). These two cases inform the analysis of the role of this low energy, but structurally significant POD mode and its relation to the unsteadiness of the coherent structures. Whilst the focus here is on a supersonic jet, the analysis of this particular POD mode in its relation to the flow unsteadiness is applicable to any flow type, where POD may be used to identify periodic, large-scale vortical structures.

2 Methodology

2.1 Proper orthogonal decomposition

For POD analysis, if each velocity snapshot is an l by m array of vectors, with a total of N snapshots, where $l\times m>> N$, the method of snapshots can be implemented to determine the dominant fluctuations of the flow (Sirovich 1987). The eigenvalue problem solved for the method of snapshots is given by Eq. (1):

$$\begin{aligned} \varvec{R}\varvec{\nu } = \lambda {}\varvec{\nu }. \end{aligned}$$

(1)

The autocovariance matrix, $\varvec{R}$, is constructed from the velocity fields, such that

$$\begin{aligned} \varvec{R} = \varvec{V}^{\text {T}} \varvec{V}, \end{aligned}$$

(2)

and

$$\begin{aligned} {\varvec{V}} = \left[ \varvec{u'}^1~\varvec{u'}^2~\cdots ~\varvec{u'}^N \right] = \left[ \begin{matrix} u_{11}^{\prime {}1} &{} u_{11}^{\prime {}2} &{} \cdots &{} u_{11}^{\prime {}N} \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ u_{lm}^{\prime {}1}&{} u_{lm}^{\prime {}2} &{} \cdots &{} u_{lm}^{\prime {}N} \\ v_{11}^{\prime {}1} &{} v_{11}^{\prime {}2} &{} \cdots &{} v_{11}^{\prime {}N} \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ v_{lm}^{\prime {}1} &{} v_{lm}^{\prime {}2} &{} \cdots &{} v_{lm}^{\prime {}N} \end{matrix} \right] . \end{aligned}$$

(3)

Unless stated otherwise, the variables used for the POD analysis will be the two planar velocity components, u and v. Solving Eq. (1) yields the eigenvalues, $\lambda$, and the eigenvectors, $\varvec{\nu }$. The eigenvalues are sorted by $\lambda _n> \lambda _{n+1}$.

The nth spatial POD mode is given by

$$\begin{aligned} {\phi }_n(\varvec{x}) = \dfrac{\varvec{V}{\varvec{\nu }}_n(t)}{\left| \right| \varvec{V}{\varvec{\nu }}_n(t)\left| \right| }, \end{aligned}$$

(4)

and the coefficients for each snapshot of the nth mode are defined as

$$\begin{aligned} \varvec{a}_n(t) = {\varvec{\nu }}_n(t)\cdot \left| \right| \varvec{V}{\varvec{\nu }}_n(t)\left| \right| . \end{aligned}$$

(5)

Flows that exhibit coherent structures that are a result of a feedback process are often spatially and temporally periodic. These periodic structures can be represented by two sinusoidal functions, with a phase difference of 90$^\circ$, such as $A {\text {e}}^{i\theta } = \cos (\theta ) + i \sin (\theta )$. Due to this phase difference, the two functions form a circular pattern when plotted against one another. In terms of POD, the mode coefficients of two modes can be plotted, and a phase portrait constructed to illustrate the phase relation of the modes. If the phase portrait forms a circular ring, then the two modes in question are a modal pair describing a periodic flow phenomenon (Oberleithner et al. 2011). In this case, the phase angle, $\theta$ for snapshot k would be given by the relation: $\hat{a_k} {\text {e}}^{i \theta _k} = a_1(t_k) + i a_2(t_k)$. Due to the turbulent nature of these flows, deviations from a perfectly periodic mode pair occur. This results in snapshots lying off the circular ring, forming an annular distribution on the phase portrait.

Fig. 2

Schematic of the LTRAC gas jet facility

2.2 Experimental setup

The PIV measurements of this flow were acquired using the LTRAC gas jet facility. A schematic of the facility is presented in Fig. 2, with facility details available in Weightman et al. (2016). The conditions for the flow are shown in Table 1, where $M_j$ is the ideally expanded Mach number, z is the standoff height, t is the nozzle lip thickness, and D is the nozzle exit diameter, which for this case is 15 mm. Here, NPR is the nozzle pressure ratio between the plenum chamber and the ambient air and the Reynolds number is $Re = \frac{M_jc_jD_j}{\nu }$, where $c_j$ is the speed of sound at the ideally expanded conditions, and $\nu$ is the kinematic viscosity. $D_j$ is the exit diameter of a converging–diverging nozzle with throat diameter D, which generates ideal expansion at these flow conditions. The impingement surface was a square plate with a side length of 17.7D.

Table 1 Experimental conditions of the PIV measurements

Single exposure image pairs were acquired using a 12-bit Imperx B6640 camera, with a resolution of 6600 $\times$ 4400 px, using a 200 mm Micro-Nikkor lens and an added Nikon PK-12 extension ring. A dual cavity pulsed Nd:YAG laser was used to illuminate the particle field with light at a wavelength of 532 nm. The light sheet was diverging and had a thickness of approximately 1 mm through the test section. Additional PIV parameters are summarised in Table 2. The flow field was seeded using a ViCount 1300 smoke generator. Previous experiments in this facility (Mitchell et al. 2013) found that the smoke particles were approximately 600 nm in diameter given a measured relaxation time of approximately $2\,\upmu \hbox {s}$ (Melling 1997), with the particles assumed to be mono-disperse. Both the jet and the entrainment field were seeded with the same smoke generator. Particle images were diffraction limited with a diameter of $18\,\upmu \hbox {m}$, equivalent to 1.5 px. This resulted in minimal pixel locking.

The 10,000 time-independent PIV snapshot pairs were processed using the multigrid cross-correlation algorithm of Soria (1996), which allows for a minimum resolvable displacement of 0.1 px. The multigrid algorithm is particularly useful due to the large velocity difference between the jet core and entrainment field. This large displacement range required an initial window size, ${\text {IW}}_0$, of $192 \times 192\,\hbox {px}$ and a final window size, ${\text {IW}}_1$, of $24\times 24\,\hbox {px}$ for the PIV processing. A normalized median threshold of 3.0 and dynamic mean test of 1.0 with a standard deviation of 1.0 were used for vector validation.

Table 2 Pertinent PIV parameters

2.3 Synthetic data set

To complement the experimental study, synthetic velocity fields of a single vortex sheet were produced. These velocity fields were constructed using a row of Stuart vortices with amplitude, A. An imposed convective velocity, $U_{\text {c}}$, allowed for the velocity field to represent a half jet flow, with a maximum mean axial velocity of $2U_{\text {c}}$. The velocity field is given by (Stuart 1967; Shariff and Manning 2013):

$$\begin{aligned} u(\varvec{x},t)= & {} U_{\text {c}}\bigg (1-\frac{\sinh (\widetilde{y})}{\cosh (\widetilde{y})+\widetilde{A}\cos (\widetilde{x})}\bigg ),\end{aligned}$$

(6)

$$\begin{aligned} v(\varvec{x},t)= & {} -U_{\text {c}}\bigg (\frac{\widetilde{A}\sinh (\widetilde{x})}{\cosh (\widetilde{y})+\widetilde{A}\cos (\widetilde{x})}\bigg ), \end{aligned}$$

(7)

where

$$\begin{aligned} \widetilde{x} = \frac{x-U_ct}{\delta _x}, \quad \widetilde{y} = \frac{y}{\delta _y}, \end{aligned}$$

(8)

with $\widetilde{A} = A/\sqrt{A^2+1}$. The width of the shear layer is $\delta _y$ and the space between vortices is $2\pi \delta _x$. For simplicity, the shear-layer centre is located at $y = 0$.

3 Results

3.1 Case 1: initial statistics and POD analysis

Basic statistics of the impinging jet are presented in Fig. 3. The mean fields illustrate the underexpanded nature of the flow, with three shock cells observable prior to the standoff shock. The contours of variance given in Fig. 3c, d illustrate a high level of velocity variation along the shear layer for both velocity components.

Fig. 3

First- and second-order statistics for the flat plate impingement at an NPR of 3.4 and z / D of 5.0

Initially motivated by a desire to categorize the azimuthal instability mode of the flow, proper orthogonal decomposition was applied to the fluctuating flow fields. An uncertainty analysis was undertaken to confirm that the high-energy modes of the resultant POD are well converged. This analysis used the jackknife method to randomly resample the PIV data set for varying sample count (Efron 1982). For a given number of samples, the POD modes were calculated for 200 resamples taken from the full data set. Using a correlation value to find like modes, the relative energy content was compared. A 95% confidence range was determined for the relative specific kinetic energy for each sample count based on the variance of the 200 resamples. These are plotted in Fig. 4 with sample count ranging from 100 to 5000 samples. Due to processing limitations, higher sample counts were not tested. The value for 5000 samples shows a 95% confidence range of less than 1.7% of mode one and two’s specific energy value. Given the actual number of samples used was over 10,000, the mode energies are sufficiently converged for the following analysis. Relevant to later discussion, mode three’s relative energy has a slightly higher 95% confidence range of 2.6%, which is again considered sufficient to support the arguments made herein.

Fig. 4

95% confidence range of the first three POD modes. Determined by applying the jackknife method, with 200 resamples, on increasing sample counts

The calculated POD mode energy spectrum is shown in Fig. 5a, illustrating that two high-energy modes are present in the decomposition, with a cumulative energy of $\approx 33.7\%$. A phase portrait of the coefficients of these high-energy modes is presented as a joint PDF in Fig. 5b. Bins of size $0.4\langle r_m \rangle$ in each direction with a 75% overlap were used, where $\langle r_m \rangle = \langle \sqrt{a_1^2 + a_2^2} \rangle$. Shown by the joint probability distribution of Fig. 5b, the data points cluster about a mean radius, forming an annulus. As discussed in Sect. 2.1, this shape suggests that these two modes are a modal pair and describe a periodic phenomenon within the flow, with mode two being $90^\circ$ out of phase with mode one.

The four highest energy spatial modes are shown in Fig. 6, with the axial and transverse components shown. The nature of the modal pairing of mode one and two can be observed, with mode two’s shear-layer maxima and minima located at the node points of mode one, and vice versa. Specifically, these modes describe the fluctuations induced by the large-scale coherent structures that drive the aeroacoustic feedback process present in impinging jets (Edgington-Mitchell et al. 2014b; Weightman et al. 2017a). Given the antisymmetric nature of the axial component of the first two POD modes, the instability represented by these modes must be asymmetric. Considering the concentration of the mode energy into only two modes, and the geometry of the nozzle and impingement surface, a helical instability mode $(m =\pm 1)$ is more likely to exist within the flow, rather than a precessing flapping mode (Edgington-Mitchell et al. 2014a).

Fig. 5

a POD energy spectrum for the first 20 modes and b Joint PDF illustrating the phase portrait for modes one and two, with the mode coefficients normalized by $\langle r_{m} \rangle$

Fig. 6

First four spatial POD modes for an underexpanded supersonic impinging jet

The next highest energy modes, with specific kinetic energies of 3.9% and 1.7%, do not appear to be a pair based on their spatial structure. Whilst not shown here, the phase portrait does not form a clear annulus shape, suggesting that there is no phase relation between the two modes. The spatial structure of the third POD mode is vastly different to the structure of the high-energy modes, instead describing fluctuations along the axial length of the jet. This structure continues into a radial flow at the wall as observed in the transverse component of the spatial mode, as shown in Fig. 6g. Unlike the dominant mode pair, the spatial extent of this third POD mode prohibits it from describing individual large-scale coherent structures within the shear layer. This mode matches those illustrated in Fig. 1, though its relative contribution to the total energy is different. For clarity and for reasons that will become clear in the following sections, this mode will now be referred to as the shear thickness mode (STM).

In flows containing aeroacoustic feedback loops, it is possible for multiple instability modes to exist. Kumar et al. (2013) observed an intermittent switching between helical and toroidal instability modes in an impinging supersonic flow, whereas Weightman et al. (2017b) found that these two instability modes occurred simultaneously. The presence of two instability modes within the current flow would be apparent in the resultant POD modes, with a portion of the specific kinetic energy being attributed with each instability mode. This, however, is not observed for the current flow condition, with no symmetric POD mode pair observed in the 20 highest energy modes. In addition, the $m = 0$ and $m = 1$ instability modes will likely result in different impingement tone frequencies. In the acoustic data, not presented here for brevity, only a single peak is observed, suggesting that only one instability mode is occurring within this flow.

3.2 Case 1: investigating the role of the STM

To illustrate the relationship between the dominant modal pair and the STM, Fig. 7a shows a reproduced phase portrait with markers representing the mode one and two coefficient values for each snapshot. Here, the marker colour is given by the snapshot’s STM coefficient. A clear correlation is visible; snapshots that have highly negative STM coefficients are largely contained in the outer regions of the phase portrait. Conversely, highly positive coefficients are localised closer to the origin. Thus, the phase portrait of Fig. 7b suggests that snapshots containing a small contribution from the dominant mode pair are likely to exhibit a positive STM contribution. Snapshots that contain a larger contribution from the helical instability mode likely have a negative contribution of the STM.

To determine if this correlation between the dominant mode pair and other POD modes is unique to the STM, a Pearson correlation coefficient (PCC) is calculated between the dominant mode pair and the first 20 POD modes. As the phase portrait illustrates a circular shape, the magnitude of the contribution of the dominant mode pair for a snapshot can be described by its radial distance in coefficient space:

$$\begin{aligned} r_{12}(t) = \sqrt{a_1^2(t) + a_2^2(t)}. \end{aligned}$$

(9)

The resultant PCC between $r_{12}$ and each mode’s coefficients are presented in Fig. 7b. A PCC of 0.74 is calculated for the STM, with each other mode having a value of less than 0.15. This illustrates that the relation with the dominant mode pair is unique to the STM in this flow case. As discussed in Sect. 1, the STM can be difficult to identify from its spatial structure. This correlation between the magnitude of the dominant mode and each other POD modes’ coefficients provides a more direct method of identifying the STM.

Fig. 7

a Phase portrait of POD mode coefficients for modes one and two, where marker colour presents that snapshot’s STM coefficient. b Correlation between $r_{12}$ and the coefficients of modes 1–20

3.3 Case 1: the relationship between the STM and shear-layer thickness

To investigate the phenomenon described by the STM, the data set is separated into five subsets, each containing a quintile of snapshots based on the STM coefficients; set 1 contains the snapshots with the most negative STM coefficients. The conditional mean axial velocity, $U_\mathrm{con}$, at $x/D = 3.6$ calculated for each subset is presented in Fig. 8a. The mean profile for the full data set is also represented by the dashed ‘All’ line. This axial location was selected to emphasise the variation between sets, but also to ensure that there are minimal effects from the radial flow at the wall. It is observed that as the STM coefficients increase, the magnitude of the axial velocity gradient in the transverse direction increases. This suggests that the spreading of the jet is associated with the STM. A more in depth analysis of the shear-layer thickness is now undertaken.

Fig. 8

Comparison of conditional a mean axial velocity profile at x/D = 3.6 and b vorticity thickness for five subsets (solid line) and all sets (dotted line). Set one contains snapshots with STM coefficients in the first quintile, Set two contains snapshots in the second quintile, etc

The vorticity thickness, $\delta _\omega$, is used as an indicator of the shear-layer thickness of the jet and is given by Eq. (10):

$$\begin{aligned} \delta _\omega = \frac{U_2 - U_1}{\left( \frac{{\text {d}}U}{{\text {d}}y}\right) _\mathrm{max}}, \end{aligned}$$

(10)

where $U_2$ is the jet exit velocity ($U_{\text {E}}$) and $U_1$ is the ambient flow velocity and is here set to 0. $\delta _\omega$ is evaluated at each axial location from x/D = 0–4.0 using the mean of the full data set and is represented in Fig. 8b by the dashed line. The conditional mean axial velocities are used to evaluate $\delta _\omega$ for each subset, which are also illustrated in Fig. 8b. The humps present in each profile occur slightly downstream of the shock reflections points located at $x/D \approx 1.4$ and $\approx 2.8$. Before $x/D = 1.4$, the vorticity thickness profiles were approximately equal for each set. After this point, the subsets begin to diverge, with an increased divergence following the second shock reflection. By $x/D = 3.6$, $\delta _\omega$ has diverged by $\approx 0.12D$ between the first and fifth subsets. This variation is equal to 27% of the full data set’s shear-layer thickness at the same axial location.

The trend of vorticity thickness variation between subsets matches that of Fig. 8a. The most positive coefficient set (set 5) has the thinnest shear layer, with the thickness increasing as the STM coefficients of each set decrease.

To summarise, the above analysis shows the following:

• The structure of the STM prohibits it from describing variation in individual vortex size due to its spatial extent.

• There is a strong correlation between the coefficients of the STM and the amplitude of the dominant modal pair.

• The STM coefficients correlate with variations in the shear-layer thickness.

This analysis suggests that the STM describes the variation in the velocity field due to a change in shear-layer thickness between snapshots as a consequence of flow unsteadiness.

Figure 9 presents contours of vorticity for two instantaneous snapshots with STM coefficients at the 5th and the 95th percentile, i.e., highly negative and highly positive coefficients, respectively. A significant difference in the structure of the vorticity is present. For the positive STM coefficient of Fig. 9a, the shape of the large vorticity regions appears almost straight along the jet flow. Conversely, the 5th percentile snapshot has large variations in the transverse location of the peak vorticity along the axial length of the jet. Furthermore, larger ‘packets’ of vorticity are present in the negative coefficient case at $x/D \approx 2.4$ and 3.2 on the top and bottom shear layer, respectively. These ‘packets’ illustrate the existence of larger vortical structures in the negative coefficient snapshot compared to those present in the positive coefficient case. As discussed, this does not appear to be due to the jet switching between instability modes, but rather a decrease in the amplitude of the helical mode present. It is thus proposed that the variation in shear-layer thickness described by the STM is a result of unsteadiness in the size of the large-scale coherent structures that drive the feedback process. To isolate the variation in shear-layer thickness due to unsteady vortex size from other flow effects, a synthetic data set of a single shear-layer containing vortices is investigated.

Fig. 9

Vorticity of instantaneous snapshot with an STM coefficient at the a 95th, and b 5th percentile

3.4 Case 2: POD of the synthetic velocity fields

To separate the varying shear-layer thickness described by the STM from other effects occurring within the real flow, synthetic databases are produced using the Stuart vortex sheet model, as described in Sect. 2.3. A set with constant vortex amplitude and shear-layer width, with the vortex motion constrained to the axial direction, is constructed as a base case. A second synthetic case also has a constant vortex amplitude; however, the characteristic width of the layer, $\delta _y$, varies between snapshots. In the experimental case, a spectrogram of the acoustic signal for the impinging jet showed that the peak tone frequency remains almost constant. As the frequency of these tones is directly related to the spacing of the large-scale vortices, this spacing is also assumed to remain constant. Hence, for the synthetic data, the vortex spacing in the axial direction, given by $\delta _x$ in Eq. (8), is unchanged between snapshots. For the second data set, the characteristic layer width in the transverse direction, $\delta _y$, is the only parameter that is varied between snapshots. For this case, a Gaussian distribution with a mean of 0.4 and standard deviation of 0.05 is used for the $\delta _y$ variation. For the Stuart vortex sheet model, this changes not only the spatial variation of the vortices, but also the inherently linked axial velocity distribution across the shear layer in the transverse direction. Both the base and varying synthetic cases contain 10,000 time independent, two component velocity fields.

Typical instantaneous fields are presented for the base case, as shown in Fig. 10. A peak velocity of $u/U_{\text {E}} = 1$ occurs at the bottom boundary, with the axial velocity decreasing to 0 at the top boundary. Modulation of the velocity field can be observed in both components centered about $y/D = 0$. For the base case, the transverse velocity ranges between $v/U_{\text {E}} = \pm 0.12$.

Proper orthogonal decomposition is applied to the synthetic fields for the base case, with the energy spectrum, as presented in Fig. 11a. The phase portrait for modes one and two is also shown in Fig. 11b, with each snapshot coloured by its mode three coefficient. An almost perfect circle is formed by the phase portrait, as expected given the periodic vortices, large sample count, and the absence of added noise. The first two modes contain approximately 99% of the specific kinetic energy.

Figure 12 illustrates the first four spatial POD modes for the base case. The spatial structures of the first mode pair are as expected, with these modes representing the fluctuations due to the vortices traveling downstream within the shear layer. The next two POD modes are also a modal pair, though the corresponding phase portrait is not shown. These modes are the first harmonic modes of the dominant mode pair. This is illustrated by the colour variation of the phase portrait of Fig. 11b, where two cycles of mode three’s coefficients are completed for one cycle of the dominant mode pair.

Most importantly, no mode similar in structure to that of the STM of the experiment is observed in the resultant modes of the synthetic POD analysis. The only variation present in this synthetic case between snapshots in the spatial shift of the position of the shear-layer vortices. This axial variation in the shear layer is captured entirely by the dominant POD modes due to the $90^\circ$ phase shift between the mode pair and thus the STM is not required to reconstruct the snapshots. This observation, though expected, is significant in showing that the STM does not occur when variations in the shear-layer instability mode amplitude are absent.

Fig. 10

Typical instantaneous a axial and b transverse flow fields of the base single vortex sheet

Fig. 11

a POD spectrum and b phase portrait for the base case synthetic fields. The phase portrait is coloured by the coefficients of mode three, which is a harmonic of the dominant mode pair

Fig. 12

Axial and transverse components of the first four spatial POD modes for the base case synthetic fields

To test the hypothesis that the STM represents variations in the shear-layer thickness, the same decomposition is performed for the case with varying $\delta _y$. The resultant energy spectrum is shown in Fig. 13a. The overall energy of modes one and two has decreased compared to the base case, with mode three now containing $\approx 6$% of the total energy. The phase portrait, with snapshot marker colour determined by mode three coefficient, is presented in Fig. 13b. The same pattern as in Fig. 7 is observed, with a strong correlation between the mode three coefficients and the amplitude of the dominant mode pair.

The spatial modes of the varying case are illustrated in Fig. 14. Mode three is shown to have the same structure as a single shear layer in the STMs of the experiments (see Figs. 1, 6). Whilst the structure of the transverse component of mode three in the synthetic data is similar to modes one and two, its peak values are an order of magnitude lower than that of mode three’s axial component. This suggests that whilst the axial component of mode three may contribute a significant amount to the fluctuations of some snapshots, the transverse fluctuations are mostly unaffected.

Finally, the varying case is split up into five subsets, each containing one quintile of the synthetic data sets. Repeating the analysis of Sect. 3.3, the mean axial velocity distribution and vorticity thickness for each subset are determined and are presented in Fig. 15. As there is no spreading rate applied to the synthetic fields, the statistics can be averaged axially, as well as temporally. This results in a slightly different plot for the vorticity thickness, compared to Fig. 8, where now, a single marker denotes the thickness for the full data set and each subset. In Fig. 15a, the same trends are exhibited as in the experimental data analysis. As the STM coefficients increase, the magnitude of the transverse gradient of the axial velocity increases. Similarly, the vorticity thickness of Fig. 15b decreases with increasing STM coefficient. This matches the observation of the role of the STM in the analysis of the PIV data.

The synthetic data set supports the hypothesis that the STM, here represented by mode three, describes variations in the shear-layer thickness of the flow. This variation is likely a direct result of unsteadiness in the size of the large-scale coherent structures that populate the shear layer.

Fig. 13

a POD spectrum and b phase portrait for the varying case synthetic fields. The phase portrait is coloured by the coefficients of mode three

Fig. 14

Axial and transverse components of the first four spatial POD modes for the varying case synthetic fields

Fig. 15

Comparison of five subsets of the varying vortex sheet synthetic fields for a axial velocity profile and b centreline, upper and lower shear-layer boundaries. The subsets are as defined in Fig. 8

3.5 Comparison of different POD basis variables

The variable used as the basis of the proper orthogonal decomposition has a significant effect on the resultant modes (Kostas et al. 2005; Gurka et al. 2006; Tang et al. 2015). To determine if the STM is sensitive to the decomposition basis, the POD analysis is repeated for different base variables for both the experimental and synthetic data. The variables often used for planar PIV data are: both u and v velocity components, a single velocity component, or the out-of-plane vorticity, $\omega _z = (\frac{{\text {d}}v}{{\text {d}}x} - \frac{{\text {d}}u}{{\text {d}}y})$. POD was performed separately on these four bases; u and v, u, v, and $\omega _z$. The decomposed modes constructed from both velocity components, as shown in the previous sections, are taken as the reference case for each data set. The modes produced by the other variables are compared with the first three reference modes. This is accomplished using a cross correlation between the mode shapes of the reference case and each spatial mode of the POD for the different base variable. The mode with the highest correlation with a particular reference mode is assumed to describe the same spatial mode. This correlation was always greater than 0.95 for like modes.

This approach allows for a comparison of the relative contribution of like modes for the different decomposition methods, which is presented in Fig. 16a for the experimental data set and Fig. 17a, b for each synthetic case. The vertical axis denotes the relative energy and the horizontal axis gives the mode number based on the reference case spatial modes. The colour of each marker shows the mode number within each decomposition. For example, the highest energy mode of the transverse velocity decomposition has the same spatial structure as the second mode of the reference decomposition. Hence, it is located at mode two on the horizontal axis, but is coloured as mode one.

From Fig. 16a, the relative contribution of the vorticity modes is significantly lower than that of the velocity derived modes. Whilst mode one and two are still the dominant mode pair, the STM occurs lower in the modal ranking at mode four rather than mode three. Whilst the trend of the modes is the same for the axial-based POD and the reference case, the order of the dominant mode pair swaps in the transverse velocity-based POD. Whilst all three velocity-based decompositions rank the STM at mode three, the energy contribution is almost twice as large in the axial decomposition compared to the transverse. This is a somewhat expected result, as the STM’s spatial coefficients are larger in the axial direction in the reference case.

The impinging jet is unusual in that the direction of the mean flow changes at the wall, unlike a free jet, wake, or mixing layer. Thus, the STM mode from the transverse decomposition would contain less relative energy if the radial wall flow was excluded. This is illustrated in Fig. 16b, where the separate u and v decompositions were applied on a reduced region of interest (ROI), which excluded $x/D> 3.6$. It is shown that the relative energy of the STM in the transverse decomposition drops to less than $\approx 1/4$ of the axial-based POD mode three in this ROI and, consequently, is ranked at mode six.

Similar results occur for the synthetic data sets. Given the lack of high magnitude radial flow, the decomposition for only the full field is considered. For the base case, little variation is observed between the resultant mode energy between the four different variables. Whilst the dominant mode order does change when applying the axial and vorticity-based POD, mode three, which in this case is the first harmonic, does not change order. For the dominant modes, the same switching of the order of modes one and two occurs as in the PIV data for the varying case. The STM, however, contains a wide range of relative energy between the different decompositions. For example, the axial-based POD exhibits a much larger energy contribution to the STM than in the reference POD case. In contrast, the STM’s relative energy for both vorticity and transverse-based decompositions is lower compared to the reference case, with the latter decreasing to almost zero energy. Like in the experimental result, this is expected due to the fluctuations of the STM being largest in the axial direction of mode three (see Fig. 14c, d).

Each variable-based decomposition is able to capture both modes of the coherent structures as the two highest energy mode pair and the STM at a lower mode. Whilst the STM’s mode energy is significantly lower for the transverse velocity-based POD on the reduced ROI, the same mode spatial structure is observed. This suggests that the presence of the STM in the modal decomposition is independent of the variables used for the basis of the POD; however, its relative contribution is not. Thus, depending on the variable used for the decomposition, specific mode structures can be of quite low-energy and overlooked in the analysis. It is important to look beyond the highest energy modes, as well as decompose the data using different variables, to determine the appropriate choice of modes that will describe the relevant flow phenomena for a given flow. This may include spatial modes that do not initially appear important to the flow structure.

Fig. 16

Comparison of POD modes for different variable base components for a the full field and b a reduced ROI excluding $x/D> 3.6$

Fig. 17

Comparison of POD modes for different variable base components for a synthetic base case and b synthetic varying case

3.6 Implications of the presence of the STM

Whilst observing the presence of the STM within the POD modes suggests an unsteadiness of the coherent structures, the form of the unsteadiness is difficult to ascertain. An attempt to isolate intermittency and amplitude of variation is performed using synthetic velocity fields as above. The STM’s relative mode energy is compared across two variation conditions. For the first condition, the standard deviation of the $\delta _y$ variation was varied from 0.04 to 0.08, with the original data set having a value of $\sigma = 0.05$. The resultant mode energy of the STM is plotted in Fig. 18a, illustrating an increase in relative mode energy with increasing deviation size from the mean $\delta _y$ value. This suggests that as the vortex size ventures further from that of the mean vortex, the STM’s relative energy increases.

The second condition seeks to illustrate the effect of intermittency on the unsteadiness behaviour. This is intermittency in the statistical sense, with an increasing percentage of the time-independent snapshots given a $\delta _y$ value that deviates from the mean. The resultant mode energy of the STM is given in Fig. 18b. With 0% variation from the mean $\delta _y$, the STM does not occur, and thus has 0% of the relative energy. As the percentage of snapshots that are constructed with a different $\delta _y$ value increases, the relative STM energy likewise increases. This suggests that the STM energy may be an indicator of the intermittency of unsteadiness within the flow.

These two conditions illustrate that not only does the variation in the spatial extent of the vortices, in this case $\delta _y$, determine the relative energy of the STM, but the intermittency of those variations also has a significant effect. Whilst these two points were expected to contribute to the STM energy, this result helps more clearly define the suggested role of the STM. It is not only the amplitude of the variation of the vortices, but also the intermittency that determines the relative contribution of the STM in describing the flow.

Fig. 18

STM energy for different a $\sigma$ values for the variation in $\delta _y$ and b percentage of snapshots that deviate from the mean $\delta _y$

4 Conclusions

The existence of a specific POD mode structure, the shear thickness mode, has been observed here in several experimental flows, in both free and impinging underexpanded jets. The coefficients of the STM have a strong correlation with the amplitude of the coefficients of the dominant mode pair, which describes the large-scale coherent structures of the flow. The spatial structure of the STM, however, prohibits it from describing such structures. By separating the data set based on the STM coefficients, a link between the shear-layer thickness, represented by the vorticity thickness, and these coefficients is observed. Specifically, the STM appears to describe the variation of the shear-layer thickness between each snapshot. This variation is suggested to be the result of the unsteadiness of the large-scale shear-layer vortices that drive the aeroacoustic feedback processes of these flows.

Synthetic velocity fields supplemented the experimental results, with a steady base case as a reference and a non-steady case, which had variations in the transverse vortex size and shear-layer width between snapshots. The STM only exists in the latter case, and is again shown to correlate with the amplitude of the dominant mode pair; the link between the STM coefficients and the shear-layer thickness is again observed. As the only variation between snapshots was restricted to the characteristic shear-layer width, $\delta _y$, this result supports the hypothesis that the STM describes the variation in shear-layer thickness between snapshots. This shear-layer variation is a result of unsteadiness of the large-scale vortices, which can either be in the form of intermittency or vortex amplitude variation.

Several flow parameters are used for the basis of the POD decomposition. The STM is present in each flow that contained unsteadiness of the shear layer, with its relative mode energy varying depending on the flow variable used. In particular, the transverse velocity-based POD resulted in lower STM energy. Thus, using this variable as the basis for POD may result in the STM, or other low-energy modes of significance, being overlooked and important flow dynamics being ignored.