Development of a novel anemometry technique for velocity and temperature measurement

Abstract

Hot-wire anemometry is a widely used measurement technique for obtaining local velocities or temperatures in a flow-field. Operated under constant temperature or constant current the small diameter wires can resolve high-frequency velocity or temperature fluctuations with a high degree of spatial and temporal resolution. Therefore, more or less sophisticated hardware, e.g. using a Wheatstone bridge for constant temperature anemometry (CTA), is used with relatively high acquisition costs. In this paper a new technique is used, where the wire temperature or current is digitally controlled via a FPGA unit. The electric circuit is simpler than the usual set-ups and the hardware used is very robust, allowing to operate the control unit under harsh environments. This allows also to reduce the cable lengths, and therefore, eventually to increase the frequency response of the hot wire. The application of this technique for measurements of aerodynamic and thermal boundary layers under varying Reynolds numbers for laminar and turbulent boundary layers is demonstrated. The results are compared to measurements with standard CTA system and show that similar results are obtained with this new technique.

Graphical abstract

1 Introduction

Accurate measurement of flow properties is, despite the advances in flow simulation, still of crucial importance for further technology development or for an increase in knowledge on flow phenomena. Nowadays several measurement techniques are available and they can be divided into steady and time discrete as well as into intrusive or non-intrusive. Hot or cold wire techniques belong to the intrusive and time discrete measurement techniques and are used to measure the time mean as well as the fluctuating part of fluid velocity or temperature. The hot-wire probe consists of a wire with a diameter of some micrometers (in general between 1 and 10 μm) attached to prongs. It is common to use tungsten, platinum or platinum-alloy as material for the wire. For platinum wires, diameters down to 0.25 μm are reported in Bruun (1995). The wire sensors are operated by applying an electrical current through the wire, and the magnitude of the current or voltage can change depending on the specific technique used, the wire resistance, and the heat transfer rate from the wire to the surrounding fluid and bodies.

The perhaps most common anemometer technique for velocity measurements is the constant temperature anemometry (CTA). The applied voltage, and therefore, the electrical current are continuously adjusted to keep the wire temperature constant. The wire is heated by the electric current and with use of a proper material an almost linear relationship between wire temperature $T_{\rm w}$ and resistance at this temperature $R_{\rm w}$ can be established

$$\begin{aligned} R_{\rm w} = R_0 [1+\alpha _0\left( T_{\rm w}-T_0\right) ], \end{aligned}$$

(1)

with $\alpha _0$ as the temperature coefficient of resistivity and $R_0$ as the wire’s electric resistance, both at the reference temperature $T_0$. Hence setting the wire resistance to a fixed value is reciprocal to setting the wire temperature constant. The wire resistance is controlled in general by hardware via a Wheatstone bridge. A schematic of such an electric circuit is given in Fig. 1. The resistance $R_2$ sets the sum of the resistances of the wire and connecting cables $R_{\rm w}+R_{\rm c}$, when the bridge is balanced. If the wire resistance changes the bridge is unbalanced and the voltage through the amplifier corrects the voltage to reset the wire resistance to the desired value. The resistance of the hot wire in constant temperature operation is usually increased to a relatively high value to increase the sensitivity towards velocity differences and decrease the sensitivity towards temperature variation. According to Bruun (1995) the sensitivity towards velocity variation follows $\left| \partial E_{\rm w}/\partial U\right| \propto \sqrt{T_{\rm w}-T_{\infty }}$, while the temperature sensitivity is governed by $\left| \partial E_{\rm w}/\partial T_{\infty }\right| \propto \left( T_{\rm w}-T_{\infty }\right) ^{-0.5}$. The overheat ratio defined by

$$\begin{aligned} a_{\rm r} = \frac{R_{\rm w}-R_0}{R_0} \end{aligned}$$

(2)

is often set to 0.8, which is in general a good compromise between a good velocity sensitivity and a wire temperature below the maximum affordable by the same.

Fig. 1

Schematic of a CTA hardware set-up with a Wheatstone bridge, refer to Nitsche and Brunn (2006)

Another common way to operate hot wires is in constant current mode (CC). Applying a low overheat ratio, the sensor in CC mode is able to capture high-frequency temperature variations while in CT mode the cut-off frequency lies two orders of magnitude below the one for the CC mode, see Stainback and Nagabushana (1993). The sensor operated as a cold wire is a common way to measure temperature and its fluctuations. To lower the velocity sensitivity, the wire is operated at a current as low as possible but high enough to insure a good signal to noise ratio.

Both operating modes require different electrical compensation circuits and hardware set-ups. High-performance anemometry systems are commonly expensive and, typically for many electric systems, can be sensitive to harsh environments, such as extreme temperatures (below 10 °C or above 50 °C), or pressures well below ambient, or high accelerations.

An alternative method for controlling the wire temperature or current can be to use a digital controller with signal acquisition and output. Field-programmable gate arrays (FPGA) are one possible choice for a digital control unit. They allow for parallel computing, and therefore, parallel processing of the measured data and computation of the output variable. In this paper, a cRIO control unit from National Instruments is used as digital controller and the voltages and current are acquired and set by A/D input and output channels at the cRIO chassis. The functionality of the whole set-up was tested for absolute pressures down to 4000 Pa and ambient temperatures of 60 °C. The controller was programmed to operate in constant temperature as well as constant current mode and fluid velocity or temperature measurements were performed inside a laminar and turbulent boundary layer on a flat plate.

Here, the theory for the application of a digital controller to perform hot wire anemometry in constant temperature is presented and the method is described in detail. Simulations of the simplified control circuit with MatLab Simulink help to identify the limits of the digital controller. Measurements of the mean and fluctuating parts of the velocity inside the laminar and turbulent boundary layer show the quality of the results with the new system in comparison with results using a commercial analog CTA system. Finally, results of the mean temperature inside the laminar boundary layer show the suitability of the controller for CCA measurements.

2 Design of the digital control circuit

Fig. 2

Schematic of the electric circuit using the digital controller

The electric circuit used to operate the wire in CT as well as in CC mode is shown in Fig. 2. The output voltage E is set by the digital controller and the signal is proportionally amplified to $E_0$ to reach the power needed to achieve the desired overheat ratio. Typical output units for the cRIO chassis achieve only a current of 20 mA which is in general not enough to heat the wire. The voltages at the resistance $R_1$ as well as at the wire plus connecting cables $R_{\rm w} + R_{\rm c}$ are measured as $E_1$ and $E_2$ respectively. The electric current I is determined with $E_1$ and $R_1$ using Ohm’s law and for CT mode the resistance $R_{\rm w}$ is determined as

$$\begin{aligned} R_{\rm w} = \frac{E_2}{I}-R_{\rm c} = \frac{E_2\cdot R_1}{E_1}-R_{\rm c}. \end{aligned}$$

(3)

A programmable digital PID controller is used to determine the output voltage $E_0$ after the analog amplifier, based on the deviation of the measured resistance from the set-point $R_{\rm s}-R_{\rm w}$. By adjusting the gain value and the integral and derivative time constants, an optimized control and frequency response can be achieved.

The frequency response for the electric circuit can be estimated with the method used by Blackwelder (1981). The author linearises the energy equation and simplifies the problem by looking at small variations of the applied power $P=E_{\rm w}\cdot I$ and the heat flow F. Following the derivations given in the appendices (Sect. 1) one obtains

$$\begin{aligned} \frac{c_{\rm p}\cdot m}{R_0\cdot \alpha _0}\frac{{\rm d}{\Delta }R_{\rm w}}{{\rm d}t} + \left[ \frac{h\cdot S}{R_0\cdot \alpha _0} - \frac{E_0^2\left( R_1+R_{\rm c}-R_{\rm w}\right) }{R_{\rm t}^3}\right] {\Delta }R_{\rm w}= \frac{2E_0\cdot R_{\rm w}}{R_{\rm t}^2}{\Delta }E_0 - \frac{\partial F}{\partial U}{\Delta }U, \end{aligned}$$

(4)

with $R_{\rm t}=\left( R_1+R_{\rm c}+R_{\rm w}\right)$, the specific heat capacity of the wire $c_{\rm p}$ and its mass m, the heat transfer coefficient h and the wire surface area S.

The PID controller computes the output voltage $E_0$ based on the error $e=R_{\rm s}-R_{\rm w}=-{\Delta }R_{\rm w}$ and using the proportional gain $K_{\rm p}$ and the time constants $t_{\rm n}$ and $t_{\rm v}$ with

$$\begin{aligned} {\Delta }E_0 = -K_{\rm p}\left( {\Delta }R_{\rm w} + \frac{1}{t_{\rm n}}\int {{\Delta }R_{\rm w} {\rm d}t} + t_{\rm v}\frac{{\rm d}{\Delta }R_{\rm w}}{{\rm d}t}\right) . \end{aligned}$$

(5)

Substituting ${\Delta }E_0$ from Eq. (5) into Eq. (4) one obtains

$$\begin{aligned} \begin{aligned}&\left( \frac{c_{\rm p}\cdot m}{R_0\cdot \alpha _0} + K\cdot t_{\rm v}\right) \frac{{\rm d}{\Delta }R_{\rm w}}{{\rm d}t} + \left[ \frac{h\cdot S}{R_0\cdot \alpha _0} - \frac{E_0^2\left( R_1+R_{\rm c}-R_{\rm w}\right) }{R_{\rm t}^3} + K \right] {\Delta }R_{\rm w} \\&\quad + \frac{K}{t_{\rm n}}\int {{\Delta }R_{\rm w} {\rm d}t} = - \frac{\partial F}{\partial U}{\Delta }U, \end{aligned} \end{aligned}$$

(6)

with the constant K defined by

$$\begin{aligned} K = \frac{2\cdot E_0R_wK_{\rm p}}{R_{\rm t}^2}. \end{aligned}$$

(7)

2.1 Discrete system control

To check the system for stability, the transfer function for Eq. 6 is computed and analysed. For a digital system with discrete value acquisition a z-transformation on Eq. 6 is performed. With

$$\begin{aligned} Z [x (kt_{\rm s} ) ] = \sum _{k=0}^{\infty }x ( kt_{\rm s} ) z^{-k} \end{aligned}$$

(8)

for k discrete samples at time step $t_{\rm s}$, and using the trapezoidal rule for the integral term of the PID controller

$$\begin{aligned} {\Delta }R\left( z\right) \left[ \frac{t_2}{t_{\rm s}}\frac{z-1}{z} + t_1 + \frac{K_{\rm c}\cdot t_{\rm s}}{2}\frac{z+1}{z-1} \right] = -\frac{\partial F}{\partial U}{\Delta }U\left( z\right) \end{aligned}$$

(9)

is obtained, with

$$\begin{aligned} t_2= & {} \frac{c_{\rm p}\cdot m}{R_0\cdot \alpha _0} + K\cdot t_{\rm v} \end{aligned}$$

(10)

$$\begin{aligned} t_1= & {} \frac{h\cdot S}{R_0\cdot \alpha _0} - \frac{E_0^2 \left( R_1+R_{\rm c}-R_{\rm w}\right) }{R_{\rm t}^3} + K \end{aligned}$$

(11)

$$\begin{aligned} K_{\rm c}= & {} \frac{K}{t_{\rm n}}. \end{aligned}$$

(12)

Using $h\cdot S\cdot {\Delta }T=E_0^2\cdot R_{\rm w}/R_{\rm t}^2$ as well as Eqs. (1) and (2), the term $t_1$ can be rewritten as

$$\begin{aligned} t_1= & {} \frac{E_0^2R_{\rm w}}{R_{\rm t}^2\left( R_{\rm w}-R_0\right) }- \frac{E_0^2\left( R_1+R_{\rm c}-R_{\rm w}\right) }{R_{\rm t}^3} + K \nonumber \\= & {} \frac{E_0^2}{R_{\rm t}^3}\left[ R_{\rm w} + \frac{R_{\rm w}^2+R_0\left( R_1+R_{\rm c}\right) }{R_{\rm w}-R_0}\right] + K \nonumber \\= & {} \frac{E_0^2}{R_{\rm t}^3}\left[ 2R_{\rm w} + \frac{R_{\rm t}}{a_{\rm R}}\right] + K, \end{aligned}$$

(13)

which shows that $t_1$ is always positive. Hence, the transfer function for the discrete system is

$$\begin{aligned} \frac{{\Delta }R\left( z\right) }{{\Delta }U\left( z\right) } = \frac{-\frac{\partial F}{\partial U} z\left( z-1\right) }{z^2\left( \frac{t_2}{t_{\rm s}}+t_1+\frac{K_{\rm c} t_{\rm s}}{2}\right) + z\left( -\frac{2t_2}{t_{\rm s}}-t_1+\frac{K_{\rm c} t_{\rm s}}{2}\right) +\frac{t_2}{t_{\rm s}}}. \end{aligned}$$

(14)

The poles of Eq. (14) can be found to be

$$\begin{aligned} z_{1,2} = \frac{4t_2+2t_1t_{\rm s}-K_{\rm c}t_{\rm s}^2\pm t_{\rm s}\sqrt{\left( 2t_1-K_{\rm c}t_{\rm s}\right) ^2-16K_{\rm c}t_2}}{4t_2+4t_1t_{\rm s}+2K_{\rm c}t_{\rm s}^2}. \end{aligned}$$

(15)

for stability reasons $|z|\le 1$ and, following the method shown in  "Appendix", one can see that the system is stable for almost any $K_{\rm p}\ge 0$, which is very convenient.

2.1.1 Inverse z-transformation

The inverse z-transformation of Eq. (14) after a step change is obtained after multiplication of the same transfer function with $z/(z-1)$ and rearranging with the poles $z_1$ and $z_2$ of Eq. (15) to

$$\begin{aligned} {\Delta }R\left( z\right) = \frac{z}{z-z_1}\frac{z}{z-z_2}\left( -\frac{\partial E}{\partial U}\right) . \end{aligned}$$

(16)

After inverse transformation, the following solution is obtained

$$\begin{aligned} \begin{aligned} {\Delta }R (kt ) =&\Biggl \lbrace \frac{2\left( -1\right) ^kC^k \cos \left[ k\cdot \arccos \left( \frac{B}{2\sqrt{AC}}\right) \right] }{A\left( AC\right) ^{k/2}} \\&+ \frac{\left( -1\right) ^kC}{2A\sqrt{\frac{B^2}{4}-AC}} \left[ \left( -z_1\right) ^{k-1}- \left( -z_2\right) ^{k-1}\right] \Biggr \rbrace \frac{\partial E}{\partial U}, \end{aligned} \end{aligned}$$

(17)

with

$$\begin{aligned} A= & {} \frac{K_{\rm c}t_{\rm s}}{2} + \frac{t_2}{t_{\rm s}} + t_1 \end{aligned}$$

(18)

$$\begin{aligned} B= & {} \frac{K_{\rm c}t_{\rm s}}{2} - \frac{2t_2}{t_{\rm s}} - t_1 \end{aligned}$$

(19)

$$\begin{aligned} C= & {} \frac{t_2}{t_{\rm s}}. \end{aligned}$$

(20)

If the poles are complex still a non-complex solution is obtained for ${\Delta }R (kt_{\rm s} )$ with

$$\begin{aligned} \begin{aligned} {\Delta }R (kt_{\rm s} ) =&\Biggl \lbrace \frac{-2\left( -1\right) ^kC^{k/2} \cos \left[ k\cdot \arccos \left( \frac{B}{2\sqrt{AC}}\right) \right] }{A^{(k+2)/2}} \\&- \frac{\left( -1\right) ^kC^{(k+1)/2} \sin \left[ \left( k-1\right) \varphi \right] }{A^{(k+1)/2}\sqrt{AC-\frac{B^2}{4}}}\Biggr \rbrace \frac{\partial E}{\partial U} \end{aligned}, \end{aligned}$$

(21)

with

$$\begin{aligned} \varphi = {\left\{ \begin{array}{ll} \arctan \frac{2\sqrt{AC-\frac{B^2}{4}}}{B} &{} {\text {for}}\quad B> 0\\ \arctan \frac{2\sqrt{AC-\frac{B^2}{4}}}{B}+\pi &{} {\text {for}}\quad B<0 \end{array}\right. }. \end{aligned}$$

(22)

It is visible from Eq. (21) that

$$\begin{aligned} \lim _{k\rightarrow \infty }{\Delta }R (kt_{\rm s} ) = -3\left( -1\right) ^{k}\left( \frac{C}{A}\right) ^{k/2}. \end{aligned}$$

(23)

Hence, Eq. (21) converges for $A>C$ (which is always true for $K> 0$) and the convergence rate increases the larger this difference is. The factor C/A can be influenced by the control parameters $t_{\rm v}$, $t_{\rm n}$ and $K_{\rm p}$ as well as the sampling time $t_{\rm s}$ and the choice of the resistance $R_1$. The effects of these parameters for strictly positive values of the same are summarized in Table 1. It becomes visible from this table that the time constants $t_{\rm v}$ and $t_{\rm n}$ as well as the resistance $R_1$ should be chosen as small as possible. Not surprisingly, K should be increased as much as possible, since the circuit should be stable for all values of $K>0$. Probably more surprising is the fact that the settling time may decrease for increasing sampling time $t_{\rm s}$. Therefore, one must obtain the minimal time $t=k\cdot t_{\rm s}$, for which the variance ${\Delta }R$ can be considered negligible, i.e. $|{\Delta }R|\le {\varXi }$, which is equivalent to find a limit for $(C{/}A)^{k/2}$.

Table 1 Influence of the parameters on the value of C/A

The solution for optimal $t_{\rm s}$ can be found by inserting $k=t/t_{\rm s}$ into Eq. (23)

$$\begin{aligned} \left[ \frac{2t_{\rm n}\left( \tau _2+Kt_{\rm v}\right) }{t_{\rm s}^2K+2t_{\rm s}t_{\rm n}\left( \tau _1+K\right) +2t_{\rm n}\left( \tau _2+Kt_{\rm v}\right) }\right] ^{\frac{t}{2t_{\rm s}}} = {\varXi }. \end{aligned}$$

(24)

The optimum value for $t_{\rm s}$ can be found by solving Eq. (24) for t and setting $\partial t/\partial t_{\rm s}=0$, which gives, after some algebraic manipulation,

$$\begin{aligned} \exp \left[ \frac{t_{\rm s}\left( \frac{Kt_{\rm s}}{t_{\rm n}}+\tau _1+K\right) }{t_{\rm s}\left( \frac{Kt_{\rm s}}{2t_{\rm n}}+\tau _1+K\right) +\tau _2+Kt_{\rm v}}\right] = \frac{t_{\rm s}\left( \frac{Kt_{\rm s}}{2t_{\rm n}}+\tau _1+K\right) }{\tau _2+Kt_{\rm v}} + 1. \end{aligned}$$

(25)

One solution of Eq. (25) is $t_{\rm s}=0$, which can be a local maximum. A second solution might exist for $\frac{t_{\rm s}\left( \frac{Kt_{\rm s}}{t_{\rm n}}+\tau _1+K\right) }{t_{\rm s}\left( \frac{Kt_{\rm s}}{2t_{\rm n}}+\tau _1+K\right) +\tau _2+Kt_{\rm v}}> 1$, but this is not mandatory. Furthermore, it can be seen from Eq. (25) that the optimal sampling time $t_{\rm s}$ is independent of the threshold value ${\varXi }$ and that the optimum sampling time can also be influenced by the choice of $K_{\rm p}$, $t_{\rm v}$ and $t_{\rm n}$, in cases where a second solution of Eq. (25) exists.

2.2 Simulation of the control system

Fig. 3

Schematic of the control circuit simulated with Simulink

A control circuit following the derivations as explained above and in the appendices was designed with Matlab Simulink and a schematic of the same is shown in Fig. 3. The PID controller has limited outputs to $0\le E_0\le 2.5$ as in reality (for simplicity the proportional gain from E to $E_0$ is omitted) and the transfer function TF is set in accordance to Eq. (4). The input disturbance ${\varPsi }$ is representative of a change ${\Delta }U$ and its effects on ${\Delta }R_{\rm w}$.

The simulated frequency output $E_0$ and $R_{\rm w}$ for a variation in ${\varPsi }$ with amplitude of ${\varPsi }=1$, i.e. ${\varPsi }=\sin \left( \omega \right)$, is shown on the left of Fig. 4 for optimized combination of control parameters. The output for $E_0$ is normalized by the value for constant ${\varPsi }$, the Reynolds number based on the wire diameter is 2.5. It can be seen that variations up to a frequency of $\omega =100\,\mathrm {Hz}$ do not have any change in the voltage output and the resistance variations are damped up to two orders of magnitude. With increasing frequency the fluctuations tend to spread further and any variation of ${\varPsi }$ above the Nyquist limit, i.e. above half the sampling frequency, spreads out without any damping. The amplification of the control voltage $E_0$ as a function of the disturbance frequency can be taken from the same plot and the measurements corrected with this filter up to the limit imposed by the sampling frequency.

Fig. 4

Bode plot of the simulated output of $R_{\rm w}$ and $E_0$ for a oscillating variation in z (left) and signal history for the wire resistance $R_{\rm w}$ and voltage $E_0$ for a step change of $\psi = - \;0.01\Omega$ at $t=0.01\,\mathrm {s}$ (right)

The time history of the wire resistance $R_{\rm w}$ and the control voltage $E_0$ for a step change of $\varvec{\psi } = - \;0.01\Omega$ at $t=0.01\,\mathrm {s}$ is shown on the right of the same figure. One can observe that both resistance and voltage are back to normal values after four samplings, which is equal to ${\Delta }t=32 \ \upmu {\rm s}$. Nevertheless, there is of course an overshoot in voltage $E_0$ right after the step change of ${\varPsi }$ to rapidly recover the datum value of the resistance $R_{\rm w}$. One must be aware that these simulations are carried out on a simplified model using linearizations and omitting other limiting factors such as the connecting cables. Additionally, inaccuracies of the data in and output ($E_1$, $E_2$ and $E_0$) will limit the gain parameters to use. Nevertheless these simulations are an aid for estimation of the limits of the control circuit and in finding optimum parameters $K_{\rm p}$, $t_{\rm n}$ and $t_{\rm v}$.

3 Implementation of the technique and validation measurements

The digital data acquisition, the PID control and the voltage output was implemented in a cRIO-9014 digital control unit from National Instruments together with a cRIO-9114 chassis. The choice of this unit was based on experience using it in unusual environments with low absolute pressures, down to 4000 Pa. The cRIO unit as a clock timing of 40 MHz and the program for the digital controller was designed using the real-time module from LabView. The voltages $E_1$ and $E_2$ are acquired with NI 9222 and NI 9205 modules respectively while the voltage $E_0$ is set by a NI 9265 module attached to the amplifier. The limiting factor for the control system is the module for acquisition of $E_2$ with an update rate of 125,000 samples per second in differential mode. The whole data acquisition and control of the output is designed similar to the schematic of Fig. 3 programming the controller on the FPGA architecture of the cRIO. The controller is able to calculate the new output variables and to set the new output value in less than 3 μs each. Since all tasks are performed in parallel, the voltage acquired at 125 kHz is always influenced by the outcome of the preceding sample, i.e. the time lag between data acquisition and output update is much smaller than the time lag between the input samples.

Single hot wire sensors 55P15 as well as hot film sensors 55R03 from Dantec where used in the experiments and the overall cable length between control output and sensor was approximately 5 m.

Fig. 5

History of the voltage $E_2$ and resistance $R_{\rm w}+R_{\rm c}$ after a square-wave superposition (${\Delta }E_2$) on the voltage output

The square-wave response of the digital control system was tested and a exemplary time history is shown in Fig. 5. The data was acquired using the 55R03 probe and the superimposed disturbance voltage had a magnitude of approximately 10% of the mean voltage. The graph for ${\Delta }E_2$ has the same scale as the graph for $E_2$.

The voltage $E_2$ was acquired by an additional A/D board built into the measurement computer and the data acquisition was not triggered. Therefore, the time stamp might be actually slightly shifted. Though no optimization of the control parameters was performed, one can see that the system recovers over a time scale of about 100 μs.

As additional outcome of Fig. 5, one can observe that the response to the positive flank is not exactly equal to the one for the negative flank of the disturbance ${\Delta }E_2$. This can be explained by the fact that the disturbance was not absolutely in phase with the signal acquisition of the digital controller (2.2–125 kHz). Therefore, the transient behavior of the hot-wire is also not captured at equal positions for different occurrences of the step change. Nevertheless, the settling time for both flanks is comparable.

Fig. 6

History of the voltage $E_2$ and E for the digital controller and the Dantec system at no flow

A slight drawback of the digital controller, is that the technique, as it is used here, exhibits higher noise than a commercial high performance unit. Figure 6 shows exemplary voltage plots over time at no flow conditions and low static pressure. Both produce similar high-frequency oscillations of approximately 3 mV. However, for completeness one must say that translating the voltage into velocity leads to approximately double the noise for the digital controller, comparing it to the Dantec CTA system. This is due to the fact that in case of the digital controller, $E_2$ is measured, whereas the output for the Dantec system is $E_1+E_2$.

3.1 Velocity measurements

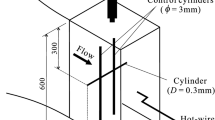
The test case for validation of the technique is a flat plate with an overall length of 0.4 m and width of 0.3 m. A schematic of the test article is shown in Fig. 7. The leading-edge shape is similar to a NACA 0012 profile.

Fig. 7

Schematic of the test specimen “flat plate”

The flow is set to a Mach number of 0.2 at Reynolds numbers, based on the overall length, of 200,000 and 800,000. The plate was installed in the High-Speed Cascade Wind Tunnel of the Federal Armed Forces University Munich. It is a continuously operating wind tunnel with open nozzle, details of which can be found in Sturm and Fottner (1985) and a drawing is depicted in Fig. 8. One of the main features is that the tunnel itself is inserted in a large pressure tank, where the static pressure can be lowered down to 4000 Pa. This allows a variation of the Reynolds and Mach numbers independent from each other. For the measurements shown here the static pressure inside the chamber varied between 11,240 Pa and 44,910 Pa depending on the Reynolds number. The nozzle exit had a cross-sectional area of $300 \times 400 \ {\rm mm}^2$ and boards at the nozzle limits above and below the plate were adjusted to control constant velocity along the plate measured by static pressure taps on the same.

Fig. 8

View of the high-speed cascade wind tunnel

Boundary-layer traverses with a single hot-wire probe 55P15 from Dantec were performed at mid span and at a distance from the leading edge of $x=300\,\mathrm {mm}$. The hot-wire probe has as sensor a tungsten wire with a diameter of 5 μm and is especially designed for boundary-layer traverses using the constant temperature technique. Reference velocity measurements were performed with a StreamLine Pro Anemometer System from the same company. Since the whole system has to be placed outside the pressure tank, an overall cable length between the Wheatstone bridge and the sensor of 20 m is used. The cut-off frequency of the low-pass filter was set to 30 kHz after optimization of the gain using the square-wave test.

The cRIO digital controller was placed inside the pressure tank and the overall cable length was 5 m.

The highest expected measurement uncertainty with the hot-wire measurement system from Dantec is between 0.1 and 1% of the measured velocity, based solely on uncertainty in the voltage acquisition. This value can be doubled when accounting for uncertainty in the calibration process and data fit by a polynomial function. Similar uncertainties for average values are expected for the system set-up with the digital controller, but more noise is possible due to poorer performance of the A/D-boards in the ranges used and smaller bandwidth of the control system. In fact for the lower Reynolds number, the bandwidth of the digital controller was limited to 8 kHz with the parameters used. Applying the declared random noise for the three A/D modules, one obtains a noise of $75\,\mathrm {V}$ for $E_0$, 650 μV for $E_1$ and 29 μV for $E_2$. Obviously the main noise contributor is the measurement of $E_1$. For very low velocities and voltages at the wire such a fluctuation would represent velocity fluctuations of approximately 0.05 m/s or 0.5 % of a mean velocity of 10 m/s. This means that close to the wall, where low velocities are measured, velocity fluctuations of around 0.5% of the mean velocity can be attributed to the noise of the A/D boards.

Fig. 9

Velocity profile (left) and fluctuations (right) along the boundary layer at $Re_x=150{,}000$

A comparison of the results using both techniques for a laminar boundary layer is shown in Fig. 9. On the left the measured velocities along the boundary layer are shown together with the analytical result found by Blasius (1908). It is clearly visible that both techniques show similar results and that they fit quite well to the theoretical solution. Close to the wall a slight shift of the velocity profile is seen for the standard technique due to wall proximity effects and different accuracies of the approximation polynomial at low velocities. On the right of the same figure, the velocity fluctuations are shown as root mean square of the velocity fluctuations $u'$ normalized by the mean velocity u for both measurement techniques. Also here the profiles lie close to each other. Again close to the wall, differences are seen, which can be explained by the higher velocities measured with the Dantec system in this region, but also to more noise using the digital control system as explained above.

Fig. 10

Velocity profile (left) and fluctuations (right) along the boundary layer at $Re_x=600{,}000$

A similar comparison is carried out for turbulent boundary layer at the higher Reynolds number and at a surface length of 300 mm, i.e. $Re_x=600{,}000$, in Fig. 10 but with $y^+$ as function of $u^+$. The semi-analytical result for the velocity profile is used as reference with $u^+=y^+$ for $y^+<10.8$ and $u^+=2.44\cdot \log (y^+ )+5$ for $y^+\ge 10.8$ as found in Kays et al. (2005). Again a very good comparison is obtained for both average velocities as well as relative velocity fluctuations. The first measurement point seems to suffer from wall proximity effects, since here the obtained velocities are too high compared to the reference curve using both measurement techniques. In the remaining part the data fits quite nicely to the expected data.

The difference in normalized rms-value of the velocity fluctuations in the near-wall region is again due to slightly different average velocities obtained with each technique.

3.2 Measurement of the local temperature

One of the great advantages of the simple hardware setup with digital controller is that it can easily be used to measure in constant current (CCA) mode. Measurements of the thermal boundary layer were carried out with the same probe operated in CCA mode at an overheat ratio of $a_{\rm r}=0.01$. According to the manufacturer, temperature fluctuations up to 10 Hz are perceivable by this type of probe. The digital controller was only slightly modified in order to cancel the offset between measured and desired current.

To create a thermal boundary layer, the same flat plate was covered with an inconel foil having a thickness of 25 μm. An electric current is set through the foil creating a constant heat flux of ${\dot{Q}}=E\cdot I$, which is corrected for heat conduction into the plate and heat radiation. To decrease the heat loss a material (Renshape BM 70 US) with a low heat conductivity of $k=0.1\,\mathrm {W/(m \ K)}$ is used.

Fig. 11

Normalized temperature profile along the boundary layer at $Re_x=150{,}000$

The measured temperature along a laminar boundary layer at $Re_x=150{,}000$ is depicted in Fig. 11 together with the analytical solution for a flat plate at constant temperature without pressure gradient, see Kays et al. (2005). The temperature is presented in normalized form defined by $\theta = \left( T_{w}-T\right) /\left( T_{\rm w}-T_{\infty }\right)$, with the wall temperature $T_{\rm w}$ and the temperature outside the boundary layer $T_{\infty }$. As said before, the heating foil creates a uniform heat along the surface. However, the heat conduction into the plate is larger with increasing wall temperature, i.e. with increasing boundary-layer thickness, which is the reason why the heat flux into the fluid reduces with increasing length x. At the end, the wall temperature is more uniform than with uniform convective heat flux into the fluid and the analytical solution for uniform wall temperature is a good comparison. It is seen that the measured temperature fits quite well to the expected curve. Only closer to the wall at a distance $\eta \le 0.1\,\mathrm {mm}$, are wall proximity effects noticeable.

4 Summary

A new measurement technology using hot and cold wire anemometry was developed and implemented using a programmable digital controller for setting the resistance of the wire or the current through the same. This new technology allows measurement of velocity and temperature of the fluid, including the fluctuating components, with the same set-up. It is versatile, allowing easy optimization to different set-ups and measurement conditions by simply adjusting the control parameters. The robustness of the system makes it even imaginable to be inserted into moving components such as in shafts of rotating test rigs. Further development and optimization of the A/D boards will allow to increase the bandwith of the control system even further.

The linearized equations for the controller are derived and the stability criteria are obtained, showing that the control loop is stable for almost any positive value of the gain parameter K. Optimized control parameters for proportional gain, derivative, and integral time are obtained using a simulation of the control loop in Matlab Simulink and it is shown that frequencies of several kHz can be in principle controlled using this set-up.

Square-wave tests with the implemented digital controller show that the simulated results are quite achievable also in reality.

The new technique is validated by measuring velocities and temperatures along laminar and turbulent boundary layers with zero pressure gradient. The measured velocities are compared to theoretical solutions as well as to measurements with a commercial CTA device. The comparisons show very good agreement among the three solutions and also good agreement in the velocity fluctuations between both measurement techniques.

The temperature measurement with the new technique along a laminar boundary layer shows also good agreement with the theoretical solution, confirming the validity of the set-up for both measurement techniques CTA and CCA.

In the future, further validation measurements are to be carried out and the implementation of faster data acquisition devices is expected to enhance even more the dynamic behavior of the control loop.

The implementation of constant voltage anemometry is also possible without large effort which could allow for simultaneous velocity and temperature measurement as reported in Stainback and Nagabushana (1993).

Appendix

1.1 Determination of the energy equation

Neglecting heat flow due to radiation, natural convection and heat conduction at the ends of the wire, the heat flow is equal to the heat transfer due to forced convection

$$\begin{aligned} F = {\dot{Q}}_{\rm c} = h\cdot S\cdot \left( T_{\rm w}-T_{\infty }\right) . \end{aligned}$$

(26)

Hence the energy equation simplifies to

$$\begin{aligned} \frac{{\rm d}{\dot{Q}}_{\rm s}}{{\rm d}t} = c_{\rm p}\cdot m\frac{{\rm d}T_{\rm w}}{{\rm d}t} = P-F. \end{aligned}$$

(27)

Assuming only finite differences of the power and heat flow and neglecting higher order derivatives, i. e. $F={\overline{F}}+{\Delta }F$ and $P={\overline{P}}+{\Delta }P$, Eq. (27) can be seen as a linear function

$$\begin{aligned} c_{\rm p}\cdot m\frac{{\rm d}{\Delta }T_{\rm w}}{{\rm d}t} = {\overline{P}}+{\Delta }P-{\overline{F}}-{\Delta }F \end{aligned}$$

(28)

or, since the time average values ${\overline{P}}-{\overline{F}}=0$,

$$\begin{aligned} c_{\rm p}\cdot m\frac{{\rm d}{\Delta }T_{\rm w}}{{\rm d}t} = {\Delta }P-{\Delta }F. \end{aligned}$$

(29)

Writing the electric power as

$$\begin{aligned} E_{\rm w}\cdot I=\frac{E_0^2\cdot R_{\rm w}}{\left( R_{\rm w}+R_{\rm c}+R_1\right) ^2} \end{aligned}$$

(30)

and inserting Eq. (1) in Eq. (29), with

$$\begin{aligned} {\Delta }P= & {} \left( \frac{\partial P}{\partial E_0}{\Delta }E_0 + \frac{\partial P}{\partial R_{\rm w}}{\Delta }R_{\rm w}\right) \\ {\Delta }F= & {} \left( \frac{\partial F}{\partial U}{\Delta }U + \frac{\partial F}{\partial R_{\rm w}}{\Delta }R_{\rm w}\right) \end{aligned}$$

one obtains after some algebraic manipulation

$$\begin{aligned} \frac{c_{\rm p}\cdot m}{R_0\cdot \alpha _0}\frac{{\rm d}{\Delta }R_{\rm w}}{{\rm d}t} + \left[ \frac{h\cdot S}{R_0\cdot \alpha _0} - \frac{E_0^2\left( R_1+R_{\rm c}-R_{\rm w}\right) }{R_{\rm t}^3}\right] {\Delta }R_{\rm w}= \frac{2E_0\cdot R_{\rm w}}{R_{\rm t}^2}{\Delta }E_0 - \frac{\partial F}{\partial U}{\Delta }U, \end{aligned}$$

(31)

1.2 Stability regions for the discrete transfer function

For obtaining the poles of Eq. (15) with $|z|\le 1$ one must distinguish between real and complex solutions as well as for $z\ge 0$ and $z<0$ for real solutions. Looking first at the real solutions and rearranging Eq. (15) one obtains setting $z\le 1$

$$\begin{aligned} \pm t_{\rm s}\sqrt{\left( 2t_1-K_{\rm c}t_{\rm s}\right) ^2-16K_{\rm c}t_2}\le 2t_1t_{\rm s} - K_{\rm c}t_{\rm s}^2. \end{aligned}$$

(32)

After substitution of $t_1=\tau _1+K$, $t_2=\tau _2+Kt_{\rm v}$, $K_{\rm c}=K/t_{\rm n}$ and squaring Eq. (32) the equation can be rearranged to

$$\begin{aligned} 8K^2\left( 2\frac{t_{\rm s}^3}{t_{\rm n}}+\frac{t_{\rm s}^4}{t_{\rm n}^2}+2\frac{t_vt_{\rm s}^2}{t_{\rm n}}\right) + 16K\left( \frac{\tau _1t_{\rm s}^3}{T_{\rm n}}+\frac{\tau _2t_{\rm s}^2}{t_{\rm n}}\right) \ge 0 \quad {\text {for}}\quad 0\le z\le 1 \end{aligned}$$

(33)

The first solution of Eq. (33) is $K\ge 0$ since all values inside the brackets are positive. The second solution is found by rearranging it to

$$\begin{aligned} 8K\left( 2\frac{t_{\rm s}^3}{t_{\rm n}}+\frac{t_{\rm s}^4}{t_{\rm n}^2}+2\frac{t_vt_{\rm s}^2}{t_{\rm n}}\right) \ge - \ 6\left( \frac{\tau _1t_{\rm s}^3}{t_{\rm n}}+\frac{\tau _2t_{\rm s}^2}{t_{\rm n}}\right) \end{aligned}$$

(34)

or finally

$$\begin{aligned} K \ge -\frac{2t_{\rm n}\left( \tau _1t_{\rm s}+\tau _2\right) }{t_{\rm s}^2+2t_{\rm n}\left( t_{\rm s}+t_{\rm v}\right) }. \end{aligned}$$

(35)

The second real case is obtained setting $z\ge - \ 1$ which gives

$$\begin{aligned} \pm t_{\rm s}\sqrt{\left( 2t_1-K_{\rm c}t_{\rm s}\right) ^2-16K_{\rm c}t_2}\ge - \ 8t_2 -6t_1t_{\rm s} -K_{\rm c}t_{\rm s}^2 \end{aligned}$$

(36)

The same steps as above are performed to obtain

$$\begin{aligned} \begin{aligned}&K^2\left[ t_{\rm v}\left( 4t_{\rm v}+6t_{\rm s}+\frac{2t_{\rm s}^2}{t_{\rm n}}\right) +2t_{\rm s}^2+\frac{t_{\rm s}^3}{t_{\rm n}}\right] \\&\quad + \ K\left[ \tau _2\left( 8t_{\rm v}+6t_{\rm s}+\frac{2t_{\rm s}^2}{t_{\rm n}}\right) + \tau _1t_{\rm s}\left( 6t_{\rm v}+4t_{\rm s}+\frac{t_{\rm s}^2}{t_{\rm n}}\right) \right] \\&\quad + \ 4\tau _2^2+6\tau _1\tau _2t_{\rm s}+2\tau _1^2t_{\rm s}^2\ge 0 \quad {\text {for}} \quad -1\le z<0 \end{aligned}. \end{aligned}$$

(37)

Solving Eq. (37) yields two negative solutions

$$\begin{aligned} K\ge & {} -\frac{\tau _1t_{\rm s}+2\tau _2}{t_{\rm s}+2t_{\rm v}} \end{aligned}$$

(38)

$$\begin{aligned} K\ge & {} -\frac{2t_{\rm n}\left( \tau _1t_{\rm s}+\tau _2\right) }{t_{\rm s}\left( t_{\rm s}+2t_{\rm n}\right) +2t_nt_{\rm v}}. \end{aligned}$$

(39)

The second solution is exactly the same as Eq. (35) and is in general closer to zero as the first solution for this second case.

The complex solutions are independent of the quadrant, and since only the route term in Eq. (15) can be complex, the solutions can be found by setting

$$\begin{aligned} \frac{\sqrt{\left( 4t_2+2t_1t_{\rm s}-K_{\rm c}t_{\rm s}^2\right) ^2+t_{\rm s}^2 \left[ \left( 2t_1-K_{\rm c}t_{\rm s}\right) ^2-16K_{\rm c}t_2\right] }}{4t_2+4t_1t_{\rm s}+2K_{\rm c}t_{\rm s}^2} \le 1. \end{aligned}$$

(40)

Expanding Eq. (40) leads to a very similar equation as the ones above and in fact one solution of the same is equal to Eq. (35), whereas the second solution can be found to be

$$\begin{aligned} K\ge \frac{- \ 2\tau _1t_{\rm n}}{2t_{\rm n}+t_{\rm s}}. \end{aligned}$$

(41)

Summarizing, the requirements listed in Table 2 can be found.

Table 2 Requirements on K for stable solutions of the control system

Requirements 2, 3(a) and 3(b) are always negative values and can, therefore, be summarized by

$$\begin{aligned} K\ge 0, \end{aligned}$$

(42)

since only positive values of $K_{\rm p}$ are considered. Further analysis can be carried out on K for obtention of real values of z, i.e. for cases 1 and 2 in Table 2. To achieve real solutions the term under the route of Eq. (15) has to be positive, i.e.

$$\begin{aligned} \left( 2t_1-K_{\rm c}t_{\rm s}\right) ^2-16K_{\rm c}t_2\ge 0. \end{aligned}$$

(43)

This restriction is achieved for

$$\begin{aligned}&K\le 2\frac{\chi _1-4\sqrt{\chi _2}}{t_{\rm n}\left( 2-t_{\rm s}/t_{\rm n}\right) ^2-16t_{\rm v}} \vee K\ge 2\frac{\chi _1+4\sqrt{\chi _1}}{t_{\rm n}\left( 2-t_{\rm s}/t_{\rm n}\right) ^2-16t_{\rm v}} \quad {\text {for}}\; \xi>0 \end{aligned}$$

(44)

$$\begin{aligned}&2\frac{\chi _1+4\sqrt{\chi _2}}{t_{\rm n}\left( 2-t_{\rm s}/t_{\rm n}\right) ^2-16t_{\rm v}} \le K \le 2\frac{\chi _1-4\sqrt{\chi _2}}{t_{\rm n}\left( 2-t_{\rm s}/t_{\rm n}\right) ^2-16t_{\rm v}} \quad {\text {for}}\;\xi <0 \end{aligned}$$

(45)

with

$$\begin{aligned} \chi _1= & {} 4\tau _2+\tau _1 t_{\rm s}-2\tau _1 t_{\rm n} \end{aligned}$$

(46)

$$\begin{aligned} \chi _2= & {} \tau _1^2 t_{\rm v} t_{\rm n}-\tau _1\tau _2 t_{\rm n}+0.5\cdot \tau _1\tau _2 t_{\rm s}+\tau _2^2 \end{aligned}$$

(47)

$$\begin{aligned} \xi= & {} \left( 2-t_{\rm s}/t_{\rm n}\right) ^2-16t_{\rm v}/t_{\rm n}. \end{aligned}$$

(48)

Hence, in most cases Eq. (42) limits the stable solutions of Eq. (14). Only for $\xi>0$ the second interval of Eq. (44) sets a different limit with a minimum value for K larger than zero.