Characterizing free-surface expressions of flow instabilities by tracking submerged features

Abstract

Under unidirectional flow, complex bottom roughness such as seagrass canopies can induce Kelvin–Helmholtz (KH) shear instabilities, and these vortices can impact the free surface and leave a signature with an inherent frequency. Therefore, one approach to inferring the presence and properties of submerged ecosystems may be to look at the behavior of the water surface. We present an imaging-based laboratory method developed to characterize this canopy-induced shear instability. Much like a lens, a curving free surface refracts light at the interface (Moisy et al., Exp Fluids 46:1021–1036, 2009). Using cameras placed above the length of a flume, the water surface slope is measured by tracking the apparent distortion of submerged model vegetation in a series of images, manifested as a slight shimmering over time. We demonstrate that the synthetic Schlieren technique can: (1) measure the spectral signature of the canopy-induced shear instability on the free surface, (2) provide high-resolution spatial information on the development of the instability over the entire canopy length, and (3) measure the propagation speed and length scale of the coherent KH rollers at the surface and detect distinguishable differences in these properties for varying canopy geometry.

1 Introduction

1.1 Physical motivation

Under unidirectional flow, bottom roughness such as seagrass canopies and other submerged aquatic vegetation can induce a Kelvin–Helmholtz shear instability (Ghisalberti and Nepf 2002). The rollers generated are critical to vertical mass and momentum transfer between flow above and within the canopy and set the dominant turbulent scale throughout the flow domain (Nepf and Ghisalberti 2008). Organized waving of both terrestrial vegetation, “honami” (Finnegan 1979), and aquatic vegetation, “monami” (Ackerman and Okubo 1993), is attributed to these vortices. Ghisalberti and Nepf (2006) and Okamoto and Nezu (2009), among other studies, found that a coherent vortex induces a strong downward sweep at its back side and a weak upward ejection at its front side, and these sweeps and ejections are concentrated in the mixing layer zone centered near the top of the canopy.

Much work in the past few decades has focused on using coherent turbulent structures for insight into subsurface flow characteristics (Pan and Banerjee 1995; Kumar et al. 1998; Savelsberg et al. 2006; Chickadel et al. 2009; Plant et al. 2009; Koltakov 2013). These turbulent structures form near bed-form irregularities but can be advected upward through the water column. When such turbulent features reach the surface, they generate signature expressions such as upwellings, downwellings, and counter-rotating vortices (Kumar et al. 1998).

Rosenzweig (2017) found that the coherent vortices of a canopy-generated shear instability can impact the free surface and leave a signature with an inherent frequency as they pass. Experimental results showed that the roller had a spreading angle between 9.5$^\circ$ and 11.5$^\circ$ from its generation at the beginning of the canopy to where it first appeared at the free surface, indicating that a canopy might leave a “footprint” on the free surface proportional to its size. However, data were limited to sparse laser Doppler anemometry (LDA) measurements at points 5 mm below the free surface, as well as a few direct point measurements of the actual surface slope. Higher-resolution measurements are needed to gain a deeper understanding of how the instability develops and evolves over the canopy, as well as how the surface behavior depends on the properties of the system. We aim to use the surface signature of the instability generated by bottom roughness features to characterize the structure of the bed, in hopes that future field and laboratory studies can reduce the number and scope of measurements required to study the dynamics of interest.

The goals of this paper are to develop a method that (1) gives spatial and temporal resolution of the free surface over a patch of model vegetation, (2) allows us to infer relationships between surface measurements and characteristics of the submerged roughness, and (3) provides insight towards a theoretical understanding of this instability.

1.2 Review of optical methods for measuring free-surface behavior

A number of of optical methods for measuring characteristics of the water surface have been developed over the past several decades. Lasers provided useful point measurements of surface slope (e.g., Lange et al. 1982). Savelsberg et al. (2006) tracked the refraction of a laser beam through the air–water interface to measure turbulence manifested on the free surface. They extended this laser refractometry method by rapidly scanning the incident laser beam along a line to obtain spatial information in one dimension in addition to temporal resolution.

Sutherland et al. (1999) and Dalziel et al. (2000), among others, leveraged distortion of background patterns to study density variations in flows using digital image correlation (DIC) techniques. These techniques fall under the umbrella of “synthetic Schlieren” and background-oriented Schlieren (BOS) methods. Building on the work of Kurata et al. (1990) and Elwell (2005), Moisy et al. (2009) developed the free-surface synthetic Schlieren (FS-SS) method, which tracks the distortion of a random dot pattern through a liquid interface using traditional particle image velocimetry (PIV) algorithms. They related these pixel displacements $\mathbf {\delta r}$ to surface slope as:

$$\begin{aligned} \nabla \eta = - \mathbf {\delta r} \left( \frac{1}{\alpha h_p} - \frac{1}{H_\mathrm{cam}} \right) \end{aligned}$$

(1)

where $\nabla \eta$ is the gradient in the location of the water surface, $\alpha$ is related to the refractive indices of the two fluids, $\alpha = 1 - n_\mathrm{air}/n_\mathrm{liq}$, $h_p$ is the distance between the pattern and the liquid interface, and $H_\mathrm{cam}$ is the height of the camera above the pattern. Essentially, the displacement field measured is linearly proportional to the actual surface slope. If the wavelength of the surface phenomenon is less than the field of view, the surface gradient field can be numerically integrated to estimate water depth. The conditions required for the linearity assumption in this method to be valid are discussed in more detail in Sect. 3.2.

Dolcetti et al. (2016) studied the free surface in shallow-water flow over a rough bottom boundary. This was perhaps the first experimental study to characterize the frequency–wavenumber spectrum and dispersion relations of the waves generated in a turbulent free-surface flow. However, because of the obstructing bottom roughness in their problem, they were unable to use optical methods and instead used two orthogonal arrays of wave probes to gain a quasi-3D characterization of the free-surface behavior.

The limitation of existing imaging methods is that they depend on a smooth, horizontal bottom with either a flat, distinct pattern (e.g., random dots or a checkerboard) or a transparent bottom through which a laser can shine. When studying flows with more complex bathymetry, such idealized setups are not possible. In the following experiments, we extend the FS-SS method to measure surface slope over bathymetric roughness.

1.3 Outline and scope of this paper

In this paper, we present an extension of the free-surface synthetic Schlieren method developed by Moisy et al. (2009), in which we track distinct features of preexisting bathymetric roughness and do not require artificial checkerboard or dot patterns. In Sect. 2, we describe the experimental setup and image processing techniques. In Sect. 3, we describe validation and sensitivity of the technique. In Sect. 4, we demonstrate the capabilities of the technique using canopy flow as an illustrative example, including tracking the development of the instability over the canopy length, computing the relevant length scales and propagation speed of the roller, and observing variation of surface behavior with flow and canopy properties.

2 Experimental setup and image processing

2.1 Experimental setup

Experiments were conducted in a 6 m long by 0.61 m wide by 0.61 m deep recirculating flume. A variable speed pump fills a constant head tank, which in turn drives flow to the inlet section of the flume. The inlet section converges through a series of homogenizing grids of decreasing size into the glass-walled rectangular test section. The test section is 3 m long with a 1.5 m buffer zone both upstream and downstream to mitigate entrance and exit effects on the flow profile. A sharp-crested downstream control weir is used in conjunction with the pump’s variable speed control to independently change flow rate and flow depth. A complete description of the facility is available in O’Riordan et al. (1993).

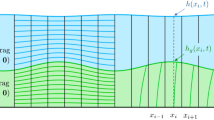
A model vegetative canopy composed of an array of rigid wooden cylinders was set up at the inlet of the test section to generate the shear instability. The canopy was 1.5 m in length, and dowels were 6.35 mm in diameter. Geometry and definitions of variables are shown in Fig. 1. The circular ends of the cylinders were painted white with one coat of Bic Wite-Out correction fluid, and a waterproofing coat of white Sally Hansen nail color. Water depth was kept constant at 31.2 cm for all experiments by varying the height of the outlet weir in conjunction with pump power. Experiments were run for three different flow speeds, with different canopy heights and densities as shown in Table 1. The Reynolds number listed is defined as:

$$\begin{aligned} Re_{\infty } = U_{\infty }H/\nu \end{aligned}$$

(2)

where $U_{\infty }$ is the free-stream velocity for given flume settings in an unobstructed channel (0.20, 0.15, and 0.10 m/s for fast, medium, and slow cases, respectively), H is the flow depth (0.312 m), and $\nu$ is the kinematic viscosity of water (1 × 10⁻⁶ m²/s). Although these same three flume settings were used for all experiments, actual free-stream and within-canopy velocities vary based on the geometry of the cylinder array present. The submergence ratio, $h_c/H$, is the ratio of the canopy height (20 and 15 cm) to water depth. The canopy density ranges from dense to intermediate for the experimental cases presented here; prior velocity measurements showed that the sparsest array did not yield as strong an instability signal at the surface due to weaker shear. Figure 2 shows the layout of the cylinder arrays, as well as the spacing between rows.

Fig. 1

Canopy geometry, showing definitions of variables and coordinate system. Flow through the canopy (left to right) creates a mixing layer, with faster fluid moving at speed $U_s$ and slower fluid moving through the canopy at speed $U_c$. Shear creates overturning Kelvin–Helmholtz rollers, shown pictorially as rotating circles, which propagate downstream over the canopy. Schematic adapted from Ghisalberti and Nepf (2002)

Table 1 Experimental runs

Fig. 2

Canopy density for the intermediate and dense cases. Variable $S_r$ indicates the streamwise spacing between rows. Cylinders are placed in polycarbonate sheets with holes drilled at 1.875 cm spacing. Here, darkened circles indicate a cylinder is present; a white circle indicates the drilled hole is empty. Canopy density controls the spatial resolution of the data collected

An array of six Basler Ace (model number acA1300-60gm) monochrome cameras was set up to image the length of the cylinder array. Camera synchronization and image logging were performed using a LabVIEW program. Cameras were triggered by a function generator (BNC Model 555 Pulse/Delay Generator), and images were transferred by Ethernet cables onto two data acquisition computers. Camera frame rate was set to 10 frames per second, with all cameras taking images simultaneously. Each camera was equipped with a Tamron lens with an f-stop of F/2.1, focal length of 35 mm, and exposure time of 8000 µs. Images were 1280 × 1024 pixels, yielding a field of view (FOV) of approximately 25 cm ${\times }$ 25 cm. Following the notation of Moisy et al. (2009), we define the camera height $H_\mathrm{cam}$ as the distance between the camera and the features being tracked. Because we are tracking the tips of the cylinders, $H_\mathrm{cam}$ changes with varying canopy height. The cameras were positioned 206 cm above the flume bottom. Figures 3 and 4 show a schematic of this setup and a photo of the facility.

Fig. 3

Experimental setup. Images taken show plan view of flume, with tips of canopy elements manifesting as white circles

Fig. 4

Experimental setup. Photo taken looking down from above the flume. Canopy elements along the centerline have white circles painted on the cylinder tips

2.2 Image processing to obtain displacement fields

Following Moisy et al. (2009), the surface gradient field of an air–water interface can be computed based on the displacement of features at a known depth:

$$\begin{aligned} \nabla \eta = - \mathbf {\delta r} c_p \left( \frac{1}{\alpha (H-h_c)} - \frac{1}{H_\mathrm{cam}} \right) . \end{aligned}$$

(3)

Here we define $\mathbf {\delta r}$ as the displacement field in pixels and calibrate from pixels to centimeters using the factor $c_p$. The factor $c_p$ was determined by computing the median circle diameter detected by the particle tracking algorithm in pixels and dividing this by the diameter of the cylinders in centimeters. Note as well that $h_p$ has been replaced by $(H-h_c)$, the distance between the free surface and the features being tracked—in this case, the circular tips of the cylinders.

To robustly detect these circular tips, images were first masked to remove spurious artifacts and thresholded. The cylinder tips were then tracked over time using particle tracking (Ouellette et al. 2005). The tilting of the surface manifests itself as a slight wobbling in the apparent location of the cylinder tips over time. Cylinders themselves were observed throughout the experiments and verified to be rigid and motionless.

Particle tracking, while usually utilized for tracking actual kinematic movement of particles in a flow, is still applicable in this case where it is used to track only apparent movement of fixed features through an air–water interface. Particle tracking codes simply assume smoothness and continuity of motion, which still holds in this case as we do not encounter caustics. To verify that particle tracking does not introduce spurious kinematics, we also utilized an alternate method in which circles are detected using a circular Hough transform (see documentation accompanying MATLAB function imfindcircles). Circle centers are sorted into a grid so that the position of each individual cylinder tip is tracked over time. This method yielded the same result as particle tracking; the data presented here are based on particle tracking algorithms.

Displacement of circle centers $[C_{x}, C_{y}]$ from their mean position was computed in a Reynolds-averaging sense (overbars indicating time average):

$$\begin{aligned} \mathbf {\delta r} = [C_{x,t}',C_{y,t}'] = [C_{x,t}, C_{y,t}] - [\overline{C}_{x}, \overline{C}_{y}] . \end{aligned}$$

(4)

This displacement field was then substituted into equation (3). Because we do not use a reference image of the setup at a fixed mean water level, our definition of $\nabla \eta$ varies from that of Moisy et al. (2009). We define the full surface slope field as $\nabla \xi$ and decompose it as $\nabla \xi = \nabla \bar{\eta } + \nabla \eta$. Thus, we are measuring instantaneous deviations ($\nabla \eta$) from the mean ($\nabla \bar{\eta }$) as indicated by the above equation.

The final result of these computations is a time series of the fluctuating surface gradient $\nabla \eta = [\partial \eta / \partial x, \partial \eta / \partial y]$ over every cylinder in the array. Sample time series of $\mathbf {\delta r}$ and $\nabla \eta$ are shown in Fig. 5. The signal $\delta r_x$ shows pixel displacements in the streamwise direction; $\delta r_y$ shows variations in the cross-stream direction. Roller expression in the surface slope is much more coherent in the streamwise direction, while more high-frequency oscillations appear in the cross-stream. We will therefore direct most of our focus on streamwise characteristics of the flow.

Spectral quantities, such as peak frequency and bandwidth of the Kelvin–Helmholtz instability, can be computed using these data. We determined the peak frequency following Rosenzweig (2017), computing spectra of the surface slope using Welch’s periodogram method with 36-s ensemble windows with 50% overlap. The frequency of the instability peak was identified visually. The power spectral density spectrum of the surface slope is simply in the units of seconds, as it represents the spectrum of the (dimensionless, m/m) surface slope. It will be shown that the relative magnitude of the spectrum is quite informative.

Each canopy element provides a time series, yielding 360 and 720 independent data points for the intermediate- and high-density array cases, respectively. Therefore, in addition to temporal information sampled at 10 Hz, we were also able to gain spatial information, such as the streamwise development of the instability, its propagation speed, and characteristic length scales.

Fig. 5

Sample signal from one canopy element. The signal $\delta r_x$ in (a) shows pixel displacements in the streamwise direction, and $\partial \eta / \partial x$ in (c) likewise shows the streamwise surface slope. The signal $\delta r_y$ in (b) shows pixel displacements in the cross-stream direction, and $\partial \eta / \partial y$ in (d) shows the cross-stream surface slope. Roller expression in the surface slope is much more coherent in the streamwise direction, and will be the focus of much of this paper. Error bars are shown in (c) and (d)

3 Validation

3.1 Comparison with established measurements

We first validated the results of the imaging technique versus prior velocity measurements just beneath the free surface to ensure that the technique yields the same spectral properties, particularly the peak frequency of the instability. We validated using Runs 1, 2, and 3, for which we have laser Doppler anemometry (LDA) data (methods and results discussed in Rosenzweig 2017). LDA measurements presented here were taken 5 mm below the free surface at the trailing edge of the canopy and used the horizontal (u) velocity component. The same spectral peak and breadth of this peak were measured using the two different techniques, to within measurement error. Figure 6 shows the power spectral density, normalized by its maximum value, from both techniques. LDA spectra are from the turbulent fluctuations in horizontal velocity ($u'$). FS-SS measurements show power spectral density of the surface slope normalized by its maximum value and are taken from a canopy element in the last row of the cylinder array. The position and shape of the spectral peak show more variation in the slow flow case, as the signal is weaker in less energetic flows.

Fig. 6

Comparison of the power spectra of the velocity fluctuations as measured by LDA (black dashed) and the surface slope fluctuations as measured by the method presented in this paper (red solid). Shown are the fast, medium, and slow flow cases for the 20 cm intermediate density canopy (Runs 1, 2, and 3)

3.2 Validity and uncertainty

We also assessed the validity of the assumptions described by Moisy et al. (2009) for our experimental setup. These assumptions include:

• 1. Paraxial approximation: The pattern-camera distance $H_\mathrm{cam}$ must be much larger than the field size L, yielding a maximum paraxial angle $\beta _\mathrm{max} \simeq L/(\sqrt{2}H_\mathrm{cam}) \ll 1$. For this setup, $H_\mathrm{cam} \sim$ 190 cm, $L \sim$ 25 cm, so $\beta _\mathrm{max} \simeq 0.09$.

• 2. Weak slope approximation: The angle $\gamma$ between the unit vector normal to the free surface and the vertical vector must be small; thus, the surface slope itself must be small. Surface slopes measured here were on the order of 5 mm over 1 m (0.005 m/m).

• 3. Weak amplitude approximation: The amplitude of perturbations from the mean must be small compared to the feature-surface distance, $H-h_c$. Viewed through the glass side walls of the flume, variations from the mean water level are on the order of millimeters, while the feature-surface distance ranges from 10.2 to 15.2 cm.

Although the camera was set up to minimize parallax distortion, we verified that the same power spectral density was found at different positions in the field of view to ensure that any spatial differences in power spectral density are physical, rather than distortion in regions of the FOV due to a failure in the paraxial approximation. We set up two cameras with overlapping fields of view and compared the raw signal and the power spectral density from a row of cylinders. In one camera, this row was seen at the top edge of the field of view; in the other, it was aligned with the center. As seen in Fig. 7, properties of the spectrum (Fig. 7c) such as peak frequency, power spectral density at this peak, and bandwidth of the peak are nearly identical for the same row captured in two different fields of view. Additionally, these quantities remain relatively fixed in the cross-stream direction. Figure 7e shows the signal from a single element, as imaged from both cameras. The raw slope signal of this element was nearly identical when located in different (streamwise) portions of the field of view. Therefore, we concluded that any observed differences in spectral properties are actual physical manifestations, and not artifacts of the imaging technique or underlying linearity assumptions.

Fig. 7

Slope spectra and raw slope signal from one row of canopy elements, viewed from two cameras. Images (a) and (b) above show the fields of view when two cameras are overlapped by 50%. Circles on the top two images indicate the single element used for comparing the spectra and the raw slope signal. Dashed lines on the spectrum in (c) and raw signal in (e) represent data from Camera 1; solid lines represent data from Camera 2. The spectra and raw signals are practically identical when measured from two different points of view. The slope signals from each are compared in (d), with the line $y=x$ showing an exact correspondence. While there is scatter, it is important to note that spectral quantities, order of magnitude, and general trends are identical when imaged from two different cameras

The largest source of uncertainty in this experimental technique are the constants used in equation (3). The bias and random error are summarized in Table 2. In order to quantify the contribution of this uncertainty to the observed signal, we followed the propagation of random errors outlined by Moffat (1988) for a sample time series of $\nabla \eta$. We defined $\nabla \eta = f(\mathbf {\delta r}, c_p, H_\mathrm{cam}, H, h_c)$, re-computed $\nabla \eta$ using the perturbed variables, and found the root-sum-square of the residuals. The resulting uncertainty as a percentage of $\partial \eta / \partial x$ was approximately $\pm \;5$%; uncertainty bars are shown in Fig. 5c, d. The potential bias error is much larger than random error for the variable $H_\mathrm{cam}$, as we have assumed the location of the camera center without performing a camera calibration, in order to reduce complexity of the technique. We believe the uncertainty in the estimated camera height is an acceptable compromise to maintain procedural simplicity, given that a change of $\pm \;10$ cm in $H_\mathrm{cam}$ yields only a $\pm \;0.1$% change in the value of $\nabla \eta$.

Table 2 Bias and random error (estimated 95% confidence intervals) in quantities used to calculate $\nabla \eta$, for $h_c$ = 15 cm

4 Results

Several capabilities of this technique can be highlighted using the illustrative example of canopy flow. The results shown below demonstrate that the technique can spatially and temporally resolve important physical features of a canopy-induced shear instability.

4.1 The spectral signature of the Kelvin–Helmholtz instability at the surface evolves over the canopy length, and indicates that the roller is growing and propagating.

Since each cylinder provides a time series of surface slope, we can examine how the power spectral density develops over the entire canopy length. For these experiments, the FOV of each camera overlapped by about 10%. To examine streamwise development, we look at the signal from a line of cylinders along the centerline of the flume. For the 20 cm cylinder case ($h_c/H = 0.64$), the spectra show that energy at the peak instability frequency increases as one moves downstream for all flow cases (Fig. 8). Colors of the spectra indicate measurements at different streamwise locations in the canopy. The peak instability frequency is noted; higher-speed flows have higher peak frequencies, i.e., shorter-period surface perturbations.

Fig. 8

Slope spectra for different slow speeds, experimental cases 1–3. Darker colors indicate upstream elements at the leading edge of the canopy; lighter colors indicate elements at the downstream, trailing edge of the canopy. The vertical line indicates where the peak instability frequency occurs. Higher-speed flows have higher peak frequencies, i.e., lower-period oscillations

Energy at the peak spectral frequency—e.g., $f_p$ = 0.7 Hz for Fig. 8a—increases in the downstream direction. This is to be expected, as the velocity profile is developing shear at the height of the canopy, before reaching a fixed flow profile. Rollers will also take time to form and grow large enough to impact the free surface. For slower flows, there is also a significant oscillation at a frequency of approximately 1.6 Hz that is present even at the leading edge of the canopy. These are likely surface ripples that are shed from the unevenness in the sidewalls at the transition from the inlet section of the flume to the test section, which is flattened out at faster speeds.

For all of these cases, we can look at a vertical slice of the spectrum at the primary peak frequency to see how energy at the peak frequency evolves with respect to downstream distance x. Figure 9 plots the power spectral density at the peak frequency versus downstream distance. The power spectral density at the peak frequency for each experimental case is normalized by the corresponding maximum value that occurs along the length of the canopy.

For both canopy geometries tested here, the roller manifests itself at the surface around 0.5 $L_c$ downstream of the leading edge of the canopy. Its energy at the surface grows at an increasing rate. The spreading angle can be computed as the tangent of canopy-surface distance divided by the location at which the signal first appears at the surface. This gives spreading angles between 8$^\circ$ and 12$^\circ$, a result that agrees well with those found from the velocity measurements of Rosenzweig (2017). However, because the roller first manifests itself at the surface at the same location along the canopy length in these experiments, the suggestion arises that instead of a constant or uniform spreading angle, there may be a constant development length that is independent of canopy height (although the canopy density may also play a role in these experimental cases). If the spreading angle or development length of this instability is known a priori, this would prove useful, as it it would allow surface measurements (in the laboratory, or in the field using existing remote-sensing techniques) to independently predict the canopy’s location.

Fig. 9

Normalized power spectral density at peak instability frequency and its streamwise development. The vertical axis shows the energy at the peak frequency for each experimental case, normalized by its corresponding maximum value along the length of the canopy. The energy in the surface slope reaches its maximum at the trailing edge of the canopy, $x/L_c = 1$

4.2 Coherent structures can be visualized and tracked, and their surface properties are predictive of subsurface flow characteristics and roughness geometry

Because we have extensive spatial resolution of a 1.5 m $\times$ 0.25 m portion of the flume, we can examine both the spatial and temporal characteristics of the free surface.

Visualizing rollers. We can look at snapshots of the free surface slope over the entire canopy at an instant in time, and visualize rollers as they develop and propagate over the domain. Figure 10 shows three snapshots in time of roller manifestation at the free surface. The plots show instantaneous streamwise surface slopes throughout the domain for one experimental case. In agreement with the spectral analysis, the rollers begin to manifest at the free surface about halfway through the length of the canopy. Dark bands represent negative slopes, and light bands represent more positive slopes. Stronger surface slopes develop as they propagate downstream. The rollers are approximately 2D, indicating that this given domain can be assumed homogeneous in y.

Fig. 10

Snapshots in time of the streamwise surface slope, $\partial \eta /\partial x$, for the 20 cm high canopy at the fast flow speed. Black-outlined circles represent the data points and actual resolution of the measurement technique; surface slope is linearly interpolated between these points to provide higher-resolution contours. Darker colors indicate more negative slopes; lighter colors indicate more positive slopes. The rollers begin to be visible at the surface around halfway through the length of the canopy. The dark band at $\frac{3}{4}L_c$ at $t=1.9$ sec represents the downward-sloping back side of the roller, and its movement can be tracked over time. The roller has moved about $\frac{1}{8}L_c$ by the third snapshot 0.8 s later

Propagation speed of the rollers. Figure 10 suggests that we can compute the speed at which these rollers propagate downstream. By cross-correlating the signal of the farthest downstream element with signals further upstream, we can estimate the propagation speed $C_p$ of the roller. Figure 11 shows a sample calculation; the approach is similar to particle image velocimetry (PIV), where a given spatial shift between two signals has an associated correlation peak in time, yielding a speed $\Delta x/\Delta t$.

Fig. 11

Sample cross-correlation of surface slope signals for elements spaced a distance $\Delta x$ apart, with a correlation peak at $\Delta t$, yielding a propagation speed of the roller

We compute these quantities for each element along the centerline of the flume for each case and plot $\Delta x$ versus $\Delta t$ as shown in Fig. 12. The slope of each line represents the propagation speed of the roller over the canopy. As might be expected, the speed of the roller increases for increasing flow speeds. Results of these calculations are summarized in Table 3. Of further note is the constant slope of the plots in Fig. 12, suggesting that the propagation speed of the rollers is constant across the cylinder array.

The propagation speed of the roller is approximately equal to the velocity at the inflection point of the velocity profile. Velocity profile measurements for these experimental cases are presented and discussed in Rosenzweig (2017), and referenced briefly in Table 3. This means that the rollers are traveling at a speed slower than most of the surrounding fluid, and that their propagation is governed by the speed of fluid in the region of peak shear, i.e., the site of roller generation. The inflection point velocity $U_i$ generally coincides with $U_h$, the velocity at the height of the canopy. Nepf and Ghisalberti (2008) note that in a free shear layer (one unbounded by a canopy below and a free surface above), the vortex is centered at the inflection point of the velocity profile, and travels at this inflection point velocity. In a canopy shear layer flow, the center of the roller is shifted upwards, and the vortex propagates at a velocity higher than that at the inflection point, or height of the canopy. Our results support this conclusion, as the rollers propagate at a speed on the order of 1–2 cm/s faster than the estimated inflection point velocity ($C_p/U_i \approx 1.1$). Ghisalberti and Nepf (2002) also measured the speed of vortices generated by a submerged canopy of flexible model vegetation, and found that the ratio of the vortex propagation speed to the mean velocity at the height of the canopy ($C_p/U_h$) ranged from 1.3 to 1.76. In terrestrial canopies, the accepted value of $C_p/U_h$ is 1.8 (Finnegan 1979).

Fig. 12

Propagation speeds of the roller, with dx computed with respect to the farthest downstream canopy element. Black = fast, red = medium, blue = slow flow cases. Elements in the first 50 cm of the canopy are excluded in linear fits, as previous figures demonstrate that the instability has not yet significantly manifested at the surface. Linear fits are computed using a robust linear model estimator with bisquare weight function

Length scale of the rollers. We can also measure a correlation length scale of the roller, defined as the distance r at which the correlation function below crosses zero:

$$\begin{aligned} R_{xx}(r,x) = \left\langle \frac{\partial \eta }{\partial x}(x,t) \cdot \frac{\partial \eta }{\partial x}(x+r,t) \right\rangle \end{aligned}$$

(5)

where angle brackets indicate a time average. Zero-crossings that fall between two spatial points are linearly interpolated.

As our previous results suggest, the roller first appears at the free surface about halfway through the canopy. This is where a dominant length scale emerges in Fig. 13, as shown by the convergence in the plot. Correlation length $L_\mathrm{corr}$ normalized by $(H-h_c)$ is plotted as a function of downstream distance. As coherence of the surface signal is weak for the upstream portion of the canopy, there is a great deal of scatter, with correlation lengths converging as the rollers gain a coherent shape. For each experimental case, we compute a single correlation length as the median value for $x/L_c > 0.65$, where the value has reached approximately steady state.

A zero-crossing in the correlation function above represents when two quasi-periodic signals are 90$^\circ$ out of phase; thus, the actual length scale or “wavelength” of the roller is four times the correlation length, $L_\mathrm{roller} = 4 \cdot L_\mathrm{corr}$. These measurements agree well with a rough estimate of the roller size obtained by dividing the speed of the roller by its dominant frequency. These results are summarized in Table 3.

Okamoto et al. (2016) found that the integral length scale of coherent structures at the top of the canopy was on the order of the vegetation height for flexible vegetation, while for rigid vegetation the structures were 1.5–2 times the vegetation height. However, our results show an inverse relationship between canopy height and roller size. The most likely reason for the difference between our scaling and that of Okamoto et al. is that our flows are more strongly confined by the free surface; for the experiments shown here, the submergence ratio $H/h_c$ ranges from 1.6 to 2.1, while the rigid vegetation tested by Okamoto et al. was significantly more submerged, at $H/h_c = 3.0$.

This results in two important differences in the flows. First, Nepf and Vivoni (2000) showed that the the distance into the canopy to which a significant turbulent stress extends asymptotes at around $H/h_c$ of 2. Their results and those of Raupach et al. (1996) suggest that for $H/h_c < 2$, the penetration depth is reduced because the shear length scale is limited by the water depth. Our measurements occur at the boundary of two regions of behavior. This supports our findings that the largest turbulent length scale in these experiments may be restricted by the canopy-surface distance $(H-h_c)$. Second, as shown by McDonald et al. (2006) for flow over corals, as the submergence ratio decreases more of the flow is forced through the canopy rather than “skimming” over it. In their case, this produced large differences in the drag coefficient over the corals and this behavior could be a significant factor in this flow as well.

In Fig. 14 we summarize the relationship between properties of the roller and properties of the flow that induced the roller by comparing two Reynolds numbers:

$$\begin{aligned} Re_\mathrm{roller} = \frac{C_{p}L_\mathrm{roller}}{\nu } \quad \mathrm {and}\quad Re_\mathrm{flow} = \frac{U_i (H-h_c)}{\nu }. \end{aligned}$$

(6)

The direct relationship between $Re_\mathrm{flow}$ and $Re_\mathrm{roller}$ indicates that the incident flow conditions and canopy geometry will set all characteristics of the coherent structures that develop. While the trend is promising and suggestive of a linear proportionality between $L_\mathrm{roller}$ and $(H-h_c)$, we recognize that our results are limited to six experimental runs. Further research is required to investigate this possible disagreement with previous results and to clarify the factors that govern KH roller size, particularly in regards to the submergence of the vegetation and degree to which the free surface confines the growth of the shear layer and the coherent structures.

Fig. 13

Correlation lengths for all experimental cases. Black = fast, red = medium, blue = slow flow cases. o = 15 cm canopy, asterisk 20 cm canopy. Black line shows where $L_\mathrm{corr} = H-h_c$. As coherence of the surface signal is weak for the upstream of the canopy, there is a great deal of scatter. Downstream values converge to 60–75% of the gap between the canopy and the free surface

Fig. 14

Comparison of Reynolds numbers. $Re_\mathrm{flow}$ is based on the previously known flow characteristics and experiment geometry; $Re_\mathrm{roller}$ is based on properties of the roller measured using this imaging technique. Definitions are provided in equation (6)

Table 3 Summary of experimental results. Values of $U_i$, the inflection point velocity, are taken from Rosenzweig (2017)

5 Conclusions

We present a laboratory remote-sensing technique to measure the surface expression of subsurface coherent structures due to a Kelvin–Helmholtz shear instability. The technique is non-intrusive and relies solely on a camera and identifiable roughness features beneath the water surface. The beauty of this methodology lies in its simplicity: flow characteristics of a commonly used experimental setup can be measured remotely with the addition of one or more uncalibrated cameras to the pre-existing setup—no lasers, complex optics, or elaborate calibration routines are required.

We demonstrate that this synthetic Schlieren technique for tracking submerged features is able to:

• 1. Measure the same spectral signature of a shear instability previously characterized using velocity measurements from within the water column.

• 2. Provide high-resolution spatial information on the development of the instability over the length of the cylinder array.

• 3. Measure the propagation speed and predominant length scale of the instability and detect distinguishable differences for varying experiment geometries.

However, this technique may not be applicable in all laboratory situations. The main limitations of the technique include:

• 1. The interface studied must be between two clear, uniform-density fluids.

• 2. The presence of caustics and ray-crossings. We have performed a set of experiments with a tall, dense, longer canopy at high flow speeds which generated significant surface-impacting boils with sharp slope changes and caustics that make this method unusable. An example image from a 2.25 m long canopy with elements 20 cm in height and at the densest case is shown in Fig. 15. Note that with ray-crossings, a single submerged feature can show up multiple times on the surface. However, useful data may still be gleaned between such occurrences.

• 3. It requires identifiable features, at a density adequate to spatially resolve the phenomenon of interest.

• 4. It requires some prior knowledge of the depth of the features in order to convert measured pixel displacements into physical quantities (i.e., surface slope). However, if only interested in the predominant frequency of the signal and other spectral properties, then the actual magnitude and units of the power spectral density are irrelevant.

Fig. 15

Sample images from an experimental case not reported here, with a longer canopy where the roller has broken up into strong surface-impacting boils. Image on left shows the surface absent of a large disturbance. Image on right shows the surface strongly distorted by a boil in the bottom center of the FOV. The boils have strong curvature, causing ray-crossings that not only make tracking of individual cylinder tips difficult but also make the assumptions required for this technique untenable

Despite these limitations, the method provides promising insight towards a deeper theoretical understanding of a canopy-generated shear instability. It also possesses a number of predictive capabilities that can be applied in future studies. By first determining parameterizations of peak frequency, propagation speed, and length scales for varying canopy geometry and flow speeds, we will be able to infer properties of the subsurface roughness based solely on surface measurements.

The method also allows us to look at lateral variation which may be due to development of secondary instabilities or spatial differences in roughness. For more strongly three-dimensional flows than the illustrative example studied here, high resolution of both the streamwise and spanwise spatial variation of the flow may be particularly useful. Preliminary results using this technique on a longer canopy found that there is increased spanwise variation farther downstream, and suggest that the 2D coherent rollers may eventually break up into multi-scale 3D structures (see caption of Fig. 15).

These results have a variety of applications and extensions. In the laboratory, this technique is an alternative to in situ measurements, provides a two-dimensional map of surface properties over a large region, and cuts down on experiment run times dramatically by providing simultaneous spatial sampling. It may be useful for studies of setup, mean water levels, and wave steepness changes over vegetation. Extending to the field, we can now work towards an understanding of how the inherent frequency, length scale, and propagation speed of the instability depends on canopy configuration, density, and submergence. These same surface expressions may be detectable in the field using existing remote sensing techniques. Additionally, the feature-tracking synthetic Schlieren technique itself may yield useful insights if adapted to drone studies over clear water, where bathymetric features are plentiful and distinct, e.g., Chirayath and Earle (2016). Laboratory studies may be necessary first to develop feature-tracking and triangulating algorithms for roughness that is irregular and varies in depth. A promising direction may be to combine feature identification and tracking algorithms developed in the computer vision community such as SIFT (Lowe 2004) and optical flow methods in conjunction with depth triangulation using stereo-refraction methods, such as those developed by Morris (2004) and Gomit et al. (2013).