1 Introduction

When a liquid jet is extruded from an orifice it may fragment into drops. This discontinuity, resulting from the capillary instability of the jet surface, was first observed more than a century ago by Savart (1833), followed by Plateau (1843). Since then, numerous experiments have been reported on this phenomenon using controlled jets, i.e., forced jets (e.g., Rutland and Jameson 1971; Gordon et al. 1973; Taub 1975; Collicott et al. 1994; Christanti and Walker 2002; Keshavarz et al. 2015). Much fewer experiments were conducted with non-controlled jets, i.e., free jets (e.g., Grant and Middleman 1966; Leroux et al. 1996; Blaisot and Adeline 2000, Christanti and Walker 2000).

Free jet experiments are generally easier to carry out. The jet destabilization does not need to be controlled (using an electric or acoustic device) or temporally monitored using a high-speed imaging system. However, a statistical analysis is required. The extraction of the characteristic quantities of the instability, such as the initial amplitude, wavelength and growth rate of the perturbation, may thus appear more challenging. The present work deals with the determination of the growth rate of the instability for free falling jets.

Linear stability theory predicts that the initial perturbation of wavenumber k and small amplitude \(a_{0}\) of a jet of diameter d, (\(a_{0} \ll d\)) will grow exponentially if \(k< \pi d\) with a k-dependant growth rate \(\alpha (k)\). For free jets, the wavenumber with the maximum growth rate, i.e., the most unstable wavenumber, \(k^{*}\) will be the mode responsible for the jet breakup. With, the maximum growth rate \(\alpha _\mathrm{max}=\alpha (k^{*})\) and \(k^{*}\) depending on the fluid properties. Inviscid fluids are characterized by Rayleigh’s relation (1878), viscous liquids by Weber’s (1931) and viscoelastic fluids by the model developed by Brenn et al. (2000). For more details on the hydrodynamics of free liquid jets, see the seminal work of Yarin (1993) and Ashgriz and Yarin (2011). These dispersion relations were experimentally validated with forced jet experiments (Goedde and Yuen 1970; Keshavarz et al. 2015). Free jet experiments are submitted to mode selection. Thus, such experiments allow to explore only a reduced domain of wavenumbers around \(k^{*}\), therefore, limiting their use for a cross-validation between theory and experimentation.

Yet, free jet experiments are encountered in diverse industrial applications, for instance in agricultural spraying. It is, therefore, of paramount importance to be able to measure the characteristic quantities of the instability, including the growth rate.

To the best of our knowledge, existing methods available in the literature to extract the growth rate of a free jet instability are based on the determination of the perturbation maxima (e.g., Cossali and Coghe 1993; Blaisot and Adeline 2000). The more accurate one is the one proposed by Blaisot and Adeline (2000), involving an imaging system and a spatial analysis of the entire jet. More precisely, the method relies on a shadow-graph imaging technique with asymmetric magnification, a subpixel edge detection, a wavelet analysis and a shape recognition procedure to localize the jet interface maxima. The asymmetric magnification allows to dilate the jet in the radial direction. The wavelet transform and the shape recognition procedure are used to localize with accuracy the maxima of deformation in the jet contour. Once the maxima are determined for different positions along the jet axis, i.e., for different times from the entrance of the jet stream, and for different jets obtained in the same experimental conditions, the growth rate is extracted by finding the best fit in the data with a technique based on the calculation of mass centers (see Blaisot and Adeline 2000 for more details).

The entire experimental method was shown to be of good accuracy for spatially resolved jet images. Yet, it is important to underline that the determination of the growth rate as previously described implies a strong reduction of the information extracted from the edge-detection procedure. Moreover, the wavelet transform has an important computational cost.

Here, an experimental method is proposed to determine the growth rate of the free jet instability based on the computation of the standard deviation of a set of jet profiles. It presents three main advantages. First, the method works with a simple imaging technique. Second, the computational cost is strongly decreased. Third, the standard deviation curve provides continuous information along the jet axis. As an example, the experimental method is applied to liquid jets for two low-viscosity solutions: a Newtonian one, the other being viscoelastic.

The theoretical foundations of the method and its application to emulated jet profiles are presented in Sect. 2. In Sect. 3 the practical implementation of the method is detailed and in Sect. 4 the method is applied to free jet experiments of a Newtonian and viscoelastic fluid.

2 Method description

2.1 Theoretical argument

Rayleigh (1878) built the first model of inviscid jet breakup into vacuum using linear stability theory. Within the framework of this theory, the evolution of a single mode perturbation to an infinite column of liquid can be described by :

$$\begin{aligned} \eta (z,t)=\eta _0 \sin (kz+\phi ) {e}^{\alpha t} \end{aligned}$$
(1)

where z is the position on the jet axis, t the time, k the wavenumber of the perturbation, \(\phi\) the spatial phase, \(\alpha\) the growth rate and \(\eta _0\) the initial amplitude of the perturbation. Note, that Eq. (1) still holds for viscous (Weber (1931)) and viscoelastic ( Brenn et al. (2000)) models. Real jets are transported with a uniform velocity U so the temporal and spatial variables are linked by an equation:

$$\begin{aligned} z=Ut \end{aligned}$$
(2)

Equation (2) also implies that we arbitrarily decided that the origin of time corresponds to the origin on the jet axis (the position of the orifice) and that \(\eta\) may be a function of the spatial coordinate z only, besides time t. Let us consider now a set of N jet profiles \(r_i\), assuming that Eqs. (1) and (2) hold:

$$\begin{aligned} r_i(z)=\frac{d}{2}+\eta _{0} \sin (kz+\phi _i) e^{\alpha z /U} \end{aligned}$$
(3)

where d is the jet diameter and \(\phi _i\) the perturbation spatial phase of the \(i^{th}\) profile. Equation (3) is then turned dimensionless using d as the length scale and Rayleigh’s time, \(t_R=\sqrt{(\rho d^3)/(8\gamma )}\), as the timescale, with \(\rho\) and \(\gamma\) the fluid density and surface tension. We obtain:

$$\begin{aligned} \overline{r_i}(\overline{z})=\frac{1}{2}+\overline{\eta _{0}} \sin \left( \overline{k} \overline{z}+\phi _i\right) e^{\overline{\alpha } \, \overline{z}/\overline{U}} \end{aligned}$$
(4)

where \(\overline{z}=z/d\), \(\overline{k}=kd\), \(\overline{\alpha }=\alpha t_R\), \(\overline{U}=U t_R/d\), \(\overline{\eta _0}=\eta _0/d\) and \(\overline{\eta _i}=\eta _i/d\). From this set the standard deviation is computed at each \(\overline{z}\) position:

$$\begin{aligned} \overline{\sigma }(\overline{z})=\frac{1}{\sqrt{N}}\sqrt{\sum _{i=1}^{N} \left( \overline{r_i}(\overline{z}) - \langle \overline{r_i}(\overline{z})\rangle \right) ^2 } \end{aligned}$$
(5)

where \(\langle \overline{r_i}(\overline{z}) \rangle\) is the mean of \(\overline{r_i}(\overline{z})\) over i at the position \(\overline{z}\). Assuming that the jet profiles are uncorrelated in time, each phase \(\phi _i\) is modeled as the realization of a random variable of uniform distribution on \([0,2\pi ]\). So, \(\langle \overline{r_i}(\overline{z}) \rangle\) tends to 1/2 when N tends to infinity. So Eq. (5) becomes:

$$\begin{aligned} \overline{\sigma }(\overline{z})=\frac{1}{\sqrt{N}}\sqrt{\sum _{i=1}^{N}\left( \overline{\eta _{0}} \sin \left( \overline{k} \overline{z}+\phi _i\right) e^{\overline{\alpha } \, \overline{z}/\overline{U}}\right) ^2} \end{aligned}$$
(6)

Using the uniform distribution of the random variable defining \(\phi _i\) and taking the logarithm of Eq. (6) we finally obtain:

$$\begin{aligned} \ln (\overline{\sigma }(\overline{z}))= \ln \left( \frac{\mid \overline{\eta _{0}} \mid }{\sqrt{2}}\right) + \overline{\alpha }\frac{\overline{z}}{\overline{U}}. \end{aligned}$$
(7)

Equation (7) allows the computation of the growth rate \(\overline{\alpha }=\alpha t_R\) in the linear regime from a set of N jet profiles considered at uncorrelated times. It also provides an indirect measurement of the initial perturbation amplitude \(\eta _{0}.\) This relation is valid for inviscid, Newtonian and viscoelastic fluids.

2.2 Validation and robustness

To estimate the robustness of the method described above, a set of \(N=5000\) profiles is created using a modified version of Eq. (4):

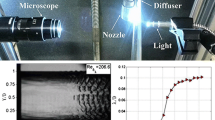
$$\begin{aligned} \overline{r_i}(\overline{z})=\frac{1}{2}+\overline{\eta _{0,i}} \sin \left( \overline{k_{i}} \overline{z}+\phi _i\right) e^{\overline{\alpha _i} \, \overline{z}/\overline{U}}+\epsilon _i(\overline{z}) \end{aligned}$$
(8)

where the parameters \(\overline{\eta _{0,i}}\), \(\overline{k_i}\) and \(\overline{\alpha _i}\) are draws of random variables of uniform distributions varying from 0.85 to 1.15 times a user-defined value. Due to the finite precision of real profiles a random noise \(\epsilon _i(\overline{z})\) was added. Each test profile is defined from \(\overline{z}=0\) to \(\overline{z}=\overline{z_{c,i}}\), with \(\overline{r_i}(\overline{z_{c,i}})=0\). The average breakup length is defined as \(\langle \overline{L} \rangle = \langle \overline{z_{c,i}} \rangle\) and all functions are shifted to have coincident breakup points at \(\langle \overline{L} \rangle\). The standard deviation is then computed. One result is presented in Fig. 1. There are three main regions. In the beginning, \(\overline{z} < 65\), the noise is dominant and hides the perturbation growth. Then, \(65< \overline{z} < 85\), the perturbation becomes dominant and \(\ln (\overline{\sigma }(\overline{z}))\) exhibits a linear evolution as predicted by Eq. (7). Finally, \(\overline{z} > 85\), perturbations are in phase near the breakup point and Eq. (7) does not hold anymore. The growth rate for various sets of parameters was measured with the standard deviation method (present work) and with the wavelet transform method (Blaisot and Adeline 2000). Both sets of results were compared to the growth rate value used to create the jet profiles. It was found that the standard deviation method tends to underestimate the growth rate (\(-6.2 \%\)) while Blaisot’s method overestimates it (\(+5.4 \%\)). Note that both methods provide results of comparable accuracy.

Fig. 1
figure 1

Standard deviation of a set of emulated jet profiles. Three regions are displayed, delimited by the two blue dash–dot lines. The averages of the parameters distributions are: \(\overline{\eta _{0}}=8\times 10^{-5}\), \(2\overline{k} = 0.7\), \(\overline{\alpha }=0.3\) and \(\epsilon =0.03\)

Full size image

3 Operating description

3.1 Jet imaging setup

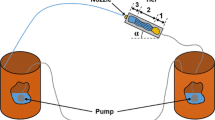
Figure 2 shows a diagram of the experimental setup to produce and image a free, vertical jet of liquid. It is composed of two parts, operating independently: the jet production system and the visualization technique. The jet production system consists of a motorized syringe pump, a liquid feed and drain system, a liquid orifice assembly and a precision balance. Free falling jets are produced by vertically ejecting liquid through a stainless steel orifice plate (Edmund optics) of orifice diameter 61.5 \(\upmu\)m from a liquid chamber. The syringe pump delivers fluid into the liquid chamber through the liquid feed system at a constant flow rate. The repeatability of the produced jet is quantified by collecting and weighing liquid drops from the disintegration of the jet with the balance (Ohaus, precision 0.1 mg). An average jet velocity is calculated, for each experimental run, based on the measurement of jet diameter, assuming mass conservation. Therefore, the balance helps us to detect any perturbation that may occur during the experiment. The liquid drain system also plays an important role in the control of the produced jet. It incorporates a pressure gauge and drain valve. The pressure gauge helps us diagnosing orifice plugging and other system changes. The drain valve is used for flushing out the liquid feed system after experiment. Sections of the produced jet are back-illuminated using a flash light source with 20-ns pulses (Mini-Strobokin). An optical configuration including a fiber and a lens was chosen to obtain the best enlightenment conditions of the jet. The flash light source is synchronized with a video camera (Lightning RDT from DRS Data and Imaging Systems, Inc.) at an acquisition frequency, \(F=25 \,\mathrm{Hz}\). Images are recorded on the camera with a resolution of \(1280\times 180\) pixels. For all experiments reported in the present work, the spatial resolution was of 5.2 \(\upmu\)m/pixel.

The experimental system is settled on a heavy marble and encaged into a Plexiglas box to isolate the jet from room air currents.

Fig. 2
figure 2

Experimental setup to produce and image a free, vertical jet of liquid

Full size image

3.2 From image to jet profile

The top image in Fig. 3 shows an example of a raw jet image captured with our imaging system. The jet and its fragments appear darker. All images are processed using the same procedure running on Matlab. First, the background is subtracted. Second, the image is cropped to eliminate the area of low enlightenment near the orifice. Then two images are created, the first one is obtained using a modified Sobel filter and the second one is the result of a morphological opening and a binary conversion. The final image is obtained as the smoothed addition of the first and second images. One example is presented in Fig. 3 (see the middle image). Then, all objects (the jet and drops) in the image are independently numbered by a labeling algorithm. The jet corresponds to the closest object from the orifice. Finally, the subpixel edge points are determined using the mean intensity level curve. The resulting list of ordered points defines the jet profile (see the bottom image in Fig. 3).

Fig. 3
figure 3

Zoomed-in image of a jet of water and isopropyl alcohol (\(5\%\) in mass). From top to bottom: raw image, processed image, jet profile. Jet velocity: 8.9 m/s

Full size image

3.3 From jet profile to standard deviation

Each jet profile is projected on the main direction of its eigenbasis using Principal Component Analysis (PCA). Jet profiles are then shifted (see Sect. 2.2) to have coincident breakup points. Afterwards, jet profiles are split into two parts, one above and one below the jet axis. The jet diameter d is calculated as twice the mean distance to the jet axis near the orifice and is averaged over the set of profiles. Finally, the standard deviation is computed at each discrete position.

3.4 Other measurements

To check the hypothesis of Rayleigh regime and free jet, we measured the average jet length \(\langle \bar{L} \rangle\) as the mean jet profile length turned dimensionless by the jet diameter d. We also measured the distribution of wavenumbers \(\bar{k}\) defined as the average of the inverse distance between two consecutive local maxima turned dimensionless by d.

In the next section, the above procedure is applied to jet images obtained with two low-viscosity solutions, one being Newtonian, the other viscoelastic.

4 Applications

4.1 Fluids and experimental conditions

We performed free falling jet experiments with two different fluid solutions and for various Weber numbers. The Weber number is here defined as \(We=\rho d U^2/\gamma\).

The two low-viscosity fluid solutions are Newtonian and viscoelastic. The first one is the solvent of the second one, a very dilute polymer solution. The polymer is the polyethylene oxide (PEO) with a high molecular weight (\(8\times 10^{6}\) g/mol according to the data of Aldrich Chemical). The very dilute polymer solution is prepared by dissolving 5 part per million (ppm) in mass of PEO in a Newtonian solvent composed of water (deionized degased filtered) and \(5\%\) in mass of isopropyl alcohol. Isopropyl alcohol is used to facilitate the dispersion of PEO powder into water and to improve conservation and stability of the solution. Because the amount of dissolved polymer is very small, the density, surface tension and shear viscosity are very similar to those of the solvent. These properties were measured at \(T=22\) °C using the Antoon Paar DMA 35 Density meter for the density \(\rho\), the Krüss DSA100 Drop Shape Analyzer for the surface tension \(\gamma\) and the Anton Paar MRC 501 rheometer for the zero-shear viscosity \(\mu\). Their values are: \(\rho =989\) kg/m\(^{3}\), \(\gamma =49\) mN/m and \(\mu =1.2\) mPa s.

The Weber number is varied by changing the mean jet velocity. Jet contraction was observed, being weakly reduced with increasing velocities and/or with polymer concentration, for the range of velocities explored in this study. This phenomenon was first reported by Middleman and Gavis (1961). The average jet velocity ranged from 5.0 to 11 m/s. Its value was chosen high enough to neglect the action of gravity but low enough to neglect the influence of the surrounding air. For each Weber number and fluid solution, we recorded a total of \(N=5000\) images, uncorrelated in time (\(F t_{\rm R} \ll 1\)), to determine the standard deviation curve.

Fig. 4
figure 4

Jet stability curve for the two fluid solutions. Comparison to the results of Mun et al. (1998) obtained with the 50-ppm PEO solution

Full size image

Before applying the method to extract the growth rate of the jet instability, the experimental conditions are more carefully specified by checking that our experiment is in Rayleigh’s regime with the jet stability curve and the distribution of jet perturbation wavenumbers.

Figure 4 shows the jet stability curve from our data points, i.e., the evolution of the dimensionless average breakup length \(\langle \bar{L}\rangle\) with the Weber number. Our results show a linear and affine dependence for the solvent and polymer solution, respectively. Our data points belong, thus, to the Rayleigh’s regime of the jet stability curve. Please note that breakup lengths of the viscoelastic jet are shorter than those of the Newtonian one, in agreement with previous results from the literature (Kroesser and Middleman 1969; Mun et al. 1998).

The distribution of jet perturbation wavenumbers \(\overline{k}\) is presented in Fig. 5. For the solvent (Fig. 5a) and the polymer solution (Fig. 5b), the mode of the distribution \(\overline{k}_{M}\) is close to Rayleigh’s theoretical prediction \(2\overline{k^{*}} \approx 0.7\). This result holds for all investigated values of \(We\). This confirms the free nature of the experiments conducted here. The inset shows that, within the experimental precision, \(\overline{k}_{M}\) does not vary much with We. Once again, this observation confirms that the effect of the surrounding air can be neglected.

To summarize, we performed free falling jet experiments in the Rayleigh’s regime, using two types of fluids. The jet stability curves for both solutions are in agreement with previous works. In the next subsections, the standard deviation curve for each solution and one fixed Weber number is presented. Growth rate measurements are extracted for various Weber numbers as well.

Fig. 5
figure 5

The distribution of jet perturbation wavenumbers for a the solvent and b the polymer solution. \(We=85\). The inset shows the influence of the Weber number on the mode of the distribution. Experimental measurements are compared to Rayleigh’s prediction for the most unstable wavenumber (see the red dashed line)

Full size image

4.2 Newtonian case

The standard deviation curve for the Newtonian solution is presented for \(We=85\) in Fig. 6a. The experimental noise, essentially due to the finite resolution of the camera, dominates the first part of the curve. Data points located below the resolution of half a pixel (the pixel resolution is delimited by the blue dash-dot line) are rejected for growth rate extraction. Note that the bump located around \(\overline{z}=60\) is due to the gradient of enlightenment in our processed images. This can be easily fixed by normalizing the raw images, an operation that was found not advantageous in our case. The second part of the curve shows a linear trend on a log–linear graph. It corresponds to the regime of exponential growth and its slope is used to compute the growth rate using relation (7). All data points located above the experimental noise were taken into account to obtain the linear fit. Note that this figure shares several features, including the phase oscillations, with Fig. 1 obtained with profiles of emulated jets for which the experimental noise was represented by the function \(\epsilon\). Growth rate measurements for several Weber numbers are reported in the inset. Results do not vary with \(We\) in good agreement with theoretical value of Rayleigh: \(\overline{\alpha } \approx 0.3\).

Fig. 6
figure 6

Standard deviation curve of a set of 5000 profiles of real jets for a the solvent and b the polymer solution. \(We=85\). The linear domain allows to extract the growth rate of the instability. The pixel resolution is represented by the blue dash–dot line. The inset shows the influence of the Weber number. Experimental measurements are compared to Rayleigh’s prediction for the maximum growth rate (see the red dashed line)

Full size image

4.3 Viscoelastic case

The standard deviation curve for the viscoelastic solution is presented in Fig. 6b. In this case we observe an additional regime of growth rate decrease following the exponential growth of amplitude perturbations. A representative image presented in Fig. 7 shows a good correspondence between the third regime and the formation of a Bead On A String (BOAS) structure in the jet. Those structures are generally encountered with viscoelastic jets (see for instance Goldin et al. 1969; Clasen et al. 2006; Bhat et al. 2010). Growth rate measurements are reported in the inset. The upper limit of the second regime, from which the growth rate of the linear instability can be extracted by linear regression, is set by a criterion on the ratio of the standard deviation and of the unperturbed jet radius. The value chosen for all Weber number experiments was 0.35. Our results are in agreement with Brenn’s model that reduces to Rayleigh’s one for low-viscosity viscoelastic solutions (see Ref. Tirel et al. 2017 for a comparison with Brenn’s model).

The fact that the measured growth rates in Newtonian and viscoelastic cases are close may at first sight contradict the important decrease of the breakup length observed on the jet stability curve due to the addition of a small amount of polymer (see Fig. 4). Initial amplitudes of the jet interface deformation are estimated based on the standard deviation curve according to relation (7). They are found to be larger by a factor of the order of 50 in the viscoelastic case. This result suggests that the breakup length reduction is caused by an increase in jet initial perturbation amplitudes.

Fig. 7
figure 7

Representative image of viscoelastic jet exhibiting a BOAS structure. The vertical lines are drawn to delimit the saturation regime detected on the standard deviation curve (see Fig. 6)

Full size image

5 Conclusion

A method to extract the growth rate of the instability in free liquid jet experiments has been presented. It is based on the computation of the standard deviation of jet profiles, uncorrelated in time but obtained in the same experimental conditions. Previous methods are based on the determination of the jet displacement maxima, as for instance the method developed by Blaisot and Adeline (2000), which is the most accurate to the best of our knowledge. The present method tends to be simpler in its formulation and implementation. Its principle has been described here and tested on a set of emulated jet profiles to validate its concept and evaluate its robustness. Results showed that the method is of comparable accuracy than the one of Blaisot and Adeline (2000). In addition, it presents three main advantages. First, it works with a simple imaging technique. Second, it has a low computational cost. Third, it uses all the information provided by edge detection to extract the growth rate. The implementation of the method has been detailed in three steps: the production of jet images with a standard shadow-graph technique, the procedure to obtain jet profiles from jet images and the one to draw the standard deviation curve from jet profiles. The method was then applied to free falling jet experiments performed with different Weber numbers and two low-viscosity solutions: a Newtonian one and a viscoelastic one.

Results on the distribution of wavenumbers and the jet stability curve for both solutions allowed us to confirm the free nature of the experiments reported here and the domain explored in this study, i.e., the Rayleigh’s regime.

The standard deviation curve was then used to extract growth rates near the maximum value for both solutions and various Weber numbers in the Rayleigh’s regime. Results were found in good agreement with linear stability theory, as one would have expected according to previous studies (see for instance Yarin 1993). These results serve to validate the present method to extract the growth rate in free liquid jet experiments. The standard deviation curve could also be used to gain insight into the breakup of low-viscosity viscoelastic jets. First it allowed us to identify the transition from exponential growth to saturation due to BOAS structures. Second, it provided us indirect measurements of the initial perturbation amplitude. Comparison between the two low-viscosity solutions revealed that initial amplitudes values are larger for the viscoelastic case, which would explain the reduction in breakup length observed on the jet stability curve. We emphasize that the access to the saturation regime and the initial perturbation amplitude does not rely on the jet stability curve as in previous studies (see Ref. Mun et al. 1998). This shows the novelty and value of our approach to explore the dynamics of free liquid jets.