Abstract
This brief review article is devoted to all the aspects related to hydrodynamics of foams. For this reason, we focused at first on the methods for studying the basic structural units of the foams—the foam films (FF) and the Plateau borders (PB), thus reviewing the literature about their drainage. After this, we scrutinized in detail the Derjaguin’s works on the electrostatic disjoining pressure along with its Langmuir’s interpretation, the microscopic and macroscopic approaches in the theory of the van der Waals disjoining pressure, the DLVO theory, the steric disjoining pressure of de Gennes, and the more recent works on non-DLVO forces. The basic methods for studying of foam drainage are presented as well. Engineering and other applications of foam are reviewed as well. All these aspects are presented from retrospective and perspective viewpoints.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Aqueous foams are dispersion of bubbles in water. They have specific structure, which depends on the foam’s liquid volume fraction. The foam starts both draining and decaying at its very generation (Exerowa and Kruglyakov 1997; Weaire and Hutzler 1999). The foam drainage is an aqueous gravity flow reducing the amount of water into the foam. This causes the formation of well-defined structures—foam films between pairs of bubbles, Plateau borders (PBs) between threesome bubbles, and nodes. The foam decay is a reduction of the total amount of bubbles into the foam due to the bubble coalescence (Exerowa and Kruglyakov 1997) and/or the trans-diffusion of the air from the smaller to the larger bubbles (Krustev and Muller 1999; Saint-Jalmes 2006) (foam coarsening).
The rate of decay of the transient foam is commensurable with the rate of their drainage, while the tenacious foams decay significantly slower than they drain. For this reason, they become dry foams containing close packed polygonal bubbles, Plateau borders (PBs), and nodes. The latter are channels, which form nodes when they cross each other (Koehler et al. 2000; Kruglyakov et al. 2008).
The drainage of the long lasting foams has been studied in the last several decades (Kruglyakov et al. 2008). It has been established that the gravity flow of the liquid occurs most of all in the Plateau borders (PBs) (Koehler et al. 2000). For this reason, their size and shape are important hydrodynamic factors. The latter are affected by the bubble coalescence which usually occurs when the foam films are in the range of the nano-scale thickness (in dry foams).
For this reason, the drainage and the stability of the foam films is one of the key factors controlling the overall behavior of the foams. Typically, when the foam films reach nano-scale thickness, they exhibit both electrostatic repulsion and van der Waals attraction (Kralchevsky and Danov 2015; Nguyen and Schulze 2003) in line with the DLVO theory (Derjaguin and Landau 1941, Verwey and Overbeek 1948) when they are in range of the nano-scale thickness. Moreover, there are a number of other (non-DLVO) interactions between the surfaces of the film, which dominate often like ion-correlation forces (Attard et al. 1988a, b), steric forces (De Gennes 1985, 1987), hydrophobic forces (Christenson et al. 1987, 1990; Qu et al. 2009), adsorption forces (Karakashev et al. 2013a, b), colloidal structural forces (Nikolov et al. 1990), etc. These non-DLVO forces act in the foam films under particular conditions. For example, the ion-correlation force is negative correction to the electrostatic disjoining pressure originating from the energy of deformation of the electrical diffusive layer. The hydrophobic and adsorption forces (Karakashev et al. 2013a, b; Tsekov and Schulze 1997) act in the foam films due to the overlapping of the surfactant adsorption layers. The steric disjoining pressure appears when polymers are dissolved into the aqueous medium. Colloidal structural forces emerge when the surfactant solutions form micelles, thus affecting the drainage of the foam films.
Other important factors, which govern the durability of the foams, are the Gibbs elasticity and the viscoelastic moduli of the foam films. Unfortunately, there are no theoretical models relating the foam lifetime and these two factors. However, there are kinetic models of drainage of both foam films and Plateau borders (PBs) accounting for the Marangoni stress and the surface viscosity.
As far as the DLVO and non-DLVO forces between the bubbles are well studied, we could pose the question if this knowledge is sufficient to control the durability of foams?
For example, the electrostatical stabilization at low ionic strength contributes to longer lifetime of foams. Higher ionic strengths allows the film surface to approach closer to each other in line with the DLVO curve. Unfortunately, the prediction of the lifetime of foams is a difficult task, especially for industrial applications. For this reason, methods for stabilization and destabilization of foams were created (Karakashev and Grozdanova 2012). In general, they consist of introducing particles with specific sizes and hydrophobicity and/or oil (Dippenaar 1982a, b, c; Kulkarni and Goddard 1977) into aqueous surfactant solutions.
This review is dealing with the basic aspects on the dynamic behavior of the foams. It scrutinizes a number of topics, related to the hydrodynamics of foams.
2 Basic structural unit of the foam: foam films and Plateau borders
The foam films and the Plateau borders (PBs) are the basic structural units of foams. Both of them are responsible for the overall behavior of foam. For example, the durability of the foam films affects the durability of the very foam. For this reason, methods for studying their properties are developed. We will present hereafter the basic methods for investigations of foam films and Plateau borders (PBs) along with some significant achievements in this field.
2.1 Types of foam films and methods for their investigation
A foam film is a thin-liquid layer entrapped between two bubbles. Its thickness is usually in the nano-scale range and can be measured by means of the interferometry. Such films are often present in foams. For example, foams with very small liquid content (dry foams) contain Newton black foam films (with thickness of 5–10 nm) or common black films (with thickness 10–20 nm) (Exerowa and Kruglyakov 1997). The more wet the foams are the thicker are their films. The standard interferometry can be applied to foam films until 1000 nm.
Derjaguin and Kussakov (1939) were the first to apply the interferometry to study the film intercalated between a bubble and a solid surface. Later on, Scheludko and Exerowa (1959a, b) applied the interferometry to determine the thickness of foam film in a double concave drop, while Mysels et al. (1961a, b) used the same technique to study foam films in rectangular vertical frame.
The setups introduced by Scheludko and Exerowa (1959a, b), and Mysels et al. (1961a, b) were designed for studying of foam films.
Another important problem is the interaction between the film surfaces across the aqueous layer. Thin-film pressure balance (TFPB) has been designed by Mysels and Jones (1966) to study the disjoining pressure of the foam film at different thicknesses. A foam film in such a case is situated in a small hole located in the middle of a porous plate. However, despite the above-mentioned methods had been proven to be trustworthy, in none of the cases, the foam film was located between two bubbles.
Yet, such a method has been introduced recently by Morokuma et al. (2015). This method is called the laser extinction method. The two bubbles are attached to hydrophobic glass plates being located oppositely to each other. The glass slides are gently approached towards each other, thus pressing against each other. The interferometry can be applied for measuring the film thicknesses of no more than 1 μm. The reason for this limit is that the aqueous core of the film scatters light, thus decreasing the intensity of the reflected by the two film surfaces light. The ticker the film is the smaller the intensity of the reflected light becomes. Moreover, the foam film must be transparent. In some cases, the foam films (and the foams) can be stabilized by particles. Scheludko et al. (1954/1955) developed the electro-conductivity method for determination of opaque (non-transparent) foam films. We will discuss briefly all these methods hereafter.
2.1.1 Foam films formed from double concave drop
Foam films formed from a double concave drop were studied by means of the interferometry first by Scheludko and Exerowa (1959a, b). Their methodology has been successfully tested and applied in a vast number of studies, including the pioneering studies on thinning and surface forces in the liquid films (Ivanov and Dimitrov 1974; Ivanov 1988; Karakashev and Nguyen 2007; Manev et al. 1997; Radoev et al. 1974, 1968; Scheludko 1967).
The method is suitable for studying under controlled condition equilibrium and thinning films of different types: free foam films, emulsion, and polymolecular films on solid/liquid substrate. It allows the experiment to cover the entire rang of film stability of vastly varying lifetime and is extensively used in many investigations.
The setup for the interferometric measurements of the film thickness is comprised of two basic units: (1) the measuring cell (‘the Scheludko–Exerowa cell’, Fig. 1) in which the film is formed and (2) the optic-electronic system for monitoring the film and registration of its thickness (Fig. 2).
Scheludko–Exerowa cell (Karakashev and Manev 2015)
Experimental setup for studying thin-liquid films (Karakashev and Manev 2015)
The method is based on the normal illumination of the film (see Figs. 1, 2) with a beam of coherent light (mono or polychromatic), which is reflected by the two surfaces of the film, thus causing the appearance of two phase-shifted beams of reflected light, which are collected together and captured by photodetector, thus producing interferograms used for calculation of the thickness. If the light is polychromatic, one can see different colors on the interferograms, corresponding to specific film thickness. In such a case, a digital filtration to the interferograms should be applied (Karakashev et al. 2007) prior the calculation of the thickness. The latter can be calculated by means of the interferometric formula:
where \(\lambda\) is wavelength of the monochromatic light after digital filtration (for green light \(\lambda = 547\) nm), \({n_0}\) is the refractive index of water (\({n_0} = 1.333\) at T = 20 °C), \(l\) is order of interference, \(\Delta = \left( {I - {I_{\min }}} \right)/\left( {{I_{\max }} - {I_{\min }}} \right)\), \(I\) is the transient strength of the signal, \({I_{\max }}\) and \({I_{\min }}\) are its maximal and minimal values, \(r = {\left( {{n_0} - {n_1}} \right)^2}/{\left( {{n_0} + {n_1}} \right)^2}\) is the Fresnel reflection coefficient, and \({n_1}\) is refractive index of the air (\({n_1} = 1\)). The minimal signal for foam a film is usually taken from the signal of a ruptured film, while the maximal signal is taken from the digital interferogram. An example of the interferogram of a planar foam film and its corresponding film thickness is presented in Fig. 3 (Karakashev and Ivanova 2010).
Example of the transient digital images of 10−5 M Tetraethylene Glycol Octyl Ether (C8E4) foam films taken at 0.9 s intervals (top left to bottom right) and the corresponding transient thicknesses of the thinning film (Karakashev and Ivanova 2010)
This method can be applied for measuring film thicknesses of no more than 1 µm, because the aqueous core film scatters light, thus decreasing the intensity of the reflected light. Usually, the films with thickness in the range of 700–800 nm have low intensity of the reflected light. Hence, the ratio of the level of the noise of the signal increases, thus enhancing the relative error of the determination to about ±5 nm. At film thickness below 200 nm, the relative error is about ±1 nm. Moreover, the typical capillary pressure achieved by means of this cell is below 100 Pa.
Several innovations have been introduced in the experimental technique, e.g., the pioneering oscillating photometric probe (Manev 1981). Measuring the thickness on a small portion of the film surface (e.g. <5% of the total area) has allowed registration of very fine deviations in the local film thickness from the variations in reflected light intensity (Fig. 4).
Evolution of the film profile during the last stages of thinning (time, indicated from 0 to 100 s is counted from an arbitrary “initial” h). The amplitude of the thickness heterogeneity is about 25 nm. Film of radius r = 1.0 mm formed from 1.0 mmol/l sodium dodecylsulfate + 0.1 mol/l KCl aqueous solutions (Manev et al. 1997)
The measuring technique with the oscillating photometric probe has further allowed the quantitative estimation of the magnitude of the film inhomogeneity, its dependence on the film radius, and the size of the thin and thick domains over the film area. Data obtained by this method have been used to establish the detailed laws of the evolution of film thickness in time.
More advanced technique for studying the film thickness inhomogeneity is the line-scan camera, which scans a selected line from the foam film during its drainage (Karakashev et al. 2005). This allows one to investigate more precisely the profile of the thin film. Thus, one can study the surface waves in the thin films or the formation of black spots (see Fig. 5).
Film thickness profiles before (the filled circles) and after (the unfilled circles) the formation of the black spot in foam films determined by means of a line-scan camera (Karakashev et al. 2005)
Another advanced procedure for studying the film thickness inhomogeneity was reported by Karakashev et al. (2013a, b) (see Fig. 6).
The procedure for obtaining of 3D images of thin-liquid films is described in detail in (Karakashev et al. 2013a, b). It can be applied to foam films, although wetting films were studied by means of this procedure. In contrast to the classical setup introduced by Scheludko and Exerowa, Karakashev et al. (2013a, b) captured the entire image of the interferograms with a digital camera and processed the latter offline by means of the image processing software (e.g., Image J, Optimas, etc). Multiple horizontal and parallel to each other lines (see Fig. 6) crossing the film are drawn by means of the graphical tool of the Image J software. Each of these lines, coinciding with the horizontal x axis, is coupled with particular spatial interferogram along the line crossing the film, obtained by “plot profile” option of the Image J software. Thus, a series of spatial interferograms corresponding to each line along the axis x are obtained and converted into real film thickness profiles by means of the interferometry formula, Eq. (1). The distances, coinciding with the vertical axis y between the lines, are known as well. Thus, the exact coordinates x and y corresponding to each film thickness are obtained. The 3D profiles are obtained by 100 × 100 matrixes via Microcal Origin software version 5.
2.1.2 Foam films formed in a rectangular frame
Mysels et al. (1961a, b) and Razouk and Mysels (1966) were the first to use the rectangular frame as a tool for studying foam lamellae. The method consists in measuring the increased tension of a foam lamella when stretching it to a measured extent, concurrently with the determination of the local film thickness of the lamella from the interference pattern.
Thus, they studied the elastic moduli of the films and the variation of the film thickness with their expansion. The method was adopted later by Prins et al. (1967), and Prins and van den Tempel (1968). These first attempts to determine the elastic moduli were critically evaluated in the literature (Kitchener 1962a, b; Mysels et al. 1961a, b). The arguments (Mysels et al. 1961a, b) were focused on the dynamic nature of the film elasticity showing that the film dynamics effects should last for milliseconds, while the time scale of the stretching covers seconds, and this is accompanied by the increased values of the film tension. Hence, a different limiting factor—presumably the depletion of surfactant in the intra-lamellar liquid—must be active in the film (Mysels et al. 1961a, b). According to Kitchener (1962a, b), the latter effect corresponds to the exact definition of the Gibbs elasticity as defined in (Gibbs 1928). This should be valid for thin films in which the electrostatic disjoining pressure is significant, but in many cases, the thickness of the foam lamella is of the order of microns, corresponding to the absence of the electrostatic disjoining pressure. The methodology of Mysels et al. (1961a, b), and Razouk and Mysels (1966) is limited to relatively stable foam lamellae with high level of surfactant adsorption in the surface layers. In addition, an expansion of the film surfaces is related only to the dilatational (not the shear) viscoelasticity. Meanwhile, Mysels at al. (1959) developed a theory of the gravitation drainage of suspended foam films, which are being withdrawn from a pool of liquid with certain velocity. According to their analysis, the thickness of the foam film can be calculated by means of the following relation:
where σ is the equilibrium surface tension of the surfactant solution, ρ is the density of water, and g is gravity acceleration, \(Ca = \mu U/\sigma\) is the capillary number, µ is the dynamic bulk viscosity of water, and U is velocity of withdrawal of the wire frame. Equation (2) known is Frankel’s law of gravitational drainage of soap films. An excellent review of the theory of gravitational drainage was published by Stein (1993). de Gennes (2001) studied withdrawal of a “young” soap film connected to the pool of liquid. He investigated the balance of the osmotic pressure and the gravity force in the suspended film. Saulnier et al. (2011) build up a similar setup allowing significant variation of the velocity of withdrawal of the suspended film. They reported that above a certain velocity of withdrawal of the foam film, Frankel’s law breaks down, and a faster drainage at the bottom of the film emerges. This effect was investigated in detail more profoundly by Sett et al. (2013) using the following experimental setup. An aluminum wire frame (4 cm × 4 cm × 0.087 cm, see Fig. 7) was dipped into a 200 ml container with surfactant solution.
Left Schematic of the experimental setup of drainage from plane films (Sett et al. 2013)
Then, the solution container was raised and lowered using a linear stage. The film was illuminated perpendicularly with coherent polychromatic light. The latter was reflected by the two surfaces of the film, thus resulting in the interference pattern (see Fig. 7), whose time evolution was captured by CCD camera and stored in computer for further offline processing. The interference pattern obtained from a certain spot of the film (right below the top wire and 2 cm from the left wire) was processed for obtaining the local film thickness at this spot versus time. A linear dependence of the film thickness on time until the formation of black film and rupture was observed. The corresponding values of the surface elasticity ε can be calculated using the equation (Sett et al. 2013):
where \(T\) is the characteristic time of film drainage until film rupture and \({h_0}\) is the film thickness at the moment of film formation.
As far as the area of the foam film is significantly larger than the one in Scheludko–Exerowa cell, the foam film must be located in the environment of with controlled humidity.
2.1.3 Spherical foam films (foam bubbles)
Bianco and Marmur (1993) developed new experimental approach for measuring the Gibbs elasticity of oscillating foam bubbles. This approach is based on the measurement of the film tension upon the expansion and shrinkage of the “soap” bubble surface at a given low frequency. This method was advanced by Kovalchuk et al. (2005). The inhomogeneous distribution of the liquid in the foam bubble due to gravity was accounted for. In contrast to the numerous works on the viscoelastic moduli of single gas/liquid surface layers, the available data on the elasticity of foam bubbles remain scarce. In addition, open questions on the origin of the Gibbs elasticity of foam films remained as well. For example, it is not clear why the tension of thick foam films (~2–3 microns) varies upon the change of the film surface area with a speed much lower than the speed of relaxation of the adsorption layer. The electrostatic disjoining pressure should not have any contribution at such large thicknesses. Hence, it should not be any depletion of surfactant molecules in such foam films. Consequently, the approach of Lucassen and van den Tempel could be applied (Blank et al. 1970; Lucassen and Van Den Tempel 1972).
They derived the following expression for the elastic modulus of the surface monolayer:
where \({\varepsilon _0} = - d\sigma /d\ln \Gamma\), and \(\Gamma\) is the surfactant concentration at the film surface, \(\omega\) is the cyclic frequency of compression/expansion, and \({\omega _0}\) is the so-called adsorption frequency of the surfactant, expressed as
In Eq. (5), \(D\) is the bulk diffusion coefficient, while \(d\Gamma /dc\) is the so-called adsorption length and \(c\) is the bulk concentration of the surfactant.
A detailed study of the elastic moduli of foam bubbles in a wide range of surfactant (tetraethylene glycol octyl ether, C8E4) concentration was conducted by Karakashev et al. (2010a, b). They made a critical evaluation of the approach of Lucassen and van den Tempel. All the measurements were conducted using a commercially available profile-analysis tensiometer (PAT 1 D module of Sinterface Technologies, Ltd., Germany) with a frequency of 0.1 Hz and amplitude of 2 mm3. The tensiometer consists of (1) a mechanical unit for creating and controlling the test fluid–liquid interface in a 2 cm × 2 cm × 2 cm cuvette made of optical grade silica, (2) an optical unit for monitoring the evolution of the interface profile, and (3) a computer with the Sinterface software, PAT-1D, and a data acquisition system for operating the instrument, storing the raw data for the interface profiles, and processing the data offline. The mechanical unit has a water bath for controlling the temperature. The foam bubble is produced (see Fig. 8) by a dual tube—a narrower internal tube situated in a wider external tube. The surfactant solution flowing in the external tube is controlled by a syringe, while air flows through the internal tube, as controlled by another syringe. The two syringes are mounted on the panel of a motorized pump, controlled by the computer. Once formed, the soap bubble was illuminated, equilibrated and its image was captured by the CCD video camera, stored, and processed by the computer software. The edge (the interface profile) of the bubble was digitally identified with sub-pixel resolution and fitted with the numerical solution of the Young–Laplace equation, allowing the determination of the film tension, volume, and area of the bubble. The cyclic time dependence of film tension was determined by changing the bubble volume as a sinusoidal function of time with maximal frequency 0.1 Hz due to the fact that the Young–Laplace equation is strictly valid for statical curved surfaces. Moreover, thickness of the soap bubble is non-uniform due to gravity. Hence, the viscoelastic modulus obtained is averaged upon the entire surface of the bubble.
This study showed that the film tension values of soap bubbles prepared from C8E4 aqueous solutions are larger than the doubled values of the surface tension. The elastic moduli values were significantly lower than the values of the Gibbs elasticity \({E_g}\), calculated by the surface tension isotherm. Their fit of the ratio \(2\varepsilon /{E_G}\), calculated with the model of Lucassen and van den Tempel [Eqs. (4) and(5)] to the experimental data on the measured \({E_{\exp }}/{E_G}\) gave a value for the bulk diffusion coefficient of the surfactant molecules \(D = 5.1 \times {10^{ - 11}}\) m2/s, which is significantly lower than expected for a single C8E4 molecule. All this indicates that there is an exchange of surfactant molecules between the film surfaces and the bulk of the film (\(2\varepsilon < < {E_G}\)), and this exchange is impeded by some unknown factor. Furthermore, increased viscous dissipation of the film liquid is very much possible during the soap bubble oscillation, as compared to the case of the surface of a semi-infinite bulk phase.
2.1.4 Foam films between two bubbles
Recent work (Morokuma et al. 2015) introduced a new experimental setup for studying foam films between two bubbles in contact (see Fig. 9). They used the laser extinction method, based on Lamber’s law, to determine the thickness of the foam film. In contrast to the other methods, where film thinning is driven by natural forces (gravity, capillary force, etc), the bubble approach velocity here is manipulated on demand.
Two bubbles in contact (a); scheme of foam film located between two bubbles (Morokuma et al. 2015)
This approach was used to study the mechanism of coalescence of two bubbles in pure water. The variation of foam-film thickness between the bubbles at the location of rupturing and the distribution of the liquid film thickness is evaluated. The governing experimental parameters are the rate of the approach of the bubbles towards each other and the measured film position. The time from the start of collision until coalescence is measured by means of a high-speed camera. When bubble coalescence occurs rapidly, the film is thinnest near the center, and this position moves towards the periphery from the center during the coalescence. The thinnest film thickness appeared just before coalescence and is evaluated to be 1.0 μm. A ring-shaped thinner area in the liquid film emerged and shifted from the center towards the periphery of the liquid film with an increase in the bubble approach velocity and close contact duration. The thinnest film thickness just before the very rupture in the ring-shaped area was approximately 300 nm.
2.1.5 Foam films in porous plate
Foam films in porous plate are designed for studying the interaction force between its two surfaces within the thin film pressure balance setup (TFPB). Derjaguin and Obuchov (1936) were the first to balance the forces in the thin film with a squeezing pressure. They trapped air bubbles underneath a glass slide which was horizontally submerged in an aqueous solution. The buoyancy force pressed the bubble to the solid surface, thus squeezing the thin film between them. After some time, the drainage stopped due to the balancing of the surface forces with the buoyancy force, thus leaving an equilibrium thin-liquid film and preventing the air from contacting the solid. Following Derjaguin and Obuchov’s original experiments, various experimental setups were constructed to directly manipulate the capillary pressure imposed on a thin-liquid film (Derjaguin and Titievskaya 1953; Deryagin and Titievskava 1957). The design which emerged as the simplest was pioneered, as mentioned beforeahead, by Scheludko and Exerowa (1959a, b). This cell is still widely used to measure film thinning and dynamics, and was modified by Platikanov and Manev (1964) and Manev et al. (1984) to investigate emulsion films. However, due to the limited range of the applied capillary pressures, the Scheludko cell has only been operated in a dynamic mode to deduce disjoining pressure isotherms (Scheludko 1967; Scheludko and Exerowa 1959a, b; Scheludko and Platikanov 1961). Mysels and Jones eliminated the restriction of the low capillary pressure of the Scheludko cell by introducing a porous porcelain disc with a circular hole, instead of a capillary tube (Mysels and Jones 1966). With this device, they measured the equilibrium disjoining pressure isotherms, for foam films, up to disjoining pressure greater than 100 kPa.
Shortly after this Exerowa and Scheludko improved the Mysels’ original porous-plate design by welding a porous glass filter to the end of a capillary tube (Ekserova and Sheludko 1971). These film holders have the advantage of not requiring any glue, which can potentially contaminate the solution, and their shape can be easily tailored to impose small capillary pressures or induce specific film profiles required for delicate low-pressure work. Exerowa et al. have measured the foam-film disjoining pressure isotherms for both ionic and nonionic surfactant solutions using porous glass frit holders (Exerowa et al. 1987; Kolarov et al. 1986), while Aronson et al. (1994) used a slightly modified version of the technique for similar systems (Aronson et al. 1994). Likewise, Bergeron and Radke (1995) measured the disjoining pressure isotherms for asymmetric air/solution/oil (i.e., pseudo-emulsion) films for the first time (Bergeron et al. 1993; Bergeron and Radke 1995) and they have extended the method to measure extremely low capillary pressures. These low-pressure extensions made it possible to measure the oscillatory forces responsible for the film stratification (Bergeron and Radke 1992). The capillary pressure can be controlled by means of proper selection of the porous frit. The narrower the pores are the larger the capillary pressure is and vice versa. For example, porous frit with pores with width of 5 µm can result in the maximal capillary pressure of about 28,000 Pa, while the 10 μm width corresponds to the capillary pressure equal to 14,000 Pa.
Thin film pressure balance setup (TFPB) is shown in Fig. 10. The porous plate is with the pores size of about 5–10 μm. Being in contact with the foam film located in the hole, the liquid is squeezed to reaching film equilibrium state. The disjoining pressure can be varied by means of variation of the pressure inside the chamber. Meanwhile, the thickness of the foam film is determined interferometrically. Thus, one can obtain the Π-h (the disjoining pressure versus film thickness) isotherms.
Schematic of the pressure cell and film holder for a thin-film-balance. The film can be optically interrogated from above and/or below (Bergeron 1999)
2.1.6 Opaque foam films
All the methods discussed above require transparent foam films. However, when the foam film stabilized by particles is opaque, = the above methods cannot be applied. For this reason, Scheludko et al. (1954/1955) developed electro-conductivity method for measuring the opaque (non-transparent) foam films. When two bubbles covered by layers of solid particles approach each other, foam film is formed (see Fig. 11). In contrast to the free foam films stabilized by surfactants, which have been widely described in the literature, scarce information on foam films stabilized by solid particles is available.
Scheme of foam-film formation upon deformation of the bubbles with surface covered by a dense layer of solid particles (or particle aggregates) (Nushtaeva and Kruglyakov 2003)
The capillary pressure \({P_\sigma }\) for the case of a particle-covered fluid interface with hexagonal packing can be expressed by the following equation (Nushtaeva and Kruglyakov 2003):
where \({\sigma _{A/W}}\) is the surface tension of air/water interface, θ is the contact angle between the particle and the air/water interface, α is angle related to the film thickness, which is the slope angle between the particle radius directed towards the three-phase contact line inside the pore space, measured with respect to the equatorial line of the particle, and \({R_p}\) is the radius of the particles. The angle α varies in the 0° to 90°—θ range. The capillary pressure in the particles stabilized film increases upon thinning of the internal phase thickness h (Nushtaeva and Kruglyakov 2003; Nushtayeva and Kruglyakov 2001). The thickness h of the internal phase film can be expressed by the following equation:
where A is the distance between the equatorial lines of the particles located on the two opposite surfaces of the film divided by the particle radius. For hexagonal packing of particles, \(A = 2\sqrt {2/3} = 1.633\); for cubic packing of the particles, \(A = 2\). One can obtain the \({P_\sigma }\) versus \(h\) isotherm by solving Eqs. (6) and (7). The very film thickness can be determined by means of conductometry. The scheme of the experimental setup is presented in Fig. 12. The experimental setup consists of a circular platinum frame with diameter approximately 4.8 mm and wire thickness about 0.26 mm. The frame is located in a porous glass plate with the thickness of about 1.5 mm and diameter of the pores of about 16 µm. The wire frame plays a role of an electrode. There is a platinum wire located at the centre of the frame. It plays a role of a second electrode. The cell is dipped into particle suspension containing surfactant solution and KCl, and after that is withdrawn, thus forming a particle stabilized foam film. The porous glass plate is connected with a mechanism for reducing the pressure inside of the pores, thus applying pressure difference on the film, which appears to be the driving force of its thinning. The capillary pressure in the film is assumed to be equal to the applied pressure drop. At the very moment of its formation, the film which consists of two interfacial layers of particle aggregates with an aqueous core between them. The film begins thinning initially due to gravity until the two interfacial layers come in contact. In such a case, it is assumed that the film reaches its equilibrium thickness \({h_e}\). It can be determined by means of the following formula (Kruglyakov and Ekserova 1998):
Scheme of the device for studying conductivity of foam film, thinning due to the applied pressure drop: 1 cell consisting of a porous plate with the film, 2 separating funnel with water, 3 conductometer, 4 U shaped manometer (Nushtaeva and Kruglyakov 2003)
where \({\kappa _f}\) is the film conductivity, \({\kappa _{sp}}\) is the specific conductivity of KCl solution, \({r_2}\) and \({r_1}\) are the radii of the inner and outer electrodes, \({n_f}\) is ratio of the film volume containing solid particles to the volume of the liquid in the film (the expansion ratio of the film), and \(B\) is an experimental coefficient, whose value is in the 1.1–2 range depending on the angle θ.
The expansion ratio \({n_f}\) usually has a value in the range of 2.5–4 depending on the film thickness and the packing of the particle aggregates. One can easily study the particle stabilized films by means of the setup in Fig. 12 measuring their dependence of the film thickness on the applied pressure and the stability of the very films.
2.2 Methods for investigation of Plateau borders
Foam drainage occurs mainly in the Plateau borders (PB) (Koehler et al. 2000; Nguyen 2002). For this reason, it is important to study experimentally and theoretically how exactly the drainage of liquid occurs in the PB. The basic methods of the experimental investigations are described in the following.
2.2.1 Plateau border apparatus (PBA)
The experiment method is similar to the one of Koczo and Racz (1987). The Plateau border (PB) and the three adjoining films are formed upon the withdrawal of a special frame from a reservoir containing the surfactant solution. The frame is precisely positioned relative to the reservoir, so that the length of the PB can be easily adjusted. Usually, the PB lengths are in the 5–15 mm range. The pool with the surfactant solution is located in a cover cell, thus producing water vapour saturation in the vicinity of the PB. The PBs stable for hours or more can be formed by this method. The frame consists of a vertical metallic cylinder with three fixed rods (of 1 mm in diameter) (see Fig. 13). To conduct an experiment on drainage in a PB, a feed channel of diameter of 10 mm is driven along the axis of the cylinder and an outlet with the diameter of 1 mm is fixed at its lower part. As far as the PB is suspended to the bottom of the metallic cylinder, this feed channel is used to dispense liquid through the PB channel. A syringe pump is used to deliver the solution into the PB at a flow rate within the 1–100 mm3/min range. These flow rates correspond to liquid velocities in the mm/s range in the PB, which are in the range of the liquid front velocities observed in the foam-drainage experiments (Durand et al. 1999). The images of the PB during the experiments are taken through windows in the cover cell. Thus, one can measure the PB length L and follow the evolution of the PB profile \(\Delta y(z)\), where \(y(z)\) is the apparent PB thickness and z is the vertical coordinate. The apparent PB thickness does not coincide with the radius of curvature, R, of the PB, but it is proportional to R, i.e., \(\Delta y(z) = kR(z)\). Measurements of \(\Delta y(z)\) for a static PB have been compared to R(z) within the region of the PB, where \(R(z) \approx \left( {\sigma /g\rho } \right)\Delta z\), and \(\Delta z\) is the height from the liquid level in the reservoir. A pressure transducer is connected to the metallic cylinder, thus allowing us to measure the liquid pressure inside of PB. One can determine the profile of PB upon z and the related pressure inside of PB at different liquid flow rates. One can read more details about these measurements in (Pitois et al. 2005).
Plateau border apparatus (PBA) (Pitoi et al. 2005)
In particular, Pitois et al. (2005) tested the validity of the Nguyen Equation (2002) to describe the flow in a single PB. A special attention was focused on characterizing the behavior of the adjoining films as the solution was injected into the PB. The authors compared the measured values for the pressure loss, ΔP, with the theoretical pressure drop given by the Nguyen equation as
The surface shear viscosity µ s was obtained by fitting Eq. (9) for different values of the surfactant solution flow rate to the experimental data. The dependence of ΔP on the flow rate \(Q\) shows that minimal ΔP is obtained for sodium dodecylsulfate (SDS) and tetradecyltrimethylammonium bromide (TTAB) surfactant solutions without adding dodecanol. It was observed that the addition of dodecanol causes an increase in the surface rigidity. Such an increase in the surface rigidity increase in the values of the Gibbs elasticity and dilatational viscosity. The observations of the variation of the film thickness showed that the thickness increases linearly with the increasing pressure drop. Due to the fact that the flat rate in the films (at a thicknesses from 200 to 600 nm) is much smaller than that in the PBs, it is not clear in which way the foam films affect the rate of the foam drainage and the energy dissipation.
2.2.2 The foam pressure drop technique (FPDT)
The foam pressure drop technique is one of the techniques for studying the foam drainage. However, model calculations developed in relation to this technique reveal the liquid flow in a single Plateau border (PB). For this reason, this method is described here as one of the methods for studying the PBs.
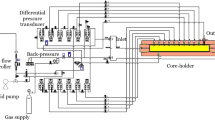
Figure 14 shows a setup for the investigating of foam drainage under an applied pressure drops. A hydrodynamic theory for this experimental setup was developed, thus providing the volumetric flat rate of drainage in a single PB averaged over all possible orientations. The foam cell made from Pyrex glass consists of two independent (lower and upper) compartments connected with the foam by porous disks. Each of the compartments is filled with the foaming solution. The foam is positioned between the two porous disks. The conductivity of the foam is measured by means of the conductometer (2) with platinum electrodes (1). The foam height of 2 cm is kept constant in all measurements. The upper and lower compartments of the cell are connected to peristaltic pump (8) through a valve (7) for regulating pressures through the pressure transducers, the pressure buffer vessels (5), and the vessels (4) for collecting the foaming solution drained from the foam. Initially, wet foam with a uniform bubble size is produced in the foam cell without the upper compartment. Then, the upper compartment filled with the foaming solution is brought into contact with the foam which closed the foam cell. The peristaltic pump is used to create a pressure drop (relative to the atmospheric pressure) in the upper and lower compartments. The pressure drop was independently controlled using valve (7) and peristaltic pump (8), and measured by the pressure transducers (6). Due to the special arrangement of the U shaped tube to level the hydrostatic pressure in the lower compartment, the pressure drop, \(\Delta p\), applied to the lower compartment (as measured by the pressure transducer) is equal to the pressure (relative to the atmospheric pressure) of the foam liquid at the foam bottom.
Schematic of the experimental setup for measuring foam drainage under applied pressures: 1 platinum electrodes, 2 conductivity meter, 3 capillary flow meter, 4 vessels for collecting the foam solution, 5 buffers for reducing the pressure fluctuations, 6 pressure transducers, 7 valves for regulating pressure in the lower and upper parts of the foam cell, and 8 peristaltic pump (Exerowa and Kruglyakov 1997)
The pressure of the foaming liquid at the top foam surface (relative to the atmospheric pressure) is equal to the pressure drop applied to the upper compartment less the hydrostatic head of the foam solution in the upper compartment. The pressure drops are changed on demand in such a way that the pressure drop applied to the upper compartment less the hydrostatic head is equal to the pressure drop applied to the lower compartment. Therefore, the foaming liquid pressures (relative to the atmospheric pressure) at the top and the bottom of the foam surfaces are approximately equal. This experimental situation is created to reinforce the uniform radius of foam Plateau borders and to simplify the drainage analysis. The pressure drop is smaller than the capillary pressure in the pores of the porous disks, and therefore, only the foam liquid drains through the disks, but the gas does not pass through them. Once the pressure drop is set, the liquid from the foam starts draining upward and downward for about 20 min until reaching hydrodynamic equilibrium, at which the PB becomes unform along the foam hight. After this, the foam solution from the upper compartment starts draining through the foam towards the lower compartment due the gravity.
The volumetric flow rate of the draining foam is measured by means of a graduated glass tube (3). The pressure drop is equal to \({P_L} = {P_0} - \Delta P\), where \({P_0}\) is the atmospheric pressure, while \(\Delta P\) is the pressure generated by the peristaltic pump. This setup allows one to demand different pressure drops on the top and the bottom of the foam \(P_L^{\max } = {P_0} - \Delta {P_{\min }}\) and \(P_L^{\min } = {P_0} - \Delta {P_{\max }}\), at the upper and low porous plates, respectively.
The basic theory of the FPDT technique is discussed next. This technique can be assumed as one of the most advanced techniques for studying foam drainage as far as one has control of the Plateau borders (PBs) radii along the foam column height.
Since the height of the foam columns used in the experiments is small (~2 cm), the radius, R, of the foam Plateau borders (PBs) can be assumed to be constant throughout the foam. This assumption is further reinforced by the application of the equal pressure drops at the top and bottom foam surface. The PB radius can be determined from the Laplace pressure on the bubble cell surface, which yields
where \({p_g}\) is the pressure in the foam bubbles and \({p_l}\) is the liquid pressure in the Plateau borders under the applied pressure drops. The pressure term on the right-hand side of Eq. (10) can be determined using the applied pressure drops and the balance between the mechanical work of the foam formation and the surface energy as described in the following.
Balancing the mechanical work, \(\left( {{p_g} - {p_0}} \right)dV\), spent for the foam formation within the volume element \(dV\), with the surface energy \(\sigma dS\), surrounded by the surface area \(dS;\) one obtains \(\left( {{p_g} - {p_0}} \right)dV = \sigma dS\), where \({p_0}\) is the atmospheric pressure. The pressure difference \(\Delta {p_g} = {p_g} - {p_0}\) is known as the excess pressure in foam bubbles which can be obtained from the energy balance equation, which yields
where a is the edge length of polyhedral bubble cells in foam and \({c_1} = 1.575\) if the Kelvin tetrakaidecahedron is used for the foam cell. Alternatively, the pentagonal dodecahedron can be used for the cell, which yields \({c_1} = 1.796\). Equation (11) is valid for dry foams but can be extrapolated to predict the pressure excess in foam bubbles with higher liquid fraction.
Furthermore, the pressure difference on the right-hand side of Eq. (10) can be re-written and determined as \({p_g} - {p_l} = \Delta {p_g} + \left( {{p_0} - {p_l}} \right) = {c_1}\sigma /a + \Delta p\), where Eq. (11) was used to determine \(\Delta {p_g}\). Here, \(\Delta p\) is the pressure drop externally applied to the foam bottom surface (or the pressure drop externally applied to the foam top surface less the hydrostatic pressure head). Equation (10) for the PB radius yields
Furthermore, the edge length, a, of foam polyhedral bubbles is also a function of the radius of the PB. Within the dry foam limit, the dependence of the liquid volume fraction, \(\varepsilon\), on the radius of the PB and its length is described as
where \({c_2} = 5.828\) is valid for the Kelvin tetrakaidecahedron cell or \({c_2} = 4.698\) is valid for pentagonal dodecahedron cell, respectively. Equations (12) and (13) are central to this theory, and can be combined to determine the radius, R, and length, a, of the PB. The solution for R reads
where \({c_3} = 3.804\) is valid for Kelvin tetrakaidecahedron cell or \({c_3} = 3.893\) for pentagonal dodecahedron cell, respectively.
The standard drainage theory assumes rigid gas–liquid interface (Weaire and Hutzler 1999). The gravity drainage velocity, W, of interstitial liquid in the individual PBs averaged over all possible orientations of the PBs in foam gives
where ρ and \(\mu\) are the foam liquid viscosity and density, respectively, and g is the acceleration due to gravity. The volumetric flow rate of liquid drainage, Q, through the foam column can be determined as \(Q = W\varepsilon A\), which yields
where \(A\) is the cross-sectional area of the foam column. Equation (16) can be used to validate the theory versus the experimental data.
The standard drainage theory has been extended to account for a number of effects relevant for foam drainage, including the foam surface shear viscosity (Desai and Kumar 1983), the surface diffusion of surfactants (Durand and Langevin 2002), and the node contributions (Durand et al. 1999; Koehler et al. 2000; Stone et al. 2003). For the foam drainage in the dry limit under an applied pressure drop, the effect of the foam surface shear viscosity can be important and the extended theory for the gravity drainage velocity, W, of interstitial liquid in individual PBs averaged over all possible orientations of PBs in foam provides the following result (Nguyen 2002):
where \(Bo = {\mu _s}/\left( {\mu R} \right)\) is the Boussinesq number and \({\mu _s}\) is the surface shear viscosity. The term in the square brackets on the right-hand side of Eq. (17) describes the deviation from the standard drainage theory. For an infinitely large surface viscosity (i.e., the rigid gas–liquid interface), the term in the brackets approaches 1, thus tending to the standard drainage equation.
The volumetric velocity of liquid drainage, Q, through the foam column can be determined as
Equation (18) is useful for validating the modified theory against the experimental data on the volumetric flow rate, as shown in the following.
The liquid flow through the foam with a constant (along the foam column height) of PB radius was first investigated by Kuznetsova and Kruglyakov (1981). It was established that the experimental drainage rate in the foam containing SDS with the common black films and the surfactant NP-20 was substantially higher (by a factor up to 9) than calculated by the Leonard–Lemlich Equation (1965a, b) with the PB radii greater than 50 µm. The latter accounts for the liquid drainage in PBs in their real geometry, but assumes rigid walls of the PBs. In this work, liquid flow through the foam stabilized by SDS and Triton X-100 with electrolyte, gelatine, and glycerol added, was investigated. The radii of the PBs varied from 30 to 100 µm. The experimental results obtained by the FPDT method were compared with the models using the Desai and Kumar equation (1982, 1983) and the Nguyen equation (17) in which the surface mobility effect is taken into account. The more recent study reported in Vilkova and Kruglyakov (2005) also showed that an immobile surface of the PBs was observed in the foam containing SDS + lauryl alcohol + gelatin. Surface mobility was observed experimentally in foam containing Triton X-100 + 0.1 mol/L NaCl, and foam containing SDS (with the common black films). For these solutions, the experimental foam-drainage velocity was significantly higher than the model predictions. The Boussinesq numbers for these solutions were equal to 2 and 10, respectively.
The investigations of flow of surfactant solution through foams stabilized by the surfactants SDS and Triton X-100 with electrolyte and gelatine as additives were reported by Vilkova and Kruglyakov (2004a, b, 2005). The minimal R min, and maximal R max, and PB radii were known as well. The PB profile \(R\left( z \right)\) was calculated assuming mobile PB surface.
It was shown that the experimental PB radii of the foam containing SDS + 0.1 M NaCl and Triton X-100 + 0.4 M NaCl were the same as the calculated values by applying the Nguyen Eq. (17) and the Desai and Kumar model at all the pressure gradients. In the foam of SDS + gelatin with the Newton black films, the PB radii were different from the calculated values. For example, in the foam containing SDS with the Newton black films, the PB radius was 20% smaller than the calculated values.
A similar decrease in the PB radii was observed with the foam of SDS + 0.2% gelatin: the experimental PB radius in this foam was different from the calculated values using the model with the surface immobility by 28%. The decrease can be caused by the surface tension gradient along the PBs.
The investigation of the liquid flow through the foam subjected to different pressure drops (\(P_L^{\max }\) and \(P_L^{\min }\)) is reported in Vilkova and Kruglyakov (2005). In this work, the experimental and theoretical volumetric flow rates through the PBs (with the immobile surface) were compared using the following expression:
This equation was obtained from the Leonard–Lemlich equation (Leonard and Lemlich 1965a, b) and the dependence \(r = \sigma /{P_\sigma }\); \({P_\sigma }\) is the capillary pressure. From Eq. (19) and the parameter β obtained in this work, the volumetric flow rate of the solution calculated taking into account the surface mobility was obtained. With the help of the Nguyen Eq. (17), the volumetric flow rate \(Q^{\prime\prime}_{{{\text{th}}}}\) of the solution through the PBs with the minimum and maximum radii (\({r_{\min }}\) and \({r_{\max }}\)) was
No significant difference between the experimental and theoretical volumetric flow rates was observed in the Triton X-100 + glycerol foam.
In the foam containing SDS + gelatine, the experimental volumetric flow rate was different from the prediction by the Leonard–Lemlich theory. The discrepancy between the theoretical and experimental drainage rates (Kruglyakov and Vilkova 2007; Vilkova and Kruglyakov 2004a, b, 2005) is probably due to the uncertainty of the measured surface viscosities (Stevenson 2005).
3 Foam drainage: basic concepts and methods for investigation
The foam drainage is relatively a new field of the dispersion science (Desay and Kumar 1982, Koehler et al. 2000; Krotov 1984; Leonard 1964; Narsimhan 1990; Verbist et al. 1996; Weaire et al. 1993). Thus, the experimental methods and theories dealing with foam drainage under different conditions were developed. A short overview of some of the basic achievements in this field follows next.
3.1 Foam drainage equations
The foam drainage can be expressed as a laminar flow driven by the capillary and the gravitational forces. The foam resists to drainage by three basic dissipative elements, associated with the Plateau borders (PBs), where three bubbles meet, the nodes, where four PBs meet, and the films, where two bubbles meets. The boundary between these dissipative elements is difficult to be distinguished and accurately described mathematically. However, they have been used to conveniently describe various dissipative effects in foam drainage. For example, in contrast to the PBs and the nodes, the foam films have a considerable dissipative effect only in very wet foams (Kruglyakov and Exerowa 1998; Exerowa and Kruglyakov 1998; Goldfarb and Sheiber 1988; Koehler et al. 2004a, b, c; Krotov 1980; Narsimhan 1990; Verbist et al. 1996; Weaire et al. 1993; Nguyen 2002). There, the drainage flow can significantly dissipate via viscous losses. The drainage flow obeys the Stokes equations (in the lubrication approximation limit) and the continuity equation, but the key element here is the boundary conditions determining the viscous losses. In terms of the viscous loses, two drainage regimes are accepted, namely, the channel-dominated drainage (with viscous losses being dominant in the PBs) and the node-dominated drainage (with viscous losses being dominant in the nodes). In contrast to the flow in the nodes, the flow in the PBs is easier to describe. Therefore, most of the theoretical models focus on the flow in the PBs. In this regard, there are two important parameters related to the flow in the PBs, i.e., the shape and surface mobility of the PB. The cross-sectional shape of the PB can be assumed as formed by three equal circular arcs which are joined together (the arcs are concave towards the center of the triangle). Due to the symmetry, the area of PB is usually modeled by 1/6th of the total area. The hydrodynamic equations are formulated in cylindrical coordinate system with the origin located at the center of the circle used to generate one of the arc-like sides of the PB. Therefore, combining the mass and momentum balance equations yields the standard foam-drainage equation, which describes the spatial and temporal evolutions of the cross-sectional area, A, of the PBs (or the liquid volume fraction, ε) (Nguyen and Schulze 2004; Verbist et al. 1996; Weaire and Hutzler 1999) as
where t and z are the time and vertical coordinate, respectively, C = 0.402, and f is the shape factor. The first and second terms on the right-hand side of Eq. (21) contain the gravitational and capillarity contributions to the driving force of drainage. The liquid volume fraction ε can be introduced into Eq. (21) by the formula \(A \cong {\delta _r}{L^2}\varepsilon\), where \({\delta _r} = 0.676385\) (Koehler et al. 2000; Verbist et al. 1996). Therefore, the alternative form of Eq. (21) is
The essence of the standard drainage equation as described by Eqs. (21) and (22) is related to the shape factor f. It is determined by the shape and mobility of the PB. For example, if the PBs are cylindrical and rigid, \(f = 8\pi\). If one assumes the rigid PBs with real shape, \(f = 50\).
The first differential equation of foam drainage can be found in the works of (Kann 1989; Kruglyakov and Exerowa 1998) and is detailed in a series of works of Exerowa and Kruglyakov (1998), Krotov (1980), and Kruglyakov and Exerowa (1998) who solved the problem for both equilibrium and non-equilibrium between the PB and the adjacent foam films. The analytical solutions of these equations were obtained for the distribution of the foam density in the vertical direction in quasi-equilibrated foams and in the foams undergoing stationary drainage flow. Krotov (1980) accounted for the viscous losses due to rigid PBs and foam films. Assuming a negligible effect of the films on dry foams, he derived the drainage equation as:
where R is the volume-equivalent radius of the foam bubbles (applied for bubbles with all the possible shapes). The shape factor, according to Eq. (23), should be \(f = 20.4.\) Krotov (1980) formulated the condition of the PB surface immobility as \(0.224r\mu /{\mu _s} < < 1\), where r is the PB radius and µs is the surface viscosity. Similar differential equations were latterly derived by Goldfarb and Sheiber (1988) and Verbist et al. (1996). In these works, the value of the shape factor was\(f = 1\).
The subsequent analysis on the influence of the physicochemical factors on the foam drainage can be found in Durand and Langevin (2002). They accounted for the effects of surface viscosity and the surfactant adsorption layer (soluble and insoluble) under the condition close to the thermodynamic equilibrium. They also assumed the cylindrical shape of the PBs and the negligible effect of the surface viscosity. According to this work, the shape factor in the case of an insoluble surfactant should be
where \({D_s}\) and \({E_g}\) are the surface diffusion coefficient and the Gibbs elasticity of the adsorption layer, respectively. The contribution of the second term on the right-hand side of Eq. (24) is usually smaller than the contribution of the first term. In the case of a soluble surfactant, the shape factor can be described as
where D is the bulk diffusion coefficient, \(\beta = {\left( {\partial \Gamma /\partial c} \right)_{{\text{eq}}}}\) is the adsorption length, \({\Gamma _{{\text{eq}}}}\)is the equilibrium surfactant adsorption, and \({c_{{\text{eq}}}}\) is the surfactant bulk concentration at equilibrium. The contribution of the second term on the right-hand side of Eq. (25) is also smaller than the contribution of the first term. Therefore, the second terms in Eqs. (24) and (25) can be neglected yielding the shape factor of the rigid cylindrical PBs, as \(1/f = 1/8\pi\).
Desai and Kumar (1982) accounted for the surface shear viscosity and employed the triangular shape for the PB cross-section, which yields the following expression for the shape factor:
with α being a function of the surface shear viscosity described as \(\alpha = 0.4387\mu \sqrt A /{\mu _s}\) and the other model parameters denoted as α i and b i tabulated by the authors.
Nguyen (2002) accounted for the PBs with real shape and the surface mobility and derived a semi-numerical expression for the shape factor as
In Eq. (27), \(Bo = {\mu _s}/\left( {\mu r} \right)\) is the Boussinesq number and r is the radius of the Plateau borders.
Narsimhan (1990) combined the approaches of Exerowa and Kruglyakov (1998), Krotov (1980), Kruglyakov and Exerowa (1998) with those of Desai and Kumar (1982, 1983). He considered the PBs with the surface viscosity and derived the following differential drainage equation:
where R is the radius of the bubbles in the foam and l is the length of the PBs. Surprisingly, the exponent of A in Eq. (28) is not identical with the standard drainage [Eq. (21)]. We will see further that this equation is valid for the node-dominated regime of drainage.
Koehler et al. (2000) have significantly contributed to the theory of foam drainage. Considering the foam as a porous medium with a permeability, \(k\left( \varepsilon \right)\), which varies dynamically with the liquid volume fraction, they derived a generalized foam-drainage equation:
where \({\delta _\varepsilon } = 0.171\), and L is the length of the edge of the Kelvin cell. In Eq. (29), permeability \(k\left( \varepsilon \right)\) accounts for the contributions from the channels and the nodes. For the channel-dominated regime, Eq. (29) yields Eq. (22) with \(f = {\delta _r}/{K_1} = 107.36\), where K 1 = 0.0063 is the coefficient related to viscous losses in the PBs. If one assumes viscous losses only in the nodes, the drainage equation is as follows:
where K 1/2 is a fitting parameter related to the viscous losses in the nodes. One can see similarities between Eqs. (28) and (30). Koehler et al. (2004a, b, c) also considered the effects of the external PB channels (in contact with the walls of the container).
Furthermore, Wang and Narsimhan (2006) considered the draining solution in the foam as a power-law (non-Newtonian) fluid, with Eq. (28) being multiplied by \({C_v} = a\left( n \right) + b\left( n \right)\beta\), and with the following viscosity coefficient:
where \(a\left( n \right)\), \(b\left( n \right)\), and \(n\) are the fitting coefficients, and \(\beta\) is a the dimensionless surface viscosity. The coefficient \(n\) is equal to 1 for Newtonian liquids, \(0 < n < 1\) for pseudo-plastic liquids, and \(n> 1\) for dilatant liquids. These authors also solved the foam-drainage equation numerically and analytically for particular cases of foam in quasi-equilibrium or foam with quasi-steady drainage. There are particular solutions for solitary wave for forced drainage. However, during the forced drainage, the foam becomes very wet locally, approaching the condition of the Kugelschaum (the spherical bubbles), at which the PBs and the nodes do not exist, but only spherical bubbles exist in a close contact.
3.2 Model calculations
The foam-drainage theory is based on the liquid mass momentum and balance equations in the lubrication approximation by considering a laminar flow in the PBs driven by the gravity and the capillary forces. The simplified governing equations yield
where µ is the liquid viscosity, U and \(\left\langle U \right\rangle\) are the liquid local and space-averaged velocity in the PBs, and A and P are the cross-sectional area and the local pressure in the PB. In addition, r, z, and ϕ are the cylindrical coordinates centered at the PB center line. There are three basic keys of modeling the foam drainage, including the BP shape, the surface boundary conditions, and the foaming liquid rheology. For the drainage of a Newtonian liquid, the integration of Eqs. (32) and (33) yields the results f depending only on the PB shape, but not on the characteristic length scale or the flow rate. Accordingly, these two equations (Nguyen and Schulze 2003) reduce to
where the shape factor \(f\) is discussed in the following. The pressure P in Eq. (34) contains the hydrostatic and capillary terms \(P = \rho gz + {p_g} - \sigma /R\), where p g is the pressure in the gas bubbles, and R is the radius of the PBs. The drainage equations discussed in the previous sub-section were obtained using Eq. (34). The shape factor, f, is central to the drainage theories. Both numerical and analytical approaches have been used to obtain f. Leonard and Lemlich (1965a, b) solved the problem numerically accounting for the real shape of PBs and the surface mobility. Desai and Kumar (1982, 1983) derived an approximate semi-numerical result described by Eq. (26). Nguyen (2002) accounted for the real shape of the PBs and the surface mobility, and derived the semi-empirical result given by Eq. (27). The asymptotic result obtained by Nguyen in the limit of the Bousinesq number tending to zero agrees with the analytical result obtained by Koehler et al. (2004a, b, c). Wang and Narsimhan (2006) solved numerically the problem for non-Newtonian liquids and were able to establish the solution only for the cylindrical rigid PB with a plug-like flow in the following form:
where R 1 is the radius of a cylinder with the cross-sectional area and A being equal to the real area of the PBs. Therefore, if n = 1, then \(f = 8\pi\).
Stevenson et al. (2007) assumed that if the inertial pressure losses are negligible, the liquid superficial net rate of foam drainage can be expressed as
where R is the radius of the gas bubbles, and m and x are the fitting parameters. Here, it is assumed that the mobility of the PB surface and the viscous losses in the nodes are implicit functions of the model parameters m and x which can only be obtained by fitting the model with the drainage data. Similarly, Neethling et al. (2002) developed a foam-drainage model by considering viscous loses in the channels and the nodes, with a set of two model fitting parameters.
Foam drainage in a rising foam column was also studied to predict the superficial liquid flow rate as a function of the gas superficial velocity and other relevant parameters (Nguyen et al. 2003; Stevenson et al. 2003). The water recovery rate, J f , from a rising foam column is determined as
where J g is the gas (bubble) velocity and ε is the average liquid holdup. The pneumatic foam appears to be more complicated as a research object as far as the foam is rising, while the liquid is draining due to the gravity.
3.3 Methods for studying foam drainage
A number of techniques and methods for producing foams suitable for studying foam drainage have been developed. Most of the techniques are described in the monographs of Exerowa and Kruglyakov (1998) and Weaire and Hutzler (1999). The progress of drainage of liquid from a foam in cylindrical columns can be divided into the following stages of liquid accumulation: (1) the stage of an increasing rate and (2) the stage of the decreasing rate (Weaire and Hutzler 1999). To set aside these complications, Saint-Jalmes et al. (2000) used a special construction (”an Eiffel tower”) which allows more liquid to be passed down than received from above, and thus, the foam can become uniformly drier with time.
The methods for studying of foam drainage can be divided into number of categories:
-
methods for determining the velocity of the liquid flow out of foam;
-
methods for determining the liquid flow (percolating) through the foam;
-
foam pressure drop technique (FPDT) (Exerowa and Kruglyakov 1998);
-
forced drainage in which a front of wet foam moving through the foam with small liquid content is registered (Koehler et al. 2000; Weaire and Hutzler 1999);
-
free drainage, i.e., a method for studying the change in the liquid volume fraction of a draining foam driven by the gravity (Jun et al. 2012; Koehler et al. 2000);
-
special setup with a single PB (Pitois et al. 2005).
To accelerate the foam drainage and to obtain very dry foams, the FPDT method is used (Vilkova and Kruglyakov 2005). In the micro-syneresis investigations, the experimental methods focus on determining liquid contents at different foam heights and monitoring liquid velocity of drainage simultaneously. Thus, the UV light was used to monitor the liquid flow by the following tracers of fluorescent salt dissolved in the liquid previously (Koehler et al. 2004a, b, c). For observing the front of the moving liquid, the light scattering technique (Cervantes-Martinez et al. 2005; Saint-Jalmes et al. 2000) or the local electrical conductivity measurements (Cervantes-Martinez et al. 2005; Durand et al. 1999) were also used. The nuclear magnetic resonance imaging technique was successfully employed to determine the liquid drainage and the volume fraction (Assink et al. 1988; McCarthy 1990; Stevenson et al. 2007). The sonic velocity method was also used to measure the liquid fraction as a function of foam height (Magrabi et al. 2001).
The experimental setup for studying foam drainage at constant radii or controlled distribution of the radii of the Plateau borders along the foam height is described in a number of works (Exerowa and Kruglyakov 1998; Kruglyakov and Vilkova 2007; Vilkova and Kruglyakov 2004a, b, 2005). The control of the PB size is achieved by the controlled reduction of the pressure at the top and at the bottom of a small foam column. The details of the FPDT method will be given in Sect. 2.2. The technique can also be used for studying the micro-syneresis and the time required for establishing the pressure equilibrium in the PBs.
A special setup with a single PB designed and used by Pitois et al. (2005); measurements of the pressure drop in the foam channel as a function of the volumetric liquid flow rate were conducted with the theoretical predictions (Nguyen 2002). The single PB and three adjoining films were obtained by withdrawing a special frame from a reservoir containing foaming solution. The typical PB length was between 5 and 15 mm. The frame consisted of a vertical metallic tube on which three rods (1 mm in diameter) were connected. The tube was used to deliver liquid to the PB.
The basic methods for studying foam drainage—the free and forced foam drainage—are considered in the following. They have commonly been used to study foam drainage. Both drainage processes are governed by gravity, surface tension, and viscous forces. Two limits of foam drainage are assumed (Koehler et al. 2000): the channel-dominated drainage regime, in which the main hydrodynamic resistance is on the PBs and the node-dominated drainage regime, in which the viscous dissipation takes place in the nodes.
3.3.1 Free drainage
The free drainage method involves the formation of a foam column of rising bubbles from a foam solution. The bubbling is then stopped to allow the liquid in the foam surrounding the bubbles to freely drain, due to gravity, back to the foam solution. The initial liquid content in the foam is usually high and uniformly distributed. The drainage leads to a gradient in the liquid fraction, with the amount of liquid decreasing for the top to the bottom of the foam. A dry front from the top to the bottom of the foam column propagating downwards can sometimes be observed. The dry front can lead to the formation of two overlapping regions in the foam body: the rear and knee regions (Koehler et al. 2000). In the rear region, the liquid volume fraction ε increases from the top towards the bottom until reaching a constant value ε main in the knee region. The “knee” is moving downwards with a constant velocity \({v_k}\), which is greater than the rear velocity \({v_r}\), thus causing the rear region to increase in time. The drainage regime (node or channel-dominated) is governed by the nature of the surfactant used and is determined by adjusting the theory to the experiment. For example, if the foam contains sodium dodecyl sulfate (Koehler et al. 2000), the free drainage at the top of the foam proceeds as \(\varepsilon \sim {t^{ - 1.2}},\) corresponding to \({v_r} \cong 6.13\varepsilon _{\text{main}}^{1/2}\), which is valid for the node-dominated regime of drainage. Accordingly, the knee is moving with the velocity \({v_k} \cong \sqrt 2 {v_r}\).
3.3.2 Forced drainage
In the forced drainage method, foam solution is added onto the top of an already dried foam causing propagation of a continuous wet wave throughout the foam column. A modification of the forced drainage is the pulsed drainage, where the foam surfactant solution is periodically added onto the foam top. The drainage wave profile consists of three regions (Koehler et al. 2000): the drained region below the traveling wet wave (ε < 10−4), the transition region in the vicinity of the front of the wet wave, and the main body region with uniform ε main. The front of the advancing wet wave has the speed, \({v_f}\), depending on the injected liquid volume flux, Φ, as: \({v_f} = \Phi /{\varepsilon _{{\text{main}}}}.\) The main liquid volume fraction ε main is measurable. In this way, each value of \(\Phi\) corresponding to the given values of \({\varepsilon _{{\text{main}}}}\) and \({v_f}\) can be determined. Therefore, the experimental data can be expressed as \({v_f}\) versus \({\varepsilon _{{\text{main}}}}\) or \({v_f}\) versus \(\Phi\). The corresponding theoretical dependencies are \({v_f} = {K_{1/2}}\rho g{L^2}\sqrt {{\varepsilon _{{\text{main}}}}} /\mu = {\left( {{K_{1/2}}\rho g{L^2}/\mu } \right)^{2/3}}{\Phi ^{1/3}}\) in the node-dominated regime, or \({v_f} = {K_1}\rho g{L^2}{\varepsilon _{{\text{main}}}}/\mu = {\left( {{K_1}\rho g{L^2}/\mu } \right)^{1/2}}{\Phi ^{1/2}}\) in the channel-dominated regime (Saint-Jalmes et al. 2004), where K 1 = 0.0063 (Koehler et al. 2000), K 1/2 is the dimensionless permeability for the liquid flow in the PBs, the nodes, L, is the length of the edge of the Kelvin foam cell, and µ is the liquid viscosity. The regime of drainage is determined by adjusting the theory to the experiment. The effects of the capillary and the gravitational forces were separated recently by the initiation of the two-dimensional forced drainage in the Hele-Shaw cell (Hutzler et al. 2005) and the pulsed drainage (Koehler et al. 2001). It was found that the capillary forces are dominant.
The experimental investigations of foam drainage using the two different drainage regimes are discussed by (Cervantes-Martinez et al. 2005; Durand et al. 1999; Saint-Jalmes and Langevin 2002; Saint-Jalmes et al. 2000, 2004). The results are also expressed by a power-law relationship between v and Φ (or ε) as \(v = {\Phi ^\alpha }\), where α = 1/2 (for the rigid channel surfaces) and α = 1/3 for the mobile surfaces. Durand et al. (1999) studied the foam drainage stabilized by the SDS surfactant [1.2 mmol/L and its mixture with dodecanol (LOH)]. They found α = 0.39 ± 0.4 (for soap Dawn) and α = 0.54 ± 0.3 for the mixture with (SDS/LOH = 103), while α = 0.39 ± 0.4 for (SDS/LOH = 2 × 103). However, it is not clear whether the difference in the drainage behavior is due to the different surface viscosities of the two systems and which of the surface shear and dilatational viscosities should be considered.
The results presented in (Saint-Jalmes and Langevin 2002) show that foam drainage depends on many parameters: gas type, liquid viscosity, surfactant type, bubble size, wetness, and the foam height. The experimental results show that changing these foam parameters can induce transition between the node- and channel-dominated regimes. The results are analyzed in terms of two dimensionless numbers: \({M_L} = \mu R/{\mu _s}\) and \({M_d} = \mu {D_s}/{E_g}z\), where \(\mu\) and \({\mu _s}\) are bulk dynamic viscosity and surface viscosity of air/water interface, \({D_s}\) is surface diffusion coefficient of the surfactant molecules, \({E_g}\) is Gibbs elasticity, and \(z\) is vertical coordinate. For the intermediate regime, they proposed to consider that the PBs and nodes are resistors connected in series, where the corresponding resistances depend on the mobility parameters M L and M d. It was established that a transition between the two drainage regimes occurs in an intermediate range of surface mobility corresponding to the point, where the channel and node resistances are equivalent. They also proposed that drainage experiments can be used as a method for measuring surface shear viscosities. The aim was to study how the free drainage behavior of SDS-dodecanol foams depends on the SDS/LOH concentration ratio in the case of very small bubbles size (<200 µm). The dependences ε/ε0 (τ) for different values of the concentration ratio (4–100) of the foams generated with C2F6 (to minimize the coarsening effect) show that a transition from a foam drainage with a high surface mobility (k = 100 or 12.8) to the plug-like drainage regime at [SDS]/[LOH] = 5. Although these experiments supply useful data on the foam drainage, they cannot be considered as a proof of the real transition between the channel-dominated and node-dominated regimes, because the coupled dissipation cannot be predicted, at its value is rather a fitting parameter between the models and the experiment.
4 Surface forces in thin-liquid films
To understand the properties of the thin-liquid film, one needs to know the fundamental forces acting on them. A thin-liquid film is a quasi-two-dimensional continuum surrounded with two interfacial layers, thus forming an unified inhomogeneous structure with specific properties. The film thickness is a fundamental quantitative parameter characterizing the deviations of the properties of a thin film from those of the bulk phase. Such deviations are adequately expressed by the disjoining pressure, introduced by B. V. Derjaguin in the early 1930s (Derjaguin and Obuchov 1935; Koehler et al. 2000) and is a fundamental value in the Deryaguin–Landau–Verwey–Overbeek, DLVO, theory of stability of lyophobic colloids (Derjaguin and Landau 1941; Deryaguin 1989; Verwey and Overbeek 1948). The classical DLVO theory combines the van der Waals and electrostatic double-layer interactions. The van der Waals interaction between the surfaces of the thin-liquid film is systematically described in many books, including (Mahanty and Ninham 1977; Verwey and Overbeek 1948). The interaction can be described by means of either the Hamaker ‘microscopic’ approach (Israelachvili 1992a, b, c), or the Lifshitz (‘macroscopic’) approach (Hamaker 1937; Lifshitz 1955; Nguyen and Schulze 2003).
4.1 Electrostatic disjoining pressure
The electrostatic disjoining pressure Π el arises in thin films of dilute electrolyte solutions and is due to the overlapping of the diffuse electric layers on the two film surfaces at small separation distances. For symmetrical electrolytes, the equation derived from the Poisson–Boltzmann equation for Π el yields (Dzaloshinskii et al. 1961; Nguyen and Schulze 2003):
where z is the valence of the binary electrolyte, \(\psi\) is the potential in the film at the position of the zero potential gradient (e.g., at the mid-plane for the symmetric foam films), e is the electron charge, c el is the electrolyte bulk concentration in the solution from which the film is formed, and k B T is the molecular thermal energy.
In foam (and emulsion) films, Π el is always positive (repulsion). With wetting films, the situation is more complex, and in some cases, electrostatic interactions can even lead to the attraction of the film surfaces (Deryagin 1989; Hunter 1994).
In addition to the long-range forces of attraction and repulsion, stability of films and the respective disperse system is also dependent on the short-range interactions in the adsorption layers (Deryagin 1989; Israelachvili 1992a, b, c; Nguyen and Schulze 2003), whose characteristics are an important factor in the formation of the stable ‘black’ films, but have little effect on film thinning.
The calculation of the disjoining pressure as a function of the film thickness is critical to validation of the drainage theories. Approximate equations are not universal. For this reason, advanced models are needed as described in the following (Exerowa and Kruglyakov 1997; Karakashev and Ivanova 2010).
The electrostatic disjoining pressure Π el can be obtained by numerical solution of the Poisson–Boltzmann equation employing the appropriate boundary conditions at the film surfaces. Under the condition of constant surface potential, the numerical solution of the nonlinear Poisson–Boltzmann equation can be semi-analytically represented as (Karakashev and Ivanova 2010):
where c el is the molar concentration of electrolytes in the solution. The Debye constant for a binary electrolyte of valence z is defined as \(\kappa = {\left\{ {2{c_{el}}{F^2}{z^2}/\left( {\varepsilon {\varepsilon _0}{R_g}T} \right)} \right\}^{1/2}}\), where \({\varepsilon _0}\) is the dielectric permittivity of the vacuum. The normalized surface potential is defined as\({y_0} = zF{\varphi _s}/\left( {{R_g}T} \right),\) where F is the Faraday constant and \({\varphi _s}\) is the surface potential. For \(\left| {{y_0}} \right| \leqslant 7\), the function \(f({y_0})\) is defined as \(f({y_0}) = 2\cosh (0.332\left| {{y_0}} \right| - 0.779)\). Equation (39) is valid up to the 120 mV value of the surface potential. Under the condition of constant surface charge density, the exact numerical solution of the Poisson–Boltzmann equation yields (Nguyen et al. 2002)
The model constants in Eq. (40) are functions of the surface potential, y 0, at the infinite separation (i.e., at the single air–water surface) which are described for \(\left| {{y_0}} \right| \leqslant 5\) as follows: \(\tilde A = \tilde B\tilde C\sinh \left( {1.854\left| {{y_0}} \right| - 0.585{{\left| {{y_0}} \right|}^2} + 0.1127{{\left| {{y_0}} \right|}^3} - 0.00815{{\left| {{y_0}} \right|}^4}} \right),\) \(\tilde B = 0.571\left| {{y_0}} \right|\exp \left( { - 0.095{{\left| {{y_0}} \right|}^{1.857}}} \right)\) and \(\tilde C = 1 - 0.00848\left| {{y_0}} \right|\).
Equation (40) is valid up the 186 mV value of the surface potential. It should be noted here that the regime of constant surface potential should be the most probable regime for thin-liquid films (TLF) with fluid interfaces (foam and emulsion films), while the regime of the constant surface charge density is most probable for TLF with solid surfaces (e.g. in suspensions). Note also that the electrostatic disjoining pressure in the case of ionic surfactants is affected by the drainage outflows from thin-liquid film (Nguyen et al. 2002). For instance, when the surface-active ions are displaced at the periphery of the film, they reduce the electrostatic repulsion at its center. Moreover, the shift of the electrical double layer (EDL) towards the periphery of the film creates streaming potential between the center and the film rim (Karakashev et al. 2010a, b). The latter causes the opposite fluxes decreasing the speed of film drainage.
4.2 Van der Waals disjoining pressure
The van der Waals disjoining pressure, Π vdW , as a function of the film thickness, h, can be described as (Karakashev and Tsekov 2011)
where А(h, \(\kappa\)) is the Hamaker–Lifshitz function, which depends on the film thickness and the Debye constant, \(\kappa\), due to the electromagnetic retardation effect and is described as
where ε 1 is the static dielectric permittivity of the dispersion phase (ε1 = 2.379 for toluene at 298.15 K), ε 2 is the static dielectric permittivity of the disperse medium (ε2 = 80 for water), \(\hbar\) = 1.055 × 10− 34 Js/rad is the Planck constant, ω is the absorption frequency in the UV region—typically around 2.068 × 1016 rad/s for water, \({n_1}\) and \({n_2}\) are the characteristic refractive indices of the dispersion phase and the medium: \(n_{_1}^2\) = 1 for air and \(n_{_2}^2\) = 1.887 for water, and q = 1.185. The characteristic wavelength is defined as \(\tilde \lambda = 2v\sqrt {2/n_2^2\left( {n_1^2 + n_2^2} \right)} /\left( {{\pi ^2}\omega } \right)\), where v is the speed of light.
4.3 Steric disjoining pressure
If polymeric molecules are adsorbed on the two surfaces of the liquid film, considerable part of their chains are located in the liquid core of the film. When the film becomes sufficiently thin, they begin to obstruct sterically its further thinning. One has to consider the following effects: the osmotic (entropic) repulsion due to the overlapping of the polymeric chains protruding from the two surfaces, the elastic effects (reducing the repulsion) due to the deformation of the chains, and the attraction between the chains from the two surfaces until the point at appropriates solvents. There exist different theories aiming at describing these interactions. One of them which has been widely accepted and validated is the theory of de Gennes (de Gennes 1997; De Gennes 1987; Israelachvili 1992a, b, c; Nguyen and Schulze 2004; Sett et al. 2014) which yields the relation for the steric disjoining pressure at significant adsorption of polymeric molecules in “good” solutions for h ≤ 2L g as
where L g is the thickness of the polymeric layer on the surfaces of the film, \({k_B}\) is Boltzmann constant, \(\Gamma\) is adsorption of polymeric molecules on the film surfaces, and \(h\) is the thickness of the foam film. These forces have stabilizing effect on the foams.
4.4 Hydrophobic disjoining pressure
Long-range attraction forces between hydrophobic surfaces were observed in some particular cases (Rabinovich and Deryagin 1988; Sett et al. 2014). There are several theories trying to explain the origin of the so-called “hydrophobic attraction”, but there is no fully acceptable explanation. One of the explanations, for example, is the ordering of water molecules in dynamic structures in close proximity to the hydrophobic surfaces (Israelachvili 1992a, b, c; Tsekov and Schulze 1997). This minimizes the free energy of the system and reduces the effect from the unfavorable contact between the hydrophobic substances and water. When non-polar molecules approach the interface, they diminish the contact area of carbon–water, which result in hydrophobic attraction. Tsekov and Schulze (1997) have thermodynamic description of the hydrophobic interactions, accounting for the change, and of the adsorption upon the thinning of the film. According to them, the following relation exists for the hydrophobic attraction:
where ΔЕ is the difference in the Gibbs elasticities of the adsorption layer of a single-phase air/water boundary relative to the bi-layer surfactant at an infinitely small film thickness. The definition of Gibbs elasticity of the adsorption layer reads
This is a very important characteristics of the adsorption layer. The Gibbs elasticity resists to the deformation of a new interphase boundary. The value D in Eq. (44) is \(D = {\left. {\frac{{d\Gamma }}{{dc}}} \right|_{h \to \infty }}\). It can be found using the adsorption isotherm of a surfactant. The physical meaning in the present case is the specific length of decay of the hydrophobic forces and depending on it they can be short—or long ranged. In a mixture of surfactants each, one of them has its own contribution to the hydrophobic interaction between the film surfaces, and Eq. (44) will express that by a sum of exponents. The hydrophobic attraction between the surfaces of the foam film results in faster drainage of the film (Israelachvili 1992a, b, c; Karakashev and Nguyen 2007) as compared to the classical DLVO theory.
4.5 Ion-correlation disjoining pressure
The electrostatic theory of thin films implies that electrolyte solution is ideal. However, the presence of electrolytes causes effects, which should be accounted for in the theory of the electrostatic disjoining pressure. The ion-correlation correction term to the disjoining pressure accounts for the energy of formation of the Debye layer referred to the bulk, the energy of deformation of the counter-ion diffusive layer due to the “image” forces, whose physical meaning stems from the propensity of the ions to transfer to medium with a higher value of the dielectric permittivity. The value of the latter is small at the air/water interface (it is between 1 and 6). The ion-correlation correction can be expressed by the following equation:
The two valent salts have a significant effect on the electrostatic disjoining pressure. This negative correction to the electrostatic disjoining pressure causes reduction of its value and results in thinner equilibrium films or faster reaching their critical thickness, which causes faster a decay of foam or the formation of black films, i.e., foam stabilization.
5 DLVO theory and electrostabilization of foams and emulsions
As mentioned above, the two basic types of disjoining pressure are related to the van der Waals and electrostatic interactions between the film surfaces. Accordingly, Derjaguin, Landau, Verwey, and Overbeek (Derjaguin and Landau 1941; Verwey and Overbeek 1948) developed the DLVO theory incorporating these two basic forces as a net force, which depends on the film thickness Π = ΠEl + Πvw. The interaction energy between the two surfaces can be expressed by the following equation:
where C and А are constants. The function f(h) is depicted in Fig. 15.
The electrostatic force of repulsion forms an energetical barrier, which prevents the film thinning. Hence, the films become equilibrium ones. If one adds electrolyte into the system, the value of κ increases, thus reducing the contribution of the electrostatic term in Eq. (47), and accordingly, the height of the barrier diminishes. At a sufficient electrolyte content, the electrostatic barrier can completely disappear, thus allowing the film to thin until reaching its critical thickness, at which the van der Waals attraction becomes significant (Verwey and Overbeek 1948). However, the DLVO theory does not account for the specificity of the counter ions in the diffusive layer. Hence, according to the DLVO theory, all the salts of the same valency should affect identically the behavior of the film. Moreover, this is not exactly true.
Pandey et al. (2003) conducted an investigation on the effect of the counter ions on the foamability and durability of foams, stabilized by Lithium Dodecylsulfate (LiDS), Sodium Dodecylsulfate (SDS), Cesium Dodecylsulfate (CsDS), and Magnesium Dodecylsulfate (Mg(DS)2). Figure 16 shows the foam lifetime versus the type of used surfactant at two concentrations—1 and 25 mM. In the first case, the foam stability increases upon the shift from LiDS to CsDS, while the dependence in the second case is more complicated due to the presence of micelles. The above-mentioned experimental dependence cannot be explained with electrostatic stabilization, according to which the electrostatic repulsion between the foam-film surfaces is the strongest in the case LiDS and the weakest in the case of CsDS. Hence, the foam stability should increase in the order CsDS < SDS < LiCl, due to the fact that the larger counter ions penetrate (e.g., Cs+) in the surfactant adsorption layer more than the smaller counter ions (e.g., Li+). The larger the penetration of the counter ions into the surfactant adsorption layer, the weaker is the repulsion between the bubbles in the foam and vice versa.
Foam stability of surfactant Dodecylsulfate at a 1mM and at b 25 mM surfactant; reprinted with the permission from Elsevier (Pandey et al. 2003)
On the contrary, the work of Schelero et al. (2010) supports the electrostabilization theory. They studied the dependence of the disjoining pressure on the film thickness of foam films stabilized by LiDS, SDS, and CsDS at different surfactant concentrations (see Fig. 17). A similar experiment has been conducted by Ivanov et al. (2011), who studied the dependence of the total disjoining pressure on film thickness of films stabilized by of 1 mM cetyltrimethyl ammonium bromide (CTAB) + 9 mM NaX (X = F, Cl, Br) (see Fig. 18).
Disjoining pressure Π versus film thickness of LiDS (filled circles), SDS (filled squares), and CsDS (filled triangles) at concentrations of DS−: 0.1 , 1, and 3.5 mM. Results from the Poisson–Boltzmann calculations are also shown by (solid curves), and for clarity, only some fitted isotherms are shown; Reprinted with the permission from Americal Chemical Society, Schelero et al. (2010)
Plot of \(\ln \Pi\) versus h for foam films stabilized by 1 mM CTAB + 9 mM NaX (X = F, Cl, Br); Reprinted with the permission from Elsevier (Ivanov et al. 2011)
One can see in Fig. 18 that even in the presence of small amount of added salt, the electrostatic stabilization of the foam films is present (Pandey et al. 2003; Slavchov et al. 2014). The strongest repulsion measured by means of the film pressure balance setup, also leading to the most stable liquid film between the bubbles occurs in the presence of NaF, while the weakest repulsion between the bubbles takes place in the presence of NaBr.
Unfortunately, explanation of film stability using this single effect is far from being complete. The counter ions affect the electrostatic repulsion between bubbles; however, it is not clear whether this effect is sufficient to predict foam and emulsion stability. In general, every surfactant solution can be characterized by its foamability (the initial foam volume after foam generation) and lifetime of the foam (Exerowa and Kruglyakov 1997; Ivanov et al. 2011; Pugh 2002; Weaire and Hutzler 1999). There are a number of factors, which affect foamability and/or the foam lifetime, as, for example, the type of the surfactant and its concentration (Karakashev et al. 2012), the air humidity (Exerowa and Kruglyakov 1997; Li et al. 2010), the presence of particles (Alargova et al. 2004; Johansson and Pugh 1992; Li et al. 2012), etc. Moreover, the foams can be classified as tenacious (with a long lifetime) and transient (short living). The border line between them is often abrupt and is related to the formation of the so-called black foam films (Kruglyakov et al. 2011), which are very durable. Moreover, the foam stability is related to the level of surfactant adsorption on the bubble surfaces (Exerowa and Kruglyakov 1997; Karakashev and Manev 2003; Karakashev et al. 2011). The latter is related to their elastic moduli (Manev and Nguyen 2005). It should be elucidated how the counter-ion type affects the stability of foams containing ionic surfactants. Repulsion from the charged surface leads to a slower adsorption of the charged surfactant molecules. For example, while a similar situation arises for emulsion droplets (Wantke and Fruhner 1998), experiments with the same system [CTAB + NaX (X = F, Cl, Br)] repeated an opposite result. These particular emulsions studied in (Ivanov et al. 2011) were the most stable in the presence of Br− ions (a larger adsorption energy) and the least stable in the presence of F− ions (a smaller adsorption energy). This intriguing result stems from the two factors affecting in two opposite directions the film stability. Namely, a stronger repulsion between the film surfaces should result in more stable foams and emulsions, while a weaker adsorption at the fluid/fluid interfaces should result in less stable. For counter-ion penetrating deeper in the surfactant layer (e.g., Br−), the net surface potential in a while would lower electrostatic repulsion towards the other bubbles (oil droplets) and prevent adsorption of the surfactant molecules. Larger adsorption of surfactant molecules facilitates formation of black stable films, which may be made even more stable electrostatically at distances smaller than the Debye length, leading to a partial expulsion of the counter-ion layer and additional charge stabilization. Depending on the specific stability challenge, however, it is not easy to predict which effect will be stronger, and sometimes, time-dependent dynamics may play a role, rather than just equilibrium considerations.
It should be emphasized that the electrostatic repulsion between bubbles, which is controlled by the added counter ions, is only one of the factors contributing to foam stabilization. The counter ions strongly affect the level of surfactant adsorption as well. The latter appears to be decisive for stabilization of the foam and the foam films. Two distinct regimes of surfactant behavior can be distinguished: (1) stabilization by added salt and (2) a rapid destabilization of the films beyond a critical counter-ion concentration. This concentration could be lower or higher than the critical micelle concentration (CMC).
6 Directions to control and design foams
As far as the foams are widely spread in our civilization, they appear to be desired or not in the different particular cases. For this reason, procedures applied for foam stabilization or destabilization were developed. Some of them are discussed in the following.
6.1 Defoaming
Defoaming dates back to the beginning of the 20th century when mechanical devices and radiation were utilized (Eddy 1932; Fanto 1907; Friedrichs 1928; Miller 1930) as, for example, air jets, special still heads, paddle wheels, perforated spiral canals, centrifuges, change of pressure, heating elements, supersonic waves, ultraviolet rays, X-rays, etc. These ways to suppress foaming were expensive due to the energy required for their implementation. To reduce the costs, chemical methods were preferred to the mechanical ones and radiation. Among the chemical methods, the addition of small quantities of caprylic alcohol, amyl alcohol, octyl alcohol, linseed oil, castor oil, rapeseed oil, trimethylcyclohexanol, phenyl ether, isoamyl isovalerate, milk, kerosene, polyamides, etc. (Gastrock and Reid 1938; Ross and McBain 1944; Jacoby and Bischmann 1948) were recommended for various aqueous foam systems. Since the late 1940s, chemical methods were commercialized and found many applications in the pharmaceutical industry (Gunderson and Denman 1948), medicine (Koffler and Goldschmidt 1949), food industry (Luisada 1950), and chemical industry (Brunner 1950), steam engines (Ross and McBain 1944), etc. The lab research on the foam inhibitors began approximately at the same time (Gunderson and Denman 1948; Robinson and Woods 1948; Ross 1950; Ross and McBain 1944; Ross and Young 1951; Ross et al. 1953).
The history of the antifoams can be split into two periods—period of “oil” antifoam products (the early 1940s–late 1970s); period of “oil + hydrophobic particles” antifoam products (the late 1970s–present) In addition, the corresponding research methods underwent development. The performance of the antifoaming agents was divided into film-breaking and foam-preventing actions. To investigate them separately, different methods were developed since the 1940s: (1) Ross–Miles method (Ross and Miles 1941); (2) Pop test by Ross and McBain (1944); (3) tests of film breaking and foam preventing by Okazaki and Sasaki (1966); (4) Japanese industrial standard (JIS) method (1967) for determining foaming characteristics of petroleum products; (5) Deutsche Industrie Norm (DIN) method (1981); and (6) Popup test by Tsuge et al. (1984).
It was assumed that oil droplets can destabilize the foam films in the following modes:
-
by acting as hydrophobic bridges between two film surfaces;
-
by displacing the adsorbed surfactant species on the film surface, thus disturbing its stabilizing action;
-
by rapidly spreading on the surface of the film, causing the liquid to be squeezed away and the film to thin and collapse.
Each antifoaming agent (Ross and Young 1951; Walker et al. 1949) has its own optimal concentration, below which it is less effective and above which it acts as foam stabilizer. A correlation between the antifoaming effect and the viscosity (Okazaki and Sasaki 1960), the spreading coefficient (Ross and Young 1951), and the entering coefficient (Harkins 1941) of each agent was sought. Thus, the entering coefficient \(E\) was defined as a measure of the ability of the antifoaming droplet (oil) to be naturally drawn into the gap between two bubbles in contact (into the foam film) which can be expressed as
where \({\sigma _{\text{F}}}\), \({\sigma _{{\text{FD}}}},\) and \({\sigma _{\text{D}}}\) are the surface tension of the air/foaming solution (subscript F), the interfacial tension between the foaming solution and defoamer (oil phase) (subscript FD), and the surface tension of air/defoamer (oil) (subscript D), respectively. If \(E> 0\), the antifoaming agent (oil droplet) should be drawn naturally into the foam film and bridge the bubbles. If \(E < 0\), the oil droplet could be ejected from the foam film and could arrive near it only by chance.
The spreading coefficient \(S\) (Robinson and Woods 1948) was defined as a measure of the ability of the antifoaming agent to spread naturally on the aqueous surface of foaming solution. It can be expressed by
If \(S> 0\), the oil should spread on the surface of the foaming solution thus forming a duplex layer, which collapses later into liquid lenses. The latter are in equilibrium with the monolayer film.
One can obtain the relation between the entering and the spreading coefficient, from Eqs. (48) and (49):
The signs of the entering and the spreading coefficient should be positive for the foam inhibitors (Harkins 1941; Ross 1950). However, the research on the antifoam action faced a number of problems when explaining the action of antifoam within the foam lamellas. For example, more detailed studies (Ross and Young 1951) showed that some agents make the foam films drain faster, but they do not affect the thickness at which they rupture. In contrast, other agents make the foam-film rupture, while they are still thick. There are reports in the literature that antifoaming agents make the black foam films (called at that time as plastic surface films) less durable (Ross and Young 1951). In addition, a correlation between viscosity, the entering and spreading coefficients, and the antifoaming action could not be found for some antifoamers (Ross 1967). Thus, even with positive signs of S and E, some antifoam agents do not act as foam suppressors. Also was found out that there exists a synergism between some pairs of antifoaming agents (Ross and Butler 1956). Some low molecular antifoamers showed even an inversion to foamers (Okazaki and Sasaki 1960). These studies were extended, furthermore, on gas emulsions in the absence of any frother (Kruglyakov and Koretskaya 1974) which revealed an increased rate of bubble coalescence in the presence of silicone antifoamers.
The power of foam prevention by a given antifoamer was further quantified by the coefficient of antifoaming efficiency (Kulkarni et al. 1977):
where \(K\) and \({K_0}\) are the rates of foam generation in the presence and absence of an antifoaming agent under the identical conditions. The coefficient \(F\) depends on the concentrations of the antifoaming agent and the frother. It was shown as well (Hobbs and Pratt 1974) that when ionic surfactants are used as a frothers, the coefficient of antifoaming efficiency \(\eta\) drops abruptly upon an increase in the surfactant concentration, when being close to CMC. This was correlated with a sudden increase in the surface potential of the oil lenses, and the surfaces of the foam films as well, corresponding to an increased electrostatic repulsion between them, hence bridging the film surfaces by the oil lens should occur more difficult. The bridging ability of the oil lenses was quantified by the film-breaking factor \({F_P}\) (Tsuge et al. 1984):
where \(\tilde t\) and \({t_D}\) are the times for rupturing of foam film in the presence and absence of oil lenses (antifoam agent). The values of the film-breaking factor \({F_P}\) vary between one (maximal) and zero (minimal). Another way to quantify the foam-film-breaking ability is to measure and compare the times for complete foam decay for the two cases—(1) a foam with positioned oil droplet on its top and (2) an oil free foam column (Kulkarni et al. 1977). The ability of the oil droplets to bridge the film surfaces can be expressed by the bridging coefficient \(B\) (Garrett 1980):
The larger the positive value of \(B\) is the stronger is the bridging ability of the oil lens. It should be noted that the entering and the spreading coefficients \(E\) and \(S\) are not sufficient to explain completely the action of the antifoams.
To enhance the efficiency of the antifoaming agents, hydrophobized silica particles were added as fillers to the oils (Kulkarni et al. 1977) (e.g., a silicone oil). This work marked the beginning of the second period (the late 1970s until present) in the history of antifoams. A significant increase in the antifoam efficiency was first explained by a fast adsorption of surfactant molecules from the two surfaces of the foam film onto the hydrophobic particles, thus forming surfactant-depleted spots on the foam lamellas. The latter should cause rupturing of the lamellas, i.e., coalescence of bubbles in contact. The overall process makes the particles more hydrophilic. It was reported as well (Aronson 1986; Dippenaar Dippenaar 1982a, b, c; Garrett 1979; Tsuge et al. 1984) that the hydrophobic particles can act as a defoamer in the absence of oil. In these studies, it was shown that the film-breaking ability of a particle depends on the critical receding contact angle \({\theta _{0R}}\) between the foam film and the particle. The latter depends on the aspect ratio of the particles. For example, for spherical particles (the aspect ratio = 1) \({\theta _{0R}} = 90^\circ,\) while for cylindrical particles with the aspect ratio of 4, \({\theta _{0R}} = 56^\circ\) (Joshi et al. 2009). If the receding contact angle of the particles is larger than the critical one (\({\theta _R}> {\theta _{0R}}),\) the particles brake the film; otherwise, the film stays intact The reason is in the emerging convex flow driven by the local capillary forces near the particle. This convex flow should make the foam-film thicker if \({\theta _R} < {\theta _{0R}}\) (the stabilizing effect) or thinner if \({\theta _R}> {\theta _{0R}}\) (the destabilizing effect) around the particle. The latter should initiate rupturing of the foam film at the locations near the particles (Frye and Berg 1989; Garrett 1979; Prins and Vantriet 1987; Torikata et al. 1991) (see Fig. 19). In addition, synergetic action between the hydrophobic particles and oil droplets together was studied in (Frye and Berg 1989). The oil was considered as a carrier of the particles. Hence, it should have sufficient spreading abilities. In addition, if the particles are completely wettable by the oil, they are encapsulated, thus forming oil droplets of a variable size with solid core. This kind of “solid” oil droplet has lower critical receding contact angle \({\theta _{0R}}\) as compared to the solid particles only (Aveyard et al. 1993). The latter increases their bridging ability. The mechanism of foam-film rupture or stabilization due to the oil lenses (“solid” or “soft”) is depicted in Fig. 20. It is apparent that the two mechanisms (with particles or oil lenses) are identical. Under given circumstances, the antifoam emulsions can become foam stabilizers (Kumagai et al. 1991). Different oils (e.g., fluorosilicone oil) were developed and tested (Aveyard and Clint 1995; Owen and Groh 1990; Wu et al. 2008a, b). The mechanism of the antifoam action was studied further by Koczo et al. (1994). They measured the critical pressure of rupturing of the pseudo-emulsion films (air/water/oil) (see Fig. 21), which are formed between the oil lenses and the water/air interfaces and established a correlation with the effectiveness of the antifoam mixture. They showed that the presence of hydrophobic particles in the oil reduces to a large extent the critical pressure of rupture of the pseudo-emulsion films. In addition, the action of the antifoam was investigated on bubbles situated on the water/air interfaces and in vertical foam films and vertical Plateau borders. They arrived at the conclusion that the antifoam activity occurs mainly at the Plateau borders (PB) of the foam.
Consecutive stages from the mechanism of rupturing of foam films containing hydrophobic particles (Karakashev and Grozdanova 2012)
Experimental procedure of Koczo et al. (1994) used to form and test the stability of pseudo-emulsion film: a capillary containing oil (with or without particles) is immersed into the surfactant solution; b capillary is lifted out of the solution; c aqueous drop from the tip of the capillary is taken away by a needle touching the end of the capillary with a small pseudo-emulsion film is formed; d pushing the oil phase out of the capillary expands the film, thus the pressure measured by the pressure transducer (PT) increases; e if the film ruptures the oil spreads on the tip of the capillary thus reducing the pressure; f if the film is stable, the pressure reaches maximum upon the further expansion of the film; g over the hemispherical shape, the pressure decreases.
Most of the oil “solid” lenses in the foam get trapped into the PB due to the fact that the basic water content (carrying the oil lenses) at the moment of foam generation is located in the PB. The pseudo-emulsion films between the oil lenses and the air/water interface of the PB rupture due to the low critical pressure (see Fig. 21). This is the first variant of the film trapping technique (FTT). Its main drawback is that it can be applied to pseudo-emulsion films with low critical pressure of rupturing. According to (Wu et al. 2008a, b), the basic mechanism of antifoam action stems from the fact that the oil lenses get trapped at the PB surface (see Fig. 22). When two or more such oil lenses in the PB get in contact, they collide resulting in the PB collapse (see Fig. 22). These conclusions were confirmed later by Koczo et al. (1994) and Basheva et al. (2000).
Comprehensive reviews of the works related to the factors controlling foam stability and the antifoam performance until the 1990s can be found in (Garrett 1992; Pugh 1996). The further development of these investigations involved the film trapping technique, FTT (Hadjiiski et al. 1996) allowing direct measurement of the water/oil/air contact angle at an oil droplet trapped into a foam film (see Fig. 23). The micro-interferometric method applied to measuring thickness of thin-liquid films was involved in this technique (Exerowa and Kruglyakov 1997). The latter was further employed in (Denkov et al. 1999) for more systematic studies of the antifoam globules behavior in the foam films. It was shown that the oil pre-spreading on the water/air surface of the foam films is very important for the antifoam performance. In lack of such pre-spreading, the antifoam action ceases to exist. The oil bridges rupturing the foam films were detected using high-speed camera recording. Unstable and meta-stable oil bridges were observed and subsequently analyzed. The rupture of the foam films caused by unstable bridges occurred on the scale of milliseconds, while with meta-stable bridges the films ruptured on the time scale from several hundred milliseconds to a couple of seconds.
Oil droplet trapped in a foam film with the corresponding interference pattern (Hadjiiski et al. 1996) (not to scale).
The stability of oil bridges was studied theoretically in more detailed in (Denkov 1999). The effect of the basic governing factors (three-phase contact angles, film thickness, size of the bridge, presence of a pre-spread oil layer) on the evolution, and stability of the oil bridges was analyzed. It was shown that the bridge stability depends primarily on two factors: (1) the contact angle at the air–water-oil triple line and (2) the relative size of the bridge (with respect to the film thickness). The bridge should be larger than a given critical size to become mechanically unstable at an appropriate contact angle at the air–water-oil contact line as defined (Garrett 1980) (for positive bridging coefficient). Otherwise, the bridge is stable at any contact angle. The pre-spread oil layer serves as a reservoir, which pumps oil into the bridges thus increasing their size beyond their critical size.
The FTT micro-interferometric technique developed in (Hadjiiski et al. 1996) (see Fig. 24) was employed further together with scanning laser microscopy (Tamura et al. 1999) to study pseudo-emulsion air–water–oil films and pseudo-wetting air–water–solid films. Oil droplets (with or without particles inside) and solid particles were trapped in wetting films on a solid plate. It was reported that the pseudo-emulsion films with the thickness of about 100 nm formed very short-living oil bridges causing film rupturing. In addition, the films on oil droplets with solid core exhibited much more thickness inhomogeneity as compared to the other cases. Such inhomogeneous films were more unstable than the other films. In addition, systematic studies with confocal laser scanning microscopy and fluorescent labeled particles (Wang et al. 1999) revealed that the oil droplets trap myriad of particles, and they are located at the very oil–water interface in the form of aggregates, while the droplets cores are free of particles.
Numerical simulations performed in (Valkovska et al. 2000) investigated the effect of the oil solubility on the stability of the pseudo-emulsion air–water–oil films. It was found that the films become more unstable if the oil is more “soluble” in water, i.e., the diffusion of oil molecules on the air/water surface forms an oil monolayer at some spots. This causes Marangoni effect, which induces sub-surface flows making the film to expand and thin faster around the locations of the oil spots. Jha et al. (2000) confirmed the important role of the oil spreading. This work studied the effect of the type of surfactant on the PDMS oil spreading and the antifoam performance. If was shown that the spreading of the oil spots is opposed by the surfactant molecules at the air/water interface via the surface shear viscosity. A surfactant series having the same heads but different lengths of the hydrocarbon tails was used in this study. An increase of the hydrocarbon tail length of the surfactant molecules causes an increase in the surface shear viscosity. This reduces spreading of the oil spots and resulting in diminished reduction of the surface tension and correlates with a weaker antifoam performance of the PDMS oil. In addition, the exhausting of the antifoam emulsions, related to weaker antifoam performance, is accompanied by removing the oil monolayer from the air/water interface as reported (Denkov et al. 2000). This work confirmed the observations reported by (Racz et al. 1996) that the “solid”–oil droplets loose a part of their oil shell thus releasing oil droplets, which are free of particles. The new “solid” droplets are enriched by solid particles and are unable to facilitate rupturing of the foam lamella. The thickness of the pre-spread oil layer reduces as the duration of foam agitation increases (Denkov et al. 2002). It is interesting to note (Denkov et al. 2000) that the exhausted antifoam can be reactivated by adding new portions of oil. The latter covers the “exhausted solid” oil droplets with new amounts of oil thus increasing their size and ability to form oil bridges within the foam lamellae. The effect of the antifoam performance of the PDMS oil in the presence of betaine (Koczo et al. 1994, Basheva et al. 2000) exploited a further developed version of the film trapping technique (FTT), allowing measurement of the critical pressure (called the entry barrier) of rupturing of the pseudo-emulsion air–oil–water film, also of (Koczo et al. 1994) but rather improved.
The theory of the FTT technique (see Fig. 24) was given by Hadjiiski et al. (2001). It should be noted that four variants of FTT were developed for the period of 1994–2001. The first one (see Fig. 21) (Koczo et al. 1994) allows for measuring the critical pressure of rupture of air/water/oil pseudo-emulsion films in some short range of pressure values. The second type of FTT (see Fig. 23) (Hadjiiski et al. 1996) allows accurate measurement of the contact angle at the antifoam globules trapped into foam films. The third one (Tamura et al. 1999) allows the interferometric monitoring of antifoam globules trapped into wetting films, and finally, the fourth type of FTT (see Fig. 24) (Basheva et al. 2000; Hadjiiski et al. 2001) allows both accurate measurements of the critical pressure of rupturing of air/water/oil pseudo-emulsion films in quite broad range of pressure values, as well as the interferometric monitoring of the trapped antifoam globules. Evidently, the last type of FTT is the most preferable for experimental studies on antifoams.
The work of Hadjiiski et al. (2001) is very useful for achieving better understanding of the antifoam action. A detailed study of different factors affecting the so-called entry barrier (the critical capillary pressure of rupturing of the pseudo-emulsion air/water/oil films) was conducted using the FTT technique (Hadjiiski et al. 2001). They reported that the entry barrier increases upon increase of the surfactant concentration especially close to CMC. A homologue series of alcanes—from octane to hexadecane—was used one by one as oil shell of the antifoam globules. It was found that the entry barrier increases upon an increase in the hydrocarbon tail of oil. In addition, the pre-spread oil on the air/water interface of pseudo-emulsion film affects the entry barrier as well. For decane and dodecane, the layer of pre-spread oil reduces the entry barrier, whereas for hexadecane, the effect is opposite. The pre-spreading of PDMS oil, which is commonly used as an antifoam, decreases the entry barrier by several times (Denkov et al. 2002). Such a role of oil spreading in the antifoaming action of oils was not reported so far. In short, (Hadjiiski et al. 2001) recommends short-chained oils applied to diluted aqueous surfactant solutions as effective antifoam agents. Despite these clarifications, Marinova and Denkov (2001) stress that the physics of antifoam action is quite complicated. This work studied the effect of several antifoams on aqueous solutions of two surfactants. It found quite different antifoam performances at similar spreading, entering, and bridging coefficients. The antifoam performance depended on the surfactant type. The ones with slow kinetics of surfactant adsorption at the air/water and oil/water interfaces exhibited a weak antifoam performance. On the contrary, the antifoams exhibited better performance if the surfactant adsorbed fast at the fluid interfaces. The further studies were focused on optimizing the procedure of antifoam preparation for achieving maximal antifoam activity (Marinova et al. 2002). An optimal hydrophobicity of solid particles was established to achieve the best antifoam action. The latter was found to correspond to the minimum of the entry barrier, as the studies employing the FTT technique revealed.
Comprehensive reviews related to antifoams can be found in Denkov (2004), Miller (2008). In short, these reviews stress that two kinds of antifoams exist—the fast and the slow ones. The fast ones make the foam decay completed in seconds, while the slow ones need hours to destroy the foam. The fast antifoams have low entry barriers, as measured by the FTT technique. Hence, their globules rupture foam films at the early stages after the foam generation. The globules of the slow antifoams possess high entry barriers. The foam films expel them at the early stages after foam generation thus forcing them to enter the Plateau borders (PB). The latter get narrower upon time due to the foam drainage, and the walls of PB squeeze the globules apparently at the top of the foam cap. This traps them at the walls of the PB, thus making the oil of the globules to spread (see Fig. 22). All these are favorite conditions for destroying the PB. The spreading, the entering, and the bridging coefficients do not play a role of the criteria of the quality of the antifoam performance. They must be positive for the active antifoams, but to conclude how active is an antifoam, the entry barrier should be measured. The value of the entry barrier can be used as a criterion of the quality of the antifoam performance in any particular case. Further studies (Joshi et al. 2005; Al-Masry 2006) on the antifoam action revealed an overall increase in the gas hold-up and non-homogeneous size distribution of the foam bubbles due to the presence of antifoam. Comprehensive studies of the oil-type antifoams and their performance extending those of (Denkov 2004; Miller 2008) are unavailable, as to our knowledge.
6.2 Foamability and stability of foams
At the first stages of foam agitation, gas emulsion is formed (myriad of bubbles appear in surfactant aqueous solution) thus allowing the surfactant molecules to begin adsorbing at the walls of the bubbles, which reduces surface tension and generates viscoelastic properties (the surface elasticity and viscosity). The bubbles rise towards the water/air level of the foaming solution due to the buoyancy force. During this stage, the bulk liquid is subjected to certain shear stress (Nguyen and Schulze 2003) acting as an external force applied to the bubbles. The drag deforms all the bubbles in the bulk liquid. These deformations, if large enough, can tear off the bubbles to smaller bubbles. When colliding, the bubbles coalesce or bounce. Hence, two important processes occur during the foam agitation—coalescence resulting in larger bubbles and breaking apart resulting in smaller bubbles. The dominating one will determine the foamability of the surfactant solution. This is dependent on the so-called critical Weber number \({W_{cr}}\) (Nguyen and Schulze 2003; Duineveld 1998). The Weber number \(W{e_1}\) is the ratio of the splitting and the capillary pressures:
where \(\rho\) is the bulk density, \({r_b}\) is the bubble radius, \(\sigma\) is the surface tension, and \(U\) is the velocity of the bubble rise. The subscript 1 expresses the fact that this is a Weber number for a single bubble. The splitting pressure originates from the kinetic energy of the bubbles and the additional shear stress (or turbulence) of the bulk liquid. It tends to break apart the bubble to smaller bubbles. The capillary pressure originates from the curvature of the bubble and its surface tension (\({P_c} = 2\sigma /{r_b})\) and tends to restore the bubble shape. If \(W{e_1}> W{e_{cr}}\), the bubbles break apart into two or more bubbles while rising up. If \(W{e_1} < W{e_{cr}}\), bubbles do not split. In addition, the Weber number, defined in Eq. (54), can also be applied to bubbles colliding with a water/air interface in the foaming solution. The bubble can coalesce with the surface if \(W{e_1} < W{e_{cr}}\) or bounce if \(W{e_1}> W{e_{cr}}\). However, the critical value of the Weber number should be different from the one corresponding to the bubble splitting. According to Duineveld (1995), the Weber number of two colliding bubbles in pure water can be expressed by
where \(W{e_2}\) corresponds to two bubbles in contact, \({r_{b1}}\) and \({r_{b2}}\) are the radii of the bubbles, and \(V = dh/dt\) (\(h\) is a film thickness and \(t\) is a time) is the velocity of thinning of the foam film. If \(W{e_2}> W{e_{cr2}}\), the bubbles bounce after colliding; on the other hand, if \(W{e_2} < W{e_{cr2}}\), they coalesce (see Fig. 25). When a surfactant is added, it inhibits the bubble coalescence, which corresponds to a decrease in the value of the critical Weber number. In such a case, the Weber number can be expressed as (Nguyen and Schulze 2003):
Basic stages of in the bubble collision (Karakashev and Grozdanova 2012)
where \({R_f}\) is the film radius. It is seen that when the bubbles collide, a foam film is formed between them. The latter begins thinning and expanding due to the capillary pressure and any additional bulk shear stress. Under such condition, the bubbles interact hydrodynamically and the foam-film drains with a low Reynolds number. The durability of the foam film depends on the rate of film thinning. There is a critical thickness (about 30 nm) at which the films rupture or underwent transition to black (common or Newtonian) films (Exerowa and Kruglyakov 1998), which are very durable. Due to the fact that the thin-liquid films are the basic factor governing stability of colloidal dispersions, a methodology for studying such films (having in mind foams, wetting and emulsions) based on the interferometry was developed (Scheludko 1967).
The bubbles, which have survived during the foam agitation, become a part of the foam body. At the very moment of its formation, the foam begins to decay due to various phenomena occurring in it: film thinning, liquid drainage due to gravity, gas diffusion from smaller to larger bubbles (Ostwald ripening), and rupturing if the foam films. The latter causes coalescence of neighboring bubbles (Exerowa and Kruglyakov 1997). In addition, foam interacts with the walls of its container (Manev and Karakashev 2001). It is well known that a stable foam contains the so-called black foam films, which consists of the adsorbed bi-layers protruding from both sides of the film. The durability of this special kind of foam films depends on the level of compactness and the surface forces in the adsorption layers.
In general, the foam stability is related to the kinetics of drainage and the lifetime of the foam films (the equilibrium or black films). The kinetics of drainage is related to the gravity force (syneresis). The drainage occurs mostly in the Plateau borders (PB). The main factor governing foam stability is the lifetime of the foam films. The stability of a foam film is dependent on the properties of the adsorption layers located on its two surfaces. When a foam film reaches a critical thickness, hcr, it ruptures or undergoes transition to a black (stable) foam film. If the population of surfactant molecules on the surface Γ exceeds a certain value Γbl (Γ > Γbl), then black and stable foam films form. Foams which are produced in this manner are very stable. However, if Γ < Γbl, the adsorption layers on both sides of the film are incapable of producing black spots in the film, and as a consequence, the generated foam decays rapidly. It is known that the total adsorption can be reduced below the critical level (Γ < Γbl) (Nemeth et al. 1997; Karakashev and Manev 2003; Manev and Karakashev 2001) by adding another surfactant forming mixed and more scarce adsorption layer. Another key factor controlling the durability of transient foams is the viscoelasticity of the air/water interfaces. Te latter depends on the adsorption layer. In general, the rule is—the stronger the viscoelasticty effects are, the more durable foam is. The following expression for the surface elasticity is used (Lucassen and Van den Tempel 1972):
where \({\varepsilon _0} = - d\sigma /d\ln \Gamma\), \(\sigma\) is the surface tension, \(\Gamma\) is surfactant molar surface concentration, \(\omega\) is cyclic frequency of compression/expansion of the water/air interface disturbing the adsorption layer, while \({\omega _0}\) is called the adsorption frequency of the surfactant expressed as: \({\omega _0} = D/2{(d\Gamma /dC)^2},\) where \(D\) is the bulk diffusion coefficient and \(C\) is the surfactant bulk concentration. The derivative \(d\Gamma /dC\) is known as the adsorption length.
The correlation of the foam durability and the viscous modulus is shown in Fig. 26. The latter depends on the adsorption layer. The adsorption layer can be modified by adding even inorganic salts into the foaming solution (Karakashev and Manev 2001). For example, 0.01 M KBr reduces both foamability and durability of foams of 5 × 10− 4 M of the nonionic surfactant C10E8. On the other hand, adding of 0.01 M NaI does not affect foamability but rather extends foam longevity. Ion-specific effects can affect both foamability and foam stability.
The air humidity has a significant effect on the durability of foams as well (Li et al. 2012). Thus, for example, it has been established that foam decays faster in a dryer air and slower in a more humid one. This has been attributed to the non-uniform evaporation (the Marangoni drying) of foam in its upper layer causing the Marangoni waves along the foam lamellae and bubble coalescence. Figure 27 shows the decay of two identical foams at two values of the relative humidity of the ambient air—50 and 65%. One can see an evident difference between the decay of the two foam columns.
Experimental viscoelastic modulus and foam durability as a function of the surfactant concentration (Karakashev et al. 2011)
Hight of decayed foam versus foam age at two different values of relative humidity (1.37 × 10−3 M CTAB solution, initial freeboard foam height = 0 mm). The bubble size, the initial foam hight, and the initial liquid fraction have been the same in both cases (Li et al. 2012).
Since the foam films drain faster in a dryer air than in humid air, the effect of humidity on the rate of foam decay is combined—dry air causes faster foam-film drainage and powerful Marangoni waves cause instability in the upper foam layer.
In summary, the compactness of the surfactant adsorption layer and the air humidity has a significant effect on foam durability. Hence, one can use both these factors to achieve a more or less durable foam. Moreover, foams in hydrophobic containers are less durable than foams in hydrophilic containers (Manev et al. 2001).
6.3 Foam production: new concept for better understanding of foams
Foaminess and foam durability are two basic characteristics describing foams. The first one can be defined in two ways—the initial foam volume (Exerowa and Kruglyakov 1997) and Bikerman’s unit of foaminess (Bikerman 1938; Li et al. 2010). The initial foam volume depends on the method of foam generation. For that reason, it was introduced (Bikerman 1938) more realistic measure, which unfortunately can be applied only to foams produced by sparging of gas into surfactant solution. This unit of foaminess is expressed by the relation \(\Sigma = {h_{\max }}/\tilde g\), where \({h_{\max }}\) and \(\tilde g\) are the maximal height of the foam and superficial gas velocity (Li et al. 2010), respectively.
Karakashev et al. (2012) suggested a parameter unifying both the foaminess and the rate of foam decay. Their ratio is called foam production. According to (Karakashev et al. 2012), the works on foams in the literature can be divided to two basic groups: (1) tenacious foams and (2) transient foams. The tenacious foams have specific internal structure, e.g., polyhedral soap bubbles forming lamellas, Plateau borders, and nodes (Saint-Jalmes 2006; Kruglyakov et al. 2008; Koehler et al. 2000; Saint-Jalmes and Langevin 2002). The foaminess is not an important parameter for such foams, but rather such phenomena as foam drainage and coarsening are related to the foam’s structure. The foam production is a concept valid for short-living foams, because the stable foams can exist up to for many hours, days, and even months, which corresponds to an infinitely large foam production. The short-living foam does not possess a well-defined structure due to the high liquid volume fraction on it. It usually consists of moving bubbles dispersed in an aqueous phase. The bubbles are subjected to mechanical stresses during generation of foam thus colliding and coalescing due their low elastic moduli. The works on such foams are scarce. Most of such works deal with the relation between the surfactants molecular structure, or mixture of surfactants with the foaminess and durability of foams generated by means of the different methods (Varadaraj et al. 1990; Samanta and Ghosh 2011; Carey and Stubenrauch 2010; Varade et al. 2011). Some other works study the parameters affecting the initial foam volume of the transient foams (Basheva et al. 2000; Rosen and Solash 1969; Koczo et al. 1994). There are also works on the so-called smart foams with switchable foam stability (Fameau et al. 2011; Middelberg and Dimitrijev-Dwyer 2011). As a rule, the foam lifetime and the foaminess have been studied separately despite an evident experimental correlation between them. Such a correlation has been overlooked, even though it implicitly contains an important information on the nature of the transient foam. This fact implies an existence of a new parameter based on this correlation, which is called the foam production (Karakashev et al. 2012). It is defined based on the Bikerman’s unit of foaminess (Bikerman 1938):
where \(\Sigma\) is Bikerman’s unit of foaminess, while \({U_d}\) is the average rate of foam decay. Unfortunately, such a parameter is applicable to only foams produced by means of gas sparging into a surfactant solution. For this reason, a second definition of foam production, which is valid for the other available methods of foam generation, has been introduced:
where \({V_0}\) is the initial foam volume. Irrespective of the method of foam generation, this parameter actually counterbalances foaminess and foam decay as the two opposite effects responsible for the foam’s nature.
Figure 28 depicts the experimental data on foaminess and the rate of foam decay versus C/CMC ratio (C is surfactant concentration, while CMC is the critical micelle concentration) of sodium octylsulfate (SOS) for foam produced by means of the Bikerman’s method of foam generation. It is seen that a correlation between these two parameters exists. An increase of the foaminess is accompanied by a faster foam decay and vice versa. Examples for such a correlation can be found in (Bikerman 1938; Karakashev et al. 2011; Freger and Vetokhin 1992; Oh and Shah 1991; Szekrenyesy et al. 1992). Yet, the results shown in Fig. 28 are ambiguous, because they do not clarify whether one produces larger amount of foam lasting for a longer time upon an increase of C/CMC ratio. Fortunately, the above-mentioned concept sheds a light on this ambiguity. Figure 29 reveals that foam production increases linearly upon increasing the C/CMC ratio.
Average rate of foam decay and Bikerman’s unit of foaminess versus C/CMC of sodium octylsulfate (SOS) (Karakashev et al. 2012)
Foam production versus C/CMC of sodium octylsulfate (SOS) (Karakashev et al. 2012)
The foaminess and the foam stability are essentially the two sides of the same coin. For this reason, they should not be studied separately. There is an old philosophical principle named “Occame’s razor” which states “Entia non sunt multiplicanda praeter necessitate” (Entities must not be multiplied beyond necessity). The foam production is the parameter which does not exceed the limits of the necessity. In his profound work “Making frothing shampoo or beer” (Durian and Raghavan 2010). Durian, one of the leading scientists in the contemporary foam field, Durian summarized the basic factors which make the ordinary water a foaming liquid. Here, again, the foaminess and foam decay compete determining whether a foam could be useful in any specific application.
7 Industrial applications of foams
Some of the most important foam properties that determine their industrial applications are discussed in this section. The foam flotation of mineral particles, ion flotation, foam accumulation and foam separation of soluble surfactants, as well as the treatment of waste waters polluted by various substances (soluble and insoluble), are based on the difference in the compositions of the initial foaming solution and the liquid phase in the foam. Due to this difference, it is possible to accelerate some reactions (foam catalysis) and to shift the chemical equilibrium of some reactions in the foam. The low heat conductivity of foams is the reason to use them as thermo-insulating materials, such as foam concrete, foam gypsum, foam-glass, polymer foams, porous casting moulds, frozen foams, and other foaming materials. Along with being thermal insulators, many foams possess another important property: a low density (a high expansion ratio). Liquid foams are also used as thermoinsulators, for example, in hothouses. Low-density foams are used in pyrotechniques, for deposition of uniform adhesion or anticorrosion coatings, for elimination of water “stoppers” in deep petroleum and natural gas wells cracks, as well as for establishing equilibrium between the pressure in geological formation and that in the drilling fluids. There are reports of using foams to lift sunken boats. The ability of a foam to absorb various gases, liquid, and solid particles and to isolate them from a medium is one of its properties of significant importance that associates in a single group foams of different purposes, such as for fire fighting; dust protection, and collection; purification from solid and liquid pollutants; isolation of hazardous gases and aerosols from the electrolysis baths; water basin protection; isolation of aggressive liquids (ammonium, isocyanite, etc) and natural gas in earth; explosive techniques; treatment of soil with solid, liquid, or gas pesticides; foams for welding in an inert gas medium; aerosol foams; etc. Foams used in enhanced oil recovery can also be included in this group. In the latter case, the ability of foams to create strong hydrodynamic resistance and their stability at high capillary pressures is important. The large specific surface area of foams promotes their application for the absorption and purification of gases in foam devices, acceleration of vacuum drying, and degasation of oils (Bickerman 1973; Rosen and Solash 1969) as well as for drying of the surfaces of such machines, as pumps, before their conservation. The industrial procedure in the production of many foods involves a stage in which they are converted into a foam. By virtue of the large surface area of the foam product, its processing can be intensified. For example, in such a way milk, coffee, egg powder, and potato paste are dried at low temperature after their previous foaming. Equally important also are some other foam properties, such as foam dispersity and a number of rheological parameters. On the basis of the mechanical foam properties, such as their high compressibility and damping, a technique has been developed for emergency aircraft landing on foam which reduces shocks and vibrations, and can prevent explosions. The strong compression of a foam with the consequent sharp pressure “dump” which leads to an increase in the foam expansion ratio and to creation of a high capillary pressure can be used as a method for foam destruction. The rheological properties of foams (the shear stress and viscosity) allow one to control permeabilities to gases and liquids of porous systems. Foams are capable of reducing pressure caused by a blast wave. The mechanical properties of foams can be used to lower the water shock in tower jumps. This can be realised by a short foaming of water with formation of a rapidly collapsing gas emulsion. Because of their good sound absorption properties, solid foaming materials are used as acoustic insulating baffles. The liquid foam can also be used to reduce the noise of some machines. The laboratory methods for the study of the structural parameters of foams (the dispersity and foam expansion ratio) are based on the measurement of the electrical and optical characteristics of foams (Sett et al. 2016; Bickerman 1973). However, there is no information about the application of these properties in technological processes (excluding the automated control of the mechanical defoaming devices). The tendency of soap bubbles to form two-dimensional hexagonal packing can be used to design a two-dimensional model of crystals following Bragg and Lambert and to study the crystal defects (vacancies and incorporations) as well as other crystal phenomena. Textile dyeing is another domain employing foams. They decrease water consumption and ensure a uniform spreading of the dye. Special requirements are imposed on such foams referring to their expansion ratio and stability (Bryant and Walter 1983; Datymer 1983; Sett et al. 2016). The stability of both foam films and the foam bulk plays an important role in the effective application of foams. They should satisfy special requirements for stability which might differ significantly even within the same group. Several techniques for controlling the quality of the products, for example, beer, tea, and whisky (Datymer 1983; Davidson 1981), or the tightness of pipe and reservoir welds, are based on the formation of a foam with a definite lifetime.
8 Conclusions
The hydrodynamics of foams stands behind many complex phenomena occurring in the life of draining foams. Foam, an ensemble of bubbles, produced by means of a certain agitation of surfactant solution is concentrated gas emulsion with very high liquid volume fraction. At the first moments of foam generation, there are no dissipative structures which are responsible for the foam drainage (Plateau borders, nodes, and foam films). The latter are formed upon reducing the liquid volume fraction by means of drainage due to gravity. The present review surveys the basic knowledge on foam drainage and individual thin foam films. The latter are the most important elementary units contributing to foam formation. It should be emphasized that the fields dealing with foam drainage and thin foam films were developed independently despite the fact that they are two different sides of the same phenomenon. The present review gives a comprehensive overview of both.
References
Alargova RG, Warhadpande DS, Paunov VN, Velev OD (2004) Foam superstabilization by polymer microrods. Langmuir 20:10371–10374
Aronson MP (1986) Influence of hydrophobic particles on the foaming of aqueous surfactant solutions. Langmuir 2:653–659
Aronson AS, Bergeron V, Fagan ME, Radke CJ (1994) The Influence of Disjoining Pressure on Foam Stability and Flow in Porous-Media. Colloids Surfaces a-Physicochemical Engineering Aspects 83:109–120
Assink RA, Caprihan A, Fukushima E (1988) Density profiles of a draining foam by nuclear magnetic resonance imaging. AIChE J 34:2077–2079
Attard P, Mitchell DJ, Ninham BW (1988a) Beyond Poisson-Boltzmann: images and correlations in the electric double layer. I. Counterions only. J Chem Phys 88:4987–4996
Attard P, Mitchell DJ, Ninham BW (1988b) Beyond Poisson-Boltzmann: images and correlations in the electric double layer. II. Symmetric electrolyte. J Chem Phys 89:4358–4367
Aveyard R, Clint JH (1995) Liquid droplets and solid particles at surfactant solution interfaces. J Chem Soc-Farad Trans 91:2681–2697
Aveyard R, Cooper P, Fletcher PDI, Rutherford CE (1993) Foam breakdown by hydrophobic particles and nonpolar oil. Langmuir 9:604–613
Basheva ES, Ganchev D, Denkov ND, Kasuga K, Satoh N, Tsujii K (2000) Role of betaine as foam booster in the presence of silicone oil drops. Langmuir 16:1000–1013
Bergeron V (1999) Measurement of forces and structure between fluid interfaces. Curr Opin Colloid Interface Sci 4:249–255
Bergeron V, Radke CJ (1992) Equilibrium measurements of oscillatory disjoining pressures in aqueous foam films. Langmuir 8:3020–3026
Bergeron V, Radke CJ (1995) Disjoining Pressure and Stratification in Asymmetric Thin-Liquid Films. Colloid Polym Sci 273:165–174
Bergeron V, Fagan ME, Radke CJ (1993) Generalized Entering Coefficients—a Criterion for Foam Stability against Oil in Porous-Media. Langmuir 9:1704–1713
Bianco H, Marmur A (1993) Gibbs Elasticity of a Soap Bubble. J Coll Interface Sci 158:295–302
Bickerman J (1973) Foams. Springer-Verlag, New York
Bikerman JJ (1938) The unit of foaminess. Trans Faraday Soc 34:0634–0638
Blank M, Lucassen J, van den Tempel M (1970) The elasticities of spread monolayers of bovine serum albumin and of ovalbumin. J Coll Int Sci 33:94–100
Brunner JR (1950) The Effectiveness of Some Antifoaming Agents in the Condensing of Skimmed Milk and Whey. J Dairy Sci 33:406–407
Bryant GM, Walter AT (1983). In: Lewin M, Sello S (eds) Handbook of Fiber Science and Technology. Marcel Dekker, New York
Carey E, Stubenrauch C (2010) Foaming properties of mixtures of a non-ionic (C(12)DMPO) and an ionic surfactant (C(12)TAB). J Colloid Interface Sci 346:414–423
Cervantes-Martinez A, Saint-Jalmes A, Maldonado A, Langevin D (2005) Effect of cosurfactant on the free-drainage regime of aqueous foams. J Colloid Interface Sci 292:544–547
Christenson HK, Claesson PM, Pashley RM (1987) The hydrophobic interaction between macroscopic surfaces. Proc Indian Acad Sci (Chem Sci) 98:379–389
Christenson HK, Fang J, Ninham BW, Parker JL (1990) Effect of divalent electrolyte on the hydrophobic attraction. J Phys Chem 94:8004–8006
Datymer A (1983) Surfactants in Textile Processing. Marcel Dekker, New York
Davidson JA (1981) Foam Stability as an Historic Measure of the Alcohol Concentration in Distilled Alcoholic Beverages. J Colloid Interface Sci 81:540–542
De Gennes PG (1985) Penetration of a coil into an adsorbed layer—application to the kinetics of exchange and to bridging processes between colloidal particles. Cr Acad Sci II 301:1399–1403
De Gennes PG (1987) Polymers at an interface; a simplified view. Adv Colloid Interface Sci 27:189–209
de Gennes P-G (1997) Friction forces on a solid experiencing more than one contact. C R Acad Sci, Ser IIb: Mec, Phys, Chim, Astron 325:7–14
de Gennes PG (2001) “Young” soap films. Langmuir 17:2416–2419
Denkov ND (1999) Mechanisms of action of mixed solid-liquid antifoams. 2. Stability of oil bridges in foam films. Langmuir 15:8530–8542
Denkov ND (2004) Mechanisms of foam destruction by oil-based antifoams. Langmuir 20:9463–9505
Denkov N, Cooper P, Martin J (1999) Mechanisms of action of mixed solid-liquid antifoams. 1. Dynamics of foam film rupture Langmuir 15:8514–8529
Denkov ND, Marinova KG, Christova C, Hadjiiski A, Cooper P (2000) Mechanisms of action of mixed solid-liquid antifoams: Exhaustion and reactivation. Langmuir 16:2515–2528
Denkov ND, Tcholakova S, Marinova KG, Hadjiiski A (2002) Role of oil spreading for the efficiency of mixed oil-solid antifoams. Langmuir 18:5810–5817
Derjaguin B, Kussakov M (1939) Anomalous Properties of Thin Polymolecular Films. V. Acta Physicochemca URSS 10:25–44
Derjaguin B, Landau L (1941) Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Phys-chim 14:633–662
Derjaguin B, Obuchov E (1935) Kolloidn Zh 1:385
Derjaguin B, Obuchov E (1936) Anomalien dünner Flüssigkeitsschichten. Acta Physic URSS 5:1–22
Derjaguin BV, Titievskaya AS (1953) Kolloid Zh 15:416
Deryagin BV (1989) Influence of surface forces on the formation of structural peculiarities of the boundary layers of liquids and boundary phases. Pure Appl Chem 61:1955–1958
Deryagin BV, Titievskava AS (1957) Static and kinetic stability of free films and froths. Proc Intern Congr Surface Activity, 2nd, London, 1957 1:211–219
Deryaguin BV (1989) Theory of the stability of colloids and thin films. Springer, New York
Desai D, Kumar R (1982) Flow through a Plateau border of cellular foam. Chem Eng Sci 37:1361–1370
Desai D, Kumar R (1983) Liquid holdup in semibatch cellular foams. Chem Eng Sci 38:1525–1534
Dippenaar A (1982a) The destabilization of froth by solids. II. The rate-determining step. Int J Miner Process 9:15–22
Dippenaar A (1982b) The Destabilization of Froth by Solids 0.1. the Mechanism of Film Rupture. Int J Miner Process 9:1–14
Dippenaar A (1982c) The destabilization of froth by solids. I. The mechanism of film rupture. Int J Miner Process 9:1–14
Durand M, Langevin D (2002) Physicochemical approach to the theory of foam drainage. European Physical Journal E: Soft Matter 7:35–44
Durand M, Martinoty G, Langevin D (1999) Liquid flow through aqueous foams: From the plateau border-dominated regime to the node-dominated regime. Phys Rev E: Stat Phys, Plasmas, Fluids, Relat Interdiscip Top 60:R6307–R6308
Durian DJ, Raghavan SR (2010) Making a frothy shampoo or beer. Phys Today 63:62–63
Dzaloshinskii IE, Lifshitz EM, Pitaerskii LP (1961) The general theory of van der Waals forces. Adv Phys 10:165–209
Eddy CW (1932) An anti-foam stillhead. Ind Eng Chem Anal Ed 4:198–199
Ekserova D, Sheludko A (1971) Porous plate method for studying microscopic foam and emulsion films. Dokl Bolg Akad Nauk 24:47–50
Exerowa D, Kruglyakov PM (1997) Foam and foam films: theory, experiment, application. Marcel Dekker, New York
Exerowa D, Kruglyakov PM (1998) Foam and foam films: Theory, experiment and application. Elsevier, Amsterdam
Exerowa D, Kolarov T, Khristov K (1987) Direct Measurement of Disjoining Pressure in Black Foam Films. I. Films from an Ionic Surfactant”. Colloids Surf 22:171–185
Fameau AL, Saint-Jalmes A, Cousin F et al (2011) Smart foams: switching reversibly between ultrastable and unstable foams. Angew Chem Int Ed 50:8264–8269
Fanto RZ (1907) Angew Chem 20:1233–1234
Freger VB, Vetokhin VN (1992) Determination of the foam destruction rate - Rupture of films. Colloid J Russ Acad Sci 54:280–284
Friedrichs F (1928) J Soc Glass Rech 12:306
Frye GC, Berg JC (1989) Antifoam Action by Solid Particles. J Coll Int Sci 127:222–238
Garrett PR (1979) The effect of polytetrafluoroethylene particles on the foamability of aqueous surfactant solutions. J Colloid Interface Sci 69:107–121
Garrett PR (1980) Preliminary considerations concerning the stability of a liquid heterogeneity in a plane-parallel liquid-film. J Coll Int Sci 76:587–590
Garrett PR (1992) The mode of action of antifoams. In: Garrett PR (ed) Defoaming: theory and industrial applications. CRC Press, Boca Raton, pp 329
Gastrock EA, Reid JD (1938) Antifoaming device for use in concentration of noninflammable liquors. Ind Eng Chem-Anal Ed 10:0440–0440
German, Government (1981) Deutsche Industrie Norm (DIN)
Gibbs JW (1928) The Collected Works of J. Willard Gibbs, Ph.D., L.L.D. Longmans, Green and Co., New York, London, Toronto
Goldfarb II, Sheiber IR (1988) Liquid flow in foams. Fluid Dyn (Trans USSR Acad Sci Mech Liquid Gas Ser) 23:244
Gunderson LO, Denman WL (1948) Polyamide foam inhibitors—mechanism of foam inhibition in steam generators. Ind Eng Chem 40:1363–1370
Hadjiiski A, Dimova R, Denkov ND, Ivanov IB, Borwankar R (1996) Film trapping technique - Precise method for three-phase contact angle determination of solid and fluid particles of micrometer size. Langmuir 12:6665–6675
Hadjiiski A, Tcholakova S, Denkov ND, Durbut P, Broze G, Mehreteab A (2001) Effect of oily additives on foamability and foam stability. 2. Entry barriers. Langmuir 17:7011–7021
Hamaker HC (1937) The London-van der Waals attraction between spherical particles. Physica 4:1058–1072
Harkins WD (1941) A general thermodynamic theory of the spreading of liquids to form duplex films and of liquids or solids to form monolayers. J Phys Chem 9:552–568
Hobbs SY, Pratt CF (1974) Modifications in bubbly flow on antifoam addition. Aiche J 20:178–180
Hunter RJ (1994) Introduction to modern colloid science. Oxford University Press, Oxford
Hutzler S, Cox SJ, Wang G (2005) Foam drainage in two dimensions. Coll Surf A 263:178–183
Israelachvili J (1992a) Interfacial forces. J Vac Sci Technol, A 10:2961–2971
Israelachvili JN (1992b) Adhesion, friction and lubrication of molecularly smooth surfaces. NATO ASI Ser, Ser E 220:351–385
Israelachvili JN (1992c) Intermolecular and surface forces. Academic Press, London
Ivanov IBE (1988) Thin liquid films. Marcel Dekker, New York
Ivanov IB, Dimitrov DS (1974) Hydrodynamics of thin liquid films. Effect of surface viscosity on thinning and rupture of foam films. Colloid Polym Sci 252:982–990
Ivanov IB, Slavchov RI, Basheva ES, Sidzhakova D, Karakashev SI (2011) Hofmeister effect on micellization, thin films and emulsion stability. Adv Colloid Interface Sci 168:93–104
Jacoby AL, Bischmann LC (1948) Steam bubble formation—effects of heating surface and use of antifoams. Ind Eng Chem 40:1360–1363
Japanese, Government (1967) Japan Industrial Standard (JIS)-K2518
Jha BK, Christiano SP, Shah DO (2000) Silicone antifoam performance: correlation with spreading and surfactant monolayer packing. Langmuir 16:9947–9954
Johansson G, Pugh RJ (1992) The influence of particle size and hydrophobicity on the stability of mineralized froths. Int J Miner Process 34:1–21
Joshi KS, Baumann A, Jeelani SAK, Blickenstorfer C, Naegeli I, Windhab EJ (2009) Mechanism of bubble coalescence induced by surfactant covered antifoam particles. J Colloid Interface Sci 339:446–453
Jun S, Pelot DD, Yarin AL (2012) Foam Consolidation and Drainage. Langmuir 28:5323–5330
Kann KB (1989) Kapillyarnaya gidrodinamika pen. Nauka, Novosibirsk
Karakashev SI, Grozdanova MV (2012) Foams and antifoams. Adv Colloid Interface Sci 176:1–17
Karakashev SI, Ivanova DS (2010) Thin liquid film drainage: Ionic vs. non-ionic surfactants. J Colloid Interface Sci 343:584–593
Karakashev SI, Manev ED (2001) Frothing behavior of nonionic surfactant solutions in the presence of organic and inorganic electrolytes. J Colloid Interface Sci 235:194–196
Karakashev SI, Manev ED (2003) Correlation in the properties of aqueous single films and foam containing a nonionic surfactant and organic/inorganic electrolytes. J Colloid Interface Sci 259:171–179
Karakashev SI, Manev ED (2015) Hydrodynamics of thin liquid films: Retrospective and perspectives. Adv Colloid Interface Sci 222:398–412
Karakashev SI, Nguyen AV (2007) Effect of sodium dodecyl sulphate and dodecanol mixtures on foam film drainage: examining influence of surface rheology and intermolecular forces. Coll Surf A 293:229–240
Karakashev SI, Tsekov R (2011) Electro-marangoni effect in thin liquid films. Langmuir 27:265–270
Karakashev SI, Nguyen AV, Manev ED, Phan CM (2005) Surface foam film waves studied with high-speed linescan camera. Colloids Surf A 262:23–32
Karakashev SI, Nguyen AV, Manev ED (2007) A novel technique for improving interferometric determination of emulsion film thickness by digital filtration. J Colloid Interface Sci 306:449–453
Karakashev SI, Tsekov R, Ivanova DS (2010a) Dynamic effects in thin liquid films containing ionic surfactants. Colloids Surf A 356:40–45
Karakashev SI, Tsekov R, Manev ED, Nguyen AV (2010b) Elasticity of foam bubbles measured by profile analysis tensiometry. Coll Surf A 369:136–140
Karakashev SI, Manev ED, Nguyen AV (2011) Effect of thin film elasticity on foam stability. Annu Sofia Univ 102/103:153–163
Karakashev SI, Georgiev P, Balashev K (2012) Foam production—ratio between foaminess and rate of foam decay. J Colloid Interface Sci 379:144–147
Karakashev SI, Nguyen AV, Tsekov R (2013a) Effect of the adsorption component of the disjoining pressure on foam film drainage. Colloid J 75:176–180
Karakashev SI, Stöckelhuber KW, Tsekov R, Heinrich G (2013b) Bubble Rubbing on Solid Surface: Experimental Study. J Colloid Interface Sci 412:89–94
Kitchener JA (1962a) Confirmation of the Gibbs theory of elasticity of soap films. Nature 194:676–677
Kitchener JA (1962b) Elasticity of soap films; an amendment. Nature 195:1094
Koczo K, Racz G (1987) Flow in a plateau border. Coll Surf 22:97–110
Koczo K, Koczone JK, Wasan DT (1994) Mechanisms of antifoaming action in aqueous systems by hydrophobic particles and insoluble liquids. J Colloid Interface Sci 166:225–238
Koehler SA, Hilgenfeldt S, Stone HA (2000) A generalized view of foam drainage: experiment and theory. Langmuir 16:6327–6341
Koehler SA, Hilgenfeldt S, Stone HA (2001) Flow along two dimensions of liquid pulses in foams: experiment and theory. Europhys Lett 54:335–341
Koehler SA, Hilgenfeldt S, Stone HA (2004a) Foam drainage on the microscale I. Modeling flow through single Plateau borders. J Colloid Interface Sci 267:420–438
Koehler SA, Hilgenfeldt S, Stone HA (2004b) Foam drainage on the microscale II. Imaging flow through single Plateau borders. J Colloid Interface Sci 267:439–440
Koehler SA, Hilgenfeldt S, Weeks ER, Stone HA (2004c) Foam drainage on the microscale—II. Imaging flow through single Plateau borders. J Colloid Interface Sci 276:439–449
Koffler H, Goldschmidt MC (1949) The effect of certain antifoam agents on penicillin yields obtained during the submerged growth of Penicillium–Chrysogenum Q-176. Am J Bot 36:811–811
Kolarov T, Ekserova D, Balinov B, Martynov GA (1986) Dependence of the charge and potential of a foam film on its thickness. Kolloidn Zh 48:1076–1080
Kovalchuk VI, Makievski AV, Kragel J et al (2005) Film tension and dilational film rheology of a single foam bubble. Coll Surf A 261:115–121
Kralchevsky PA, Danov KD (2015) Chemical Physics of Colloid Systems and Interfaces. In: Birdi KS (ed) Handbook of Surface and Colloid Chemistry. 4 edn. CRC Press, Boca Raton
Krotov VV (1980) Theory of syneresis of foams and concentrated emulsions. 2. Local hydroconductivity of polyhedral disperse systems. Kolloidnyi Zhurnal 42:1092–1101
Krotov VV (1984) Generalized equations of syneresis. Kolloidnyi Zhurnal 46:15–22
Kruglyakov PM, Exerowa DR (1990) Pena i pennye plenki. Chemie, Moscow
Kruglyakov PM, Ekserova DR (1998) Foam and foam films. Elsevier, Amsterdam
Kruglyakov PM, Koretskaya TA (1974) Inversion of Antifoaming Ability in Fatty Alcohol Series. Colloid J Ussr 36:627–630
Kruglyakov PM, Vilkova NG (2007) Investigation of Plateau border profile shape with flow of surfactant solution through under constant pressure drop using the FPDT method. In: Tadros T (ed) Colloid Stability: The role of surface forces. WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, pp. 109
Kruglyakov PM, Karakashev SI, Nguyen AV, Vilkova NG (2008) Foam drainage. Curr Opin Colloid Interface Sci 13:163–170
Kruglyakov PM, Elaneva SI, Vilkova NG (2011) About mechanism of foam stabilization by solid particles. Adv Colloid Interface Sci 165:108–116
Krustev R, Muller HJ (1999) Effect of film free energy on the gas permeability of foam films. Langmuir 15:2134–2141
Kulkarni RD, Goddard ED (1977) Droplet-foam bubble interactions as applied to antifoaming. Croat Chem Acta 50:163–179
Kulkarni RD, Goddard ED, Kanner B (1977) Mechanism of antifoaming action. J Colloid Interface Sci 59:468–476
Kumagai H, Torikata Y, Yoshimura H, Kato M, Yano T (1991) Estimation of the stability of foam containing hydrophobic particles by parameters in the capillary model. Agric Biol Chem 55:1823–1829
Kuznetsova LL, Kruglyakov PM (1981) Issledovanie zakonomernostey techeniya rastvorov PAV po kanalam PlatoGibbsa peny.. Dokl Akad Nauk SSSR 260:928
Leonard RA (1964) A theoretical and experimental study of intertitial liquid flow in foam Chemical Engineering. University of Cincinnati, Cincinnati, pp. 248
Leonard RA, Lemlich R (1965a) A study of interstial liquid flow in foam. Part I. Theoretical model and application to foam fractionation. AlChE J 11:18–25
Leonard RA, Lemlich R (1965b) A study of interstial liquid flow in foam. Part II. Experimental verification and observations. AlChE J 11:214–216
Li XL, Shaw R, Stevenson P (2010) Effect of humidity on dynamic foam stability. Int J Miner Process 94:14–19
Li X, Karakashev SI, Evans GM, Stevenson P (2012) Effect of environmental humidity on static foam stability. Langmuir 28:4060–4068
Lifshitz EM (1955) The theory of molecular attractive forces between solid bodies. J Exp Theor Phys USSR 29:83–94
Lucassen J, Van Den Tempel M (1972) Dynamic measurements of dilational properties of a liquid interface. Chem Eng Sci 27:1283–1291
Luisada AA (1950) Therapy of paroxysmal pulmonary edema by antifoaming agents. Circulation 2:872–879
Magrabi SA, Dlugogorski BZ, Jameson GJ (2001) Free drainage in aqueous foams: model and experimental study. AIChE J 47:314–327
Mahanty JH, Ninham BW (1977) Colloid Science: Dispersion Forces. Academic Press, London
Manev E (1981) Study of thickness nonhomogeneity and rate of thinning of free microscopic liquid films. Godishnik na Sofiiskiya Universitet Sv Kliment Okhridski, Khimicheski Fakultet 75:174–183
Manev E, Karakashev S (2001) Effect of adsorption of short-chained organic ions on the stability of foam from aqueous solution of a non-ionic surfactant. Godishnik na Sofiiskiya Universitet "Sv Kliment Okhridski", Khimicheski Fakultet 92–94:167–173
Manev ED, Nguyen AV (2005) Effects of surfactant adsorption and surface forces on thinning and rupture of foam liquid films. Int J Miner Process 77:1–45
Manev ED, Sazdanova SV, Wasan DT (1984) Emulsion and foam stability—the effect of film size on film drainage. J Colloid Interface Sci 97:591–594
Manev E, Tsekov R, Radoev B (1997) Effect of thickness non-homogeneity on the kinetic behavior of microscopic foam films. J Dispers Sci Technol 18:769–788
Manev ED, Karakashev SI, Milushev AM (2001) Influence of some organic and inorganic additivities on the stability of foams of tetraethilelene glycol mono octyl ether. Bulg Chem Comm 33(2):133–147
Marinova K, Denkov N (2001) Foam destruction by mixed solid-liquid antifoams in solutions of alkyl glucoside: electrostatic interactions and dynamic effects. Langmuir 17:2426–2436
Marinova KG, Denkov ND, Branlard P, Giraud Y, Deruelle M (2002) Optimal hydrophobicity of silica in mixed oil-silica antifoams. Langmuir 18:3399–3403
McCarthy MJ (1990) Interpretation of the magnetic resonance imaging signal from a foam. AIChE J 36:287–290
Middelberg APJ, Dimitrijev-Dwyer M (2011) A designed biosurfactant protein for switchable foam control. Chemphyschem 12:1426–1429
Miller RW (1930) Can Chem Met 14:19–21
Miller CA (2008) Antifoaming in aqueous foams. Curr Opin Colloid Interface Sci 13:177–182
Morokuma T, Utaka Y, Shoji M (2015) Measurement of liquid film thickness between coalescing twin air bubbles in a water pool using a modified laser extinction method. Heat Transfer Eng 36:1266–1274
Mysels KJ, Jones MN (1966) Direct measurement of variation of double-layer repulsion with distance. Discuss Faraday Soc 42:42–50
Mysels KJ, Shinoda K, Frankel S (1959) Soap films studies of their thinning and bibliography. Pergamon Press, London
Mysels KJ, Cox MC, Skewis JD (1961a) Measurement of film elasticity. J Appl Phys 65:1107
Mysels KJ, Cox MC, Skewis JD (1961b) The measurement of film elasticity. J Phys Chem 65:1107
Narsimhan G (1990) Unsteady state drainage of a standing foam. AIChE Symp Ser 86:76–86
Neethling SJ, Lee HT, Cilliers JJ (2002) A foam drainage equation generalized for all liquid contents. J Phys Condens Matter 14:331–342
Nemeth Z, Racz G, Koczo K (1997) Antifoaming action of polyoxyethylene-polyoxypropylene-polyoxyethylene-type triblock copolymers on BSA foams. Coll Surf A 127:151–162
Nguyen AV (2002) Liquid drainage in single Plateau borders of foam. J Colloid Interface Sci 249:194–199
Nguyen AV, Schulze HJ (2003) Colloidal Science of Flotation. Marcel Dekker, New York
Nguyen AV, Schulze HJ (2004) Colloidal science of flotation. Marcel Dekker, New York
Nguyen AV, Evans GM, Jameson GJ (2002) Approximate calculations of electrical double-layer interaction between spheres. In: Hubbard AT (ed) Encyclopedia of surface and colloid science. Marcel Dekker, New York
Nguyen AV, Harvey PA, Jameson GJ (2003) Influence of gas flow rate and frothers on water recovery in a froth column. Miner Eng 16:1143–1147
Nikolov A, Wasan DT, Denkov N, Kralchevskii P, Ivanov I (1990) Drainage of foam films in the presence of nonionic micelles. Prog. Colloid Polym Sci 82:87–98
Nushtaeva AV, Kruglyakov PM (2003) Capillary Pressure in Thinning Emulsion Film Stabilized with Solid Spherical Particles. Colloid J (Translation of Kolloidnyi Zhurnal) 65:341–349
Nushtayeva AV, Kruglyakov PM (2001) Capillary pressure in a thinning emulsion film stabilised by spherical solid particles. Mendeleev Commun 6:235–237
Oh SG, Shah DO (1991) Relationship between micellar lifetime and foamability of sodium dodecyl-sulfate and sodium dodecyl-sulfate 1-hexanol mixtures. Langmuir 7:1316–1318
Okazaki S, Sasaki T (1960) 2 Types of antifoamers and their cooperating action. Bull Chem Soc Jap 33:564–565
Okazaki S, Sasaki S (1966) Tenside 3
Owen MJ, Groh JL (1990) Fluorosilicone antifoams. J Appl Pol Sci 40:789–797
Pandey S, Bagwe RP, Shah DO (2003) Effect of counterions on surface and foaming properties of dodecyl sulfate. J Colloid Interface Sci 267:160–166
Pitois O, Fritz C, Vignes-Adler M (2005) Liquid drainage through aqueous foam: study of the flow on the bubble scale. J Colloid Interface Sci 282:458–465
Platikanov D, Manev E (1964) Thin liquid films in another liquid: model of emulsion. Izvestiya na Instituta po Fizikokhimiya, Bulgarska Akademiya na Naukite 4:185–191
Prins A, van den Tempel M (1968) Composition and elasticity of thin liquid films. J Phys Chem 73:2828
Prins A, Vantriet K (1987) Proteins and surface effects in fermentation—foam, antifoam and mass-transfer. TIBTECH 5:296–301
Prins A, Arcuri C, van den Tempel M (1967) Elasticity of thin liquid films. J Colloid Interface Sci 24:84
Pugh RJ (1996) Foaming, foam films, antifoaming and defoaming. Adv Colloid Interface Sci 64:67–142
Pugh RJ (2002) Foams and foaming. Handb Appl Surf Colloid Chem 2:23–43
Qu X, Wang LG, Karakashev SI, Nguyen AV (2009) Anomalous thickness variation of the foam films stabilized by weak non-ionic surfactants. J Colloid Interface Sci 337:538–547
Rabinovich YI, Deryagin BV (1988) Interaction of hydrophobized filaments in aqueous electrolyte solutions. Colloids Surf 30:243–251
Racz G, Koczo K, Wasan DT (1996) Mechanisms of antifoam deactivation. J Colloid Interface Sci 181:124–135
Radoev BP, Manev ED, Ivanov IB (1968) Flow of thin liquid films. I. Diffusion kinetics. Annu Sofia Univ 60:59–72
Radoev BP, Dimitrov DS, Ivanov IB (1974) Hydrocynamics of thin liquid films. Effect of the surfactant on the rate of thinning. Colloid Polym Sci 252:50–55
Razouk RI, Mysels KJ (1966) Progress in measurement of film elasticity. J Am Oil Chem Soc 43:A130
Robinson JV, Woods WW (1948) A method of selecting foam inhibitors. J Soc Chem Ind-London 67:361–365
Rosen MJ, Solash J (1969) Factors affecting initial foam height in the Ross–Miles foam test. J Am Oil Chem Soc 46:399–402
Ross S (1950) The inhibition of foaming. II. A mechanism for the rupture of liquid films by anti-foaming agents. J Phys Chem 54:429–436
Ross S (1967) Mechanisms of foam stabilization and antifoaming action. Chem Eng Prog 63:41–47
Ross S, Butler JN (1956) The inhibition of foaming 0.7. Effects of antifoaming agents on surface-plastic solutions. J Phys Chem 60:1255–1258
Ross S, McBain JW (1944) Inhibition of foaming in solvents containing known foamers. Ind Eng Chem 36:570–573
Ross J, Miles GD (1941) An apparatus for comparison of foaming properties of soaps and detergents. Oil soap 18:99
Ross S, Young JG (1951) Action of Antifoaming Agents at Optimum Concentrations. Ind Eng Chem 43:2520–2525
Ross S, Hughes AF, Kennedy ML, Mardoian AR (1953) The inhibition of foaming. V. Synergistic effects of antifoaming agents. J Phys Chem 57:684–686
Saint-Jalmes A (2006) Physical chemistry in foam drainage and coarsening. Soft Matter 2:836–849
Saint-Jalmes A, Langevin D (2002) Time evolution of aqueous foams: drainage and coarsening. J Phys Condens Matter 14:9397
Saint-Jalmes A, Vera MU, Durian DJ (2000) Free drainage of aqueous foams: container shape effects on capillarity and vertical gradients. Europhys Lett 50:695–701
Saint-Jalmes A, Zhang Y, Langevin D (2004) Quantitative description of foam drainage: transition with surface mobility. Eur Phys J E 15:53
Samanta S, Ghosh P (2011) Coalescence of bubbles and stability of foams in brij surfactant systems. Ind Eng Chem Res 50:4484–4493
Saulnier L, Restagno F, Delacotte J, Langevin D, Rio E (2011) What is the mechanism of soap film entrainment? Langmuir 27:13406–13409
Schelero N, Hedicke G, Linse P, Klitzing RV (2010) Effects of counterions and co-ions on foam films stabilized by anionic dodecyl sulfate. J Phys Chem B 114:15523–15529
Scheludko A (1967) Thin liquid films. Adv Colloid Interface Sci 1:391–464
Scheludko A, Exerowa D (1959a) Electrostatic pressure in foam films of aqueous electrolyte solutions. Kolloid Z 165:148–151
Scheludko A, Exerowa D (1959b) Electrostatic repulsion between diffusion electrical layers in two-sided liquid films. Doklady Akademii Nauk SSSR 127:149–151
Scheludko A, Platikanov D (1961) Investigation of thin liquid layers on mercury. Kolloid-Z 175:150–158
Scheludko A, Dessimirov K, Nikolov A (1954/1955) On the drainage of aqueous solution from foam lamelas. Ann Sofia Univ 49:127–141
Sett S, Sinha-Ray S, Yarin AL (2013) Gravitational drainage of foam films. Langmuir 29:4934–4947
Sett S, Sahu RP, Pelot DD, Yarin AL (2014) Enhanced foamability of sodium dodecyl sulfate surfactant mixed with superspreader trisiloxane-(poly)ethoxylate. Langmuir 30:14765–14775
Sett S, Sahu RP, Sinha-Ray S, Yarin AL (2016) Experimental investigation of eletrokinetic stabilization of gravitational drainage of ionic surfactants films. Electrochim Acta 187:693–703
Slavchov RI, Karakashev SI, Ivanov IB (2014) Ionic Surfactants and Ion-Specific Effects: Adsorption, Micellization, Thin Liquid Films. In: Romsted LS (ed) Surfactant Science and Technology: Retrospects and Prospects. Taylor & Francis Group, pp. 593
Stein HN (1993) The drainage of free liquid-films. Coll Surf A 79:71–80
Stevenson P (2005) Remarks on the shear viscosity of surfaces stabilized with soluble surfactants. J Colloid Interf Sci 290:603
Stevenson P, Stevanov C, Jameson GJ (2003) Liquid overflow from a column of rising aqueous froth. Miner Eng 16:1045
Stevenson P, Mantle MD, Sederman AJ, Gladden LF (2007) Analitative Measurments of liquid Holdup and Drainage in foam using NMRI. AIChEJ 53:290
Stone HA, Koehler SA, Hilgenfeldt S, Durand M (2003) Perspectives on foam drainage and the influence of interfacial rhelogy. J Phys Conden Mat 15:S283–S290
Szekrenyesy T, Liktor K, Sandor N (1992) Characterization of foam stability by the use of foam models. 2. Results and discussion. Colloids Surf 68:275–282
Tamura T, Kageyama M, Kaneko Y, Kishino T, Nikaido M (1999) Direct observation of foam film rupture by several types of antifoams using a scanning laser microscope. J Colloid Interface Sci 213:179–186
Torikata Y, Kato M, Kumagai H, Yano T (1991) Estimation of foam stability by parameters in the capillary model. Agric Biol Chem 55:1307–1312
Tsekov R, Schulze HJ (1997) Hydrophobic forces in thin liquid films: adsorption contribution. Langmuir 13:5674–5677
Tsuge H, Ushida J, Hibino SI (1984) Measurement of film-breaking ability of antifoaming agents. J Colloid Interface Sci 100:175–184
Valkovska DS, Danov KD, Ivanov IB (2000) Effect of surfactants on the stability of films between two colliding small bubbles. Colloids Surf A 175:179–192
Varadaraj R, Bock J, Valint P, Zushma S, Brons N (1990) Relationship between fundamental interfacial properties and foaming in linear and branched sulfate, ethoxysulfate, and ethoxylate surfactants. J Colloid Interface Sci 140:31–34
Varade D, Carriere D, Arriaga LR et al (2011) On the origin of the stability of foams made from catanionic surfactant mixtures. Soft Matter 7:6557–6570
Verbist G, Weaire D, Kraynik AM (1996) The foam drainage equation. J Phys: Condens Matter 8:3715–3731
Verwey EJW, Overbeek JTG (1948) Theory of the stability of lyophobic colloids. Elsevier, Amsterdam
Vilkova NG, Kruglyakov PM (2004a) Influence of a liquid flow through a foam under a pressure drop on the Plateau border curvature profile. Mendeleev Commun 14:22–23
Vilkova NG, Kruglyakov PM (2004b) Investigation of foam and emulsion destruction under the great pressure gradients. Adv Colloid Interface Sci 108–109:159–165
Vilkova NG, Kruglyakov PM (2005) Liquid flow through the foam: Comparison of experimental data with the theory. Colloids Surf A: Physicochem Eng Aspects 263:205–209
Walker HW, Morrow RW, du Pont de Nemours EI (1949). USA
Wang Z, Narsimhan G (2006) Model for Plateau border drainage of power-law fluid with mobile interface and its application to foam drainage. J Colloid Interf Sci 300:327
Wang G, Pelton R, Hrymak A, Shawafaty N, Heng YM (1999) On the role of hydrophobic particles and surfactants in defoaming. Langmuir 15:2202–2208
Wantke KD, Fruhner H (1998) The relationship between foam stability and surface rheological properties. Prog Trends Rheol V, Proc Eur Rheol Conf, 5th:315–316
Weaire D, Hutzler S (1999) Physics of foams. Oxford University Press, Oxford
Weaire D, Pittet N, Hutzler S, Pardal D (1993) Steady-state drainage of an aqueous foam. Phys Rev Lett 71:2670–2673
Wu F, Cai C, Wang L, Cao ZP, Yi WB (2008a) Breaking and inhibiting foam performance of modified silicone oils in oil-based systems. J DIsp Sci Tech 29:792–795
Wu F, Cai C, Yi WB, Cao ZP, Wang Y (2008b) Antifoaming performance of polysiloxanes modified with fluoroalkyls and polyethers. J App Polym Sci 109:1950–1954
Acknowledgements
Stoyan Karakashev thanks to the Fulbright organization for the financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Karakashev, S.I. Hydrodynamics of foams. Exp Fluids 58, 91 (2017). https://doi.org/10.1007/s00348-017-2332-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-017-2332-z