Measurement of velocity fluctuations in microfluidics with simultaneously ultrahigh spatial and temporal resolution

Abstract

Although unsteady and electrokinetic flows are widely used in microfluidics, there is unfortunately no velocimeter today that can measure the random velocity fluctuation at high temporal and spatial resolution simultaneously in microfluidics. Here we, for the first time, theoretically study the temporal resolution of laser induced fluorescence photobleaching anemometer (LIFPA) and experimentally verify that LIFPA can have simultaneously ultrahigh temporal $({\sim } 4\,\upmu \hbox {s})$ and spatial $({\sim }203\,\hbox {nm})$ resolution and can measure velocity fluctuation up to at least 2 kHz, whose corresponding wave number is about $6\times 10^6\,{/}\hbox {m}$ in an electrokinetically forced unsteady flow in microfluidics.

1 Introduction

Transport phenomena play a key role for performance of microfluidics devices. To understand the phenomena, we have to characterize the flows first. Currently, the most premier velocimetry in microfluidics is micro particle image velocimetry $(\mu \hbox {PIV})$ and its derivatives, which have the superior capability of measuring 2D and 3D microflow field on mean flow field, if the flow is steady or at most weakly disturbed (Klein and Posner 2010; Raben et al. 2013; Kinoshita et al. 2007; Santiago et al. 1998; Wereley and Meinhart 2010; Westerweel et al. 2004). However, for unsteady flows with random high velocity gradients, e.g., chaotic or turbulent flows where fluctuation $u'$ of velocity u could be strong, continuously measurement of $u'$ with sufficiently high spatiotemporal resolution becomes challenging for current $\mu \hbox {PIV}$, which has difficulty in exploring the spatial structure of flows down to sufficiently small spatial scales, because of its limited resolution (Burghelea et al. 2004). We have recently successfully generated micro electrokinetic turbulence in a microchannel at low Reynolds number (Wang et al. 2014). Then, the question is how to measure and characterize the turbulent flows in microchannels. To our knowledge, there is even no published power spectrum density (PSD) of $u'$ in microfluidics for frequency higher than $100\,\hbox {Hz}$.

For the widefield microscope, to reach a high spatial resolution, a large numerical aperture (NA) and magnification lens is necessary. If the particle concentration is low, there could be the risk that the interrogation window will not have sufficient particles in each image. This will reduce the temporal resolution and cause extra error. To ensure the capture of particles in interrogation spots, high particle volume fraction is then required. However, this will result in: (1) more serious out-of-focus noise which limits the signal-to-noise ratio (SNR) of image; (2) worse SNR of correlation field that leads to high probability of erroneous velocity (Klein and Posner 2010); and (3) change in viscosity of fluids (Breuer 2005), which in turn will alter the physical and chemical specifications, such as the local electric field and fluid viscosity that can cause the change in flows as well. In fact, even using a large NA lens cannot increase the spatial resolution by reducing depth of correlation and the out-of-focus influence (Rossi et al. 2012).

To reduce the out-of-focus influence and achieve high temporal resolution, Kinoshita et al. (2007) used confocal microscope with high-speed rotating Nipkow disk to capture the instant particle images in moving droplets. A continuous-wave (cw) laser was used as light source. This work claimed a $2\,\hbox {kHz}$ capture rate. However, to increase the relatively low SNR, ensemble average of correlation fields was applied which restricts the temporal resolution (Klein and Posner 2010). Later, Klein and Posner (2010) applied similar facilities with high-power laser in electrokinetic instability experiments. A great improvement was achieved, and instant velocity fields were successfully measured. But the local velocity structures are not reliable due to the erroneous velocity, which also makes continuous measurement for spectrum analysis unreliable. To reduce the percentage of erroneous velocity, Raben et al. (2013) combined confocal-based $\mu \hbox {PIV}$ with robust phase correlation and tested in steady Poiseuille flow. These authors found this combination could apparently reduce the erroneous vectors in steady flow. However, for a highly fluctuated flow, such as electrokinetic flow with high electric field intensity and high conductivity ratio, to our knowledge, there are no reliable measurements on velocity field published.

This situation becomes worse when $\mu \hbox {PIV}$ is used in any flow, where particles have different velocity from their surrounding fluids, such as electrokinetics (EK) and near wall flow, magnetophoresis, acoustophoresis, photophoresis and thermophoresis. This is because that particles, which are used as tracers of fluid velocity in $\mu \hbox {PIV}$, have their own velocity, which is essentially different from that of fluids, and the difference is unpredictable in many cases. When used in these flows, which are widely applied in lab-on-a-chip, $\mu \hbox {PIV}$ suffers from several uncertainties. For instance, in EK flows, the infilled particles may not monitor the fluid flow faithfully, because they experience electric force (e.g., dielectrophoresis due to the different permittivity and conductivity of particle from solution and Coulomb force) and have different velocity from local fluids (Breuer 2005; Posner and Santiago 2006; Kirby 2010). The well-known particle lagging makes it difficult to measure strong and high frequency $u'$. Since most particles may have more or less charge, erroneous velocity due to electrostatic force cannot be avoided, not only in the presence of EK, but also in flows without EK when particles are close to the polarized wall (Sadr et al. 2007).

Although in some circumstance, such as a simple AC EOF, the dielectrophoresis effect is easy to be distinguished and corrected (for instance, by two-color $\mu \hbox {PIV}$ (Wang and Meinhart 2005)), in most of the cases, the uncertainties are hard to be distinguished and unable to remove. Posner and Santiago (2006) noticed the possible error between the measured and real velocity field in the weakly fluctuated EK chaotic flow. This error could be too complicated to be corrected. This makes $\mu \hbox {PIV}$ measurement dubious in electrokinetic flows. In addition, these PIV-based methods also require expensive pulsed laser and camera.

There are also several other restrictions of $\mu \hbox {PIV}$ on achieving simultaneously high spatial and temporal resolution. To the best of our knowledge, to reach high repetition rate, all the high-speed cameras for $\mu \hbox {PIV}$ are so far made by CMOS sensor and the relevant derivations (such as SCMOS by LaVision Inc.). CMOS sensor has intrinsically high background noise. To achieve high SNR, the fluorescent signal should be high enough to conquer the background noise. For pulsed laser, this may not be an issue. However, no measurement with pulsed laser of high repetition rate in microfluidics has been reported. Also, Klein and Posner (2010) pointed out that the pulsed laser cannot work with a Nipkow disk. Hence, the combination of the pulsed laser and confocal microscope with a Nipkow disk to achieve the high spatial resolution $\mu \hbox {PIV}$ measurement with high repetition rate is yet to be developed. For cw laser, while high capturing rate is applied, the short exposure time and weak excitation light means shot noise is not negligible. Both of low signal and high background noise will cause very low SNR, which in turn will create a large amount spurious vectors while calculating. These vectors will mislead the measurement of highly spatiotemporal random velocity, and the actual temporal resolution of $\mu \hbox {PIV}$ is decreased. High power cw laser can enhance the SNR, but will also cause additional defects, such as heating. This may cause additional and unexpected influence. Thus, so far $\mu \hbox {PIV}$ with simultaneously high spatial and temporal resolution is yet to be developed.

Some other flow diagnostic methods are also developed in microfluidics, such as molecular tagging velocimetry (MTV) (Hu and Koochesfahani 2006; Koochesfahani and Nocera 2007), hot-wire anemometer (HWA) and its derivatives (Nguyen 1997), laser Doppler velocimetry (LDV) (Dinther et al. 2012) etc. However, to our knowledge, they all have intrinsic disadvantages on measuring $u'$ with high fluctuation frequency in unsteady microflows with complex circumstances. For example, MTV is slow and can only measure slowly varying flow velocities. HWA and its derivatives are single-point measurement methods. Although they can reach high temporal resolution, to get a fast response, the spatial resolution should be sacrificed, as summarized by Nguyen (1997). To the authors’ knowledge, so far the highest temporal and spatial resolution that reported in microfluidics measurements is on the order of $10\,\hbox {kHz}$ with $12\,\upmu \hbox {m}$ filament diameter (Simes et al. 2005), where they focused only on the frequency of flow. Besides the limited spatial resolution, HWA and its derivatives have difficulty in measuring velocity at the positions away from the wall as they are fabricated on the microchannel and are inaccurate when external electric field is present. These features significantly restrict the application of HWA and its derivatives in microfluidics, especially in EK flows. LDV and LDA are also single-point velocimetries. They normally have high repetition rate, i.e., high temporal resolution. The spatial resolution, to the best of authors’ knowledge, is not better than 4 by $16\,\upmu \hbox {m}$ (Voigt et al. 2008). This is also limited in microfluidics. As in LDV measurement, particles are still required. The flow diagnostic methods will also suffer the same uncertainty as $\mu \hbox {PIV}$ as introduced above. Due to these reasons, Kuang et al. (2009) developed a new velocity measurement technique called laser induced fluorescence photobleaching anemometer (LIFPA) based on the relation between fluorescence intensity and velocity of flow due to photobleaching process. This technique has several advantages: (1) noninvasive; (2) high spatiotemporal resolution; and (3) capable of far-field nanoscopic measurement.

The present work primarily focuses on the relations between flow velocity and photobleaching for velocity measurement. Meanwhile, the theoretical study is equally important and can be potentially applied to the fundamental influence of fluid flow on chemical process (i.e., photobleaching here) in biology and medicine, since fluorescence and its photobleaching plays a key role in biomedical research. For instance, fluorescence recovering after photobleaching (FRAP) has been widely applied in biology and medicine to measure diffusivity of proteins and other biochemicals within a cell. However, FRAP often faces a challenge: there is no diffusion behavior (Lippincott-Schwartz et al. 2003; Phair and Misteli 2001). The reason is that in FRAP, the signal depends on not only molecular diffusion, but also local fluid flow driven by molecular motors or membrane tension flow. Understanding the relation between flow velocity and photobleaching could enable FRAP to measure protein dynamics more accurately and provide more comprehensive information on protein dynamics within a live cell.

In this manuscript, we theoretically analyze and experimentally demonstrate the unprecedented high temporal resolution (TR) of the recently developed LIFPA system (Kuang et al. 2009) for $u'$ measurement in unsteady EK flows. Both unprecedented high spatial and temporal resolution can be achieved. The results are also compared with $\mu \hbox {PIV}$ measurement.

2 Analysis of LIFPA’s temporal resolution

2.1 Scheme of photobleaching process in laser focus

LIFPA bases on the photobleaching phenomenon of a small molecular fluorescent dye tracer (not micro- or nanoparticles) under the illumination of laser beam (Sugarman and Prudhomme 1987; Ricka 1987; Wang 2005). When an electrically neutral dye is used, it can avoid aforementioned issues with particles in $\mu \hbox {PIV}$. Generally, if laser power density ($P_{d}$) is uniform in focus area, the fluorescence intensity $I_{f}$ decreases exponentially in a quiescent fluid with bleaching time t as:

$$I_{f}=I_{f0}\exp \left( -\frac{t}{\tau }\right)$$

(1)

where $I_{f0}$ is the initial $I_{f}$ at $t=0$ and $\tau$ is a half decay time constant. Both $I_{f0}$ and $\tau$ are determined by $P_{d}$, dye concentration, fluorescent efficiency, quantum yield of photobleaching of dye at the laser wavelength, pH value of solution, etc. With Galilean transformation on Eq. 1, $I_{f}$ can be related to the instantaneous flow velocity u, as:

$$I_{f, {\mathrm{uni}}}(u;x',y')=I_{f0}\exp \left( -\frac{x'}{u\tau }\right)$$

(2)

where the subscript “uni” means that $P_{d}$ is uniform in the detection volume. As the laser beam is axisymmetric, all the flows perpendicular to laser beam axis have the same photobleaching process. Hence, in this part, we use the photobleaching process of flow in streamwise direction with velocity u to study the temporal resolution of LIFPA measurement. Here, $x'$ is the local streamwise position within the laser focus and $y'$ is the lateral position, with $x'\in [0,\,d_{f}]$ and $y'\in [0,\,d_{f}]$. If $P_{d}$ is not uniform, but Gaussian distribution, $I_{f0}$ and $\tau$ cannot be assumed to be constant as they depend on the bleaching history along pathline due to non-uniform $P_{d}$.

Fig. 1

Diagram of photobleaching process under uniform and non-uniform laser power density. a The diagram of four cases of $P_{d}$. Curve (i) and (ii) indicate high and low $P_{d}$, respectively. Curve (iii) is a rough model of non-uniform $P_{d}$. And curve (iv) is the related uniform $P_{d}$ whose value equals to the mean value of curve (iii). b The evolutions of $C_{\mathrm{eff}}$ normalized by their initial values under different $P_{d}$

To better describe the photobleaching process, the effective dye concentration and $I_{f}$ along $x'$ under both uniform and non-uniform $P_{d}$ are diagramed in Fig. 1. From curve (i) (dot-dashed line) and (ii) (short dashed line), where uniformly high and low $P_{d}$ are applied, respectively (Fig. 1a), it can be seen the effective dye concentration ($C_{\mathrm{eff}}$, the ratio between the concentration of unbleached dye and the initial dye concentration) of both cases decreases exponentially (Fig. 1b). And so does the $I_{f}$ (Fig. 2). The only difference is the time constant $\tau$ which is smaller for case (i) and larger for case (ii).

When a non-uniform $P_{d}$ is considered, as shown by curve (iii) (light yellow color) in Fig. 1a, both the $C_{\mathrm{eff}}$ and $I_{f}$ experience a complicated progress. In Fig. 1b, as indicated by the arrow, $C_{\mathrm{eff}}$ first decreases along the short dashed line, due to the low $P_{d}$. Then, under the exposure of high $P_{d}$, $C_{\mathrm{eff}}$ will decrease faster along the solid line (which is part of curve (i)) till the edge of high $P_{d}$. When the $P_{d}$ becomes smaller again, $C_{\mathrm{eff}}$ has already been significantly photobleached and results in a much flatter variation of $C_{\mathrm{eff}}$. The corresponding $I_{f}$ can be found by curve (iii) in Fig. 2. In the diagram, $I_{f}$ first decreases along curve (ii) (short dashed line), which is the same as in low $P_{d}$ case. Then, a sudden increase in $I_{f}$ caused by the high $P_{d}$ can be seen, as indicated by the solid line and arrow. Later, also a rapidly decreasing $I_{f}$ emerges while the edge of the lower $P_{d}$ is reached, followed by a small $I_{f}$ which also varies slowly.

Fig. 2

Diagram of $I_{f}$ variation in laser focus area, under the four cases shown in Fig. 1a

For comparison, a case with uniform $P_{d}$ which has the same mean value of $P_{d}$ as case (iii) is investigated and demonstrated by curve (iv) (long dashed line), as shown in both Figs. 1 and  2. It can be seen although both the $C_{\mathrm{eff}}$ and $I_{f}$ exhibit apparent differences between curve (iii) and (iv), their integrations in the laser focus region showed no much difference. This is the reason why in the following discussions sometimes we arbitrarily approximate our general model to the uniform case.

Due to the complexity of photobleaching process (intrinsically nonlinear, molecule diffusion becomes important at small scales and the convective transport and reaction equation cannot be simplified, laser and fluorescent signal absorbed by fluid, molecule broken by laser, etc), there is no reliable mathematical model so far to explicitly describe the related physical-chemical process. Although several works (Sugarman and Prudhomme 1987; Ricka 1987) have attempted to solve this problem, it is still far from being solved. Here, for general purpose, a weight function $\psi (u;x',y')$ is introduced to account the influence of non-uniform $P_{d}$ and we have:

$$I_{f}(u;x',y')=I_{f0}\psi (u;x',y')\exp \left( -\frac{x'}{u\tau }\right)$$

(3)

Approximating the cross section of exposure region to be a square with width of $d_{f}$ (not accurate, but sufficient to evaluate the influence of high $P_{d}$ region), the total $I_{f}(u;x',y')$ in the laser focus area, i.e., $I_{f,{\mathrm{total}}}$ can be calculated as below:

$$I_{f,{\mathrm{total}}}(u)=\int _0^{d_{f}}\int _0^{d_{f}}I_{f}(u;x',y')\,{\mathrm{d}} x'\,{\mathrm{d}} y'+I_{f,end}$$

(4)

where $I_{f, {\mathrm{end}}}$ is a positive constant since the fluorescence signal is not zero when the flow is at rest. As $\psi (u;x',y')>0$ and is continuous in the region, then:

$$\begin{aligned} I_{f,{\mathrm{total}}}(u)\,= & \,I_{f0}\psi _{s}(u)\int _0^{d_{f}}\int _0^{d_{f}}\exp \left( \frac{-x'}{u\tau }\right) \,{\mathrm{d}} x'\,{\mathrm{d}} y'+I_{f,end} \\=\, & \,d_{f}I_{f0}\psi _{s}(u)u\tau \left[ 1-\exp \left( \frac{-d_{f}}{u\tau }\right) \right] +I_{f,end} \end{aligned}$$

(5)

where $\psi _{s}(u)$ is a slowly varying function compared to $u\left[ 1-\exp \left( {-d_{f}}/{u\tau }\right) \right]$ for evaluating the overall effect of non-uniform $P_{d}$, with $\psi _{s}(0) = \psi _{s}(\infty )$. Hence, $I_{f,{\mathrm{tota}l}}(u)$ is a monotonically increasing function of u.

2.2 LIFPA response to u fluctuation

In highly and rapidly fluctuated flows, the temporal response of a velocimeter to u variation is of most interest. It should be sufficiently fast to capture the instant structures of varying u. Since the bleaching is behind the mechanism of LIFPA and the bleaching time can be approximately seen as the residence time of a dye molecule within the laser beam, LIFPA’s temporal response to u variation is normally determined by $\tau$ and $d_{f}$. The bleaching process of the dye in convection can be equivalently estimated from the bleaching process in a quiescent flow.

The relation between bleaching processes in flow and quiescent flow can be schematically explained by Fig. 3. As shown, at an arbitrary $u_{1}$, we can have a relevant $I_{f, {\mathrm{total}}}$, which in turn, in the photobleaching curve of the dye in the quiescent flow, corresponds to a $t_{{\mathrm{quie}}, 1}$ at which $I_{f, {\mathrm{total}}}=I_{f, {\mathrm{total}}, {\mathrm{quie}}}$. During a short time variation ${\mathrm{d}}t$ (where t without subscript “${\mathrm{quie}}$” means the real time of LIFPA measurement), the velocity decreases to $u_{2}$, which then has a corresponding $t_{{\mathrm{quie}}, 2}$ in the quiescent flow. If the LIFPA system is fast enough, when the velocity changes, the relevant photobleaching dynamics should respond immediately. In other words, when the velocity change from $u_{1}$ to $u_{2}$ needs time of ${\mathrm{d}}t$, the related photobleaching time change is ${\mathrm{d}}t_{\mathrm{quie}}\,({=}t_{{\mathrm{quie}}, 2}-t_{{\mathrm{quie}}, 1})$, which should be no more than ${\mathrm{d}}t$. Hence, the maximum ${\mathrm{d}}u/{\mathrm{d}}t$ that LIFPA can measure should be confined by ${\mathrm{d}}u/{\mathrm{d}}{t_{{\mathrm{quie}}}}$ which corresponds to the highest acceleration that LIFPA can measure.

Fig. 3

Diagram of relationship between the fluorescent intensity $I_{f, {\mathrm{total}}}$ measured in the flow of velocity u with the photobleaching time $t_{{\mathrm{quie}}}$ in a quiescent flow where $I_{f,{\mathrm{total}}}(u) \equiv I_{f,{\mathrm{total,quie}}}(t_{{\mathrm{quie}}})$

The relation of $I_{f, {\mathrm{total,quie}}}\sim t_{{\mathrm{quie}}}$ in quiescent flow can be described as:

$$\begin{aligned} I_{f,{\mathrm{total,quie}}}(t_{\mathrm{quie}})= & \,\psi _{s}(0)\int _0^{d_{f}}\int _0^{d_{f}}\exp \left( \frac{-t_{\mathrm{quie}}}{\tau }\right) \,{\mathrm{d}} x'\,{\mathrm{d}} y'+I_{f,{\mathrm{end}}} \\= & \,\psi _{s}(0){d_{f}^2}I_{f0}\exp \left( \frac{-t_{{\mathrm{quie}}}}{\tau }\right) +I_{f,end} \end{aligned}$$

(6)

Let $I_{f,{\mathrm{total}}}(u)\equiv I_{f,{\mathrm{total,quie}}}(t_{\mathrm{quie}})$, we find:

$$d_{f}I_{f0}\psi _{s}(u)u\tau \left[ 1-\exp \left( -\frac{d_{f}}{u\tau }\right) \right] =\psi _{s}(0){d_{f}^2}I_{f0}\exp \left( -\frac{t_{\mathrm{quie}}}{\tau }\right)$$

(7)

From Eq. 7, u is related directly to $t_{\mathrm{quie}}$ by a $u\sim t_{\mathrm{quie}}$ curve. Its slope determines the maximum temporal change in u that LIFPA can measure. If

$$|R|=\left| \frac{{\mathrm{d}} u}{{\mathrm{d}} {t_{quie}}} \right| \ge \left| \frac{{\mathrm{d}} u}{{\mathrm{d}} t} \right|$$

(8)

i.e., the actual temporal change in u ($|{{\mathrm{d}} u}/{{\mathrm{d}} t}|$) is smaller than the slope R of $u\sim t_{{\mathrm{quie}}}$ curve which stands for the upper limit of LIFPA response ability, LIFPA can measure the variation of u faithfully. Reversely, if

$$|R|=\left| \frac{{\mathrm{d}} u}{{\mathrm{d}} {t_{{\mathrm{quie}}}}} \right| <\left| \frac{{\mathrm{d}} u}{{\mathrm{d}} t} \right|$$

(9)

LIFPA cannot grasp u structures and results in underestimation of $u'$. By taking time derivatives ($t_{{\mathrm{quie}}}$) on both sides of Eq. 7, with plugging Eq. 7 in, R can be estimated as below:

$$\begin{aligned}&\left( \frac{{\mathrm{d}} u}{{\mathrm{d}} {t_{{\mathrm{quie}}}}} \right) \left\{ \frac{{\mathrm{d}} {\psi _{s}(u)}}{{\mathrm{d}} u}u\tau \left[ 1-\exp \left( -\frac{d_{f}}{u\tau }\right) \right] +\,\psi _{s}(u)\tau \left[ 1-\exp \left( -\frac{d_{f}}{u\tau }\right) \right] \right. \\&\left. -\psi _{s}(u)\frac{d_{f}}{u}\exp \left( -\frac{d_{f}}{u\tau }\right) \right\} =\,-\psi _{s}(u)u\left[ 1-\exp \left( -\frac{d_{f}}{u\tau }\right) \right] \end{aligned}$$

(10)

The photobleaching mechanism of fluorescent dyes is a very complicated, nonlinear physical-chemical process and is far from well understanding. Therefore exact solution of Eq. 5 is not available. Also, the explicit theoretical expression of ${{\mathrm{d}}u}/{{\mathrm{d}} {t_{{\mathrm{quie}}}}}$ is difficult to achieve from Eq. 10 and simplification is required. Here, as $\psi _{s}(u)$ is a slowly varying function of u, we assume ${{\mathrm{d}} {\psi _{s}(u)}}/{{\mathrm{d}} u}\sim 0$. (Note this is a rough approximation and will lead to some error on evaluating LIFPA’s temporal resolution, but it can help us theoretically estimate the feature of the LIFPA system approximately, without causing essential mistake and the corresponding error should be small as the variation of the velocity range we considered is relatively small. Furthermore, by careful calibration, the errors can be significantly reduced indirectly.) Then, we will have two cases.

If ${d_{f}}/{u\tau }\gg 1$, i.e., for low u, it is obtained $R=-u/{\tau }$. Or in other words,

$$\left| \frac{{\mathrm{d}} u}{{\mathrm{d}} t}\right| \le {\frac{u}{\tau }}$$

(11)

If ${d_{f}}/{u\tau }\ll 1$, i.e., for much larger u, and assume we only take into account the first order of exponential term ($\exp (-{d_{f}}/{u\tau })=1-{d_{f}}/{u\tau }$), then it is obtained that $R=-u^2/{d_{f}}$, and:

$$\left| \frac{{\mathrm{d}} u}{{\mathrm{d}} t}\right| \le \frac{u^2}{d_{f}}$$

(12)

This means, at small magnitude of u, the response speed of LIFPA to u variation is proportional to u by a factor of $-1/\tau$, and $u\sim t_{quie}$ curve is exponential. While at high u, R is dominated by $d_{f}$ and u itself, and $u\sim t_{{\mathrm{quie}}}$ curve becomes power-law. A simplified $u\sim t_{\mathrm{quie}}$ relation can further illustrate the mechanism of high TR of LIFPA. Let $\tilde{t}={t_{\mathrm{quie}}}/{\tau }$, $\tilde{u}={u\tau }/{d_{f}}$, and arbitrarily assume $\psi _{s}(u)$ to be a constant, from Eq. 7, we have dimensionless equation:

$$\tilde{t}= -\log \left\{ \tilde{u} \left[ 1-\exp \left(-\frac{1}{\tilde{u}}\right)\right] \right\}$$

(13)

The $\tilde{u}\sim \tilde{t}$ relation is plotted in Fig. 5a. Furthermore, $\tilde{t}$ can also be related to the resident time $t_{r}={d_{f}}/{u}$ as:

$$\tilde{t}= -\log \left\{ \frac{\left[ 1-\exp ({ -\tilde{t_{r}}})\right] }{\tilde{t_{r}}}\right\}$$

(14)

where $\tilde{t_{r}}={t_{r}}/{\tau }$. Larger u and smaller $t_{r}$ are equivalent to shorter $t_{quie}$ in quiescent flow, and vice versa. $\left| {{\mathrm{d}} \tilde{u}}/{{\mathrm{d}} \tilde{t}}\right| \sim \tilde{u}$ curve is plotted in Fig. 5b. A monotonic increasing relation can be found between $\left| {{\mathrm{d}} \tilde{u}}/{{\mathrm{d}} \tilde{t}}\right|$ and $\tilde{u}$. The higher u, the faster LIFPA responds.

2.3 Temporal resolution of LIFPA

Equations 11 and 12 describe the velocity acceleration, which is closely related to temporal resolution. Below we will connect the acceleration to the temporal resolution. When $\tau$ of LIFPA is small, its influence on TR can be elucidated by a simple model. Take square on both sides of Eq. 11, and assume instant velocity of a flow can be approximately described as a periodic function, i.e., $u=U+u_a\sin (\omega t)$ (where U is the mean velocity, $u_a$ is the amplitude and $\omega$ is the angular frequency) with ${\mathrm{d}} {u}/{\mathrm{d}} {t}=\omega u_a\cos (\omega t)$, we have:

$$\left( \frac{u_{a}^2}{\tau ^2}+{u_{a}^2}\omega ^2\right) \sin ^2(\omega t)+\frac{2Uu_{a}}{\tau ^2}\sin (\omega t)+\left( \frac{u_{a}^2}{\tau ^2}-{u_{a}^2}\omega ^2\right) \ge 0$$

(15)

where $u_{a}$ and $\omega =2\pi f$ are the amplitude and angular frequency of u fluctuation, respectively. Equation 15 indicates, when this quadratic equation is satisfied, LIFPA can respond fast enough. To make Eq. 15 satisfied, the following two conditions must be met:

$$\begin{aligned} \left\{ \begin{array}{lll} \left( u_a+U\right) ^2/\tau ^2\ge 0 \\ \left( u_a-U\right) ^2/\tau ^2\ge 0 \\ \left( U^2-u^2_{a}\right) -u^2_{a}{\omega }^2{\tau }^2 \ge 0,\quad \text{ if }\quad U\le u_a\left( 1+\omega ^2\tau ^2\right) \\ \end{array} \right. \end{aligned}$$

(16)

or

$$\begin{aligned} \left\{ \begin{array}{lll} \left( u_a+U\right) ^2/\tau ^2\ge 0 \\ \left( u_a-U\right) ^2/\tau ^2\ge 0 \\ U> u_a\left( 1+\omega ^2\tau ^2\right) \\ \end{array} \right. \end{aligned}$$

(17)

As all the physical quantities are real, the first two terms of both Eqs. 16 and  17 are naturally satisfied. Then, the required conditions are simplified to:

$$\sqrt{U/u_a-1}/2\pi \tau \le f\le \sqrt{U^2/u^2_{a}-1}/2\pi \tau \quad \text{ or }\quad 0<f< \sqrt{U/u_a-1}/2\pi \tau$$

(18)

For the case $f=0$, i.e., steady flow, the reliability of LIFPA is not an issue at all. Hence, to meet the requirement of Eq. 18, the time scale of TR (i.e., $t_{s}$) should be:

$$t_{s}\sim \frac{1}{f}\ge 2\pi \tau \left( \frac{U^2}{u_{a}^2}-1\right) ^{-1/2}$$

(19)

with $U\ge u_{a}$ (i.e., no reverse flow) and $U+u_{a}\sin (\omega t)\ll d_{f}/\tau$ (which can be relaxed to $U\ll d_{f}/2\tau$). The typical relations between $\tau$ and TR are plotted in Fig. 5c, where $u_{\mathrm{rms}}/U$ is used as a parameter, which, compared to $u_{a}/U$, is more proper for estimating the velocity fluctuations. In sinusoidal model, $u_{\mathrm{rms}}=u_{a}/\sqrt{2}$. It can be seen that the higher the $u_{\mathrm{rms}}/U$, the larger the value of $t_{s}$. Large value of $t_{s}$ indicates a poor TR. However, $u_{\mathrm{rms}}$ cannot be infinitely small and should be larger than the noise level of LIFPA. Normally, for a small $u_{\mathrm{rms}}$, $t_{s}$ is assumed to be no less than $\tau$.

Fig. 4

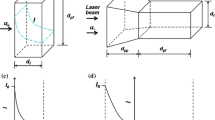
Schematic of the LIFPA setup and microchannel. a Schematic of the microchannel. AC electric field is applied to the two gold electrodes from the function generator. The basic flow is supplied by the syringe pump. x, y and z are the streamwise, spanwise and vertical directions of microchannel, respectively. The origin point of coordinate locates on the center of the tip of trailing edge. b Setup of LIFPA system in this experiment. L1, L2 and L3 lenses, PH1 and PH2 pinholes, DM1 and DM2 dichroic mirrors, M1 and M2 mirrors, BP band-pass filter, OL objective lens from Olympus, CP carrier plate, NS nanocube piezo stage (PI, 3-D), TS manual translation stage, ADC NI A/D converter

3 Experimental setup

3.1 AC EK flow in microchannel

The present work aims at developing a technique with simultaneously high spatial and temporal resolution for velocity fluctuation measurement in microfluidics. Ideally, a flow with known velocity field and spectrum should be used as a standard flow to evaluate the method. However, unfortunately in microfluidics, to our knowledge, so far no such a flow is available that has both large velocity fluctuations and high frequency. Therefore, in this manuscript, an unsteady, EK forced pressure-driven flow with external AC electric field in a microchannel is investigated to demonstrate the high TR of LIFPA. A quasi T-channel with side walls of 5$^\circ$ divergent angle was fabricated as shown in Fig. 4a. Both top and bottom layer of the channel are made by transparent acrylic plastic substrates. The sidewalls of the microchannel are conductive (gold) so that they are used as electrodes for forcing a pressure-driven flow electrokinetically. The channel has a rectangular cross section. At entrance, the width (W) is $130\,\upmu \hbox {m}$. The height is $240\,\upmu \hbox {m}$ which is constant for the entire 5-mm-long channel. Two streams are pumped into the channel by a Harvard Apparatus PHD 2000 infusion pump. They are separated by a plastic (Acrylic) splitter plate that has a sharp trailing edge. The two streams have different conductivities, one side is approximately $1\, \upmu \hbox {S/cm}$ and the other side is $5000\,\upmu \hbox {S/cm}$. The flow rate of each stream is about $2 \upmu \hbox {L/min}$. Hence, the bulk flow Reynolds number ($Re=U_{b}d/\nu$, where $U_{b}=2\, \hbox {mm/s}$ is the bulk flow velocity, d is the hydraulic diameter of channel at the entrance, and $\nu$ is the kinematic viscosity of water) is around 0.4. To generate a unsteady flow, an AC signal from a Tektronix function generator, Model AFG3102, is applied to the pressure-driven flow. Two channels of the function generator are separately connected to the two electrodes of the microchannels sidewalls. Sinusoidal signals with the same amplitude and frequency but 180$^\circ$ phase difference are applied to maximum the disturbance and increase velocity fluctuations.

Fig. 5

a Typical relation between $\tilde{u}$ and $\tilde{t}$, b $\left| {{\mathrm{d}} \tilde{u}}/{{\mathrm{d}} \tilde{t}}\right|$ vs $\tilde{u}$. c $t_{s}$ vs $\tau$ at different velocity fluctuation intensities. d LIFPA calibration curve fitting by both theoretical curve (Eq. 5) and $5{\hbox {th}}$ order polynomial. e Rise time of EOF. The transient process of the initial stage of the EOF with time step of $1\,\upmu \hbox {s}$ during a $15\,\upmu \hbox {s}$ period. The result shows that TR of the LIFPA is better than $5\,\upmu \hbox {s}$, because values can be easily discriminated during the $5\,\upmu \hbox {s}$ time intervals

3.2 LIFPA setup

The LIFPA measurement system consisted of a confocal microscopy system (CMS) and data acquisition system (DAS), as shown in Fig. 4b. Briefly say, the home-developed CMS consists of a light source ($405\,\hbox {nm}$ continuous-wave laser to be compatible with Coumarin 102 fluorescent dye for LIFPA measurement), complicated optics, high-accuracy nano-translation stage (Physik Instrumente (PI) piezo nanocube 3D positioning stage P-611.3SF) and Olympus objective of PlanApo100× NA 1.4 oil immersions. The laser power at its output is $50\, \hbox {mW}$. The concentration of Coumarin 102 is $20\,\upmu \hbox {M}$. The DAS is also shown in Fig. 4b schematically. After an optical band-pass filter (to eliminate noise) and pinhole (as spatial filter), the fluorescence signal is collected by a high-sensitive photomultiplier (PMT, HAMAMATSU, R-928). The current signal from the PMT is amplified by a low-noise current preamplifier SR570 (Stanford Research System) which generates a voltage signal. A cutoff frequency of low-pass filter from the preamplifier is used to reduce the shot noise from the fluorescence signal. The signal is later sent to the computer by an A/D convertor (NI-6259 from National Instruments) and recorded by LabVIEW SignalExpress (National Instruments). In this experiment, the laser diameter at the focus point and the depth of focus are estimated to be about $203\,\hbox {nm}$ and $1000\,\hbox {nm}$, respectively. The spatial resolution of LIFPA dictated by the diffraction limit at the focus is ${\sim } 203^2\times 1000$ nm$^3$. Similar to the criterion used in HWAs, where the wire diameter is used as the spatial resolution, in LIFPA, we claim the spatial resolution is also the diameter of the laser focus which is $203\,\hbox {nm}$. The sampling rate here is selected to be $12.8\,\hbox {kHz}$ to be high enough to measure the highest frequency signal, but as low as possible to minimize shot noise.

3.3 $\mu \hbox {PIV}$ measurements

To evaluate the measurement of LIFPA, a LaVision $\mu \hbox {PIV}$ system is also used to measure the velocity fluctuation for comparison. The $\mu \hbox {PIV}$ system consisted of a PCO Sensicam high-sensitivity camera, NewWave SOLO III pulse laser, self-assembled microscope with 60× NA 0.85 Plan microscope objective and Newport 3D precision translation stage. $1\,\upmu \hbox {m}$ polystyrene fluorescent particle (Thermo Scientific Fluoro-Max Red) is used as tracer. The velocity field is calculated by Davis 7 software (from LaVision Inc.). The interrogation window size is $64\times 64$ pixels $(8.1 \times 8.1\, \upmu \hbox {m})$ with 50 % overlap. The depth of correlation should be larger than $30\,\upmu \hbox {m}$ if estimated from the work of Rossi et al. (2012). The measured plane is at $z=-4\,\upmu \hbox {m}$ from centerline (Bown et al. 2006) which is a sufficient approximation of flow at centerline. For calculating the root-mean-square $(\hbox {rms})$ of velocity fluctuations, 200 velocity fields are processed in this manuscript.

3.4 LIFPA measurement

Similar to a hot-wire anemometer (HWA), LIFPA should be calibrated before measurement. In this experiment, LIFPA was calibrated in the same microchannel that experiments were conducted. To ensure accurate measurement, the syringe pump was calibrated by particle tracing method. The calibration curve $u=u(I_{f,{\mathrm{total}}})$ is nonlinearly fitted by both $5{\hbox {th}}$ order polynomial curve (i.e., $u(I_{f,{\mathrm{total}}})=\sum _{n=0}^5 a_{n}I_{f,{\mathrm{total}}}^n$) and the theoretical curve from Eq. 5, where the effect $\psi _{s}(u)$ is assumed to be a constant. Both methods exhibit good fitting as shown in Fig. 5d. The $5{\hbox {th}}$ order polynomial is adopted for u calculation because of the better fitting. In practical measurement, as LIFPA cannot distinguish direction of flow, the velocity measured by LIFPA is its magnitude, i.e., $u_{s}=\sqrt{u^2+v^2}$, where u and v are the instant velocity components in x and y directions, respectively. Therefore, in the following sections, $u_{s}$ is used for more explicit expression. The calibration relation is not affected. Due to the fast photobleaching and pre-photobleaching, the z directionally moved molecule of fluorescent dye could be immediately photobleached before entering the focus area. The corresponding directional correction factor of LIFPA in z direction in this investigation is much smaller than $1\,\%$ (Zhao et al. 2015). Based on this theoretical estimation, the difference between with and without considering w component (the velocity component in z direction) in $u_s$ is significantly less than $1\,\%$, while considering isotropic hypothesis. In fact, adjacent to the trailing edge, the velocity component in z direction should be less stronger than the corresponding x and y components. The z directional correction factor should be even smaller than predicted. Therefore, the contribution of velocity component in z direction to LIFPA measurement is approximately negligible, and w is not presented in $u_{s}$ in this manuscript.

4 Experimental results

4.1 Time series of velocity and its derivation

LIFPA is single-point measuring technique and can have very high sampling rate, which is limited by its TR. The time series of $u_{s}$ in EK-forced flow is plotted in Fig. 6a, where three cases are investigated. Without forcing, $u_{s}$ is nearly constant with negligible small fluctuations probably due to vibration of the setup and shot noise. Under forcing with voltage V = 8 V$_{p-p}$ (peak-to-peak value of AC signal), $f=100\,\hbox {kHz}$, the flow is slightly and randomly disturbed. However, when V is increased to $20\,\hbox {V}_{p-p}$, $u_{s}$ signal becomes random with large and rapid fluctuation, and large local gradient as shown in Fig. 6b.

By fitting Eq. 5 (as shown in Fig. 5d), $\tau$ is found to be about $4\,\upmu \hbox {s}$. As ${d_{f}}/{u_{s}\tau }\gg 1$, $\left| \left( {{\mathrm{d}} u_{s}}/{{\mathrm{d}} t} \right) _{LIFPA}\right|$ is estimated to be 500 m/s$^2$ according to Eq. 11, when $u_{s}$ = 2 mm/s. This is much larger than the maximum $\left| \left( {{\mathrm{d}} u_{s}}/{{\mathrm{d}} t} \right) _{flow}\right|$ (about $35\,\hbox {m/s}^2$) in Fig. 6b. Hence, the LIFPA measurement is theoretically fast enough to measure $u'_{s}$ (${=}u_{s}-\bar{u_{s}}$, i.e., the measured velocity fluctuation, where the bar means ensemble average) in this flow. Although $\left| \left( {{\mathrm{d}} u_{s}}/{{\mathrm{d}} t} \right) _{LIFPA}\right|$ decreases to 50 m/s$^2$ when $u_{s}$ is reduced to $0.2\, \hbox {mm/s}$ (already a small value for most lab-on-a-chip applications), it is still sufficiently fast to accurately measure the velocity fluctuations. Figure 6 indicates that in the electrokinetically forced flow, the velocity fluctuation and its acceleration increase rapidly with the voltage. The flow is no more steady, but highly unsteady with random motion.

To ensure the high TR character of LIFPA, the rise time $\tau _{r}$ of DC electroosmotic flow (EOF) under sudden applied electric field is also investigated to validate the ultrahigh TR of the LIFPA, since this is one of the most basic transient electrokinetic flows with a very fast dynamic process. (The flow rate of each stream is still $2 \,\upmu \hbox {L/min}$. In this case, two electrodes were placed at the inlets and outlet with $20\, \hbox {V}$ difference. The two streams have the same conductivity of $1\,\upmu \hbox {S/cm}$ to minimize flow disturbance and meanwhile generate a thick electric double layer. The EOF was measured at $1\,\upmu \hbox {m}$ from the bottom of the channel. (The sampling rate of signal in this experiment is $1\,\hbox { MHz}$.) As shown in Fig. 5e, the rise time of EOF flow is about $10 \,\upmu \hbox {s}$. The increase in EOF can be clearly distinguished from the basic flow. As commonly known, to distinguish a signal properly, the TR of a measuring technique should be at least two times higher than the signal. Therefore, the experimental result indirectly shows that the temporal resolution of LIFPA should be apparently better than $10\,\upmu \hbox {s}$ for the rise time measurement of the DC EOF. The rapid response of LIFPA is undisputed, and the theoretically predicated temporal resolution (i.e., $4\,\upmu \hbox {s}$) is reasonable. Note, the starting EOF has a slight overshoot similar to the case in a RC circuit, and after the velocity reaches the peak, there is a small roll-off (Kuang et al. 2011).

Fig. 6

Time series and acceleration of velocity along center line of the channel at $x=10\,\upmu \hbox {m}$ downstream from the trailing edge. a Time series of $u_s$ for the unforced and forced flows at different voltages and $f=100\,\hbox {kHz}$. b ${{\mathrm{d}}u_{s}}/{{\mathrm{d}} t}$ at $V=20\, \hbox {V}_{p-p}$ and $f=100\,\hbox {kHz}$

4.2 Power spectrum density of velocity fluctuation

In unsteady or turbulent flows, PSD is one of the most important parameters, which can reveal the multiscale features involved in the flows. Currently there are few measurements on PSD because of the lack of the velocimeters that can measure the PSD in unsteady flows in microfluidics. Fortunately, LIFPA now can, for the first time (to the best of our knowledge), measure the PSD with high frequency in microfluidics. The PSD of $u'_{s}$ at $V=20\,\hbox {V}_{p-p}$, $f=100\,\hbox {kHz}$ measured by LIFPA at $x= 10\,\upmu \hbox {m}$ (i.e., $10\,\upmu \hbox {m}$ downstream of trailing edge.) is plotted in Fig. 7a, which shows that the PSD in the forced flow is much higher than that in the unforced flow. It can be seen there are 4 different regions in the PSD of the forced flow. At the low frequency range from 1 to $80\,\hbox {Hz}$, the spectrum is almost flat due to the non-equilibrium process under strong forcing. From 80 to $300\,\hbox {Hz}$, the slope of PSD is about $-$1.7. Because of the nature of low Reynolds number, the viscous dissipation is high and a slope of $-$4 from the PSD is developed from 300 to $2\, \hbox {kHz}$. Beyond $2\,\hbox {kHz}$, there is no detectable velocity signal and the PSD is dominated by noise.

The PSD of the forced flow is about four decade higher than that of the unforced flow near $100\,\hbox {Hz}$. The PSD from the wide bandwidth of the frequency of the forced flow indicates the existence of multiple scale eddies in the microflow. The slope of the PSD can be larger than $-$3. Therefore, this unsteady flow behaves differently from the temporally random but spatially smooth chaotic flow (Fouxon and Lebedev 2003; Burghelea et al. 2004). The detectable $u_s$ signal in the frequency domain in the EK forced flow can be up to $2\,\hbox {kHz}$. The corresponding wave number is about $6\times 10^6$ 1/m), which to our knowledge cannot be measured by current $\mu \hbox {PIV}$. It seems LIFPA is the only technique that can measure velocity signal of such a high frequency so far, while the spatial resolution is kept in the submicrometer to be able to measure high wave number signal.

Specially, in fluorescence measurement, the shot noise can significantly contaminate the statistical results at high frequency (Wang and Fiedler 2000). Each flow has a highest cutoff frequency, beyond which noise starts to dominate. To reduce the noise from higher frequency to increase signal-to-noise ratio (SNR), proper low-pass frequencies (higher than the cutoff frequencies of velocity signal) of the electric filter from the SR-570 current amplifier are selected for different flows and spatial positions. For the forced flow, the low-pass frequency is $10\,\hbox {kHz}$. For the unforced flow, the low-pass frequency is selected to be $3\,\hbox {kHz}$, which is sufficiently high to show the noise feature of the flow. Because of the low-pass filter, the PSD of the unforced flow beyond $1.5\,\hbox {kHz}$ decays with the increase in the frequency. The purpose of showing the PSD of unforced flow is to demonstrate: (1) beyond $20\,\hbox {Hz}$, there is no additional high-frequency velocity fluctuations caused by laser heating, vibration of channel, unstable pump and other unexpected factors in the unforced flow and (2) the noise level is low and the SNR is sufficiently high for the measurement of the forced flow. Hence, the higher-frequency components above $1\,\hbox {kHz}$ is arbitrarily removed for the unforced case in Fig. 7a. It should be also noted that the noise levels of PSD in the unforced and forced flows are different. This is probably because the signal is higher in the forced flow than that in the unforced flow, and the shot noise increases with the signal (Wang and Fiedler 2000).

Fig. 7

a Velocity PSD along centerline at $x = 10\,\upmu \hbox {m}$. bComparison of $u_{s, {\mathrm{rms}}}^*$ measured along x direction by both LIFPA and $\upmu \hbox {PIV}$ at the centerline of channel under $V=20\, \hbox {V}_{p-p}$, $f = 100\,\hbox {kHz}$

4.3 Comparison between LIFPA and $\mu \hbox {PIV}$ measurements

The $\hbox {rms}$ of velocity fluctuation, $u_{s, {\mathrm{rms}}}^*(={\sqrt{\bar{{u'}_{s}^2}}}/{U_{b}}$) at $V=20\, \hbox {V}_{p-p}$, $f = 100\,\hbox {kHz}$ was measured by both LIFPA and $\mu \hbox {PIV}$ at different streamwise positions. The result is plotted in Fig. 7b. Since LIFPA cannot distinguish velocity directions, the measured velocity by LIFPA is actually the velocity magnitude, i.e., $u_s$. For comparison of LIFPA with PIV, the magnitude of velocity $(u_s)$ is first calculated from PIV based on u and v components and then the $u_s$ fluctuation is calculated and compared with LIFPA’s results. Note, due to the fast photobleaching and the noninvasive nature of LIFPA, unlike the HWA, where z velocity component can also have an influence on $u_s$, LIFPA suffers less influence of the z velocity component along the axis of laser beam on the measurement of $u_s$, as investigated by Zhao et al. (2015). Therefore, even if the flow is 3D, it is still reasonable to compare $u_s$ measurement for LIFPA and $\mu \hbox {PIV}$. It can be seen, adjacent to the inlet, $u_{s, {\mathrm{rms}}}^*$ is very large. Here, $u_{s, {\mathrm{rms}}}^*$ measured from $\mu \hbox {PIV}$ exhibits apparent discrepancies from LIFPA and is at least 24 % smaller than that measured by LIFPA. After ${x}/{W}=0.4$ (i.e., around $x\sim 50\,\upmu \hbox {m}$) downstream, where $u_{s, {\mathrm{rms}}}^*$ is much weaker due to rapid viscous dissipation, $\mu \hbox {PIV}$ exhibits consistent values as LIFPA. This can verify that LIFPA is reliable.

The reason why the measured $u_{s, {\mathrm{rms}}}^*$ by $\mu \hbox {PIV}$ is lower than that measured by LIFPA is not fully understood. Ideally, it is better to use a standard and reliable flow field with high-frequency signal and strong velocity fluctuations to test both LIFPA and $\mu \hbox {PIV}$. However, to the best of our knowledge, such a flow in microfluidics is yet to be found. One reason could be that because of the 3D flow, the z directional velocity component may cause some contribution and error for the measurement of $u_{s, rms}^*$ (although, theoretically say, the contribution is negligibly small as introduced above), as the detection point has a $1000\,\hbox {nm}$ depth of focus.

Compared to LIFPA technique, $\mu \hbox {PIV}$ is intrinsically improper for such a complicated flow field and will suffer several influences which will result in unpredictable measurement errors. One reason could be that $\mu \hbox {PIV}$ has difficulty in measuring the fast fluctuated velocity due to intrinsic particle lagging [although the discrepancy could be small according to theoretical analysis (Adrian 1991)], especially for the high-frequency small-scale structures, which are crucial for transport phenomena.

Another cause could be the EK force (e.g., dielectrophoresis (DEP), electrophoresis, etc) loaded on the particles. In this experiment, the DEP effect is inevitable for the $1\,\upmu \hbox {m}$ particles used for $\mu \hbox {PIV}$. The real part of Clausius–Mossotti factor is between $-$0.5 to 0.74 and varies at different positions with time, due to the varying solution conductivity and permittivity. The local DEP effect will vary spatially and temporally and result in an unpredictable varying DEP force which may drive the particles in a different direction from the flow of the fluid. As the particle is slightly negatively charged, the influence of AC electric body force on particles is also unpredictable. These influences will also cause the measured velocity through $\mu \hbox {PIV}$ departure from the actual one.

The third reason may be due to the relatively low spatial resolution of $\mu \hbox {PIV}$, not only in xy plane, but also the large depth of correlation in z direction (Rossi et al. 2012). As mentioned in the introduction, it is almost impossible to use a confocal $\mu \hbox {PIV}$ to measure the highly fluctuated electrokinetic flow with high frequency. We can only use the conventional non-confocal microscopy system for the unsteady electrokinetic flows. The actual z directional resolution of the conventional $\mu \hbox {PIV}$ is the depth of correlation (i.e., the effective averaging depth for velocity measurement) which is significantly larger than the theoretically predicted one and affected by both microscopy system and even particle size (Rossi et al. 2012). As has been mentioned, in our $\mu \hbox {PIV}$ system, the depth of correlation is estimated to be larger than $30\,\upmu \hbox {m}$. In contrast, LIFPA can be applied to a confocal microscope for the unsteady electrokinetic flows without the issues involved in $\mu \hbox {PIV}$ and the effective depth of focus of the present confocal LIFPA is ${\sim}1000\,\hbox {nm}$. All these uncertainties could cause smaller magnitude of velocity fluctuations measured by $\mu \hbox {PIV}$ in this EK flow, compared to LIFPA method.

5 Discussion and conclusion

In this manuscript, the ultrahigh temporal resolution of LIFPA under submicrometer spatial resolution is theoretically investigated and experimentally demonstrated. Measurements of $\hbox {rms}$ of velocity fluctuation are also compared between LIFPA and $\mu \hbox {PIV}$. Simultaneous submicrometer spatial resolution with microsecond temporal resolution has been achieved. The corresponding wave number is estimated to be on the order of $10^6\,{/}\hbox {m}$. To the best of our knowledge, this is the highest wave number that has been reported in the field of fluid mechanics. To evaluate and verify the theory of the temporal resolution of LIFPA, ideally a well-known and standard flow should be used for comparison. Unfortunately, unlike conventional flow, in microfluidics flow, it is difficult to have a standard flow with defined velocity oscillating at high frequency on the order of $100\,\hbox {kHz}$. The measured $2\,\hbox {kHz}$ signal should not be the limit of the temporal resolution of LIFPA, but either the maximum frequency of velocity fluctuations in the flow or the highest frequencies of the fluorescence signal, beyond which noise starts to dominate. Therefore, although it is verified that LIFPA can have temporal resolution of about 5 μs, experimental evaluation of its corresponding higher frequency resolution is yet to be developed.

Similarly to the HWA, LIFPA also uses a calibration between fluorescence intensity and flow velocity and adopts the quasi-steady approximation used in HWA (Comte-Bellot 1976). The calibration is measured under a steady flow, and the velocity fluctuations are measured based on the quasi-steady approximation as long as the temporal resolution is sufficiently high for the time-resolved measurement. In other word, if the temporal resolution is shorter than the shortest characteristic time, then the quasi-steady approximation is satisfied. Although LIFPA can offer velocity measurement with unprecedented simultaneously high spatial and temporal resolution, unfortunately, currently the single laser beam based LIFPA has also the following disadvantages: (1) cannot take the measurement of the entire velocity field in a flow as PIV can; (2) cannot distinguish the velocity direction; and (3) must rely on the Taylor hypothesis in order to measure spatial PSD of velocity. The latter two difficulties can cause measurement errors. Proper error analysis and correction methods for LIFPA on statistical measurement flow velocity have been investigated in detail by Zhao et al. (2015). Also, as mentioned previously, compared to HWA, LIFPA has apparently better measurement accuracy due to the smaller influence of 3D flow in z direction (parallel to laser beam). This is why in the definition of $u_{s}$, only u and v are considered.

The LIFPA system is intrinsically stable if two factors are carefully taken care of. One is the laser power, and the other is the effective dye concentration. The laser should be sufficiently warmed up before acquiring data to ensure it work stably. Since the fluorescent dye is very sensitive and photobleaches fast, the effective dye concentration in each measurement may be different if the dye is not carefully stored. Therefore, the dye should be well protected from photobleaching. As investigated by Kuang et al. (2009), by comparing with the velocity profile predicted theoretically in a laminar flow of a tube, the relative error of LIFPA measurement is only $3\,\%$ on average.

Currently, LIFPA technique is still on its early stage and has large potency for development and improvement. By increasing laser intensity at focus point or developing new fluorescent dye, the bleaching time constant $\tau$ can be further reduced to significantly increase the temporal resolution. Combining with the technique of super-resolution microscope, i.e., stimulated emission depletion microscope, LIFPA can even overcome classical diffraction limit in physics and reach to at least $70\,\hbox {nm}$ spatial resolution (Kuang and Wang 2010). Since the neutral dye is molecularly dissolved in the fluid, there are always sufficient particles of molecular size as flow tracer to avoid the issues of particle seeding and interaction with electric field in $\mu \hbox {PIV}$ and to ensure continuously high-frequency sampling with sufficiently long time measurement. Therefore, LIFPA can be a new technique for statistical measurement of high-frequency and small-scale flow velocity with simultaneously high spatiotemporal resolution in complex flows in microfluidics.