1 Introduction

The local volumetric heat release rate is an important quantity for flame measurements. For example, it is the dominant coupling parameter between combustion and acoustics in combustion instability. However, the volumetric heat release rate is a value defined theoretically and cannot be measured directly.

A flame property that is easy to measure is its own radiation. The measurement is non-invasive and requires limited measurement effort. In the past, the radiation of excited radicals like hydroxyl (\({\hbox {OH}^*}\)) or methylidine (\({\hbox {CH}^*}\)) has often been used as markers for the heat release rate. Sometimes, even a quantitative correlation between the spatial radiation emissivity and the volumetric heat release rate is assumed.

The validity of this assumption has been investigated in numerous studies. However, most of these studies were focused on premixed hydrocarbon flames. This is due to two reasons: first, non-premixed flames tend to soot, which masks the radical emission and makes it hard to measure. Second, the measurement of the heat release rate is important for the stability analysis of lean premixed gas turbine combustors, which are prone to be unstable. Nevertheless, non-premixed non-sooting flames can also exhibit combustion instability, for example in rocket combustion.

A detailed review of the correlation between heat release and flame emission for premixed hydrocarbon flames is given by Lauer (2011). It is generally agreed that both \({\hbox {OH}^*}\) and \({\hbox {CH}^*}\) chemiluminescence are poor quantitative markers in turbulent flames for the local volumetric heat release rate (Najm et al. 1998; Ayoola et al. 2006), but that the overall flame emission is linked to the overall heat release (Clark and Bittker 1954; Hardalupas and Orain 2004).

Due to the different nature, the results from the studies mentioned above cannot be directly transferred to non-premixed flames. The correlation between heat release and flame emission for non-premixed flames has been studied by only a few authors: Panoutsos et al. (2009) numerically investigated a counterflow non-premixed methane-air flame and came to the conclusion that \({\hbox {OH}^*}\) radiation can be used as a topological marker for heat release rate because the distance between the peak in heat release and chemiluminescence peak is small for this combination of fuel and oxidizer. They did not propose any quantitative relationship. Yoo et al. (2002) performed a similar study on spherical low-pressure nitrogen-diluted hydrogen–air flames. In their study, the peaks of heat release rate and \({\hbox {OH}^*}\) are at different locations. Recently, Hossain and Nakamura (2014) compared the numerically simulated profiles of the heat release rate and the \({\hbox {CH}^*}\) concentration in atmospheric counterflow diffusion flames of methane and propane burning with air. Within the laminar flame, both \({\hbox {CH}^*}\) and heat release rate peak at close spatial locations, but the general shapes are very different from each other. They applied the procedure by Lauer et al. (2011), which was developed for premixed counterflow flames, to compare the flamelet-integrated heat release rate with the flamelet-integrated \({\hbox {CH}^*}\) radiation at varying strain rates. For low strain rates, a linear relationship (but not direct proportionality) is observed. It becomes highly nonlinear near the extinction strain rate. The authors numerically studied the influences of fuel types, the chemical mechanisms used for the ground-state and the excited species, the diluents, and the diffusion properties of \({\hbox {CH}^*}\) by parameter variation. They concluded that the computation of the precursors for the chemiluminescent reaction (\(\hbox {C}_{2}\hbox {H}\) and \(\hbox {C}_{2}\hbox {H}_{2}\)) has the most significant impact on the modeled \({\hbox {CH}^*}\) radiation. Although Hossain and Nakamura (2014) included \({\hbox {OH}^*}\) in their simulation, they did not elaborate on its radiation.

Experimentally, the relationship between \({\hbox {OH}^*}\) radiation and heat release rate has not been discussed thoroughly in the literature for non-premixed flames. The only work touching this context is by Burrows and Razner (1964), Burrows and Povinelli (1962), and Burrows (1965), who, however, only used the \({\hbox {OH}^*}\) radiation within a rocket combustion chamber to mark the reaction zone. Bedard et al. (2014) recently published their first approach on this subject. Besides presenting the measured, time-resolved spectrum of a single injector burning methane with decomposed hydrogen peroxide, they compared the heat release rate with the \({\hbox {OH}^*}\) and \({\hbox {CH}^*}\) radiation obtained from a numerical simulation. As the simulation was performed with a significantly reduced mechanism, the radiation was modeled in a post-processing step. The radiation was approximated by just taking into account the chemical excitation rates, thus ignoring any thermal influence. While the comparison of the numerical data yields some spatial correlation between the heat release rate and radiation, the simulated radiation did not match the experimentally observed values, which questions their modeling approach. Nevertheless, they concluded that both \({\hbox {CH}^*}\) and \({\hbox {OH}^*}\) are insufficient to provide both the spatial and temporal details to resolve the heat release rate in their combustor.

Non-premixed hydrogen flames are popular in liquid rocket propulsion for their high efficiency. However, combustion instability is a dangerous hazard. Its understanding is crucial to designing future engines without risking costly full-scale engine failures, like it has been necessary for the F-1 engine of the Saturn V (Yang and Anderson 1995). To experimentally investigate the phenomenon under the hostile conditions in rocket engines, a proportionality between flame radiation and the heat release rate would be convenient.

The absence of molecules containing carbon in hydrogen flames rules out sophisticated methods that rely on combined measurements of (stimulated) radiation from excited hydrocarbons like \({\hbox {CH}^*}\) (Hardalupas et al. 2010). Instead, hydrogen flames emit only radiation from the excited hydroxyl radical \({\hbox {OH}^*}\) and a continuous radiation peaking in the blue.Footnote 1 While the origin of the latter is not proven beyond doubt, recent results confirm earlier studies which propose a chemiluminescence reaction forming \({\hbox {H}_{2}\hbox {O}_{2}^{*}}\) responsible for the blue radiation (Fiala 2015; Vanpee and Mainiero 1979; Diederichsen and Wolfhard 1956):

$$\begin{aligned} \hbox {OH}+\hbox {OH}\longrightarrow \hbox {H}_{2}\hbox {O}_{2}^{*}\longrightarrow \hbox {H}_{2}\hbox {O}_{2} + h\, \upnu \end{aligned}$$
(1)

In liquid rocket engines, hydrogen is burned with pure oxygen at elevated pressure. This results in flame temperatures above 3500 K. At this temperature, the excitation of \({\hbox {OH}^*}\) is mostly due to thermal excitation instead of chemical excitation, which causes radiation at lower temperatures (Gaydon and Wolfhard 1952; Gardiner et al. 1969; Hidaka et al. 1982; Kathrotia et al. 2010; Koike and Morinaga 1982; Leo et al. 2007; Wolfhard and Parker 1952). The different physical origin might also have an influence on a possible correlation between radiation and heat release rate.

1.1 Focus and outline

This study compares the \({\hbox {OH}^*}\) and blue radiation from non-premixed hydrogen flames to the volumetric heat release rate in a hybrid approach: to correctly capture the physical effects, the radiation is recorded from a jet flame experiment. The heat release is computed from a numerical simulation featuring detailed chemistry. The flame burns in the laminar regime to fully resolve the flame structure. The pressure is varied between atmospheric conditions and 40 bar. The experiment is also used to validate radiation models.

To transfer the findings from the laminar to the turbulent regime, counterflow flame simulations are conducted. If a turbulent flame is imagined to consist of an ensemble of laminar counterflow flames, the results from the laminar study can be transferred by a statistical approach.

The experimental and numerical setups of the jet flame as well as the setup of the counterflow flame simulations are described in the next section. Afterward, the radiation and the heat release rate of the jet flame are compared on an integral basis as a function of pressure as well as on a spatial basis. The underlying physical mechanisms are explained based on the counterflow flame simulations. By analyzing the correlation for flamelet ensembles, radiation and the heat release rate within turbulent flames are compared. Finally, the results are summarized in a conclusion.

2 Experimental and numerical setups

To properly examine the physical flame radiation, a laboratory-scale experiment is set up. However, the determination of the molecular structure and especially the heat release rate is not possible from the experiment alone with reasonable measurement effort. Therefore, the experiment is complemented by a numerical simulation that provides these parameters. To ensure that the numerical data are reliable, the flame is chosen to burn in the laminar regime. This avoids the great uncertainty of turbulence–chemistry interaction. The hybrid approach further resolves the detailed laminar flame structure. To be able to transfer these findings on to turbulent flames, counterflow flame simulations are conducted.

2.1 Jet flame experiment

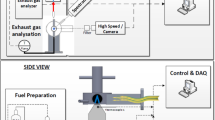
A sketch of the experimental combustor setup is shown in Fig. 1. The laminar flame is established by oxygen burning in a hydrogen co-flow. A mass flow rate of 40 mg/s oxygen is fed through a quartz fuel lance with an outer diameter of 10 mm and a wall thickness of 1 mm. This corresponds to a Reynolds number of 332 with respect to the lance inner diameter. At the tip of the lance, a steady anchored diffusion flame is stabilized. Hydrogen is supplied through an annular duct at a mass flow rate of 20 mg/s and a Reynolds number of 303 with respect to the hydraulic diameter of the duct. The great excess of hydrogen (equivalence ratio 4) leads to a manageable exhaust gas temperature.

Fig. 1
figure 1

Schematic drawing of the experimental high-pressure burner

Full size image

The flame is shielded by a 1-mm-thick quartz tube with an internal diameter of 20 mm. It is housed inside a partially water-cooled pressure vessel. Nitrogen flows between the flame shield and the vessel walls to prevent the test rig from overheating and to further reduce the exhaust temperature. The test rig is designed to withstand pressures of up to 40 bar.

The pressure is built up and regulated by an electrically assisted needle valve in the exhaust. The pressure is monitored by a pressure transducer mounted at the nitrogen inlet. Hydrogen, oxygen, and nitrogen are supplied by standard gas cylinders. Their mass flow rates are controlled by Bronkhorst mass flow controllers. The oxygen is fed into the burner through the lance which is long enough to establish a fully developed Hagen–Poiseuille flow. The hydrogen flows through six radial jets into a plenum, from which it enters the annular duct through an open porous metal foam to ensure a homogeneous flow. The nitrogen enters the pressurized chamber directly through six radial jets.

To suppress back-flow at the end of the flame shield, the combustion products impinge onto a top quartz window. Here, the flow is reversed and mixed with the nitrogen. Six peripheral holes vent the exhaust into an eccentric duct, which collates the gases into the exhaust pipe. Before entering the exhaust valve, the flow is cooled by an air-cooled heat exchanger.

Optical access to the flame is provided by quartz windows on the sides of the burner. An image-intensified Photron Ultima APX I\(^2\) CMOS camera records the radiation of the flame. The camera is able to capture 2048 frames resolving 1024 \(\times\) 1024 pixels at 10 bit. To record images of the stationary flame, the lowest available frame rate of 50 frames/s and the lowest recommended image intensifier gain are used. To further minimize the random noise, 204 frames are captured sequentially and averaged in a post-processing routine. The camera is equipped with a Nikkor 105-mm F/4.5 UV lens. The aperture value of the lens is set to a very small value of F/22 so that the detection system can be approximated as a pinhole camera. This is important to ensure that each pixel can be attributed to a single ray through the flame and that a (modified) inverse Abel transform can be applied. Two optical filters can be mounted in front of the UV lens: to record only the radiation of the OH spectrum, an Andover Corporation 307FS10-50 band-pass optical filter with a central wavelength of 308.501 nm and a FWHM of 10.646 nm is used. To distinguish the broad-band blue radiation from possible side effects, its radiation is filtered by an Andover Corporation 020FC34-50/4560 band-pass optical filter with a central wavelength of 456.27 nm and a FWHM of 2.370 nm. The detection setup is placed 500 mm away from the flame center, which results in a resolution of 30 px/mm.

To attest the right choice of filters, the spectrum of the flame is additionally recorded. An Acton Research Cooperation SpectraPro 275 Czerny–Turner-type diffraction spectrograph with a focal length of 275 mm is used. It is placed between the camera and the UV lens (without the above filters). The spectrograph is mounted such that the \(10\,\upmu \hbox {m}\) wide entrance slit is horizontal. The lens focuses an approximately 0.5-mm-thick horizontal slice of the flame 5 mm above the fuel lance onto the entrance slit of the spectrograph. The quantum efficiency of the entire setup is calibrated using a tungsten lamp with a known spectral irradiation. The spectral resolution is checked against mercury line measurements. A grating showing 150 grooves/mm with a blaze wavelength of 500 nm is used, resulting in a resolution of approximately 3 nm. The spectrum is shown for four pressure levels in Fig. 2. The \(\Delta v = 1\) band around 285 nm, the \(\Delta v = 0\) band around 310 nm, and the \(\Delta v = -1\) band around 340 nm of the OH radical are dominating the UV range. The continuous blue radiation is much weaker, but clearly visible for higher pressure levels. Its influence is noticeable starting at 340 nm, it is partially masked by the high-wavelength region of the OH bands around 340 nm, and it extends beyond the end of the spectrum displayed in Fig. 2. By evaluating the spectrum around 308.501 and 456.27 nm, it can be verified that the \({\hbox {OH}^*}\) and blue filters only record \({\hbox {OH}^*}\) and blue radiation, respectively. Due to the very high intensity of both \({\hbox {OH}^*}\) and blue radiation, a possible impact of IR radiation transmitted through the filter can be ruled out.

Fig. 2
figure 2

Radiance spectrum of the flame 5 mm above the burner lance

Full size image

During operation, a steady flame is observed up to approximately 33 bar for the described configuration and mass flow rates. For higher pressures, the flame becomes unstable due to buoyancy effects.

2.2 Jet flame simulation

To provide detailed insight into the flame structure, the experimentally studied flame is computed using a computational fluid dynamics (CFD) simulation. The commercial program Ansys Fluent 14.0 (ans 2011) is found to be the best choice to simulate this setup because it supports multi-component diffusion.

As the experimental setup shows rotational symmetry, it is sufficient to simulate the radial profile of the flame in 2D. The entire flow field inside the 463-mm-long quartz tube is modeled (see Fig. 1). The quartz tube itself as well as the quartz fuel lance is included in the simulation as solid regions and coupled to the flow using the conjugate heat flux model. The boundary condition for the outer glass tube is set as a convection cooling boundary condition.

For the oxygen inlet, a fully developed Hagen–Poiseuille velocity profile is assumed. The 182-mm-long hydrogen duct is too short to show a fully developed laminar velocity profile. Therefore, the entire annular duct is included in the simulation. A block velocity profile is assumed at the exit plane of the metal foam. The temperatures of both hydrogen and oxygen are set according to values measured in the experiment. The top end of the domain is modeled as a pressure outlet.

The domain is meshed with 17,792 nodes, corresponding to a grid size of approximately 0.5 mm per rectangular cell. The grid is the result of refining an originally 4\(\times\) coarser grid. Further refinements by factors of 4\(\times\) and 16\(\times\) do not lead to significant deviations from the coarsest solution (Fiala 2015).

Due to the stationary behavior of the flame and the low flow velocities, Fluent’s steady state pressure-based incompressible solver is used. No turbulence model is applied since laminar flow is considered. Gravity is included as a volumetric force. Since very high temperature levels are present in hydrogen–oxygen combustion, the thermal infrared radiation cannot be neglected. Fluent’s discrete transfer radiation model (DTRM) is used to take radiative heat losses into account (this is different from the modeling of \({\hbox {OH}^*}\) and blue radiation, which is described below). This model is applicable to the range of optical densities in the infrared varying with pressure. It assumes gray radiation. The infrared absorption coefficients are computed by the weighted sum of gray gases model (WSGGM) considering the molecules \(\hbox {H}_{2}\)O and \(\hbox {CO}_{2}\). As the blue and \({\hbox {OH}^*}\) radiation only account for a small percentage of the overall radiative heat flux, their effect on the overall flow field is ignored (Daguse et al. 1996).

The chemical reactions are modeled using the detailed mechanism of Ó Conaire et al. (2004). The original mechanism contains ten species (H, \(\hbox {H}_{2}\), O, \(\hbox {O}_{2}\), OH, \(\hbox {H}_{2}\)O, \(\hbox {H}_{2}\hbox {O}_{2}\), \(\hbox {HO}_{2}\), \(\hbox {N}_{2}\), and Ar) and 19 reactions. It had to be extended to include \(\hbox {CO}_{2}\) as a non-reacting species, which is required by Fluent for the weighted sum of gray gases model to work, although this does not have an impact on the simulation result.

Additionally, the summed-up electronically excited \(A^2\varSigma ^+\) state of OH is included as a separate species \({\hbox {OH}^*}\). If the flame is considered to be optically thin, the volumetric emissivity of the \({\hbox {OH}^*}\) radiation is proportional to the concentration of the separate species \({\hbox {OH}^*}\). By taking thermodynamic data for \({\hbox {OH}^*}\) from Burcat and Ruscic (2005) thermalized excitation is inherently provided. The reaction rates for the chemical excitation and quenching of \({\hbox {OH}^*}\) are taken from Kathrotia et al. (2010). The transport data for \({\hbox {OH}^*}\) are assumed to be identical as for ground-state OHFootnote 2. Since \({\hbox {OH}^*}\) is present in only very small amounts and \(\hbox {CO}_{2}\) does not occur at all, the underlying reaction mechanism is not found to be influenced by these modifications.

To compare the simulation \({\hbox {OH}^*}\) radiance to the experiment, the line-of-sight-integrated \({\hbox {OH}^*}\) radiation is computed using a modified forward Abel transform (Fiala et al. 2014; Fiala 2015). This is applicable as long as the gas is optically thin. However, particularly at elevated pressures, this assumption is not justified. To account for self-absorption, the \({\hbox {OH}^*}\) radiation is simulated in a second way by a spectral modeling approach (Fiala 2015): the emissivities and absorptivities of each spectral line within the investigated spectral range are obtained from an object-oriented implementation of the HITRAN 2012 database (Rothman et al. 2009). The code has been verified against HITRAN’s own implementation, the LIFBASE data base (Luque and Crosley 1999), and TDLAS measurements (Fiala 2015). By evaluating the radiative transfer equation along the lines of sight attributed to each camera pixel and afterward convoluting the spectral data with the transmission of the optical filter, the radiation as recorded by the camera can be simulated.

The blue radiation is assumed to originate from \({\hbox {H}_{2}\hbox {O}_{2}^{*}}\) produced by Reaction (1). If its formation is the rate-determining step, then the concentration of \({\hbox {H}_{2}\hbox {O}_{2}^{*}}\) is proportional to the rate of production. Neglecting temperature and pressure influences, the rate is dominated by the concentration of the reactants. Thus, the blue radiation is modeled to be directly proportional to the square of the OH concentration. Although not physically proven, this approach yields good results (Fiala 2015; Vanpee and Mainiero 1979).

The local volumetric heat release rate is computed natively by Fluent.

2.3 Counterflow flame setup

A schematic view of the considered counterflow flame configuration is shown in Fig. 3. Two axis-symmetric jets of fuel and oxidizer impinge each other from opposed nozzles, thus creating an axis-symmetric flow field which can be described by the axial coordinate z and the radial coordinate r. Only the axial coordinate z has to be resolved to specify the flame (Kee et al. 2003). In theory, counterflow flames are fully characterized by the operating pressure p and a strain rate a, for a given set of fuel and oxidizer compositions and temperatures.

Fig. 3
figure 3

Schematic view of the counterflow flame configuration

Full size image

The Cantera software package (version 2.2b) is used to compute the counterflow flames (Goodwin et al. 2014), which solves the well-known governing partial differential equations described by Kee et al. (2003). In practice, each counterflow flame simulation is defined by setting the boundary conditions, the grid size, the operating pressure, and a chemical reaction mechanism. For this paper, the base reaction mechanism of Ó Conaire et al. (2004) extended by the \({\hbox {OH}^*}\) chemiluminescence addition by Kathrotia et al. (2010) is used. Pure hydrogen and pure oxygen 300 K are set at the fuel and oxidizer inlets. The mass flow rates and the grid size are varied to span up a range of strain rates following the efficient routines introduced by Fiala and Sattelmayer (2014).

In the literature, several variants exist to define the strain rate in non-premixed counterflow flames. However, all of them are approximately proportional to each other (Fiala 2015). In this paper, only the qualitative change of the strain rate is of interest. The choice of the strain rate definition does not influence the results. The maximum axial velocity gradient is used to characterize the strain rate (Fiala 2015; Fiala and Sattelmayer 2014; Turns 2000). It is computed from the simulation results.

For each pressure and strain rate, the profile of the heat release rates and both types of radiation are calculated as a function of the axial coordinate z. The heat release rate is computed from the heat of reaction of each reaction. As will be justified later on, the assumption of negligible optical density is required for a meaningful quantitative correlation between the line-of-sight-integrated radiation and heat release rate. Therefore, the \({\hbox {OH}^*}\) radiation can be assumed proportional to the concentration of the \({\hbox {OH}^*}\) species. The \({\hbox {OH}^*}\) spectral radiation model is not performed for the analysis of counterflow flames. Similar to the jet flame simulation, the blue radiation is assumed to be proportional to the square of the concentration of ground-state OH.

3 Radiation and heat release in laminar flames

In the following, the heat release rate is compared to both types of radiation. Featuring all essential physical effects, the results for laminar flames are described first.

3.1 Overall radiation of the jet flame

By summing up the counts of each camera pixel, the overall radiation of the laminar jet flame experiment is measured as a function of pressure. It is plotted for both \({\hbox {OH}^*}\) and blue radiation in Fig. 4. At low pressures, \({\hbox {OH}^*}\) and blue radiation increase approximately linearly and quadratic with pressure, respectively. This is due to the fact that the overall flame shape is similar and the \({\hbox {OH}^*}\) and blue radiation are mainly dependent on [OH] and [OH]2, respectively. Between 10 and 30 bar, the flame straining due to buoyancy leads to smaller radiating volumes and therefore stagnating radiation. Above 32 bar, the flame is essentially flat, and flame straining becomes less important. The blue radiation then resumes to increase. The \({\hbox {OH}^*}\) radiation, on the other hand, additionally suffers from a reduction in temperature due to radiative heat losses and from self-absorption and, therefore, is further reduced.

Fig. 4
figure 4

Total \({\hbox {OH}^*}\) and blue radiation of the jet flame experiment and simulation. a \({\hbox {OH}^*}\). b Blue radiation

Full size image

In the experiment, the oxygen mass flow rate is kept constant for all pressure levels. Due to the large excess of hydrogen, the oxygen is assumed to be completely consumed. Since the overall heat release rate is directly proportional to the consumption of oxygen, it is considered to be constant as well.

If a direct proportionality between heat release rate and radiation existed, then the radiation should be insensitive to pressure. Figure 4 shows that this is clearly not the case: between 1 and 40 bar, the \({\hbox {OH}^*}\) radiation increases by a factor of approximately 80 and the blue radiation by a factor of approximately 1000. Therefore, it can be concluded that there is no general proportionality between the heat release rate and either \({\hbox {OH}^*}\) or blue radiation on the integral level.

To validate the numerical modeling of radiation, the simulated data are added to Fig. 4. Generally, a very good agreement of the spectral radiation model ([\({\hbox {OH}^*}\)] SM) for \({\hbox {OH}^*}\) and the blue radiation model ([OH]2) can be testified. The \({\hbox {OH}^*}\) radiation modeled by the detailed chemistry \({\hbox {OH}^*}\) species ([\({\hbox {OH}^*}\)] DC) significantly over-predicts the increase of radiation with pressure. This is due to the neglecting of self-absorption of \({\hbox {OH}^*}\) radiation by this model.

3.2 Spatial profiles within the jet flame

Figure 5 shows the radially deconvoluted experimental and numerical profiles of the \({\hbox {OH}^*}\) and blue radiation. In addition, the numerically computed heat release rate is shown. The contour plots can be directly compared. Here, the spatial profiles are evaluated at 1 bar. With increasing pressure, the flame reduces in size due to buoyancy straining. However, the comparison between radiation and heat release rate is similar for all pressure levels (Fiala 2015).

Fig. 5
figure 5

Comparison between the local (filtered) \({\hbox {OH}^*}\) emissivity of the jet flame with the local heat release rate at 1 bar. a Measured \({\hbox {OH}^*}\) radiance, inverse Abel transformed. b \([{\hbox {OH}]^*}\) from simulation. c Measured blue radiance, inverse Abel transformed. d [OH]2 from simulation. e Volumetric heat release rate

Full size image

It is observed that radiation and heat release rate have significantly different spatial distributions. The \({\hbox {OH}^*}\) and blue radiation show the typical crescent shape of an under-ventilated flame, with little intensity at the flame base and most radiation at the tip of the flame. The heat release rate, on the other hand, peaks directly at the anchoring point at the lance rim. Here, the heat of reaction is mostly transferred to the lance. From there on, two regions of heat release emerge: one at the inner (oxygen) side and one at the outer (hydrogen) side. On a volumetric basis, the oxygen branch appears to be more intense. However, the hydrogen branch shows a larger radius and, in total, accounts for approximately the same amount. In between the two branches, the heat release drops almost to zero. This shape is very reasonable, as will be discussed in the next section. It is also in agreement with observations from other diffusion jet flames in the literature (Grcar et al. 2003; Sullivan et al. 2002).

Spatially, there is obviously no qualitative correlation between the local volumetric heat release rate and either the local \({\hbox {OH}^*}\) or blue radiation for the laminar jet flame.

3.3 Counterflow flame profiles

A better understanding of the spatial distributions of heat release and radiation observed above can be gained from counterflow flame simulations. Their one-dimensional data allow for more detailed and quantitative analysis of the processes happening within a non-premixed flame.

Figure 6 shows the key structural aspects of a typical hydrogen–oxygen diffusion flame. Since pure hydrogen is used as fuel and pure oxygen as oxidizer, their mole fractions \(X_{\mathrm{H_2}}\) and \(X_{\mathrm{O_2}}\) are unity at their corresponding boundaries. Within the flame, their mole fractions overlap due to diffusion. The products of combustion, mostly \(\hbox {H}_{2}\hbox {O}\) and OH, are present in the center of the flame.

Fig. 6
figure 6

Structure of a counterflow flame at p = 1 bar and \(a_{\mathrm{max}} = 5.8\times 10^{2}\,1/\hbox {s}\)

Full size image

The total heat release rate resulting from the chemical reactions is also shown in Fig. 6. It exhibits a complex structure with two dominating peaks. To understand the origin of this structure, it is split into the most important reactions in Fig. 7, similar to the analysis presented by Law (2006). The peak on the hydrogen side is mostly due to the reaction \(\hbox {H}+\hbox {OH}+ \hbox {M} \longrightarrow \hbox {H}_{2}\hbox {O}+ \hbox {M}\), whereas the peak on the oxygen side is caused by the combination of the same reaction, the reaction \(\hbox {H}+ \hbox {O}_{2} (+\hbox {M})\longrightarrow \hbox {HO}_{2} (+\hbox {M})\), and the reaction \(\hbox {HO}_{2}+ \hbox {OH} \longrightarrow \hbox {H}_{2}\hbox {O}+ \hbox {O}_{2}\). These reactions reasonably dominate the heat release rate, because they are the chain-terminating reactions (indirectly) forming water vapor. In between the two peaks, there is less formation of \(\hbox {H}_{2}\hbox {O}\). Instead, the endothermic reaction \(\hbox {H}+ \hbox {O}_{2}\longrightarrow \hbox {O} + \hbox {OH}\) forming OH actually removes heat from the flow.

Fig. 7
figure 7

Contribution of the most important reactions to the total heat release within a counterflow flame. Data at p = 1 bar and \(a_{\mathrm{max}} = 5.8\times 10^{2}\,1/\hbox {s}\)

Full size image

The double-peak structure can also be explained in an intuitive way: the effect of heat release is the increase in temperature. In non-premixed flames, the two streams of oxidizer and fuel are each heated up before they reach the stagnation plane. It is natural that heat release coincides with the gradients in temperature. The endothermic reactions sustaining the flame are most effective in the regions of the highest temperature, thus reducing the amount of heat release in this zone.

This behavior is so clearly visible because of the high diffusivity of (atomic and molecular) hydrogen and the absence of dilution like nitrogen. It is insensitive to pressure, but slightly influenced by strain: with an increasing strain rate, the flame thickness is reduced and the diffusion velocities cannot keep up with the free stream velocities. The two zones of heat release move closer together and partially overlap, but still show the characteristic structure.

The spatial emissivities of the \({\hbox {OH}^*}\) and blue radiation are also shown in Fig. 6. Their normalized (filtered) emissivities are assumed to be proportional to the simulated concentration of \({\hbox {OH}^*}\) for the \({\hbox {OH}^*}\) radiation and the square of the OH concentration for the blue radiation. Both profiles show a single, sharp peak in the center of the flame at approximately equal locations.

The emissivity of \({\hbox {OH}^*}\) can be best explained from analytical considerations: if thermal excitation is assumed, then the \({\hbox {OH}^*}\) concentration is directly proportional to the concentration of OH and exponentially depending on temperature (Fiala and Sattelmayer 2013b):

$$\begin{aligned}{}[\hbox {OH}^{*}] \sim [\hbox {OH}] \cdot \exp \left( - \frac{\Delta g^\ominus _m}{R_m ~ T} \right) \end{aligned}$$
(2)

As explained in the previous paragraphs, OH is formed from an endothermic reaction which is most prominent in the hottest region of the flame. Its profile is centered around this zone. The exponential temperature influence leads to an even narrower peak of \({\hbox {OH}^*}\) compared to OH, with a maximum at the highest temperature.

Similarly, taking the square of the OH concentration to model the blue radiation results in a profile that is based on the shape of the ground-state OH distribution, but sharper.

Both the \({\hbox {OH}^*}\) and the blue radiation have a shape which is significantly different to the heat release rate. The reasons are the different underlying physical mechanisms leading to radiation or heat release. A correlation between the two values within laminar non-premixed flames is therefore not given. Comparing the results to the observations from the jet flame experiment, the numerical findings are confirmed and the reasons for the difference between radiation and heat release are explained.

4 Radiation and heat release in turbulent flames

As shown in the previous section, the flame radiation is not a good marker for the heat release within laminar non-premixed flames. However, almost all problems with combustion instability arise in turbulent flames. Practically, a correlation between the line-of-sight-integrated radiation and the corresponding heat release rate is of greater interest than a spatial correlation within the laminar structure.

This section attempts to transfer the findings from the investigation of laminar flames onto turbulent flames. The approach is reasonable, as the turbulent flame is often imagined as an ensemble of laminar counterflow flames, then referred to as flamelets (Peters 1984). Therefore, the underlying physical processes leading to radiation and heat release learned from laminar flames still apply. However, if a turbulent flame is considered, the relation between heat release rate and radiation has to be evaluated for stochastic distributions of flamelet ensembles. The effects of turbulence are modeled by the straining of the individual flamelets forming the flamelet ensembles.

In practical turbulent flames in rocket engines, the pressure is high and flamelets experience high strain. The thickness of flamelets scales inversely with the square root of pressure and strain (Fiala and Sattelmayer 2014; Law 2006; Poinsot and Veynante 2005; Peters 2004):

$$\begin{aligned} \delta \sim \frac{1}{\sqrt{p ~ a}} \end{aligned}$$
(3)

Effectively, the thicknesses of the flamelets are therefore well below 1 mm. Typical measurement equipment for large-scale rocket engines provides a resolution of this order. The detailed structure of the underlying flamelets cannot be resolved.

Fig. 8
figure 8

Illustration of the assumed flamelet ensemble

Full size image

Additionally, radiation measurements are typically line-of-sight-integrated measurements. Therefore, the exact spatial flame structure is not of interest. Instead, the radiation measured along the ray entering the detector is compared to the heat release rate of the measurement volume (see Fig. 8). From this integral point of view, three general cases are possible from basic consideration:

  1. 1.

    The measurement volume contains only unburnt reactants: in this case, there is no OH present and neither \({\hbox {OH}^*}\) nor blue radiation can take place. Similarly, as no reaction can take place, the heat release rate is zero.

  2. 2.

    Several flamelets are within the measurement volume: Both luminous and heat release zones are contained and their integral absolute values are positive.

  3. 3.

    The measurement volume consists of fully burnt products: The reaction is completed, and no heat release takes place. However, radiation can still occur if OH is present and the temperature is high enough (see also Burrows and Razner (1964)). Nevertheless, if the equivalence ratio is not stoichiometric, the mixing of the combustion products with the species in excess results in lower temperature and substantially less OH compared to the flame zone. The emissivity of \({\hbox {OH}^*}\) and blue radiation would, therefore, be significantly lower compared to case 2.

Qualitatively, both \({\hbox {OH}^*}\) and blue radiation are markers for the line-of-sight-integrated heat release rate, if the combustor is operated at globally non-stoichiometric conditions.

The question remains whether a quantitative relation exists. The experience from premixed hydrocarbon flames indicates that there might exist a correlation: As reviewed in the introduction, turbulent ensembles of flamelets can have equal property distributions, such that the integral flame radiation is proportional to the integral heat release rate. Additionally, Lauer et al. (2011) introduced an approach for premixed flames, which provides a correction parameter to account for unequal strain rate distributions. To investigate non-premixed flames, the application of this technique is analyzed in the following.

Nevertheless, one limitation on the quantitative relation is evident: if self-absorption is significant, this affects only the line-of-sight-integrated radiation. A direct proportionality between absolute radiation and absolute heat release rate is thus impossible. Within this section, self-absorption is ignored to derive quantitative results.

4.1 Flamelet-integrated correlation of single flamelets

If the line of sight is broken down into separate flamelets, and each flamelet is assumed to be cut normal to the flame surface, then the quantities of interest are the flamelet-integrated values. They are obtained by an integration along the axial flame coordinate z:

$$\begin{aligned} A_f = \int \limits _{-\infty }^{\infty } A(z) ~ \mathrm{d}z \end{aligned}$$
(4)

In the following, this operation is denoted by the subscript \(_f.\) This operation is applicable to any volumetric quantity A. For a single flamelet, the flamelet-integrated value \(A_f\) thus represents a quantity with respect to the flame surface area.

For combustion of constant reactant composition at constant initial temperatures, the only two parameters influencing the structure of flamelets are pressure p and strain rate a. To investigate both influences, batches of counterflow flame simulations at varying pressures and strain rates are computed. The flamelet-integrated heat release rate \(\dot{q}_f\), the flamelet-integrated \({\hbox {OH}^*}\) emissivity \([\hbox {OH}^{*}]_f\), and the flamelet-integrated blue emissivity \([\hbox {OH}]_{f}^{2}\) are plotted as a function of pressure and strain rate in Fig. 9.

Fig. 9
figure 9

Flamelet-integrated heat release rate (a), OH\(^*\) radiation (b), and blue radiation (represented by [OH]2) (c) as a function of maximum strain rate \(a_{\mathrm{max}}\) and pressure p

Full size image

These quantities are shown appropriately scaled by the empirically learned relations:

$$\begin{aligned}&\dot{q}_f \sim a^{1/2} ~ p^{1/2} \end{aligned}$$
(5)
$$\begin{aligned}&[\hbox {OH}^{*}]_f \sim a^{-1/2} ~ p^{1} \end{aligned}$$
(6)
$$\begin{aligned}&[\hbox {OH}]_{f}^{2} \sim a^{-1/2} ~ p^{3/2} \end{aligned}$$
(7)

The relations especially hold for flamelets far from extinction. With increasing pressure, the extinction strain rate greatly increases, and the relations are valid for a larger strain rate range.

Pressure and strain rate thus have a significant impact on the flamelet-integrated heat release rate and radiation. More importantly, the impact is not identical: while the flamelet-integrated heat release rate increases with the square root of strain rate, both flamelet-integrated radiation decrease with the square root of strain rate. This contradicts the hypothesis of direct proportionality between flamelet-integrated heat release rate and radiation: if two arbitrary flamelets with not-equal strain rates are considered, the flamelet with the higher strain rate will have a higher heat release rate but a lower radiation compared to the flamelet with the lower strain rate. A general direct proportionality between heat release rate and radiation of single flamelets is therefore not possible. This already holds at constant pressure. If the flamelets to be compared show unequal pressure levels, the discrepancy for the relation between heat release rate and radiation is even larger following the above equations.

4.1.1 Justification of Equations (5–7)

Equations (5–7) show a very simple form. Indeed, they can also be derived analytically: if all fuel is assumed to be consumed by the flame, then the heat release rate per flame surface area should be proportional to the fuel mass flux. The fuel mass flux is proportional to the inflow velocity multiplied by the density at the beginning of the flame. The difference in the velocities between the inlet, divided by the flame thickness, defines the mean axial strain rate. As the velocity ratio between fuel and oxidizer is constant, the velocity at the beginning of the flame is directly proportional to the strain rate multiplied by the flame thickness. Using Eq. (3), and substituting these relations into each other, Eq. (5) can be derived (Fiala and Sattelmayer 2013a, 2014):

$$\begin{aligned} \dot{q}_f \sim \mathring{m}_f = \rho _f \cdot u_f \sim p \cdot a \cdot \delta \sim p \cdot a \cdot \frac{1}{\sqrt{a ~ p}} \sim \sqrt{a ~ p} \end{aligned}$$
(8)

This relation is in agreement with previous results from counterflow flame simulations in the literature (Ribert et al. 2008; Pons et al. 2007).

The scaling of the flamelet-integrated emissivities can be explained by evaluating the integration (4) itself. This is first presented for the blue radiation. The shape of the blue radiation is similar at all pressures and strain rates (Fiala 2015). The area under the curve, which corresponds to the integral, is under this condition proportional to the product of the peak-squared OH concentration \([\hbox {OH}]^2_{\mathrm{peak}}\) and the width of the profile, which, in turn, is proportional to the flame thickness \(\delta\). Applying the equation of state for ideal gases, the peak OH concentration can be substituted by an expression consisting of the pressure p, the mixture-averaged gas constant R, the temperature T, and the peak mole fraction of OH \(X_{\mathrm{OH}, \text {peak}}\). Among these, only the pressure changes significantly, while the others are approximately constant. If all of these relations are substituted into each other and only the similarity is considered, Eq. (7) can be derived:

$$\begin{aligned}{}[\hbox {OH}]^2_f&= {} \int _{-\infty }^{\infty } \left( [\hbox {OH}](z) \right) ^2 ~ \mathrm{d}z\sim [\hbox {OH}]^2_{\mathrm{peak}} \cdot \delta \nonumber \\&= {} \left( \frac{p}{R ~ T} X_{\mathrm{OH}, \text {peak}} \right) ^ 2 \cdot \delta \nonumber \\&\sim p^2 \cdot \frac{1}{\sqrt{a ~ p}} \sim p^{3/2} ~ a^{-1/2} \end{aligned}$$
(9)

Similarly, the flamelet-integrated \({\hbox {OH}^*}\) emissivity can be derived. In addition to the above steps, Eq. (2) is employed to compute the \({\hbox {OH}^*}\) concentration from the OH concentration and the temperature. Due to the exponential dependency on the temperature, the change in temperature can no longer be neglected. While the strain rate does not influence the peak temperature far from extinction, an increase in pressure leads to a significant rise. The overall impact of the exponential term can be studied from a zero-dimensional analysis in Cantera: using Cantera’s equilibrate method, the adiabatic temperature \(T_{\mathrm{ad}}\) of stoichiometric hydrogen–oxygen mixtures can be computed as a function of pressure. If the maximum temperature \(T_{\mathrm{max}}\) is assumed to be about the adiabatic flame temperature \(T_{\mathrm{ad}}\), the exponential term in Eq. (2) can be evaluated. It is found that it scales approximately with:

$$\begin{aligned}&\frac{[\hbox {OH}]^*}{[\hbox {OH}]} \sim \exp \left( - \frac{h ~ c}{k_\mathrm{B} ~ \lambda ~ T_{\mathrm{max}}} \right) \nonumber \\&\quad\quad \sim \exp \left( - \frac{h ~ c}{k_\mathrm{B} ~ \lambda ~ T_{\mathrm{ad}}} \right) \sim p^{0.5} \end{aligned}$$
(10)

Using this information, Eq. (6) is obtained:

$$\begin{aligned}{}[\hbox {OH}]^{*}_f&= {} \int _{-\infty }^{\infty } [\hbox {OH}^{*}](z) ~ \mathrm{d}z \sim [\hbox {OH}^{*}]_{\mathrm{peak}} \cdot \delta \nonumber \\&= {} \frac{p}{R ~ T} X_{\mathrm{OH}^*, \text {peak}} \cdot \delta \nonumber \\&= {} \frac{p}{R ~ T} X_{\mathrm{OH}, \text {peak}} \cdot \exp \left( - \frac{h ~ c}{k_\mathrm{B} ~ \lambda ~ T_{\mathrm{max}}} \right) \cdot \delta \nonumber \\&\sim p \cdot p^{0.5} \cdot \frac{1}{\sqrt{a ~ p}} \sim p^{1} ~ a^{-1/2} \end{aligned}$$
(11)

4.2 Flamelet-integrated correlation of flamelet ensembles

After describing the influence of strain rate and pressure on individual flamelets, the subsequent question is whether the integral heat release rate and radiation are correlated for an ensemble of flamelets forming a turbulent flame. Typically, the absolute pressure is approximately constant throughout the ensemble. However, the strain rate of each flamelet along the line of sight varies significantly. From the results presented above for individual flamelets, it is evident that a general direct proportionality between heat release rate and radiation is not given for arbitrary turbulent flames.

Lauer et al. (2011) faced a comparable influence of straining on heat release rate and \({\hbox {OH}^*}\) radiation in premixed counterflow flamelets. Similarly, a general direct proportionality was attested to be false. However, they were able to develop a model-based correction technique to still be able to obtain the heat release rate experimentally from \({\hbox {OH}^*}\) measurements. In this study, the strategy is followed accordingly.

Moreover, the simple dependencies of heat release rate and radiation from strain rate and pressure derived in Sect. 4.1 greatly simplify the procedure. A single line of sight is considered (see Fig. 8), along which the integrated radiance \(L_{\mathrm{LoS}}\) is measured. The task is to obtain the heat release rate \(\dot{q}_{\mathrm{LoS}}\) corresponding to the interrogation volume. Within this volume, an ensemble of several flamelets forms the turbulent flame. According to Yeung et al. (1990), the strain rate in flames is approximately normally distributed around a mean value \(\bar{a}\) for a sufficiently large number of flamelets. If the number of flamelets within the volume is assumed to be N, the overall heat release rate \(\dot{q}_{\mathrm{LoS}}\) is the sum of the flamelet-integrated heat release rates \(\dot{q}_{f,i}\) of all flamelets contained. Using Eq. (5), \(\dot{q}_{f,i}\) can be expressed to be proportional to \(a_i^{1/2}~p_i^{1/2}\). Normally, the pressure p can be assumed to be constant throughout the turbulent flame. By applying the law of large numbers, the sum can be replaced by the number of flamelets multiplied by the expected value of the summands:

$$\begin{aligned} \dot{q}_{\mathrm{LoS}} = \sum \limits _{i=1}^N \dot{q}_{f,i} \sim \sum \limits _{i=1}^N a_i^{1/2}~p_i^{1/2} \approx N \cdot \bar{a}^{1/2} \cdot p^{1/2} \end{aligned}$$
(12)

Correspondingly, this derivation can be performed for the radiances of \({\hbox {OH}^*}\) and the blue radiation, which are again assumed to be proportional to the \({\hbox {OH}^*}\) concentration and the square of the OH concentration, respectively:

$$\begin{aligned}&L_{[\mathrm{OH}^{*}],{\mathrm{LoS}}} \sim [{\hbox {OH}^{*}]}_{\mathrm{LoS}} = \sum \limits _{i=1}^N {[\hbox {OH}^{*}]}_{f,i} \sim \sum \limits _{i=1}^N a_i^{-1/2}~p_i^{1}\nonumber \\&\quad\quad\quad\quad\quad\quad\quad\quad\quad \approx N \cdot \bar{a}^{-1/2} \cdot p^{1} \end{aligned}$$
(13)
$$\begin{aligned}&L_{\mathrm{[OH]}^{2},\text {LoS}} \sim {[\hbox {OH}]}^2_{\mathrm{LoS}} = \sum \limits _{i=1}^N {[\hbox {OH}]}^2_{f,i} \sim \sum \limits _{i=1}^N a_i^{-1/2}~p_i^{3/2}\nonumber \\&\quad \approx N \cdot \bar{a}^{-1/2} \cdot p^{3/2} \end{aligned}$$
(14)

Generally, the number of flamelets N is not known. However, by solving Eqs. (13) and (14) for N and substituting the results in Eq. (12), two expressions for the line-of-sight heat release rate can be derived:

$$\begin{aligned}&\dot{q}_{\mathrm{LoS}} \sim \bar{a} ~ p^{-1/2} ~ L_{[{\mathrm{OH}}^{*}],{\mathrm{LoS}}} = c_{f, {[{\mathrm{OH}}^{*}]}} ~ L_{[\mathrm{{OH}}^{*}],{\mathrm{LoS}}} \end{aligned}$$
(15)
$$\begin{aligned}&\dot{q}_{\mathrm{LoS}} \sim \bar{a} ~ p^{-1} ~ L_{\mathrm{{[{OH}]}}^{2},{\mathrm{LoS}}} = c_{f, {[{\mathrm{OH}}]}^2} ~ L_{{\mathrm{[OH]}}^{2},\text {LoS}} \end{aligned}$$
(16)

These equations represent a formulation to determine the heat release rate from \({\hbox {OH}^*}\) and blue radiation measurements. The proportionality constants \(c_{f, {[{\mathrm{OH}}^{*}}]}\) and \(c_{f, [{\mathrm{OH}}^{2}]}\) correspond to the non-linear proportionality constant introduced by Lauer et al. (2011). They are also shown as a function of strain rate and pressure in Fig. 10.

Fig. 10
figure 10

Proportionality constants between the flamelet-integrated heat release rate and a the OH\(^*\) radiation or b the blue radiation, as a function of the maximum strain rate \(a_{\mathrm{max}}\) and the pressure p (scaled appropriately)

Full size image

If the strain rate is viewed as an inverse flame thickness, Eqs. (15) and (16) can also be explained intuitively: Flames with a high strain rate are very thin. If radiation is proportional to the flame thickness, there will be little radiation originating from such a flame, even though there is a certain heat release. Inversely, lowly strained flames are very thick and thus radiate considerably even though they are associated with little heat release. Asymptotically, the latter describes the case of the final products of a globally stoichiometric combustion, which are hot and radiate, but do not release further heat.

Thus, the determination of the heat release rate from radiation measurements in turbulent non-premixed flames is possible in principle. However, there is no general proportionality. Instead, the radiances have to be weighted accordingly with the mean strain rate \(\bar{a}\) of the flamelet ensemble and the pressure.

Practically, the scaling with pressure is achievable in experiments with reasonable effort: either it is assumed to be constant, or, in the case of large pressure amplitude combustion instability, it can be obtained from pressure field reconstruction (Gröning et al. 2012; Fiala et al. 2011). Nevertheless, the measurement of the mean strain rate is more demanding: for example, the steady mean strain rate can be determined from PIV experiments by measuring the Kolmogorov time scale (Lauer et al. 2011). However, the application of this technique is hardly feasible in confined combustion chambers, especially if time-resolved measurements are of interest. This imposes a major drawback of using flame radiation as a quantitative marker for the heat release rate.

Additionally, it should be mentioned again that the derivations above are only valid for low optical densities, i.e., negligible self-absorption.

Within the framework of this paper, no direct experimental proof of this method on a turbulent flame was possible. Nevertheless, the results from Lauer et al. (2011) generally support the findings. Furthermore, the radiation data of the laminar burner studied in Sect. 3.1 indirectly validate the theory: As the total heat release rate is kept constant throughout all experiments, the strain rate should decrease inversely with pressure (Eq. 12). Substituted into Eqs. (15) and (16), the total \({\hbox {OH}^*}\) and blue radiation should increase with \(p^{3/2}\) and \(p^{2}\), respectively. Although key effects like the flame straining due to gravity and the self-absorption of \({\hbox {OH}^*}\) radiation is neglected in this simple estimation, the results agree by trend with the data presented in Fig. 4.

5 Conclusions

The comparison of \({\hbox {OH}^*}\) and blue radiation of non-premixed hydrogen–oxygen flames to heat release rate is summarized as follows:

  • Generally, there exists little connection between the heat release rate and both types of radiation in non-premixed flames.

  • Within the laminar flame structure, heat release rate and radiation occur at spatially different locations.

  • The reason for the dissimilarity is the different physical origin of both quantities: radiation originates from the center of the reactive zone, in which both temperature and OH concentration peak. The total amount of flame radiation increases with pressure and is linearly dependent on the flame thickness, which is heavily influenced by flame straining. The heat release, on the other hand, leads to the spatial increase in temperature and is present in a much broader region.

  • In turbulent flames, in which the spatially resolved laminar flame structure is not important, there is still no general quantitative proportionality between the line-of-sight-integrated radiation and the heat release rate because of flame straining.

  • Self-absorption only affects the line-of-sight-integrated radiance but not the line-of-sight-integrated heat release rate. Therefore, a direct correlation fails naturally in optically thick media.

  • In optically thin media, the line-of-sight-integrated heat release rate can be obtained from radiation measurements if it is weighted with the mean strain rate of the flamelets within the probe volume.

The requirement of the additional measurement of the strain rate distribution reduces the advantage of simple radiation measurements for evaluating the heat release rate. In many situations, the measurement of the strain rate distribution is even unfeasible. However, the crude assumption of constant mean strain rate might be justified in certain situations. For example, along a certain line of sight through the flame burning at constant operating conditions, the strain rate distribution might be considered to be constant in time. In this case, the fluctuation of radiation would be proportional to the fluctuation of the heat release rate. On the other hand, two different spatial flame regions are likely to have very different strain rate distributions. For this situation, the assumption of direct proportionality between flame radiation and the heat release rate would lead to false results.

However, it should not be concluded that radiation measurements are useless. In fact, the opposite is the case: Sometimes, qualitative results are already sufficient, like the characterization of the flame zone for the description of the stratified acoustic field in the combustor. Also, if radiation measurements are not compulsively used to represent the heat release rate, its pure interpretation can be useful. Additionally, radiation data can serve for the validation of CFD simulations if these are sufficiently resolved and thus able to directly calculate flame radiation (Fiala 2015). If validated, the CFD simulation can be assumed to provide the accurate heat release rate.