Experimental characterization of the unsteady natural wake of the full-scale square back Ahmed body: flow bi-stability and spectral analysis

Abstract

In recent years, the increasing interest in reducing the aerodynamic drag of vehicles, such as station wagons, minivans or buses, has led research to focus on the characterization of square back bluff geometries. In this paper, the results of an extensive experimental campaign on the full-scale well-known body of Ahmed et al. (1984) are presented, for two height-based Reynolds numbers, $Re_{\rm H} = 5.1 \times 10^5$ and $7.7 \times 10^5$. Eighty-one measurement points were used to map the base pressure field, while the wake topology was investigated by means of a series of ten 2D Particle Image Velocimetry planes. These measurements clearly show that the wake presents a bi-stable behavior, characterized by a random succession of switches between two well-defined mutually symmetric configurations, confirming the results from Grandemange et al. (J Fluid Mech 722:51–84, 2013b. doi:10.1017/jfm.2013.83) for the same model. For the presented results, the timescale of this phenomenon is of the order of $800 \, V_{\infty} / H$. The sensitivity of the bi-stability to the yaw angle was also investigated, and considerations on how to take such a behavior into account in post-processing this kind of field are given. High-frequency measurements were also carried out with four piezoelectric transducers and a synchronized two-component hot-wire. The results show a low-frequency spectral activity: peaks at $St_{\rm H} = 0.13$ and 0.19, corresponding to vortex shedding modes, were found on the lateral base pressures and in the far wake, whereas a signature at $St_{\rm H} = 0.08$ was visible on the vertical base centerline and in the recirculation bubble shear layer. Correlation analysis and proper orthogonal decomposition confirm the interpretation of the latter mode as the pumping of the recirculation bubble.

1 Introduction

Ever since the influence of aerodynamic drag on the overall moving resistance was first pointed out, aerodynamic optimization of the external shape has been an important step when designing a new vehicle. Whether performance or low fuel consumption is required, the most common research topic on ground vehicle aerodynamics is the reduction in the drag coefficient. It is known that this is not a trivial task, since ground vehicles can be considered as bluff bodies, which are characterized by complex three-dimensional flow structures. For this kind of study, the great variability in the shapes of ground vehicles (e.g., notchback or fastback cars, vans, buses, trains) has also to be considered. This variety makes it difficult to provide general guidelines about the best strategies to adopt for reducing aerodynamic drag.

These are the reasons why fundamental research is mostly performed on bluff bodies with elementary shapes, so that only a specific aspect of an actual vehicle can be analyzed. One of the simplified vehicle models is the well-known shape introduced by Ahmed et al. (1984). This body consists of a parallelepiped with the global proportions of a common hatchback car, presenting four rounded edges at the front and a slanted plane at the rear. The goal of the latter is to model the rear window of a hatchback car. The authors found that the drag of this body was highly sensitive to the slant angle of the plane, and they were able to relate it to the different wake topologies. In particular, for slant angles between $0^{\circ }$ and $12.5^{\circ }$, the flow is attached to the slanted plane and separates at the rear, the wake consisting of a recirculation bubble which, qualitatively, is no different from the ones obtained from elementary bluff bodies. When the slanted plane inclination is between $12.5^{\circ }$ and $30^{\circ }$, a considerable drag enhancement is documented, associated with a reattachment on the slant and the formation of two counter-rotating vortices developing from the upper corners. Beyond $30^{\circ }$, the flow is no longer able to reattach on the slanted plane: A wake consisting of a recirculation bubble is formed again, and the drag suddenly decreases to the value of the square back configuration.

With time, the Ahmed body has become a reference for the study of vehicle aerodynamics. Most research has focused on the $25^{\circ }$ or $30^{\circ }$ slanted geometry, mainly for the interest in finely characterizing this complex 3D configuration. For example, the visualizations by Spohn and Gilliéron (2002) and the analysis by Vino et al. (2005) and Wang et al. (2013) gave more insight into the topology of the longitudinal structures and their interaction with the slanted plane separation region. The measurements and proper orthogonal decomposition (POD) analysis by Thacker et al. (2012) also highlighted the spectral properties of the recirculating flow. The natural flow of the $25^{\circ }$ body was numerically simulated with large eddy simulations by Krajnović and Davidson (2005) and by Minguez et al. (2008).

Another reason is that since it presents many sources of drag, the slanted Ahmed body is a good starting point for testing drag control strategies. Drag reductions were registered with passive geometry modifications (Thacker et al. 2012) or with devices such as splitter plates (Gilliéron and Kourta 2010), flaps (Beaudoin and Aider 2008) or deflectors (Fourrié et al. 2011). Active control techniques such as pulsed jets (Joseph et al. 2012) or synthetic jets (Kourta and Leclerc 2013) have also been successfully used.

However, in recent years, more and more studies have been carried out on square back Ahmed bodies, because of the increasing demand for station wagons or mini wagons. The different kind of wake of the square back geometry does not allow the application of most of the control strategies developed for the $25^{\circ }$ configuration.

As far as drag reduction is concerned, the usual approach is to attempt to recover pressure at the base. The motivation for this is that for a square back-like wake, 70 % of the total drag comes from the base pressure distribution, as shown by Ahmed et al. (1984) on their body. Khalighi et al. (2001) showed that substantial drag reductions can be achieved by creating a cavity with four deflectors or with steady blowing jets (Khalighi et al. 2012), as Wassen et al. (2010) also showed numerically.

One interesting finding derives from the work of Grandemange et al. (2013b), who documented and characterized a bi-stable flow behavior on a 1:4 scale model square back Ahmed body. This bi-stability consists in the dynamic switch of the wake topology between two well-defined configurations which are mutually symmetric with respect to the vertical center plane. The succession of these switches is random with a timescale of the order of $1000 \, V_{\infty} / H$ ($V_{\infty}$ being the free-stream velocity and H the height of the model). This means that the well-described symmetric flow configuration typical of this body derives from the averaging of the two asymmetric configurations, requiring a long acquisition time when studying this kind of problem. Complementary studies were carried out by the same authors, who found out that bi-stability can be suppressed by reducing the ground clearance (Grandemange et al. 2013a) or by perturbing the wake with the insertion of horizontal or vertical control cylinders (Grandemange et al. 2014). The bi-stability phenomenon has also been reported for a double-backward-facing step by Herry et al. (2011). Courbois et al. (2014) also showed that under precise wind yaw angle conditions, the evolution of the lift force of an actual minivan can have a bi-stable behavior. The numerical simulation of bi-stability is a difficult task, due to its very long timescale. However, the wake of the square back Ahmed body as calculated by Wassen et al. (2010) presented an unexpected asymmetry in the horizontal plane. The two-state evolution of the side force of the simulation by Östh et al. (2014) might also be related to bi-stability.

The recent findings by Rigas et al. (2014) indicate that the instantaneous pressure field behind their axisymmetric body is actually antisymmetric and randomly rotates. As in the previously cited works, when averaging on long-time runs, the pressure field becomes symmetric. Also, the timescale associated with this phenomenon is about 500 times the characteristic time calculated on free-stream velocity and on the diameter of the body. These properties suggest a multistable behavior of the wake, developing over an infinite number of states.

The wake bi-stability does not seem to interfere with the other periodic modes that can be detected by means of spectral analysis. As far as the periodic modes are concerned, many authors agree with the identification of the low-frequency modes associated with vortex shedding, both from the left-/right-side planes and from the roof and the floor of the vehicle (Grandemange et al. 2013b; Östh et al. 2014; Lahaye et al. 2014). A lower-frequency mode was also found by Khalighi et al. (2001, 2012) for the Ahmed body and by Duell and George (1999) on a bluff body similar to the one from Ahmed, but with a square section. This mode is usually explained as a pumping of the whole recirculation bubble (Berger et al. 1990). Khalighi et al. (2001) associated their 20 % drag reduction with the suppression of this spectral peak.

The work presented in this paper aims at further developing the experimental data base on the study of the square back Ahmed geometry and tries to establish the points of agreement between the previous studies. The final goal of this research is to provide as detailed as possible experimental information on the unsteady phenomena related to the wake of the square back Ahmed body, with a view to the development of optimized flow control strategies.

All the presented results derive from experimental measurements on a full-scale geometry. After the description of the experimental setup in Sect. 2, the dependence of the drag coefficient on the Reynolds number is discussed in Sect. 3. In Sect. 4, the unsteady topology of the wake is discussed, by means of pressure base measurements and PIV in the wake. The bi-stable behavior of the wake is clearly identified and documented. High acquisition frequency pressure and velocity measurements were also carried out, and spectra and correlations are shown in Sect. 5. Then, in Sect. 6, a complementary analysis based on the POD of the pressure signals is presented, before concluding with some final considerations.

2 Experimental setup

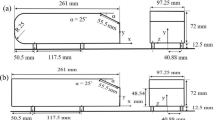
The experimental campaigns took place in the subsonic “Lucien Malavard” closed-loop wind tunnel of the PRISME laboratory at the University of Orléans, France. Its test chamber section is 2 m by 2 m wide, with a free-stream turbulence level lower than 0.4 %. The 1:1 scale Ahmed body (length $L = 1.044\,\hbox {m}$, height $H =0.288\,\hbox {m}$, width $W = 0.389\, \hbox {m}$, ground clearance 50 mm) is placed over a raised floor, as shown in Fig. 1. The same figure also depicts the Cartesian coordinate system used in this paper. The $X$ axis is directed toward the flow direction, whereas the $Z$ axis coincides with the vertical direction. Its origin is placed on the floor, the $X = 0$ point corresponding to the base plane position, with the $Y = 0$ point aligned with its vertical centerline. Two free-stream velocities were chosen, $V_{\infty} = 26.7$ and $40\,\hbox {m}\,\hbox {s}^{-1}$. The corresponding Reynolds numbers, calculated on the Ahmed body height, are $Re_{\rm H} = 5.1 \times 10^5$ and $7.7 \times 10^5$, respectively. Before testing the Ahmed body, the boundary layer profiles over the floor were investigated. Transition occurs before the position of the model nose. Just below the rear base, the boundary layer is fully turbulent, and for 26.7 m s⁻¹, its 99 % boundary layer thickness $\delta _{99} = 24\,\hbox {mm}$, whereas its displacement thickness is $\delta _1 = 3.7\,\hbox {mm}$. These values are smaller than the 50 mm model ground clearance. The raised floor presents, at its end, a trailing edge flap. Its deflection was set up before inserting the Ahmed model so that the pressure distribution around the ground plane is uniform. The aerodynamic forces on the Ahmed body were measured by means of an external strain gauge balance, linked to the model via a plate-beam structure embedded in the floor, and a mast sheltered from the flow with a streamlined fairing. The balance is equipped with a turntable. The yaw angle between the model and the flow was measured with an absolute encoder whose precision is $0.08^{\circ }$.

Fig. 1

Experimental setup

The characterization of the mean wake topology was performed in two steps: A cartography of the pressure field over 81 points placed at the rear of the body was obtained by means of three MicroDAQ$^{\mathrm{TM}}$ pressure scanners, as shown in Fig. 2a; pressure data were sampled at 20 Hz for 900 s. Because of the bi-stability phenomenon typical of this kind of wake (Grandemange et al. 2013b), it is necessary to analyze the pressure histories acquired with this instrumentation. Thus, it is important to determine what their frequency response is. The connecting pressure tubes used were 0.6 m long with a 1.56 mm internal diameter. According to Bergh and Tijdeman (1965), the first resonance frequency of the probe-transducer system is 125 Hz. This frequency is high enough to avoid a distortion effect on the pressure reading: In fact, the spectral analysis carried out with piezoelectric transducers showed that most of the dynamic activity is found at low frequencies (in the worst case, at 26 Hz for $V_{\infty} = 40\, \hbox {m}\, \hbox {s}^{-1}$), see Sect. 5. Also, the bi-stable behavior pressure switches are very rapid, shorter than the sampling period of 0.05 s of the pressure scanners. This means that the energy associated with this phenomenon is at even lower frequencies. Indeed, if a bi-stable switch is modeled with a Heaviside function, its Fourier transform will be:

$$\begin{aligned} {\mathcal {F}} \left\{ H(t) \right\} = \frac{\delta (f)}{2} + \frac{1}{2\pi j f} \end{aligned}$$

(1)

where $\delta (f)$ is the Dirac function and $j$ the imaginary unit. Furthermore, the presence of a phase shift induced by the tubing is not of great concern, since all the tubes were of the same length so that the 81 pressure measurement acquisitions can be assumed to be practically synchronized. It has to be mentioned that this measurement system was not synchronized with the other equipment.

Two-dimensional PIV on a series of orthogonal planes was performed by means of a LaVision$^{\mathrm{TM}}$ system, in order to characterize the mean topology of the wake recirculation bubble, as shown in Fig. 2b. In particular, the five horizontal ($XY$) planes are $612 \times 408\, \hbox {mm}^2$ with a spatial resolution of one vector every 1.22 mm and were acquired for 500 s at 2 Hz, whereas the sizes of the vertical ($XZ$) planes are $558 \times 490\, \hbox {mm}^2$, their resolution is 1.95 mm/vect, and their acquisition time was 400 s at 1 Hz.

Four piezoelectric Kulite$^{\mathrm{TM}}$ transducers were used to capture high-frequency parietal pressure fluctuations near the rear edges, on a total of 16 measurement points, as shown in Fig. 2c. The sampling frequency was 2 kHz for an acquisition time of 525 s.

As far as the velocity is concerned, 2D hot-wire measurements were performed on a series of 87 points, on the wake shear layer and behind the reattachment point of the recirculation bubble, as shown in Fig. 2d. For each point, data were gathered at 20 kHz for 450 s. During these tests, further unsteady pressure measurements were carried out, at the middle of the edges of the base section (in red in Fig. 2c). It was not possible to synchronize these two measurement devices by means of a trigger. However, an electric reference signal was acquired at the same time with the two different instruments. By computing the point of maximum cross-correlation between the two reference acquisitions, it was possible to resynchronize the measurements when post-processing the data, allowing the calculation of the coherence between pressure and velocity.

Fig. 2

Pressure and velocity exploration. Mean field measurements: a positions of the pressure taps and b the ones of the 2D PIV planes; c spectral analysis probed positions with the piezoelectric transducers, and d with the hot-wire probe

3 Ahmed body drag

In this section, the global drag of the Ahmed body is compared to the pressure drag generated at the base of the body. The aerodynamic global drag coefficient, obtained via balance measurements, is defined as follows:

$$\begin{aligned} C_{\rm D} = \frac{D}{0.5 \rho S V_{\infty} ^{2}} \end{aligned}$$

(2)

where $D$ is the measured drag force, $\rho$ is the air density, $S = 0.112\, \hbox {m}^2$ is the projected frontal surface, and $V_{\infty}$ is the free-stream velocity. The contribution of the base pressure drag is calculated by integration of the pressure coefficient field, measured from the rear tappings:

$$\begin{aligned}&\displaystyle C_{\rm p} = \frac{p - p_{\infty} }{0.5 \rho V_{\infty} ^{2}} \nonumber \\&\displaystyle C_{\rm D,base} = - \frac{1}{S} \iint \limits _S C_{\rm p} \cdot \hbox {d}S \end{aligned}$$

(3)

in which $p_{\infty}$ is the reference static pressure, measured in the unperturbed upstream flow.

The Reynolds dependence of the two drag coefficients is presented in Fig. 3. The Reynolds number $Re_{\rm H}$ was calculated on the reference height of the model and free-stream velocity. Free-stream velocity was varied between 15 and 45 m ${\text{s}}^{-1}$, the corresponding Reynolds number being $Re_{\rm H} = 3.67 \times 10^5$ and $8.15 \times 10^5$, respectively. For both coefficients, a slight dependence on the Reynolds number is noticeable.

Specifically, the measured global drag coefficient varies from $C_{\rm D} = 0.329$ for $Re_{\rm H} = 3.67 \times 10^5$ to $C_{\rm D} = 0.315$ at $Re_{\rm H} = 8.15 \times 10^5$. This range of values is higher than the $C_{\rm D} = 0.250$ result from Ahmed et al. (1984). However, also the results of other previous works show global drag coefficients greater than the one from Ahmed et al. (1984). In particular, it is found that the global drag for the square back configuration varies between $C_{\rm D} = 0.274$ by Grandemange et al. (2013b) and $C_{\rm D} = 0.364$ from Eulalie et al. (2014).

The base pressure drag shows a slow increase with Reynolds number. In particular, the $C_{\rm D,base}$ value calculated from the highest Reynolds dataset is greater by 2.7 % than the one obtained at $Re_{\rm H} = 3.67 \times 10^5$. The contribution of $C_{\rm D,base}$ on the global drag varies between 71 and 76 %, which is in agreement with recent researches on this geometry (Grandemange 2013; Eulalie et al. 2014).

The difference between the two coefficients is representative of the amount of drag generated by the front of the vehicle and by the cylindrical stilts, as well as of the friction drag with the other walls of the body.

Fig. 3

Reynolds dependence of the global drag coefficient $C_{\rm D}$ and of the base pressure drag coefficient $C_{\rm D,base}$

4 Unsteady topology characterization

4.1 Bi-stable behavior of the wake

The cartography of the parietal mean pressure field is reported in Fig. 4a, for the lower free-stream velocity. As for the global forces, no significant dependence of the pressure coefficient on the Reynolds number was noticed.

It can be observed that the time-averaged field is quite homogeneous, the spatial averaged pressure coefficient being −0.22. This result is in agreement with the literature on the same body (Khalighi et al. 2001; Grandemange et al. 2013b; Wassen et al. 2010). In fact, a slight horizontal pressure gradient exists: The pressure increases by 10 % close to the vertical edges, when compared to the base center values.

What could appear surprising is the RMS value of the $C_{\rm p}$ field, as shown in Fig. 4b, which is large, when compared to the mean value. At its worst, for the taps situated in ($Y/H = \pm 0.32$, $Z/H = 0.67$), the RMS value is up to 25 % of the steady coefficient value. The only exception is in the vertical centerline of pressure taps ($Y/H = 0$), where the fluctuation level is low, compared to neighboring taps.

These high RMS values result mainly from the bi-stable behavior of the pressure field, which was already observed by Grandemange et al. (2013b) on the same geometry, at a 1/4 scale, and by Herry et al. (2011) on a double-backward-facing step. Further evidence for this is provided in Fig. 5a which reports the temporal evolution of the synchronized measurements of two piezoelectric transducers, located at symmetric points of the lower edge, at $Y/H = \pm 0.32$. At these points, the highest $C_{\rm p}$ RMS values of the piezoelectric transducer data were measured. As can be seen, the pressure coefficient of the two taps continuously switches between two well-defined levels. This is even more evident when the probability density functions (PDFs) computed on the whole acquisition time interval are plotted, as shown in Fig. 5b, since the pressure data distribute as a bimodal statistical function.

The same kind of unsteady pressure behavior was also detected with the pressure scanners, as shown in Fig. 5c. In this figure, the evolution of the pressure coefficient from the two points presenting the highest RMS from Fig. 4b is considered. In Fig. 5d, the PDFs at these points are compared to the one obtained from the evolution of the $C_{\rm p}$ at the base center. It can be seen here that the pressure distributes as a typical gaussian function, indicating that there is no bi-stable behavior. This explains the lower $C_{\rm p}$ RMS value observed at the vertical taps centerline.

The results shown are for a free-stream velocity of $26.7\, \hbox {m}\, \hbox {s}^{-1}$, and it has to be added that the bi-stable behavior was visible for both the free-stream velocities.

The pressure switches randomly occur on long timescales, as detailed in Sect. 4.2. The changes in stable position are synchronous, not only when considering left-to-right symmetric pressure taps, as shown in Fig. 5a, c, but also when measurement points on the same part of the base are considered, as illustrated in Fig. 5e.

Fig. 4

Rear pressure field cartography, $Re_{\rm H} = 5.1 \times 10^5$, the black dots representing the positions of the taps: a canonical time averaging, b RMS value

Fig. 5

Bi-stable behavior of the pressure field. Piezoelectric transducer measurements, $Y/H = \pm$0.32, $Z/H = 0.23$, $Re_{\rm H} = 7.2 \times 10^5$, a excerpt of the $C_{\rm p}$ evolutions and, b related PDFs, pressure scanner measurements, $Y/H = \pm 0.32$ and $Y/H = 0$, $Z/H = 0.67$, $Re_{\rm H} = 5.1 \times 10^5$, c excerpt of the $C_{\rm p}$ evolutions, and d related PDFs, e synchronization of the bi-stability for four different pressure taps

The bi-stability phenomenon was not only detected for pressure cartography measurements, butt was also highlighted in the velocity field measured with PIV, as shown for the points in Fig. 6. The PIV data acquired in the vertical centerplane show no evidence of bi-stable behavior, confirming what was observed for the pressure cartography in Fig. 5d.

Fig. 6

Velocity bi-stability: a–d non-dimensionalized velocities evolutions for four points inside the recirculation bubble, $Re_{\rm H} = 5.2 \times 10^5$, e visualization of points positions

The two distinct stable positions of the pressure field can be visualized by means of a conditional averaging of the unsteady data, provided that it is possible to identify, at a given instant, in which stable configuration the wake is. Since the pressure switches happen at the same instants for all the pressure positions, the phase identification process can be based on the time history of at least one significant measurement point. In the case of the pressure scanners, the taps situated at ($Y/H = {\pm } 0.32,\,Z/H = 0.67$) were chosen (i.e., those considered in Fig. 5c), since the highest values of $C_{\rm p}$ RMS are reported there. The unsteady data of all the pressure taps were sorted into two groups, according to the sign of the function $\Delta C_{\rm p,CA}$:

$$\begin{aligned} \Delta C_{\rm p,CA}&=C_{\rm p} \left( \frac{Y}{H} = 0.32, \frac{Z}{H} = 0.67, t \right) \nonumber \\&\quad- C_{\rm p} \left( \frac{Y}{H} = - 0.32, \frac{Z}{H} = 0.67, t \right) \end{aligned}$$

(4)

This criterion is qualitatively the same as the one used by Grandemange et al. (2013b), in which the conditional averaging of the rear pressure field was based on the calculation of the base pressure gradient in the $Y$ direction.

The conditionally averaged pressure fields of the two separate phases are represented in Fig. 7a, b. It can be seen that strong left-to-right imbalances are visible for each bi-stable field. The pressure field corresponding to the bi-stable configuration for which $\Delta C_{\rm p,CA} > 0,$ shown in Fig. 7a, presents a low-pressure region on the left base side. As can be seen from Fig. 13b, the related velocity field also looks dissymmetric. So, in the following, this position will be identified with the letter “L”. Similarly, when $\Delta C_{\rm p,CA} < 0$, the fields appear to be antisymmetric relative to the centerline vertical axis with the previous one, so the corresponding phase will be named “R”.

Whatever stable position is considered, the lowest pressure deriving from the bi-stability differs by 27 % with respect to the related long-time-averaged value. These values are registered where the greatest RMS variations are also seen, at ($Y/H = \pm 0.32,Z/H = 0.67$). The two stable fields are symmetric to the vertical centerplane. Figure 7c plots the spatial average between the two stable phases, defined as:

$$\begin{aligned} C_{\rm p,LR} (i,j) = \frac{C_{\rm p,L} (i,j) + C_{\rm p,R} (i,j)}{2} \end{aligned}$$

(5)

where $C_{\rm p,L}$ and $C_{\rm p,R}$ are the conditionally averaged values for the generic pressure tap of the coordinates $(i,j)$. The obtained field is uniform and is almost identical to the long-time average presented in Fig. 4a, as can be clearly seen in Fig. 7d, where the mid-height $C_{\rm p}$ distribution is compared for the two stable positions and the two averaged fields. The $C_{\rm p}$ recalculated with Eq. 5 differs by 0.1 % at most from the canonical averaged field.

Fig. 7

Conditional averaging of pressure data: a rear pressure phase L, b rear pressure phase R, c spatial average of the two identified phases, d comparison of the pressure distributions at $Z/H = 0.67$

Thus, the conditionally averaged base pressure field alternates between two well-defined schemes. Since the base drag makes the largest contribution to the global $C_{\rm D}$, it is interesting to calculate it for the stable positions as shown in Fig. 7a, b. It was found that, for $Re_{\rm H} = 5.1 \times 10^5, C_{\rm D,base,L} = C_{\rm D,base,R} = C_{\rm D,base} = 0.221,$ and for $Re_{\rm H} = 7.7 \times 10^5, C_{\rm D,base,L} = C_{\rm D,base,R} = C_{\rm D,base} = 0.227$. So, the bi-stability phenomenon does not affect the mean value of the base drag, because the pressure variation on the left or right base part is balanced on the other side, as can be clearly seen from Fig. 7d. Even if this has an effect on the yawing moment, this result has also to be taken into account when trying to reduce drag on a body showing such bi-stability. In fact, when drag is investigated, the bi-stability phenomenon does not induce bias on the results. An important consequence is that the previous results obtained on this kind of body do not have to be reconsidered. On the other hand, the $C_{\rm p}$ variation on a single point can be substantial, so, if local effects are being studied, greater care has to be taken, because part of the recorded variations can derive from bi-stability rather than from the effect of the drag control strategy.

Conditional averaging can also be applied to the PIV data, as shown in Fig. 8. In this case, the sorting criterion is based on the sign of the function $\Delta V_{i,{\rm CA}}$, depending on one significant measurement point:

$$\begin{aligned} \Delta V_{i,{\rm CA}} = V_{i} \left( \tilde{x},\tilde{y},\tilde{z}, t \right) - \overline{V}_i \left( \tilde{x},\tilde{y},\tilde{z} \right) \end{aligned}$$

(6)

where $i$ is the direction of the velocity component, $\tilde{x},\tilde{y},\tilde{z}$ are the coordinates of the considered point, and $\overline{V}_i$ is the velocity average for the considered measurement. For the horizontal PIV planes, the $V_y$ velocity component for the points at ($\tilde{x} = 0,\tilde{y} = 0$) was used, whereas for the vertical planes bi-stability was evident on the $V_x$ component at ($\tilde{x} = 0.75H, \tilde{z} = 0.29H$). The sorted phases were assembled by topology coherence and interpolated on a 3D volume. Figure 8 shows the $V / V_\infty = 0.1$ isosurfaces of the obtained velocity fields. The points shown in Fig. 6 lie on these surfaces. As seen for the pressure fields, the two bi-stable conditionally averaged configurations of the wake show a left-to-right antisymmetry and their averaging yields the well-known symmetric recirculation bubble.

Fig. 8

Conditional averaging of velocity data, $V/V_\infty = 0.1$ isosurfaces: a phase L, b phase R, c spatial average of the two identified phases

4.2 Statistical analysis of the stable phase duration

The excerpt of the temporal evolution of the pressure field from Fig. 5c shows that the bi-stable phenomenon is not periodic. In order to characterize its timescale, a statistical approach is necessary.

The random variables chosen as parameters for this study are the durations of each stable position, $t_{{\rm phase},i}$ (with $i = \hbox{L, R}$), defined as the time elapsed between two successive phase switches. The populations for the analysis were obtained from the conditional averaging operation explained in Eq. 4.

In the following, it is verified that the transitions between the two phases can be assumed as purely random. One method to perform this is checking if the process can be modeled as a stationary Markov chain. For this, the switching process has to satisfy the following properties:

• 1. it evolves in a discrete number of states;

• 2. the PDF of the time duration for each state is a decreasing exponential;

• 3. each state transition depends only on the starting phase and not on the previous states (memorylessness property).

The first property is satisfied by the bi-stability phenomenon itself. For the second, the PDFs of $t_{{\rm phase},i}$, deriving from the experiments at the higher free-stream velocity, are shown in Fig. 9a. During the considered run 190 phase switches were recorded, meaning that the statistics on the left and right positions are computed on two populations of $N_{\rm L} = N_{\rm R} = 95$ observations. The obtained PDFs have decreasing trends, well matched with an exponential probability distribution of the type $f(t_{\rm phase}) = \lambda e^{-\lambda t_{\rm phase}}$. To verify this hypothesis, the cumulative density function of the experimental data was calculated, so that a Kolmogorov–Smirnov test could be performed, as shown in Fig. 9b, c. The null hypothesis is that the experimental data fit an exponential distribution of parameter $\lambda = 1 / t_{\rm phase}$. The results are reported in Table 1: The null hypothesis is rejected if the maximum distance between experimental and theoretical distributions, $D_{\exp}$, is greater than the statistical test $KS_{\alpha}$. This is not verified with the present data, so the statistical test is passed and the two populations derive from exponential distributions.

To verify the memorylessness property, the probability of change of state after exactly $t^*$ seconds was calculated. If the transition does not depend on the past phases, the formula is given [the demonstration is found in Grandemange et al. (2013b)]:

$$\begin{aligned} P(S(t + t^*) \ne S(t)) = P_{\rm shift} (1 - P_{\rm shift})^{t^*} \end{aligned}$$

(7)

where $P_{\rm shift}$ is the probability of changing its stable position in a 1 s acquisition. The results are plotted in Fig. 9d. Equation 7 fits the experimental data reasonably well. Thus, the randomness of the bi-stability phenomenon can be modeled with a Markov chain.

Fig. 9

Statistical analysis of the phase time duration $t_{{\rm phase},i}$, $Re_{\rm H} = 7.7 \times 10^5$: a probability density functions, b, c cumulative distribution functions for each phase, d PDF of remaining in the same phase

Table 1 Kolmogorov–Smirnov test on the $t_{{\rm phase},i}$ populations

The timescale of the bi-stability phenomenon was estimated by calculating the mean duration $\overline{t}_{\rm phase}$ of the two stable positions. This time was compared to the characteristic aerodynamic times, calculated on free-stream velocity and both the height H and the width W of the Ahmed body. The results are presented in Table 2, and the comparison with the ones from Grandemange et al. (2013b) is also proposed. It is evident that the mean is significantly greater than the characteristic Ahmed body time, confirming that the bi-stability phenomenon affects the longest timescales.

Even if the results of the presented work have an order of magnitude that is compatible with those reported in Grandemange et al. (2013b), our bi-stability timescales are lower. It is thought that this discrepancy derives from the different sampling frequency, which is 1 Hz in the case from the literature, whereas it is 20 Hz for the results presented here. In fact, we detected phase durations shorter than 1 s, which contributed to decreasing the value of $t_{\rm phase}$. When our data were artificially resampled at 1 Hz, the agreement with Grandemange’s results was significantly improved.

Table 2 Timescales of the bi-stability phenomenon

An important consequence of this bi-stable behavior is that when analyzing the flow on this body, the large value of the bi-stability timescale requires averaging on a long acquisition time. If the run is too short, one of the stable positions may become predominant and an asymmetric field is obtained after data averaging. Let us consider Fig. 10, which shows the time percentage during which the phase identified at $t = 0$ is present. The dotted black line indicates equal distribution between the two phases.

With the Ahmed body perfectly aligned to the wind flow, in the first 120 s, the initial phase is slowly balanced by its opposite. The two phases tend to be reasonably distributed (60 vs 40 % distribution at worst) after 320 s, corresponding to 40–45 times the mean transition time (i.e., on the order of $10^4 \, V_\infty /H$). We are aware that this result is specific for the present tests. Still, this shows the importance of setting up long-time acquisitions when dealing with a bi-stable wake. If acquisitions are too short, the bi-stability can bias the results and mislead the data interpretation.

Hopefully, as will be detailed in the next section, the perfect balance between the two stable positions is not strictly necessary to characterize the mean field when bi-stability is involved, provided that it is possible to identify the two phases.

Fig. 10

Presence of the initial phase during the acquisition

4.3 Bi-stability sensitivity to yaw angle

As previously seen from Figs. 7 and 8, the topology of each stable position exhibits a left-to-right asymmetry. Complementary tests were carried out for different values of the yaw angle $\beta$, as shown in Fig. 11, in order to study the effects of a small angle of yaw induced by a misplacement of the body into the flow. It is important to point out that for these new measurements, the acquisition time is still 900 s, as for the previous results.

First, the pressure fields obtained from canonical averages at $\beta = -1^{\circ }$ and $-2^{\circ }$ were compared to the most similar bi-stable position . The data previously presented correspond to the $\beta = 0^{\circ }$ curve. This is done in Fig. 11b, in which the measurements at the base mid-height are compared. It can be observed that the three distributions are qualitatively very similar. In fact, the differences between the zero-drift conditionally averaged field and the long-time-averaged yawed fields are mostly situated toward the vertical centerline: for example, at $Y/H = 0$, and for $\beta = 1^{\circ }$, the difference is 7 %.

Then, the bi-stable behavior of the yawed wake was studied by tracing the PDFs of the $C_{\rm p}$ evolution at the point indicated in the sketch from Fig. 11c. When the body is correctly aligned to the flow, the two PDF maxima are nearly at the same level, meaning that the presence of the two bi-stable phases is equiprobable. In other words, none of the stable positions predominates, so that on a sufficiently long acquisition, the averaged pressure field is not asymmetric. If a yaw angle of $0.4^{\circ }$ is imposed, a bimodal distribution of the $C_{\rm p}$ coefficient is still obtained, but this time the lower pressure position is preferred. The wake still has a bi-stable behavior, but in this case, one stable position is most seen during the acquisition. When the yaw angle is further increased up to $1^{\circ }$, only one phase is detected, meaning that the bi-stability behavior is suppressed.

A finer analysis was carried out for yaw angles close to $0^{\circ }$. For these sets of data, the two stable positions were identified in the same way as for Fig. 7 and the persistence time of each one was expressed as a percent of the whole acquisition. The dependence of the latter quantity on the yaw angle $\beta$ is plotted in Fig. 11d, for both the free-stream velocities. The dotted line represents the equiprobability of the two bi-stable positions. A clear trend is not visible, and the curves are not antisymmetric relative to the $\beta = 0^{\circ }$ position, as could be thought. This can be attributed to the randomness of the bi-stable behavior, which can scatter the data. However, a clear predominance of one phase is visible when $\left| \beta \right| > 0.2^{\circ }$. It is also worth noting that only at these two angles, the phase time distribution is different for the two free-stream velocities, whereas for other values of $\beta$, the results are coherent.

Fig. 11

Sensitivity of the bi-stable wake behavior to the yaw angle $\beta$: a reference system, b pressure distribution at $Z/H = 0.67$ for different values of $\beta$, c probability density functions of the indicated pressure tap for different values of $\beta$, d sensitivity of the permanence time of the “L” phase, expressed as time percentage, to the yaw angle

Another interesting result from Fig. 11c is the fact that the points of maxima of the PDF functions do not significantly shift with $\beta$. This indicates that when the wake presents bi-stability, the yaw angle mostly affects the permanence time, but has little effect on the topology of each stable position.

A confirmation analysis was carried out by imposing a yaw angle of $-0.35^{\circ }$ on the Ahmed body. If the pressure distribution measured at the mid-height pressure taps is compared to the one at $0^{\circ }$, as shown in Fig. 12, a slight asymmetry is visible. The analysis of the pressure evolution showed that the “R” phase is now visible for 70.5 % of the time, which creates the asymmetry when averaging all the data of the acquisition. However, the two topologies of the conditionally averaged “R” phase are almost identical.

Thus, it is interesting to perform the spatial average of the two stable phases identified, as previously done for Figs. 7 and 8. All of the steps of the spatial averaging analysis are reported in Fig. 13, in the case of the whole pressure field and for the velocity measured at the model mid-height ($Z/H = 0.67$).

When spatially averaging the two stable positions, as shown in Fig. 13d, the non-yawed symmetric pressure field was again observed. The trace of the toric recirculation bubble in the wake is also symmetric. This means that for a correct study of the wake in the case of bi-stability, the perfect alignment of the body to the flow is not mandatory, since it is possible to reconstruct the long-time steady field by processing the data. In the least favorable case, it is even possible to reconstruct the long-time symmetric field from the characterization of a single stable phase, since the bi-stable fields are mutually symmetric. This can be an important point in the case of numerical simulations, where the calculation of the unsteady field on very long timescales can be time-consuming, if not impossible.

Fig. 12

Mid-height pressure distribution at $Re_{\rm H} = 5.1 \times 10^5$: results of the canonical average and of the stable position R for $\beta = 0^{\circ }$ and $-0.35^{\circ }$

Fig. 13

Bi-stability sensitivity analysis for $Re_{\rm H} = 5.1 \times 10^5$ and $\beta = -0.35^{\circ }$, rear $C_{\rm p}$ field and non-dimensional velocity of the mid-height plane $Z/H = 0.67$: a long-time canonical average, b stable position R, c stable position L, d spatial average of the two separated phases

5 Spectral analysis

In this section, our study focuses on the periodic wake dynamics, for which the timescale is comparable to the characteristic aerodynamic time. As seen in Sect. 4.2, these properties are not relative to the bi-stability phenomenon. This is the reason why conditional averaging was not performed for these analyses. However, the acquisition time of all the data presented in this section was 450 s, which is long enough to obtain a reasonable equipresence of the two bi-stable positions previously presented. Nevertheless, as will be seen in the next section, it is still possible to identify the bi-stability signature from the analysis of their power spectra.

5.1 Spectra of the pressure and velocity signals

The spectra deriving from the measurements of the piezoelectric transducers are presented in Fig. 14. Figures 15, 16, 17 and 18 report the most interesting results from the hot-wire tests. The results are presented in the form of power spectral densities (PSDs); the dotted lines represent the −7/3 and −5/3 logarithmic decaying laws, for the pressure and velocity spectra, respectively. In Figs. 15, 16, 17 and 18, the PSDs were vertically shifted, so that the peak frequencies can be easily identified for all the measurements. In the following, all the non-dimensional frequencies are expressed as Strouhal numbers, $St_{\rm H}$, calculated on the free-stream velocity $V_\infty$ and the height of the model $H$.

$$\begin{aligned} St_{\rm H} = \frac{f H}{V_\infty } \end{aligned}$$

(8)

The pressure spectra present energy peaks at $St_{\rm H} \approx 0.45$ that do not appear in the hot-wire measurements. Additional investigations showed that these peaks are not related to the Ahmed body, but may be attributed to the raised floor structure within the wind tunnel. These frequencies will therefore not be further discussed in this study.

These results show that most of the spectral activity is observable at low frequency. The most recurrent peak is found at $St_{\rm H} = 0.13$. Should this number be non-dimensionalized with the width of the Ahmed model, we obtain $St_W = 0.175$, which is compatible with a Von Kármán vortex shedding mode, developing on the left and right sides of the Ahmed body. This result is also documented in the literature (Grandemange et al. 2013b; Lahaye et al. 2014). This peak is found for all the pressure measurements taken outside the vertical centerline, as shown in Fig. 14a, b, and for the hot-wire probings made downstream the recirculation bubble, when the transverse velocity component $V_y$ is considered, as shown in Figs. 15b, 17b and 18b.

It is still worth mentioning that this Von Kármán mode is independent of the bi-stable behavior characterized in the previous section, in spite of what the left-to-right symmetry of the two phenomena could suggest. As seen in Sect. 4.2, the mean timescale of the bi-stability is way greater than the characteristic aerodynamic time. Thus, bi-stability only affects the lowest aerodynamic frequencies. In the pressure spectra in Fig. 14, both the $St_{\rm H} = 0.13$ peak and an energy increase at the lowest frequencies are visible. Indeed, Grandemange (2013) demonstrated that:

$$\begin{aligned} {\mathbb {E}} \left( \left| A_q \left( f \right) \right| ^2 \right) \underset{\overline{t}_{\rm phase} f \ll 1}{\sim } \frac{1}{f^2} \end{aligned}$$

(9)

where $A$ is the autospectrum function. Then, the spectrum associated with a bi-stable quantity decreases with a −2 law for very low frequencies, and this is compatible with the present spectra.

The other Von Kármán frequency corresponding to the vortex shedding from the floor and the roof of the model was also found, only for the hot-wire measurements, as shown in Figs. 16a, c and  18b, where peaks at $St_{\rm H} = 0.19$ are visible. This result agrees with the findings of Lahaye et al. (2014) and Östh et al. (2014). Once again, this frequency was detected downstream the recirculation bubble; also, the peak becomes more marked when the distance to the base increases.

Our results show the presence of a lower energy peak, for $St_{\rm H} \approx 0.07 - 0.08$, found for the pressures at the vertical centerline probing, as shown in Fig. 14a, and mostly in the shear layers for the longitudinal and vertical components $V_x$ and $V_z$ of the hot-wire probings, as shown in Figs. 15a, c, 16c and 17a. More precisely, this frequency was found in the longitudinal mid-plane ($Y/H = 0$) and at mid-height ($Z/H = 0.67$).

This low-frequency mode has been observed on the square back Ahmed body by Khalighi et al. (2001, 2012). Its existence was, however, doubted by Grandemange et al. (2013b). We have reasons to think that the results presented here are not in contradiction with those of the latter authors: In their case, most of the hot-wire probing was made at $X/H > 1.5$, i.e., behind the recirculation bubble. Our results show that at these locations, the predominant modes are those deriving from vortex shedding, which is coherent with Grandemange’s conclusions. In our case, the $St_{\rm H} = 0.08$ peak is rather found in the shear layer measurements, as also found by Khalighi et al. (2001).

A possible interpretation of this low-frequency activity is the nonlinear interaction of the two vortex shedding modes in the wake. Indeed, $St_{\rm H} = 0.08$ is close to the difference of the other two characteristic frequencies, $0.19$ and $0.13$, as also remarked in Lahaye et al. (2014). In the literature, a similar result was obtained from the direct numerical simulations of Ehrenstein and Gallaire (2008), regarding the wake of a flow passing over a bump at low Reynolds number. Here, they showed that the dynamics resulting from the unstable modes is at the origin of a lower-frequency wake beating.

The occurrence of a very low frequency in 3D wakes is often reported. To the best of our knowledge, this phenomenon was first described by Berger et al. (1990) for both the wakes of a circular disk and of a sphere. In their flow visualization experiments, they showed that the wake moves periodically in the streamwise direction at a non-dimensional frequency of $St = 0.05$. This kind of behavior of the wake is often given the name of “bubble pumping” phenomenon.

Duell and George (1999) also referred to the bubble pumping mechanism when studying the pressure field at the rear of a body similar to the Ahmed model, but presenting a square section. In particular, they found a strong coherence between the unsteady pressure fluctuations of the left and right side, for $St = 0.07$. They interpreted this as indicating that the pumping phenomenon derives from the pairing of eddies shed from the model edges. The eddies grow until they reach the separation point, where they shed.

However, it is worth noting that Duell and George (1999) also made hot-wire measurements on the upper shear layer and the $St = 0.07$ peak was not visible in their spectra, unlike the present results or those of Khalighi et al. (2001).

Fig. 14

Pressure power spectral densities on the rear of the model: a probings on the middle points of the rear edges, b probings on the corners

Fig. 15

Velocity power spectral densities on the upper shear layer of the wake, $Y/H = 0$: a longitudinal component $V_x$, b transverse component $V_y$, c vertical component $V_z$, d probing positions superposed on the PIV streamlines

Fig. 16

Velocity power spectral densities downstream the recirculation bubble, $Y/H = 0$: a vertical component $V_z$, $X/H = 1.5$, b probe positioning, c vertical component $V_z$, $X/H = 2$, d probing positions superposed on the PIV streamlines

Fig. 17

Velocity power spectral densities on the right-side shear layer of the wake, $Z/H = 0.67$: a longitudinal component $V_x$, b transverse component $V_y$, c probing positions superposed on the PIV streamlines

Fig. 18

Velocity power spectral densities on the right-side shear layer of the wake, $Z/H = 0.87$: a longitudinal component $V_x$, b transverse component $V_y$, c probing positions superposed on the PIV streamlines

5.2 Coherence analysis

In this section, the correlation between the fluctuations of the rear pressure field and those of the velocity in the wake is studied by computing the coherence function and the phase shift between the two signals. First, the coherence between the pressure signals, measured at the points shown in Fig. 14, is considered, as shown in Fig. 19. The coherence between two synchronized signals was calculated as follows:

$$\begin{aligned} \gamma _{12} \left( f \right) = \frac{ \left| P_{12} \left( f \right) \right| ^2 }{P_{11} \left( f \right) P_{22} \left( f \right) } \end{aligned}$$

(10)

where $P_{12}$ is the cross-spectrum and $P_{11}$ and $P_{22}$ are the auto spectra of signals 1 and 2. The phase between the two signals is defined as the angle of the complex cross-spectrum function:

$$\begin{aligned} \varphi _{12} \left( f \right) = \arctan \left( \frac{\text{ Im } \left[ P_{12} \left( f \right) \right] }{Re \left[ P_{12} \left( f \right) \right] } \right) \end{aligned}$$

(11)

where Im and Re are the imaginary and real parts of the complex $P_{12}$ function.

When left-to-right opposite probing locations are considered, it is found that the pressure fluctuations show a strong coherence toward the lowest frequencies. In particular, it is interesting to state that the two signals tend to be perfectly coherent, while being in phase opposition. This is another confirmation of the left-to-right bi-stable behavior of the wake. The signals in Fig. 19a present, as expected, strong coherence for $St_{\rm H} = 0.13$. Once again, when the phase shift is checked, the signals are in phase opposition, which confirms the interpretation of this peak of energy as a Von Kármán mode.

As far as the measurements on the centerpoints of the horizontal edges are concerned, as shown in Fig. 19b, coherence is high at low frequencies and slowly decreases until, at $St_{\rm H} = 0.1$, the signals become incoherent. The decreasing trend is only interrupted by the peak found at $St_{\rm H} = 0.08$, the frequency of the bubble pumping phenomenon. In the range of Strouhal numbers considered, the pressure signals are phased.

As expected from the auto spectra results from Fig. 19b, the coherence functions of the measurements taken from the rear corners present local peaks for the left-to-right Von Kármán mode. However, low but non-negligible levels of coherence (around 20 %) are visible at the bubble pumping frequency. It is also possible to find coherence for the top-to-bottom vortex shedding mode, when measurements of the corners of the same side are taken, as shown in Fig. 19c. The weak coherence peak visible at $St_{\rm H} = 0.04$ could be compatible with low-frequency acoustic noise. The phase shifts observed for the corner point measurements at the Strouhal numbers of $St_{\rm H} = 0.13$ and 0.19 are consistent with the interpretation of vortex shedding, whereas in the case of the coherence peak at $St_{\rm H} = 0.08$, the pressure signals are phased in the vertical direction and are in opposition in the transverse direction. This does not agree with the axisymmetric bubble pumping seen by Berger et al. (1990). It should be remembered, however, that at the considered frequencies, the coherence is weak.

Fig. 19

Coherence of the unsteady pressure measurements, $Re_{\rm H} = 4.66 \times 10^5$: a between the centers of the vertical edges, b between the centers of the horizontal edges, c between the two left corners, d between the two upper corners, e between two opposite corners

As far as the synchronized pressure/hot-wire measurements are concerned, it was decided to place the piezoelectric transducers in the configuration of Fig. 14a, since their spectra efficiently detected most of the unsteady phenomena previously described (i.e., the bi-stability, the $St_{\rm H} = 0.08$ mode, the vortex shedding developing from the lateral surfaces). The results are shown in Figs. 20 and 21.

When considering the upper shear layer, the coherence between the velocity components $V_x$ and $V_z$ and the upper pressure measurement has a frequency behavior similar to the one seen in Fig. 19b. A peak of strong correlation at $St_{\rm H} = 0.08$ is also visible. The upper central shear layer is also correlated with the lateral phenomena, as shown in Fig. 20b. The transverse velocity $V_y$ is strongly correlated with the pressure measured on the vehicle side at the lowest frequencies, whereas the correlation at $St_{\rm H} = 0.13$ increases with the distance to the rear surface. The same behavior is also seen for coherence of the side shear layer $V_y$ velocity with the same pressure tap, as shown in Fig. 21a.

It is also interesting to consider the phase shift between the two signals. In the upper shear layer, at the lowest frequencies, the pressure and the $V_x$ and $V_z$ velocity components are in phase opposition. This is not surprising, since a steady enhancement of the velocity induces low pressure. However, for $St_{\rm H} = 0.08$, the phase shift does not show a visible spatial gradient. This behavior was also seen for the lower central shear layer. Since the $St_{\rm H} = 0.08$ peak was detected on the recirculation bubble, this means that at this frequency, there is a low-frequency movement of the wake in the longitudinal direction. In other words, the pressure fluctuations in the vertical longitudinal center plane are induced by the periodic shrinking and expansion of the recirculating part of the wake, as shown in Fig. 22, which agrees with the bubble pumping interpretation.

On the contrary, the phase shift evolves with distance for $St_{\rm H} = 0.13$, as we expected from the vortex shedding interpretation of this spectral mode. In particular, from these phase shifts it is possible to calculate the time lag, $t_{\rm lag}$, between the pressure and velocity signals, as shown in Fig. 23. This quantity increases with distance and can be reasonably approximated with a linear dependence. This means that the convection velocity of the eddies is constant. More specifically, it was found, for the present data, that the convection velocity is $0.44 V_\infty$ for the upper shear layer and $0.6 V_\infty$ for the one on the side.

Fig. 20

Pressure/velocity coherence along the upper shear layer, $Y/H = 0$: a longitudinal velocity $V_x$ versus pressure at $(Y/H = 0, Z/H = 1.07)$, b transverse velocity $V_y$ versus pressure at $(Y/H = 0.62, Z/H = 0.67)$, c vertical velocity $V_z$ versus pressure at $(Y/H = 0, Z/H = 1.07)$, d positions of the hot-wire measurements

Fig. 21

Pressure/velocity coherence along the side shear layer, $Z/H = 0.67$: a transverse velocity $V_y$ versus pressure at $(Y/H = 0.62, Z/H = 0.67)$, b positions of the hot-wire measurements

Fig. 22

Interpretation of the $St_{\rm H} = 0.08$ spectral peak in the $Y/H = 0$ plane, according to phase shift results between pressure and velocity: a positive pressure fluctuations, b negative pressure fluctuations

Fig. 23

Evolution of the phase time $t_{\rm lag}$ between the pressure and the hot-wire signals, at $St_{\rm H} = 0.13$

6 Proper orthogonal decomposition of the base pressure field

In this section, the Proper Orthogonal Decomposition technique (POD) from Lumley (1967) is applied to the pressure measurements we collected from the two measurement systems employed.

As is well known, this method decomposes the fluctuation field $p'(\mathbf {x},t) = p(\mathbf {x},t) - \overline{p}(\mathbf {x})$ into a set of basis functions (or POD modes) $\mathbf {\Phi }$ so that:

$$\begin{aligned} p' \left( \mathbf {x}, t \right) = \sum _{n = 1}^{N_{\rm m}} a^{\left( n \right) } \left( t \right) \mathbf {\Phi }^{\left( n \right) } \left( \mathbf {x} \right) \end{aligned}$$

(12)

where $N_{\rm m}$ is the number of measurement points and $a^{(n)}(t)$ is the modal coefficient relative to the nth POD mode $\mathbf {\Phi }^{(n)}$.

It can be demonstrated that the solution of Eq. 12 is the same as that of the eigenvalue problem:

$$\begin{aligned}&\displaystyle R {\mathbf {\Phi }}^{\left( n \right) } = \lambda ^{\left( n \right) } {\mathbf {\Phi }}^{\left( n \right) } \left( \mathbf {x} \right) \nonumber \\&\displaystyle R = \left[ \begin{matrix} R_{11} &{} \ldots &{} R_{1 N_{\rm m}} \\ \vdots &{} \ddots &{} \vdots \\ R_{N_{\rm m} 1} &{} \ldots &{} R_{N_{\rm m} N_{\rm m}} \end{matrix} \right] \nonumber \\&\displaystyle R_{ij} = \frac{1}{N_{\rm t}} \sum _{k=1}^{N_{\rm t}} p' \left( x_i, t_k \right) \cdot p' \left( x_j, t_k \right) \end{aligned}$$

(13)

in which $N_{\rm t}$ is the number of the available time samples.

Figure 24 shows the eigenvalues $\lambda (n)$ resulting from the solution of Eq. 12, when the datasets obtained with both the pressure scanners and the piezoelectric transducers are used. These curves also correspond to the percent of energy associated with each mode. The results obtained from the two measurement systems are coherent, in that the first two modes have high energy levels (greater than 10 %). The different amount of energy obtained from the scanners and from the piezoelectric transducers is mainly due to the difference in number and disposition of the pressure taps in each case, as will be clearer when the modal forms are discussed.

When the cumulative energy is calculated, it is found that the first two modes from the piezoelectric transducer dataset are 77.3 % of the overall energy, whereas when the scanner data are used, 84.4 % of the energy is reached with only 4 POD modes.

Fig. 24

Energy of the POD modes derived from the pressure fields

It is then interesting to show the aspect of the corresponding eigenvectors, by representing them in the form of cartographies on the rear of the model. This is done in Figs. 25 and  26. It can be seen that the first POD mode from the two measurement systems shows a left-to-right antisymmetry. This POD mode is therefore compatible with both bi-stability and the Von Kármán mode seen in the pressure spectra, as shown in Fig. 14. The PSD of this POD mode coefficient $a^{(1)}(t)$, calculated on the piezoelectric transducer dataset, as shown in Fig. 27, has a clear peak at $St_{\rm H} = 0.13$ and the −2 law low-frequency energy increase, typical of bi-stability behavior.

The second POD mode obtained with both measurement systems is similar. In particular, this mode enhances the pressure taps of the vertical centerline, and the corresponding spectrum from piezoelectric transducers has a peak at $St_{\rm H} = 0.08$. The vertical centerline taps all have the same sign, meaning that for this mode, pressure fluctuations are phased at $Y/H = 0$. This agrees with the phase shift results seen previously in Fig. 19b. This mode can be associated with the bubble pumping phenomenon. This mode appears to be more energetic when using the piezoelectric transducer dataset simply because in the case of the pressure scanners the energy is distributed over a wider number of locations, most of which contribute to the first POD mode.

The third and fourth POD modes are identified in reverse order on the two available datasets. However, the results of the two POD analyses are consistent: In both cases, the energy levels of these modes are approximately the same. The most interesting mode between the two is the one in which the eigenvector shows an up-to-down antisymmetry, compatible with the up-to-down Von Kármán mode. In fact, the related spectrum shows a very weak peak at $St_{\rm H} = 0.19$.

Fig. 25

POD modes eigenvector representation, derived from the pressure scanner dataset: a–d first to fourth modes

Fig. 26

POD modes eigenvector representation, derived from the piezoelectric transducers dataset: a–d first to fourth modes

Fig. 27

Spectra of the POD modal coefficients, derived from the piezoelectric transducers dataset. The curves are shifted along the vertical axis

7 Summary and conclusions

An extensive measurement campaign was carried out on the natural wake of a full-scale square back Ahmed body with the final goal of studying its unsteady dynamics modes. The experiments were performed at two different height-based Reynolds numbers, $Re_{\rm H} = 5.1 \times 10^5$ and $7.7 \times 10^5$. The results provide evidence of a bi-stability phenomenon and of a low-frequency spectral activity.

The bi-stable behavior of the wake was detected with three different measurement systems, showing that both the base pressure and the velocity fields switch between two mutually symmetric left-to-right positions. The well-documented symmetric configuration corresponds to the averaging of the signal time series on a long time interval.

By means of a conditional averaging of the different signals, it was then possible to characterize the topology of each stable phase. It has been demonstrated that one phase is the reflexion symmetric of the other, relatively to the vertical median plane. Furthermore, the field reconstructed from their spatial averaging is the same as the one obtained from canonically averaging the acquired data.

The statistical analysis made on the time duration of each bi-stable position highlighted the completely random behavior of this bi-stability. The calculation of the average duration between two phase switches indicates that the timescale of the bi-stability is large and of the order of $800 \, V_\infty / H$. This means that to properly characterize the two stable positions, acquisitions must be done on long runs. As an example, for the specific cases discussed in this paper, the acquisitions had to last at least $10^4 \, V_\infty / H$.

The temporal distribution of the two stable positions proved to be sensitive to the yaw angle. In fact, when a low yaw angle of $0.4^{\circ }$ is imposed, a 70 % of the time phase predominance appears. The canonical averaging of the bi-stable signal then provides the expected yawed field. Moreover, the bi-stability disappears when the yaw angle is further increased beyond $1^{\circ }$. However, independently of the yaw angle, provided it is small, the topologies of the phases are qualitatively the same, and the correct long-time-averaged symmetric wake can be reconstructed by spatial average of the two phases.

As far as the spectral analysis of base pressure and wake velocity is concerned, we have been able to detect, in addition to the bi-stability, three other low-frequency activities. In particular, we have found two modes, at $St_{\rm H} = 0.13$ and 0.19, associated with vortex shedding, developing from the vertical and horizontal walls of the Ahmed body, respectively. We also detected a lower-frequency activity, at $St_{\rm H} = 0.08$, which was previously found by only a few authors. The physical origin of this phenomenon is under investigation. One possible explanation of this low-frequency mode could be the nonlinear interaction of the vortex shedding modes.

These periodic activities have been localized in specific places. When considering the base pressure measurements, the $St_{\rm H} = 0.08$ mode was found in the vertical centerline, whereas the $St_{\rm H} = 0.13$ may be identified on both sides of this line. The POD analysis confirms this result, by assigning the most energetic mode to both the left-to-right vortex shedding and the bi-stability, whereas the second mode corresponds to the $St_{\rm H} = 0.08$ spectral peak. In the case of velocity measurements, this latter mode was found in the shear layer of the recirculation bubble, for the longitudinal and vertical component. Downstream of the reattachment point, the two modes associated with vortex shedding are visible.

In order to provide an interpretation for the $St_{\rm H} = 0.08$ spectral peak, correlation analyses of the synchronized pressure and velocity signals were carried out. At this Strouhal number, the pressure signals of the taps at the middle of the horizontal edges are phased. Furthermore, there is little phase shift between the pressure and velocity measurements, suggesting that at $St_{\rm H} = 0.08$, the recirculation bubble periodically shrinks and expands. These results are coherent with the “bubble pumping” phenomenon as an explication for this low-frequency mode.