1 Introduction

In spite of the wide variety of applications of orifice jets, also related to the ease of manufacturing, as in marine propulsion, pollutant discharge or studies on the cardio-circulatory system, the number of studies regarding them is still limited (Quinn 1989, 2005; Boersma et al. 1998; Mi et al. 2001, 2007; Romano and Falchi 2010; Zhang et al. 2014).

The reason presumably lies in the complexity of their velocity field, especially in the near field, so that the behaviour of these jets is still not fully understood. The vena contracta occurrence can be elected as an example of it. In fact, due to the necessity for the flow to pass through the orifice, which has a limited diameter in comparison to the plenum size upstream, the streamlines of the jet tend to converge. Downstream of the plate they should recover the undisturbed direction, and consequently, they should change it to get the original one, but they are not able to perform this abruptly. Therefore, the contraction persists further downstream until a minimum section, named the “vena contracta”. This was probably first described by Evangelista Torricelli in his experiment on atmospheric pressure in 1643 (Torricelli 1644).

With the aim to describe this phenomenon, a characteristic dimensionless quantity can be defined, though this quantity will not be evaluated in this work, being the attention focused on the velocity features. Given the area of the vena contracta A and the area of the orifice A 0, the coefficient of contraction results:

$$C_c=\frac{A}{A_0}$$

For a sharp circular orifice, its value is generally near to 0.6 (Michell 1890), but it is also dependent on the specific shape of the contraction (Batchelor 2000) and of the orifice, increasing (in all) by 10 % moving from the circular shape to the square, the triangular and the rectangular (King 1918).

Regarding the small scales, one of the most challenging problems in the study of jets is their behaviour in the near field especially in connection to isotropic conditions. First of all, Kolmogorov, in his work Kolmogorov (1941), introduced the hypothesis that, at sufficiently high Reynolds numbers, the flow displays statistically isotropic features at small scales, regardless to the possible anisotropy of larger ones. An immediate application of this hypothesis can be found in the assessment of turbulent kinetic energy dissipation rate, present in the turbulent kinetic energy budget equation. Its value in general depends on 12 quantities involving mean square derivatives of velocity components, combinations of them and their statistical moments (Hinze 1975). Therefore, an evaluation of all those terms is very challenging both experimentally and numerically due to the requirements of high temporal and spatial resolutions. Several ways of extending spatial resolution in particle image velocimetry (PIV) have been worked out. Keane et al. (1995) and later Stitou and Riethmuller (2001), e.g. used the knowledge of the velocity field from cross correlation of large sub-regions and particle tracking PTV in order to achieve an high spatial resolution, and Westerweel et al. (1997) made use of a window offset in the analysis, whereas Scarano (2002, 2003) developed an adaptive window shaping. Westerweel et al. (2004) and later Billy et al. (2004) and Kähler and Scholz (2006) applied a two-point ensemble correlation at single-pixel resolution, while Lavoie et al. (2007) compared PIV spatial resolution with the one of hot-wire anemometry, suggesting spectral corrections in order to improve PIV results. However, even when these effective procedures are employed, the simplest way to attain an higher spatial resolution in the study of a fixed area is still to consider the overlapping of several flow regions as small as possible (in terms of flow scales). This work aims to find a guideline for appropriately choosing the extent of the framed area, i.e. the magnification factor, as related to flow scales, and its originality resides in this purpose. Specifically, the simultaneous analysis of large- and small-scale statistics allows to understand whether the extension of the framed area could increase and change the range of scales and to which limit correct results are obtained. A first limited study on magnification factor influence can be found in Kähler et al. (2012), based on different particle image diameters in synthetic images. We aim to perform instead an experimental study having particles dimension near to 1-2 pixels, while their diameters ranged between 3 and 20 pixels.

1.1 Velocity derivative background

In general, the turbulent kinetic energy dissipation rate is defined as (Hinze 1975):

$$\epsilon _T=\nu \left( \left\langle \frac{\partial u_i}{\partial x_j} \frac{\partial u_i}{\partial x_j}\right\rangle + \left\langle \frac{\partial u_i}{\partial x_j} \frac{\partial u_j}{\partial x_i} \right\rangle \right) \quad \text{ for } \,i,j=1,\ldots ,3$$
(1)

where u i and u j are the generic velocity components, ν denotes the kinematic viscosity and the indexes i and j identify the orthogonal axes set. Writing explicitly its terms, Eq. (1) becomes:

$$\begin{aligned} \epsilon _T&= \nu \left\{ 2 \left[ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial v}{\partial y} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial w}{\partial z} \right) ^2 \right\rangle \right] \right. \nonumber \\ &\quad\left. +\, \left[ \left\langle \left( \frac{\partial u}{\partial y} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial v}{\partial x} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial u}{\partial z} \right) ^2 \right\rangle \right. \right. \\ &\quad\left. \left. +\,\left\langle \left( \frac{\partial w}{\partial x} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial v}{\partial z} \right) ^2 \right\rangle + \left\langle \left( \frac{\partial w}{\partial y} \right) ^2 \right\rangle \right] \right. \nonumber \\ &\quad\left. +\,2 \left( \left\langle \frac{\partial u}{\partial y} \frac{\partial v}{\partial x}\right\rangle + \left\langle \frac{\partial u}{\partial z} \frac{\partial w}{\partial x}\right\rangle + \left\langle \frac{\partial v}{\partial z} \frac{\partial w}{\partial y}\right\rangle \right) \right\} \end{aligned}$$
(2)

The intrinsic difficulty of evaluating this quantity is now clear. Referring to the local isotropy hypothesis (Kolmogorov 1941), Eq. (2) gets a more simple expression associated to a single quantity, e.g. the mean quadratic derivative of streamwise velocity with respect to the streamwise coordinate:

$$\epsilon _T=15 \nu \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle$$
(3)

This much simpler expression in comparison with (2) was not confirmed experimentally (Browne et al. 1987), in particular for orifice jets.

There exists a different formulation, firstly expressed by Batchelor (1946) and Chandrasekhar (1950) and then proposed by George and Hussein (1991) more recently, based on the less stringent hypothesis of axial symmetry to rotation. Thanks to this approximation, the functional dependency of Eq. (2) can be reduced to four quantities, e.g. in the plane (x, y), the derivatives of velocity components in the same plane.

$$\begin{aligned} \epsilon _T&= \nu \left[ - \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle + 2 \left\langle \left( \frac{\partial u}{\partial y} \right) ^2 \right\rangle \right. \\&\quad\left. +\,2\left\langle \left( \frac{\partial v}{\partial x} \right) ^2 \right\rangle + 8 \left\langle \left( \frac{\partial v}{\partial y} \right) ^2 \right\rangle \right] \end{aligned}$$

It is still not clear under which conditions a phenomenon shows local isotropy or axial symmetry conditions, albeit a good amount of works have confirmed the goodness of the second one in correspondence to several turbulent flows, such as quasi-homogeneous shear flows, boundary layers, pipe jets, circular jets, round plumes, plane jets, mixing layers and two dimensional cylinder wakes (George and Hussein 1991). However, this has rarely been studied on orifice jets (Romano and Falchi 2010). A possible way of testing the fulfilment of those conditions is making use of some non-dimensional parameters (George and Hussein 1991). They are as follows:

$$K_1 = \frac{\left\langle \left( \frac{\partial v}{\partial y} \right) ^2 \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle } \quad K_2=\frac{\left\langle \left( \frac{\partial w}{\partial z} \right) ^2 \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle } \quad K_3=\frac{\left\langle \left( \frac{\partial u}{\partial y} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle }$$
(4)
$$K_4 = \frac{\left\langle \left( \frac{\partial v}{\partial x} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle } \quad K_5=\frac{\left\langle \left( \frac{\partial u}{\partial z} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle } \quad K_6=\frac{\left\langle \left( \frac{\partial w}{\partial x} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle }$$
(5)
$$K_7= \frac{\left\langle \left( \frac{\partial v}{\partial z} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle } \quad K_8=\frac{\left\langle \left( \frac{\partial w}{\partial y} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle } \quad K_9=\frac{\left\langle \frac{\partial u}{\partial y} \frac{\partial v}{\partial x} \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle }$$
(6)
$$K_{10} = \frac{\left\langle \frac{\partial u}{\partial z} \frac{\partial w}{\partial x} \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle } \quad K_{11}=\frac{\left\langle \frac{\partial v}{\partial z} \frac{\partial w}{\partial y} \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle }$$
(7)

Usually, a planar PIV investigation allows to derive K 1, K 3, K 4 and K 9.

In addition, with the aim of confirming axial symmetry, some different parameters should be introduced (George and Hussein 1991):

$$\begin{aligned} R_1&= \frac{\frac{1}{3} \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle + \frac{1}{3} \left\langle \left( \frac{\partial v}{\partial z} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial v}{\partial y} \right) ^2 \right\rangle } \\ R_2&= \frac{\frac{1}{6} \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle - \frac{1}{3} \left\langle \left( \frac{\partial v}{\partial z} \right) ^2 \right\rangle }{ \left\langle \frac{\partial v}{\partial z} \frac{\partial w}{\partial y} \right\rangle } \end{aligned}$$
(8)

If local isotropy conditions were fulfilled, we should get, as demonstrated by Taylor (1935), the following relations (George and Hussein 1991):

$$K_1 = 1; \quad K_2=1; \quad K_3=2; \quad K_4=2$$
(9)
$$K_5 = 2; \quad K_6=2; \quad K_7=2; \quad K_8=2$$
(10)
$$K_9 = -0.5; \quad K_{10}=-0.5; \quad K_{11}=-0.5$$
(11)

On the other hand, if the axial symmetry conditions were fulfilled, it would be got (George and Hussein 1991):

$$\begin{aligned} K_1&= K_2; \quad K_3=K_5; \quad K_4=K_6; \\ K_7&= K_8; \quad K_9=K_{10}=-0.5 \end{aligned}$$
(12)
$$\begin{aligned}K_1&= \frac{1}{3}+\frac{1}{3}K_7 \quad ({\rm that \, is} \, R_1=1); \\ K_{11}&= \frac{1}{6}-\frac{1}{3}K_7 \quad ({\rm that \, is} \, R_2=1) \end{aligned}$$
(13)

As already mentioned, the first and main aim of this work is finding a guideline for appropriately choosing the extent of the acquired flow region in PIV. To do this, PIV technique is applied to a challenging problem, where a high spatial and temporal resolution is required, such as the near field of a circular turbulent orifice jet. The focus is on both large scales, aiming to define where the effects of inlet conditions are lost so that useful simplifications can be applied, and small scales, following previous guidelines on velocity derivatives.

2 Experimental setup

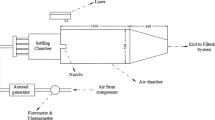
The experimental setup is divided into the jet apparatus and the acquisition systems. The first consists of a closed loop hydraulic circuit starting from an auxiliary tank, from where a centrifugal pump moves water to a secondary constant level head tank to avoid artificial velocity fluctuations, as displayed in Fig. 1. Once flowed out of the head tank, the water enters through a honeycomb into the test tank, which is subdivided by the orifice plate into a settling chamber (38 cm, upstream) and the proper test chamber (58 cm, downstream). Finally, a second plate delimits a discharge chamber, downstream to the test one, through which the water comes back to the main tank, closing the loop.

Experimental conditions are determined mainly by the Reynolds number defined by \(Re=\frac{U_0 D}{\nu }\) (where U 0 is the exit bulk velocity, D is the diameter of the orifice, equal to 3 cm, and ν the kinematic viscosity of fluid) set to 35,000 and the Taylor microscale Reynolds number defined by \(Re_\lambda =\frac{u^\prime \lambda }{\nu }\) (where u′ is the longitudinal velocity rms value and λ is the longitudinal Taylor microscale) which is ~300. Moreover, Kolmogorov length scale, derived by employing Kolmogorov local isotropy hypothesis for evaluating ε T , was about η = 10−4 m, and Taylor microscale, obtained by the auto-correlation function as the intercept of the parabola that matches it at the origin, was about λ = 2.1 × 10−3 m.

The present study has been carried out by means of PIV technique. The acquisition system is composed first of all by a light source, namely a double-pulse Nd-Yag laser having 200 mJ energy per pulse and a pulse duration of 8 ns, and by a digital high-speed camera (2,000 frames/s), with 1,024 × 1,024 pixel resolution and a 10 bit CMOS sensor. Between them, a BNC 575 pulse generator allows the synchronization between laser illumination and camera recording. Table 1 summarizes the main timing settings and their outcomes. The resolution decreases from 1 to 4 as shown in the following (Table 3).

Table 1 Timing settings
Full size table

The camera had a 17 μm sensor pixel size, a 50 mm focal length objective, an aperture equal to F = 1.8 and the working distance was near to 20 cm thanks to an extension tube set. The water was seeded by glass hollow beads having a diameter ranging from 8 to 12 μm and 1.05−1.15 g cm−3 density. Table 2 gives details about particle image densities and particle image size for each resolution. The particle image densities, evaluated as number of particles per pixel (N ppp), were always near to 0.045–0.05. These values are in agreement with the recommendations of Cierpka et al. (2013) (0.03 < N ppp < 0.05) and close to the optimal value N ppp = 0.035 prescribed by Willert and Gharib (1991). Particle image size was mainly between 1.5 and 2.3 pixels. As shown in the fourth column of Table 2, where the volume fraction ratio between 1.5 and 2.3 pixels particles is reported, the effect of decreasing the magnification manifests itself in a rising amount of smaller (1.5 pixel) image particles compared to the larger (2.3 pixel) ones.

The laser sheet thickness was approximately 1 mm.

Table 2 Particle image features
Full size table

Acquired images have been analysed by LaVision Davis 7 software making use of a multipass algorithm made of two passes in correspondence to a larger window size equal to 64 × 64 pixels and four passes in correspondence to a smaller window of 32 × 32 pixels, in both cases using 75 % overlapping. In addition, a vector validation algorithm, based on a regional median filter and group removing, is applied to eliminate spurious vectors. Thus, the final spacing between velocity vectors was eight pixels. Davis 7 has been one of the contributors of the third PIV challenge (Stanislas et al. 2008) when its performance has been studied, and it was evaluated able to reach a bias error as less as 0.5 % and an RMS error around 5 %, obviously depending on the quality of PIV images.

This work consists of a comparison between different conditions, discussed later. In correspondence to each of them, 10,000 couples of images have been acquired in subsets of 1,000 at a repetition rate of 10 Hz, so that each acquisition took 100 s. Being the integral length scale near to 6 × 10−3 m, estimated integrating velocity autocorrelation, the integral time scale can be evaluated making reference to the local mean velocity, about 1.3 ms−1, to be equal to ~4 ms. Due to the fact that, in the processing of random signals, samples are statistically independent if they are separated by a period of the least two times the integral time scales (George 1978) and being the time distance between each couple of images equal to 0.1 s (25 times the integral time scale), the statistical independence between all samples can be stated.

Fig. 1
figure 1

Experimental setup

Full size image

Anyway, in order to evaluate the effectiveness of the number of acquired images, tests on statistical convergence have been performed. In Figs. 2 and 3, the PDFs of the axial velocity and of its spatial derivative in the same direction, with a different number of images, namely 100, 1,000 and 10,000, are compared at the centreline, two diameters downstream of the orifice (Falchi and Romano 2009). A gradual smoothing of the PDF raising the number of samples can be firstly pointed out. The selected number of samples for the present study, 10,000, seems to give a quite smooth converged PDF for both velocity and spatial derivative.

Fig. 2
figure 2

Probability density functions of the axial velocity evaluated with different sample number in correspondence to the jet centreline

Full size image
Fig. 3
figure 3

Probability density functions of the axial velocity spatial derivative evaluated with different sample number in correspondence to the jet centreline

Full size image

3 Results

3.1 Statistical moments

The main aim of present work was studying the effect of varying the optical magnification on the orifice jet near-field statisitics. For this reason, acquisitions with different framed areas have been performed. In detail 2D × 2D, being D orifice diameter (3 cm), 3D × 3D, 4D × 4D and 5D × 5D areas have been acquired at the same Reynolds number, i.e. 35,000. In Table 3, the different experimental conditions are summarized. It is interesting to note that for the first two resolutions the full image size is between 25 and 40 Taylor microscales, whereas for the other two is larger than 50.

Table 3 Parameters of present study
Full size table

The column reporting the ratio between vector spacing and Taylor microscale offers a hint for an observation concerning Nyquist–Shannon sampling theorem. In fact, the different spatial resolutions sampling ability of the inertial range (Taylor microscale λ) gets worse moving from Resolution 1 to Resolution 4 reaching the limit value of half of the Taylor microscale each vector spacing (sampling rate; Nogueira et al. 2005).

Moreover, it has been understood that the effect of magnification in PIV can be viewed as a low-pass filtration of the data (Foucaut et al. 2004). Figure 4 shows a comparison between the power spectral densities of the axial velocity component (E 11) at jet centreline evaluated in correspondence to the four different magnification factors. Clearly, by increasing the magnification factor, the PSD is extended towards the high frequencies. The improved resolution allows not only to increase the maximum Kλ by a factor 3, but also to derive a better description of the inertial scales (Kλ around 1). The slope −5/3 is not fulfilled due to the strong anisotropic flow field in the near jet outlet.

Fig. 4
figure 4

Comparison between the power spectral densities evaluated at different magnifications

Full size image

Figures 5 and 6 show two overall results in the case of 5D, the poorest resolution, with the aim to provide an overview of the phenomenon. The mean velocity confirms the fact reported in literature for this jet flow (Mi et al. 2007) that the mean flow spreads out axisymmetrically and longitudinal velocity reaches its maximum a few diameters downstream to the orifice (vena contracta), as discussed and shown later (Fig. 8). Moreover, it should be pointed out that the radial RMS component v′ exhibits a distinct peak around one diameter downstream of the outlet, exactly where is the section of vena contracta. In addition, all those jet features developing from \(\frac{x}{D}=0\) in a contraction jet are now displayed at \(\frac{x}{D}=0.5-1\) due to the vena contracta phenomenon (Rajaratnam 1976).

Fig. 5
figure 5

Axial velocity mean field contours

Full size image
Fig. 6
figure 6

Radial velocity RMS contours

Full size image

In order to get a better knowledge of the near field of this jet, in Fig. 7, the longitudinal mean velocity radial profiles have been plotted at downstream positions (0.1D, 1D, 2D, 3D and 4D), at Resoluton 4. First of all, it can be clearly seen the distinctive shape of the mean velocity exit profile of an orifice jet, with the two velocity peaks near the edges (Mi et al. 2001). This is different from the top hat profile of a nozzle jet and the power law profile \(\left( \frac{1}{7} \right)\) of a pipe jet (Mi et al. 2001). Then, the interaction between jet and the surrounding fluid starts, and velocity tends to be smoothed in space and the profile to enlarge over and over.

Fig. 7
figure 7

Transverse profiles of axial velocity in correspondence to different positions downstream to the orifice

Full size image

Aiming to highlight the vena contracta, first of all, the profiles of longitudinal velocity along the axis of the jet should be drawn. Such a plot is shown in Fig. 8. Here, U c and U max denote the centreline mean velocity and its maximum value at the vena contracta. The position of the maximum velocity about one diameter downstream to the orifice is clearly seen. This is just an evidence of vena contracta phenomenon. No substantial effect of optical magnification affects such a large-scale plot.

Fig. 8
figure 8

Centreline longitudinal velocity behaviour

Full size image

The effect of optical magnification can be better pointed on transverse profiles of the statistical moments and Reynolds stress tensor, as presented in Figs. 9, 10, 11, 12, 13, 14 and 15.

Figures 9 and 10 show the transversal profiles of axial mean velocity, respectively, at 0.1D and 2D downstream to the orifice. It can be noticed the slight difference between the results of the higher resolution setups (Resolutions 1 and 2, Table 3) and the lower ones (Resolutions 3 and 4). Indeed, data coming from Resolutions 3 and 4 are averaged onto a large framed area, i.e. containing the moving fluid inside the jet and the quite still ambient fluid. On the other hand, at the downstream profile presented in Fig. 10, the effect of optical magnification almost vanishes.

Fig. 9
figure 9

Transverse profile of axial velocity at 0.1D downstream to the orifice

Full size image
Fig. 10
figure 10

Transverse profile of axial velocity at 2D downstream to the orifice

Full size image

In the same Fig. 9, a comparison between the very near-field axial velocity transverse profiles of the present work and two references is shown. The one by Mi et al. (2001) is a hot-wire anemometry (HWA) measurement on an orifice jet at Re = 16,000, while the one by Zhang et al. (2014) is a Large Eddy Simulation of an orifice jet at Re = 50,000. First of all, the high spatial resolution HWA data ~10−5 m lie near to the present results which have highest resolution (Resolutions 1 and 2).

This ensures goodness of a proper PIV study compared to HWA measurements, preserving the advantage of non-intrusivity. Moreover, a good agreement is achieved between the higher resolution results and the numerical simulation.

The vena contracta phenomenon can also be observed in Fig. 11 representing the radial velocity transverse profile in the very near zone (0.05D downstream to the orifice). In contrast to the results from other turbulent jets, the radial velocity preserves a univocal sign along each of the two sides of the jet that are determined by jet centreline. This means that, very close to the outlet, the jet does not spread outwards, as pipe and contraction jets, but rather reduces its section due to the orifice and this reduction persists downstream to the orifice plate.

Fig. 11
figure 11

Transverse profile of radial velocity at 0.05D downstream to the orifice

Full size image

Also in RMS radial profiles, a relevant effect of optical magnification is observed close to the orifice. Figures 12 and 13 display the transverse profile of the root mean square of the axial component of velocity, respectively, at a distance 0.1D and 2D downstream to the orifice. As for the mean velocity field, also the RMS exit profiles exhibit a distinctive shape: low values at the centre of the jet and two sharp peaks at the edges (Mi et al. 2001; Quinn 2005). Due to the different optical magnifications, these peaks appear as sharper as higher the resolution (Resolution 1), and then, more and more smoothed as the spatial resolution decreases. The effect is less evident in the radial profiles at a distance x = 2D from the orifice, as presented in Fig. 13. The results in correspondence to 0.1D are also compared with those of Quinn (2005), obtained by HWA. Again, the present results seem to split into two groups, one at high resolution (Resolutions 1 and 2), which remains near to the HWA results, and those at lower resolution (Resolutions 3 and 4) which are quite smoothed.

Fig. 12
figure 12

Transverse profile of axial velocity RMS at 0.1D downstream to the orifice

Full size image
Fig. 13
figure 13

Transverse profile of axial velocity RMS at 2D downstream to the orifice

Full size image

For higher-order statistical moments, the effect of spatial resolution is felt also farther from the orifice. In Figs. 14 and 15, radial profiles of skewness and flatness factors are presented at a distance x = 2D from the orifice. Reference data about these higher-order statistics of an orifice jet cannot be found in literature. The larger framed areas generate a result much smoother than the one resulting from the smaller areas, especially near the centre of the jet. Actually, the effect of lowering the resolution seems to give an illusory larger intermittency (positively skewed and leptokurtic) in correspondence to the centreline (Rajaratnam 1976).

Fig. 14
figure 14

Transverse profile of axial velocity skewness at 2D downstream to the orifice

Full size image
Fig. 15
figure 15

Transverse profile of axial velocity flatness at 2D downstream to the orifice

Full size image

3.2 Large- and small-scale isotropy

In order to study the occurrence of large-scale isotropy, a characteristic parameter can be evaluated, i.e. the ratio of streamwise to vertical rms velocities, i.e. \(\frac{u^{\prime }}{v^{\prime }}\) (Browne et al. 1984; Djeridane et al. 1996). This is an indicator of the energy supplied to the large scales, due to the fact that the second order structure functions \(\langle (\delta u^{\prime })^{2} \rangle (x,r) = \overline{(u^{\prime }(x+r)-u^{\prime }(x))^{2}}\) and \(\langle (\delta v^{\prime })^{2} \rangle (y,r)=\overline{(v^{\prime }(y+r)-v^{\prime }(y))^{2}}\) tend to \(2u^{\prime ^{2}}\) and \(2v^{\prime ^{2}}\) when \(r \rightarrow \infty\) (Romano and Antonia 2001). If the phenomena were isotropic at large scales, this parameter should be equal to 1, being equivalent the transversal and the axial directions. In Fig. 16, the results of this evaluation are reported.

Fig. 16
figure 16

Axial evolution of large-scale isotropy parameter \(\frac{u^{\prime }}{v^{\prime }}\)

Full size image

For \(\frac{x}{D}<5\), the flow field is far from isotropy in correspondence to large scales. Indeed, the parameter tends towards a value near to 1.3 moving along the jet axis. This fact is confirmed by the existing data on orifice jets (OP) (Mi et al. 2007; Romano and Falchi 2010), both made using PIV technique and having a pixel resolution of 100 and 95 pixel cm−1, respectively (~10−3 m). These results are confirmed also on long pipe jets (LP) (Djeridane et al. 1996), as obtained by Laser Doppler Velocimetry, having a spatial resolution around 10−4 m, and on smooth contraction jets (SC) (Xu and Antonia 2002), by hot-wire anemometry having a spatial resolution of ~10−5 m. No relevant influence seems to be related to the different optical magnifications. Therefore, the large scales, which mainly affect the results of \(\frac{u^{\prime }}{v^{\prime }}\), have only a slight dependence on the choice of the magnification in use unless \(\frac{x}{D}\le 1\) , as also observed from the analysis of low order statistical moments.

With regard to the small-scale isotropy, the parameters to be derived from the data available through a PIV study have been measured, namely K 1, K 3, K 4 and K 9, as presented in Sect. 1. The results are shown in Figs. 17, 18, 19 and 20 compared with the ones of Romano and Falchi (2010) on the same jet in correspondence to Re = 20,000 with a pixel resolution of 95 pixel cm−1. Spatial derivatives have been evaluated making use of finite difference approximations with second order accuracy.

The parameter

$$K_1=\frac{\left\langle \left( \frac{\partial v}{\partial y} \right) ^2 \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle }$$

compares the spatial evolution of longitudinal and transversal velocities along their own direction. In an isotropic phenomenon, all the directions are equivalent, and therefore, this ratio should be equal to 1, as given in Eq. (9). The results, depicted in Fig. 17, show a univocal tendency towards the fulfilment of this hypothesis, already in the near zone \(\left( \frac{x}{D}<5 \right)\), in correspondence to all resolutions. In the very near-field zone \(\left( \frac{x}{D}<2 \right)\) spatial gradients are more intense, and therefore, the effects of magnification and related spatial resolution are more pronounced there and tend to diminish moving downstream as the spatial gradients are smeared out by viscosity.

Fig. 17
figure 17

Axial evolution of small-scale isotropy parameter \(K_1\)

Full size image

The parameter

$$K_3=\frac{\left\langle \left( \frac{\partial u}{\partial y} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle }$$

estimates the relative importance, with regard to the longitudinal velocity component, of the transversal evolution with respect to the axial one. If isotropy conditions were fulfilled, this parameter should be equal to 2, as given in Eq. (9). From Fig. 18, this condition does not seem to be fulfilled in the near zone, in agreement with Romano and Falchi results. Here, the optical magnification only affects the very near zone and not the rest of the jet.

Fig. 18
figure 18

Axial evolution of small-scale isotropy parameter \(K_3\)

Full size image
$$K_4=\frac{\left\langle \left( \frac{\partial v}{\partial x} \right) ^2 \right\rangle }{ \left\langle \left( \frac{\partial u}{\partial x} \right) ^2 \right\rangle }$$

is corresponding and opposite of \(K_3\) concerning axial evolution of transversal velocity. The isotropic value is equal to 2, and again this condition does not seem to be satisfied (Fig. 19) in the studied zone, in agreement with Romano and Falchi (2010). Once more, the effect of different optical magnifications is noticeable in the very near zone and to a lesser degree moving downstream along the axis of the jet \(\left( \frac{x}{D}<2\div 3 \right)\). The isotropy condition is far to be satisfied.

Fig. 19
figure 19

Axial evolution of small-scale isotropy parameter \(K_4\)

Full size image

The last studied parameter

$$K_9=\frac{\left\langle \frac{\partial u}{\partial y} \frac{\partial v}{\partial x} \right\rangle }{\left\langle \left( \frac{\partial u}{\partial x} \right) ^2\right\rangle }$$

depends on the cross derivatives of axial and transversal velocities. The isotropy condition prescribes that its value should be equal to −0.5 and again does not seem to be satisfied, irrespective of the framed area, Fig. 20, showing, however, a splitting of the results between high magnification and low magnification ones.

In this cross derivative moment, the effect is much higher than in the other ones.

Fig. 20
figure 20

Axial evolution of small-scale isotropy parameter \(K_9\)

Full size image

4 Conclusions

The near zone of a sharp edged round orifice jet has been investigated, focusing particularly on the influence of optical magnification on the study of a jet based on the PIV technique. To this aim, both large- and small-scale features of the jet have been studied varying the size of the framed area through the object plane distance. Such results on high-order statistics and on spatial derivatives of orifice jets cannot be easily found in the literature. The selected optical magnifications are larger than what usually employed in PIV (except for the lower one). Regarding the large scales, first of all, the occurrence of the vena contracta phenomenon for an orifice jet has been shown in several ways. In addition, it has been highlighted the limited influence of optical magnification on low order statistical moments, which slightly rises as the order of the statistics becomes higher due to local averaging. This shows the importance of a proper choice of the setup, in particular as regard to the optical magnification. Then small-scale features of the jet have been examined, particularly with interest to the evaluation of spatial derivatives of velocity components and then to the fulfilment of isotropy hypotheses of the jet. Based on those data, an incomplete local isotropy condition is attained, although restricted to the near zone, and an influence of optical magnification that is moderate on the overall behaviour of the phenomenon (spatial derivatives and deductions about symmetry hypotheses) and high on the determination of local features of such a jet. Generally speaking, a practical regulation can be pointed out: the size of the acquired region should not exceed a limiting value that is around 30–40 Taylor microscales. For smaller magnifications (i.e. for an acquired region which is larger than 50 Taylor microscales), the statistical moments are smoothed in the near field starting from mean velocity and this effect propagates further downstream for higher-order moments, due to the bigger relationship with small scales.