1 Introduction

The discovery of the Talbot effect dates back by almost two-hundred years, when Henry Fox Talbot [1] shone a white light to a periodic grating and detected the repeated multicolored light patterns that shared the shape of the grating at some specific distances. Lord Rayleigh [2] later explained the effect as repercussions of a Fresnel or near-field diffraction phenomenon of a highly coherent light beam, and the lensless self-images of the diffraction grating appear repeatedly at longitudinal intervals from the grating plane, separated by so-called Talbot length \(L_T\), which can be approximated using paraxial optics as \(D^2/\lambda\), where D is the grating period and \(\lambda\) represents the wavelength of the optical source. Since then, numerous advancements related to this near-field effect have been reported. Spatial manifestation of the Talbot carpets, the optical carpets originated from integer, and fractional Talbot effects were demonstrated using a coherent optical source [3]. The light carpet was demonstrated to be capable of prime number decomposition [4]. Demonstrations of the Talbot effect associated with other optical elements including a mask grating, a lens, and a double-slit were examined [5,6,7]. High contrast Talbot patterns were obtained through an approach using two overlapping gratings [8]. It was also shown that an appropriate spherical wave front, formed via a monochromatic beam and a microscopic objective, could bring about the angular Talbot carpet in angular spectrum [9], where the phase of the angular Talbot carpet was later investigated using a far-field holography method [10]. The Talbot effect idea was extended to create temporal Talbot carpets, which could be produced by bright or dark pulse trains transmitted in dispersive optical components and observed in single-mode fibers [11, 12]. Using space-time wave packets, the temporal Talbot effect in free space [13] and the veiled space–time Talbot effect [14, 15] were achieved. The nonlinear Talbot phenomenon from nonlinear optical beams was explored experimentally and theoretically as well [16,17,18]. The Talbot patterns based on periodic structures of Bose–Einstein condensates [19, 20] and electromagnetic induced transparency atomic medium [21, 22] were formulated—displaying atom–light interactions. The Talbot sources are not only restricted to optical beams, but the effect was also demonstrated for ultrasonic and water waves [23, 24]. Moreover, the Talbot effect was applied in the production of an optical lattice [25], to the detection of diffraction grating period [26], spectral measurements [27,28,29], characterization of optical vortices with multiple topological charges [30,31,32,33,34,35], lithography processes [36], and to optical manipulation of minuscule particles [37].

The Talbot idea was also expanded by Lau for spatially incoherent sources using a double setup with same-period gratings, later named as the Talbot–Lau effect [38]. Incoming waves are made transversely coherent by the first grating and interfered to form the Fresnel diffraction patterns by the second grating [3, 39]. These patterns almost resemble those of the Talbot effect, except for having no lateral phase shifts of the self-images for odd multiples of the Talbot length. The Lau studies found applications in optical lithography and medical X-ray imaging. The Talbot–Lau fringes produced by light-emitting diode (LED) arrays were scrutinized for photolithography [40]. In medical imaging, X-ray Talbot–Lau phase-contrast interferometers were employed for detecting human organs [41, 42]. Recent techniques for X-ray Talbot–Lau interferometry involve enhanced phase gratings composed of gold [43], a scanning configuration which could picture large target samples [44], and mechanical systems that could adapt the Talbot–Lau setup to function for conventional X-ray imaging [45]. Due to de Broglie wave nature of incoherence, many works have also focused on matter wave interferometry based on the near-field Talbot–Lau effect to probe particle quantum properties [46, 47]. These near-field interferometers were used with various particles including rubidium atoms [48], fullerenes [49], positrons [50], oligoporphyrins [51], and antibiotic polypeptides [52]. The Talbot–Lau structure was proposed for inertial detection for particle beams [53]. The Talbot–Lau interferometer was used with a neutron beam and exploited for investigation of the inner frameworks of electrical steel sheets [54], magnetic field spatial distribution [55], and the splitting of the spin states [56].

In this paper, studies to further enrich our knowledge on the Talbot and Talbot–Lau effects for different types of spatially coherent and incoherent optical sources, such as a 483 nm external cavity diode laser, and a common single 635 nm LED, are reported. Talbot carpet weaved by the overlapping grating method [8] and Talbot–Lau carpets fabricated via same- and different-period diffraction gratings were implemented. The characteristics of transverse phase shifts in the Talbot–Lau images with high clarity appeared when using a first grating having a period twice that of the second grating. Led by the results in these studies, the concept of a wavemeter for incoherent light is proposed as well.

2 Talbot effect with 483 nm tunable diode laser

Fig. 1
figure 1

a A coherent beam diffracts through the grating \(G_1\). The first grating self-image of \(G_1\) at \(L_1=L_T\) delivers another diffraction via \(G_2\). A smaller open fraction of the Talbot pattern can be obtained by selecting an appropriate transverse shift \(\delta\). b An incoherent beam propagates through the Talbot–Lau setup with \(G_1\) and \(G_2\) to a screen along the x-axis over distances \(L_1\) and \(L_2\), respectively

Full size image
Fig. 2
figure 2

Optical carpet generated with 483 nm tunable diode laser in two-grating Talbot setup for \(0.76L_T<L_2<3.24L_T\) with 25 \(\mu m\) steps used in scanning, and D=100 \(\mu\)m: a simulation according to \(I_1=\psi _1^*\psi _1\), and b experiment. The effective open fraction was set as \(f_{eff}\simeq 0.25\)

Full size image

First, we implement the optical carpet using the 483 nm tunable diode laser in the Talbot effect with two overlapping gratings. This laser source is an external cavity diode laser. Figure 1(a) schematically illustrates the set-up, consisting of a plane wave of light with wavelength \(\lambda\) diffracting through a grating \(G_1\) by a distance \(L_1\) to another grating \(G_2\) having the same period D. The grating open fraction f provides a grating window size \(a = fD\), such as \(f=0.5\) for a typical Ronchi grating. Adjusting the transverse shift \(\delta\) provides a smaller open fraction f and can deliver an interference pattern with higher contrast behind the grating \(G_2\). The grating transmission function can be written as, \(T_G(x_0)=\Sigma _n A_n \exp (2 \pi i n x_0/D)\). Therefore, in the near-field regime with the Fresnel approximation, the exact wave function on the screen in Fig. 1(a) is given by [8]

$$\begin{aligned}{} & {} \psi _1(x,L_1,L_2)=\sum _{{n_1},{n_2}} A_{n_1} A_{n_2} \exp \left\{ \frac{2\pi i}{D} [({n_1}+{n_2})x-{n_2}\delta ]\right\} \nonumber \\{} & {} \quad ~~~~~~\times \exp \left\{ \frac{i\pi \lambda }{D^2}[{n_1}^2L_1+({n_1}+{n_2})^2L_2]\right\} , \end{aligned}$$
(1)

where \(A_{n_1}=\sin (n_1 \pi f)/n_1 \pi\), and \(A_{n_2}=\sin (n_2 \pi f)/n_2 \pi\) are the Fourier component associated with the periodicity and the open fraction of grating [3]. At \(L_1=L_T\), the transverse shift \(\delta\) equal to \(f_{eff}d\) with \(f_{eff}<0.5\) is expected to provide a narrower effective open fraction as presented in Ref. [8]. Figure 2 illustrates a simulation of the optical carpet according to \(I_1=\psi _1^*\psi _1\) in comparison to the experimental results for \(\lambda =483\) nm with D=100 \(\mu\)m for both gratings (i.e., diffraction gratings with 10 lines/mm, PHYWE). The theoretical simulation matches the experiment when setting \(f_{eff}\simeq 0.25\). The experiment can be set to this \(f_{eff}\simeq 0.25\) by scanning the second grating \(G_2\) transversely.

Our results confirmed that the method of overlapping gratings for small open fraction was able to create high-contrast fractional and integer Talbot patterns  [8, 57] comparable to those optical carpets formed by a single symmetric grating. The external cavity diode laser with a wavelength of 483 nm is essential for two-photon Rydberg excitation of rubidium atoms, which could be incorporated with electromagnetically induced Talbot carpet for optical imaging that provides a diagnostic tool for neutral atoms or molecules. This novel concept will be further tested in our laboratory in the near future.

3 Talbot effect with 635 nm light-emitting diode

Fig. 3
figure 3

Experimental Talbot setup for 635 LED with varied distances between LED and grating (L)

Full size image

We explore the implications of an incoherent and spherical wavefront to the near-field pattern. The incoming beam, from a LED, propagates along the z-axis with a wavefront on the \(x_0\)-axis (Fig. 3). For the spatial incoherent beam, we utilize an initial wave function \(\psi _0(x_0)=\exp (i k_{\theta } x_0)\) where \(k_{\theta }= k \sin \theta\) represents the projection of the incident wave vector (\(k=2\pi / \lambda\)) onto the \(x_0\)-axis [3]. The spherical wavefront is considered by applying the transmission function \(T_{R}(x_0)=\exp (-ikx_0^2/2R)\) with R representing a radius of curvature. Subsequently, the grating transmission function \(T_G(x_0)\) is used to obtain a wave function behind the grating, \(G_1\) (Fig. 3). Therefore, the diffracted wave function on the xz plane is obtained by applying the Huygens-Fresnel integral

$$\begin{aligned} \psi _2(x,z)= & {} \hat{F}(x,z;x_0,0)T_G(x_0)T_{R}(x_0)\psi _{0}(x_0). \end{aligned}$$
(2)

Here, \(\hat{F}(x,z;x_0,z_0)\) is assigned as a transition operator

$$\begin{aligned} \hat{F}(x_b,z_b;x_a,z_a)\equiv \sqrt{\frac{ik}{2 \pi (z_b-z_a)}} e^{-ik(z_b-z_a)} \int _{-\infty }^{\infty }dx_a~e^{\frac{-ik(x_b-x_a)^2}{2(z_b-z_a)}}. \end{aligned}$$
(3)

The longitudinal positions (\(z_a\) and \(z_b\)) can be reduced to \(z_a=0\) and \(z_b=z\), then \(z_b-z_a=z\). The analytic calculation yields

$$\begin{aligned} \psi _2(x,z)= & {} \sum _{{n}} A_{n} \exp \left\{ \frac{2\pi i n (x+z \sin \theta )}{MD}+\frac{i\pi n^2 z}{M(D^2/\lambda )} \right\} , \end{aligned}$$
(4)

where the \(M=1+(z/R)\) in the obtained expression can be interpreted as the magnification to the fringe period and the Talbot length, respectively. The factor constants including the phase constant were neglected.

The influence of spatial incoherence can be included by taking the sum over all \(\theta\) contributing to the intensity [3],

$$\begin{aligned} I_{2}= & {} \sum _{\theta =-\pi /2}^{\pi /2}\psi _2^*\psi _2. \end{aligned}$$
(5)

We use the approximation \(\sin \theta \simeq \theta\) to replace the summation with an integral over small angles. Consequently, the calculation can be done analytically and yields

$$\begin{aligned} I'_2= & {} \int _{-\theta _{max}}^{\theta _{max}}d\theta ~ \psi _2^*\psi _2 =\sum _{{n,m}} A_{n}A_{m}\frac{MD}{\pi (n-m)z} \sin \left[ \frac{2\pi (n-m)z\theta _{max}}{MD}\right] \nonumber \\{} & {} ~~~~~\exp \left\{ \frac{2\pi i (n-m) x)}{MD}+\frac{i\pi (n^2-m^2) z \lambda }{M D^2} \right\} , \end{aligned}$$
(6)

where \(\theta _{max}\) is less than 10 degrees to justify the approximation [58]. Lastly, the spectral bandwidth of the wavelength of the emitted light from the diode has to be involved. We assume a wavelength distribution following the Gaussian. Hence, the intensity pattern will be

$$\begin{aligned} I''_{2}= & {} \sum _{\lambda '=0}^{\infty }e^{-\frac{(\lambda '-\lambda )^2}{\sqrt{2}\beta ^2}}I'_{2}, \end{aligned}$$
(7)

where \(\beta\) represents the radius of the wavelength distribution [59]. Figure 3 is a sketch of the setup. A LED with \(\lambda =635~\)nm was used as an incoherent source. The distance, L between the LED and the grating (\(G_1\), \(D=100 \mu\)m, PHYWE) was varied, but the distance between the grating and the CCD camera (MT9J003 1/2.3-inch 10 Mp CMOS with pixel size p of 1.1 \(\mu\)m) was fixed as one Talbot length (\(z=L_T=\)15.75 mm). The experimental results are shown in Fig. 4 for different distances L. The visibility of the pattern increases with distance as discussed above. In our recent experiment, the distance L larger than 300 mm, provides the starting of clear visibility. In Fig. 5, the theoretical simulations \(I''_2\) match well the experimental results when fixing \(\theta _{max}=10^o\) and FWHM \(\beta =16~nm=2.5~\%\) of the center wavelength \(\lambda =635~ nm\). The magnifications \(M=\) 1.40, 1.16, 1.07, and 1.03 to match the extended interference fringes depend on the distances from the light source to the grating L.

Fig. 4
figure 4

Interference patterns in the Talbot setup with varied distances between LED and grating of a L= 30 mm, b 100 mm, c 300 mm, and d 500 mm. Visibility increases with the distance L

Full size image
Fig. 5
figure 5

The experimental interference patterns (the cross sections from Fig. 4) and the simulations (solid lines) according to Eq. (7) at \(z=L_T\)=15.75 mm with D = 100 \(\mu m\) and M=1.40 (a), 1.16 (b), 1.07 (c) and 1.03 (d). Please see the text for details

Full size image

The results in this section exhibit significant benefits as the Talbot effect can be applied even with spatially incoherent light if the distance from the light source to the grating is large enough. One possible application is shown in the last section.

4 Talbot–Lau effect with 635 nm light-emitting diode

For this section, we consider the Talbot–Lau effect used an incoherent beam with two gratings. We employ the initial wave \(\psi _0(x_0)\) with the wavenumber projection \(k_{\theta }\) used in the previous section, but the light source is close to the grating. The wave diffracts through the grating \(G_1\) to \(G_2\), and these two gratings have periods (\(D_1\), \(D_2\)), and open fractions (\(f_1\), \(f_2\)), as depicted in Fig. 1(b).

Fig. 6
figure 6

Optical carpets of Talbot–Lau effect with \(f_1=f_2=0.5\) and a \(D_1=D_2= 200 ~\mu\)m (experiment with no phase shift), b \(D_1=200 ~\mu\)m, \(D_2= 100 ~\mu\)m (experiment with phase shift), c \(D_1=D_2= 200 ~\mu\)m (simulation (Eq. 17) with no phase shift), and d \(D_1=200 ~\mu\)m, \(D_2= 100 ~\mu\)m (simulation with phase shift). The vertical dashed lines mark the phase shift of the condition (b) and (d)

Full size image

According to the grating transmission function \(T_G\) and the defined transition operator Eq. (3), the wave function on the \(xL_2\)-plane is given by

$$\begin{aligned} \psi _3(x,L_1,L_2)= & {} \hat{F}(x,L_2;x_1,0)T_{G_2}(x_1)\hat{F}(x_1,L_1;x_0,0)\nonumber \\{} & {} T_{G_1}(x_0)\psi _{0}(x_0). \end{aligned}$$
(8)

With analytic integrations, similar to Eq. (5), the intensity pattern including the spatial incoherence can be written as

$$\begin{aligned} I_{3}= & {} \sum _{\theta =-\pi /2}^{\pi /2}\psi _3^*\psi _3=\sum _{{n_1,n_2}}\sum _{{m_1,m_2}} A_{n_1}(f_1)A_{n_2}(f_2)A_{m_1}(f_1)A_{m_2}(f_2) \nonumber \\{} & {} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\times \exp \left( iPx+iQ\lambda +iW\sin \theta \right) , \end{aligned}$$
(9)

where

$$\begin{aligned} P= & {} 2\pi \left( \frac{n_1-m_1}{D_1}+\frac{n_2-m_2}{D_2}\right) , \end{aligned}$$
(10)
$$\begin{aligned} Q= & {} \frac{\pi L_1 \left( n_1^2-m_1^2\right) }{D_1^2}+\pi L_2 \left( \left( \frac{n_1}{D_1}+\frac{n_2}{D_2}\right) ^2-\left( \frac{m_1}{D_1}+\frac{m_2}{D_2}\right) ^2\right) , \end{aligned}$$
(11)
$$\begin{aligned} W= & {} 2 \pi \left( \frac{\left( L_1+L_2\right) \left( n_1-m_1\right) }{D_1}+\frac{L_2 \left( n_2-m_2\right) }{D_2}\right) . \end{aligned}$$
(12)

Using the small-angle approximation as in Eq. (6), we obtain

$$\begin{aligned} I'_3= & {} \int _{-\theta _{max}}^{\theta _{max}}d\theta ~\psi _3^*\psi _3 \nonumber \\= & {} \sum _{{n_1,n_2,m_1,m_2}}A_{n_1}A_{n_2}A_{m_1}A_{m_2} \frac{2\sin (W \theta _{max})}{W} e^{ \left( iPx+iQ\lambda \right) } \end{aligned}$$
(13)

However, the mixture of \(k\sin \theta\) in each orientation results in the interference pattern disappearing unless the \(\theta\)-dependence that corresponds to the factor \(\sin (W \theta _{max})/W\) has a maximum value equal to 1 when W goes to zero. The vanishing of the function W is achieved under some particular conditions. As an example, in the case of \(D_1=D_2=D\), the W will be zero only if

$$\begin{aligned} L_2=L_1 \frac{n_1-m_1}{(m_1-n_1)+(m_2-n_2)}. \end{aligned}$$
(14)

If we choose \(L_1=L_2=L\), the function \(W=0\) in the series when \((n_2-m_2)=-2(n_1-m_1)\) [3] that makes \(\sin (W \theta _{max})/W=1\) and the exponent reduced to

$$\begin{aligned} iPx+iQ\lambda =\frac{2\pi i(m_1-n_1)x}{D}+ \frac{\pi i(m_1-n_1)(m_2+n_2)L}{D^2/\lambda }. \end{aligned}$$
(15)

The above expression is similar to \(\psi _1^*\psi _1\) (Eq.(1)), which can produce the optical carpet behind \(G_2\) by maintaining \(L_1=L_2\). Not only the case \(D_1=D_2\) works, but also different grating periods can be used. For example, in the case \(D_1=2D_2=D\) with \(L_1 =L_2\), the condition \(W=0\) is satisfied in the series when \(n_2-m_2=m_1-n_1\)

$$\begin{aligned} iPx+iQ\lambda =\frac{2\pi i(m_1-n_1)x}{D}+ \frac{\pi i(m_1-n_1)(m_2+n_2)L}{2D^2/\lambda }. \end{aligned}$$
(16)

The fraction 1/2 in the second term causes a longitudinal phase shift in the optical carpet compared to the typical case. Then, the theoretical simulations involving Gaussian wavelength distribution can be calculated as

$$\begin{aligned} I''_{3}= & {} \sum _{\lambda '=0}^{\infty }e^{-\frac{(\lambda '-\lambda )^2}{\sqrt{2}\beta ^2}}I'_{3}, \end{aligned}$$
(17)

Our demonstration was done for these two cases, i.e., \(D_1=D_2= 200 ~\mu\)m and \(D_1=200 ~\mu\)m, \(D_2= 100 \mu\)m, and the results are shown in Fig. 6. All gratings are binary grating with \(f = 0.5\). The phase shifts (marked with the vertical dashed lines) at Talbot distances, which typically occur only with the Talbot effect, can happen here with the condition that the second grating has half the period of the first grating. To the best of our knowledge, an appearance of this phase shift in the Talbot–Lau effect is here shown for the first time. Also, with this configuration, the interference contrast with at least twice the value can be clearly measured compared to a normal setup (\(D_1=D_2\)). This makes benefit when working with low contrast sources such as in matter wave optics.

5 Application

Fig. 7
figure 7

Near-field wavemeter for incoherent light sources. a shows the experimental setup, while b and c are the optical carpets of green LED and calibration laser, respectively. The distance L from the grating to the camera was varied, allowing the optical carpet to be captured on a single image of the camera. Please see the text for details

Full size image

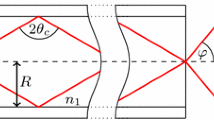
A near-field Talbot wavemeter was earlier demonstrated with coherent light, such as a laser source [27, 28, 60, 61]. These schemes cannot be applied to spatially incoherent light sources. For these, a two-grating Talbot–Lau interferometer is required. We demonstrated the use of the Talbot effect with spatially incoherent light with the help of an optical fiber and a collimating lens [34]. The distance between the source and the grating must be large enough in order to obtain the interference pattern as presented in section 3. This can be satisfied using an optical fiber to stretch this length. Our experimental setup, illustrated in Fig. 7(a), is suited for this purpose. It has a multi-mode fiber (MF, M42L01, Thorlabs) and lens (A390TM-B, Thorlabs) for adapting the incoherent light source to provide a transversely coherent wave. The inclined grating, G (80 Grooves/mm, Edmund optics) configuration can then generate an optical carpet which was detected by the camera (MT9J003 1/2.3-inch 10 Mp CMOS with pixel size p of 1.1 \(\mu\)m). In order to obtain the optical carpet, the periodicity of the grating must be aligned with the x-axis. Figure 7(b) and (c) represent the experimental optical carpets with a green light-emitting diode (LED) and a 780.24 nm tunable laser, respectively. Our tunable laser [62] with stable single-wavelength operation at around 780.24 nm (\(\lambda _{Cal}\)) was used for calibration. Therefore, the measured wavelength of an unknown light source (\(\lambda\)) can be extracted as

$$\begin{aligned} \lambda = \lambda _{Cal} L_{T(Cal)}/L_T, \end{aligned}$$
(18)

where \(L_T\) and \(L_{T(Cal)}\) are the Talbot lengths of the unknown light source and the calibrated laser (780.24 nm laser), respectively.

With this method, the empirical parameters, i.e., the grating period, the tilt angle (\(\phi\)), and the camera pixel size, do not need to be known. According to our results, the wavelength of the green LED when calculated according to Eq. (18) was 535.92 nm. This is a typical value for this particular LED. The accuracy was based on that of the calibration laser.

6 Conclusion

Talbot and Talbot–Lau effects have a number of potential applications. In our work, a broadband spatially incoherent light can also be used for the Talbot effect, provided a long enough distance between the light source and the grating, for which an optical fiber can also be applied. In our example, the good contrast starts at the distance of about 300 mm. This is a good distance matching with the use of such fiber cables. Second, good interference contrast in the Talbot–Lau experiments can be gained if the second grating period is half that of the first grating. From our recent experiments, this contrast can be increased at least twice. In addition, the phase shift at each Talbot distance (which normally occurs only in the Talbot effect) can also be seen in this Talbot–Lau configuration. This observation might be useful in optics applications and even in matter wave optics. In the last section, a wavemeter for measuring a spatially incoherent light source has been demonstrated as one possible application. Our demonstration deals with the wavelength measurement of a green LED. The measured wavelength of 535.92 nm can be obtained nicely. We are convinced that our recent studies provide useful information to the optics community for both research and applications.