Uncertainty quantification for high-temperature gas sensing using direct laser absorption spectroscopy

Abstract

We performed a detailed numerical uncertainty quantification of the fixed- and scanned-wavelength direct absorption spectroscopy method (DA) at high temperature. A transition near 2551 nm, relevant to water vapor sensing in a shock tube facility, was considered. The uncertainty quantification for this transition was based on a critical evaluation of the uncertainty associated with each parameter required for DA modeling. The results show a non-negligible uncertainty on the water concentration with a standard deviation on the order of $7\%$ when perturbing all the parameters separately at their maximum uncertainty. This uncertainty originates mainly from the uncertainty on temperature, pressure, line strength, and lower state energy. The non-negligible error induced by finite scanning time in scanned-DA was also discussed and a local optical Damköhler number was introduced to characterize such a phenomenon. The uncertainty for practical temperature measurement using the two-color DA approach was also estimated. Depending on the selected absorption line pair, the minimum uncertainty can be as low as 5.1% or as high as 18%.

1 Introduction

Shock tube is widely used in combustion research, owning to the wide range of test-gas conditions that can be achieved in such a facility, i.e., temperature range from 600 to 3000 K and pressure range from sub-atmospheric to 100 MPa [1]. Measuring species-time histories and thermodynamic conditions within a shock tube is required for accurately characterizing the dynamics of chemical systems, and improving chemical kinetics mechanisms, via the fine-tuning of specific reaction rate constants [2]. For species-time histories, laser absorption techniques can provide a non-intrusive, fast-response measurement, and are particularly well suited for monitoring combustion experiments in shock tube. Direct laser absorption (DA) has been widely applied in shock tube species-time histories measurements [2,3,4]. Infrared (IR) and ultraviolet (UV) active species, such as CO, $\hbox {CO}_2$, $\hbox {H}_2\hbox {O}$, and OH, can be monitored with IR or UV direct absorption.

However, the measuring procedure will inevitably introduce uncertainties. Previous studies estimated the measurement uncertainties in shock tube from different aspects. Petersen et al. [5] estimated the temperature measurement uncertainties based on the uncertainties of shock–velocity measurement. During a shock tube experiment, the temperature and pressure behind the reflected shock wave change mainly due to the reactivity of the mixture and the non-ideal pressure rise [2]. For DA measurement in shock tube, the temperature and pressure are needed to calculate species concentration based on measured data. Alturaifi et al. [2] discussed the species-time histories’ uncertainty due to different assumptions on the temperature and pressure profiles in shock tube. Up to $5\%$ difference in CO mole fraction was reported in their work when considering a constant volume or a variable-volume reactor model. Zaczek et al. [6] examined the uncertainties of rate coefficient measurement for the reaction $\hbox {CH}_3$OH + OH $\Rightarrow$ products. Various sources of uncertainties have been estimated in their research including the temperature behind reflected shock ($\hbox {T}_5$), the overall reaction mechanism, and the overall OH absorption coefficients. The overall OH absorption coefficients’ uncertainty was estimated to be $3\%$ in their research. Laser sensors developed in shock tube environment can be extended to other high-temperature reactive flows such as detonation. For example, Peng et al. [7] reported uncertainties induced by absorption parameters on the temperature and water concentration they measured using laser absorption in a rotating detonation engine. The uncertainties on the spectroscopic parameters reported by Goldenstein et al. [8] were employed to determine the overall uncertainty on the measured species concentration and temperature.

In all these previous studies, no detailed uncertainty quantification (UQ) has been done for absorption parameters, which are of the utmost importance for the accurate application of laser absorption techniques in shock tube and other high-temperature reacting media. The known parameters are used to generate simulation results and fit the experimental measurements, allowing to extract the species concentration. The HITRAN database [9] is a widely used open database which provide line-by-line spectroscopic parameters to calculate the absorption coefficient. These parameters are mainly obtained by experimental measurement and inevitably include uncertainty and, possibility errors. The impact of the uncertainty of each spectroscopic parameters on DA measurements in shock tube experiments remains unknown and a detailed uncertainty analysis is required to identify the main source of uncertainty and further improve high-temperature DA measurements. Given the complexity of the DA absorption equations, the classical error propagation approach is hardly applicable and employing a more advanced method such as uncertainty quantification with Monte Carlo sampling of perturbed input parameters is required.

The present paper aims at performing a detailed uncertainty quantification of the direct absorption technique and identify the dominant sources of uncertainty. For this purpose, we employed simulated water vapor profiles generated in hydrogen–oxygen–argon mixtures under shock tube relevant conditions. In Sect. 2, fundamentals of DA in shock tube are presented in detail. In Sect. 3, the uncertainties associated with each spectroscopic and thermodynamics parameter are discussed. In Sect. 4, the UQ calculation method for DA is described. In Sects. 5 and 6, UQ results for different DA approaches are discussed in detail. In Sect. 7, the UQ analysis is extended to another practical case: the two-color temperature measurement with DA. In the last section, concluding remarks are given.

2 Fundamentals of direct absorption in shock tube

Direct laser absorption (DA) is based on Beer–Lambert law [10]

$$\begin{aligned} T_\nu =\left( \frac{I_{t}}{I_{0}}\right) _\nu = \exp \left( -k_\nu L\right) , \end{aligned}$$

(1)

where $T_\nu$ is the transmittance at laser frequency $\nu$; $I_t$ and $I_0$ are the transmitted and incident laser intensity, respectively; $k_\nu$ is the spectral absorption coefficient; L is the absorption path-length. For gas species with fingerprint spectral features associated with individual quantum transitions, the spectral absorption coefficient $k_\nu$ can be further expanded into

$$\begin{aligned} k_\nu = P\chi _i S \phi (\nu ), \end{aligned}$$

(2)

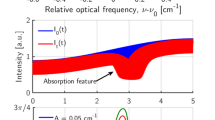
where P is the total pressure of the gas, $\chi _i$ is the mole fraction of the absorbing species, and S and $\phi (\nu )$ are the line strength and line-shape function of the absorption feature. For shock tube laser absorption measurement, an IR or UV laser is typically used to generate incident laser beam. The incident laser travels across the shock tube cross-section at a location close to the end wall. Both transmitted and incident laser intensities are recorded with detectors. This process is shown in Fig. 1.

Fig. 1

Schematic of laser direct absorption in shock tube

For tunable laser diodes, both fixed- and scanned-DA can be applied. For fixed-DA, the frequency of laser light is fixed at the line center of the selected absorption feature. A detailed example of fixed-DA in the IR range is described by Alturaifi et al. [2]. Fixed-DA allows fast sampling rate of species concentration and gas conditions inside the shock tube. The sampling rate can reach up to 1 GHz (estimated based on the time constant of a Vigo PVI-3TE detector which is widely used in the combustion community). However, fixed-DA only records one point in the full absorption spectrum and the measurement can be affected by pressure-induced absorption line frequency shift, which inevitably introduces uncertainty. By recording the whole absorption spectrum, this potential shift of frequency can be ignored. This approach corresponds to the scanned-DA (or scanned-wavelength DA) which uses a periodic signal such as a sawtooth wave to tune simultaneously the intensity and frequency of the laser diodes. Within a small scanning range, the relationship between laser intensity and laser frequency/wavenumber may be considered to be essentially linear. For scanned-DA, the schematic of incident and transmitted laser intensity are shown in Fig. 1. The full absorption feature $T_\nu$ can be extracted and the species concentration can be deduced by fitting the measured $T_\nu$. One important limitation in scanned-DA is the scanning rate. For shock tube experiments, gas conditions can change rapidly especially in the vicinity of the ignition event. Low scanning rate may cause distortion in the measured spectral features due to the rapid changes of species concentration, temperature, and pressure during a single scan period. The sampling rate is mainly limited by the technical characteristics of the laser diode. While near-IR tunable laser diodes can be scanned at up to few gigahertz, mid-IR and far-IR tunable laser can be scanned only at a rate on the order of few hundreds kHz or lower.

3 Uncertainty on spectroscopic parameters

3.1 List of parameters for DA modeling

In this paper, we have considered IR-DA for water vapor measurement under high-temperature conditions. As indicated in Eq. 2, the line strength and the line shape need to be calculated.

For line strength of transition j reported in the HITRAN database [9], a reference temperature of 296 K is used ($S_j(296)$). For calculating the line strength at different temperatures ($S_j(T)$), the lower state energy $E''$ and partition function Q(T) are required, as indicated by

$$\begin{aligned} S(T)= & {} S(T_0)\frac{Q(T_0)}{Q(T)}\exp \left[ -\frac{hcE''}{k}\left( \frac{1}{T}-\frac{1}{T_0}\right) \right] \nonumber \\&\left[ 1-\exp \left( -\frac{hc\nu _0}{kT}\right) \right] \left[ 1-\exp \left( -\frac{hc\nu _0}{kT_0}\right) \right] ^{-1}, \end{aligned}$$

(3)

where h is the Planck’s constant, c is the light speed in a vacuum, k is the Boltzmann’s constant, and $T_0$ is the reference temperature. Q(T), $S(T_0)$, and $E''$ are also available in HITRAN database.

The calculation of the line-shape function ($\phi (\nu )$) requires selecting a line-shape model, and calculating the collisional broadening coefficient ($\Delta \nu _C$) and Doppler broadening coefficient ($\Delta \nu _D$), respectively, defined as (under the configuration of our targeted conditions)

$$\begin{aligned} \Delta \nu _{C}= & {} P\left( {\mathrm{X}}_{\mathrm{H}_2\mathrm{O}}2\gamma _\mathrm{self}+{\mathrm{X}}_\mathrm{Ar}2\gamma _{\mathrm{H}_2\mathrm{O}-i}\right) \end{aligned}$$

(4)

$$\begin{aligned} \Delta \nu _{D}= & {} \nu _0\left( 7.1623 \times 10^{-7}\right) \left( \frac{T}{M_{\mathrm{H}_2\mathrm{O}}}\right) ^{1/2}, \end{aligned}$$

(5)

where $M_{\mathrm{H}_2\mathrm{O}}$ is the molar mass of water and $2\gamma _\mathrm{self}, 2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{i}}$ are the self/i-broadened half-width at half-maximum (HWHM) coefficients. It is noted that $\Delta \nu _{D}$ uses the practical equations given by Hanson et al. [10]. The Voigt profile was selected as the line-shape function due to its wide range of applicability and its good accuracy under near-ambient pressure [11]. The uncertainty induced by the Voigt profile was neglected in the present paper.

The self-broadened HWHM coefficient ($2\gamma _\mathrm{self}$), i-broadened Lorentzian HWHM coefficient ($2\gamma _{\mathrm{H}_2\mathrm{O}-i}$), and temperature exponent for the i-broadened HWHM ($n_i$) are used to calculate $\Delta \nu _C$ [10], where i represents the diluting species. HITRAN database only provides $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$ and $n_\mathrm{air}$. In shock tube experiments, argon is widely used as diluent because of its high isentropic coefficient which enable efficient heating of the test gas. However, measurement of $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{Ar}}$ and $n_\mathrm{Ar}$ is scarce in the literature; Li et al. [12] provide such data for a transition near 7299.431 $\hbox {cm}^{-1}$, whereas Li et al. [13] measured these data for two transitions near 7185.6 $\hbox {cm}^{-1}$ and 7154.35 $\hbox {cm}^{-1}$. The comparison between $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{Ar}}$, $n_\mathrm{Ar}$ and $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$, $n_\mathrm{air}$ for these transitions demonstrates a differences of two-to-three times. Because the present paper is concerned with the uncertainty quantification, and in the absence of specific and reliable measurement for $2\gamma _{\mathrm{H}_2O-\mathrm{Ar}}$ and $n_\mathrm{Ar}$, using the values reported for $2\gamma _{\mathrm{H}_2O-\mathrm{air}}$ and $n_\mathrm{air}$ seems a reasonable approach to generate the absorption profile. Thus, the further analysis in this paper uses $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$ and $n_\mathrm{air}$ instead of $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{Ar}}$ and $n_\mathrm{Ar}$, because these two later parameters are not always available in the literature.

To summarize, the spectroscopic parameters required to apply DA are listed as follows:

• 1. $\nu _0$: Transition central wavenumber

• 2. S(296): Line strength at 296 K

• 3. $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$: Air-broadened Lorentzian HWHM

• 4. $2\gamma _\mathrm{self}$: Self-broadened HWHM

• 5. $E''$: Lower state energy

• 6. $n_\mathrm{air}$: Temperature exponent for the air-broadened HWHM

• 7. $\delta _\mathrm{air}$: Pressure shift induced by air, taken at a reference pressure of 101.3 kPa

• 8. Q(T): Partition function

In addition, the shock tube conditions are also needed:

• 9. $P_5$: Pressure behind reflected shock wave

• 10. $T_5$: Temperature behind reflected shock wave.

Other parameters, such as the optical path-length, can also induce error during shock tube DA measurement. The dimension of shock tube can be precisely measured, so that the error induced by the uncertainty on the optical path-length can be reasonably neglected. For devices induced error, such as background determination and non-ideal laser tuning response, specific procedures, as applied by Alturaifi et al. [2], can be employed to minimize them.

3.2 Uncertainty for HITRAN data

HITRAN database provides values for parameters No. 1–8. It is noted that $\nu _0$ (parameter No.1) was not considered as a source of uncertainty in the following analysis. For fixed-DA, the absorption line-center ($\nu _0$) and the frequency of the laser light can be precisely matched using a static gas cell as done in [2]. For scanned-DA, the whole absorption feature is recorded, which means that the line-center can be selected when processing the data. Thus, the measuring uncertainty of $\nu _0$ does not affect the DA measuring process. On the other hand, the uncertainty of the nine other parameters need to be carefully estimated. The uncertainty levels for the parameters are also provided in HITRAN except for $E''$ and Q(T). In HITRAN, an error code from 0 to 9 (for the line position and air pressure-induced line shift parameters) or 0 to 8 (for the line intensity and broadening parameters) is provided for each item in the HITRAN database [14]. The corresponding uncertainty of the error code used in HITRAN is explained in [14]. In this case, the HITRAN provided uncertainties are used in priority. For $E''$ and Q(T), the uncertainties are estimated based on other researches, as explained in the following sub-sections.

3.3 Uncertainty for partition function

For the partition function ($Q_{\mathrm{H}_2\mathrm{O}}(T)$), our investigation suggests that no direct uncertainty analyses were presented in previous studies. The full partition function Q of a molecule in the ideal gas state is the product of the internal partition function ($Q_\mathrm{int}$) and the translational partition function ($Q_\mathrm{trans}$) [15]. The expressions for $Q_\mathrm{int}$ and $Q_\mathrm{trans}$ are, respectively, shown in Eqs. 6 and  7

$$\begin{aligned} Q_\mathrm{int}= & {} \sum _{i}^{} g_i\left( 2J_i+1\right) \exp \left( \frac{-c_2Ei}{T}\right) , \end{aligned}$$

(6)

$$\begin{aligned} Q_\mathrm{trans}= & {} V\Lambda ^{-3}, \end{aligned}$$

(7)

where $c_2 = hc/k_\mathrm{B}$ is the second radiation constant, $J_i$ is the rotational quantum number, $E_i$ is the rotational-vibrational energy level given in $\hbox {cm}^{-1}$, T is the thermodynamic temperature in K, $g_i$ is the nuclear spin degeneracy factor, and the index i runs over all possible rovibronic energies considered, V is the volume of the system, $\Lambda = h/(2\pi m k_\mathrm{B} T)^{1/2}$ is the de Broglie wavelength, h is the Planck constant, and m is the molecule mass [15].

Among the parameters used to calculate $Q_\mathrm{int}$ and $Q_\mathrm{trans}$, energy levels $E_i$ and T are the major sources for the uncertainties of Q. Their respective effects were treated separately. The uncertainties of $E_{\mathrm{H}_2\mathrm{O}}$ was obtained using the comparisons presented by Tennyson et al. [16]. In their work, the standard deviation of $E_{\mathrm{H}_2\mathrm{O}}$ was estimated as 0.0462 $\hbox {cm}^{-1}$. Then, based on this results and the average energy levels showed in their work, the percentage of uncertainty for $Q_{\mathrm{H}_2\mathrm{O}}(T)$ corresponding to one standard deviation was taken as $0.01944\%$.

3.4 Uncertainty for lower state energy

The uncertainty for lower state energy $E''$ is also not reported in HITRAN database for all available lines. Sung et al. [17] reported measured uncertainty of the lower state energy for water absorption lines near 6576 $\hbox {cm}^{-1}$. The average uncertainty was $5\%$, while the minimum uncertainty was $0.6\%$ and the maximum uncertainty was $8\%$. Despite our efforts, only one paper dealing with the uncertainty on $E''$ could be found. As a consequence, the values presented in this paper should be considered with caution. We have deliberately used the largest possible uncertainty in the main body of the paper. For completeness, Sect. 7 in the appendices presents an additional UQ analysis obtained using the lowest uncertainty value for $E''$.

3.5 Uncertainty for reflected shock conditions

The gas mixture we employed is hydrogen–oxygen mixtures diluted with argon. $P_5$ is set to 0.1 MPa to avoid line-mixing induced by high pressure [18]. The uncertainty of $T_5$ and $P_5$ was estimated based on the uncertainties on the Mach number of incident shock $M_1$, initial pressure $P_1$, and temperature $T_1$ in the driven section. The SDToolbox written by Browne et al. [19] was used to calculate $T_5$ and $P_5$ based on $P_1$, $T_1$ and $M_1$. Table 1 shows two condition sets selected for generating water species profile. Theses cases were selected to represent different water concentration profiles. Case 01 represents a case for which the final water concentration is large and is rapidly reached. In addition, a large temperature change is taking place during the oxidation process. Case 02 represents a case for which the final water concentration is low and is slowly reached. Also, the temperature change is small under these conditions.

Table 1 Compositions and conditions for the Ar-diluted hydrogen–oxygen mixtures used in our analysis

The uncertainty for $T_1$ is known as $\pm 1$ K; the uncertainty for $P_1$ can be neglected based on high-precision gauge usually employed in shock tube experiments, see Knott and Robinson [20]; the uncertainty for $M_1$ was selected as $\pm 1 \%$ based on the analysis of Petersen et al. [5]. The nominal values of $T_1$, $P_1$ and $M_1$ corresponding to the selected $T_5$ and $P_5$ were first calculated via an optimization process using the SDToolbox. Then, perturbations on $T_1$ and $M_1$ were applied either separately or simultaneously to calculate the differences in $T_5$ and $P_5$. The uncertainty on $T_5$ is calculated as $2\%$ and the uncertainty of $P_5$ is calculated as $3\%$. In previous studies, Urzay et al. [21] reported $\pm 10$ K and Sun et al. [22] reported $\pm 30$ K. Based on these previous results, the $T_5$ and $P_5$ uncertainties we estimated were considered to correspond to a $2\sigma$ uncertainty. It is noted that, if considering a $1\sigma$ uncertainty, then the uncertainties on $P_5$ and $T_5$ are 1% and 1.5%, respectively.

4 Method of uncertainty quantification for DA

The error propagation is a widely used method for experimental error estimation. However, for complex phenomenon, such as the one discussed in this paper, error propagation relations are very hard or impossible to establish. In this case, uncertainty quantification based on Monte Carlo sampling of perturbed input parameters is used to estimate the uncertainty.

Once the uncertainty for each parameters are available, the uncertainty analysis for water concentration profile measured with DA can be performed. The shock tube simulations were performed with the adiabatic constant volume (CV) reactor in Cantera [23]. The calculated water concentration profiles for both two cases are shown in Fig. 2.

Fig. 2

Simulated water concentration (solid lines) and temperature (dashed lines) profiles for two conditions

The transition we selected for water is near 2551 nm, and its spectroscopic parameters are given in Table 2. This transition has been used in several previous studies for measuring water concentration. [7, 24, 25].

Table 2 Spectroscopic parameters of the $\hbox {H}_2\hbox {O}$ transition used in the present study

As discussed in Sect. 3, the uncertainty of the parameters was obtained from both the HITRAN database and our literature review. The parameters with uncertainty levels are listed here: (in the order of minimum uncertainty, average uncertainty, and maximum uncertainty)

• 2. S(296): $0.1\%$, $0.55\%$, $1\%$ for $1\sigma$ (HITRAN)

• 3. $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$ (HITRAN)

• 4. $2\gamma _\mathrm{self}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$ (HITRAN)

• 5. $E''$: $0.6\%$, $5\%$, $8\%$ for $1\sigma$ (literature review, section 3.4)

• 6. $n_\mathrm{air}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$ (HITRAN)

• 7. $\delta _\mathrm{air}$: 1E-7 $\hbox {cm}^{-1}$, 5.5E-7 $\hbox {cm}^{-1}$, 1E-6 $\hbox {cm}^{-1}$ for $1\sigma$ (HITRAN)

• 8. Q(T): $0.01944\%$ for $1\sigma$ (literature review, Sect. 3.3)

• 9. $P_5$: $3\%$ for $2\sigma$ (literature review and calculations, section 3.5)

• 10. $T_5$: $2\%$ for $2\sigma$ (literature review and calculations, Sect. 3.5).

The maximum uncertainties in the list above are used for most analyses in the present paper, otherwise specified.

The uncertainty quantification for DA is performed according to the following steps: (i) the absorbance $\alpha (\nu ) = k_\nu L$ is calculated at each time based on the simulated water mole fraction ($\hbox {X}_{\mathrm{H}_2\mathrm{O}}$) and the nominal values for each parameters; (ii) using a Monte Carlo sampling approach, one out of the nine parameters (No. 2–10 in the list of Sect. 3) is selected randomly and perturbed based on the uncertainty levels given in Sect. 4; (iii) with the group of parameters generated in step (ii), the $\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$, referred to as “measured” water concentration, is calculated using an optimization procedure with the absorbance profile calculated in step (i) as the target. This procedure is illustrated in Fig. 3. It is noted that, although our approach is purely numerical, it could be similarly applied to experimental results. In this case, the absorbance profile generated in step (i) would be replaced by an experimental profile. Since all the parameters are known when applying the fully numerical procedure, an accurate determination of the effects of the parameters uncertainty is possible whereas when using experimental data, the actual $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ remains unknown.

Fig. 3

Schematic of UQ for DA. Only one time point on the profile with one perturbation attempt is shown in this figure. $p_i$ represents one of the parameters required to calculate the absorption profile. While the full spectral feature is shown in this figure for clarity, for fixed-DA, only the absorbance at the line-center is calculated

For step (ii), the uncertainty on each parameter is assumed to be characterized by a log-normal distribution

$$\begin{aligned} \frac{\ln {p_i}}{\ln {f_i}}\sim {\mathcal {N}} (0,1), f_i=\frac{^{n}p_i+\Delta p_i}{^{n}p_i}, \end{aligned}$$

(8)

where ${\mathcal {N}} (0,1)$ is the normal distribution, and $f_i$ is the uncertainty factor defined by uncertainty level $\Delta p_i$ and nominal value $^{n}p_i$ for parameter $p_i$. This method has been widely employed in evaluating the kinetics-induced uncertainty and in optimizing kinetics models [21, 26, 27]. Following previous studies [26, 28], the sampling of the parameters values is limited to the range of $\pm 3\sigma$ of normal distribution.

5 Results and discussion

5.1 Fixed-DA uncertainty quantification

The UQ for fixed-DA was first performed with the method described in Sect. 4. For each time of the water concentration profile, a total of 1 million perturbations (attempts) of the parameters were performed. For each attempt, only one parameter was randomly selected to be perturbed. The number of times each parameter has been sampled and perturbed has been recorded and is shown in Fig. 4. It is obvious that the perturbed parameters were effectively randomly selected.

Fig. 4

Number of times each parameters has been sampled and perturbed. The total number of run is 1 million

5.1.1 Single time point analysis

One time point ($t = 3.4604$ ms) was selected in case 01 to show detailed results. The probability distribution function (PDF) of “measured” water concentration obtained as one of the nine parameters was perturbed is shown in Fig. 5. The overall PDF for water concentration shows a combination of features: (i) Around $40\%$ of the results are located in the same section corresponding to the nominal value (View 1); (ii) despite of this high central bar, the remaining of the PDF demonstrates a Gaussian distribution with a heavy tail shape (View 2); (iii) further zoom-in indicates that the heavy tail in View 2 appears to be another Gaussian distribution with larger standard deviation (View 3). Analysis of the individual PDF for each parameter is needed to further understand the overall shape of the results. These are shown in Fig. 6.

Fig. 5

Probability distribution function of “measured” water concentration ($\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$) at $t = 3.4604\hbox { ms}$ for case 01 using fixed-DA. (a)–(c) Employed three different Y scales for the same figure. Blue stem in (a) shows the nominal value of water concentration. 500 sections were evenly defined within the range between the minimum and the maximum $\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$. $T = 1889.5$ K, $P = 118.7$ kPa, $\hbox {X}_{\mathrm{H}_2\mathrm{O}} = 0.0166$, $L = 25\hbox { cm}$. The mean value for this data set is 0.0166 and the standard deviation is 0.0013

Fig. 6

Probability distribution function of “measured” water concentration (backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ or $\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$) at $t = 3.4604$ ms for case 01 using fixed-DA. Blue stem shows the nominal value of water concentration. 200 sections are evenly defined within the range of minimum-to-maximum backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ to visualize about 111,000 runs for each parameter. $T = 1889.5$ K, $P = 118.7$ kPa, $\hbox {X}_{\mathrm{H}_2\mathrm{O}} = 0.0166$, $L = 25\hbox { cm}$. The standard deviation $\sigma$ for subfigures are (a) 4.6e–4, (b) 4.9e–5, (c) 1.7e–4, (d) 1.0e–7, (e) 1.7e–5, (f) 2.7e–16, (g) 3.9e–3, (h) 2.5e–4, (i) 2.6e–4. The mean values for subfigures are all equal to 0.0166

Figure 6 clearly indicates why a high central bar is observed in Fig. 5(a). Three out of nine parameters, including $\delta _\mathrm{air}$, $2\gamma _\mathrm{self}$ and Q(T), have essentially no impact on the uncertainty of the “measured” water concentration. The PDF plot for pressure also indicates a very limited impact on the uncertainty of the “measured” water concentration using the fixed-DA method. While pressure has a weak impact on the absorption at the line-center, it has a larger impact on the line-broadening phenomenon. Thus, the uncertainty on pressure is expected to have a larger influence on the results obtained using the scanned-DA because of its impact on the shape of the absorption feature. Lower state energy shows great impact on the uncertainty of “measured” water concentration, which results in the heavy tail feature in Fig. 5(c). Both higher maximum uncertainty and exponential dependence on the lower state energy of Eq. 3 lead to a pronounced impact of lower state energy uncertainty on the overall UQ results. A non-symmetric distribution is seen when perturbing the lower state energy. We attribute this behavior to the exponential dependence of the absorption on the lower state energy, i.e., in the absorption calculation equations, the lower state energy appears in the exponential part of the line strength S(T) at temperature T [10]. The perturbation of the lower state energy using a Gaussian distribution induces a non-symmetric distribution of the model’s output. The two $2\gamma$ broadening coefficients ($2\gamma _\mathrm{air}$ and $2\gamma _\mathrm{self}$) share similar uncertainty but have different impact on the uncertainty of the “measured” water concentration. This can be explained by the large difference between the concentration of water and of the diluent gas in our simulations (97–99% dilution was employed). The uncertainty on temperature shows a relatively large impact on the uncertainty of the water concentration. The two parameters $n_\mathrm{air}$ and $2\gamma _\mathrm{air}$ show similar PDF with widths slightly wider than that of the PDF obtained by perturbing the line strength value.

Based on these analyses, a mixed-Gaussian distribution can be used to fit the PDF shown in Fig. 5. The parameters contributing to the central bar were removed (P, $\delta _\mathrm{air}$, $2\gamma _\mathrm{self}$ and Q(T)). Two different Gaussian distributions were used to fit, respectively, the “tail”, related to the uncertainty of the lower state energy, and the central part, related to the uncertainties of the remaining parameters. The fitting results are shown in Fig. 7. It is noted that in this figure, probability density function (PdF) instead of PDF is used to help fitting with mixed-Gaussian distribution. In this case, a good agreement between the PdF and the fit is obtained. For the central part, the Gaussian distribution characteristics were noted with standard deviation $\sigma _1$ and mean value $\mu _1$, while for the “tail” part, and the Gaussian characteristics were noted as $\sigma _2$ and $\mu _2$.

Fig. 7

Probability density function of “measured” water concentration ($\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$) at $t = 3.4604\hbox { ms}$ for case 01 using fixed-DA. Only the parameters whose uncertainty induces a Gaussian response of the predicted $\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$ were included to perform the fit. These parameters are S(296), $2\gamma _{\mathrm{H}_2\mathrm{O}-air}$, $E''$, $n_\mathrm{air}$, and $T_5$. $T = 1889.5$ K, $P = 118.7$ kPa, $\hbox {X}_{\mathrm{H}_2\mathrm{O}} = 0.0166$, $L = 25\hbox { cm}$

5.1.2 Time profile analysis

Using a similar method, the uncertainty for complete water profiles shown in Fig. 2 was analyzed. The results for the two simulation cases are presented in two ways: (1) using the $\sigma$ of the Gaussian distribution (noted as $\sigma _{1}$) and (2) using the standard deviation $\sigma _\mathrm{std}$ of all “measured” water concentration. For (1), $\sigma _{1}$ is also known as the standard deviation for Gaussian distribution. The probability density function of the Gaussian distribution is defined as follows:

$$\begin{aligned} f(x) = \frac{1}{\sqrt{2\pi }\sigma _{1}}\exp {-\frac{{(x-\mu )}^2}{2\sigma _{1}^2}}, \end{aligned}$$

(9)

where $\mu$ is the expectation or mean of the distribution and $\sigma _{1}$ is the standard deviation. For (2), the standard deviation $\sigma _\mathrm{std}$ for a group of discrete data is described as follows:

$$\begin{aligned} \sigma _\mathrm{std} = \sqrt{\frac{1}{N}\sum _{i=1}^{N}(x_i-\mu )^2}, \end{aligned}$$

(10)

where $\mu$ is the mean of the discrete data.

The UQ results are shown in Fig. 8 for both cases 01 and 02. It is noted that the uncertainty shown in these figures corresponds to $\sigma _1$, the standard deviation for the first Gaussian used to fit the PdF data in Fig. 7, which is representative of the effect of the uncertainty on $\delta _\mathrm{air}$, Q(T), $2\gamma _\mathrm{self}$, and P. For both cases, the uncertainties seem to be smaller within the period of rapidly increasing water concentration. However, this is only a visual effect due to the low concentration and rapidly increasing concentration. The relative uncertainty, defined as $\frac{\sigma _1}{\mu _1}$, was calculated to be on average around 0.017 and is essentially constant after 0.1 ms in both cases.

Fig. 8

Water, temperature, and uncertainty profiles for cases 01 and 02 using fixed-DA. $\sigma _1$ was used to represent the probability area

To show the individual impact of all the parameters, method (2) was used and the uncertainty results are shown in Fig. 9. Compared with Fig. 8, standard deviation $\sigma _\mathrm{std}$ is used and the impacts of all nine parameters are shown in Fig. 9 for case 01. It shows that the parameters whose impact is illustrated in Fig. 8(a) induce a lower uncertainty than in Fig. 9(a). This is because the overall $\sigma _\mathrm{std}$ is greatly influenced by the $\sigma _\mathrm{std}$ induced by the lower state energy uncertainty. The overall uncertainty is a combination of the individual $\sigma _\mathrm{std}$ for, on the one hand, P, $\delta _\mathrm{air}$, $2\gamma _\mathrm{self}$ and Q(T), and on the other hand, for $E''$. No significant differences are observed between case 01 and case 02.

Similar to the work of Klein et al. [29], we have investigated the effect of noise by introducing a constant noise with signal-to-noise ratio (SNR) of 217. The results with noise for case 02 are shown in Figs. 10 and 11. The uncertainty profiles with noise show rough edges. This feature is more obvious in case 02 than in case 01, because of the lower water concentration in case 02, while the noise level applied is constant. Despite these differences, no significant changes for uncertainty tendency along the profiles are observed for both cases.

Fig. 9

Water, temperature, and uncertainty profile for case 01 using fixed-DA with (a) all parameters randomly perturbed and (b) only the lower state energy perturbed. $\sigma _\mathrm{std}$ was employed

Fig. 10

Water, temperature, and uncertainty profile for case 02 with noise using fixed-DA. $\sigma _1$ is used to represent the probability area

Fig. 11

Full water profile UQ for case 02 with noise using fixed-DA: (a) all parameters randomly perturbed and (b) only the lower state energy perturbed. $\sigma _\mathrm{std}$ was employed

5.2 Scanned-DA uncertainty quantification

For scanned-DA, we used the area below the absorption profile as the target function for optimization. The absorption feature we used is within the wavenumber range of 3919.8–3920.4 $\hbox {cm}^{-1}$. An example of this absorption profile is shown in Fig. 12.

Fig. 12

An example of selected absorption profile. The conditions are selected from case 01 at $t = 3.4604$ ms. Nominal values are used for all the parameters. $T = 1889.5$ K, $P = 118.7$ kPa, $\hbox {X}_{\mathrm{H}_2\mathrm{O}} = 0.0166$, $L = 25\hbox { cm}$

In the following, we first quantify the uncertainty when neglecting the finite scanning time of the absorption feature. In a second time, we relax this assumption to more closely match the conditions and limitations of shock tube experiments.

5.2.1 Analyses under ideal-scanning conditions

Single time point analysis For single time point analyses, the same conditions as the ones used in Fig. 5 were employed. The UQ results for the overall analysis are shown in Fig. 13. No significant differences are observed compared to Fig. 5. The PDF has a rougher envelope compared with fixed-DA cases. The detailed single-parameter analyses are presented in Fig. 14

Fig. 13

Probability distribution function of “measured” water concentration (backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$) at $t = 3.4604$ ms for case 01 using scanned-DA. (a)–(c) The three different Y scales for the same figure. Blue stem in (a) shows the nominal value of water concentration. 500 sections were evenly defined within the range of minimum-to-maximum backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ to visualize one million cases. $T = 1889.5$ K, $P = 118.7$ kPa, $\hbox {X}_{\mathrm{H}_2\mathrm{O}} = 0.0166$, $L = 25$ cm. The mean value for this data set is 0.0166 and the standard deviation $\sigma _\mathrm{std}$ is 0.0013

Fig. 14

Probability distribution function of “measured” water concentration (backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$) at $t = 3.4604$ ms for case 01 using scanned-DA. Blue stem shows the nominal value of water concentration. 200 sections were evenly defined within the range of minimum-to-maximum backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ to visualize about 111,000 cases for each parameter. The standard deviation $\sigma _\mathrm{std}$ for subfigures are (a) 4.9e–4, (b) 2.3e–4, (c) 1.7e–4, (d) 2.6e–16, (e) 2.7e–16, (f) 2.6e–16, (g) 3.7e–3, (h) 2.4e–5, (i) 2.5e–5. The mean values for subfigures are all equal to 0.0166 except for (g) 0.0169

The rougher PDF envelope seen for the overall results is mainly attributed to the lower state energy uncertainty, as shown in Fig. 14(g). Both $n_\mathrm{air}$ and $2\gamma _\mathrm{air}$ show less impact on the uncertainty compared with the fixed-DA case. On the contrary, pressure shows stronger impact than observed from the fixed-DA analyses. This is because the full absorption features are considered, which increases the contribution of line shape to the final result. The line shape is strongly dependent on pressure, which can explain why pressure becomes a more important factor when using scanned-DA. In addition, the impact of $n_\mathrm{air}$ and $2\gamma _\mathrm{air}$ are minimized due to the area fitting of absorption feature. The remaining absorption parameters show a similar behavior in both fixed- and scanned-DA. Based on these analyses, the full species profile analyses are performed. Due to the similarity of the two cases in fixed-DA, we only show the results for case 01. It is noted that the Gaussian fitting is not used in scanned-DA analyses, because the UQ results are more randomly distributed which complicates obtaining Gaussian distribution fit with good agreement.

Time profile analysis Only rapidly increasing part of the water concentration profile of case 01 (from about 0.02 to 0.14 ms) was analyzed in details under a ideal-scanning situation. The results are shown in Figs. 15 and 16.

Fig. 15

Full water profile UQ for case 01 with ideal-scanning

Fig. 16

Full water profile UQ for case 01 with ideal-scanning. All nine absorption parameters are shown separately. It is noted that for some figures, the colored areas are too small, so the areas are shown as blue lines

Similar uncertainty ranges are observed for each parameter in Figs. 14 and 16. For the species profiles obtained with scanned-DA, the uncertainty comes mostly from the uncertainty on lower state energy, line strength, temperature, and pressure. This can be explained by the use of the area-based optimization for calculating water concentration. The parameters 3, 4, and 6 mainly affect the line shape, while the area below the absorption profile is relatively constant. The overall UQ shown in Fig. 15 is very similar with the fixed-DA result. The detailed comparison also indicates that there are no significant differences.

The analysis with noise described in Sect. 5 was also performed for scanned-DA. The results are shown in Fig. 17.

Fig. 17

Full water profile UQ for case 01 with ideal-scanning. Noise was added to the simulated absorption data, as described in Sect. 5

Unlike what we observed for fixed-DA, no significant differences are observed before and after noise is introduced. The noise we introduced is a Gaussian noise featured with zero mean. The area-based optimization process we used minimizes this zero-mean noise when calculating the area below the absorption profile. This also shows another advantage of scanned-DA compared with fixed-DA.

5.2.2 Analyses under non-ideal-scanning conditions

Time profile analysis As mentioned in Sect. 2, the scanning process will take a finite time in reality. When the scanning period is relatively long compared with the characteristic chemical time-scale, the measured single full absorption features might be affected by non-constant temperature and species concentration. This non-ideal effect will cause deformation of the measured absorption feature. This is illustrated in Fig. 18.

Fig. 18

Example of the effect of finite-rate scanning on the absorption profile. The water profile used is from case 01. The scanning period is 1e$-5$ s (or scanning frequency of 100 kHz). The $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$, temperature and pressure are normalized with their values at the initial time shown in this figure

In Fig. 18, the $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ is increased by more than $300\%$ during the scanning period. The simulated absorption feature affected by this rapid increase (blue line) shows significant difference when comparing with the ideal-scanning case (red line). To further analyze the uncertainty of water measurement under this non-ideal conditions, the overall contribution as well as the individual contributions of each parameter were extracted, as shown in Figs. 19 and 20. Compared with the results shown in Fig. 15, the overall uncertainty in Fig. 19 shows no significant difference. The main difference between these two figures is the large offset observed in Fig. 19 between the actual/nominal profile and the “measured” one at time up to 90 $\upmu$s. This is caused by the non-ideal-scanning effect. A sudden jump is also observed in Fig. 19 near 0.065 ms, see inset. This can be explained by the low but rapidly increasing water concentration. The rapidly increasing water concentration leads to a great deformation of the absorption features. When combined with the low water concentration, the results become much less accurate. The PDF of “measured” water concentration before and after the sudden jump is shown in Fig. 21. A non-uniform, rather random distribution is observed before the jump point, while a uniform, Gaussian-like distribution is observed after this jump point. The per-parameters results shown in Fig. 20 show similar characteristics as those shown in Fig. 16. Nevertheless, the offset induced by the finite-rate scanning is present for all the parameters, regardless of the uncertainty they generate.

Fig. 19

Full water profile UQ for case 01 with non-ideal-scanning. Noise was added to the simulated absorption data, as described in Sect. 5

Fig. 20

Full water profile UQ for case 01 with non-ideal-scanning. The effects of the nine absorption parameters are shown separately. Noise was added to the simulated absorption data, as described in Sect. 5. It is noted that for some figures, the colored areas are too small and are only shown as blue lines. The main difference induced by non-ideal-scanning is the large offset between the nominal profile and the “measured” one; see Fig. 19 for ideal-scanning case

Fig. 21

The probability distribution function for points (a) before and (b) after the jump point in Fig. 19. $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ are normalized by each corresponding $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ for the bar with maximum value in the PDF

Local optical Damköhler number To characterize the conditions for which finite-rate scanning can be of significant importance for DA application, we introduce the concept of local optical Damköhler number Da$_o$. Similar to the classical Damköhler number, which compares the relative time-scale of the flow and the chemical reaction in combustion [30], the optical Damköhler number intents to compare the relative time-scale of scanning and conditions rate of change, and is defined as

$$\begin{aligned} Da_o = \frac{P_{max}}{P_\mathrm{min}} \times \frac{T_\mathrm{max}}{T_\mathrm{min}} \times \frac{X_\mathrm{max}}{X_\mathrm{min}}, \end{aligned}$$

(11)

where $_\mathrm{max}$ and $_\mathrm{min}$ are the maximum and minimum values during the scanning period for P, T, and X. The “measured” water concentration and Da$_o$ profiles are shown in Fig. 22.

Fig. 22

Da$_o$ profile for 100 kHz scanned-DA in Fig. 19. The lower sub-figure shows the difference between nominal $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ and “measured”(backward) $\hbox {X}_{\mathrm{H}_2\mathrm{O}}'$ in percentage

The jump seen in Fig. 19 also appears in Fig. 22 and we will only focus on the area which follows this discontinuity. The value of Da$_o$ is strongly connected with the error percentage which reaches a maximum value above 50%. A smaller Da$_o$ will lead to smaller error in the measured concentration. It is possible to apply Da$_o$ for scanning frequency selection for scanned-DA measurement in combustion. A large amount of simulations under various conditions are needed to precisely determined which range of values of Da$_o$ should be employed to ensure accurate measurement under high-temperature conditions. Nevertheless, it is clear that Da$_o$ should tend to 1 to minimize inaccurate measurement during fast transients.

5.3 UQ analyses for two-color DA temperature measurement

Two-color DA technique is a practical method for temperature measurement in combustion systems. This method uses two different transitions of the same species. For scanned-DA, the two areas below two absorption profiles can be used to calculate the temperature

$$\begin{aligned} R_\mathrm{area} = \frac{A_1}{A_2} = \frac{\int _{-\infty }^{+\infty } P\chi _\mathrm{target}S_{1}(T) \phi _1(\nu ) L\,\mathrm{d}\nu }{\int _{-\infty }^{+\infty } P\chi _\mathrm{target}S_{2}(T) \phi _2(\nu ) L\,\mathrm{d}\nu } = \frac{S_1(T)}{S_2(T)}. \end{aligned}$$

(12)

Only $\phi _i(\nu )$ is the function of $\nu$ and its integration is equal to 1. Using HITRAN database, the ratio $R_\mathrm{area}=\frac{S_1(T)}{S_2(T)}$ can be calculated as a known function of temperature. In practice, using the measured areas to calculate the ratio, the temperature can be obtained by checking a pre-calculated $R_\mathrm{area}$ table.

However, for fixed-DA, no area can be obtained during the measurement. The actual ratio in this case will become

$$\begin{aligned} R_\mathrm{center} = \frac{P\chi _\mathrm{target}S_{1}(T) \phi _1(\nu _1) L}{P\chi _\mathrm{target}S_{2}(T) \phi _2(\nu _2) L} = \frac{S_1(T)\phi _1(\nu _1)}{S_2(T)\phi _2(\nu _2)}, \end{aligned}$$

(13)

where $\nu _1$ and $\nu _2$ are the center frequencies of the two selected absorption features. The line-shape function at line-center is mainly determined by collisional broadening coefficient $\Delta \nu _C$, which is directly proportional to pressure [10]. Then, by measuring pressure at the same time, the gas temperature can be inferred from the measured ratio $R_\mathrm{center}$, using simulations of the ratio as a function of temperature at the measured pressure [3].

The uncertainty for the ratio $R_\mathrm{area}$ and $R_\mathrm{center}$ can be estimated using error propagation function

$$\begin{aligned} \Delta R_\mathrm{center}= & {} \sqrt{(\Delta S_1(T))^2+(\Delta \phi _1(\nu _1))^2+(\Delta S_2(T))^2+(\Delta \phi _2(\nu _2))^2}, \end{aligned}$$

(14)

$$\begin{aligned} \Delta R_\mathrm{area}= & {} \sqrt{(\Delta S_1(T))^2+(\Delta S_2(T))^2}. \end{aligned}$$

(15)

The $(\Delta \phi _i(\nu _i))^2$ terms may be neglected due to the small uncertainty on pressure in shock tube experiments, which leads to the uncertainty of both scanned- and fixed-DA two-color methods

$$\begin{aligned} \Delta R = \sqrt{(\Delta S_1(T))^2+(\Delta S_2(T))^2}. \end{aligned}$$

(16)

A transition near 2551 nm was already selected in the previous sections. Based on this selected transition, another absorption line was selected to form a two-color scheme. To select the proper line couple, the selection rules developed by Zhou et al. [31] were used. The main ideal of this set of selection rules is to select two strong transitions with a large lower state energy difference ($\Delta E'' > 300$ $\hbox {cm}^{-1}$), which provides a maximum ratio-temperature sensitivity. The second transition we selected is near 3948.177 $\hbox {cm}^{-1}$ (2532.8 nm); see the spectroscopic characteristics of the line in Table 3. Similar uncertainty assignment method used in Sect. 3 was applied to this new transition. The list of uncertainty is shown as follows: (minimum uncertainty, average uncertainty, maximum uncertainty)

• 2. S(296): $0.1\%$, $0.55\%$, $1\%$ for $1\sigma$

• 3. $2\gamma _{\mathrm{H}_2\mathrm{O}-\mathrm{air}}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$

• 4. $2\gamma _\mathrm{self}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$

• 5. $E''$: $0.6\%$, $5\%$, $8\%$ for $1\sigma$

• 6. $n_\mathrm{air}$: $1\%$, $1.5\%$, $2\%$ for $1\sigma$

• 7. $\delta _\mathrm{air}$: 1E–6 $\hbox {cm}^{-1}$, 5.5E–6 $\hbox {cm}^{-1}$, 1E–5 $\hbox {cm}^{-1}$ for $1\sigma$

• 8. Q(T): $0.01944\%$ for $1\sigma$

• 9. $P_5$: $3\%$ for $2\sigma$

• 10. $T_5$: $2\%$ for $2\sigma$.

Table 3 Spectroscopic parameters of the $\hbox {H}_2\hbox {O}$ transition used in two-color method. Data were acquired from the HITRAN database [9]

To analyze the $\Delta S_i(T)$, all absorption parameters listed are perturbed at the same time in the calculation. For different uncertainty levels, both maximum group (all parameters at their maximum uncertainty, all parameters perturbed at same time) and minimum group (all parameters at their minimum uncertainty, all parameters perturbed at same time) were tested for the different time step under the conditions of case 02. The calculated $S_i(T)$ show a Gaussian-like distribution for both two groups (see Fig. 24). Different time points selected in case 02 show a relatively constant ratio of mean and standard deviation $\sigma _{1}/\mu$. This ratio can be used as relative $\Delta S_i(T)$ corresponding to 1$\sigma$ in Gaussian distribution. For $\Delta S_1(T)$ (near 2551 nm), the averaged value is $3.18\%$ for minimum group and $21.52\%$ for maximum group; For $\Delta S_2(T)$ (near 2532 nm), the averaged value is $3.49\%$ for minimum group and $33.50\%$ for maximum group. Then, the minimum $\Delta R$ is $4.72\%$ and the maximum $\Delta R$ is $39.82\%$ for two-color temperature measurement. For each line couple, the uncertainty on temperature depends on $\Delta R$ and on the sensitivity of the ratio to temperature change. The line couple presented in this section, noted as ratio 1, (2551–2532 nm) and a water line couple used in the work of Peng et al. [7], noted as ratio 2, (2551– 2481 nm) are compared to show the importance of both $\Delta R$ and R(T) for temperature measurement. The $\Delta R_1$ for (2551 nm - 2532 nm) couple is equal to $4.72\%$. The $\Delta R_2$ for (2551–2481 nm) couple is equal to $7.14\%$. For a target temperature of 2000 K, $\Delta T_1$ for (2551–2532 nm) couple is $-290$ K or $+431$ K, and $\Delta T_2$ for (2551–2481 nm) couple is $-93$ K or $+110$ K. The second line couple presents a smaller uncertainty on temperature despite having a larger uncertainty on line strength ratio R. This is due to the lower temperature sensitivity to the ratio of the second line couple. In addition, it is important to note that, although $\Delta R$ is the same when considering $S_{1}/S_{2}$ or $S_{2}/S_{1}$, this is not the case for R(T). This results in a different $\Delta T$ when considering the ratio or its reciprocal. For example, considering the line pair of Peng et al. [7], using $S_{2551\; \mathrm{nm}}/S_{2481\; \mathrm{nm}}$ leads to a range of $-93$ K or $+110$ K whereas using $S_{2481\; \mathrm{nm}}/S_{2551\; \mathrm{nm}}$ leads to a range of $-100$ K or $+102$ K. The full temperature profile (case 02) with the UQ results for the two-color method is shown in Fig. 23. It is noted that for both line pairs, no significant difference was observed when using the ratio or its reciprocal. Lower temperature sensitivity is observed for (2551 nm - 2481 nm) pair, which is consistent with single-point analysis results.

Fig. 23

$\Delta S_i(T)$ estimation for both two transitions. Probability density function with its Gaussian fitting is shown in the figure. Only one case in each group is shown

Our UQ analysis led to a minimum of $5.1\%$ for the temperature uncertainty at 2000 K for the water line couple used in the work of Peng et al. [7]. The temperature measurement uncertainty we calculated is about $3.3\%$ when using the uncertainty reported in Peng et al. [7] for the spectroscopic parameters. However, the major uncertainty contributor we have identified in the present paper, the lower state energy ($E''$), is not reported as an uncertainty source by Goldenstein et al. [8]. It is acknowledged that for some parameters we have included in our uncertainty analysis, no specific uncertainty data could be found and only estimated values could be obtained. Nevertheless, our estimated values are based on the thorough and critical review of data from the literature. As similar uncertainty results were obtained for our study and the study of Peng et al. [7], it is reasonable to conclude that the uncertainty on temperature measurement using the two-color DA approach is around 5% at best. In the work of Pinkowski [32], multi-wavelength laser absorption inside a shock tube was performed using an IR dual-comb, and an uncertainty on temperature of around $1.8\%$ was reported. Although the use of multiple transitions enables to greatly minimize the measurement uncertainty, dual-comb spectroscopy remains a complex and un-common laser diagnostics. Until such high-accuracy capabilities become more widely available, the uncertainty of the DA technique can be lowered by improved measurement of the spectroscopic parameters.

Fig. 24

Temperature measurement uncertainty ranges for case 02. UQ for both line pairs $S_{2551\; \mathrm{nm}}/S_{2481\; \mathrm{nm}}$ and $S_{2551\; nm}/S_{2532\; \mathrm{nm}}$ are presented

6 Conclusion

Based on the present detailed UQ analysis, the uncertainties induced by the uncertainty on the spectroscopic parameters are non-negligible when applying fixed- or scanned-DA. The parameters that dominate the uncertainty are the line strength, pressure, temperature, and lower state energy. The parameters that determine the line shape have relatively small impact on the measured uncertainty, which makes the scanned-DA more robust than fixed-DA. The relative uncertainty on the “measured” water concentration is basically constant during the whole simulation time, even in the initial part when water concentration is extremely low. A realistic noise level was introduced to the tested cases to verify the impact of signal-to-noise ratio on the measurement. The main impact is the reduced quality of the water profile when noise is introduced.

Further testing with non-ideal scanned-DA shows a great impact of scanning frequency on the measured results. A case with scanning frequency equal to 100 kHz was tested. The largest difference in water concentration between the nominal value and “measured” value is approximately $70\%$. The concept of local optical Damköhler number was defined to characterize the conditions under which the finite rate of scanning induces significant errors. A clear connection between large Da$_o$ and large errors was observed and future research should focus on identifying the critical value for Da$_o$ for which the finite-rate scanning has negligible impact.

At last, the uncertainty of two-color temperature measurement with DA was estimated based on our UQ analyses. The two-color measurement ratio R has an uncertainty of $4.72\%$ when all parameters have minimum uncertainty. When maximum uncertainties are considered for all species,$\Delta R$ is equal to $39.82\%$. The corresponding uncertainty on temperature depends heavily on the selected line couples. A minimum uncertainty of $5.1\%$ on temperature was obtained for the line couple selected by Peng et al. [7]. It is noted that the uncertainties of some spectroscopic parameters used in our analyses were not specifically measured, but were based on a critical literature review. To further improve the accuracy of species concentration and temperature measurement via laser absorption in combustion environments, more precise measurements of fundamental spectroscopic parameters are required.

Appendices

Appendices

1.1 Additional uncertainty analyses

1.1.1 Error due to the optical path-length uncertainty

The error on the optical path-length is mainly due to the non-ideal alignment of the laser beam with respect to the shock tube windows. This error varies with different combination of shock tube diameter and window size. Our estimations consider two tubes of very different diameters.

The first tube is a shock tube with 250 mm diameter equipped with round windows with diameter of 10 mm. The nominal optical length for this shock tube is 250 mm and the maximum optical length is estimated as $\sqrt{250^2+10^2} = 250.20$ mm. The maximum uncertainty for this shock tube is about $0.08\%$.

The second tube has a diameter of 80 mm and is equipped with round windows with diameter of 8 mm. The nominal optical length for this shock tube is 80 mm and the maximum optical length is estimated as $\sqrt{80^2+8^2} = 80.40$ mm. The maximum uncertainty for this shock tube is about $0.5\%$.

Based on these estimations, the error induced by the uncertainty on the optical path-length is relatively small, especially for the tube with the largest diameter. Based on the linear relation between the optical path-length L and the absorbance $\alpha$ (see Eq. 17), this estimated error can be easily added via simple error propagation equations

$$\begin{aligned} \alpha = \hbox {PS(T)XL}. \end{aligned}$$

(17)

1.1.2 Error due to the line-center uncertainty

The uncertainty on the line-center is provided in the HITRAN database for most absorption lines. HITRAN database uses an error code to identify the uncertainty level for each parameter. The error code for $\nu _0$ for the transition we selected near 2551 nm is 5, which corresponds to an uncertainty range for $\nu _0$ from 0.00001 to 0.0001 $\hbox {cm}^{-1}$. The maximum uncertainty is employed and a similar simulation as the one presented in Fig. 6 was performed. It is noted that this maximum uncertainty of 0.0001 $\hbox {cm}^{-1}$ is considered as a 1$\sigma$ error in our calculation. The results are shown in Fig. 25. The PDF mainly concentrates very close to the nominal value of $\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$. In this case, the error induced by the uncertainties of $\nu _0$ can be essentially neglected.

Fig. 25

Probability distribution function of “measured” water concentration ($\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$) at $t = 3.4604$ ms for case 01 using fixed-DA with the line-center perturbed. Blue stem shows the nominal value of water concentration. 200 sections were evenly defined within the range of minimum-to-maximum backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ to visualize about 111,000 cases for line-center UQ analysis

1.1.3 Further UQ analysis for the lower state energy

For most calculations shown in this paper, the maximum uncertainty on the lower state energy ($8\%$) was employed as the input of our calculations. Additional calculations based on the minimum uncertainty on the lower state energy ($0.6\%$) are presented in Fig. 26. The same approach as the one employed to obtain the results shown in Fig. 6 was used. By applying a much smaller uncertainty on the lower state energy, the PDF width is shrunk to a level similar to the uncertainty induced by the uncertainty on temperature. However, it should be noted that the temperature uncertainty is larger than $0.6\%$ when considering a 1$\sigma$ uncertainty. This further demonstrate the large impact of the uncertainty on the lower state energy for DA measurement.

Fig. 26

Probability distribution function of “measured” water concentration ($\hbox {X}_{\mathrm{H}_2\mathrm{O}}^{'}$) at $t = 3.4604$ ms for case 01 using fixed-DA with the lower state energy perturbed. Blue stem shows the nominal value of water concentration. 200 sections were evenly defined within the range of minimum-to-maximum backward $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ to visualize about 111,000 cases for lower state energy UQ analysis. The minimum lower state energy uncertainty ($0.6\%$) was employed

1.1.4 Error estimation on $\hbox {P}_1$

The uncertainty of the driven section pressure $\hbox {P}_1$ can be essentially neglected for the present analysis. $\hbox {P}_1$ can be measured using various gauges of different accuracy. Downes et al. [33] estimated the uncertainty on $\hbox {P}_1$ to be of $\pm 100$ Pa for a nominal value of 101,309 Pa, which is about $0.1\%$. This uncertainty can be even lower when using an optimal set of gauges. The uncertainty on $\hbox {P}_1$ only affects the UQ results by affecting the value of $\hbox {P}_5$, which was analyzed in detailed in Sect. 3. Thus, the actual error on $\hbox {P}_1$ has no relevance for the present analysis.

1.2 Optical Damköhler number: further analysis

Four different scanning frequencies (1 kHz, 100 kHz, 500 kHz, and 1 MHz) were selected to further analyze the Optical Damköhler Da$_o$. The results are shown in Fig. 27. For all cases, the Da$_o$ reaches its maximum value at the begin and eventually decrease to 1. The maximum Da$_o$ value is decreasing with the scanning frequency increase. For a scanning frequency of 500 kHz, the average error on the “measured” mole fraction is about 5%. In this case, the maximum Da$_o$ number is less than 1.3, which provides a relatively low uncertainty. The results also show the marginal benefit of further increasing the scanning frequency; see Fig. 27(d). For tunable laser diode, the actual wavenumber scanning range is typically decreased when a higher tuning frequency is applied. In this case, a trade-off between the scanning frequency and the uncertainty induced by the finite scanning rate needs to be considered.

Fig. 27

Da$_o$ profile for 1 kHz, 100 kHz, 500 kHz, and 1 MHz scanned-DA. The lower sub-figure shows the difference between nominal $\hbox {X}_{\mathrm{H}_2\mathrm{O}}$ and “measured”(backward) $\hbox {X}_{\mathrm{H}_2\mathrm{O}}'$ in percentage