1 Introduction

The amount of information transmitted all over the world has grown exponentially over the last 40 years. Therefore, it is obvious that guided-wave optical technologies are also developing rapidly to meet the ever-increasing demands. A promising method of increasing both speed and amount of information transmitted is the generation of optical frequency combs. This method is applied in high-precision optical sensors [1], optical signal processing [2], optical metrology [3], ultrafast information processing and transmission [4,5,6]. All these applications require a fixed distance between the comb lines, whose phase should also differ by a known and unchangeable value. The generators of frequency combs are the base for providing high data rates for long distances in optical communication systems [7].

The methods of frequency comb generation can be divided into three main groups. The first one is the generation using a mode-locked laser and an internal or external reference to stabilize the repetition rate and the phase of the carrier signal envelope [8,9,10]. The second one is the generation of frequency combs by means of electro-optical modulation. This method provides a broad range of adjustments of the central frequency and the distance between the peaks and their number [11,12,13]. The generation and tuning are performed using analog methods, i.e., by changing the amplitude and phase of the control signal applied to the modulator. Such methods require either precise synchronization of the amplitude and phase of control signals or strict control of offset signals using intensity modulators or nested modulators [12,13,14]. The third group is the usage of microresonators in the form of rings with optical pumping [15,16,17]. All these methods allow achieving a distance between peaks of hundreds of GHz. However, the creation of an optical frequency comb generator with continuously changing parameters is still a challenge. Another difficulty is with regard to the fact that the comb lines located near the central frequency of the pump pulse have a higher intensity, and consequently the efficiency and the signal-to-noise ratio for every single line gets worse.

There are methods that combine the formation of frequency combs and the creation of an ultrashort subpulse sequence in the time domain [18, 19]. The work toward a temporal sequence of subpulses formation has been conducted for the last 30 years. For example, in [20], a femtosecond pulse sequence was created by spectral filtering of ultrashort pulses. To achieve this, a femtosecond 4f-shaper was used. The spectrally decomposed femtosecond pulse was filtered by a mask located in the spectral plane of the shaper. Its second part produced the spectral addition of the radiation diffracted on the mask synthesizing a sequence of pulses with a shape given by the Fourier transform. In further works, a spatial light modulator (SLM) was used instead of the mask [21]. In other series of studies, the sequence was generated based on the diffraction of a spectrally decomposed wave in a photorefractive crystal [22] due to four-wave mixing in a nonlinear crystal [23] located in the spectral plane of the shaper. These methods allowed to form sequences of femtosecond pulses with a terahertz repetition rate. However, the duration of the sequence was limited to a temporal window of the shaper, which is commonly a dozen picoseconds.

As already mentioned, there is an alternative method of forming a frequency comb with its corresponding sequence in time domain which is described in [19, 24, 25]. The method is featured by the possibility of performing pulse shaping without the usage of special spectral masks or modulators. These studies showed experimentally that a sequence of ultrashort light subpulses with THz repetition rate can be formed as a result of the interference of two femtosecond phase-modulated pulses with a time delay between them smaller than their duration. This method allows achieving a subpulse repetition rate of more than 10 THz, which depends on the delay between the pulses, though it is impossible to control such a sequence since it can be formed in the overlapping region only. Additionally, the possibility of controlling such a sequence of subpulses by means of time-spectral multiplexing was demonstrated in [19] for the pulse delay shorter than its duration and a subpulse repetition rate of less than 1 THz. However, this paper shows indirect estimates of the possibility of controlling the sequence only experimentally. Thus, there is no clear correlation between the spectral and temporal structures of the sequence formed. It is worth noting that the subpulse repetition rate depends on the width of the spectrum directly [7]. Therefore, the usage of a highly coherent supercontinuum with an ultrawide spectrum as a source, for example, in [26], can help to increase the repetition rate above 1 THz.

This paper analytically investigates the possibility of controlling a sequence of subpulses of any duration with a terahertz repetition rate formed by the method described in [19]. The main contributions of this paper are the following:

  • The possibility of controlling a sequence of pulses of any duration with a terahertz repetition rate is shown, considering the discrepancy coefficient.

  • The discrepancy coefficient of the central frequency of subpulses in the quasidiscrete temporal structure with respect to the central frequency of the spectral lines in the quasidiscrete spectral structure is determined analytically for femtosecond pulses with linear frequency modulation.

  • The existence of analytically obtained discrepancy is confirmed by means of numerical simulation and experiment. Its influence on the distortion of the encoded sequence is demonstrated.

  • It is shown that the duration and repetition rate, considering the discrepancy determined, can be arbitrary.

The paper is organized as follows. Section 2 presents and describes the mathematical model of the interference of two phase-modulated pulses, as a result of which a sequence of ultrashort subpulses is generated. Section 3 is devoted to the theoretical analysis of the possibility of controlling the sequence of femtosecond subpulses with a terahertz repetition rate. Section 4 shows the experimental confirmation of the results obtained from theoretical analysis. Section 5 provides the conclusions on the research conducted and the prospects for future work.

2 Mathematical model

A quadratic modulation of the ultrashort pulse phase (linear frequency modulation) occurs after passing through a dispersive medium. It results in a pulse duration increase. For high-intensity pulses, the phenomenon of self-phase modulation occurs and leads to a stronger frequency modulation in the temporal structure. This frequency modulation can be described by a linear function [27]. Thus, a pulse with electric field oscillation E having a linear frequency modulation can be described by the following equation (Fig. 1):

$$\begin{aligned} E(t) = E_0 \times \exp \left( -2\frac{t^2}{\tau ^{2}_{0}} \right) \sin \left( \omega _0 \left( 1+\frac{\alpha _0}{\tau _{0}}t \right) t \right) , \end{aligned}$$
(1)

where \(E_0\) is the pulse amplitude, \(\omega _0\) is the pulse central frequency, \(\tau _0\) is the pulse duration, and \(\alpha _0\) is a linear frequency modulation coefficient.

Fig. 1
figure 1

Chirped pulse and its chirp

Full size image

The interference of a femtosecond phase-modulated pulse of form (1) with its copy shifted by a time delay \(\varDelta \tau\) can be represented as:

$$\begin{aligned} E = \, & {} E_1+ E_2\nonumber \\= \,&{} E_0 \times \exp \left( -2\frac{t^2}{\tau ^{2}_{0}} \right) \sin \left( \omega _0 \left( 1+\frac{\alpha _0}{\tau _{0}}t \right) t \right) \nonumber \\&+ E_0 \times \exp \left( -2\frac{\left( t+\varDelta \tau \right) ^{2}}{\tau ^{2}_{0}} \right) \nonumber \\&\times \sin \left( \omega _0 \left( t+\varDelta \tau \right) +\frac{\alpha _{0}}{\tau _{0}} \omega _0 \left( t+\varDelta \tau \right) ^{2} \right) , \end{aligned}$$
(2)

where \(E_1\) and \(E_2\) are the electric field of the pulse and its delayed copy. Equation (2) can be transformed to the form:

$$\begin{aligned} E= \,& {} E_0 \times \exp \left( -2\frac{t^2}{\tau ^{2}_{0}}\right) \nonumber \\&\times \left[ 2\sin \left[ \left( \omega _0+\omega _{\mathrm{mod}} \right) t+\frac{\alpha _0}{\tau _0}\omega _0 t^2+\phi _0 \right] \right. \nonumber \\&\left. \times \cos \left( \omega _{\mathrm{mod}}+\phi _0 \right) +\left( \exp \left[ \frac{-4t \varDelta \tau -2 \varDelta \tau ^2}{\tau _{0}^{2}} \right] -1 \right) \right. \nonumber \\&\left. \times \sin \left( \omega _0 \left( t+\varDelta \tau \right) +\frac{\alpha _0}{\tau _0}\omega _0 \left( t+\varDelta \tau \right) ^2 \right) \right] , \end{aligned}$$
(3)

where \(\phi _0=\frac{\omega _0 \varDelta \tau }{2}\left( 1+\frac{\alpha _0}{\tau _0}\varDelta \tau \right)\) is the initial phase, \(\omega _{\mathrm{mod}}=\frac{\alpha _0}{\tau _0}\omega _0 \varDelta \tau\) is the interference field modulation frequency.

For \(\varDelta \tau \ll \tau _0\) the last term in (3) can be neglected and the equation for the superposition of the light fields of the two pulses takes the following form:

$$\begin{aligned} E= & {} E_0 \times \exp \left( -2\frac{t^2}{\tau ^{2}_{0}}\right) \nonumber \\&\times \left[ 2\sin \left[ \left( \omega _0+\omega _{\mathrm{mod}} \right) t+\frac{\alpha _0}{\tau _0}\omega _0 t^2+\phi _0 \right] \right. \nonumber \\&\left. \times \cos \left( \omega _{\mathrm{mod}}+\phi _0 \right) \right] , \end{aligned}$$
(4)

where the cosine is responsible for modulating the signal, and the sine represents its internal structure.

At the same time, according to the Fourier shift theorem, the spectrum of such an interference can be represented in the form:

$$\begin{aligned} \left| G_s(\omega ) \right| ^2=2\left| G(\omega ) \right| ^2 \times \left[ 1+cos \left( 2\pi \omega \varDelta \tau \right) \right] , \end{aligned}$$
(5)

where

$$\begin{aligned} G(\omega )= & {} \frac{1}{2i} \sqrt{\frac{\pi }{\frac{2}{\tau _{0}^{2}}-i\omega _0 \frac{\alpha _0}{\tau _0}}} \times \exp \left( \frac{-\left( \omega -\omega _0 \right) ^2}{4 \left( \frac{2}{\tau _{0}^{2}}-i\omega _0 \frac{\alpha _0}{\tau _0} \right) } \right) \nonumber \\&-\frac{1}{2i} \sqrt{\frac{\pi }{\frac{2}{\tau _{0}^{2}}+i\omega _0 \frac{\alpha _0}{\tau _0}}} \times \exp \left( \frac{-\left( \omega +\omega _0 \right) ^2}{4 \left( \frac{2}{\tau _{0}^{2}}+i\omega _0 \frac{\alpha _0}{\tau _0} \right) } \right) . \end{aligned}$$
(6)

3 Theoretical analysis

Figure 2a shows an example of the result of the femtosecond phase-modulated pulse interference in the spectral region with its copy shifted by a time delay \(\varDelta \tau\) (5). Here, \(\delta \omega\) is the period of a quasidiscrete spectrum, \(\varDelta \omega\) is the spectrum half-width, \(\omega _0\) is the central frequency, and \(\omega _i\) is the ith peak frequency. Then, \(\frac{\varDelta \omega }{\delta \omega }=N\) stands for the number of peaks in the quasidiscrete spectrum, and the frequency of the ith peak can be calculated as:

$$\begin{aligned} \omega _i = \omega _0 \pm i\delta \omega , \end{aligned}$$
(7)

where \(\delta \omega =\frac{1}{\varDelta \tau }.\)

Figure 2b shows an example of the femtosecond phase-modulated pulse interference amplitude in the time domain (3). Here, \(\delta \tau\) is the period of temporal peaks, \(\varDelta \tau\) is the time delay between two pulses, and \(\tau _0\) is the duration of one pulse.

Fig. 2
figure 2

The interference results of two phase-modulated femtosecond pulses in a spectral and b time domains

Full size image

As mentioned, when \(\varDelta \tau \ll \tau _0\), the form of the interference structure for Eq. (4) is identical to the result of Eq. (3). Therefore, to calculate the frequency of an individual peak of the temporal sequence, it is possible to take the derivative of the phase in Eq. (4): \(\omega (t)=\left[ \left( \omega _0+\omega _{\mathrm{mod}} \right) t+\frac{\alpha _0}{\tau _0}\omega _0 t^2 +\phi _0 \right] '=\omega _0+\omega _{\mathrm{mod}}+2\frac{\alpha _0}{\tau _0}\omega _0 t\). Then, \(\omega _i = \omega _0 \pm \frac{i}{\delta \tau } \pm \omega _{\varDelta \tau }\), where \(\frac{1}{\delta \tau }=\omega _{\mathrm{mod}}\), and \(\omega _{\varDelta \tau }=\omega (\varDelta \tau )-\omega (0)=2\frac{\alpha _0}{\tau _0}\omega _0 \varDelta \tau = 2\omega _{\mathrm{mod}}\) is the frequency increment due to the difference in the interference temporal width of the two pulses shifted by the time delay \(\varDelta \tau\) and the temporal width of each pulse separately. Therefore, the ith peak frequency in the temporal structure for the total interference field with small \(\varDelta \tau\) can be calculated from the formula:

$$\begin{aligned} \omega _i = \omega _0 \pm \omega _{mod}(i+2). \end{aligned}$$
(8)

It can be seen from Eqs. (7) and (8) that the central frequencies of the ith peaks in the frequency and time domains differ by a value \(2\omega _{\mathrm{mod}}\). This value depends on the phase modulation coefficient \(\alpha _0\), time delay between pulses \(\varDelta \tau\) and center frequency \(\omega _0\) directly. The presence of this additional term leads to a discrepancy between the temporal and spectral interference structures.

Figure 3 shows two phase-modulated pulses with \(\tau _0\) = 80 fs and \(\alpha _0 = 0.4\) calculated by formula (1) and shifted by the time delay \(\varDelta \tau = 10\,\hbox {fs}\). The result of their interference in time and spectral domains is shown in Fig. 4a, b, respectively, where \(\omega _{\mathrm{norm}}=\frac{\omega _i}{\omega _0}\) is the normalized frequency.

Fig. 3
figure 3

Two phase-modulated pulses shifted by a time delay \(\varDelta \tau = 10\,\hbox {fs}\)

Full size image

One can see a correlation between the peaks in the spectral and temporal domains. Usually, it is easier to cut out the spectral components and then observe the change in the temporal shape of the pulse in an experiment. Here, the correlation patterns of the central frequencies of the ith peaks in the temporal and spectral structures (7, 8) are derived. Regarding the numerical simulation, to trace the inconsistency of this correlation, it is more convenient to cut out the temporal structure of the ith peak and control the shift of \(i+1\) and \(i-1\) peaks in the spectral structure. Based on Eqs. (7, 8), this shift is equal to discrepancy coefficient \(k=2\omega _{\mathrm{mod}}\).

Fig. 4
figure 4

The result of the interference of two phase-modulated pulses shifted by time delay in the a time and b spectral domains

Full size image

Figure 5 shows the simulation results of the temporal structure cutting out (Fig. 5a) and the change in the spectral structure (Fig. 5b, c).

Fig. 5
figure 5

The result of cutting out one of the peaks in the time domain for \(\varDelta \tau = 10\,\hbox {fs}\). Sequence of pulses in the a time and b spectral domains. c Zoomed area with visible shift of the minimum after cutting out one of the peaks

Full size image

It can be seen that the shift of the minimum after cutting out one of the peaks is around 0.1 of the normalized frequency. The same value can be obtained using derived analytical formula for discrepancy coefficient (8): \(k=2 \frac{\alpha _0}{\tau _0} \omega _0 \varDelta \tau =0,1\omega _0\).

To validate the results obtained, a simulation for a larger time delay between pulses \(\varDelta \tau = 20\,\hbox {fs}\) was performed. Figure 6 shows the result of cutting out one of the peaks in the time domain. As seen, after cutting out one of the central peaks, the shift of the minimum cannot be determined as a residual interference term is formed (Fig. 6c).

Fig. 6
figure 6

The result of cutting out one of the peaks in the time domain for \(\varDelta \tau = 20\,\hbox {fs}\). Sequence of pulses in a time and b spectral domains. c Zoomed area with visible shift of the minimum after cutting out one of the peaks

Full size image

To eliminate the latter term, the entire left side should be cut out. The results are shown in Fig. 7. The shift of the minimum after cutting out the peaks is about 0.2 of the normalized frequency, which corresponds to the discrepancy coefficient for this case \(k=2 \frac{\alpha _0}{\tau _0} \omega _0 \varDelta \tau =0.2\omega _0\), obtained analytically (8).

Fig. 7
figure 7

The result of cutting out all the peaks to the left of the central in the time domain for \(\varDelta \tau = 20\,\hbox {fs}\). The sequence of pulses in the a time and b spectral domains. c Zoomed area with visible shift of the minimum after cutting out one of the peaks

Full size image

The discrepancy coefficient obtained can be translated into a temporal domain since the coefficient of linear frequency modulation of the pulse is known. The linear chirp can be defined by \(\phi (t)=\alpha _0 t+b\) (Fig. 8), where \(\alpha _0\) is the linear frequency modulation coefficient, and b is the constant coefficient of the linear function. Supposing that the discrepancy in the frequency domain leads to discrepancy in the time domain \(t_1-t_2\), with \(t_1>t_2\), temporal discrepancy coefficient is related to the spectral one as follows (Fig. 8):

$$\begin{aligned} k=\phi (t_1-t_2)=\alpha (t_1-t_2). \end{aligned}$$
(9)
Fig. 8
figure 8

Conversion of the spectral discrepancy coefficient of the central frequency of subpulses in the quasidiscrete temporal structure k into the temporal one

Full size image

For the case shown in Fig. 5, \(k = 0.1\), and therefore \(t_1-t_2=\frac{k\tau _0}{\alpha _0} =2\varDelta \tau =\) 20 fs. To confirm the values obtained, numerical simulation was performed. Its results are shown in Fig. 9. It can be seen that the shift of the minimum after cutting out one of the peaks is about 20 fs, which corresponds to the value previously obtained.

Fig. 9
figure 9

The result of cutting out one of the frequency domain peaks for \(\varDelta \tau = 10\,\hbox {fs}\). Sequence of pulses in the a spectral and b time domain. c Zoomed area with visible discrepancy after cutting out one of the peaks

Full size image

4 Experimental confirmation

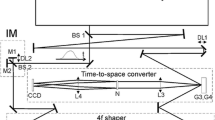
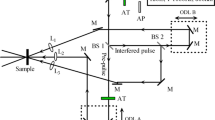
To verify the results obtained, they are compared with the experimental study on the femtosecond sequence of subpulses’ spectral–temporal coding presented in [19]. The experimental setup is presented in Fig. 10. The source is a femtosecond Ti:sapphire laser system based on a regenerative amplifier (Regulus 35f1k, Avesta-Project). The pulse duration is 30 fs, the repetition rate is 1 kHz, and the energy of a single pulse is up to 2 mJ. The sequence of pulses is formed in the Michelson interferometer with interference of two chirped pulses with a delay between them shorter than their duration. The sequence is coded using 4f-shaper by modulating the spectral quasidiscrete structure with the help of an SLM located in its spectral plane. To visualize the received signal, a time-to-space conversion device is used [28].

Fig. 10
figure 10

Experimental setup [19]. M1, M2 mirrors interferometer Michelson (IM), BS1, BS2 beam splitters, DL1, DL2 delay lines, G1, G2, G3, G4 gratings, L1, L2, L3, L4 lens, SLM spatial light modulator, N nonlinear crystal, CCD camera

Full size image

Figure 11 shows the result of the experiment of coding the temporal sequence by cutting out the spectral components (Fig. 11a), as well as the results of numerical simulation with the same parameters (Fig. 11b–d). It can be seen that when the spectral lines are cut out, the corresponding subpulses in the time sequence are incorrectly cut out. As can be seen from Fig. 11a-insert, the minimum is shifted by 800 fs. The numerical simulation results showed a similar shift in the generated sequence as a result of time-domain coding equal to a doubled time delay.

Fig. 11
figure 11

a The result of the experiment of coding the temporal sequence by cutting out the spectral components. The pulse duration is 1200 fs, and the time delay is 400 fs. Insertion is the result of discrepancy in the time domain as a result of the coding experiment. b Uncoded (red) and coded (blue) quasidiscrete spectrum. c The result of simulating the temporal sequence coding. The red curve is the original sequence, and the blue one is the coded one. The pulse duration is 1200 fs, the time delay is 400 fs, and the phase modulation factor is 0.0085. d Result of the discrepancy in encoding sequence

Full size image

Regarding the results obtained and the assumption for a chirped pulse, sequences with any repetition rate of any duration can be generated and controlled. Figure 12 shows an example of numerical simulation of sequence control with a repetition rate of 0.2–0.4 THz for a chirped pulse of 100 ps duration and a phase modulation coefficient of 0.015. The repetition rate was varied by changing the time delay between the interfering pulses from 1.5 to 3 ps. Figure 12III illustrates the uncoded sequence of pulses with repetition rate of 0.4 THz. It can be seen that individual subpulses of temporal structure do not overlap down to the level of \(10^{4}\). As a result of information coding for the repetition rate of 0.4 THz, temporal sequence distortion occurs (Fig. 12c-II), because the temporal discrepancy coefficient (9) for this case is 2.4 times greater than the duration of one subpulse and residual interference term is formed.

Fig. 12
figure 12

The result of numerical simulation of temporal sequence coding by cutting out the spectral components for a pulse of 100 ps duration and a repetition rate of a 0.2 THz, b 0.25 THz, and c 0.4 THz. The red curves are the original quasidiscrete spectrum (I) and the initial sequence of subpulses (II), and the blue curves are coded ones. (III) The uncoded temporal sequence of subpulses with repetition rate of 0.4 THz and for initial pulses with duration of 100 ps in log scale

Full size image

Sequences with THz repetition rate require very fine-tuning of the interferometer for correct operation. Such systems demand maintaining a constant time delay for the formation of a subpulse sequence. This requires vibration isolation and spatial and thermal stabilization. There are linear piezo-stages with a step accuracy of 10 nm. This means that it can maintain the stability of the temporal structure of subpulses with an accuracy of 70 attoseconds. This illustrates the possibility of the sequence stability control. In the case of fiber delay line, the same situation is observed. Moreover, because the pulses in the time structure spread out so that the adjacent wavelengths do not overlap with each other in space during propagation, neither timing jitter nor cross-talking occurs.

5 Conclusion and future work

In conclusion, the numerical simulation methods demonstrate the possibility of forming an ultralong sequence of subpulses with any repetition rate and of controlling it considering the discrepancy coefficient. The results show the formation of a controlled sequence with a duration of more than 100 ps, which is difficult to achieve by existing methods. This paper has analytically justified the discrepancy between the temporal and spectral structures formed with the interference of two femtosecond phase-modulated pulses shifted by a time delay less than their duration. The numerical simulation methods have determined the presence of the discrepancy coefficient of the central frequency of subpulses in the quasidiscrete temporal structure with respect to the central frequency of the spectral lines in the quasidiscrete spectral structure. The discrepancy coefficient can be represented analytically both in time and spectral domains. The possibility of controlling the temporal structure by cutting out the “corresponding” spectral lines is demonstrated experimentally. As a result, the temporal shift due to the discrepancy in the temporal structure of the subpulses during the modulation of the spectral quasidiscrete structure is measured experimentally. The shift is equal to the temporal discrepancy coefficient described analytically. Considering the discrepancy coefficient, the quality of information coding can be improved. Based on this, it is possible to make an a priori assessment of the advisability of using a particular configuration of the system for the most efficient data transmission in such areas as ultrafast information transfer and optical coherence tomography.

Future work involves collaboration with colleagues and the implementation of these guided-wave optical technology into existing optical communication systems. In the future, it is necessary to investigate the propagation of coded sequences of subpulses in conventional optical fibers and free space. It is also necessary to study the possibility of using these sequences to control fast processes.