Accuracy of non-resonant laser-induced thermal acoustics (LITA) in a convergent–divergent nozzle flow

Abstract

Non-resonant laser-induced thermal acoustics (LITA) was applied to measure Mach number, temperature and turbulence level along the centerline of a transonic nozzle flow. The accuracy of the measurement results was systematically studied regarding misalignment of the interrogation beam and frequency analysis of the LITA signals. 2D steady-state Reynolds-averaged Navier–Stokes (RANS) simulations were performed for reference. The simulations were conducted using ANSYS CFX 18 employing the shear-stress transport turbulence model. Post-processing of the LITA signals is performed by applying a discrete Fourier transformation (DFT) to determine the beat frequencies. It is shown that the systematical error of the DFT, which depends on the number of oscillations, signal chirp, and damping rate, is less than $1.5\%$ for our experiments resulting in an average error of $1.9\%$ for Mach number. Further, the maximum calibration error is investigated for a worst-case scenario involving maximum in situ readjustment of the interrogation beam within the limits of constructive interference. It is shown that the signal intensity becomes zero if the interrogation angle is altered by $2\%$. This, together with the accuracy of frequency analysis, results in an error of about $5.4\%$ for temperature throughout the nozzle. Comparison with numerical results shows good agreement within the error bars.

1 Introduction

This paper presents laser-induced thermal acoustics (LITA) measurements performed along the centerline of a convergent–divergent nozzle in the Mach number range of 0.25–1.7. LITA classifies as a non-intrusive, seedless, four-wave mixing point measurement technique. It involves forming of a laser-induced density grating originating from two intersecting coherent laser beams. A third laser beam, focused on the density grating, is partly scattered and, thus, forms the signal beam that holds direct information on the speed of sound. Challenges arising from measurements in a convergent–divergent nozzle originate from strong flow gradients resulting in a loss of signal quality. Förster et al. [1] recently compared LITA with well-established laser-based techniques (tunable diode laser absorption spectroscopy, TDLAS, laser-induced fluorescence, LIF, and coherent anti-Stokes Raman spectroscopy, CARS) on their application to shock-heated flows. They point out that a unique feature of LITA is that signal analysis is independent on its intensity since the speed of sound and Mach number can be determined solely from a frequency analysis. This makes LITA a valuable diagnostic tool for the current flow conditions.

The LITA signal has been theoretically studied and mathematically described [2,3,4] and has since then been widely used to measure speed of sound (temperature) and Mach number (velocity) [5,6,7,8,9]. Further, it has been demonstrated to measure transport properties, species concentration and pressure [10]. In the present paper, the accuracy of LITA is systematically addressed. Schlamp et. al investigated the effect of low signal-to-noise ratios [11] and of translational interrogation beam misalignment [12]. However, the systematic errors arising from interrogation angle misalignment and frequency post-processing are still unquantified to the author’s knowledge.

2 Methods

2.1 Experimental methods

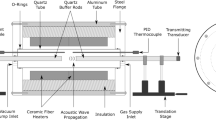
The experiments presented here were performed at the supersonic test facility of the Institute of Aerospace Thermodynamics (ITLR) at the University of Stuttgart. A schematic of the facility is shown in Fig. 1.

Fig. 1

ITLR supersonic test facility

Air is supplied by a screw compressor and passes an air dryer and an electrical heater before reaching the test section. The maximum continuous mass flow rate amounts to ${1.45}\,\mathrm{kg\ s}^{-1}$ at a total pressure of ${10}\,{\mathrm{bar}}$. A three-staged heater allows for a maximum total temperature up to ${1300}\,\mathrm{K}$. The test facility is further equipped with a mass flow meter (Endress + Hauser, Prowirl 77H DN 100, accuracy $<1\%$ of reading) and a total pressure sensor (Omega, PAA21-C-10, accuracy $<0.5\%$ of full scale) at the inlet of the test section.

The flow channel consists of three segments with a constant width of ${40}\,{\mathrm{mm}}$. The first segment connects the heater outlet with the optically accessible test section (segments 2 and 3). Air passes a rectangular convergent–divergent nozzle with a nozzle throat height of ${26.3}\,{\mathrm{mm}}$ designed for an exit Mach number of $\mathrm{Ma}=1.7$ in the second segment (Fig. 2).

Fig. 2

Second segment of the flow channel

The third segment has a constant height of ${35.4}\,{\mathrm{mm}}$. Optical access is provided by flat quartz glass windows from both sides of the test section. Static pressure taps (Scanivalve, DSA 3016, accuracy $<0.05\%$ of full scale) are aligned slightly off the symmetry plane of the flow channel throughout the top wall. A calibrated thermocouple (Type K, accuracy $\pm {1.5}\,\mathrm{K}$) is placed upstream of the nozzle in the first segment to measure the total temperature. The flow channel contour and the window positions are given in Fig. 3 together with the coordinate system used for presenting the measurement results. The wall-coordinates of the convergent–divergent nozzle are further shown in the “Appendix” (Table 2).

Fig. 3

Flow channel contour

Operating conditions were set to a total pressure of ${2.5}\,{\mathrm{bar}}$ and a total temperature of ${380}\,\mathrm{K}$ ensuring supersonic flow conditions throughout the whole duct downstream of the nozzle throat. All results presented were measured along the centerline of the convergent–divergent nozzle within the first window (segment 2).

2.2 Numerical methods

A 2D numerical simulation of the flow field was performed to compare with the experimental data. The numerical domain comprises the whole test section of ${664}\,{\mathrm{mm}}$ length (${-184.8}\,{\mathrm{mm}} \le x \le {479.2}\,{\mathrm{mm}}$, see Fig. 3). The mesh consists of an H-grid topology throughout the whole duct and features about 1 Mio nodes. The steady-state Reynolds-averaged Navier–Stokes equations (RANS) were solved using the commercial implicit flow solver ANSYS CFX 18. For turbulence modelling, the shear stress transport (SST) turbulence model developed by Menter [13] was used. Furthermore, the following boundary conditions were applied: the inflow conditions were defined according to the mass flow rate and the total temperature recorded during the experiments. The turbulence intensity was set to $I=4.2\%$ according to the experiments reported here and the eddy viscosity ratio was set to $\nu _t /\nu = 100$, which is appropriate for high Reynolds number flow. All walls were set adiabatic and were treated as no-slip smooth walls. The outlet static pressure was set to ${0.4}\,{\mathrm{bar}}$.

3 Laser-induced thermal acoustics (LITA)

3.1 Fundamentals

Excitation phase

During the excitation phase, two coherent laser beams are crossed under an angle $\theta$ as depicted in Fig. 4.

Fig. 4

Density grating formed by two crossed coherent laser beams

In the intersection area, the electric field is modulated forming an ellipsoidal intensity grating [4]. The fringe spacing $\Lambda _{\mathrm{grid}}$ depends on the wavelength of the excitation beams $\lambda _{\mathrm{exc}}$ and the crossing angle

$$\begin{aligned} \Lambda _{\mathrm{grid}}=\frac{\lambda _{\mathrm{exc}}}{2\sin (\theta /2)}. \end{aligned}$$

(1)

In the ellipsoidal measurement volume, the electric field modulations cause a density grating with identical fringe spacings. The two underlying optoacoustic effects are electrostriction and thermalisation [14]. The latter only contributes if radiation with wavelength $\lambda _{\mathrm{exc}}$ is absorbed by the test medium, leaving electrostriction the only mechanism for these experiments. In this case, the molecules of the dielectric test medium are polarized within the interference area and accelerated towards the high-energy regions of the grating. The acceleration results in the generation of two sound waves propagating in opposite directions and perpendicular to the grating fringes. These sound waves are convected with the local test medium velocity. The wavelength of the individual wave packages is equal to the fringe spacing $\Lambda _{\mathrm{grid}}$.

Interrogation phase

The physical basis underlying the interrogation phase is the Brillouin light scattering (BLS) [15], i.e., the inelastic scattering of monochromatic laser light on sound waves as sketched in Fig. 5.

Fig. 5

Brillouin light scattering of the interrogation beam on the density grating

The scattering vector $\varvec{q}$ is defined as the difference between the propagation vector of the interrogation and the signal light beam, $\varvec{k}_{int}$ and $\varvec{k}_{\mathrm{sig}}$,

$$\begin{aligned} \varvec{q} = \varvec{k}_{\mathrm{int}}-\varvec{k}_{\mathrm{sig}} \end{aligned}$$

(2)

and its magnitude can be determined as:

$$\begin{aligned} q = \left| \varvec{q} \right| = 2 k_{\mathrm{int}} \sin (\varphi /2). \end{aligned}$$

(3)

Here, $k_{\mathrm{int}}=2 \pi n / \lambda _{\mathrm{int}}$ is the wave vector written as a function of the refractive index n and $\lambda _{\mathrm{int}}$ is the interrogation wave length.

Since the scattering is inelastic, each photon either loses (Stokes process) or gains (anti-Stokes process) energy when interacting with the sound waves. Therefore, the frequency of the interrogation beam $f_{\mathrm{int}}$ undergoes a Doppler shift, resulting in the so-called Brillouin frequency

$$\begin{aligned} f_{\mathrm{Brillouin}} = f_{\mathrm{int}} \pm \frac{a}{2 \pi } q , \end{aligned}$$

(4)

where a is the speed of sound. Both frequencies (from the Stokes and anti-Stokes process) interfere with each other, so that the beat frequency recorded by a high-speed detector corresponds to twice the Brillouin frequency shift

$$\begin{aligned} f_{2a} = \frac{4a}{\lambda _{\mathrm{int}}}\sin (\varphi /2) . \end{aligned}$$

(5)

It becomes apparent that the frequency of the signal beam only depends on the interrogation beam wavelength $\lambda _{int}$ and interrogation angle $\varphi$, but not on the fringe spacing $\Lambda _{\mathrm{grid}}$ of the sound waves.

Maximum signal intensity is obtained when the reflected light interferes constructively. For a coherent signal beam, the Bragg condition

$$\begin{aligned} \frac{\lambda _{\mathrm{int}}}{2\sin (\varphi _{\mathrm{opt}}/2)}=\frac{\lambda _{\mathrm{exc}}}{2\sin (\theta /2)}= \Lambda _{\mathrm{grid}} \end{aligned}$$

(6)

has to be fulfilled. Hence, the condition for maximum signal intensity directly prescribes the geometrical setup of excitation and interrogation beams for given laser wavelengths.

3.2 Optical setup

The optical setup used for the experiments is similar to the one recently used at our facilities [1, 5, 6, 16]. Figure 6 outlines all relevant components of the setup.

Fig. 6

Optical LITA setup

For the excitation beams, a pulsed Nd:YAG laser (Spectra-Physics PIV-200-10, $\lambda {\mathrm{exc}}={1064}\,{\mathrm{nm}}$, $\tau _{\mathrm{pulse}}={10}\,{\mathrm{ns}}$) is used. After passing a beam splitter, the two beams are focused via a lens (AR-coated, $f={700}\,{\mathrm{mm}}$) to form the density grating. For the given LITA setup, the ellipsoidal measurement volume has a diameter of $\Omega _{\mathrm{exc}} \approx {300}\,{{\upmu }\mathrm{m}}$ and a length of approximately ${7}\,{\mathrm{mm}}$. The beam originating from a continuous wave DPSS laser (Coherent Verdi V8, $\lambda _{\mathrm{int}}={532}\,{\mathrm{nm}}$) is split into an interrogation and a reference beam at a ratio of 90/10. The former is focused on the measurement volume to a spot size of $\Omega _{\mathrm{int}} \approx {140}\,{{\upmu }\mathrm{m}}$ and is partly scattered into the signal beam. The latter passes a variable ND filter before it is focused by the lens such that it interferes with the signal beam. The mode in which the signal beam and an adjustable amount of the reference beam are mixed before reaching the detector is referred to as heterodyne detection. Homodyne detection is present if the reference beam is cut off. The LITA signal is directed to an avalanche photo detector (Thorlabs APD110) using an optical coupler and a multi-mode fiber (${10}\,{{\upmu }\mathrm{m}}$ in diameter). The entire setup is mounted on a 3-axis optical translation table that allows to shift the probe volume inside the flow channel. For protection of the windows, the energy of the excitation laser was limited to ${91}\,\mathrm{mJ}$. The power of the continuous interrogation laser is restricted to ${5}\,\mathrm{W}$ through scattered light originating from the lens and glass windows.

3.3 Signal acquisition and processing

Fig. 7

Example LITA signals detected in a, b subsonic and c, d supersonic flow from a, c homodyne and b, d heterodyne detection together with the corresponding frequency spectra

From the time resolved signal, certain flow properties can be derived in two different ways. First, the signal can be compared to a theoretical model proposed by Cummings et al. [14]. The theoretical model takes the governing optoacoustic effects into account and predicts the signal intensity variations in time. Curve fitting of the obtained signal allows for the calculation of flow velocity and speed of sound. Secondly, a frequency analysis of the LITA signal can be performed in order to identify the dominating frequencies and to calculate the flow Mach number and the speed of sound. This method provides the best results for noisy signals with a short life time and it is, therefore, applied to the presented data set. Typical homodyne signals detected in subsonic and supersonic flow and their frequency spectra are shown in Fig. 7a, c. For purely non-resonant measurements, the modulation of the signal occurs with $f_{2a}$. Knowing the signal frequency and the interrogation angle of the geometrical setup, the speed of sound can be calculated according to Eq. 5. The systematic errors in the determination of the interrogation angle can be reduced using calibration measurements in a resting fluid and the speed of sound becomes

$$\begin{aligned} a = a_{\mathrm{calib}} \frac{f_{2a,\mathrm{calib}}}{f_{2a}}. \end{aligned}$$

(7)

Assuming ideal gas conditions and known gas composition, the local temperature follows directly from the speed of sound as:

$$\begin{aligned} T = \frac{a^2}{\gamma R}. \end{aligned}$$

(8)

Calculation of the flow velocity from a given signal requires heterodyne detection. Mixing of the reference beam and the two signal parts from Stokes and anti-Stokes scattering causes two additional beat frequencies in the spectrum of the heterodyne signal. Typical heterodyne signals and their frequency spectra are shown in Fig. 7b, d. In quiescent air, the beat frequency is the same for both sound waves and the two peaks in the signal’s spectrum coincide at $f_a$. This peak splits into two frequencies $f_{v-}$ and $f_{v+}$ if the flow velocity is non-zero. From their difference to $f_a$, the flow velocity $v_{\mathrm{flow}}$ can be calculated according to

$$\begin{aligned} |v_{\mathrm{flow}} |=\frac{f_{v+} \mp f_{v-}}{2} \frac{\lambda _{\mathrm{int}}}{2\sin (\varphi /2)} \end{aligned}$$

(9)

for subsonic and supersonic flow, respectively. The Mach number then results from Eqs. 9 and  5 as

$$\begin{aligned} {\mathrm{Ma}} = 1 \mp \frac{2f_{v-}}{f_{2a}}. \end{aligned}$$

(10)

Note that no calibration is required to determine the Mach number.

At every measurement point, 200 homodyne and 200 heterodyne signals were recorded separately. For frequency analysis, a Matlab routine that automatically picks the 50 signals exhibiting the best signal-to-noise ratio was applied. The frequency spectra of the signals were analyzed using a discrete Fourier transformation (DFT) and the dominant frequency was automatically detected ($f_{2a}$ from homodyne and $f_{v-}$ from heterodyne detection). The corresponding mean values were calculated as well as the standard deviation based on a confidence interval of ${66}{\%}$. The temperature and Mach number were obtained from the averaged frequencies and error propagation was applied to estimate the uncertainty of the flow properties.

4 Results

The results are organized in three parts: first, the calibration measurement and its accuracy are discussed. This involves the evaluation of the systematic error of interrogation angle misalignment. Secondly, the results from experimental and numerical investigation of the nozzle flow are presented including Mach number, temperature and turbulence level distributions along the centerline. Finally, the signal quality and the accuracy of frequency analysis are addressed.

4.1 Accuracy of LITA calibration

Fig. 8

Average of 100 LITA signals each from calibration measurements at varying interrogation angle $\varphi$

Calibration measurements have been conducted in quiescent air at room temperature. As discussed before, the signal intensity reaches its maximum if the Bragg condition (Eq. 6) is fulfilled. For the current setup ($\lambda _{\mathrm{int}}=\lambda _{\mathrm{exc}}/2$), the Bragg condition simplifies to $\varphi _{\mathrm{opt}} \approx \theta /2$ applying the sine approximation for small angles. Consequently, the beams were aligned in such a way that the interrogation angle $\varphi \approx {0.7424}^{\circ }$ is half the excitation angle $\theta \approx {1.4848}^{\circ }$. For the calibration signal with the maximum intensity, a peak frequency of $f_{2a,\mathrm{calib}}=33.34 \pm {0.25}\,{\mathrm{MHz}}$ was observed (see Figs. 8, 9). According to Eq. 5, the corresponding interrogation angle is $\varphi _{\mathrm{opt}}=0.7429 \pm {0.0055}^{\circ }$. This is in perfect agreement with the geometrical setup.

Fig. 9

Frequency distributions determined from calibration measurements at varying interrogation angle $\varphi$ of 100 LITA signals each

Table 1 Effect of interrogation beam misalignment

As the flow is accelerated to supersonic speed, the density along the nozzle centerline decreases and, thus, the refractive index causing a change in beam alignment. Strong vibrations outside of the flow channel can further cause gradual misalignment of the laser beams over the test period. That is why in situ readjustment of the interrogation angle is indispensable in order to obtain good LITA signals. This interferes with the calibration of the LITA setup since the calibration frequency is proportional to the interrogation angle $f_{2a} \propto \varphi /2$ in the small angle approximation (see Eq. 5). Hart et al. [17] overcome this issue using a reference cell that allows for in situ calibration. This was not possible with the current setup because our optical translation table does not allow for a focus point outside of the flow channel. That is why the influence of the interrogation angle on the calibration frequency has to be evaluated.

As discussed above, the interrogation angle is conditioned by the need of constructive interference. Purely constructive interference is present if the Bragg condition (Eq. 6) is fulfilled. The signal intensity resulting from interference can theoretically be predicted assuming quasi-elastic scattering. Figure 10 shows that the signal intensity drops below half of its maximum if the interrogation angle differs by only $1.22\%$ from the Bragg condition and becomes zero at $2\%$ deviation.

These limits have been verified experimentally. To ensure that the signal beam is captured even if the interrogation angle is out of adjustment, the scattered light was reduced by removing the windows to allow for the usage of a multimode fiber of ${105}\,{{\upmu }\mathrm{m}}$ in diameter. Starting from the optimum interrogation angle, which fulfills the Bragg condition, the interrogation beam was moved to each direction until the maximum signal intensity dropped below half of the maximum signal output (see Fig. 8). The frequency distribution depicted in Fig. 9 illustrates the resulting frequency shift and the corresponding calculated interrogation angles are summarized in Table 1.

Fig. 10

Theoretically predicted signal intensity together with experimental results at varying interrogation angle $\varphi$ deviating from the Bragg condition $\varphi _{opt}$

The experiments fit the theory very well (see Fig. 10). Since readjustment of the interrogation beam during the experiments is only sensible within the limits set by constructive interference, the accuracy of calibration can be estimated from the theoretically predicted signal intensity. Starting the experiments with the optimum interrogation angle from calibration measurements, the interrogation beam cannot be moved beyond the point where the signal intensity drops to zero. Therefore, an overall calibration error of $2\%$ was considered.

4.2 Nozzle flow

Fig. 11

Experimental (EXP) and numerical (CFD) wall static pressure

Fig. 12

Numerical pseudo-schlieren of the nozzle flow and positions of LITA measurements at $x={-40,-35,-25,-20,-15,-10,-5,6,10,15,20,26,35,40}\,{\mathrm{mm}}$

The LITA results presented here were recorded along the centerline of a convergent–divergent nozzle involving high pressure, temperature and density gradients. Reference data are provided by a 2D numerical simulation of the entire flow field. Wall static pressure measurements are utilized to validate the numerical result: Figure 11 shows the wall static pressure as a function of axial coordinate, where $x={0}\,{\mathrm{mm}}$ denotes the position of the nozzle throat. Note that error bars are not plotted because they are minor ($< \pm \, {0.035}\,{\mathrm{bar}}$). The measured static pressure along the channel walls is overall well predicted by the simulation. The deviation in pressure increase downstream of the nozzle indicates that the boundary layer grows faster in the experiment than in the simulation. This can be easily explained with 3D effects, which cannot be captured by the 2D simulation, namely the side wall boundary layers and the interaction between the boundary layers in the corners of the rectangular channel. Figure 12 shows the numerically predicted pseudo-schlieren image of the nozzle flow and the locations of all LITA measuring positions. It clearly shows the expansion fans that form at the nozzle throat and the position of their crossing point located at $x \approx {25}\,{\mathrm{mm}}$.

Temperature and Mach number

The measured temperature and Mach number along the centerline are presented in Fig. 13, together with numerical results for comparison.

Fig. 13

Experimental (LITA) and numerical (CFD) temperature and Mach number along the nozzle centerline together with their uncertainty $\sigma$ and divergence $\delta$

The uncertainty $\sigma$ of the flow property and the deviation $\delta$ compared to numerical data are enlarged below. The uncertainty is determined from error propagation taking into account the standard deviations of the beat frequencies $f_{v-}$ and $f_{2a}$ as well as the maximum error of frequency analysis (discussed below) and, concerning only the temperature, the maximum calibration error. The measurement error of the temperature is comparatively large ($\pm 13 \ldots {19}\,{\mathrm{K}}$) throughout the whole nozzle. This is due to uncertainties resulting from the in situ readjustment of the interrogation angle, which are an order of magnitude larger than uncertainties resulting from standard deviations of the beat frequencies. The numerical solution deviates up to $5 \%$ but lies within these error bars indicating that the error estimation is valuable. The uncertainties of the measured Mach numbers are relatively minor since the Mach number does not rely on the calibration measurement but only on the frequency analysis. In this case, the numerical solution deviates less than $3.2 \%$ everywhere. We believe that this can be attributed to uncertainties in determining the boundary conditions of the numerical solution or experimental deviations in pressure and temperature that are not captured by the simulation. However, the overall agreement of both, temperature and Mach number, between experimental and numerical data is good.

Free-stream turbulence intensity

The free-stream turbulence intensity is defined as:

$$\begin{aligned} I = \frac{1}{\overline{u}} \sqrt{\frac{2}{3} k} \end{aligned}$$

(11)

with $\overline{u}$ being the free-stream mean velocity and the turbulence kinetic energy

$$\begin{aligned} k = \frac{1}{2} \left( \overline{{u}'_x{ u}'_x} + \overline{{u}'_y {u}'_y} + \overline{{u}'_z {u}'_z} \right) . \end{aligned}$$

(12)

Here, $\overline{{u}'_x {u}'_x}$, $\overline{{u}'_y {u}'_y}$, and $\overline{{u}'_z {u}'_z}$ are the time-averaged, squared velocity fluctuations in all three axes of space (x, y, z). LITA signals from heterodyne detection allow for the statistical analysis of the streamwise turbulence intensity calculated from the root mean square (rms) of the velocity fluctuations ${u}'_{x,\mathrm{rms}}$ divided by the corresponding mean velocity $\overline{u_x}$. For this, the velocity fluctuations and the mean velocity are expressed in terms of the averaged ($\overline{f_{2a}}$, $\overline{f_{v-}}$) and instantaneous ($f_{2a,i}$, $f_{v-,i}$) beat frequencies:

$$\begin{aligned} \frac{{u}'_{x,\mathrm{rms}}}{\overline{u_x}}= & {} \frac{\sqrt{\overline{{u}'_x {u}'_x}}}{\overline{u_x}} = \frac{1}{\overline{u_x}} \sqrt{ \frac{1}{N} \sum _{i=1}^{N} (u_{x,i} - \overline{u_x})^2 }\nonumber \\= & {} \frac{1}{\overline{f_{2a}} - 2\overline{f_{v-}}} \sqrt{\frac{1}{N}\sum _{i=1}^{N}(f_{2a,i}-2f_{v-,i}-\overline{f_{2a}}+2\overline{f_{v-}})^2} \end{aligned}$$

(13)

The statistical analysis relies on the accurate frequency detection of both beat frequencies from single shot LITA measurements making it prone to errors. That is why only high-quality LITA signals, which clearly exhibit both beat frequencies for $\ge 6$ oscillations (e.g., Fig. 7a), are considered. Figure 14 includes the results of a streamwise turbulence intensity analysis obtained from heterodyne LITA signals at different positions along the nozzle centerline upstream of the nozzle throat.

Fig. 14

Experimental (LITA) and numerical (CFX) decay of streamwise turbulence intensity along the nozzle centerline together with the measurement uncertainty $\sigma$

The measurement uncertainties, which take into account the standard deviations of the time-averaged beat frequencies and $0.5\%$ systematical error of the instantaneous beat frequencies, are plotted below. (The accuracy of frequency analysis as a function of number of oscillations is discussed in the following section.) In the region of the nozzle entry, the measured velocity fluctuations correspond to about $4.2\%$ streamwise turbulence intensity. Further, the LITA measurements reveal a strong decay in turbulence intensity in flow direction, which is typical for a strongly accelerated flow [18, 19]. Figure 14 further shows results from numerical RANS simulations with various turbulence inlet intensities (2, 4.2, 10 and $20\%$). The respective velocity fluctuations are calculated from Eq. 12, which simplifies to $\overline{{u}'_x {u}'_x}=2/3k$ under the assumption of isotropic turbulence ($\overline{{u}'_x{u}'_x}=\overline{{u}'_y{u}'_y}=\overline{{u}'_z{u}'_z}$) of the SST model. Figure 14 reveals that the predicted streamwise turbulence intensity in the nozzle region is practically insensitive to the inlet condition and differs considerably from the experimental results. The strong, non-physical decay of turbulence variables in an inviscid uniform flow, which gets stronger with increasing inlet turbulence intensity, is a known issue with the SST model [20]. This results from the k-$\epsilon$ model, which is used in the outer region of the boundary layer, together with the assumption of locally isotropic turbulence [21]: from this assumption follows that local mean flow gradients are suppressed in the free-stream and, thus, no turbulence kinetic energy can be produced. Here, the k-$\epsilon$ equation reduces to

$$\begin{aligned} \overline{u} \frac{\partial k}{\partial x} = -\epsilon , \end{aligned}$$

(14)

where k is the turbulence kinetic energy and $\epsilon$ is the turbulence dissipation. This leads to a strong overprediction of the decay of turbulence kinetic energy in non-isotropic turbulent flows such as channel flows [22], where energy is transferred at a turbulent length scale. However, the correct simulation of turbulence variables is a huge field of research and it is not the purpose of this paper to entirely cover this topic.

4.3 Signal quality

High pressure, temperature and density gradients affect the signal life time and the signal intensity. In the following, both aspects are discussed by means of LITA results from homodyne detection.

Chirp effect

The life time of the homodyne LITA signal significantly decreases as the flow accelerates following from the decreasing residence time of the sound waves. As a consequence, the number of detectable oscillations drops from 6–8 in the subsonic to 2–4 in the supersonic flow region (compare Fig. 7a, c).

Fig. 15

Single oscillation frequencies of the average of 50 LITA signals each from homodyne detection at different positions throughout the nozzle

Furthermore, it was observed that the first oscillation of the homodyne LITA signals exhibits a chirp as outlined in Fig. 8. This, in combination with a varying number of oscillations, can lead to an error in frequency detection. The chirp effect is investigated systematically by means of the average of 50 LITA signals at each position in the range of $-40 \le x \le {20}\,{\mathrm{mm}}$. (The signal quality does not allow for single oscillation analysis further downstream.) All single oscillation frequencies were identified by applying a simple computerized peak-detection routine after smoothing the averaged signal with a Savitzky–Golay filter. Note that the accuracy of chirp quantification is restricted by the temporal resolution of the oscilloscope: a single oscillation comprises about 135–165 time samples, thus, a deviation of one single time sample corresponds to $<0.75\%$. The resulting frequencies, normalized with respect to the corresponding dominant frequency of a DFT, are depicted in Fig. 15. In the region of the nozzle inlet, the first oscillation is a little bit delayed compared to the following oscillations. This (positive) chirp becomes less prone when the flow is accelerated throughout the nozzle and turns to a considerable negative chirp in the supersonic flow region. Apart from that, the following oscillations are not chirped but oscillate at a roughly constant frequency.

A chirp effect in homodyne LITA signals has been documented before [9, 23]. Schlamp et al. [23] reported a negative chirp measured in a supersonic free jet, which matches our observations made in the supersonic flow region. However, in their experiments the chirp persisted throughout the whole signal ($\approx 10$ oscillations). Schlamp et al. could not physically explain the chirp but argued that initial heating of the probe volume or deviations from the plane wave assumption might be the reason. Hart et al. [9] also reported a (weak) chirp but did not quantify it. They believed that the chirp was caused by their geometrical setup ($\Omega _{\mathrm{int}}> \Omega _{\mathrm{exc}}$) and the associated changing scattering angle with respect to the locally fixed detector as the acoustic waves pass the interrogation beam’s focus region. This can be excluded for the current experiments because the diameter of the interrogation beam was smaller than the diameter of the excitation beam. Further, the chirp is also present in the calibration measurement (Fig. 8) at which a multimode fiber of ${105}\,{{\upmu }\mathrm{m}}$ in diameter was used making the signal detection independent of the scattering angle.

We believe that the change in sign of the chirp in our experiments is connected with the readjustment of the interrogation angle during the test day and the linked shift of its initial position within the probe volume. However, this still does not explain the underlying physical effect. Following the idea of Schlamp et al., another reason could be that the initial heating of the probe volume is only present if the flow temperature is cold enough in our experiments.

Accuracy of the frequency analysis (DFT)

The quality of a discrete Fourier analysis (DFT) depends (among other things) on the number of oscillations and on the damping rate of the input signal. It is known that a DFT tends to underestimate the frequency if only a limited number of oscillations can be analyzed. In order to quantify this (systematic) error, a DFT was performed on a model homodyne LITA signal without chirp and a varying number of oscillations was analyzed. The result is depicted in Fig. 16 (continuous line), where a normalized frequency of 1 refers to the actual oscillating frequency.

Fig. 16

Accuracy of a DFT as a function of number of oscillations

It is shown that the error is considerable for two oscillations but drops below $1\%$ for more than four oscillations. Figure 16 further shows exemplary results of chirped signals from our experiments. Consequently, the uncertainty of a DFT is enhanced if the signal exhibits a positive chirp and reduced if the signal exhibits a negative chirp. In our experiments, a positive chirp was only observed in the subsonic flow region where the signal quality was good ($\ge 6$ oscillations). A negative chirp was documented further downstream ($x \ge -10\,{\mathrm{mm}}$) where the signal quality significantly deteriorates and the number of detectable oscillations locally drops to 2. According to Fig. 16, this leads to a maximum error of $1.5\%$ that has to be considered for frequency analysis. This inaccuracy has been already included in the error estimation of Fig. 13.

Pressure and temperature dependency

The LITA signal intensity is known to be a function of static pressure and temperature [1, 23, 24]. As a consequence, for a given total flow condition, the signal intensity decreases with increasing Mach number. Therefore, a significant drop of the signal intensity was observed in our experiments. This allows us to investigate the influence of static pressure and temperature on the LITA signal intensity. The results plotted in Fig. 17 rely on numerical data for the static pressure and temperature along the nozzle centerline. All signal intensities are averaged over $\ge 50$ signals at each position to level signal shot-by-shot fluctuations of the excitation laser.

Fig. 17

LITA signal intensity as a function of static pressure and temperature

A quadratic fit of the form $p^{2}T^{\mathrm{const}}$ shows best agreement (coefficient of determination $R^{2}=0.969$) with the experimental data for $\mathrm{const} = -2.85$. This value is close but just below the temperature exponent documented in literature: Danehey [24] predicts that for purely non-resonant LITA in quiescent fluids the peak signal intensity $I_{\mathrm{sig}}$ scales with $p^2$ and $T^{-3}$. Experimental works by Schlamp et al. [23] ($I_{\mathrm{sig}} \propto T^{-4.25}$) and Förster at al. [1] ($I_{\mathrm{sig}} \propto p^2 T^{-3.4}$) reveal a stronger dependence on temperature. However, we believe that the decrease in signal intensity in our experiments cannot be solely explained with the change in static pressure and temperature. Most likely, some other effects caused by (instationary) expansion fans, a decrease of turbulence as the flow is accelerated, or readjustment of the interrogation beam are superimposed.

5 Conclusion

Laser-induced thermal acoustics (LITA) measurements were performed in an undisturbed, strongly accelerated nozzle flow in the Mach number range of 0.25–1.7 involving strong gradients and a related loss of LITA signal quality along the nozzle centerline. These conditions allow for the comprehensive investigation of systematic errors arising from interrogation beam misalignment and frequency analysis: Changing flow conditions along the nozzle centerline together with strong vibrations and changing ambient temperature in the laboratory require in situ readjustment of the interrogation beam. This is a common procedure to obtain good LITA signals, however, the alternation of the interrogation beam angle interferes with the preceded calibration of the optical setup. It was shown that the signal intensity drops to zero if the interrogation angle differs $2\%$ from the optimum resulting from the Bragg condition. Post-processing of the LITA signals further involves frequency analysis of the oscillating time signals, typically performed by a discrete Fourier transformation (DFT). The accuracy of a DFT depends on the signal quality, i.e., on the signal intensity (signal-to-noise ratio), the chirp, and the number of oscillations. It was observed that all three characteristics decrease as the flow is accelerated resulting in a maximum systematic error of $1.5\%$ in frequency detection.

In addition, the temperature and Mach number along the nozzle centerline were analyzed and compared with results from a 2D URANS simulation. The results showed very good agreement within the error bars indicating that the estimation of systematical errors is reasonable. It was further demonstrated that high-quality LITA signals that allow for accurate single-shot post-processing of the velocity can be used to determine the velocity fluctuations in flow direction. The results reveal a drop of free-stream, streamwise turbulence intensity from 4.2 to $2.2\%$ within the first ${30}\,{\mathrm{mm}}$ of the convergent–divergent nozzle (up to ${15}\,{\mathrm{mm}}$ upstream of the nozzle throat). Finally, the strong gradients in pressure and temperature along the nozzle centerline were utilized to investigate their influence on the signal intensity. A quadratic fit of the form $I_{\mathrm{sig}} \propto p^2 T^{-2.85}$ showed best agreement.

Appendix

See Table 2.

Table 2 Dimensions (mm) of the Mach 1.7 nozzle with subsonic section