1 Introduction

Material technology is evolving rapidly toward creating new materials with particular electromagnetic (EM) and optical properties that do not exist in natural materials. One of the frontiers at which great conquests are being made is graphene formations. Since it was first synthesized in 2004 [1], graphene has been used in numerous applications in electronics [2, 3], optoelectronics [3], and photonics [4] and in the development of bioelectric sensory devices [5]. Graphene has several EM and optically unique properties such as high charge carrier mobility, electronic energy spectrum without a gap between the valence and conduction bands, and frequency-independent absorption of EM radiation [6–8].

Recently, significant attention has been focused on EM analysis and characterization of graphene [9–11]. Several investigations were carried out on the interaction of EM fields with graphene. EM absorbance and reflectance properties of graphene composites for different applications [12], EM wave absorption properties of graphene modified with carbon nanotube composites [13], and EM interference shielding of flexible graphene/polymer composite films in sandwiched structures [14] have been presented recently in the literature. Other studies demonstrated that both polarized plasmons (TE/TM) can be supported in graphene [15, 16]. The giant Faraday rotation influence on graphene coupled to metallic nanoparticles was theoretically investigated in [17]. The propagation of surface plasmon polaritons (SPP) in a graphene-based resonator-coupled waveguide system was numerically and theoretically investigated in [18]. Analytical models based on transformation optics for subwavelength gratings coupled into the plasmons of graphene were presented in [19]. Reflection, transmission, and absorption of EM waves by a super lattice graphene layer in the presence of an external magnetic field were investigated in [20]. Hyperbolic wavevector dispersions at mid- and far-infrared frequencies in multilayer graphene-dielectric stacks were studied in [21]. Waveguide modes in multilayer graphene-dielectric structures and the effective medium theory of graphene structures in the infrared band were presented in [22]. The conditions of large wavevector propagating EM waves in a subwavelength periodic multilayer graphene structure was theoretically investigated in [23].

In the presence of an external static magnetic field, graphene becomes gyrotropic [24–27]. In addition, under an external magnetic field, graphene rotates the polarization of a normally incident linearly polarized plane wave and the rotation angle depends on both the magnetic field and the chemical potential of the graphene [24]. In a wide frequency range and at large incidence angles, the graphene-dielectric stack under the effect of an external magnetic field is transparent for one circularly polarized wave, and opaque for the other [25]. Polarization-selective nonreciprocal isolation for circularly polarized waves using monolayer graphene in the presence of an external static magnetic field is theoretically demonstrated in [26].

Further notable behavior of optical waves in graphene structures have been noticed and reported by researchers. The visual transparency of the graphene can be defined in terms of its fine-structure constants as discussed in [9]. Perfect absorption in graphene multilayers and absorption in the magneto-optical response of graphene were discussed in [10, 28, 29]. The interaction between the transitions of both the interband and intraband in graphene allows the properties of graphene-dielectric multilayer structures to be changed to be electromagnetically opaque or transparent in terahertz (THz) or infrared frequency bands [30]. However, in general, at THz frequencies, the spatial dispersion introduced by the periodicity of graphene can be neglected, as proposed by [21]. Similar studies on other optical and electromagnetic periodic waveguiding structures have described similar wave behaviors [31, 32]. Such wave behavior can be utilized in many applications in photonics and optoelectronics, such as in photonic devices, polarization control, filtering, surface plasmon resonance, and tuning of light-emitting diodes and lasers and total internal reflection fluorescence microscopes [33].

In this work, an infinite graphene-dielectric stack placed in an anisotropic ambient medium is considered to examine the coupling of the evanescent waves and the formation of the discrete trapped modes in the dispersive gyrotropic graphene stack, the feasible resonances, and the associated transmission and field anomalies. The transfer matrix method (TMM) is utilized to develop expressions for the transmission coefficients in both the non-resonant and the resonant states. The instantaneous tangential field components are presented to confirm the field amplifications at the resonant frequencies. Effects of the chemical potential and the magnitude of the external magnetic field on the number of trapped modes and subsequently the transmission resonances are studied as well.

Fig. 1
figure 1

a Physical geometry of the problem. b Graphene-dielectric stack

Full size image

2 Analytical formulations

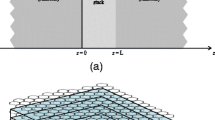
To investigate the behavior of the evanescent and propagating EM waves around a graphene-dielectric stack, consider the physical model shown in Fig. 1, showing a graphene-dielectric stack in an anisotropic ambient medium. The anisotropic ambient media supports both propagating and evanescent modes at the same parallel wavevector. The following constitutive relations represent the anisotropic medium:

$$\begin{array}{l} \bar{D}=\overline{\overline{\varepsilon }}\bar{E} \\ \bar{B}=\overline{\overline{\mu }}\bar{H} \\\end{array},$$
(1)

where \(\overline{\overline{\varepsilon }}\) is the \(3\times 3\) permittivity tensor and \(\overline{\overline{\mu }}\) is the \(3\times 3\) permeability tensor given by

\(\overline{\overline{\varepsilon }}=\left[ \begin{array}{lll} {{\varepsilon }_{xx}} & {{\varepsilon }_{xy}} & {{\varepsilon }_{xz}} \\ {{\varepsilon }_{yx}} & {{\varepsilon }_{yy}} & {{\varepsilon }_{yz}} \\ {{\varepsilon }_{zx}} & {{\varepsilon }_{zy}} & {{\varepsilon }_{zz}} \\\end{array} \right]\) and \(\overline{\overline{\mu }}=\left[ \begin{array}{lll} {{\mu }_{xx}} & {{\mu }_{xy}} & {{\mu }_{xz}} \\ {{\mu }_{yx}} & {{\mu }_{yy}} & {{\mu }_{yz}} \\ {{\mu }_{zx}} & {{\mu }_{zy}} & {{\mu }_{zz}} \\\end{array} \right]\).

Consider general obliquely incident plane waves with time dependency \({{e}^{-i\omega t}}\). The fields are defined as

$$\mathbf{E}\left( x,y,z;\,t \right)={{\mathbf{E}}_{0}}{{e}^{i\left( {{k}_{x}}x+{{k}_{y}}y+{{k}_{z}}z-\omega t \right)}}=\left[ \begin{matrix} {{E}_{x}}(z) \\ {{E}_{y}}(z) \\ {{E}_{z}}(z) \\\end{matrix} \right]{{e}^{i\left( {{k}_{x}}x+{{k}_{y}}y-\omega t \right)}},\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }$$
(2a)
$$\mathbf{H}\left( x,y,z;\,t \right)={{\mathbf{H}}_{0}}{{e}^{i\left( {{k}_{x}}x+{{k}_{y}}y+{{k}_{z}}z-\omega t \right)}}=\left[ \begin{matrix} {{H}_{x}}(z) \\ {{H}_{y}}(z) \\ {{H}_{z}}(z) \\\end{matrix} \right]{{e}^{i\left( {{k}_{x}}x+{{k}_{y}}y-\omega t \right)}},\text{ }\!\!~\!\!\text{ }$$
(2b)

where \(\kappa =({{k}_{x}},\text{ }\!\!~\!\!\text{ }{{k}_{y}})\) is the wavevector parallel to the gyrotropic graphene stack and \(\omega\) is the angular frequency of the incident plane wave. Using the Berreman \(4\times 4\) matrix method [34], the Maxwell equations are reduced to four ordinary differential equations in terms of tangential electric and magnetic field components:

$$\frac{d\Psi (z)}{dz}=i~J~A\Psi \left( z \right),~$$
(3)

where \(A\) is a \(4\times 4\) matrix that depends on the properties of the medium (\(\overline{\overline{\varepsilon }}\) and \(\overline{\overline{\mu }}\)), the tangential wavevector components, and the frequency of the incident wave. It is given by

$$A=\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} \\ {{a}_{21}} & {{a}_{22}} \\\end{matrix} \right].~$$
(4)

The elements of the above matrix \(A\) are given for a general anisotropic medium as

$$a_{{11}} = \left[ {\begin{array}{*{20}c} {\frac{\omega }{c}\varepsilon _{{xx}} - \frac{c}{\omega }\frac{{k_{y}^{2} }}{{\mu _{{zz}} }} - \frac{\omega }{c}\frac{{\varepsilon _{{xz}} \varepsilon _{{zx}} }}{{\varepsilon _{{zz}} }}} & {\frac{\omega }{c}\varepsilon _{{xy}} + \frac{c}{\omega }\frac{{k_{x} k_{y} }}{{\mu _{{zz}} }} - \frac{\omega }{c}\frac{{\varepsilon _{{xz}} \varepsilon _{{zy}} }}{{\varepsilon _{{zz}} }}} \\ {\frac{\omega }{c}\varepsilon _{{yx}} + \frac{c}{\omega }\frac{{k_{x} k_{y} }}{{\mu _{{zz}} }} - \frac{\omega }{c}\frac{{\varepsilon _{{yz}} \varepsilon _{{zx}} }}{{\varepsilon _{{zz}} }}} & {\frac{\omega }{c}\varepsilon _{{yy}} - \frac{c}{\omega }\frac{{k_{x}^{2} }}{{\mu _{{zz}} }} - \frac{\omega }{c}\frac{{\varepsilon _{{yz}} \varepsilon _{{zy}} }}{{\varepsilon _{{zz}} }}} \\ \end{array} } \right],$$
$${{a}_{12}}=\left[ \begin{matrix} {{k}_{y}}\left( \frac{{{\varepsilon }_{xz}}}{{{\varepsilon }_{zz}}}-\frac{{{\mu }_{zx}}}{{{\mu }_{zz}}} \right) & -{{k}_{x}}\frac{{{\varepsilon }_{xz}}}{{{\varepsilon }_{zz}}}-{{k}_{y}}\frac{{{\mu }_{zy}}}{{{\mu }_{zz}}} \\ {{k}_{x}}\frac{{{\mu }_{zx}}}{{{\mu }_{zz}}}+{{k}_{y}}\frac{{{\varepsilon }_{yz}}}{{{\varepsilon }_{zz}}} & {{k}_{x}}\left( \frac{{{\mu }_{zy}}}{{{\mu }_{zz}}}-\frac{{{\varepsilon }_{yz}}}{{{\varepsilon }_{zz}}} \right) \\\end{matrix} \right],$$
$${{a}_{21}}=\left[ \begin{matrix} {{k}_{y}}\left( \frac{{{\varepsilon }_{zx}}}{{{\varepsilon }_{zz}}}-\frac{{{\mu }_{xz}}}{{{\mu }_{zz}}} \right) & {{k}_{x}}\frac{{{\mu }_{xz}}}{{{\mu }_{zz}}}+{{k}_{y}}\frac{{{\varepsilon }_{zy}}}{{{\varepsilon }_{zz}}} \\ -{{k}_{x}}\frac{{{\varepsilon }_{zx}}}{{{\varepsilon }_{zz}}}-{{k}_{y}}\frac{{{\mu }_{yz}}}{{{\mu }_{zz}}} & {{k}_{x}}\left( \frac{{{\mu }_{yz}}}{{{\mu }_{zz}}}-\frac{{{\varepsilon }_{zy}}}{{{\varepsilon }_{zz}}} \right) \\\end{matrix} \right],~\text{and}$$
$$a_{{22}} = \left[ {\begin{array}{*{20}c} {\frac{\omega }{c}\mu _{{xx}} - \frac{c}{\omega }\frac{{k_{y}^{2} }}{{\varepsilon _{{zz}} }} - \frac{\omega }{c}\frac{{\mu _{{xz}} \mu _{{zx}} }}{{\mu _{{zz}} }}} & {\frac{\omega }{c}\mu _{{xy}} + \frac{c}{\omega }\frac{{k_{x} k_{y} }}{{\varepsilon _{{zz}} }} - \frac{\omega }{c}\frac{{\mu _{{xz}} \mu _{{zy}} }}{{\mu _{{zz}} }}} \\ {\frac{\omega }{c}\mu _{{yx}} + \frac{c}{\omega }\frac{{k_{x} k_{y} }}{{\varepsilon _{{zz}} }} - \frac{\omega }{c}\frac{{\mu _{{yz}} \mu _{{zx}} }}{{\mu _{{zz}} }}} & {\frac{\omega }{c}\mu _{{yy}} - \frac{c}{\omega }\frac{{k_{x}^{2} }}{{\varepsilon _{{zz}} }} - \frac{\omega }{c}\frac{{\mu _{{yz}} \mu _{{zy}} }}{{\mu _{{zz}} }}} \\ \end{array} } \right]$$

Additionally, \(\text{ }\!\!\Psi\!\!\text{ }\left( z \right)\) and J are given, respectively, by

$${\text{ }}\Psi {\text{ }}(z) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {E_{x} (z)} \\ {E_{y} (z)} \\ \end{array} } \\ {\begin{array}{*{20}c} {H_{x} (z)} \\ {H_{y} (z)} \\ \end{array} } \\ \end{array} } \right],{\text{ }}~{\text{ }}{\text{and}}{\text{ }}~{\text{ }}J = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & \quad 0 \\ 0 & \quad 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & \quad 1 \\ { - 1} & \quad 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & \quad { - 1} \\ 1 & \quad 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & \quad 0 \\ 0 & \quad 0 \\ \end{array} } \\ \end{array} } \right]$$

and \(c\) is the speed of light in vacuum.

3 Fields in the anisotropic ambient medium

The anisotropic ambient medium has the following properties:

\({{\overline{\overline{\varepsilon }}}_{a}}=\left[ \begin{matrix} {{\varepsilon }_{xa}} & 0 & 0 \\ 0 & {{\varepsilon }_{ya}} & 0 \\ 0 & 0 & {{\varepsilon }_{za}} \\\end{matrix} \right],\text{ }\!\!~\!\!\text{ }\) and \(\text{ }\!\!~\!\!\text{ }{{\overline{\overline{\mu }}}_{a}}=\left[ \begin{matrix} {{\mu }_{xa}} & 0 & 0 \\ 0 & {{\mu }_{ya}} & 0 \\ 0 & 0 & {{\mu }_{za}} \\\end{matrix} \right].\)

In this work, these properties have been selected to provide two real and two imaginary z-directional wavenumbers corresponding to propagating and evanescent modes. These wavenumbers are the eigenvalues of the matrix \(iJA\) in the medium and the wave modes in that medium are represented by the associated eigenvectors.

At \({{k}_{y}}=0\), the z-directional propagating and evanescent wavenumbers in the anisotropic ambient medium are given, respectively, by

$$k_{z}^{ap}=\pm \sqrt{\frac{{{\omega }^{2}}}{{{c}^{2}}}{{\varepsilon }_{ya}}{{\mu }_{xa}}-\frac{{{\mu }_{xa}}}{{{\mu }_{za}}}{{k}_{x}}^{2}\,}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ },\,\,\text{and }\!\!~\!\!\text{ }$$
(5)
$$k_{z}^{ae}=\pm \sqrt{\frac{{{\omega }^{2}}}{{{c}^{2}}}{{\varepsilon }_{xa}}{{\mu }_{ya}}-\frac{{{\varepsilon }_{xa}}}{{{\varepsilon }_{za}}}{{k}_{x}}^{2}}\text{ }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ }$$
(6)

where the superscripts ‘ap’ and ‘ae’ refer to the propagating and evanescent modes in the ambient medium, respectively. The corresponding tangential field components (eigenvectors) associated with these wavenumbers are given by

$$\user2{v}_{ \pm }^{{ap}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\frac{\omega }{c}\mu _{{xa}} } \\ \end{array} } \\ {\begin{array}{*{20}c} { \mp k_{z}^{{ap}} } \\ 0 \\ \end{array} } \\ \end{array} } \right],{\text{~and~}}$$
(7)
$$\user2{v}_{ \pm }^{{ae}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \pm k_{z}^{{ae}} } \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ {\frac{\omega }{c}\varepsilon _{{xa}} } \\ \end{array} } \\ \end{array} } \right].{\text{~}}$$
(8)

The propagating z-directional wavenumber \((k_{z}^{ap})\) should be real, while the evanescent z-directional wavenumber \((k_{z}^{ae})\) should be imaginary. Therefore, for the anisotropic ambient medium, the elements of the permittivity tensor \({{\overline{\overline{\varepsilon }}}_{a}}\) and permeability tensor \(\text{ }\!\!~\!\!\text{ }{{\overline{\overline{\mu }}}_{a}}\) must satisfy the following conditions:

$${{\varepsilon }_{ya}}{{\mu }_{za}}>\frac{{{k}_{x}}^{2}}{{{\left( \frac{\omega }{c} \right)}^{2}}}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }, \,\,\text{ and }\,\,\text{ }{{\mu }_{ya}}{{\varepsilon }_{za}}<\frac{{{k}_{x}}^{2}}{{{\left( \frac{\omega }{c} \right)}^{2}}}$$
(9)

which implies that \({{\varepsilon }_{ya}}{{\mu }_{za}}>{{\mu }_{ya}}{{\varepsilon }_{za}}.\)

3.1 Fields in the gyrotropic graphene stack

The electromagnetic properties of graphene are described in terms of the surface conductivity \(\sigma\). The Kubo model of conductivity is used for the graphene sheet, which takes into account the interband and intraband transitions and is given by [29]:

$$\sigma ={{\sigma }_{\text{inter}}}+{{\sigma }_{\text{intra}}}~$$
(10)

where the intraband and interband conductivity are given, respectively, by

$${{\sigma }_{intra}}=\frac{i4{{e}^{2}}{{k}_{B}}T}{\hbar \left( \omega +i/\tau \right)}\left( \frac{{{\mu }_{c}}}{{{k}_{B}}T}+2\ln \left( {{e}^{-{{\mu }_{c}}/{{k}_{B}}T}}+1 \right) \right)\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }$$
(11)
$${{\sigma }_{\text{inter}}}=\frac{i4{{e}^{2}}{{k}_{B}}T}{\hbar }\underset{0}{\overset{\infty }{\mathop \int }}\,\frac{{{f}_{d}}\left( -E \right)-{{f}_{d}}\left( E \right)}{{{\left( \omega +i/\tau \right)}^{2}}-4{{\left( E/\hbar \right)}^{2}}}\text{dE}\approx \frac{i{{e}^{2}}}{{{\hbar }^{2}}}\ln \left( \frac{2\left| {{\mu }_{c}} \right|-\left( \omega +i/\tau \right)\hbar }{2\left| {{\mu }_{c}} \right|+\left( \omega +i/\tau \right)\hbar } \right),~$$
(12)

where \({{\mu }_{c}}\) is the chemical potential, \(\omega\) is the angular frequency, \({{k}_{B}}\) is the Boltzmann’s constant, \(\hbar\) is the reduced Planck constant, \(T\) is the temperature (in Kelvin), \(e\) is the charge of the electron, \(\tau\) is the relaxation time, \(E\) is the Fermi energy, \({{f}_{d}}\left( E \right)\) is the Fermi–Dirac distribution given by \({{f}_{d}}(E)~=1/({{e}^{(E-\mu c)/{{k}_{B}}T}}+~1)\), and \(i=\sqrt{-1}\).

In the presence of an external static magnetic field \({{\bar{B}}_{0}}\text{ }\!\!~\!\!\text{ }\)applied parallel to the interfaces of the layer and perpendicular to the direction of the plane wave propagation, graphene becomes gyrotropic and its anisotropic permittivity is given by [27]:

$${{\overline{\overline{\varepsilon }}}_{s}}=\left[ \begin{matrix} {{\varepsilon }_{\text{gd}}} & 0 & i{{\varepsilon }_{\text{god}}} \\ 0 & {{\varepsilon }_{2\text{g}}} & 0 \\ -i{{\varepsilon }_{\text{god}}} & 0 & {{\varepsilon }_{\text{gd}}} \\\end{matrix} \right],~$$
(13)

where \({{\varepsilon }_{\text{gd}}}={{\varepsilon }_{\text{inter}}}-\omega _{p}^{2}\left( \omega +\text{i}/\tau \right)/\left( \omega \left( {{\left( \omega +\text{i}/\tau \right)}^{2}}-\omega _{c}^{2} \right) \right)\), \({{\varepsilon }_{\text{god}}}=-\omega _{p}^{2}{{\omega }_{c}}/\left( \omega \left( {{\left( \omega +\text{i}/\tau \right)}^{2}}-\omega _{c}^{2} \right) \right)\), \({{\varepsilon }_{\text{2g}}}={{\varepsilon }_{y}}\), \({{\omega }_{c}}=e{{B}_{0}}/{{m}^{*}}c\) is the cyclotron frequency, \({{\omega }_{p}}=\sqrt{\left( N{{e}^{2}} \right)/\left( {{m}^{*}}{{\varepsilon }_{0}} \right)}\) is the plasma (or cutoff) frequency, \({{m}^{*}}\) is the effective mass of the electron, and \({{\varepsilon }_{\text{inter}}}=1\text{ }\!\!~\!\!\text{ }+\text{ }\!\!~\!\!\text{ }i{{\sigma }_{\text{inter}}}/\omega {{\varepsilon }_{0}}{{t}_{\text{g}}}\).

Using the effective medium theory (EMT) [25], the graphene-dielectric stack shown in Fig. 1b can be characterized by the gyrotropic permittivity tensor, given by

$${{\overline{\overline{\varepsilon }}}_{s}}=\left[ \begin{matrix} {{\varepsilon }_{\text{xs}}} & 0 & i{{\varepsilon }_{\text{gs}}} \\ 0 & {{\varepsilon }_{\text{ys}}} & 0 \\ -i{{\varepsilon }_{\text{gs}}} & 0 & {{\varepsilon }_{\text{zs}}} \\\end{matrix} \right].~$$
(14)

The parameters of this tensor are given by \({{\varepsilon }_{\text{xs}}}={{\varepsilon }_{\text{zs}}}=f~{{\varepsilon }_{\text{gd}}}+(1-f){{\varepsilon }_{d}},\) \({{\varepsilon }_{\text{ys}}}={{\left( f/{{\varepsilon }_{2g}}+(1-f)/{{\varepsilon }_{d}} \right)}^{-1}},\) \({{\varepsilon }_{\text{gs}}}=f\times {{\varepsilon }_{\text{god}}},\) where \(f={{t}_{\text{g}}}/({{t}_{\text{g}}}+{{t}_{d}}),\) \({{\varepsilon }_{d}}\) is the permittivity of the dielectric layer, \({{t}_{\text{d}}}\) is the thickness of the dielectric layer, and \({{t}_{\text{g}}}\) is the thickness of the graphene layer.

The z-directional propagating and evanescent wavenumbers for \({{k}_{y}}=0\) are

$$k_{z}^{\text{sp}}=\pm \sqrt{\frac{{{\omega }^{2}}}{{{c}^{2}}}\left( \frac{{{\varepsilon }_{\text{xs}}}^{2}-{{\varepsilon }_{\text{gs}}}^{2}}{{{\varepsilon }_{\text{xs}}}} \right)-{{k}_{x}}^{2},}\;\text{and}$$
(15)
$$k_{z}^{\text{se}}=\pm \sqrt{\frac{{{\omega }^{2}}}{{{c}^{2}}}{{\varepsilon }_{\text{ys}}}-{{k}_{x}}^{2}}\text{ }\!\!~\!\!\text{ }.\text{ }\!\!~\!\!\text{ }$$
(16)

The field components associated with these wavenumbers are deduced as

$$\user2{v}_{ \pm }^{{{\text{sp}}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { \pm \varepsilon _{{1s}} k_{z}^{{sp}} + i\varepsilon _{{{\text{gs}}}} k_{x} } \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ {\frac{\omega }{c}\left( {\varepsilon _{{1s}} ^{2} - \varepsilon _{{{\text{gs}}}} ^{2} } \right)} \\ \end{array} } \\ \end{array} } \right]{\text{~and~}}$$
(17)
$$\user2{v}_{ \pm }^{{{\text{se}}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - \frac{\omega }{c}} \\ \end{array} } \\ {\begin{array}{*{20}c} { \pm ~k_{z}^{{{\text{se}}}} } \\ 0 \\ \end{array} } \\ \end{array} } \right]~.{\text{~~}}$$
(18)

The propagating z-directional wavenumber \(\left( k_{z}^{\text{sp}} \right)\) should be real, while the evanescent z-directional wavenumber \(\left( k_{z}^{\text{se}} \right)\) should be imaginary. Therefore, for a gyrotropic graphene-dielectric stack that supports these two modes instantaneously, the elements of the permittivity tensor \({{\overline{\overline{\varepsilon }}}_{s}}\) must satisfy the following conditions:

$$\frac{{{\varepsilon }_{\text{xs}}}^{2}-{{\varepsilon }_{\text{gs}}}^{2}}{{{\varepsilon }_{\text{xs}}}}>\frac{{{k}_{x}}^{2}}{{{\left( \frac{\omega }{c} \right)}^{2}}},{\text{ and }} {{\varepsilon }_{\text{ys}}}<\frac{{{k}_{x}}^{2}}{{{\left( \frac{\omega }{c} \right)}^{2}}},$$
(19)

which implies that \(\left( {{\varepsilon }_{\text{xs}}}^{2}-{{\varepsilon }_{\text{gs}}}^{2} \right)/{{\varepsilon }_{\text{xs}}}>{{\varepsilon }_{\text{ys}}}\).

The trapped modes in the gyrotropic graphene-dielectric stack are characterized by \(k_{z}^{\text{sp},e}=0\) (no z-directional propagation), and their frequencies belong to the continuous interval I bounded by the dispersion curves of the propagating and evanescent waves of the gyrotropic graphene-dielectric stack given by Eqs. 15 and 16, respectively, that is, \({{k}_{x}}\sqrt{{{\varepsilon }_{\text{xs}}}/\left( {{\varepsilon }_{\text{xs}}}^{2}-{{\varepsilon }_{\text{gs}}}^{2} \right)}\le I\le {{k}_{x}}/\sqrt{{{\varepsilon }_{\text{ys}}}}\). Evanescent wave coupling arises when the incident frequencies belong to the continuous spectrum intervalI and the tangential field components of the anisotropic ambient evanescent modes match those of the propagating modes in the gyrotropic graphene-dielectric stack. If the normalized parallel wavevector is perturbed, resonances occur around the trapped modes.

Therefore, the construction of the trapped modes can be determined by matching the evanescent fields in the ambient medium with the propagating fields in the graphene-dielectric stack so that

$$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {{E_x}} \\ {{E_y}} \\ {\begin{array}{*{20}{c}} {{H_x}} \\ {{H_y}} \end{array}} \end{array}} \right] = {A_1}\left[ {\begin{array}{*{20}{c}} { - k_z^{ae}} \\ 0 \\ {\begin{array}{*{20}{c}} 0 \\ {\frac{\omega }{c}{\varepsilon _{xa}}} \end{array}} \end{array}} \right]{e^{ - ik_z^{ae}z}}\quad \left( {z < 0} \right) \hfill \\ = {A_2}\left[ {\begin{array}{*{20}{c}} {{\varepsilon _{xs}}k_z^{sp} + i{\varepsilon _{gs}}{k_x}} \\ 0 \\ {\begin{array}{*{20}{c}} 0 \\ {\frac{\omega }{c}\left( {{\varepsilon _{xs}}^2 - {\varepsilon _{gs}}^2} \right)} \end{array}} \end{array}} \right]{e^{ik_z^{sp}z}} + {A_3}\left[ {\begin{array}{*{20}{c}} { - {\varepsilon _{xs}}k_z^{sp} + i{\varepsilon _{gs}}{k_x}} \\ 0 \\ {\begin{array}{*{20}{c}} 0 \\ {\frac{\omega }{c}\left( {{\varepsilon _{xs}}^2 - {\varepsilon _{gs}}^2} \right)} \end{array}} \end{array}} \right]{e^{ - ik_z^{sp}z}}(0 < z < L) \hfill \\ = {A_4}\left[ {\begin{array}{*{20}{c}} {k_z^{ae}} \\ 0 \\ 0 \\ {\frac{\omega }{c}{\varepsilon _{xa}}} \end{array}} \right]{e^{ik_z^{ae}(z - L)}}\quad (z> L) \hfill \\ \end{gathered}$$
(20)

where \({{A}_{1}}\), \({{A}_{2}}\), \({{A}_{3}}\), and \({{A}_{4}}\) are constants to be determined by applying the correct boundary conditions.

Equation (20) presents the tangential field components inside and outside the graphene-dielectric stack. \({{E}_{x}}\) and \({{H}_{y}}\) are the evanescent fields in the regions \((z<0\) and \(z>L)\). These fields are propagation fields in region \((0<z<L)\). The continuity of the tangential field components at the interfaces \((z=0;~z=L)\) yields the following:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - k_{z}^{{ae}} } & { - \left( {\varepsilon _{{xs}} k_{z}^{{sp}} + i\varepsilon _{{gs}} k_{x} } \right)} \\ {\varepsilon _{{xa}} } & { - \left( {\varepsilon _{{xs}} ^{2} - \varepsilon _{{gs}} ^{2} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} { - \left( { - \varepsilon _{{xs}} k_{z}^{{sp}} + i\varepsilon _{{gs}} k_{x} } \right)} & 0 \\ { - \left( {\varepsilon _{{xs}} ^{2} - \varepsilon _{{gs}} ^{2} } \right)} & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\left( {\varepsilon _{{xs}} k_{z}^{{sp}} + i\varepsilon _{{gs}} k_{x} } \right)e^{{ik_{z}^{{sp}} L}} } \\ 0 & {\left( {\varepsilon _{{xs}} ^{2} - \varepsilon _{{3s}} ^{2} } \right)e^{{ik_{z}^{{sp}} L}} } \\ \end{array} } & {\begin{array}{*{20}c} {\left( { - \varepsilon _{{xs}} k_{z}^{{sp}} + i\varepsilon _{{gs}} k_{x} } \right)e^{{ - ik_{z}^{{sp}} L}} } & { - k_{z}^{{ae}} } \\ {\left( {\varepsilon _{{xs}} ^{2} - \varepsilon _{{gs}} ^{2} } \right)e^{{ - ik_{z}^{{sp}} L}} } & { - \varepsilon _{{xa}} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} {A_{3} } \\ {A_{4} } \\ \end{array} } \\ \end{array} } \right] = 0.~$$
(21)

For the above matrix to have a non-trivial solution, its determinant must be equal to zero. Then, the condition of trapped modes is given by

$$\begin{array}{l} 2\cos \left( {k_z^{{\rm{sp}}}L} \right)\\ \, + \,i\frac{{{\varepsilon _{{\rm{xs}}}}^2{\varepsilon _{{\rm{xa}}}}^2\left( {{{\left( {k_z^{{\rm{sp}}}} \right)}^2} + {k_x}^2} \right) + {{\left( {{\varepsilon _{{\rm{xs}}}}^2 - {\varepsilon _{{\rm{gs}}}}^2} \right)}^2}{{\left( {k_z^{{\rm{ae}}}} \right)}^2}}}{{{\varepsilon _{{\rm{xs}}}}{\varepsilon _{{\rm{xa}}}}k_z^{{\rm{ae}}}k_z^{{\rm{sp}}}\left( {{\varepsilon _{{\rm{gs}}}}^2 - {\varepsilon _{{\rm{xs}}}}^2} \right)}}\sin \left( {k_z^{{\rm{sp}}}L} \right) = 0.{\rm{ }}~{\rm{ }}~{\rm{ }} \end{array}$$
(22)

When an electromagnetic field is incident on the graphene-dielectric stack, part of this field will be transmitted to the other side and the other part of the field will be reflected. If the incident field hits the graphene-dielectric stack at \(z=0\), the resulting field outside the stack will be as follows:

$$\psi \left( z \right)=\left\{ \begin{matrix} v_{+}^{\text{ap}}~{{e}^{ik_{z}^{\text{ap}}z}}+r_{-}^{p}~v_{-}^{\text{ap}}~{{e}^{-ik_{z}^{\text{ap}}z}}+r_{-}^{e}~v_{-}^{\text{ae}}~{{e}^{-ik_{z}^{\text{ae}}z}}~~~~~~~~~~~~~~~~~~~~~&(z<0) \\ t_{+}^{p}~v_{+}^{\text{ap}}{{e}^{ik_{z}^{\text{ap}}(z-L)}}+t_{+}^{e}~v_{+}^{\text{ae}}~{{e}^{ik_{z}^{\text{ae}}(z-L)}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~&(z>L) \\\end{matrix} \right.~~,~~$$
(23)

where \(v_{+}^{\text{ap}}{{e}^{ik_{z}^{\text{ap}}z}}\) is the incident field, \(v_{\pm }^{\text{ap},e}\) are the eigenvectors associated with the eigenvalues (z-directional wavenumbers) \(\pm k_{z}^{\text{ap},e}\) in the anisotropic ambient medium, and \(r_{-}^{p,e}\) and \(t_{+}^{p,e}\) are the amplitudes of the reflected and transmitted fields, respectively.

The tangential field components at the interfaces of the graphene-dielectric stack are continuous, so the field inside the stack can be found using the transfer matrix method (TMM) [34]:

$$\psi \left( L \right)=T\left( 0,L \right)\psi \left( 0 \right)\,\,\text{ and }\!\!~\!\!\text{ }$$
(24)
$$t_{+}^{p}\text{ }\!\!~\!\!\text{ }v_{+}^{p}+t_{+}^{e}\text{ }\!\!~\!\!\text{ }v_{+}^{e}=T\left( 0,L \right)\left( \text{ }\!\!~\!\!\text{ }v_{+}^{p}+r_{-}^{p}\text{ }\!\!~\!\!\text{ }v_{-}^{p}+r_{-}^{e}\text{ }\!\!~\!\!\text{ }v_{-}^{e} \right),\text{ }\!\!~\!\!\text{ }$$
(25)

where \(T\left( 0,L \right)={{\text{e}}^{iJ{{A}_{s}}L}}\) is the transfer matrix of the gyrotropic graphene layer. Then, the transmission and reflection coefficients can be determined directly from Eq. 25.

4 Results and discussion

In this section, the previously derived analytical formulations are used to investigate the dispersion relations, trapped mode condition, transmission coefficients for both non-resonance and resonance, and field anomalies at the resonance frequencies.

Consider the ambient medium to have the following properties:

\({{\overline{\overline{\varepsilon }}}_{a}}=\left[ \begin{matrix} 1.1 & 0 & 0 \\ 0 & 10 & 0 \\ 0 & 0 & 1 \\\end{matrix} \right]\), and \({{\overline{\overline{\mu }}}_{a}}=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\end{matrix} \right]\).

The gyrotropic graphene-dielectric stack has the following properties (in SI units); the thickness of the graphene sheet is 1 nm, the thickness of the dielectric layer is 50 \(\text{nm}\), and the dielectric constant \({{\varepsilon }_{d}}=1.1\). In this work, we set \(~T=300~\text{K}\), \(\tau =1~\text{ps}\), and the effective mass of the electron \({{m}^{*}}=0.1\times 0.9\times {{10}^{-30}}~\text{kg}\), as given in [27].

The complex conductivity of the graphene sheet and its equivalent permittivity varying with the normalized frequency (\({{\omega }_{n}}=\omega a/c;a={{10}^{-6}}\);where \(\omega\) is the actual angular frequency in rad/s) for different values of the chemical potential are shown in Fig. 2. The equivalent permittivity of the graphene sheet is presented in Fig. 3. The permittivity tensor elements of the graphene-dielectric stack when the external magnetic field \({{\bar{B}}_{0}}=1\text{ }\!\!~\!\!\text{ Tesla}\) are shown in Fig. 4. Increasing the magnetic field \({{\bar{B}}_{0}}\) has an effect in the low frequencies (less than 5 THz) on the elements of the effective permittivity tensor as shown in Fig. 5. As the cyclotron frequency \({{\omega }_{c}}\) grows closer to \(\omega\), the values of the elements of the permittivity tensor approach their pole values. Higher frequencies (greater than 5 THz) have a small change in values of the elements of the permittivity tensor when the magnetic field is increased.

The dispersion relations between the angular frequency and the real z-directional wavevector (\({{k}_{z}}\)) when the parallel wavevector \(\kappa =\left( {{k}_{x}},{{k}_{y}} \right)=(0.5,0)\) for three different values of the chemical potential \({{\mu }_{c}}\) are depicted in Fig. 6. It is clearly shown that the continuous frequency spectrum interval \(I\) where the trapped modes are embedded decreases as the chemical potential increases. Therefore, the number of possible discrete trapped modes embedded in this interval and, accordingly, the frequencies of these trapped modes will be reformed. There is a noticeable variation in the values of the effective permittivity tensor elements observed at a specific frequency that is apparently controlled by the magnetic field. The effect of this pole in the elements of the permittivity tensor appears on the dispersion relation as shown in Fig. 7.

Fig. 2
figure 2

The conductivity of graphene

Full size image
Fig. 3
figure 3

The equivalent permittivity of graphene

Full size image
Fig. 4
figure 4

The permittivity elements of the graphene-dielectric stack: a \({{\varepsilon }_{1s}}\), and b \({{\varepsilon }_{gs}}\)

Full size image
Fig. 5
figure 5

The effect of the magnetic field on the permittivity tensor elements

Full size image
Fig. 6
figure 6

The dispersion relation. The blue and red lines show the ambient medium propagating and evanescent z-directional wavenumber, respectively. The black and green lines are the propagating z-directional wavenumber of the graphene-dielectric stack for four different values of the chemical potential. The interval I is bounded by the z-directional wavenumbers of the graphene-dielectric stack

Full size image
Fig. 7
figure 7

The effect of the external magnetic field on the dispersion relation

Full size image

For example, when \({{\mu }_{c}}=0.175~\text{eV}\), the interval \(I\) is extended from \({{\omega }_{n}}=0.187081\) to \({{\omega }_{n}}=0.496731;\) for \({{\mu }_{c}}=0.20~\text{eV}\), I is extended from \({{\omega }_{n}}=0.2017\) to \({{\omega }_{n}}=0.496731\); for \({{\mu }_{c}}=0.25~\text{eV}\), I is extended from \({{\omega }_{n}}=0.229086~\) to \({{\omega }_{n}}=0.496731\); and for \({{\mu }_{c}}=0.300~\text{eV}\), I is extended from \({{\omega }_{n}}=0.254578~\) to \({{\omega }_{n}}=0.496731\). The upper bound of I does not change because there is no variation in the y-direction of the permittivity tensor.

Fig. 8
figure 8

Trapped modes with their numbers versus the thickness of the graphene-dielectric stack: a \({{\mu }_{c}}=0.175~\text{eV}\), b \({{\mu }_{c}}=0.200~\text{eV}\), and c \({{\mu }_{c}}=0.300~\text{eV}\)

Full size image

The patterns of the trapped modes versus the thickness of the graphene stack for three different values of the chemical potential are depicted in Fig. 8. Each trapped mode line represents a possible trapped mode and its frequency at the stack thickness value L. As a result of varying the chemical potential, the number of trapped modes and their frequency locations are changed. For instance, for \({{\mu }_{c}}=0.175\text{ }\!\!~\!\!\text{ eV}\), there are four trapped modes embedded in the continuum interval I when the thickness \(L=8\) units in length, located at \({{\omega }_{n}}=0.222162\), \({{\omega }_{n}}=0.303411\), \({{\omega }_{n}}=0.398530,\) and \({{\omega }_{n}}=0.480127\). However, when \({{\mu }_{c}}=0.200\text{ }\!\!~\!\!\text{ eV}\), there are four trapped modes but at different frequencies. Three trapped modes are obtained only when \({{\mu }_{c}}=0.300\text{ }\!\!~\!\!\text{ eV}\). Table 1 summarizes that observation of the trapped modes. At these trapped modes, the evanescent modes in the ambient medium tend to couple to the gyrotropic graphene stack as propagating modes.

Table 1 Trapped mode frequencies in the gyrotropic graphene stack
Full size table

Figure 9 depicts the transmission coefficient across the 8-unit-length graphene-dielectric stack. When the parallel wavevector is set to \(~\kappa =\left( 0.5,0 \right)\), the graphene-dielectric stack shows four trapped modes and three trapped modes when \({{\mu }_{c}}=0.2~\text{eV}\) and \({{\mu }_{c}}=0.3~\text{eV}\), respectively. These trapped modes are unstable with wavevector perturbations. Hence, when the parallel wavevector is perturbed to\(~\kappa =\left( 0.5,~0.03 \right)\), resonances occur around these trapped modes. The resonances around the trapped modes are due to the interaction between the incident EM wave and the conceivable trapped modes. So, for small perturbations of \(~{{k}_{y}}\), when the frequency of the incident EM wave matches the trapped mode frequency, resonance will occur. However, when \(\kappa =\left( 0.5,~0.0 \right)\), the trapped mode is perfect and is decoupled from the propagating modes in the ambient medium. These resonances are presented by sharp transmission anomalies (total transmission and total reflection) with intense field amplification, as shown in Figs. 10 and 11. The trapped modes are obtained when the parallel wavevector \(\kappa =(0.5,0)\). For large values of \({{k}_{y}}\), the trapped mode conditions will be destroyed, while changing \({{k}_{x}}\) will only change the position of the continuum interval I and cause a shift in the trapped mode frequencies. The field amplification associated with resonance state is due to the coupling between the propagating modes in the anisotropic ambient medium and the trapped modes in the graphene-dielectric stack. Figure 10a shows the instantaneous tangential fields at the trapped mode (mode 1) when \({{\mu }_{c}}=0.200~\text{eV}\) and \(\kappa =(0.5,~0)\), which in this case show no resonance around the trapped mode. However, Fig. 10b depicts the amplification around the trapped mode at resonance around the trapped mode (mode 1) when \({{\mu }_{c}}=0.200~\text{eV}\), \(\kappa =(0.5,~0.03)\), and normalized frequency \(\omega =0.321675\). Fig. 11a shows the instantaneous tangential fields at the trapped mode (mode 1) when \({{\mu }_{c}}=0.200~\text{eV}\) and \(\kappa =(0.5,0)\), which in this case shows no resonance around the trapped mode. However, Fig. 11b shows the amplification around the trapped mode at resonance around the trapped mode (mode 1) when \({{\mu }_{c}}=0.300~\text{eV}\), \(\kappa =(0.5,0.02)\), and normalized frequency \(\omega =0.38\).

Fig. 9
figure 9

Transmission coefficient in the gyrotropic-graphene stack: a \({{\mu }_{c}}=0.2~\text{eV}\), and b \({{\mu }_{c}}=0.3~\text{eV}\)

Full size image
Fig. 10
figure 10

Instantaneous tangential fields in the gyrotropic graphene stack for a \({{\mu }_{c}}=0.2\text{ }\!\!~\!\!\text{ eV}\) and \(\kappa =(0.5,0)\), and b \({{\mu }_{c}}=0.2\text{ }\!\!~\!\!\text{ eV}\), \(\kappa =(0.5,\text{ }\!\!~\!\!\text{ }0.03)\), and \(\omega =0.321675\)

Full size image
Fig. 11
figure 11

Instantaneous tangential fields in the gyrotropic graphene stack for a \({{\mu }_{c}}=0.3\text{ }\!\!~\!\!\text{ eV}\), \(\omega =0.321575\), and \(\kappa =(0.5,\text{ }\!\!~\!\!\text{ }0)\), and b \({{\mu }_{c}}=0.3\text{ }\!\!~\!\!\text{ eV}\), \(\kappa =(0.5,\text{ }\!\!~\!\!\text{ }0.02)\), and \(\omega =0.38\)

Full size image

5 Conclusions

This paper explores propagation and resonances of electromagnetic fields in graphene-dielectric stacks placed in an external static magnetic field. In the presence of the external magnetic field, graphene acquires gyrotropic characteristics. The dispersion relations, trapped mode condition, and the propagating and evanescent modes in the gyrotropic graphene stack have been derived and numerically quantified. The evanescent modes supported in the ambient medium couple as propagating modes in the gyrotropic graphene-dielectric stack at the discrete frequencies of the trapped modes. Field resonances with sharp transmission/reflection anomalies and with intense amplification in the magnetized graphene stack transpire by perturbing the parallel wavevector of the incident field around the trapped mode frequencies. Increasing the chemical potential of the graphene noticeably decreases the width of the continuous interval where the trapped modes are embedded. However, the magnitude of the applied magnetic field has a noticeable effect on the trapped modes formation only at the normalized lower frequency band. The number of trapped modes and the discrete resonances can be effectively controlled by changing the chemical potential of the dispersive graphene and the thickness of the stack.