1 Introduction

In recent years, the study of superconductivity has focused on the search for materials with increasingly higher transition temperatures, as well as the study of those superconducting materials whose behaviour deviates from that predicted by the Bardeen, Cooper and Schrieffer theory (BCS) [1,2,3]. The BCS theory is the most successful in describing the superconducting state [4]. Those superconductors that are described by the BCS theory are called conventional. Despite the success of the BCS theory in describing the superconducting state, it should be noted that many superconductors cannot be described entirely through this theory, and they are generically known as unconventional superconductors [5].

A family of superconductors that deviates from the guidelines of the BCS theory are the so-called heavy fermions [6, 7]. In 2004, the compound \(\hbox {CePt}_\mathrm{3}\hbox {Si}\), a heavy fermion with a transition temperature to the superconducting state \(T_c=0.75\) K and an antiferromagnetic ordering at \(T_N=2.25\) K, was reported [8]. The crystal structure of this superconductor is orthorhombic and lacks inversion symmetry. The electronic properties exhibited by \({\mathrm {CePt_3Si}}\) are different from those of a conventional superconductor. After this discovery, attention has been paid to materials in which the crystal structure lacks an inversion center and presents intense electronic correlations. Examples of this kind of materials are: \({\mathrm {CePt_3Si}}\), \({\mathrm {CeRhSi_3}}\), \({\mathrm {CeIrSi_3}}\), \({\mathrm {CeCoGe_3}}\), \({\mathrm {UIr}}\) and \({\mathrm {Th_{44}Be_{33}Pt_{16}}}\)[2, 3, 9, 10]. In these compounds, the presence of elements with f electronic bands that are partially filled is characteristic at first sight, although there are superconductors without an inversion center that do not contain rare-earth elements, in which the electronic interactions are not so intense. The absence of elements with f electronic bands, as occurs in heavy fermions, makes them good candidates to study the effects caused by spin–orbit coupling on superconducting properties, evading magnetic interactions between localized and itinerant f-electrons, which can give rise to magnetic fluctuations and electronic instabilities. Examples of this kind of superconductors are: \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) [11], \(\hbox {Li}_\mathrm{2}\hbox {Pd}_\mathrm{3}\hbox {B}\) [12], \(\hbox {Li}_\mathrm{2}\hbox {Pt}_\mathrm{3}\hbox {B}\) [13], \({\mathrm {Li_2Pd_{3-x}Cu_xB}}\) [14], \({\mathrm {Li_2Pd_{3-x}Ag_xB}}\) [15], \({\mathrm {W_3Al_2C}}\) [16], \({\mathrm {Mo_{3-x}Nb_xAl_2C}}\) and \({\mathrm {Mo_{3-x}Ru_xAl_2C}}\) [17], \({\mathrm {Mo_{3-x}Re_xAl_2C}}\) [18], \({\mathrm {W_4IrC_{1-x}}}\) [19], \({\mathrm {CaPtAs}}\) [20] and \({\mathrm {Mo_3P}}\) [21].

In unconventional superconductors, there can be a spontaneous breaking of the time inversion symmetry as well as of the structural inversion symmetry. This condition gives the possibility that the electron Cooper pairs can exhibit a triplet state coupling. One of the effects produced by the lack of an inversion center in the crystal structure is the presence of an inhomogeneous electric field; as a result, the spin–orbit interactions become more intense, and is known as antisymmetric spin–orbit coupling (ASOC) [22]. It has been shown that ASOC acts unfavorably on spin–triplet pairing states [23]. The presence of ASOC leads to a splitting of the electronic bands by lifting the spin degeneracy and consequently splitting the Fermi surface. The mixture of singlet and triplet coupling gives rise to an anisotropic superconducting gap that can include nodes and lines of nodes [24].

The theory proposed by Werthamer, Helfand and Hohenberg (WHH) [25] can be used to determine the influence of Cooper pair breaking due to Pauli paramagnetism and spin–orbit interaction. This effect is observed in the behaviour of the upper critical field \(H_{c2}\) as a function of temperature. The deviation of \(H_{c2}\) with respect to the WHH theory can be taken as an indication of the presence of nodes or lines of nodes in a superconductor without an inversion center.

The substitution of an element in a superconducting material is often used as a way to modify its electronic properties’ behaviour, which allows studying the effects of substitution on the superconducting properties. The possibility of an unconventional superconducting state and the promise of spin–triplet pairing superconductivity in the \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) attracts considerable attention [11, 26, 27]. In this study, we present the effect of partial substitution of Al by Pd on the superconducting properties of \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\). The above analyzing the system \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) with x = 0.00, 0.05 and 0.10. The reason for choosing the substitution of Al by Pd was to generate a negative chemical pressure effect, due to the difference in the atomic radius (Al: 1.25 Å, Pd: 1.40 Å) [28], on the crystalline structure and therefore modify the superconducting properties. On the other hand, the effect produced by the Al substitution by Pd on \(H_{c2}\) is analyzed to determine whether the dispersions due to the spin–orbit interaction influence the breaking of Cooper pairs. The parameters of the normal and superconducting state are estimated, and the strength of the electron–phonon coupling.

2 Experimental details

Polycrystalline samples of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) with x = 0.00, 0.05 and 0.10 were synthesized with stoichiometric quantities of high-purity elements, Mo \(99.95\%\) (Strem Chemicals), Al \(99.999\%\) (Alfa Aesar Puratronic), C \(99.95\%\) (Sigma-Aldrich) and Pd \(99.95\%\) (Strem Chemicals). An excess of Al, 10 wt% was added to compensate for the Al loss because of its low melting point. The materials were mixed and pelleted; subsequently, the pellet was arc melted under a continuous flow of high-purity Argon gas. The produced sample was turned and remelted several times to obtain an homogeneous sample.

X-ray diffraction patterns were obtained at room temperature in a Siemens (D5000) diffractometer with Co \(K_{\alpha }\) radiation (\(\lambda\)=1.79026 Å) and Fe filter in steps of 0.02\(^{\circ }\) at 8 s/step in the 2\(\theta\) range of 20\(^{\circ }\)-110\(^{\circ }\). Rietveld refinement analysis of the diffraction patterns was performed with the topasV5 package [29].

The study of the magnetic properties as a function of temperature T of the samples was carried out using a magnetometer based on a SQUID (Quantum Design model MPMS-5). Measurements were made in the zero field cooled (ZFC) and field cooled (FC) modes with presence of magnetic field of 20 Oe in a temperature interval of 2-10 K.

Electrical resistance as function of temperature T and magnetic field H was measured in a Physical Properties Measurement System (PPMS) (Quantum Design) using the four-probe method. Measurements were made in a temperature range of 2-10 K with H varying between 0 and 9 T.

Specific heat measurements were determined using relaxation method between room temperature and 2.5 K in the PPMS system. The sample was attached to the measuring stage using Apiezon N grease to ensure a good thermal contact. The contribution to the heat capacity of the sample holder and grease was subtracted from the sample measurement.

3 Results and discussion

3.1 Structural characterization

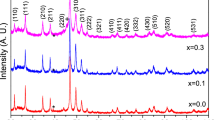
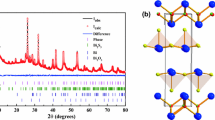
Rietveld refinement of powder X-ray diffraction patterns of synthesized polycrystalline samples of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) with x = 0.00, 0.05 and 0.10 is shown in Fig. 1. Most of the reflections of each pattern can be well indexed to a cubic unit cell of the \(\beta\)-Mn type. The starting crystal structure model for the Rietveld refinements of the \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) phase had the \(P4_132\) space group (\(\#213\)), and other impurities phases as \({\mathrm {Mo_2C}}\), \({\mathrm {Mo_3Al}}\) and \({\mathrm {Mo_3Al_8}}\) were necessary to achieve a reasonable refinement of the phase mixture. The content of impurities are listed in table 1. These impurities have been previously reported in works associated with \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) [11, 17, 18, 27]. Here, it is worth mentioning that the \({\mathrm {Mo_3Al_8}}\) phase does not show superconducting transition, while \({\mathrm {Mo_2C}}\) is reported to exhibit superconducting transition below 2.5 K [30].

Fig. 1
figure 1

Rietveld refinement result of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) with a x=0.00, b 0.05 and c 0.10. In a, the Miller indexes of each plane for \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) are indicated. The R factors of refinement are summarized in Table 1. The vertical bars indicate the Bragg reflections of \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\)(1), \({\mathrm {Mo_2C}}\)(2) and \({\mathrm {Mo_3Al_8}}\)(3)

Full size image

The Rietveld analyses show a linear increase of the lattice parameter, a, as the nominal composition of Pd increases. The lattice parameter gradually increases from 6.8650(14) Å (x = 0.00) to 6.87851(6) Å (x = 0.10). This is consistent with the Vegard’s law, since Pd (1.40Å) has a greatest atomic radius than Al (1.25Å) [28]. This suggests successful doping of Pd into the Al sites in \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\). Samples with higher Pd doping levels (x >0.1) were also synthesized; however, the amount of impurities such \({\mathrm {Mo_2C}}\) and \({\mathrm {Mo_3Al_8}}\) significantly increase, and the under the criterion of doping with the minimum impurity levels, the \(x=0.00,0.05\) and 0.10 samples were selected. The structural parameters and R-factors of the Rietveld refinements are summarized in Table 1.

Table 1 Structural parameters and \(R-\)factors of the Rietveld refinements
Full size table

3.2 Magnetic and electrical measurements

Figure 2 shows the temperature dependence of the magnetization M(T) of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\), which is measured in a magnetic field of 20 Oe under ZFC and FC modes. A diamagnetic signal below the superconducting transition is observed in each sample. The superconducting transition temperature, \(T_c\), was determined as the onset of the transition. Notably, the magnetic study does not reflect the presence of the \({\mathrm {Mo_2C}}\) superconducting impurity.

Fig. 2
figure 2

FC and ZFC magnetization measurements as a function of temperature of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) under an external constant magnetic field of 20 Oe

Full size image

The estimated values of \(T_c\) decrease gradually with doping of Pd, from 9.01 K until 8.38 K. The fact that the lattice parameter a increases with the Al-by-Pd doping suggests a negative pressure that produces a decrease in \(T_c\). For \({\mathrm {Mo_3Al2C}}\) has been reported that by applying external pressure up to 25 kbar, the \(T_c\) value increases up to 9.35 K [26]. The results obtained in \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) regarding the effect of the Al by Pd substitution on a and \(T_c\) values can be related through the nominal content of Pd. The magnetic measurements shows that the fraction corresponding to the Meissner effect (FC) is lower than the shielding effect (ZFC), which is common to observe in bulk polycrystalline metallic superconductors [12, 31]. The magnetic study reveals that the presence of the impurity phases does not show visible influence on the superconducting properties of the \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) phase, which permits to assume that the content of impurities is relatively low.

The electrical resistance measurements as a function of temperature, normalized to 10 K, are shown in Fig. 3. As can be observed, the transition to the superconducting state is presented as an abrupt decrease in resistance. From this plot, the \(T_c\) values were determined as the temperature associated with the point where the resistance decreased to one half of its value in the transition onset. The values obtained were 9.00, 8.88 and 8.68 K for the nominal Pd content values x = 0.00, 0.05 and 0.10, respectively. The width of the transition temperature was estimated to be 0.3 K, determined between 90% and 10% of the resistance at the transition range. The Al-by-Pd substitution effect in \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) is to decrease the \(T_c\) values. The rate of change of \(T_c\) is about -6.8 K/x, where x is the nominal at% Pd into the samples.

Fig. 3
figure 3

Electrical resistance as a function of the temperature normalized to the value of the resistance at 10 K of the system \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\)

Full size image

Assuming that Al and Pd contribute with 3 and 2 electrons per atom, respectively, to the conduction band, it can be said that the decrease in \(T_c\) may be a consequence of a decrease in the density of electronic states at the Fermi energy \(N(E_F)\); however, it cannot be ruled out that the difference in mass of these atoms produces changes in the density of phononic states, producing a decrease in \(T_c\).

As is well known, when a superconductor is subjected to a magnetic field, H, the \(T_c\) decreases. From this, measurements of R vs T at different H allow us to determine the upper critical field as a function of temperature \(H_{c2}(T)\). Figure 4 shows the electrical resistance as a function of temperature by applying different magnetic fields to the samples under study.

Fig. 4
figure 4

Electrical resistance as a function of temperature at different magnetic fields corresponding to system \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\). The nominal content of Pd is: a x=0.00, b x=0.05 and c x=0.10

Full size image

From the measurements of electrical resistance to different magnetic fields, the associated \(T_c\) with each magnetic field was determined, corresponding to \(H_{c2}\). As shown in Fig. 5, the temperature dependence of \(H_{c2}\) is practically linear in the studied range of temperature. In the same figure, a linear fit of data close to \(T_c\) is shown; the slope of this line allows to determine the critical field at T=0 K, using the Werthamer–Helfand–Hohenberg theory (WHH) [25]

$$\begin{aligned} \mu _0 H_{c2}(0)=- 0.693 \left( \frac{dH_{c2}}{dT}\right) _{T=T_c} T_c. \end{aligned}$$
(1)

This theory has been used in works related to non-centrosymmetric superconducting materials [11, 14,15,16, 31,32,33,34].

The values of \(\mu _{0}H_{c2}(0)\) obtained are 15.22±1.58 T, 15.45±0.96 T and 13.89±0.29 T for x = 0.0, 0.05 and 0.10, respectively. The value for the sample x = 0.00 is comparable with the reported value, \(\mu _0H_{c2}=\) 15.08 T [11].

The Ginzburg–Landau coherence length \(\xi _{GL}\) can be calculated from the upper critical field \(\mu _0H_{c2}\) using [35]

$$\begin{aligned} H_{c2}(0)=\frac{\varPhi _0}{2\pi \xi _{GL}^2}, \end{aligned}$$
(2)

where \(\varPhi _0=2.0678\times 10^{-15}\) T m\(^2\) is the magnetic flux quantum, yielding \(\xi _{GL}=42.69\pm 0.47\) Å, \(\xi _{GL}=41.78\pm 0.44\) Å and \(\xi _{GL}=42.93\pm 0.54\) Å for x = 0.00, 0.05 and 0.10, respectively.

For non-centrosymmetric superconductors, the comparison between the upper limit field and the Pauli limit field, \(\mu _0H_P\), gives information about the importance of the triplet component of pairing. If the upper critical field exceeds the Pauli limit, this suggests a substantial contribution from the spin–triplet component to the pairing amplitude, presumably because of the brokenness of the inversion symmetry [36]. The Pauli limit field is obtained with the expression \(\mu _0H_P=\varDelta _0/\sqrt{2}\mu _B\) [37], where \(\varDelta _0\) are obtained through the measurements of specific heat and are reported in Table 2. In our case, the values obtained from the Pauli limit field are \(\mu _0H_P=19.06\pm 1.23\) T, \(\mu _0H_P=26.86\pm 0.74\) T and \(\mu _0H_P=22.59\pm 0.65\) T, for x = 0.00, 0.05 and 0.10, respectively. As we can see the Pauli limiting field is greater than the upper critical fields, which suggest that the Cooper pairs are in a spin-singlet state.

Fig. 5
figure 5

Upper critical field as a function of temperature determined from magnetoresistance measurements of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) (x = 0.00, 0.05 and 0.10). The continuous lines are linear fit

Full size image

3.3 Specific heat

Figure 6 shows the \(T^2\) dependence of the specific heat as a function of temperature, \(C_P(T)/T\), of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) samples. A jump around \(T_c\), characteristic of a superconducting transition demonstrates bulk superconductivity in the samples under study.

Fig. 6
figure 6

Heat capacity of \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\). The nominal content of Pd is: a x= 0.00, b x=0.50 and c x= 0.10. The solid line represents the best fit to \(C_P/T=\gamma +\beta T^2\) in the normal state

Full size image

In the normal state, above the transition temperature, the specific heat can be analyzed using \(C_p(T)/T=\gamma +\beta T^2\), where \(\gamma\) and \(\beta\) are coefficients related to the electron and phonon contributions to the specific heat, respectively [38]. In Fig. 6, the solid line represents the best linear fit to \(C_P/T\) vs \(T^2\) data of the \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) system, with x = 0.00, 0.05 and 0.10, yielding the Sommerfeld coefficient \(\gamma\) and the Debye constant \(\beta\). The Debye temperature, \(\varTheta _D\), was calculated via

$$\begin{aligned} \theta _D=\left( \frac{12\pi ^4nR}{5\beta }\right) ^{\frac{1}{3}}, \end{aligned}$$
(3)

where \(n=3\) is the number of atoms per formula and \(R=8.314\) Jmol\(^{-1}\)K\(^{-1}\) is the ideal gas constant. The parameter that indicates the intensity of the electron-phonon interaction is the electron–phonon coupling constant, \(\lambda _{e-p}\). The \(\lambda _{e-p}\) was estimated using the McMillan formula [39]:

$$\begin{aligned} \lambda _{e-p}=\frac{1.04+\mu ^{*}\ln (\theta _D / 1.45 T_c)}{(1-0.62\mu ^*)\ln (\theta _D/1.45T_c)-1.04}, \end{aligned}$$
(4)

where \(\mu ^*\) represents the repulsive screened Coulomb potential. To estimate \(\lambda _{e-p}\) from the above equation, we can use the Debye temperature obtained from specific heat measurements and assume a Coulomb pseudopotential parameter \(\mu ^*=0.13\). This value is used for intermetallic superconductors [39, 40]. We further estimate the density of states at the Fermi level, \(N(E_F)\), by the formula

$$\begin{aligned} N(E_F)=\frac{3\gamma }{\pi ^2k_B^2N_A}, \end{aligned}$$
(5)

with \(k_B\) the Boltzmann’s constant and \(N_A\) the Avogadro’s number.

The obtained \(N(E_F)\) value for the sample without doping is less than the reported experimental value of 3.32 eV\(^{-1}\), determined from specific heat measurements [30]. Band structure calculations for \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) give \(N(E_F)\) values of 5.48 eV\(^{-1}\) and 2.5 eV\(^{-1}\); however, when the spin–orbit interaction is considered, it increases to 3.5 eV\(^{-1}\) [41]. The \(N(E_F)\) value obtained in this work is considered acceptable, given the data previously reported in the literature [18]. For this reason, the observed trend in the superconducting phenomenological parameters for samples with different Pd content can be taken as valid; \(N(E_F)\) decreases with increasing the nominal Pd content. The values of \(\lambda _{e-p}\) allow us to classify the electron-phonon coupling in the \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) system, as an intermediate coupling considered for \(\lambda _{e-p}<1\) [39].

It is of special interest to know the aspects related to superconductivity parameters, particularly the gap in the superconducting state, \(2\varDelta _0\). To determine this parameter, it is necessary to know the behaviour of the specific heat of superconducting electrons. To determine the electronic specific heat, \(C_e(T)\), the term associated with the phonon contribution, is subtracted from \(C_P(T)\), that is, \(C_e(T)=C_P(T)-\beta T^3\) [38]. Once the phonon contribution to the specific heat has been subtracted, the \(T_c\) value is determined from the \(C_e(T)\) curves by taking the temperature corresponding to the midpoint of the jump in specific heat \(\varDelta C_e\). It is noteworthy that the \(T_c\) value for x = 0 is lower than for the sample corresponding to x = 0.5 and higher than for x = 0.1. This trend has been observed in the \({\mathrm {Mo_{3-x}Re_xAl_2C}}\) system [18].

The calculation of the superconducting gap, \(2\varDelta _0\), is obtained by determining the condensation energy from [35]

$$\begin{aligned} \varDelta U(0)=-\frac{1}{2}\gamma T_c^2+\int _{0}^{T_c} C_e(T) \,dT, \end{aligned}$$
(6)

where \(C_e(T)\) is the electronic specific heat in the superconducting state. The integral contained in the equation 6 was obtained by adjusting the electronic specific heat in the superconducting state as \(C_e(T)=AT^n\). Once \(\varDelta U(0)\) is obtained, the value of \(2\varDelta _0\) is determined through the expression \(\varDelta U(0)=\frac{1}{2}N(E_F)\varDelta _0^2\). The \(2\varDelta _0\) value obtained for the sample without Pd, 3.12 meV, agrees with the previously reported [11]. Extensive point-contact Andreev reflection spectroscopy studies confirmed that \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) is a moderately strong-coupling superconductor with \(2\varDelta /k_B T_c\simeq 4\) [42], and this value is close to that obtained for the sample without Pd.

Fig. 7
figure 7

\(C_e/\gamma T_c\) versus \(T/T_c\) curves of \({\mathrm {Mo_{3-x}Re_xAl_2C}}\); a x=0.00, b x = 0.05 and c x = 0.10. The solid line represents the best fit to a power law

Full size image

At low temperatures, \(T<T_c\), the behaviour of the linear coefficient in \(C_e(T)\) is an indicator of the superconducting gap structure. The \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) has been reported as a BCS-type superconductor; from this point of view, the electronic specific heat at temperatures less than \(T_c\) must have an exponential behaviour; however, the adjustments to an exponential behaviour were not satisfactory. We use a power law to fit the electronic specific heat, \(C_e(T)\), for \(T<T_c\). The solid line in Fig. 7 represents the best fit to a power law in the temperature region 4 K\(<T<T_c\). Power laws in \(C_e/T\) generally indicate the existence of gapless excitations and nodes or lines of nodes in the gap [11, 43, 44]. In our case, since there are considerable amounts of \({\mathrm {Mo_2C}}\) impurity, our conclusion on the gap symmetry needs further studies on single crystals to be clarified.

Table 2 Parameters obtained from the specific heat of the system \(\hbox {Mo}_{3}\hbox {Al}_{2-{x}}\hbox {Pd}_{x}\hbox {C}\) (x = 0.00, 0.05 and 0.10); \(T_c\) (K), \(\gamma\) (mJ/mol K\(^2\)), \(\beta\) (mJ/mol K\(^4\)), \(\varDelta U(0)\) (mJ/mol), \(\theta _{D}\) (K), \(N(E_F)\) (eV\(^{-1}\)), \(\varDelta C/\gamma T_{c}\), \(2\varDelta _0\) (meV), \(2\varDelta _0/k_BT_c\) and \(\lambda _{ep}\)
Full size table

In Table 2, all the thermodynamic and superconducting parameters mentioned above are summarized.

4 Conclusions

In summary, we reported the effects of partial substitution of Al by Pd in \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\), on the superconducting critical temperature and the upper critical field. The results shown that the Al substitution by Pd produces a decrease in \(T_c\) with a rate of change of -6.8/%Pd. From the point of view of WHH theory, the upper critical field as a function of temperature shows that the Cooper pairs are in spin-singlet state. At low temperatures, our best fit to the experimental electronic specific heat data is a power law, and this suggests that the presence of Pd in \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) affects the Fermi surface and possibly initiates the formation of nodes or nodal lines. We conclude that the impurity effects or disorder in the polycrystallines samples may have generated a anisotropic gap and the admixture of the triplet pairing component due to a lack of inversion symmetry. The above allows having a basis to confirm that \(\hbox {Mo}_{3}\hbox {Al}_{2}\hbox {C}\) is not a conventional superconductor.