Abstract
Recently, a reversible and a giant rotating magnetocaloric effect has been pointed out in the multiferroic TbMn2O5 single crystal, opening the way for new designs of low-temperature magnetic cooling. In this paper, we report a preliminary theoretical work with the aim of enlarging our understanding on the electronic, magnetic and accordingly magnetocaloric features of the TbMn2O5 compound. Particularly, the TbMn2O5 magnetic anisotropy is analyzed in terms of X-ray magnetic circular dichroism (XMCD) and X-ray absorption spectroscopy (XAS) spectra.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The discovery of new multiferroic compounds exhibiting a strong magnetoelectric coupling has aroused great interest since the beginning of the century, justified both by the fundamental issues involved and the prospects for technological applications [1]. The interest of these compounds lies in the coupling between orders, magnetic and electrical, with the possibility, from a static point of view, to manipulate the magnetization by applying an electric field [2]. The more recent discovery of magnetoelectric excitations has opened up a new field investigation [3]. In multiferroics, these hybrid excitations called electromagnons can be understood as magnons excited by the electrical component of a wave electromagnetic and are the signature in the dynamic regime of magnetoelectric coupling [4, 5]. Understanding the mechanisms behind these new excitations is one of the recent challenges of condensed matter physics, and the possibility of modulating these excitations via a field electric and/or magnetic is also an avenue explored for future applications to be defined in the field of information transport, magnetic refrigeration and spintronic devices for example. These materials in which the magnetism and the ferroelectricity are coupled have been widely studied [6,7,8]. Studies on RMn2O5 oxides have shown an important magnetocaloric effect (MEE) that is associated with a unique commensurate–incommensurate magnetic transition [1,2,3,4,5,6,7,8,9].
In this way, by using relatively low magnetic fields a highly reversible switching of electrical polarization was reported in TbMn2O5 [10]. On the other hand, it was recently shown that the same compound unveils a giant and reversible rotating magnetocaloric effect (RMCE). Habitually, this compound exhibits an insulating behavior. Its crystalline structure consists of edge-shared Mn4+O6 octahedra arranged along the c-axis and linked by pairs of Mn3+O5 pyramids [11,12,13,14]. The multiferroic TbMn2O5 material is characterized also by different exchange interactions involving Mn4+, Mn3+ and rare earth R3+ ions sublattices, leading to a complex magnetism character. As a result, TbMn2O5 reveals various magnetic and electric phase transitions [15, 16]. At TN = 43 K, it shows an incommensurate antiferromagnetic (ICM) state with a propagation vector k (0.50, 0, 0.30) that transforms into a commensurate antiferromagnetic (CM) phase at TCM = 33 K with k = (0.5, 0, 0.25), while a ferroelectric order takes place at TFE = 38 K [15].
Recently, it has been demonstrated that a large thermal effect can be simply produced by rotating the TbMn2O5 single crystal within the ac plane in relatively low constant magnetic fields rather than using the conventional magnetization–demagnetization method [1]. Under a constant magnetic field of 2 T, the resulting maximum entropy change from the rotation motion is more than 6 J/kg K, while the associated adiabatic temperature change is found to exceed 8 K. Such a large RMCE was attributed to different factors such as strong magnetocrystalline anisotropy, low specific heat as well as the enhancement of the magnetization under magnetic fields lower than 3 T. In this work, the first principles calculations (DFT) are used to investigate the electronic and magnetic properties of TbMn2O5; we aim at opening the way for the understanding of the physics behind the RMCE in TbMn2O5 single crystals and the promising RMn2O5 family of multiferroics [16].
2 Computational method
The TbMn2O5 compound crystallizes in an orthorhombic symmetry with Pbam space group (number 55). Its lattice parameters are given by: a = 7.2643 Å, b = 8.4768 Å and c = 5.6700 Å [17]. The electronic and magnetic properties of TbMn2O5 have been studied using ab initio calculations with full-potential linearized augmented plane wave (FP-LAPW) [18] involving the gradient generalized approximation GGA [19], GGA + U and spin–orbit coupling.
Conventional approaches such as the local density approximation (LDA) [20], or that of generalized gradients (GGA) [21], used in density functional theory (DFT), are standards and widely used as an approach to describe the ground state of a large number of insulating, semiconductor and metallic systems. However, it seems to us that they are insufficient to obtain a satisfactory qualitative description of the structure electronics and magnetic properties of correlated systems, so it is necessary to go beyond the DFT to properly treat strong electronic correlations. Several corrections have been developed to provide solutions to this DFT deficiency.
Among those which have been applied, we find the GGA + U method [22, 23], where "U" is the Hubbard parameter which designates the intra-atomic Coulomb interaction applying to localized orbitals (in general d or f) to correct errors in the DFT.
In TbMn2O5, U is equal to 8 eV for Tb and 4 eV for Mn, while J is assumed to be zero for both atoms [19]. The total and partial electron densities are calculated at equilibrium state. The self-consistent calculations are considered to converge with a convergence criterion fixed by a variation of the sixth decimal place in the electronic charge density and with 7 × 6x9 Monkhorst–Pack mesh implemented in the code WIEN2k [24]. In this work, calculations are performed on the Pbam orthorhombic structure of TbMn2O5 reported in Fig. 1 using the reported crystallographic parameters in ref [17].
To determine the magnetic anisotropy, we have utilized DIPAN program implemented in WIEN2K code [18] that calculates the magnetic dipolar hyperfine field and the dipolar magnetocrystalline anisotropy.
It is theoretically possible to measure the XMCD signal of any compound having at least one paramagnetic moment and for which the spin–orbit coupling is not zero. The analysis of XMCD spectra allows, with the "sum rules," to go back to the moment of spin and orbit of the studied element TbMn2O5. It is necessary for that, firstly, to have the absorption field in zero field and calculate its integral; secondly, to make the difference of the two absorptions obtained for the two polarizations, it is the signal XMCD [24]. This signal is employed to estimate the value of the spin and orbital moments in TbMn2O5 compound.
Also, the XMCD spin moment sum rule to the M4,5 edges of Tb is used for the calculation of orbital and spin moments. Considering the transition 3d (c = 2) into 4f final states (l = 3) with the number of holes n = 4 l + 2−n4f, the following equations are obtained [25]:
where the Sz and Lz are the spin and orbital moment of Tb atoms, respectively.
3 Results and discussion
The compound TbMn2O5 has an orthorhombic structure consisting of octahedra of Mn4+O6 and bipyramids of Mn3+O5 linked by their edges and their corners. This structure is illustrated in Fig. 1. Perfect knowledge of the magnetic orders of the Mn3+ and Mn4+ ions is essential for a good understanding of the multiferroic character of the compound TbMn2O5.
This material has several magnetic transitions. Below 10 K, the magnetic order of the Tb ion spins appears and adopts an antiferromagnetic order. Given the complexity of these magnetic orders, we will simplify the diagram of these configurations by looking at the ab plane, in which the ion spins Mn are almost confined.
The front view of the ab plane shows that the crystal structure of TbMn2O5 is formed by two loops of manganese ions. Each loop consists of a chain of manganese ions Mn4+–Mn3+–Mn3+–Mn4+–Mn3+ which forms a pentagonal loop. The two loops share two neighboring Mn3+O5 pyramids. However, if an antiferromagnetic coupling between two neighboring spins is established, it should favor an antiparallel arrangement along the entire chain. However, this is not the case. Indeed, geometrically, one cannot form an antiferromagnetic order along a loop formed by five manganese ions. This creates a frustrated magnetic structure which gives rise to more complex magnetic orders.
Figure 1 shows the magnetic configuration of TbMn2O5 in the commensurable antiferromagnetic phase, the spins of which are ordered antiparallelically along the zigzag chain along the b-axis. The neighboring pairs Mn3+− Mn4+ are alternately coupled in a quasi-ferromagnetic and quasi-antiferromagnetic manner along the axis a (ellipses in red and blue dotted lines).
3.1 Electronic properties
As we had discussed previously, TbMn2O5 crystallizes in an orthorhombic structure of space group Pbam. The manganese in this structure have two valences: Mn3+ and Mn4+, corresponding to two crystallographic sites. The cations Mn4+ have an octahedral environment of six oxygen (Fig. 2).
The octahedra are joined together by a ridge and form continuous chains along the c-axis. The Mn3+ environment has pyramids with a square base of five oxygen.
They are organized in dimers in which the two pyramids share an edge. Octahedra and bipyramids constitute the elementary building bricks. Along the c-axis, there is an alternation of planes of pyramids Mn3+O5, octahedra Mn4+O6 and rare earth Tb3+.
The crystallographic sites and the coordinates of the ions in the mesh are given in Table 1.
In order to explain the impact of electronic structure on the magnetic properties, we have calculated the total and partial densities of states (PDOS) of TbMn2O5 with GGA and GGA + U approximations as they are displayed in Fig. 3(a) and Fig. 3(b). The lower valence bands situated in the range (−7.0 eV) to (−5.0 eV) are due to the Tb-f states. The main contribution to the magnetism comes from 4f states of Tb atoms.
The detail of the structure strongly depends on the nature of terbium. It is not only the order of moments of Tb3+ which differs from one compound to another of the same family, but also the order of moments of Mn can also be influenced [15, 26]. This indicates the role of Tb in the magnetic ordering of manganese ions. Indeed, with its strong spin–orbit coupling, the Tb3+ ion has a strong anisotropy. Since that of manganese ions is much weaker, it is expected that the magnetic order in TbMn2O5 will depend on the anisotropy of terbium.
The filling of the d orbitals in a pyramidal environment with a square base and in an octahedral environment is done by respecting Hund's rule. (The energy of repulsion is minimized by adopting a maximum spin state.)
The environment of the terbium, having eight first neighbors, and the nature of the 4f orbitals being more complex, the estimation of the degeneration and the filling of these orbitals require more detailed calculations based on a precise crystallographic structure. The nature of the occupied 3d and 4f orbitals and the fine crystallographic structure are essential parameters for the calculation of the exchange integrals.
The Pbam symmetry of TbMn2O5 allows a position freedom of Mn3+ ions along the pyramid axis. Such motion alters the Mn–O bonds and thus the hybridization between the manganese 3d and oxygen 2p states. It is worth noting that the U value is taken from ref [27].
The density of states for Mn1 shows that the t2g level gives rise to two levels: a level which remains stable with a pure metallic character dxy and a level formed by the two hybrid molecular orbitals with a metallic character dxz and dyz; this level is a little destabilized because of the decrease in the binding character metal ligand. The level eg generates an undisturbed level formed predominantly of dx2-y2, and a dz2 level which is stabilized (see Figs. 4 and 5).
3.2 Magnetic properties
In order to well understand the magnetic interactions in the TbMn2O5 compound, we have calculated the values of Tb and Mn spins and their orbital magnetic moments [28]. The sign of the XMCD signal and that of its integral give the relative orientation of the magnetic moments between them and with respect to the applied external field.
For the total magnetic moment given in the self-consistent field (SCF) calculation, it is difficult to distinguish between the contributions from the spins and orbitals since it is equivalent to the difference between up and down spin densities of state.
For these reasons, XMCD can give more details about the value of spin–orbit coupling and calculate separately the spin and orbital moments. The absorption and dichroic spectra XAS and XMCD of TbMn2O5 are shown in Fig. 6(a) and Fig. 6(b). At the M edge, the absorption spectrum presents a peak situated at 1208.0 eV. At the L2 edge, the spectrum presents one contribution at 1244.5 eV. The integral of XMCD and XAS allows the calculation of orbital morb and spin ms moments.
The number of 4f electrons (3d) is calculated by integrating the 4f-projected (3d) density of states inside each atomic sphere. According to relations (1) and (2) and using GGA approximation, the values of morb and ms are given in Table 2 for both Tb and Mn atoms. These values indicate on the strong contribution of Tb ions to the total magnetic moment [29]. On the other hand, the obtained moment for Tb compares well with that experimentally reported in Refs [1] and [30].
In TbMn2O5 compound, giant magnetocrystalline anisotropy is remarked where the magnetization tends to orient preferentially along the a-axis [1, 30] (along the b-axis for HoMn2O5 [32]). As mentioned before, the DFT calculations using xdipan program enabled us to determine the minimal energy corresponding to the easy axis of magnetization. Thus, the magnetic anisotropy is defined as:
ΔE = E(easy axis) − E(hard axis).
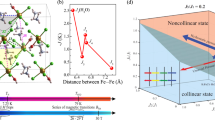
The spin–orbit term is included to observe the change in density of states. For 4f states and 3d states, it is known that there is a competition between the spin–orbit effect and the crystal field. The latter is usually strong in the case of 3d states (transition metals). Also, the rare earth elements require a spin–orbit calculation. So, it is highly important to see the charge distribution in 3d and 4f states in the case of spin–orbit coupling (SOC). To understand the anisotropy shown by TbMn2O5, we calculated the energy of the compound following each axis using DIPAN package implemented in WIEN2k program. The calculation consists to compute the total energy for different axes to find the minimal one. For TbMn2O5, the lower value corresponds to the a-axis, confirming early reported experimental works [1, 33].
The Hubbard U potential makes it possible to localized f and d states or the electrons which are delocalized.
The localization of these bands which are responsible for the magnetisms makes it possible to better calculate the magnetic moment and the most stable magnetic phase, as well as the spin orientation of each electron which gives access to the orientation of the magnetization in the compound. In fact, we obtain the most probable value of magnetic anisotropy energy (MAE).
It seems from Table 3 that the calculations without applying the potential U give the easy magnetization axis on the a-axis, while the correction U gave a minimum energy on the [011] axis or the (001) plane.
It should be noted that the magnetic anisotropy is given by the Wien2k code using the DIPAN package, which just gives an anisotropy contribution; in particular, it is the anisotropy created by the network. For the correction U, the easy magnetization axis is located between the z-axis and the yz plane, which confirms the non-collinearity of the spins of magnetic atoms [34].
4 Conclusion
In summary, our preliminary calculations using the density functional theory study of TbMn2O5 unveil that it is possible to determine some key parameters such as magnetic moments and electronic structures that are of great interest for the investigation of its entropic behavior (MCE). Particularly, the obtained magnetic moments as well as the anisotropic energies are in fair agreement with previous experimental reports. However, the main challenge remains the simulation of some important magnetothermal parameters of TbMn2O5 such as specific heat, entropy and adiabatic temperature changes. This point is currently under investigation in our group, and any relevant results will be published in a forthcoming publication.
References
M. Balli, S. Jandl, P. Fournier, D.Z. Dimitrov, Appl. Phys. Lett 108, 102401 (2016)
H. Katsura, N. Nagaosa, A.V. Balatsky, Phys. Rev. Lett. 95, 057205 (2005)
M. Fiebig, J. Phys. D: Appl. Phys. 38, R123 (2005)
G.E. Johnstone, Neutron and X-ray scattering study of magnetic manganites (University of Oxford, Oxford, 2012)
S.-W. Cheong, M. Mostovoy, Nat. Mater. 6, 13 (2007)
A.B. Sushkov, R.V. Aguilar, S. Park, S.-W. Cheong, H.D. Drew, Phys Rev Lett. 98, 027202 (2007)
J. Varignon, S. Petit, A. Gellé, M.B. Lepetit, J Phys Condens Matter. 25(49), 496004 (2013)
L.C. Chapon, P.G. Radaelli, G.R. Blake, S. Park, S.-W. Cheong, Phys. Rev. Lett. 96, 097601 (2006)
A. Ramirez, Geometrical Frustration, chapter 4, p. 423, Elsevier Science B.V., 2001
N. Hur, S. Park, P.A. Sharma, J.S. Ahn, S. Guha, S.-W. Cheong, Nature 429, 392 (2004)
G.R. Blake, L.C. Chapon, P.G. Radaelli, S. Park, N. Hur, S.-W. Cheong, J. Rodríguez-Carvajal, Phys. Rev. B 71, 214402 (2005)
T.-R. Chang, H.-T. Jeng, C.-Y. Ren, C.-S. Hsue, Phys. Rev. B 84, 024421 (2011)
N. Hur, S. Park, P.A. Sharma, S. Guha, S.-W. Cheong, Phys. Rev. Lett. 93, 107207 (2004)
D. Tzankov, V. Skumryev, M. Aroyo, R. Puzniak, M.D. Kuzmin, M. Mikhov, Solid. Stat. Comm. 147, 212 (2008)
L.C. Chapon, G.R. Blake, M.J. Gutmann, S. Park, N. Hur, P.G. Radaelli, S.W. Cheong, Phys. Rev. Lett. 93, 177402 (2004)
I.A. Sergienko, E. Dagotto, Phys. Rev. B. 73, 094434 (2006)
A. Muñoz, J.A. Alonso, M.T. Casais, M.J. Martínez-Lope, J.L. Martínez, M.T. Fernández-Díaz, Phys. Rev. B 65, 144423 (2002)
P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka, J. Luitz, WIEN 2k (Augmented Plane Wave Local Orbitals Program for Calculating Crystal Properties, Vienna, Austria, 2001)
J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996)
J.P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple. Phys. Rev. Lett. 77(18), 3865–3868 (1996)
L. Hedin, B.I. Lundqvist, Explicit local exchange-correlation potentials. J. Phys. C: Solid State Phys. 4(14), 2064 (1971)
S.Y. Savrasov, G. Kotliar, Phys. Rev. Lett. 84, 3670 (2000)
B.-T. Wang, H. Shi, W. Li, P. Zhang, Phys. Rev. B 81, 045119 (2010)
H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13, 5188 (1976)
P. Carra, B.T. Thole, M. Altarelli, X. Wang, Phys. Rev. Lett. 70, 694 (1993)
P.G. Radaelli, C. Vecchini, L.C. Chapon, P.J. Brown, S. Park, S.-W. Cheong, Incommensurate magnetic structure of YMn2O5: a stringent test of the multiferroic mechanism. Phys Rev B 79, 020404 (2009)
C. Tay-Rong, J. Horng-Tay, R. Chung-Yuan, H. Chen-Shiung, Phys Rev B 84, 024421 (2011)
B.T. Thole, P. Carra, F. Sette, G. van der Laan, Phys. Rev. Lett. 68, 1943 (1992)
C. Wilkinson, P.J. Brown, T. Chatterji, Phys. Rev. B. 84, 224422 (2011)
M. Balli, S. Jandl, P. Fournier, D.Z. Dimitrov, Crystals 7, 44 (2017)
J. Jensen, A.R. Mackintosh, Rare Earth Magnetism (Oxford Univ. Press, Oxford, 1991)
H. Bouhani, A. Endichi, H. Zaari, A. Benyoussef, M. Hamedoun, M. Balli, A. El Kenz, O. Mounkachi, J. Mater. Chem. Phys. 231, 366 (2019)
C. Wang, G-C Guo, L. He, Mater. Sci. 2007, arXiv:0711.2539v1
M. Balli, B. Roberge, P. Fournier, et S. Jandl, Review of the Magnetocaloric Effect in RMnO3 and RMn2O5 Multiferroic Crystals , Crystals, vol 7, no 2, p. 44, févr. 2017, 10.3390/cryst7020044
Acknowledgements
This work was supported by PHC Toubkal/17/49-36812NJ project and by the MESRSFC (Ministere de l’Enseignement Supérieur, de la Recherche Scientifique et de la formation des cadres) in the framework of the national program PPR under contract No. PPR/2015/57.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Endichi, A., Bouhani, H., Zaari, H. et al. Electronic and magnetic properties of the multiferroic TbMn2O5. Appl. Phys. A 126, 410 (2020). https://doi.org/10.1007/s00339-020-03585-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-020-03585-4