1 Introduction

Advances in technologies of MEMS and electronics industries allow the widespread use of portable devices, wireless sensors, and implantable medical devices. However, one unavoidable problem is that uninterrupted energy supply to these electronics is still not realized, which seriously hinders them from developing their own potential. Currently, conventional electrochemical batteries and micro fuel cells are the main power sources for electronics; however, they require periodic charging or regular replacement. In addition, disposal of the expired batteries may cause environmental pollutions. Therefore, harvesting energy from the ambient energy sources such as light [1], wind [2, 3], thermal [4, 5] and vibration [6,7,8,9] provides an alternative solution as it has the potential to continuously power electronics. Among these ambient energy sources, vibration is the most attractive because it is ubiquitous, inexhaustible and versatile in nature.

Vibration energy harvesters convert the ambient vibration energy into electrical energy using piezoelectric [10], electrostatic [11], and electromagnetic [12,13,14] mechanisms. Most vibration harvesters employ a spring–mass–damper system, which needs to work at their resonance frequencies for maximizing output. Moreover, these resonance-based harvesters typically require a relatively high resonant frequency to obtain a considerable power output, since the power generated by a vibration energy harvester increases with its resonant frequency [15]. Unfortunately, most ambient vibrations are in a low-frequency range (less than 100 Hz) and the external excitation cannot always match the resonant frequency of the energy harvester. Therefore, a vibration energy harvester with wide operating bandwidth is desirable for scavenging the ambient vibrations.

To achieve this goal, a number of methods have been proposed to widen the operating bandwidth, for instance, multimodal oscillators [16,17,18], frequency-tuning methods [19, 20], frequency up-conversion [21, 22] technique and piecewise linear methods [23,24,25]. Among them, the piecewise linear method has gained substantial attention as the method really enables energy harvesters to work at a broad frequency bandwidth, which could be beneficial for enhancing the performance of the harvester. Ashraf et al. [26] designed an energy harvester prototype able to convert the low-frequency ambient vibrations (10–18 Hz) into electricity. The harvester employs a piecewise linear oscillator to widen the range of operating frequency. Liu et al. [27] studied a piezoelectric energy harvester based on a piecewise linear system with a wide operating bandwidth (18 Hz). Miah et al. [28] presented an impact-based frequency up-converted piezoelectric vibration harvester coupled with the piecewise linear system, which can produce higher output power within a wide operating bandwidth.

Only widening the operating bandwidth is not enough, the undesired internal loss is hard to avoid. To alleviate this problem, diamagnetic stabilized levitation has been introduced in energy harvesters [29,30,31,32,33]. Unlike mechanical contact structure, diamagnetic levitation is used to construct a non-contact structure eliminating the internal friction, which is beneficial to reduce the internal loss. Liu et al. [33] proposed a nonlinear vibration energy harvester based on stabilized magnetic levitation using diamagnet. In the proposed harvester, two spiral coils made by bismuth were employed as the inductance coils and diamagnetic materials. Wang et al. [34] theoretically and experimentally studied a magnetically levitated vibration energy harvester. The proposed harvester achieves a power of 0.74 μW at an excitation frequency of 2.7 Hz. Palagummi et al. [35] designed a horizontal diamagnetic levitation based on low-frequency energy harvester. In this structure, the weight of the floating magnet was balanced by the attractive force of two coaxial lifting magnets in vertical directional and the floating magnet will move in parallel with two pyrolytic graphite plates when the harvester was excited. Experimental results indicated that the harvester can generate a maximum root-mean-square (RMS) power of 3.6 μW at a frequency of 1.2 Hz. Gao et al [36] improved Palagummi’s structure and designed a diamagnetic levitation vibration harvester with a bistable potential well. The improved harvester could harvest a peak power of 33.7 μW from a vibration level of 0.6 m/s [2] over a frequency range of 0.5–4.5 Hz. By reviewing the relevant literatures, it is also found that these energy harvesters based on diamagnetic levitation are capable of capturing the low-frequency vibration.

To combine the characteristics of the piecewise linear system and the advantages of diamagnetic levitation mechanism, a low-frequency wideband electromagnetic vibration energy harvester was studied in this paper. With their common contribution, the proposed energy harvester is especially suitable for the low frequency, such as human-body-induced vibration (less than 10 Hz). This paper is organized as follows. In Sect. 2, the energy harvester structure with elastic films is introduced and its operating mechanism is discussed; In Sect. 3, the electromechanical model of the energy harvester with a piecewise linear system is established and the frequency response of the piecewise linear system is analyzed; experiments under the vibration exciter and hand shaking are carried out to verify the performance of the harvester in Sect. 4; and conclusions are drawn in Sect. 5.

2 Device configuration and operating mechanism

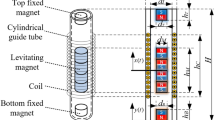
The schematic of the proposed energy harvester is shown in Fig. 1. The diamagnetic stabilized levitation system [37] is adopted as the main structure of the harvester. The harvester mainly includes a lifting magnet with 12.7 mm diameter and 5 mm height, two pyrolytic graphite sheets of 25 mm diameter and 5 mm thickness, a floating magnet of 12 mm diameter and 4 mm height, four 140-turn planar coils made of 0.07 mm diameter copper wire and a ring elastic film (depicted in red in Fig. 1). The four planar coils are divided into two groups which are attached to the bottom of the upper highly oriented pyrolytic graphite (HOPG) sheet and the top of the lower HOPG sheet, respectively.

Fig. 1
figure 1

Schematic of the proposed energy harvester

Full size image

The magnets are all NdFeB-52 (1.45T) permanent magnets magnetized axially, with the same magnetization direction. The gravity of the floating magnet is balanced by the attraction force between the floating magnet and the lifting magnet, and the diamagnetic forces from two HOPG sheets are used to maintain the stability of the floating magnet in the direction. HOPG is an anisotropic material, and the magnetic susceptibility χ‖ parallel to the horizontal plane is − 8.0 × 10−5, while the magnetic susceptibility χ⊥ perpendicular to the horizontal plane is − 45 × 10−5. Since the magnetic field of the lifting magnet is circumferentially symmetrical, the floating magnet automatically aligns with the lifting magnet to obtain a balance condition. When the floating magnet deviates from the axis of the lifting magnet, the centripetal force that the horizontal component of the magnetic force exerted on the magnet rotor will push it back to its equilibrium position. When the harvester is subjected to vibrations in the horizontal direction, the floating magnet is free to move along the radial directions due to the centripetal force and, thus, an inductive voltage is generated within the coils.

3 Theoretical modeling

3.1 Electromechanical model

In this analysis, it is assumed that the floating magnet moves only in the horizontal plane. The centripetal force is proportional to the horizontal deviation distance, which has been demonstrated by Yuta [38]. Therefore, the centripetal force can be equivalent to a spring force from a mechanical spring with stiffness k0 and damping c0.

For ease of explanation, the proposed energy harvesting system was simplified to a piecewise linear model with stoppers on two sides, which is illustrated in Fig. 2. The elastic film, which works as a flexible stopper, is considered as a mechanical spring with spring stiffness k1 and damping c1. When the energy harvester is excited by a horizontal vibration u(t), a relative motion will occur between the floating magnet and the tube; the relative displacement is recorded as y(t). Based on the amplitude of the relative displacement y, the response of the system could be classified into two cases. In the first case, if the relative displacement y is smaller than the gap r, there is no impact between the floating magnet and the elastic films. Correspondingly, the stiffness and damping of the system are k0 and c0, respectively. In the second case, when y is bigger than r, the floating magnet will impact the elastic films, and then they stick together to vibrate until they separate. With the elastic film involved, the overall stiffness and damping of the system increase to k0+ k1 and c0+ c1, respectively. As k1> k0, the effective resonant frequency of the harvester is increased and, in turn, the operating bandwidth of the system is broadened to a wider frequency range [39]. Therefore, the piecewise linear governing equations of the proposed energy harvester can be written as

Fig. 2
figure 2

a Equivalent piecewise linear vibration system, b system stiffness of the piecewise linear system

Full size image
$$\begin{aligned} m\ddot{y} + \left( {c_{0} + c_{1} } \right)\dot{y} + {\text{F}}_{\text{L}} \left( {\text{i,y}} \right) + \left( {k_{0} + k_{1} } \right)y - k_{0} r = - m\ddot{u}{\text{ y}} \ge {\text{r}} \hfill \\ m\ddot{y} + c_{0} \dot{y} + k_{0} y + {\text{F}}_{\text{L}} \left( {\text{i,z}} \right) = - m\ddot{u} \, \left| y \right| < r \hfill \\ m\ddot{y} + \left( {c_{0} + c_{1} } \right)\dot{y} + {\text{F}}_{\text{L}} \left( {\text{i,y}} \right) + \left( {k_{0} + k_{1} } \right)y{ + }k_{0} r = - m\ddot{u}{\text{ y}} \le - {\text{r}} \hfill \\ \dot{i}L_{{\text{coil}}} + i\left( {R_{{\text{load}}} + R_{{\text{coil}}} } \right) = V\left( {y,\dot{y}} \right) \hfill \\ \end{aligned}$$
(1)

where \({\text{u}}\left( {\text{t}} \right){\text{ = U}}\sin (\omega {\text{t}})\), ω represents the excitation frequency, U is the excitation amplitude, FL(i,y) is the electrical damping force, i is the current in the coil, Lcoil is the inductance of the coil, Rcoil is the internal impedance and Rload is the external load. \(V\left( {y,\dot{y}} \right)\) is the induced voltage and the dot over a variable represents the derivative with time. The voltage function (\(V\left( {y,\dot{y}} \right)\)) in Eq. (2) is determined by the Faraday’s law of induction. By summing over the infinitesimal areas (rdθdr) as shown in Fig. 3a, \(V\left( {y,\dot{y}} \right)\) can be given as follows:

Fig. 3
figure 3

Schematic of the coil geometry for a voltage-induced calculation for each loop of the coil, b Lorentz force calculation for each loop of the coil

Full size image
$${\text{V}}\left( {y,\dot{y}} \right) = - \frac{{\text{d}\varphi }}{{\text{d}t}} = - \frac{{\text{d}\varphi }}{{\text{d}y}}\frac{{\text{d}y}}{{\text{d}t}} = - 2\dot{y}\frac{\text{d}}{{\text{d}{\text{y}}}}\sum\limits_{{z\text{coil= h}^{ - } }}^{{z\text{coil} = h^{ + } }} {\sum\limits_{{r\text{coil} = r_{\text{int}} }}^{{r\text{coil} = r_{{\text{out}}} }} {\int\limits_{0}^{{r\text{coil}}} {\int\limits_{0}^{\pi } {B_{z} \left( {\rho_{,} {\text{z}}_{{\text{coil}}} } \right){\text{rd}}{\text{rd}}\theta } } } }$$
(2)

where \(\rho = \sqrt {(y - r\cos \theta )^{2} + \left( {r\sin \theta } \right)^{2} }\), zcoil is the vertical distance from the center of the floating magnet to the coil, \(t = h^{ + } - h^{ - }\), t is the thickness of the coils, rin is the inner radius of the coil and rout is the outer radius of the coil. The axial magnetic field component Bz is written in terms of the cylindrical coordinates with respect to the center of the floating magnet, which is determined by modeling the floating magnet as a thin coil [40].

The electrical damping force FL(i,y) is defined by Lorentz law. By summing the damping force due to each part of the coil (rdθ) as shown in Fig. 3b, FL(i,y) can be written as follows:

$$F_{L} \left( {i,y} \right) = 2i\sum\limits_{{z\text{coil} = h^{ - } }}^{{z\text{coil} = h^{ + } }} {\sum\limits_{{r = r_{{\text{in}}} }}^{{r = r_{{\text{out}}} }} {\int\limits_{0}^{\pi /2} {\left( {B_{z} \left( {\rho_{{\text{right}}} ,z_{{\text{coil}}} } \right) - B_{z} \left( {\rho_{{\text{left}}} ,z_{{\text{coil}}} } \right)} \right)} } } r\text{d}\theta$$
(3)

where \(\rho_{{\text{left}}} = \sqrt {(y + r\cos \theta )^{2} + \left( {r\sin \theta } \right)^{2}}\), \(\rho_{right} { = }\sqrt {({\text{y - rcos}}\theta )^{ 2} { + }\left( {{\text{r}}sin\theta } \right)^{ 2} }\), the subscripts ‘left’ and ‘right related to the left and right part of the current carrying coils.

3.2 Frequency response

When the coils in the energy harvester are open circuit, the electromagnetic damping from coils can be ignored. Therefore, Eq. (1) can be rewritten as:

$$\begin{aligned} \ddot{y} + 2\left( {\zeta_{0} \omega_{0} + \zeta_{1} \omega_{1} } \right)\dot{y} + \left( {\omega_{0}^{2} + \omega_{1}^{2} } \right)y - \omega_{1}^{2} r = - \ddot{u} \, y \ge r \hfill \\ \ddot{y} + 2\zeta_{0} \omega_{0} \dot{y} + \omega_{0}^{2} y = - \ddot{u} \, \left| y \right| < r \hfill \\ \ddot{y} + 2\left( {\zeta_{0} \omega_{0} + \zeta_{1} \omega_{1} } \right)\dot{y} + \left( {\omega_{0}^{2} + \omega_{1}^{2} } \right)y + \omega_{1}^{2} r = - \ddot{u} \, y \le - r \hfill \\ \end{aligned}$$
(4)

where ω0 and ζ0 are the resonant frequency and the damping ratio of the equivalent spring, ω1 and ζ1 are the resonant frequency and the damping ratio of the mechanical spring, respectively. The four parameters can be denoted as:

$$\omega_{0} = \sqrt {\frac{{k_{0} }}{m}} ,\omega_{1} = \sqrt {\frac{{k_{1} }}{m}} ,\zeta_{0} = \frac{{c_{0} }}{{2m\omega_{0} }},\zeta_{1} = \frac{{c_{1} }}{{2m\omega_{1} }},$$

Let us consider \(\tau = \omega_{0} t\),\(\rho = \frac{\omega }{{\omega_{0} }}\),\(\rho_{1} = \frac{{\omega_{1} }}{{\omega_{0} }}\),\(\mu = \frac{y}{U}\),\(\upsilon = \frac{u}{U}\), \(\delta = \frac{r}{U}\)

Therefore, Eq. (4) can be written as:

$$\ddot{\mu } + 2\zeta_{0} \dot{\mu } + \mu = \rho^{2} \sin \left( {\rho \tau } \right) + f\left( {\mu ,\dot{\mu }} \right)$$
(5)

where

$$f\left( {\mu ,\dot{\mu }} \right) = \left\{ \begin{aligned} - 2\rho_{1} \zeta_{1} \dot{\mu } - \rho_{1}^{2} \mu + \rho_{1} \delta \, \mu > \delta \hfill \\ 0 \, \left| \mu \right| < \delta \, \hfill \\ - 2\rho_{1} \zeta_{1} \dot{\mu } - \rho_{1}^{2} \mu - \rho_{1} \delta \, \mu < - \delta \hfill \\ \end{aligned} \right. \,$$
(6)

The method of averaging was used to obtain a closed-form solution of this function. We assume the first-order approximate solution as:

$$\mu = a\left( \tau \right)\sin \left( {\varphi \left( \tau \right)} \right)$$
(7)
$$\dot{\mu } = a\left( \tau \right)\rho \cos \left( {\varphi \left( \tau \right)} \right)$$
(8)
$$\varphi \left( \tau \right) = \rho \tau + \beta \left( \tau \right)$$
(9)

where \(a\left( \tau \right)\) is a slowly varying amplitude, \(\beta \left( \tau \right)\) is a slowly varying phase difference between the base excitation and the response. Equations (7) and (8) imply that

$$\dot{a}\sin \varphi + a\dot{\beta }\cos \varphi = 0.$$
(10)

Substituting Eqs. (7) ~ (9) into Eq. (5) yields

$$\dot{a}\rho \cos \varphi - a\dot{\beta }\rho \sin \varphi = a\left( {\rho^{2} - 1} \right)\sin \varphi + \rho^{2} \sin \left( {\varphi - \beta } \right) - 2\zeta_{0} a\rho \cos \varphi + f\left( {\mu ,\dot{\mu }} \right)$$
(11)

Solving Eqs. (11) and (12) for \(\dot{a}\) and \(\dot{\beta }\), we get

$$\dot{a}\rho = [a(\rho^{2} - 1) + \rho^{2} cos\beta ]sin\varphi cos\varphi - \left( {2\zeta_{0} a\rho + \rho^{2} \sin \beta } \right)\cos^{2} \varphi + f\left( {\mu ,\dot{\mu }} \right)\cos \varphi$$
(12)
$$a\dot{\beta }\rho = - [a(\rho^{2} - 1) + \rho^{2} cos\beta ]sin^{2} \varphi + \left( {2\zeta_{0} a\rho + \rho^{2} \sin \beta } \right)\cos \varphi + f\left( {\mu ,\dot{\mu }} \right)\sin \varphi$$
(13)

Since \(\dot{a}\) and \(\dot{\beta }\) change very slowly with time, their values can be assumed as constant over a period of 2π:

$$2\pi \dot{a}\rho = \int_{0}^{2\pi } {\left[ {\left( {a(\rho^{2} - 1) + \rho^{2} cos\beta } \right)sin\varphi cos\varphi - \left( {2\zeta_{0} a\rho + \rho^{2} \sin \beta } \right)\cos^{2} \varphi + f\left( {\mu ,\dot{\mu }} \right)\cos \varphi } \right]} \text{d}\varphi$$
(14)
$$2\pi a\dot{\beta }\rho = \int_{0}^{2\pi } { - \left[ {\left( {a\left( {\rho^{2} - 1} \right) + \rho^{2} \cos \beta } \right)\sin^{2} \varphi - \left( {2\zeta_{0} a\rho + \rho^{2} \sin \beta } \right)\sin \varphi \cos \varphi + f\left( {\mu ,\dot{\mu }} \right)\sin \varphi } \right]} \text{d}\varphi$$
(15)
$${\text{f}}\left( {\mu ,\dot{\mu }} \right) = \left\{ \begin{aligned} - 2\rho_{1} \zeta_{1} a\rho \cos \varphi - \rho_{1}^{2} a\sin \varphi + \rho_{1}^{2} \delta \, \varphi_{1} < \varphi < \pi - \varphi_{1} \hfill \\ - 2\rho_{1} \zeta_{1} a\rho \cos \varphi - \rho_{1}^{2} a\sin \varphi - \rho_{1}^{2} \delta \, \pi { + }\varphi_{1} < \varphi < 2\pi - \varphi_{1} \hfill \\ \end{aligned} \right.$$
(16)

and

$$\varphi_{1} = \text{sin}^{ - 1} \left( {\delta /a} \right)$$
(17)

For the steady-state response solution of the system, the time derivatives on left-hand sides of Eqs. (14) and (15) are considered to be zero. Then, we have

$$\pi \rho^{2} \sin \beta { = } - 2\zeta_{0} {\text{a}}\rho \pi - 4\rho \rho_{1} \xi_{1} \delta \cos \varphi_{1} - 2\rho \rho_{1} \xi_{2} a(\pi - 2\varphi_{1} )$$
(18)
$$\pi \rho^{2} \cos \beta {\text{ = - a}}\pi \rho^{2} + a\pi \left( {1 + \rho_{1}^{2} } \right) - 2a\varphi_{1} \rho_{1}^{2} - 2\rho_{1}^{2} \delta \cos \varphi_{1}$$
(19)

Combining Eqs. (18) and (19), the implicit equation for the amplitude as a function of the excitation frequency ρ is given by

$$\pi^{2} \rho^{4} = X_{1}^{2} + X_{2}^{2}$$
(20)

where X1 and X2 are the right-hand sides of Eqs. (17) and (18), respectively. Based on the frequency function (20), the amplitude of the floating magnet against the excitation frequency can be obtained accordingly.

To understand the frequency response characteristic of a piecewise linear model, the simulation results are shown in Fig. 4. In the simulation, the gap r is set as 6.5 mm; the amplitude of the external excitation is 5 mm; the damping is assumed to be ξ0 = 0.1 and ξ1= 0.36; and the frequency characteristics are supposed to be ω0 = 2.5 and ω1 = 7. As shown in Fig. 4, the frequency response of the floating magnet is divided into three stages. In the initial stage, the frequency response of the floating magnet is consistent with that of a spring–mass–damper model (without stoppers), the relative displacement increases from point A to point B with the excitation frequency increases. When the relative displacement reaches point B, the relative displacement is up to 6.5 mm, and the frequency response enters the second stage. In this stage, the floating magnet hits the elastic films, and the relative motion no longer follows the frequency response of the linear model until it reaches point C where the relative displacement drops immediately to point D, at which the frequency response reverts to the original trace of the linear model. Subsequently, the relative displacement decreases slowly from point D to point E with the increase in the excitation frequency. Compared to the linear model, the effect of the piecewise linear model to widen the operating bandwidth is clearly demonstrated. Figure 5 shows the simulated open-circuit RMS voltage according to Eq. 2. It can be seen that the voltage response curve is also divided into three stages. The voltage increases with the excitation frequency in each stage. The trend of the voltages is consistent with the relative displacement in the first two stages, but it is opposite in the third stage.

Fig. 4
figure 4

Relative displacement of the floating magnet versus different excitation frequency

Full size image
Fig. 5
figure 5

Simulated open-circuit voltages versus different excitation frequencies

Full size image

4 Experimental

4.1 Prototype fabrication

In this work, the prototype of the vibration harvester was fabricated by 3D printing technology, which is shown Fig. 6 (a). It is composed of a hollow tube with an internal thread, two threaded end covers, and intermediate support. Two HOPG sheets are embedded in the bottom cover and the internal support, respectively. The lifting magnet is bonded to the top cover using adhesive. To mount the elastic film, two opposite rectangular holes are opened on the side wall of the hollow tube. The thickness of the elastic film is 30 μm. To maximize the induced voltage, four coils are connected in series, and the total resistance is 112 Ω. The total weight of the main body (including four planar coils) is 104 g. Other parameters of the harvester, as well as the magnets, have been mentioned before. Next, the prototype will be used to evaluate the performance of the harvester experimentally.

Fig. 6
figure 6

a Energy harvester prototype and b experimental setup

Full size image

4.2 Experimental setup

The experimental setup for testing the performance of the prototype is shown in Fig. 6b. The harvester was fixed on a vibration exciter (LT-50-ST250; ECON) connected to a power amplifier (LSA-V5000A; ECON) in conjunction with a vibration controller (VT9002; ECON) which provided various excitation signals to the vibration exciter. The amplitude of the output vibration was monitored by an accelerometer (EA-YD-188; ECON) mounted on the base of the vibration exciter, connected to the vibration controller. A digital oscilloscope (Tektronix TBS 1052-B-EDU) was used to measure and record the output voltage of the prototype.

4.3 Experimental results under harmonic excitation

Figure 7 shows the open-circuit RMS voltages frequency responses of the energy harvester versus different excitation amplitudes. It could be observed that the inductive voltage gradually increases until the resonant frequency and then drops sharply. Moreover, the dramatic reduction in the output voltage increases with the excitation amplitude. Under 5 mm excitation amplitude, the output voltage drops from 159 to 74.8 mV; when the frequency sweeps from 5.1 to 5.2 Hz, the reduction of the voltage reaches 84.2 mV. The resonant frequency of the system increases with the amplitude of the external excitation. The resonant frequency is from 2.5 to 5.1 Hz, while the amplitude increases from 1.5 to 5 mm. The output voltage curve of the harvester is similar to the frequency response curve of a linear spring–mass–damper system when the amplitude is 1.5 mm, and a maximum output RMS voltage of 54 mV at a low resonant frequency of 2.6 Hz. When the excitation amplitude exceeds 2 mm, it was observed that the floating magnet impacted the elastic film. The frequency response demonstrates that the operating bandwidth is broadened and continuously to widened with the excitation amplitude. When the excitation amplitude is 5 mm, the operating bandwidth is widened to a frequency range of 3 Hz (2.1–5.1 Hz). The output voltage increases steadily from 59 mV to 159 mV within this frequency range.

Fig. 7
figure 7

Open-circuit RMS voltage frequency responses of the energy harvester versus different excitation amplitudes

Full size image

To further explore the potential of the energy harvester, we tried to characterize its output under the excitation frequency higher than 10 Hz. Unfortunately, the vibration generated by the exciter is not stable when the frequency goes beyond 15 Hz and, thus, the voltage output of the harvester is unbelievable. So we just show the results at the excitation frequencies between 10 to 15 Hz. As shown in Fig. 8, the induced voltage continues to increase with the excitation frequency. The experimental results demonstrate that the proposed harvester is also capable of scavenging vibration with a frequency greater than 10 Hz. In other words, the operating bandwidth of the proposed harvester is further widened. For example, the operating bandwidth exceeds 3 Hz under excitation amplitude of 5 mm. To understand the underlying reasons, we carefully observed the movement of the floating magnet and found that the floating magnet vibrates slightly near the stable equilibrium position when the excitation frequency reaches a certain value. And the relative displacement of the floating magnet is almost equal to the excitation amplitude. This phenomenon will cause the change rate of the magnetic flux through the coils to increase with excitation frequency. Therefore, the induced voltage increases with the excitation frequency.

Fig. 8
figure 8

Open-circuit RMS voltages from the harvester versus the excitation frequency ranged from 10 to 15 Hz

Full size image

Figure 9 summarizes the start frequency and stop frequency at which the floating magnet impacts the elastic film at different amplitudes. The start frequency is near 2 Hz, and it gradually decreases with the increase in the excitation amplitude, but the decrement is not obvious. The stop frequency increases exponentially with the increase in the excitation amplitude, which can be used to guide the design of a desirable harvester. In addition, it is seen that the impact bandwidth increases with the excitation amplitude.

Fig. 9
figure 9

Impact bandwidth that the floating magnet impacts the elastic film at different amplitudes

Full size image

Subsequently, the energy harvester was characterized by a vibration exciter under excitations with 5 Hz frequency and various accelerations; the results are shown in Fig. 10. The output voltage increases with the load resistance, and the maximum power could reach 152 μW when the load resistance matches the internal resistance.

Fig. 10
figure 10

Peak-peak voltages and output power of the harvester versus different load resistances

Full size image

4.4 Experimental results under hand shaking vibration

As shown in Fig. 11, the fabricated prototype was shaken horizontally by hand. A 9-axis attitude angle sensor (JY901, Wit Motion) mounted on the top of the prototype was used to monitor the hand shaking motion. The optimum resistance is connected to the energy harvester as its load, and the output voltage waveform across the resistance is shown in Fig. 12 under hand shaking excitation. The maximum peak–peak load voltage is 328 mV, and the maximum acceleration generated by hand shaking is 0.502g. The frequencies of the output voltage and the applied excitation were analyzed by Fast Fourier Transform (FFT), which is shown in Fig. 13. It can be seen that the frequency of the output voltage waveform is 12.49 Hz when the energy harvester is excited at the frequency of 5.395 Hz. This clearly indicates the frequency up-conversion behavior of the harvester.

Fig. 11
figure 11

Prototype was excited by hand shaking

Full size image
Fig. 12
figure 12

Output voltage waveform generated by the harvester under hand shaking excitation

Full size image
Fig. 13
figure 13

Frequency components (by FFT) of the output voltage waveform generated by (a) the harvester and (b) the applied excitation obtained from hand shaking

Full size image

An AC signal is generated by the prototype, which cannot be used directly to power electronic devices before being rectified and boosted. At first, we tried to rectify the AC signal generated by the harvester using a full-bridge rectifier which consists of four detector diodes (1N60) with a forward voltage of 267 mV. The maximum voltage across the capacitor (47 μF, 50 V) connected to the rectifier is 232 mV under 5 Hz and 0.5g acceleration, which is too low to power electronic devices. Obviously, the conventional bridge rectifier circuit is not suitable for this harvester. To obtain a high DC output voltage, a 12-stage Villard’s voltage multiplier circuit was utilized, which is shown in Fig. 14a. The circuit was composed of 12 detector diodes and 12 electrolytic capacitors (47 μF, 50 V). The boost and rectification effects of the circuit were tested at 5 Hz under 0.5g acceleration, which is shown in Fig. 14b. It can be seen that a 2.48 V DC voltage was obtained after 25 s.

Fig. 14
figure 14

a Circuit diagram of a 12-stage voltage multiplier. b Boost and rectification effects of the circuit

Full size image

To demonstrate the practical application of the energy harvester as an efficient power source, it was excited by hand shaking to power an LED. The output of the harvester was connected to the input of the multiplier circuit whose output (DC) drives the electronic load. The LED can be lit in real time during handshaking, but the brightness of the LED is not stable. A power management circuit matching this proposed harvester will be studied better in the next stage.

5 Conclusions

In this work, a low-frequency wideband electromagnetic is proposed for harvesting the low-frequency vibration energy. The diamagnetic stabilized levitation structure is introduced into the proposed harvester to reduce the internal loss and offer an equivalent low stiffness spring. With elastic films as stoppers, the energy harvester is analyzed to have a piecewise linear characteristic. Experimental results show that the proposed harvester has the potential to work in a broadband and low-frequency range. The operating bandwidth reaches 3 Hz at excitation amplitude of 5 mm. The maximum power generated by the harvester at 5 Hz under 0.8 g was 152 μW. In human hand shaking test, an LED is successfully illuminated by the energy harvester connected to a 12-stage Villard’s voltage multiplier circuit. Similar research results have not been reported in the published diamagnetic levitation energy harvester. The performance could be further improved by optimizing the parameters of the elastic films, the coils and the two magnets.