1 Introduction

The materials with perovskite structure have been extensively investigated due to their interesting dielectric, ferroelectric, pyroelectric and piezoelectric properties for applications in a variety of electronic devices [1,2,3]. Some particular industries including automotive, aerospace and deep oil well logging have expressed the demands for high-temperature ceramic capacitors (HTCC), which require that the HTCC can possess a high permittivity, low dielectric loss and good dielectric temperature stability at the operating temperature more than 200 °C [4,5,6,7,8]. A typical temperature involving capacitors on the wheel is required to work as high as 250 °C, and the temperature is 200–300 °C in the cylinder [4]. The filter capacitors in silicon carbide power invertor are generally in need of operating beyond 200 °C [6]. The BaTiO3-based dielectrics with high permittivity have been widely used as capacitors for many years [9]. However, their operating temperatures are normally insufficient high due to the low Curie temperature (TC) of BaTiO3 (~ 120 °C) [10,11,12].

K0.5Na0.5NbO3 (KNN) ceramics possess a potential for high-temperature applications because of the high TC of this system [13]. However, the dielectric peaks at ~ 200 °C (TO–T) and ~ 410 °C (TC) corresponding to orthorhombic–tetragonal (O–T) and tetragonal–cubic (T–C) phase transitions deteriorate the dielectric temperature stability [14]. To overcome the performance deterioration near phase transitions, an alternative way of developing high-temperature KNN-based dielectrics is to form relaxor ferroelectrics with a relative flat permittivity in a wide temperature range by introducing modified compositions or dopants [15,16,17,18,19].

Recently, relaxor behavior has been found in KNN–AZrO3 binary system, such as (1 − x)KNN–xSrZrO3 [20], (1 − x)KNN–xBaZrO3 [21], and (1 − x)KNN–x(Bi0.5Na0.5)ZrO3 [22]. Permittivity peaks in KNN–AZrO3 system become much broader than that in undoped KNN, resulting in an enhanced permittivity temperature stability and an extended temperature usage range. Unfortunately, the Tc declines hugely with the addition of compositions, and consequently limits the high-temperature applications. Moreover, it was reported by Naama Klein et al. [23] that Li substitution at A site of KNN could shift TC to high temperatures. In addition, previous studies showed that the addition of Bi3+ could effectively improve the electrical properties of KNN ceramics [24, 25]. However, there is few investigation on the influence of (Bi0.5Li0.5)ZrO3 content on the high-temperature dielectric properties of KNN.

In this study, (Bi0.5Li0.5)ZrO3 was selected to modify the structure and properties of KNN. In addition, dielectric behavior of the system was focused on to disclose the high-temperature dielectric loss mechanism by impedance spectroscopy.

2 Experimental procedures

(1 − x)K0.5Na0.5NbO3–x(Bi0.5Li0.5)ZrO3 (labeled as (1 − x)KNN–xBLZ, x = 0.00, 0.03, 0.05 and 0.08) lead-free ceramics were fabricated via the solid-state reaction route. Starting materials K2CO3 (99%), Na2CO3 (99.8%), Li2CO3 (98%), Nb2O5 (99.99%), ZrO2 (99%) and Bi2O3 (99%) were dried at 120 °C for 24 h before weighting. The dried powders were thoroughly weighted according to the stoichiometric ratio and mixed using a planetary mill for 8 h. The mixture was calcined at 900 °C for 4 h and mixed again using a planetary mill for 8 h. The calcined powder was granulated with 5 wt% PVA as a binder and then pressed under ~ 350 MPa into discs of 12 mm in diameter and ~ 1.2 mm in thickness. The discs with different BLZ content were sintered in a temperature range of 1100–1140 °C for 4 h in air.

Ceramic density was measured by the Archimedes method. Typical X-ray diffraction (XRD) patterns of the (1 − x)KNN–xBLZ ceramics were obtained by an automated diffractometer (X’Pert PRO, PANalytical) with Cu K α (λ = 1.5418 Å) radiation at room temperature. For dielectric measurement, the sintered discs were polished into about 1 mm in thickness. Silver paste electrodes were coated at both surfaces of the samples and fired at 650 °C for 0.5 h. The permittivity on elevated temperature was taken using a precision impedance analyzer (Agilent 4294A) in the temperature range of 30–550 °C varied in 3 °C. The Rietveld refinements were performed using the GSAS-EXPGUI software. The space groups, cell parameters, and atom positions were selected according to the reference [26]. The scaling ratio, zero point, background, cell parameters, atom positions, isotropic displacement parameters and profile shape parameters were fitted during the refinement.

3 Results and discussion

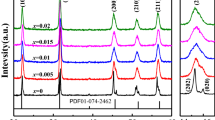
XRD patterns of the (1 − x)KNN–xBLZ ceramics at room temperature (RT) are plotted in Fig. 1. A small amount of secondary phase (K2Nb4O11) is detected for undoped KNN by X’Pert HighScore Plus software. With the addition of BLZ, the secondary phase disappears and single perovskite structure is obtained for the samples with x ≥ 0.03, which suggests that BLZ could efficiently suppress the secondary phase as a fine sintering aid. Moreover, it is noticeable that the increase of BLZ gradually changes crystal symmetry of the ceramics. Undoped KNN exhibits an orthorhombic structure (Amm2) at RT, which could be confirmed by splitting of (022) and (200) diffraction peaks near 2θ of 45° and higher relative intensity of the (022) peak. With increasing BLZ, the (022) peak is depressed and the relative intensity of (200) peak increased, thus a typical O–T mixed phase is detected in the x = 0.03 sample. Further addition of BLZ leads to the suppression of orthorhombic phase, and then the tetragonal phase (P4mm) with higher relative intensity of (200) peak occurs at the sample of x = 0.05 [27,28,29,30,31]. Subsequently, two peaks gradually merges into a symmetric peak corresponding to (200) peak for x = 0.08, implying appearance of a rhombohedral phase (R3m) in agreement with BaZrO3 modified KNN [21].

Fig. 1
figure 1

XRD patterns of the (1 − x)KNN–xBLZ ceramics at room temperature

Full size image

Lattice parameter of all samples was determined using Rietveld refinement software (GSAS-EXPGUI) [27] based on X-ray diffraction data and listed in Table 1. The unit cell parameter decreases with the addition of BLZ, which could be ascribed to ionic substitution. For (1 − x)KNN–xBLZ solid solution, since (Bi0.5Li0.5)2+ for (K0.5Na0.5)+ displaces A site while Zr4+ for Nb5+ locates at B site, the size of (Bi0.5Li0.5)2+ (1.30 Å, CN = 12) is much smaller than that of (K0.5Na0.5)+ (1.515 Å, CN = 12) in contrast with the larger size of Zr4+ (0.72 Å, CN = 6) than that of Nb5+ (0.64 Å, CN = 6) [32, 33]. Great lattice distortion is present with the increase of BLZ. Furthermore, the larger size ions at B site could enhance the stability of rhombohedral phase, which is in agreement with the XRD results.

Table 1 Phase, lattice parameters, cell volume, and relative density of the (1 − x)KNN–xBLZ ceramics
Full size table

Figure 2 depicts temperature dependence of permittivity (ε′) for the (1 − x)KNN–xBLZ ceramics at 1 MHz. For undoped KNN with orthorhombic structure at RT, two permittivity peaks corresponding to TO–T and TC above RT can be seen clearly. With the addition of BLZ, both TO–T and TC dramatically shift to lower temperatures, while the TO–T around RT can be observed in the x = 0.03 sample, which suggests the O–T mixed phase is present at RT in agreement with the XRD results [23, 31]. Further increasing BLZ, the TO–T disappears while only TC exists above RT in the composition of x = 0.05. For x = 0.08, it is found that permittivity peak exhibits a step-like behavior near RT, which could be ascribed to increase of rhombohedral–tetragonal (R–T) transition in correspondence with the dielectric behavior reported in KNN-based system [34, 35]. All results further verify crystal symmetry of the (1 − x)KNN–xBLZ ceramics, which is consistent with the XRD analysis. Moreover, it is noticeable that the T–C transition peaks are sharp for the compositions with x = 0 and 0.03, while for the samples of x = 0.05 and 0.08, the transition peak becomes much broader and shows an apparent characteristic of relaxor behavior with the diffuse phase transition.

Fig. 2
figure 2

Temperature dependence of permittivity (ε′) for the (1 − x)KNN–xBLZ ceramics at 1 MHz

Full size image

To further quantitatively characterize the relaxor behavior of diffuse phase transition for the (1 − x)KNN–xBLZ system, the characterizations of relaxor behavior have been described. The permittivity of normal ferroelectrics above Curie point (Tc) obeys the Curie–Weiss law as follows [36]:

$$1/\varepsilon ^{\prime}=(T - {T_0})/C\quad (T>{T_{\text{C}}}),$$
(1)

where C is the Curie–Weiss constant which can reflect the nature of ferroelectric transition, and T0 is the Curie–Weiss temperature. Figure 3 shows the reciprocal of permittivity for the (1 − x)KNN–xBLZ ceramics at 1 MHz as a function of temperature. It is clear that permittivity deviates from the Curie–Weiss law for the samples with x ≥ 0.05. The deviation degree (ΔTm) from the Curie–Weiss law can be defined as [36]:

Fig. 3
figure 3

The reciprocal of permittivity for the (1 − x)KNN–xBLZ ceramics at 1 MHz as a function of temperature

Full size image
$$\Delta {T_{\text{m}}}={T_{{\text{CW}}}} - {T_{\text{m}}}$$
(2)

where TCW is the temperature at which the permittivity begins to deviate from the Curie–Weiss law and Tm is the temperature at permittivity maxima as shown in Fig. 3. The perfect linear fittings above TCW are obtained and the best fitting parameters are listed in Table 2. The inset of Fig. 3 shows that ΔTm increases with the addition of BLZ. It suggests that the diffuse phase transition behavior of the (1 − x)KNN–xBLZ system is evidently enhanced by introducing BLZ.

Table 2 Curie–Weiss temperature (T0), Curie–Weiss constant (C), temperature at which the permittivity starts to deviate from the Curie–Weiss law (TCW), temperature at the maximum of permittivity (Tm), deviation degree (ΔTm) and diffuse factor (γ) for the (1 − x)KNN–xBLZ ceramics at 1 MHz
Full size table

Generally, the diffuseness of phase transition for relaxor ferroelectrics with diffuse phase transition follows a modified Curie–Weiss law as depicted by [37]:

$$\frac{1}{{\varepsilon ^{\prime}}} - \frac{1}{{\varepsilon _{{\text{m}}}^{\prime }}}=\frac{{{{(T - {T_{\text{m}}})}^\gamma }}}{C},$$
(3)

where \(\varepsilon _{{\text{m}}}^{\prime }\) is the permittivity maxima, C is the Curie–Weiss constant, and γ (1 ≤ γ ≤ 2) is the diffuse factor. Generally, γ = 1 and γ = 2 present the Curie–Weiss behavior for normal ferroelectrics and classical relaxor ferroelectrics, respectively [37]. To further verify the effect of the BLZ on the phase transition behavior of KNN, the plots of log(1/ε′ − \({1 \mathord{\left/ {\vphantom {1 {\varepsilon _{{\text{m}}}^{\prime }}}} \right. \kern-0pt} {\varepsilon _{{\text{m}}}^{\prime }}}\)) versus log(T − Tm) for the (1 − x)KNN–xBLZ ceramics at 1 MHz are displayed in Fig. 4. The γ can be obtained from the slope of linear fitting as shown by solid lines in Fig. 4. It is found that γ increases monotonously from 1.25 to 1.94 with the addition of BLZ, implying that the (1 − x)KNN–xBLZ ceramics change from normal ferroelectrics to relaxor ferroelectrics. Generally, ionic substitutions [i.e., (Bi0.5Li0.5)2+ for (K0.5Na0.5)+ at A site and Zr2+ for Nb5+ at B site] give rise to size and valence mismatches. Nb5+and Zr4+ have ionic radii of 0.64 and 0.72 Å, respectively. A more pronounced off-center shift of the smaller Nb atoms is observed in their oxygen octahedral cage in comparison to the larger Zr atom. Then, the substitutions of K+/Na+ with Li+/Bi3+ (exhibiting a stereochemically active lone electron pair) and Nb5+ with Zr4+ not only disturbs the long-range Nb5+ displacement, but also results in substantial local lattice strain. Local size mismatch could produce random strains, while local valence mismatch could result in quenched random electric fields (RFs). The RFs hinder long-range ferroelectric ordering and generate polar nano-regions (PNRs) [38, 39]. The existence of PNRs has been confirmed by the neutron elastic diffuse scattering and TEM in PMN relaxor ferroelectric [40, 41]. When the substitution concentration is not very high, the PNRs are isolated and embedded in the (1 − x)KNN–xBLZ ceramics matrix, which lead to the relaxor behavior.

Fig. 4
figure 4

Log(1/ε′ − \({1 \mathord{\left/ {\vphantom {1 {\varepsilon _{{\text{m}}}^{\prime }}}} \right. \kern-0pt} {\varepsilon _{{\text{m}}}^{\prime }}}\)) as a function of log(T − Tm) for the (1 − x)KNN–xBLZ ceramics at 1 MHz with various BLZ content. The red solid lines is the linear fittings according to Eq. (3)

Full size image

Figure 5 presents temperature coefficient curves of permittivity \(({{\Delta \varepsilon ^{\prime}} \mathord{\left/ {\vphantom {{\Delta \varepsilon ^{\prime}} {\varepsilon _{{200^\circ {\text{C}}}}^{\prime }}}} \right. \kern-0pt} {\varepsilon _{{200^\circ {\text{C}}}}^{\prime }}},\;\Delta \varepsilon ^{\prime}=\varepsilon ^{\prime} - \varepsilon _{{200^\circ {\text{C}}}}^{\prime })\) and dielectric loss (tanδ) as a function of temperature for the (1 − x)KNN–xBLZ ceramics at 1 MHz. In Fig. 5a, the temperature coefficient curve of the permittivity near Tc is hugely influenced by the addition of BLZ. Particularly, the composition with x = 0.08 exhibits a high and stable permittivity (~ 1317) from 55 to 445 °C based on ± 15% variation, which is the tolerance of electronic industries alliance (EIA) X8R/X9R capacitors assigned currently for operating at elevated temperatures [8]. Moreover, it is found from Fig. 3b that low tanδ (≤ 0.06) extends from 120 to 400 °C. Therefore, the 0.92KNN–0.08BLZ ceramic is hugely attractive for high-temperature capacitors. However, tanδ of the samples increases hugely at higher temperatures due to a thermally activated conductivity [42].

Fig. 5
figure 5

Temperature coefficient of permittivity (a) and dielectric loss (b) as a function of temperature for the (1 − x)KNN–xBLZ ceramics at 1 MHz

Full size image

Impedance spectroscopy is usually utilized to study the dielectric behavior of ceramic materials [43]. To further understand high-temperature dielectric loss behavior of the samples, normalized imaginary parts of impedance for the (1 − x)KNN–xBLZ ceramics as a function of frequency at measured temperatures are plotted in Fig. 6. Each curve of the samples at given temperatures exhibits a symmetric peak with a frequency maximum (relaxation frequency). The relaxation frequency gradually shifts to the higher frequency side with the increase of temperature. It suggests a thermally activated relaxation behavior. The relation between relaxation frequency and temperature follows the Arrhenius law:

$${f_{\hbox{max} }}={f_0}\exp \left( {\frac{{ - {E_{{\text{rel}}}}}}{{{k_{\text{B}}}T}}} \right),$$
(4)

where fmax is the relaxation frequency, fo is the pre-exponential factor, Erel is the activation energy of relaxation, kB and T are the Boltzmann constant and measured Kelvin temperature, respectively. From the slope of the straight lines obtained from ln (fmax) versus (1000/T) plots in Fig. 7, the Erel can be calculated: Erel = 1.009 eV for x = 0, Erel = 1.014 eV for x = 0.03, Erel = 1.627 eV for x = 0.05 and Erel = 1.106 eV for x = 0.08. The Erel first increases then declines with increasing BLZ.

Fig. 6
figure 6

Normalized imaginary parts of impedance for the (1 − x)KNN–xBLZ ceramics as a function of frequency at measured temperatures, a x = 0, b x = 0.03, c x = 0.05, d x = 0.08

Full size image
Fig. 7
figure 7

Arrhenius plots of relaxation frequency (fmax) for the (1 − x)KNN–xBLZ ceramics. The symbols are the experimental data and the solid lines are the linear fittings according to Eq. (4)

Full size image

Figure 8 plots ac conductivity (σac) of the (1 − x)KNN–xBLZ ceramics as a function of frequency at measured temperatures. The σac of all samples declines with the decrease of frequency, and then exhibits a fixed value close to dc conductivity at low frequencies. This conductivity behavior normally obeys the “universal dielectric response” (UDR) law [44]:

Fig. 8
figure 8

Ac conductivity (σac) of the (1 − x)KNN–xBLZ ceramics as a function of frequency at measured temperatures, a x = 0, b x = 0.03, c x = 0.05, d x = 0.08. The solid lines are the fittings according to Eq. (5)

Full size image
$${\sigma _{{\text{ac}}}}={\sigma _{{\text{dc}}}}+{\sigma _0}{f^s},$$
(5)

where σdc is the dc conductivity, σ0 is pre-exponential factor, f and s are the frequency and exponential term (0 < s ≤ 1). The UDR law depicts one phenomenon connected with many-body interactions between charges and dipoles. The perfect fittings between σac and frequency with Eq. (5) as shown by solid lines in Fig. 8 are carried out to achieve σdc values at different temperatures. The relation between obtained σdc and temperature obeys the Arrhenius law:

$${\sigma _{{\text{dc}}}}={T^{ - 1}}{\sigma _0}\exp \left( { - \frac{{{E_{{\text{con}}}}}}{{{k_{\text{B}}}T}}} \right),$$
(6)

where σ0 is pre-exponential factor, Econ is the activation energy of dc conductivity, kB and T are the Boltzmann constant and measured Kelvin temperature, respectively. From the slope of straight lines obtained from ln (T σdc) versus (1000/T) plots in Fig. 9, the Econ can be calculated: Econ = 0.634 eV for x = 0, Econ = 0.644 eV for x = 0.03, Econ = 1.246 eV for x = 0.05 and Econ = 0.864 eV for x = 0.08. The Econ first increases then declines with increasing BLZ, which agrees with the variation of Erel. It has been reported that the activation energies for single- and doubly ionized oxygen vacancies are in the range of 0.3–0.5 and 0.6–1.2 eV in perovskite oxides, respectively [42, 44]. Thus, both Erel and Econ for the (1 − x)KNN–xBLZ ceramics should be related to the doubly ionized oxygen vacancies.

Fig. 9
figure 9

Arrhenius plots of the dc conductivity for the (1 − x)KNN–xBLZ ceramics. The symbols are the experimental data and the solid lines are the linear fittings according to Eq. (6)

Full size image

It is known that the volatilization of K/Na/Li/Bi during sintering gives rise to oxygen vacancies, meanwhile the possible Nb5+ substitution by Zr4+ occurs, as described in the Kroger–Vink notation by Eq. (7−9):

$${A_{\text{A}}} \to A+V_{{\text{A}}}^{\prime }+\frac{1}{2}V_{O}^{{ \bullet \bullet }},$$
(7)
$${\text{B}}{{\text{i}}_{{\text{Bi}}}} \to {\text{Bi}}+V_{{{\text{Bi}}}}^{{\prime \prime \prime }}+\frac{3}{2}V_{{\text{O}}}^{{ \bullet \bullet }},$$
(8)
$${\text{Z}}{{\text{r}}_{{\text{Zr}}}} \to {\text{Zr}}_{{{\text{Nb}}}}^{\prime }+\frac{1}{2}V_{{\text{O}}}^{{ \bullet \bullet }},$$
(9)

where \(V_{{\text{A}}}^{\prime }\) is vacancies of K/Na/Li, \(V_{{\text{O}}}^{{ \bullet \bullet }}\) is the doubly ionized oxygen vacancy, \(V_{{{\text{Bi}}}}^{{\prime \prime \prime }}\) is the Bi vacancy, and \({\text{Zr}}_{{{\text{Nb}}}}^{\prime }\) is the quadruply ionized Zr4+ which occupies at the Nb5+ site. Since one Bi vacancy induces more oxygen vacancies than that of K/Na/Li and the compensated oxygen vacancies is formed due to the creation of the negatively charged defect \({\text{Zr}}_{{{\text{Nb}}}}^{\prime }\), the high concentration of oxygen vacancies results in the decrease of activation energy with increasing BLZ. In this work, why do both Erel and Econ first increases and then decrease with the increase of BLZ? Considering the change of lattice parameter for the (1 − x)KNN–xBLZ system as mentioned above, it is assumed that the magnitude of activation energy could be associated with both lattice distortion and the concentration of oxygen vacancies. With the addition of BLZ, lattice parameter of the samples of x = 0.03 and 0.05 dramatically drops due to the change of crystal symmetry, and the higher energy barrier for oxygen vacancies hopping results in the increase of activation energy [45]. Further increasing BLZ, the lattice parameter of the sample of x = 0.08 slightly decreases, and the enhanced concentration of oxygen vacancies plays a dominant role on the decrease of activation energy.

4 Conclusions

(1 − x)K0.5Na0.5NbO3–xBi0.5Li0.5O3 ceramics were prepared by the solid-state reaction method. The stability of rhombohedral phase and relaxor behavior are enhanced with the increase of BLZ. The 0.92KNN–0.08BLZ ceramic shows a high and stable permittivity (~ 1317, ± 15% variation) from 55 to 445 °C and low dielectric loss (≤ 6%) from 120 to 400 °C, which is hugely attractive for HTCC applications. The high-temperature conduction presents a thermally activated behavior, which might be attributed to lattice distortion and the concentration of oxygen vacancies.