1 Introduction

Electromagnetically induced transparency (EIT) is a quantum interference phenomenon that renders an opaque medium transparent in a narrow spectral region with low absorption and steep dispersion [1, 2]. These properties have been exploited to show different applications in these systems, such as slow light, sensing and data storage [2–5]. However, it was realized that EIT-like behaviors are not uniquely associated with quantum systems and can be extended to classical systems [2–4]. In this context, several classical systems have been designed to demonstrate the classical analogue of EIT. Among these systems, one can cite plasmonic nanostructures [6–9], planar metamaterials [10, 11], photonic crystal waveguides coupled to cavities [12–16], coupled microresonators [17–20], micro- and radiowave circuits [21–23] and acoustic slender tube waveguides [24, 25]. The EIT resonance can be obtained using two coupled resonators (or oscillators) with closely spaced frequencies.

The resonators with high (dark resonator) and low (radiative resonator) Q factors give rise to the so-called Λ-type configuration [1] in three atomic levels, whereas the resonators with low Q factors (radiative resonators) give rise to the so-called V-type configuration [6, 7, 22–25]. In few recent works, the V-type resonances in double-stub resonators connected at the same site along a waveguide have been shown in photonic [22, 23], acoustic [24, 25] and plasmonic [26, 27] structures.

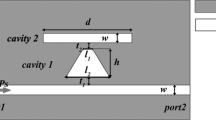
In this work, we studied the plasmonic analogue of EIT in a two-side-coupled cavity to a waveguide. The geometry of the system is considered in either Λ- or V-like configuration. This is to provide a plasmonic system design giving rise to EIT-like resonance in both configurations. The cavities are embedded in a metal and filled with air and are considered to have the same width (w = 100 nm), whereas their lengths L 1 and L 2 can be detuned. We show the possibility of the existence of EIT resonance by detuning the size of the two cavities in Λ- and V-type configurations (Fig. 1a, b). Their separation from the waveguide is referred to as g (metallic gap that enables evanescent coupling).

Fig. 1
figure 1

a Geometry of a metal–insulator–metal waveguide side-coupled (through a metallic gap g) to two cavities situated symmetrically on each side of the bus waveguide. b Same as in (a) but such as both cavities are placed on the same side of the main waveguide, and coupled to each other through a metallic gap g 2. In this configuration, the three atomic levels (analogously with atomic systems) are sketched within the structure

Full size image

2 Method of numerical simulation

The cladding of the waveguide and the cavities is a silver metal whose dielectric function is described by the lossy Drude model

$$\varepsilon \left( \omega \right) = \varepsilon_{\infty } - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} + i\varGamma \omega }} ,$$
(1)

where \(\varepsilon_{\infty }\) is the relative permittivity at infinite frequency, \(\omega_{\text{p }}\) is the plasma frequency, and \(\varGamma\) is the collision frequency. The corresponding values are given by [28]: \(\varepsilon_{\infty } = 12.5\), \(\omega_{\text{p}} = 2.05 \times 10^{16}\)  rad/s, and \(\varGamma = 10^{14}\) rad/s. The waveguide width (d) is set out to be equal to 50 nm, and the incident plane wave is a TM-polarized one, i.e., the magnetic field is perpendicular to the plane of Fig. 1 (\(\vec{H} / /\vec{z}\)). The frequency domain we are interested in here corresponds to the vacuum wavelength ranging from 600 to 820 nm. In this frequency interval, the waveguide is strictly monomode and antisymmetric [29]. It corresponds to a surface plasmon polariton (SPP)-like mode in which the electric field is strongly confined along the dielectric–metal interface and decays exponentially away from it [30, 31].

The optical properties of the structure such as transmission (T), reflection (R) and absorption (A) are obtained using finite element method (Comsol-Multiphysics package) [32]. R and T are calculated, respectively, by means of the scattering matrix elements of the system, namely

$$R = \left| {S_{11} } \right|^{2} \quad {\text{and}}\quad T = \left| {S_{21} } \right|^{2} ,$$
(2)

whereas the absorption is deduced by A = 1 − R − T.

3 Plasmonic design system in V-type state

In order to show the possibility of existence of EIT resonance, i.e., a resonance squeezed between two transmission zeros, we have to take \(L_{1}\) and \(L_{2}\) slightly different. This is true whether the system design is set into a V- or Λ-like configuration. We will focus first on the V-type system and then treat the Λ-like case. Figure 2a–c gives, respectively, the transmission, reflection and absorption spectra (pink curves) for L 1 = 240 nm and L 2 = 258 nm (\(\Updelta L = L_{2} - L_{1} = 18 \;{\text{nm}}\)) and g = 12 nm. One clearly notes, in Fig. 1a, the emergence of a resonance peak at \(\lambda_{r} = 672\) nm between the two dips situated at \(\lambda_{1} = 654\;{\text{nm }}\) and \(\lambda_{2} = 693\;{\text{nm}}\). As a matter of comparison, we have also plotted the transmission, reflection and absorption for each resonator alone (black and red curves). While the zeros of transmission are originated from the resonances of the cavities [30], the peak of resonance is the consequence of an interaction between the cavities.

Fig. 2
figure 2

a Transmission spectra when a single cavity is coupled to the waveguide with L 1 = 240 nm (black curve) and L 2 = 258 nm (red curve). The pink curve corresponds to the case when both cavities are present in the system (L 1 = 240 nm and L 2 = 258 nm). b The same as in (a) but for the reflection. c The same as in (a) but for the absorption. The metallic gap is kept fixed at g = 12 nm

Full size image

Figure 3a, b represents the magnetic field distribution at the incident wavelengths (of the dips) \(\lambda_{1} = 654\;{\text{nm}}\) and \(\lambda_{2} = 693\;{\text{nm}}\). At these wavelengths, the field is trapped in each cavity and does not propagate in the system. This result has already been explained and reported deeply in [30].

Fig. 3
figure 3

a, b Magnetic field maps at the transmission dip wavelengths \(\lambda_{1} = 652\;{\text{nm }}\) and \(\lambda_{2} = 692\;{\text{nm }}\), respectively. c Same as (a, b) but for the resonance peak at \(\lambda_{r} = 672\;{\text{nm}}\). Notice the different color scales at the left-hand side of the figures

Full size image

Besides, the magnetic field map at the wavelength of the resonant peak, i.e., \(\lambda_{r} = 672\) nm, is depicted in Fig. 3c. It can be clearly seen that the wave is now transmitted through the waveguide. This phenomenon can be explained as an out-of-phase oscillation of one cavity with respect to the other. Indeed, the cavities, acting like radiative oscillators, interfere destructively (via the bus waveguide) at the wavelength of the EIT resonance. As a result, the guided mode at the resonance is transmitted to the end of the waveguide giving rise to the EIT phenomenon.

In addition to the study of the amplitudes of the transmission, it is interesting to analyze other information of the scattering parameters such as the dispersion behavior. The latter is related to the phase \(\phi\) of the transmission. An example of the variation of the phase as a function of the wavelength is given in Fig. 4a for \(\Delta L = 18\;{\text{nm}}.\) As predicted, the phase shows two phase drops around the transmission zeros (Fig. 2a). The phase drops do not reach \(\pi\) because of the large absorption in the metal. Similar behavior has been observed experimentally in coaxial cables [23]. A clear signature of the phase drops is observed in the delay time defined as \(\tau = \frac{{{\text{d}}\phi }}{{{\text{d}}\omega }}\) giving rise to negative delay time in Fig. 4b. The delay time gives the time spent by electromagnetic waves in the cavities (time of capture) before their transmission.

Fig. 4
figure 4

a Variation of the phase of the transmission as a function of the wavelength for the structure depicted in Fig. 1a with L 1 = 240 nm and L 2 = 258 nm. b Same as (a) for the delay time. The metallic gap is kept fixed at g = 12 nm

Full size image

In order to study the effect of the detuning \(\Delta L = L_{2} - L_{1}\) on the EIT resonance, we have fixed the length of the lower cavity at L 1 = 240 nm and changed the length L 2 of the upper cavity (results not shown). As predicted, the dip associated with the fixed cavity falls at the same wavelength; however, the wavelengths induced by the second cavity and the EIT resonance increase when \(\Delta L\) increases.

We have also been interested in the behavior of the transmission, reflection and absorption magnitudes with respect to \(\Delta L\) at the EIT resonance wavelength. The corresponding results are summarized in Fig. 5. One could notice that the transmission and reflection coefficients cross each other when the absorption reaches a maximum value at around \(\Delta L \approx 5.5 \;{\text{nm}}\). This is similar to what has been reported recently in photonic circuits [23]. The wavelengths of the EIT resonance and the zeros of transmission are depicted in the inset in Fig. 5.

Fig. 5
figure 5

Transmission, reflection and absorption versus \({\Updelta} L = L_{2} - L_{1}\) for the EIT resonance depicted in the inset. The wavelengths of the transmission zeros \(\lambda_{1}\) and \(\lambda_{2}\) are also sketched in the inset. The length of the lower cavity is fixed to L 1 = 240 nm, and the metallic gap is kept equal to g = 16 nm

Full size image

The characteristics of the EIT resonance depend strongly on the gap parameter g separating the cavities and the waveguide, as it is described in Fig. 6a. When g decreases, (1) the wavelengths associated with the transmission dips and the EIT resonance increase (Fig. 6b). (2) The width and the intensity of the resonance decrease which renders the system less transparent because of the absorption. (3) The dips reach zero intensity which means that the system becomes more opaque at the cavities wavelengths.

Fig. 6
figure 6

a Transmission spectra versus wavelength for g = 16 nm (black curve), 12 nm (red curve), 9 nm (green curve) and 6 nm (pink curve). The lengths of the two cavities are fixed to L 1 = 240 nm and L 2 = 258 nm. b Transmission zeros and EIT resonance wavelengths versus g

Full size image

4 Plasmonic design system in a Λ-type state

After having grafted the cavities resonators aside of the bus waveguide in a V-like configuration, we now put both cavities on the same side of the waveguide as depicted in Fig. 1b. In this geometry, the system clearly resembles a Λ-like atomic state [1].

The interaction between the incident wave in the waveguide and the two cavities placed on the same side of the waveguide is quite different from the case where the cavities are placed on each side of the waveguide. Indeed, let us call \(\left| 2 \right\rangle\) and \(\left| 3 \right\rangle\) the eigenmodes (states) associated with higher and lower cavities, respectively. Given that the cavities are placed close to each other, they interact strongly (depending on the gap g 2), which produces a new system (cavity) characterized by two new states, namely \(|a \rangle= \left( {|2\rangle + |3\rangle} \right)/\sqrt 2\) and \(|b\rangle = \left( {|2\rangle - |3 \rangle} \right)/\sqrt 2\) (Fig. 1b). The coupling of the incident wave with this system gives rise to two dips associated with the states \(|a\rangle\) and \(|b\rangle\). An example of the transmission spectra of such a system is shown in Fig. 7 for L 1 = 240 nm and L 1 = 252 nm (i.e., ΔL = L 2 − L 1 = 12 nm), and g = g 2 = 10 nm. Both frequency wavelengths (\(\lambda_{1} = 630\;{\text{nm}}\) and \(\lambda_{2} = 730\;{\text{nm}}\)) are eigenmodes of the coupled cavities. This is quite explicit in Fig. 8a, b where the magnetic field maps are presented within the system at these specific wavelengths. As a matter of fact, at these frequencies the incident waves are trapped inside the cavities and reflected back to the entrance of the waveguide.

Fig. 7
figure 7

Transmission spectra versus wavelength of the system of Fig. 1b for \(L_{1} = 240 \;{\text{nm}}\), \(L_{2} = 252\;{\text{nm}}\) and g = g 2 = 10 nm

Full size image
Fig. 8
figure 8

a, b Modulus of the magnetic field maps at transmission dips at \(\lambda_{1} = 630\;{\text{nm }}\) and \(\lambda_{2} = 730\;{\text{nm }}\), respectively. c Same as (a) and (b) but for the EIT resonance peak wavelength at \(\lambda_{r} = 700\;{\text{nm}}\). Notice the different color scales at the right-hand side of the figures

Full size image

One notes the appearance of a relatively large transparency window (EIT resonance) between the transmission zeros induced by the cavities. The magnetic field map at the middle wavelength of the transmitted window (≈\(\lambda_{r} = 700\;{\text{nm}}\)), corresponding to the EIT resonance wavelength, is presented in Fig. 8c. This result shows that the transmission (transparency) appears as a consequence of the interaction of the incident wave with the upper cavity mode. This can be explained by the fact that the EIT resonance lying between the two states \(|a\rangle\) and \(|b\rangle\) is a linear combination of the two states, namely \(\left( {|a\rangle + |b\rangle} \right)/\sqrt 2\). However, this state is exactly the eigenmode \(|2\rangle\) of the upper cavity which explains the behavior of the magnetic field trapped inside this cavity and its extinction in the lower cavity (Fig. 8c).

One could have noticed the relatively large width of the transparency window that opened up, which indicates a quite low quality factor of the EIT resonance. In order to improve Q, we studied the influence of the metallic gap g 2 on the full width at half maximum (FWHM) of the resonance. This parameter permits the control of the evanescent coupling intensity between upper and lower cavities. In Fig. 9, we give the transmission spectra of the system versus wavelength for different values of g 2, and such that L 1 = 240 nm, L 2 = 252 nm and g = 10 nm. We remark a significant decrease of the width of the EIT resonance with increasing g 2. Specifically, Q ≈ 13 for g 2 = 10 nm and Q ≈ 27 for g 2 = 20 nm. The drawback of increasing Q is the energy loss associated with EIT peak. Indeed, one can see that at g 2 = 10 nm (Q ≈ 13), approximately 75% of the incident power is transmitted, while for g 2 = 20 nm, only 60% of the power is transferred. Nonetheless, 60% of transmitted power is still quite reasonable value, and a trade-off should always be reached at that point.

Fig. 9
figure 9

Transmission spectra versus wavelength of the system for different values of g 2 such that \(L_{1} = 240\;{\text{nm }}\) and \(L_{2} = 252\;{\text{nm}}\) and g = 10 nm

Full size image

Another important feature of a classical analogue system of EIT is whether it is easy to adjust the resonance peak or not. In order to show the possibility of EIT resonance frequency tuning, we studied the effect of the upper cavity length on the transmission properties of the system.

Specifically, we calculated the transmission spectra versus wavelength for L 2 = 246, 252, 258 and 264 nm, whereas \(L_{1} = 240\;{\text{nm}}\), g = 10 nm and g 2 = 17 nm are kept constant. The value of g 2 = 17 nm offers a good rate of transmitted power at EIT resonance (about 65%) and a relatively small FWHM of the associated peak. The corresponding results are presented in Fig. 10, where one can notice an almost linear increase of the EIT resonance wavelength with increasing L 2. Actually, it is shown in Fig. 9 that the intensity of the evanescent coupling between the two cavities resonators represented by g 2 enables the tuning of the EIT resonance as well. Nevertheless, it also modifies the FWHM of the resonance peak, which might be undesirable. Consequently, it is best to adjust L 2 such that only the wavelength resonance can be tuned.

Fig. 10
figure 10

Transmission spectra versus wavelength of the system for different values of L 2 such that \(L_{1} = 240\;{\text{nm}},\) \(g_{2} = 17\;{\text{nm}}\) and g = 10 nm

Full size image

5 Conclusion

In this paper, we have demonstrated numerically the possibility of existence of plasmonic analogue of EIT in metal–air–metal waveguide coupled to two nanocavities resonators placed in either V- or Λ-type configurations. Both cavities are filled with air but with different sizes. The waveguide and the cavities are embedded in a metal, and the interaction between the confined mode within the waveguide and the cavities depends on the type of configuration the system is set into. In a V-like state, the incident light-wave couples with both cavities (put aside) evanescently through a small metal gap. In this case, the EIT resonance is shown and explained by destructive interference between the cavities acting like radiative oscillators. We have shown that the behavior of the EIT resonance in the transmission can be detuned via the difference in size of the two cavities depending on the value of the gap separating the cavities from the waveguide. On the other hand, when the same system is placed in a Λ-type state, the incident wave couples directly (evanescently) with the lower cavity, and only indirectly (via the former) with the upper one. In this situation, The EIT resonance existence is proven as well, and it is explained analogously with atomic systems as destructive interference between the upper and lower cavities. The possibility of tuning the frequency and improving the quality factor of the EIT resonance peak is demonstrated. As a matter of completeness of this work, we predict to use the properties of the EIT resonance in designing an optical demultiplexer made of one input waveguide and two output waveguides [33]. This work is in progress. Besides, the available results may have important applications for designing integrated devices such as narrow-frequency optical filters, novel sensors and high-speed switches.