Diffuse phase transition and impedance spectroscopy analysis of Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅ (x = 0.25) ferroelectric ceramic

Abstract

A new rare earth ferroelectric tetragonal tungsten bronze compound with general formula Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅ (x = 0.25) was elaborated as ceramic and investigated using X-ray diffraction and dielectric measurements. The results show a tetragonal phase with the space group P4bm. Special emphasis was done to characterize diffuse phase transition (DPT) that occurs close to 472 °C. Using dielectric measurements in a frequency range of (10 Hz–1 MHz) and in a temperature range (25–550 °C), we have shown that the real part of the permittivity close to DPT is well described by Santos–Eiras phenomenological model. Space charge polarization, relaxation phenomena and free charges conductivity have been analyzed using dielectric, impedance spectroscopy and Nyquist plots showed non-Debye (polydispersive) type relaxation. In paraelectric phase, the Arrhenius activation energies were determined. Frequency dependence of ac conductivity at different temperatures follows the Jonscher’s universal law (Jonscher et al. in J Mater Sci 20:4431, 1985).

1 Introduction

Among ferroelectric of the oxygen-octahedral type, the most numerous and practically the most important (after the perovskite family) are complex oxides with the structure of the tetragonal tungsten bronze (TTB) type. They present several advantages as the specific manifestation of the ferroelectric properties, the relatively low (tetragonal) symmetry of the paraelectric phase and the relationship of ferroelectric and ferroelastic properties. This makes them very interesting for theoretical and experimental studies. In addition, because of their high electrooptical and piezoelectric coefficients, the high Curie temperature and substantial anisotropy of piezoelectric properties, the TTB used in technology as material for high-efficiency electrooptical and piezoelectric applications [2, 3]. So the study of new compounds and solid solutions with TTB structure is of great interest both from the viewpoint of further development of the ferroelectricity physics and for new materials creation, especially lead free ferroelectrics. Novel materials of this structure type are to be fully exploited for future applications [4]. Because of this great interest and taking into account the standards of environmental protection and on the basis of recent work on the effect of the Ba and Nb substitutions by Na and W on the ferroelectric properties of the solid solution Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅, we are oriented to explore in details the new representative of BNNW samples (called further as BNNW25, Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅ where x = 0.25) and investigate their electrical properties by impedance spectroscopy method.

This paper reports on the dielectric properties of solid-state synthesized BNNW25 ceramics. The ceramic’s symmetry is P4bm. Dielectric experiments show that the ferroelectric niobate ceramic BNNW025 presents a phase transition at T = 472 °C. This result was confirmed by X-ray analysis and Raman studies in previous work [5]. The origin of frequency dispersion of dielectric constant was analyzed by complex impedance spectroscopy technique. Details of these results and their discussion are presented below.

2 Experiment

The BNNW25 powders were prepared using the solid-state reaction method. First, we started with Nb₂O₅ (99.5 %), NaCO₃ (99.99 %) and BaCO₃ (99 %). These materials (carbonates and oxides) were mixed in a desired stoichiometry. The mixture was ground in ethanol medium for 1 h with agate mortar before each thermal treatment. The obtained powder was calcined at 900 °C/4 h. The formation of the single-phase compound was confirmed by X-ray powder diffraction (XRD) technique. The granulated powder was compacted under 250 MPa hydraulic pressure into disk of 6 mm diameter and of 1 mm thickness approximately. The obtained pellets were then placed into alumina crucible and sintered at 1270 °C/2 h. The obtained sintered ceramic samples were crack-free.

To study the electrical properties of the compound, two electrodes were deposited on both flat surfaces of the sintered pellets, with air-drying conducting silver paste. An impedance analyzer connected to a personal computer was used to measure the capacitance, loss tangent and impedance versus frequency in the temperature range (25–550 °C).

Dielectric measurements were taken using the SOLARTRON SI-1260 spectrometer in the frequency range of 10–10⁶ Hz. A source of 1 V was applied to the electroded pellets. Temperature variation was performed using a Linkam TS 93 hot stage with a temperature stability of ±0.1 K. Platinum electrodes were deposited on two circular faces of the ceramic to get the capacitor-shaped samples.

3 Results and discussion

3.1 X-ray diffraction (XRD) analysis

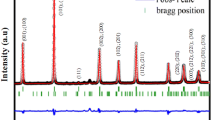
Figure 1 shows the obtained room temperature XRD pattern on BNNW025 ceramic made in previous work [5]. This figure shows an excellent agreement between the calculated and the observed diffractograms. The BNNW025 was refined basing on the tetragonal structure with the space group P4bm and refined in profile fitting mode using the FullProf software. Substituting the barium and the niobium by the sodium and the tungsten leads to a progressive decreasing of crystallographic parameters. The crystal structure of this composition is formed by an arrangement of octahedra (Nb/W)O₆ which constitute the basic skeleton of the structure. The Ba²⁺ and Na⁺ ions occupy the sites of coordination numbers 12 and 15 [4].

Fig. 1

X-ray diffraction patterns of the ceramic BNNW25

3.2 SEM micrograph

Figure 2 shows the SEM micrograph of the ceramic sample sintered at 1270 °C. The surface morphology shows the existence of polycrystalline microstructure comprising good grain growth with shape anisotropy. The grains of unequal size appear to be distributed inhomogeneously over the entire volume of the sample. As reveled from the histogram in the inset, the sample shows a narrow grain size distribution with average grain size of 2.8 µm.

Fig. 2

SEM micrograph of ceramic sintered at 1270 °C. The inset histogram shows the grains size distribution

3.3 Dielectric analysis

Dielectric measurements were taken on ceramic. These measurements have given the real and imaginary values of the BNNW025 dielectric permittivity ε _r expressed by: “$\varepsilon^{*} = \varepsilon^{\prime } + j\varepsilon^{\prime \prime }$’’, for various frequencies and temperatures. As it can be seen for the obtained results presented in Fig. 2, the broad maxima of $\varepsilon_{\text{r}}^{\prime }$ have been observed at the temperature T _c = 472 °C. The paraelectric–ferroelectric phase transition, which is observed around T _c, is diffused in nature, and wide frequency dispersion is observed in the dielectric constant in the paraelectric phase (Fig. 3). The observed diffusion is most likely caused by the domain walls or topological defects motion in the nucleating ferroelectric phase [6, 7].

Fig. 3

Temperature dependence of real part $\varepsilon_{\text{r}}^{\prime }$ of dielectric permittivity on heating

The dielectric permittivity at T _C changes as: $\varepsilon_{\text{r}}^{\prime } \left( {T_{\text{C}} } \right)$ = 1600, 1346, 940 and 774 at 50, 100, 500 and 1000 kHz, respectively. For frequencies range <50 kHz, the dielectric constant is very high at T _C and keeps ascending which is due to high space charge concentration at high temperatures.

Figure 4 shows the susceptibility $1/\varepsilon_{{\text{r}}}^{\prime }$ as function of temperature at 1 MHz for the BNNW025. Beyond T _c, the curve can be fitted by the linear Curie–Weiss law $\varepsilon_{\text{r}}^{\prime } = \frac{C}{{\left( {T - T_{0} } \right)}} \left( {T > T_{\text{c}} } \right)$. However, $\varepsilon_{{\text{r}}}^{\prime }$ starts to deviate from the Curie–Weiss law at the temperature noted T _b. This deviation from the linear behavior could be due to the non-uniform distribution of the critical temperatures in the ceramic sample. The following parameters are determined: T _c = 472 °C, T ₀ = 327 °C, C = 1.34 × 10⁵ K and ΔT = T _b − T _c = 15 °C. The large value of C, characteristic for oxygen octahedra ferroelectrics [8, 9], indicates that the transition is mostly of displacive type [10]. Otherwise, the small value of T ₀, when compared to the transition temperature T _c, is a characteristic feature of the first-order ferroelectric phase transition [11].

Fig. 4

Temperature dependence of inverse susceptibility $1/\varepsilon_{\text{r}}^{\prime }$ at 1 MHz

3.4 Diffusive nature of ferroelectric transition

The diffusive nature of the ferroelectric phase transition can be determined based on the Santos–Eiras phenomenological equation [12]:

$$\varepsilon_{\text{r}}^{\prime } = \frac{{\varepsilon_{\text{m}}^{\prime } }}{{1 + \left( {\frac{{T - T_{\text{m}} }}{\Delta }} \right)^{\gamma } }}$$

(1)

where $\varepsilon_{\text{m}}^{\prime }$ is the dielectric permittivity maximum, T _m is the temperature that corresponds to $\varepsilon_{\text{m}}^{\prime }$, γ indicates the character of the phase transition, and ∆ is the parameter that defines the transition diffuseness degree. If γ = 1, Eq. (1) fits a “conventional” first- or second-order ferroelectric phase transition, described by the Landau–Devonshire theory. If γ = 2, Eq. (1) represents the so-called complete DPT, described by Kirilov and Isupov [13]. For 1 < γ < 2, the transition is “incomplete”. This means that the interaction between nucleating ferroelectric clusters in paraelectric matrix begins far above Tm and plays an important role in its diffusive character [12].

The experimental results fit, modeled by Eq. (1) for T > T _m, is shown in Fig. 5. The used fitting parameters are illustrated in Table 1. The parameters γ for BNNW025 are found close to 1.45–1.95, which leads to the conclusion that DPT in BNNW025 is of “incomplete” nature. This behavior is often observed in TTB ceramics, whose explanation is related to the movement of domain walls in ferroelectric materials [6, 14].

Fig. 5

Temperature dependence of $\varepsilon_{\text{r}}^{\prime }$ at different frequencies. Solid lines present the theoretical fit of BNNW25

Table 1 Dielectric parameters obtained from Santos–Eiras’ equation

3.5 Complex impedance analysis

The polycrystalline ceramic materials heterogeneity is the origin of a large variety of frequency-dependent effects [15]. The bulk material properties can be separated from the grain, the grain boundaries and electrodes contribution using the frequency-dependent impedance spectroscopy. The main studied parameters are: complex dielectric permittivity $\varepsilon^{*}$, complex impedance $Z^{*}$, complex admittance $Y^{*}$ and dielectric loss tan δ defined by [16]:

$$\varepsilon^{*} = \varepsilon^{\prime } + j\varepsilon^{\prime \prime }$$

(2)

$$Z^{*} = Z^{\prime } - jZ^{\prime \prime } = \frac{1}{{j\omega C_{0} \varepsilon^{*} }}$$

(3)

$$Y^{*} = Y^{\prime } + jY^{\prime \prime } = j\omega C_{0} \varepsilon^{*}$$

(4)

$$\tan \delta = \frac{{\varepsilon^{\prime \prime } }}{{\varepsilon^{\prime } }} = \frac{{Z^{\prime } }}{{Z^{\prime \prime } }} = \frac{{Y^{\prime } }}{{Y^{\prime \prime } }}$$

(5)

where ω = 2πf is the pulsation (f is the frequency in Hz), C ₀ = ε ₀ S/e is the vacuum capacitance having the same electrodes surface S, the thickness e, and the permittivity ε ₀. Figure 6a, b illustrates the variation of the real and imaginary parts of impedance ($Z^{\prime }$ and $Z^{\prime \prime }$) versus frequency within the interval (10 Hz–1 MHz), for several values of temperature (T = 450 − 500 °C).

Fig. 6

Variation of a real ($Z^{\prime }$) and b imaginary (−$Z^{\prime \prime }$) parts of impedance versus frequency for different temperatures

It can be seen from Fig. 6a that, for low frequencies, the $Z^{\prime }$ magnitudes are large and decrease with the temperature. This can be explained by the space charge polarization. Nevertheless, for high frequencies, the $Z^{\prime }$ magnitudes are no more temperature dependent and decrease with frequency. This leads to ionic conductivity enhance.

Figure 6b shows that the $Z^{\prime \prime }$ magnitudes present peaks that shift toward high frequencies with the temperature increase indicating the relaxation time increase and the space charge loss [17].

Figure 7 illustrates the normalized imaginary part of the impedance ($Z^{\prime \prime } /Z_{ \hbox{max} }^{\prime \prime }$) as a function of frequency for values of temperature. The curve shows asymmetrical peak, indicating the ionic conductivity relaxation release at high temperatures.

Fig. 7

Normalized imaginary parts Z _i /Z _imax of impedance as a function of frequency for different temperatures

The relaxation time is defined by: τ _m = 1/ω _m, where ω _m is the peak position which obeys the Arrhenius low:

$$\omega_{\text{m}} = \omega_{0} e^{{ - \frac{{E_{\tau } }}{{k_{\text{B}} T}}}}$$

(6)

Figure 8 shows the relaxation time τ _m plotted versus the inverse of temperature.

Fig. 8

Arrhenius plot of temperature dependence of relaxation frequency

According to Eq. (6) and using the slope of log τ _m versus 1/T, the activation energy E _a can be estimated. Its value is approximately 0.56 eV in the paraelectric phase (T > T _c) and 0.80 eV in the ferroelectric phase (T < T _c).

To identify the contribution of grain, grain boundary and electrodes to the ceramic overall dielectric response, the impedance spectroscopy seems to be an interesting tool.

Figure 9 illustrates the equal axis Nyquist plot (−$Z^{\prime \prime }$ vs $Z^{\prime }$) for T = 450–500 °C in the (10–10⁶ Hz) frequencies range. When temperature increases, the semicircles become smaller and their centers shift toward lower |Z|. This indicates a reduction of grain and grain boundary resistance and negative temperature coefficient of resistance (NTCR) like in semiconductors [18, 19]. The semicircles are not perfect, but inclined with their centers placed below the real ($Z^{\prime }$) axis by an angle (α − 1)π/2, where 0 < α < 1 [20]. That means the relaxation phenomena are a non pure non-Debye type, because of relaxation time distribution.

Fig. 9

Nyquist plot at different temperatures of BNNW025 ceramics

To distinguish between the grains, grain boundaries and electrodes dielectric properties, the ceramic material can be modeled by a sequence of three parallel RC elements connected in series (Fig. 10). The first element model represents the grain dielectric properties, the second represents grain boundaries dielectric properties, and the last one represents electrodes dielectric properties.

Fig. 10

Complex impedance and deconvoluted plots (a). Equivalent circuit used for fitting experiment (b)

The complex impedance ($Z^{*}$) of a parallel RC element is given by:

$$Z^{*} = \frac{R}{{1 + \left( {j\omega RC} \right)}} = \frac{R}{{1 + \left( {j\omega \tau } \right)}}$$

(7)

where $\tau = RC$ is the relaxation time constant and $\omega$ is the angular frequency.

In the complex impedance plan plot, the frequency $\omega$ at which the semicircular arc maximum occurs is determined by the relaxation time constant $\tau$ and can be deduced from [21, 22]:

$$\omega_{\hbox{max} } = \tau^{ - 1} = (RC)^{ - 1}$$

(8)

The real and imaginary parts of the total impedance $Z^{*}$, versus the couples (resistances, capacitances) of grains (R _g, C _g), grain boundaries (R _gb, C _gb) and electrodes (R _e, C _e), can be expressed as:

$$Z^{\prime } = \frac{{R_{\text{g}} }}{{1 + \left( {\omega R_{\text{g}} C_{\text{g}} } \right)^{2} }} + \frac{{R_{\text{gb}} }}{{1 + \left( {\omega R_{\text{gb}} C_{\text{gb}} } \right)^{2} }} + \frac{{R_{\text{e}} }}{{1 + \left( {\omega R_{\text{e}} C_{\text{e}} } \right)^{2} }}$$

(9)

$$Z^{\prime \prime } = R_{\text{g}} \left( {\frac{{\omega R_{\text{g}} R_{\text{g}} }}{{1 + \left( {\omega R_{\text{g}} C_{\text{g}} } \right)^{2} }}} \right) + R_{\text{gb}} \left( {\frac{{\omega R_{\text{gb}} C_{\text{gb}} }}{{1 + \left( {\omega R_{\text{gb}} C_{\text{gb}} } \right)^{2} }}} \right) + R_{\text{e}} \left( {\frac{{\omega R_{\text{e}} C_{\text{e}} }}{{1 + \left( {\omega R_{\text{e}} C_{\text{e}} } \right)^{2} }}} \right)$$

(10)

R _g and R _gb could directly be obtained from the intersection with $Z^{\prime }$-axis. C _g and C _gb can be calculated using the relation:

$$f_{\hbox{max} } = \, 1/(2pt) \, = \, 1/(2pRC)$$

(11)

However, this mathematical model is valid exclusively for “ideal” systems, where the Nyquist plot is described by perfect semicircles with centers on the x-axis. In most materials, it is not the case: the semicircle centers are located below the real axis by a finite angle referred as the depression angle (α _d). This behavior is due to a distributing impedance response that is associated with a relaxation time spread. Thus, the classical Debye equation employing a single relaxation time cannot describe correctly the relaxation. This problem can be avoided by replacing the capacitor C in the equivalent schemes by a constant phase element (CPE) to account for the shape of the depressed semicircle [23, 24]. This is one of the most common and precise model of phenomena for ionic conductors having a contribution of bulk grain, grain boundary and electrodes [20].

The impedance of the constant phase element (CPE) is given by [23, 25]:

$$Z_{\text{CPE}} = \frac{1}{{Q\left( {i\omega } \right)^{p} }}$$

(12)

where $\omega$ is the angular frequency, Q and p are constants with $0 \le p \le 1$.

The constant phase element (CPE) corresponds to an ideal capacitor with C = Q for p = 1 and to an ideal resistor with $R = 1/Q$ for p = 0. Therefore, p can be used to represent the degree of perfection of the capacitor and represents a measure of arc distortion below the real impedance axis. The parameter p is related to the depression angle α _d as follow:

$$\alpha_{d} = (1 - p) \times \frac{\pi }{2}$$

(13)

The complex impedance ($Z^{*}$) of each element (CPE//R) is given by:

$$Z^{*} \left( \omega \right) = \frac{R}{{1 + RQ\left( {j\omega } \right)^{p } }} = \frac{R}{{1 + \left( {j\omega \tau } \right)^{p } }}$$

(14)

where $\tau^{p} = RQ$.

Then, Eq. (8) can be modified as:

$$\omega_{\hbox{max} } = \tau^{ - 1} = \left( {RQ} \right)^{ - 1/p}$$

(15)

The real and imaginary parts of impedance ($Z^{*}$) in the equivalent circuit become:

$$Z^{\prime} = \frac{{R\left( {1 + RT\omega^{p} \cos \left( {\frac{p}{2}} \right)} \right)}}{{1 + 2RT\omega^{p} \cos \left( {\frac{p}{2}} \right) + \left( {RT\omega^{p} } \right)^{2} }}$$

(16)

$$Z^{\prime\prime} = \frac{{R^{2} T\omega^{p} \sin \left( {\frac{p}{2}} \right)}}{{1 + 2RT\omega^{p} \cos \left( {\frac{p}{2}} \right) + \left( {RT\omega^{p} } \right)^{2} }}$$

(17)

Note that:

• The electrode impedance was found to be very small and will be further neglected.

• There are no series resistances that can be attached to the equivalent circuit since semicircles start from origin.

As a result, the resistance R and the parameters p and Q of the CPE are obtained for each temperature. The values of p are found between 0.95 and 0.98. The constant time τ of grain and grain boundary relaxation are then obtained using the relationship given in Eq. (15). The effective grain and grain boundary parameters R _g, R _gb as well as the relaxation times τ _g and τ _gb as functions of temperature are shown in Fig. 11a, b. When Q increases the R _gb is found to be less than R _g, which means that conductivity occurs through the grains boundaries. It is also understandable that relaxation times τ _g and τ _gb decrease with temperature. Plots of R _g and R _gb versus temperature respect the Arrhenius law. The slopes of these plots, collected in Table 2, give the conduction of the material and the relaxation activation energy for grains and grain boundaries. It follows that conduction mechanism is dominated by grains boundaries [26].

Fig. 11

Variation of resistance (a) and relaxation time of grain and grain boundary (b) with temperature BNNW025

Table 2 Activation energy values of conduction, relaxation for grain and grain boundary in BNNW025 ferroelectric phase

3.6 Conductivity

Figure 12 presents the frequency dependence of AC conductivity (σ _AC) at several temperatures. It shows a plateau at low frequencies and dispersion at high frequencies. The plateau region corresponding to DC conductivity is found to extend to higher frequencies when temperature increases [27]. The frequency at which the dispersion takes place, also known as hopping frequency, increases with temperature. This behavior suggests that electrical conductivity occurs via hopping mechanism, which is governed by the Jonscher’s power law [28]:

$$\sigma_{\text{AC}} = \, \sigma_{\text{DC}} + A \cdot \left( \omega \right)^{n} .$$

(18)

where, σ _DC is the direct current conductivity of the sample and ω is the angular frequency of measurement. The n parameter reflects the degree of interaction between mobile ions and the lattices around them, while A is a constant which introduces the polarizability strength.

Fig. 12

Frequency dependence of the AC conductivity at various temperatures of the BNNW25 compound

The experimental conductivity curves of the sample are fitted using Eq. (18). The fitting results are presented in Table 3.

Table 3 Nonlinear fitting data of the conductivity of BNNW025 compound

This table shows a decreasing tendency of n when temperature increases which is reasonable according to the model based on classical hopping of electrons over barrier. In addition and according to Funke [29], when the n value is equal to 1, it means that the hopping motion involves a translational motion with a sudden hopping and when n is greater than 1, it means that the motion involves localized hopping without the species leaving the neighborhood [30, 31]. The change of tendency in slope takes place at a frequency known as hopping frequency of the polarons (ω _p), which depends on temperature. The AC conductivity follows the Almonde West relation [32] as σ(ω) = Aω _p[1 + (ω/ω _p)ⁿ], where ω _p is the hopping frequency and n is the Jonscher’s constant [33]. In the literature [34] has been reported that σ _DC = Aω _p, so the relationship becomes σ(ω) = σ _DC[1 + (ω/ω _p)ⁿ]. The AC conductivity is calculated using the relationship σ = ωεε ₀tan δ. The plateau region of the conductivity at higher frequencies and temperatures may be linked to the space charge. This assumption is reasonable since the space charge effect vanishes at higher temperatures and frequencies. This typical behavior suggests the existence of hopping mechanism between the allowed sites.

4 Conclusion

In this paper, we worked on a new ferroelectric TTB structure ceramic compound Ba_2.15−x Na_0.7 + xNb_5−x W _x O₁₅ (BNNW025). It has been synthesized using the solid-state reaction method. Analyzing its ferroelectric phase transition shows a diffusive one, of displacive type.

The Santos–Eiras phenomenological model was used to study the characteristics of the ferroelectric-to-paraelectric phase transition in the compound at Curie temperature (472 °C). The studied parameters were: $\varepsilon_{\text{m}}^{\prime }$, T _m (°C), ∆ (°C) and γ.

Dielectric properties of the BNNW025 ceramic were as well analyzed and showed an “incomplete” DPT phase transition around the temperature of the maximum dielectric permittivity (diffusivity 1.66 < γ < 1.95). This phase transition can be explained by the intrinsic disorder of Barium sites and the TTB unit cells distortions.

Dielectric impedance spectroscopy analysis shows a non-relaxor type behavior and low frequency dispersion. However, the interaction between space charge polarization and the grain decreases at high frequencies.

Nyquist plots showed a non-Debye (polydispersive) type relaxation. Only grain and grain boundaries contribute to the impedance, while the effect of material electrode interface can be neglected. The activation energy was estimated from Arrhenius behavior in paraelectric region as 0.56 and 0.8 eV in ferroelectric region. The ac conductivity and dielectric behavior in BNNW025 have been studied also as function of frequency.

Such a new class of lead free ferroelectric Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅ is of great interest for environment-friendly applications. This work anticipates our future investigation of ferroelectric TTB family Ba_2.15−x Na_0.7+x Nb_5−x W _x O₁₅ that will allow to understand the mechanism of conduction in this ceramics and the effect of the substitution of Ba and Nb by Na and W on dielectric proprieties.