1 Introduction

Electroactive polymers (EAPs) are a rapidly developing class of ‘active’ and ‘smart’ materials that could produce actuation through deformations in response to both mechanical forces and applied electric fields [1–3]. Moreover, it is found that EAPs have attractive features including large actuation strains, low mass, high response speed and compliance [3–9]. As a typical class of EAPs, dielectric elastomer actuators (DEAs) have received increasing interests for applications in energy harvesting, artificial muscles, adaptive optical elements, soft robots and electromechanical actuators [1, 8–13]. Indeed, some aspects of DEAs have surprised us and cannot be explained by everyone’s common experience. For example, it has been reported that the strain in a statically deformed dielectric elastomer membrane (DEM) with a fully fixed frame may increase over 100 % in terms of in-plane extension before breakdown [14]. However, when the frame is replaced by a mechanical weight, the maximum strain may reach 380 % [15]. Therefore, the dynamical systems consisting of soft materials (e.g., dielectric elastomers) are becoming a new research topic in the field of mechanics of physics and solid.

The early theoretical models for DEAs adopted linear elasticity and free boundary conditions in predicting the behaviors of DEAs under small strains (<10 %) [16, 17]. In order to overcome the limitations of linear elasticity and small strain assumptions, various nonlinear models (see, e.g., [18]) describing DEA behaviors were developed based on hyperelasticity theories [19–21]. Moreover, in order to better predict the large deformation behavior of DEAs, some researchers tried to develop models based on the theory of thermodynamics [22].

The typical structure of DEAs is a soft dielectric membrane sandwiched between a pair of compliant electrodes [23]. DEAs are susceptible to an electromechanical instability when actuated electrostatically. Therefore, early studies on the electromechanical behavior of DEAs considered the static deformation [12, 24–26] by neglecting the effect of inertia. Researches on the electrostatic instability have been reported analytically as well as experimentally [16, 27, 28].

However, time-dependent voltages or mechanical forces are frequently applied to a DEA in experiments [29, 30] and practical applications [31]. In such cases, inertia can play a significant role in the performances of DEAs, and hence the dynamic analysis is necessary. In the past decade, indeed, considerable efforts in analyzing the dynamic responses of DEAs subjected to mechanical and/or electrical loadings have been exerted. Some interesting works considering the dynamic responses of DEAs include Zhu et al. [32, 33], Xu et al. [18], Li et al. [34, 35], Sheng et al. [36], Feng et al. [37], Zhang et al. [38, 39] and Keplinger et al. [2].

Because of their potential applications in artificial muscles, adaptive morphing wings and soft robots for the purpose of dynamic operations/motions [8, 31], DEAs usually have the initial state of a pre-stretched/pre-compressed deformation due to the initial disturbances. However, most previous works assumed the DEA system is activated from the rest configuration and chose an undeformed configuration as the initial stretch ratio when investigating the dynamic responses of DEAs under in-plane deformation. To the authors’ best knowledge, the effect of initial stretch ratio on the dynamic responses of DEAs has not been systematically addressed so far. To this end, this paper studies the dynamic responses of DEAs with stretching deformation under an electrical load, with particular interest of investigating the effect of various initial stretch ratios on the electromechanical behavior of such dynamical systems.

2 Analytical model

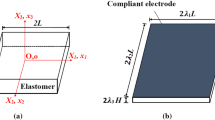
The DEA model under consideration is shown in Fig. 1. As plotted in Fig. 1a, the DE in the actuator in its reference state has an original size of 2L × 2L × 2H. Suppose that the DEA has a density ρ and it is incompressible, satisfying the incompressibility relation λ 1 λ 2 λ 3 = 1 (λ 1, λ 2 and λ 3 are the stretch ratios). Due to the symmetry in the x–y plane, the incompressibility relation may be further written as λ 1 = λ 2 = \(\lambda_{3}^{ - 1/2}\). For simplicity, we neglect the subscript of λ 3 and denote λ = λ 3 in the following analysis. It is also assumed that the stretch ratio λ is independent of the space variables and is only a function of time t [18]. Although the DEA is generally sandwiched between two electrodes, the electrodes are made of an even softer material, with mechanical stiffness much lower than that of the dielectric elastomer. Therefore, the current work assumes the mechanical stiffness of electrodes is negligible.

Fig. 1
figure 1

a The reference state of the DEA with the original size of 2L × 2L × 2H; b the excited state of the DEA with 2λ 1 L × 2λ 2 L × 2λ 3 H

Full size image

Next, to describe the behavior of the DEAs, we adopt a material model known as the ideal dielectric elastomer [40], where the dielectric behavior of the elastomer is taken to be liquid like, unaffected by deformation. Thus, the true electric displacement is linear in the true electric field, and the permittivity is independent of deformation. The elastomer is also taken to obey the Gaussian statistics, so that the elastic behavior of the elastomer is neo-Hookean [33]. As reported in [40, 41], such material model is able to explain some experimental data.

If the damping effect is either neglected or absent, by considering the kinetic energy and the Helmholtz free energy (elastic energy and dielectric energy) in the DEA system and using the Euler–Lagrange equation, the differential equation governing the oscillations of the DEAs for λ may be given by [18]

$$\frac{{{\text{d}}^{2} \lambda }}{{{\text{d}}t^{2} }} - \frac{3}{{2\lambda (1 + c_{1} \lambda^{3} )}}\left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}t}}} \right)^{2} +\, c_{2} \frac{{\lambda^{4} - \lambda + e}}{{1 + c_{1} \lambda^{3} }} = 0$$
(1)

in which c 1 = 2H 2/L 2 and c 2 = 6 μ/ρL2 are constants, with μ being the shear modulus of the DEA, and e is the normalized electrical load described by

$$e(t) = \frac{\varepsilon }{\mu }\left[ {E_{0} (t)} \right]{\kern 1pt}^{2}$$
(2)

where ε is the permittivity of the elastomer and E 0(t) = V/2H is the nominal electric field with V being the applied electric potential, which may be time dependent. For details on the derivation of Eq. (1), the reader is referred to Ref. [18].

Before closing this section, it should be mentioned that Eq. (1) is only valid for small to moderate stretch ratios. Zhao and Suo [42] have developed a model of nonideal dielectric elastomers, which is capable of predicting large deformations of DEAs and couples the quasilinear dielectric behavior with nonlinear elastic behavior.

3 Electromechanical responses of the DEAs

In the following, the dynamical behaviors of the DEA will be analyzed based on Eq. (1). Several system parameters utilized in the calculations are the same as those used by Xu et al. [18]: i.e., H = 1.0 × 10−3 m, L = 5.0 × 10−3 m, μ = 6.71 × 104 Pa, ρ = 1.2 × 103 kg/m3, ε = 6.198 × 10−11 F/m. The rate of initial stretch ratio is set to be \(\dot{\lambda }(0) = 0\). In the calculations, it is found that the initial stretch ratio of the DEA may significantly influence the dynamical behaviors of the system, as shown in the following.

Firstly, the case of constant electric loading is considered. In such a case, \(e = \varepsilon E_{0}^{2} /\mu\) is time independent. We plot a bifurcation diagram in Fig. 2 to show the detailed effect of initial stretch ratio on the minima and maxima of the DEA oscillations for several different values of E 0. In the calculations, the transient solutions of Eq. (1) were not considered. Then, whenever the oscillation velocity \(\dot{\lambda }(t)\) is zero, the oscillation displacement \(\lambda (t)\) was recorded, thus for a given E 0 producing two bifurcation branches in Fig. 2. It is seen from this figure that the system is usually experiencing periodic motions when the initial stretch ratio λ(0) is successively increased from 0.5 to 1.2. When E 0 = 0, it is easy to calculate the static equilibrium of Eq. (1) by ignoring the time-dependent terms. If the initial stretch ratio is chosen as λ(0) = 1, the DEA would keep static with λ(t) = 1 since the static equilibrium is found to be λ s  = 1. As shown in Fig. 2, the static equilibrium value of λ becomes smaller with increasing E 0. If λ(0) ≠ λ s , however, periodic oscillation fairly occurs. The phase portrait diagrams for two typical values of λ(0) are presented in Fig. 3.

Fig. 2
figure 2

Bifurcation diagram for the periodic oscillations of the DEA under constant nominal electric field E 0 = 0, 12, 18, and 20 kV/mm, respectively, for various initial stretch ratios

Full size image
Fig. 3
figure 3

Phase portraits for the periodic oscillations of the DEA with two different initial stretch ratios and E 0 = 0 kV/mm, showing the pronounced effect of initial stretch ratios

Full size image

Since the response of the DEA is periodic for λ(0) ≠ λ s , there exist a minimum value and another maximum value of λ(t) during one oscillation period. For example, when E 0 = 0 and λ(0) = 0.8, the minimum value of λ(t) is found to be λ(t)min = 0.8, as shown in Fig. 3. When E 0 = 0 and λ(0) = 1.1, the maximum value of λ(t) is found to be λ(t)max = 1.1.

Next, it is also interesting to see how the dynamical behavior of the DEA would evolve when the electrical load is time dependent. Unlike linear cases, the dynamic responses of the nonlinear DEA system under time-dependent electric loading may be very complicated. For calculation purpose, a harmonic electrical load E 0 = E a sin(Ωt) = E a sin(2πft) is applied to the DEA. The dependence of the DEA performance on the initial stretch ratio is investigated. The excitation amplitude (E a ) and frequency (f) of the electric loading are set to be E a  = 18.5 kV/mm and f = 300 Hz, respectively. With these parameter values and λ(0) = 1, the oscillation trajectory in the phase portrait diagram (see Fig. 4a) would be bounded in a reasonable region, and hence the vibration is stable. The Poincaré map plotted in Fig. 4b forms a closed loop, showing that the oscillation is quasiperiodic. The essential feature of such quasiperiodic oscillation may be further observed in the power spectra (PS) diagram, as shown in Fig. 4c.

Fig. 4
figure 4

Nonlinear oscillation of the DEA under harmonic electric excitation with E 0 = 18.5 kV/mm, f = 300 Hz and λ(0) = 1, showing a quasiperiodic motion; a phase portrait, b Poincaré map, and c Power spectra of the stretch ratio

Full size image

More calculations have shown that the dynamic responses of the DEA under harmonic electrical load may be significantly affected by the initial stretch ratio λ(0). The initial stretch ratio may be either decreased or increased gradually from λ(0) = 1. Typical results stressing the main qualitative features that may be observed are shown in Figs. 5 and 6.

Fig. 5
figure 5

Nonlinear oscillation of the DEA under harmonic electric excitation with E 0 = 18.5 kV/mm, f = 300 Hz and λ(0) = 0.75785, showing a chaotic motion; a phase portrait, b Poincaré map, and c Power spectra of the stretch ratio

Full size image
Fig. 6
figure 6

Nonlinear oscillation of the DEA under harmonic electric excitation with E 0 = 18.5 kV/mm, f = 300 Hz and λ(0) = 0.7578, showing a chaotic divergent motion (i.e., the numerical solution of the oscillation amplitude goes to infinitesimal with increasing time steps); a phase portrait, b Poincaré map, and c Power spectra of the stretch

Full size image

The results plotted in Fig. 5 are obtained with λ(0) = 0.75785, which is smaller than 1. It is seen from the phase portrait, Poincaré map and PS diagram that the oscillation of the DEA is chaotic-looking with frequency content of relatively wide band. The Poincaré map of Fig. 5b has spread out and contains an infinite number of points, yet the map does not fill the space.

Moreover, when λ(0) is slightly below 0.75785, e.g., λ(0) = 0.7578, the oscillation would become unstable, as seen in Fig. 6. Overall, the phase plane portrait shown in Fig. 6a is different from that in Fig. 5a. The phase portrait of Fig. 6a suggests a chaotic motion for a time. However, the oscillation eventually becomes a divergent oscillation. Here, this transient chaos is termed as “chaotic divergence.” It is also noted that the divergent trajectory eventually moves towards to zero value of λ. This implies that extreme contraction in height of the DEA would occur. Consequently, the DEA is undergoing a blowup in length. Such a divergent oscillation of the DEA is unstable.

Indeed, when λ(0) is increased from 1 to a relatively large value, chaotic divergent oscillation is also possible. For example, if the initial stretch ratio is gradually increased to λ(0) = 1.741495, chaotic divergence could occur.

In Figs. 5 and 6, the excitation frequency (f) of the electrical load is fixed to be 300 Hz. When f is varied, it is expected that the oscillation of the DEA may be either stable or unstable (i.e., the DEA undergoes a divergent oscillation). Evidently, the stability of the oscillation is still related to the initial stretch ratio considered. Thus, the parameter region in the (f, λ(0)) plane might be divided into a network with certain steps of f and λ(0), and then numerical simulations were carried out by solving Eq. (1) directly at every net point. By summarizing the obtained results, one can divide approximately the parameter region into two subregions according to the different behaviors of the DEA, as shown in Fig. 7. It reveals that the instability boundaries of the oscillations occurred in the ranges of 100 Hz < f < 300 Hz and 0.4 < λ(0) < 2.5. For a specific excitation frequency, there exists a certain range of λ(0) within which the oscillation is stable. In the case of f = 150 Hz or f = 250 Hz, in fact, it is seen that the oscillation is stable for moderate values of λ(0), while it is unstable for small and large values of λ(0). However, in the case of f = 190 Hz, it is recognized that when λ(0) is gradually increased from 0.4 to 2.5, the oscillations of the DEA would follow a instability–stabilization–instability–restabilization–reinstability sequence. Such a complex evolution of the DEA oscillations, once again, demonstrates the dramatic effect of initial stretch ratio on the dynamical behavior of the system.

Fig. 7
figure 7

Stability region in the (f, λ(0)) plane for the dynamical behavior of the DEA with E 0 = 18.5 kV/mm. The DEA with system parameters within the unstable region is subjected to a chaotic divergent oscillation

Full size image

4 Conclusions

This paper mainly investigates the nonlinear dynamics of DEAs subjected to an electrical load with the consideration of initial stretch ratio effect. The results show that the initial stretch ratio has significant influence on the dynamical behaviors of the DEA system, especially in the case when the DEA is subjected to a harmonic electric loading, resulting in quasiperiodic, chaotic, and chaotic divergent oscillations. The occurrence of chaotic divergent oscillations implies that the dynamical system becomes unstable from a viewpoint of dynamics. Consequently, issues on predicting such a type of DEA failure are of significant importance in applications of DEAs. We hope that our theoretical predictions, e.g., quasiperiodic, chaotic and chaotic divergent oscillations, can be validated by future experimental observations.

Another important issue for the DEAs is about the possibility of dielectric breakdown, which is not considered in this work. Is it possible that the DEAs fail by dielectric breakdown before they show chaotic divergent oscillations? This needs further theoretical and experimental investigations.