1 Introduction

Graphene is a one-atom-thick layer of graphite with hexagonal lattice structure, which attracted a lot of research attention due to its excellent strength, flexibility, and electrical/thermal conductivity [1–3]. Graphene can be obtained by micromechanical cleavage or repeatedly peeling process with adhesive tape [4, 5]. Recently, graphene has been recognized as a promising novel material applicable in flexible displays, optical devices, chemical sensing, biosensors, ultra-capacitors, super-small transistors, and flash-like memory [2, 4, 6, 7]. For advance application, it is important to have some understanding about mechanical properties of graphene or graphite so that further development would become feasible.

Some experimental attempts [8–10] have been performed to characterize the properties of graphene. However, it still remains a challenge for experimentalists to carry out test and analyze experimental data at such small scale. Both theoretical [11, 12] and numerical methods, e.g., atomistic-continuum modeling [13, 14], first principle method [15], and molecular dynamics simulation [16–19], have been employed to investigate the elastic properties of graphene or graphite. Li and Chou [13] proposed a structural mechanics method combined with molecular mechanics, which replaced the C–C bonds by an equivalent beam based on deformation energy equivalence. Shokrieh and Rafiee [11] presented analytical formulations to predict Young’s moduli of graphene sheets using a linkage between lattice molecular structure and equivalent discrete frame structure proposed by Li and Chou [13]. Hwu and Yeh [12] derived explicit closed-form expressions of mechanical properties for graphene and carbon nanotubes on the basis of force constants of carbon covalent bonding. Contrary to single bond equivalent concept, Cheng and Shi [14] developed the stick-spiral models based on the energy equivalence with the graphene basic cell and found that their model could provide more accurate elastic properties of graphene, especially the Poisson ratio, than the existing molecular structural mechanics models.

Molecular dynamics method has become a widely used atomic-scale simulation scheme with obvious advantage of dealing with complicated and relatively large atom systems. Several molecular dynamics simulations were implemented to examine the thickness and chirality effects on mechanical properties of graphene/graphite. Mortazavi et al. [18] studied the mechanical response of bulk graphite and few-layer graphene consisting of 2–7 atomic planes and found that the bonding strength between neighboring layers improved by increasing of the number of graphene layers, which would reduce the elastic modulus and ultimate strength. Ni et al. [19] investigated both the elastic and fracture behaviors of finite-size graphene sheet along different directions, and they observed that the fracture strain and the rupture process was loading direction dependent. Unlike the theoretical derivations and structural mechanics modeling, molecular dynamics simulations could directly deal with nonlinear interatomic interactions and large deformation condition. However, the computational efficiency of molecular dynamics method still restricts the simulated system size.

In this study, we proposed to examine the mechanical properties of both infinite graphene sheet and bulk graphite under small and large deformation based on molecular mechanics method. Instead of replacing the interatomic bonding with energy equivalent continuum structure, the deformation energy of the graphene/graphite under loading would be directly related to the bond changes. Considering the representative unit cell, the changes of bond lengths and angles under uniform loadings could be realized numerically under the geometry relations and minimum energy assumption. Various loadings, e.g., uniaxial, biaxial, simple tension, and pure shear, could be applied on the representative unit cell in order to extract the elastic properties of graphene/graphite at small deformation. Moreover, the fracture behavior of graphene/graphite along different loading directions would be studied as well.

2 Theoretical modeling

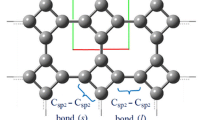
Both graphene and graphite are consisted by carbon hexagonal honeycomb lattice structure as shown in Fig. 1. The graphite is composed of interlacing graphene sheets. From the viewpoint of molecular mechanics, the carbon atoms are taken as mass points and the interaction between atoms could be described by force fields. The interactions energy between covalent-bonded atoms was firstly introduced by Cornell et al. [20] as

$$U = U_{\rho } + U_{\theta } + U_{\omega } + U_{\tau } + U_{\text{vdw}} + U_{\text{es}}$$
(1)

where U ρ , U θ , U ω , and U τ are bonded energies of stretching, angle, inversion, and torsion, respectively; U vdw and U es are energies of non-bonded van der Waals interaction and electrostatic interaction. Regarding the in-plane loading of graphene, the energies of bond inversion and torsion, which involve out-of-plane deformation, are negligible. Moreover, the non-bonded interactions, i.e., van der Waals interaction and electrostatic interaction, have less contribution on a covalent system and will be neglected in the graphene sheet as well. Hence, the total interatomic potential energy is mainly contributed by bond stretching and angle variation for graphene, which can be described by spring models as

$$U = \frac{1}{2}\sum {K_{r} \left( {\Delta r} \right)^{2} } + \frac{1}{2}\sum {K_{\theta } \left( {\Delta \theta } \right)^{2} }$$
(2)

where ∆r and ∆θ are the changes of bond length and bond angle from the equilibrium state; K r and K θ are the corresponding force constants of bond stretching and angle variation. For the consideration of bulk graphite, the non-bonded van der Waals interactions will be included in the interatomic potential energy.

Fig. 1
figure 1

Schematic illustration of a 2D graphene and b 3D graphite

Full size image

2.1 2D graphene

First, consider an infinite graphene sheet under in-plane uniform loading; it is obvious that every hexagonal lattice would deform in the same way. Hence, we could consider the deformation of a representative unit cell, instead of the whole graphene sheet. The representative unit cell of the graphene, as shown in Fig. 2a, is chosen as the smallest periodic cell which could yield behavior representative of the whole. At equilibrium, the equilibrated C–C bond length, a, and bond angle, θ, of the graphene are 1.42 Å and \(\frac{2}{3}\pi\), respectively; the side lengths of the representative unit cell, L x and L y , are \(\sqrt 3 a\) and 3a. We will consider two types of in-plane uniform loadings, i.e., biaxial and shear. Assume the graphene is sustaining biaxial loading, ɛ x and ɛ y , as shown in Fig. 2b, the deformation of the representative unit cell could be described by two bond lengths, a x and a y , and two bond angles, α and β, due to symmetry and periodicity. The angle between the bond lengths, a x and a y , is denoted as α and that between the bond lengths, a x and a x , is named as β. Under biaxial loading, i.e., given ɛ x and ɛ y , there are three geometry constraints needed to be satisfied.

Fig. 2
figure 2

Schematic illustrations of graphene a at equilibrium and b under biaxial loading (The representative unit cell is indicated by red dash line)

Full size image
  1. 1.

    Angle relation

    $$2\alpha + \beta = 2\pi$$
    (3)
  2. 2.

    Length condition along y-direction

    $$L_{y} \left( {1 + \varepsilon_{y} } \right) = L_{y} +\Delta L_{y} = 2a_{y} + 2a_{x} \cos \frac{\beta }{2}$$
    (4)
  3. 3.

    Length condition along x-direction

    $$L_{x}^{2} \left( {1 + \varepsilon_{x} } \right)^{2} = \left( {L_{x} +\Delta L_{x} } \right)^{2} = 2a_{x}^{2} \left( {1 - \cos \beta } \right)$$
    (5)

where ∆L x,y is the unit cell length variation along x- and y directions under biaxial strains, ɛ x and ɛ y . The total deformation energy of the representative unit cell caused by the biaxial loading can be expressed as

$$U = 4 \times \frac{1}{2}K_{r}\Delta a_{x}^{2} + 2 \times \frac{1}{2}K_{r}\Delta a_{y}^{2} + 8 \times \frac{1}{2}K_{\theta }\Delta \alpha^{2} + 4 \times \frac{1}{2}K_{\theta }\Delta \beta^{2}$$
(6)
$$\Delta a_{x} \left( {\Delta a_{y} } \right) = a_{x} \left( {a_{y} } \right) - a$$
(7)
$$\Delta \alpha \left( {\Delta \beta } \right) = \alpha \left( \beta \right) - \frac{2}{3}\pi$$
(8)

where ∆a x,y and ∆α(∆β) are bond length and angle changes from the equilibrium values. In order to prevent double counting the deformation energy of the graphene, only the energies contributing by six bond length changes and 12 angle variations are included due to the periodicity. Here in this research, it is assumed the force constants K r = 6.517 × 10−18 J Å−2 and K θ = 8.754 × 10−19 J [20]. At equilibrium, the total deformation energy of the unit cell is obviously zero. The deformation of the representative unit cell could be described by six unknowns, i.e., ∆L x , ∆L y , a x , a y , α and β. Given the biaxial loading strains, ɛ x and ɛ y , combining with three geometry constraint conditions, it is still required to have one more equation in order to realize the deformation of the unit cell. It is assumed that the changes of bond lengths and angles will make the total deformation energy of the representative unit cell minimum. Under minimum energy assumption, all the six unknowns that illustrate the bond length/angle changes under biaxial loading could be easily figured out, and thus, the deformation energy of the unit cell could be computed as well.

Therefore, the elastic properties of the graphene could be calculated based on small loading strains and deformation energy density. Besides, it is also straightforward to work out the deformation of the graphene under uniaxial loading (given ɛ x , zero ɛ y ; given ɛ y , zero ɛ x ), which is the special case for in-plane biaxial loading. As for simple tension loading (given ɛ x , zero σ y ; given ɛ y , zero σ x ), either ∆L x or ∆L y is given. Combined with three geometry constraint conditions, we need to determine two unknowns based on minimum energy assumption. Nelder–Mead multidimensional unconstrained minimization method is adopted to find the two parameters that would minimize the total deformation energy of the representative unit cell. Thus, the deformation of the graphene under simple tension loading could be determined.

Similarly for pure shear uniform loading, γ xy , as shown in Fig. 3a, the deformation of the representative unit cell could be described by three bond lengths, a x1, a x2, a y and three bond angles, α 1, α 2, β. Since it is pure shear loading, the side lengths, L x and L y , of the unit cell would remain the same. However, the bond length/angle changes need to satisfy some geometry constraints under the limitation of periodic and symmetric conditions. These constraints are

Fig. 3
figure 3

Schematic illustrations of graphene under pure shear loading. a The unit cell and b the top half of the unit cell (The representative unit cell is indicated by red dash line)

Full size image
  1. 1.

    Length condition

    $$\frac{1}{2}L_{y} \cos \gamma = L_{1} \cos \theta_{1} + a_{y} \cos \theta_{2}$$
    (9)
    $$\frac{1}{2}L_{y} \sin \gamma = L_{1} \sin \theta_{1} + a_{y} \sin \theta_{2}$$
    (10)
  2. 2.

    Bond length conditions

The geometry relations of bond length, a x1 and a x2, can be generated by using the law of cosines applied to the angle \(\angle ADB\) and \(\angle A^{\prime} DB\) of the triangles ∆ADB and ∆A′DB as shown in Fig. 3b

$$a_{x1}^{2} = L_{1}^{2} + \left( {\frac{{L_{x} }}{2}} \right)^{2} - 2L_{1} \left( {\frac{{L_{x} }}{2}} \right)\cos \left( {\frac{\pi }{2} + \theta_{1} } \right)$$
(11)
$$a_{x2}^{2} = L_{1}^{2} + \left( {\frac{{L_{x} }}{2}} \right)^{2} - 2L_{1} \left( {\frac{{L_{x} }}{2}} \right)\cos \left( {\frac{\pi }{2} - \theta_{1} } \right)$$
(12)
  1. 3.

    Bond angle conditions

The geometry relations for bond angles, α 1, α 2, and β, can be expressed using the law of cosines applied to the angle \(\angle ABD\), \(\angle A^{\prime } BD\) and \(\angle ABA^{\prime }\) of the triangles ∆ADB, ∆A′DB, ∆ABA′

$$\left( {\frac{{L_{x} }}{2}} \right)^{2} = a_{x1}^{2} + L_{1}^{2} - 2a_{x1} L_{1} \cos \left( {\pi - \alpha_{1} - \left( {\theta_{1} - \theta_{2} } \right)} \right)$$
(13)
$$\left( {\frac{{L_{x} }}{2}} \right)^{2} = a_{x2}^{2} + L_{1}^{2} - 2a_{x2} L_{1} \cos \left( {\pi - \alpha_{2} - \left( {\theta_{1} - \theta_{2} } \right)} \right)$$
(14)
$$L_{x}^{2} = a_{x1}^{2} + a_{x2}^{2} - 2a_{x1} a_{x2} \cos \beta$$
(15)

The total deformation energy caused by pure shear loading due to the changes of the bond lengths and bond angles in the unit cell can be expressed as

$$U = 2 \times \frac{1}{2}K_{r}\Delta a_{x1}^{2} + 2 \times \frac{1}{2}K_{r}\Delta a_{x2}^{2} + 2 \times \frac{1}{2}K_{r}\Delta a_{y}^{2} + 4 \times \frac{1}{2}K_{\theta }\Delta \alpha_{1}^{2} + 4 \times \frac{1}{2}K_{\theta }\Delta \alpha_{2}^{2} + 4 \times \frac{1}{2}K_{\theta }\Delta \beta^{2}$$
(16)
$$\Delta a_{x1} \left( {\Delta a_{x2} } \right) = a_{x1} \left( {a_{x2} } \right) - a$$
(17)
$$\Delta \alpha_{1} \left( {\Delta \alpha_{2} ,\Delta \beta } \right) = \alpha_{1,2} \left( {\alpha_{2} ,\beta } \right) - \frac{2}{3}\pi$$
(18)

The number of variables used in describing the deformation of the unit cell under pure shear is 10 (L 1, θ 1, θ 2, a x1, a x2, a y , α 1, α 1, β, and γ). Given the shear strain, γ, combining with seven geometry constraint equations, we could reduce the number of unknowns to two in order to realize the deformation of the unit cell. Nelder–Mead multidimensional unconstrained minimization method is employed to find these two parameters that would minimize the deformation energy of the unit cell. Consequently, the shear properties of the graphene could be calculated based on the deformation energy density under small strain loading. However, it is worth to mention that the deformation of the representative unit cell under either biaxial or shear loading could be realized irrespective of small or large strain. The fracture strain could be predicted using the critical bond length as the fracture criteria. It is assumed that the bond would break when the bond length reaches 1.83 Å [19].

2.2 3D graphite

The infinite bulk graphite consisting of interlocking layers of graphene sheets (types A and B) is shown in Fig. 1b and the representative unite cell for 3D graphite is periodic in both in-plane and out-of-plane directions as illustrated in Fig. 4. The interlayer distance, d, between each graphene layer is the same. The initial positions of eight carbon atoms in the unit cell are \(A_{1} \left( {0, \frac{{L_{y} }}{2} - a_{y} , \frac{3}{2}d} \right),\,A_{2} \left( {0, \frac{{L_{y} }}{2}, \frac{3}{2}d} \right),\,A_{3} \left( { \frac{{L_{y} }}{2}, L_{y} - a_{y} , \frac{3}{2}d} \right),\,A_{4} \left( { \frac{{L_{x} }}{2}, L_{y} , \frac{3}{2}d} \right),\) \(B_{1} \left( {0, \frac{{L_{y} }}{2} + a_{y} , \frac{1}{2}d} \right),\,B_{2} \left( {0, \frac{{L_{y} }}{2}, \frac{1}{2}d} \right),\,B_{3} \left( { \frac{{L_{y} }}{2}, a_{y} , \frac{1}{2}d} \right),\) and \(B_{4} \left( {\frac{{L_{x} }}{2}, 0, \frac{1}{2}d} \right)\). The positions of all the other atoms in the graphite could be easily figured out by stacking the unit cell along x, y, z directions with translational distances, L x , L y , and 2d. The van der Waals force is much weaker than the covalent bonding force. Thus, van der Waals interaction is only considered for atoms locating at different graphene layers and neglected for those at the same layers. The long-range van der Waals interaction can be expressed by Lennard–Jones potential function as

$$U_{\text{vdw}} = 4\varepsilon \left[ {\left( {\frac{{r_{0} }}{r}} \right)^{12} - \left( {\frac{{r_{0} }}{r}} \right)^{6} } \right]$$
(19)

where the parameters, ɛ and r 0, are 3.8630 × 10−22 J and 3.4 Å [21], respectively. The equilibrium distance between graphene layers is not necessary equal to 3.4 Å, and the equilibrated bond length might not remain as 1.42 Å while taking van der Waals interaction into account. The bond angel of the graphite at equilibrium will still remain as \(\frac{2}{3}\pi\) due to threefold symmetry. The equilibrium distance and bond length, a, in graphite can be determined under the assumption of minimum energy numerically. However, it is not feasible to consider van der Waals interactions between all atom pairs for the pair number would increase as O(N 2). Since the energy contribution from far away atoms is negligible due to the rapid decay of attractive part of van der Waal force, only the atom pairs within certain distance need to be considered. Hence, convergence test on the number of the nearest atom pairs across graphene layers would be performed in order to attain the equilibrium interlayer distance and bond length in graphite.

Fig. 4
figure 4

Schematic diagram of the graphite representative unit cell. a Side view and b top view

Full size image

In order to obtain the elastic properties of the graphite, either in-plane biaxial, shear or out-of-plane loading would be applied to the equilibrated unit cell. It is reasonable to recognize that each graphene layer inside the graphite representative unit cell would be indifferentiable, that is the deformation at each graphene layer would be the same. The solution procedure of determining the deformation under in-plane loading is similar to 2D graphene model except with one more unknown, the interlayer distance d. For in-plane biaxial loading (given ɛ x , ɛ y , zero σ z ), the total strain energy of the graphite unit cell can be expressed as

$$U = 2 \times \left( {4 \times \frac{1}{2}K_{r}\Delta a_{x}^{2} + 2 \times \frac{1}{2}K_{r}\Delta a_{y}^{2} + 8 \times \frac{1}{2}K_{\theta }\Delta \alpha^{2} + 4 \times \frac{1}{2}K_{\theta }\Delta \beta^{2} } \right) +\Delta U_{\text{vdw}}$$
(20)

where ∆U vdw is the van der Waals energy change after loading. Since there are two graphene layers inside the graphite representative unit cell, the deformation energy due to bond length/angle changes is double. The deformation of the unit cell (i.e., ∆α x , ∆α y , ∆α, ∆β, and d) could be numerical determined under the minimum energy assumption. The situation is similar for in-plane pure shear loading (given γ xy , zero ɛ x , ɛ y , σ z , γ xz , γ yz ).

As for out-of-plane pure shear loading (given γ xz or γ yz ), the deformation is only the relative displacement between different graphene layers along x or y direction. Hence, there is no bond length variation in the in-plane direction, i.e., zero ɛ x , ɛ y , and the height, 2d, of the graphite unit cell, would remain the same, i.e., zero ɛ z . Similar energy minimization scheme could be applied to compute the interlayer distance change and the deformation energy under the applied strain.

3 Results and discussion

The displacements of atoms, determining by bond lengths and angles, inside the representative unit cell of both two-dimensional graphene and three-dimensional graphite were calculated purely from the atomic bonding (stretching and bending) and non-bonding (van der Waal) energies using molecular mechanics method. Various loading conditions were applied to extract the elastic properties of graphene/graphite at small deformation and examine their fracture behaviors at large loading.

3.1 2D graphene

The strain energy density of the graphene under various loading conditions can be calculated based on minimum energy assumption as

$$u = \frac{U}{{L_{x} L_{y} d_{0} }}$$
(21)

where d o is the thickness of graphene and taken as 3.4 Å. Since graphene is a single-layer material, the elastic stiffness matrix can be simplified as

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{16} } \\ {C_{12} } & {C_{22} } & {C_{26} } \\ {C_{16} } & {C_{26} } & {C_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\}$$
(22)

The relation between strain energy density and strains can be expressed as

$$u = \int {\sigma_{x} d\varepsilon_{x} } + \int {\sigma_{y} d\varepsilon_{y} } + \int {\sigma_{xy} d\gamma_{xy} }$$
(23)

The elastic constants of graphene can be calculated from various in-plane loadings. Take uniaxial loading in x direction (given ɛ x , zero ɛ y , γ xy ) as an example, the strain energy density can be written as \(u = \frac{1}{2}C_{11} \varepsilon_{x}^{2}\). Figure 5 illustrates the relation between strain energy density of the graphene and the applied strain under uniaxial and simple tension loadings along both in-plane (x and y) directions. From our molecular mechanics calculation, it is clear to observe that strain energy density, u, is proportional to ɛ 2 at small deformation (strain < 0.001) and directional independent. At larger strain, the strain energy density is always higher while the load is applied along x direction than along y direction under the same strain for both uniaxial and simple tension loadings.

Fig. 5
figure 5

Relations between strain energy densities and applied strains under a uniaxial and b simple tension loading (Dash line indicates loading along x direction; solid line represents tension along y direction)

Full size image

Hence, the stiffness matrix of the graphene could be computed under various small strain loading conditions based on molecular mechanics as

$$\left[ C \right] = \left[ {\begin{array}{*{20}c} {870.4} & {236.7} & 0 \\ {} & {870.4} & 0 \\ {({\text{symm}})} & {} & {317.2} \\ \end{array} } \right] \;\left( {\text{GPa}} \right)$$
(24)

It is noticed that the elastic constants are the same along both in-plane directions. If simple tension is applied on the zigzag edge of the unit cell, i.e., given ɛ x and zero σ y , γ xy , Young’s modulus of the graphene could be calculated from strain energy density, \(u = \frac{1}{2}E_{x} \varepsilon_{x}^{2}\), and Poisson’s ratio relating to transverse contraction could be figured out from the deformation of the unit cell (∆L x , ∆L y ). It is found that the Young’s moduli (E x , E y ) and Poisson’s ratios (ν xy , ν yx ) of the graphene are 805.6 GPa and 0.27, respectively. It is observed that the shear modulus, C 66, Young’s modulus, and Poisson’s ratio satisfy the relation \(C_{66} = \frac{E}{{2\left( {1 + \nu } \right)}}\), which indicates that the graphene is in-plane isotropic. Furthermore, our calculated Young’s moduli and Poisson’s ratios are consistent with the values based on the closed-form solution derived in the literature [12] and stick-spiral model [14] while adopting the same set of force constants.

Since the deformation of the graphene under loading could be determined under minimum energy assumption, it is interesting to examine the strain distribution inside the unit cell if the conventional strain definition is adopted. The atom arrangement is discrete and not symmetric in y direction. Hence, the unit cell is divided into two zones based on geometry similarity as shown in Fig. 6a. The normal and shear strain at each zone are defined following the conventional definitions as

Fig. 6
figure 6

a The illustration of the divided zones based on geometry similarity. The strain distributions at two zones under b simple tension loading along y direction and c pure shear strain

Full size image
$$\varepsilon_{y}^{(1)} = \frac{{\left( {a_{x} \cos \frac{\beta }{2} - \frac{1}{2}a} \right)}}{{\frac{1}{2}a}},\;\varepsilon_{y}^{(2)} = \frac{{\left( {a_{y} - a} \right)}}{a},\;\gamma_{xy}^{(1)} = \theta_{1} ,\;\gamma_{xy}^{(2)} = \theta_{2}$$
(25)

Figures 6b and c show the strain distributions of these two zones under simple tension loading along y direction and pure shear. It is obvious to notice that the strain along y direction is not uniform inside the unit cell and becomes nonlinear when the applied strain is large. Zone 1 is more flexible under simple tension but stiffer under shear loading as compared to zone 2.

The fracture strain for graphene can be estimated based on fracture criteria of critical bond length, at which the bond will tend to break. The critical bond length is assumed as 1.83 Å [19]. Here, the fracture strains under simple tension along two in-plane directions could be predicted.

The bond lengths of graphene subjected to simple tension loading could be evaluated based on minimum energy assumption and the bond length changes (∆a x , ∆a y ) under different strains are shown in Fig. 7. The dotted line indicates the critical bond length change, from which the fracture strain could be determined. It is also noticed that one of the bonds (a y ) almost remain the same as the equilibrium bond length and a x bond would break first while loading on armchair edge, i.e., x direction. The a y bond would reach critical bond length faster when loading on zigzag edge. Moreover, the fracture strains are 0.43 and 0.38, respectively, while loading on armchair and zigzag edges of graphene. This trend is consistent with the observation in molecular dynamics simulation [19].

Fig. 7
figure 7

Bond length changes of graphene under simple tension loading on a armchair and b zigzag edges

Full size image

The fracture behavior of graphene is directional dependent while contrasting to the elastic behavior. Moreover, it is worth to point out that the estimation of fracture strain is not limited to simple tension loading. Similar prediction on fracture strain based on critical bond length could be applied to various loading conditions, e.g., shear, biaxial, combined loadings, and simple tension along various chiral directions.

3.2 3D graphite

In order to determine the equilibrium layer distance and bond length in graphite, various nearest atom pairs across graphene layers were considered. Figure 8 illustrates the convergence test on the number of nearest atom pairs across graphene layers. It is found that the equilibrium interlayer distance would converge to 3.391 Å after considering sixth nearest atom pairs. Therefore, van der Waals energy is considered up to sixth nearest atom pairs across graphene layers in the following study. The equilibrating bond length of graphite is calculated as 1.419 Å, which is slightly shorter than the one in graphene.

Fig. 8
figure 8

Calculated equilibrium interlayer distance while considering nth nearest atom pairs across graphene layers

Full size image

After obtaining the equilibrium state of graphite, various in-plane and out-of-plane loadings could be applied to extract the elastic properties of graphite. The graphite is an orthotropic material, at which we could find three orthogonal planes of symmetry. Thus, the elastic matrix of the graphite can be written as

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ \end{array} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{11} } \\ {} \\ {} \\ \end{array} } \\ {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{12} } \\ {C_{22} } \\ {} \\ \end{array} } \\ {} \\ {({\text{symm}})} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{13} } \\ {C_{23} } \\ {C_{33} } \\ \end{array} } \\ {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {C_{44} } \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ {C_{55} } \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ {C_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ \end{array} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\}$$
(26)

There are nine independent elastic moduli that could be computed from the relation of the deformation energy and strain under various loadings using molecular mechanics. The variations in bond length, bond angle, and interlayer distance were estimated under minimum energy assumption. For example, the elastic constants C 44 and C 55 could be calculated from out-of-plane pure shear loading. Hence, the stiffness matrix of the graphite could be obtained as

$$[C] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {871.6} \\ {} \\ {} \\ \end{array} } \\ {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {234.2} \\ {870.8} \\ {} \\ \end{array} } \\ {} \\ {({\text{symm}})} \\ {} \\ \end{array} \begin{array}{*{20}c} { \begin{array}{*{20}c} {4.175} \\ {4.173} \\ {26.48} \\ \end{array} } \\ {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {0.101} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ {0.101} \\ {} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ {318.2} \\ \end{array} } \right]\;\left( {\text{GPa}} \right)$$
(27)

It is found that the graphite meets the definition of transversely isotropic material, i.e., C 11 ≅ C 22, C 13 ≅ C 23, C 44 ≅ C 55, \(C_{66} \cong \frac{{C_{11} - C_{12} }}{2}\). The axis of symmetry, with respect to which the material has identical properties, is along out-of-plane direction, i.e., z axis. The in-plane elastic constants of graphite are approximately equal to those of graphene. The elastic stiffness is much smaller in out-of-plane direction since the interlayer carbon atoms are van der Waals interaction, which is much weaker than covalent bonding in the in-plane direction. Similarly, Young’s moduli and Poisson ratios of graphite can be obtained by simple tension on the representative unit cell as E x  ≅ E y  = 808 GPa, E z  = 26 GPa, ν xy  ≅ ν yx  = 0.27, ν xz  ≅ ν yz  = 0.12, ν zx  ≅ ν zy  = 0.004. It is clear to see that the van der Waals interaction between layers does not significantly influence the in-plane elastic properties. The in-plane Young’s moduli of graphite are only slightly higher than those of graphene. Moreover, the predicted in-plane fracture strain of graphite is similar to that of graphene, which depends on the loading direction. We did not consider out-of-plane fracture in current research. Since the out-of-plane loading would not have much effect on the in-plane carbon bonds, different fracture criteria needs to be imposed in order to predict the fracture strain.

It is worth to mention that our molecular mechanics method could be applied to calculate both small and large deformation of graphene and graphite, i.e., elastic and fracture behavior. Even though we did not obtain an analytical expression for elastic constants, the elastic properties could be easily estimated numerically with the atomic interaction strength (K r , K r , ɛ and r 0). Furthermore, the bond length or angle change is nonlinear at larger strain, which could be captured using the proposed method.

4 Conclusions

In this study, the representative unit cell of 2D graphene and 3D graphite were considered, and the deformation of the unit cell under various uniform loading conditions, e.g., in-plane/out-of-plane, biaxial/shear, could be realized based on molecular mechanics. In molecular mechanics, the interaction between carbon atoms could be described by force fields. It is assumed that the deformation of the unit cell needs to satisfy the geometry constraints and minimum energy requirement. The elastic properties of graphene/graphite could be calculated from the strain energy density of the unit cell at small deformation (strain < 0.001). It is found in elastic region that graphene is in-plane isotropic, while graphite is transversely isotropic with axis of symmetry pointing along out-of-plane direction. And the in-plane elastic properties of graphite are approximately equal to those of graphene even with the consideration of van der Waals interaction across graphene layers. When the loading strain is large, it is noticed that strain is not uniform and become nonlinear inside the unit cell. Zone 1 is more compliant under uniaxial tension but stiffer under shear loading as compared to zone 2. Adopting critical bond length as the fracture criteria, it is predicted that the fracture strain while loading on zigzag edge is lower than that on armchair edge of graphene/graphite, which is consistent with molecular dynamics simulation results. It is concluded that the fracture behavior of graphene/graphite is directional dependent contrasting to the elastic behavior.