Existence and Stability of Traveling Waves for Degenerate Reaction–Diffusion Equation with Time Delay

Abstract

This paper deals with the existence and stability of traveling wave solutions for a degenerate reaction–diffusion equation with time delay. The degeneracy of spatial diffusion together with the effect of time delay causes us the essential difficulty for the existence of the traveling waves and their stabilities. In order to treat this case, we first show the existence of smooth- and sharp-type traveling wave solutions in the case of $c\ge c^*$ for the degenerate reaction–diffusion equation without delay, where $c^*>0$ is the critical wave speed of smooth traveling waves. Then, as a small perturbation, we obtain the existence of the smooth non-critical traveling waves for the degenerate diffusion equation with small time delay $\tau >0$. Furthermore, we prove the global existence and uniqueness of $C^{\alpha ,\beta }$-solution to the time-delayed degenerate reaction–diffusion equation via compactness analysis. Finally, by the weighted energy method, we prove that the smooth non-critical traveling wave is globally stable in the weighted $L^1$-space. The exponential convergence rate is also derived.

1 Introduction and Main Results

In this paper, we consider the degenerate reaction–diffusion equation with time delay

$$\begin{aligned} \frac{\partial u}{\partial t} -D\Delta u^m +d(u)=f(u_\tau ), \quad t\ge 0, \quad x\in {\mathbb {R}} \end{aligned}$$

(1.1)

with initial datum $u_0(s,x)$, $s\in [-\tau ,0]$. This equation models the population of the Australian sheep-blowfly Lucilia cuprina, where $u=u(t,x)\ge 0$ represents the population density of the blowflies at time t and location x, $u_\tau =u(t-\tau ,x)$ is the time-delayed population, and $\tau \ge 0$ is the generation time (the matured age); mathematically, we call it time delay. $D\Delta u^m$ with $m>1$ is the nonlinear diffusion with more ecological sense, that is, the diffusive velocity of population depends on the current population density, and the smaller population, the slower diffusion, in particular, when $u=0$ (the zero population), the diffusion speed is zero. The function $f(u_\tau )$ is the birth rate function, and d(u) represents the death rate. Without loss of generality, throughout this paper we take $f(u_\tau )$ and d(u) as the followings, captured as Nicholson’s birth rate function and death rate function

$$\begin{aligned} f(u_\tau )=pu_\tau {e}^{-au_\tau }, \quad d(u)=du, \end{aligned}$$

(1.2)

where $p>0$ is the maximum per capita daily egg production rate, $\frac{1}{a}>0$ is the size at which the blowfly population reproduces at its maximum rate, d with $d\in (0, p)$ is the per capita daily adult death rate. Besides the degenerate diffusion case ($m>1$), we also give a brief discussion for the singular diffusion case, that is $0<m<1$.

The degenerate equation with time delay (1.1) possesses two constant equilibria

$$\begin{aligned} u_-=0 \quad \text{ and } \quad u_+=\frac{1}{a}\ln \frac{p}{d}, \quad \text{ and }\quad u_+>u_- \ \text{ when } \frac{p}{d}>1. \end{aligned}$$

The initial data $u_0(s,x)\ge 0$ satisfies

$$\begin{aligned} u_0(s,x) \rightarrow u_\pm \text{ as } x\rightarrow \pm \infty , \quad \text{ uniformally } \text{ in } s\in [-\tau ,0]. \end{aligned}$$

(1.3)

In this paper, we are interested in the existence and uniqueness (up to shift) of the traveling wave solutions to Eq. (1.1), as well as their asymptotic stability. By a traveling wave solution, we mean a solution of the form $u(t,x)=\varphi (x+ct)$ connecting the constant states $u_\pm$ with the wave speed $c>0$:

$$\begin{aligned} {\left\{ \begin{array}{ll} c\varphi '(\xi )-D(\varphi ^m)''(\xi )+\mathrm{d}\varphi =p\varphi _{c\tau } {e}^{-a\varphi _{c\tau }},\\ \phi (\pm \infty )=u_\pm , \end{array}\right. } \end{aligned}$$

(1.4)

where $\varphi _{c\tau }=\varphi (\xi -c\tau )$.

In the past years, the existence of traveling wave solutions and their stabilities for the time-delayed diffusion equations have been studied intensively. Speaking of which, Schaaf (1987) firstly investigated the existence of traveling wavefronts for the linear diffusion equation with time delay, more precisely, for the time-delayed Fisher-KPP equation

$$\begin{aligned} \frac{\partial u}{\partial t} =\frac{\partial ^2 u}{\partial x^2}+u(t-\tau ,x)(1-u(t,x)), \end{aligned}$$

there is a minimal wave velocity $c^*(\tau )>0$, such that

• (i) if $c<c^*$, there are only trivial waves;

• (ii) if $c>c^*$, there are nontrivial wave solutions determined uniquely.

Thereafter, Wu and Zou (2001) studied the traveling waves for the following equation

$$\begin{aligned} \frac{\partial u}{\partial t} =\frac{\partial ^2 u}{\partial x^2}+u(t,x)(1-u(t-\tau ,x)), \end{aligned}$$

where the delay occurs in the removal term instead of the first factor, and they showed that for any given $c>2$, there exists $\tau ^*(c)>0$ such that if $\tau \le \tau ^*(c)$, the above equation has a traveling wave front with wave speed c. But two questions arise: for the existent traveling wave, how small the time delay $\tau$ should be, and once $\tau$ is big, what should we expect? These are unclear in Wu and Zou (2001). Later, Kwong and Ou (2010) gave the explicit estimate on the size of $\tau$. Namely, for any given $c\ge 2$, there exists a critical value $\tau ^*(c)>0$, which is determined by

$$\begin{aligned} \tau ^*(c)=\sup \{\tau >0; \lambda ^2+c\lambda -{e}^{c\lambda \tau }=0 \quad \text {has a positive root } \lambda \}, \end{aligned}$$

such that the equation has a monotone traveling wave with wave speed c if $\tau \le \tau ^*$, but no monotone traveling wave if $\tau >\tau ^*$. Besides the Fisher-KPP model, there are also some interesting studies related to Nicholson’s blowflies model, Eq. (1.1) with $m=1$. For example, So and Zou (2001) showed that when $1<\frac{p}{d}\le e$, for any time delay $\tau$, the monotone traveling waves exist when $c\ge c^*$, where $c^*>0$ is the critical wave speed; while when $\frac{p}{d}>e$, the problem becomes more challenging because the birth function loses monotonicity, and the solutions may be oscillating as numerically reported. As shown in Faria and Trofimchuk (2006, 2007), Ma (2007), Trofimchuk et al. (2008) and Trofimchuk and Trofimchuk (2008), when $e<\frac{p}{d}\le {e}^2$, for any time delay, the traveling waves exist when $c\ge c^*$, but the traveling waves may be non-monotone for some cases; when $\frac{p}{d}>{e}^2$, the existence is proved only for small time delay $\tau <\tau ^*$. Beside these, there are some significant research concerning with the traveling waves for the linear diffusion equations with nonlocal time delay, see, for example Li et al. (2007) and Xu and Xiao (2016).

On the other hand, the topic on the stability of traveling waves for time-delayed reaction–diffusion equations is also one of the hot research spots from both mathematical and physical points of view (Chern et al. 2015; Huang et al. 2012, 2016; Lin et al. 2014; Mei et al. 2009a, b, 2004, 2010; Mei and Wang 2011; Wu et al. 2011). For the non-degenerate case, namely $m=1$ in Eq. (1.1), Schaaf (1987) proved the linear stability of traveling wavefronts by the spectral method. Since then, the topic was not touched until Mei et al. (2004) showed the nonlinear stability of traveling waves by the weighted energy method when the initial perturbation around the wave is small enough. Furthermore, Mei and his collaborators (Huang et al. 2012; Mei et al. 2009a, b, 2010; Mei and Wang 2011) obtained the global stability for the traveling waves, while the non-critical traveling waves are exponentially stable and the critical traveling waves are algebraically stable. The adopted approach is the combination of the comparison principle, Fourier transform and the weighted energy method. When the birth rate function $f(u_\tau )$ is non-monotone for $u_\tau \in [0,u_+]$ under consideration, the equation losses its monotonicity, and when the time delay $\tau$ is bigger, then both the traveling waves and the original solution are oscillating around $u_+$. In this case, Lin et al. (2014) first proved the exponential stability for the non-critical oscillatory traveling wave, and Chern et al. (2015) showed the stability for the critical oscillatory waves, but no convergence rates are addressed. The approach for proof is the anti-weighted energy method with help of Hanalay’s inequality. A similar result for the nonlocal diffusion case was obtained by Huang et al. (2016). Very recently, by using Fourier transform to derive the fundamental solution for the linearized equation with delay, Mei et al. (submitted) further obtained the optimal exponential/algebraic convergence rates for the non-critical/critical oscillatory waves.

However, when the time-delayed equation is degenerate in its diffusion, namely, $m>1$ in Eq. (1.1), the study on the existence of traveling waves and their stability was not related yet as we know. In fact, even for the degenerate diffusion equations without time delay, there are only limited research works dealing with this subject. Aronson (1980) studied the porous medium equation with Fisher-KPP source

$$\begin{aligned} u_t=(u^m)_{xx}+u(1-u), \quad \text{ with } \ m>1, \end{aligned}$$

and confirmed the existence of the sharp-type traveling wave with the critical wave speed $c^*$. In particular, when $m=2$, Gilding and Kersner (2005) obtained the exact traveling wave solution corresponding to $c^*$. De Pablo and Vázquez (1991) studied the equation

$$\begin{aligned} u_t=(u^m)_{xx}+u^n(1-u), \quad \text{ with } \ m>1. \end{aligned}$$

From these studies, we see that the most obvious difference between the linear diffusion equations and the degenerate diffusion equations is that there may exist traveling waves of sharp type for the degenerate diffusion equation, that is, the solution is piecewise smooth and decreases to 0 at a finite spatial position, at which the solution is non-differentiable.

The degeneracy for $m>1$ with the effect of time delay $\tau >0$ causes us some essential difficulties. To attack such a problem will be the main target in the present paper. Here, we focus on the degenerate equation (1.1) with Nicholson blowflies’ birth rate function and death rate function (1.2), and investigate the existence, the uniqueness and the stability of traveling waves for Eq. (1.1). Note that, $u_-=0$ is an unstable node and $u_+$ is the stable node, which makes Eq. (1.1) as the so-called mono-stable equation just like the classical Fisher-KPP equation. For the existence of traveling waves to the regular time-delayed equations without degenerate diffusion, the usual approaches adopted are the monotonic method based on the comparison principle (Wu and Zou 2001; So and Zou 2001), the Leray Schauder fixed point theorem (Ma 2007) and the spectral method (Faria and Trofimchuk 2006, 2007; Trofimchuk et al. 2008; Trofimchuk and Trofimchuk 2008) based on the good regularity of differential operators. Due to the degeneracy of the time-delayed equation, the existing methods for treating regular diffusion equations seem not directly applicable to our case. So, we have to try some new techniques. The idea is that, to show the existence of traveling waves for the time-delayed equation, we first solve the problem without time delay by using phase plane analysis and some comparison methods, and then, we use the perturbation method to establish the existence of traveling waves for the equation with a small time delay. Unfortunately, this technique does not work for the case with large time delay. Furthermore, by using the technical compactness analysis, we prove the global existence and uniqueness of the original solution to the time-delayed reaction–diffusion equation with degeneracy, and the $C^{\frac{1}{4m},\frac{1}{2m}}$-regularity. Finally, by using the weighted energy method, we prove that the smooth traveling waves with $c>c^*$ are $L^1$-exponentially stable. Note that the $L^1$-stability was obtained by Mei et al. (2010) for the non-degenerate time-delayed Nicholson’s equation, where the comparison principle guarantees that $\int |v|\mathrm{d}x=\int v\mathrm{d}x$ once the initial perturbations are positive. In the present paper, the initial perturbations are allowed to change sign, by introducing a smooth approximation of sign functions, and taking compactness analysis, we get the $L^1$-stability for the case with time delay and degenerate diffusion.

Our main results are as follows.

Theorem 1.1

(Smooth and sharp traveling waves without time delay) For the degenerate reaction–diffusion equation (1.1) without time delay (i.e., $\tau =0$),

• 1. when $m>1$, there exists a critical wave speed $c^*>0$, such that for any $c\ge c^*$, the non-delayed equation (1.1) admits a unique (up to shift) monotone traveling wavefront $\varphi (x+ct)$ connecting $u_{\pm }$; and no monotone traveling wavefront exists for $0<c<c^*$. Here,

  $$\begin{aligned} c^*=\sup _{g\in \mathcal D_1}\left\{ 2\sqrt{D}\int _0^{u_+}\sqrt{-mg(s)s^m(p{e}^{-as}-d)g'(s)} \mathrm{d}s\right\} , \end{aligned}$$

  (1.5)

  where

  $$\begin{aligned} {\mathcal D}_1= & {} \Big \{g\in C^1(0, u_+); \ g(u_+)=0, \ \int _0^{u_+}g(s)\mathrm{d}s=1, \\&-\,g'(\varphi )>0 \quad \text { for any }\ \varphi \in (0,u_+)\Big \}. \end{aligned}$$

  In particular,

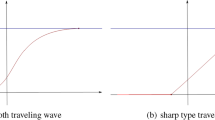
  • when $c>c^*$, the traveling wave is smooth: $\varphi (\xi )\in C^2({\mathbb {R}})$;

  • when $c=c^*$, the traveling wave is a semi-finite traveling wave, that is, there exists $\xi _0$ such that $\varphi (\xi )=0$ for $\xi \le \xi _0$ and $0<\varphi (\xi )<u_+$ for $\xi >\xi _0$, and $\varphi \in C^2(\xi _0, +\infty )$. In this case, when $1<m<2$, the traveling wave is smooth; and when $m\ge 2$, the traveling wave is sharp type.

  Furthermore, the traveling waves satisfy

  $$\begin{aligned} \varphi (\xi )\sim {e}^{\frac{p-d}{c}\xi }, \quad \text {as}\ \xi \rightarrow -\infty , \quad \text {for any}\ c>c^*, \end{aligned}$$

  and

  $$\begin{aligned} u_+-\varphi (\xi )\sim {e}^{\lambda _{1}^+\xi }, \quad \text {as}\ \xi \rightarrow +\infty , \quad \text {for any}\ c\ge c^*, \end{aligned}$$

  where

  $$\begin{aligned} \lambda _1^+=\frac{cu_+^{1-m}-\sqrt{c^2u_+^{2-2m}+4mDadu_+^{2-m}}}{2mD}; \end{aligned}$$

• 2. when $0<m<1$, then no nonnegative traveling wave solution connecting $u_\pm$ exits for Eq. (1.1) with $\tau =0$.

Remark 1.1

The types of traveling waves for the degenerate diffusion equation described in Theorem 1.1 can be sketched as follows: when $1<m<2$, all traveling waves $\phi (x+ct)$ with $c\ge c^*$ are smooth (see the first part of Fig. 1), and when $m\ge 2$ and $c=c^*$, the traveling wave $\phi (x+c^*t)$ is non-differentiable (see the second part of Fig. 1 for the sharp-type traveling wave). This is essentially different from the non-degenerate diffusion equations, where the traveling waves all are smooth.

Fig. 1

Smooth traveling waves and sharp-type traveling waves

Theorem 1.2

(Smooth traveling waves with small time delay) Assume $\tau >0$ and $m>1$ in the degenerate reaction–diffusion equation with time delay (1.1). Then, for any $c_0>c^*$ ($c^*$ is defined in (1.5)), there exists a sufficiently small constant $\tau _0>0$, and a continuously differentiable function $c=c(\tau )>0, \tau \in [0,\tau _0)$ with $c(0)=c_0$, such that the problem (1.4) admits a traveling wave front $\varphi (x+ct)=\varphi (\xi )\in C^2({\mathbb {R}})$ corresponding to $\tau$ and $c(\tau )$. Furthermore, it holds

$$\begin{aligned} \varphi (\xi )\sim {e}^{\lambda _*(\tau )\xi }, \quad \text {as}\ \xi \rightarrow -\infty , \end{aligned}$$

and

$$\begin{aligned} u_+-\varphi (\xi )\sim {e}^{\lambda _-(\tau )\xi }, \quad \text {as}\ \xi \rightarrow +\infty , \end{aligned}$$

where $\lambda _*(\tau )$ is the eigenvalue of the characteristic equation

$$\begin{aligned} c\lambda +d=p{e}^{-\lambda c\tau }, \end{aligned}$$

and $\lambda _-(\tau )$ is the negative root of

$$\begin{aligned} -Dmu_+^{m-1}\lambda ^2+c\lambda +d-d(1-au_+){e}^{-\lambda c\tau }=0. \end{aligned}$$

Remark 1.2

Different from the case without time delay in Theorem 1.1, the time delay, no matter how small it is, causes us a particular difficulty for the proof of uniqueness of the smooth traveling wave obtained in Theorem 1.2. The existing approach used in Aguerrea et al. (2012) and Yu and Mei (2016) for time-delayed equations seems not able to be applied to the degenerate case $m>1$, because the maximum principle does not hold for the time-delayed equation with degenerate diffusion. So the uniqueness of smooth traveling waves in the case with time delay still remains open. In this sense, we can also see that the dual effects made by the time delay and the degeneracy are essential.

Theorem 1.3

(Global existence and $C^{\alpha ,\beta }$-regularity of original solutions) For the degenerate diffusion equation (1.1) with time delay (i.e., $m>1$ and $\tau >0$), let the initial data be $0\le u_0\in L^\infty ([-\tau , 0] \times {\mathbb {R}})$, and

$$\begin{aligned}\lim _{x\rightarrow -\infty }u_0(s,x)=0, \lim _{x\rightarrow +\infty }u_0(s,x)=u_+, \quad \text{ uniformally } \text{ in } s\in [-\tau ,0]. \end{aligned}$$

Then the cauchy problem of Eq. (1.1) admits a uniquely global solution $u\in \mathcal D_2$, where

$$\begin{aligned} {\mathcal D}_2= & {} \{u\in L^\infty ({{\mathbb {R}}}_+\times {\mathbb {R}})\cap C^{\alpha ,\beta }({{\mathbb {R}}}_+\times {\mathbb {R}}); (u^m)_x\in L^\infty ({\mathbb {R}}_+; L^2_{loc}({\mathbb {R}})), \\ (u^m)_t\in & {} L^2_{Loc}({\mathbb {R}}_+\times {\mathbb {R}})\} \end{aligned}$$

with $\alpha =\frac{1}{4m}$ and $\beta =\frac{1}{2m}$, and

$$\begin{aligned} 0\le \Vert u\Vert _{L^\infty }\le \max \left\{ \Vert u_0\Vert _{L^\infty }, \frac{p}{aed}\right\} . \end{aligned}$$

Theorem 1.4

($L^1$-global stability of smooth traveling waves) Let $m>1$, and $\tau \in [0,\tau _0)$, and $\phi (x+ct)$ be a smooth traveling wave with $c>c^*(\tau )$, and $w(x+ct)=w(\xi )={e}^{-\lambda \xi }$ with $\xi =x+ct$ be the weight function, where $\lambda \in (\lambda _1,\lambda _2)$, and $\lambda _1>0$ and $\lambda _2>0$ are the roots of

$$\begin{aligned} J_\tau (c,\lambda )=d+c\lambda -Dm\kappa ^{m-1}\lambda ^2-p{e}^{-\lambda c\tau }=0 \end{aligned}$$

with $\kappa =\max \{\Vert u_0\Vert _{L^\infty }, \frac{p}{aed}\}$, $c^*(\tau )$ satisfies that $J_\tau (c^*,\lambda )=0$ admits a unique positive solution $\lambda ^*$, see Fig. 5. When the initial perturbation around the smooth traveling wave satisfies

$$\begin{aligned} v_0(s,\xi ):=u_0(s,x)-\phi (x+cs) \in C(-\tau ,0;L^1_w(\mathbb {R}), \end{aligned}$$

where $L^1_w(\mathbb {R})$ is the weighted $L^1$-space with the weight $w(\xi )$, then

$$\begin{aligned} v(t,\xi ):=u(t,x)-\phi (x+ct) \in C(-\tau ,0;L^1_w(\mathbb {R})) \end{aligned}$$

and

$$\begin{aligned} \Vert (u-\phi )(t)\Vert _{L^1_w(\mathbb {R})}\le Ce^{-\mu t} (\Vert v_0\Vert _{L^1(-\tau ,0;L^1_w(\mathbb {R}))}+\Vert v_0(0)\Vert _{L^1_w(\mathbb {R})}) \end{aligned}$$

for some positive constant $\mu >0$. Particularly, when $\tau =0$, the above stability also holds.

The paper is organized as follows. In Sect. 2, we prove Theorem 1.1, namely the existence and asymptotic behavior of uniquely monotonic traveling waves for Eq. (1.1) without time delay, and in Sect. 3, we prove the existence and asymptotic behavior of smooth traveling waves with small time delay (Theorem 1.2). Then, we prove Theorem 1.3 in Sect. 4, that is, the existence, uniqueness and regularity of solutions for the cauchy problem of (1.1). Finally, we prove the global $L^1$-stability of smooth traveling waves (Theorem 1.4) in Sect. 5.

2 Existence of Traveling Waves for the Equation Without Time Delay

In this section, we first consider the existence of traveling wave front connecting two equilibrium points $u_-=0$ and $u_+=\frac{1}{a}\ln \frac{p}{d}>0$ for the equation without time delay, that is

$$\begin{aligned} {\left\{ \begin{array}{ll} c\varphi '(\xi )-D(\varphi ^m)''(\xi )+\mathrm{d}\varphi =p\varphi {e}^{-a\varphi },\\ \varphi (\pm \infty )=u_\pm . \end{array}\right. } \end{aligned}$$

(2.1)

In what follows, we will discuss the existence of smooth traveling waves. Here, the smooth traveling waves means that the solution $\varphi \in C^2({\mathbb {R}})$, which satisfies (2.1) in the classical sense.

Let $\psi (\xi )=({\varphi ^m})'(\xi )$. Then, Eq. (2.1) is transformed into

$$\begin{aligned} \left\{ \begin{aligned}&\varphi '(\xi )=\frac{1}{m}\varphi ^{1-m}(\xi )\psi (\xi ) \\&\psi '(\xi )=\frac{c}{m D}\varphi ^{1-m}\psi +\frac{d}{D}\varphi -\frac{p}{D}\varphi {e}^{-a\varphi }. \end{aligned}\right. \end{aligned}$$

(2.2)

The equilibrium point $(u_+, 0)$ is a saddle point. Its two real eigenvalues are

$$\begin{aligned} \lambda _+=\frac{cu_+^{1-m}+\sqrt{c^2u_+^{2-2m}+4mDadu_+^{2-m}}}{2mD}, \end{aligned}$$

and

$$\begin{aligned} \lambda _-=\frac{cu_+^{1-m}-\sqrt{c^2u_+^{2-2m}+4mDadu_+^{2-m}}}{2mD}. \end{aligned}$$

Note that if $\varphi '(\xi )>0$ for $0<\varphi <u_+$, then (2.2) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}\psi }{\mathrm{d}\varphi }=\frac{c}{D}-\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{D\psi }, \\&\psi (u_+)=0. \end{aligned}\right. \end{aligned}$$

(2.3)

Let $\psi _c(\varphi )$ be the solution of the above equation, and we have

$$\begin{aligned} \psi _c(\varphi )\sim mu_+^{m-1}\lambda _-\left( \varphi -u_+\right) , \quad \text {as} \ \varphi \rightarrow u_+. \end{aligned}$$

(2.4)

Then, the existence of traveling wavefront of (2.1) connecting 0 and $u_+$ is equivalent to that $\psi _c(0)=0$.

Now, we are going to prove Theorem 1.1. The proof is divided in 4 steps, and the adopted approach is the phase plane analysis method.

Step 1. The existence of traveling waves for $c\ge c_*$ Inspired by Yin and Jin (2010), by a direct calculation, it is not difficult to see that $\psi _c(\varphi )$ is decreasing on the wave speed c. That is, for any positive constants $c_1$, $c_2$ with $c_1>c_2$, we have

$$\begin{aligned} \psi _{c_1}(\varphi )<\psi _{c_2}(\varphi ) \end{aligned}$$

(2.5)

for $\psi _{c_1}(\varphi )\ge 0$. In fact, by (2.4), one sees that (2.5) holds when $\varphi$ is sufficiently close to 0. Suppose that there exists $\varphi _1\in (0, u_+)$ such that $\psi _{c_1}(\varphi _1)=\psi _{c_2}(\varphi _1)=\psi ^*$, and $\psi _{c_1}(\varphi )<\psi _{c_2}(\varphi )$ for any $\varphi \in (\varphi _1, u_+)$. Then we have $\psi _{c_1}'(\varphi _1)<\psi _{c_2}'(\varphi _1)$. While by (2.3), we see that

$$\begin{aligned} \psi _{c_1}'(\varphi _1)=\frac{c_1}{D}-\frac{m\varphi _1^m(p{e}^{-a\varphi _1}-d)}{D\psi ^*}> \frac{c_2}{D}-\frac{m\varphi _1^m(p{e}^{-a\varphi _1}-d)}{D\psi ^*}= \psi _{c_2}'(\varphi _1), \end{aligned}$$

it is a contradiction.

Denote the curve ${\tilde{\psi }}(\varphi ) =\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{c}$ by $\varGamma _c$, see Fig. 2, which divides the upper half plane into two parts $E_1$, $E_2$. From Eq. (2.2), we see that $\psi _c'(\varphi )<0$ in $E_1$, and $\psi _c'(\varphi )>0$ in $E_2$. By (2.4), it is not difficult to see that $\psi <{\tilde{\psi }}$ when $\varphi <u_+$ and $\varphi$ is close to $u_+$ sufficiently. Therefore, for trajectory $\varGamma (\varphi , \psi )$ of (2.2) starting from point $(u_+, 0)$ must be increasing before intersecting with $\varGamma _c$. Also, it is clear that $\varGamma (\varphi , \psi )$ does not intersect with $\varphi$-axis when $\varphi \in (0, u_+)$, that is $\psi (0)\ge 0$ for any wave speed c.

Fig. 2

The graph of ${\tilde{\psi }}(\varphi )$

Next, we show that when c is appropriately large, $\varGamma (\varphi , \psi )$ will arrive at the point (0, 0). Let $\phi (\varphi )=B\varphi ^r$ with $1\le r\le m$. Then,

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}\varphi }\le \frac{c}{D}-\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{D\phi } \end{aligned}$$

is equivalent to

$$\begin{aligned} Br\varphi ^{r-1}+\frac{m\varphi ^{m-r}(p{e}^{-a\varphi }-d)}{DB}<\frac{c}{D}. \end{aligned}$$

When c is appropriately large, the above inequality holds. Note that $\phi (u_+)>0=\psi _c(u_+)$, then by comparison, we arrive at

$$\begin{aligned} 0\le \psi _c(\varphi )\le \phi (\varphi ),\quad \text {for} \ \varphi \in [0,u_+], \end{aligned}$$

(2.6)

which implies that $0\le \psi _c(0)\le \phi (0)=0$ for the large wave speed c.

On the other hand, if $\psi _c(0)=0$, then we have

$$\begin{aligned} \psi _c'(\varphi )\le \frac{c}{D}, \end{aligned}$$

which implies $\psi _c(\varphi )\le \frac{c}{D}\varphi$. Integrating the equation in (2.3) from 0 to $u_+$, we have

$$\begin{aligned} \frac{cu_+}{D}=\int _{0}^{u_+}\frac{ms^{m}(p{e}^{-as}-d)}{D\psi (s)}\mathrm{d}s\ge \int _{0}^{u_+}\frac{ms^{m-1}(p{e}^{-as}-d)}{c}\mathrm{d}s, \end{aligned}$$

which implies that

$$\begin{aligned} c\ge \sqrt{\frac{D}{u_+}\int _0^{u_+}ms^{m}(p{e}^{-as}-d)\mathrm{d}s}. \end{aligned}$$

(2.7)

Let

$$\begin{aligned} c^*=\sup \{c\ge 0; \psi _c(\varphi )\quad \text {does not arrive at the point }\ (0,0)\}. \end{aligned}$$

Then, $c^*>\sqrt{\frac{D}{u_+}\int _0^{u_+}ms^{m}(p{e}^{-as}-d)\mathrm{d}s}$ is well defined. By the monotonicity of $\psi _c$ on c, it holds that $\psi _c(0)=0$ for any $c\ge c^*$, and $\psi _c(0)>0$ for any $0<c<c^*$.

Step 2. Uniqueness (up to shift) of traveling waves. If there are more than one traveling wave $\phi (x+ct)$ with the same wave speed $c\ge c_*$, we may assume that $\psi _1(\varphi )$, $\psi _2(\varphi )$ are the two solutions of (2.3), then there exists $\varphi _0\in (0, u_+)$ such that $\psi _1(\varphi _0)\not =\psi _2(\varphi _0)$. Then, we have

$$\begin{aligned} \frac{d(\psi _1^2-\psi _2^2)}{\mathrm{d}\varphi }=\frac{2c}{D}\frac{\psi _1^2-\psi _2^2}{\psi _1+\psi _2}, \end{aligned}$$

by a direct calculation, we see that

$$\begin{aligned} (\psi _1^2-\psi _2^2)(\varphi )=(\psi _1^2-\psi _2^2)(\varphi _0){e}^{\frac{2c}{D} \int _{\varphi _0}^\varphi \frac{1}{\psi _1+\psi _2}\mathrm{d}s}, \end{aligned}$$

then we have $(\psi _1^2-\psi _2^2)(u_+)\not =0$. This is a contradiction, and the uniqueness of solutions for the problem (2.3) is proved. It means that the corresponding equation (2.1) admits a unique solution (up to shift). In fact, if $\varphi _1$ $\varphi _2$ are the two solutions of (2.1), then there exists $\xi _1$, $\xi _2$ such that $\varphi _1(\xi _1)=\varphi _2(\xi _2)=\frac{u_+}{2}$. Using the property of inverse function, and recalling (2.2), we see that $\xi '(\varphi )=\frac{1}{\varphi '(\xi )}=\frac{m\varphi ^{m-1}}{\psi _c}$. Therefore, we have

$$\begin{aligned} \xi -\xi _1= & {} \int _{\frac{u_+}{2}}^{\varphi _1(\xi )} \frac{ms^{m-1}}{\psi (s)}\mathrm{d}s,\\ \xi -\xi _1= & {} (\xi -\xi _1+\xi _2)-\xi _2=\int _{\frac{u_+}{2}}^{\varphi _2(\xi -\xi _1+\xi _2)} \frac{ms^{m-1}}{\psi (s)}\mathrm{d}s, \end{aligned}$$

which means that $\varphi _1(\xi )=\varphi _2(\xi -\xi _1+\xi _2)$.

Step 3. Variational characterization of $c^*$, and the asymptotic decay rate of the traveling wavefronts at far fields

Let $\psi _c(\varphi )$ be the solution of (2.3) connecting the equilibrium points (0, 0) and $(u_+, 0)$, and then we have that

$$\begin{aligned} \psi _c(\varphi )\sim \frac{m(p-d)}{c}\varphi ^m \end{aligned}$$

(2.8)

as $\varphi \rightarrow 0^+$ for any $c>c^*$.

In fact, from (2.3), we see that $\psi _c(\varphi )\sim \frac{m(p-d)}{c}\varphi ^m$ or $\psi _c(\varphi )\sim \frac{c}{D}\varphi$. However, from (2.6), we see that for large c, $\psi _c(\varphi )\le \phi (\varphi )= B\varphi ^m$ for any $\varphi \in (0, u_+)$ with some positive constant B. Thus, (2.8) holds for large wave speed, while for the other wave speeds, this result can be obtained by the monotonicity of $\psi _c(\varphi )$ on the wave speed c, that is $\psi _c(\varphi )$ is decreasing on the wave speed c. Suppose to the contrary, there exists a wave speed $c_0>c^*$, such that $\psi _{c_0}(\varphi )\sim \frac{c_0}{D}\varphi$, then $\psi _c(\varphi )\sim \frac{c}{D}\varphi$ for $c^*\le c<c_0$, which means that $\psi _{c_0}>\psi _c(\varphi )$. This is a contradiction.

Next, we consider the case for the critical wave speed. We show that

$$\begin{aligned} \psi _{c^*}(\varphi )\sim \frac{c^*}{D}\varphi \end{aligned}$$

(2.9)

as $\varphi \rightarrow 0^+$. Let $\psi _c(\varphi )$ be the solution of (2.3), and then for any $c<c^*$, we have $\psi _c(0)>0$. Consider the following problem

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}\psi }{\mathrm{d}\varphi }=\frac{c}{D}-\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{D\psi }, \\&\psi (0)=0. \end{aligned}\right. \end{aligned}$$

(2.10)

Denote ${\tilde{\psi }}_c(\varphi )$ be the maximal solution of (2.10), that is take $\psi (0)=\varepsilon >0$ in (2.10), and the maximal solution is obtained as $\varepsilon \rightarrow 0$. Then, ${\tilde{\psi }}_c'(0)=\frac{c}{D}$. By the comparison principle for solutions of the problem (2.10), we obtain

$$\begin{aligned} {\tilde{\psi }}_c(\varphi )\le \psi _c(\varphi ), \quad \text {for any } c<c^*, \end{aligned}$$

which means that ${\tilde{\psi }}_c$ goes to zero at some point $\varphi _c$ with $\varphi _c<u_+$ for $c<c^*$, and ${\tilde{\psi }}_c(\varphi )(\varphi )>0$ for any $\varphi \in (0, \varphi _c)$. By a direct calculation, it is also easy to obtain if $c_1<c_2$,

$$\begin{aligned} {\tilde{\psi }}_{c_1}(\varphi )< \tilde{\psi }_{c_2}(\varphi ), \quad \text {for any} \, \varphi \in (0, \min \{\varphi _{c_1}, u_+\}). \end{aligned}$$

Note that when $c>c^*$,

$$\begin{aligned} \tilde{\psi }_c(\varphi )>\psi _c(\varphi ), \quad \text {for any}\ \varphi \in (0, u_+). \end{aligned}$$

Then, we have ${\tilde{\psi }}_{c^*}(u_+)=0$. Note that ${\tilde{\psi }}_{c^*}(\varphi )\ge \psi _{c^*}(\varphi )$, by the first equation of (2.3) or (2.10), we have ${\tilde{\psi }}_{c^*}'(\varphi )\ge \psi _{c^*}'(\varphi )$ for any $\varphi \in (0, u_+)$, which implies that ${\tilde{\psi }}_{c^*}(\varphi )\equiv \psi _{c^*}(\varphi )$ for any $\varphi \in [0, u_+]$ since ${\tilde{\psi }}_{c^*}(0)=\psi _{c^*}(0)$ and ${\tilde{\psi }}_{c^*}(u_+)=\psi _{c^*}(u_+)$. Then (2.9) is obtained.

Inspired by Benguria and Depassier (1996), we give the variational characterization of $c^*$. Let $g\in c^1(0,u_+)$ be a nonnegative function such that $-g'>0$ and $\int _0^{u_+}g(s)\mathrm{d}s<+\infty$. Multiplying the first equation of (2.3) by g and integrating it from 0 to $u_+$, we obtain

$$\begin{aligned} \frac{c^*}{D}\int _0^{u_+}g(s)\mathrm{d}s&=\int _0^{u_+} \left( \frac{mg(s)s^{m}(p{e}^{-as}-d)}{D\psi _{c^*}(s)}-\psi _{c^*}(s)g'(s)\right) \mathrm{d}s \\&\ge \frac{2}{\sqrt{D}}\int _0^{u_+}\sqrt{-mg(s)s^m(p{e}^{-as}-d)g'(s)} \mathrm{d}s \end{aligned}$$

since $\psi _{c^*}, -g', p{e}^{-as}-d \ge 0$. The above equality holds if $g={\hat{g}}$, where ${\hat{g}}$ satisfies

$$\begin{aligned} \frac{m{\hat{g}}(s)s^{m}(p{e}^{-as}-d)}{D\psi _{c^*}(s)}=-\psi _{c^*}(s){{\hat{g}}}'(s). \end{aligned}$$

Combining with (2.3), we also have

$$\begin{aligned} -\frac{{{\hat{g}}}'}{{\hat{g}}}=\frac{c^*}{D\psi _{c^*}}-\frac{\psi _{c^*}'}{\psi _{c^*}}, \end{aligned}$$

which implies that

$$\begin{aligned} {\hat{g}}(\varphi )=\frac{D\psi _{c^*}}{c^*}{e}^{-\int _{a}^{\varphi }\frac{c^*}{D\psi _{c^*}} \mathrm{d}s}, \end{aligned}$$

where $0<a<u_+$. By (2.4) and (2.9), we can obtain ${\hat{g}}(u_+)=0$, and $0<{\hat{g}}(0)<\infty$. Then we can normalize ${\hat{g}}$ such that $\int _0^{u_+}g(s)\mathrm{d}s=1$. Thus we prove (1.5).

In what follows, we show the asymptotic behavior at infinity. Note that $\varphi (\xi )$ is monotone, then for any fixed ${\tilde{\varphi }}>0$, using inverse function derivation rule, and recalling (2.2), we see that $\xi '(\varphi )=\frac{1}{\varphi '(\xi )}=\frac{m\varphi ^{m-1}}{\psi _c}$, then we get

$$\begin{aligned} \xi ({\tilde{\varphi }})-\xi (\varphi )=\int _{\varphi }^{{\tilde{\varphi }}}\xi '(s)\mathrm{d}s =\int _{\varphi }^{{\tilde{\varphi }}}\frac{ms^{m-1}}{\psi _c(s)}\mathrm{d}s. \end{aligned}$$

Combining with (2.8) and (2.9), we see that $\xi \rightarrow -\infty$ as $\varphi \rightarrow 0^+$ for $c>c^*$; and $\xi$ goes to a finite number, say $\xi _0$, as $\varphi \rightarrow 0^+$ for $c=c^*$. Without loss of generality, let us take $\xi _0=0$, namely, $\varphi (0)=\varphi (\xi _0)=0$. Then $(\varphi ^m)'(0)=0$, and by (2.9), we further have $\varphi _l'(0)=0$ and

$$\begin{aligned} \varphi _r'(0)=\left\{ \begin{array}{l@{\quad }l} 0, &{} \text {if } \ m<2,\\ \frac{c^*}{mD}, &{}\text {if } \ m=2,\\ +\infty , &{} \text {if } \ m>2, \end{array}\right. \end{aligned}$$

where $\varphi _l'$ and $\varphi _r'$ denote the left-sided and right-sided derivatives, respectively. It implies that $\varphi$ is still a smooth traveling wave for any $m<2$, and $\varphi$ is a sharp-type traveling wave for any $m\ge 2$. Furthermore, for $c>c^*$, using L’Hospital’s rule, we further have

$$\begin{aligned} \lim _{\varphi \rightarrow 0^+}\frac{\xi (\varphi )}{\ln \varphi }= \lim _{\varphi \rightarrow 0^+}\frac{m\varphi ^m}{\psi _c}=\frac{c}{p-d}, \end{aligned}$$

that is,

$$\begin{aligned} \varphi (\xi )\sim {e}^{\frac{p-d}{c}\xi }, \quad \text {as}\ \xi \rightarrow -\infty . \end{aligned}$$

Similarly, for any fixed $\hat{\varphi }\in (0,u_+)$, we have

$$\begin{aligned} \xi (\varphi )-\xi (\hat{\varphi })=\int _{\hat{\varphi }}^{\varphi }\frac{ms^{m-1}}{\psi _c(s)}\mathrm{d}s. \end{aligned}$$

Recalling (2.4), for any $c\ge c^*$, we see that $\xi \rightarrow +\infty$ as $\varphi \rightarrow u_+^{-}$, and

$$\begin{aligned} \lim _{\varphi \rightarrow u_+^{-}}\frac{\xi (\varphi )}{\ln (u_+-\varphi )}=\frac{1}{\lambda _1^+}, \end{aligned}$$

which implies $u_+-\varphi \sim {e}^{\lambda _1^+\xi }$ as $\xi \rightarrow +\infty$.

Step 4. No traveling waves exist for $0<m<1$ We first show that Eq. (1.1) with $m<1$ and $\tau =0$ admits no monotone traveling wave solution. Suppose to the contrary, say, $\psi (\varphi )$ is the solution of (2.3) connecting (0, 0) and $(u_+, 0)$, then we will have a contradiction. In fact, by integrating Eq. (2.3) from 0 to $\varphi$, we have

$$\begin{aligned} \psi (\varphi )\le \frac{c}{D}\varphi . \end{aligned}$$

For any $\varepsilon$ with $0<\varepsilon <p-d$, we further have

$$\begin{aligned} \frac{\mathrm{d}\psi }{\mathrm{d}\varphi }=\frac{c}{D}-\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{D\psi } \le \frac{c}{D}-\frac{m(p-\varepsilon -d)}{c\varphi ^{1-m}} \end{aligned}$$

when $\varphi$ is sufficiently small such that $p{e}^{-a\varphi }>p-\varepsilon$. By integrating the above inequality from 0 to $\varphi$, it yields

$$\begin{aligned} \psi (\varphi )\le \frac{c}{D}\varphi -\frac{p-\varepsilon -d}{c}\varphi ^m, \end{aligned}$$

which means that $\psi (\varphi )<0$ for small $\varphi$. This is a contradiction.

Next, we show that Eq. (1.1) does not admit any nonnegative and smooth traveling wave solution. If the argument is false, then there exists at least a solution $\varphi (\xi )$ for (2.1). From the above proof, $\varphi$ is not monotonous. Note that $\varphi (\pm \infty )=u_\pm$, then there exists a local minimum point $\xi _0\in {\mathbb {R}}$ such that $\varphi '(\xi _0)=0$, $-(\varphi ^m)''\le 0$, by the first equation of (2.1), we see that

$$\begin{aligned} 0\ge c\varphi '(\xi _0)-D(\varphi ^m)''(\xi _0)=\varphi (p{e}^{-a\varphi }-d), \end{aligned}$$

which means that $\varphi (\xi _0)=0$ or $\varphi (\xi _0)\ge u_+$. If $\varphi (\xi _0)=0$, then there exist $\xi _1<\xi _0<\xi _2$ such that $\varphi (\xi _1)=\varphi (\xi _2)>0$, $\varphi '(\xi _1)\le 0$, $\varphi '(\xi _2)\ge 0$ and $0\le \varphi (\xi )<u_+$ for $\xi \in (\xi _1, \xi _2)$. Then, integrating the first equation in (2.1) from $\xi _1$ to $\xi _2$ yields

$$\begin{aligned} 0\ge D(\varphi ^m)'(\xi _1)-D(\varphi ^m)'(\xi _2)=\int _{\xi _1}^{\xi _2}\varphi (s) (p{e}^{-a\varphi (s)}-d) \mathrm{d}s>0. \end{aligned}$$

It is a contradiction. While if $\varphi (\xi _0)\ge u_+$, then there exists $\xi ^*<\xi _0$, such that $\xi ^*$ is a local maximum with $\varphi (\xi ^*)>u_+$, then there exist $\xi _3$, $\xi _4$ with $\xi _3<\xi ^*<\xi _4$ such that $u_+<\varphi (\xi _3)=\varphi (\xi _4)<\varphi (\xi ^*)$, $\varphi '(\xi _3)\ge 0$, $\varphi '(\xi _4)\le 0$, and $\varphi (\xi )>u_+$ for $\xi \in (\xi _1, \xi _2)$. Then integrating the first equation in (2.1) from $\xi _3$ to $\xi _4$ yields

$$\begin{aligned} 0\le D(\varphi ^m)'(\xi _3)-D(\varphi ^m)'(\xi _4)=\int _{\xi _3}^{\xi _4}\varphi (s) (p{e}^{-a\varphi (s)}-d) \mathrm{d}s<0. \end{aligned}$$

It is a contradiction. It implies that $\varphi$ is not a solution.

Finally, combining Steps 1–4, we immediately prove Theorem 1.1.

3 Existence of Traveling Waves for Equation with Small Time Delay

In this section, we are going to prove Theorem 1.2. Based on Theorem 1.1, by the perturbation method and the implicit function theory, we can obtain the existence of smooth traveling waves $\phi (x+ct)$ for the time-delayed degenerate diffusion equation (1.1), where the wave speed c is selected as $c=c(\tau )>c_0\ge c^*$ with $\tau \in (0,\tau _0]$, and $\tau _0>0$ is a specified number. At the end of this section, we will give one remark on the uniqueness of traveling waves and one proposition on the case of sharp-type traveling waves.

Proof of Theorem 1.2

Firstly, we reduce Eq. (2.1) into the following system

$$\begin{aligned} \left\{ \begin{aligned}&\varphi '(\xi )=\frac{1}{m}\varphi ^{1-m}(\xi )\psi (\xi ), \\&\psi '(\xi )=\frac{c}{m D}\varphi ^{1-m}\psi +\frac{d}{D}\varphi -\frac{p}{D}\varphi {e}^{-a\varphi }+\frac{p}{D} \left( \varphi {e}^{-a\varphi }-\varphi _{c\tau } {e}^{-a\varphi _{c\tau }}\right) . \end{aligned}\right. \end{aligned}$$

(3.1)

The existence of smooth monotone traveling waves connecting the two equilibrium points 0 and $u_+$ is equivalent to the existence of positive solutions for the following problem

$$\begin{aligned}&\frac{\mathrm{d}\psi }{\mathrm{d}\varphi }=\frac{c}{D}-\frac{m\varphi ^{m-1}(p\varphi _{c\tau }{e}^{-a\varphi _{c\tau }}-\mathrm{d}\varphi )}{D\psi }, \nonumber \\&\psi (0)=0, \quad \psi (u_+)=0, \end{aligned}$$

(3.2)

where $\varphi _{c\tau }$ is defined as

$$\begin{aligned} \varphi _{c\tau }=\inf \left\{ r; \varphi \ge r\ge 0, \text {and}\ \int _{r}^\varphi \frac{ms^{m-1}}{\psi (s)}\mathrm{d}s\le c\tau \right\} . \end{aligned}$$

(3.3)

When $\tau =0$, by using Theorem 1.1, we see that (3.2) admits a solution $\psi =F(\varphi , c)$ connecting the points (0, 0) and $(u_+, 0)$ for $c> c^*$. We consider Eq. (3.2) with the initial data $\psi (u_+)=0$, by (3.3), we see that $\varphi _{c\tau }\rightarrow u_+$ as $\varphi \rightarrow u_+$, we consider the linearized equation near $(\varphi , \psi )=(u_+, 0)$, that is

$$\begin{aligned} -Dmu_+^{m-1}\varphi ''+c\varphi '+d(\varphi -u_+)-p(1-au_+){e}^{-au_+}(\varphi _{c\tau }-u_+) =G_1, \end{aligned}$$

(3.4)

where

$$\begin{aligned} G_1&=Dm(\varphi ^{m-1}-u_+^{m-1})\varphi ''+Dm(m-1)u_+^{m-2}|\varphi '|^2 \\&\quad +p(\varphi _{c\tau }-u_+)({e}^{-a\varphi _{c\tau }}-{e}^{-au_+}) \\&\quad +pu_+(\varphi _{c\tau }-u_+) \left( ae^{-au_+}+\frac{{e}^{-a\varphi _{c\tau }}-{e}^{-au_+}}{\varphi _{c\tau }-u_+}\right) . \end{aligned}$$

Note that $p{e}^{-au_+}=d$, then the characteristic equation of (3.4) is

$$\begin{aligned} \Delta (c, \lambda )=-Dmu_+^{m-1}\lambda ^2+c\lambda +d-d(1-au_+){e}^{-\lambda c\tau }=0. \end{aligned}$$

(3.5)

Denote $y_1(\lambda )=-Dmu_+^{m-1}\lambda ^2+c\lambda +d$, $y_2(\lambda ,\tau )=d(1-au_+){e}^{-\lambda c\tau }$.

Fig. 3

The graphs of $y_1$, $y_2$

Clearly, from Fig. 3, the above equation admits two real roots $\lambda _-$ and $\lambda _+$ with $\lambda _-(\tau )<0<\lambda _+(\tau )$, where $\lambda _-(\tau )$ and $\lambda _+(\tau )$ are increasing on $\tau$. Then, we have

$$\begin{aligned} \psi \sim mu_+^{m-1}\lambda _-(\tau )\left( \varphi -u_+\right) , \text {as} \ \varphi \rightarrow u_+^{-}, \end{aligned}$$

(3.6)

which means that $\psi (\varphi )>0$ when $\varphi$ is in a small left neighborhood of $u_+$. We denote the trajectory of (3.2) starting from the point $(u_+, 0)$ by

$$\begin{aligned} \psi =f_1(\varphi , c, \tau ), \quad f_1(u_+, c, \tau )=0. \end{aligned}$$

Notice that $\lambda _-(\tau )>\lambda _-(0)$, then we have

$$\begin{aligned} f_1(\varphi , c, \tau )<f_1(\varphi , c, 0), \end{aligned}$$

(3.7)

when $\varphi$ is in a small left neighborhood of $u_+$. We denote the trajectory of (3.2) starting from the point (0, 0) by

$$\begin{aligned} \psi =f_0(\varphi , c, \tau ), \quad f_0(0, c, \tau )=0. \end{aligned}$$

Consider the linearized equation near $(\varphi , \psi )=(0, 0)$, that is

$$\begin{aligned}&c\varphi '+\mathrm{d}\varphi -p\varphi _{c\tau } \nonumber \\&\quad =Dm(m-1)\varphi ^{m-2}|\varphi '|^2+Dm\varphi ^{m-1}\varphi '' +p\varphi _{c\tau } ({e}^{-a\varphi _{c\tau }}-1) \nonumber \\&\quad =G_2. \end{aligned}$$

(3.8)

Then, the characteristic equation of (3.8) is

$$\begin{aligned} \Delta (c, \lambda )=c\lambda +d-p{e}^{-\lambda c\tau }. \end{aligned}$$

(3.9)

Clearly, the above equation admits a real root $\lambda ^*(\tau )>0$. Then

$$\begin{aligned} f_0(\varphi , c, \tau )\sim m\varphi ^{m}\lambda ^*(\tau ), \quad \text {as} \ \varphi \rightarrow 0^+. \end{aligned}$$

(3.10)

Note that

$$\begin{aligned} f_0(\varphi , c, 0)=f_1(\varphi , c, 0)=F(\varphi , c), \quad \text {for any} \ c\ge c^*, \end{aligned}$$

(3.11)

by continuous dependence of solution trajectories on parameters, the trajectories must cross the line $\varphi =\frac{1}{2}u_+$ when $\tau$ appropriately small. For any fixed wave speed $c_0\ge c^*$, the unperturbed problem corresponds to the solution $\psi =F(\varphi , c_0)$. In what follows, we show that there exists a unique $c=c(\tau )$ near $c_0$ such that $f_0(\frac{1}{2}u_+, c, \tau )=f_1(\frac{1}{2}u_+, c, \tau )$. Let

$$\begin{aligned} H(c, \tau )=f_0\left( \frac{1}{2}u_+, c, \tau \right) -f_1\left( \frac{1}{2}u_+, c, \tau \right) . \end{aligned}$$

Obviously, $H(c_0, 0)=0$. In what follows, we show that

$$\begin{aligned} \frac{\partial H}{\partial c}(c_0, 0)\not =0. \end{aligned}$$

(3.12)

Let

$$\begin{aligned} g_0(\varphi )=\frac{\partial f_0}{\partial c}(\varphi , c_0, 0). \end{aligned}$$

Then, $g_0(0)=0$, and

$$\begin{aligned} \frac{\mathrm{d} g_0}{\mathrm{d}\varphi }=\frac{\partial }{\partial c}\left. \left( \frac{\partial f_0}{\partial \varphi }(\varphi , c, 0) \right) \right| _{c=c_0}=\frac{1}{D}+\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{DF^2}g_0, \end{aligned}$$

where F is defined in (3.11), and we further have

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\varphi }\left( g_0 {e}^{\int _\varphi ^{\frac{1}{2}u_+}\frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s} \right) = \frac{1}{D} {e}^{\int _\varphi ^{\frac{1}{2}u_+}\frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s}. \end{aligned}$$

Integrating it from 0 to $\frac{1}{2}u_+$ yields

$$\begin{aligned} g_0\left( \frac{1}{2}u_+\right) = \frac{1}{D}\int _0^{\frac{1}{2}u_+} {e}^{\int _\varphi ^{\frac{1}{2}u_+}\frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s}\mathrm{d}\varphi . \end{aligned}$$

(3.13)

Let

$$\begin{aligned} g_1(\varphi )=\frac{\partial f_1}{\partial c}(\varphi , c_0, 0). \end{aligned}$$

Then, $g_1(u_+)=0$, and

$$\begin{aligned} \frac{\mathrm{d} g_1}{\mathrm{d}\varphi }=\frac{\partial }{\partial c}\left. \left( \frac{\partial f_1}{\partial \varphi }(\varphi , c, 0) \right) \right| _{c=c_0}=\frac{1}{D}+\frac{m\varphi ^m(p{e}^{-a\varphi }-d)}{DF^2}g_1, \end{aligned}$$

and we further have

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\varphi }\left( g_1 {e}^{-\int _{\frac{1}{2}u_+}^\varphi \frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s} \right) =\frac{1}{D} {e}^{-\int _{\frac{1}{2}u_+}^\varphi \frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s}. \end{aligned}$$

Similarly, integrating the above equation from $\frac{1}{2}u_+$ to $u_+$, we have

$$\begin{aligned} g_1\left( \frac{1}{2}u_+\right) =- \frac{1}{D}\int _{\frac{1}{2}u_+}^{u_+} {e}^{-\int _{\frac{1}{2}u_+}^\varphi \frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s}\mathrm{d}\varphi . \end{aligned}$$

(3.14)

Combining (3.13) and (3.14), we obtain

$$\begin{aligned} \frac{\partial H}{\partial c}(c_0, 0)=g_0\left( \frac{1}{2}u_+\right) -g_1\left( \frac{1}{2}u_+\right) =\frac{1}{D}\int _0^{u_+} {e}^{\int _\varphi ^{\frac{1}{2}u_+}\frac{ms^m(p{e}^{-as}-d)}{DF^2(s, c)}\mathrm{d}s}\mathrm{d}\varphi >0. \end{aligned}$$

By using the implicit function theorem, for sufficiently small $\tau$, we have $H(c(\tau ), \tau )=0$. Thus, we have proved Theorem 1.2.$\square$

Now, we give one remark on the uniqueness of traveling waves and one proposition on the possible sharp-type traveling waves.

Remark 3.1

Different from the case without time delay, the degenerate diffusion equation with time delay loses its comparison principle, and the uniqueness of traveling waves for the case with time delay (even it is small enough) is still open. It seems that the existing techniques for treating uniqueness cannot be directly applied.

Proposition 3.1

If $\varphi (\xi )\in L^\infty ({\mathbb {R}})$ is a piecewise smooth monotone traveling wave solution, then $\varphi \in C^2({\mathbb {R}})$ if $\varphi (\xi )>0$ for any $\xi \in {\mathbb {R}}$. However, when $\varphi (\xi )=0$ at some point $\xi$, then a sharp-front type traveling wave is possible to exist.

Fig. 4

Piecewise smooth solution

Proof

Let $u(t,x)\in L^\infty ({\mathbb {R}}\times {\mathbb {R}})$ be a piecewise smooth solution of (1.1). Assume that u(t, x) is not smooth or not continuous on the curve $\varGamma : x=x(t)\in Q$, and $x=x(t)$ divides the domain Q into two parts $Q_1$ and $Q_2$, where $Q\subset {\mathbb {R}}^2$ is a bounded domain (Fig. 4). Then, for any $\varPhi (t,x)\in C_0^\infty (Q)$, we have

$$\begin{aligned} -\iint _Q u\varPhi _t \mathrm{d}x\mathrm{d}t-D\iint _Q u^m\varPhi _{xx} \mathrm{d}x\mathrm{d}t+\mathrm{d}\iint _Q u\varPhi \mathrm{d}x\mathrm{d}t=\iint _Q f(u_\tau )\varPhi \mathrm{d}x\mathrm{d}t. \end{aligned}$$

(3.15)

Let $u_l$, $u_r$ be the left/right-sided limits, and $(u^m)_{xl}$, $(u^m)_{xr}$ denote the left-sided and right-sided derivatives, respectively. By a direct calculation, we see that

$$\begin{aligned}&-\iint _Q u\varPhi _t \mathrm{d}x\mathrm{d}t=-\iint _{Q_1} u\varPhi _t \mathrm{d}x\mathrm{d}t-\iint _{Q_2} u\varPhi _t \mathrm{d}x\mathrm{d}t \nonumber \\&\quad =\int _\varGamma u_r\varPhi x'(t)\mathrm{d}t-\int _\varGamma u_l\varPhi x'(t)\mathrm{d}t+\iint _{Q_1} u_t\varPhi \mathrm{d}x\mathrm{d}t +\iint _{Q_2} u_t\varPhi \mathrm{d}x\mathrm{d}t, \end{aligned}$$

(3.16)

and

$$\begin{aligned}&-D\iint _Q u^m\varPhi _{xx} \mathrm{d}x\mathrm{d}t\nonumber \\&\quad =-D\iint _{Q_1} u^m\varPhi _{xx} \mathrm{d}x\mathrm{d}t-D\iint _{Q_2} u^m\varPhi _{xx} \mathrm{d}x\mathrm{d}t \nonumber \\&\quad =-D\int _\varGamma u^m_r\varPhi _x \mathrm{d}t+D\int _\varGamma u^m_l\varPhi _x \mathrm{d}t+D\iint _{Q_1} (u^m)_x\varPhi _x \mathrm{d}x\mathrm{d}t \nonumber \\&\qquad +\,D\iint _{Q_2} (u^m)_x\varPhi _x \mathrm{d}x\mathrm{d}t \nonumber \\ \nonumber&\quad =-D\int _\varGamma (u^m_r-u^m_l)\varPhi _x \mathrm{d}t+D\int _\varGamma ((u^m)_{rx}-(u^m)_{lx})\varPhi \mathrm{d}t \\&\qquad -\,D\iint _{Q_1} (u^m)_{xx}\varPhi \mathrm{d}x\mathrm{d}t-D\iint _{Q_2} (u^m)_{xx}\varPhi \mathrm{d}x\mathrm{d}t. \end{aligned}$$

(3.17)

Substituting (3.16) and (3.17) into (3.15), and we obtain

$$\begin{aligned}&\int _\varGamma \Big ( (u_r-u_l)x'(t)+D((u^m)_{rx}-(u^m)_{lx})\Big )\varPhi \mathrm{d}t -D\int _\varGamma (u^m_r-u^m_l)\varPhi _x \mathrm{d}t \\&\quad \quad +\,\iint _{Q_1}\Big ( u_t-D(u^m)_{xx}+du-f(u_\tau )\Big )\varPhi \mathrm{d}x\mathrm{d}t\\&\quad \quad +\,\iint _{Q_2}\Big ( u_t-D(u^m)_{xx}+du-f(u_\tau )\Big )\varPhi \mathrm{d}x\mathrm{d}t \\&\quad =0. \end{aligned}$$

By the arbitrariness of $\varPhi$, we have

$$\begin{aligned} (u_r-u_l)x'(t)+D((u^m)_{rx}-(u^m)_{lx})=0, \quad \text {and}\ u^m_r-u^m_l=0, \end{aligned}$$

which implies that

$$\begin{aligned} u_r=u_l, \quad (u^m)_{rx}=(u^m)_{lx}. \end{aligned}$$

Note that $\varphi (\xi )=\varphi (x+ct)=u(t,x)$, then $\varphi _r(\xi )=\varphi _l(\xi )$, and ${\varphi ^m}_r'(\xi )={\varphi ^m}_l'(\xi )$. If $\varphi _r(\xi )=\varphi _l(\xi )\not =0$, $\varphi '_{r}=\varphi '_{l}$. Recalling (1.4), we further have $\varphi ''_{r}=\varphi ''_{l}$. That is, $\varphi \in C^2({\mathbb {R}})$. While if $\varphi _r(\xi )=\varphi _l(\xi )=0$, then it is possible for $\varphi _r'(\xi )\not =\varphi _l'(\xi )$. For this cases, so $\varphi (\xi )$ is a sharp traveling wave, which is not smooth only at the point $\varphi =0$. The proof is complete.$\square$

4 Global Existence and Regularity of Time-Delayed Degenerate Solution

Recalling (1.1), we see that $\tilde{u}(t,\xi )=u(t, \xi -ct)=u(t, x)$ with $\xi =x+ct$ and $c>c^*>0$ satisfies the following equation

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial \xi }-D\Delta u^m+du=f(u_\tau ), \\&\lim _{\xi \rightarrow -\infty } u(t,\xi )=0, \quad \lim _{\xi \rightarrow +\infty } u(t,\xi )=u_+, \\&u(s,\xi )=\tilde{u}_0(s, \xi )=u_0(s,\xi -cs), \quad s\in [-\tau , 0], \end{aligned}\right. \end{aligned}$$

(4.1)

where $f(s)=pse^{-as}$. For simplicity, we still denote the solution by $u(t,\xi )$. We are going to prove Theorem 1.3 in the equivalent form to Eq. (4.1).

Let $u^l_0(s,\xi )$ with $0\le u^l_0(s,\xi )\le \tilde{u}_0(s, \xi )$ be a sufficiently smooth function with $u^l_0(s,\xi )\rightarrow \tilde{u}_0(s,\xi )$ as $l \rightarrow \infty$, uniformly in $\xi$ and s. Consider the following problem

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial \xi }-D\Delta u^m+du=f(u_\tau ), \quad \xi \in (-l, l), \quad t>0 \\&u(-l, t)=\frac{1}{l},\quad u(l,t)=\frac{1}{l} {e}^{-\mathrm{d}t}+u_+, \quad t>0 \\&u(s,\xi )=u^l_0(s,\xi )+\frac{1}{l}, \quad s\in [-\tau , 0]. \end{aligned}\right. \end{aligned}$$

(4.2)

It is easy to show that $f(u_\tau )=pu_\tau {e}^{-au_\tau }\le \frac{p}{ae}$. By a direct calculation, $\frac{1}{l}e^{-\mathrm{d}t}$ is a lower solution of (4.2), and $\max \{u_++\frac{1}{l}, \Vert \tilde{u}_0\Vert _{L^\infty }+1, \frac{p}{aed}\}$ is an upper solution of (4.2). Then, by the comparison principle, we obtain

$$\begin{aligned} \frac{1}{l}e^{-\mathrm{d}t}\le u(t,\xi )\le \max \left\{ u_++\frac{1}{l}, \Vert \tilde{u}_0\Vert _{L^\infty }+1, \frac{p}{aed}\right\} , \end{aligned}$$

(4.3)

and the problem (4.2) admits a smooth solution $u_l(t,\xi )$. Next, we show the $C^{\alpha ,\beta }$-estimate of $u_l$. For any $a\in (-l+2, l-2)$, multiplying Eq. (4.2) by $u^r\eta ^2$ ($r>0$) with $\eta (\xi )\in C^{\infty }_0(a-2,a+2)$, and $0\le \eta (\xi )\le 1$, $|\eta '(\xi )|\le 1$, $\eta =1$ for $\xi \in (a-1, a+1)$, we see that

$$\begin{aligned}&\frac{1}{r+1}\frac{\mathrm{d}}{\mathrm{d}t}\int u^{r+1}\eta ^2\mathrm{d}\xi +Dmr\int u^{m+r-2}|u_\xi |^2\eta ^2 \mathrm{d}\xi +\mathrm{d}\int u^{r+1}\eta ^2\mathrm{d}\xi \\&\quad =-Dm\int u^{m+r-1}u_\xi \eta \eta _\xi \mathrm{d}\xi +\frac{2c}{r+1}\int u^{r+1}\eta \eta _\xi \mathrm{d}\xi +\int f(u_\tau )u^r\eta ^2\mathrm{d}\xi \\&\quad \le \frac{Dmr}{2}\int u^{m+r-2}|u_\xi |^2\eta ^2 \mathrm{d}\xi +C. \end{aligned}$$

Then, for any given $\sigma >0$, and for any $t>0$, we have

$$\begin{aligned} \int _{t}^{t+\sigma }\int u^{m+r-2}|u_\xi |^2\eta ^2 \mathrm{d}\xi \mathrm{d}s \le C, \end{aligned}$$

(4.4)

where C only depends on r and $\sigma$. By using the mean value theorem of integrals, we further prove that there exists $t_0\in (t, t+\sigma )$ such that

$$\begin{aligned} \int u^{m+r-2}(t_0)|u_\xi (t_0,\xi )|^2\eta ^2(\xi ) \mathrm{d}\xi \le C. \end{aligned}$$

(4.5)

Multiplying Eq. (4.2) by $(u^m)_t\eta ^4$, we have

$$\begin{aligned}&m\int u^{m-1}u_t^2\eta ^4\mathrm{d}\xi +\frac{D}{2}\frac{\mathrm{d}}{\mathrm{d}t}\int |(u^m)_\xi |^2\eta ^4 \mathrm{d}\xi +\frac{dm}{m+1}\int u^{m+1}\eta ^4\mathrm{d}\xi \\&\quad =-m^2\int u^{2m-2}u_\xi u_t\eta ^3\eta _\xi \mathrm{d}\xi -cm\int u^{m-1}u_tu_\xi \eta ^4 \mathrm{d}\xi +\int f(u_\tau )u^{m-1}u_t\eta ^4\mathrm{d}\xi \\&\quad \le \frac{m}{2}\int u^{m-1}u_t^2\eta ^4\mathrm{d}\xi +C\int u^{3(m-1)}|u_\xi |^2 \eta ^2\mathrm{d}\xi \\&\quad \quad +\, C\int u^{m-1}|u_\xi |^2\eta ^4 \mathrm{d}\xi +C\int f^2(u_\tau )u^{m-1}\eta ^4\mathrm{d}\xi . \end{aligned}$$

Combining with (4.4) and (4.5), we further have

$$\begin{aligned} \int _t^{t+\sigma }\int u^{m-1}u_t^2\eta ^4\mathrm{d}\xi +\sup _{t}\int |(u^m)_{\xi }|^2\eta ^4 \mathrm{d}\xi \le C, \end{aligned}$$

(4.6)

where C is independent of l. Let us denote the solution of (4.2) by $u_l$ and its weak limit by u as $l\rightarrow \infty$. Letting $l\rightarrow \infty$, we obtain the existence of the generalized solutions for the problem (4.1) satisfying (4.4), (4.6) and

$$\begin{aligned} 0\le u\le \max \Big \{\Vert \tilde{u}_0\Vert _{L^\infty }, \frac{p}{aed}\Big \}. \end{aligned}$$

By the boundedness of u, we also have

$$\begin{aligned} \int _t^{t+\sigma }\int |(u^m)_t|^2\eta ^4\mathrm{d}\xi +\sup _{t}\int |(u^m)_\xi |^2\eta ^4 \mathrm{d}\xi \le C. \end{aligned}$$

(4.7)

Then, by Sobole embedding inequality, we have $u^m\in L^\infty ((0,\infty ), C^{1/2}({\mathbb {R}}))$, because of $u^m\in L^\infty ((0,\infty ), H^1_{loc}({\mathbb {R}}))$. We further obtain $u^m(t,\xi )\in C^{\frac{1}{4},\frac{1}{2}}({{\mathbb {R}}}_+\times {\mathbb {R}})$ due to $(u^m)_t\in L^2((t,t+\sigma )\times (a-1, a+1))$. In fact, for any $t_1, t_2\in {\mathbb {R}}^+$, $x\in {\mathbb {R}}$, (without loss of generality, we assume that $t_2\le t_1$.) take a ball $B_r$ of radius r centered at x, with $r=|t_1-t_2|^{\frac{1}{2}}$. Recalling (4.7) and using Poincáre inequality, we have

$$\begin{aligned}&\int _{B_r}|u^m(t_1,y)-u^m(t_2,y)|dy=\int _{B_r} \left| \int _{t_2}^{t_1}\frac{\partial u^m(t,y)}{\partial t} \mathrm{d}t\right| dy \\&\quad \le C \left( \int _{t_2}^{t_1}\int _{B_r} \left| \frac{\partial u^m(t,y)}{\partial t}\right| ^2 dydt\right) ^{1/2}|t_1-t_2|^{1/2}r^{1/2} \\&\quad \le C|t_1-t_2|^{1/2}r^{1/2}. \end{aligned}$$

By the mean value theorem, there exists $x^*\in B_r$ such that

$$\begin{aligned} |u^m(t_1,x^*)-u^m(t_2,x^*)|\le C|t_1-t_2|^{1/2}r^{-1/2}= C|t_1-t_2|^{1/4}. \end{aligned}$$

Then, we have

$$\begin{aligned}&|u^m(t_1,x)-u^m(t_2,x)| \\&\quad \le |u^m(t_1,x)-u^m(t_1,x^*)|+|u^m(t_1,x^*)-u^m(t_2,x^*)| +|u^m(t_2,x^*)-u^m(t_2,x)|\\&\quad \le C(|x-x^*|^{\frac{1}{2}}+|t_1-t_2|^{\frac{1}{4}}) \\&\quad \le C|t_1-t_2|^{\frac{1}{4}}, \end{aligned}$$

which implies that $u^m(t,\xi )\in C^{\frac{1}{4},\frac{1}{2}}({{\mathbb {R}}}_+ \times {\mathbb {R}})$. It means that $u(t,\xi )\in C^{\frac{1}{4m},\frac{1}{2m}}({{\mathbb {R}}}_+ \times {\mathbb {R}})$.

Next, we show the uniqueness. Let $u_1, u_2\in \mathcal D_2$ be the solutions of (4.1), and assume $u=u_1-u_2$. For simplicity, we replace $u(t,\xi )$ by u(t, x) with $\xi =x+ct$, and note that when $t\in (0,\tau )$, $t-\tau \in (-\tau , 0)$,then $f(u_{1,\tau })=f(u_{2,\tau })=f(\tilde{u}_0(t-\tau ,x))$. Thus, we have

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u}{\partial t}-D\Delta (u_1^m-u_2^m)+du=0, \quad (t, x)\in {\mathbb {R}}\times (0,\tau ), \\&\lim _{x\rightarrow -\infty } u(t,x)=0, \quad \lim _{x\rightarrow +\infty } u(t,x)=0, \quad t\in (0,\tau ), \\&u(s,x)=0, \quad s\in [-\tau , 0]. \end{aligned}\right. \end{aligned}$$

(4.8)

Take the test function $\psi _n(t,x)=\alpha _n(x)\int _\tau ^t(u_1^m-u_2^m)\mathrm{d}s$, where $\alpha _n(x)\in C_0^\infty ({\mathbb {R}})$, which is a concave function with $0\le \alpha _n(x)\le 1$, $|\alpha _n'(x)|\le 1$, and

$$\begin{aligned} \alpha _n(x)= {\left\{ \begin{array}{ll} 1, &{}|x|\le n;\\ 0, &{} |x|\ge n+1. \end{array}\right. } \end{aligned}$$

(4.9)

Then, $\psi _n(t,x)\in {\mathring{H}}^{1}({\mathbb {R}}\times (0,\tau ))$. Note that $u(0,x)=\psi _n(\tau ,x)\equiv 0$, we obtain

$$\begin{aligned}&\iint _{Q_\tau }ue^{\mathrm{d}t}\alpha _n(x)(u_1^m-u_2^m)\mathrm{d}x\mathrm{d}t \\&\quad = D\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n(x)(u_1^m-u_2^m)_x\left( \int _\tau ^t(u_1^m-u_2^m)_x\mathrm{d}s\right) \mathrm{d}x\mathrm{d}t \\&\quad \quad +\,D\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n'(x)(u_1^m-u_2^m)_x\left( \int _\tau ^t(u_1^m-u_2^m)\mathrm{d}s\right) \mathrm{d}x\mathrm{d}t \\&\quad =\frac{D}{2}\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n(x)\frac{\mathrm{d}}{\mathrm{d}t}\left( \int _\tau ^t(u_1^m-u_2^m)_x\mathrm{d}s\right) ^2\mathrm{d}x\mathrm{d}t \\&\quad \quad +\,D\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n'(u_1^m-u_2^m)_x\left( \int _\tau ^t(u_1^m-u_2^m)\mathrm{d}s\right) \mathrm{d}x\mathrm{d}t\\&\quad =-\frac{D}{2}\iint _{Q_\tau }\alpha _n(x)\left( \int _\tau ^0(u_1^m-u_2^m)_x\mathrm{d}s\right) ^2\mathrm{d}x\mathrm{d}t\\&\quad \quad -\,\frac{dD}{2}\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n(x)\left( \int _\tau ^t(u_1^m-u_2^m)_x\mathrm{d}s\right) ^2\mathrm{d}x\mathrm{d}t \\&\quad \quad +\,D\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n'(x)(u_1^m-u_2^m)_x\left( \int _\tau ^t(u_1^m-u_2^m)\mathrm{d}s\right) \mathrm{d}x\mathrm{d}t \\&\quad \le D\iint _{Q_\tau }{e}^{\mathrm{d}t}\alpha _n'(x)(u_1^m-u_2^m)_x\left( \int _\tau ^t(u_1^m-u_2^m)\mathrm{d}s\right) \mathrm{d}x\mathrm{d}t, \end{aligned}$$

where $Q_\tau =(0,\tau )\times (-\infty ,+\infty )$. Note that $\alpha _n'(x) =0$ for $|x|<n$ and $|x|>n+1$, by using (4.6), we further have

$$\begin{aligned}&\iint _{Q_\tau }ue^{\mathrm{d}t}\alpha _n(x)(u_1^m-u_2^m)\mathrm{d}x\mathrm{d}t \nonumber \\&\quad \le D\sqrt{\tau }{e}^{\mathrm{d}\tau }\left( \iint _{Q_\tau }|\alpha _n'(x)||(u_1^m-u_2^m)_x|^2\mathrm{d}x\mathrm{d}t\right) ^{1/2} \nonumber \\&\qquad \times \,\left( \iint _{Q_\tau }|\alpha _n'(x)|(u_1^m-u_2^m)^2 \mathrm{d}x\mathrm{d}t\right) ^{1/2}\nonumber \\&\le C\left( \iint _{Q_\tau }|\alpha _n'(x)|(u_1^m-u_2^m)(u_1-u_2) \mathrm{d}x\mathrm{d}t\right) ^{1/2}. \end{aligned}$$

(4.10)

Note that $\alpha _n'(x) =0$ for $|x|<n$ and $|x|>n+1$, from the above inequality, we have

$$\begin{aligned} \iint _{Q_\tau }ue^{\mathrm{d}t}\alpha _n(x)(u_1^m-u_2^m)\mathrm{d}x\mathrm{d}t \end{aligned}$$

is bounded uniformly. It means that

$$\begin{aligned} \iint _{Q_\tau }|\alpha _n'(x)|(u_1^m-u_2^m)(u_1-u_2) \mathrm{d}x\mathrm{d}t\rightarrow 0, \quad \text {as} \ n\rightarrow \infty . \end{aligned}$$

Let $n\rightarrow \infty$, we have

$$\begin{aligned} \iint _{Q_\tau }{e}^{\mathrm{d}t}u(u_1^m-u_2^m)\mathrm{d}x\mathrm{d}t=0, \end{aligned}$$

which implies that $u_1=u_2$ in $Q_\tau$. Repeating the above procedure on $(\tau ,2\tau )$, $(2\tau , 3\tau ), \ldots$, we then prove

$$\begin{aligned} u_1(t,x)=u_2(t,x), \quad \text{ for } (t,x)\in {{\mathbb {R}}}_+\times {\mathbb {R}}. \end{aligned}$$

The uniqueness is proved.

5 Global Stability of Smooth Traveling Waves

In this section, we study the global stability of smooth traveling waves.

Let u(t, x) be the solution of Eq. (1.1) with initial datum $u_0(s,x)$, $s\in [-\tau , 0]$, $\varphi (x+ct)=\varphi (\xi )$ be a given smooth traveling wave connecting 0 and $u_+$ with $c>c^*$, and let $v(t,\xi ):=u(t,x)-\varphi (\xi )$, $v_0(s,\xi ):=u_0(s,\xi -cs)-\varphi (\xi )$. Then, $v(t,\xi )$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial v}{\partial t}+c\frac{\partial v}{\partial \xi }-D\Delta (u^m-\varphi ^m)+dv=f(u_\tau )-f(\varphi _{c\tau }), \\&v(s,\xi )=v_0(s,\xi ), \quad s\in [-\tau , 0], \end{aligned}\right. \end{aligned}$$

(5.1)

where $f(s)=pse^{-as}$.

Let $w(\xi )>0$ be a weight function, and then we define the weighted $L^1_w({\mathbb {R}})$ by

$$\begin{aligned} v\in L^1_w({\mathbb {R}}) \Leftrightarrow \Vert v\Vert _{L^1_w({\mathbb {R}})}=\int _{{\mathbb {R}}} |v(\xi )|w(\xi ) \mathrm{d}\xi \le C, \end{aligned}$$

(5.2)

and for any $T>0$, $L^\infty ([0,T]; L^1_w({\mathbb {R}}))$ by

$$\begin{aligned} \Vert v\Vert _{L^\infty ([0,T];L^1_w({\mathbb {R}}))}=\sup _{t\in [0,T]}\Vert v(t)\Vert _{L^1_w({\mathbb {R}})}. \end{aligned}$$

We are going to prove Theorem 1.4. The proof is divided into 3 steps.

Step 1. Weighted $L^1_w$-regularity for the perturbed solution: $v \in L^\infty ({{\mathbb {R}}}_+; L^1_w({\mathbb {R}}))$ Let $J_\varepsilon (s)\in C^1(R)$ be the approximation of the sign function satisfying $J_\varepsilon '(s)\ge 0$, and $J_\varepsilon (s)\rightarrow \mathrm{sgn} (s)$, $J_\varepsilon '(s)\rightarrow \delta (s)$, as $\varepsilon \rightarrow 0$, where $\delta (s)$ is the Delta function. Multiplying the first equation of (5.1) by $J_\varepsilon ({\hat{v}})w(\xi )\alpha _n(\xi )$, where $w(\xi )={e}^{-\lambda \xi }$ is the weight function, $\alpha _n(\xi )$ is defined in (4.9), and ${\hat{v}}=u^m-\varphi ^m$, and integrating the resultant equation on ${\mathbb {R}}$, we have

$$\begin{aligned}&\int _{{\mathbb {R}}}\partial _t(\alpha _nvw) J_\varepsilon ({\hat{v}})\mathrm{d}\xi + D\int _{{\mathbb {R}}} \alpha _nJ_\varepsilon '({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi + D\int _{{\mathbb {R}}} \alpha _n'J_\varepsilon ({\hat{v}})w\partial _\xi {\hat{v}} \mathrm{d}\xi \\&\quad \quad +\,D\int _{{\mathbb {R}}} w'(\xi )\alpha _nJ_\varepsilon ({\hat{v}}) \partial _\xi {\hat{v}}\mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}} \alpha _n vw J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad = \int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) wJ_\varepsilon ({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

Let $h_\varepsilon ({\hat{v}}):=\int _0^{{\hat{v}}}J_\varepsilon (s) \mathrm{d}s$, and then we further have

$$\begin{aligned}&\int _{{\mathbb {R}}}\partial _t(\alpha _nvw) J_\varepsilon ({\hat{v}})\mathrm{d}\xi + D\int _{{\mathbb {R}}} \alpha _nJ_\varepsilon '({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \\&\quad \quad -\,D\int _{{\mathbb {R}}} (\lambda ^2 w(\xi )\alpha _n-2\lambda w(\xi )\alpha _n'+w\alpha _n'') h_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad \quad +\,\mathrm{d}\int _{{\mathbb {R}}} \alpha _n vw J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad = \int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) wJ_\varepsilon ({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

Letting $\varepsilon \rightarrow 0$, and noting that $h_\varepsilon ({\hat{v}})\rightarrow |{\hat{v}}|$, we obtain

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\int _{{\mathbb {R}}}\alpha _n|v|w \mathrm{d}\xi + D\int _{{\mathbb {R}}} \alpha _n\delta ({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi -D\int _{{\mathbb {R}}}w\alpha _n'' |{\hat{v}}|\mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}} \alpha _n |v|w \mathrm{d}\xi \\&\quad =D\lambda ^2\int _{{\mathbb {R}}}\alpha _n|{\hat{v}}|w \mathrm{d}\xi -2\lambda D\int _{{\mathbb {R}}} w(\xi )\alpha _n' |{\hat{v}}|\mathrm{d}\xi +\int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) w \ \mathbf{sgn}({\hat{v}}) \mathrm{d}\xi \\&\quad \le M\int _{{\mathbb {R}}}w(\xi )\alpha _n|v|\mathrm{d}\xi -2\lambda D\int _{{\mathbb {R}}} w(\xi )\alpha _n' |{\hat{v}}|\mathrm{d}\xi +p\int _{{\mathbb {R}}} \alpha _n|u_\tau -\varphi _{c\tau }|w \mathrm{d}\xi . \end{aligned}$$

Note that $\alpha _n''\le 0$, $\alpha _n'(\xi )\ge 0$ for $-n-1\le \xi \le -n$, and $\alpha _n'(\xi )\le 0$ for $n\le \xi \le n+1$, and then we obtain

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _{{\mathbb {R}}}\alpha _n|v|w \mathrm{d}\xi\le & {} (M-d)\int _{{\mathbb {R}}}\alpha _n|v|w\mathrm{d}\xi +2\lambda D\int _n^{n+1} {e}^{-\lambda \xi }|{\hat{v}}|\mathrm{d}\xi \\&+\,p\int _{{\mathbb {R}}} \alpha _n|u_\tau -\varphi _{c\tau }|w \mathrm{d}\xi , \end{aligned}$$

which implies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {e}^{-(M-d)t}\int _{{\mathbb {R}}}\alpha _n|v|w \mathrm{d}\xi \right) \le Ce^{-(M-d)t}, \quad \text {for }\ 0\le t\le \tau . \end{aligned}$$

Letting $n\rightarrow \infty$, we obtain

$$\begin{aligned} \sup _{t\in (0,\tau )}\int _{{\mathbb {R}}}|v|w \mathrm{d}\xi \le C. \end{aligned}$$

Repeating the same procedure on $(\tau ,2\tau )$, $(2\tau , 3\tau ), \cdots$, then we prove

$$\begin{aligned} \sup _{t\in {{\mathbb {R}}}_+}\int _{{\mathbb {R}}}|v(t,\xi )|w(\xi ) \mathrm{d}\xi \le C. \end{aligned}$$

The proof is complete.

Similarly to Step 1, we also have the following $L^1-$regularity of the solution $v(t,\xi )$ without weight function.

Step 2. $L^1$-regularity of perturbed solution: $v\in L^\infty ({{\mathbb {R}}}_+;L^1({\mathbb {R}}))$ For simplicity, we do not take the approximation of the sign function. Multiplying the equation by $\alpha _n(x)\mathbf{sgn}({\hat{v}})$, and integrating it over ${\mathbb {R}}$, we obtain

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\int _{{\mathbb {R}}}\alpha _n|v| \mathrm{d}\xi + D\int _{{\mathbb {R}}} \alpha _n\delta ({\hat{v}}) |\partial _\xi {\hat{v}}|^2\mathrm{d}\xi -D\int _{{\mathbb {R}}}\alpha _n'' |{\hat{v}}|\mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}} \alpha _n |v| \mathrm{d}\xi \\&\quad =\int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) \mathbf{sgn}({\hat{v}}) \mathrm{d}\xi + c\int _{{\mathbb {R}}} \alpha _n'|v|\mathrm{d}\xi \\&\quad \le C\int _{{\mathbb {R}}}|u_\tau -\varphi _{c\tau }|\mathrm{d}\xi +C, \end{aligned}$$

where $\alpha _n$ is defined in (4.9). Then, for any given $t>0$, we obtain

$$\begin{aligned} \int _{{\mathbb {R}}}\alpha _n|v| \mathrm{d}\xi \le C, \end{aligned}$$

where C is independent of n. Letting $n\rightarrow \infty$, we prove

$$\begin{aligned} \int _{{\mathbb {R}}}|v(t,\xi )| \mathrm{d}\xi \le C \quad \text{ for } t\in {{\mathbb {R}}}_+. \end{aligned}$$

The proof is complete.

Step 3. Global stability of traveling waves: $\Vert v(t)\Vert _{L^1_w({\mathbb {R}})} \le Ce^{-\mu t} (\Vert v_0\Vert _{L^1(-\tau ,0;L^1_w(R))} +\Vert v_0(0)\Vert _{L^1_w})$ Next, we are going to show the global stability of smooth traveling waves in the weighted $L^1$-space. By Theorem 1.3, we see that the solution of (5.1) satisfies

$$\begin{aligned} \Vert u\Vert _{L^\infty }\le \max \Big \{\Vert u_0\Vert _{L^\infty }, \frac{p}{aed}\Big \}=\kappa , \end{aligned}$$

which means $\frac{{\hat{v}}}{v}< m \kappa ^{m-1}$, where $v=u-\phi$ is the solution of (5.1), and ${{\hat{v}}}=u^m-\phi ^m$ as defined before. Define

$$\begin{aligned} J_\tau (c, \lambda ):=d+c\lambda -Dm\kappa ^{m-1}\lambda ^2-p{e}^{-\lambda c\tau }. \end{aligned}$$

(5.3)

Denote $y_3(\lambda , c)=d+c\lambda -Dm\kappa ^{m-1}\lambda ^2$, $y_4(\lambda , c)=p{e}^{-\lambda c\tau }$. From Fig. 5, we see that, there exists $c^*(\tau )>0$ such that $J_\tau (c^*, \lambda )=0$ admits only one real root $\lambda ^*$, especially, $c^*(0)=2\sqrt{Dm\kappa ^{m-1}(p-d)}$, and for any $c>c^*$, $J_\tau (c, \lambda )=0$ has two positive real roots $\lambda _1, \lambda _2$ with $0<\lambda _1<\lambda ^*<\lambda _2$.

Fig. 5

The graphs of $y_3$ and $y_4$

Firstly, similarly to the proof of above Step 1, we multiply the first equation of (5.1) by $\alpha _nJ_\varepsilon ({\hat{v}})w$, where $w={e}^{-\lambda \xi }$, $\alpha _n(\xi )$ is defined in (4.9), and ${\hat{v}}=u^m-\varphi ^m$, then integrate the resultant equation on ${\mathbb {R}}$ to have

$$\begin{aligned}&\int _{{\mathbb {R}}}\partial _t(\alpha _nvw) J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\qquad -\,c\int _{{\mathbb {R}}}v\Big (\alpha _n'(\xi )w(\xi ) J_\varepsilon ({\hat{v}}) +\alpha _n(\xi )w'(\xi )J_\varepsilon ({\hat{v}})+\alpha _n(\xi )w(\xi )J_\varepsilon '({\hat{v}})\partial _\xi {\hat{v}}\Big )\mathrm{d}\xi \\&\qquad +\, D\int _{{\mathbb {R}}}\alpha _n J_\varepsilon '({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi + D\int _{{\mathbb {R}}}\alpha _n' J_\varepsilon ({\hat{v}})w\partial _\xi {\hat{v}}\mathrm{d}\xi \\&\qquad + \,D\int _{{\mathbb {R}}}\alpha _n J_\varepsilon ({\hat{v}})w'\partial _\xi {\hat{v}}\mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}}\alpha _n vw J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad = \int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) wJ_\varepsilon ({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

Letting $h_\varepsilon ({\hat{v}})=\int _0^{{\hat{v}}}J_\varepsilon (s) \mathrm{d}s$, we further have

$$\begin{aligned}&\int _{{\mathbb {R}}}\partial _t(\alpha _nvw) J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\qquad -\,c\int _{{\mathbb {R}}}v\Big (\alpha _n'(\xi )w(\xi )J_\varepsilon ({\hat{v}}) +\alpha _n(\xi )w'(\xi )J_\varepsilon ({\hat{v}})+\alpha _n(\xi )w(\xi )J_\varepsilon '({\hat{v}})\partial _\xi {\hat{v}}\Big )\mathrm{d}\xi \\&\qquad +\,D\int _{{\mathbb {R}}}\alpha _n J_\varepsilon '({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi - D\int _{{\mathbb {R}}} h_\varepsilon ({\hat{v}})(\alpha _n''w+2\alpha _n'w'+\alpha _nw'')\mathrm{d}\xi \\&\qquad +\,\mathrm{d}\int _{{\mathbb {R}}}\alpha _n vw J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad = \int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) wJ_\varepsilon ({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

By (4.6), we see that $v, \partial _\xi {\hat{v}}\in L^2_{loc}({{\mathbb {R}}})$, then let $\varepsilon \rightarrow 0$, we have

$$\begin{aligned} \int _{{\mathbb {R}}}v\alpha _n(\xi )w(\xi )J_\varepsilon '({\hat{v}})\partial _\xi {\hat{v}} \mathrm{d}\xi \rightarrow \int _{{\mathbb {R}}}v\alpha _n(\xi )w(\xi )\delta ({\hat{v}})\partial _\xi {\hat{v}} \mathrm{d}\xi =0. \end{aligned}$$

Thus, we have

$$\begin{aligned}&\frac{d}{\mathrm{d}t}\int _{{\mathbb {R}}}\alpha _n|v|w\mathrm{d}\xi -c\int _{{\mathbb {R}}}\Big (|v|\alpha _n'(\xi )w(\xi ) +|v|\alpha _n(\xi )w'(\xi )\Big )\mathrm{d}\xi +D\int _{{\mathbb {R}}}\alpha _n \delta ({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \\&\qquad -\,D\int _{{\mathbb {R}}}|{\hat{v}}|(\alpha _n''w+2\alpha _n'w'+\alpha _nw'')\mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}}\alpha _n vw J_\varepsilon ({\hat{v}})\mathrm{d}\xi \\&\quad =\int _{{\mathbb {R}}} \alpha _n\left( f(u_\tau )-f(\varphi _{c\tau })\right) wJ_\varepsilon ({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

By the weighted $L^1_w$ -regularity for the perturbed solution showed in the above Step 1, we see that for any $t>0$, $|v|w\in L^1({\mathbb {R}})$. By taking $n\rightarrow \infty$, we then have

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\int _{{\mathbb {R}}}|v|w \mathrm{d}\xi -c\int _{{\mathbb {R}}}|v|w'(\xi )\mathrm{d}\xi + D\int _{{\mathbb {R}}} \delta ({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \\&\qquad -\,D\int _{{\mathbb {R}}} w''(\xi ) |{\hat{v}}| \mathrm{d}\xi +\mathrm{d}\int _{{\mathbb {R}}} |v|w \mathrm{d}\xi \\&\quad = \int _{{\mathbb {R}}} f'(\varphi _{c\tau }+\theta v(t-\tau ,\xi -c\tau ))v(t-\tau ,\xi -c\tau )w\ \mathrm{sgn}({\hat{v}}) \mathrm{d}\xi . \end{aligned}$$

Multiplying the above equation by ${e}^{\mu t}$, and integrating it from 0 to t, we then have

$$\begin{aligned}&\int _{{\mathbb {R}}} {e}^{\mu t}|v(t,\xi )|w \mathrm{d}\xi +\int _0^t\int _{{\mathbb {R}}}\left( d-c\frac{w'}{w}-D\frac{w''}{w}\frac{{\hat{v}}}{v}-\mu \right) {e}^{\mu s}|v|w\mathrm{d}\xi \mathrm{d}s \nonumber \\&\qquad +\,D\int _0^t\int _{{\mathbb {R}}} {e}^{\mu s}\delta ({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \mathrm{d}s\nonumber \\&\quad =\int _0^t\int _{{\mathbb {R}}} {e}^{\mu s} f'(\varphi _{c\tau }+\theta v(s-\tau ,\xi -c\tau ))v(s-\tau ,\xi -c\tau )w(\xi )\ \mathrm{sgn}({\hat{v}}) \mathrm{d}\xi \mathrm{d}s \nonumber \\&\quad \quad +\,\int _{{\mathbb {R}}}|v(0,\xi )|w(\xi ) \mathrm{d}\xi \nonumber \\&\quad =: I_1(t)+\int _{{\mathbb {R}}}|v(0,\xi )|w(\xi ) \mathrm{d}\xi . \end{aligned}$$

(5.4)

Next, we estimate $I_1$. Clearly, we have $u(t,x)\ge 0$ since $u_0(s,x)\ge 0$, and note that $f'(s)=p(1-as){e}^{-as}$, then $|f'(s)|\le p$ for any $s\ge 0$, therefore, we have

$$\begin{aligned} |I_1|&\le p\int _0^t\int _{{\mathbb {R}}} {e}^{\mu s}|v(s-\tau ,\xi )| w(\xi +c\tau ) \mathrm{d}\xi \mathrm{d}s \\&= p{e}^{\mu \tau }\int _{-\tau }^{t-\tau }\int _{{\mathbb {R}}} {e}^{\mu s}|v(s,\xi )| w(\xi +c\tau )\mathrm{d}\xi \mathrm{d}s \\&\le p{e}^{\mu \tau }\int _{-\tau }^0 \int _{{\mathbb {R}}} {e}^{\mu s}|v_0(s,\xi )| w(\xi +c\tau )\mathrm{d}\xi \mathrm{d}s \\&\quad +\, p{e}^{\mu \tau }\int _0^{t}\int _{{\mathbb {R}}} {e}^{\mu s}|v(s,\xi )| w(\xi +c\tau )\mathrm{d}\xi \mathrm{d}s. \end{aligned}$$

Substituting it into (5.4), we arrive at

$$\begin{aligned}&{e}^{\mu t}\int _{{\mathbb {R}}}|v(t,\xi )|w \mathrm{d}\xi +\int _0^t\int _{{\mathbb {R}}}{e}^{\mu s}\left( d+c\lambda -D\frac{{\hat{v}}}{v}\lambda ^2-\mu - p{e}^{-\lambda c\tau }{e}^{\mu \tau }\right) |v|w\mathrm{d}\xi \mathrm{d}s \\&\qquad +\,D\int _0^t\int _{{\mathbb {R}}}{e}^{\mu s} \delta ({\hat{v}})w|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \mathrm{d}s \\&\quad \le p{e}^{\mu \tau }\int _{-\tau }^0 \int _{{\mathbb {R}}} {e}^{\mu s}|v_0(s,\xi )| w(\xi +c\tau )\mathrm{d}\xi \mathrm{d}s +\int _{{\mathbb {R}}}|v(0,\xi )|w(\xi ) \mathrm{d}\xi . \end{aligned}$$

For any fixed $\lambda \in (\lambda _1,\lambda _2)$, then there exists a constant $m_1>0$, such that $J_\tau (c, \lambda )>2m_1$, where $J_\tau (c,\lambda )$ is defined in (5.3), and take $\mu >0$ appropriately small such that

$$\begin{aligned} d+c\lambda -D\frac{{\hat{v}}}{v}\lambda ^2-\mu -p{e}^{-\lambda c\tau }{e}^{\mu \tau }>m_1. \end{aligned}$$

Then, we obtain

$$\begin{aligned}&\int _{{\mathbb {R}}}|v(t,\xi )|w \mathrm{d}\xi +m_1\int _0^t\int _{{\mathbb {R}}}{e}^{\mu (s-t)}|v|w\mathrm{d}\xi \mathrm{d}s \\&\quad \le p{e}^{-\mu t}{e}^{\mu \tau }\int _{-\tau }^0 \int _{{\mathbb {R}}} {e}^{\mu s}|v_0(s,\xi )| w(\xi +c\tau )\mathrm{d}\xi \mathrm{d}s +{e}^{-\mu t}\int _{{\mathbb {R}}}|v(0,\xi )|w(\xi ) \mathrm{d}\xi , \end{aligned}$$

which implies the weighted $L^1_w$-stability:

$$\begin{aligned} \Vert (u-\phi )(t)\Vert _{L^1_w(\mathbb {R})}\le Ce^{-\mu t} (\Vert v_0\Vert _{L^1(-\tau ,0;L^1_w(\mathbb {R}))}+\Vert v_0(0)\Vert _{L^1_w(\mathbb {R})}). \end{aligned}$$

When $\tau =0$, similar to (5.4), we have

$$\begin{aligned}&\int _{{\mathbb {R}}} {e}^{{\tilde{\mu }} t}|v(t,\xi )|\tilde{w} \mathrm{d}\xi +\int _0^t\int _{{\mathbb {R}}}\left( d-c\frac{\tilde{w}'}{\tilde{w}}- D\frac{{\hat{v}}}{v}\frac{\tilde{w}''}{\tilde{w}} -{\tilde{\mu }}\right) {e}^{{\tilde{\mu }} s}|v|\tilde{w}\mathrm{d}\xi \mathrm{d}s \\&\quad \quad +\,D\int _0^t\int _{{\mathbb {R}}} {e}^{{\tilde{\mu }} s}\delta ({\hat{v}})\tilde{w}|\partial _\xi {\hat{v}}|^2\mathrm{d}\xi \mathrm{d}s \\&\quad =\int _0^t\int _{{\mathbb {R}}} {e}^{{\tilde{\mu }} s} f'(\varphi +\theta v(s,\xi ))|v(s,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi \mathrm{d}s +\int _{{\mathbb {R}}}|v(0,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi \\&\quad \le p\int _0^t\int _{{\mathbb {R}}} {e}^{{\tilde{\mu }} s}|v(s,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi \mathrm{d}s +\int _{{\mathbb {R}}}|v(0,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi . \end{aligned}$$

Taking $\tilde{w}(\xi )={e}^{-{\tilde{\lambda }}\xi }$, then

$$\begin{aligned}&\int _{{\mathbb {R}}}|v(t,\xi )|\tilde{w} \mathrm{d}\xi +\int _0^t\int _{{\mathbb {R}}}\left( d+c\tilde{\lambda }-D\frac{{\hat{v}}}{v}\tilde{\lambda }^2-{\tilde{\mu }}-p\right) {e}^{{\tilde{\mu }} (s-t)}|v|\tilde{w}\mathrm{d}\xi \mathrm{d}s \\&\quad \le {e}^{-{\tilde{\mu }} t}\int _{{\mathbb {R}}}|v(0,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi . \end{aligned}$$

For any fixed ${\tilde{\lambda }}\in ({\tilde{\lambda }}_1,{\tilde{\lambda }}_2)$, then there exists a constant $\tilde{m}_1>0$, such that $J_0(c, {\tilde{\lambda }})>2\tilde{m}_1$, and take ${\tilde{\mu }}>0$ appropriately small such that

$$\begin{aligned} d+c{\tilde{\lambda }}-D\frac{{\hat{v}}}{v}{\tilde{\lambda }}^2-{\tilde{\mu }}-p>\tilde{m}_1. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \int _{{\mathbb {R}}}|v(t,\xi )|\tilde{w} \mathrm{d}\xi +\tilde{m}_1\int _0^t\int _{{\mathbb {R}}} {e}^{{\tilde{\mu }} (s-t)}|v|\tilde{w}\mathrm{d}\xi \mathrm{d}s \le {e}^{-{\tilde{\mu }} t}\int _{{\mathbb {R}}}|v(0,\xi )|\tilde{w}(\xi ) \mathrm{d}\xi . \end{aligned}$$

The proof is complete.$\square$

Based on the above Steps 1–3, we immediately prove Theorem 1.4.

Remark 5.1

When $\tau =0$, namely, the degenerate reaction–diffusion equation (1.1) without time delay, from Theorem 1.4, we see that $v(t,\xi )\in L^1({\mathbb {R}})$ for any $t>0$ if $v_0(0,\xi )\in L^1({\mathbb {R}})$. By Theorem 1.3, we also see that $v\in L^\infty ({{\mathbb {R}}}_+\times {\mathbb {R}})\cap C^{\alpha , \beta }({{\mathbb {R}}}_+\times {\mathbb {R}})$. Then, we always have

$$\begin{aligned} \lim _{\xi \rightarrow \infty }|u(t,\xi )-\varphi (\xi )| =0. \end{aligned}$$