Potential Singularity for a Family of Models of the Axisymmetric Incompressible Flow

Abstract

We study a family of 3D models for the incompressible axisymmetric Euler and Navier–Stokes equations. The models are derived by changing the strength of the convection terms in the equations written using a set of transformed variables. The models share several regularity results with the Euler and Navier–Stokes equations, including an energy identity, the conservation of a modified circulation quantity, the BKM criterion and the Prodi–Serrin criterion. The inviscid models with weak convection are numerically observed to develop stable self-similar singularity with the singular region traveling along the symmetric axis, and such singularity scenario does not seem to persist for strong convection.

1 Introduction

The 3D incompressible Euler and Navier–Stokes equations govern the motion of ideal incompressible fluid and take the following simple form

$$\begin{aligned} {\mathbf {u}}_t+{\mathbf {u}}\cdot \nabla {\mathbf {u}}=-\nabla p+\nu \Delta {\mathbf {u}}, \quad \nabla \cdot {\mathbf {u}}=0, \end{aligned}$$

(1.1)

where ${\mathbf {u}}(x,t): R^3\times [0, T)\rightarrow R^3$ describes the 3D velocity field of the fluid, and $p(x,t): R^3\times [0, T)\rightarrow R$ describes the pressure in the fluid. The divergence-free condition $\nabla \cdot {\mathbf {u}}=0$ guarantees the incompressibility of the fluid. The Laplace term $\nu \Delta {\mathbf {u}}$ models the viscosity in the fluid; for inviscid fluid with $\nu =0$, Eq. (1.1) are called the Euler equations, and for the viscous case $\nu >0$, Eq. (1.1) are called the Navier–Stokes equations. The 3D Euler and Navier–Stokes equations are among the most fundamental nonlinear PDEs in nature yet far from being fully understood. The fundamental question regarding the global regularity of the 3D Euler and Navier–Stokes equations with smooth initial data remains open and is viewed as one of the most important open questions in mathematical fluid mechanics; see Fefferman (2006).

The Euler and Navier–Stokes equation (1.1) enjoy the energy identity,

$$\begin{aligned} \frac{1}{2}\Vert {\mathbf {u}}(x,t)\Vert _{L^2(R^3)}^2+\nu \int _0^t \Vert \nabla {\mathbf {u}}(x,s)\Vert _{L^2(R^3)}^2=\frac{1}{2}\Vert {\mathbf {u}}(x,0)\Vert _{L^2(R^3)}^2, \end{aligned}$$

(1.2)

where $\frac{1}{2}\int _{R^3}|{\mathbf {u}}(x,t)|^2\mathrm{d}x$ and $\nu \int _0^T\int _{R^3}|\nabla {\mathbf {u}}(x,t)|^2\mathrm{d}x\mathrm{d}t$ seem to be the only known coercive a priori estimates of smooth solutions to (1.1). The difficulty for the global regularity of the Navier–Stokes equations lies in the fact that these known a priori estimates are supercritical with respect to the invariant scaling of the equations; see Tao (2008) for more about this supercritical barrier. For the Euler equations, due to the lack of regularization mechanism, to establish global regularity of the solutions becomes even more challenging.

In this work, we investigate a family of 3D models for the 3D Euler and Navier–Stokes equations with axial symmetry. The family of models are derived by changing the strength of the convection terms in the equations written using a set of transformed variables, $u_1=\frac{u^\theta }{r}$, $\omega _1=\frac{\omega ^\theta }{r}$, where $u^\theta$ and $\omega ^\theta$ are the angular components of the velocity and vorticity fields, respectively. The family of 3D models can be written in terms of $u_1$ and $\omega _1$ as follows,

$$\begin{aligned} u_{1,t}+u^ru_{1,r}+u^zu_{1,z}&= \nu \left( \partial _r^2+\frac{3}{r} \partial _r+\partial _z^2\right) u_1+2u_1\phi _{1,z},\\ \omega _{1,t}+u^r\omega _{1,r}+u^z\omega _{1,z}&= \nu \left( \partial _r^2+\frac{3}{r}\partial _r+\partial _z^2\right) \omega _1+\left( u_1^2\right) _z,\\ -\left[ \partial _r^2+(3/r)\partial _r+\partial _z^2\right] \phi _1&=\omega _1, \end{aligned}$$

with the Biot–Savart law given by

$$\begin{aligned} u^r=-\epsilon r\phi _{1,z}, \quad u^z=\epsilon (2\phi _1+r\phi _{1,r}). \end{aligned}$$

The parameter $\epsilon$ is used to control the strength of the convection terms. The case $\epsilon =1$ corresponds to the original axisymmetric Euler and Navier–Stokes equations, and the case $\epsilon =0$ corresponds to the 3D model proposed by Hou and Lei (2009). It has been numerically shown in Hou and Lei (2009) and Hou et al. (2012, 2014) that the above inviscid model with $\epsilon =0$ can develop potential finite-time singularity.

In this work, we study the above 3D models with the parameter $\epsilon \in [0, 2)$ to demonstrate the subtle balance between the nonlinear convection and the nonlinear vortex stretching. Our study shows that the competition between the convection and the vortex stretching may be responsible for the potential singularity formation or depletion of nonlinearity of the equations.

The family of models share several regularity results with the Euler and Navier–Stokes equations, including an energy identity, the conservation of a modified circulation quantity, a BKM-type criterion for the inviscid model, and a Prodi–Serrin type criterion for the viscous model. The energy functional for the models is equivalent to that of the original Euler and Navier–Stokes equations. We derive an equivalent formulation of the models written in the velocity–pressure formulation, and they can be viewed as the original Eq. (1.1) with an added stirring forcing term. To control this additional term in our proof of the regularity criteria, we need to use some estimates for the Sobolev norms of axisymmetric solenoidal vector fields.

Despite the similarities between the proposed models and the original Euler equations, the inviscid models demonstrate very different regularity properties based on our numerical computation. Our numerical results suggest that for weak convection, the inviscid models develop finite-time singularity with local self-similar structure, and the singular region is not stationary but traveling along the symmetric axis. To resolve the singular numerical solutions, we employ an adaptive moving mesh method proposed in Luo and Hou (2014), which adaptively puts a certain portion of the grid points in the singular region of the solutions. We numerically observe that as we increase the strength of the convection terms, such singularity scenario is destroyed. Specifically, this singularity scenario does not seem to persist for the original Euler equations.

We also employ a dynamic rescaling formulation to demonstrate the stability of the self-similar singularity. In the dynamic rescaling formulation, we add scaling and shifting terms to the models according to the scaling and translational invariance properties of the equations, and the resulting equations govern the evolution of the spatial profiles in the original solutions. The self-similar profiles in the singular solutions correspond to the steady state of the dynamic rescaling equations, and we demonstrate the stability of the self-similar profiles by linearizing the discretized dynamic rescaling equations at the steady state. We observe that for weak convection, the real parts of the eigenvalues of the Jacobian matrix are all negative, which demonstrates the linear stability of the traveling wave self-similar singularity scenario. However, as the strength of the convection increases, the dominating eigenvalues of the Jacobian matrix with the largest real parts seem to approach the imaginary axis. This implies that the steady state of the dynamic rescaling equations becomes less stable as the strength of the convection increases.

The rest of the paper is organized as follows. In Sect. 2, we derive the models and give a brief review of some of the previous works on the regularity of the 3D Euler and Navier–Stokes equations. In Sect. 3, we prove some regularity results for the family of models, including some conserved quantities and non-blow-up criteria. In Sect. 4, we solve the inviscid models numerically and present some features of the finite-time singularity. We also present stability results for the self-similar singularity of the inviscid models using the dynamic rescaling formulation. Concluding remarks are made in Sect. 5.

2 Derivation of the Models and Review of Previous Works

In this section, we derive the models and give a brief review of some of the previous works for 3D Euler and Navier–Stokes equations.

2.1 Derivation of the Models

Let $\mathbf {e_r}$, $\mathbf {e_\theta }$ and $\mathbf {e_z}$ be the standard orthonormal vectors defining the cylindrical coordinate system,

$$\begin{aligned} \mathbf {e_r}=\left( \frac{x_1}{r}, \frac{x_2}{r}, 0\right) ^T,\quad \mathbf {e_\theta }=\left( \frac{x_2}{r}, -\frac{x_1}{r}, 0\right) ^T,\quad \mathbf {e_z}=(0,0,1)^T, \end{aligned}$$

where $r=\sqrt{x_1^2+x_2^2}$ and $z=x_3$. Then the 3D velocity field ${\mathbf {u}}(x,t)$ is called axisymmetric if it can be written as

$$\begin{aligned} {\mathbf {u}}=u^r(r, z, t)\mathbf {e_r}+u^\theta (r, z, t)\mathbf {e_\theta }+u^z(r, z, t)\mathbf {e_z}, \end{aligned}$$

where $u^r$, $u^\theta$ and $u^z$ do not depend on the $\theta$ coordinate.

The Euler and Navier–Stokes equations with axisymmetric velocity field can be written in the cylindrical coordinates as

$$\begin{aligned} u^\theta _t+u^ru^\theta _r+u^zu_z^\theta&= \nu \left( \Delta -\frac{1}{r^2}\right) u^\theta -\frac{u^ru^\theta }{r}, \end{aligned}$$

(2.1a)

$$\begin{aligned} \omega ^\theta _t+u^r\omega _r^\theta +{u^z}\omega _z^\theta&= \nu \left( \Delta -\frac{1}{r^2}\right) \omega ^\theta +\frac{2}{r}u^\theta u^\theta _z+\frac{u^r\omega ^\theta }{r}, \end{aligned}$$

(2.1b)

$$\begin{aligned} -\left[ \Delta -\frac{1}{r^2}\right] \phi ^\theta&=\omega ^\theta , \end{aligned}$$

(2.1c)

where the radial and angular velocity fields $u^r$ and $u^\theta$ are recovered from $\phi ^\theta$ based on the Biot–Savart law

$$\begin{aligned} u^r=-\partial _z\phi ^\theta ,\quad u^z=r^{-1}\partial _r(r\phi ^\theta ). \end{aligned}$$

(2.2)

Note that Eqs. (2.1–2.2) have a formal singularity on the axis $r=0$ due to the $\frac{1}{r}$ terms. Because the angular components $u^\theta (r,z)$, $\omega ^\theta (r,z)$ and $\phi ^\theta (r,z)$ can all be viewed as odd functions of r (Liu and Wang 2006), one can introduce the following transformed variables (Hou and Li 2008) to remove the formal singularity in (2.1),

$$\begin{aligned} u_1=u^\theta /r,\quad \omega _1=\omega ^\theta /r,\quad \phi _1=\phi ^\theta /r. \end{aligned}$$

(2.3)

Then one can get the equations for $u_1$ and $\omega _1$ as the following:

$$\begin{aligned} u_{1,t}+u^ru_{1,r}+u^zu_{1,z}&= \nu \left( \partial _r^2+ \frac{3}{r}\partial _r+\partial _z^2\right) u_1+2u_1\phi _{1,z}, \end{aligned}$$

(2.4a)

$$\begin{aligned} \omega _{1,t}+u^r\omega _{1,r}+u^z\omega _{1,z}&= \nu \left( \partial _r^2+ \frac{3}{r}\partial _r+\partial _z^2\right) \omega _1+(u_1^2)_z, \end{aligned}$$

(2.4b)

$$\begin{aligned} -\left[ \partial _r^2+(3/r)\partial _r+\partial _z^2\right] \phi _1&= \omega _1, \end{aligned}$$

(2.4c)

with the Biot–Savart law given by

$$\begin{aligned} u^r=-r\phi _{1,z}, \quad u^z=2\phi _1+r\phi _{1,r}. \end{aligned}$$

(2.5)

For axisymmetric flow, the incompressibility condition becomes

$$\begin{aligned} \partial _r(ru^r)+\partial _z(ru^z)=0. \end{aligned}$$

(2.6)

The Euler and Navier–Stokes equations with axial symmetry have an additional conserved quantity besides the energy (1.2). The total circulation $\Gamma =ru^\theta =r^2u_1$ satisfies the maximum principle,

$$\begin{aligned} \partial _t\Gamma +u^r\Gamma _r+u^z\Gamma _z= \nu \left( \Delta -\frac{2}{r}\partial _r\right) \Gamma ,\quad \Vert \Gamma (\cdot , t)\Vert _{L^\infty }\le \Vert \Gamma (\cdot , 0)\Vert _{L^\infty }. \end{aligned}$$

(2.7)

We change the strength of the convection terms in the Euler and Navier–Stokes equation (2.4) by a factor of $\epsilon$ and get the following Biot–Savart law and models of the Euler and Navier–Stokes equations,

$$\begin{aligned} u^r=-\epsilon r\phi _{1,z},\quad u^z=2\epsilon \phi _1+\epsilon r\phi _{1,r}. \end{aligned}$$

(2.8)

In this work, we study the family of models (2.8) with $\epsilon \in [0, 2)$ to demonstrate the balance between the convection terms and the vortex stretching terms in (2.4), and the potential stabilizing effect of convection.

Note that we change the strength of the convection in a form of the Euler and Navier–Stokes equations written using transformed variables $u_1$ and $\omega _1$ (2.3), not the original velocity–pressure form (1.1). Next we derive an equivalent formulation for the family of models (2.8) in the velocity–pressure formulation.

Multiplying Eq. (2.4) by r and using (2.8), we get

$$\begin{aligned} u^\theta _t+u^r u^\theta _r+u^z u^\theta _z- \frac{u^ru^\theta }{r}&=-\frac{2}{\epsilon }\frac{u^ru^\theta }{r}+\nu \left( \Delta -\frac{1}{r^2}\right) u^\theta , \end{aligned}$$

(2.9)

$$\begin{aligned} \omega ^\theta _t+u^r \omega _r+u^z \omega _z-\frac{u^r\omega ^\theta }{r}&=\frac{(u^\theta )^2_z}{r}+\nu \left( \Delta -\frac{1}{r^2}\right) \omega ^\theta . \end{aligned}$$

(2.10)

Because the $\frac{1}{\epsilon }$ term does not allow $\epsilon =0$, we make change of variables

$$\begin{aligned} v^r=\frac{u^r}{\epsilon }=-r\phi _{1,z}, \quad v^z=\frac{u^z}{\epsilon }=2\phi _1+r\phi _{1, r},\quad v^\theta =\frac{u^\theta }{\epsilon ^{3/2}}. \end{aligned}$$

(2.11)

Based on (2.8) and (2.4c), we have

$$\begin{aligned} \omega ^\theta =(\partial _z v^r-\partial _r v^z). \end{aligned}$$

(2.12)

Then we denote $F_r(t, r, z)$ and $F_z(t,r,z)$ as

$$\begin{aligned} F_r(t,r,z)&=v^r_t+\epsilon v^rv^r_r+\epsilon v^zv^r_z-\epsilon \frac{(v^\theta )^2}{r}-\nu \left( \Delta -\frac{1}{r^2}\right) v^r,\\ F_z(t,r,z)&=v^z_t+\epsilon v^rv^z_r+\epsilon v^zv^z_r-\nu \Delta v^z. \end{aligned}$$

Comparing $\partial _z F^r-\partial _r F^z$ with (2.10), we obtain

$$\begin{aligned} \partial _z F^r(t, r, z)-\partial _r F^z(t,r,z)=0, \end{aligned}$$

so there exists a scalar field p such that $F^r=\partial _z p$, $F^z=\partial _r p$. Namely,

$$\begin{aligned} v^r_t+\epsilon v^rv^r_r+\epsilon v^zv^r_z-\epsilon \frac{(v^\theta )^2}{r}+\partial _r p&= \nu \left( \Delta -\frac{1}{r^2}\right) v^r, \end{aligned}$$

(2.13)

$$\begin{aligned} v^z_t+\epsilon v^rv^z_r+\epsilon v^zv^z_r+\partial _z p&=\nu \Delta v^z. \end{aligned}$$

(2.14)

And p is determined by the incompressibility condition (2.6).

Then we denote the new velocity field ${\mathbf {v}}$ as

$$\begin{aligned} {\mathbf {v}}=v^r \mathbf {e_r}+v^\theta \mathbf {e_\theta }+v^z\mathbf {e_z}. \end{aligned}$$

Changing Eqs. (2.13), (2.14) back to the physical coordinates, we get

$$\begin{aligned} {\mathbf {v}}_t+\epsilon {\mathbf {v}}\cdot \nabla {\mathbf {v}}=-\nabla p+\nu \Delta {\mathbf {v}}+(2\epsilon -2)\frac{v^\theta v^r \mathbf {e_\theta }}{r}. \end{aligned}$$

(2.15)

So the family of models, (2.4) and (2.8), which are originally derived by changing the strength of the convection terms in the governing equations of a set of transformed variables $\frac{u^\theta }{r}$ and $\frac{\omega ^\theta }{r}$, can also be derived by changing the strength of convection in (1.1) and adding a stirring forcing of the form

$$\begin{aligned} {\mathbf {F}}=(2\epsilon -2)\frac{v^\theta v^r \mathbf {e_\theta }}{r}. \end{aligned}$$

Remark 2.1

The third change of variable in (2.11) requires $\epsilon >0$, without which we will get an additional radial forcing term $\frac{(v^\theta )^2}{r}\mathbf {e_r}$ in (2.15), and our proof of the regularity results in Sect. 3 still goes through.

2.2 Review of Regularity Results for the 3D Euler and Navier–Stokes Equations

A lot of important progresses have been made concerning the regularity of the Euler and Navier–Stokes equations. In the 2D case, the global regularity holds (Majda and Bertozzi 2002) because one can get a priori estimate of the maximum vorticity $\mathbf {\omega }=\nabla \times {\mathbf {u}}$. For the Euler equations, the celebrated BKM criterion (Beale et al. 1984; Ferrari 1993) asserts that if $\int _0^T \Vert \mathbf {\omega }(t)\Vert _\infty \mathrm{d}t <+\infty$, then the solutions remain smooth up to time T. We will prove the same criterion for the inviscid model (2.8) in Sect. 3. The non-blow-up criterion of Constantin et al. (1996) focuses on the geometric aspects the 3D Euler flows and asserts that there can be no blowup if the velocity field ${\mathbf {u}}$ is uniformly bounded and the vorticity direction $\xi =\omega /|\omega |$ is sufficiently “well behaved” near the point of maximum vorticity. The theorem of Deng et al. (2005, 2006) is similar in spirit to the Constantin–Fefferman–Majda criterion, but confines the analysis to localized vortex line segments. They assert that if the vorticity direction is well behaved on a local region near the maximum vorticity, then the solutions remain regular. To be specific, their theorems allow the area of the region to collapse to zero.

For the 3D Navier–Stokes equations, if the initial data are small in certain critical norm, say $\Vert {\mathbf {u}}\Vert _{L^2}\Vert \nabla {\mathbf {u}}\Vert _{L^2}$, then the solutions will remain bounded and smooth for all time. See Koch and Tataru (2001) for an essentially optimal result in this direction. The criterion of Prodi (1959) and Serrin (1963) claims that for $\frac{3}{p} + \frac{2}{q} =1$, $3<p\le +\infty$, if $\Vert {\mathbf {u}}(x,t)\Vert _{L^q(L^p(R^3), [0, T))}<+\infty$, then the solutions can be extended smoothly beyond time T. The critical case of $p=3$ and $q=+\infty$ also implies regularity of the solutions, and this result was proved by Escauriaza et al. (2003) using essentially different techniques, which rely on a unique continuation property for the backward heat equations. We will prove a Prodi–Serrin type criterion for the viscous model (2.8) in Sect. 3.

To demonstrate the supercritical barrier in the 3D Navier–Stokes equations, Tao recently proposed a 3D model (Tao 2016) where the nonlinearity term $B({\mathbf {u}}, {\mathbf {u}})$ in (1.1) is replaced by a highly non-trivial averaging term ${{\tilde{B}}}({\mathbf {u}}, {\mathbf {u}})$. The averaged bilinear operator ${{\tilde{B}}}(\cdot , \cdot )$ shares several estimates with $B(\cdot , \cdot )$, and it is proved that the averaged model can develop finite-time singularity.

There also exist a lot of works in the literature that focus on the numerical search of a finite-time singularity for the Euler equations. See Grauer and Sideris (1991), Pumir and Siggia (1992) and Weinan and Shu (1994) for the numerical study of the axisymmetric Euler equations, and Kerr (1993), Hou and Li (2006) for Euler flows generated by perturbed antiparallel vortex tubes. The numerical results mentioned above have been non-conclusive since there is no stable structure in the potentially singular solutions. In a recent numerical computation by Luo and Hou (2014) for the 3D axisymmetric Euler equations, the solutions were observed to develop singularity on the boundary with local self-similar structure. Several works were motivated by this computation, including two 1D models (Hou and Luo 2013; Choi et al. 2014, 2015) and a self-similar singularity result (Hou and Liu 2015) for one of the models. For the inviscid models that we study in this work, the singular solutions also develop stable local self-similar structure, and the singular region is not stationary but traveling along the symmetric axis.

3 Some Regularity Results

The velocity field ${\mathbf {v}}$ in Eq. (2.15) is divergence-free according to (2.6),

$$\begin{aligned} \partial _r (r v^r)+\partial _z (r v^z)=\partial _r(-r^2\phi _{1,z})+\partial _z(2 r\phi _1+ r^2\phi _{1,r})=0, \end{aligned}$$

and thus the 3D models (2.15) are still incompressible.

The inviscid models (2.8) with $\nu =0$ enjoy the following scaling invariance,

$$\begin{aligned} u_1(r, z, t)\rightarrow \frac{1}{\tau }u_1\left( \frac{r}{\lambda }, \frac{z}{\lambda },\frac{t}{\tau }\right) , \quad \omega _1(r, z,t)\rightarrow \frac{1}{\lambda \tau }\omega _1\left( \frac{r}{\lambda }, \frac{z}{\lambda }, \frac{t}{\tau }\right) ; \end{aligned}$$

(3.1)

while for the viscous models $\nu >0$, we have,

$$\begin{aligned}&u_1(r, z,t)\rightarrow \frac{1}{\tau }u_1\left( \frac{r}{\tau ^{1/2}}, \frac{z}{\tau ^{1/2}}, \frac{t}{\tau }\right) , \nonumber \\&\omega _1(r, z,t)\rightarrow \tau ^{-3/2} \omega _1\left( \frac{r}{\tau ^{1/2}}, \frac{z}{\tau ^{1/2}}, \frac{t}{\tau }\right) . \end{aligned}$$

(3.2)

Note that the introduction of viscosity $\nu >0$ restricts the two-parameter symmetry group in (3.1) to the one-parameter group in (3.2).

The models also enjoy translational invariance in the axial direction,

$$\begin{aligned} u_1(r, z,t)\rightarrow u_1(r, z-c, t), \quad \omega _1(r, z,t)\rightarrow \omega _1 (r, z-c, t). \end{aligned}$$

(3.3)

The scaling and translational invariances (3.1), (3.3) allow for the traveling self-similar singularity of the inviscid models that will be demonstrated in Sect. 4.

The Laplace operators in the evolution equations of $u_1$ (2.4a), $\omega _1$ (2.4b), and the Biot–Savart law (2.4c), namely

$$\begin{aligned} \partial _r^2+\frac{3}{r}\partial _r+\partial _z^2 \end{aligned}$$

are essentially five-dimensional Laplace operator with axial symmetry. It is convenient to view the 3D model (2.8) as defined on $y\in R^5$ with

$$\begin{aligned} y=(y_1, y_2, y_3, y_4, z)\in R^5, \quad r=\left( y_1^2 + y_2^2+y_3^2+y_4^2\right) ^{1/2}, \end{aligned}$$

and the solutions are symmetric with respect to $y_i$, $i=1,2 \dots 4$.

The new 3D models (2.8) enjoy the following energy identity for $\epsilon <2$.

Theorem 3.1

For smooth solutions to the 3D model (2.8) with $\epsilon <2$, the following identity holds,

$$\begin{aligned}&\frac{1}{2}\frac{d}{\mathrm{d}t}\int _{-\infty }^\infty \int _0^\infty \left( |u_1|^2+(2-\epsilon )|\nabla _y \phi _1|^2\right) r^3\mathrm{d}r\mathrm{d}z \nonumber \\&\quad +\, \nu \int _{-\infty }^\infty \int _0^\infty \left( |\nabla _y u_1|^2+(2-\epsilon )|\Delta _y\phi _1|^2\right) r^3\mathrm{d}r\mathrm{d}z=0. \end{aligned}$$

(3.4)

Remark 3.2

We denote the energy functional in the above identity as,

$$\begin{aligned} E_\epsilon = \int _{-\infty }^\infty \int _0^\infty \left( |u_1|^2+(2-\epsilon )|\nabla _y \phi _1|^2\right) r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

(3.5)

For $\epsilon =1$, $E_1$ is the same as the $L^2$ energy of the original Euler and Navier–Stokes equations in the energy identity (1.2),

$$\begin{aligned} E_1=\frac{1}{2\pi }\int _{R^3}|{\mathbf {u}}|^2\mathrm{d}x. \end{aligned}$$

For $\epsilon <2$, $E_\epsilon$ is equivalent to the $L^2$ energy of Euler and Navier–Stokes equations. To be specific, we have that

$$\begin{aligned} \min (1, 2-\epsilon )E_1\le E_\epsilon \le \max (1, 2-\epsilon )E_1. \end{aligned}$$

Proof

Multiplying the first Eq. (2.4a) by $u_1r^3$, and integrating over d r d z, which is equivalent to the 5D Lebesgue measure d y, we get

$$\begin{aligned}&\frac{1}{2}\frac{d}{\mathrm{d}t}\int u_1^2r^3\mathrm{d}r\mathrm{d}z+\frac{1}{2}\int (u^rr) r^2 \left( u_1^2\right) _r\mathrm{d}r\mathrm{d}z+\frac{1}{2}\int (u^zr) r^2\left( u_1^2\right) _z\mathrm{d}r\mathrm{d}z\\&\quad =\int 2u_1^2\phi _{1,z}r^3\mathrm{d}r\mathrm{d}z-\nu \int |\nabla _y u_1|^2r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

For the convection terms, using integration by part, one can get

$$\begin{aligned}&\frac{1}{2}\int (u^rr) r^2 \left( u_1^2\right) _r\mathrm{d}r\mathrm{d}z+\frac{1}{2}\int (u^zr) r^2 \left( u_1^2\right) _z\mathrm{d}r\mathrm{d}z=\\&\quad -\frac{1}{2}\int \left( (u^rr)_r+(u^zr)_z\right) r^2 u_1^2\mathrm{d}r\mathrm{d}z-\int u^rr^2u_1^2 \mathrm{d}r\mathrm{d}z. \end{aligned}$$

Using the divergence-free condition $(ru^r)_r+(ru^z)_z=0$, one can get

$$\begin{aligned} \frac{1}{2}\int (u^rr) r^2 \left( u_1^2\right) _r\mathrm{d}r\mathrm{d}z+\frac{1}{2}\int (u^zr) r^2\left( u_1^2\right) _z\mathrm{d}r\mathrm{d}z=-\int u^rr^2u_1^2\mathrm{d}r\mathrm{d}z. \end{aligned}$$

Then we have

$$\begin{aligned} \frac{1}{2}\frac{d}{\mathrm{d}t}\int u_1^2r^3\mathrm{d}r\mathrm{d}z-\int u^rr^2u_1^2\mathrm{d}r\mathrm{d}z =\int 2u_1^2\phi _{1,z}r^3\mathrm{d}r\mathrm{d}z-\nu \int |\nabla _y u_1|^2r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

Using the Biot–Savart law $u^r=-\epsilon r\phi _{1,z}$, we get that

$$\begin{aligned} \frac{1}{2}\frac{d}{\mathrm{d}t}\int u_1^2r^3\mathrm{d}r\mathrm{d}z=\int (2-\epsilon )u_1^2\phi _{1,z}r^3\mathrm{d}r\mathrm{d}z-\nu \int |\nabla _y u_1|^2r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

(3.6)

Multiplying (2.4b) by $\phi _1r^3$, and using $-\Delta \phi _1=\omega _1$, we have

$$\begin{aligned}&\frac{1}{2}\frac{d}{\mathrm{d}t}\int |\nabla \phi _1|^2r^3\mathrm{d}r\mathrm{d}z+\int (u^rr)\omega _{1,r}\phi _1r^2\mathrm{d}r\mathrm{d}z+\int (u^zr)\omega _{1,z}\phi _1r^2\mathrm{d}r\mathrm{d}z\\&\quad =-\int u_1^2\phi _{1,z}r^3\mathrm{d}r\mathrm{d}z-\nu \int |\Delta _y\phi _1|^2r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

For the convection terms, using integration by part we get

$$\begin{aligned}&\int (u^rr)\omega _{1,r}\phi _1r^2\mathrm{d}r\mathrm{d}z+\int (u^zr)\omega _{1,z}\phi _1r^2\mathrm{d}r\mathrm{d}z=\\&\quad -\int \left( (u^rr)_r+(u^zr)_z\right) \omega _1\phi _1r^2\mathrm{d}r\mathrm{d}z \\&\quad -\int \left[ u^rr\omega _1\left( \phi _1r^2\right) _r+ u^zr\omega _1\left( \phi _1r^2\right) _z\right] \mathrm{d}r\mathrm{d}z. \end{aligned}$$

The first term in the RHS vanishes due to (2.6), and the second term also vanishes based on the Biot–Savart law (2.8). Then we have

$$\begin{aligned} \frac{1}{2}\frac{d}{\mathrm{d}t}\int |\nabla \phi _1|^2r^3\mathrm{d}r\mathrm{d}z =-\int u_1^2\phi _{1,z}r^3\mathrm{d}r\mathrm{d}z-\nu \int |\Delta _y\phi _1|^2r^3\mathrm{d}r\mathrm{d}z. \end{aligned}$$

(3.7)

Adding up (3.6) and (3.7), we can complete the proof. $\square$

For the family of 3D models (2.8) with $\epsilon >0$, we define the modified circulation as

$$\begin{aligned} \Gamma ^\epsilon =r^{2/\epsilon }u_1, \end{aligned}$$

(3.8)

which plays the same role as the circulation $\Gamma$ for the axisymmetric Euler and Navier–Stokes equations in (2.7). We can derive the equation of $\Gamma ^\epsilon$ as

$$\begin{aligned} \partial _t\Gamma ^\epsilon +u^r\Gamma ^\epsilon _r+u^z\Gamma ^\epsilon _z =\nu \left( \Delta -\frac{2}{r} \left( \frac{2}{\epsilon }-1\right) \partial _r+ \frac{1}{r^2}\frac{2}{\epsilon } \left( \frac{2}{\epsilon }-2\right) \right) \Gamma ^\epsilon . \end{aligned}$$

(3.9)

Then for the inviscid model with $\nu =0$, or the viscous model with $\nu >0$, $\epsilon \ge 1$, we have the maximal principle

$$\begin{aligned} \Vert \Gamma ^\epsilon (r, z, t)\Vert _{L^\infty }\le \Vert \Gamma ^\epsilon (r, z, 0)\Vert _{L^\infty }. \end{aligned}$$

And in the viscous models with $\epsilon >1$, the quantity $\Gamma ^\epsilon$ is indeed subcritical with respect to the scaling of the equations in (3.2).

For the inviscid 3D model (2.8) with $\nu =0$, we have the following Beale–Kato–Majda type non-blow-up criterion for ${\mathbf {v}}=v^r \mathbf {e_r}+v^z \mathbf {e_z}+v^\theta \mathbf {e_\theta }$.

Theorem 3.3

For initial data ${\mathbf {v}}(x,0)\in H^4(R^3)$, if

$$\begin{aligned} \int _0^T\Vert \nabla \times {\mathbf {v}}(t)\Vert _{\mathrm{BMO}}\mathrm{d}t<+\infty , \end{aligned}$$

(3.10)

then ${\mathbf {v}}(x,T)\in H^4(R^3)$, and the solutions can be extended beyond time T.

We need the following estimate proved by Kozono and Taniuchi (2000). For divergence-free velocity field ${\mathbf {v}}(x)$ in $R^3$, the following holds:

$$\begin{aligned} \Vert \nabla _x {\mathbf {v}}\Vert _{L^\infty }\le C\left[ 1+\Vert \nabla \times {\mathbf {v}}\Vert _{\mathrm{BMO}}\ln \left( 1+\Vert {\mathbf {v}}\Vert ^2_{H^4}\right) \right] . \end{aligned}$$

(3.11)

We also need the following estimates of Klainerman and Majda (1981):

$$\begin{aligned} \Vert fg\Vert _{H^m}\le c\Vert f\Vert _{L^\infty }\Vert D^m g\Vert _{L^2(R^N)}+c\Vert D^mf\Vert _{L^2(R^N)}\Vert g\Vert _{L^\infty }, \end{aligned}$$

(3.12)

$$\begin{aligned} \begin{aligned}&\sum _{0\le |\alpha |\le m} \Vert D^\alpha (fg)-fD^\alpha g\Vert _{L^2(R^N)}\\&\quad \le c\Vert \nabla f\Vert _{L^\infty } \Vert D^{m-1}g\Vert _{L^2(R^N)}+c\Vert D^m f\Vert _{L^2(R^N)}\Vert g\Vert _{L^\infty }. \end{aligned} \end{aligned}$$

(3.13)

To estimate the stirring term in (2.15), we use the following Lemma.

Lemma 3.4

For smooth axisymmetric solutions to (2.15), ${\mathbf {v}}\in H^4(R^3)$,

$$\begin{aligned} \left\| D^4 \frac{v^rv^\theta \mathbf {e_\theta }}{r}\right\| _{L^2(R^3)}\le \Vert \nabla {\mathbf {v}}\Vert _{L^\infty } \Vert {\mathbf {v}}\Vert _{H^4}. \end{aligned}$$

We prove Lemma 3.4 using the estimates for axisymmetric solenoidal vector fields that are obtained in Liu and Wang (2006). Denote the operator ${\mathcal {L}}$ as

$$\begin{aligned} {\mathcal {L}}=-\Delta _3+\frac{1}{r^2}, \end{aligned}$$

where $\Delta _3$ is the three-dimensional Laplace operator

$$\begin{aligned} \Delta _3=\partial _r^2+\frac{1}{r}\partial _r+\partial _z^2. \end{aligned}$$

Then for every smooth axisymmetric solenoidal vector field

$$\begin{aligned} {\mathbf {F}}=F^\theta \mathbf {e_\theta }-\partial _z\varphi ^\theta \mathbf {e_r}+\frac{\partial _r(r\varphi ^\theta )}{r}\mathbf {e_z}, \end{aligned}$$

(3.14a)

we have

$$\begin{aligned} \Vert D^4{\mathbf {F}}\Vert ^2_{L^2(R^3)}=\Vert {\mathcal {L}}^2 F^\theta \Vert ^2_{L^2(R^3)}+\Vert {\mathcal {L}}^2\varphi ^\theta \Vert _*^2, \end{aligned}$$

(3.14b)

where

$$\begin{aligned} \Vert f\Vert _*^2=\Vert \partial _r f\Vert _{L^2(R^3)}^2+\Vert \partial _z f\Vert _{L^2(R^3)}^2+\left\| \frac{f}{r}\right\| _{L^2(R^3)}^2. \end{aligned}$$

(3.14c)

One can easily verify that the operator ${\mathcal {L}}$ can be represented as

$$\begin{aligned} {\mathcal {L}}(\cdot )=-r\Delta _5 \left( \frac{\cdot }{r}\right) , \end{aligned}$$

(3.15)

where $\Delta _5$ is the 5D Laplace operator

$$\begin{aligned} \Delta _5=\partial _r^2+\frac{3}{r}\partial _r+\partial _z^2. \end{aligned}$$

With the above preparation (3.14), (3.15), we can now prove Lemma 3.4.

Proof

Using (3.14) with $F^\theta =\frac{v^rv^\theta }{r}$, $\varphi =0$, we have

$$\begin{aligned} \left\| D^4 \frac{v^rv^\theta \mathbf {e_\theta }}{r}\right\| _{L^2(R^3)}=\left\| {\mathcal {L}}^2 \frac{v^rv^\theta }{r}\right\| _{L^2(R^3)}. \end{aligned}$$

Then using (3.15), we have

$$\begin{aligned} \left\| {\mathcal {L}}^2 \frac{v^rv^\theta }{r}\right\| _{L^2(R^3)}=\left\| r\Delta _5^2 \frac{v^rv^\theta }{r^2}\right\| _{L^2(R^3)}=\left\| \Delta _5^2 \frac{v^rv^\theta }{r^2}\right\| _{L^2(R^5)}=\left\| D^4 \frac{v^rv^\theta }{r^2}\right\| _{L^2(R^5)}. \end{aligned}$$

Then using estimate (3.12), we have

$$\begin{aligned} \left\| D^4 \frac{v^rv^\theta \mathbf {e_\theta }}{r^2}\right\| _{L^2(R^3)}\le c\left\| \frac{v^r}{r}\right\| _{L^\infty } \left\| D^4\frac{v^\theta }{r}\right\| _{L^2(R^5)}+ c\left\| \frac{v^\theta }{r}\right\| _{L^\infty } \left\| D^4\frac{v^r}{r}\right\| _{L^2(R^5)}. \nonumber \\ \end{aligned}$$

(3.16)

Since $v^r$, $v^\theta$ vanish on the symmetric axis, we have

$$\begin{aligned} \left| \frac{v^r}{r}\right| , \quad \left| \frac{v^\theta }{r}\right| \le \left\| \nabla {\mathbf {v}}\right\| _{L^\infty }. \end{aligned}$$

(3.17)

Next, we estimate $\Vert D^4\frac{v^\theta }{r}\Vert _{L^2(R^5)}$ and $\Vert D^4\frac{v^r}{r}\Vert _{L^2(R^5)}$. We have that

$$\begin{aligned} \left\| D^4\frac{v^\theta }{r}\right\| _{L^2(R^5)}=\left\| \Delta _5^2 \frac{v^\theta }{r}\right\| _{L^2(R^5)}=\left\| \frac{1}{r}{\mathcal {L}}^2 v^\theta \right\| _{L^2(R^5)}=\left\| {\mathcal {L}}^2 v^\theta \right\| _{L^2(R^3)}, \end{aligned}$$

(3.18)

where we have used (3.15) in the second equality and change of measure in the third equality. Therefore, using (3.14) with ${\mathbf {F}}={\mathbf {v}}$, we have

$$\begin{aligned} \left\| D^4\frac{v^\theta }{r}\right\| _{L^2(R^5)}=\Vert {\mathcal {L}}^2 v^\theta \Vert _{L^2(R^3)}\le \Vert {\mathbf {v}}\Vert _{H^4(R^3)}. \end{aligned}$$

(3.19)

Similarly, using (3.15) and change of measure as in (3.18), we have

$$\begin{aligned} \left\| D^4\frac{v^r}{r}\right\| _{L^2(R^5)}=\Vert {\mathcal {L}}^2 v^r\Vert _{L^2(R^3)}=\Vert \partial _z{\mathcal {L}}^2 \phi ^\theta \Vert _{L^2(R^3)}. \end{aligned}$$

(3.20)

Then according to (3.14) with ${\mathbf {F}}={\mathbf {v}}$, we have

$$\begin{aligned} \left\| D^4\frac{v^r}{r}\right\| _{L^2(R^5)}=\Vert \partial _z{\mathcal {L}}^2 \phi ^\theta \Vert _{L^2(R^3)}\le \Vert {\mathbf {v}}\Vert _{H^4(R^3)}. \end{aligned}$$

(3.21)

Finally using (3.17), (3.19) and (3.21) in (3.16), we finish the proof. $\square$

Now we prove the BKM Theorem 3.3 for the inviscid model (2.15).

Proof

Taking $D^\alpha$ with $|\alpha |=4$ for both sides of Eq. (2.15), and computing its $L^2$ inner product with $D^\alpha v$, we get

$$\begin{aligned} \frac{1}{2}\frac{d}{\mathrm{d}t}\Vert D^\alpha {\mathbf {v}}\Vert ^2_{L^2(R^3)}=-\epsilon (D^\alpha {\mathbf {v}}, D^\alpha ({\mathbf {v}}\cdot \nabla {\mathbf {v}}))+\left( D^\alpha {\mathbf {v}}, D^\alpha \frac{v^rv^\theta \mathbf {e^\theta }}{r}\right) , \end{aligned}$$

(3.22)

where we have used $(\cdot , \cdot )$ to denote the $L^2$ inner product on $R^3$.

Using the divergence-free condition, we have

$$\begin{aligned} (D^\alpha {\mathbf {v}}, {\mathbf {v}}\cdot D^\alpha {\mathbf {v}})=0. \end{aligned}$$

Then for the first term on the right-hand side of (3.22), we have

$$\begin{aligned} -(D^\alpha {\mathbf {v}}, D^\alpha ({\mathbf {v}}\cdot \nabla {\mathbf {v}}))=-(D^\alpha {\mathbf {v}}, D^\alpha ({\mathbf {v}}\cdot \nabla {\mathbf {v}})-{\mathbf {v}}\cdot D^\alpha {\mathbf {v}}). \end{aligned}$$

Using the Hölder inequality and estimate (3.13), we have

$$\begin{aligned} -(D^\alpha {\mathbf {v}}, D^\alpha ({\mathbf {v}}\cdot \nabla {\mathbf {v}}))\le C\Vert D^\alpha {\mathbf {v}}\Vert _{L^2(R^3)}\Vert \nabla {\mathbf {v}}\Vert _{L^\infty }\Vert D^\alpha {\mathbf {v}}\Vert _{L^2(R^3)}. \end{aligned}$$

For the second term on the right-hand side of (3.22), using Lemma (3.4), we have

$$\begin{aligned} \left( D^\alpha {\mathbf {v}}, D^\alpha \frac{v^rv^\theta \mathbf {e_\theta }}{r}\right) \le C\Vert \nabla {\mathbf {v}}\Vert _{L^\infty }\Vert D^\alpha {\mathbf {v}}\Vert _{L^2(R^3)}^2. \end{aligned}$$

Putting these estimates in (3.22), we have

$$\begin{aligned} \frac{d}{\mathrm{d}t}\Vert D^\alpha {\mathbf {v}}\Vert _{L^2(R^3)}^2\le C\Vert \nabla {\mathbf {v}}\Vert _{L^\infty } \Vert {\mathbf {v}}\Vert _{H^4}^2. \end{aligned}$$

(3.23)

This together with the $L^2$ estimate (3.4), and the estimate (3.11), gives

$$\begin{aligned} \begin{aligned}&\Vert {\mathbf {v}}(t)\Vert _{H^4}^2-\Vert {\mathbf {v}}(0)\Vert _{H^4}^2\\&\quad \le C\int _0^t \Vert {\mathbf {v}}(s)\Vert _{H^4}(1+\Vert \nabla \times {\mathbf {v}}\Vert _{\mathrm{BMO}}\ln (1+\Vert {\mathbf {v}}(s)\Vert ^2_{H^4}))\mathrm{d}s. \end{aligned} \end{aligned}$$

Then using the Gronwall’s inequality and (3.10), we finish the proof that

$$\begin{aligned} \Vert {\mathbf {v}}(T)\Vert _{H^4(R^3)}<+\infty . \end{aligned}$$

$\square$

For the viscous model (2.15) with $\nu >0$ , we have the following Prodi–Serrin type non-blow-up criterion.

Theorem 3.5

For smooth solutions to (2.15) with ${\mathbf {v}}(x, 0)\in H^1(R^3)$, if

$$\begin{aligned} {\mathbf {v}}(x,t)\in L^q( L^p(R^3), [0, T)), \end{aligned}$$

(3.24)

with

$$\begin{aligned} \frac{3}{p}+\frac{2}{q}=1, \quad 3<p\le +\infty , \end{aligned}$$

then the solutions can be smoothly extended beyond T.

We need the following 1D Hardy inequality to estimate the additional stirring term in (2.15); see Hardy et al. (1952).

Lemma 3.6

If $\lambda >1$, $\sigma >1$, f(r) is a nonnegative measurable function, and F(r) is defined by

$$\begin{aligned} F(r)=\int _0^r f(t)\mathrm{d}t, \end{aligned}$$

then

$$\begin{aligned} \int _0^\infty r^{-\sigma }F^\lambda \mathrm{d}r\le \left( \frac{\lambda }{\sigma -1}\right) ^\lambda \int _0^\infty r^{-\sigma }(rf)^\lambda \mathrm{d}r. \end{aligned}$$

(3.25)

Now we prove Theorem 3.5 using Lemma (3.6). We only consider the case that $3<p<+\infty$, and the case that $p=+\infty$ is easier.

Proof

Multiplying both sides of Eq. (2.15) by $-\Delta {\mathbf {v}}$, we get

$$\begin{aligned} \frac{1}{2}\frac{d}{\mathrm{d}t} \Vert \nabla {\mathbf {v}}\Vert _{L^2}^2\le \int _{R^3} |\Delta {\mathbf {v}}||{\mathbf {v}}||\nabla {\mathbf {v}}|\mathrm{d}x+\int _{R^3} |\Delta {\mathbf {v}}|\left| \frac{v^rv^\theta }{r}\right| \mathrm{d}x-\nu \Vert \Delta {\mathbf {v}}\Vert ^2_{L^2}. \end{aligned}$$

(3.26)

Using the Hölder inequality, we have the following estimate for the first term on the right-hand side of (3.26),

$$\begin{aligned} \begin{aligned} \int _{R^3} |\Delta {\mathbf {v}}| |{\mathbf {v}}| |\nabla {\mathbf {v}}|\mathrm{d}x&\le \frac{\nu }{4}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2+C\int _{R^3} |{\mathbf {v}}|^2|\nabla {\mathbf {v}}|^2\mathrm{d}x\\&\le \frac{\nu }{4}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2+C\Vert {\mathbf {v}}\Vert _{L^p}^2\Vert \nabla {\mathbf {v}}\Vert _{L^{2p/(p-2)}}^2. \end{aligned} \end{aligned}$$

(3.27)

For the second term on the right-hand side of (3.26), using Hölder inequality twice, we have

$$\begin{aligned} \begin{aligned} \int _{R^3} |\Delta {\mathbf {v}}| |v^\theta |\left| \frac{v^r}{r}\right| \mathrm{d}x&\le \frac{\nu }{4}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2+C\int _{R^3} |v^\theta |^2\left| \frac{v^r}{r}\right| ^2\mathrm{d}x\\&\le \frac{\nu }{4}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2+C\Vert {\mathbf {v}}\Vert _{L^p}^2\left( \int _{R^3} \frac{(v^r)^{2p/(p-2)}}{r^{2p/(p-2)}}\mathrm{d}x\right) ^{\frac{p}{p-2}}.\qquad \qquad \end{aligned} \end{aligned}$$

(3.28)

Changing the integral to the cylindrical coordinates, we have

$$\begin{aligned} \int _{R^3} \frac{(v^r)^{2p/(p-2)}}{r^{2p/(p-2)}}\mathrm{d}x=\int _R \int _0^\infty \frac{(v^r)^{2p/(p-2)}}{r^{(p+2)/(p-2)}}\mathrm{d}r\mathrm{d}z. \end{aligned}$$

(3.29)

Since $v^r=0$ on the symmetric axis, using estimate (3.25) with $F(r)=v^r, f(r)=\partial _r v^r, \sigma =\frac{p+2}{p-2}, \lambda =\frac{2n}{n-2}$, we get

$$\begin{aligned} \begin{aligned} \int _R \int _0^\infty \frac{(v^r)^{2p/(p-2)}}{r^{(p+2)/(p-2)}}\mathrm{d}r\mathrm{d}z&\le C\int _R \int _0^\infty r (v^r_r)^{2p/(p-2)}\mathrm{d}r\mathrm{d}z\\&\le C \int _{R^3} |\nabla {\mathbf {v}}|^{2p/(p-2)} \mathrm{d}x. \end{aligned} \end{aligned}$$

(3.30)

Substituting (3.30) and (3.29) in (3.28), we get

$$\begin{aligned} \int |\Delta {\mathbf {v}}| |v^\theta |\left| \frac{v^r}{r}\right| \mathrm{d}x\le \frac{\nu }{4}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2+C\Vert {\mathbf {v}}\Vert _{L^p}^2\Vert \nabla {\mathbf {v}}\Vert _{L^{2p/(p-2)}}^2. \end{aligned}$$

(3.31)

Finally we use the Gagliardo–Nirenberg interpolation inequality (Nirenberg 1959),

$$\begin{aligned} \Vert \nabla {\mathbf {v}}\Vert ^2_{L^{2p/(p-2)}}\le C\Vert \nabla {\mathbf {v}}\Vert _{L^2}^{4/q}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^{6/p}. \end{aligned}$$

(3.32)

Putting the estimates (3.27), (3.31), (3.32) in (3.26), we have

$$\begin{aligned} \frac{d}{\mathrm{d}t} \Vert \nabla {\mathbf {v}}\Vert _{L^2}^2\le C\Vert {\mathbf {v}}\Vert _{L^p}^2\Vert \nabla {\mathbf {v}}\Vert _{L^2}^\frac{4}{q}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^{6/p}-\frac{\nu }{2}\Vert \Delta {\mathbf {v}}\Vert _{L^2}^2. \end{aligned}$$

Then using the Hölder inequality and the fact that $\frac{2}{q}+\frac{3}{p}=1$, we get

$$\begin{aligned} \frac{d}{\mathrm{d}t} \Vert \nabla {\mathbf {v}}\Vert _{L^2}^2\le C\Vert {\mathbf {v}}\Vert _{L^p}^q \Vert \nabla {\mathbf {v}}\Vert ^2_{L^2}. \end{aligned}$$

(3.33)

Using (3.24) in (3.33), we can finish the proof of the theorem. $\square$

4 Self-Similar Singularity of the Inviscid Models with Weak Convection

In this section, we numerically study the inviscid models (2.8) with different values of $\epsilon$. We employ two approaches in our numerical investigation, the direct numerical simulation and the dynamic rescaling formulation. In the direct numerical simulation, we observe that with weak convection the numerical solutions develop self-similar singularity with the singular region traveling along the symmetric axis, and such singularity formation scenario does not persist for strong convection. Then we introduce the dynamic rescaling formulation that governs the evolution of the spatial profiles in the singular solutions and demonstrate the linear stability of the traveling self-similar singularity.

4.1 Direct Numerical Simulation of the Models

We consider solving the inviscid models (2.8) in a periodic cylinder,

$$\begin{aligned} (r, z)\in [0,1]\times [0,2], \end{aligned}$$

with no-flow boundary condition. The no-flow boundary condition requires the following boundary condition for the Poisson equation (2.4c),

$$\begin{aligned} \phi _1|_{r=1}=0. \end{aligned}$$

For $\epsilon =0$, we choose the following initial data

$$\begin{aligned} \omega _1(r,z)=0,\quad u_1(r,z)=300 \sin ^{20}\left( \frac{\pi }{2} z\right) (r^2-1)^{40}. \end{aligned}$$

(4.1)

Then according to Eq. (2.4), $\omega _1$ will remain odd at $z=0$ and $z=1$, and $u_1$ will remain even at $z=0$ and $z=1$. Thus in our numerical simulation, we only need to solve the equations on a computational domain

$$\begin{aligned} D=(r, z)\in [0,1]\times [0,1]. \end{aligned}$$

(4.2)

The stream function $\phi _1$ will also remain odd at $z=0$ and $z=1$, so in solving the Poisson equation (2.4c), we can use the following boundary condition

$$\begin{aligned} \phi _1|_{\partial D}=0. \end{aligned}$$

Our preliminary numerical results suggest that the models with weak convection develop finite-time singularity on the symmetric axis. To resolve the singularity, one needs a very fine mesh in the singular region, and in our numerical simulation, we employ an adaptive mesh method introduced by Luo and Hou (2014). We consider a change of variables that maps $(\rho , \eta )\in [0,1]^2$ to $(r, z)\in [0, 1]^2$, with the derivatives $r_\rho (\rho )$ and $z_\eta (\eta )$ parameterized as

$$\begin{aligned} r_\rho&=\alpha _1+\alpha _2e^{-\pi (\rho -1)^2/\sigma _1^2}, \end{aligned}$$

(4.3a)

$$\begin{aligned} z_\eta&=\alpha _3+\alpha _4e^{-\pi \eta ^2/\sigma _2^2}+\alpha _5e^{-\pi (\eta -1)^2/\sigma _3^2}. \end{aligned}$$

(4.3b)

We use a uniform mesh in the $(\rho , \eta )$ space in our simulation and choose the parameters $\alpha _i$ and $\sigma _j$ in (4.3) such that a certain portion of the node points is put in the “singular region.” In the r direction we would like to put $\delta$ portion of the node points in the “singular region” $[0, r_0]$. We first choose

$$\begin{aligned} \sigma _1=(1-\delta )\times \frac{2}{5}, \end{aligned}$$

(4.4)

such that the exponential part in $r_\rho$ is negligible for $\rho \in [0, \delta ]$,

$$\begin{aligned} e^{-\pi (\rho -1)^2/\sigma _1^2}\le e^{-\frac{25\pi }{4}}\approx 0, \end{aligned}$$

(4.5)

which means we use a nearly uniform mesh in the “singular region” $[0, r_0]$.

Then we choose $\alpha _1$ and $\alpha _2$ such that

$$\begin{aligned} r(\rho )|_{\rho =\delta }=r_0,\quad r(\rho )|_{\rho =1}=1, \end{aligned}$$

which according to (4.5) leads to the following linear system

$$\begin{aligned} \alpha _1 \delta =r_0, \quad \alpha _1+\frac{1}{2}\sigma _1\alpha _2=1\Rightarrow \alpha _1=r_0/\delta ,\quad \alpha _2=\frac{5(\delta -r_0)}{\delta (1-\delta )}. \end{aligned}$$

(4.6)

Thus for $r_0\le \delta$, we can uniquely determine $\alpha _{1}>0, \alpha _2>0$ and $\sigma _1>0$ in (4.3).

In the z direction, we would like to put $\delta$ portion of the node points in the “singular region” $[z_1, z_2]$. We first determine the portion of node points put in the left and right intervals $[0, z_1]$ and $[z_2, 1]$, denoted by $\delta _1$ and $\delta _2$, as

$$\begin{aligned} \delta _1=\frac{z_1}{z_1+1-z_2}(1-\delta ),\quad \delta _2=\frac{1-z_2}{z_1+1-z_2}(1-\delta ), \end{aligned}$$

(4.7)

which guarantees that the portions of node points in the “regular regions,” $[0, z_1]$ and $[z_2, 1]$, are proportional to the length of the intervals.

Next we choose $\sigma _2$ and $\sigma _3$ based on $\delta _1$ and $\delta _2$ (4.7) as

$$\begin{aligned} \sigma _2=\delta _1\times \frac{2}{5},\quad \sigma _3=\delta _2\times \frac{2}{5}, \end{aligned}$$

(4.8)

such that the exponential part in $z_\eta$ is negligible for $\eta \in [\delta _1, 1-\delta _2]$,

$$\begin{aligned} e^{-\pi \eta ^2/\sigma _2^2}, \ e^{-\pi (\eta -1)^2/\sigma _3^2} \approx 0. \end{aligned}$$

(4.9)

Finally we choose $\alpha _3$, $\alpha _4$ and $\alpha _5$ such that

$$\begin{aligned} z(\eta )|_{\eta =\delta _1}=z_1,\quad z(\eta )|_{\eta =1-\delta _2}=z_2,\quad z(\eta )|_{\eta =1}=1, \end{aligned}$$

which according to (4.9) leads to the linear system

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _3 \delta _1+\frac{1}{2}\alpha _4\sigma _2=z_1,\\ \alpha _3 (\delta _1+\delta )+\frac{1}{2}\alpha _4\sigma _2=z_2,\\ \alpha _3+\frac{1}{2}\alpha _4\sigma _2+\frac{1}{2}\alpha _5\sigma _3=1, \end{array}\right. } \ \Rightarrow \ {\left\{ \begin{array}{ll} \alpha _3=\frac{z_2-z_1}{\delta },\\ \alpha _4=5 \frac{\delta (1-z_2+z_1)-(1-\delta )(z_2-z_1)}{(1-\delta )\delta },\\ \alpha _5=5 \frac{\delta (1-z_2+z_1)-(1-\delta )(z_2-z_1)}{(1-\delta )\delta }. \end{array}\right. } \end{aligned}$$

(4.10)

Then for $z_2-z_1\le \delta$, we can determine $\sigma _{2},\sigma _3>0$ and $\alpha _{j}>0 \ (j=3,4,5)$ in (4.3).

The conditions (4.5), (4.9) guarantee that the transforms (4.3) are even at $r=0$ and $z=0, 1$. With the change of variables, Eqs. (2.4) become

$$\begin{aligned} u_{1,t}+u^r\frac{u_{1,\rho }}{r_\rho }+u^z\frac{u_{1,\eta }}{z_\eta }&=2u_1\frac{\phi _{1,\eta }}{z_\eta }, \end{aligned}$$

(4.11a)

$$\begin{aligned} \omega _{1,t}+u^r\frac{\omega _{1,\rho }}{r_\rho }+u^z\frac{\omega _{1,\eta }}{z_\eta }&=2u_1^2\frac{u_{1,\eta }}{z_\eta }, \end{aligned}$$

(4.11b)

with the velocity field given by

$$\begin{aligned} u^r=-\epsilon r\frac{\phi _{1, \eta }}{z_\eta },\quad u^z=2\epsilon \phi _1+\epsilon r\frac{\phi _{1, \eta }}{r_\eta }. \end{aligned}$$

(4.11c)

The weak form of the Poisson equation (2.4c) becomes,

$$\begin{aligned} \begin{aligned} a(\phi _1, \psi )&=\int _{[0,1]^2} \left( \frac{\phi _{1, \rho }}{r_\rho }\frac{\psi _\rho }{r_\rho }+\frac{\phi _{1, \eta }}{z_\eta }\frac{\psi _\eta }{z_\eta }\right) r^3r_\rho z_\eta \mathrm{d}\rho d\eta \\&=\int _{[0,1]^2}\omega _1 \psi r^3r_\rho z_\eta \mathrm{d}\rho d\eta ,\quad \forall \psi \in V, \end{aligned} \end{aligned}$$

(4.11d)

where

$$\begin{aligned} V= & {} \mathrm {span}\{ \psi \in H^1[0, 1]^2: \psi (-\rho ,\eta )=\psi (\rho , \eta ), \\&\psi (1, \eta ) = \psi (r, 0)=\psi (r, 1)=0\}. \end{aligned}$$

We discretize the computational domain $(\rho , \eta )$ using a uniform mesh

$$\begin{aligned} (\rho _i, \eta _j)=(ih_\rho , jh_\eta ),\quad 0\le i\le N_R,\quad 0\le j\le N_Z, \end{aligned}$$

where $h_\rho =\frac{1}{N_R}$ and $h_\eta =\frac{1}{N_Z}$ are the uniform mesh sizes.

We use a second-order center difference scheme to compute the derivatives $\phi _{1,z}$ and $\phi _{1,r}$ in (4.11c), the derivatives in the convection terms of (4.11a) and (4.11b), and the derivatives in the nonlinear vortex stretching terms.

We discretize the Poisson equation (4.11d) using a finite- element method with trial space

$$\begin{aligned} V_h=\{\psi (r,z)\in V: \psi (r,z) \text { is piecewise bilinear}\}. \end{aligned}$$

In the temporal direction, we use the fourth-order explicit Runge–Kutta method and choose the time step size $\Delta t$ such that the CFL number

$$\begin{aligned} \frac{|u^r| \Delta t}{h_\rho },\quad \frac{|u^z| \Delta t}{h_\eta }\le 0.5, \end{aligned}$$

(4.12a)

and the growth of maximum $\omega _1$ in each time step does not exceed $1\%$, namely

$$\begin{aligned} \Vert w^{n+1}_1\Vert _{L^\infty }-\Vert w^n_1\Vert _{L^\infty }\le (\Vert w^n_1\Vert _{L^\infty }+10)\times 1\%. \end{aligned}$$

(4.12b)

In our simulation, we identify the “singularity region” of the solutions as

$$\begin{aligned} (r, z)\in [0, L]\times \left[ -\frac{L}{2}+c, \frac{L}{2}+c\right] , \end{aligned}$$

where $(r,z)=(0, c)$ is the position where maximum $\omega _1$ is attained, $\omega _1(0, c)=\Vert \omega _1\Vert _{L^\infty }$, and L is chosen such that $\omega _1(L, c)=\frac{1}{2}\omega _1(0,c)$.

We use two sets of mesh in our simulation with

$$\begin{aligned} N_R=N_Z=512,\quad \text {and}\quad N_R=N_Z=1024. \end{aligned}$$

(4.13)

We simulate the model (4.11) with $\epsilon =0$ using initial data (4.1) until $\Vert \omega _1\Vert _{L^\infty }$ reaches $1.1\times 10^8$. In the simulation, we keep track of $\Vert \omega _1(t)\Vert _{L^\infty }$, $\Vert u_1(t)\Vert _{L^\infty }$, which are attained on the symmetric axis, and record the numerical solutions at time steps corresponding to different $\Vert \omega _1(t)\Vert _{L^\infty }$. The growth of $\log \Vert u_1(t)\Vert _{L^\infty }$ and $\log \Vert \omega _1(t)\Vert$ is plotted in Fig. 1, and we can see that there exists very small difference between the results obtained on the two meshes (4.13). In the rest of this paper, we will only present numerical results on the fine mesh.

Fig. 1

Resolution study using two meshes. a $\log \Vert \omega _1(t)\Vert _{L^\infty }$. b $\log \Vert u_1(t)\Vert _{L^\infty }$

Then we use the numerical solutions for $\epsilon =0$ at the time step $\Vert \omega _1\Vert _{L^\infty }=3\times 10^4$ as initial data for the model with different $\epsilon$,

$$\begin{aligned} \epsilon =0.1, \quad \epsilon =0.2, \quad \epsilon =0.3,\quad \epsilon =0.4. \end{aligned}$$

The decay of the inverse of $\Vert u_1(t)\Vert _{L^\infty }$ is plotted in Fig. 2. We can see that for weak convection, $\Vert u_1(t)\Vert _{L^\infty }$ goes to infinity and the models develop finite-time singularity, while for strong convection, such finite-time singularity scenario does not persist. Moreover, we can see that close to the singularity time, $\Vert u_1(t)\Vert _{L^\infty }^{-1}$ decays approximately linearly for weak convection,

$$\begin{aligned} \Vert u_1(t)\Vert _{L^\infty }^{-1}\approx C(T-t). \end{aligned}$$

Fig. 2

Finite-time singularity for weak convection

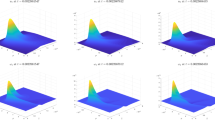
For the case $\epsilon =0.2$, the numerical solutions restricted on the symmetric axis at several different time steps are plotted in Fig. 3, and we can see that the center of the singularity region is not stationary but traveling along the symmetric axis. The singularity scenario for $\epsilon =0, 0.1, 0.3$ is similar.

Fig. 3

The traveling of the singularity region. a $\omega _1(0, z, t)$. b $u_1(0, z, t)$

Next we consider the spatial profiles in the solutions as approaching the potential singularity time. In this paper we refer to “profile” as normalized solutions. At time t, the spatial profiles U(t) and W(t) are obtained as

$$\begin{aligned} U(t)=\frac{1}{\tau }u_1\left( \frac{r}{\lambda }, \frac{z-c}{\lambda },t\right) , \quad W(t)= \frac{1}{\lambda \tau }\omega _1\left( \frac{r}{\lambda }, \frac{z-c}{\lambda }, t\right) , \end{aligned}$$

(4.14a)

where the scaling and shifting are based on the scaling and translational invariance property of the model (3.1), (3.3). We choose the parameter c in (4.14) such that the singularity region is shifted to the origin. The solution $\omega (0, z, t)$ crosses zero once in the singularity region, and we choose c such that

$$\begin{aligned} W(0,0,t)=0. \end{aligned}$$

(4.14b)

And we choose $\lambda$ and $\tau$ to normalize $W_z(0, 0, t)$ and U(0, 0, t),

$$\begin{aligned} W_z(0, 0, t)=C_1,\quad U(0,0, t)=C_2. \end{aligned}$$

(4.14c)

For $\epsilon =0.2$, we consider the spatial profiles in the singular solutions at different time steps corresponding to different $\Vert \omega _1\Vert _{L^\infty }$. To simplify our presentation, we only plot the profiles restricted on the symmetric axis in Fig. 4. We can see that the profiles at different time steps close to the singularity time collapse, which implies the self-similar nature of the finite-time singularity. In this paper, by self-similar singularity we mean that the spatial profiles in the singular solutions converge as approaching the singularity time. For the cases $\epsilon =0, 0.1, 0.3$, the singular solutions also exhibit self-similar feature.

Fig. 4

Profiles of the singular solutions on the symmetric axis

Based on the singularity scenario described above, we make the following self-similar ansatz for the singular solutions close to the singularity time:

$$\begin{aligned} u_1&=(T-t)^{c_u} U\left( \frac{r}{(T-t)^{c_l}}, \frac{z-c(t)}{(T-t)^{c_l}}\right) , \end{aligned}$$

(4.15a)

$$\begin{aligned} \omega _1&=(T-t)^{c_\omega } W\left( \frac{r}{(T-t)^{c_l}}, \frac{z-c(t)}{(T-t)^{c_l}}\right) . \end{aligned}$$

(4.15b)

In the above ansatz, $(r,z)=(0, c(t))$ is the center of the singularity region, and U(r, z), W(r, z) are the self-similar profiles of the singular solutions. The exponents $c_u$, $c_\omega$ and $c_l$ characterize the blow-up rate of the solutions.

Plugging the above self-similar ansatz into Eq. (2.5), and matching the order of $(T-t)$ for each term in the equations, we get

$$\begin{aligned} c_u=-1, \quad c_\omega =-1-c_l, \quad \frac{d}{\mathrm{d}t}c(t)=c(T-t)^{c_l-1}, \end{aligned}$$

(4.16a)

and the following self-similar equations governing the self-similar profiles,

$$\begin{aligned} U+(c_lr+U^r)U_{r}+(c_lz+U^z-c)U_{z}&=2U\Psi _{z}, \end{aligned}$$

(4.16b)

$$\begin{aligned} (c_l+1)W+(c_lr+U^r) W_{r}+(c_lz+U^z-c)W_{z}&=(U^2)_z, \end{aligned}$$

(4.16c)

$$\begin{aligned} -\left[ \partial _r^2+(3/r)\partial _r+\partial _z^2\right] \Psi&=W, \end{aligned}$$

(4.16d)

where

$$\begin{aligned} U^r=-\epsilon r\Phi _z, \quad U^z=2\epsilon \Phi +\epsilon r\Phi _r. \end{aligned}$$

(4.16e)

To study the self-similar Eq. (4.16), we can make the following scaling transformation,

$$\begin{aligned} U_c(r,z)\rightarrow U\left( \frac{r}{c},\frac{z}{c}\right) ,\quad W_c(r,z)\rightarrow \frac{1}{c}W\left( \frac{r}{c},\frac{z}{c}\right) , \end{aligned}$$

and the scaled profiles $W_c$ and $U_c$ will satisfy the same self-similar equations with c changed to $c = 1$. In another word, the unknown parameter c can be chosen to be 1 based on scaling of the profiles.

However, the exponent $c_l$ in (4.16) cannot be determined by a simple scaling argument and it is the only unknown scaling parameter. In the literature (Barenblatt and Zel’Dovich 1972; Sedov 1993), such singularity is called self-similar singularity of the second kind, and to solve Eq. (4.16), one needs to find $c_l$ such that the equations have non-trivial solutions, which is essentially a nonlinear eigenvalue problem.

In Fig. 2, we can see that for weak convection, the inverse of $\Vert u_1(t)\Vert _{L^\infty }$ decays linearly close to the singularity time, which agrees with the scaling exponent $c_u=-1$ obtained in (4.16a). Using this we compute the approximate singularity time T by linear regression on a time interval close to singularity,

$$\begin{aligned} \Vert u_t(t)\Vert ^{-1}_{L^\infty }\approx C_1t+C_2,\quad T\approx -\frac{C_2}{C_1}. \end{aligned}$$

(4.17)

Next we use the estimated singularity T from (4.17) in linear regression

$$\begin{aligned} \log \Vert \omega _1(t)\Vert _{L^\infty }\approx c_\omega \log (T-t)+C, \end{aligned}$$

(4.18)

on the same time interval as (4.17) to determine the scaling exponent $c_\omega$. And after we get $c_\omega$, the exponent $c_l$ can be obtained as

$$\begin{aligned} c_l=-c_\omega -1. \end{aligned}$$

The region of linear regression (4.18) in the case that $\epsilon =0.2$ is plotted in Fig. 5. The estimated $c_l$ for $\epsilon =0, 0.1, 0.2, 0.3$ are listed in Table 1. We can see that as the strength of the convection increases, the scaling exponent $c_l$ becomes smaller; namely, the length scale of the solutions decays slower.

Fig. 5

Linear regression to determine $c_\omega$. a $\log \Vert \omega _1(t)\Vert _{L^\infty }$. b Linear regression region

Table 1 The scaling exponent $c_l$ for different $\epsilon$

Due to the nonlinear and nonlocal nature of the self-similar Eq. (4.16), it is difficult to prove the existence of $c_l$ such that (4.16) has non-trivial solutions, which is essentially a nonlinear eigenvalue problem. In the next subsection, we employ a dynamic rescaling formulation, which governs the evolution of the spatial profiles (4.14) in the singular solutions, to numerically demonstrate the stability of the observed self-similar singularity.

4.2 Stability of the Self-Similar Singularity

According to the self-similar Eq. (4.16), if the solutions to (2.8) start from initial data equal to the self-similar profiles, then the profiles in the singular solutions will remain the same, and the solutions will develop singularity exactly as the ansatz (4.15). In this subsection, we consider the stability of the self-similar profiles and demonstrate that the solutions to (2.8) develop singularity asymptotically as (4.15) if starting from initial data that are perturbed from the self-similar profiles.

We demonstrate the stability of the self-similar profiles using the dynamic rescaling formulation. We add scaling terms to Eq. (2.4) and get

$$\begin{aligned} u_{1,t}+(c_l(t)r+u^r)u_{1,r}+(c_l(t)z+u^z+c(t))u_{1,z}&=2u_1\phi _{1,z}+c_u(t)u_1, \end{aligned}$$

(4.19a)

$$\begin{aligned} \omega _{1,t}+(c_l(t)r+ u^r)\omega _{1,r}+(c_l(t)z+u^z+c(t)) \omega _{1,z}&=(u_1^2)_z+c_\omega (t) \omega _1, \end{aligned}$$

(4.19b)

$$\begin{aligned} -\left[ \partial _r^2+(3/r)\partial _r+\partial _z^2\right] \phi _1&=\omega _1, \end{aligned}$$

(4.19c)

where the velocity field above is the same as the original equations,

$$\begin{aligned} u^r=-\epsilon r\phi _{1,z},\quad u^z=2\epsilon \phi _1+\epsilon r\phi _{1,r}. \end{aligned}$$

In the above formulation, the $c_l(t)r\partial _r$, $c_l(t)z\partial _z$ terms stretch the solutions in the spatial direction; the $c(t)\partial _z$ term shifts the solutions along the axial direction; the $c_\omega (t)\omega _1$ and $c_u(t)u$ terms rescale the solutions $\omega _1$ and $u_1$ in amplitude, respectively. According to the scaling invariance property of the model (3.1), we need to choose the following condition for the scaling parameters in (4.19),

$$\begin{aligned} c_\omega (t)=c_u(t)-c_l(t) \end{aligned}$$

(4.19d)

such that the dynamic rescaling equations are equivalent to the 3D models.

To be specific, let $u_1(r,z,t)$, $\omega _1(r,z,t)$ be solutions to the model (2.5), then

$$\begin{aligned} u_1(r,z,t)&=C_u(t)u_1\left( C_l(t)r, C_l(t)z-z(t), \tau (t)\right) , \end{aligned}$$

(4.20a)

$$\begin{aligned} \omega _1(r,z,t)&=C_\omega (t)\omega _1\left( C_l(t)r, C_l(t)z-z(t), \tau (t)\right) , \end{aligned}$$

(4.20b)

are solutions to the dynamic rescaling Eq. (4.19), where

$$\begin{aligned} \frac{d}{\mathrm{d}t}\tau (t)&=\exp \left( \int _0^t c_u(s)\mathrm{d}s\right) , \end{aligned}$$

(4.20c)

$$\begin{aligned} C_u(t)&=\exp \left( \int _0^t c_u(s)\mathrm{d}s\right) , \end{aligned}$$

(4.20d)

$$\begin{aligned} C_\omega (t)&=\exp \left( \int _0^t c_\omega (s)\mathrm{d}s\right) , \end{aligned}$$

(4.20e)

$$\begin{aligned} C_l(t)&=\exp \left( \int _0^t -c_l(s)\mathrm{d}s\right) , \end{aligned}$$

(4.20f)

$$\begin{aligned} z(t)&=\int _0^t c(s)C_l(s) \mathrm{d}s. \end{aligned}$$

(4.20g)

In another word, the solutions to the dynamic rescaling Eq. (4.19) are simply rescaling of the solutions to the original Eq. (2.4).

To fix the scaling parameters in the above dynamic rescaling formulation, we need suitable normalization conditions. We first fix the center of the solution at the origin. In another word, we choose c(t) in (4.19) such that

$$\begin{aligned} \omega _1(0,0,t)=0. \end{aligned}$$

(4.21a)

The above condition leads to

$$\begin{aligned} c(t)=\frac{2u_1u_{1,z}(0,0)}{\omega _{1,z}(0,0)}-u^z(0,0). \end{aligned}$$

(4.21b)

Then we choose $c_l(t)$ and $c_u(t)$ to normalize the derivatives of w and the value of u at the origin. Namely, we choose $c_l(t)$ and $c_u(t)$ such that

$$\begin{aligned} \frac{d}{\mathrm{d}t} \omega _{1,z}(0,0)=0,\quad \frac{d}{\mathrm{d}t}u(0,0)=0. \end{aligned}$$

(4.21c)

And this leads to the following $c_l(t)$ and $c_u(t)$,

$$\begin{aligned} c_u(t)&=\frac{2(u_{1,z})^2}{\omega _{1,z}}-2\phi _{1,z}, \end{aligned}$$

(4.21d)

$$\begin{aligned} c_l(t)&=\frac{(u_{1,z})^2}{\omega _{1,z}}-\phi _{1,z}- \frac{u_1u_{1,z}\omega _{1,zz}}{\omega _{1,z}^2}-u^z_z+ \frac{u_1u_{1,zz}+(u_{1,z})^2}{\omega _{1,z}}. \end{aligned}$$

(4.21e)

With the normalization conditions (4.21) and the equivalent relation (4.20), we conclude that the dynamic rescaling equations govern the evolution of the spatial profiles in the solutions (4.14). The self-similar profiles correspond to a steady state of the dynamic rescaling equations, and we will numerically study the stability of the steady state of (4.19) to demonstrate the stability of the singularity scenario described in the previous subsection.

A similar dynamic rescaling formulation has been employed to study the singularity of nonlinear Schrödinger equations in McLaughlin et al. (1986), Landman et al. (1988), LeMesurier et al. (1988), Landman et al. (1992) and Papanicolaou et al. (1994). In those works, the dynamic rescaling formulation is primarily used as an approach to accurately solve the equations numerically. In this work, we employ this formulation to investigate the stability of the self-similar profiles. In the works we just mentioned above, the singular region is not traveling, so there is no need to add the shifting term $c(t)\partial _z$ as in (4.19). The normalization condition (4.21) is also different from those in the study of Schrödinger equations.

The dynamic rescaling Eqs. (4.19) are defined on unbounded domain

$$\begin{aligned} (r,z)\in R^+\times R, \end{aligned}$$

and to numerically solve the equations, we need to first truncate the equations to a bounded computational domain

$$\begin{aligned} (r,z)\in D=[0, M]\times [-M, M],\quad M=120, \end{aligned}$$

(4.22)

and discretize D using a uniform mesh

$$\begin{aligned} (r_i, z_j)=\left( i r_h, \left( j-\frac{nz}{2}\right) z_h\right) ,\quad 0\le i\le nr, \quad 0\le j\le nz, \end{aligned}$$

(4.23)

where $r_h=M\times \frac{1}{nr}$, $z_h=M\times \frac{2}{nz}$.

To truncate the solutions $\omega _1$ and $u_1$ to the computational domain D, we introduce the following projection operators,

$$\begin{aligned} P_u f(r, z)&=P^r P_u^z f(r,z), \end{aligned}$$

(4.24a)

$$\begin{aligned} P_\omega f(x)&=P^r P_\omega ^z f(r,z), \end{aligned}$$

(4.24b)

where $P^r$, $P^z_u$ and $P^z_\omega$ are defined as

$$\begin{aligned} P^r f(r,z)&=f(r,z)-\frac{r^2}{M^2}f(M, z), \end{aligned}$$

(4.24c)

$$\begin{aligned} P^z_u f(r,z)&=f(r,z)-f(r, M)\frac{z(z+M)}{2M^2}-f(r, -M) \frac{z(z-M)}{2M^2}, \end{aligned}$$

(4.24d)

$$\begin{aligned} P^z_\omega f(r,z)&=f(r,z)-f(r, M)\frac{z^2(z+M)}{2M^3}+f(r, -M)\frac{z^2(z-M)}{2M^3}. \end{aligned}$$

(4.24e)

Putting the above truncation operator in Eq. (4.19), we get

$$\begin{aligned} u_{1,t}&=P_u(-(c_l(t)r+u^r)u_{1,r}-(c_l(t)z+u^z+c(t))u_{1,z}+2u_1\phi _{1,z}+c_u(t)u_1),\\ \omega _{1,t}&=P_\omega (-(c_l(t)r+ u^r)\omega _{1,r}-(c_l(t)z+u^z+c(t))\omega _{1,z}+(u_1^2)_z+c_\omega (t) \omega _1). \end{aligned}$$

The projection operators (4.24) do not change the evenness of $\omega _1$ and $u_1$ with respect to r or violate the normalization condition (4.21). Moreover, if $u_1$ and $\omega _1$ decay fast and are small on the boundary of the computational domain, then the error introduced by the projection operators is also small.

To compute the velocity field $u^r$ and $u^z$, one needs to solve the Poisson equation (2.4c) on the computational domain D (4.22). To get the appropriate boundary condition for $\phi _1$, we write it using the 5D Green’s function as

$$\begin{aligned} \phi _1(y)=\frac{1}{8\pi ^2} \int _{R^5} \omega _1(y')\frac{1}{|y-y'|^3}\mathrm{d}x'. \end{aligned}$$

(4.25)

Since $\phi _1$ and $\omega _1$ are symmetric with respect to $y_{1,2,3,4}$, it is convenient to transform the integral (4.25) using the 4D spherical coordinates, and we get

$$\begin{aligned} \phi _1(r,z)= & {} \frac{1}{8\pi ^2} \int _R \mathrm{d}z'\int _0^\infty \mathrm{d}r'\int _0^\pi \mathrm{d}\theta _1\int _0^\pi \mathrm{d}\theta _2\int _0^{2\pi }\mathrm{d}\theta _3 \\&r'^3\sin ^2\theta _1\sin \theta _2 ((r-r'\cos \theta _1)^2 +r'^2\sin ^2\theta _1+(z-z')^2)^{-3/2}\omega _1(r',z'). \nonumber \end{aligned}$$

(4.26)

And it can be simplified as

$$\begin{aligned} \phi _1(r,z)=\frac{1}{8\pi ^2} \int _Rdz'\int _0^\infty \mathrm{d}r' \omega _1(r', z')G(r, r', z), \end{aligned}$$

(4.27)

where

$$\begin{aligned} G(r, r', z)= & {} \frac{-4\pi r'\left( (z-z')^2+(r+r')^2\right) \mathrm {EllipticE} \left( \frac{4rr'}{(z-z')^2+(r+r')^2}\right) }{r^2\sqrt{(z-z')^2+(r+r')^2}} \nonumber \\&+\frac{4\pi r'\left( (z-z')^2+r^2+r'^2\right) \mathrm {EllipticK}\left( \frac{4rr'}{(z-z')^2+(r+r')^2}\right) }{r^2\sqrt{(z-z')^2+(r+r')^2}}.\qquad \quad \end{aligned}$$

(4.28)

Here the function $\mathrm {EllipticE}$ is the complete elliptic integral of the second kind, and $\mathrm {EllipticK}$ is the complete elliptic integral of the first kind.

So to compute the velocity field, we first recover $\omega _1$ as a piecewise bilinear function based on its values on the node points (4.23), and then we compute the value of $\phi _1$ on the boundary of the computational domain using the integral formula (4.27). In evaluating the integral (4.27), we use the fourth-order Gaussian quadrature rule on each local piece of the domain. Then with the boundary condition, we solve the Poisson equation (4.19c) using a second-order finite element method and get the velocity field based on (2.8).

We use the upwind scheme to discretize the spatial derivatives in the convection terms in (4.19) and use the second-order center difference scheme to discretize the spatial derivatives in the vortex stretching terms. After the spatial discretization, we get an ODE system of $\vec {\omega }$ and $\vec {u}$,

$$\begin{aligned} \frac{d}{\mathrm{d}t}\vec {u}=F_u(\vec {u}, \vec {\omega }),\quad \frac{d}{\mathrm{d}t}\vec {\omega }=F_\omega (\vec {u}, \vec {\omega }). \end{aligned}$$

(4.29)

Note that the determination of the scaling parameters (4.21), the numerical computation of the Biot–Savart law (4.27) and the truncation operators (4.24) are all encoded in the forcing functions $F_u$ and $F_\omega$ in (4.29).

We use the forward Euler scheme to numerically solve the ODE (4.29), and the time step size $\mathrm{d}t$ is chosen such that the CFL number is less than 0.5.

We use the rescaling of numerical solutions from direct numerical simulation of the models close to the singularity time as initial data for the dynamic rescaling Eq. (4.19). We observe that for small $\epsilon$, the solutions converge to a steady state, which according to the equivalent relation between the solutions of the dynamic rescaling equations and the original model, (4.20), implies the asymptotic self-similar singularity of the models.

The scaling exponents $c_l$ corresponding to different $\epsilon$ are listed in Table 2. We can see that $c_l$ decays as we increase $\epsilon$, which agrees with what we have observed in the direct numerical simulation of the models in Table 1.

Table 2 The scaling exponent $c_l$ obtained from dynamic rescaling

Fig. 6

Distribution of the first several eigenvalues

However, there is some discrepancy between the scaling exponent $c_l$ obtained from direct simulation of the models and the dynamic rescaling formulation. This is because of the error introduced by the truncation operators (4.24).

Next we numerically study the stability of the self-similar profiles. Recall that the self-similar profiles are the steady-state solutions of the dynamic rescaling equations, and the stability of the self-similar singularity is the stability of the steady state of the dynamic rescaling Eq. (4.19).

We numerically study the linear stability of the steady state of the ODE and compute the Jacobian matrix of its right-hand side

$$\begin{aligned} J=\begin{bmatrix} \nabla _{\vec {u}}F_u&\nabla _{\vec {\omega }} F_u\\ \nabla _{\vec {u}} F_\omega&\nabla _{\vec {\omega }} F_\omega \end{bmatrix}. \end{aligned}$$

(4.30)

The first few dominating eigenvalues with the largest real parts of the Jacobian matrix for $\epsilon =0.2$ are plotted in Fig. 6. We can see that the eigenvalues have negative real part, which demonstrates the stability of the steady state and therefore the stability of the traveling wave self-similar singularity.

Table 3 Largest real part of the eigenvalues

For different $\epsilon$, the largest real parts of the eigenvalues of the Jacobian matrix (4.30) are listed in Table 3. From the table, we can see that for larger $\epsilon$, the largest eigenvalue of the Jacobian matrix becomes larger, which means the self-similar singularity becomes less stable. This demonstrates the subtle balance between the convection and nonlinear vortex stretching terms and might explain the depletion of nonlinearity for strong convection.

5 Concluding Remarks

A family of 3D models for the axisymmetric incompressible Euler and Navier–Stokes equations are proposed. These models are derived by changing the strength of the convection terms of the axisymmetric Euler and Navier–Stokes equations written using a set of transformed variables. The family of models share several regularity results with the original Euler and Navier–Stokes equations, including an energy identity, the conservation of a modified circulation quantity and some non-blow-up criteria. Despite the similarities between the proposed models and the Euler equations, our numerical results suggest that the inviscid models with weak convection develop stable self-similar singularity with the singular region traveling along the symmetric axis, and such singularity scenario does not seem to persist for the original Euler equations. We use a dynamic rescaling formulation that governs the evolution of the spatial profiles in the singularity solutions to demonstrate the stability of the traveling self-similar singularity scenario. We observe that as the strength of the convection terms increases, the self-similar profiles become less stable, which shows the subtle balance between the nonlinear convection terms and the nonlinear vortex stretching terms.