Heteroclinic Networks in Homogeneous and Heterogeneous Identical Cell Systems

Abstract

We prove results that enable realization of heteroclinic networks in coupled homogeneous and heterogeneous systems of identical cells. We also consider various models for network dynamics, which allow variation in the number of inputs to identical cells.

1 Introduction

In this work, we provide methods for constructing interesting realizations of heteroclinic cycles and networks in homogeneous and heterogenous networks of identical coupled cells. We also address a number of general issues about the structure of networks of dynamical systems.

In the next section, we give a careful review of past work on heteroclinic networks, their realizations and their interest and significance. For the remainder of the introduction, we give basic definitions and describe our main results. Throughout, we let $\mathbb {N}$ denote the (strictly positive) natural numbers and, given $n\in \mathbb {N}$, use the convention that $\mathbf {n} = \{1,\ldots ,n\}$.

Let $\Gamma (N,E) = \Gamma$ be a directed graph with $N \ge 2$ vertices, $\mathbf {v}_1, \ldots ,\mathbf {v}_N$, and directed edges $e_\alpha$, $\alpha \in \mathbf {E}$. The edges connect vertices of $\Gamma$. If $e_\alpha$ is an edge from $\mathbf {v}_j$ to $\mathbf {v}_i$, we often write $\mathbf {v}_j\rightarrow \mathbf {v}_i$ rather than $e_\alpha$. Note, however, that we allow multiple edges between vertices. Let $d_i^{\,\text {out}}$ denote the out-degree of vertex $\mathbf {v}_i$: total number of edges from $\mathbf {v}_i$ to other vertices. We may analogously define the in-degree $d_i^{\,\text {in}}$

Unless the contrary is indicated, we assume throughout the article that every graph $\Gamma$ is directed and satisfies

• (C1) There are no self-connections $\mathbf {v}_i\rightarrow \mathbf {v}_i$, $i \in \mathbf {N}$.

• (C2) For every (ordered) vertex pair $\mathbf {v}_i, \mathbf {v}_j$, there is a chain of (directed) edges $\mathbf {v}_j \rightarrow \mathbf {v}_{k_1}$, $\mathbf {v}_{k_1}\rightarrow \mathbf {v}_{k_2}, \ldots$, $\mathbf {v}_{k_s} \rightarrow \mathbf {v}_i$ joining $\mathbf {v}_j$ to $\mathbf {v}_i$ (note $i = j$ is allowed).

Conditions (C1, C2) imply that $\Gamma$ is strongly connected and that every vertex lies on a cycle of length at least two.

Let $\Gamma (N,E)=\Gamma$ be a graph and $M$ be a connected differential manifold of dimension at least two. We say that $\Gamma$ has a realization as a heteroclinic network $\Sigma$ in $M$, if we can choose a $C^1$ vector field $X$ on $M$ such that

• (H1) $X$ has hyperbolic saddles $\mathbf {p}_i \in M$, $i \in \mathbf {N}$.

• (H2) Associated with every edge $e_\alpha$ from $\mathbf {v}_j$ to $\mathbf {v}_i$, there is a unique $X$-trajectory $\phi _\alpha :\mathbb {R}\rightarrow M$ from $\mathbf {p}_j$ to $\mathbf {p_i}$ (that is, $\phi _\alpha (\mathbb {R}) \subset W^s(\mathbf {p}_i) \cap W^u(\mathbf {p}_j)$ and $\alpha \ne \beta$ implies $\phi _\alpha (\mathbb {R}) \ne \phi _\beta (\mathbb {R})$).

• (H3) $\Sigma = \bigcup _{i\in \mathbf {N}} \{\mathbf {p}_i\} \cup \bigcup _{\alpha \in \mathbf {E}} \phi _\alpha (\mathbb {R})$.

The realization is robust if (H1–3) hold for all $C^1$ vector fields $Y$ in a $C^1$ open neighbourhood of $X$ (we assume equilibria and connections depend continuously on the deformation $Y$ of $X$).

It is easy to show that every graph $\Gamma$ can be realized as a heteroclinic network in $M$ if $\text {dim}M \ge 4$ ($\Gamma (2,8)$ cannot be realized in a 3-dimensional manifold if $d_1^{\,\text {out}} = 4$). Without further restrictions, robustness will always fail because cycles of intersecting stable and unstable manifolds (forced by (C2)) can always be destroyed by arbitrarily small $C^\infty$ perturbations (transversality of invariant manifolds of hyperbolic equilibria is generic by the Kupka-Smale theorem Peixoto 1966). However, if we restrict to classes of vector fields with additional structure, for example, equivariant vector fields or Lotka-Volterra population models, then there may be subspaces of $M$ that are invariant for all vector fields in the class and this can lead to the presence of robust heteroclinic cycles and networks. In our case, we are interested in the realization of robust heteroclinic cycles in networks of interacting dynamical systems and this will constrain the type of equilibria we consider.

We briefly review the idea of a (dynamical) network (more details are in the next section). Let ${\mathcal {N}}$ be a network consisting of $\ell \ge 2$ nodes $A_1,\ldots ,A_\ell$ each with phase space $M$ and denote the phase variable corresponding to the node $A_i$ by $\mathbf {x}_i \in M$. We suppose dynamics on ${\mathcal {N}}$ is given by a $C^1$ vector field $\mathbf {f}$ on $M^\ell$. In terms of differential equations, we may write

$$\begin{aligned} \mathbf {x}_i' = f_i(\mathbf {x}_i; \mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)}),\; i \in \varvec{\ell }. \end{aligned}$$

(1.1)

We do not assume that $k_i$ is independent of $i$—the network is heterogeneous—and the map $j_i: \mathbf {k}_i \rightarrow \varvec{\ell }$ need be neither injective nor surjective (even if $k_i \ge \ell$). The presence of the variable $\mathbf {x}_{j_i(s)}$ in the arguments of $f_i$ means that the evolution of $A_i$ depends on the state of $A_{j_i(s)}$ or, equivalently, that there is a ‘connection’ from $A_{j_i(s)}$ to $A_{j_i(s)}$.

Associated with the network ${\mathcal {N}}$, we may define the network graph $G({\mathcal {N}})$ to consist of $\ell$-vertices $a_i$, corresponding to the nodes $A_i$, and edges $e_\alpha$, $a_{j_i(s)} \rightarrow a_i$, for every $\alpha = (i,j_i(s))$, $s \in \mathbf {k_i}$. We allow self-edges—though they will not play a major role in what follows. We always assume that ${\mathcal {N}}$ (that is, $G({\mathcal {N}})$) is connected. We do not assume inputs are symmetric—the component functions $f_i$ need not be symmetric functions of $\mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)}$.

If $f_i = f$, $k_i = k \ge 1$, for all $i \in \varvec{\ell }$, we say the network is a homogeneous network of identical cells.

Let ${\mathcal {N}}$ be a homogeneous network of identical cells $A_1,\ldots ,A_\ell$. Let $\varvec{\Delta }(M)=\{(\mathbf {x}_1,\ldots , \mathbf {x}_\ell ) \;|\;\mathbf {x}_1 = \cdots = \mathbf {x}_\ell \}$ denote the diagonal subspace of $M^\ell$ (we also write $\varvec{\Delta }_\ell (M)$ if we need to emphasize the number of factors). The subspace $\varvec{\Delta }(M)$ is flow-invariant for all network vector fields and is partitioned into trajectories along which all cells are synchronized. Depending on the connection structure, there may be many other invariant subspaces, each of which will correspond to a subset (or subsets) of synchronized nodes. In some cases, the invariant subspace structure will support robust heteroclinic cycles and networks.

We may now state our main result.

Theorem 1.1

Let $M$ be any connected differential manifold. There exists a sequence $({\mathcal {P}}_n)_{n\ge 3}$ of homogeneous networks, with ${\mathcal {P}}_n$ having $n$ nodes $A_1,\ldots ,A_n$ and node phase space $M$, such that if $\Gamma (N,E)=\Gamma$ is a graph satisfying (C1,C2), then we can realize $\Gamma$ as a robust heteroclinic network $\Sigma$ in ${\mathcal {P}}_{E+1}$. Furthermore, if we denote the equilibria on $\Sigma$ by $\mathbf {p}_i$, $i \in \mathbf {N}$, we have

• (1) $\mathbf {p}_i \in \varvec{\Delta }_{E+1}(M)$, $i \in \mathbf {N}$. (The equilibria are all synchronized.)

• (2) If $\alpha \in E$ corresponds to a connection $\mathbf {p}_j \rightarrow \mathbf {p}_i$, then there exists $k = k(\alpha ) \in \mathbf {E+1}$ such that

  • (a)
    $$\begin{aligned} \phi (\mathbb {R}) \subset P_k = \{\mathbf {x} \;|\;\mathbf {x}_a = \mathbf {x}_b,\; a,b \ne k\}. \end{aligned}$$

    (Node $A_{k}$ desynchronizes from the other nodes along the connection $\mathbf {p}_j \rightarrow \mathbf {p}_i$).

  • (b) If $\alpha , \beta \in E$, $\alpha \ne \beta$, then $k(\alpha ) \ne k(\beta )$.

Remark 1.2

• (1) We prove Theorem 1.1 in the most difficult case of 1-dimensional node dynamics ($M = \mathbb {R}$ or $\mathbb {T}$) and the vector fields we construct are $C^\infty$. The heteroclinic network structure persists under $C^1$ perturbations (by $C^r$ network vector fields, $r \ge 1$).

• (2) We may require additive input structure for the network ${\mathcal {P}}_n$—we give the definition in Sect. 2.4 . This allows for time varying connection structures (Bick and Field 2015).

• (3) The network ${\mathcal {P}}_3$ previously appeared in Aguiar et al. (2011, § 5) in connection with the existence of heteroclinic cycles in coupled cell systems.

• (4) Theorem 1.1 has some formal resemblance with the result on cylinder realization in Ashwin and Postlethwaite (2013, Proposition 2) though their results do not address realization in identical cell networks (see also the general discussion in Sect. 2).

We also have partial results related to Theorem 1.1 that apply to heterogeneous networks (for which $\varvec{\Delta }(M)$ may or may not be an invariant subspace) as well as different realizations of $\Gamma$ in ${\mathcal {P}}_n$, which connect equilibria that are not fully synchronized.

We conclude by describing the contents of the paper by section. In Sect. 2, we give an overview of heteroclinic cycles and networks as well as review past work on the realization problem. We conclude the section with generalities on networks of coupled dynamical systems. In Sect. 3, we construct the sequence $({\mathcal {P}}_n)$ referred to in Theorem 1.1 (and also a related sequence $({\mathcal {Q}}_n)$). In Sect. 4, we prove Theorem 1.1. In Sect. 5, we prove that Theorem 1.1 continues to hold with the assumption of additive input structure, and also show how to apply our results to heterogeneous networks. In Sect. 6, we discuss generalizations where we connect groups of synchronized cells, rather than fully synchronized equilibria. We conclude in Sect. 7 with discussion and a description of some outstanding problems. Readers who are familiar with heteroclinic networks and coupled cell systems should probably skim quickly through the background material in Sect. 2.

2 Preliminaries and Past Work

2.1 Heteroclinic Cycles and Networks

We start with a definition of a heteroclinic network that suffices for our needs.

Definition 2.1

Let $X$ be a $C^1$ vector field on the connected differential manifold $M$. A compact, connected, flow-invariant subset $\Sigma \subset M$ is a heteroclinic network if we can write

$$\begin{aligned} \Sigma = \bigcup _{i\in I} \mathbf {p}_i \cup \bigcup _{b\in J} \gamma _b(\mathbb {R}) \end{aligned}$$

where

• (1) $\mathbf {S} = \{\mathbf {p}_i \;|\;i \in I\}$ is a finite non-empty set of hyperbolic saddle equilibria for $X$.

• (2) $\mathbf {C} = \{\gamma _b:\mathbb {R}\rightarrow M \;|\;b \in J\}$ is a finite set of connecting trajectories between equilibria in $\mathbf {S}$ satisfying the conditions

  • (a) For every $\gamma _b \in \mathbf {C}$, there exist $\mathbf {p}_i, \mathbf {p}_j$, $i \ne j$, such that $\gamma _b$ is a connection from $\mathbf {p}_j$ to $\mathbf {p}_i$ ($\gamma _b(\mathbb {R}) \subset W^u(\mathbf {p}_j)\cap W^s(\mathbf {p}_i)$).

  • (b) For every ordered pair $\mathbf {p}_i,\mathbf {p}_j \in \mathbf {S}$, there exists a sequence of connections $\mathbf {p}_j \rightarrow \mathbf {p}_{k_1}, \mathbf {p}_{k_1}\rightarrow \mathbf {p}_{k_2},\ldots , \mathbf {p}_{k_s} \rightarrow \mathbf {p}_i\in \mathbf {C}$, with $s \ge 1$ and $k_1,\ldots ,k_s \ne i,j$.

If $\Sigma$ contains an equal number of equilibria and connections, $\Sigma$ is a heteroclinic cycle. If $W^u(\mathbf {p}_i)$ is 1-dimensional for all $i \in I$, we say $\Sigma$ is a simple heteroclinic network (or cycle).

Remark 2.2

• (1) If $\Sigma$ is a heteroclinic network, then every equilibrium point of $\Sigma$ lies on a cycle of length at least two.

• (2) For our definition, we deny homoclinic loops (no self-connections).

• (3) If $\Sigma$ is a heteroclinic cycle, then the number of connections equals the number of equilibria. In the case of $G$-equivariant systems, a $G$-invariant heteroclinic network $\Sigma$ is usually called a heteroclinic cycle if $\Sigma$ is the $G$-orbit of a heteroclinic cycle. If $\Sigma /G$ is a homoclinic loop, it is common to call $\Sigma$ a homoclinic cycle.

• (4) If we let $\Gamma (|I|,|J|) = \Gamma$ have vertices $\mathbf {v}_i$, $i \in I$, and require the number of connections from $\mathbf {v}_j$ to $\mathbf {v}_i$ to be $|\{ \gamma _b \;|\;\gamma _b(\mathbb {R}) \subset W^u(\mathbf {p}_j)\cap W^s(\mathbf {p}_i)\}|$, then $\Gamma$ satisfies (C1,C2) and $\Sigma$ will be a realization of $\Gamma$.

Heteroclinic and homoclinic cycles can occur in low-codimension bifurcations of vector fields and have been intensively studied by many authors (see, for example, the volumes by Shilnikov et al. (1998), Shilnikov et al. (2002)). Of particular interest are the mechanisms whereby homoclinic bifurcations can lead to complex dynamics and chaos. In a related direction that dates back to Duffing (1918), and follows on earlier work by Wang and Ott (2011), Mohapatra and Ott have recently shown how periodic forcing of homoclinic loops and heteroclinic cycles can lead to the formation of non-uniformly hyperbolic attractors—these works address the difficult problem of finding explicit examples of non-uniform hyperbolicity and build on earlier work of Young et al.’s shear-induced chaos and rank-one attractors Lin and Young (2008), Wang and Young (2003).

On account of the Kupka-Smale theorem, robust heteroclinic cycles and networks only occur when vector fields possess additional structure that is invariably associated with the presence of invariant subspaces. They are a well-known phenomenon in models of population dynamics, ecology and game theory based on the Lotka-Volterra equations (for example, May and Leonard 1975; Hofbauer 1987, 1994; Hofbauer and Sigmund 1988, 1998). Typically, these systems are defined on a simplex or the positive orthant $\mathbb {R}^n_+ = \{x \in \mathbb {R}^n \;|\;x_i \ge 0, i = 1,\ldots ,n\}$ and have the ‘extinction’ hyperplanes $x_i = 0$ as invariant subspaces. The first example of a heteroclinic cycle in the literature known to the author appears in the 1975 paper by May and Leonard (1975)¹. This example has been used to model the ‘rock-paper-scissors’ game and winnerless competition (for example,  May and Leonard 1975; Chi et al. 1998; Afraimovich et al. 2004; Rabinovich et al. 2001).

Another large and well-studied class of dynamical systems with invariant subspaces are differential equations that are equivariant with respect to a compact Lie group of symmetries (for example, dos Reis 1984; Melbourne et al. 1989; Krupa and Melbourne 1995; Field and Richardson 1992; Krupa and Melbourne 2004; Krupa 1997; Ashwin and Field 1999; Field 1996, 2007). Robust heteroclinic cycles and networks occur because generic intersections of stable and unstable manifolds of equilibria in equivariant dynamics need not be transverse (Field 1970, 1977, 1980). This breakdown of transversality is closely associated with a rich invariant subspace structure. Specifically, if a finite or compact Lie group $G$ acts smoothly on the phase space $M$, and $H$ is any non-empty subset of $G$, then the submanifold $M^H = \{x \in M \;|\;hx = x,\,\forall h \in H\}$ is invariant by the flow of every $C^1$ $G$-equivariant vector field on $M$.

From the mathematical point of view, robust heteroclinic networks often lead to interesting complex dynamics. For example, the phenomenon of random switching between nodes (Homburg and Knobloch 2010; Aguiar et al. 2005; Ashwin et al. 2010; Kirk et al. 2010). Evidence of heteroclinic switching has even been observed in vivo in Abeles et al. (1995). From the point of view of applications, there has been recent interest in robust heteroclinic cycles that appear in neural microcircuits where they give nonlinear models with ‘winnerless competition’— there is a local competition between different states but not necessarily a global winner Rabinovich et al. (2008). These models seem useful for explaining sequence generation and spatio-temporal encoding and have been found in rate-based (Afraimovich et al. 2004) and other models (Nowotny and Rabinovich 2007). They can also be found in phase oscillator models derived from Hodgkin-Huxley models (Hansel et al. 1993) or more general phase oscillator models (Ashwin et al. 2007). Heteroclinic networks can be used to perform finite-state computations in phase oscillator systems (Ashwin and Borresen 2004; Ashwin et al. 2010) (see also Neves and Timme 2009, 2012 for pulse coupled systems). Analogous behaviour is also found in hybrid models of neural systems such as the networks of unstable attractors in systems of delay-pulse coupled oscillators (Memmesheimer and Timme 2006) as well as in coupled chemical reaction systems (Kiss et al. 2007).

The class of equivariant dynamical systems is very large, and of course, many of the possible groups and group actions appear quite uninteresting for applications. It is useful to define a subclass of group actions, which results in heteroclinic cycles and networks that naturally complement those occurring in Lotka-Volterra models. Let $\Delta _n$ denote the group of diagonal matrices acting on $\mathbb {R}^n$

$$\begin{aligned} \Delta _n = \text {diag}(\pm 1, \ldots ,\pm 1) \approx \mathbb {Z}_2^n. \end{aligned}$$

Let $H$ be a subgroup of $S_n$ (the symmetric group on $n$ symbols acting on $\mathbb {R}^n$ by permutation of coordinates) and define the group $G\subset \text {O}(n)$ to consist of all linear maps $A:\mathbb {R}^n\rightarrow \mathbb {R}^n$ of the form

$$\begin{aligned} A (x_1 ,\ldots , x_n) = (\pm x_{\sigma (1)}, \dots , \pm x_{\sigma (k)}),\quad ((x_1,\dots , x_k)\in \mathbb {R}^k)\,, \end{aligned}$$

where $\sigma \in H$ ($G$ is a group of signed permutation matrices). We may write $G$ as the semidirect product $\Delta _n \rtimes H$. If $H$ is the trivial subgroup group $\{e\}$, we obtain the action of $\Delta _n$ on $\mathbb {R}^n$. The case $n = 3$ leads to the first explicit example of robust heteroclinic cycles in equivariant dynamics by dos Reis (1984). Much later, the case $n = 4$ leads to one of the first investigations of a robust heteroclinic network by Kirk and Silber (1994). There is a rich theory for heteroclinic cycles and networks when $H$ is a transitive subgroup of $S_n$ (and $G$ acts irreducibly on $\mathbb {R}$). We refer to Field (2007) for details and more references as well as to Dias et al. (2000) who investigate more general linear actions by wreath products.

We may define a natural class of dynamical systems on $\mathbb {R}^n$ (more generally $\prod _{i=1}^k \mathbb {R}^{m_i}$) intermediate between Lotka-Volterra systems and actions of groups of signed permutation matrices on $\mathbb {R}^n$. This class will have a natural connection with network dynamics.

Definition 2.3

(Field 1996, [Chapter7]) A semi-linear feedback system on $\mathbb {R}^n$ is a system of differential equations of the form

$$\begin{aligned} x'_i = f_i(x_i) + x_iF_i(x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n), \; i \in \mathbf {n} \end{aligned}$$

where $f_i(0) = 0$, $i \in \mathbf {n}$ and the maps $f_i,F_i$ are all at least $C^1$.

Remark 2.4

• (1) Lotka-Volterra systems define semi-linear feedback systems on $\mathbb {R}^n$ (typically with $F_i$ linear, $f_i(x_i) = a_i x_i - b_ix_i^2$, and $a_i, b_i > 0$).

• (2) Signed permutation group actions $G = \Delta _n \rtimes H$ on $\mathbb {R}^n$ define semi-linear feedback systems if we restrict to cubic truncations (this usually suffices for the study of heteroclinic cycles, see Field 2007 [Chapter5]). In this situation, $f_i$ will be a odd cubic map $f_i(x_i) = a_ix_i - b_i x_i^3$ (with all the $f_i$ equal if $H$ is transitive).

• (3) The ‘extinction’ hyperplanes $x_i = 0$ are invariant for semi-linear feedback systems.

• (4) In general, we may define semi-linear feedback systems on $\mathbb {R}^m = \prod _{i=1}^n \mathbb {R}^{m_i}$ in the obvious way by replacing $x_iF_i$ by $\langle \mathbf {x}_i,\mathbf {F}_i\rangle _i$, where $\langle \;,\;\rangle _i$ is an $\mathbb {R}^{m_i}$-valued bilinear form on $\mathbb {R}^{m_i}$. In this case, the subspaces $\mathbf {x}_i = 0$ are invariant.

For a semi-linear feedback system, the evolution of ${x}_i$ according to ${x}_i' = f_i({x}_i)$ is modified by the linear feedback term $x_iF_i$ that may depend nonlinearly on the remaining variables, see Fig. 1. The feedback loop can lead to bistability of equilibria on the $x_i$-axes. For example, in the Lotka-Volterra case, $f_i$ has equilibria at $x_i = 0, a_i/b_i > 0$. Along a trajectory $\bar{\mathbf {x}} = (x_1,\ldots , x_{i-1},x_{i+1},\ldots ,x_n)$, variation of $x_i F_i(\bar{x})$ can result in switching between a single stable equilibrium at $x_i = 0$ and a stable equilibrium at $x_i > 0$. This mechanism easily leads to the formation of heteroclinic cycles. We refer to (Field 1996, [Chapter7,§2]) where this approach is used to construct edge and face heteroclinic cycles in symmetric systems (though symmetry plays no essential role, see Field 1996 [Chapter 7] and Field 2005). In recent work, Ashwin and Postlethwaite (2013) have shown that every heteroclinic network, with cycle lengths at least three, can be realized in a semi-linear feedback network. The realization is achieved using explicit cubic vector fields (with $F_i$ linear in $x_j^2$, $j \ne i$).

Fig. 1

The model for a semi-linear feedback system

Heteroclinic cycles (or networks) that occur for Lotka-Volterra equations or semi-linear feedback systems have the following network interpretation. Equilibria on the cycle correspond to groups of saturated (fully active) nodes and dead nodes. For example, the equilibrium $(1,0,0)$ will correspond to one saturated node (the first), and two dead nodes. An equilibrium of the form $(a,b,0,0)$, with $a,b > 0$, corresponds to two saturated nodes and two dead nodes. If $(1,0,0)$ lies on a heteroclinic cycle, which has a connection $(1,0,0)\rightarrow (0,1,0)$, then along the connection node 3 will be dead, node 1 will be active and damped and node 2 will be active and growing.

From the point of view of much contemporary research on networks, in particular neural dynamics, it is interesting to consider networks of coupled nonlinear oscillators and look for patterns of synchronization. The simplest models of this type are Kuramoto style coupled phase oscillators where node dynamics is defined on the circle $\mathbb {T} = \mathbb {R}/\mathbb {Z}$. In this context, the previously described models of heteroclinic networks comprised of connections between equilibria are not directly relevant as nodes cannot be naturally grouped into dead and active/saturated. One approach, due to Ashwin and Swift (1992), is to look at all-to-all coupled systems of $n$-cells with $S_n$ symmetry where there is often synchronization into clusters of cells combined with heteroclinic phenomena (see, for example, Hansel et al. 1993, 1993; Orosz et al. 2009; Ashwin et al. 2010). We instead consider networks of interacting dynamical systems with no symmetries (local or global) but where the network architecture can lead to invariant subspaces comprised of groups of synchronized cells. An advantage of this approach is that we avoid higher multiplicity of eigenvalues resulting from the group action and the unavoidable $S_n$-invariance of heteroclinic cycles and networks.

2.2 Network Dynamics and Coupled Cell Systems

A general theory of networks of coupled cells has been formalized by Stewart et al. (2003), Golubitsky et al. (2004), Golubitsky et al. (2005) (a survey and review of some of this work appears in Golubitsky and Stewart (2006)). Their approach is relatively algebraic in character and depends on groupoid formalism, graphs and the idea of a quotient network. Although we use some of their formalism and terminology, we follow a more synthetic and combinatorial way of describing coupled systems that fits better with our intended applications of constructing networks with particular properties—for example, additive input structure, intrinsic cell dynamics and realistic coupling models. We use a ‘flow-chart’ formalism similar to that used in electrical and computer engineering. We give necessary definitions, establish notational conventions and refer the reader to Agarwal and Field (2010), Aguiar et al. (2011), Agarwal and Field (2010), Field (2004) for more details, discussion and examples. We remark that we generally use the term coupled cell network to refer to the network architecture—a directed network graph codifying the connection structure and node types—and use coupled cell system to refer to a specific realization of a coupled cell network as a system of coupled differential equations (Agarwal and Field 2010). On occasions, it is convenient to abuse this convention and allow network structure notation to represent a coupled cell system.

Recall from the introduction that dynamics on a network ${\mathcal {N}}$ with $\ell \ge 2$ nodes (or ‘cells’) $A_1,\ldots ,A_\ell$, each with same phase space $M$, is given by a $C^1$ vector field $\mathbf {f}$ on $M^\ell$. In terms of differential equations, we have

$$\begin{aligned} \mathbf {x}_i' = f_i(\mathbf {x}_i; \mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)}),\; i \in \varvec{\ell }. \end{aligned}$$

(2.1)

We do not yet assume that $k_i$ is independent of $i$ —the network is heterogeneous.

Remark 2.5

• (1) At this level of generality, nothing is said about the input structure or intrinsic node dynamics (see  Bick and Field 2015, §2) for an extended discussion on this point and the role of reductionism).

• (2) The model assumes that the evolution of each node depends on complete information about the states of the other nodes. This is an unrealistic assumption for most systems. For example, in biology, technology and control, communication of information is expensive (in terms of energy and resources devoted to communication channels) and efficiency is obtained through communicating the essential minimal information for the task in hand. One more realistic approach is to assume that each node $A_i$ has an associated observable $\xi _i: M \rightarrow \mathbb {R}^s$ (often with $s = 1$) and that network equations are of the form

  $$\begin{aligned} \mathbf {x}_i' = f_i(\mathbf {x}_i; \xi _{j_i(1)}(\mathbf {x}_{j_i(1)}),\ldots ,\xi _{j_i(k_i)}(\mathbf {x}_{j_i(k_i)})),\; i \in \varvec{\ell }. \end{aligned}$$

  This is the scalar signalling model described in (Agarwal and Field 2010, §2.5), which allows for situations where there is only partial communication of information between nodes, such as pulse coupling or spiking models. Scalar signalling models are also appropriate for situations where the node phase spaces vary across the network or there is a diffusive or additive input structure. None of this matters in the simplest case when $M$ is 1-dimensional ($\mathbb {R}$ or $\mathbb {T}$) since the tangent bundle $TM \approx M \times \mathbb {R}$ and we may always assume evolution depends on 1-dimensional node states. The 1-dimensional case will be of primary concern in this article, and so we assume the model given by (2.1) rather than the more realistic scalar signalling model. We discuss extensions of our main results to scalar signalling networks in the concluding section of this paper.

We regard each node of a network as a cell with a possibly variable number of inputs and an output. Diagrammatically, we represent a cell as shown in Fig. 2. Referring to Fig. 2, cell $A_i$ receives single inputs from the cells $A_2, A_7, A_9$ and three inputs from $A_3$ ($k_i = 6$). The identical arrowheads indicate that inputs 2 and 3 are the same (and so the connections from $A_3, A_9$ can be interchanged without affecting the dynamics or network structure). The remaining inputs are all different (and any interchange of inputs to 1, 4–6 will potentially change dynamics and certainly changes the network structure). We shall mainly be concerned with the case of asymmetric inputs (Agarwal and Field 2010): no inputs can be interchanged without changing network dynamics—rather than the case of symmetric inputs (Agarwal and Field 2010). We explain why shortly.

Fig. 2

A cell with six inputs and one output. Inputs of the same type (for example the second and third input) can be permuted without affecting the output

Since we are assuming all cells have the same phase space, any cell can be connected to any input of any other cell in the network. A coupled cell network ${\mathcal {N}}$ will then consist of the cells $A_i$ together with connections between cells. If each cell has a fixed number of inputs, then we require that all inputs are filled. Associated with the coupled cell network ${\mathcal {N}}$, we define the network graph $G({\mathcal {N}})$ exactly as in the introduction. We always assume that ${\mathcal {N}}$ (that is, $G({\mathcal {N}})$) is connected.

If $f_i = f$, $k_i = k \ge 1$ for all $i \in \varvec{\ell }$, the network is a homogeneous network (of identical cells²).

Let ${\mathcal {N}}$ be a homogeneous network with cells $\mathbf {A} = \{A_1,\ldots ,A_\ell \}$. Suppose that $\mathcal {X} = \{X^j\;|\;j \in \mathbf {p}\}$ is a partition of $\mathbf {A}$ such that each $X^j$ contains at least one cell and at least one $X^j$ contains two or more cells. Let $d(j) = |X^j|$ be the number of cells in $X^j$, $j \in \mathbf {p}$. Label cells in $X^j$ as $A_{j_1},\ldots , A_{j_{d(j)}}$ and define $J_j = \{j_1,\ldots ,j_{d(j)}\}$. We have $\cup _{j\in \mathbf {p}}J_j = \varvec{\ell }$.

If $\mathbf {x} = (\mathbf {x}_1,\ldots ,\mathbf {x}_n)\in M^\ell$ denotes the state of the network, then we may group states according to the partition $\mathcal {X}$ and write

$$\begin{aligned} \mathbf {x} = (\mathbf {x}^1,\ldots ,\mathbf {x}^p), \end{aligned}$$

where $\mathbf {x}^j = (\mathbf {x}_{j_1}, \ldots , \mathbf {x}_{j_{d(j)}})\in M^{d(j)}$ will denote the state of the $d(j)$ cells in $X^j$. Define

$$\begin{aligned} \varvec{\Delta }_j = \{\mathbf {x}^j \;|\;\mathbf {x}_{j_1}= \ldots = \mathbf {x}_{j_{d(j)}}\},\;\; j \in \mathbf {p} \end{aligned}$$

and

$$\begin{aligned} \varvec{\Delta }(\mathcal {X}) = \{\mathbf {x} = (\mathbf {x}^1,\ldots ,\mathbf {x}^p) \;|\;\mathbf {x}^j\in \Delta _j,\;\;j \in \mathbf {p}\}. \end{aligned}$$

Definition 2.6

(Aguiar et al. 2011; Agarwal and Field 2010; cf Stewart et al. 2003; Golubitsky et al. 2005; Golubitsky and Stewart 2006) The partition $\mathcal {X}$ is a synchrony class for the coupled cell network ${\mathcal {N}}$ if the subspace $\varvec{\Delta }(\mathcal {X})$ is dynamically invariant for every realization of ${\mathcal {N}}$ as a coupled cell system. If $\mathcal {X}$ is a synchrony class, then we say $\varvec{\Delta }(\mathcal {X})$ is a synchrony subspace or invariant subspace.

If the network is homogeneous, then $\mathcal {X} = \{A_1,\ldots ,A_\ell \}$ is always a synchrony class: the maximal synchrony class. The associated invariant space is the trivial or minimal synchrony subspace and is the synchrony subspace of minimal dimension for any given realization of a coupled cell network (this should be contrasted with the null synchrony class that is the set-theoretic complement of the union of all synchrony classes and is the open invariant set consisting of desynchronized cells). We usually denote the minimal synchrony subspace by $\varvec{\Delta }(M)$ (or $\varvec{\Delta }_\ell (M)$ if we wish to emphasize the number of cells).

We remark the following elementary proposition characterizing synchrony classes.

Proposition 2.7

(cf  Golubitsky and Stewart 2006, §7) Let ${\mathcal {N}}$ be a coupled cell network as above. Suppose that $\mathcal {X} = \{X^j\;|\;j\in \mathbf {p}\}$ is a partition of $\mathbf {A}$. Then $\mathcal {X}$ is a synchrony class iff for all $i,j \in \mathbf {p}$ and every input type $k$, every cell in $X^i$ receives the same number of inputs of type $k$ from cells in $X^j$.

Proof

One implication is an immediate consequence of the existence and uniqueness theorem for differential equations.

For the converse, it is enough to show that if the condition fails, then $\mathcal {X}$ cannot define an invariant subspace for all systems with the given architecture. It is enough to find one example. Our assumption is that there exist $i,j \in \mathbf {p}$ and an input type $\ell$ such that there exists two cells $A_a, A_b$ in $X^i$ which receive a different number of inputs of type $\ell$ from cells in $X^j$. Suppose cells have $r_\ell$ inputs of type $\ell$. Without loss of generality, take $\ell = 1$ and set $r_\ell = r$. Assume the phase space is $\mathbb {R}$ and take as model $f(x_0;x_1,\ldots ) = x_1+x_2+\cdots +x_r$ (sum linearly over inputs of type $\ell$). Initialize cells in $X^j$ so that their initial state is $1 \in \mathbb {R}$. Initialize to zero cells not in $X^j$ (note the case $i = j$ is covered). Observe that the value of the model function $f$ will be different on the two cells $A_a, A_b$ ($f$ sums to the number of inputs of type $\ell$ from cells in $X^j$). Hence $\mathcal {X}$ is not a synchrony class. $\square$

2.3 Notation for Synchrony Classes and Subspaces

Let $\varvec{\Delta }(\mathcal {X})$ be the synchrony subspace determined by the synchrony class $\mathcal {X} = \{X^j\;|\;j\in \mathbf {p}\}$. Let $\mathcal {X}' = \{X^j \;|\;d(j) > 1\}$. Each $X^j \in \mathcal {X}'$ corresponds to a group of at least two cells. If $\mathcal {X}'= \{X^{j_1},\ldots ,X^{j_k}\}$, we denote the synchrony subspace (or class) by $\{X^{j_1} \Vert X^{j_2} \Vert \ldots \Vert X^{j_k}\}$. Typically, we expand each $X^{j_i}$ to identify the individual cells. For example, suppose that $\mathcal {X}' = \{X^1,X^2\}$ and $X^1 = \{{A}_1,A_2,A_5\}$, $X^2 = \{{A}_3,{A}_4\}$, then we denote the associated synchrony subspace by $\{{A}_1,{A}_2,{A}_5 \Vert {A}_3,{A}_4\}$. The notation indicates that both groups of cells ${A}_1,{A}_2,{A}_5$ and $A_3,{A}_4$ may be synchronized, but not necessarily to the same state. Indeed, $\{{A}_1,{A}_2,{A}_3,A_4,{A}_5\}$ may not be a synchrony class (see Aguiar et al. 2011, §7.1) for a simple example).

Example 2.8

In Fig. 3, we show two identical cell networks comprised of three cells, each cell with two inputs. Suppose first that the cells have symmetric inputs. Then the two networks are dynamically identical (see Agarwal and Field 2010, §3) for formal definitions). Both networks have $\{A_1,A_2\}$, $\{A_1,A_3\}$ and $\{A_2,A_3\}$, as non-trivial synchrony classes.

Now suppose that the cells in both networks have asymmetric inputs. Then the two networks are dynamically different. Indeed, the network of Fig. 3a has two non-trivial synchrony classes $\{A_1,A_2\}$, $\{A_1,A_3\}$, while the second network has no non-trivial synchrony classes.

Based on the invariant subspace structure, one might guess that robust heteroclinic cycles are most likely when inputs are symmetric. This turns out not to be so: there are no robust heteroclinic cycles when there are symmetric inputs. This is a consequence of multiplicities forced in eigenvalues at fully synchronized equilibria. On the other hand when there are asymmetric inputs, the network of Fig. 3a supports robust simple heteroclinic cycles, even when $M$ is 1-dimensional. We refer to (Aguiar et al. 2011, [§5]) and the next section. We remark that robust heteroclinic networks can occur in systems of at least four all-to-all symmetrically coupled phase oscillators (see  Ashwin et al. 2008, 2010, but note the restrictions placed on coupling functions). On account of eigenvalue multiplicities that are often absent in systems with asymmetric inputs, we concentrate on realizing heteroclinic networks in networks of identical cells with asymmetric inputs.

Fig. 3

Two 3 identical cell networks, each cell with two inputs

2.4 Additive Input Structure, Heterogeneous Networks

While the all-to-all coupled identical cell model is attractive mathematically, it is not very realistic in some applications. In particular, we are interested in networks for which cells have well defined dynamics when uncoupled and to which one can add (or subtract) inputs in a coherent way. We give a general definition of additive input structure, which is applicable to general networks, and then specialize to systems that can synchronize into clusters and have a weak form of diffusive coupling.

Definition 2.9

Suppose that ${\mathcal {N}}$ is a dynamical network with cells $A_1,\ldots ,A_\ell$ and dynamics given by

$$\begin{aligned} \mathbf {x}_i' = f_i(\mathbf {x}_i; \mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)}),\; i \in \varvec{\ell }. \end{aligned}$$

The network (or cells) has additive input structure if there exist $P \in \mathbb {N}$, $C^1$ families of vector fields $h_j: M\times M \rightarrow TM$, $j \in \mathbf {P}$, and maps $\tau ^i:\mathbf {k}_i\rightarrow \mathbf {P}$, $i \in \varvec{\ell }$, such that

$$\begin{aligned} f_i(\mathbf {x}_i;\mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)})=\sum _{s=1}^{k_i} h_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_{j_i(s)}), \; i \in \varvec{\ell }. \end{aligned}$$

(2.2)

Remark 2.10

• (1) We regard the second variable of $h_j$ as the parameter: $h(\mathbf {x},\mathbf {y}) \in T_{\mathbf {x}}M$ for all $\mathbf {y} \in M$.

• (2) If $P = 1$, then the network has symmetric inputs—there is just one input type. If the maps $\tau ^i$ are all injective and at least one $k_i > 1$, then the network will have asymmetric inputs.

• (3) The additive input structure allows the addition and deletion of connections. In particular, the connection structure may be time dependent (cf. Bick and Field 2015).

Additive input structure requires that there are no nonlinear interactions between different inputs to the cell $A_i$ though each input may certainly interact in a nonlinear way with the state variable $x_i$. Kuramoto style phase oscillator networks, most pulse coupled networks, and the $N$-body problem of celestial mechanics all have additive input structure with $g_j(\mathbf {x}_0,\mathbf {x}_j) = G_j(\mathbf {x}_j - \mathbf {x}_0)$ (diffusive coupling—this requires an additive structure on each phase space).

Example 2.11

• (1) Consider the homogeneous 4 identical cell network with dynamics defined by

  $$\begin{aligned} f(x_0;x_1,x_2,x_3) = x_0x_1x_2x_3, \; x_i \in \mathbb {R}. \end{aligned}$$

  (We do not specify the connection structure.) The input structure is not additive: there is no natural way to remove (or add) a connection.

• (2) Consider the homogeneous 4-cell semi-linear feedback network with dynamics defined by

  $$\begin{aligned} f(x_0;x_1,x_2,x_3) = x_0 - x_0^3 + x_0\left( 2x_1 + 3x_3 - 4x_3\right) ,\; x_i \in \mathbb {R}. \end{aligned}$$

  This system has additive input structure (asymmetric inputs).

The decomposition (2.2) is far from unique. However, if we define

$$\begin{aligned} F_i(\mathbf {x}_i)= & {} \sum _{s=1}^{k_i}h_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_i), \\ g_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_{j_i(s)})= & {} h_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_{j_i(s)}) - h_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_i), \end{aligned}$$

then we have

$$\begin{aligned} f_i(\mathbf {x}_i;\mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)})= & {} F_i(\mathbf {x}_i) +\sum _{s=1}^{k_i} g_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_{j_i(s)}), \end{aligned}$$

(2.3)

$$\begin{aligned} g_j(\mathbf {x}.\mathbf {x})= & {} 0, \; \text {for all } j \in \mathbf {P},\; \mathbf {x} \in M. \end{aligned}$$

(2.4)

and this decomposition of $f_i$, subject to (2.4), is unique.³ If all the $F_i$ are equal, say to $F_0$, then ${\mathcal {N}}$ will be a heterogeneous network of identical cells with additive input structure and the ‘intrinsic’ dynamics of each cell is given by $\mathbf {x}' = F_0(\mathbf {x})$. This formulation of additive input structure is appropriate for the analysis of synchronization in the network and allows for variable numbers of inputs across the network.

Example 2.12

For Example 2.11(2), the $g_j$ will be selected from the maps $E(x,y) = 2x(x-y)$, $F(x,y) = 3x(x-y)$, $G(x,y) = -4x(x-y)$ according to the connection structure. The $F_i$ will depend on the specific connection structure and the resulting ‘intrinsic’ dynamics is artificial and unnatural: dynamics of semi-linear feedback systems does not naturally lead to clustering and synchronization.

The next examples fit well in the additive input model given by (2.3, 2.4).

Example 2.13

• (1) Suppose

  $$\begin{aligned} f(\theta _0;\theta _1,\theta _2,\theta _3,\ldots ,\theta _{\ell }) = \omega + \sum _{i=1}^\ell a \sin (\theta _i - \theta _0), \; \theta _i \in \mathbb {T}, 0 \le i \le \ell . \end{aligned}$$

  This defines the classic Kuramoto phase oscillator model. The intrinsic dynamics is given by $\theta ' = \omega$ and we can add or subtract connections without changing the intrinsic dynamics. Similar comments hold if we replace $\sin (\theta _i - \theta _0)$ by any odd trigonometric polynomial in $\theta _i - \theta _0$. We can easily generalize and let the coefficient $a$ depend on $i$.

• (2) Suppose $J_i \subset \varvec{\ell }\backslash \{i\}$, $i \in \varvec{\ell }$, and

  $$\begin{aligned} f_i(\theta _i;\theta _1,\theta _2,\theta _3,\ldots ,\theta _{\ell }) = \omega _i + \sum _{j\in J_i}^\ell a \sin (\theta _j - \theta _i + \psi _{ij} ), \; \theta _i \in \mathbb {T}, i\in \varvec{\ell }. \end{aligned}$$

  In this case, adding an input $j \rightarrow i$ will result in a frequency change for $A_i$ from $\omega _i$ to $\omega _i + a \sin (\psi _{ij})$. This situation is relevant for power grid models based on a second-order differential equation model of phase oscillators (see Filatrella et al. 2008; Dörfler and Bullo 2012; Dörfler et al. 2013; Rohden et al. 2012).

• (3) Spiking neural networks typically have additive input structure.⁴ Similar remarks hold for pulse coupled systems (Neves and Timme 2012).

Remark 2.14

(Diffusive coupling) If the phase space $M$ has an additive structure (for example, $M$ is either $\mathbb {R}^n$ or $\mathbb {T}^n$), then we can write the input maps $g_j$ of (2.3, 2.4) as functions of $\mathbf {x}, \mathbf {y}-\mathbf {x}$ (a weak form of diffusive coupling). Specifically, if we define $G_j(\mathbf {x},\mathbf {z}) = \int _0^1 \frac{d}{dt} g_j(\mathbf {x},\mathbf {x} + t\mathbf {z})\, dt$, then we may rewrite (2.3) in the form

$$\begin{aligned} f_i(\mathbf {x}_i; \mathbf {x}_{j_i(1)},\ldots ,\mathbf {x}_{j_i(k_i)}) = F_i(\mathbf {x}_i) + \sum _{s=1}^{k_i} G_{\tau ^i(s)}(\mathbf {x}_i,\mathbf {x}_{j_i(s)}-\mathbf {x}_i), \end{aligned}$$

(2.5)

where now $G_j(\mathbf {x},0) = 0$ for all $j \in \mathbf {P}$, $\mathbf {x} \in M$. We can extend this model to phase spaces with no additive structure using scalar signalling: replace $\mathbf {y}-\mathbf {x}$ by $\xi (\mathbf {y})-\xi (\mathbf {x}) \in \mathbb {R}^s$.

Suppose we are given a coupled cell system with additive input structure (2.3,2.4) with all cells in the network having identical intrinsic dynamics. Even though the cells in the network may have different numbers of inputs, the minimal synchrony subspace $\varvec{\Delta }(M)$ is always an invariant subspace of $M^\ell$ and there may exist many synchrony subspaces of $M^\ell$. We give examples later in Sect. 5.1.

3 Two Classes of Identical Cell Homogeneous Coupled Cell Systems that Support Heteroclinic Networks

We follow the notational conventions given in the previous section. Up to equivalence Dias and Stewart (2005), Agarwal and Field (2010), there are exactly two connected two identical cell networks with each cell having exactly one input. In Fig. 4, we show representative networks for each equivalence class.

Fig. 4

The two inequivalent connected two cell networks

Referring to the figure, cells in either network are assumed identical with one input. The phase space of each cell is an unspecified manifold $M$ and state variables are denoted by $\mathbf {x}_1, \mathbf {x}_2$. The only synchrony subspace of either ${\mathcal {P}}_2$ or ${\mathcal {Q}}_2$ is the minimal synchrony subspace $\varvec{\Delta }_2(M) = \{(\mathbf {x}_1,\mathbf {x}_2) \;|\;\mathbf {x}_1 = \mathbf {x}_2\}$.

Dynamics on a two identical cell network can never support robust heteroclinic cycles (see Aguiar et al. 2011, §4).

We will extend the networks ${\mathcal {P}}_2$ and ${\mathcal {Q}}_2$ to sequences $({\mathcal {P}}_n)_{n\ge 2}$ and $({\mathcal {Q}}_n)_{n\ge 2}$, where ${\mathcal {P}}_n$, ${\mathcal {Q}}_n$ are identical $n$-cell homogeneous networks, with each cell having $n-1$ inputs. Either network ${\mathcal {P}}_n$ or ${\mathcal {Q}}_n$ will have $\{{A}_1,{A}_j\} = \{\mathbf {x}_1 = \mathbf {x}_j\}$ as a synchrony subspace for $j > 1$. We start with the case $n = 3$ which was previously considered in Aguiar et al. (2011, §5).

3.1 3-Cell Networks with Two Non-trivial Synchrony Subspaces

In Fig. 5, we show the two equivalence classes of the two asymmetric input three cell identical cell networks that admit two non-trivial synchrony subspaces. Observe that ${\mathcal {P}}_3$ and ${\mathcal {Q}}_3$ are both obtained from ${\mathcal {P}}_2$ and ${\mathcal {Q}}_2$ by adding an input and one cell which is connected to the original cells the same way (for both networks). Note that we use different arrowheads to distinguish between different input types.

Fig. 5

The two inequivalent three cell networks with non-trivial synchrony classes $\{\mathbf {A}_1,\mathbf {A}_2\}$, $\{\mathbf {A}_1,\mathbf {A}_3\}$

3.1.1 Heteroclinic Networks on ${\mathcal {P}}_3$, ${\mathcal {Q}}_3$

The networks ${\mathcal {P}}_3$, ${\mathcal {Q}}_3$ have non-trivial synchrony subspaces $\{{A}_1,{A}_2\}$ and $\{{A}_1,{A}_3\}$. It is shown in (Aguiar et al. 2011, §5) that ${\mathcal {P}}_3$ and ${\mathcal {Q}}_3$ support robust heteroclinic cycles. More precisely, if we assume each cell has phase space $\mathbb {R}$ (analysis for the phase space $\mathbb {T}$ is similar; higher-dimensional dynamics is easier), then we can choose network dynamics so that there is a simple heteroclinic cycle connecting hyperbolic saddle equilibria $\mathbf {p}, \mathbf {q}$ lying in the trivial synchrony subspace $\varvec{\Delta }_3(\mathbb {R})$, with 1-dimensional connections lying in $\{{A}_1,{A}_2\}$ and $\{{A}_1,{A}_3\}$. Both equilibria have a 1-dimensional unstable manifold lying in one of the 2-planes $\{{A}_1,{A}_2\}$ and $\{{A}_1,{A}_3\}$ (but not in $\varvec{\Delta }_3(\mathbb {R})$). We refer to Fig. 6 for one possible configuration. We have only shown $\mathbf {p}, \mathbf {q}$ connections in one half plane, but it is possible (see Aguiar et al. 2011) to construct network dynamics so that there are two connections $\mathbf {p} \rightarrow \mathbf {q}$ in $x_1 = x_3$ and two connections $\mathbf {q} \rightarrow \mathbf {p}$ in $x_1 = x_2$. In case cells have 2-dimensional dynamics, Agarwal has constructed an explicit low degree polynomial vector field which realizes all four connections (Aguiar et al. 2011, §5).

Fig. 6

A simple heteroclinic cycle connecting $\mathbf {p}, \mathbf {q}$

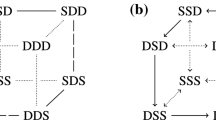
Referring to Fig. 6, along each connection one of the three cells desynchronizes from the other two (which remain synchronized) and then resynchronizes at the end of the trajectory. For example, ${A}_2$ desynchronizes from the pair $\{{A}_1,{A}_3\}$ along the connection $\mathbf {q} \rightarrow \mathbf {p}$. This is precisely the type of desynchronization and resynchronization that occurs along the connections given in our main theorem.

Remark 3.1

Along similar lines to those used in Aguiar et al. (2011), it is not hard to show⁵ that any simple heteroclinic $n$-cycle can be realized in either of the networks ${\mathcal {P}}_3$ and ${\mathcal {Q}}_3$ provided that $n$ is even. Indeed, we use the obvious generalization of the setup in Fig. 6—see Fig. 7. If $n$ is odd, it is not possible to realize a simple heteroclinic $n$-cycle if we assume 1-dimensional node dynamics. If node dynamics are 2-dimensional, realization is straightforward.

Fig. 7

A simple heteroclinic cycle connecting $2m$ nodes: $\mathbf {p}_1,\ldots , \mathbf {p}_{2m}$

In general, the graph of any heteroclinic network, with out- and in-degrees at most two for each node, can easily be realized as a simple heteroclinic network in either ${\mathcal {P}}_3$ or ${\mathcal {Q}}_3$ provided that we allow cell dynamics to be 2-dimensional. In many (possibly all) cases, we can realize using 1-dimensional cell dynamics (we have not found any counterexamples to realization by 1-dimensional node dynamics for graphs with at most 6 nodes).

Example 3.2

Both graphs shown in Fig. 8 can be realized using 1-dimensional cell dynamics as a simple heteroclinic network. To see why this is so, observe that for realization as a heteroclinic network, the connections between equilibria lie either in $x_1 = x_2$ or in $x_1 = x_3$. Once we have decided which subspace $W^u(p)$ is contained in, all the other subspaces are determined. Thus in Fig. 8a, $W^u(p), W^u(r)$ are contained in one invariant subspace, say $x_1 = x_2$, the remaining connections lie $x_1 = x_3$ (broken lines). If we apply the same argument to Fig. 8b, $W^u(s), W^u(p)$ lie in the same subspace and so must intersect. However, if we place $s$ between $q$ and $r$, $W^u(s), W^u(p)$ no longer have to intersect and we can realize the graph as a heteroclinic network. Similar arguments work for every 4-node network.

Fig. 8

Graphs with 4 nodes that can be realized in ${\mathcal {P}}_3$, ${\mathcal {Q}}_3$ as simple heteroclinic networks connecting $4$ cells with 1-dimensional cell dynamics

3.2 The Sequences $({\mathcal {P}}_n)_{n \ge 3}$, $({\mathcal {Q}}_n)_{n \ge 3}$

Proposition 3.3

We may construct a sequence $({\mathcal {P}}_n)_{n \ge 2}$ of coupled cell networks uniquely characterized by the following properties:

• (1) ${\mathcal {P}}_n$ consists of $n$ identical cells ${A}_1,\ldots ,{A}_n$, each with $n-1$ (asymmetric) inputs.

• (2) For $2 \le i \le n$, $\{{A}_1,{A}_i\}$ is a synchrony class of ${\mathcal {P}}_n$.

• (3) For $n \ge 2$, ${\mathcal {P}}_{n+1}$ is built from ${\mathcal {P}}_{n}$ by taking a new cell ${A}_{n+1}$ with $n$-input types $i_1,\ldots ,i_n$ and then

  • (a) Connecting the first $n$ cells ${A}_1,\ldots ,{A}_n$ according to the pattern of ${\mathcal {P}}_{n}$ using only the input types $i_1,\ldots ,i_{n-1}$.

  • (b) Connecting the output of cell ${A}_{n+1}$ to the $i_n$ inputs of ${A}_1,\ldots ,{A}_n$.

  • (c) Connecting the output of ${A}_j$ to the $i_{j-1}$-input of ${A}_{n+1}$, $1 \le j \le n$ where our convention is that the output of ${A}_1$ goes to the $i_n$-input of ${A}_{n+1}$.

• (4) ${\mathcal {P}}_2$ is the coupled cell network of Fig. 4.

Proof

By (3b), the cells ${A}_1,\ldots ,{A}_n$ of ${\mathcal {P}}_{n+1}$ see the same inputs from ${A}_{n+1}$. It is immediate from (3a) and proposition 2.7 that if ${\mathcal {P}}_n$ has synchrony classes $\{{A}_1,{A}_i\}$, $2 \le i \le n$, the same will be true for ${\mathcal {P}}_{n+1}$. Hence, by (3c) and proposition 2.7, $\{{A}_1,{A}_{n+1}\}$ is a synchrony class for ${\mathcal {P}}_{n+1}$. The proof is immediate by the obvious induction. $\square$

Remark 3.4

An easy consequence of proposition 2.7 is that $\{{A}_i,{A}_j\}$ is not a synchrony class of ${\mathcal {P}}_n$ if $i,j \ge 2$.

Example 3.5

In Fig. 9 we illustrate the construction of ${\mathcal {P}}_4$ used in the proof of Proposition 3.3.

Fig. 9

Constructing ${\mathcal {P}}_4$ from ${\mathcal {P}}_3$

We have an analogous result to proposition 3.3 but starting with the network ${\mathcal {Q}}_2$. We omit the proof.

Proposition 3.6

We may construct a sequence $({\mathcal {Q}}_n)_{n \ge 2}$ of coupled cell networks uniquely characterized by the following properties:

• (1) ${\mathcal {Q}}_n$ consists of $n$ identical cells ${A}_1,\ldots ,{A}_n$, each with $n-1$ (asymmetric) inputs.

• (2) For $2 \le i \le n$, $\{{A}_1,{A}_i\}$ is a synchrony class of ${\mathcal {Q}}_n$.

• (3) For $n \ge 2$, ${\mathcal {Q}}_{n+1}$ is built from ${\mathcal {Q}}_{n}$ by taking a new cell ${A}_{n+1}$ with $n$-input types $i_1,\ldots ,i_n$ and then

  • (a) Connecting the first $n$ cells ${A}_1,\ldots ,{A}_n$ according to the pattern of ${\mathcal {Q}}_{n}$ but using only the input types $i_1,\ldots ,i_{n-1}$.

  • (b) Connecting the output of cell ${A}_{n+1}$ to the $i_n$ inputs of ${A}_1,\ldots , {A}_n$.

  • (c) Connecting the output of ${A}_1$ to the $i_n$ input of ${A}_{n+1}$, and the output of ${A}_2$ to the $i_{1}$-input of ${A}_{n+1}$.

  • (d) Connecting the output of ${A}_j$ to the $i_{j}$ input of ${A}_{n+1}$, $3 \le j \le n$.

• (4) ${\mathcal {Q}}_2$ is the coupled cell network ${\mathcal {Q}}_2$ of Fig. 5.

4 Realization of Heteroclinic Networks in ${\mathcal {P}}_n$ and ${\mathcal {Q}}_n$

Let $\Gamma = \Gamma (N,E)$ be a graph with $N\ge 2$ vertices $\mathbf {v}_1,\ldots ,\mathbf {v}_N$ and $E$ edges joining vertices (as usual, we assume conditions $(C1,C2)$ hold).

We show that there exists $n \le E+1$ such that $\Gamma$ can be realized as a robust heteroclinic network for a coupled cell system with network architecture either ${\mathcal {P}}_n$ or ${\mathcal {Q}}_n$. The representation will be implemented in an interesting way that reflects the possibilities of synchronization in ${\mathcal {P}}_n$ and ${\mathcal {Q}}_n$ (this will require $n = E+1$). In more detail, we prove our result in the hardest case where cell dynamics is 1-dimensional and dynamics is $C^\infty$. Each vertex $\mathbf {v}_i \in \Gamma$ will correspond to a fully synchronized hyperbolic saddle $\mathbf {p}_i \in \varvec{\Delta }_n(\mathbb {R})$, and edges $\mathbf {v}_j \rightarrow \mathbf {v}_j$ will correspond to connecting orbits $\mathbf {p}_j \rightarrow \mathbf {p}_i$ lying in a 2-dimensional invariant (synchrony) subspace. The robustness of the realization will follow in the standard way from the hyperbolicity of nodes and the (trivial) transversality of stable and unstable manifolds within invariant subspaces. Finally, the realization will reflect synchronization and desynchronization patterns in ${\mathcal {P}}_n$ and ${\mathcal {Q}}_n$. To explain this, we need new definitions and notation.

Unless stated to the contrary, we henceforth assume that each cell has phase space $\mathbb {R}$—the extension to the case where the phase space is a general connected manifold is routine. For ${\mathcal {P}}_n$ and ${\mathcal {Q}}_n$, let $P_2,\ldots ,P_n\subset \mathbb {R}^n$ be the 2-planes defined by

$$\begin{aligned} P_2= & {} \{(x_1,x_2, x_1,\ldots ,x_1) \;|\;(x_1,x_2) \in \mathbb {R}^2\} = \cap _{i \ne 2} \{{A}_1,{A}_i\}\\ P_3= & {} \{(x_1,x_1,x_3, x_1,\ldots ,x_1) \;|\;(x_1,x_3) \in \mathbb {R}^2\} = \cap _{i \ne 3} \{{A}_1,{A}_i\}\\ \ldots= & {} \ldots \\ P_n= & {} \{(x_1,x_1,x_1, x_1,\ldots ,x_n) \;|\;(x_1,x_n) \in \mathbb {R}^2\} = \cap _{i \ne n} \{{A}_1,{A}_i\}. \end{aligned}$$

As the planes $P_j$ are synchrony subspaces, they are invariant by network dynamics.

Definition 4.1

Let ${\mathcal {N}}$ be a coupled cell system with network architecture either ${\mathcal {P}}_n$ or ${\mathcal {Q}}_n$. Denote the cells of ${\mathcal {N}}$ by ${A}_1, \ldots , {A}_n$. Assume networks dynamics given by the vector field $X$.

• (1) Let $k \ge 2$. A connecting trajectory $\mathbf {p}\rightarrow \mathbf {q}$ between hyperbolic equilibria $\mathbf {p}, \mathbf {q} \in \varvec{\Delta }(\mathbb {R})$ is $k$ -simple if the cells $\{{A}_j \;|\;j\in \mathbf {n}, j \ne k\}$ are synchronized along the connection and ${A}_k$ is desynchronized from $\{{A}_j \;|\;j\in \mathbf {n}, j \ne k\}$. If the connection is $k$-simple, set $\mathfrak {s}(\mathbf {p}\rightarrow \mathbf {q}) = k$.

• (2) A heteroclinic network for $X$ is well-adapted if all connections are simple.

• (3) The representation of a connected graph as a well-adapted heteroclinic network in ${\mathcal {N}}$ is strict if given connections $\gamma , \rho$ then $\mathfrak {s}(\gamma ) = \mathfrak {s}(\rho )$ if and only if $\gamma = \rho$.

Remark 4.2

• (1) The $k$-simplicity of a connection $\mathbf {p}\rightarrow \mathbf {q}$ is equivalent to requiring that the connection lies in the 2-plane $P_k$.

• (2) It is convenient to weaken our definition of strictness—at least for the case of 1-dimensional cell dynamics—and say that the representation of a connected graph as a well-adapted heteroclinic network in ${\mathcal {N}}$ is strict if (a) there are at most two connections in each $P_k$, and (b) they connect the same nodes in the same direction.

Example 4.3

• (1) The heteroclinic cycle of Fig. 6 is well-adapted and strict.

• (2) The heteroclinic cycle of Fig. 7 is well-adapted but not strict (unless $m=1$).

• (3) Realizations of the graphs of Fig. 8 as heteroclinic networks in ${\mathcal {P}}_3$ are well-adapted but never strict.

Theorem 4.4

Let $\Gamma = \Gamma (N,E)$ be a graph which satisfies conditions (C1,C2). Then we can realize $\Gamma$ as the graph of a robust heteroclinic network $\Sigma$ in ${\mathcal {P}}_n$, where $n = E+1$ and $\Sigma$ is well-adapted and strict.

We may similarly represent $\Gamma$ as the graph of a heteroclinic network $\Sigma$ in ${\mathcal {Q}}_n$, $n = E+1$.

In either case, we may require the network vector field to be smooth ($C^\infty$). The heteroclinic network $\Sigma$ will persist under sufficiently small $C^1$ perturbations by $C^r$ network vector fields, $r \ge 1$.

Before giving the detailed proof of Theorem 4.4, we summarize the main steps. We assume throughout that $n = E+1$. In Sect. 4.3, we construct $N$ affine linear vector fields with hyperbolic equilibria $\mathbf {Z} = \{\mathbf {p}_1,\ldots ,\mathbf {p}_N\}\subset \varvec{\Delta }_n(\mathbb {R})$ with preassigned stabilities. We patch these vector fields together to define a smooth map $f$ on a neighbourhood $D$ of $\varvec{\Delta }(\mathbb {R})$ in $\mathbb {R}^n$ so that the set of equilibria for the associated network vector field contains $\mathbf {Z}$. Working on the invariant subspaces $P_j$, we next choose for each $j \in \mathbf {n}$, $j > 1$, a connection between a pair of equilibria in $\mathbf {Z}$ and then smoothly extend $f$ from $D$ to this set of connections. Finally, we extend $f$ to $\mathbb {R}^n$. The tricky step is defining $f$ so the network vector field has the right connections. As each connection will lie in a unique 2-dimensional synchrony subspace, there will not be a problem of possible intersection of connections (unlike in Example 3.2). The difficulty comes from the constraints that the network architecture imposes on the restriction $F^j$ of the network vector field to the invariant subspace $P_j$: the vector fields $F_j$ all have the same ‘vertical’ components. We include a few details needed for the proof of Proposition 3.6.

4.1 Linearization at Synchronized Equilibria: Architecture ${\mathcal {P}}_n$

We continue to assume 1-dimensional node dynamics (results are similar for $k$-dimensional node dynamics with constants $\alpha$, $\beta _i$ replaced by general $k\times k$ real matrices $A$, $B_i$).

Evolution of the nodes is given by

$$\begin{aligned} x_1'= & {} f(x_1; x_2,x_3,\ldots ,x_n)\\ \ldots= & {} \ldots \\ x_n'= & {} f(x_n;x_2,\ldots ,x_{n-1},x_1), \end{aligned}$$

where $f: \mathbb {R}\times \mathbb {R}^{n-1} \rightarrow \mathbb {R}$ determines cell dynamics. Denote the associated vector field on $\mathbb {R}^n$ defining network dynamics by $F$. Suppose that $\mathbf {p} \in \varvec{\Delta }(\mathbb {R})$ is an equilibrium of the system. Define

$$\begin{aligned} \alpha = \frac{\partial f}{\partial x_1} (\mathbf {p}), \beta _2 = \frac{\partial f}{\partial x_2} (\mathbf {p}), \ldots , \beta _n = \frac{\partial f}{\partial x_n} (\mathbf {p}). \end{aligned}$$

Here we regard $f = f(x_1;x_2,\ldots ,x_n)$.

Lemma 4.5

The rows $R_1,\ldots ,R_n$ of the Jacobian matrix $J(F)(\mathbf {p})$ of $F$ at $\mathbf {p}$ are given by

$$\begin{aligned} R_j = [\beta _2, \ldots , \beta _j,\alpha ,\beta _{j+1}, \ldots ,\beta _n],\; j \in \mathbf {n}. \end{aligned}$$

The eigenvalues of $J(F)(\mathbf {p})$ are

$$\begin{aligned} \alpha + \sum _{i=2}^n \beta _i, \alpha - \beta _2,\ldots ,\alpha - \beta _n. \end{aligned}$$

The eigenvalue $\alpha + \sum _{i=2}^n \beta _i$ has eigenspace the minimal synchrony subspace $\varvec{\Delta }_n(\mathbb {R})$. The eigenspace associated with $\alpha - \beta _k$ lies in the 2-dimensional synchrony subspace $P_k$, $k \ge 2$.

Proof

Routine elementary computations using row and column operations to identify eigenvalues. $\square$

Remark 4.6

Each synchrony subspace $P_k$ is invariant by the Jacobian matrix $J(F)(\mathbf {p})$ and $J(F)(\mathbf {p})|P_k$ has eigenvalues $\alpha + \sum _{i=2}^n \beta _i$ and $\alpha - \beta _k$ ($\alpha + \sum _{i=2}^n \beta _i$ is an eigenvalue for each $J(F)(\mathbf {p})|P_k$ since $\varvec{\Delta }_n(\mathbb {R})\subset P_k$ for all $k \ge 2$).

4.2 Linearization at Synchronized Equilibria: Architecture ${\mathcal {Q}}_n$

As above, let $F$ denote the vector field defining network dynamics on ${\mathcal {Q}}_n$ and assume $\mathbf {p} \in \varvec{\Delta }(\mathbb {R})$ is an equilibrium of the system.

Lemma 4.7

The eigenvalues of the Jacobian matrix $J(F)(\mathbf {p})$ are

$$\begin{aligned} \alpha + \sum _{i=2}^n \beta _i, \alpha , \alpha - \beta _3,\ldots ,\alpha - \beta _n. \end{aligned}$$

The eigenvalue $\alpha + \sum _{i=2}^n \beta _i$ has eigenspace $\varvec{\Delta }(\mathbb {R})$. The eigenspace associated with $\alpha$ lies in the synchrony subspace $P_2$ and the eigenspace associated to $\alpha - \beta _k$ lies in the synchrony subspace $P_k$, $k = 3,\ldots ,n$.

4.3 Constructing Network Compatible Vector Fields Near $\varvec{\Delta }(\mathbb {R})$

Our goal in this section is to show that given $n \ge 3$, we can choose (smooth) network dynamics on ${\mathcal {P}}_n$ with a pre-specified set of equilibria on $\varvec{\Delta }(\mathbb {R})$ and pre-specified Jacobian matrices at these equilibria (consistent with the matrix structure given by Lemma 4.5).

Lemma 4.8

Let $N \ge 2$. Choose distinct points $\mathbf {p}_\ell \in \varvec{\Delta } (\mathbb {R})$, $\ell \in \mathbf {N}$. Given real constants $\alpha ^\ell$, $\beta ^\ell _j$, $\ell \in \mathbf {N}$, $2 \le j \le n$, define the $n \times n$ matrices $\mathbf {J}_\ell$ by requiring that $\mathbf {J}_\ell$ has rows $R^\ell _j$ given by

$$\begin{aligned} R_j^\ell = [\beta ^\ell _2, \ldots , \beta ^\ell _j,\alpha ^\ell ,\beta ^\ell _{j+1}, \ldots ,\beta ^\ell _n],\; j \in \mathbf {n}. \end{aligned}$$

Then there exists a smooth ($C^\infty$) $f: \mathbb {R}\times \mathbb {R}^{n-1} \rightarrow \mathbb {R}$ such that the associated network vector field $F$ on ${\mathcal {P}}_n$ has the following properties:

• (1) $\mathbf {p}_\ell \in \varvec{\Delta }(\mathbb {R})$ is an equilibrium of $F$, $\ell \in \mathbf {N}$.

• (2) $F$ is affine linear in a neighbourhood of each $\mathbf {p}_\ell$, and

  $$\begin{aligned} J(F)(\mathbf {p}_\ell ) = \mathbf {J}_\ell ,\; \ell \in \mathbf {N} \end{aligned}$$

Proof

Let $g,h_1,\ldots ,h_n:\mathbb {R}\rightarrow \mathbb {R}$ be $C^\infty$. Let $\pi : \mathbb {R}^n \rightarrow \varvec{\Delta }(\mathbb {R})$ be the orthogonal projection on the diagonal. Define the smooth map $f: \mathbb {R}\times \mathbb {R}^{n-1} \rightarrow \mathbb {R}$ by

$$\begin{aligned} f(x_1;x_2,\ldots ,x_n) = g(\pi (x_1,\ldots ,x_n)) + \sum _{i=1}^n h_i(\pi (x_1,\ldots ,x_n))x_i \end{aligned}$$

Observe that

$$\begin{aligned} f(x) = g(x) + x \sum _{i=1}^n h_i(x),\; x \in \varvec{\Delta }(\mathbb {R}) \approx \mathbb {R}. \end{aligned}$$

Choose the maps $h_i$ so that (a) each $h_i$ is constant near $\mathbf {p}_\ell$, $\ell \in \mathbf {N}$, and (b) $h_1(\mathbf {p}_\ell ) = \alpha ^\ell$, $h_i(\mathbf {p}_\ell ) = \beta ^\ell _i$, $i > 1$. Now choose $g$, constant near each $\mathbf {p}_\ell$, so that $f(\mathbf {p}_\ell ) = 0$ for $\ell \in \mathbf {N}$. $\square$

4.4 Compatibility Conditions for Network Vector Fields

We consider the case where cells have 1-dimensional phase space $\mathbb {R}$. The case where the phase space is of dimension at least two is easier and omitted (see Aguiar et al. 2011, §5). Recall that dynamics on ${\mathcal {P}}_n$ is given by the system of differential equations

$$\begin{aligned} x_1'= & {} f(x_1; x_2,x_3,\ldots ,x_n)\\ x_2'= & {} f(x_2; x_1,x_3,\ldots ,x_n)\\ \ldots= & {} \ldots \\ x_n'= & {} f(x_n;x_2,\ldots ,x_{n-1},x_1), \end{aligned}$$

where $f: \mathbb {R}\times \mathbb {R}^{n-1} \rightarrow \mathbb {R}$ is smooth. Restricted to the flow-invariant 2-plane $P_j$, dynamics is given by the system

$$\begin{aligned} x_1'= & {} f(x_1;x_1,\ldots , x_1,x_j,x_1,\ldots ,x_1)\end{aligned}$$

(4.1)

$$\begin{aligned} x_j'= & {} f(x_j;x_1,\ldots , x_1,x_1,x_1,\ldots ,x_1). \end{aligned}$$

(4.2)

Denote the vector field defined by (4.1, 4.2) on $P_j$ by $F^j = (H_j,V_j)$, $j \ge 2$. We need to choose $f$ so that the vector fields $F^j$ have the properties necessary for the heteroclinic network. Already we have constructed $f$ so that on a neighbourhood $D$ of $\varvec{\Delta }(\mathbb {R})$ in $\mathbb {R}^n$, we have the required equilibria with assigned stabilities. Observe that outside of a neighbourhood $D\subset \mathbb {R}^2$ of the diagonals $x_i = x_j$, $j > 1$, the $x_1$-component $H_j$ of the vector fields on $P_j$ can be chosen freely. On the other hand, the vertical components must satisfy

$$\begin{aligned} V_i(u,v) = V_j(u,v)\; (= f(v;u,\ldots ,u)), \;(u,v) \in \mathbb {R}^2, \;\text {all }i,j \in \mathbf {n}. \end{aligned}$$

(4.3)

Set $V(u,v) = f(v;u,\ldots ,u)$, $(u,v) \in \mathbb {R}^2$. Outside of a neighbourhood $D$ of $\varvec{\Delta }(\mathbb {R})$, we can choose $V$ freely and, in particular, not affect choices made for $H_1,\ldots , H_n$.

4.5 Proof of Theorem 4.4

Suppose $\Gamma$ has $N$ vertices $\mathbf {v}_1,\ldots ,\mathbf {v}_N$ and $E$ edges $e_1,\ldots ,e_E$. Take $n = E+1$ and choose distinct points $\mathbf {p}_i \in \varvec{\Delta }(\mathbb {R})$, $i \in \mathbf {N}$. If $e_i$ connects $\mathbf {v}_s$ to $\mathbf {v}_r$, set $S(e_i) = s$, $T(e_i) = r$ and note that by (C1), $s \ne r$. For each $\ell \in \mathbf {N}$, let $O(\ell ) = \{j \;|\;S(e_j) = \ell \}$ and set $d_\ell = |O(\ell )|$ ($d_\ell$ is the out-degree $d^{\;\text {out}}_\ell$). By conditions (C1,C2), $1 \le d_\ell < E$. Set $d_0 = 2$ and define a partition of $\{2,\ldots ,E+1\}$ by

$$\begin{aligned} E_1= & {} \{d_0,d_0+1,\ldots ,d_1+d_0-1\},\\ E_2= & {} \{d_0+d_1,\ldots ,d_1+ d_2+d_0-1\},\\ \ldots= & {} \ldots \\ E_{N}= & {} \left\{ \sum _{i=0}^{N-1} d_i,\ldots ,\sum _{i=0}^{N}d_i -1 = E+1\right\} . \end{aligned}$$

Relabelling the edges $e_i$, we may suppose that

• (1) If $S(e_i) = s$, then $i \in E_s$.

• (2) if $i < j \in E_s$, then $T(e_i) \le T(e_j)$.

For $\ell \in \mathbf {N}$, choose $\alpha ^\ell , \beta _2^\ell , \ldots ,\beta _n^\ell \in \mathbb {R}$ such that

$$\begin{aligned} \alpha ^\ell - \beta _j^\ell< & {} 0,\; \text {if } j \notin E_\ell \\ \alpha ^\ell - \beta _j^\ell> & {} 0, \; \text {if } j \in E_\ell ,\\ \alpha ^\ell + \sum _{j=2}^N \beta _j^\ell< & {} 0. \end{aligned}$$

Apply Lemma 4.8 to construct $f$ which has the specified Jacobian matrices $\mathbf {J}_\ell$ at each equilibrium $\mathbf {p}_\ell$, $\ell \in \mathbf {N}$. Perturbing the $\alpha ^\ell , \beta _j^\ell$ if necessary, we may further assume that the set of 1-dimensional eigenspaces at each equilibrium are distinct when viewed as subsets of $\mathbb {R}^2$ (identify each $P_j$ with $\mathbb {R}^2$).

Let $d$ denote the Euclidean distance on $\mathbb {R}^n$. Given $\delta > 0$, set $D = \{\mathbf {x}\in \mathbb {R}^n \;|\;d(\mathbf {x},\varvec{\Delta }(\mathbb {R})) \le \delta \}$. Let $\pi :D\rightarrow \varvec{\Delta }(\mathbb {R})$ denote the associated tubular neighbourhood of $\varvec{\Delta }(\mathbb {R})$ ($\pi$ will be the restriction to $D$ of orthogonal projection on $\varvec{\Delta }(\mathbb {R})$). Choose $\delta > 0$ sufficiently small so that for each $\ell \in \mathbf {N}$, we can choose an interval neighbourhood $U_\ell$ of $\mathbf {p}_\ell$ in $\varvec{\Delta }(\mathbb {R})$ such that the network vector field $F$ associated with $f$ is linear on $\pi ^{-1}(U_\ell )$. In particular, the trajectories along the 1-dimensional eigenspaces (in the stable and unstable manifolds at $\mathbf {p}_\ell$) will intersect $\partial D$ transversally.

Thus far we have defined $f$ and the network vector field $F$ on $D$. It remains to extend $f$ to $\mathbb {R}^n$ to obtain the desired heteroclinic connection structure. We do this by first extending $F$ smoothly to the set of connecting trajectories and then extending to the network phase space.

Given $i \in E_j$, make a smooth connection $\gamma _i$ in $P_i$ from $\mathbf {p}_j$ to $\mathbf {p}_t$, where $t = T(\gamma _i)$. We do this so that $\gamma _i \cap D$ is contained in the eigenspace of $\alpha ^\ell - \beta _i^\ell$ and is a trajectory of $F|D$ (note Lemma 4.5 and that $\alpha ^\ell - \beta _i^\ell > 0$). Taking the projection into $\mathbb {R}^2$, it is clear that there may be multiple intersections between different $\gamma _i$. By perturbing the constants $\alpha ^\ell , \beta ^\ell _i$, we may adjust the trajectories in $P_j \cap D$ so that the trajectories in $P_j \cap D$ are all disjoint when projected into $\mathbb {R}^2$. Next observe that if we have connections $\gamma _i$ from $\mathbf {p}_u \rightarrow \mathbf {p}_v$ and $\gamma _r$ from $\mathbf {p}_a \rightarrow \mathbf {p}_b$ then if either $(\mathbf {p}_u,\mathbf {p}_v) \supset [\mathbf {p}_a,\mathbf {p}_b]$ or $(\mathbf {p}_a,\mathbf {p}_b) \supset [\mathbf {p}_u,\mathbf {p}_v]$, then we can always smoothly deform the connections outside of $D$ so that their projections in $\mathbb {R}^2$ do not intersect. In the remaining case, we can deform the connections so that there is at most one intersection that we can assume is transverse (within $\mathbb {R}^2$). We may further require that the intersection points are distinct (within $\mathbb {R}^2$). A formal proof is based on the obvious inductive argument over $i \in \mathbf {E}$.

Denote the points of intersection of connections in $\mathbb {R}^2$ by $z_1,\ldots ,z_k$. Choose $\varepsilon > 0$, so that the closed disc neighbourhoods $\{D_\varepsilon (z_i)\;|\;i \in \mathbf {k}\}$ are mutually disjoint: $D_\varepsilon (z_i) \cap D_\varepsilon (z_j) = \emptyset$ if $i \ne j$. There are two cases we need to consider. Referring to Fig. 10a, observe that at the intersection point $z_i$ the vertical components of $\gamma _a'$ and $\gamma _b'$ point in the same direction. Reparameterizing $\gamma _a$, we can assume the vertical components are identical (alternatively, multiply the vector field $\gamma _a'(t)$ by an appropriate strictly positive smooth function equal to $1$ outside $D_\varepsilon (z_i)$).

Fig. 10

Intersections of connecting trajectories

In the second case, where the vertical components point in opposite directions, we deform one of the curves to achieve the situation of (a)—see Fig. 10c. Note that this case handles the situation where one of the curves has zero vertical component at the intersection. All of these changes are supported inside the family of discs $D_\varepsilon (z_i)$. Now extend the vector field $F$ as a network vector field from $D$ to $D \cup _{i\in \mathbf {E}} \gamma _i(\mathbb {R})$ by defining $F(\gamma _i(t)) = \gamma _i'(t)$. This defines $f$ as a smooth map on a closed subset of $\mathbb {R}^{n}$. Now smoothly extend $f$ to all of $\mathbb {R}^n$ using either the Whitney extension theorem or a simple partition of unity argument.

Finally, we remark that the heteroclinic network we have constructed is robust under $C^1$ perturbations of network vector fields. This is a standard argument: equilibria are hyperbolic and, within the 2-dimensional invariant subspace, we have a connection from a saddle point to a sink which is not destroyed under perturbation by network vector fields. $\square$

We conclude this section with two examples and a remark about the effect of removing the requirement of strictness.

Example 4.9

• (1) The heteroclinic cycle of Fig. 7 can be realized in ${\mathcal {P}}_n$ as a strict network provided $n \ge 2m+1$. The same is true if we require pairs of connections from $\mathbf {p}_i \rightarrow \mathbf {p}_{i+1}$ (note Remark 4.2(2)).

• (2) Suppose $\Gamma = \Gamma (2,E)$ satisfies conditions (C1,C2). Then we can realize $\Gamma$ as a strict heteroclinic network $\Sigma$ in ${\mathcal {P}}_n$ for $n \ge E+1$. In this case we can do better if we pair connections between nodes and use Remark 4.2(2)). For example, if $E$ is even and there are $2k$ connections from $\mathbf {v}_1 \rightarrow \mathbf {v}_2$, we can realize $\Gamma$ by a strict heteroclinic network $\Sigma$ in ${\mathcal {P}}_n$ for $n \ge \frac{E}{2} +1$.

Remark 4.10

If we drop the requirement of strictness, we can realize graphs as robust heteroclinic networks in much smaller coupled cell networks. We have already indicated that the heteroclinic cycle of Fig. 7 can be realized in ${\mathcal {P}}_3$ as a well-adapted network for all $m \ge 2$. Similarly, heteroclinic cycles with an odd number of nodes can always be realized as well-adapted heteroclinic networks in ${\mathcal {P}}_4$. The graph $\Gamma = \Gamma (2,E)$ of Example 4.9 can be represented as a well-adapted heteroclinic network in ${\mathcal {P}}_5$. Briefly, suppose hyperbolic equilibria $\mathbf {p}, \mathbf {q} \in \varvec{\Delta (\mathbb {R})}$. Assume (a) $\mathbf {p},\mathbf {q}$ are both sinks for dynamics restricted to $\varvec{\Delta }(\mathbb {R})$, (b) the unstable manifolds of $\mathbf {p}$, $\mathbf {q}$ are 2-dimensional and $W^u(\mathbf {p}) \subset P_2 \times P_3$, $W^u(\mathbf {q}) \subset P_4 \times P_5$, (c) $W^u(\mathbf {p})$ intersects $W^s(\mathbf {q})$ transversally in $n$ connections, and $W^u(\mathbf {q})$ intersects $W^s(\mathbf {p})$ transversally in $m$ connections, where $n+m = E$ and $n$ gives the number of connections in $\Gamma$ from $\mathbf {p} \rightarrow \mathbf {q}$.

5 Additive Input Structure

In the previous section, we made no assumptions about cell dynamics beyond assuming that dynamics on a cell with $k$ inputs and state space $M$ was determined by a smooth map $f: M \times M^k \rightarrow TM$. In applications, it is often important to assume an additive input structure that allows variation in the number of inputs between cells.

Proposition 5.1

We may require additive input structure in Theorem 4.4. Specifically, given a graph $\Gamma (N,E)$ satisfying (C1,C2), there exist smooth functions $F_0: \mathbb {R}\rightarrow \mathbb {R}$ and $g_2,\ldots ,g_{E+1} : \mathbb {R}^2 \rightarrow \mathbb {R}$ such that the requirements of Theorem 4.4 are satisfied if network dynamics are defined by

$$\begin{aligned} f(x_1;x_2,\ldots ,x_{E+1}) = F_0(x_1) + \sum _{j=2}^{E+1} g_j(x_1,x_j), \end{aligned}$$

(5.1)

where $g_j(x,x) = 0$, all $x \in \mathbb {R}$, $2 \le j \le E+1$.

Proof

By Theorem 4.4, there exists a smooth map $f: \mathbb {R}\times \mathbb {R}^E \rightarrow \mathbb {R}$ which realizes $\Gamma$ as a heteroclinic network in ${\mathcal {P}}_n$, where $n = E+1$. We have to prove that $f$ can be chosen in the desired form. Observe that if (5.1) holds then

$$\begin{aligned} F_0(x) = f(x;x,\ldots ,x),\; x \in \mathbb {R}. \end{aligned}$$

(5.2)

As usual we identify the 2-plane $P_j$ with $\mathbb {R}^2$ and take coordinates $(x_1,x_j)$ on $P_j$. Denote the network vector field associated with $f$ by $F: \mathbb {R}^n \rightarrow \mathbb {R}^n$. For $j = 2,\ldots , E+1$, define $(H_j,V_j) = F|P_j$.

We have

$$\begin{aligned} H_2(x_1,x_2)= & {} f(x_1;x_2,x_1,x_1,\ldots ,x_1)\\ H_3(x_1,x_3)= & {} f(x_1;x_1,x_3,x_1,\ldots ,x_1)\\ \ldots= & {} \ldots \\ H_{E+1}(x_1,x_{E+1})= & {} f(x_1;x_1,x_1,\ldots ,x_{E+1})\\ V_j(x_1,x_j)= & {} f(x_j;x_1,\ldots ,x_1), \; 2 \le j \le E+1. \end{aligned}$$

Viewed as functions on $\mathbb {R}^2$, the $H_j : \mathbb {R}^2 \rightarrow \mathbb {R}$ can be chosen freely, subject only to $H_j(x,x) = F_0(x)$, for all $x\in \mathbb {R}^2$, $2 \le j \le n$. On the other hand, we have $V_2 = \ldots = V_{E+1}$ and $V_j(x,x) = F_0(x)$, for all $x\in \mathbb {R}^2$, $2 \le j \le n$. Set $V(x,y) = V_2(x,y) = \ldots = V_{E+1}(x,y)$. Assume then that $H_2, \ldots ,H_n,V, F_0$ are given. Substituting in (5.1), we must find smooth functions $g_2,\ldots ,g_{E+1}$ so that

$$\begin{aligned} H_2(x,y)= & {} F_0(x) + g_2(x,y)\\ H_3(x,y)= & {} F_0(x) + g_3(x,y)\\ \ldots= & {} \ldots \\ H_{E+1}(x,y)= & {} F_0(x) + g_{E+1}(x,y)\\ V(x,y)= & {} F_0(y) + \sum _{j=2}^{E+1} g_j(y,x). \end{aligned}$$

Solve the first $E$ equations uniquely for the unknowns $g_2,\ldots ,g_{E+1}$: $g_j(x,y) = H_j(x,y) - F_0(x)$, $0 \le j \le 2$. Without further work, we cannot satisfy the final equation for the vertical component since this, together with (5.1), implies the relation

$$\begin{aligned} f(x;y^E) + (E-1)f(x;x^E) = \sum _{j=0}^{E-1} f(x;x^j,y,x^{E-j-1}), \end{aligned}$$

(5.3)

where $x^s$ is abbreviated notation for $s$ copies of $x$, $0 \le s \le E$. Obviously (5.3) fails for general maps $f:\mathbb {R}\times \mathbb {R}^{n-1} \rightarrow \mathbb {R}$. However, since the common vertical components satisfy

$$\begin{aligned} V(x,y) = F_0(y) + \sum _{j=2}^{E+1} g_j(y,x), \;(x,y) \in \mathbb {R}^2, \end{aligned}$$

(5.4)

it follows that if we insist the connection in $P_j$ is always made by a trajectory in $\Delta _j^+ = \{(x_1,x_j) \;|\;x_j > x_1\}$, then the vertical component $V_j(x_1,x_j) = F_0(x_j) + \sum _{j=2}^{E+1} g_j(x_j,x_1)$ depends only on the values of $g_2,\ldots ,g_{E+1}$ in $\Delta _j^- = \{(x_1,x_j) \;|\;x_j < x_1\}$, which are not used in the connection construction for the horizontal vector fields. We can modify the original proof of Theorem 4.4 in the following way. We start as before by constructing a vector field giving the required fully synchronous equilibria and stabilities on a tubular neighbourhood of the diagonal—there is no difficulty with the additive input structure on $D$. Let $\pi :\mathbb {R}^2 \rightarrow \mathbb {R}^2$ denote the reflection in the diagonal: $\pi (x,y) = (y,x)$. Choose connections $\gamma _j\subset \Delta _j^+$ so that the curves $\pi (\gamma _j)$ intersect transversally in at most one point. Just as in the proof of Theorem 4.4 we do a local deformation of $H_j$ (in $\Delta _j^-$) so that the vertical components match at points of intersection. $\square$

Remark 5.2

In the proof of Proposition 5.1, we assumed connections lay in $\Delta _j^+ = \{(x_1,x_j) \;|\;x_j > x_1\}$, $2 \le j \le E+1$. It is not hard to extend the proof to allow for connections in $\Delta _j^\pm$. In particular, we can require both additive input structure and pairs of connections in each $P_k$ between equilibria (see Remark 4.2(2)).

5.1 Heterogeneous Networks

Our results can be applied to heterogeneous networks consisting of identical cells with additive input structure. We give an example to illustrate the general idea.

Example 5.3

In Fig. 11 we show a 4-cell network with additive input structure. We assume there are 3 input types and identical dynamics on the uncoupled cells. Cells 1, 2 and 3 have three inputs; cell 4 has two inputs (of types 2 and 3). The network has synchrony subspaces $\{{A}_1,{A}_2\}$, $\{{A}_1,{A}_3\}$, $\{{A}_1,{A}_2,{A}_3\}$, $\{{A}_1,{A}_2,{A}_4\}$, and $\{{A}_1,{A}_2,{A}_3,{A}_4\}$.

Fig. 11

A 4-cell heterogenous network with additive input structure

It is straightforward to show that we can choose 1-dimensional cell dynamics and an additive input structure so that there is a robust heteroclinic cycle joining equilibria $\mathbf {p}, \mathbf {q} \in \{(x_1,\ldots ,x_4) \;|\;x_1 = x_2 = x_3\}$. Indeed, the verification is simpler than in proposition 5.1 as we can ensure the projections into $\mathbb {R}^3$ of the connecting trajectories between $\mathbf {p}, \mathbf {q}$ do not intersect. It is also straightforward to construct a robust simple heteroclinic cycle joining equilibria $\mathbf {p}, \mathbf {q} \in \varvec{\Delta }_4(\mathbb {R})$, with connections in the 2-dimensional synchrony subspaces $\{{A}_1,{A}_2,{A}_3\}$ and $\{{A}_1,{A}_2,{A}_4\}$. Here we have a heteroclinic cycle between cells with different numbers of inputs.

Remark 5.4

The previous example shows that a heterogeneous network ${\mathcal {N}}$ consisting of identical cells with additive input structure may support robust heteroclinic networks. Of course, one can build complex heterogeneous networks ${\mathcal {N}}$ which contain a subnetwork ${\mathcal {N}}^\star$ with $N \ge 3$ cells such that

• (a) every cell in ${\mathcal {N}}^\star$ has the same number of inputs,

• (b) if we delete all inputs to cells of ${\mathcal {N}}^\star$ coming from outside ${\mathcal {N}}^\star$, then the resulting network is either ${\mathcal {P}}_N$ or ${\mathcal {Q}}_N$ (up to a relabelling of cells),

• (c) when we reinsert the deleted connections then the invariant subspace structure of ${\mathcal {N}}^\star$ is unchanged

Under these conditions, we expect to be able to choose 1-dimensional dynamics on nodes so that ${\mathcal {N}}^\star$ supports heteroclinic cycles along the lines of Proposition 5.1. More generally, we expect the same result if instead of (c) we assume an invariant subspace structure on ${\mathcal {N}}$ which induces the given invariant subspace structure on ${\mathcal {N}}^\star$. In particular, for the heteroclinic network on ${\mathcal {N}}^\star$, cells outside ${\mathcal {N}}^\star$ may need to be synchronized. We refer to Fig. 12 for a simple variation on example 5.3. In this case, we take ${\mathcal {N}}^\star$ to be the network with cells ${A}_1,{A}_2,{A}_3$. If we remove all inputs to cells in ${\mathcal {N}}^\star$ from cells outside ${\mathcal {N}}^\star$, we recover the network ${\mathcal {P}}_3$. In this case, $\{{A}_1,{A}_2\}$, $\{{A}_1,{A}_3\}$, $\{{A}_1,{A}_2,{A}_3\}$ are not invariant subspaces for ${\mathcal {N}}$. However, $\{{A}_4,{A}_5\}$ is an invariant subspace and so also are

$$\begin{aligned} \{{A}_1,{A}_2 \Vert {A}_4,{A}_5\}, \{{A}_1,{A}_2 \Vert {A}_4,{A}_5\}, \{{A}_1,{A}_2,{A}_3\Vert {A}_4,{A}_5\}. \end{aligned}$$

We follow the notational conventions of Sect. 2.

Fig. 12

A 6-cell heterogenous network with additive input structure

6 Generalizations

The heteroclinic networks constructed in the previous sections have the feature that transition between nodes is marked by a desynchronization of one cell along the trajectory. With the exception of the examples on heterogeneous networks, in the constructed heteroclinic networks, nodes always correspond to fully synchronized equilibria. In the past, there have been a number of works considering heteroclinic networks where trajectories correspond to patterns of desynchronization and resynchronization and transition between synchronized clusters, for example, the work of Ashwin et al. on computation and systems of phase oscillators with $S_N$-symmetry (Ashwin and Borresen 2004; Ashwin et al. 2007, 2010; Orosz et al. 2009), and that of Timme et al. on pulse coupled symmetric networks (Memmesheimer and Timme 2006; Neves and Timme 2009, 2012). Elsewhere, (Field 1996, [Chapter7]) constructs robust heteroclinic cycles between groups of active and quiescent nodes.

It is not hard to realize in ${\mathcal {P}}_n$ robust heteroclinic networks that exhibit more complex patterns of desynchronization and resynchronization. As a general rule, for simple heteroclinic networks, we expect desynchronization of just one cell along connecting trajectories. If unstable manifolds are of dimension greater than 1, then two or more cells may desynchronize along connecting trajectories. This behaviour is well known for phase oscillator systems with $S_n$-symmetry. Rather than give a general result, we give an example that illustrates the general method and concludes with a conjecture.

Example 6.1

We construct a simple heteroclinic network $\Sigma$ in ${\mathcal {P}}_4$ such that

• (1) Cell dynamics is 1-dimensional.

• (2) $\Sigma$ has three equilibria $\mathbf {p}_j \in P_j\backslash \varvec{\Delta }(\mathbb {R})$ and three connections $\gamma _j \subset \{\mathbf {x} \;|\;x_1 = x_j\}$, $j \in \{2,3,4\}$.

Each node of $\Sigma$ corresponds to a cluster of 3 synchronized cells. Along a connection, just two cells are synchronized and the equilibria at the ends of the connection correspond to synchronized clusters with exactly two cells in common. We refer to Fig. 13 showing how $\Sigma$ relates to the underlying invariant subspace structure in ${\mathcal {P}}_4$.

We start by choosing the points $\mathbf {p}_j \in P_j\backslash \Delta$. It is straightforward to choose network dynamics $F$ on a neighbourhood $U$ of $\{\mathbf {p}_j \;|\;j =2,3,4\}$ such that each $\mathbf {p}_j$ is a hyperbolic saddle of index 1 and

• (a) $W^u(\mathbf {p}_2) \subset \{\mathbf {x} \;|\;x_1 = x_3\}$, $W^u(\mathbf {p}_4) \subset \{\mathbf {x} \;|\;x_1 = x_2\}$ and $W^u(\mathbf {p}_2) \subset \{\mathbf {x} \;|\;x_1 = x_4\}$ (see Fig. 13).

• (b) Restricted to $P_j$, $\mathbf {p}_j$ is an attracting equilibrium.

Fig. 13

The heteroclinic cycle $\Sigma$ in ${\mathcal {P}}_4$

Just as in the proof of Theorem 4.4, we choose connections $\gamma _j \subset \{\mathbf {x} \;|\;x_1 = x_j\}$ joining the equilibria such that within $U$ each connection is a trajectory of $F$. Consider the connection $\gamma _3$ joining $\mathbf {p}_2$ to $\mathbf {p}_4$. In order that $\gamma _3$ be a trajectory in the network dynamics, we must be able to choose $f:\mathbb {R}\times \mathbb {R}^3 \rightarrow \mathbb {R}$ so that along $\gamma _3$ we have

$$\begin{aligned} x_1'= & {} f(x_1; x_2,x_1,x_4)\\ x_2'= & {} f(x_2; x_1,x_1,x_4)\\ x_4'= & {} f(x_4; x_2,x_1,x_1) \end{aligned}$$

Outside of the neighbourhood $U$, we can certainly choose $f$ along $\gamma _3$ to satisfy these equations (note that near $\mathbf {p}_2$ and $\mathbf {p}_3$ there are constraints). The corresponding equations for $\gamma _2$ are

$$\begin{aligned} x_1'= & {} f(x_1; x_1,x_3,x_4)\\ x_3'= & {} f(x_3; x_1,x_1,x_4)\\ x_4'= & {} f(x_4; x_1,x_3,x_1) \end{aligned}$$

Observe that the second component of both vector fields is the same. So choose $\gamma _2$, $\gamma _3$ so that the projections into $P_4$ are either disjoint or meet transversally at one point. We handle similarly the projections of $\gamma _2, \gamma _4$ in $P_3$ and $\gamma _3, \gamma _4$ in $P_2$ and, with the usual identification of $P_j$ with $\mathbb {R}^2$, we may require that the set of intersection points is distinct. Now deform the $\gamma _j$ in a small neighbourhood of each intersection point to achieve compatibility—just as in the proof of Theorem 4.4. Finally extend $f$ from $U\cup \cup _j \gamma _j$ to all of $\mathbb {R}\times \mathbb {R}^3$. We remark that using the same technique, we can require $W^u(\mathbf {p}_j) \subset W^s(\mathbf {p}_{j-1})$, $j = 2,3,4$ (where $\mathbf {p}_1$ is to be taken as $\mathbf {p}_4$) and that the corresponding heteroclinic network is attracting.

Conjecture

Suppose $\Gamma (N,E)=\Gamma$ is a graph satisfying (C1, C2). Let $m, r$ be chosen such that $m \ge 2$, $m > r \ge 1$ and $E \le \left( {\begin{array}{c}m\\ r\end{array}}\right) (m-r)^2$. Then we may realize $\Gamma$ as the graph of a heteroclinic network $\Sigma$ in ${\mathcal {P}}_{m+1}$ and $\Sigma$ is well-adapted and strict. Each equilibrium in $\Sigma$ will lie in an invariant subspace $x_1 = x_{i_1} = \cdots = x_{i_{r+1}}$, where $1 < i_1 < \cdots < i_{r+1}$ and each connection will lie in an invariant subspace $x_1 = x_{j_1} = \cdots = x_{j_{r}}$, where $1 < j_1 < \cdots < j_{r}$.

The conjecture holds in case $r+1 = m = E$ by Theorem 4.4. Example 6.1 verifies the conjecture when $m = 3$, $r=1$ and $E = 3$ ($3 \le \left( {\begin{array}{c}3\\ 1\end{array}}\right) \times 4$ and note that method used in the example continues to work in case we allow for twin connections both ways in which case $E = 12$).

7 Discussion and Concluding Comments

We conclude with some open questions relating to our results and examples.

The use of general sequences of identical coupled cells designed to realize all heteroclinic networks necessarily comes at a price. For example, the sequences $({\mathcal {P}}_n)$, $({\mathcal {Q}}_n)$ are highly connected and use asymmetric inputs. While the connectivity can certainly be reduced (for example, if we use a heterogeneous additive input model), it is not so easy to reduce the number of input types. However, it is possible to realize quite complex heteroclinic networks in ${\mathcal {P}}_n$ for small values of $n$—where $n$ depends mainly on the maximal out- and in-degrees of vertices in the graph of the heteroclinic network (see Sect. 3).

While asymmetric inputs are appropriate for some classes of model (for example, power grid models Filatrella et al. 2008; Dörfler and Bullo 2012), many spiking neural models effectively assume symmetric inputs (and additive input structure). It would be helpful to have an idea of the extent to which one can realize robust heteroclinic networks in identical cell systems with symmetric inputs but no global symmetries. In particular, are there sequences of identical cells with symmetric inputs that allow realization of large classes of heteroclinic networks? Is it necessary to consider networks with multiple cell types but with most cells of the same type?

The sequences $({\mathcal {P}}_n)$, $({\mathcal {Q}}_n)$ handle the general embedding problem. It is natural to ask whether we can construct other sequences for which we can efficiently realize specific classes of heteroclinic network. For example, ‘scale free heteroclinic networks’ which have some highly connected vertices or ‘hubs’ (likely relevant for applications tied to computing Ashwin and Borresen 2004; Neves and Timme 2012). Here it might well be appropriate to consider sequences with more than one cell type (one cell type for highly connected nodes – hubs – and a different cell type for cells with low connectivity). Indeed, introducing more than one cell type is already suggested by the special role that the node $A_1$ plays in our realization theorem (a similar phenomenon happens in Ashwin and Postlethwaite’s cylinder realization Ashwin and Postlethwaite 2013).

Is there a natural way to move from realization of heteroclinic networks in a semi-linear feedback model to an identical coupled cell system? (See Field for some past work, emphasizing heteroclinic cycles).

There is the question of why the realization is more difficult when there is 1-dimensional cell dynamics. While 1-dimensional cell dynamics is often favoured from the mathematical point of view, in physical problems nodes will rarely have 1-dimensional dynamics. It is not, however, that higher-dimensional cell dynamics is easier; the problem lies with the unrealistic assumption that inputs depend on the states of other cells. At this time, as far as we are aware, very little is known about the dynamics of coupled systems with more realistic coupling such as the scalar signalling model briefly discussed in Sect. 2. For example, is there any physical reason why 1-dimensional signals might be preferred over 2-dimensional signals (for example, signals containing both amplitude and phase information)? This question relates to problems in control theory—how much information needs to be communicated for effective control? In terms of synchronization of spiking neurons, does information on spike times alone suffice to ensure synchronization in networks where there is 1-dimensional signalling but high-dimensional node dynamics?

Finally, the heteroclinic networks we construct are not usually attractors—a consequence of our assumptions that allow unstable manifolds of equilibria to be of dimension 2 or greater. There is the difficult question of whether or not we can construct the realization so that it is contained in a ‘minimal’ heteroclinic attractor. Outside the case of realization of heteroclinic cycles as attractors, rather little appears to be known about this problem (see also the discussion in Ashwin and Postlethwaite 2013, §2).