Abstract
We study the evolutionary stability of dispersal strategies, including but not limited to those that can produce ideal free population distributions (that is, distributions where all individuals have equal fitness and there is no net movement of individuals at equilibrium). The environment is assumed to be variable in space but constant in time. We assume that there is a separation of times scales, so that dispersal occurs on a fast timescale, evolution occurs on a slow timescale, and population dynamics and interactions occur on an intermediate timescale. Starting with advection–diffusion models for dispersal without population dynamics, we use the large time limits of profiles for population distributions together with the distribution of resources in the environment to calculate growth and interaction coefficients in logistic and Lotka–Volterra ordinary differential equations describing population dynamics. We then use a pairwise invasibility analysis approach motivated by adaptive dynamics to study the evolutionary and/or convergence stability of strategies determined by various assumptions about the advection and diffusion terms in the original advection–diffusion dispersal models. Among other results we find that those strategies which can produce an ideal free distribution are evolutionarily stable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background and motivation
The fact that ecological and evolutionary processes occur across a range of timescales has long been recognized as a significant challenge in ecological theory; see for example Hastings (1983) and Levin (1992, 2000). The goal of this paper is to use models for populations where the movement occurs on a faster timescale than population dynamics to study the evolution of dispersal in spatially heterogenous environments when evolution occurs on a slower timescale than population dynamics. To describe movement we use the modeling approach of aggregating (i.e. amalgamating) spatial models for dispersal, specifically reaction–diffusion–advection models, to obtain ordinary differential equations at the scale of population dynamics. This approach is developed and described in some detail by Auger et al. (2012) where it is applied to a reaction–diffusion system describing competition. To describe the evolution of dispersal we use a version of adaptive dynamics, specifically pairwise invasibility analysis, to study the evolutionary stability of dispersal strategies in the aggregated population models to study the evolution of dispersal from the viewpoint of adaptive dynamics. That approach is discussed in Brännström et al. (2013) and Geritz et al. (1997). It embodies an assumption that evolutionary change arises from mutations that occur rarely, that is, on a slow timescale, relative to population dynamics. What is novel in our work is that we consider spatially heterogeneous environments and conditional dispersal as well as simple diffusion in the spatial models that we aggregate to obtain ordinary differential equations, and we link those aggregated equations to a slower evolutionary timescale via adaptive dynamics. We envision dispersal patterns as traits arising from local movement processes based on diffusion and advection, but allow those local processes to be conditional on environmental quality as measured by local population growth rates at low densities. The assumption that movement occurs by advection and diffusion is not essential for aggregating the spatial models, but it allows us to make a mechanistic connection to yet another timescale. This is because diffusion and advection models for movement on relatively large spatial scales and a given timescale arise as the continuum limits of possibly biased random walks by individuals on smaller spatial scales at a faster timescale; see for example Aronson (1985), Farnsworth and Beecham (1999), Okubo and Levin (2001) and Potapov et al. (2014). The traits that determine how individuals perform random walks determine the forms of diffusion and advection that can arise as continuum limits, which in turn determine the patterns that those processes can produce, which then determine the evolutionary stability of the strategies arising from the traits. We study this process in detail starting with local movement by diffusion and advection on what we consider a fast timescale, then moving up to the level of population dynamics and global spatial patterns at an intermediate timescale, and then onward to the level of evolution at a slow timescale. Thus, we explicitly consider the effects and evolution of dispersal across three distinct timescales, with implicit connections to a fourth scale (even faster in time and smaller in space) on which individual movement determines the details of the forms of diffusion and advection can arise at our fast timescale.
There are two key features of our modeling approach that may be advantageous. First, the assumption that dispersal occurs on a faster timescale than population dynamics may be more realistic for some populations than the assumption embodied in the reaction–advection–diffusion approach, and its nonlocal and spatially discrete analogues, that dispersal and population dynamics occur on the same timescale. Second, the separation of timescales using weighted spatial averages allows us to employ methods from the theory of ordinary differential equations and real analysis rather than partial differential equations and functional analysis to study the models. The analysis of the models is still nontrivial, but at least the methods are more elementary and hence may be more accessible to a wider range of researchers, and we can still capture effects due to spatially heterogeneous patterns of population distribution arising from dispersal strategies that are conditional on environmental quality.
Our models are not universally applicable; specifically, they do not apply to organisms such as plants, sessile animals, or other animals where movement is strictly by natal dispersal, since for those organisms the processes of dispersal and population dynamics do occur on the same timescale. They are not intended to replace reaction–advection–diffusion models, which in effect assume that population dynamics and dispersal occur on the same timescale, but rather as a complement to such models. Furthermore, there may not always be a separation of timescales between population dynamics and evolution; see Hairston et al. (2005). In this paper we assume that the spatial environment in which dispersal, population dynamics and species interactions, and evolution occur is constant in time but heterogeneous in space. The way that we connect dispersal and population dynamics at different timescales is by using the quasi-equilibrium hypothesis that dispersal patterns go to an equilibrium at the fast timescale, as in Auger et al. (2012), so that we can describe the effects of dispersal in spatially heterogeneous environments on population dynamics by systems of ordinary differential equations with coefficients depending on averages of environmental variables such as resource densities weighted by the spatial distributions of populations instead of using reaction–advection–diffusion systems. We will take the formulation of models in terms of ordinary differential equations with coefficients based on weighted spatial averages as a modeling ansatz, but the methods of Auger et al. (2012) could be adapted to give a more detailed derivation. The weighted spatial averages occurring in the coefficients of the systems we study connect the reaction–diffusion–advection approach to spatial ecology and the evolution of dispersal as in Cantrell and Cosner (2003) and Cosner (2014) with the ideas of scale transition and spatial moment approaches developed in Bolker and Pacala (1999), Chesson (2009, 2012) and Chesson et al. (2005). The way that we connect population dynamics to evolution which occurs at a slower timescale is by using the approach of pairwise invasibility analysis from the theory of adaptive dynamics, which is based on the assumption that evolutionary changes occur rarely, by means of invasion and displacement of a resident population by a small population of mutants with a novel trait; see for example Brännström et al. (2013) and Geritz et al. (1997). That general approach has been widely used to study the evolution of dispersal traits; see Averill et al. (2012), Cantrell et al. (2006, 2010, 2012a, b), Chen et al. (2008), Dockery et al. (1998), Hambrock and Lou (2009), Hastings (1983), Kao et al. (2010), Korobenko and Braverman (2012, 2014) and the discussion and references in section 4 of Cosner (2014).
There has been a considerable amount of work of various kinds on modeling ecological and evolutionary systems with multiple timescales, and on ways of connecting models that operate on different scales, including an entire issue of the journal Ecological Complexity, see Auger et al. (2000) and Morozov and Poggiale (2012). The review (Auger et al. 2000) provides many references, see also Bravo de la Parra et al. (1997, 1999, 2013, 2016), Constable (2014), Hastings (2010), Mose et al. (2012), Nguyen-Ngoc et al. (2012) and Sanz and Bravo de la Parra (2000). As noted previously, separation of ecological and evolutionary timescales is the basis for adaptive dynamics, but also arises in other approaches to evolutionary ecology, for example quantitative genetics (Polechová and Barton 2015). Patch occupancy models in metapopulation and metacommunity theory are based on the assumption that population dynamics within patches are fast relative to the rates of colonizations and extinctions among patches (Law and Leibold 2005). Aggregation across space based on a separation of timescales is used to study population models that are initially set in discrete space in Mose et al. (2012) and Nguyen-Ngoc et al. (2012) in the case of continuous time and Bravo de la Parra et al. (1997, 1999, 2013, 2016), Sanz and Bravo de la Parra (2000) in the case of discrete time. [See Auger et al. (2000) for additional references.] Stochastic population models with fast timescales are considered in Constable (2014) and Sanz and Bravo de la Parra (2000).
There has also been a considerable amount of work based on using invasibility analysis to compare dispersal strategies and identify evolutionarily stable or convergence stable strategies, or stable polymorphisms of strategies, in the context of reaction–advection–diffusion models and their discrete and nonlocal analogues. Much of the literature in that area prior to 2012 is cited and discussed in Cosner (2014), so we will only give a brief review of the area and describe more recent work here. In a classic paper (with the same title), Hastings (1983) asked the question “Can spatial variation alone lead to selection for dispersal?” and used a version of invasibility analysis to give the answer “No”, at least in the case of dispersal by diffusion modeled by Fick’s law and the analogous form of discrete diffusion. That conclusion was reaffirmed a few years later by Dockery et al. (1998), who used a somewhat more sophisticated form of invasibility analysis which has since become a standard approach to such questions. More precisely, Hastings (1983) and Dockery et al. (1998) showed that in environments that vary in space but not in time, among dispersal strategies based on simple diffusion, there is selection for slower diffusion rates so that the strategy of not diffusing at all is convergence stable. It turns out that this property holds for various types of dispersal models where dispersal is not conditioned on environmental factors; see for example Hutson et al. (2003) for the case of nonlocal dispersal, or the discussion in section 4 of Cosner (2014). However, when diffusion cannot be avoided (for example because of small scale random movements due to searching for resources or avoiding enemies), there are circumstances where invasibility analysis of reaction–advection–diffusion models suggests that there is selection for some amount of directed movement, or alternatively if individuals always advect rapidly up resource gradients there may be selection for faster diffusion. See again the discussion and references in section 4 of Cosner (2014), and Averill et al. (2012), Cantrell et al. (2006, 2007, 2010, 2012a, b), Chen et al. (2008), Hambrock and Lou (2009) and Lam and Lou (2014a, b). In particular, Lam and Lou (2014a, b) obtained conditions where there are evolutionarily and convergent stable strategies for dispersal in the context of suitable classes of strategies combining diffusion and advection. A related but different type of result is that in some cases a competitor using a small to moderate amount of advection up a resource gradient can exclude a competitor that disperses by simple diffusion, but if the advection up the resource gradient is too fast the populations will coexist because the rapidly advecting population concentrates on resource peaks; see Cantrell et al. (2007), Lam (2011) and Lam and Ni (2010).
In the present paper we compare strategies involving diffusion and advection on environmental gradients with strategies such as simple diffusion which produce a spatially constant population distribution. We also compare strategies with different ratios of advection and diffusion rates. The results we obtain are generally consistent with those obtained in reaction–advection–diffusion models. Furthermore, we consider a special class of dispersal strategies that can produce an ideal free distribution of populations that use them. In the context of spatially explicit population models in temporally static environments a population achieves an ideal free distribution if the fitness of individuals (which in this setting is typically measured by local per capita population growth rate) is constant in space, and there is no net movement at population equilibrium. In the presence of population dynamics the only way that fitness can be constant at equilibrium is for it to be zero, which in models of logistic type typically means that the distribution of population must exactly match the distribution of resources. [See Cosner (2014) section 4 for additional discussion and references.] Dispersal strategies that can produce an ideal free distribution have been shown to be evolutionarily stable, versus those that cannot in various different types of models and classes of strategies, including reaction–diffusion–advection models and their nonlocal and discrete analogues; see for example Averill et al. (2012), Cantrell et al. (2010, 2012a, b), Korobenko and Braverman (2012, 2014). We find that this is also true in the modeling framework in this paper, and in fact can be established by means of phase plane analysis.
1.2 Organization of the paper
The paper is divided into sections by general topics. The sections are divided into subsections that treat more specific topics. The subsections are further subdivided. They generally start with statements of results and/or discussions of their interpretation which include most of the key ideas of the paper. Lengthy mathematical proofs and calculations, and some abstract discussions of mathematical background issues, are presented in subsubsections whose titles contain terms such as “technical” or “technicalities”. Readers who are primarily interested in the biological interpretations and applications of the ideas and results and want to get the “big picture” may want to skip the technical subsections, at least on the first reading. In Sect. 2 we develop the models and discuss their general properties, aspects of their dynamics, and connections to other models. In Sect. 3 we present three case studies of interacting populations that are ecologically identical in terms of resource use but which have different dispersal traits and thus different spatial distributions: first, where one population can achieve an ideal free distribution and the other cannot, second, where one population diffuses and advects on resource gradients but the other has a spatially uniform distribution, as would arise from fast simple diffusion, and third, where both populations advect and diffuse but may have different ratios of advection rate to diffusion rate. Depending on the case we find conditions for coexistence or competitive exclusion on the timescale of population dynamics, which allow us to then draw conclusions about the evolutionary or convergence stability of certain dispersal strategies, or the coexistence of others, on the timescale of evolution. In Sect. 4 we summarize our conclusions from the modeling.
2 Modeling framework
2.1 Dispersal
2.1.1 Description of the models
The key idea underlying the modeling in this paper is that the timescale of dispersal for the organisms in the models is sufficiently fast compared to timescale of their population dynamics that it is reasonable to assume the spatial distribution of the organisms is always effectively at equilibrium when viewed on the timescale of population dynamics. We will generally assume that the organisms disperse by some combination of diffusion and advection, although either or both of those may be conditioned on environmental conditions. Specifically, we will assume that the spatial region where the dispersal processes occur is a bounded region \(\Omega \subset {\mathbb {R}}^n\) (where \(n=1,2\) or 3), and we will usually assume that dispersal processes are described on the fast timescale by an advection–diffusion equation
where L is a second order elliptic partial differential operator of the form
with \( \mu _1, \mu _2 \ge \mu _0\) for some constant \(\mu _0>0\). Operators of this type arise naturally as continuum limits for biological diffusion processes where organisms may condition their small scale movement probabilities on various environmental factors and/or may engage in directed movement or be subject to physical advection. The derivation of such movement models from the underlying mechanisms operating at the level of stochastic movements by individuals is discussed in some detail in Aronson (1985) and Okubo and Levin (2001). We will supplement the operator L with no-flux boundary conditions:
Such boundary conditions incorporate the assumption that individuals do not cross the boundary of \(\Omega \) when they encounter it. We use no-flux boundary conditions so that there is no loss or gain of population arising from dispersal (specifically, dispersal across the boundary of \(\Omega \)). This can be seen by integrating the Eq. (1) over \(\Omega \) and using the divergence theorem to obtain \(\frac{d}{dt} \int _\Omega udx=0\).
If the coefficients in (2) and (3) and the boundary of the region \(\Omega \) are smooth, then the operator L in (2) with the boundary conditions (3) has a unique principal eigenvalue, whose eigenfunction \(\phi (x)\) is positive. The theory underlying this fact is based on results analogous to the Perron-Frobenius Theorem for nonnegative matrices. It turns out that the principal eigenvalue is 0. In the absence of population dynamics, solutions to (1) with positive initial densities converge to multiples of \(\phi \) as \(t \rightarrow \infty \). This observation will be a key element of our modeling approach. The details are described in Theorem 1, which is stated after a brief discussion of some technicalities. Readers interested mainly in the applications of the models may want to skip those and go directly to the theorem.
2.1.2 Some technical points
We will assume that \(\partial \Omega \) and the coefficients of L are sufficiently smooth that standard existence and regularity theory apply to (1) and the corresponding equilibrium equation, and that the adjoint operator \(L^*\) is well defined and has coefficients smooth enough that standard existence and regularity theory apply to it as well. [It is sufficient to have \(\partial \Omega \) of class \(C^{2+\gamma }\), with \(\mu _1, \mu _2 \in C^{2+\gamma }({\bar{\Omega }})\), and \(\vec {P}\in [C^{1+\gamma }({\bar{\Omega }})]^n \); see López-Gómez (2013) or (Cantrell and Cosner 2003, section 1.6), and the references therein]. The adjoint operator \(L^*\) associated with L is given by
with Neumann boundary condition
It follows from the maximum principle that the operator \(L^*\) has a positive resolvent, and elliptic regularity theory implies that the resolvent is compact on appropriate spaces, for example Hölder or Sobolev spaces. Thus, the spectrum of \(L^*\) consists of eigenvalues, and the Krein–Rutman theorem can be applied to \(L^*\) to show that \(L^*\) has a principal eigenvalue. (To be more precise, the Krein–Rutman theorem applies to the resolvent of \(L^*\)). A statement of the Krein–Rutman theorem and some references and discussion are given in section 2.5.1 of the book by Cantrell and Cosner (2003). Detailed discussions of the Krein–Rutman theorem and its applications to principal eigenvalues of second order elliptic operators such as \(L^*\) are given by López-Gómez (2013). It is easy to see that \(L^*u=0\) if \(u\equiv 1\), so the principal eigenvalue is 0. It follows that the principal eigenvalue of L is also zero. Furthermore, because L and \(L^*\) are second order elliptic operators, we have that \(Re\; \lambda <0\) for any other eigenvalue \(\lambda \) of \(L^*\) or L. This last observation is based on results that are specific to second order elliptic operators; a result of this type was proved by Protter and Weinberger (1966); see López-Gómez (2013) for a more general and unified treatment. Thus, all the terms in the eigenfunction expansions for solutions to (1) which are multiples of higher eigenfunctions will decay to 0 as \(t \rightarrow \infty \).
2.1.3 A fundamental result about dispersal
Recall that (1) keeps \(\int _\Omega u(x,t)dx\) fixed because of the no-flux boundary condition. Combining our previous observations, we have the following:
Theorem 1
Let \(\phi _0(x)>0\) be the eigenfunction corresponding to the eigenvalue 0 for the operator L in (2) with boundary condition (3), normalized so that \(\int _\Omega \phi _0(x)dx=1\). If u(x) is a solution to (1) with \(u(x,0)=u_0(x) \ge 0\) then \(u(x,t) \rightarrow U_0\phi _0(x)\) as \(t \rightarrow \infty \), where \(U_0=\int _\Omega u_0(x)dx\).
In some cases we can explicitly characterize \(\phi _0\). Specifically, if
for some function q(x) then
The fact that \(\phi _0\) as defined in (7) is an eigenfunction for L for the eigenvalue 0 can be seen by direct calculation. We will use the result of Theorem 1 to formulate our models for population dynamics.
2.2 Population dynamics
2.2.1 The logistic equation: modeling
Suppose that the dispersal process reaches equilibrium on the fast timescale of dispersal, so that we can write \(u(x,t)=U(t)\phi _0(x)\) where \(U(t)=\int _\Omega u(x,t)dx\). If we substitute this into the equation
where L is as in (2) with boundary conditions (3), and integrate over \(\Omega \), we obtain
(Here we would normally assume \(b(x)>0\).) The interpretation of (9) is that the population it describes interacts locally with the environmental quality, which is determined by levels of risks and resources, and with itself, according to the principle of mass action, but the local population density is given by the spatial distribution arising from dispersal on the fast timescale multiplied by the total population. The coefficients of the terms describing linear growth and logistic self-interaction can be viewed as spatial averages of the local values of the corresponding quantities weighted by the spatial distribution of the population.
Remark
We have \(u(x,t)=U(t)\phi _0(x)\) where by the normalization of \(\phi _0\) we have \(U(t)=\int _\Omega u(x,t)dx\). The forms of the coefficients in (9) are closely related to those that have been used to provide a currency to compare dispersal strategies or to formulate models in other contexts in theoretical ecology. Note that under our modeling formulation the first term in (9) could be written as \( \int _\Omega a(x)u(x,t)dx. \) Fagan et al. (2017) used this formulation, with a(x) allowed to depend on time and denoted as m(x, t), to define a currency to assess the effectiveness of the use of nonlocal information by foraging organisms in acquiring resources in spatiotemporally varying environments. There is an important body of work on general scaling properties of ecological models developed largely by Chesson (2009, 2012) and Chesson et al. (2005), and often referred to as scale transition theory, that relates population dynamic terms that are similar to those in (9) to means and variances of local population growth rates (or more broadly local fitness) and environmental quality. To see the connection, denote the mean of u(x, t) as \({\overline{u}}(t)=U(t)/|\Omega |\), and similarly the means of a, \(\phi _0\), and products of those quantities by \({\overline{a}}\), \(\overline{\phi _0}\), etc. Note that by our scaling of \(\phi _0\) we have \(\overline{\phi _0}=1/|\Omega |\), \({\overline{u}}=U/|\Omega |\), and \(u(x,t)=|\Omega |{\overline{u}}\phi _0(x)\). Using these definitions and observations, a standard identity relating the average of a product with the averages of its factors and their covariance, and the linearity of covariance in each of its arguments, we can then write the first term on the right of (9) as
Variations on this equation or related equations based on these general ideas appear in Chesson (2012) and Chesson et al. (2005). See “boxed” equations 12.B2.6 and 12.B2.7 and equations 12.4, 2.14-17 of Chesson et al. (2005) or equations 2–7 of Chesson (2012). Related ideas were used to set up simulation models by Bolker and Pacala (1999).
2.2.2 The logistic equation: additional technical comments on connections to scale transition theory
We can also rewrite the linear growth model corresponding to (9) in terms of the average density \({\overline{u}}(t)\) by dividing by \(|\Omega |\) and use the scaling of \(\phi _0\) and the equations in (10) to get
Analogously to (10), if b(x) is constant (reflecting the idea that crowding effects do not depend on resource levels), and using \(\hbox {Cov}(X,X)=Var(X)\) the second term on the right of (9) can be written as
Combining (9), (10), and (12) we get
which is very much in the spirit of models developed from Chesson’s modeling viewpoint.
2.2.3 Lotka–Volterra competition models
If we start with a competition system
where the operators \(L_1\) and \(L_2\) are of the form shown in (2) with no-flux boundary conditions as in (3) we can follow the derivation of (9) to obtain the analogous competition system. (In this case we would assume that the competitive interactions occur on the same timescale as the population dynamics arising from the birth and death rates of each competitor in the absence of the other rather than on the faster timescale of dispersal. This would probably be a reasonable assumption for many cases of resource competition but might not be appropriate if competition is mediated, for example, by direct aggressive behavior or transmission of a disease that is lethal for one competitor but not the other. In what follows we will be thinking primarily about resource competition between populations that are ecologically similar, so the assumption should be reasonable in that context.)
If we denote the total populations of the competitors as U and V, and the normalized principal eigenfunctions of \(L_1\) and \(L_2\) as \(\phi _1\) and \(\phi _2\) respectively, the resulting model takes the form
where the functions b, c, e, and f describing intra- and inter-species interactions are assumed to be positive. The system (15) is a standard Lotka–Volterra competition model. We could also derive the analogous predator–prey model by making one of the interspecific interaction terms negative. The general type of modeling approach that we have introduced here could be used in the context of any type of Lotka–Volterra model for any number of interacting species. However, the approach is completely based on assumption that local population interactions can be described by the mass action principle, so it is not clear if it can be extended to other types of interactions in a reasonable way. The dynamics of the Lotka–Volterra system are well understood. It will have single-species equilibria \((U^*,0)\) and \((0, V^*)\) if and only if \(\int _\Omega a(x)\phi _1(x)dx >0\) and \(\int _\Omega d(x)\phi _2(x)dx >0\), respectively. If the single species equilibrium for the first population is linearly unstable then the second population will persist if it is initially present. If in addition there is no coexistence equilibrium, which will be true in particular if the single-species equilibrium for the second species is linearly asymptotically stable, then the second will exclude the first. The analogous results hold if the roles of the species are reversed. If both the single species equilibria are linearly unstable then the model has a unique globally attracting coexistence equilibrium, so the populations will coexist. If both are linearly asymptotically stable then there is an unstable coexistence equilibrium and which competitor will persist is determined by initial conditions. The equilibrium \((U^*,0)\) is linearly asymptotically stable if \(\sigma <0\) and unstable when \(\sigma >0\), where
Similarly, the equilibrium \((0,V^*)\) is linearly asymptotically stable if \(\tau <0\) and unstable when \(\tau >0\), where
In what follows our primary interest will be the evolution of dispersal for a single population. To describe that we will use competition models where the two competitors are assumed to be ecologically identical except for their dispersal strategies.
2.3 Evolution
We will approach the question of evolution of dispersal from a viewpoint suggested by evolutionary game theory and the theory of adaptive dynamics. Specifically, we will look for strategies that can arise from evolution, specifically convergent stable strategies or neighborhood invader strategies, and strategies that can persist if they evolve, namely evolutionarily stable strategies. We assume that mutations affecting dispersal strategies are relatively rare, so that evolution acts on a timescale that is even slower than population dynamics. To determine what the outcome of evolution will be we will use pairwise invasibility analysis. What that means is that we will consider situations where there is a resident population that is using some strategy and a small population of mutants using some other strategy, but otherwise identical to the resident population is introduced. The models then predict whether the mutant population can invade the resident population. A strategy that can resist invasion by any population using any other available strategy is considered to be evolutionarily stable. A strategy that allows a population using it to invade some populations using other strategies is considered to be a neighborhood invader strategy. In cases where strategies are restricted to some class that can be parameterized, the properties of being evolutionarily stable or being a neighborhood invader can be either local or global in parameter space. Also, within a class of strategies that can be parameterized, a strategy is said to be convergent stable if strategies closer to it in parameter space can invade those that are farther away, at least within some subset of parameter space. To study the evolution of dispersal we will consider the invasibility of single species equilibria in the special case where \(a(x)=d(x)\) and \(b(x)=c(x)=e(x)=f(x)\). This assumption embodies the idea that the two competitors are ecologically equivalent and differ only in their dispersal strategies. A more specific version of this assumption about population interactions where \(a(x)=d(x)=m(x)\) and \(b(x)=c(x)=e(x)=f(x)=1\) has been used widely in models for the evolution of dispersal; see for example Averill et al. (2012), Cantrell et al. (2006, 2007, 2010, 2012b), Chen et al. (2008), Dockery et al. (1998), Hambrock and Lou (2009), Kao et al. (2010) and Lam and Lou (2014a, b). It embodies the additional assumption that only the linear birth or death rates for the interacting populations, which would serve as proxies for their local fitness when the populations are at low densities, are spatially dependent. However, we note that for each species by itself, in the case where the birth or death rate m(x) is always positive, the logistic equation for local population dynamics at the point x in the absence of dispersal could be written as
Thus, in that case, one could use the formulation of the logistic equation in terms of r and K to make the interpretation \(m(x)=r=K\) at the point x. In our study of the evolution of dispersal and related questions in the special case used in Averill et al. (2012), Cantrell et al. (2006, 2007, 2010, 2012b), Chen et al. (2008), Dockery et al. (1998), Hambrock and Lou (2009), Kao et al. (2010) and Lam and Lou (2014a, b), the Eqs. (16), (17) take the special forms
We will make use of (19), (20) in what follows.
A common theme in many results about the evolution of dispersal is that in spatially variable but temporally constant environments, “the slower diffuser wins”. This was observed by Hastings (1983); related results are proved in Dockery et al. (1998) and Hutson et al. (2003). However, in the modeling approach we use here, all dispersal, diffusive or otherwise, is fast. Our approach distinguishes between strategies only if they lead to distinct equilibrium distributions as given by the principal eigenfunctions \(\phi _1\) and \(\phi _2\). Thus, if constant diffusion is combined with advection up the gradient of m(x), as was studied in models on a single timescale in Cantrell et al. (2006, 2007), Chen et al. (2008) and Hambrock and Lou (2009), the only thing that matters is the ratio of the diffusion rate to the advection rate, since that determines the principal eigenfunction via (7). An important class of dispersal strategies are those that lead to an ideal free distribution. In models on a single timescale those are exactly the dispersal strategies that allow a population to match the local quality of the environment, that is, for which the unique positive equilibrium of the Eq. (8) or the analogous spatially discrete or nonlocal models is given by the equilibrium that would arise without any dispersal at all, namely \(u^*(x)=a(x)/b(x)\) provided \(a(x)>0\) on \({\bar{\Omega }}\), or in the special case where \(a(x)=m(x)\) and \(b(x)=1\), by \(u^*(x)=m(x)\); see for example Averill et al. (2012), Cantrell et al. (2010, 2012a, b), and Korobenko and Braverman (2012, 2014) and the references therein. In (Averill et al. 2012; Cantrell et al. 2012a, b; Korobenko and Braverman 2012, 2014), strategies leading to ideal free distribution have been shown to be globally evolutionarily stable and also to be global neighborhood invaders. We will see that something similar is true in the context of our models with multiple timescales, where the corresponding condition is that the principal eigenfunction of the dispersal operator is a scalar multiple of a(x) / b(x). There are various ways in which a dispersal operator of the form (2) can have a scalar multiple of a(x) / b(x), or in the more special case m(x), as its principal eigenfunction. For example in the case where \(a(x)=m(x)>0\) and \(b(x)=1\), operators of the form \(\nabla \cdot \mu (x)\nabla (u/m(x))\) will have that property for any \(\mu (x)>0\). Those include the special cases \(\mu =1\), which leads to \(Lu=\nabla ^2(u/m(x))\), as used in Korobenko and Braverman (2012, 2014), and \(\mu =1/m(x)\), which leads to \(Lu=\nabla \cdot [\nabla u-(u/m) \nabla m]\) as used in Averill et al. (2012) and Cantrell et al. (2010) among other possibilities. In the case of a general dispersal operator as in (2) in a logistic equation such as (8) the condition for the operator to lead to an ideal free distribution is that
It is interesting to consider how ideal free dispersal can act on the fitness of a population of fixed size. It turns out that in the special case of the logistic equation where only the density dependent self-regulation term varies, ideal free dispersal acts to increase population level fitness. Specifically, suppose that the local rate of growth or decline for a population on the slow timescale is given by \(r(1-u/K(x))\) (so that in the formulation of (8) we would have \(a(x)=r \) and \(b(x)=r/K(x)\)). Looking at the system on the fast timescale of dispersal, we can suppose that the overall population remains constant but its spatial distribution varies, and use the local fitness weighted by the population distribution as a proxy for population level fitness:
For such a population the distribution of the population would change on the fast timescale as governed by (1).
Proposition 1
Suppose that the dispersal operator L has the form (2) with boundary conditions (3), and that L supports an ideal free distribution with respect to K(x), that is, \(L K(x)=0\) on \(\Omega \), so that (21) holds with \(a/b=K\). Suppose that u(x, t) is a population density corresponding to a fixed population (so that \(\int _\Omega udx\) is assumed to be constant on the fast timescale) but that the spatial distribution of the population changes according to (1). Then F as defined in (22) is increasing on the fast timescale.
Proof
Differentiating F with respect to t (which is currently being interpreted as representing the fast timescale of dispersal) and using (1) yields
The first term in the last integral is zero because of the boundary conditions on L. Using (2) and the divergence theorem we can then rewrite (23) as
By using (21) with \(a/b=K\) and direct calculation we obtain
so that (24) can be written as
proving the claim. \(\square \)
The property of ideal free dispersal shown in Proposition 1 does not appear to extend directly to logistic equations with other forms of spatial variation; however, we shall see that on the slow timescale ideal free dispersal strategies in general are evolutionarily stable in a strong sense relative to strategies that do not produce an ideal free distribution.
3 Case studies
3.1 Ideal free dispersal
3.1.1 Main result and remarks
Consider the case of (15) where \(a(x)=d(x)>0\) and \(b(x)=c(x)=e(x)=f(x)>0\). This corresponds to a scenario of competition between ecologically identical populations. In that setting the first population has an ideal free dispersal strategy if
We have the following:
Theorem 2
In the setting of (15) with \(a(x)=d(x)>0\) and \(b(x)=c(x)=e(x)=f(x)>0\), any ideal free dispersal strategy is a global evolutionarily stable strategy and a global neighborhood invader strategy relative to any class of strategies that does not include any other ideal free strategy.
Remark
We will see that any population using an ideal free strategy will exclude any population that is not using an ideal free strategy if both populations are present initially. This result is analogous to those obtained in Averill et al. (2012), Cantrell et al. (2012a, b) and Korobenko and Braverman (2014) for various sorts of models on a single timescale.
Whether or not a population can disperse so as to achieve an ideal free distribution by using diffusion, or a combination of diffusion and advection, depends on behavioral traits at the spatiotemporal scale of random walks. That scale is faster in time and smaller in space than the scales where diffusion and advection models operate. The ability to develop traits that can ultimately produce an ideal free distribution depends on the sensory and motor capabilities of individuals. Roughly speaking, to achieve an ideal free distribution, individuals must be able to sense and respond to environmental quality or more generally local fitness, or gradients of such quantities, at the scale of random walks. This point is noted in Cosner (2014) and discussed in detail in Farnsworth and Beecham (1999) and Potapov et al. (2014); see Aronson (1985) and Okubo and Levin (2001) for background material. In particular, diffusive movement at the scale of random walks which is not conditioned on the local environment, for example, classical diffusion as described by Fick’s law, cannot produce an ideal free distribution.
3.1.2 Technicalities: proof of Theorem 2
Suppose that the first competitor uses an ideal free dispersal strategy. The dynamics of the system (15) can be determined from the invasion criteria arising from (16) and (17). We have
It follows that \((U^*,0)\) is always linearly neutrally stable. Also,
The sign of \(\tau \) is the same as the sign of
Since \((a(x)/b(x)^{1/2})^2=a(x)^2/b(x)\), \((b(x)^{1/2}\phi _2(x))^2=b(x)\phi _2(x)^2\), and \((a(x)/b(x)^{1/2})(b(x)^{1/2}\phi _2(x))=a(x)\phi _2(x)\), it follows from the Cauchy-Schwartz inequality that \(\tau \) is positive unless \(a(x)/b(x)^{1/2}\) is a constant multiple of \(b(x)^{1/2}\phi _2(x)\), which will be true only if \(\phi _2(x)\) is a constant multiple of a(x) / b(x), that is, only if the strategy used by the second competitor is also ideal free. Thus, a population using an ideal free dispersal strategy can always invade a population using any strategy that is not ideal free. The existence or nonexistence of a positive equilibrium in this case of (15) is determined by a system equivalent to
The determinant of the coefficient matrix of (31) is the expression that occurs in (30) multiplied by \(\int _\Omega [a(x)/b(x)]dx\), so if the second competitor is using a strategy that is not ideal free then the determinant is nonzero. Solving for \(V^{**}\) then yields \(V^{**}=0\). Hence there is no positive equilibrium. (The isoclines of the system (15) intersect at \((U^{**},0)\) in this case.) It then follows by general competition theory that since the system (15) does not have a positive equilibrium and the equilibrium \((0,V^*)\) is unstable, the equilibrium \((U^*,0)\) is globally asymptotically stable. Thus, a population using an ideal free dispersal strategy can resist invasion by any population using a dispersal strategy that is not ideal free, and furthermore can invade any such population. It follows that ideal free dispersal strategies are globally evolutionarily stable relative to strategies that are not ideal free, as claimed. They are also global neighborhood invader strategies.
3.2 Diffusion versus diffusion with advection
3.2.1 Background and main results
In the case where \(a(x)>0\) and all dispersal strategies of the form (2) are available to a population, ideal free dispersal strategies are possible, and the results of the previous section show that they can be expected to evolve and persist. However, there may be situations where \(a(x)<0\) for some values of x, which would reflect ecological situations where any sort of diffusive movement leads to source-sink dynamics even if arbitrary choice of advection is possible. Also, the dispersal strategies available to organisms may be limited in ways that prevent them from achieving an ideal free distribution. In this section and the next we will explore some scenarios where ideal free dispersal is not feasible for one reason or another. Specifically, we will consider cases where \(a(x)=d(x)=m(x)\) and \(b(x)=c(x)=e(x)=f(x)=1\) and where the only available strategies are simple diffusion or simple diffusion with advection on \(\nabla m(x)\). In this section we will consider competition between a population that simply diffuses and one that diffuses and advects on \(\nabla m(x)\). In the next section we will study the evolution of the rate of advection on \(\nabla m(x)\) when both competitors can use arbitrary rates of advection on \(\nabla m(x)\). Models on a single timescale with these features were studied in Cantrell et al. (2006, 2007), Chen et al. (2008), Hambrock and Lou (2009) and Lam and Lou (2014a, b).
The first observation in the case where m(x) can change sign is that since the principal eigenfunction corresponding to the case of simple diffusion is constant, our models predict that a population that simply diffuses will persist only if \(\int _\Omega m(x)dx>0\). On the other hand, if a population diffuses at a constant rate and advects on \(\nabla m(x)\) with rate \(\alpha \) times as large [for example if \(\mu _1=\mu _2=1\) and \(\vec {P}(x)=\alpha \nabla m(x)\) in (2)] then the principal eigenfunction is a multiple of \(e^{\alpha m(x)}\) and our models predict persistence if \(\int _\Omega m(x)e^{\alpha m(x)}dx>0\), which will always be true for \(\alpha \) sufficiently large if m(x) is differentiable and \(m(x)>0\) somewhere. The same condition is sufficient for persistence in the analogous reaction–diffusion–advection model on a single timescale; see for example Cantrell and Cosner (2003, p. 106). Suppose that we allow m(x) to change sign but assume that \(\int _\Omega m(x)dx>0\) so that our models predict persistence for a single population for all \(\alpha \ge 0\). Suppose further that the first competitor diffuses at a fixed rate and advects on \(\nabla m(x)\) at \(\alpha \) times the diffusion rate, while the second competitor just diffuses. In that case the condition for a small population of the first competitor to be able to invade a resident population of the second, as given by \(\tau >0\) in (20), is
It turns out that (32) holds for \(\alpha >0\) provided m(x) is not constant.
Let \({\bar{m}}=\frac{1}{|\Omega |} \int _\Omega mdx\).
Proposition 2
Assume that the second competitor simply diffuses at a constant rate while the first competitor diffuses and also advects on \(\nabla m\) at a rate equal to \(\alpha \) times its diffusion rate. Assume further that \({\bar{m}} >0\) so that \((0,V^*)\) exists. If m(x) is not identically equal to \({\bar{m}}\) then for all \(\alpha >0\) the inequality (32) holds so that \((0,V^*)\) is unstable and hence the first competitor can invade a resident population of the second competitor if a small population of the first competitor is introduced.
Proof
Observe that \(\int _\Omega (m(x)-{\bar{m}})dx=0\) and that if m(x) is not identically equal to \({\bar{m}}\) then \(\frac{d}{d\alpha }\int _\Omega e^{\alpha (m(x)-{\bar{m}})}(m(x) - {\bar{m}})>0\), so that \(\int _\Omega e^{\alpha (m(x)-{\bar{m}})}(m(x) - {\bar{m}})>0\) for \(\alpha >0\). Dividing by \(e^{-\alpha {\bar{m}}}\) and distributing \(e^{\alpha m(x)}\) yields \(\int _\Omega e^{\alpha m(x)}m(x)dx-{\bar{m}}\int _\Omega e^{\alpha m(x)}dx>0\), which is equivalent to (32). \(\square \)
Although a competitor that advects on \(\nabla m\) can always invade a competitor that simply diffuses in the setting of Proposition 2, it cannot always resist invasion by such a competitor. This phenomenon was shown to occur in some cases for models on a single timescale in Cantrell et al. (2007) when the competitor that both diffuses and advects on \(\nabla m\) has a sufficiently large advection rate. In that situation the mechanism that allows invasion by the purely diffusing competitor is that the density of the advecting and diffusing competitor concentrates at certain maxima of m(x); see Lam (2011) and Lam and Ni (2010). A similar mechanism appears to produce the analogous effect in our models on multiple timescales. Additionally, in our models the purely diffusing competitor can also invade the advecting and diffusing competitor when the advection rate is large in cases where m(x) has a positive lower bound. The condition for a small population of the second (purely diffusing) competitor to be able to invade a resident population of the first, as given by \(\sigma >0\) in (19), is equivalent to
Observe that \(G(0)=0\) and that for non-constant m(x)
by the Cauchy-Schwartz inequality. Thus for small positive values of \(\alpha \) we have \(G(\alpha )<0\) and hence the second competitor cannot invade a resident population of the first. For large \(\alpha \) there are conditions on m(x) under which \(G(\alpha )>0\) so the second competitor can invade the first. We have the following:
Lemma 1
Suppose that m(x) attains its global maximum on \({\bar{\Omega }}\) at finitely many points and all global maxima are non-degenerate. Then
Lemma 1 implies that for \(\alpha \) large (33) holds so that there is mutual invasibility by the competitors so they can coexist. We have:
Corollary 1
If the hypotheses of Proposition 2 and Lemma 1 are satisfied then the equilibrium \((U^*,0)\) is unstable so a small population of the second competitor can invade a resident population of the first competitor if the first competitor advects on \(\nabla m\) at a sufficiently large rate \(\alpha \). In that case, since each population can invade the other if introduced at low density, the competitors can coexist.
The condition in Lemma 1 is not the only one that implies coexistence for sufficiently large \(\alpha \):
Proposition 3
Suppose that \(m_0=min\{m(x): x \in {\overline{\Omega }}\} >0\). If \(\alpha >1/m_0\) then the equilibrium \((U^*,0)\) is unstable, so there is mutual invasibility by the two competitors and hence they can coexist.
To summarize the case where one competitor simply diffuses and the other advects up the gradient of m at a rate \(\alpha >0\), by combining the previous results in this section with the known dynamics of the Lotka–Volterra competition model, we have the following:
Theorem 3
Suppose that the hypotheses of Proposition 2 are satisfied and m(x) is not identically equal to \({\bar{m}}\). For all \(\alpha >0\) the competitor that both diffuses and advects up the gradient of m can persist and can invade a resident population of the competitor that simply diffuses. If the advection rate \(\alpha \) is sufficiently small the competitor that advects up the gradient of m will exclude the competitor that simply diffuses. If in addition the hypotheses of Corollary 1 or Proposition 3 are satisfied then for \(\alpha \) sufficiently large the competitor that simply diffuses can invade a resident population of the competitor that diffuses and advects up the gradient of m, so the two competitors can coexist.
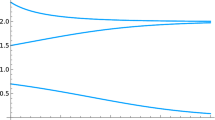
The conditions given in the hypotheses of Corollary 1 and Proposition 3 are sufficient for our model to predict that the competitor which simply diffuses can invade a resident population of the competitor that both advects on the gradient of m and diffuses, provided that the advection rate \(\alpha \) is large, but they are not necessary for that prediction. Also, in general we do not know if there is a unique value of \(\alpha \) where the prediction of the model changes from competitive exclusion to coexistence, or whether it may switch between those more than once. As an example, if \(\Omega =(0,1)\) then \(m(x)=x\) does not satisfy the hypotheses of either Corollary 1 or Proposition 3, but the conclusion that the model predicts coexistence for large \(\alpha \) still holds. Specifically, the global maximum of m(x) is not nondegenerate in the sense of Corollary 1 in the example, and m(x) does not have a positive minimum. Furthermore, in that example, it turns out that the value of \(\alpha \) where the prediction switches from exclusion to coexistence is unique. Details of that example are worked out in the next subsubsection.
3.2.2 Technicalities: proofs and analysis of the example \(m(x)=x\)
Proof of Lemma 1
Suppose that \(max_{{\bar{\Omega }}}\; m(x)=m(x_i)=m_0\) for \(i=1 \ldots N\). Assume that \(x_i \in \Omega \) for each i. (The case where \(x_i \in \partial \Omega \) for some i is similar.) By Taylor’s theorem and the fact that m has a nondegenerate maximum at \(x_i\), for each i
where \(\nabla ^2 m(x_i)\) denotes the Hessian of m at \(x_i\). By hypothesis, \(\nabla ^2 m(x_i)\) is strictly negative definite. Hence, since the set of local maxima is finite, there exists some \(\delta >0\) such that for \(i=1 \ldots N\), if \(|x-x_i|<\delta \), then
and for some \(\epsilon >0\), \(m(x)<m_0-\epsilon \) for \(x \in \Omega \backslash \{\cup _{i=1}^N \{|x-x_i|<\delta \}\). We then have
For any given i let \(y=\sqrt{\alpha }(x-x_i)\). Then \(dx=\alpha ^{-n/2}dy\) and
where \(C_i=\int _{{\mathbb {R}}^n} e^{\frac{1}{4}y^T \nabla ^2 m(x_i)y}dy\). Combining (37) and (38) we obtain
It follows from (39) that
On the other hand, we have
Again, for any given i let \(y=\sqrt{\alpha }(x-x_i)\), and we have
There exists a constant \(c_i>0\) such that for \(\alpha \ge 1/\delta \) we have
Thus, for \(\alpha \ge 1/\delta \) we have
so that
Letting \(C=\sum _{i=1}^N C_i\) and \(c=\sum _{i=1}^N c_i\) it follows from (39), (41), and (44) that for \(\alpha \ge 1/\delta \) we have
Since
the estimate (45) implies (35). \(\square \)
Proof of Proposition 3
Let
Observe that (33) holds if \(H(\alpha )>0\). Note that
so that for any constant c we can write \(H(\alpha )\) as
Also, the integrand in (47) must change sign, which means that there are points \(x \in {\overline{\Omega }}\) where \(m(x)=a\) such that
that is, \(e^{\alpha a}=\int _\Omega e^{2\alpha m}/\int _\Omega e^{\alpha m}\), so that \(a=(1/\alpha )ln(\int _\Omega e^{2\alpha m}/\int _\Omega e^{\alpha m})\). For nonconstant m,
so we have \(a>m_0\), and then by hypothesis \(a>1/\alpha \). For \(z>1/\alpha \), \(ze^{-\alpha z}\) is decreasing. Choose \( c=ae ^{-\alpha a}\) in (48). Since \(m \ge m_0\), \(a \ge m_0\), and \(m_0>1/\alpha \), it follows that if \(m>a\) then \(me^{-\alpha m}-ae^{-\alpha a}<0\). Also, \(e^{\alpha m}>e^{\alpha a}=\int _\Omega e^{2 \alpha m(x)}dx/\int _\Omega e^{ \alpha m(x)}dx\) so multiplying by \(e^{ \alpha m(x)}\) and rearranging terms gives \(e^{ 2\alpha m(x)}/\int _\Omega e^{2 \alpha m(x)}dx>e^{ \alpha m(x)}/\int _\Omega e^{ \alpha m(x)}dx\). Thus, if \(m>a\), both factors in the integrand in (48) are negative so their product is positive. Similarly, both factors are positive in the case \(m<a\), so again the product is positive. It follows that \(H(\alpha )>0\) for \(\alpha >1/m_0\), so that (33) holds, implying instability of \((U^*,0)\) and hence coexistence. \(\square \)
Example 1
Let \(\Omega =(0,1)\) and \(m(x)=x\). Direct calculations give
from which we obtain
We will see that there is a unique value \(\alpha ^\# > 0\) such that \(G'(\alpha ) <0\) for \(0<\alpha < \alpha ^\#\) and \(G'(\alpha ) >0\) for \(\alpha > \alpha ^\#\), from which it follows that \(G(\alpha )\) changes sign exactly once, from negative to positive, for \(\alpha \in (0, \infty )\). Direct calculations show that
For convenience, we consider the numerator of \(-G'(\alpha )/2\) and expand it to determine the sign of \(G'(\alpha )\). Let
We want to show that there is a unique value \(\alpha ^\# > 0\) such that \(S(\alpha ) >0\) for \(0<\alpha < \alpha ^\#\) and \(S(\alpha ) <0\) for \(\alpha > \alpha ^\#\). Note that \(S(0)=0\) and the dominant term in \(S(\alpha )\) as \(\alpha \rightarrow \infty \) is \(-\alpha e^{2\alpha }\) so that \(S(\alpha ) \rightarrow -\infty \) as \(\alpha \rightarrow \infty \). Computing derivatives of S yields
We have \(S^{(4)}(0)=0\), and \(S^{(4)}(\alpha )=\alpha e^\alpha (\alpha +5-16e^\alpha )\). Since \(16e^\alpha >16+16\alpha \) for \(\alpha >0\), we have \(S^{(4)}(\alpha )<0\) for \(\alpha >0\). We have \(S'''(0)=1>0\), and the dominant term in \(S'''(\alpha )\) is \(-8\alpha e^{2\alpha }\), which is negative for \(\alpha >0\), so \(S'''(\alpha ) < 0\) for \(\alpha \) sufficiently large. It then follows that for some unique \(\alpha _1>0\) we have \(S'''(\alpha )>0\) for \(\alpha <\alpha _1\) and \(S'''(\alpha )<0\) for \(\alpha >\alpha _1\). Furthermore, \(S''(0)=0\) and the dominant term in \(S''(\alpha )\) is \(-4\alpha e^{2\alpha }\), which is negative for \(\alpha >0\), so \(S''(\alpha ) < 0\) for \(\alpha \) sufficiently large. Hence, \(S''(\alpha )\) is positive and increasing on \((0, \alpha _1)\), has a maximum at \(\alpha = \alpha _1\), and then decreases toward \(-\infty \), so there exists a unique \(\alpha _2\) so that \(S''(\alpha )>0\) for \(0<\alpha <\alpha _2\) and \(S''(\alpha )<0\) for \(\alpha >\alpha _2\). Similarly, we have \(S'(0)=0\) and \(S'(\alpha )<0\) for \(\alpha \) sufficiently large, so repeating the last argument shows there is a unique \(\alpha _3\) so that \(S'(\alpha )>0\) for \(0<\alpha <\alpha _3\) and \(S'(\alpha )<0\) for \(\alpha >\alpha _3\). Finally, since \(S(0)=0\) and \(S(\alpha ) <0\) for \(\alpha \) large, the same argument shows that there is a unique \(\alpha ^{\#}>0\) so that \(S(\alpha )>0\) for \(0<\alpha <\alpha ^{\#}\) and \(S(\alpha )<0\) for \(\alpha >\alpha ^{\#}\), which gives the desired result.
3.3 Evolution of advection rates
3.3.1 Background and main results
In this section we will consider the case where both competitors must diffuse at the same fixed rate but both advect on the gradient of the local population growth rate at low density and can choose the size of their advection rates relative to the diffusion rate. Again, we will consider cases where \(a(x)=d(x)=m(x)\) and \(b(x)=c(x)=e(x)=f(x)=1\), with \(\int _\Omega mdx>0\). Suppose that the first competitor advects on \(\nabla m\) at a rate equal to \(\alpha \) times the diffusion rate while the second competitor advects on \(\nabla m\) at \(\beta \) times the diffusion rate. In that case the condition \(\sigma >0\) in (19) for the equilibrium \((U^*,0)\) to be unstable, so that a small population of the second competitor can invade a resident population of the first, is equivalent to
Using \({\tilde{\sigma }}\) as a proxy for \(\sigma \), we see that the strategy corresponding to an advection rate \(\alpha ^*\) will be evolutionarily singular if \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ^*,\alpha ^*)=0\) and will be convergence stable if \(\displaystyle \frac{\partial }{\partial \alpha } \left( \displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\alpha )\right) \Big |_{\alpha ^*}<0\). See Geritz et al. (1997). What we will actually show is that under suitable conditions on m(x) there is an evolutionarily singular strategy \(\alpha ^*\) with the property that for \(\alpha \approx \alpha ^*\), we have \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\alpha )>0\) for \(\alpha <\alpha ^*\) and \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\alpha )<0\) for \(\alpha >\alpha ^*\), which is still sufficient for convergence stability. A simple computation yields
It follows immediately from Hölder’s inequality that for nonconstant m(x), \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha =0}>0\). To show there exist evolutionarily singular strategies we will find conditions so that \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }<0\) for large \(\alpha \). The first is similar to those in Lemma 1:
Lemma 2
Suppose that m(x) attains its global maximum on \({\bar{\Omega }}\) at finitely many points \(x_i \in \Omega \) and all global maxima are non-degenerate. Then for \(\alpha \) sufficiently large,
The second set of conditions for the existence of evolutionary singular strategies are similar to those given for coexistence of populations dispersing by simple diffusion and by diffusion with advection up the gradient of m in Proposition 3.
Proposition 4
Let \(m_0=min\{m(x): x \in {\overline{\Omega }}\}\) and \(m_1=max\{m(x): x \in {\overline{\Omega }}\}.\) Suppose that \(m_0>0\). Then for \(0\le \alpha <1/m_1\),
For \(\alpha >1/m_0\),
We can now give conditions for the existence of \(\alpha ^*\) such that the strategy of advection on \(\nabla m\) at a rate equal to \(\alpha ^*\) times the diffusion rate is locally convergence stable:
Theorem 4
Suppose that m(x) is nonconstant and that the hypotheses of either Lemma 2 or Proposition 4 are satisfied. Then there exists at least one value \(\alpha ^*\) such that advection on \(\nabla m\) at a rate equal to \(\alpha ^*\) times the diffusion rate is a local convergence stable strategy. If the hypotheses of Proposition 4 are satisfied then \(\alpha ^* \in [1/m_1,1/m_0]\) where \(m_0, m_1\) are as in Proposition 4.
Proof
We always have \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha =0}>0\). Under the hypotheses of either Lemma 2 or Proposition 4 we have \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }<0\) if \(\alpha \) is sufficiently large. Thus, there must be at least one value \(\alpha ^*\) where \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }=0\), and if the hypotheses of Proposition 4 are satisfied we have \(\alpha ^* \in [1/m_1,1/m_0]\) where \(m_0, m_1\) are as in Proposition 4. It is easy to see that \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }\) is an analytic function of \(\alpha \) and is not identically zero, so at \(\alpha =\alpha ^*\) it must have at least one nonzero derivative. If the lowest order nonzero derivative is positive for every such \(\alpha ^*\) then \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }\) cannot change sign from positive to negative, which yields a contradiction, so there must be some value \(\alpha ^*\) such that the lowest order nonzero derivative is negative. For any such value of \(\alpha ^*\) we have \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\alpha )>0\) for \(\alpha <\alpha ^*,\alpha \approx \alpha ^*\) and \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\alpha )<0\) for \(\alpha >\alpha ^*,\alpha \approx \alpha ^*\), which is sufficient for local convergence stability.
As in the case of diffusion with advection versus simple diffusion, the sufficient conditions we have derived for the existence of a convergence stable strategy are not necessary, and we do not know if the value \(\alpha ^*\) which determines a convergence stable strategy is unique. The fact the our conditions are not necessary can be seen in the case \(\Omega =(0,1)\) with \(m(x)=x\), which is worked out in the next subsection. It turns out that the value \(\alpha ^*\)is unique in that case. \(\square \)
3.3.2 Technicalities: proofs and analysis of the example \(m(x)=x\)
Proof of Lemma 2
As in Lemma 1, suppose that \(max_{{\bar{\Omega }}}\; m(x)=m(x_i)=m_0\) for \(i=1 \ldots N\) with that \(x_i \in \Omega \). Let
It is clear that \(g(\alpha )\) has the same sign as \(\displaystyle \frac{\partial {\tilde{\sigma }}}{\partial \beta }(\alpha ,\beta )\Big |_{\beta =\alpha }\). Since m has a nondegenerate maximum at \(x_i\), for each i, the Hessian \(\nabla ^2 m(x_i)\) is strictly negative definite. Let
Note that \(m_1 \le 0\). Since the set of global maxima is finite, for any sufficiently small \(\epsilon >0\) we can choose \(\delta >0\) so that if \(|x-x_i|<\delta \) then
and \(m(x)<m_0-\epsilon \) for \(x \in \Omega \backslash \Omega _\delta \). We can express the first integral in (55) as
and observe that
for some constant C, and similarly for the remaining integrals in (55). If we multiply out the decomposed integrals then since \(m\le m_0\) everywhere and \(m<m_0-\epsilon \) on \(\Omega \backslash \Omega _\delta \), any of the resulting product terms with a factor where one of the integrals is taken over \(\Omega \backslash \Omega _\delta \) will be bounded by \(Ce^{\alpha (3m_0-\epsilon )}\) so that
If we now write \(m=m_0+m_1\) in (60), expand and combine or cancel like terms, then rearrange we obtain
The second term in the second line of (61) is nonpositive. To estimate the first term in the second line of (61) observe that by (56)
Since \(M_i(x)\) is a negative definite quadratic form, for each i we can make the substitution \(y=\alpha ^{1/2}(1-\epsilon )^{1/2}(x-x_i)\) and obtain
for some generic constant C which can be chosen independent of \(\epsilon \) and \(\delta \). It follows that
Using the analogous substitutions where \(y=2^{1/2}\alpha ^{1/2}(1-\epsilon )^{1/2}(x-x_i)\) we also have
Thus, the first term in the second line of (61) is bounded by \(C\alpha ^{-(n+2)}e^{3\alpha m_0}\). To estimate the terms in the first line of (61) we observe that they can be rewritten as
Recalling that \(m_1\le 0\) and \(M_i\le 0, i=1\ldots N\), and using (57) we have
where the term in the first line of right hand side of the inequality is negative and the term in the second line is positive. We can estimate those terms by substitution as in (62)–(65). Using \(y=\alpha ^{1/2}(1+\epsilon )^{1/2}(x-x_i)\) in the first integral on the right in (67) yields
Making the analogous substitutions in the remaining integrals on the right in (67) yields
Let
We have
Using (68)–(70) in (67) yields
As \(\alpha \rightarrow \infty \) the expression inside the brackets on the right side of (72) approaches
For sufficiently small \(\epsilon >0\) we have \(C_{ij}<0\). Thus, for \(\alpha \) sufficiently large, we have by (66)–(73)
for some constant \(C_0>0\). Hence, choosing \(\epsilon >0\) sufficiently small, it follows from (61), (64), (65), and (74) that for \(\alpha \) large,
so that \(g(\alpha ) <0\) for large \(\alpha \), which proves the lemma. \(\square \)
Proof of Proposition 4
By direct calculation and proper rearrangement we have
Since
we have, for any constant c,
Since
there exists some \(x^*\in {{\bar{\Omega }}}\) such that
Choose \(c=m(x^*)\) we have
Recall that the function \(ze^{-\alpha z}\) is increasing if \(z<1/\alpha \) and decreasing if \(z>1/\alpha \). It follows that the last two factors in the integrand in (79) have the same sign if \(m(x)<1/\alpha \) on \(\Omega \), which will be true if \(\alpha <1/m_1\), and of opposite signs if \(m(x)>1/\alpha \) on \(\Omega \), which will be true if \(\alpha >1/m_0\). The first factor in the integrand is always positive, so \(\frac{\partial {\tilde{\sigma }}}{\partial \beta }-c{\tilde{\sigma }}(\alpha , \beta )\) is positive for \(\alpha <1/m_1\) and negative for \(\alpha >1/m_0\). This together with \({\tilde{\sigma }}(\alpha , \alpha )=0\) proves the proposition. \(\square \)
Example 2
As in Example 1, let \(\Omega =(0,1)\) and \(m(x)=x\). In this case there is a unique value of \(\alpha ^*\) that determines a convergence stable strategy. We have
Direct calculation of g in the case \(\alpha =0\) and l’Hospital’s rule show \(g(0)=\displaystyle \lim _{\alpha \rightarrow 0}g(\alpha )=1/12.\)
The proof of the first part of Proposition 4 is still valid for this case and implies that \(g(\alpha )>0\) for \(0<\alpha <1/m_1=1\). Direct calculations yield
Numerical evaluation gives \(g(1)>0\) so \(g(\alpha )>0\) for \(0\le \alpha \le 1.\) Further calculations give
The quantity \(-2\alpha ^2+3\alpha -6\) is always negative because its discriminant is negative, so we have \(g'(\alpha )<0\) for \(\alpha >2\), and by numerical evaluation \(g(2)<0\). Hence we have \(g(\alpha )<0\) for \(\alpha \ge 2\). Furthermore, by numerical evaluation, \(g'(1)>0\). We will show that \(g'(\alpha )\) changes sign exactly once on (1, 2), which then implies that \(g(\alpha )\) changes sign exactly once on (1, 2), which yields the desired result. It will be convenient to write \( 4\alpha ^5g'(\alpha )=V(\alpha )=T(\alpha )-Z(\alpha )\), where
Clearly the signs of V and \(g'\) are the same. Also, \(Z(\alpha )\ge 0\) for \(\alpha \ge \sqrt{3}\). Note that the expression \(2\alpha ^2-3\alpha +6\) is increasing on [1, 2] and equals 8 when \(\alpha =2\), and that \(e^\alpha >1+\alpha \ge 2\). Thus, \(T(\alpha ) < -6(\alpha -2)^2e^{2\alpha }-8(\alpha -2)e^\alpha -12\) on [1, 2]. Viewing the last expression as a quadratic in \((\alpha -2)e^\alpha \) we see that the discriminant is negative, so that \(T(\alpha )<0\) on [1, 2]. It follows that \(V(\alpha ) <0\) on \([\sqrt{3},2]\) so we can restrict our attention to \(\alpha \in [1,\sqrt{3})\). Direct calculations yield
By numerical evaluation we have \(V'(1)=-3e^3+8e^2+e>0\) and \(V''(1)=3e^3-8e^2-e<0\). Clearly \(V'''(\alpha )< (-81\alpha ^2+162\alpha -54)e^{3\alpha }+(-32\alpha ^2-96\alpha +8)e^{2\alpha }\) on \([1,\sqrt{3}]\). We claim that \(V'''(\alpha )< 0\) on \([1,\sqrt{3}]\). Let \(k(\alpha )=(-81\alpha ^2+162\alpha -54)e^\alpha +(-32\alpha ^2-96\alpha +8)\), so that \(V'''(\alpha )<0\) if \(k(\alpha )<0\). Numerical evaluation gives \(k(1)<0\). We have \(k'(\alpha )=(-81\alpha ^2+108)e^\alpha -64\alpha -96=(-81\alpha +81)e^\alpha +27e^\alpha -64\alpha -96\). For \(\alpha \in [1,\sqrt{3})\) we have \(64\alpha +96 \ge 160\) and (by numerical evaluation) \(27e^\alpha< 27e^{\sqrt{3}}<153\) so that \(k'(\alpha )<0\). It follows that \(V'''(\alpha )<0\) on \([1,\sqrt{3})\), and hence that \(V''(\alpha )<0\) on \([1,\sqrt{3})\) since \(V''(1)<0\). We know that \(g'(1) >0\) and \(g'(\alpha )<0\) for \(\alpha \in [\sqrt{3},2]\), so the same is true for \(V(\alpha )\), so that \(V'(\alpha )\) must be negative somewhere in the interval \([1,\sqrt{3})\). Since \(V'(1)>0\), this together with \(V''(\alpha )<0\) implies that \(V'(\alpha )\) changes sign exactly once, from positive to negative, in the interval \([1,\sqrt{3})\). Since \(V(1) >0\) and \(V(2)<0\) it follows by the same logic that \(V(\alpha )\) and hence \(g'(\alpha )\) changes sign exactly once, from positive to negative, in [1, 2]. Applying the same argument once again, since \(g(1)>0\), \(g(2)<0\), and \(g'(\alpha )\) changes sign exactly once from positive to negative, we conclude that \(g(\alpha )\) must do the same, as desired.
4 Conclusions
Our fundamental conclusion about modeling, supported by our case studies, is that by using systems of ordinary differential equations whose coefficients are weighted spatial averages of parameters describing environmental heterogeneity where the weights are given by eigenfunctions of reaction–diffusion–advection operators describing the dispersal of populations, we can recover many of the sorts of results about the effects and evolution of dispersal which have been developed for models based on reaction–diffusion–advection systems and their nonlocal analogues. This suggests that for populations where dispersal occurs on a more rapid timescale than population dynamics, the method of aggregation discussed in Auger et al. (2012) can be used effectively to address questions related to conditional dispersal in spatially heterogeneous environments. The reduction of models from partial differential equations to ordinary differential equations represents a significant simplification, although teasing out the effects of dispersal strategies in heterogeneous environments is still a nontrivial problem in the simplified setting. Additionally, our methods and results give a way to connect population models incorporating mechanistic descriptions of dispersal based on reaction–diffusion–advection models to landscape models based on spatial averaging of the type discussed in Chesson (2009, 2012) and Chesson et al. (2005). Our fundamental conclusion about the biological implications of models is that many of the qualitative conclusions about the evolution of dispersal and related topics that have been developed using models that operate on a single timescale (Averill et al. 2012; Cantrell et al. 2006, 2007, 2010, 2012a, b; Chen et al. 2008; Cosner 2014; Hambrock and Lou 2009; Kao et al. 2010; Korobenko and Braverman 2012, 2014; Lam and Lou 2014a, b) still obtain. Thus, predictions about the effects and evolution of dispersal made by various types of models where dispersal and population dynamics act on a single timescale appear to be robust relative to the presence and separation of different timescales for those processes. Specific examples are the predictions that an appropriate amount of advection on environmental gradients (not too much or too little) is advantageous, and that dispersal strategies that can produce an ideal free distribution are evolutionarily stable relative to strategies that cannot.
We believe that there are many possible extensions of the ideas in this paper that might be worth pursuing. There are many questions about the ways that the interplay of dispersal strategies and environmental heterogeneity which could be addressed using the same approach. We only considered a few specific questions about the effects of dispersal strategies on competition, and only in the context of the evolution of dispersal in otherwise identical populations. There are many more possibilities. The same methods could be applied to predator–prey systems, or systems with several trophic levels, or with several species interacting in a mixture of ways (for example, one might consider a predator with two prey species and ask how dispersal patterns influence apparent competition.) The reduction from partial differential equations to ordinary differential equations might be even more useful in studying models with several populations, or for models of the coevolution of dispersal in pairs of interacting species (leading to a system of four equations) than in the relatively simple context of the monotone systems describing pairwise competition.
References
Aronson DG (1985) The role of diffusion in mathematical population biology: Skellam revisited. In: Capasso V, Grosso E, Paveri-Fontana SL (eds) Mathematics in biology and medicine. Lecture notes in biomathematics, vol 57. Springer, Berlin, pp 2–6
Auger P, Poggiale J-C, Charles S (2000) Emergence of individual behaviour at the population level. Effects of density-dependent migration on population dynamics. Comptes Rendus de l’Academie des Sciences - Series III - Sciences de la Vie 323:119–127
Auger P, Poggiale JC, Sánchez E (2012) A review on spatial aggregation methods involving several time scales. Ecol Complex 10:12–25
Averill I, Lou Y, Munther D (2012) On several conjectures from evolution of dispersal. J Biol Dyn 6:117–130
Bolker BM, Pacala SW (1999) Spatial moment equations for plant competition: understanding spatial strategies and the advantages of short dispersal. Am Nat 53:575–602
Brännström Å, Johansson J, von Festenberg N (2013) The Hitchhiker’s guide to adaptive dynamics. Games 4:304–328
Bravo de la Parra R, Sánchez E, Auger P (1997) Time scales in density dependent discrete models. J Biol Syst 5:111–129
Bravo de la Parra R, Sánchez E, Arino O, Auger P (1999) A discrete model with density dependent fast migration. Math Biosci 157:91–110
Bravo de la Parra R, Marvá M, Sánchez E, Sanz L (2013) Reduction of discrete dynamical systems with applications to dynamics population models. Math Model Nat Phenom 8:107–129
Bravo de la Parra R, Marvá M, Sansegundo F (2016) Fast dispersal in semelparous populations. Math Model Nat Phenom 11:120–134
Cantrell RS, Cosner C (2003) Spatial ecology via reaction–diffusion equations. Wiley, Chichester
Cantrell RS, Cosner C, Lou Y (2006) Movement toward better environments and the evolution of rapid diffusion. Math Biosci 204:199–214
Cantrell RS, Cosner C, Lou Y (2007) Advection-mediated coexistence of competing species. Proc R Soc Edinb A 37:497–518
Cantrell RS, Cosner C, Lou Y (2010) Evolution of dispersal and the ideal free distribution. Math Biosci Eng 7:17–36
Cantrell RS, Cosner C, Lou Y (2012a) Evolutionary stability of ideal free dispersal strategies in patchy environments. J Math Biol 65:943–965
Cantrell RS, Cosner C, Lou Y, Ryan D (2012b) Evolutionary stability of ideal free dispersal in spatial population models with nonlocal dispersal. Can Appl Math Q 20:15–38
Chen X, Hambrock R, Lou Y (2008) Evolution of conditional dispersal: a reaction–diffusion–advection model. J Math Biol 57:361–386
Chesson P (2009) Scale transition theory with special reference to species coexistence in a variable environment. J Biol Dyn 3:149–163
Chesson P (2012) Scale transition theory: its aims, motivations and predictions. Ecol Complex 10:52–68
Chesson P, Donahue MJ, Melbourne BA, Sears ALW (2005) Scale transition theory for understanding mechanisms in metacommunities. In: Holyoke M, Leibold MA, Holt RD (eds) Metacommunities: spatial dynamics and ecological communities. The University of Chicago Press, Chicago, pp 279–306
Constable GWA (2014) Fast timescales in stochastic population dynamics. Dissertation, University of Manchester
Cosner C (2014) Reaction–diffusion–advection models for the effects and evolution of dispersal. Discret Contin Dyn Syst A 34:1701–1745
Dockery J, Hutson V, Mischaikow K, Pernarowsk M (1998) The evolution of slow dispersal rates: a reaction diffusion model. J Math Biol 37:61–83
Fagan WF, Gurarie E, Bewick S, Howard A, Cantrell RS, Cosner C (2017) Perceptual ranges, information gathering, and foraging success in dynamic landscapes. Am Nat 189:474–489
Farnsworth KD, Beecham JA (1999) How do grazers achieve their distribution? A continuum of models from random diffusion to the ideal free distribution using biased random walks. Am Nat 153:509–526
Geritz S, Metz JAJ, Kisdi E, Meszéna G (1997) Dynamics of adaptation and evolutionary branching. Phys Rev Lett 78:2024–2027
Hairston NG Jr, Ellner SP, Geber MA, Yoshida T, Fox JA (2005) Rapid evolution and the convergence of ecological and evolutionary time. Ecol Lett 8:1114–1127
Hambrock R, Lou Y (2009) The evolution of conditional dispersal strategies in spatially heterogeneous habitats. Bull Math Biol 71:1793–1817
Hastings A (1983) Can spatial variation alone lead to selection for dispersal? Theor Pop Biol 24:244–251
Hastings A (2010) Timescales, dynamics, and ecological understanding. Ecology 91:3471–3480
Hutson V, Martínez S, Mischaikow K, Vickers GT (2003) The evolution of dispersal. J Math Biol 47:483–517
Kao C-Y, Lou Y, Shen W (2010) Random dispersal vs. nonlocal dispersal. Discret Contin Dyn Syst A 26:551–596
Korobenko L, Braverman E (2012) On logistic models with a carrying capacity dependent diffusion: stability of equilibria and coexistence with a regularly diffusing population. Nonlinear Anal RWA 13:2648–2658
Korobenko L, Braverman E (2014) On evolutionary stability of carrying capacity driven dispersal in competition with regularly diffusing populations. J Math Biol 69:1181–1206
Lam K-Y (2011) Concentration phenomena of a semilinear elliptic equation with large advection in an ecological model. J Differ Equ 250:161–181
Lam K-Y, Lou Y (2014a) Evolutionarily stable and convergent stable strategies in reaction–diffusion models for conditional dispersal. Bull Math Biol 76:261–291
Lam K-Y, Lou Y (2014b) Evolution of dispersal: ESS in spatial models. J Math Biol 68:851–877
Lam K-Y, Ni W-M (2010) Limiting profiles of semilinear elliptic equations with large advection in population dynamics. Discret Contin Dyn Syst A 28:1051–1067
Law R, Leibold MA (2005) Assembly dynamics in metacommunities. In: Holyoke M, Leibold MA, Holt RD (eds) Metacommunities: spatial dynamics and ecological communities. The University of Chicago Press, Chicago, pp 263–278
Levin SA (1992) The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture. Ecology 73:1943–1967
Levin SA (2000) Multiple scales and the maintenance of biodiversity. Ecosystems 3:498–506
López-Gómez J (2013) Linear second order elliptic operators. World Scientific, Singapore
Morozov A, Poggiale J-C (2012) From spatially explicit ecological models to mean-field dynamics: The state of the art and perspectives. Ecol Complex 10:1–11
Mose VN, Nguyen-Huu T, Auger P, Western D (2012) Modelling herbivore population dynamics in the Amboseli National Park, Kenya: application of spatial aggregation of variables to derive a master model. Ecol Complex 10:42–51
Nguyen-Ngoc D, Nguyen-Huu T, Auger P (2012) Effects of fast density dependent dispersal on pre-emptive competition dynamics. Ecol Complex 10:26–33
Okubo A, Levin SA (2001) Diffusion and ecological problems. Springer, New York
Polechová J, Barton NH (2015) Limits to adaptation along environmental gradients. PNAS 20:6401–6406
Potapov A, Schlägel U, Lewis MA (2014) Evolutionarily stable diffusive dispersal. Discret Contin Dyn Syst B 19:3319–3340
Protter MH, Weinberger HF (1966) On the spectrum of general second order operators. Bull Am Math Soc 72:251–255
Sanz L, Bravo de la Parra R (2000) Time scales in stochastic multiregional models. Nonlinear Anal RWA 1:89–122
Acknowledgements
Some of the ideas in this paper arose from discussions in workshops at the Banff International Research Station: Multiscale Analysis of Self-Organization in Biology (09w5070) July 12–July 17, 2009, organizers B. Perthame and T. Hillen, and Emerging Challenges at the Interface of Mathematics, Environmental Science and Spatial Ecology (11w5106) July 3–July 08, 2011, organizers R. S. Cantrell, R. Holt, and M. A. Lewis. CC thanks Odo Diekmann for discussions that helped motivate this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The paper should be listed for the special issue S.I. : In honor of Alan Hastings’ 65th birthday.
Research partially supported by NSF Grants DMS-1118623 and DMS-1514752 (RSC, CC), NSF Grant DMS-1411476 (YL), NSFC Grant No. 11571364 (YL), and an NSERC Discovery Grant (ML)
Rights and permissions
About this article
Cite this article
Cantrell, R.S., Cosner, C., Lewis, M.A. et al. Evolution of dispersal in spatial population models with multiple timescales. J. Math. Biol. 80, 3–37 (2020). https://doi.org/10.1007/s00285-018-1302-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-018-1302-2