Modelling the fear effect in predator–prey interactions

Abstract

A recent field manipulation on a terrestrial vertebrate showed that the fear of predators alone altered anti-predator defences to such an extent that it greatly reduced the reproduction of prey. Because fear can evidently affect the populations of terrestrial vertebrates, we proposed a predator–prey model incorporating the cost of fear into prey reproduction. Our mathematical analyses show that high levels of fear (or equivalently strong anti-predator responses) can stabilize the predator–prey system by excluding the existence of periodic solutions. However, relatively low levels of fear can induce multiple limit cycles via subcritical Hopf bifurcations, leading to a bi-stability phenomenon. Compared to classic predator–prey models which ignore the cost of fear where Hopf bifurcations are typically supercritical, Hopf bifurcations in our model can be both supercritical and subcritical by choosing different sets of parameters. We conducted numerical simulations to explore the relationships between fear effects and other biologically related parameters (e.g. birth/death rate of adult prey), which further demonstrate the impact that fear can have in predator–prey interactions. For example, we found that under the conditions of a Hopf bifurcation, an increase in the level of fear may alter the direction of Hopf bifurcation from supercritical to subcritical when the birth rate of prey increases accordingly. Our simulations also show that the prey is less sensitive in perceiving predation risk with increasing birth rate of prey or increasing death rate of predators, but demonstrate that animals will mount stronger anti-predator defences as the attack rate of predators increases.

1 Introduction

Studying the mechanisms driving predator–prey systems is a central topic in ecology and evolutionary biology. The long-standing view, is that predators can impact prey populations only through direct killing. Predation events are relatively easy to observe in the field and by removing individuals from the population, it stands to reason that direct killing would be involved (Creel and Christianson 2008; Lima 1998, 2009; Cresswell 2011). An emerging view, however, is that the mere presence of a predator may alter the behaviour and physiology of prey to such an extent that it can exert an effect on prey populations even more powerful than direct predation (Creel and Christianson 2008; Lima 1998, 2009; Cresswell 2011).

All animals in every taxa respond to perceived predation risk and show a variety of anti-predator responses including changes in habitat usage, foraging behaviours, vigilance and physiological changes (Cresswell 2011; Svennungsen et al. 2011; Peacor et al. 2013; Preisser and Bolnick 2008; Pettorelli et al. 2011). For example, when prey assess predation risk, they may choose to abandon the original high-risk habitat and relocate to low-risk habitats, which can carry an energetic cost especially if the low-risk habitats are of suboptimal quality (Cresswell 2011). Similarly, scared prey are well-known to forage less, which could reduce the birth rate and survival through mechanisms like starvation (Creel and Christianson 2008; Cresswell 2011). High levels of acute predation risk can cause prey to leave habitats or foraging sites temporarily, returning only when the acute risk has passed and the prey are relatively safe (Cresswell 2011). Moreover, fear may affect the physiological condition of juvenile prey and leave harmful impacts on their survival as adults (Clinchy et al. 2013; Creel and Christianson 2008). Birds, for example, respond to the sounds of predators with anti-predator defences (Creel and Christianson 2008; Cresswell 2011), and when nesting, will flee from their nests at the first sign of danger (Cresswell 2011). Such an anti-predator behaviour may be beneficial in increasing the probability of survival, but can carry some long-term costs on reproduction that may affect population numbers (Cresswell 2011).

Although some theoretical ecologists and evolutionary biologists have realized that the interactions between prey and predators should not be simply described by direct predation alone and that the cost of fear should be considered (Preisser and Bolnick 2008; Peacor et al. 2013; Pettorelli et al. 2011), no mathematical models have been proposed to quantitatively investigate whether or the extent to which fear can affect prey populations. This is mainly due to lack of direct experimental evidence demonstrating that fear can affect the populations of terrestrial vertebrates.

Recently, however, Zanette et al. (2011) conducted a manipulation on song sparrows during an entire breeding season to determine whether perceived predation risk could affect reproduction even in the absence of direct killing. The authors manipulated predation risk by broadcasting predator sounds to some populations of song sparrows while others heard non-predator sounds. At the same time, all nests in the manipulation were protected from direct killing ensuring that any effects on reproduction could only be ascribed to fear. Zanette et al. (2011) found that the fear of predators alone led to a $40~\%$ reduction in the number of offspring of the song sparrows parents could produce. The reason this effect was so dramatic, is because predation risk had effects on both the birth rate and survival of offspring because song sparrow females laid fewer eggs (the birth rate), fewer of those eggs hatched (survival) and more nestlings died in the nest (survival). Moreover, the authors showed that a variety of anti-predator responses led to these effects on demography. For example, scared parents fed their nestlings less, their nestlings were lighter and much more likely to die. Correlational evidence in birds (Eggers et al. 2005, 2006; Ghalambor et al. 2013; Hua et al. 2013, 2014; Fontaine and Martin 2006; Orrock and Fletcher 2014; Ibáñez-Álamo and Soler 2012), elk (Creel et al. 2007), snowshoe hares (Sheriff et al. 2009) and dugongs (Wirsing and Ripple 2011) also provide some evidence that fear can affect populations.

Predator–prey models have been studied extensively, but no models to date have incorporated the plastic anti-predator behaviour of prey in addition to the behaviour of the predator. Following the classic Lotka–Volterra model, Holling (1965) proposed the well-known Holling type II functional response of predators. The population dynamics of predator–prey systems with the Holling type II functional response have been studied by many scholars and the existence of a unique stable limit cycle for such a model has been confirmed (Kooij and Zegeling 1997; Kuang and Freedman 1988; Sugie et al. 1997). There have been many other predator–prey systems that have modelled more complicated functional responses. For example, within the prey dependent functional responses, May (1972), Seo and DeAngelis (2011) and Huang et al. (2014) considered some monotone response functions and Zhu et al. (2003), Ruan and Xiao (2001), Freedman and Wolkowicz (1986) and Wolkowicz (1988) studied some non-monotone response functions. In addition to functional responses dependent on prey numbers only, there are also studies considering functional responses dependent on both prey and predators numbers, among which are the Beddington–DeAngelis functional responses (Cantrell and Cosner 2001; Beddington 1975; DeAngelis et al. 1975; Hwang 2003, 2004) and ratio dependent functional response (Song and Zou 2014a, b).

No matter how sophisticated functional responses may be when incorporated into predator-prey models, they still only reflect what can happen regarding direct killing. In this paper, we propose and analyze a predator-prey model incorporating the cost of fear (indirect effects) to explore the impact that fear can have on population dynamics in predator–prey systems. In Sect. 2, we formulate the model incorporating the cost of fear generated by anti-predator behaviors. In Sect. 3, we analyze the model for the case when the functional response is a linear function of the prey population. In Sect. 4, we consider the Holling type II functional response for the model, and present some results on the stability of equilibria, existence of Hopf bifurcation and direction of Hopf bifurcation. Our mathematical results show that while incorporating fear (i.e. predation risk) effects into predator–prey models do not affect the structure of the equilibria, it may change the stability of the equilibria. Moreover, the existence of Hopf bifurcation and its direction in our model will be different from the classic model ignoring fear effects. In Sect. 5, we provide some numerical simulation results which reveal some potential roles that the fear effect may play in predator–prey interactions. We end the paper by Sect. 6, consisting of some conclusions and we also, discuss the biological implications of our mathematical results and possible future projects.

2 Model formulation

Assume that the prey obey a logistic growth in the absence of predation and the cost of fear. The logistic growth of prey can be separated into three parts: a birth rate, a natural death rate and a density dependent death rate due to intra-species competition. This leads to the following ODE

$$\begin{aligned} \frac{du}{dt}=r_0 u-d\,u-a\,u^2, \end{aligned}$$

(2.1)

where u represents the population of the prey, $r_0$ is the birth rate of prey, d is the natural death rate of prey, a represents the death rate due to intra-species competition.

Let v represent the population of the predator. Since fields experiments show that the fear effect will reduce the production, we modify (2.1) by multiplying the production term by a factor f(k, v) which accounts for the cost of anti-predator defence due to fear, leading to

$$\begin{aligned} \frac{du}{dt}=[f(k,v)\, r_0]\, u -d\,u-a\,u^2. \end{aligned}$$

(2.2)

Here, the parameter k reflects the level of fear which drives anti-predator behaviours of the prey. By the biological meanings of $k,\,\,v$ and f(k, v), it is reasonable to assume that

$$\begin{aligned} \left\{ \begin{aligned}&f(0,v)=1,\;\;\;\;f(k,0)=1,\;\;\;\;\lim \limits _{k\rightarrow \infty } f(k,v)=0,\;\;\;\;\lim \limits _{v\rightarrow \infty } f(k,v)=0,\\&\frac{\partial f(k,v)}{\partial k}<0,\;\;\;\;\frac{\partial f(k,v)}{\partial v}<0. \end{aligned} \right. \end{aligned}$$

(2.3)

Although there are arguments and beliefs (e.g., Clinchy et al. 2013) that fear may lead to lower survival rate of adults due to physiological impacts when they are young, by far there are no direct experimental evidences showing such an impact. As such, we do not incorporate this factor into modelling in this work, meaning that we regard d and a as constants.

Next, we incorporate a predation term g(u) v into (2.2) to obtain the following general prey–predator model with cost of fear reflected:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{du}{dt}=u\,r_0\,f(k,v)-d\,u-a\,u^2-g(u)\,v,\\&\frac{dv}{dt}=v\,(-m+c\,g(u)).\\ \end{aligned} \right. \end{aligned}$$

(2.4)

Here $g: \mathbb {R}_+ \rightarrow \mathbb {R}_+$ is the functional response of predators, v represents the density of predators, c is the conversion rate of prey’s biomass to predators’ biomass, m is the death rate of predators. Typically, g(u) is of the form up(u) with $p: \mathbb {R}_+ \rightarrow \mathbb {R}_+$. When $p(u) =p$ is a constant, g(u) gives a linear functional response, and when $p(u)= p/(1+qu)$, g(u) represents the Holling type II functional response.

By the standard basic theory of ODE systems, one can easily show that for any initial value $(u_0,v_0) \in \mathbb {R}_+^2$, (2.4) has a unique solution, and with the form $g(u)= p(u) u$, it is easily seen that the solution remains positive and bounded, and hence it exists globally.

From the first equation in (2.4), we have $u'(t) \le (r_0-d) u$ which establishes a linear comparison equation from the above for the first equation. By a comparison argument, we conclude that if $r_0<d$, then $u(t) \rightarrow 0$ as $t \rightarrow \infty$, and applying the theory of asymptotically autonomous systems (see, e.g. Castillo-Chavez and Thieme 1995) to the second equation in (2.4), we also obtain $v(t) \rightarrow 0$ as $t \rightarrow \infty$. This means that when $r_0<d$, both prey and predator species will go to extinction, regardless of the fear effect and particular predation mechanism. Therefore, we only need to consider the case when $r_0>d$ which will be assumed in the rest of the paper.

3 Model with the linear functional response

For the case of linear functional response $g(u)=p u$, we consider general function f(k, v) that satisfies conditions (2.3), reducing the model (2.4) to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{du}{dt}=r_0\,u\,f(k,v)-d\,u-a\,u^2-p\,u\,v,\\&\frac{dv}{dt}=c\,p\,u\,v-m\,v. \end{aligned} \right. \end{aligned}$$

(3.1)

In addition to the trivial equilibrium $E_0=(0,0)$, this system also has a boundary equilibrium $E_1=((r_0-d)/a,0)$ under the condition $r_0>d$. In addition, there exists a unique positive (co-existence) equilibrium for system (3.1) given by $E_2=(\overline{u},\overline{v})$ if

$$\begin{aligned} r_0>d + \frac{am}{cp} \end{aligned}$$

(3.2)

holds, where $\overline{u}=m/(c\,p)$ and $\overline{v}$ satisfies

$$\begin{aligned} r_0\,f(k,\overline{v})-d-a\,\overline{u}-p\,\overline{v}=0. \end{aligned}$$

(3.3)

If (3.2) is reversed, (3.3) has no positive solution and hence system (3.1) has no positive (coexistence) equilibrium.

The following theorem describes the local stability of all three equilibria.

Theorem 3.1

The following statements hold:

• (i) The semi-trivial equilibrium $E_1$ is locally asymptotically stable if (3.2) is reversed and is unstable if (3.2) holds.

• (ii) The positive equilibrium $E_2$, as long as it exists (i.e., when (3.2) is satisfied), is locally asymptotically stable.

Proof

We only show the proof of the local stability of $E_2$ because the proof for the local stability of $E_1$ is similar. The Jacobian matrix of system (3.1) at $E_2$ is

$$\begin{aligned} J=\left[ \begin{array}{cc} J_{11}&{}J_{12}\\ J_{21}&{}J_{22}\\ \end{array} \right] , \end{aligned}$$

(3.4)

where

$$\begin{aligned}&J_{11}=r_0\,f(k,\overline{v})-d-2\,a\,\overline{u}-p\,\overline{v}= -a \bar{u}<0, \quad J_{12}=r_0\,\overline{u}\,\frac{\partial f(k,v)}{\partial v}\Bigg |_{v=\overline{v}}-p\,\overline{u}<0,\nonumber \\&J_{21}=c\,p\,\overline{v}>0, \quad J_{22}=c\,p\,\overline{u}-m =0. \end{aligned}$$

(3.5)

Obviously, ${{\mathrm{tr}}}(J)= -a \bar{u}<0$, and by (2.3), $\det (J)=-J_{12}J_{21} >0$. Thus, $E_2$ is locally asymptotically stable. $\square$

The above theorem shows that, as the parameter $r_0$ increases, the model experiences two bifurcations of equilibrium: when $r_0 \in (0, d)$, $E_0$ is the only equilibrium which is globally asymptotically stable; when $r_0$ passes d to enter the interval $(d, d+ am/cp)$, $E_0$ loses its stability to a new equilibrium $E_1$; and when $r_0$ further passes $d+am/cp$, $E_1$ loses its stability to another new equilibrium $E_2$. The next theorem further confirms that the stability claimed in Theorem 3.1 is actually global for both $E_1$ and $E_2$.

Theorem 3.2

The boundary equilibrium $E_1$ is globally asymptotically stable if $r_0 \in (d, d+am/cp)$, and the unique positive equilibrium $E_2$ is globally asymptotically stable if $r_0> d+am/cp$.

Proof

Assume $r_0>d+am/cp$ and let $P(u,v),\,Q(u,v)$ represent the two functions on the right hand side of system (3.1). Choose the Dulac function $B(u,v)=1/(u\,v).$ After calculations, we obtain

$$\begin{aligned} D=\frac{\partial {(P\,B)}}{\partial u}+\frac{\partial {(Q\,B)}}{\partial v}=-\frac{a}{v}<0 \end{aligned}$$

(3.6)

for $(u,v) \in (0,\infty )\times (0,\infty ).$ Therefore, by the Dulac–Bendixson theorem (Perko 1996, Theorem 2, p 265), there is no periodic orbit in $(0,\infty )\times (0,\infty )$ for system (3.1). Moreover, $E_2$ is the unique positive equilibrium in $(0,\infty )\times (0,\infty )$ if (3.2) holds; hence, every positive solution will tend to $E_2$. This together with the local stability confirmed in Theorem 3.1 implies that $E_2$ is indeed globally asymptotically stable, if (3.2) holds.

When $r_0 \in (d, d+am/cp)$, there is no other equilibrium other than $E_0$ and $E_1$ in $\mathbb {R}_+^2$, and hence, there can not be any periodic orbit in $\mathbb {R}_+^2$, implying that every positive solution will either approach $E_0$ or $E_1$. It can be easily seen that $E_0$ is repelling (under $r_0>d$), and thus, every positive solution actually approaches $E_1$. This together with Theorem 3.1 again implies that $E_1$ is indeed globally asymptotically stable if $r_0 \in (d, d+am/cp)$. $\square$

4 Model with the Holling type II functional response

In this section, we consider the Holling type II functional response $g(u)=pu/(1+qu)$, and in the mean time, for convenience of analysis, we adopt the following particular form for the fear effect term f(k, v):

$$\begin{aligned} f(k,v)=\frac{1}{1+k\,v}. \end{aligned}$$

(4.1)

With g(u) and f(k, v) specified as above, the model (2.4) becomes

$$\begin{aligned} \begin{aligned}&\frac{du}{dt}=\frac{r_0\,u}{1+k\,v}-d\,u-a\,u^2-\frac{p\,u\,v}{1+q\,u},\\&\frac{dv}{dt}=\frac{c\,p\,u\,v}{1+q\,u}-m\,v.\\ \end{aligned} \end{aligned}$$

(4.2)

4.1 Existence of equilibria and dynamical behaviours in boundary

In addition to the trivial equilibrium $E_0=(0,0)$, system (4.2) has one semi-trivial equilibrium $E_1=((r_0-d)/a,0)$ if $r_0>d,$ which is assumed in the rest of the paper. We address the local stability of $E_1$ in the following theorem.

Theorem 4.1

Semi-trivial equilibrium $E_1$ is locally asymptotically stable if

$$\begin{aligned} (r_0-d)(c\,p-m\,q)<a\,m \end{aligned}$$

(4.3)

is satisfied and is unstable if

$$\begin{aligned} (r_0-d)(c\,p-m\,q)>a\,m \end{aligned}$$

(4.4)

holds.

The proof for Theorem 4.1 is similar to the proof in Theorem 3.1 and is thus omitted. We will see later that under (4.4), the model (4.2) actually has a positive equilibrium.

Note that $E_0$ is unstable, $E_1$ is locally asymptotically stable and there is no other equilibrium provided that

$$\begin{aligned} c\,p \,\le \, m\,q. \end{aligned}$$

(4.5)

Then this implies that $E_1$ is indeed globally asymptotically stable if (4.5) holds. Thus, we have the following theorem.

Theorem 4.2

The boundary equilibrium $E_1$ is globally asymptotically stable if (4.5) is satisfied.

By Theorem 4.2, the dynamical behaviour of system (4.2) is clear when (4.5) holds. In the sequel, we only need to study the case when

$$\begin{aligned} c\,p>m\,q. \end{aligned}$$

(4.6)

In order to simplify the analysis, we make the following transformations for system (4.2) by

$$\begin{aligned} dt= & {} \frac{(1+q\,u)(1+k\,v)}{m} \,d \overline{t},\nonumber \\ \overline{u}= & {} \frac{c\,p-m\,q}{m}\,u,\overline{v}=k\,v. \end{aligned}$$

(4.7)

Dropping the bars system (4.2) is transformed to the following equivalent system

$$\begin{aligned} \frac{du}{dt}= & {} u(a_1+a_2\,u-a_3\,v-a_4\,u\,v-a_5\,u^2-a_6\,v^2-a_5\,u^2\,v),\nonumber \\ \frac{dv}{dt}= & {} v\,(u-1)(1+v), \end{aligned}$$

(4.8)

where

$$\begin{aligned} a_1= & {} \frac{r_0-d}{m}, \, \, a_2=\frac{(r_0-d)\,q-a}{c\,p-m\,q}, \,\, a_3=\frac{d\,k+p}{m\,k},\nonumber \\ a_4= & {} \frac{d\,q+a}{c\,p-m\,q},\, \, a_5=\frac{a\,m\,q}{(c\,p-m\,q)^2}, \, \, a_6=\frac{p}{m\,k}. \end{aligned}$$

(4.9)

By (4.6), we have $a_i>0$ where $i=1,\,3,\,4,\,5,\,6$. Thus, there exists a positive equilibrium $E_2=(1,\overline{v}_2)$ for system (4.8) if

$$\begin{aligned} a_1+a_2>a_5 \,\,\, ( \Longleftrightarrow a_5-a_1< a_2 ), \end{aligned}$$

(4.10)

where $\overline{v}_2$ is the positive root of the following quadratic equation under (4.10):

$$\begin{aligned} a_6\,\overline{v}_2^2+(a_3+a_4+a_5)\,\overline{v}_2-(a_1+a_2-a_5)=0. \end{aligned}$$

(4.11)

By (4.11), we actually obtain

$$\begin{aligned} \overline{v}_2=\frac{-(a_3+a_4+a_5)+\sqrt{(a_3+a_4+a_5)^2+4\,a_6(a_1+a_2-a_5)}}{2\,a_6}. \end{aligned}$$

(4.12)

We point out that straightforward calculation shows that (4.10) is equivalent to the condition (4.4), implying that $E_1$ loses its stability to the occurrence of the positive equilibrium $E_2$ when inequality (4.3) is reversed to (4.4). The local stability of $E_2$ is addressed in the following theorem.

Theorem 4.3

The positive equilibrium $E_2$ is locally asymptotically stable if

$$\begin{aligned} a_5-a_1<a_2 \le 2\,a_5, \end{aligned}$$

(4.13)

or

$$\begin{aligned} a_2>2\,a_5 \quad \,\,\, \text{ and } \quad \,\,\, \overline{v}_2>\frac{a_2-2\,a_5}{a_4+2\,a_5}; \end{aligned}$$

(4.14)

it is unstable if

$$\begin{aligned} a_2>2\,a_5 \quad \,\,\,\text{ and } \quad \,\,\, \overline{v}_2<\frac{a_2-2\,a_5}{a_4+2\,a_5}. \end{aligned}$$

(4.15)

Proof

Jacobian matrix of system (4.8) at $E_2(1,\overline{v}_2)$ is

$$\begin{aligned} J^{*} =\left[ \begin{array}{cc} J_{11}&{}J_{12}\\ J_{21}&{}J_{22}\\ \end{array} \right] , \end{aligned}$$

(4.16)

where

$$\begin{aligned} J_{11}= & {} a_1+2\,a_2-a_3\,\overline{v}_2-2\,a_4\,\overline{v}_2-3\,a_5-a_6\,\overline{v}_2^2-3\,a_5\,\overline{v}_2,\nonumber \\ J_{12}= & {} -a_3-a_4-2\,a_6\,\overline{v}_2-a_5<0,\,J_{21}=\overline{v}_2\,(1+\overline{v}_2)>0,\,J_{22}=0.\qquad \end{aligned}$$

(4.17)

Obviously, $\det (J)=-J_{12}J_{21} >0$ by (4.10) and then the stability of $E_2$ is determined by ${{\mathrm{tr}}}(J^{*})=J_{11}.$ Direct calculations show that ${{\mathrm{tr}}}(J^{*})<0$ is equivalent to

$$\begin{aligned} (a_2-2\,a_5)<(a_4+2\,a_5)\,\overline{v}_2. \end{aligned}$$

(4.18)

Because $\overline{v}_2,\,a_4,\,a_5$ are all positive, (4.18) is satisfied if (4.13) holds. Furthermore, if $a_2>2\,a_5,$ the local stability of $E_2$ further requires $\overline{v}_2>(a_2-2\,a_5)/(a_4+2\,a_5),$ as presented in (4.14). Equilibrium $E_2$ loses stability when (4.15) holds. $\square$

Note that (4.13) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&r_0>\frac{a\,m}{c\,p-m\,q}+d,\\&r_0 \le d+\frac{a\,(c\,p+m\,q)}{q\,(c\,p-m\,q)},\\ \end{aligned} \right. \end{aligned}$$

(4.19)

and (4.14) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}&r_0>d+\frac{a\,(c\,p+m\,q)}{q\,(c\,p-m\,q)},\\&k>\frac{q\,(c\,p-m\,q)^2\left( (r_0-d)\,q\,(c\,p-m\,q)-a\,(c\,p+m\,q)\right) }{c^2\,p\,a\,\left( q\,d(c\,p-m\,q)+a\,(c\,p+m\,q)\right) }.\\ \end{aligned} \right. \end{aligned}$$

(4.20)

Then, by Theorem 4.3, we obtain that prey and predators will tend to a steady state if (4.19) holds. In this case, the stability of $E_2$ is not affected by the cost of fear, which is similar to the results we obtained from the previous Sect. 3. In other words, the stability of the co-existence equilibrium will not change if the birth rate of prey is not large enough to support oscillations no matter how sensitive prey are to predation risks. However, in contrast to the results of model with linear functional response (3.1), for the model with the Holling type II functional response (4.2), conditions in (4.20) imply that the stability of $E_2$ is affected by the level of anti-predator defence. Conditions in (4.20) indicate that when the birth rate of prey is large enough, prey and predators still tend to a steady state if prey are sensitive enough to perceive potential attacking by predators and show anti-predation behaviours accordingly but lose stability if not. It is well-known that the classic predator-prey model without the cost of fear but with the Holling type II functional response admits the occurrence of Hopf bifurcation when the carrying capacity of prey is large enough. The phenomenon ‘paradox of enrichment’ (McAllister et al. 1972; Riebesell 1974; Rosenzweig 1971; Gilpin and Rosenzweig 1972) appears as a consequence. However, as discussed above, incorporating the cost of fear into predator–prey models can rule out such phenomenon ‘paradox of enrichment’ by choosing large enough k.

4.2 Global stability of positive equilibrium

In the above section, we have shown that $E_2$ is locally asymptotically stable if (4.13) or (4.14) holds. The following theorem confirms that $E_2$ is globally symptomatically stable under (4.13) and another condition.

Theorem 4.4

The positive equilibrium $E_2$ is globally asymptotically stable if

$$\begin{aligned} a_5-a_1<a_2 \le 2\,a_5 \quad \,\,\,\text{ and }\quad \,\,\, 1 \le a_2+a_4. \end{aligned}$$

(4.21)

Proof

Denote the right-hand sides of system (4.8) by $P(u,v),\,Q(u,v)$ respectively. Take the following function as a Dulac function: $B(u,v)=u^{-1}\,v^{\beta }$ where $\beta$ is to be specified later. Then the divergence of the vector is

$$\begin{aligned} D= & {} \frac{\partial (P(u,v)\,B(u,v))}{\partial u}+\frac{\partial (Q(u,v)\,B(u,v))}{\partial v}\nonumber \\= & {} u^{-1}\,v^{\beta }\left( f_1(u)\,v+f_2(u)\right) , \end{aligned}$$

(4.22)

where

$$\begin{aligned} f_1(u,\beta )= & {} -2\,a_5\,u^2+u\,(2+\beta -a_4)-(\beta +2), \nonumber \\ f_2(u,\beta )= & {} -2\,a_5\,u^2+u\,(a_2+\beta +1)-(\beta +1). \end{aligned}$$

(4.23)

By (4.23) and (4.21), we have

$$\begin{aligned} f_1(u,\beta )=f_2(u,\beta )+\left( u(1-a_4-a_2)-1\right) \le f_2(u,\beta ) \end{aligned}$$

(4.24)

for u in $[0,\infty )$. Thus, we have $D \le 0$ for $(u,v) \in \mathbb {R}^2_+$ if

$$\begin{aligned} f_2(u,\beta ) \le 0,\;\;\mathrm{for}\;\; u \;\;\in [0, \infty ). \end{aligned}$$

(4.25)

Therefore, it suffices to find a $\beta$ such that (4.25) holds. Because $a_5>0,$ (4.25) is satisfied if

$$\begin{aligned} \Delta (\beta )=(a_2+\beta +1)^2-8\,a_5\,(\beta +1) \le 0 \end{aligned}$$

(4.26)

holds. For convenience, let $\beta +1=\overline{\beta }.$ Then (4.26) becomes

$$\begin{aligned} \overline{\Delta }(\overline{\beta })=\overline{\beta }^2+2\,(a_2-4\,a_5)\overline{\beta }+a_2^2 \le 0. \end{aligned}$$

(4.27)

The existence of $\overline{\beta }$ satisfying (4.27) is implied by $\overline{\Delta } (4a_5-a_2) \le 0$ which is equivalent to

$$\begin{aligned} a_5\,(2\,a_5-a_2) \ge 0. \end{aligned}$$

(4.28)

But this is ensured by the first inequality in (4.21). Thus, under (4.21), there exists $\beta$ such that $D \le 0$ for $(u,v) \in \mathbb {R}^2_+$, and by the well-known Dulac–Bendixson theorem (Perko 1996, Theorem 2, p 265), $E_2$ is globally asymptotically stable. $\square$

4.3 Existence of limit cycles and Hopf bifurcation

In the above section, we have shown that there is no limit cycle if (4.21) holds. Now we show that there exists a limit cycle if (4.15) is satisfied.

Theorem 4.5

There exists a limit cycle if (4.15) holds.

Proof

By (4.15) and Theorem 4.3, $E_2=(1,\overline{v}_2)$ is unstable and $E_1=(\overline{u}_1,0)$ is a saddle point. Note that by (4.15) we have

$$\begin{aligned} \bar{u}_1= \frac{a_2+\sqrt{a_2^2+4a_1 a_5}}{2a_5}>1. \end{aligned}$$

Let $L_1=u-\overline{u}_1.$ Then

$$\begin{aligned} \frac{du}{dt}\Big |_{L_1=0}=\overline{u}_1(-a_3\,v-a_4\,\overline{u}_1\,v -a_6\,v^2-a_5\,\overline{u}_1^2\,v) <0, \end{aligned}$$

(4.29)

since $a_3,\,a_4,\,a_5,\,a_6$ are all positive.

Next, let $L_2=v-\lambda$ with $\lambda >0$ to be specified later. By calculations, we obtain

$$\begin{aligned} \frac{dL_2}{dt}\Bigg |_{L_2=0}= & {} \frac{dv}{dt}\Bigg |_{v=\lambda }\nonumber \\= & {} \lambda \,(u-1)\,(1+\lambda )<0, \,\,\,\text{ for }\,\,\, u \in (0,1). \end{aligned}$$

(4.30)

Moreover, let

$$\begin{aligned} L_3=2\,(\overline{u}_1-1)(v-\lambda )+\lambda \,(u-1). \end{aligned}$$

(4.31)

Calculations give

$$\begin{aligned} \frac{dL_3}{dt}\Bigg |_{L_3=0}= & {} 2\,(\overline{u}_1-1)\frac{dv}{dt}+\lambda \,\frac{du}{dt}\nonumber \\= & {} 2\,(\overline{u}_1-1)v\,(u-1)\,(1+v)\nonumber \\&+\lambda \,u\,(a_1+a_2\,u-a_3\,v-a_4\,u\,v-a_5\,u^2-a_6\,v^2-a_5\,u^2\,v)\nonumber \\&\le -\frac{a_6\,u}{4}\,\lambda ^3+\lambda ^2\,\left( 2\,(\overline{u}_1-1)^2-\frac{u}{2}\,(a_3+a_4\,u+a_5\,u^2)\right) \nonumber \\&+\lambda \,((a_1+a_2\,u -a_5\,u^2)u+2\,(\overline{u}_1-1)^2). \end{aligned}$$

(4.32)

Because $a_6>0$ and $0<u<\overline{u}_1$, it follows from (4.32) that $dL_3/dt<0$ for sufficiently large $\lambda >0$.

By Poincaré–Bendixson theorem (Meiss 2007, Theorem 6.12), there exists a limit cycle if (4.15) holds. $\square$

From the above analysis, we see that when (4.15) holds, the positive equilibrium $E_2$ becomes unstable and a limit cycle comes into existence. Such a limit cycle is a result of Hopf bifurcation. Indeed, from the proof of Theorem 4.3, we see that $E_2$ loses its stability and Hopf bifurcation occurs when ${{\mathrm{tr}}}(J^{*})=J_{11}$ in (4.17) changes sign from negative to positive. Thus, ${{\mathrm{tr}}}(J^{*})=J_{11}=0$ gives the condition for Hopf bifurcation. Making use of (4.11), the formula for $J_{11}$ in (4.17) can be simplified to

$$\begin{aligned} J_{11}= -(a_4+2a_5) \bar{v}_2 +a_2- 2 a_5. \end{aligned}$$

(4.33)

Therefore, sign change of $J_{11}$ from negative to positive is actually equivalent to switch from condition (4.14) to condition (4.15) implying that the limit cycle arises from a Hopf bifurcation.

Next, we deal with the direction of Hopf bifurcation, intending to understand the impact of the fear effect on the Hopf bifurcation and its direction in terms of the fear effect parameter k. We first have the following general theorem on the bifurcation direction.

Theorem 4.6

Let

$$\begin{aligned} \sigma:= & {} -8\,a_5\,(a_2-2\,a_5)^2\,a_6^2-(a_4+2\,a_5)\,(-a_4+6\,a_4\,a_5-2\,a_5+8\,a_3\,a_5+4\,a_5^2)\nonumber \\&\quad \,(a_2-2\,a5)\,a_6-a_5\,(a_4+2\,a_5)^2\,(2\,a_3+a_4)\,(a_3+a_4+a_5). \end{aligned}$$

(4.34)

Then, the Hopf bifurcation is supercritical if $\sigma <0$ and it is subcritical if $\sigma >0.$

Proof

Let $x=u-1,y=v-\overline{v}_2.$ Then system (4.8) becomes

$$\begin{aligned} \frac{dx}{dt}= & {} J_{11}\,x+J_{12}\,y+f_1(x,y),\nonumber \\ \frac{dy}{dt}= & {} J_{21}\,x+J_{22}\,y+f_2(x,y), \end{aligned}$$

(4.35)

where $J_{11},J_{12},J_{21},J_{22}$ are shown in (4.17) and $f_i(x,y)$ for $i=1,2$ represent higher order terms of x, y. We have seen in the above that the Hopf bifurcation occurs when $J_{11}=0$, or equivalently

$$\begin{aligned} \overline{v}_2=\frac{a_2-2\,a_5}{a_4+2\,a_5}. \end{aligned}$$

(4.36)

Moreover, by the transformation

$$\begin{aligned} X=x,Y=J_{11}\,x+J_{12}\,y=J_{12}\,y \end{aligned}$$

and noting that $J_{22}=0$, system (4.35) is further transformed to

$$\begin{aligned} \frac{dX}{dt}= & {} Y+f_1\left( X,\frac{Y}{J_{12}}\right) ,\nonumber \\ \frac{dY}{dt}= & {} J_{12}\,J_{21}X+J_{12}\,f_2\left( X,\frac{Y}{J_{12}}\right) . \end{aligned}$$

(4.37)

Let

$$\begin{aligned} \gamma =-J_{12}\,J_{21}>0,\overline{X}=-X,\overline{Y}=Y/\sqrt{\gamma }. \end{aligned}$$

Then system (4.37) becomes

$$\begin{aligned} \frac{d\overline{X}}{dt}= & {} -\sqrt{\gamma }\,\overline{Y}-f_1\left( -\overline{X},\frac{\sqrt{\gamma }}{J_{12}}\,\overline{Y}\right) ,\nonumber \\ \frac{d\overline{Y}}{dt}= & {} \sqrt{\gamma }\,\overline{X}+\frac{J_{12}}{\sqrt{\gamma }}\, f_2\left( -\overline{X},\frac{\sqrt{\gamma }}{J_{12}}\,\overline{Y}\right) . \end{aligned}$$

(4.38)

Now the Jacobian matrix of (4.38) at (0, 0) is of the Jordan Canonical form

$$\begin{aligned} \left[ \begin{array}{cc} 0&{}-\sqrt{\gamma }\\ \sqrt{\gamma }&{}0\\ \end{array} \right] . \end{aligned}$$

(4.39)

Define $F_1$ and $F_2$ by

$$\begin{aligned} F_1(\overline{X},\overline{Y})= & {} -f_1\left( -\overline{X},\frac{\sqrt{\gamma }\,\overline{Y}}{J_{12}}\right) ,\\ F_2(\overline{X},\overline{Y})= & {} \frac{J_{12}}{\sqrt{\gamma }}\,f_2\left( -\overline{X},\frac{\sqrt{\gamma }\,\overline{Y}}{J_{12}}\right) . \end{aligned}$$

Then the direction of Hopf bifurcation is determined by the sign of the quantity

$$\begin{aligned} \sigma ^*:= & {} \frac{1}{16}\left( \frac{\partial ^3F_1}{\partial \overline{X}^3}+\frac{\partial ^3F_1}{\partial \overline{X} \partial \overline{Y}^2}+\frac{\partial ^3 F_2}{\partial \overline{X}^2 \partial \overline{Y}}+\frac{\partial ^3 F_2}{\partial \overline{Y}^3}\right) \nonumber \\&+\,\frac{1}{16\omega }\bigg (\frac{\partial ^2F_1}{\partial \overline{X} \partial \overline{Y}}\left( \frac{\partial ^2 F_1}{\partial \overline{X}^2}+\frac{\partial ^2 F_1}{\partial \overline{Y}^2}\right) -\frac{\partial ^2 F_2}{\partial \overline{X} \partial \overline{Y}}\left( \frac{\partial ^2 F_2}{\partial \overline{X}^2}+\frac{\partial ^2 F_2}{\partial \overline{Y}^2}\right) \nonumber \\&-\,\frac{\partial ^2 F_1}{\partial \overline{X}^2}\frac{\partial ^2 F_2}{\partial \overline{X}^2}+\frac{\partial ^2 F_1}{\partial \overline{Y}^2}\frac{\partial ^2 F_2}{\partial \overline{Y}^2}\bigg ), \end{aligned}$$

(4.40)

where $\omega =\sqrt{\gamma }=\sqrt{-J_{12}\,J_{21}}.$ Using (4.36) and with the help of Maple software, $\sigma ^{*}$ is calculated and simplified to the formula given by $\sigma$ in (4.34). By Perko (1996) (Theorem 1 on page 34), Hopf bifurcation is supercritical if $\sigma <0$ and it is subcritical if $\sigma >0$. $\square$

In order to analyze how the fear affects the direction of Hopf bifurcation, we may choose k as a bifurcation parameter. By (4.9), it is clear that only $a_3$ and $a_6$ depend on the parameter k. Letting $h=d/m$, we see that

$$\begin{aligned} a_3=a_6+h. \end{aligned}$$

(4.41)

By $a_6=\frac{p}{m}\, \frac{1}{k}$, we can equivalently take $a_6$ (instead of k) as the bifurcation parameter in the re-scaled model (4.8). By using (4.41), (4.36) can be simplified to

$$\begin{aligned} a_6=\frac{(a_4+2\,a_5)(a_4\,a_5+a_4\,a_1+a_5\,a_2+2\,a_5\,a_1+2\,a_5\,h-h\,a_2)}{(a_2+a_4)(a_2-2\,a_5)}=:a_6^*\qquad \end{aligned}$$

(4.42)

an equation with the right hand side independent of k, giving the critical value of $a_6$ for Hopf bifurcation.

Regarding $a_6$ as a bifurcation parameter which is chosen at the critical value $a_6^*$, $\sigma$ in (4.34) can be expressed, in terms of $a_1$ as a quadratic function, as

$$\begin{aligned} \sigma _0=A_1\,a_1^2+A_2\,a_1+A_3, \end{aligned}$$

(4.43)

the sign of which determines the direction of Hopf bifurcation. In (4.43), we have

$$\begin{aligned} A_1= & {} -2\,a_5\,(a_4+2\,a_5)^2\,(2\,a_2-2\,a_5+a_4)^2,\nonumber \\ A_2= & {} -(a_4+2\,a_5)\,(B_{1}\,h+B_{2}),A_3=D_1\,h^2+D_2\,h+D_3, \end{aligned}$$

(4.44)

where

$$\begin{aligned} B_{1}= & {} -4\,a_5\,(-2\,a_5+a_2)^2\,(2\,a_2-2\,a_5+a_4),\nonumber \\ B_{2}= & {} (a_2+a_4)(-2\,a_5\,a_2^2+6\,a_4\,a_5\,a_2^2+20\,a_2^2\,a_5^2-a_2^2\,a_4-44\,a_5^3\,a_2+3\,a_2\,a_5\,a_4^2\nonumber \\&+\,4\,a_4\,a_2\,a_5+8\,a_5^2\,a_2-8\,a_4\,a_5^3-2\,a_4^2\,a_5^2-4\,a_4\,a_5^2-8\,a_5^3+24\,a_5^4),\nonumber \\ D_1= & {} -2\,a_5\,(-2\,a_5+a_2)^4,\nonumber \\ D_2= & {} (a_2-2\,a_5)^2\,(a_2+a_4)\,(-a_4\,a_2+3\,a_4\,a_2\,a_5+10\,a_5^2\,a_2-2\,a_5\,a_2\nonumber \\&-2\,a_4\,a_5^2+4\,a_5^2-12\,a_5^3+2\,a_4\,a_5),\nonumber \\ D_3= & {} -a_5\,(a_2+a_4)^2\,(a_4^2\,a_2^2+12\,a_2^2\,a_5^2-2\,a_5\,a_2^2+7\,a_4\,a_5\,a_2^2-a_2^2\,a_4-12\,a_2\,a_4\,a_5^2\nonumber \\&-a_2\,a_5\,a_4^2-28\,a_5^3\,a_2+8\,a_5^2\,a_2+4\,a_4\,a_2\,a_5-8\,a_5^3+4\,a_4\,a_5^3-4\,a_4\,a_5^2+16\,a_5^4).\nonumber \\ \end{aligned}$$

(4.45)

From (4.44), it is clear that $A_1<0$ because $a_5>0.$ Let $\Delta =A_2^2-4\,A_1\,A_3.$ Mathematical analysis show that $A_2,\,A_3$ and $\Delta$ can be positive or negative under different conditions. Numerical simulations show that all reasonable combinations of $A_2,A_3,\Delta$ are possible (see Figs. 1, 2, 3).

Fig. 1

$A_1<0,A_2<0,A_3<0,\Delta >0$ and $A_1<0,A_2<0,A_3<0,\Delta <0$. Parameters are: $a_2=9.0639,a_4=8.8393,a_5=4.4733,h=0.8866$ and $a_2=8.7964,a_4=3.82,a_5=1.4757, h=1.3037$ respectively

Fig. 2

$A_1<0,A_2>0,A_3<0,\Delta <0$ and $A_1<0,A_2<0,A_3>0,\Delta >0.$ Parameters are: $a_2=3.9703,a_4=7.6983,a_5=0.0715,h=35.7226$ and $a_2=6.9741, a_4=0.1337, a_5=0.1194, h=0.0032$ respectively

Fig. 3

$A_1<0,A_2>0,A_3>0,\Delta >0$ and $A_1<0,A_2>0,A_3<0,\Delta >0.$ Parameters are: $a_2=8.0115,a_4=0.2414,a_5=0.0256,h=0.0131$ and $a_2=7.1134,a_4=7.3037,a_5=0.0436, h=0.7421$ respectively

Notice that $A_1,\,A_2,\,A_3,\,\Delta$ are all expressions of $a_2,\,a_4,\,a_5,\,h.$ Then, by taking different values of $a_1$, $\sigma _0$ can be positive or negative. Let

$$\begin{aligned} a_1^{+}=\frac{1}{2}\frac{\left( a_4+\sqrt{a_4^2-4\,a_5\,h}\right) (a_2+a_4)}{a_5}-h, \end{aligned}$$

(4.46)

and

$$\begin{aligned} a_1^{-}=-\frac{1}{2}\frac{\left( -a_4+\sqrt{a_4^2-4\,a_5\,h}\right) (a_2+a_4)}{a_5}-h. \end{aligned}$$

(4.47)

By using $a_1^+$ and $a_1^-$, the possibilities of the direction of Hopf bifurcation are summarized in Table 1, which shows that the direction of Hopf bifurcation can be supercritical or subcritical depending on different combinations of $a_1,a_2,a_4,a_5,h.$

Table 1 Direction of Hopf bifurcation by taking $a_6$ as a bifurcation parameter

Fig. 4

Available region of Hopf bifurcation on $r_0,\,q$ plane. Parameters are: $a=0.01,p=0.5, c=0.4,m=0.05,d=0.01$

Fig. 5

Different patterns for prey and predators. Parameters for a are: $r_0=0.03,k=0.1, d=0.01, a=0.01, p=0.5, q=0.1, m=0.05, c=0.4.$ Parameters for b are: $r_0=0.05,k=10, d=0.01, a=0.01, p=0.5, q=0.6, m=0.05,c=0.4$. a Global stable positive equilibrium. b Stable limit cycle

5 Numerical simulations

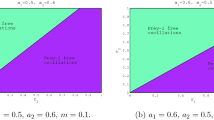
In order to better explore the role that the cost of fear plays in our predator–prey model, we conducted a series of numeric simulations for model (4.2) with parameters in their original scales. In Fig. 4, the solid curve represents the critical curve which determines the Hopf bifurcation without the fear effect (i.e. $k=0$) by setting $r_0$ and q as free parameters. Figure 4 shows that the model incorporating the cost of fear requires larger $r_0$ to admit the existence of Hopf bifurcation, compared to the models without it. From a biological point of view, the cost of fear in prey requires higher compensation for the prey’s birth rate to support periodic oscillations in prey and predator populations. As indicated in Fig. 5a, the population of the prey and predator tend toward a globally stable steady state if $r_0$ and q are located in the region between the dashed curve and the solid curve in Fig. 4. In this case, no matter how sensitive the prey is to predation risk, periodic oscillations can not occur. Figure 5b shows that the populations of prey and predator oscillate periodically due to supercritical Hopf bifurcation if the parameters are chosen in the region between the solid line and the dotted line in Fig. 4. In Fig. 4, by choosing $q=0.6,$ we can obtain a vertical line which intersects with the solid line and the dotted line when increasing the value of $r_0$. This indicates that increasing $r_0$ or equivalently increasing k may lead to change of directions of Hopf bifurcation from forward to backward. Figure 6 is a subcritical Hopf bifurcation diagram plotted using Matcont software (Dhooge et al. 2003, 2008). As shown in Fig. 6, taking k as a bifurcation parameter, there are two branches for the period of oscillation where the lower one corresponds to an unstable limit cycle and the upper one accounts for a stable limit cycle. Biologically, increasing the level of the fear effect in prey may induce a transition from the state where the populations of the prey and predator oscillate periodically to a bi-stability situation. When bi-stability happens, multiple limit cycles occur, as shown in Fig. 7. In this scenario, the eventual pattern for prey and predators depend on their initial population sizes. Prey and predators tend to a steady state if initial populations are relatively small and stay inside the unstable limit cycle. The populations of prey and predators oscillate periodically if initial populations are relatively large and locate outside the unstable limit cycle. Figure 8 shows the relationship between $(k,\,q)$ and $(k,\,r_0)$ along the critical line determining Hopf bifurcation. Figure 8b indicates that when increasing the value of the prey’s birth rate, lower levels of fear are required to obtain Hopf bifurcation no matter how the handling time of food by predators varies. Biologically, this implies that with a higher birth rate, the prey becomes less sensitive in perceiving predation risk.

Fig. 6

Bifurcation diagram for subcritical Hopf bifurcation. Parameters are: $r_0=2.671,d=0.0246,a=0.0004,p=0.0673,q=0.0058,c=0.0952,m=0.0505$

Fig. 7

Subcritical Hopf bifurcation/bi-stability. Parameters are: $r_0=0.12,k=60,d=0.01,a=0.01,p=0.5, q=0.6,m=0.05,c=0.4$

Fig. 8

Two dimensional projection of Hopf bifurcation curve when $k \ne 0$ into k, q and $k,r_0$ respectively. a k, q along Hopf bifurcation curve. b $k,r_0$ along Hopf bifurcation curve

Fig. 9

Available region of Hopf bifurcation on $r_0,\,p$ plane. Parameters are: $q=0.5,c=0.5,m=0.1,d=0.05,a=0.01$

Fig. 10

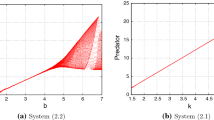
Two dimensional projection of Hopf bifurcation curve when $k \ne 0$ into $p-k$ plane and $r_0-k$ plane respectively, with the parameter values given in Fig. 9. a k, p along Hopf bifurcation curve. b $k,r_0$ along Hopf bifurcation curve

Similarly, Fig. 9 again shows that as fear effects become more extreme, it can induce a change in the direction of Hopf bifurcation, from supercritical to subcritical by holding p fixed at some point. The difference between Figs. 4 and 9 lies in that p needs to be large enough to support subcritical bifurcation whereas q has to be in an intermediate interval. Biologically, the attack rate by predators needs to be large enough to instill fear in prey; otherwise, fear will not affect dynamical behaviours of predator–prey systems and bi-stability can not happen. Figure 10a shows that prey are more willing to show anti-predator behaviours when the attack rate of predators increases and Fig. 10b again confirms that the prey show weaker anti-predator behaviours when the prey’s birth rate is greater, regardless of the change in the predators’ attack rate.

Another interesting observation is that the natural death rate of predators m needs to be relatively small in order for the model to permit a subcritical Hopf bifurcation, as indicated in Fig. 11. Biologically, a relatively high density of predators is required to evoke anti-predator defenses in prey that carry costs large enough to affect prey populations. The cost of fear can not be observed if the population of predators drops too quickly whereby cues signifying predation risk are low, as will be the anti-predator responses of prey (Fig. 12).

We also apply different functions in modelling the cost of fear when conducting simulations. Particularly, we test the following two functions

$$\begin{aligned} f(v)=e^{-k\,v}, \end{aligned}$$

(5.1)

and

$$\begin{aligned} f(v)=\frac{1}{1+k_1\,v+k_2\,v^2}. \end{aligned}$$

(5.2)

Both functions (5.1) and (5.2) are decreasing functions with respect to v, but with different decreasing rates, compared with (4.1). Our simulation results for Hopf bifurcation and its direction are qualitatively unchanged with either (5.1) or (5.2), which implies that our results are applicable for general monotone decreasing function of v. Moreover, for (5.2), we also obtain a relationship between $k_1$ and $k_2$ along the Hopf bifurcation curve as demonstrated in Fig. 13 indicating that $k_2$ is indeed linearly decreasing with $k_1$ on the Hopf bifurcation.

Fig. 11

Available region of Hopf bifurcation on $r_0,\,m$ plane. Parameters are: $q=0.5,p=0.5,c=0.6,a=0.01,d=0.05$

Fig. 12

Two dimensional projection of Hopf bifurcation curve when $k \ne 0$ into $m-k$ plane and $r_0-k$ plane respectively, with the parameter values given in Fig. 11. a k, m along Hopf bifurcation curve. b $k,r_0$ along Hopf bifurcation curve

Fig. 13

Relationship between $k_1$ and $k_2$ along the Hopf bifurcation line when taking fear function (5.2)

Fig. 14

The biomass for predators and prey from periodic solutions with varying k due to supercritical Hopf bifurcation. Parameters are: $r_0=2,d=0.2,a=0.04,p=0.4,q=0.2,c=0.3,m=0.1$

In the context of population control, if all solutions of (4.2) tend to a steady state eventually, then the fear effect will not affect the prey population over the long-term. However, under the same scenario, the predator’s eventual population will decrease when k increases (see 4.12). On the other hand, the populations of the prey and predator may oscillate periodically due to supercritical or subcritical Hopf bifurcation. In this case, Fig. 14 indicates that the biomass of prey and predators decrease with increasing k along periodic solutions due to supercritical Hopf bifurcation. Biologically, this implies that anti-predator behaviours of prey may impact their long-term overall growth rate, as a cost of fear. Moreover, Fig. 14 confirms the theoretical arguments that stronger levels of defence result in higher costs, which can decrease the prey’s long-term population size. Simulations are also conducted for biomass of prey and predators along periodic solutions with varying k due to subcritical Hopf bifurcation. Results for such a case are consistent with the former one where Hopf bifurcation is supercritical and is thus omitted.

6 Conclusions and discussions

In this paper, we have studied a predator–prey model that has incorporated the effect that the fear of predators have on prey with either the linear functional response or the Holling type II functional response. For the case with the linear functional response, mathematical results show that the cost of fear does not change dynamical behaviours of the model and a unique positive equilibrium is globally asymptotically stable when it exists.

However, for the model with the Holling type II functional response, the cost of fear affects predator–prey interactions in several ways. Analytical results show that there exists a globally stable positive equilibrium if the birth rate of prey is not large enough to support fluctuations. In this case, the populations of prey and predators tend to generate positive constants eventually, no matter how sensitive the prey is to potential dangers from predators. When the birth rate of prey is large enough to support oscillations, the positive equilibrium of the predator–prey system is locally asymptotically stable if the fear level is high. In this case, the cost of fear can stabilize the predator–prey system by ruling out periodic solutions. This offers a new mechanism to avoid the “paradox of enrichment” in ecosystems. Periodic solutions can still exist when the fear level is relatively low. Conditions for existence of Hopf bifurcation and conditions determining the direction of Hopf bifurcation are obtained, which indicate that the cost of fear will not only affect the existence of Hopf bifurcation but also change the direction of Hopf bifurcation. Indeed, we have shown that Hopf bifurcation in the model incorporating the cost of fear can be both supercritical and subcritical, which is in contrast to the classic predator–prey models that ignore the predation risk effects where Hopf bifurcation can only be supercritical.

Numerical simulations are conducted to show the potential role that fear effects can play in predator–prey interactions by releasing one or two more parameters free rather than the single k. Under conditions of Hopf bifurcation, increasing fear level may cause a change in the direction of Hopf bifurcation, from supercritical to subcritical, when the birth rate of prey increases accordingly. Fear generates rich dynamical behaviours including bi-stability, where the solutions tend to a steady state or oscillate periodically depending on the initial population size. Numerical simulations also show that the prey is less sensitive to perceived predation risk when the birth rate of prey is high, regardless of how other parameters change. Moreover, the prey would be more willing to show anti-predator defences when the attack (i.e. predation) rate is high, and would perceive fewer potential dangers as the death rate of predators increases. Simulations with different functions modelling the cost of fear indicate that the results we have obtained in this paper remain valid when other general monotone decreasing functions are adopted.

In our model formulation, we have assumed that the perceived predation risks only reduce the birth rate and survival of offspring, and have ignored the possible impact on the death rate of adult prey. Although Zanette et al. (2011) and Clinchy et al. (2013) argue that fear may increase the adult death rate due to long-term physiological impacts, there is still a lack of direct experimental evidence. For the same reason, we have only considered the case when fear does not affect intra-specific competition in our model, although there is also a theoretical argument in Cresswell (2011) that the fear effect may change the strength of intra-specific competition because of the complexity of food web. Once some experimental evidence becomes available, these should all be incorporated into the model, and such a model would be able shed more light on the prey–predator interactions.