Delay differential systems for tick population dynamics

Abstract

Ticks play a critical role as vectors in the transmission and spread of Lyme disease, an emerging infectious disease which can cause severe illness in humans or animals. To understand the transmission dynamics of Lyme disease and other tick-borne diseases, it is necessary to investigate the population dynamics of ticks. Here, we formulate a system of delay differential equations which models the stage structure of the tick population. Temperature can alter the length of time delays in each developmental stage, and so the time delays can vary geographically (and seasonally which we do not consider). We define the basic reproduction number ${\mathcal R}_0$ of stage structured tick populations. The tick population is uniformly persistent if ${\mathcal R}_0>1$ and dies out if ${\mathcal R}_0<1$. We present sufficient conditions under which the unique positive equilibrium point is globally asymptotically stable. In general, the positive equilibrium can be unstable and the system show oscillatory behavior. These oscillations are primarily due to negative feedback within the tick system, but can be enhanced by the time delays of the different developmental stages.

1 Introduction

Lyme disease is spread by ticks of the genus Ixodes which are infected with the bacterium Borrelia burgdorferi. If humans are bitten by an infectious tick, a characteristic skin rash, called erythema migrans, can appear. Other symptoms of infection can include tiredness, headache, and swollen lymph glands. Lyme disease can also affect the joints, heart, and nervous system. Severe human infection can lead to death.

Lyme disease has a wide distribution in the northern temperate regions of the world including the United States, Europe, and East Asia. Ticks of the genus Ixodes are the major vectors of Lyme disease, which normally feed on mice, deer, and other mammals. They can transmit the Borrelia burgdorferi bacteria to humans when they acquire blood meals from human beings. Usually, the tick nymphs are involved in the transmission of Lyme disease, which are most likely to feed on a person and are rarely noticed due to their small size (less than 2 mm).

The life cycle of most ticks has four main stages: egg, larva (or seed tick), nymph and adult. All main stages except the egg stage have at least three substages (or phases): questing, feeding and engorged ticks. The larval stage has an additional hardening phase and the adult stage an additional egg-laying phase.

To survive and pass from one stage to the next, one blood meal is required each time, i.e., to pass from the larval to the nymph stage, from the nymph to the adults stage, and to produce eggs for the adults.

The majority of ticks require three different hosts to complete their full life cycle; they will die before transition to the next stage if they do not find a suitable host for their next feeding.

The survival and development of ticks also depend on temperature and humidity, among other factors. According to Ogden et al. (2005), the continuing existence of tick populations and the establishment of new populations is constrained by biotic factors (host densities and habitats) and abiotic factors such as climate. Climate impacts tick survival mostly during non-parasitic periods of the life cycle. In general, the lower the temperature, the longer it takes the ticks to finish the development in a stage and the higher is the chance of dying during that stage.

Various works [Caraco et al. (2002); Ghosh and Pugliese (2004); Hartemink et al. (2008); Norman et al. (1999); Rosà et al. (2003); Zhao (2012)] have considered the impact of tick demographics on the transmission of tick-borne diseases. In order to keep the size of the model systems at bay, they typically have not considered all the stages and substages of ticks.

In 2005, Awerbuch-Friedlander et al. (2005) formulated a nonlinear system of difference equations that models the three-stage life cycle of the deer tick over four seasons. They studied the effect of seasonality on the stability and oscillatory behavior of the tick population by comparing analytically the seasonal model with a non-seasonal one. One of the main results of their work is that seasonality in the life cycle of deer ticks can increase the stability of the system.

There are also some works that classify tick development into twelve stages like Awerbuch and Sandberg (1995) and Ogden et al. (2005). Awerbuch et al. proposed a model of 12 monthly stage-structured matrices and use it to follow the annual changes in the tick population. They found that oscillations due to fluctuating environments are strongly affected by the magnitude of the eigenvalues. Thus both inherent and environmental oscillations determine patterns of tick population growth. In a non-fluctuating environment, tick population structure ultimately converges to a stable stage distribution regardless of whether the population thrives or declines.

Ogden et al. (2005) proposed a computational model (created by STELLA 7.0.3 for Windows software) with twelve sequential developmental stages of ticks. The model was developed to simulate effects of temperature on tick survival and seasonality. Temperature-dependent time delays were calculated from monthly normal temperature date. Temperature also influenced host-seeking success in the model. The model contains negative feed-back of tick density in the various feeding stages on stage survival and of tick density in the feeding adult stage on the later fecundity in the egg-laying stage.

The model simulations in (Ogden et al. 2005) predicted that the maximum equilibrium numbers of ticks were the lower the further north they were located, due to a steady increase in mortality of all life stages with decreasing temperature. A regression analysis provided theoretical limits for the establishment of I. scapularis in Canada. Maps of these limits suggested that the range of southeast Canada, where temperature conditions are currently suitable for the tick, is much wider than the existing distribution of I. scapularis. So there is potential for the tick population to move north.

Wu et al. (2013) adapted a model of 12 ordinary differential equations of the tick vector of Lyme disease, Ixodes scapularis, from the computational model in (Ogden et al. 2005). They used temperature normals smoothed by Fourier analysis to generate seasonal temperature-driven development rates and host biting rates. Using the spectral radius of a next generation operator on a suitable space of periodic functions, values were obtained for the basic reproduction number ${\mathcal R}_0$ for I. scapularis at locations in southern Canada where the tick has become established. ${\mathcal R}_0$ at Long Point, Point Pelee and Chatham sites, where I. scapularis is established, was estimated at 1.5, 3.19 and 3.65, respectively. The threshold temperature conditions for the survival of tick populations (${\mathcal R}_0=1$) were shown to be the same as those identified using the computational model in (Ogden et al. 2005) (2800 to 3100 cumulative annual degree days with reference temperature of $0$ degree Celsius).

By their very nature, the dynamics in the models in (Ogden et al. 2005; Wu et al. 2013) are oscillatory because of the seasonally varying developmental rates, and it is difficult to see whether the models are capable of self-sustained oscillations. Following (Ogden et al. 2005), we therefore consider a time-autonomous twelve-stage tick model with twelve developmental delays nine of which are discrete and three are exponentially distributed. The sum of those time delays roughly equals the the time required for ticks to finish their development which is usually two to three years. The lengths of the exponentially distributed delays depend on the availability of appropriate hosts. Our model focuses on the negative feed-back from feeding to egg-laying adults and ignores density-dependent per capita mortality rates in the feeding substages.

Because of this focus, our twelve-stage model has a closed submodel of five delay differential equations which is still too difficult to analyze and is therefore approximated by a system of three delay differential equations (Sect. 2). The approximate system is mathematically well-posed and has positive bounded solutions (Sects. 4 and 8).

The original system and the approximate system have the same positive equilibrium and the same basic reproduction number $\mathcal {R}_0$. We show for the approximate system that ${\mathcal R}_0$ has the familiar threshold properties. If ${\mathcal R}_0 < 1$, the tick population dies out while it persists (uniformly) if ${\mathcal R}_0 > 1$ (Sect. 5). We derive conditions for the local and global asymptotic stability of the positive equilibrium which state ${\mathcal R}_0 >1$ should be close enough to 1 (Sects. 5 and 9.2). We also find analytic evidence that, for certain feedback functions, the positive equilibrium can easily lose its stability indicating the existence of solutions exhibiting undamped oscillations. This stability loss occurs even if all discrete developmental delays are set to zero. This shows that the negative feed-back structure of the tick system is the primary cause of undamped oscillations which, however, can be enhanced by the discrete time delays.

For other feedback functions, however, the positive equilibrium is globally stable for all parameter values for which it exists. This is consistent with the simulation results of Ogden et al. [see (2005, Sec. 3)] where the solutions “came to a steady, cyclical equilibrium after approximately 10 years”. Recall that the model in (Ogden et al. 2005) is seasonally forced (with a 1 year period), so all equilibrium solutions are periodic except the extinction state.

From our analytic results, it is difficult to predict whether the dynamics of tick populations are more complex at warmer than at colder locations because lower temperatures increase time delays but decrease ${\mathcal R}_0$ which two effects seem to counteract each other when it comes to generate undamped oscillations.

We numerically compare the solutions of the original and the approximate system using the parameters from (Ogden et al. 2005) and find that they are not too different from each other qualitatively. Both our analytic and numerical results indicate that complex behavior of solutions does occur for certain feedback functions, but apparently not at parameter ranges that presently are realistic for tick populations.

2 The model

Following (Ogden et al. 2005), we consider four tick stages and twelve substages:

• one egg stage, $E$;

• four larval stages: hardening, $L_h$; questing, $L_q$; feeding, $L_f$; and engorged, $L_g$;

• three nymph stages: questing, $N_q$; feeding, $N_f$; and engorged, $N_g$;

• four adult stages: questing, $A_q$; feeding, $A_f$; engorged, $A_g$; and egg-laying, $A_e$.

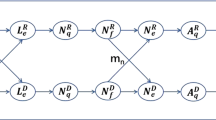
A diagram of the (sub)stages and the flows between them can be found in [Ogden et al. (2005), Fig. 1].

Fig. 1

Time evolution of total number of questing ticks for systems (2.2) (dotted line) and (2.6) (solid line). Fix $\gamma ^L=\gamma ^N=0.13$ and vary $\gamma ^A=0.003, 0.013, 0.03$ from the top to the bottom figure

For all stages except the questing stages, the length is determined by physiological development and they are rather the same for everyone in the stage than exponentially distributed. The lengths of the questing stages depend on the availability of appropriate hosts to feed on. The questing stages end and the feeding stages start when the tick happens to be picked up by or otherwise get attached to a suitable host. Therefore, the lengths of the questing stages are assumed to be exponentially distributed.

The model with equations for all stages is displayed in Table 1. A detailed list of the model parameters (together with their numerical values) can be found in Table 2.

Table 1 Model equations

Table 2 Parameter comparison in the model (3.3) and (Ogden et al. 2005)

The stage lengths are denoted by the letter $\tau$ labeled with superscripts and subscripts with superscripts E, L, N, A specifying “egg, larva, nymph and adult” and subscripts $h,q,f, g,e$ specifying “hardening, questing, feeding, engorged, egg-laying”. For instance, $\tau ^\mathrm{N}_g$ is the length of the stage in which nymphs are engorged.

Analogously, per capita death rates are denoted by the letter $d$ and labeled similarly. For instance, $d^\mathrm{A}_g$ is the per capita death rate of engorged adult ticks.

The time length $\tau ^\mathrm{A}_e$ does not only give the length of the egg-laying period but also the remaining length of life after entering the egg-laying stage.

The letter $\gamma$ denotes the per capita transition rates from the questing to the feeding phases with superscripts L, N, A again specifying the stage. So $\gamma ^A$ is the per capita transition rate from questing to feeding adults. These are compound rates that combine the questing activity rates with the availability of appropriate hosts.

In Table 1, $B(t)$ denotes the population recruitment rate at time $t$, in this case the overall rate at which eggs are being laid. We will specify later how $B$ depends on the dependent variables of the system. Differently from (Ogden et al. 2005), population recruitment will be the only process that we assume to be prone to nonlinear feedback from the other stages. In (Ogden et al. 2005), ticks in the feeding stages exert a negative feedback on themselves by inducing an immune reaction in the host that increases their mortality. Such instantaneous nonlinear self-feedbacks are not able to lead to undamped oscillations by themselves because they do not destroy the monotonicity of the dynamical system. They are neglected here, which will allow us to reduce the system to fewer equations.

2.1 The smallest closed subsystem

According to (Ogden et al. 2005), fertility of egg-laying adults is reduced by an immune reaction or resistance of the host which are triggered by the feeding adults that were feeding on the same host at the same time, i.e., a time $\tau ^\mathrm{A}_g$ ago. Hence

$$\begin{aligned} B(t)=\psi \big (A_f(t-\tau ^\mathrm{A}_g)\big ) A_e(t), \end{aligned}$$

(2.1)

with a decreasing function $\psi :{ \mathbb {R}}_+ \rightarrow { \mathbb {R}}_+$.

A closer look at Table 1 shows that several differential equations are decoupled from the rest of the system. For instance, the symbol $N_g$ that denotes the number of engorged nymphs only appears in the differential equation for $N_g$ but not in any of the other differential equations.

In the following system, together with (2.1), all decoupled equations have been removed, and it is the smallest mathematically closed subsystem of the model in Table 1,

$$\begin{aligned} \begin{aligned} L_q'(t)=&B(t-\tau ^\mathrm{E}-\tau ^\mathrm{L}_h) e^{-d^\mathrm{E} \, \tau ^\mathrm{E}- d^\mathrm{L}_h \tau ^\mathrm{L}_h} -\gamma ^\mathrm{L} L_q (t)-d^\mathrm{L}_q L_q(t),\\ N_q'(t)=&\gamma ^\mathrm{L} L_q (t-\tau ^\mathrm{L}_f-\tau ^\mathrm{L}_g) e^{-d^\mathrm{L}_f \tau ^\mathrm{L}_f-d^\mathrm{L}_g \tau ^\mathrm{L}_g} -\gamma ^\mathrm{N} N_q(t) - d^\mathrm{N}_q N_q(t),\\ A_q'(t)=&\gamma ^\mathrm{N} N_q(t-\tau ^\mathrm{N}_f-\tau ^\mathrm{N}_g ) e^{-d^\mathrm{N}_f \tau ^\mathrm{N}_f-d^\mathrm{N}_g \tau ^\mathrm{N}_g } -\gamma ^\mathrm{A} A_q(t) - d^\mathrm{A}_q A_q(t),\\ A_f' (t)=&\gamma ^\mathrm{A} A_q(t) -\gamma ^\mathrm{A} A_q(t-\tau ^\mathrm{A}_f) e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f } -d^\mathrm{A}_f A_f(t),\\ A_e'(t)=&\gamma ^\mathrm{A} A_q(t-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g) e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f-d^\mathrm{A}_g \tau ^\mathrm{A}_g}\\&- \gamma ^\mathrm{A} A_q(t-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g-\tau ^\mathrm{A}_e) e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f- d^\mathrm{A}_g \tau ^\mathrm{A}_g}\!. \end{aligned} \end{aligned}$$

(2.2)

2.2 A reduced approximate system

The nonlinearity (2.1) causes unusual analytic problems, similarly as in (Fan et al. 2014). Even boundedness of solutions will be hard to prove. These problems arise because $B$ depends on both $A_f$ and $A_e$ where these are even evaluated at different times.

So we make the following approximations which make $B$ depend only on one dependent variable, $A_q$, which is evaluated at the same time. The differential equations for $A_f$ and $A_e$ are solved by

$$\begin{aligned} \begin{aligned} A_f (t)=&\int _{t-\tau ^\mathrm{A}_f}^t \gamma ^\mathrm{A } A_q(s) e^{-d^\mathrm{A}_f (t-s)} ds,\\ A_e(t)=&e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f-d^\mathrm{A}_g \tau ^\mathrm{A}_g} \int _{t-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g-\tau ^\mathrm{A}_e}^{t-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g } \gamma ^\mathrm{A } A_q(s)ds. \end{aligned} \end{aligned}$$

(2.3)

We approximate the right hand sides of these equations by replacing $A_q(s)$ in the integrands by the value of $A_q$ at one of the integration limits,

$$\begin{aligned} \begin{aligned} A_f (t) \approx&\gamma ^\mathrm{A } A_q(t- \tau ^\mathrm{A}_f )\int _{t- \tau ^\mathrm{A}_f}^t e^{-d^\mathrm{A}_f (t-s)} ds,\\ A_e(t) \approx&e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f - d^\mathrm{A}_g \tau ^\mathrm{A}_g} \tau ^\mathrm{A}_e \gamma ^\mathrm{A } A_q(t- \tau ^\mathrm{A}_f -\tau ^\mathrm{A}_g) . \end{aligned} \end{aligned}$$

(2.4)

In the first approximation, we have chosen the lower integration limit and, in the second approximation, the upper integration limit. These choices have been made for obtaining the most convenient formulas in the model below.

The errors in these approximations are small if the integration intervals are short. So these approximations are justified if the stage lengths $\tau ^\mathrm{A}_f$ and $\tau ^\mathrm{A}_e$ are sufficiently short. In (Ogden et al. 2005), the length of the egg-laying adult stage $\tau ^\mathrm{A}_e$ is chosen to be about 1 day and the length of the feeding adult stage $\tau ^\mathrm{A}_f$ to be about 10 days. So the approximation of $A_e$ seems justified, the one for $A_f$ may be problematic. We simplify,

$$\begin{aligned} \begin{aligned} A_f (t) \approx&\gamma ^\mathrm{A } A_q(t- \tau ^\mathrm{A}_f ) \frac{1 - e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f}}{d^\mathrm{A}_f},\\ A_e(t) \approx&e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f - d^\mathrm{A}_g \tau ^\mathrm{A}_g} \tau ^\mathrm{A}_e \gamma ^\mathrm{A } A_q(t- \tau ^\mathrm{A}_f -\tau ^\mathrm{A}_g). \end{aligned} \end{aligned}$$

(2.5)

The first relation means that the number of feeding adults as a function of time $t$ is proportional to the number of questing adults at time $t - \tau ^A_f$ with $\tau ^A_f$ being the length of the feeding stage. The second relation means that the number of egg-laying adults as function of time $t$ is proportional to the number of questing adults at time $t - \tau ^A_f - \tau _g^A$, where the delay is the sum of the lengths of the feeding and engorged adult stages. With equal mathematical justification, we could also have chosen $t - \tau ^A_f - \tau _g^A - \tau _e^A$, but $\tau _e^A$ is just one day. Our choices are motivated by our ends, the upcoming system (2.6) with the nonlinearity (2.7).

We substitute these approximations into (2.2) using (2.1),

$$\begin{aligned} \begin{aligned} L_q'(t)=&F \big ( A_q (t - \tau ^\mathrm{E} - \tau ^\mathrm{L}_h - \tau ^\mathrm{A}_f -\tau ^\mathrm{A}_g)\big ) e^{-d^\mathrm{E} \tau ^\mathrm{E}- d^\mathrm{L}_h \tau ^\mathrm{L}_h -d^\mathrm{A}_f \tau ^\mathrm{A}_f - d^\mathrm{A}_g \tau ^\mathrm{A}_g}\\&- (\gamma ^\mathrm{L} +d^\mathrm{L}_q) L_q(t),\\ N_q'(t) =&\gamma ^\mathrm{L} L_q (t - \tau ^\mathrm{L}_f -\tau ^\mathrm{L}_g) e^{-d^\mathrm{L}_f \tau ^\mathrm{L}_f - d^\mathrm{L}_g \tau ^\mathrm{L}_g} - (\gamma ^\mathrm{N} + d^\mathrm{N}_q)N_q(t),\\ A_q'(t) =&\gamma ^\mathrm{N} N_q(t - \tau ^\mathrm{N}_f - \tau ^\mathrm{N}_g ) e^{-d^\mathrm{N}_f \tau ^\mathrm{N}_f - d^\mathrm{N}_g \tau ^\mathrm{N}_g } - (\gamma ^\mathrm{A} + d^\mathrm{A}_q) A_q(t), \end{aligned} \end{aligned}$$

(2.6)

with

$$\begin{aligned} F(A_q) = A_q \gamma ^\mathrm{A } \psi \Big ( A_q \gamma ^\mathrm{A } \frac{1 - e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f}}{d^\mathrm{A}_f}\Big ) \tau ^\mathrm{A}_e . \end{aligned}$$

(2.7)

To appreciate the new system, one should look back at (2.1). There the population recruitment rate depends on $A_f$ and $A_e$ evaluated at different times; now it only depends on $A_q$ evaluated at the same time.

Notice that (2.6) retains all the parameters of the original system; so, biologically, it models the tick system in all its detail though mathematically we only need to consider the questing substages.

The following delays have been chosen temperature dependent in (Ogden et al. 2005): $\tau ^E$, $\tau ^\mathrm{L}_g$, $\tau ^\mathrm{N}_g$, $\tau ^\mathrm{A}_g$. The delay $\tau ^\mathrm{A}_e$ has been chosen to be one day in the model in (Ogden et al. 2005) but is said to be temperature dependent in nature. The activity rates contained in $\gamma$ are also temperature dependent. Since our model is time-autonomous, it can only consider geographic but not seasonal temperature variations.

As announced before, we have ignored density dependence of the per capita mortalities in the feeding stages as it has been assumed in (Ogden et al. 2005). Such density dependence would make a reduction to three delay differential equations impossible.

The other dependent variables can be obtained by (2.3) and

$$\begin{aligned} E(t)&=\int _{t - \tau ^\mathrm{E}}^{t} B(s)e^{-d^\mathrm{E}(t-s)}ds,\nonumber \\ L_h(t)&=e^{-d^E\tau ^E}\int _{t - \tau ^\mathrm{E} - \tau ^\mathrm{L}_h}^{t - \tau ^\mathrm{E}} B(s)e^{-d_h^\mathrm{L}(t - \tau ^\mathrm{E}-s)}ds,\nonumber \\ L_f(t)&= \int _{t - \tau _f^\mathrm{L}}^{t}\gamma ^L L_q(s) e^{-d_f^\mathrm{L}(t-s)}ds,\nonumber \\ L_g(t)&=e^{-\tau _f^\mathrm{L}d_f^\mathrm{L}}\int _{t - \tau _f^\mathrm{L}- \tau _g^\mathrm{L}}^{t-\tau _f^L} \gamma ^L L_q(s) e^{-d_g^\mathrm{L}(t- \tau _f^L-s)}ds, \end{aligned}$$

(2.8)

and

$$\begin{aligned} N_f(t)&= \int _{t - \tau _f^\mathrm{N}}^{t}\gamma ^N N_q(s) e^{-d_f^\mathrm{N}(t-s)}ds,\nonumber \\ N_g(t)&=e^{-\tau _f^\mathrm{N}d_f^\mathrm{N}} \int _{t - \tau _f^\mathrm{N}- \tau _g^\mathrm{N}}^{t-\tau _f^\mathrm{N}}\gamma ^N N_q(s) e^{-d_g^\mathrm{N}(t- \tau _f^\mathrm{N}-s)}ds,\nonumber \\ A_g(t)&=e^{-\tau _f^\mathrm{A}d_f^\mathrm{A}}\int _{t - \tau _f^\mathrm{A}- \tau _g^\mathrm{A}}^{t-\tau _f^\mathrm{A}}\gamma ^A A_q(s) e^{-d_g^\mathrm{A}(t- \tau _f^\mathrm{A}-s)}ds. \end{aligned}$$

(2.9)

If one prefers to calculate these amounts via the delay differential equations, the integral equations in (2.3), (2.8), and (2.9) must be satisfied for the initial data at t = 0 (Busenberg and Cooke 1980). If the initial data are chosen in an arbitrary way, solutions can become negative. Notice that, once it has been shown that $L_q$, $N_q$ and $A_q$ are nonnegative (Theorem 4.1), also the other dependent variables given by (2.3), (2.8) and (2.9) have nonnegative values.

2.3 The negative feedback function

The function $\psi : { \mathbb {R}}_+ \rightarrow { \mathbb {R}}_+$ which expresses the negative feedback of feeding adults on the fertility of egg-laying adults is of particular importance. A natural property of $\psi$ is that it is (not necessarily strictly) decreasing. A possible choice is

$$\begin{aligned} \psi (s) = \beta e^{-\alpha s}, \qquad s \ge 0. \end{aligned}$$

(2.10)

Here $\beta >0$ is the per capita egg-laying rate of adults without any immune reaction of the hosts of adult ticks, and $\alpha >0$ scales the strength of the negative feedback. Such a form is chosen in (Rosà and Pugliese 2007) except that there all ticks rather than the feeding adult ticks are involved in the negative feedback. Another possible choice is

$$\begin{aligned} \psi (s) = \beta (1 + (\alpha s)^\xi )^{-\zeta }, \qquad s \ge 0, \end{aligned}$$

(2.11)

with $\xi , \zeta > 0$. Odgen et al. (2005)‘ suggest

$$\begin{aligned} \psi ( s) = \beta ( 0.99 - 0.04 \ln (1.01 + (s/D)), \qquad s \ge 0, \end{aligned}$$

(2.12)

where $D$ is the density of deer. This is a surprising choice for various reasons: First, (2.12) implies $\psi (0) < \beta$ while one expects equality. So it should be

$$\begin{aligned} \psi ( s) = \beta [ 1 - 0.04 \ln (1 + (s/D))], \qquad s \ge 0. \end{aligned}$$

(2.13)

A more serious issue is that $\psi$ becomes negative for large $s$. Actually, it is assumed in (Ogden et al. 2005) that fertility is reduced to at most half its maximum, i.e., $\psi (s)/\beta \ge 0.5$ for all $s \ge 0$, which (2.12) only meets for a restricted range of the independent variable $s$. To model such a limited fertility reduction, we make the ansatz

$$\begin{aligned} \psi ( s/\alpha )/\beta = \frac{ 1 + p \phi ( s)}{1 + \phi ( s)}=: \psi _0(s). \end{aligned}$$

(2.14)

Here $\phi$ is an increasing function with $\phi (0)=0$ and $\phi (s) \rightarrow \infty$ as $s \rightarrow \infty$. Then $\psi _0(s) \rightarrow p$ as $s \rightarrow \infty$ where $p$ is the maximum fraction to which the fertility is supposed to be reduced. Notice that

$$\begin{aligned} \psi _0(s) = \frac{1 - (1-p) \phi (s) - p \phi ^2(s)}{1 - \phi ^2(s)}. \end{aligned}$$

This expression is approximated for small $s$ by

$$\begin{aligned} 1 - (1-p) \phi (s), \end{aligned}$$

which is of the form of (2.13) with $\phi (s) = a \ln (1+s)$.

Notice that the function $F$ in (2.7) associated with $\psi$ in (2.14) is unbounded if $p>0$.

To summarize, a mathematically sound choice having some of the desired features in (Ogden et al. 2005) would be

$$\begin{aligned} \psi _0(s) = \frac{ 1 + p a \ln (1+ s)}{1 + a \ln (1+ s)}, \qquad s \ge 0. \end{aligned}$$

(2.15)

3 A lean formulation for analyzing the approximate model

We let $y_1 = L_q$, $y_2 = N_q$, and $y_3= A_q$ be the amount of questing larvae, nymphs, and adults. Then model (2.6) can be rewritten as

$$\begin{aligned} y_1'(t) =&\gamma _3p_3F ( y_3 (t - \tau _3)) - \eta _1 y_1(t),\nonumber \\ y_2'(t) =&\gamma _1p_1y_1(t - \tau _1) - \eta _2 y_2(t),\nonumber \\ y_3'(t) =&\gamma _2p_2y_2(t- \tau _2) - \eta _3 y_3(t). \end{aligned}$$

(3.1)

The egg-laying function (2.7) becomes

$$\begin{aligned} F(y_3)=y_3 \psi (\kappa y_3) \tau _e^\mathrm{A} \quad \mathrm {and}\quad \kappa =\gamma ^\mathrm{A} \frac{1 - e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f}}{d^\mathrm{A}_f} . \end{aligned}$$

(3.2)

Further

$$\begin{aligned} \gamma _1 = \gamma ^\mathrm{L} ,\quad \gamma _2 = \gamma ^\mathrm{N} ,\quad \gamma _3 = \gamma ^\mathrm{A} \end{aligned}$$

are the per capita transition rates from the larval, nymph, and adult questing stages into the respective feeding stages. The parameters

$$\begin{aligned} \eta _1 = \gamma _1 + d^\mathrm{L}_q, \quad \eta _2 = \gamma _2 + d^\mathrm{N}_q, \quad \eta _3 = \gamma _3 + d^\mathrm{A}_q \end{aligned}$$

are the per capita exit rates from the larval, nymph, and adult questing stages. The parameters $p_j$ are defined by

$$\begin{aligned} p_1 = e^{-d^\mathrm{L}_f \tau ^\mathrm{L}_f - d^\mathrm{L}_g \tau ^\mathrm{L}_g}, \quad p_2 = e^{-d^\mathrm{N}_f \tau ^\mathrm{N}_f - d^\mathrm{N}_g \tau ^\mathrm{N}_g}, \quad p_3 = e^{-d^\mathrm{E} \tau ^\mathrm{E}- d^\mathrm{L}_h \tau ^\mathrm{L}_h -d^\mathrm{A}_f \tau ^\mathrm{A}_f - d^\mathrm{A}_g \tau ^\mathrm{A}_g}. \end{aligned}$$

Here $p_1$ is the probability of surviving the feeding and engorged larval stages, $p_2$ is the probability of surviving the feeding and engorged nymph stages, and $p_3$ is the probability of surviving the feeding and engorged adult stages and the egg stage and the hardening larval stage.

The delays are given by

$$\begin{aligned} \tau _1 = \tau ^\mathrm{L}_f +\tau ^\mathrm{L}_g, \quad \tau _2 = \tau ^\mathrm{N}_f +\tau ^\mathrm{N}_g, \quad \tau _3 = \tau ^\mathrm{E} + \tau ^\mathrm{L}_h + \tau ^\mathrm{A}_f +\tau ^\mathrm{A}_g. \end{aligned}$$

Notice that the parameters $p_j$ and $\tau _j$ are not independent of each other. For example, $p_1$ and $\tau _1$ both depend on the delays $\tau _f^\mathrm{L}$ and $\tau _g^\mathrm{L}$.

We set $x_j= \kappa y_j$ and the model (3.1) becomes

$$\begin{aligned} \begin{aligned} x_1'(t) =&\gamma _3p_3 G(x_3(t-\tau _3))-\eta _1 x_1(t),\\ x_2'(t) =&\gamma _1p_1 x_1(t-\tau _1)-\eta _2 x_2(t),\\ x_3'(t) =&\gamma _2p_2 x_2(t-\tau _2)-\eta _3 x_3(t). \end{aligned} \end{aligned}$$

(3.3)

with

$$\begin{aligned} G(s) = s \psi (s) \tau _e^\mathrm{A}. \end{aligned}$$

(3.4)

Similarly, any other parameters sitting in the argument of $\psi$ can be scaled out. So, as for examples, we can restrict ourselves to

$$\begin{aligned} \psi (s) = \beta e^{-s} \end{aligned}$$

(3.5)

or

$$\begin{aligned} \psi (s) = \frac{\beta }{1 + s^\alpha }, \qquad \end{aligned}$$

(3.6)

with $\alpha > 0$, or to

$$\begin{aligned} \psi (s) = \beta \frac{ 1 + p a \ln (1+ s)}{1 + a \ln (1+ s)} \end{aligned}$$

(3.7)

with $a >0$ and $0 \le p <1$.

Here $\beta$ is the egg-laying rate of an adult tick and $\beta \tau ^\mathrm{A}_e$ is the average total amount of eggs a typical adult tick lays under optimal conditions.

We assume nonnegative continuous initial data for $\theta \in [-\tau , 0]$ as follows:

$$\begin{aligned} \begin{aligned}&x_j(\theta )=x_{j0}(\theta )\ge 0,\quad \theta \in [-\tau _j,0], \qquad j =1,2,3, \end{aligned} \end{aligned}$$

(3.8)

with at least one of them being not identically equal to zero.

Otherwise, the tick population will remain to be zero forever.

4 Positivity and boundedness of solutions

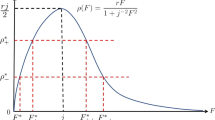
Define the reproduction number of ticks at (scaled) level $s$ of questing adults as

$$\begin{aligned} \mathcal {R}(s)=\tau _e^\mathrm{A}\psi (s)\frac{\gamma _1}{\eta _1}p_1 \frac{\gamma _2}{\eta _2} p_2 \frac{\gamma _3}{\eta _3}p_3. \end{aligned}$$

(4.1)

Recall that $\tau _e^\mathrm{A}$ is the time adults have available for laying eggs while $\psi (s)$ is the egg-laying rate at questing adult level $s$. Further, $\gamma _1$ is the per capita transition rate from the questing larval to the next larval stage while $\eta _1$ is the overall rate of leaving the questing larval stage including death. So $\frac{\gamma _1}{\eta _1}$ is the probability of surviving the questing larval stage while $p_1$ is the probability of surviving all the other larval stages. Similarly, $\frac{\gamma _2}{\eta _2}$ and $\frac{\gamma _3}{\eta _3}$ are the probabilities of surviving the questing nymph and adult stages, respectively. Finally, $p_2$ is the probability of surviving all the other nymph stages, while $p_3$ is the combined probability of surviving the feeding and engorged adult stages, the egg stage, and the hardening larval stage. So ${\mathcal R}(s)$ is the reproduction number at level $s$, indeed, the expected number of eggs in the next generation resulting from one typical egg in this generation if the level of questing adult ticks is at $s$ all the time.

$$\begin{aligned} {\mathcal R}_0= {\mathcal R}(0) \end{aligned}$$

(4.2)

is called the basic reproduction number. Notice that ${\mathcal R}(s)$ is a decreasing function of $s$. We define

$$\begin{aligned} {\mathcal R}_\infty = \lim _{s \rightarrow \infty } {\mathcal R}(s). \end{aligned}$$

(4.3)

Theorem 4.1

Consider system (3.3) with nonnegative initial data (3.8) and birth function $G(s)$ in (3.4). Any solution of (3.3) is nonnegative, becomes strictly positive at some time, and remains positive thereafter.

If ${\mathcal R}_\infty <1$, solutions are uniformly bounded for initial data in a bounded set.

Next we show that there is a bounded attractor for all solutions of the model. Notice that if ${\mathcal R}_\infty < 1$, then ${\mathcal R}(s) < 1$ for all sufficiently large $s>0$.

Theorem 4.2

Assume that ${\mathcal R}_\infty < 1$. Let $s \ge 0$ and ${\mathcal R}(s)<1$. Then $\limsup _{t \rightarrow \infty } x_3(t) \le s$ holds for any solution of (3.3).

For the proofs of these results we refer to Sect. 8. We mention that nonnegativity and positivity results analogous to those in Theorem 4.1 also hold for the original model (2.2). However, we have not been able to prove analogous boundedness results for (2.2) which is part of the motivation to work with the approximate system.

5 Equilibria and their stability

Equilibria of differential equations are time-independent solutions. Notice that (2.2) and (2.6), of which (3.3) is the lean formulation, have the same equilibria. Proofs of the subsequent results can be found in Sect. 9.

Theorem 5.1

Consider system (3.3). If $\mathcal {R}_0\le 1$, the system has only the trivial equilibrium $(0,0,0)$.

The trivial equilibrium is locally asymptotically stable if ${\mathcal R}_0 < 1$. The tick population dies out, $x_i(t) \rightarrow 0$ as $t \rightarrow \infty$, $i=1,2,3$, if ${\mathcal R}_0 < 1$ or if ${\mathcal R}_0 = 1$ and $\psi (s) < \psi (0)$ for all $s > 0$.

If $\mathcal {R}_0>1$, the trivial equilibrium loses stability. If $\mathcal {R}_0>1> {\mathcal R}_\infty$, positive equilibria $(x_1^*, x_2^*, x_3^*)$ exist,

$$\begin{aligned} \begin{aligned} {\mathcal R}(x_3^*)=1,\quad x_2^*=\frac{\eta _3}{\gamma _2p_2}x_3^*,\quad x_1^*=\frac{\eta _2}{\gamma _1p_1}x_2^*. \end{aligned} \end{aligned}$$

If there is such an equilibrium with $\psi '(x_3^*)< 0$, then it is the only one.

If, in addition, $\psi '(x_3^*)x_3^* \ \ge -2\psi (x_3^*)$, the positive equilibrium is unique and locally asymptotically stable.

The global stability of the zero equilibrium (the extinction state) if ${\mathcal R}_0 < 1$ is a straightforward consequence of Theorem 4.2. It can also been shown for the original system (2.2), but Theorem 4.2 can no longer be used. A possible proof for the original system uses truncated Laplace transforms similarly as in the proof of [Smith and Thieme (2011), Thm.5.39].

The instability of the extinction equilibrium $(0,0,0)$ if ${\mathcal R}_0 >1$ even comes the form of uniform weak persistence.

Introduce the following notations. Let $h:[b,\infty )\rightarrow \mathbb {R}$. Then the limit superior and the limit inferior of $h$ as $t\rightarrow \infty$ are defined as

$$\begin{aligned} h^{\infty }:&=\displaystyle \lim \sup _{t\rightarrow \infty }h(t)=\inf _{a\geqslant b}\sup \{h(t);t\geqslant a\},\\ h_{\infty }:&=\displaystyle \lim \inf _{t\rightarrow \infty }h(t)=\sup _{a\geqslant b}\inf \{h(t);t\geqslant a\}. \end{aligned}$$

Theorem 5.2

If ${\mathcal R}_0 > 1$, the questing adult ticks are uniformly weakly persistent: There exists some $\epsilon >0$ such that $x_3^{\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

It may be worthwhile to spell out the limit superior notation.

There exists some $\tilde{\epsilon }> 0$ such that for any solution of (3.3) whose initial data satisfy (3.8) there exists a sequence $(t_n)$ with $t_n \rightarrow \infty$ as $n \rightarrow \infty$ and $x_3(t_n) > \tilde{\epsilon }$ for all $n \in {\mathbb {N}}$.

The analogous result, with the same ${\mathcal R}_0$, also holds for the original system (2.2). The proof is the same as in Sect. 9.1, though one has to apply the Laplace transform to more equations.

If ${\mathcal R}_0 > 1 > {\mathcal R}_\infty$, the instability of the extinction equilibrium $(0,0,0$) takes the stronger form of uniform persistence. We were not able to prove an analogous result for (2.2) because we could not prove boundedness of solutions for that system.

Theorem 5.3

Consider system (3.3). If $\mathcal {R}_0 >1> {\mathcal R}_\infty$, the tick population is uniformly persistent: There exists some $\epsilon >0$ such that $x_{1\infty }\geqslant \epsilon$, $x_{2\infty }\geqslant \epsilon$ and $x_{3\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

Let us spell out what this means for $x_3$: There exists some $\tilde{\epsilon }>0$ such that for any solution of (3.3) whose initial data satisfy (3.8) there exists some $r \ge 0$ such that $x_3(t) \ge \tilde{\epsilon }$ for all $t \ge r$.

So all the numbers of all questing substages are eventually bounded away from 0 with a bound that does not depend on their initial data as long as those satisfy (3.8).

One can build on the last result to prove global stability of the interior equilibrium for some special cases. To this end, one derives one integral equation for $x_3$ and uses a global stability result for scalar integral equations (Thieme 2003). See Sect. 9.2.

Corollary 5.4

Let $1 < {\mathcal R}_0 \le e^2$ and $\psi (s) = \beta e^{-\alpha s}$ for $s \ge 0$. Then, whatever the discrete delays, the interior equilibrium is globally asymptotically stable for all solutions of (3.3) whose initial data satisfy (3.8).

We do not need to put a bound on the basic reproduction number in order to obtain global stability of the interior equilibrium if the negative feedback function $\psi$ is weakly density-dependent in the manner specified in the next result.

Corollary 5.5

Let ${\mathcal R}_0 > 1> {\mathcal R}_\infty$. Let $\psi '(s)< 0$ for all $s >0$ and $s^2 \psi (s)$ be a strictly increasing function of $s\ge 0$. Then, whatever the discrete delays, the interior equilibrium is globally asymptotically stable for all solutions of (3.3) whose initial data satisfy (3.8).

The assumption that $s^2 \psi (s)$ is a strictly increasing function of $s\ge 0$ can be interpreted as weak density-dependence of the feedback function. It implies that $\psi '(s)s \ \ge -2\psi (s)$ for all $s \ge 0$. Notice that local asymptotic stability of the interior equilibrium in Theorem 5.1 follows if this just holds for $s= x_3^*$.

Example 5.6

The following examples match Corollary 5.5,

$$\begin{aligned} \psi (s) = \beta (1 + b s^\xi )^{-\zeta } \end{aligned}$$

with $b > 0$, $\beta > 1$ and $\xi , \zeta > 0$ and $\xi \zeta \le 2$ [Thieme (2003) p.98], and

$$\begin{aligned} \psi (s) = \beta \frac{1 + p \phi (s)}{1 + \phi (s)} \end{aligned}$$

with $\beta > 1> p\beta$, $0 \le p < 1$, $\phi$ differentiable with $\phi '(s) >0$ for all $s >0$, $\phi (s) \rightarrow \infty$ as $s \rightarrow \infty$, and $s^{-2} \phi (s)$ decreasing as a function of $s>0$.

The property that $s^2 \psi (s)$ increases as a function of $s$ follows from

$$\begin{aligned} s^2 \psi (s) =\beta \frac{1 + p \phi (s)}{s^{-2} + s^{-2} \phi (s)}. \end{aligned}$$

The feedback function $\psi$ which has been modified from (Ogden et al. 2005) falls under this category with $\phi (s) = a \ln (1 + bs)$ where $a,b>0$. In this case, we even have that $G$ with $G(s) = s \psi (s) \tau ^\mathrm{A}_e$ is increasing.

The stability conditions in the previous theorems hold for all delays and may be overly strong for small delays. To explore this, we investigate the characteristic equation for $\tau _1 = \tau _2 = \tau _3=0$ which takes the form

$$\begin{aligned} \lambda ^3 + (\eta _1 + \eta _2 + \eta _3) \lambda ^2 + (\eta _1 \eta _2 + \eta _1 \eta _3 + \eta _2 \eta _3 ) \lambda + \xi \eta _1 \eta _2 \eta _3=0 \end{aligned}$$

with $\xi = - \frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} >0$. By the Routh-Hurwitz criterion, the characteristic polynomial has no roots with nonnegative real part if and only if

$$\begin{aligned} (\eta _1 + \eta _2 + \eta _3) (\eta _1 \eta _2 + \eta _1 \eta _3 + \eta _2 \eta _3 ) > \xi \eta _1 \eta _2 \eta _3. \end{aligned}$$

This inequality is satisfied if $\xi \le 3$. Let us calculate $\xi$ for the special case $\psi (x) = \beta e^{-\alpha x}$. Then

$$\begin{aligned} \xi = \alpha x_3^* = \ln {\mathcal R}_0. \end{aligned}$$

By Rouché’s theorem, the interior equilibrium is locally asymptotically stable, if $\ln {\mathcal R}_0 \le 3$ and the delays $\tau _1, \tau _2, \tau _3$ are sufficiently small. For sufficiently large ${\mathcal R}_0$, the characteristic polynomial has complex roots with positive real parts. Since all coefficients of the characteristic polynomial are positive, there is a root with positive real part and nonzero imaginary part. This means, again by Rouché’s theorem, that for sufficiently large ${\mathcal R}_0$, the interior equilibrium is unstable for sufficiently small delays in an oscillatory manner. One would expect that this is even more the case for intermediate delays.

Theorem 5.7

Let $\psi (x) = \beta e^{-\alpha x}$, $1 < {\mathcal R}_0 \le e^3$. Then the interior equilibrium is locally asymptotically stable if the delays $\tau _1$, $\tau _2$, $\tau _3$ are sufficiently small. If ${\mathcal R}_0$ is sufficiently large, the interior equilibrium is unstable if the delays $\tau _1$, $\tau _2$, and $\tau _3$ are sufficiently small.

6 Numerical simulations

In this section, we present numerical simulations of the approximate system (2.6) (solid lines in Figs. 1, 2), check whether they are consistent with our analytical results, and compare them with numerical simulations of the original system (2.2) (dotted lines in Figs. 1, 2). For the numerical simulations, we use the package DDE23 in Matlab.

Fig. 2

Time evolution of total number of questing ticks for systems (2.2) (dotted line) and (2.6) (solid line). Fix $\gamma ^A=0.03$ and vary $\gamma ^L,\gamma ^N=0.015, 0.13, 0.65$ from the top to the bottom figure

We choose the growth function (2.7) with $\psi (s)=\beta e^{-s}$. We borrow most of the parameter values from (Ogden et al. 2005). In Table 2, we list all parameters shared in both models with exceptional parameters given in the next paragraph. It needs to be pointed out that in (Ogden et al. 2005), the per capita mortalities $d_f^L$, $d_f^L$, or $d_f^L$ are assumed to be density dependant. In model 2.2, we ignore the density dependance; so we take the mean values of those in (Ogden et al. 2005). The parameters $\tau ^E$, $\tau _g^L$, $\tau _g^A$ and $\tau _g^N$ vary with temperature, see Fig. 1 in (Ogden et al. 2005). We give their ranges in the table. For other parameter values, we just copy them.

The remaining parameters $\gamma _L$, $\gamma _N$, and $\gamma _A$ in model (2.2) do not appear in (Ogden et al. 2005) as such. Based on (Ogden et al. 2005), the main hosts for both larvae and nymphs are rodents the numbers of which are chosen as $R= 200$. The main hosts for adults are deer the numbers of which is chosen as $D=20$. The relations between our parameters and those in (Ogden et al. 2005) are

$$\begin{aligned} \gamma _L = (\lambda _{ql}/7) \theta ^i, \qquad \gamma _N = (\lambda _{qn}/7) \theta ^i \qquad \gamma _A = (\lambda _{qa}/7) \theta ^a. \end{aligned}$$

Note that $\lambda _{ql}$ is the weekly host finding rate of questing larvae. We divide it by 7 to convert to a daily host finding rate. From (Ogden et al. 2005),

$$\begin{aligned} \lambda _{ql}&= 0.0089*R^{0.515}=0.0089*(200)^{0.515}\approx 0.1363,\\ \lambda _{qn}&= \lambda _{ql}\approx 0.1363,\\ \lambda _{qa}&= 0.06*D^{0.515}=0.06*(20)^{0.515}\approx 0.2807. \end{aligned}$$

The parameters $\theta ^i$ and $\theta ^a$ in (Ogden et al. 2005) are the activity probabilities of immature and adult ticks, respectively; they are temperature dependant and have a range of $[0,1]$ [Ogden et al. (2005), Fig.3].

Therefore $\gamma ^L= \lambda _{ql}*\theta ^i/7$ and $\gamma ^N=\lambda _{qn}*\theta ^i/7$ are in the interval $[0, 0.0194]$, and $\gamma ^A= \lambda _{ql} * \theta ^a$ is in the interval $[0,0.0401]$. Wu et al. (2013) have calculated ${\mathcal R}_0$ values for various sites using the parameters in (Ogden et al. 2005) (which are changing over the year) with the largest value being 3.65. For these values, since they are below $e^2 \approx 7.39$, our analysis based on (2.6) predicts extinction or convergence to a positive equilibrium which is consistent with the findings in (Ogden et al. 2005) where the simulations show extinction or convergence to periodic solutions (their model is periodically forced). In order to check our analytic results and to make the comparison between the original and the approximate system interesting, we therefore choose considerably larger values for $\gamma ^L, \gamma ^N$, and $\gamma ^A$.

In Fig. 1, we choose $\gamma ^L=\gamma ^N=0.13$ and $\gamma ^A=0.003, 0.013$ or $0.03$ from top to the bottom. For such choice of parameters, we have ${\mathcal R}_0=7.36,\ 14.18$ or $16.83$. By our analytical results, the system is uniformly persistent for all three cases. For $\gamma ^A=0.003$, we have $\ln ({\mathcal R}_0)=\ln (7.36)\approx 1.9961<2$, by Corollary 5.4, the unique positive equilibrium is globally asymptotically stable.

In Fig. 2, we fix $\gamma ^A=0.03$ and choose $\gamma ^L=\gamma ^N=0.015, 0.13, 0.65$ from top to bottom. For such choice of parameters, we have ${\mathcal R}_0=9.79,\ 16.83$ or $17.98$. Since we have basic reproduction numbers that are larger than 1, the system is uniformly persistent by Theorem 5.3. Notice that $\ln 9.79 \approx 2.281$ which is slightly above the threshold $\ln {\mathcal R}_0 =2$ for global stability of the persistence equilibrium (Corollary 5.4). This shows nicely the destabilizing influence of the discrete delays because the threshold for local stability without the discrete delays is larger than $\ln {\mathcal R}_0 =3$ (Theorem 5.7).

For all simulations we have chosen constant initial conditions $L_q=N_q=A_q=200$. For system (2.2), we need to make sure that its initial conditions satisfy (2.3) for $A_f$ and $A_e$ at $t=0$,

$$\begin{aligned} A_f (0)&= \int _{-\tau ^\mathrm{A}_f}^0 \gamma ^\mathrm{A } A_q(s) e^{d^\mathrm{A}_f s} ds =\int _{-\tau ^\mathrm{A}_f}^0 \gamma ^\mathrm{A } 200 e^{d^\mathrm{A}_f s} ds,\\&= 200 \int _{t-\tau ^\mathrm{A}_f}^t \gamma ^\mathrm{A } e^{d^\mathrm{A}_f (s-t)} ds =200 \gamma ^\mathrm{A } \frac{1-e^{-d^\mathrm{A}_f \tau _f^A}}{d^\mathrm{A}_f} \end{aligned}$$

and

$$\begin{aligned} A_e(0)&= e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f-d^\mathrm{A}_g \tau ^\mathrm{A}_g} \int _{-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g-\tau ^\mathrm{A}_e}^{-\tau ^\mathrm{A}_f-\tau ^\mathrm{A}_g } \gamma ^\mathrm{A } A_q(s)ds\\&= 200 e^{-d^\mathrm{A}_f \tau ^\mathrm{A}_f-d^\mathrm{A}_g \tau ^\mathrm{A}_g} \tau _e^\mathrm{A} \gamma ^\mathrm{A }. \end{aligned}$$

From Figs. 1 and 2, we can see that system (2.2) (dotted lines) and its approximate system (2.6) (solid lines) have qualitatively similar numerical dynamics. So system (2.6) seems a good approximation to system (2.2) giving reasonable confidence that the study of system (2.6) can qualitatively reveal the dynamics of system (2.2). One should keep in mind that the complex behavior of the solutions of both systems is due to an exaggerated range of some of the parameters which makes the basic reproduction numbers more than twice as large as the largest value determined from realistic parameter ranges. These too large parameters were chosen to illustrate our analytic results and to spice up the comparison between the original and the approximate system. A further bifurcation analysis would be mathematically interesting but may presently lack biological relevance for dynamics of tick populations.

7 Discussion

Ticks, which are the vectors of bacterial and viral diseases, have a complicated life cycle that can be divided into four main stages and 12 substages. Moreover, the lengths of the substages depend on environmental conditions like temperature and the availability of suitable hosts to feed on and so vary a lot geographically and seasonally. Models like the one in (Ogden et al. 2005) that want to use realistic parameters obtained from natural data need to take all substages into account. If such detailed models are extended to study the spread of tick-borne infectious diseases, one ends up with very large systems that are too unwieldy to be analyzed mathematically for their qualitative behavior. The models of tick-borne disease in the literature therefore do not consider all the substages of ticks. Ghosh and Pugliese (2004) and Norman et al. (1999) only consider the main stages of larvae, nymphs and adults. Caraco et al. (2002) and Zhao (2012) consider the questing substages of larvae and nymphs and the adult stage, and (Hartemink et al. 2008) considers the feeding substages of larvae, nymphs and adults and the egg stage. Rosà and Pugliese (2007) considers the questing and feeding substages of larvae, nymphs and adults.

It is one aim of this paper to build a bridge between detailed tick models and less detailed models that can be extended into disease models. Truly enough, less detailed models can be and have been formulated without reducing them from very detailed models. But then they involve parameters that have no counterparts in the naturally occurring system. A reduction procedure reveals how the parameters of the less detailed model are compounded from parameters that can be obtained from observations. The reduction procedure may also show the kind of realism that is lost by choosing a model with little detail and explain why such a model produces solutions that are not a perfect quantitative fit to the natural observations.

To connect the detailed model in (Ogden et al. 2005), which is a computational model, to the type of disease models considered in the literature, we translate it into a system of differential equations. The lengths of most stages are determined by physiological development, and they are rather of fixed length than exponentially distributed. The lengths of the questing substages depend on random events like meeting a suitable host and so are rather exponentially distributed than the same for all questing ticks in that stage. Nevertheless, all twelve differential equations have delays differently from [Fan et al. (2014); Wu et al. (2013)] where all differential equations are ordinary. The use of delays makes it possible to leave out the majority of these equations and consider a subsystem of five equations only.

To reduce this system even further requires approximations, and we study what kind of errors are created this way and whether the reduced model can be used with some confidence. To make this comparison easier, we do not consider time-dependent parameters. So the models we consider are not suited as quantitatively predictive tools because the seasonal variation of parameters in pronounced in reality. It is also futile to compare their numerical simulations quantitatively to real observations.

We find that one of the two approximations we preform for system reduction looks analytically harmless because the length of the integration integral is short (1 day). The second is problematic because the length of the integration integral is much larger (10 days). The original system and the approximative system have the same equilibria and the same basic reproduction number which acts in identical ways as threshold between tick extinction and tick persistence.

If the feedback functions are weakly density-dependent (Corollary 5.5) or if the parameters are kept in a realistic range (Corollary 5.4), our analytic results show that the approximate system displays simple qualitative behavior. The numerical simulations show the same for the original system with the parameters in realistic range. This is consistent with the findings in (Ogden et al. 2005) where the solutions under time-periodic forcing converge to periodic solutions with the same period.

To have a more conclusive numerical comparison between our original model and its approximation, we ramp up some parameters (availability of suitable hosts for adults and for larvae and nymphs) way above their natural range. Since one of our approximations was problematic, it does not come as a surprise that the numerical solutions of the original system and those of the approximative system show quantitative differences. But their qualitative behavior, in particular as far as its complexity is concerned, is similar enough that one can confidently use the reduced model for qualitative studies.

The numerical computations also show that the tick system has the potential for complex behavior though it does not occur in a realistic parameter range. For realistic parameters, the solutions of the approximative system converge to the extinction equilibrium or to a globally stable persistence equilibrium, and the numerical computations suggest that the same hold for the original system. For strongly density-dependent feedback functions like $\psi (x) = \beta e^{-\alpha x}$, both systems show the potential for complex behavior in the case of dramatic climatic changes. Global warming may play out in counteracting directions though because warmer temperatures decrease the developmental delays but increase the basic reproduction number; our analytic results suggest that the first has a stabilizing and the second a destabilizing effect.

Appendices

Appendix 1: Proofs for Sect. 4

Proof of Theorem 4.1

Consider system (3.3) with nonnegative initial data (3.8) and birth function $G(s)$ in (3.4). Any solution of (3.3) is nonnegative, becomes strictly positive at some time, and remains positive thereafter.

Without loss of generality, we assume that the number of adult ticks $x_{30}(\theta )$ is not identically zero for $\theta \in [-\tau _3,\ 0]$. There exists $\theta ^*\in (-\tau _3,\ 0)$ such that $x_{30}(\theta ^*)>0$. By the continuity of the function, there exists a neighborhood $(\theta ^*-\delta ,\theta ^*+\delta )$ such that $x_{30}(\theta )>0$, where $\delta$ is a small positive number. For any $t^*\in [0,\ \tau _3]$ and $t^*>\theta ^*+\tau _3+\delta$,

$$\begin{aligned} x_1(t^*)&= \int _0^{t^*}\gamma _3p_3 e^{-\eta _1(s-t^*)}G(x_{30}(s - \tau _3))\mathrm {d}s+x_{10}(0) e^{-\eta _1t^*}\\&> \int _{\theta ^*-\delta }^{\theta ^*+\delta }\gamma _3p_3 e^{-\eta _1(s-t^*)}G(x_{30} (s - \tau _3))\mathrm {d}s \; >0. \nonumber \end{aligned}$$

(8.1)

After time $t^*$, $x_1(t)$ can never become zero again since

$$\begin{aligned} x_1'(t)>- \eta _1 x_1 (t) \quad \mathrm {and}\quad x_1(t)\geqslant x_1(t^*)e^{-\eta _1(t-t^*)}>0. \end{aligned}$$

If $\theta ^*=-\tau _3$ or $0$, we can modify the proof a little bit and take the neighborhood $(-\tau _3,-\tau _3+\delta )$ or $(-\delta ,0)$. Our proof still works. Similarly we can prove that $x_2(t)$ and $x_3(t)$ are strictly positive at some $\bar{t}>0$ and remain strictly positive thereafter.

Let $T> 0$ be arbitrary. From the integral equation for $x_1$ like in (8.1), we have that

$$\begin{aligned} \sup _{-\tau _1 \le t \le T} x_1(t) \le \sup _{-\tau _1 \le t \le 0} x_{10}(t) + \frac{\gamma _3 p_3}{\eta _1} \sup _{-\tau _3 \le t \le T} G(x_3(t)). \end{aligned}$$

After integrating the differential equation for $x_2$,

$$\begin{aligned}&\sup _{-\tau _2 \le t \le T} x_2(t) \le \sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _1 p_1}{\eta _2} \sup _{-\tau _1 \le t \le T} x_1(t)\\ \le&\sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _1 p_1}{\eta _2}\sup _{-\tau _1 \le t \le 0} x_{10}(t) + \frac{\gamma _1 p_1}{\eta _2}\frac{\gamma _3 p_3}{\eta _1} \sup _{-\tau _3 \le t \le T} G(x_3(t)). \end{aligned}$$

We integrate the differential equation for $x_3$,

$$\begin{aligned}&\sup _{-\tau _3 \le t \le T} x_3(t) \le \sup _{-\tau _3 \le t \le 0} x_{30}(t) + \frac{\gamma _2 p_2}{\eta _3} \sup _{-\tau _2 \le t \le T} x_2(t)\nonumber \\ \le&c_3 + \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \sup _{-\tau _3 \le t \le T} G(x_3(t)) \end{aligned}$$

(8.2)

with

$$\begin{aligned} c_3 = \sup _{-\tau _3 \le t \le 0} x_{30}(t) + \frac{\gamma _2 p_2}{\eta _3} \sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _2 p_2}{\eta _3}\frac{\gamma _1 p_1}{\eta _2} \sup _{-\tau _1 \le t \le 0} x_{10}(t) . \end{aligned}$$

(8.3)

Assume that ${\mathcal R}_\infty < 1$ and let $x >0$ such that ${\mathcal R}(x) <1$. Since $\psi$ is decreasing, from (3.4),

$$\begin{aligned} G(s) \le s \psi (x) \tau ^\mathrm{A}_e, \qquad s \ge x. \end{aligned}$$

So

$$\begin{aligned} G(s) \le c_x + s \psi (x) \tau ^\mathrm{A}_e, \qquad s \ge 0, \end{aligned}$$

where $c_x = \sup _{0\le s\le x} G(x)$. By (8.2), for some $\tilde{c}_x>0$, which does not depend on the solution,

$$\begin{aligned} \sup _{-\tau _3 \le t \le T} x_3(t) \le c_3 + \tilde{c}_x + {\mathcal R}(x) \sup _{-\tau _3 \le t \le T} x_3(t). \end{aligned}$$

We reorganize,

$$\begin{aligned} \sup _{-\tau _3 \le t \le T} x_3(t) \le (1 - {\mathcal R}(x))^{-1} (c_3 + \tilde{c}_x). \end{aligned}$$

Since the right hand side does not depend on $T$, $x_3$ is bounded on $[-\tau _3, \infty )$ and

$$\begin{aligned} x_3(t) \le (1 - {\mathcal R}(x))^{-1} (c_3 + \tilde{c}_x). \end{aligned}$$

Notice from (8.3) that this is a uniform bound for a bounded set of initial data. Now $x_1$ and $x_2$ are bounded as well with the bounds being uniform for bounded sets of initial data. $\square$

Note that the method we used to prove the positiveness of solutions is also used in (Gourley et al. 2009).

Next we show that there is a bounded attractor for all solutions of the model.

Proof of Theorem 4.2

Assume that ${\mathcal R}_\infty < 1$. Let $x \ge 0$ and ${\mathcal R}(x)<1$. Then $\limsup _{t \rightarrow \infty } x_3(t) \le x$ holds for any solution of (3.3).

By Theorem 4.1, any solution is bounded. By the fluctuation method [Hirsch et al. (1985); Smith and Thieme 2011, A.3], [Thieme 2003, Prop.A.22]), for each $j \in \{1,2,3\}$, there exists a sequence $(t_k)$ with $t_k \rightarrow \infty$,

$$\begin{aligned} x_j(t_k) \rightarrow x_{j}^\infty := \limsup _{t\rightarrow \infty } x_{j}(t), \qquad x_{j}'(t_k) \rightarrow 0, \qquad k \rightarrow \infty . \end{aligned}$$

From (3.3),

$$\begin{aligned} x_1^\infty =&\frac{\gamma _3 p_3}{\eta _1} \lim _{k\rightarrow \infty } G(x_3(t_k - \tau _3)),\nonumber \\ x_{j+1}^\infty \le&\frac{\gamma _j p_j}{\eta _{j+1}} x_j^\infty , \qquad j=1,2. \end{aligned}$$

(8.4)

We substitute these inequalities into each other,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \lim _{k\rightarrow \infty } G(x_3(t_k - \tau _3)). \end{aligned}$$

We can assume that $x_3^\infty > 0$. Since $x_3$ is bounded on ${ \mathbb {R}}_+$, after choosing a subsequence, $x_3(t_k - \tau _3) \rightarrow s$ for some $s \in [0, x_3^\infty ]$. Since $G$ is continuous,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} G(s) . \end{aligned}$$

Since $G(0) =0$, $s \in (0, x_3^\infty ]$. By definition of $G$,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} s \psi (s) \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} x_3^\infty \psi (s) . \end{aligned}$$

Since we have assumed that $x_3^\infty > 0$, this implies

$$\begin{aligned} 1 \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} \psi (s)= {\mathcal R}(s) . \end{aligned}$$

Since $0 < s \le x_3^\infty$ and ${\mathcal R}$ is decreasing and ${\mathcal R}(x) < 1$ we have $x_3^\infty \le x$. By (8.4),

$$\begin{aligned} x_1^\infty = \frac{\gamma _3 p_3}{\eta _1} \beta \tau ^\mathrm{A}_e x , \qquad x_{2}^\infty \le \frac{\gamma _1 p_1}{\eta _{2}} x_1^\infty . \end{aligned}$$

$\square$

Appendix 2: Proofs for Sect. 5

Proof of Theorem 5.1

At first, we will consider the equilibria of system (3.3). Suppose $(x_1^*,x_2^*,x_3^*)$ is an equilibrium, then

$$\begin{aligned} \begin{aligned} 0 =&\gamma _3p_3 G(x_3^*)-\eta _1x_1^*,\\ 0 =&\gamma _1p_1 x_1^*-\eta _2 x_2^*,\\ 0 =&\gamma _2p_2 x_2^*-\eta _3 x_3^*. \end{aligned} \end{aligned}$$

It is easy to see $x_1^*=\frac{\eta _2}{\gamma _1p_1}x_2^*$, $x_2^*=\frac{\eta _3}{\gamma _2p_2}x_3^*$ and $x_3^*$ satisfies

$$\begin{aligned} x_3^*\Big (\psi (x_3^*)-\frac{\eta _1\eta _2\eta _3}{\gamma _1p_1\gamma _2p_2\gamma _3p_3\tau _e^A} \Big ) =x_3^* \Big (\psi (x_3^*)-\frac{\psi (0)}{\mathcal {R}_0}\Big )=0. \end{aligned}$$

(9.1)

Solving (9.1), we have $x_3^*=0$ if $\mathcal {R}_0\le 1$ and $x_3^*=0$ and any $x_3^*>0$ with $\psi (x_3^*)=\frac{\psi (0)}{\mathcal {R}_0}$ if $\mathcal {R}_0> 1$ since $\psi$ is (not necessarily strictly) monotone decreasing and continuous on $[0,\infty )$. If $\psi '(x_3^*) < 0$, $x_3^*$ is uniquely determined and the nonzero equilibrium is unique.

Conversely, if ${\mathcal R}_0 >1 > {\mathcal R}_\infty$, there exists a number $x^*_3 >0$ satisfying ${\mathcal R}(x_3^*) = 1$, and defining $x_1^*$ and $x_2^*$ as above provides an equilibrium of system (3.3) in $(0,\infty )^3$.

If $\mathcal {R}_0 < 1$, then $\limsup _{t\rightarrow \infty } x_3(t) =0$ by Theorem 4.2. If ${\mathcal R}_0 =1$ and $\psi (s) < \psi (0)$, for all $s >0$, then ${\mathcal R}(s) < 1$ for all $s>0$. By Theorem 4.2, $\limsup _{t\rightarrow \infty } x_3(t)<s$ for all $s >0$ and so equals 0. It follows from the proof of Theorem 4.2 that $x_j(t) \rightarrow 0$ as $t \rightarrow \infty$ for $j=1,2$.

Local asymptotic stability of the trivial equilibrium if ${\mathcal R}_0< 1$ follows from a standard analysis of a characteristic equation which is similar to the one we will do for the positive equilibrium and is therefore omitted.

Let $\mathcal {R}_0>1$. To study the local asymptotic stability of the positive equilibrium, we use the principle of linearized stability [see Hale and Verdyun Lunel (1993), e.g.]. The linearization of system (3.3) at the positive equilibrium leads to the characteristic equation

$$\begin{aligned} (\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3) = (\psi (x_3^*)+\psi '(x_3^*)x_3^*)\tau _e^A\gamma _1p_1\gamma _2p_2\gamma _3p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}. \end{aligned}$$

(9.2)

By (4.1) and ${\mathcal R}(x_3^*)=1$,

$$\begin{aligned} (\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3) = \Big (1 +\frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \Big ) \eta _1 \eta _2 \eta _2 e^{-\lambda (\tau _1+\tau _2+\tau _3)}. \end{aligned}$$

(9.3)

Since $\psi '(x_3^*) < 0$, there is no nonnegative root.

Suppose that there is a root $\lambda$ with $\mathfrak {R}\lambda \ge 0$ and $\mathfrak {I}\lambda \ne 0$. Then, by taking absolute values,

$$\begin{aligned} \eta _1 \eta _2\eta _3 < \Big |1 +\frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \Big | \eta _1 \eta _2 \eta _2. \end{aligned}$$

(9.4)

This implies

$$\begin{aligned} \frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} < -2. \end{aligned}$$

(9.5)

By contraposition, the interior equilibrium is locally asymptotically stable if

$$\begin{aligned} \frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \ge -2. \end{aligned}$$

(9.6)

$\square$

1.1 Persistence

Proof of Theorem 5.2

If ${\mathcal R}_0 > 1$, the questing adult ticks are uniformly weakly persistent: There exists some $\epsilon >0$ such that $x_3^{\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

Let $\epsilon >0$. Assume that there exists a solution $(x_1(t),x_2(t),x_3(t))$ satisfying (3.8) and

$$\begin{aligned} x_3^{\infty }=\lim _{t\rightarrow \infty } \sup x_3(t)< \epsilon . \end{aligned}$$

(9.7)

Then we have $x_3(t-\tau _3)< \epsilon$ for sufficiently large $t$. Since $\psi (x_3)$ is a decreasing function, we have $\psi (x_3(t-\tau _3))\geqslant \psi (\epsilon )$. After a shift forward in time, we have the following inequality

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm {d}x_1(t)}{\mathrm {d}t}&\geqslant \displaystyle x_3(t - \tau _3)\gamma _3p_3\tau _e^A \psi (\epsilon )-\eta _1x_1(t), \qquad t \ge 0. \end{aligned} \end{aligned}$$

Using the method in (Smith and Thieme 2011), we take the Laplace transform in both sides of the above inequality with $\lambda > 0$,

$$\begin{aligned} \lambda \fancyscript{L}(x_1(t))&\geqslant -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon ) \int _0^{\infty }e^{-\lambda s}x_3(s-\tau _3)\mathrm {d}s\\&= -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3}\int _{-\tau _3}^{\infty } e^{-\lambda s}x_3(s)\mathrm {d}s\\&\geqslant -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3} \int _{0}^{\infty }e^{-\lambda s}x_3(s)\mathrm {d}s. \end{aligned}$$

We drop the term $\int _{-\tau }^0e^{-\lambda s}x_3(s)\mathrm {d}s$ because $x_3(s)$ is nonnegative. Rearranging gives

$$\begin{aligned} \fancyscript{L}(x_1(t))\ge \frac{\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3}}{\lambda +\eta _1}\fancyscript{L}(x_3(t)). \end{aligned}$$

(9.8)

Similarly, we take Laplace transform on both sides of equations for $x_2(t)$ and $x_3(t)$ in (3.3). Simplification gives

$$\begin{aligned} \fancyscript{L}(x_2(t))\ge \frac{\gamma _1p_1e^{-\lambda \tau _1}}{\lambda +\eta _2} \fancyscript{L}(x_1(t)) \end{aligned}$$

(9.9)

and

$$\begin{aligned} \fancyscript{L}(x_3(t))\ge \frac{\gamma _2p_2e^{-\lambda \tau _2}}{\lambda +\eta _3} \fancyscript{L}(x_2(t)). \end{aligned}$$

(9.10)

We combine (9.8), (9.9) and (9.10),

$$\begin{aligned} \begin{aligned} \fancyscript{L}(x_1(t))\ge \frac{\tau _e^A\psi (\epsilon ) \gamma _1p_1\gamma _2 p_2\gamma _3 p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}}{(\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3)} \fancyscript{L}(x_1(t)). \end{aligned} \end{aligned}$$

Noting that $\fancyscript{L}(x_1(t))>0$ because $x_1(t)$ is eventually positive, we divide by $\fancyscript{L}(x_1(t))$ on both sides and obtain

$$\begin{aligned} \begin{aligned} 1\ge \frac{\tau _e^A\psi (\epsilon )\gamma _1p_1\gamma _2 p_2\gamma _3 p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}}{(\lambda +\eta _1)(\lambda +\eta _2) (\lambda +\eta _3)}. \end{aligned} \end{aligned}$$

If the questing adults ticks are not uniformly weakly persistent as formulated in the theorem, the last inequality holds for all $\lambda >0$ and $\epsilon >0$. Letting $\lambda \rightarrow 0$ and $\epsilon \rightarrow 0$, we obtain

$$\begin{aligned} \begin{aligned} 1\ge \frac{\tau _e^A\psi (0)\gamma _1p_1\gamma _2 p_2\gamma _3 p_3 }{\eta _1\eta _2\eta _3} = {\mathcal R}_0. \end{aligned} \end{aligned}$$

Recall (4.1) and (4.2). By contraposition, the questing adult ticks are uniformly weakly persistent if $\mathcal {R}_0>1$. $\square$

Proof of Theorem 5.3

Consider system (3.3). If $\mathcal {R}_0 >1> {\mathcal R}_\infty$, the tick population is uniformly persistent: There exists some $\epsilon >0$ such that $x_{1\infty }\geqslant \epsilon$, $x_{2\infty }\geqslant \epsilon$ and $x_{3\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

We will use Theorem 4.12 in (Smith and Thieme 2011) to prove the uniform persistence for questing adult ticks.

Choose the state space $X$ as the cone of nonnegative functions in $C [-\tau _1,0] \times C[-\tau _2,0] \times C[-\tau _3,0]$.

Assume that $x(t)=(x_1(t),\ x_2(t),\ x_3(t))$ is a solution of (3.3) with nonnegative initial data $\phi \in X$. Define a subset

$$\begin{aligned} D=\{x_t(\phi )\in X: 0\leqslant x_t^i (\phi )\leqslant M_i,\ i=1,2,3, \ t\geqslant \tau \}, \end{aligned}$$

where $\tau = \max _{i=1}^3 \tau _i$, $x_t^i(\phi )$ is the $i$-th component of $x_t$ and the $M_i$ have been chosen that $\limsup _{t \rightarrow \infty } x_i(t) < M_i$ (see Theorem 4.2).

It is easy to verify that $D$ is a bounded subset of $X$ and, by construction, attracts all $x\in X$. It follows that $|x'(t)|$ is uniformly bounded by a constant $\bar{M}=\bar{M}(M_1,M_2,M_3)$ on $\{t\geqslant \tau \}$ independent of the solution in $D$. From the Ascoli-Arzela Theorem [Ch.8.3 in McDonald and Weiss (1999)], the subset $D$ has compact closure because $\{x_t(\phi )\in D, t\geqslant \tau \}$ is an equicontinuous and equibounded subset of $C [-\tau _1,0] \times C[-\tau _2,0] \times C[-\tau _3,0]$.

So we have found a compact set that attracts all points in $X$.

We define $\rho :X\rightarrow \mathbb {R}_+$ by

$$\begin{aligned} \rho (x_0)= x_{30}(0),\qquad x_0=(x_{10},x_{20},x_{30})\in X. \end{aligned}$$

Then $\rho$ is continuous and $\rho (x_t(\phi ))=x_3(t)$.

We check the three assumptions $\hat{\heartsuit }_1-\hat{\heartsuit }_3$ in [Smith and Thieme (2011) Thm.4.13]. Assumption $\hat{\heartsuit }_1$ and $\hat{\heartsuit }_2$ are true because the set $D$ attracts all $x\in X$ and the closure of $D$ is compact. By (3.3), $\rho (x_0)>0$ implies $\rho (x_t(\phi ))>0$ for all $t\geqslant \tau$. This verifies $\hat{\heartsuit }_3$. By Theorem 5.2, system (3.3) is uniformly weakly $\rho$-persistent.

By Theorem 4.12 in (Smith and Thieme 2011), the system (3.3) is uniformly $\rho$-persistent whenever it is uniformly weakly $\rho$-persistent. So there exists some $\epsilon _3 >0$ such that

$$\begin{aligned} \liminf _{t\rightarrow \infty } x_3(t) \ge \epsilon _3 \end{aligned}$$

for all solutions of (3.3) whose initial data satisfy (3.8).

We apply the fluctuation method to the differential equation for $x_1$,

$$\begin{aligned} x_1'(t) = \gamma _3 p_3 G (x_3(t-\tau _3)) - \eta _1 x_1(t). \end{aligned}$$

There exists a sequence $(t_k)$ with $t_k \rightarrow \infty$, $x_1(t_k) \rightarrow x_{1\infty }$, $x_1'(t_k ) \rightarrow 0$ as $k \rightarrow \infty$. So

$$\begin{aligned} x_{1\infty } = \lim _{k\rightarrow \infty } \frac{\gamma _3 p_3}{\eta _1} G (x_3(t_k-\tau _3)) \ge \frac{\gamma _3 p_3}{\eta _1} \min \{G(x_3); \epsilon _3 \le x_3 \le M_3\} =: \epsilon _1 > 0. \end{aligned}$$

Similarly, one finds some $\epsilon _2 >0$ that does not depend on the initial conditions such that $x_{2\infty } \ge \epsilon _2$.

By Theorem 4.1, any solution whose initial data satisfies (3.8) fulfills $\rho (x_3(r)) >0$ for some $r >0$ and so $x_{j\infty } \ge \epsilon _j$ for $j =1,2,3$. $\square$

1.2 Global stability of the positive equilibrium

To prove the global stability result for the interior equilibrium, we will rewrite (3.3) as a scalar integral equation for $x_3$ and use Theorem B.40 in (Thieme 2003).

All equations of the system (3.3) are of the form

$$\begin{aligned} u'(t) = \alpha v(t-\tau ) - \mu u(t), \qquad t \ge 0. \end{aligned}$$

(9.11)

By the variation of constants formula,

$$\begin{aligned} u(t)&= \int _0^t \alpha v(s-\tau ) e^{-\mu (t-s)} ds + u(0) e^{-\mu t} = \int _{-\tau }^{t-\tau } \alpha v(s) e^{-\mu (t-s - \tau )} ds\\&+ u(0) e^{-\mu t}. \end{aligned}$$

Then $u$ can be written as

$$\begin{aligned} u(t) = \int _0^t v(s) k(t-s) ds + u_0 (t), \end{aligned}$$

(9.12)

where

$$\begin{aligned} k(t) = \left\{ \begin{array}{cc} \alpha e^{-\mu (t-\tau )} ; &{}\quad t \ge \tau \\ 0 ; &{} t \le \tau \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} u_0(t ) = \int _{-\tau }^0 \alpha v(s) k(t-s) ds + u(0) e^{-\mu t}. \end{aligned}$$

Notice that $u_0(t) \rightarrow 0$ as $t \rightarrow \infty$ and

$$\begin{aligned} \int _0^\infty k(t) dt = \frac{\alpha }{\mu }. \end{aligned}$$

(9.13)

Now let $v$ also be given in the form

$$\begin{aligned} v(s) = \int _0^s w(r) \ell (s-r) dr + v_0(s), \qquad s \ge 0, \end{aligned}$$

with $v_0(s) \rightarrow 0$ as $s \rightarrow \infty$. Then

$$\begin{aligned} u(t) = \int _0^t \Big ( \int _0^s w(r) \ell (s-r) dr + v_0(s) \Big ) k(t-s) ds + u_0(t). \end{aligned}$$

We change the order of integration

$$\begin{aligned} u(t) = \int _0^t w(r) \Big (\int _r^t \ell (s-r) k(t-s) ds \Big ) dr + \int _0^t v_0(s) k(t-s) ds + u_0(t). \end{aligned}$$

After a substitution,

$$\begin{aligned} u(t) = \int _0^t w(r) \Big (\int _0^{t-r} \ell (s) k(t-r-s) ds \Big ) dr + \tilde{u}_0(t) \end{aligned}$$

with

$$\begin{aligned} \tilde{u}_0(t) = \int _0^t v_0(s) k(t-s) ds + u_0(t). \end{aligned}$$

Finally,

$$\begin{aligned} u(t) = \int _0^t w(r) m (t-r) dr + \tilde{u}_0(t) \end{aligned}$$

(9.14)

with

$$\begin{aligned} m (t) = \int _0^t \ell (s) k(t-s) ds \end{aligned}$$

and

$$\begin{aligned} \tilde{u}_0(t) \rightarrow 0, \quad t \rightarrow \infty . \end{aligned}$$

Notice that

$$\begin{aligned} \int _0^\infty m(t) dt = \Big ( \int _0^\infty \ell (t) dt \Big ) \Big ( \int _0^\infty k(t) dt \Big ). \end{aligned}$$

(9.15)

We apply this procedure to (3.3),

$$\begin{aligned} x_1(t) =&\int _0^t G(x_3(s)) K_1(t-s)ds + \tilde{x}_1(t),\nonumber \\ x_2(t) =&\int _0^t x_1(s) K_2(t-s) ds + \tilde{x}_2(t),\nonumber \\ x_3(t) =&\int _0^t x_2(s) K_3(t-s) ds + \tilde{x}_3 (t), \end{aligned}$$

(9.16)

with $\tilde{x}_j(t) \rightarrow 0$ and

$$\begin{aligned} \int _0^\infty K_1(t)dt = \frac{\gamma _3 p_3}{\eta _1}, \qquad \int _0^\infty K_2(t)dt = \frac{\gamma _1 p_1}{\eta _2}, \qquad \int _0^\infty K_3(t) dt = \frac{\gamma _2 p_2}{\eta _3}. \end{aligned}$$

We substitute these integral equations into each other; by the procedure above we obtain the integral equation

$$\begin{aligned} x_3(t) = \int _0^t G(x_3(s)) K(t-s) ds + \bar{x}_3(t), \end{aligned}$$

(9.17)

with $\bar{x}_3(t) \rightarrow 0$ as $t \rightarrow \infty$ and

$$\begin{aligned} \int _0^\infty K(t) dt = \prod _{j=1}^3 \int _0^\infty K_j(t) dt = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j}. \end{aligned}$$

(9.18)

All solution of (3.3) satisfying (3.8) are solutions of (9.17) that are bounded and bounded away from zero. The latter follows from Theorem 5.3.

To bring this equation into the form of Theorem B.40 in (Thieme 2003), we normalize $K$ and set

$$\begin{aligned} f(x_3) = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} G(x_3) = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} x_3 \psi (x_3) . \end{aligned}$$

(9.19)

By (4.1),

$$\begin{aligned} f(x_3) = x_3 {\mathcal R}( x_3 ). \end{aligned}$$

(9.20)

We see that a fixed point of $f$, $f(x_3) = x_3$, corresponds to the third coordinate of an interior equilibrium for which ${\mathcal R}(x_3)=1$. Since ${\mathcal R}_0 > 1$, $f(x_3) > x_3$ if $x_3 > 0$ is small and $f(x_3) < x_3$ if $x_3 >0$ is large. By Theorem B.40 in (Thieme 2003), all solutions of (9.17) that are bounded and bounded away from zero converge to $x_3^*$ if $x^*_3$ is the only $z > 0$ with $f(f(z)) = z$.

The latter condition is satisfied if all solutions of the difference equation $z_{n+1} = f(z_n)$ converge to $x_3^*$ if the initial datum satisfies $z_0 >0$.

Proof of Corollaries 5.5 and 5.4

If $s^2 \psi (s)$ is a strictly increasing function of $s$, i.e., $s f(s)$ is a strictly increasing function of $s \ge 0$, this follows from [Thieme (2003), Cor.9.9].

If $\psi (s) = \beta e^{-\alpha s}$, we rescale $z_n = x^* y_n$. Notice that ${\mathcal R}_0 = e^{\alpha x_3^*}$. Then

$$\begin{aligned} y_{n+1} = y_n e^{x^*(1-y_n)}. \end{aligned}$$

By [Thieme (2003), Thm.9.16], all solutions $(y_n)$ of this difference equation converge to 1 for $y_0 > 0$ if and only if $2 \ge \alpha x_3^* = \ln {\mathcal R}_0$. This proves that the interior equilibrium attracts all solutions with nontrivial initial conditions.

For the local stability, Notice that $\psi '(x_3^*)=-\alpha \beta e^{-\alpha x^*}=-\alpha \psi (x_3^*)<0$. The stability condition in Theorem 5.1 becomes $\alpha x_3^* \le 2$. Since $\psi (x_3^*)= \frac{\psi (0)}{{\mathcal R}_0}$, $e^{-\alpha x_3^*} = 1/{\mathcal R}_0$ and $\alpha x_3^* = \ln {\mathcal R}_0$. This implies the assertion. $\square$