Nanomechanics of minerals: understandings and developments through instrumented nanoindentation techniques

Abstract

Understanding the dynamics of the lithosphere relies heavily on the scale-dependent rheology of minerals. While quartz, feldspar, and phyllosilicates are the key phases to govern the rheology of the crust and tectonic margins, olivine and other mafic phases control the same in the upper mantle. Phase transition, solid-state substitution, polymorphism, etc. also affect mineral phase rheology. High pressure–temperature deformation tests with natural, synthetic and analog materials have improved our interpretation of the geodynamic state of the lithosphere. However, deforming and studying a single crystal is not easy, because of the scarcity of specimens and laborious sample preparations. Experimental micro- to nanoindentation at room and/or elevated temperatures has proven to be a convenient method over mesoscale compressive testing. Micro- to nanoindentation technique enables higher precision, faster data acquisition and ultra-high resolution (nanoscale) load and displacement. Hardness, elastic moduli, yield stress, fracture toughness, fracture surface energy and rate-dependent creep of mono- or polycrystalline minerals are evaluated using this technique. Here, we present a comprehensive assessment of micro- to nano-mechanics of minerals. We first cover the fundamental theories of instrumented indentation, experimental procedures, pre- and post-indentation interpretations using various existing models followed by a detailed discussion on the application of nanoindentation in understanding the rheology and deformation mechanisms of various minerals commonly occur in the crust and upper mantle. We also address some of the major limitations of indentation tests (e.g., indentation size effect). Finally, we suggest potential future research areas in mineral rheology using instrumented indentation.

Introduction

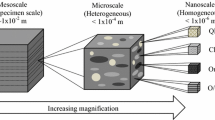
Since the 1980s, instrumented indentation has been widely utilized to explore mineral and rock rheology, submicron-scale deformation mechanisms, as well as various geotechnical applications relating to rock fracturing and associated phenomena. Indentation tests employ probing mechanism, in which an indenter tip probes the specimen surface with a regulated force and displacement to characterize its mechanical properties. Instrumented indentations are scale-dependent experiments, hence macro-, micro-, and nanoindentation terms necessitates to specify dimensional limitations and magnitude of the load. To standardize the definition, ISO (2002, 14577-1) established load and load-induced displacement threshold values to distinguish between mesoscale uniaxial compression, micro-, and nanoindentation (Fig. 1). The morphological characteristics of indents provide essential information about a material's strength, and its nature of scale-dependent deformation (Lips and Sack 1936).

Fig. 1

Schematic illustrations depicting the load, maximum displacement (h_max) and grain size resolution of macroscale uniaxial compressive tests, microindentation, and nanoindentation as per the ISO 2002 standards. Instrumented indentation can also be achieved through Atomic Force Microscopy (AFM), which provides even finer load and displacement resolution (modified after Weaver et al. 2016)

Since indentation hardness depends on the indented area, the mechanical properties obtained from hardness are highly sensitive to indenter geometry. For indentation, various geometrical forms are used (Table 1), and the internal angles between different sides of all indenters are calibrated to yield equivalent hardness for the same applied load. Technological advancements allowing low-load capacity and improved precision emerged in the nineteenth century, paved the way for integrated study of tribology (Brinell 1900; Ludwik 1908; Rockwell 1922; Smith and Sandland 1925; Alekhin et al. 1971; Grodzinski 1953; Kinosita 1972). Later, sophisticated instrumentation enabled simultaneous load and indentation displacement monitoring (Ternovskij et al. 1973). This improved the mathematical underpinnings for estimating a material's hardness-derived elastic modulus and contact stiffness from the indentation load–displacement curves. Subsequently, ultra-low-load indentation tests permitted in-situ nm-scale displacement measurements (Newey et al. 1982; Pethicai et al. 1983) which was later theorized by Oliver and Pharr (1992).

Table 1 Indenter geometry, shape of the indentation contact area, and formulae for calculating Hardness and indentation depth for different testing methods (after Mukhopadhyay and Paufler 2006)

With progressive technological advancements, instrumented indentation became one of the fundamental scaffoldings of materials science research, envisaging the understanding of lattice dynamics of metals, alloys and composites. The potential of this method inspired geologists to incorporate this tool for characterizing the physicochemical properties of geomaterials, covering brittle, brittle-ductile, and ductile deformation of minerals. Micro- to nanoindentation permits instantaneous plastic deformation at ambient temperature and pressure through a locally confined applied stress that governs brittle fracturing; making the procedure quick and least destructive (Kranjc et al. 2016; Ma et al. 2020). The micro- to nanoscale load–displacement resolutions, allow direct experimental evaluation of lattice scale deformation mechanisms (Fischer-Cripps 2011). Infinitesimal contact area and minuscule load along with manual regulation over strain rates, creep deformation can be easily achieved even at room temperatures. It is also possible to investigate the microstructural heterogeneity of a composite rock system through indentation, which is otherwise difficult to obtain from a conventional compressive test (Ma et al. 2020; Manjunath and Jha 2019). Modern instrumentations come with integrated in-situ heating mechanism, Scanning Electron Microscopy (SEM), Electron Backscattered Diffraction (EBSD), and Atomic Force Microscopy (AFM) which further facilitates investigations of temperature-dependent micro- to nano-mechanics of minerals and subsequent sophisticated analyses.

This article aims to provide a comprehensive understanding of the theories and applications of micro- to nanoindentation together with several reported applications of instrumented indentation technique in understanding the rheology of rock forming minerals. We begin with the mathematical underpinnings of instrumented indentation, followed by the experimental to analytical methodologies. We then discuss the micro- to nanoindentation studies on some of the important minerals and their scale-dependent deformation mechanisms that occur in the crust and upper mantle. In this direction, we finally suggest the potential future research areas regarding the application of instrumented indentation.

Mechanical parameters via indentation hardness tests

Hardness and elastic modulus from load–displacement curve

In indentation hardness tests, the indenter penetrates a material surface with a load (P) that initiates elastoplastic deformation of the material. A maximum target load (P_max) is fixed before indentation, and the indentation stops when the targeted load is achieved (Fig. 2a). Then, the hardness is defined as the maximum load applied normal to per unit contact area (Fischer-Cripps 2011; Oliver and Pharr 1992).

$$H\, = \,\frac{{P_{\max } }}{{A_{c} }}.$$

(1)

Fig. 2

Illustrates a loading and unloading of an indenter and associated displacements. ${h}_{c}, {h}_{max},$ and ${h}_{f}$ indicate contact depth (1), maximum indentation depth (2) and final depth (3), respectively. ${A}_{c}$ is the contact area of the indenter. b A typical load–displacement curve representing the same described in (a). c Illustrates a situation where “nose” in the unloading curve forms due to viscous flow of a material

Here, A_c is the surface contact area of an indenter tip (Fig. 2a), which is a function of the indenter geometry and determined from the load–displacement curve. However, since the indented region is bounded by curved sloping surfaces, accurate calculation of the contact area is not possible only through microscopic observations, especially when the measurements are carried out on a non-instrumented indentation setup. In that case, a projected contact area is considered based on the indenter geometry. For instance, in case of a Vickers indenter (Table 1), the ideal projected contact area is a square and hence the Vickers hardness (H_V) is given by (Mukhopadhyay and Paufler 2006):

$${H}_{V}= \frac{2{P}_{max}Sin\frac{136^\circ }{2}}{{d}^{2}}= \frac{2{P}_{max}sin68^\circ }{{d}^{2}}=1.8544\frac{{P}_{max}}{{d}^{2}},$$

(2)

where, d is the average diagonal length of the indentation area. The face angle for the Vickers square pyramid is 136°. In case of a Berkovich indenter, the ideal projected contact area is an equilateral triangle (Table 1), and depending upon the geometry of the contact area, Berkovich hardness (H_B) is calculated as (Mukhopadhyay and Paufler 2006):

$${H}_{B}= \frac{2{P}_{max}}{{a}^{2}\sqrt{3}},$$

(3)

where, a is the side length of the equilateral triangle.

The preceding calculations are basic and easy to use because theoretically, the geometry of the indenter tip is considered undistorted. However, in practice, an indenter tip undergoes friction and abrasion while entering a specimen. Repeated indentation causes tip rounding and the geometry at the contact region suffers distortion (Fischer-Cripps 2011). Consequently, the mechanics at the indenter-specimen contact becomes more complex (Broitman 2017). In that case, hardness, and elastic modulus is obtained by analyzing the instrumented indentation load (P)—displacement (h) curve, which consists of a loading and an unloading segment (Fig. 2b). ${h}_{max}$ is the maximum indentation depth achieved at P_max. During removal of the indenter tip from specimen surface, the unloading/rebound displacement is recorded until zero load is reached, and then the final depth (${h}_{f}$) is measured. Theoretically, a tangent drawn at the upper part of the unloading segment provides the material’s Contact Stiffness (S), which is the change in load with respect to per unit change in the indentation depth, i.e. $\left(S= \frac{dP}{dh}\right)$ (Fig. 2b). However, in practice, a power-law relation (Oliver and Pharr 1992) estimates S from the P as a function of h:

$$P= \beta {(h- {h}_{f})}^{m},$$

(4)

where, $\beta$ and $m$ are empirically derived parameters fitted to the P–h polynomial curve. S is then obtained as:

$$S\, = \,\left[ {\left( {\frac{dP}{{dh}}} \right)_{{h = h_{max} }} } \right] \, = \,\beta m\left( {h_{max} - h_{f} } \right)^{m - 1} .$$

(5)

Using S, contact depth (${h}_{c}$) is estimated from the following equation:

$${h}_{c}= {h}_{max}- \epsilon \left(\frac{{P}_{max}}{S}\right),$$

(6)

where, $\epsilon (0\le \epsilon \le 1)$ is Sneddon’s correction factor, which considers the influence of indenter geometry on specimen deformation. $\epsilon$ =1 suggest a flat punch, 0.72 for Vickers indenter and 0.72–0.78 for Berkovich tip indenter (Lepienski and Foerster 2004; Oliver and Pharr 2004; Shuman et al. 2007). Subsequently, ${A}_{c}$ is obtained as a complex polynomial function of ${h}_{c}$ as:

$$A_{c} \, = \, C_{0} h_{c}^{2} + C_{1} h_{c} + C_{2} h_{c}^{1/2} + C_{3} h_{c}^{1/4} + C_{4} h_{c}^{1/6} \, + \ldots ,$$

(7)

where, C_i ($i=1 \mathrm{to} n$) and C₀ denote the numerical coefficients of the indenter shape and the indenter type geometry, respectively. C₀ is 24.56 and 24.5 for Berkovich and Vickers tip, respectively. These coefficients are calibrated experimentally using a fused silica specimen of known mechanical properties.

Because of the elastoplastic deformation at the indenter-specimen contact, the instrument fails to estimate the true elastic modulus of the specimen, rather generates a data on equivalent elastic modulus of the combined indenter-specimen system. This is called the reduced elastic modulus (E_r) and is calculated in conjunction with A_c and S according to the following equation (Oliver and Pharr 1992):

$${E}_{r}= \frac{\sqrt{\pi }}{2B}\frac{S}{\sqrt{{A}_{c}}},$$

(8)

where, B is an empirically derived correction factor that depends on the indenter geometry and is expressed as:

$$B=1+ \frac{1-2{\nu }_{s}}{4\left(1-{\nu }_{s}\right)tan\phi },$$

(9)

where, ${\nu }_{s}$ is the Poisson’s ratio of the target material, and $\phi$ is the half-apical angle of the indenter tip. For conical indenter ($\phi$ ≈70˚), and fused silica as target material, B = 1.034 (Lucca et al. 2010). Using E_r, the true elastic modulus of a material (E_s) can be estimated, given the Poisson’s ratio of the specimen (${\nu }_{s}$) is known:

$$\frac{1}{{E}_{r}}= \frac{1- {\nu }_{s}^{2}}{{E}_{s}}- \frac{1- {\nu }_{i}^{2}}{{E}_{i}},$$

(10)

where, E_i and ${\nu }_{i}$ denotes the true elastic modulus and Poisson’s ratio of the indenter, respectively. For diamond indenter tip, E_i = 1140 GPa and ${\nu }_{i}$ = 0.07 (Broitman 2017).

Although Oliver and Pharr (1992)’s method explains the elastic–plastic behavior of indented materials, it does not explain the viscoelastic deformation (Broitman 2017). Beyond a critical load, materials may exhibit viscous flow, causing a reduction in unloading rate or holding duration. This could imply that the h may continue to increase at a rapid rate even when the indenter is being unloaded, causing a “nose” in the unloading segment of the load–displacement curve (Liu et al. 2021) (Fig. 2c), making S calculations incorrect. Feng and Ngan (2002) proposed a rectification process of the measured S with a linear viscoelastic relation:

$$\frac{1}{{S}_{e}}= \frac{1}{S}+ \frac{{\dot{h}}_{h}}{\left|\dot{P}\right|},$$

(11)

where, S_e is the true elastic contact stiffness, $\dot{P}$ is the loading/unloading rate and ${\dot{h}}_{h}$ is the creep rate prior to unloading, estimated using a polynomial equation fitted into the unloading curve (Liu et al. 2021). The S to S_e ratio provides a dimensionless creep-corrected factor ($\vartheta$) defined as,

$$\vartheta = \frac{S}{{S}_{e}}=S\left(1+ \frac{{\dot{h}}_{h}}{\left|\dot{P}\right|}\right)= 1+ \frac{S{\dot{h}}_{h}}{\left|\dot{P}\right|}.$$

(12)

Applying this correction factor in the elastic–plastic equations (Eq. 7 and 8), we get

$${h}_{c}= {h}_{max}- \epsilon \left(\frac{\vartheta {P}_{max}}{S}\right),$$

(13)

$${E}_{r}= \frac{\sqrt{\pi }}{2B\vartheta }\frac{S}{\sqrt{{A}_{c}}}.$$

(14)

Accordingly, the creep-corrected hardness for Berkovich tip nanoindentation test can be calculated as following:

$${H}_{B}= \frac{{P}_{max}}{24.56{\left[{h}_{max}-\varepsilon \left(\frac{\vartheta {P}_{max}}{S}\right)\right]}^{2}}.$$

(15)

$\vartheta$ accurately estimates the S and E_r of a viscoelastic material exposed to nanoindentation (Liu et al. 2021).

During the loading stage, the peripheral area of the contact zone of a specimen surface may displace laterally, causing a distinctive pattern reflected in the indent morphology (Fig. 3). These features are classified as (i) Pile-up, where the specimen surface is displaced upwards along the edge of the contact zone and then spread out laterally creating an upward curvature of the surface (Fig. 3a), and (ii) Sink-in, where the specimen surface is dragged down along the edge of the contact zone, creating an inward curvature of the surface (Fig. 3b). The degree of pile-up or sink-in can be estimated from the curvature of the loading segment of an indentation load–displacement curve. A polynomial function fitted to the loading segment determines the curvature (${K}^{^{\prime}}$), and relates the material displacement factor according to the following equation:

$$\chi = \frac{{K}^{^{\prime}}}{{C}_{0}H},$$

(16)

where, dimensionless $\chi$ is an indicator of piling-up or sinking-in of displaced material around an indenter. $\sqrt{\chi }>1$ and $\sqrt{\chi }<1$ indicate piling-up and sinking-in, respectively (Kranjc et al. 2016; Mata and Alcalá 2003). $\chi$ is also a function of $\left(\frac{{h}_{f}}{{h}_{max}}\right)$. $\left(\frac{{h}_{f}}{{h}_{max}}\right)\approx 1$, and $\left(\frac{{h}_{f}}{{h}_{max}}\right)<0.7$ for a constant P and $\dot{P}$ test indicates piling-up and sinking-in, respectively (Fischer-Cripps 2011; Oliver and Pharr 2004).

Fig. 3

a Pile-up, and b Sink-in of material around the indenter during indentation, which creates convex outward and convex inward indent morphology, respectively (modified after Fischer-Cripps 2011)

Hardness-derived yield stress and low temperature plasticity (LTP)

Yield stress models

Tabor (1970) provided a linear equation based on slip-line field theory (Hill et al. 1947; Prandtl 1920) that allows conversion between H and uniaxial yield stress (${\sigma }_{y})$ of the material:

$$H=C{\sigma }_{y},$$

(17)

where, C is an empirically obtained constraint factor. This model assumes that the indented material is a perfectly rigid plastic, i.e., no plastic deformation occurs until the yield stress is reached. Since micro- and nanoindentation are scale-dependent processes, the conversion to ${\sigma }_{y}$ allows direct estimation of the uniaxial mechanical properties and constitutive flow laws (Sly et al. 2020). The conversion depends upon the C. Experimental observations suggests that the range of C is 1.1 ≤ C ≤ 3.0, where 1.1 represents the elastic limit and values near to it is observed in materials with high $\left( {E/\sigma_{y} } \right)$ ratio, and 3.0 is the plastic limit, generally observed in materials with low $\left( {E/\sigma_{y} } \right)$ ratio (Evans and Goetze 1979; Fischer-Cripps 2011; Johnson 1970; Shaw and DeSalvo 2012; Swain and Hagan 1976). C can be estimated using several models, however, four of them are extensively used for minerals. They are described briefly in the following paragraphs.

(1) Johnson (1970) proposed that the ratio of H to ${\sigma }_{y}$ of a material is a function of the indenter geometry and E of that material. The indenter forces a fraction of the mass of a material inward, generating a depression of uniform dimension like a bubble inflating by internal hydrostatic pressure (Bishop et al. 1945) (Fig. 4a). The following equation estimates the ${\sigma }_{y}$ of an elastic–plastic solid:

Fig. 4

a Schematic representation of spherical cavity expansion model in a homogeneous and isotropic material. Theoretically, the plastic deformation zone underneath the indenter is considered to expand uniformly resembling a sphere inflating due to internal hydrostatic pressure. The strain gradient decreases gradually from the hydrostatic core near the tip of the indenter to the theoretical Elastic–Plastic boundary (red dashed line), and the strain contours are assumed to be ideally spherical. However, the actual elastoplastic deformation zone expands in an oblate spheroidal form with diverging strain contours away from the indenter tip, and the actual Elastic–Plastic boundary is not spherical (modified after Mukhopadhyay and Paufler 2006). b Schematic representation of an indentation stress–strain curve. The initial linear segment (green color) represents elastic deformation during loading stage, followed by plastic deformation (red color), and again elastic deformation (blue color) during unloading. The slope of the initial linear segment is used to calculate the ${E}_{s}$ of the material. Onset of plastic deformation is marked by the change in the curvature of the curve and is demarcated by the ${\sigma }_{y}$ of the material

$$\frac{H}{{\sigma }_{y}}= \frac{2}{3}\left[1+\mathrm{ln}\left(\frac{\frac{Etan\theta }{{\sigma }_{y}}+4\left(1-2\nu \right)}{6\left(1-\nu \right)}\right)\right].$$

(18)

Here, $\theta$ is the angle between the surface of a conical indenter and the indented surface. $\theta$ will change according to the indenter geometry, and accordingly the $H/\sigma_{y}$ ratio (Fischer-Cripps 2011; Mukhopadhyay and Paufler 2006; Sly et al. 2020). For an ideal incompressible material, $\nu$ = 0.5, and hence Eq. (18) simplifies to:

$$\frac{H}{{\sigma }_{y}}= \frac{2}{3}\left[1+\mathrm{ln}\left(\frac{Etan\theta }{3{\sigma }_{y}}\right)\right].$$

(19)

(2) Evans and Goetze (1979) empirically modified Johnson’s equation for Vickers indenter as:

$$\frac{H}{{\sigma }_{y}}= 0.19+1.6\mathrm{log}\left(\frac{Etan\theta }{{\sigma }_{y}}\right).$$

(20)

(3) Mata et al. (2002) and Mata and Alcalá (2003) included finite element analysis (FEA) into Johnson's model by incorporating reference stress (${\sigma }_{r})$, which is the stress at 10% strain. Their model is described by:

$$\frac{H}{{\sigma }_{r}}= \sum_{i=0}^{4}{c}_{i}{\left[\mathrm{ln}\left(\frac{E}{{\sigma }_{r}}\right)\right]}^{i}.$$

(21)

Here, ${c}_{i}$ is an empirical constant. ${c}_{i}$ and ${\sigma }_{r}$ are determined by finite element analysis. The model also shows that ${\sigma }_{r}$ is also comparable with ${\sigma }_{y}$ in other models. However, this model is valid for materials with 50 ≤ ${\sigma }_{y}$  ≤ 1000 MPa and 7 ≤ $E$  ≤ 200 GPa (Sly et al. 2020).

(4) Ginder et al. (2018) accommodated power-law rheology for creeping solids in Johnson's model by theorizing two constitutive equations correlating uniaxial compression (Eq. 22) with indentation creep (Eq. 23) using Bower’s model (Bower et al. 1993):

$$\dot{\varepsilon }= \alpha {\sigma }_{y}^{n},$$

(22)

$$\dot{{\varepsilon }_{i}}= {\beta }_{i}{H}^{n}.$$

(23)

Here $\dot{\varepsilon }$ and $\dot{{\varepsilon }_{i}}$ are the uniaxial, and indentation strain rates, respectively. $n$ is the stress exponent. ${\beta }_{i}$ is an empirical term in indentation creep and related to $\alpha$ as in the following equation:

$$\alpha = {\beta }_{i}{F}^{n},$$

(24)

where, F is the reduced contact pressure. Ginder’s model holds well for n $\le$ 7. n $>$ 7 results in underestimation of the yield stress (Sly et al. 2020).

Stress–strain relations from spherical indentation

Spherical and/or sphero-conical indenters are used to derive the indentation stress–strain relation which can provide the information about the onset of plastic deformation during an indentation test. Thus, ${\sigma }_{y}$ can be determined from the Indentation stress (${\sigma }_{i}$) vs Indentation strain (${\varepsilon }_{i}$) curve. The blunt tip of a spherical indenter obeys the elastic contact theory, and therefore produces distinguishable elastic and plastic deformation during indentation. ${\sigma }_{i}$ is generally expressed in the following form (Field and Swain 1993):

$${\sigma }_{i}= \frac{P}{\pi {a}_{r}^{2}},$$

(25)

where, ${a}_{r}$ is the radius of contact boundary at any given P. According to elastic contact theory, P and ${a}_{r}$ are expressed as:

$$P= \frac{4}{3}{E}_{r}{R}_{r}^\frac{1}{2}{h}_{max}^\frac{3}{2},$$

(26)

$${a}_{r}=\sqrt{{R}_{r}{h}_{e}}.$$

(27)

${h}_{e}$ (Eq. (27)) is the recoverable displacement (${h}_{e}={h}_{max}-{h}_{f}$) signifying the elastic deformation component. ${R}_{r}$ is the relative radius of indentation curvature, produced as a combined result of indenter (${R}_{i}$) and sample (${R}_{s}$) radii during indentation. It is expressed as:

$$\frac{1}{{R}_{r}}=\frac{1}{{R}_{i}}+\frac{1}{{R}_{s}}.$$

(28)

Basu et al. (2006) proposed a simple equation to derive ${a}_{r}$, and subsequently ${\varepsilon }_{i}$, which are expressed in the following forms:

$${a}_{r}=\sqrt{2{R}_{i}{h}_{c}-{h}_{c}^{2}},\, {\varepsilon }_{i}=\frac{4{a}_{r}}{3\pi {R}_{i}}.$$

(29)

Kalidindi and Pathak (2008) proposed another set of equations for determining ${a}_{r}$ and ${\varepsilon }_{i}$ by analyzing the P–h curves and using ${R}_{r}$:

$${a}_{r}={\left(\frac{3P{R}_{r}}{4{E}_{r}}\right)}^\frac{1}{3},\quad \, {\varepsilon }_{i}=\frac{4{h}_{max}}{3\pi {a}_{r}}.$$

(30)

One can use any combination of ${a}_{r}$ and ${\varepsilon }_{i}$ from Eqs. (29 and 30), all of which may produce significantly different ${\sigma }_{i}$ and ${\varepsilon }_{i}$. However, the slope of the linear (or elastic deformation) segment of the ${\sigma }_{i}-{\varepsilon }_{i}$ curve obtained from all the combinations remain same, implying that ${E}_{s}$ (${E}_{s}=\frac{{\sigma }_{i}}{{\varepsilon }_{i}})$ can be precisely estimated through the ${\sigma }_{i}-{\varepsilon }_{i}$ curves. The point in the ${\sigma }_{i}-{\varepsilon }_{i}$ space from which the curve starts to bend and produces a nonlinear segment is the yield point (Fig. 4b), and the corresponding ${\sigma }_{i}$ is the ${\sigma }_{y}$ for the given ${P}_{max}$ and ${\dot{\varepsilon }}_{i}$ (Pathak and Kalidindi 2015). However, for accurate estimation of ${\sigma }_{y}$, one must determine the zero point of the ${\sigma }_{i}-{\varepsilon }_{i}$ curves. There are several methods for determining the zero point, and (Pathak and Kalidindi 2015) have elaborately reviewed them all. Apart from the mentioned equations of ${\varepsilon }_{i}$, there are several other forms used such as, ${\dot{\varepsilon }}_{i}=\frac{d}{D}, {\dot{\varepsilon }}_{i}=tan\theta$, etc. (Pathak and Kalidindi 2015). Spherical nanoindentation has been used on Olivine (Kumamoto et al. 2017), Biotite (Lanin et al. 2021), and Muscovite (Basu et al. 2009) for determining ${\sigma }_{y}$ from the indentation stress–strain relation.

Low-temperature plasticity (LTP)

Low-temperature plasticity (LTP) refers to instantaneous plastic deformation by dominantly dislocation glide of a material, at room temperature (Frost and Ashby 1982; Tsenn and Carter 1987). The constitutive equation for an obstacle-limited dislocation is (Orowan 1940):

$$\dot{\varepsilon }= \rho b{\overline{v} }_{d},$$

(31)

where, $\rho$ is the dislocation density, a nonlinear function of ${\sigma }_{y}$, $b$ is the Burger’s vector for a particular slip system and ${\overline{v} }_{d}$ is the average dislocation velocity for the given slip system. ${\overline{v} }_{d}$ varies exponentially as a function of activation enthalpy (Q) and absolute temperature (T) of the material according to the following equation (Frost and Ashby 1982):

$${\overline{v} }_{d} \propto {e}^{-\frac{Q}{RT}},$$

(32)

where, R is the universal gas constant. The Q(T) depends on the zero-stress activation enthalpy (${Q}_{0}$), ${\sigma }_{y}$ and athermal Peierls stress (${\sigma }_{P}$), defined as the critical stress required for obstacle-free dislocation at $T=0K$ for a kind of plastic deformation constrained by lattice friction (Frost and Ashby 1982; Karato 2008). The following nonlinear equation describes their relationship:

$$Q\left(T\right)= {Q}_{0}{\left[1-{\left(\frac{{\sigma }_{y}}{{\sigma }_{P}}\right)}^{p}\right]}^{q},$$

(33)

where, $p (0<p\le 1)$ and $q (1\le q\le 2)$ are the dimensionless flow-law constants that depend on the energy barrier to dislocation (Kocks et al. 1975; Kranjc et al. 2016).

Since the $\rho$ is a function of ${\sigma }_{y}^{2}$, substituting Q in Eq. (32) and $\rho$ by ${\sigma }_{y}^{2}$ in Eq. (31), the constitutive equation for LTP is:

$${{\dot{\varepsilon }}_{LTP}=A\sigma }_{y}^{2}{e}^{-\left[\left(\frac{{Q}_{0}}{RT}\right){\left(1-{\left(\frac{{\sigma }_{y}}{{\sigma }_{P}}\right)}^{p}\right)}^{q}\right]},$$

(34)

where, ${\dot{\varepsilon }}_{LTP}$ is the LTP strain-rate, A is a material-dependent empirically derived preexponential constant. For a particular material, when ${\sigma }_{y}$ tends to ${\sigma }_{P}$, it shows plastic deformation where the $\dot{\varepsilon }$ virtually becomes independent of temperature.

Fracture toughness and fracture surface energy

Fracture toughness (K_C) of any brittle substance describes its resistance to crack propagation when subjected to external loads. The degree and duration of preexisting fractures affect K_C. The longer a crack is, the lower the stress required to cause a fracture, causing a lower K_C. It is also proportional to the energy expended during plastic deformation (Fischer-Cripps 2011; Vaidya and Pathak 2019). Generally, radial and lateral cracks appear during indentation. While microindentation causes frequent fracturing of the indented specimens, nanoindentation tests show no significant fracturing of the same. During the loading stage, the plastic deformation zone expands, causing tensile stress to develop. While unloading, the elastically stretched material around the indented area tends to revert to its previous shape, causing fractures due to the resistance from the plastically deformed zone. The cracking intensity increases with stress. Here we present the two most generally used methods for determining K_C—the geometrical and energy analysis approaches, addressed in the following sections.

Crack-length based method

In this method, the length of radial cracks, whose orientation is greatly influenced by the indenter geometry, quantifies K_C. The length of radial cracks is measured from the indented corner to the material’s undeformed area (Fischer-Cripps 2011). K_C is a function of $E/H$ (Lawn et al. 1980) and estimated using the following equation:

$$K_{C} = k\left( \frac{E}{H} \right)^{N} \frac{P}{{c^{3/2} }},$$

(35)

where, k is an empirically derived calibration constant. The suggested values of N and k are 0.5, 0.016 (Lawn et al. 1980) and 1.5, 0.0098 (Anstis et al. 1981), respectively. c is the radial crack length measured from the center to the tip of the crack (Fig. 5a, b). $\frac{P}{{c^{3/2} }}$ is a material-specific constant and varies depending on the mechanical properties of a substance. Laugier (1987) redefined K_C as:

$$K_{C} = x_{\nu } \left( {\frac{{a_{c} }}{l}} \right)^{\frac{1}{2}} \left( \frac{E}{H} \right)^{\frac{2}{3}} \frac{P}{{c^{3/2} }},$$

(36)

where, ${x}_{\nu }$ is a constant initially determined to be 0.015, a_c and l are length dimensions calculated from center to the tip of the crack, and corner to the end of the crack, respectively (Fig. 5a, b). Dukino and Swain (1992) modified Eq. (36) for Berkovich tip using the method of Ouchterlony (1976), and proposed:

$$K_{C} = 1.073x_{\nu } \left( {\frac{{a_{c} }}{l}} \right)^{\frac{1}{2}} \left( \frac{E}{H} \right)^{\frac{2}{3}} \frac{P}{{c^{3/2} }}.$$

(37)

Fig. 5

Crack geometry around a Vickers indentation, and b Berkovich indentation (after Fischer-Cripps 2011). Here, c is the radial crack length, a_c and l are the crack lengths measured from center of the indentation to the end of the crack, and edge of the indentation to the end of the crack, respectively. c Plastic energy (U_p) and Elastic energy (U_e) calculated from area under the load–displacement curve (after Ma et al. 2022)

Energy analysis method

In this method, K_C is indirectly estimated by balancing the total mechanical energy during indentation. The total mechanical energy (U) is divided into two parts viz., elastic- (${U}_{e})$ and plastic- (${U}_{p})$ energies. The ${U}_{p}$ contains a fraction of induced fracture energy (${U}_{f})$ and the remaining part is attributed to purely plastic deformation (${U}_{pp})$. The energy balance equation is as follows (Cheng et al. 2002, Ma et al. 2020):

$$U= {U}_{e}+ {U}_{p}= {U}_{e}+{U}_{f}+{U}_{pp}.$$

(38)

Hence, ${U}_{f}$ can be expressed in terms of residual energy accordingly:

$$U_{f} = U - U_{e} - U_{pp} .$$

(39)

By combining elastic fracture mechanics conditions with the existing energy balance approach, ${K}_{C}$ can be estimated according to the following equations:

$${\text{K}}_{{\text{C}}} = \sqrt {{\text{G}}_{C}^{\prime} {\text{E}}_{{\text{r}}} } \,({\text{applicable for plane stress condition)}}$$

(40)

$$K_{C} = \sqrt {G_{C}^{\prime} E_{r} \left( {1 - \nu ^{2} } \right)} ({\text{applicable}}\, {\text{for}}\,{\mkern 1mu} {\text{plane}}\,{\mkern 1mu} {\text{strain}}\,{\mkern 1mu} {\text{condition}}),$$

(41)

where, $G_{C}^{\prime }$ is the strain energy discharge density defined as:

$$G_{C}^{\prime } = \frac{{U_{f} }}{{A_{C} }}.$$

(42)

The ${U}_{f}$ must be calculated from the energy balance equation. U and ${U}_{e}$ can be determined from area under the load displacement curve (Fig. 5c) in the form of integrals, $U= \underset{0}{\overset{{h}_{max}}{\int }}Pdh$, ${U}_{e}= \underset{{h}_{f}}{\overset{{h}_{max}}{\int }}Pdh$. However, the ${U}_{pp}$ is obtained empirically. Cheng et al. (2002) estimated ${U}_{pp}$ using FEA and experimental observations. The concerned relation is:

$${U}_{pp}=2\left[\left(\frac{{h}_{f}}{{h}_{max}}\right)-1\right]U.$$

(43)

By combining Eqs. (38, 39, 40, 41, 42 and 43), ${K}_{C}$ is calculated using:

$$K_{C} \, = \, \left[ {\frac{{E_{r} }}{{A_{C} }}\left\{ {U\left( {3 - \frac{{2h_{f} }}{{h_{max} }}} \right) - U_{e} } \right\}} \right]^{\frac{1}{2}} \left( {{\text{applicable}}\,{\text{for}}\,{\text{plane}}\,{\text{stress}}\,{\text{condition}}} \right),$$

(44)

$$K_{C} \, = \, \left[ {\frac{{E_{r} }}{{A_{C} }}\left\{ {U\left( {3 - \frac{{2h_{f} }}{{h_{max} }}} \right) - U_{e} } \right\}\left( {1 - \nu^{2} } \right)} \right]^{\frac{1}{2}} \left( {{\text{applicable }}\,{\text{for}}\,{\text{plane }}\,{\text{stress}}\,{\text{condition}}} \right).$$

(45)

Fracture surface energy

Fracture surface energy $(\Gamma$) of various silicate minerals is determined to understand phase transition-related mechanical weakening under external load and at high temperatures (Atkinson and Avdis 1980; Darot et al. 1985; Swain and Atkinson 1978; Swain and Lawn 1976). $\Gamma$ is defined as the energy required per unit area to form a new fractured surface. If c >  > d, the ratio of P to c obeys a linear relationship with $\Gamma$ according to the following equation (Lawn and Wilshaw 1975; Lawn and Swain 1975):

$$\frac{P}{c}={A}_{i}\frac{E}{(1-{\nu }^{2}){(1-2\nu )}^{2}}\frac{\Gamma }{{H}_{M}},$$

(46)

where, ${H}_{M}$ is the Meyer-Vicker hardness (H_M $=1.079{H}_{V}$). Equation (46) is applicable to conical indenters, while for a spherical indenter the equation is modified to a nonlinear relation:

$$\frac{{P}^{2}}{{c}^{3}}={B}_{i}\frac{E}{g(\nu )}\Gamma .$$

(47)

Here, B_i is an empirically derived factor and $g(\nu )$ is a function of Poisson’s ratio of the material.

$\Gamma$ is measured from the slope of a ${(P}^{2}-{c}^{3})$ curve where E is considered constant. However, as E decreases with increasing temperature, it causes a similar decrease in hardness as well as $\Gamma$ of a material.

Ideally, if there is no dissipation of ${U}_{pp}$, then $\Gamma$ approximates the thermodynamic surface energy ($\xi$) (Swain and Atkinson 1978), which is expressed as (Lawn and Wilshaw 1975):

$$\xi \approx \frac{E{d}_{0}}{{\pi }^{2}},$$

(48)

where, ${d}_{0}$ is the lattice spacing along a specific crystallographic direction. Since the variation of ${d}_{0}$ with temperature is negligible compared to E, variation of $\xi$ with temperature manifests as a function of E only. Experimental observations suggest that $\Gamma =\xi$ at low temperatures. However, at higher temperatures, secondary slip systems within the plastic zone assists the lateral cracks to generate shear stress on the dislocations, causing a drag that is dissipated as an extra amount of energy other than Γ (Darot et al. 1985; Gaboriaud et al. 1981). In that case, $\Gamma >\xi$ and the difference between those two is expressed as (Darot et al. 1985):

$$\Gamma - \xi = \mathop \sum \limits_{i} \tau_{{c_{i} }} b_{i} ,$$

(49)

where, ${\tau }_{{c}_{i}}$ is the crack induced shear stress on ith dislocation and ${b}_{i}$ is the Burger’s vector for that slip system.

Specimen preparation, instrumentation and experimental methods

Specimen preparation and instrument setup

Indentation tests require smooth and solid specimen surface devoid of any roughness or asperities. Hence, specimen preparation involves grinding and polishing of the surface. Diamond film polishing is done with progressively finer particle sizes up to 0.25 μm after the specimen has been cut to the required dimensions. Colloidal silica, Hydrofluoric acid etching, and high-temperature KOH are employed to provide an even finer polish (e.g. Evans 1984). For mircoindentation tests, specimen surface should be polished to a roughness < 5%, according to ISO-2002 requirements. For nanoindentation, the influence of surface roughness is often minimized either by performing statistically larger numbers of tests or by assigning higher indentation depths (Lucca et al. 2010). Specimen dimensions are subject to the scale of indentation. For microhardness tests, a minimum thickness of 5 mm is required. Lateral dimensions may vary according to instrument specifications. For nanoindentation tests, on the other hand, specimen thickness can be as minimum as 0.1 μm, generally known as thin film specimens (Li and Bhushan 2002). In general, the thickness of the specimen should be at least ten times greater than ${h}_{max}$, and the distance between two consecutive indentations should be at least three times greater than d, so that the plastic deformation zone can expand uniformly inside the material (ISO 2002, 14577-1). Depending on the mode of microscopy (reflected or transmission), specimen thickness can be reduced to petrographic standards for post-indentation optical analysis. Specimens are commonly mounted on epoxy stubs for room temperature indentation tests, however for high-temperature studies, aluminum or steel stubs are utilized, with the specimens attached on them using heat resistant thermally conductive adhesives. Specimens are placed on a holder, which is subsequently placed on a motorized stage with a < 0.5 μm displacement resolution x–y–z translation facility. Optical rotary systems or linear track encoders are commonly used to track movement, and the entire instrument setup is integrated by a program provided by the manufacturer for automatic specimen positioning under the indenter. The load is applied to the indenter shaft using an electromagnetic coil or an expanding piezoelectric element. The corresponding displacement is measured either by monitoring the variation of capacitance or the inductance signal (Fischer-Cripps 2011).

Instrument modifications such as heating stage, thermocouples, and oxidation-free environment are required for high-temperature tests. Temperatures as high as 1500 °C have been reported (e.g. Evans and Goetze 1979). Generally, to avoid surface-oxidation related consequences, Argon filled chambers are used (e.g. Darot et al. 1985). The specimen is placed atop the heating stage; both specimen and indenter are brought to the same temperature by either separate heating mechanisms or keeping them together in contact. Attaining thermal equilibrium prior to indentation is necessary to avoid the thermal drift effect, an influencing factor in interpreting indentation results. The temperature of the specimen surface and the indenter is continuously monitored during indentation using thermocouples while increasing it in a regular interval. Indentations are made on different locations of the specimen surface at different temperatures. Materials such as diamond, tungsten carbide, sapphire, etc. can retain almost constant mechanical properties for fairly high temperatures. Therefore, they are used as indenters (Lucca et al. 2010). Depending on the nature of the test, different indenters can be used. A pointed indenter, such as a Berkovich tip, can easily achieve plastic deformation. It provides information about a material's yielding and subsequent flow laws. Spherical or sphero-conical indenters, on the other hand, are used to observe elastic deformation and determine a material's elastic modulus (ISO 2002, 14577-1, Lucca et al. 2010).

Testing methods in instrumented indentation

Load-unload-reload-unload, cyclic and multistep tests

Load and displacement resolutions differ largely between micro- and nanoindentation. For microindentation, the minimum load is 1 to 10 mN and reaches 2 N with 1 mN load and 10 nm displacement precision. Nanoindentation typically employs $\le$ 100 mN with 1 nN load and 1 nm displacement resolution (ISO 2002, 14577-1). Loading and unloading rates are usually constant for indentation tests with a short holding period, but they can be changed based on the test’s purpose. When monitoring elastic–plastic deformation, the unloading rate is often kept higher than the loading rate to avoid indentation creep.

Three types of tests are performed: (a) load–unload–reload–unload test (Fig. 6a-i), (b) cyclic loading–unloading test (Fig. 6a-ii), and (c) multistep test (Fig. 6a-iii) (Shuman et al. 2007). The loading and unloading rates are kept constant in load–unload–reload–unload and cyclic loading–unloading tests, while the load is incremented in each step in a multistep test. A load–unload–reload–unload curve can compare hardness, whereas a cyclic loading–unloading curve, which is a multiple repetition of the load–unload–reload–unload curve, is used to evaluate elastic modulus. The multistep test qualitatively analyses a material's yield strength, onset of plastic deformation, and elastic modulus at several depths from a single indent. Multistep tests are better than single indentation tests for studying polycrystalline aggregates, since it is often performed on a single site, so the relative orientation of a single grain to the indentation axis remains constant during the indentation, resulting in a more homogeneous data than applying individual indentations on grains with diverse orientations.

Fig. 6

a Typical load–displacement curves for (i) Load-unload-reload-unload, (ii) Cyclic, and (iii) Multistep indentation testing (after Shuman et al. 2007). b Load–displacement curve for continuous stiffness measurement (CSM). c Comparison between macroscale creep test and nanoindentation creep. A conventional creep test consists of (A) Transient, (B) Steady-state, and (C) Tertiary creep stages. Whereas, in nanoindentation, only the first two stages are observed. d Nature of the load-time curves for linear loading rate ($\dot{P})$ test (green), which is used to characterize elastoplastic behavior, and constant strain rate ($\dot{\varepsilon }$) test (red), which is used to characterize viscoelastic and/or viscoplastic behavior of materials. t₁, t₂, and t₃ indicates loading period, holding period, and unloading period, respectively. e Load–displacement curves for materials of different rheology (after Fischer-Cripps 2011)

When the maximum load is attained, the indenter is held for a specified time, where most materials exhibit creep displacement due to dislocation along specific slip systems activated under high static pressure in the indentation stress field (Fischer-Cripps 2006). However, this displacement is not always due to creep; it can also be due to thermal drift, where the h may change over time. Temperature differences at the indenter-specimen contact can produce undesirable thermal expansion, causing a change in the indenter's dimension relative to the specimen surface and an apparent increase/decrease in h (Fischer-Cripps 2011, 2006). ISO 2002, 14577-1 recommends putting the indentation system in a thermally insulating container to prevent thermal drift and maintain the temperature equilibrium.

Continuous stiffness measurement (CSM)

In Continuous Stiffness Measurement (CSM), a low-amplitude external sinusoidal signal is superimposed over the DC signal, causing the indenter to oscillate at a steady frequency. The signal is filtered using a frequency-selective amplifier to obtain the P–h data. CSM allows immediate measurement of mechanical parameters from the loading curve, without the need for a discrete unloading cycle (Fig. 6b) (Oliver and Pharr 1992; Pethica and Oliver 1988; Syed Asif and Pethica 1997). The measurements are acquired from infinitesimally small h, appropriate for high precision nanoindentation testing on optically thin films, since the test is performed at a single spot on the specimen surface with a high frequency of loading cycle (40 Hz). Both P and h are stated using the simple harmonic equation during CSM:

$$P = P_{0} \exp \left( {i\omega t} \right), h = h_{0}^{^{\prime}} \exp \left( {i\omega t + \varphi } \right).$$

(50)

Here, $\omega$ is the angular frequency and $\varphi$ is the phase difference between P ($\omega$) and h ($\omega$). Solving for the in- and out-phase of the output signal yields the S in case of CSM:

$$S= {\left[\frac{1}{\frac{{P}_{0}}{h(\omega )}cos\varphi -({K}_{s}-M{\omega }^{2})}- {{K}_{f}}^{-1}\right]}^{ -1},$$

(51)

where, M is the mass of the indenter, ${K}_{s}$ is the spring constant of the leaf spring that supports the indenter during its oscillation and ${K}_{f}$ is the stiffness of the indenter frame. This equation shows that S varies continuously as a function of h and is determined for any position along the P–h curve of CSM (Li and Bhushan 2002). The change in h(t) is continuously monitored to measure indentation-creep. Since the indenter tip is insensitive to drift, it can accurately measure creep in small indents over a longer period (Li and Bhushan 2002). CSM is effective in determining the indentation-creep behavior of bulk and multilayered materials. during the holding stage in a CSM test, H is measured as a function of h. Creep occurs when the h increases with time whereas H decreases. Simultaneous monitoring of H and h, thus provides proper quantification of indentation-creep.

Indentation creep tests

A typical macroscale creep test comprises of three stages of deformation viz., Primary or Transient creep, Secondary or Steady-state creep and Tertiary creep. However, indentation-creep only shows the first two stages (Fig. 6c). The initial creep displacement occurs at a high $\dot{\varepsilon }$, decreasing with time and maintaining a steady state. Room temperature indentation creep is generally accommodated by dislocation motions on preexisting slip planes; With rising temperature, new slip planes are triggered, and dislocation interactions promote strain hardening. The indentation stress (${\sigma }_{i}$) decreases with increasing creep displacement (h_creep) as a function of time according to the following equation (Hackney et al. 2012; Sun et al. 2021):

$${\sigma }_{i}= \frac{\beta P}{{h}^{2}(t)},$$

(52)

where h(t) is the instantaneous indentation depth. ${\dot{\varepsilon }}_{i}$ can be expressed as a first order time derivative of h(t) as follows:

$${\dot{\varepsilon }}_{i}= \frac{d{\varepsilon }_{i}}{dt}= \frac{1}{h(t)}\frac{dh(t)}{dt}\approx \frac{\dot{P}}{P}.$$

(53)

Integrating the above equation for the total holding time provides the total strain:

$$\varepsilon =\mathrm{ln}\left(\frac{{h}^{^{\prime}}\left(t\right)}{{h}_{0}}\right),$$

(54)

where, ${h}_{0}$ is the initial depth prior to creep and ${h}^{^{\prime}}\left(t\right)$ is the final depth. h_creep, thus, can be calculated as:

$${h}_{creep}= {h}^{^{\prime}}\left(t\right)- {h}_{0}$$

(55)

Constant ${\dot{\varepsilon }}_{i}$ can be achieved by constant $\dot{P}$ indentation tests. In that case, the nature of P–t curve becomes parabolic (Fig. 6d).

${\dot{\varepsilon }}_{i}$ can be converted to $\dot{\varepsilon }$ using Eqs. 22, 23 and 24. However, for precise estimation of the uniaxial property, one needs to incorporate the “sink-in” or “pile-up” related corrections along with the effect of indenter geometry. The modified version of Eq. (24) is therefore given below (Su et al. 2013; Thom and Goldsby 2019):

$$\alpha = \frac{\beta {F}^{n}{\chi }^{2n-1}}{tan\theta }.$$

(56)

The viscoelastic deformation of minerals can be quantified using several curve-fitting models that estimate the viscous and elastic parameters of a material. These models are constructed using springs (elastic component) and dashpots (viscous component) connected in several combinations of series and parallel alignments to replicate the experimental data. Some of the models are briefly described below.

Three element Voigt model

This model represents a Kelvin-Voigt material (a spring and a dashpot attached in parallel connection) with a spring attached in series connection. A Semi-empirical equivalent of this model of indentation-creep uses h(t) to determine viscoelastic parameters (Ashraf and Tian 2016; Fischer-Cripps 2004; Shi et al. 2020; Wang et al. 2022):

$${h}^{2}\left(t\right)= \frac{\pi }{2}{P}_{max}cot\phi \left[ \frac{1}{{E}_{1}}+ \frac{1}{{E}_{2}}\left(1-{e}^{-\frac{{E}_{2}t}{{\eta }_{1}}}\right)\right],$$

(57)

where, ${E}_{1}$ and ${E}_{2}$ represents the instantaneous and long-term reversible creep elastic modulus, respectively. ${\eta }_{1}$ is the long-term creep viscosity.

Four element Burger’s model

This model represents a Kelvin-Voigt element attached with a spring and a dashpot in a series connection. The following equation describes the indentation-creep phenomenon in terms of h and P_max (Liu et al. 2018; Shi et al. 2020):

$${h}^{2}\left(t\right)= \frac{\pi }{2}{P}_{max}cot\phi \left[ \frac{1}{{E}_{1}}+ \frac{1}{{E}_{2}}\left(1-{e}^{-\frac{{E}_{2}t}{{\eta }_{21}}}\right)+ \frac{t}{{\eta }_{1}}\right].$$

(58)

Here, ${\eta }_{21}$ is the creep time constant. The above equation can be simplified to the following form:

$${h}^{2}= {B}_{0}+ {B}_{1}\left(1-{e}^{-\frac{t}{{\eta }_{21}}}\right)+ {B}_{2}t,$$

(59)

where, ${B}_{0}$ represents the post-loading elastic deformation component; ${B}_{1}$, ${B}_{2}$ are the primary creep coefficients. Equation (59) is iteratively fitted into the h-t curve to obtain the viscoelastic parameters.

Two dashpot/Five element Kelvin model

This model represents two Kelvin-Voigt elements attached with a spring in series connection. The following equation, represents the indentation-creep deformation of a material (Menčík et al. 2009; Shi et al. 2020):

$${h}^{2}\left(t\right)= \frac{\pi }{2}{P}_{max}cot\phi \left[ \frac{1}{{E}_{3}}+ \frac{1}{{E}_{1}}\left(1-{e}^{-\frac{{E}_{1}t}{{\eta }_{21}}}\right)+ \frac{1}{{E}_{2}}\left(1-{e}^{-\frac{{E}_{2}t}{{\eta }_{22}}}\right)\right].$$

(60)

This model consists of five elements where ${E}_{1}, {E}_{2}$ and ${E}_{3}$ are the elastic moduli and ${\eta }_{22}$ is the creep time constants. Equation (60) can be simplified to a quadratic equation of the following form:

$${h}^{2}= {B}_{0}+ {B}_{1}\left(1-{e}^{-\frac{t}{{\eta }_{21}}}\right)+ {B}_{2}\left(1-{e}^{-\frac{t}{{\eta }_{22}}}\right)$$

(61)

Like Eq. (59), ${B}_{0}$ is the term represents post-loading elastic deformation and ${B}_{1}$, ${B}_{2}$ are the primary creep coefficients.

Among the three creep models, the two-dashpot Kelvin model best replicates the experimental data and offers a statistically reliable estimate of viscoelastic properties, since consists of more fitting parameters than the other two. However, it is computationally expensive because of multiple parameters. That is why, the four element Burger’s model seems appropriate to understand the indentation-induced viscoelasticity (Ma et al. 2022; Shi et al. 2020; Wang et al. 2022).

Pre- and post-indentation analysis

P–h data is the 1st-order output from an indentation test that offers qualitative information about mechanical properties. By comparing loading–unloading curvatures, one can identify if a material is brittle, ductile, or viscoelastic (Fig. 6e). However, to characterize a material’s rheology, its chemical composition, impurity concentration, and crystallographic orientation must be constrained. Therefore, indentation tests require associated material characterizations. Before indentation, X-Ray Diffraction (XRD) and Energy Dispersive X-Ray Analysis (EDXA) are used to detect a mineral's elemental composition (Dorner & Stöckhert 2004). EDXA maps the elemental make-up by evaluating near-surface elements and their proportions at several sites. This technique is preferred for analyzing polycrystalline aggregates since it does not require specimen pulverization. Secondary Ion Mass Spectrometry (SIMS) (e.g. Strozewski et al. 2021) and Fourier Transform Infrared Spectroscopy (FTIRS) (e.g. Dorner 2002) are the two most widely used techniques for determining water content or any impurity in the molecular structure of a mineral. Before indentation, the crystallographic orientation of the specimen surface must be known to document mechanical anisotropy across different directions and faces of a mineral crystal. For this aim, pole-figure goniometry via X-Ray diffraction (XRD) (e.g. Kollenberg 1988, 1986) or Electron Back-Scatter Diffraction (EBSD) is used (e.g. Ceccato et al. 2022; Dorner and Stöckhert 2004; Hansen et al. 2020; Kumamoto et al. 2017; Strozewski et al. 2021; Wallis et al. 2020). Post-indentation analyses include AFM to assess slip plane orientation and displacement, which helps us distinguish between different slip systems. Cathodoluminescence, Micropillar compression through Focused Ionic Beam (FIB) (e.g. Sly et al. 2020), and other techniques are also employed in the post-indentation analyses.

Indentation size effect (ISE)

During micro- and nanoindentation, H, E and ${\sigma }_{y}$ etc., can either decreases with increasing P, h, and/or A_c, or decrease with decreasing P, h, and/or A_c (Fig. 7a). These phenomena are known as the Indentation Size Effect (ISE) and Reverse Indentation Size Effect (RISE), respectively. These are important influencing factors that imparts uncertainties in determining the mechanical properties of materials. Various hypotheses were offered to explain these phenomena like, chemical contamination (Pethica and Tabor 1979), abrasion and oxidation of the indented surface (Turley and Samuels 1981), elastic recovery of the indented surface and inadequacy of measurements of small surface area and indenter-surface friction (Li et al. 1993), etc. Based on micromechanics theory, elastic recovery, energy balance, strain gradient plasticity (SGP), and friction, several empirical and theoretical models for explaining ISE exist, e.g., Meyer’s Power-law Model (Bückle 1965; Mott 1956), Minimum Resistance Model (Hays and Kendall 1973), Proportional Specimen Resistance Model (Li and Bradt 1993, 1991), Energy Balance Model (Quinn and Quinn 1997), Meyer's Power-law and Energy Balance Model combination (Mukhopadhyay 2005), Elastic–Plastic Deformation Model (Bull et al. 1989), Indentation-Induced Cracking Model (Li and Bradt 1991) and Strain Gradient Plasticity Model (Acharya and Bassani 2000; Huang et al. 2000; Ma and Clarke 1995; Nix and Gao 1998). Even though the interpretations obtained from these models assist in comprehending the influence of these phenomena, the genesis and mechanics of ISE and RISE remain unknown (Mukhopadhyay and Paufler 2006).

Fig. 7

a Concept of Indentation Size Effect (ISE) and Reverse Indentation Size Effect (RISE). Below a critical limit (vertical dotted black line) of load (P_c), depth (h_c) or grain size (g_c), the mean hardness and associated properties show a power-law relation (red curve for ISE and solid blue curve for RISE), with random fluctuations (blue dashed line for ISE and green dashed line for RISE), depending upon the ${P}_{max}$, h, and/or $\dot{P}$. Beyond the critical limit, mechanical parameters tend to remain constant following the conventional plasticity (modified after Broitman 2017). b Schematic representation (not to scale) of the activation of slip systems and formation of Geometrically Necessary Dislocations (GND) by a rigid conical indenter. Dislocation glide along slip direction produces step like features. Here, $\lambda$ and $\Omega$ are the angles between load and slip direction, and load and normal to the slip plane, respectively. $\theta$ is the angle between the surface of the conical indenter and the specimen surface. $h$ is the indentation depth (after Mukhopadhyay and Paufler 2006)

ISE and RISE depend on the scale of indentation, material type and indenter geometry (Bull 2003; Li et al. 2023). For example, materials like ceramics, quasicrystals, intermetallics, and few minerals like quartz, feldspar, etc., which are mechanically “hard” at room temperature–pressure conditions, shows brittle deformation through intense fracturing during indentation along with significant elastic recovery. In that case, Elastic–Plastic Deformation (EPD) model and Indentation-Induced Cracking (IIC) model are appropriate choices for describing the ISE and RISE. On the other hand, materials like metals, alloys, and minerals such as olivine, mica, etc., show ductile deformation during indentation. Hence, for these kinds of materials, Strain Gradient Plasticity (SGP) model (dislocation density-based model) satisfactorily describes the ISE (Bull 2003). Scale of indentation and indenter geometry significantly affects the mechanism of ISE. For example, microindentation with Vickers tip at higher loads (≥ 100 mN) produces fractures and instantaneous plastic deformation with little elastic recovery. Therefore, IIC will be a good choice for describing the ISE in that case (Sangwal 2009, 2000). However, at same scale and load, when indented with a spherical tip, significant elastic recovery is observed and hence EPD model may be used to account for the ISE. Similarly, low-load (≤ 10 mN) nanoindentation inhibits fracturing (Kranjc et al. 2016) and indentations with Berkovich tip at nanoscale produces instantaneous plastic deformation which may account for the dislocation assisted LTP. Therefore, the SGP model may be used to describe the ISE in that case. On the other hand, spherical nanoindentation produces dislocation assisted LTP as well as significant elastic recovery during unloading. Therefore, both SGP and EPD model may be combinedly used to describe the ISE. Hence, a material can show different mechanisms of ISE at different indentation scales with different indenter geometry. Since most of the minerals show brittle fracturing, elastic recovery, as well as dislocation assisted LTP at different scales, we have discussed the three major ISE models, i.e. the EPD, IIC and SGP model in the following subsections.

Elastic–plastic deformation (EPD) model

The EPD model proposed by Bull et al. (1989) describes the ISE of H as a function of P for hard materials where the elastic deformation is significant, with yielding or cracking occurring after a critical load. The material may show both elastic and plastic deformation during loading stage, where the plastic deformation occurs in discrete phases to accommodate the stress produced during the elastic flexure of the material surface around the indenter-specimen contact. With increasing load, the extension of ${A}_{c}$ causes yielding of the material along the outer edge of the indent in the form of tensile fractures. However, during unloading, significant elastic recovery occurs, which produces sink-in morphology of the indent. Therefore, to determine the true H, an elastic recovery correction ($\Delta$) is applied. The measured indentation diagonal length/radius (${d}_{m})$, in that case, is expressed as:

$${d}_{m}={d}_{i}-\Delta ,$$

(62)

where, ${d}_{i}$ is the ideal indentation diagonal/radius. If the hardness of an ideally plastic material independent of ISE is ${H}_{0}$, and the ISE affected measured hardness is ${H}_{m}$, then following the Meyer’s power-law formulation, ${H}_{0}$ and ${H}_{m}$ can be expressed in terms of P and d including $\Delta$ as follows-

$${H}_{0}={k}_{0}P{d}_{i}^{-2}={k}_{0}P{({d}_{m}+\Delta )}^{-2}, { H}_{m}={k}_{0}P{d}_{m}^{-2}$$

(63)

Therefore, ${H}_{m}$ can be expressed in terms of ${H}_{0}$ and $\Delta$ as following:

$${H}_{m}={H}_{0}{\left(1+\frac{\Delta }{{d}_{m}}\right)}^{2}$$

(64)

${H}_{m}$ and ${d}_{m}$ can be obtained experimentally, therefore ${H}_{0}$ and $\Delta$ can be determined iteratively through Eq. (64). It can be explained that higher P values will produce higher ${d}_{m}$ and consequently higher ${A}_{c}$. Therefore, at higher P, ${d}_{m}\gg \Delta$ and ${H}_{m}$ tends to ${H}_{0}$. However, at lower P values ${d}_{m}$ becomes small, thus causing a significant contribution from the $\frac{\Delta }{{d}_{m}}$ fraction and subsequently higher ${H}_{m}$ values. Hence, for a brittle solid, scales at which elastic recovery and fracturing becomes dominant mechanical response to indentation, this model can be implemented to estimate the ${H}_{0}$ (Mukhopadhyay and Paufler 2006).

Indentation induced cracking (IIC) model

The fundamental consideration of the IIC model proposed by Li and Bradt (1991) is that during indentation, the mechanical response from a material can be grouped into four components viz., (1) Elastic deformation, (2) Plastic deformation, (3) Indenter-specimen contact friction, and (4) Specimen cracking. According to their explanations, while the first three components only attribute to a normal ISE, specimen cracking can cause both ISE and RISE. The apparent microhardness ${H}_{A}$ (ISE dependent hardness) in case of cracking can be expressed in the following form:

$${H}_{A}={\Lambda }_{1}{k}_{1}\left(\frac{P}{{d}^{2}}\right)+{k}_{2}\left(\frac{{P}^\frac{5}{3}}{{d}^{3}}\right),$$

(65)

where, ${\Lambda }_{1}$, ${k}_{1}$, and ${k}_{2}$, are constants. The term ${\Lambda }_{1}{k}_{1}\left(\frac{P}{{d}^{2}}\right)$ describes the plastic deformation component, in which ${\Lambda }_{1}=1$ for an ideally plastic material, and ${k}_{1}$ is an empirical constant which depends on the indenter geometry. For perfectly plastic deformation ${k}_{2}=0$, hence ${H}_{A}$ is represented as ${k}_{1}\left(\frac{P}{{d}^{2}}\right).$ On the other hand, for a perfectly brittle solid, ${\Lambda }_{1}=0$, and ${k}_{2}$ becomes a function of P. In that case, ${H}_{A}$ is represented as ${k}_{2}\left(\frac{{P}^\frac{5}{3}}{{d}^{3}}\right)$. Since H is expressed as a function of d, it is assumed that the relation d = 7 h (Table 1) holds true. (Sangwal 2000) tested the applicability of this model on different alloys to examine the ISE and RISE through Vickers microindentation, and provided a generalized empirical formula as following:

$$H_{V} \propto \left( {\frac{{P^{5/3} }}{{d^{3} }}} \right)^{{m_{0} }} ,$$

(66)

where ${m}_{0}$ is a constant, independent of P and material properties. By testing different type of crystalline materials (Sangwal 2000) reported that the average value of ${m}_{0}$ (${\overline{m} }_{0}$) is 0.636. If the slope of the $\mathrm{ln}({H}_{V})$ vs $\ln \left( {\frac{{P^{5/3} }}{{d^{3} }}} \right)$ curve, ${m}_{r}$ is greater than ${m}_{0}$, then it is normal ISE. For ${m}_{r}<{m}_{0}$ it is RISE. Although this model is well constrained to demonstrate the modes of ISE through empirical methods, the underlying mechanism as how fracturing leads to RISE is still unknown (Mukhopadhyay and Paufler 2006; Sangwal 2009).

Strain gradient plasticity (SGP) model

Dislocation nucleation within the plastic field around an indenter can be classified into two categories: (a) statistical dislocations (SSD) that are already present in the material, and (b) geometrically necessary dislocations (GND) that form during indentation to accommodate the plastic strain, can explain the variation of hardness and hardness-derived mechanical parameters observed particularly for minerals (Ma and Clarke 1995; Nix and Gao 1998). Since the indentation strain remains constant due to its geometrical attributes, a smaller A_c or a lower P causes the strain gradient to rise, increasing the GND density. Consequently, dislocation interactions rise and eventually increase H or ${\sigma }_{y}$, reflecting strain hardening (Hall–Petch mechanism). The shear stress (${\tau }_{i}$) generated by the indenter in the plastic field can be expressed according to the following equation:

$${\tau }_{i}= \frac{1}{C}Gb\sqrt{{\rho }_{g}+ {\rho }_{s}},$$

(67)

where, $G$ is shear modulus, ${\rho }_{g}$ and ${\rho }_{s}$ are the densities of GND and SSD, respectively. According to Ma and Clarke (1995), ${\rho }_{g}$ is inversely proportional to d, and varies as a function of average shear strain ($\gamma )$ in the plastic field as expressed below:

$${\rho }_{g}= \frac{4\gamma }{bd}.$$

(68)

Since H can be related to ${\tau }_{i}$ through $C$, Eq. 68 can be modified as (Ma and Clarke 1995):

$$H= Gb\sqrt{{\rho }_{s}+ \frac{4\gamma }{bd}}.$$

(69)

Equation (69) tells that for smaller d (i.e. smaller A_c) ${\rho }_{g}$ > > ${\rho }_{s}$, and H increases with decreasing A_c. However, beyond a critical value of d, there is no role of ${\rho }_{g}$ and it becomes insignificant in comparison to ${\rho }_{s}$. In that case, H is expressed as a function of ${\rho }_{s}$ according to the following equation:

$${H}^{2}= {H}_{0}^{2}\left(1+ \frac{4\gamma }{{\rho }_{s}bd}\right),$$

(70)

where, ${H}_{0}$ is the ISE independent hardness. Since the average strain can be assumed to be constant, therefore, by plotting ${H}^{2}$ as a function of $1/d$, one can derive ${H}_{0}$ from the intercept and ${\rho }_{s}$ from the slope (Mukhopadhyay and Paufler 2006).

Nix and Gao (1998) proposed an equation like Eq. (70) for conical indenters, where the H is a nonlinear function of h instead of d. The equation is as follows:

$${\left(\frac{H}{{H}_{0}}\right)}^{2}=1+ \frac{{h}^{*}}{h}.$$

(71)

Here, ${h}^{*}$ is ISE independent depth, dimensionally equivalent to $\left(\frac{4\gamma }{{\rho }_{s}b}\right)$. In a similar way, ${\rho }_{g}$ can also be expressed in terms of h (Fig. 7b), as:

$${\rho }_{g}= \frac{3}{2bh}{tan}^{2}\theta .$$

(72)

Equations 71 and 72 yield a similar explanation as Eq. (70), i.e., ${\rho }_{g}$ increases with decreasing h and eventually leads to strain hardening. However, Eqs. 71 and 72 are not valid when the critical h becomes less than 100 nm. This is because (Broitman 2017): (a) as the model was developed using a conical indenter, the effect of “tip radius” of spherical indenter has not been examined, and (b) for nanoindentation, dislocations are not limited only to the hemisphere under the indenter.

Mechanisms of RISE

The origin and mechanisms of RISE is not well understood or well documented. IIC may be one of the few models that account for RISE, although it does not distinguish between a normal ISE and RISE (Sangwal 2009, 2000). However, it has been observed that unlike normal ISE, a material displaying RISE does not undergo significant elastic recovery or produce resistance to plastic deformation, instead shows relaxation through releasing the indentation stress away from the point of indentation towards the surrounding. This may produce a piling-up indent morphology that increases ${A}_{c}$ and subsequently lowers the hardness. Sangwal (2000) argued that RISE is likely to occur in mechanically “softer” phases which readily undergoes plastic deformation, and at higher load produces work hardening through dislocation multiplication, cross-slip interactions, and activation of Frank-Red sources.

Recently, (Li et al. 2023) postulated that RISE may also occur due to external factors such as surface undulations and indenter tip irregularity. According to their FEM-based model, the same depth variation $\Delta$ can occur either through blunting of indenter tip or by encountering nanoscopic groove contact on the specimen surface that can lead to inaccuracy in experimentation. This can occur either because of submicroscopic heterogeneities present on the specimen surface or abrasion of the tip during multiple loading. Since ${A}_{c}$ is a function of h, therefore, incorporating $\Delta$ as an external measurement error can provide a better estimation of the true H of the material, expressed through the following set of equations:

$$H={H}_{0}{\left(1-\frac{1}{1-\frac{h}{\Delta }}\right)}^{2},$$

(73)

$$H={H}_{0}{\left(1-\frac{1}{1+\frac{h}{\Delta }}\right)}^{2},$$

(74)

where, Eqs. 73 and 74 describes the normal ISE and RISE observed in H as a function of h ($\Delta$), respectively.

Although the mechanics behind ISE and RISE is not fully understood, and there is no generalized equation to describe it, researchers concur that ISE occurs when an indentation approaches the critical microstructural dimensions of lattice defects (Gouldstone et al. 2007; Mukhopadhyay and Paufler 2006; Pharr et al. 2010). Therefore, by determining the critical P and/or h, H₀ can be constrained and correlated with the uniaxial compressive data to a material’s mechanical behavior (Broitman 2017). Normal ISE has been reported for many minerals like Quartz, Feldspar, Olivine, Mica, Gypsum, Calcite, etc., in different forms such as variation of H as functions of P, h, ${A}_{c}$, etc. however, there is still no report of RISE observed in geomaterials.

Instrumented indentation studies on minerals

Application of instrumented indentation in studying the mechanical properties of minerals yielded many fundamental contributions in unfolding the lattice scale deformation mechanisms of complex silicate minerals that led towards a better understanding of the rheology of earth’s crust and the mantle. Although limited in number, micro- and nanoindentation tests on several silicate (e.g. quartz, olivine, pyroxenes, amphiboles, feldspar and aluminosilicates, clay minerals, etc.), oxide (hematite, magnetite, sapphire, etc.) and carbonate minerals (calcite, dolomite) are present in the literature. Figure 8a, b depicts P–h curves of some important rock forming, derived by room PT nanoindentation testing by various authors at various load–displacement resolutions. H, K_C, and E of single and polycrystalline mineral phases have been extensively studied. Table 2 lists all the indentation-derived mechanical data of various minerals. Much of the recent indentation research are focused on determining the LTP of rock forming minerals and correlating the results with uniaxial/triaxial compressive data. In the following subsections we discuss the current status of research on the aforementioned minerals, their mechanical anisotropy, temperature-dependent H and ${\sigma }_{y}$, and ISE.

Fig. 8

Examples of nanoindentation load–displacement curve of some common minerals at room pressure and temperature. a Load in mN resolution. Olivine (Kumamoto et al. 2017), Quartz and Orthoclase (Ma et al. 2021a, b), Muscovite (Zhang et al. 2009), Antigorite (Hansen et al. 2020). b Load in μN resolution. Calcite (Sly et al. 2020), Microcline (Ayatollahi et al. 2020), and Margarite and Biotite (Zhang et al. 2013)

Table 2 Room pressure temperature Microindentation Hardness, Nanoindentation Hardness, Elastic Modulus and Fracture Toughness of some common mineral phases

Quartz

Room temperature indentation tests on quartz

Quartz has been extensively studied using instrumented indentation (Brace 1963; Ceccato et al. 2022; Darot et al. 1985; Evans 1984; Evans and Goetze 1979; Goldsby et al. 2004; Parks 1984; Strozewski et al. 2021). Room temperature hardness of natural and synthetic quartz varies from 9.3 GPa (microindentation) to 19 GPa (nanoindentation) and displays low to moderate mechanical anisotropy depending on the crystallographic orientation of the plane of indentation. Multiple studies have reported $\sim$ 15% hardness anisotropy between ($10\overline{1 }1)$, $(1\overline{1 }01)$, ($10\overline{1 }0)$, and (0001) crystallographic planes (Brace 1963; Evans 1984; Nadeau 1970; Strozewski et al. 2021), and is independent of the scale of indentation. Quartz shows considerable ISE both in micro- and nanoscale. H of quartz decreases with increasing P (Brace 1963) (Fig. 9a), and h in micron- (Li et al. 2021; Viktorov et al. 2014) as well as nanometer-scale (Strozewski et al. 2021) (Fig. 9b).

Fig. 9

Summary of instrumented indentation tests on Quartz. A power-law relation between a Microindentation Hardness vs. load (Brace 1963), and b Nanoindentation Hardness vs. indentation depth (Strozewski et al. 2021) illustrates the ISE on Quartz. c Variation of nanoindentation hardness of quartz as a function of structural hydroxyl content plotted for different temperatures (after Strozewski et al. 2021). d Variation of the Constraint Factor (C) as a function of temperature for Quartz. The elastic to plastic transition occurs abruptly, as C increases suddenly to the peak value just above 573 °C, because of $\alpha -\beta$ phase transition (after Evans and Goetze 1979). e Variation of fracture surface energy of Quartz as a function of temperature along different crystallographic planes. Abrupt decrease in the energy at 573 °C suggests that microfracturing becomes the dominant deformation mechanism during phase transition (after Darot et al. 1985). f Effect of phase transition is also reflected in the Hertzian fracture load of quartz, which practically becomes zero at the transition point (after Lawn et al. 2021)

Quartz undergoes brittle fracturing and twinning under microindentation (Brace 1963; Darot et al. 1985; Evans 1984). In LTP, dislocation assisted plasticity becomes the main deformation mechanism (Goldsby et al. 2004; Masuda et al. 2000; Strozewski et al. 2021; Thom et al. 2018). However, even at a constant load, the mechanical response of quartz depends on the geometry of the indenter. Indentation carried out on a specific plane using spherical indenter produces secondary Dauphiné twinning and microcracks, whereas using sharp indenter on the same plane generates plastic flow through activation of slip planes (Brace 1963). Amongst indentation-induced slip planes in quartz, $\left\{ {1\bar{1}01} \right\}$ slip system is the most prominent one (Brace 1963; Shubnikov and Tsinzerling 1932).

Room temperature nanoindentation studies on monocrystalline quartz using AFM and TEM imaging revealed that quartz is not brittle below a critical stress range and display immediate plastic deformation upon indentation (Masuda et al. 2000). However, post-indentation photomicrography shows that the plastic-strain is not always accommodated by slip planes through dislocation glide. They argued that the predominant deformation mechanism, in this case, would have been lattice creasing, which was later validated by Goldsby et al. (2004) and Thom et al. (2018). Lattice creasing is a hypothetical solid-state plastic deformation mechanism in which the strain is concentrated within regular lattice intervals in restricted deformed zones. The deformed zones may face complete lattice distortion and even amorphization (Ferguson et al. 1987; Hemley et al. 1994; Kingma et al. 1993). Lattice creasing is a short-scale phenomenon and can accommodate limited plastic strain. Hence, this mechanism can be analogous to superplastic deformation of crystalline material, as proposed by Zelin and Mukherjee (1996) and Sakai and Muto (1998). Lattice creasing may be a precursor to dislocation glide. It has only been observed for indentation tests with a very short holding time before unloading, which might be insufficient enough for the slip systems to be activated at room temperature.

Effect of impurities on the hardness of quartz

The trace of foreign elements (e.g. [OH], Al, Na, K, and Li) as an impurity the lattice structure affects the mineral's mechanical properties (Atkinson 1979; Brace 1963; Evans 1984; Kekulawala et al. 1981; Linker and Kirby 1981; Nadeau 1970). Brace (1963) reported that increasing Al, Na, and Li concentration in synthetic quartz lowers H. Nadeau (1970) employed high-temperature annealing and carbon electrolysis to study the fluctuation in microhardness of quartz with temperatures up to 1000 °C and controlled proportions of Al, Na, K, Li, and H in the interstitial lattice spaces. This work revealed that the microhardness of quartz increases with degree of annealing in the 500–1000 °C range. In contrast, impure crystals showed a constant decline in hardness over a temperature range of 450 °C to 900 °C. Natural quartz crystals with minimal element impurity showed a sharp increase in hardness at 865 °C, possibly due to thermal annealing of preexisting crystal defects. Aside from proportion, the distribution of elemental impurities inside a crystal lattice plays a crucial role in the manifestation of a mineral's mechanical properties. Al or Li, for example, can exist in significant amounts at non-weakening structural locations in quartz does not alter its mechanical properties (Evans 1984). A similar finding was made for structural hydroxyl in natural quartz, where the hardness did not vary as the (H/106 Si) ratio was changed. However, because hydroxyls exist in gel form rather than structural form in manufactured quartz, there is a negative association between hydroxyl content with hardness (Evans 1984; Kekulawala et al. 1981, 1978).

Earlier studies on hydrolytic weakening of quartz have reported that for crystals with a H/10⁶ Si ratio > 1000, weakening occurred beyond a critical temperature of 400 °C to 500 °C (Blacic and Christie 1984; Griggs 1967; Griggs and Blacic 1965; Hobbs et al. 1972). However, recent nanoindentation studies by Strozewski et al. (2021) and Ceccato et al. (2022) on natural and synthetic quartz found that the (H/10⁶ Si) ratio in the structural site of quartz crystals does not impart any significant variation in mechanical strength up to 500 °C (Fig. 9c). This suggests that the critical temperature for hydrolytic weakening probably varies as a function of strain-rate or stress, and, during nanoindentation, the rate of diffusion of hydrogen defects may be lower than the rate of dislocation glide (Strozewski et al. 2021).

α–β phase transition of Quartz

Within a temperature window of 550–600 °C, indentation-derived mechanical properties of quartz fluctuate abruptly with a sharp gradient around 573 °C, which demarcates α to β phase transition of quartz (Darot et al. 1985; Lawn et al. 2021; Strozewski et al. 2021; Westbrook 1958). Microhardness of quartz decreases rapidly near the transition point with an abrupt increase in microfracture intensity around the indentation (Darot et al. 1985; Lawn et al. 2021). Change in mechanical response of quartz is also reflected through the abrupt variation of C that correlates the ${\sigma }_{y}$ with H (Eq. (17)). Below 573 °C, C remains constant at 1.1, implying that α quartz behaves elastically. However, just above 573 °C, C increases abruptly, which soon reaches to 3.0 within 800 °C (Fig. 9d) suggesting that β quartz undergoes plastic deformation more readily than α quartz because of the decrease in ${\sigma }_{y}$ (Evans and Goetze 1979). Deformation mechanism also changes across the α to β transition temperature. Below 573 °C quartz shows LTP through dislocation glide. The abrupt decrease in $\Gamma$(Eq. (46)) around the transition point (Fig. 9e) causes rapid tensile fracturing of the indented surface, which becomes the major deformation mechanism during the phase transition (Darot et al. 1985). It is also reflected in the Hertzian fracture load that decreases to zero at 573 °C (Fig. 9f) (Lawn et al. 2021).

Hardness-derived yield stress of Quartz and relationship with temperature

H and ${\sigma }_{y}$ of quartz decrease with increasing temperature (Brace 1963; Darot et al. 1985; Evans 1984; Evans and Goetze 1979; Lawn et al. 2021; Nadeau 1970; Strozewski et al. 2021; Westbrook 1958) (Fig. 10a, b). Below 600 °C quartz behaves elastically (Evans and Goetze 1979). However, beyond 600 °C, yield strength drops gradually because of the decrease in E, owing to the α to β phase transition during indentation. Strozewski et al. (2021) estimated ${\sigma }_{y}$ of synthetic and natural quartz crystals through nanoindentation tests using four different models discussed in section “Yield stress models”. Since quartz behaves elastically up to 600 °C, C = 1.1 in the $H-{\sigma }_{y}$ relation is used to obtain ${\sigma }_{y}$. A comparison between room temperature ${\sigma }_{y}$ obtained from all four models has been provided in Table 3. ${\sigma }_{y}$ values obtained from standard nanoindentation test (Strozewski et al. 2021) are higher than microindentation data (Evans 1984; Evans and Goetze 1979) or high load nanoindentation tests (Goldsby et al. 2004). This discrepancy can be attributed to the ISE, differences in $\dot{\varepsilon }$, and different methods in assessing the contact area (Strozewski et al. 2021). ${\sigma }_{y}$ derived from all the models show a consistent decrease with increasing temperature and the trend of variation is described with a flow-law within LTP limit. Strozewski et al. (2021) used Frost and Ashby’s model (1982) (Eq. (34)) to describe the flow law and estimate ${\sigma }_{P}$. Considering ($p=0.5, q=1)$ and ($p=1, q=2)$ and Q₀ $=135 {\mathrm{kJmol}}^{-1}$ (Hirth et al. 2001, Strozewski et al. 2021), Eq. (34) yields ${\sigma }_{P}$ ranging from 7.0 GPa to 27.3 GPa depending upon the model and constitutive parameters.

Fig. 10

Variation of a Hardness, and b Hardness-derived yield stress Evans and Goetze (1979) model of different minerals as a function of temperature. NI, MI, NIH and MIH stands for Nanoindentation, Microindentation, Nanoindentation Hardness and Microindentation Hardness, respectively. Quartz Nanoindentation (Strozewski et al. 2021), Quartz Microindentation (Evans 1984), Olivine Nanoindentation (Kranjc et al. 2016), Olivine Microindentation (Evans and Goetze 1979), Jadeite and Diopside (Dorner and Stockhert 2004), Hematite (Kollenberg 1986), Calcite (Sly et al. 2020)

Table 3 Room pressure temperature indentation-derived Yield stress (in GPa) of Quartz, Calcite and Olivine, estimated using four different models

Olivine

Olivine has been extensively studied using both low and high-temperature indentation to understand its rheology and deformation mechanisms (Darot et al. 1985; Dorner 2002; Evans and Goetze 1979; Hansen et al. 2019; Kranjc et al. 2016; Kumamoto et al. 2017; Swain and Atkinson 1978; Wallis et al. 2020). Depending on the scale of indentation and the indenter geometry, the H and E of olivine at the room temperature range from 10 to 15 GPa and 200 to 180 GPa, respectively. Unlike quartz, structurally incorporated hydroxyls or other ionic impurities have a negligible effect on the hardness of olivine (Dorner 2002).

Hardness anisotropy of Olivine

Olivine shows low to moderate H anisotropy depending on the crystallographic orientation of the plane of indentation and indenter geometry. The average H of monocrystalline olivine varies from 10 GPa on (100) plane to 9.4 GPa on (010) plane at room temperature. This anisotropy could range between 10 and 45% depending on P (Darot et al. 1985; Dorner 2002; Evans and Goetze 1979). The same anisotropy decreases below 8% when indented using spherical indenter because of the ISE (Kumamoto et al. 2017). However, this anisotropy decreases with increasing temperature, and beyond 500 °C it becomes negligible (Darot et al. 1985).

Hardness-derived yield stress of Olivine and relationship with temperature

The hardness of monocrystalline olivine decreases with increasing temperature (Fig. 10a) (Darot et al. 1985; Dorner 2002; Evans and Goetze 1979; Kranjc et al. 2016), with decrement rate of 5 MPa/K up to 500 °C when tested with a Vickers microindenter (Dorner 2002). Beyond 500 °C, H becomes constant (Darot et al. 1985). Due to the ISE, the decrement rate can reach 7.5 MPa/K at low temperatures below 200 °C (Kranjc et al. 2016). Uniaxial compressive data shows no appreciable fluctuations of E up to 1000 °C (Evans and Goetze 1979, Graham Jr. and Barsch 1969). While nanoindentation tests show that E of olivine largely varies with temperature than H (Kranjc et al. 2016), even showing a considerable anisotropy (Kumamoto et al. 2017).

${\sigma }_{y}$ also decreases with increasing temperature (Fig. 10b) (Dorner 2002; Evans and Goetze 1979; Kranjc et al. 2016), depending on the model used to estimate ${\sigma }_{y}$ (Table 3). Microindentation-derived ${\sigma }_{y}$ of olivine estimated using Eqs. (18 and 19) can vary from 5 to 9.5 GPa at room temperature to as low as 0.02 GPa at 1500 °C with a steeper slope of decrement above 1000 °C (Dorner 2002; Evans and Goetze 1979) and the flow law fitted to the ${\sigma }_{y}-T(\mathrm{^\circ{\rm C} })$ curve (Eq. (34)) yields an average ${\sigma }_{P}$ of 9.1 $\pm$ 0.3 GPa (Evans and Goetze 1979), which can vary between 5.32 and 6.45 GPa depending on different models and flow-law exponents. C shows a steady increase with temperature for olivine. at room temperature C lies close within, the elastic–plastic transition range (1.5 to 2), suggesting that olivine deforms elastically only up to a certain temperature. However, C reaches 3.0 at a temperature just above 1000 °C, where olivine shows plastic flow (Fig. 11a). At room temperature, olivine is more prone to plastic deformation than quartz (Evans and Goetze 1979; Kranjc et al. 2016).

Fig. 11

Instrumented indentation tests on Olivine: a Variation of the Constraint Factor (C) as a function of temperature for olivine. The constant increase in C indicates that the elastic to plastic transition occurs gradually for Olivine (after Evans and Goetze 1979). b A power-law relation between Hardness and contact radius represents the ISE on Olivine (after Kumamoto et al. 2017). c Compilation of yield stress data of Olivine plotted against corresponding characteristic dimension (contact radius and/or grain size) to validate the ISE dependent and ISE independent grain size (i.e., $\ge$ 300 μm) domain of polycrystalline mantle olivine. The orange boundary indicates the range of ISE observed in all yield stress data. A: Kranjc et al. 2016 (Recalculated); B: Raterron et al. 2004; C: Kawazoe et al. 2009; D: Faul et al. 2011; E: Evans and Goetze 1979; F: Mei et al. 2010; G: Long et al. 2011; H: Hansen et al. 2019; I: Druiventak et al. 2011; J: Kumamoto et al. 2017. d Variation of fracture surface energy of Olivine as a function of temperature along different crystallographic planes. The energy becomes practically constant beyond 500 °C (after Darot et al. 1985)

Indentation size effect (ISE) in Olivine

The indentation-derived polycrystalline ${\sigma }_{y}$ of olivine in the LTP regime is higher than uniaxial compressive data because of the ISE (Kranjc et al. 2016; Kumamoto et al. 2017; Wallis et al. 2020). Recent studies on geodynamic modeling of the lithosphere and lower-mantle, coupled with high-PT rock deformation experiments have shown that the ${\sigma }_{y}$ of polycrystalline olivine is in the order of$\sim {10}^{2}\mathrm{ MPa}$, which is significantly lower than the indentation values. A probable explanation of this could be the back stress generated within the dislocations during the reversal of load, when single crystals are repeatedly subjected to shortening followed by an extension which causes a long-range elastic interaction amongst the dislocations (Kinematic hardening) (Hansen et al. 2019; Wallis et al. 2020). In addition to the ISE brought on by the choice of the indentation scale, P, and indenter shape, estimating ${\sigma }_{y}$ through indentation involves another subjectivity: the choice of model. Although the constitutive equations from each model depict a comparable trend of ${\sigma }_{y}$ as a function of T, absolute values differ by several orders, producing inconsistencies in the mechanical characterization. For example, a study by Kranjc et al. (2016) showed that the average nanoindentation-derived ${\sigma }_{y}$ of olivine at room temperature using Mata and Alcalá (2003) model (Eq. (21)) is at least 5 GPa less than the microindentation-derived ${\sigma }_{y}$ estimated through Evans and Goetze's (1979) model (Eq. (20)). Re-estimated values using Eq. (20), showed average ${\sigma }_{y}$ is higher than the microindentation data, revealing the scale-dependent response of indentation. This dependance can be quantified using a power-law proportional to ${r}^{{n}^{^{\prime}}}$ where r is the contact radius of the indenter and ${n}^{^{\prime}}$ is the power-law exponent (Fig. 11b). For spherical and Berkovich tip, ${n}^{^{\prime}}$= − 0.09 and $-0.08\le {n}^{^{\prime}}\le -0.07$, respectively (Kumamoto et al. 2017). Koizumi et al. (2020) have reported a similar power-law relation between H and h, while describing microscale ISE on olivine. This apparent increment in H and ${\sigma }_{y}$ can probably be explained in terms of indentation-induced GNDs (Kumamoto et al. 2017). When the A_c beneath the indenter becomes infinitesimally small, the strain gradient across the indentation becomes so high that it triggers high-density GNDs within the plastic zone causing strain hardening through short- and long-range dislocation interactions. When indented, polycrystalline olivine aggregate also shows strain hardening through dislocation interactions at the grain boundaries. Thus, with decreasing grain size and increasing grain boundary area, the magnitude of dislocation interaction increases, causing a steady increment in H through strain hardening—a classic example of the Hall–Petch effect. By compiling all published data on ${\sigma }_{y}$ of olivine, Kumamoto et al. (2017) have proposed a threshold grain size of 300 m$\upmu$ for polycrystalline olivine (Fig. 11c), below which the Hall–Petch effect will be effective, indicating that H and ${\sigma }_{y}$ will increase with decreasing grain size in the LTP regime.

Slip systems of Olivine

Studies on LTP have shown that for olivine, dislocation glide is the major deformation mechanism at this regime. However, depending upon the scale of indentation and P, ${\rho }_{g}$ can vary drastically, which can significantly influence the ${\sigma }_{y}$ and steady-state flow stress (Hansen et al. 2019; Kranjc et al. 2016; Kumamoto et al. 2017; Wallis et al. 2020). Morphological analysis of the indents both from micro- and nanoindentation tests reveal that the major slip systems in olivine are (100) [001] and {110}[001] with minor traces of (010) [100], (010) [001], and (001) [100] with edge dislocation (Dorner 2002; Wallis et al. 2020).

Slip systems activated through external load play a critical role in controlling the hardness anisotropy. One way of quantifying this variation is to use the Critically Resolved Shear Stress (CRSS), where the anisotropy can be correlated with the Schmid and Brookes factor using (Brookes et al. 1971; Dorner 2002):

$${\tau }_{CR}= \frac{1}{2}\frac{P}{{A}_{C}}cos\lambda cos\Omega \left(cos\psi +sin\delta \right).$$

(75)

Here, ${\tau }_{CR}$ is the CRSS, $\lambda$ is the angle between the loading direction and the slip direction, $\Omega$ is the angle between the loading direction and the normal of the slip plane (Fig. 7b), $\psi$ is the angle between the indent facet and the axis of rotation of the slip plane, and δ is the angle between the indent facet and the slip direction. Schmid factor is S_CR = $cos\lambda cos\Omega$ and the Brookes factor is B_CR = $\frac{1}{2}cos\lambda cos\Omega (cos\psi +sin\delta )$. The hardness of olivine decreases with increasing S_CR or B_CR, and the best correlation between these parameters is observed within 300 to 350 °C, typical of the LTP regime (Dorner 2002). Generally, for olivine, below 700 °C only the predominant slip systems such as {110}[001] remain active. This causes an increase in S_CR or B_CR with increasing load, allowing easy glide along the slip planes, consequently a decrease in the hardness. However, above 700 °C, secondary slip systems get activated, causing an enhanced dislocation interaction. This interaction produces strain hardening through dissociation into partial dislocations bounding stacking faults, because of which the hardness of the crystal apparently increases (Dorner 2002; Wallis et al. 2020). This phenomenon can possibly explain the invariance of the hardness beyond 500 °C as observed for olivine (Darot et al. 1985).

Fracture surface energy $(\Gamma$) of Olivine

Olivine shows good fracturing along (010), (100) and (001) during microindentation where (010) and (001) are the cleavage planes. The average $\Gamma$ of olivine at room temperature ranges from 0.98 to 1.6 Jm⁻² depending upon the crystallographic direction, since the elastic modulus shows moderate directional anisotropy (Darot et al. 1985; Swain and Atkinson 1978).$\Gamma$, however, decreases with increasing temperature with a steady slope, suggesting that it would require lesser energy to generate new surface areas through fracturing because of decreasing thermodynamic surface energy, until 500 °C where it becomes flat, and $\Gamma$ becomes constant (Fig. 11d). This abrupt change can occur due to the dislocation crack interactions, since at high temperature, secondary dislocations get activated. This causes dragging of dislocations at one side of the crack, and the energy dissipated because of this drag compensates the decreasing ξ $,$ thus making $\Gamma$ constant (Darot et al. 1985; Lawn and Wilshaw 1975).

Calcite

The room temperature hardness of calcite varies from $2.59 \pm 0.10$ GPa to 2.86 $\pm$ 0.13 GPa, showing a moderate anisotropy of about 10% (Sly et al. 2020). H of calcite, like quartz or olivine, also decreases with increasing temperature (Fig. 10a), and at 175 °C, the average H of calcite ranges between 1.98 and 2.16 GPa with 9.2% anisotropy, like that obtained in room temperature. This suggests that the hardness anisotropy is independent of temperature, particularly in the LTP regime. For calcite, A_C and h increases with temperature even at a constant load, while the microfracture intensity decrease. All these observations suggest that calcite shows a high $\dot{{\varepsilon }_{i}}$ at the LTP regime.

The viscoplastic nature of calcite has been examined through the variation of ${\sigma }_{y}$ estimated using different models (Table 3). ${\sigma }_{y}$ at room temperature of calcite varies widely, starting from 0.83 $\pm$ 0.05 GPa (Ginder et al. 2018) to 1.88 $\pm$ 0.19 GPa (Johnson 1970), with an average anisotropy of 11% across all models. While the ${\sigma }_{y}$ of calcite decreases with temperature (Fig. 10b), the anisotropy of ${\sigma }_{y}$ shows an increasing trend, suggesting that the crystallographic orientation strongly influences the indentation-creep with increasing temperature. ${\sigma }_{P}$ of calcite, as estimated from Frost and Ashby (1982) model ranges between 1.2 and 9.9 GPa depending on the ${\sigma }_{y}$.

For calcite, crystallographic planes that are favorable for twinning show considerably lesser ${\sigma }_{y}$ than those which are unfavorable for twinning. However, ${\sigma }_{y}$ that are obtained from nanoindentation are at least an order of magnitude higher than the uniaxial compression results, due to ISE. H and ${\sigma }_{y}$ of calcite vary with increasing A_c following a power-law with ${n}^{^{\prime}}$ = -0.05 (Fig. 12). However, H at LTP regime remains practically constant at a particular temperature for an indenter tip radius greater than 1 μm.

Fig. 12

A power-law relation between Hardness and contact radius describes the ISE on Calcite (after Sly et al. 2020)

Phyllosilicates

Phyllosilicates such as micas, serpentines, chlorite, smectite, kaolinite, etc., are transversely isotropic sheet silicates, having different interlayer cations and varying interlayer thicknesses. Hydrous phyllosilicates contain water molecules between the layers, making them considerably weaker than other silicate minerals. These minerals are generally characterized either by discrete or complex combinations of 1:1 and/or 2:1 interlayer sequence. Electrostatic interactions between the layers and the interlayer cations, cation hydration and Born repulsion etc. are the major physical phenomena that directly influence the mechanical behavior of these minerals, contributing to the layer parallel and layer normal anisotropy. This anisotropy controls the overall elastic nature of the phyllosilicates, which affects the seismic wave propagation in crustal environments (Vernik and Liu 1997; Wang et al. 2001; Zhang et al. 2010). Systematic investigations of the nanomechanical behavior of some of the major phyllosilicates such as muscovite, biotite, talc, antigorite, etc. in response to nanoindentation have revealed that the average hardness of these minerals varies mostly because of their interlayer spacing and the said electrostatic interactions (Zhang et al. 2010, 2009).

Nanoindentation of 2:1 Phyllosilicates such as Muscovite, Margarite, Talc, Biotite, Pyrophyllite, etc., have shown H and E of these layered minerals decreases with decreasing interlayer charge. For instance, E_r of pyrophyllite (interlayer charge z = 0) is 23.5 GPa, whereas the same is 165.5 GPa for Margarite (interlayer charge z = 1.823). The nanoindentation P–h curves of these minerals reveals that the LTP of phyllosilicates is mostly controlled by interlayer cohesiveness attributed to their interstitial structure and charge concentration. Talc and pyrophyllite readily deform when subjected to indentation, the main reason being their low resistance against applied load originated because of the weak interlayer Van der Waals force and the absence of interlayer charge. Mica, like muscovite or biotite on the other hand, shows considerably higher resistance to penetration during indentation and consequently higher ${\sigma }_{y}$ because of the strong interlayer electrostatic attractions (Fig. 13a, b) (Zhang et al. 2010).

Fig. 13

Instrumented indentation tests on Phyllosilicates: a Load–displacement curves, and b Variation of representative elastic modulus as a function of interlayer charge density of some of the common Phyllosilicates. Note that the Phyllosilicates with higher charge density (e.g. Margarite, Muscovite, etc.) shows higher mechanical strength and hence, higher resistance to deformation as compared to weak Phyllosilicates (e.g. Talc or Pyrophyllite) (Reproduced after Zhang et al. 2010). c Power-law relation between the Normalized Elastic moduli and indentation displacement describes the ISE on various Phyllosilicates (Reproduced after Zhang et al. 2010)

LTP of phyllosilicates can be explained in several ways including dislocation glide, incipient kink band formation, sliding on shear fractures along basal planes, delamination, and even ripplocations of layers (Aslin et al. 2019; Basu et al. 2009; Hansen et al. 2020; Zhang et al. 2010). The interlayer charge of the phyllosilicates and consecutive interactions are also heavily influenced by these processes. For instance, muscovite, biotite, or other phyllosilicates with interlayer cations will show longer delay in delamination of layers than talc, pyrophyllite, or antigorite and instead undergo ripplocation, which is a nanoscale bending mechanism of the layers (Aslin et al. 2019). A recent study on nanoindentation of biotite coupled with atomistic simulations has shown that ripplocation in 2:1 layered phyllosilicate substantially decreases the H, E_r, and indentation modulus in these minerals (Lanin et al. 2021). The brittleness of phyllosilicates is also attributed to their lattice structures and interlayer interactions. For instance, margarite cracks during indentation due to its strong interlayer electrostatic attraction and lesser interlayer spacing. In contrast, muscovite and rectorite show indentation creep because of weak interactions and larger interlayer spacing along with the presence of water molecules, as evidenced from large pop-ins in the load–displacement curves (Zhang et al. 2010, 2009). Layer normal indentation on micas causes piling-up of materials around the indenter. Consequently, it produces incipient kink bands (IKB) which are the precursors to kink bands (KB) and serves as a major deformation mechanism for these minerals in LTP regime. The impurities and intracrystalline defects influence the formation of incipient kink bands; the larger the preexisting defects such as ripplocations (Aslin et al. 2019; Lanin et al. 2021), the more readily micas undergo kinking. The quality of mica largely affects the threshold stress for kinking. High quality mica shows higher threshold stress (~ 8 GPa) over low quality mica (threshold stress ~ 1.6 GPa) (Basu et al. 2009; Yin and Zhang 2011). Studies on linear loading, cyclical loading–unloading and CSM tests on phyllosilicates have reported indentation size effect that influences the hardness and hardness-derived yield stress of these minerals (Fig. 13c) (Yin and Zhang 2011; Zhang et al. 2010, 2013).

Pyroxenes

Microindentation hardness tests carried out on Jadeite and Diopside (Dorner and Stöckhert 2004) reveals that Jadeite is stronger than Diopside in LTP regime. Between the temperature range from 300 to 750 °C, H of Jadeite and Diopside varies from 7.4 to 8.5 GPa and 4.9 to 6.1 GPa, respectively. Since Jadeite and Diopside are the two end members of the Omphacite solid solution series, variation in H between these two minerals can be attributed to their compositional differences. Both jadeite and diopside hardness data show weak dependence on temperature with an average gradient of − 2 MPa/K (Fig. 10a) and negligible anisotropy with respect to crystallographic orientation of the planes of indentation. ${\sigma }_{y}$ of jadeite and diopside varies from 6.1 ± 0.6 to 5.0 ± 0.3 GPa and 4.1 ± 0.3 to 3.0 ± 0.3 GPa, respectively. ${\sigma }_{P}$ of these minerals varies between 8.4 (Jadeite) and 6.5 GPa (Diopside), estimated through Frost and Ashby’s model (1982). The normalized $({\sigma }_{P}$/G) of these minerals shows a similar value, suggesting that they belong to an iso-mechanical group. Linear microcracks developed during low temperature indentations in these clinopyroxenes, gradually reducing with increasing temperature. The LTP is accommodated by dislocation glides in multiple slip systems, amongst which (100) [001] is the dominant slip system observed in both the minerals. In the high temperature (~ 0.8 T_m, T_m: Homologous temperature) dislocation creep regime, diopside becomes stronger than jadeite. The transition from LTP to dislocation creep regime occurs at 0.8 T_m for both minerals. However, since the melting point of jadeite is much lower than diopside, it shows early transition from LTP to dislocation creep, which causes the apparent decrease in strength compared to diopside (Fig. 10b) (Dorner and Stöckhert 2004; Orzol et al. 2002; Stöckhert and Renner 1998).

Creep of minerals during nanoindentation

Nanoindentation creep has been tested mostly on shale, sandstone and granitoid rocks. So far, quartz, orthoclase, muscovite, halite, and clay mineral such as kaolinite has been studied for indentation creep (Goldsby et al. 2004; Ma et al. 2022; Shi et al. 2020; Sun et al. 2021; Thom and Goldsby 2019; Wang et al. 2022). Stress exponents obtained for quartz, feldspar, and mica are much greater than 3, conferring that dislocation along activated slip planes facilitates creep deformation in these minerals at LTP. Although, it has been observed that the stress exponent slowly decreases with increasing holding time (Ma et al. 2022). Indentation strain rate as well as the creep displacement varies proportionately with P_max only during the transient stage. Still, it becomes independent of applied load during the steady-state stage. Since H and E of quartz is higher than orthoclase, for the same P_max orthoclase shows higher creep displacement than quartz during the transient stage. However, their displacement trends at the steady-state stage are quite similar, suggesting that orthoclase and quartz undergo a similar deformation process at low temperature indentations (Ma et al. 2022; Wang et al. 2022). On the other hand, muscovite shows higher creep displacement during the transient stage at a much lower peak load because of its low hardness and elastic modulus compared to quartz or orthoclase (Fig. 14). Kaolinite and halite also show same trends as muscovite (Sun et al. 2021; Thom and Goldsby 2019), which establishes the fact that rheologically, these minerals can be grouped as “soft”, whereas quartz and orthoclase can be grouped as “hard”. Stress exponents obtained for halite shows a variation with hardness, where, for higher hardness the stress exponent reaches 25, which is indicative of low temperature plasticity. However, with increasing holding time during indentation creep, this value reduces to 5, suggesting that dislocation creep becomes the major deformation mechanism at that condition (Thom and Goldsby 2019).

Fig. 14

Nanoindentation creep of some common minerals: Quartz, Orthoclase, Muscovite (Ma et al. 2021a, b), and Kaolinite (Sun et al. 2021)

Goldsby et al. (2004) first explored the application of indentation creep in understanding the rate-and-state friction law that operates during earthquakes. According to their observations, the contact stiffness of quartz increases with creep time which suggests that in a quasi-static condition, friction between two contact surfaces increases, similar to a stick–slip model of rock friction proposed as a mechanism to explain episodic earthquakes. The fractional contact area in the indentation-creep experiment increases linearly as a function of the logarithm of time, similar to in a “slide-hold-slide” experiment, suggesting that increasing contact area increases the magnitude of static friction coefficient with time.

Investigating the viscoelastic nature of nanoindentation creep of quartz in shale and sandstone yields that the instantaneous elastic modulus ${E}_{1}$, modulus of long-term reversible creep ${E}_{2}$ and the creep time constant ${\eta }_{21}$ decreases, whereas the long-term creep viscosity ${\eta }_{1}$ increases with increasing peak load, suggesting that quartz behaves less elastically during the transient stage of creep deformation (Sun et al. 2021; Wang et al. 2022). The decreasing trend of elastic parameters with increasing load can be attributed to the indentation size effect. On the other hand, clay minerals like kaolinite show an opposite trend, increasing viscoelastic parameters with increasing peak load (Sun et al. 2021). This reverse trend can occur possibly either because of grain compaction, rearrangement, and friction along grain boundaries of clay minerals or mechanical interaction of clay minerals with much stiffer quartz along grain boundaries since the average elastic parameters of quartz are larger in magnitude than that of clay minerals (Sharma et al. 2019; Wang et al. 2022).

Future research directions and conclusions

Over the past six decades, many applications of instrumented indentation have brought to us some fascinating details about the deformation mechanisms of single crystal and polycrystalline aggregate of major crustal and/or mantle mineral phases, in which, integrated advanced imaging techniques such as Transmission Electron Microscopy (TEM) (e.g. Marrow et al. 2022; Masuda et al. 2000) and/or HR-EBSD (Kumamoto et al. 2017; Wallis et al. 2020) have expanded the understanding of lattice scale dislocation dynamics of materials undergoing plastic deformation at low temperatures. However, there are only a few studies that have reported the mechanical response of minerals at higher temperatures using microindentation (e.g., Dorner and Stöckhert 2004; Evans 1984; Evans and Goetze 1979), and the nanoscale deformation mechanism of crustal minerals at high-temperature domain needs to explore further. High temperature plasticity is characterized by combined dislocation glide and climb assisted creep, with complex dislocation interactions (Frost and Ashby 1982). Nanoindentation is arguably the best method for investigating such complex lattice scale thermomechanical behavior of minerals.

Atomic force and scanning probe microscopy (AFM and SPM) are examples of techniques that are recently being used as new ways to assist instrumented indentation. Several studies have reported application of AFM on shale to understand its mechanical properties (e.g. Eliyahu et al. 2015, Emmanuel et al. 2016, Li et al. 2018a). Indentation using AFM can be achieved in two ways: (a) a very low range load indentation to measure only the elastic behavior of materials, and (b) high load indentation to measure the viscoelastic parameters of a material. One of the major advantages of AFM indentation is that it provides homogeneous mechanical mapping along with the surface topography of a preassigned submicron-scale scan area by continuously probing into the material surface at a high frequency and high probing density (Sobhbidari and Hu 2021). This provides a localized map of the material surface which could elucidate the effect of preexisting defects and impurities on the surface mechanical properties of a material. For instance, Chakoumakos et al. (1991) applied nanoindentation to investigate the surface mechanical properties of a chemically zoned zircon crystal damaged by in-situ alpha-decay event and reported that the hardness measured along a profile on the surface fluctuates as a function of the radioactive decay dose. Variation in the concentration of U and Th in the crystal had resulted in contrasting degree of amorphization, consequently a similar variation in hardness and elastic modulus. This work sets an example for a potential research problem: mapping mechanical properties along a physicochemically heterogeneous material surface to understand the role of preexisting defects and lattice impurities in its mechanical manifestations. Coupled with EPMA (Electron Probe Micro Analyzer), a similar study conducted by Wu et al. (2021) reported the nanomechanical variability along a profile of compositionally heterogeneous layered surface of calcareous concretions from glacial varve deposits. Same methodology should also be employed to study single crystal or polycrystalline minerals. AFM based Infrared Spectroscopy (AFM-IRS) provides in-situ chemical characterization of material surface along with mechanical mapping (e.g. Yang et al. 2017), and hence can be employed to investigate the mechanical heterogeneity of a chemically zoned mineral grain such as garnet.

One of the major concerns of employing instrumented indentation is the ISE and scale-dependent mechanical response of a material. Therefore, while using AFM indentation, one must be particularly aware of the fact that the results obtained from this technique would yield at least an order of magnitude higher values than micro- or macroscale indentation or mesoscale compressive tests. Hence, a great deal of work needs to be carried out in this regard—understanding the underlying mechanisms for indentation size effect and correlating the mechanical data across all scales of observations. Scale dependent plasticity has a profound effect on understanding the mechanical changes during phase transformation of minerals. For instance, high-temperature microindentation experiments on quartz (Darot et al. 1985; Lawn et al. 2021) reveals rapid microfracturing during $\alpha -\beta$ phase transition, however, fracturing during indentation is a function of load and contact area. Therefore, there is a possibility that the mechanical response of quartz during phase transition observed through microindentation might not be the same compared to nanoindentation data, thus bringing out a new problem for future investigations. In particular, as the process of phase transition alters the crystallographic dimensions and subsequently the lattice structure, it may give rise to intrinsic ISE and even RISE. Therefore, phase transition, dehydration, and chemical alteration, etc. are some of the major processes that affect the mechanical response of a mineral and should be addressed with varying experimental parameters such as load, loading rate, strain rate and holding time (e.g., Alao and Yin 2014, Shi et al. 2019a).

In this regard, real-time imaging of multiscale indentation processes on various crystalline materials through in-situ SEM and TEM based nano- to picoindentation (with load resolution ~ 1 nN, displacement resolution ≤ 1 nm) techniques have shed light on the understandings of dislocation dynamics at room temperature as well as high-temperature ambient conditions (Carlton and Ferreira 2012; Nili et al. 2013). One of the first in-situ SEM-based nanoindentation studies was reported by Rabe et al. (2004), where they indented layered titanium nitride and silicon nitride films to map the onset of plastic deformation and the evolution of the specimen surface with progressive increase of load. At each incremental stage of load, the real-time changes in pop-in behavior, piling-up of material around the indenter were captured through Back Scattered Electron (BSE) imaging, and the evolution of contact area as a function of load was monitored continuously. With further technological advancement, Moser et al. (2005, 2006) applied SEM-based instrumented nanoindentation tests on zirconium-based bulk metallic glasses that allowed to quantify the magnitude of pop-ins or displacement bursts in the P–h curve which were correlated with the simultaneous occurrence of fracture as well as intracrystalline shear band formations. Rzepiejewska-Malyska et al. (2008, 2009) developed the first SEM-based depth sensing indentation (DSI) setup to study the nano-mechanics of titanium nitride, and reported that at higher loads, adhesive as well as cohesive failure creates anomaly in the P–h curves. Real time visualization of the surface evolution during indentation can provide significant information about the indent morphology, especially the pile-up or sink-in effect. These state-of-the-art techniques can be implemented for studying intracrystalline behavior of minerals, particularly for layered and transversely isotropic minerals such as micas and other hydrous phases, where the formation of Incipient Kink Band (IKB), shear localization, and layer perpendicular delamination can be observed in discrete time-resolved stages. In situ SEM-based experiments can also provide insights into the effects of surface undulation, tip-surface interaction, and errors due to tip abrasion that contributes to ISE in different scales.

SEM-based indentation techniques have two major limitations. First, is the inability to view fracture propagation through depth of crystal grains. Second, the lack of true nanoscale real-time imaging such as observation of stress-induced phase and structural transition of individual crystals or grains and the ability to study the propagation of the plastic deformation zone beneath the indenter (Nili et al. 2013). TEM based nano- to picoindentation methods provide better insights in these cases. Minor et al. (2004, 2002) first reported the in-situ TEM based instrumented nanoindentation studies on aluminum thin film that provided information about the formation of nanoscale incipient plastic bands that developed with progressive load and accommodated plastic strain during indentation. Ultra-sensitive capacitive transducers integrated with the TEM indentation setup allows stepwise measurement of load and displacement in discrete phases with true nanoscale imaging of the deforming sample. Ultra-thin specimen fitted inside the TEM holder even allows to test tensile properties of individual crystal grains during indentation (Kiener and Minor 2011). Although the sample preparation and instrumentation setup are extremely difficult and laborious for TEM based experiments, the results provide one of the finest insights into the real-time lattice dynamics of crystals. Since nanoindentation generates extremely high confining pressure at the tip of the indented region, the in-situ TEM based indentations on quartz, olivine, and even anisotropic phases such as calcite, gypsum and mica at ambient and/or high-temperature conditions can provide information about the stress-induced phase transition, dehydration, and deformation mechanisms such as grain boundary migration (GBM), diffusion creep (DC), dissolution precipitation creep (DPC), ripplocations, etc. that can be directly correlated with the real-time observations of the microstructural changes.

To gain insights into the intracrystalline fracture propagation, tensile strength, and compressive strength of individual crystal grains a new type of nanomechanical experiments is conducted on micro- to nanopillars and beams that are fabricated using Focused Ionic Beam (FIB) milling process (Sebastiani et al. 2015b). These experiments are extended versions of in-situ SEM-based nanoindentation tests, and comprises of mainly four types viz., single cantilever beams (e.g., Maio and Roberts 2005), double cantilever beams (e.g., Liu et al. 2013), clamped beams (e.g., Jaya and Jayaram 2014), and pillars (e.g., Sebastiani et al. 2015a; Sly et al. 2020). High energy ionic beams (such as Ga +) are charged on the specimen surface to produce beams with notches at predefined positions and wells inside which cylindrical micropillars are fabricated. The milled specimens are then indented using either flat punch or sharp indenter with controlled load and strain rates to produce tensile cracks. The deformation process is monitored in real time through SEM imaging and the onset of fracturing is directly correlated with the load–displacement profile to get the yield strength of the individual phases. Recently, Sly et al. (2020) applied FIB fabricated micropillar compression on calcite on different crystallographic orientations to estimate the anisotropy of uniaxial compressive yield strength. Similar technique can also be applied to other anisotropic mineral phases such as mica, gypsum, etc. to examine deformation mechanisms such as delamination of layers, propagation of median cracks, formation of kink bands and piling-up, etc. FIB micropillar compression is also a novel technique to accurately estimate K_C of minerals (Sebastiani et al. 2015b). The length by diameter ratio of these micropillars are set to 2:1 (Sly et al. 2020) to replicate the mesoscale compressive tests, thereby miniaturizing the conventional experiments to submicron scale. This provides a direct insight into the scale-dependent deformation mechanism of materials.

Apart from experimental studies, ab-initio simulations of instrumented indentation provide important insights into the mechanical response of a material of ideal composition. Simulations like Density Functional Theory (DFT) or Molecular Dynamic Simulation (MDS) are frequently used in materials science research for generating defect free lattice structures to compare the simulation results with experimental data. Running these simulations on geomaterials are computationally expensive and often produces erroneous results because of their complex crystal structure and chemical composition. However recently, some of the studies have reported the use of MD simulation (e.g., Ma et al. 2021a, b) and DFT (e.g. Lanin et al. 2021) alongside nanoindentation tests to correlate the experimental data with the simulation results for crustal minerals. Ab-initio simulations are fast, efficient and reliable methods for evaluating lattice scale dynamics of minerals and can generate valuable data on the mechanical parameters of minerals at all possible scales of observation. Therefore, it is expected that more simulation-based studies on assessing the physical properties of minerals will be conducted in future, and the cross-scale correlation of experimental as well as simulation data will help us to understand the scale-dependent mechanical variability of important rock forming minerals and their geologic implications.