Introduction

Knowing the elastic properties of minerals is of crucial importance in geosciences for the correct interpretation of seismological data (e.g., Birch 1952; Jackson 1983; Brown and McQueen 1986; Duffy et al. 1995; Li and Liebermann 2007; Bass et al. 2008). Since both pressure and temperature increase as a function of depth, much experimental and theoretical work has been done to understand how these two variables affect the physical properties of minerals (e.g., Karki et al. 1997; Steinle-Neumann et al. 2001; Speziale et al. 2004; Murakami et al. 2012; Lu et al. 2013; Yang et al. 2014; Mao et al. 2015; Pamato et al. 2016; Zhang and Bass 2016; Duan et al. 2018).

Most of the minerals relevant to geophysics (e.g., olivine, spinel, garnet, magnesiowüstite) are solid solutions between two (or more) endmember compositions; therefore, an in-depth understanding of the relationships between their chemical composition and physical properties is of great relevance. Experimental results obtained at high pressure and high temperatures can be well described and modeled according to widely accepted thermodynamic approaches (eulerian finite strain, thermal equation of state; e.g., Birch 1938, 1947; Davies and Dziewonski 1975; Jackson and Rigden 1996; Angel 2000; Li and Zhang 2005; Stixrude and Lithgow-Bertelloni 2005). On the opposite, the influence of chemical composition on elasticity is not yet fully understood (sometimes it is even ambiguous), and overall it is not satisfactorily modeled by a well-defined theoretical approach. Many extant studies have tried to tackle the problem of understanding how chemical substitutions and their effects on structural properties influence the elasticity of solid solutions, (e.g., Slagle and McKinstry 1967; Isaak and Graham 1976; Jackson et al. 1978; Giri and Mitra 1986; Tatli and Özkan 1987; Angel et al. 1988; Duffy and Vaughan 1988; Zhang and Reeder 1999; Reichmann et al. 2000; Jacobsen et al. 2002; Angel 2004; Jiang et al. 2004; Speziale et al. 2004; Nestola et al. 2006; Marquardt et al. 2009; Pamato et al. 2016; Buchen et al. 2017; Kurnosov et al. 2017). However, some review studies discuss samples with different origin, thermobaric history or synthesis methods, thus lacking internal consistency. Furthermore, most of these works are limited to either natural samples of complex chemical compositions or to synthetic endmember compositions.

Recently, Reichmann and Jacobsen (2006) and Riechmann et al. (2013) explored the systematic relations between crystal chemistry and elastic properties of oxides and silicates with spinel structure, and pointed out that systematic trends of density and elastic moduli of spinels with transition metals in both the octahedrally (M) and tetrahedrallycoordinated sites (T) violate the empirical Birch’s law (1961), and the transition metal-rich compositions are prone to low pressure phase transitions. Transition metals (especially, Fe) are known to affect the crystal structure and elasticity in rather complex ways (e.g., Syono et al. 1971; Lin et al. 2013). Since Fe is widespread on the Earth (dominates the core and is the fourth most abundant element in the mantle; Jackson 2000), it is of interest to systematically investigate how Fe–Mg substitution influences the structural and elastic response of Earth materials. To explore such an effect, we have chosen to investigate spinels in the series MgAl2O4–FeAl2O4 (spinel–hercynite). Minerals of the spinel–hercynite solid solution series (MgAl2O4–FeAl2O4) are important accessory phases in upper mantle assemblages and relevant components in solid inclusions of diamonds (e.g., Nestola et al. 2015).

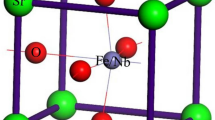
Spinel crystals belong to the cubic system (space group: \(Fd{\overline{3}}m\)). The structure of spinel can be described in terms of anion and cation sublattices (Sickafus et al. 1999). The anions in the sublattice are arranged in a pseudo-cubic close-packed lattice, being slightly shifted in the <111> directions. The oxygen fractional coordinate is usually identified by the letter u. When u = 0.25 (assuming the origin of the unit cell at the octahedral vacancy with point symmetry \(\overline{3}m\)), the anion sublattice is a perfect cubic close packed (ccp) lattice. The cation sublattice corresponds to the cubic MgCu2 Laves phase (Galasso 2016). The overall unit cell consists of 32 oxygen atoms with 64 tetrahedral and 32 octahedral interstices, but only 24 of these interstices are occupied by cations (8 cations in tetrahedral coordination and 16 cations in octahedral coordination). The general chemical formula of spinel is AB2X4, where X represents anions and A and B are divalent and trivalent cations, respectively, and there are eight formula units in a unit cell. A very interesting feature of the spinel structure is the possibility to incorporate a wide range of chemical species by adjusting the three structural degrees of freedom: (1) cell parameter (a), (2) oxygen fractional coordinate (u) and (3) degree of inversion (i) (Sickafus et al. 1999). The degree of inversion i quantifies the fraction of the B cation in the tetrahedrally coordinated site according to the formula: T(A1−iBi)M(AiB2−i)X4. The two opposite configurations are: (1) i = 0: no B cations in tetrahedra (normal spinel) and (2) i = 1: the T-site is fully occupied by B cations (inverse spinel). Both spinels with i = 0 and i = 1 are defined as ordered. However, only few spinels are exactly normal or inverse, very often indeed the cations can be disordered among the M and T sites and hence i can take values between 0 and 1. The maximum disorder is reached when i = 2/3. Equilibration temperature has a very important effect on the inversion degree of a spinel: higher equilibration temperatures promote cation disorder (e.g., Andreozzi et al. 2000). In principle, also pressure could affect the cation distribution of a spinel, although there is not yet a general consensus on the role of pressure in modifying the degree of disorder (e.g., Hazen and Navrotsky 1996; Nestola et al. 2007). Spinels virtually offer the possibility of understanding in which way cations in different coordination environments may affect the elastic properties of binary solid solution series (Recio et al. 2001; Mori-Sánchez et al. 2003; Bruschini et al. 2015). Many papers have already dealt with the elasticity of oxides and silicates with spinel structure, but a thorough experimental investigation of the systematic effects of Fe–Mg substitution is still missing. To the best of our knowledge, the only available data on Fe-bearing aluminate spinels are given by Wang and Simmons (1972), who reported the full set of elastic parameters for a synthetic FeAl2O4 and a natural (Mg,Fe)Al2O4 spinel. Recently, Nestola et al. (2015) studied the high pressure equation of state of FeAl2O4.

In the present study, we investigate the effects of Fe2+–Mg substitution on the elasticity of cubic spinels in the system (Mg1−xFe2+x)Al2O4 with 0 ≤ x < 0.5. Six gem-quality synthetic crystals were studied following a multi-analytical approach including electron microprobe analysis (EMPA), single-crystal X-ray diffraction and Brillouin scattering (BS).

Experimental methods

Crystal synthesis and sample preparation

The single crystals investigated in this study were previously synthesized and described by Andreozzi et al. (2000), Andreozzi and Lucchesi (2002) and Hålenius et al. (2002). Here, it is worth remembering that all the crystals were synthesized at the very same experimental conditions to ensure a high degree of internal consistency. Gem-quality inclusion-free crystals were selected for the crystal chemical and Brillouin scattering measurements and were manually ground into double-side polished platelets having a thickness of 40–60 µm. The starting crystals showed a well-developed octahedral shape and for this reason all the produced platelets were parallel (or very close) to {111}, with the exception of He5a which is almost parallel to {100}. Some crystals coming from the same batch of materials from which we picked up the samples from this study were already chemically and structurally characterized (Andreozzi and Lucchesi 2002; Hålenius et al. 2002). For the sake of accuracy, we repeated the chemical and crystallographic characterization on the very same samples used for the Brillouin scattering measurements.

Single-crystal structure refinement

For X-ray data collection, the six crystal fragments used for Brillouin scattering measurement were mounted on a Bruker KAPPA APEX-II diffractometer, equipped with a CCD area detector (6.2 × 6.2 cm2 active detection area, 512 × 512 pixels) and a graphite crystal monochromator, using MoKα radiation from a fine-focus sealed X-ray tube. The sample-to-detector distance was 4 cm. More than 5000 exposures per sample were collected (step = 0.2°, time/step = 10 s) covering the full reciprocal sphere with an average redundancy of about 20. Final unit cell parameters were refined using the Bruker AXS SAINT program from about 2000 recorded reflections with I > 10 σI in the range 8° < 2θ < 90°. The intensity data were processed and corrected for Lorentz, polarization and background effects with the APEX2 software program of Bruker AXS. The data were corrected for absorption using the multi-scan method (SADABS), leading to a significant improvement in Rint (merging residual value). No violation of \(Fd{\overline{3}}m\) symmetry was noted.

Structure refinement was done with the SHELXL-2013 program (Sheldrick 2013). All reflections were used in the refinement. Variable parameters during the structural refinement were: overall scale factor, oxygen coordinate, site-scattering values, atomic-displacement parameters, and extinction parameter. Setting the origin at \(\overline{3}m\), the initial atomic positions for oxygen atoms were taken from Bosi et al. (2010). The T site was modeled with Mg vs. Fe and the M site with Al (except for crystal MgAl2O4, which was modeled considering only TMg and MAl because of being Fe free). Convergence was attained when the shifts in all refined parameters were less than their estimated standard deviation. Table 1 summarizes the structural parameters and refinement details.

Table 1 Selected X-ray diffraction data for the spinels in the (Mg,Fe)Al2O4 series studied
Full size table

Electron microprobe analysis and cation partitioning

The same crystals used for Brillouin scattering measurements were mounted on a glass slide and polished for electron microprobe analysis on a Cameca SX50 instrument equipped with four wavelength-dispersive spectrometers (WDS mode) and operated at an accelerating potential of 15 kV and a sample current of 15 nA, with an incident beam diameter of about 1 µm. For each sample, we collected 7–20 point analysis. Standards used were synthetic MgAl2O4 spinel and corundum (for Al), Fe3O4 (for Fe) and MgO (for Mg). PAP computer program was applied for raw data reduction (Pouchou and Pichoir 1984). Atomic fractions were calculated on the basis of four oxygen atoms (atoms per formula unit, apfu). The results, given in Table 2, are well supported by the match between the number of electrons per formula unit derived from chemical and structural analysis.

Table 2 Chemical composition of the investigated Fe–Mg spinel samples
Full size table

The intersite cation distribution was obtained by minimizing the residuals between calculated and observed chemical-structural data according to the procedure of Lavina et al. (2002). Optimized cation distributions are reported in Table 3.

Table 3 Calculated cation site population in the investigated Fe–Mg samples
Full size table

Brillouin scattering measurements and data reduction

Brillouin scattering measurements were performed in the Brillouin Laboratory at GFZ German Research Centre for Geosciences in Potsdam, Germany. During the Brillouin scattering measurements, the samples were loaded into a sample holder obtained by sandwiching a 250 mm thick, face parallel, stainless steel disk (with a 2 mm diameter drilled chamber) between two diamond disks. The sample platelets were placed inside the sample chamber in contact with one of the two diamond plates. We found this system to be very useful for ambient condition measurements for two main reasons: (1) the sample can be quickly and easily removed from the holder and (2) diamond has a very high thermal conductivity, which allows to efficiently dissipate heat potentially produced by light absorption in the sample. We used a forward symmetric scattering geometry (e.g., Whitfield et al. 1976) and an external incidence angle of 60°. The mirror distance in the interferometer was 6 mm. We used a Verdi V2 solid state Nd:YVO4 laser with a power at the sample of about 100 mW. To change systematically the orientation of the sample, the platelets were rotated along a horizontal axis starting from an arbitrary orientation in an angular range of 180° collecting a spectrum every 10°. The total number of probed velocities ranges between 31 and 48. The collection time for each spectrum was in the order of 1–2 h. Since iron tends to increase the absorption of light in our crystals (they become more opaque with increasing iron content), we reduced the incident laser intensity to avoid overheating of the sample and hence any possible Fe2+ oxidation and associated defects. As a consequence, the collection time for iron-rich samples (He5a and He6a) was significantly longer (2–3 h). Since the investigated materials become opaque for high iron content, we could not analyze crystals with Fe2+ > 0.5 apfu.

In a typical Brillouin scattering measurement, a beam of coherent light is shone into the sample to be investigated. A very small fraction of the scattered radiation is found to be frequency shifted with respect to the incident beam (Cummins and Schoen 1972; Grimsditch 2001). The frequency shift (\(\varDelta \omega\)) is proportional to the speed of sound (\(\nu\)) in the probed direction, according to Whitfield et al. (1976):

$$\nu =\frac{{\Delta \omega {\lambda _0}}}{{2\sin {\theta _{{\text{ext}}}}}}.$$
(1)

In Eq. (1), \({\lambda }_{0}\) is the wavelength of the laser and \({\theta _{{\text{ext}}}}\) is the external angle of incidence in symmetric scattering geometry. In elastically anisotropic materials (like the vast majority of crystalline compounds including those belonging to the cubic system), the velocity and the polarization of an acoustic wave may change as a function of crystallographic direction. By measuring the velocities in two or more directions, it is possible to retrieve the full set of elastic constants (Every 1980; Newnham 2005).

Spinels crystallize in the cubic system (space group \(Fd{\overline{3}}m\)) and their elastic tensor is fully described by only three stiffness coefficients: C11, C12 and C44 (in Voigt contracted index notation).

The full elastic tensors and the crystallographic orientations of the sample platelets were refined by performing a non-linear least-square fit of the set of Christoffel’s equations corresponding to probed acoustic waves (Every 1980; Shimizu 1995). Uncertainties on the retrieved Cij depends on errors associated with measured velocities, which in turn depend on uncertainties associated with peak position determination (frequency shift). The last step was to convert the single-crystal stiffnesses into an ideal isotropic polycrystalline bulk modulus (KS0) and shear modulus (GVRH) values using the Voigt–Reuss–Hill (VRH) averaging scheme (Eq. 2–5; Watt et al. 1976):

$${K_{{\text{S0}}}}={K_{\text{V}}}={K_{\text{R}}}=\frac{{\left( {{C_{11}}+2{C_{12}}} \right)}}{3},$$
(2)
$${G_{{\text{VRH}}}}=\frac{{{G_{\text{V}}}+{G_{\text{R}}}}}{2},$$
(3)

where

$${G_{\text{V}}}=\frac{{\left( {{C_{11}} - {C_{12}}+3{C_{44}}} \right)}}{5},$$
(4)
$${G_{\text{R}}}=\frac{{5\left( {{C_{11}} - {C_{12}}} \right){C_{44}}}}{{4{C_{44}}+3\left( {{C_{11}} - {C_{12}}} \right)}}.$$
(5)

The subscripts “V” and “R” refer to the Voigt and Reuss bound values.

Results

Crystal chemistry

The results of the single-crystal X-ray diffraction measurements are reported in Table 1 and shown in Fig. 1. All the parameters increase linearly with increasing Fe content. As already noted by Andreozzi and Lucchesi (2002), the cation–oxygen distances in tetrahedra (T-O) increase at a much higher rate than cation–oxygen distances in octahedra (M-O); therefore, the increase of the unit cell can be mainly attributed to the expansion of tetrahedra. In iron-poor compositions, T-O are shorter than M-O, while for iron-rich compositions the opposite is true. At about 0.20–0.25 Fe2+ apfu, T-O and M-O are expected to have the same value (Fig. 1c).

Fig. 1
figure 1

The main crystallographic parameters plotted against Fe2+ content for the investigated Fe–Mg spinel samples: a unit cell parameter (a); b oxygen positional parameter (u); c cation–oxygen bond length in tetrahedra (T-O) and octahedra (M-O). Blue diamond symbols are for T-O, while red square symbols are for M-O. The open symbol represents sample He3a (see text for “Discussion”). Error bars are sometimes smaller than symbol size. Dashed lines are guides to the eye

Full size image

The chemical composition of the investigated (Mg1−x,Fex)Al2O4 spinel crystals is summarized in Table 2. The Fe2+ content progressively increases up to 0.48 apfu substituting for Mg, while Al content keeps almost stoichiometric with a minor substitution by Fe3+ at the highest Fetot contents. Most of the Fe2+ is found in tetrahedral coordination, with only a little fraction (reaching a maximum value of 0.07 apfu in He6a) hosted in the octahedra (Table 3). The very small amount of Fe3+ is found in tetrahedra. The tetrahedrally coordinated Al (which summed with the tetrahedrally coordinated Fe3+ corresponds to the inversion degree) decreases slightly but steadily along the investigated range, while the amounts in the octahedra remain constant. Overall, we can state that the increase of Fe2+, which substitutes Mg in tetrahedra, is mainly responsible for the crystallographic variations observed in the MgAl2O4–FeAl2O4 solid solution. The results described here are in agreement with those reported in Andreozzi and Lucchesi (2002) for crystals grown in the same experimental batches, with the only important exception of sample He3a (x = 0.202) for which the structural parameters are significantly lower than expected (Table 1; Fig. 1).

Elasticity

In many spectra, we observed the longitudinal and both shear wave peaks (Fig. 2). The peak positions (that is the frequency shifts) were determined by least-square fits to pseudo-Voigt functions and velocities were calculated with Eq. (1). Fitted velocities are plotted in Fig. 3. The peaks in the spectra were fitted with a mixed Gaussian–Lorentian model. The R2 coefficient ranged between 0.8 and 0.9.

Fig. 2
figure 2

Typical Brillouin spectrum. qL quasi-longitudinal wave, qT2 and qT1 quasi-transverse waves (fast and slow, respectively). The central peak corresponds to the unshifted radiation (Rayleigh scattering). At the far ends of the image, there are the qT wave of diamond and higher-order repetition of the central line (ghost). Intensity in arbitrary units (a.u.)

Full size image
Fig. 3
figure 3

Velocities measured as a function of rotation angle starting from an arbitrary direction. Blue circles are for quasi-longitudinal waves, green diamonds are for fast quasi-transverse waves and, red triangles are for slow quasi-transverse waves. The names of the samples and the crystallographic orientation of the platelets are shown at the center of each plot

Full size image

The Cijs determined for the (Mg,Fe2+)Al2O4 series are reported in Table 4 along with the Fe2+ content, density, calculated from measured composition and unit cell volume, aggregate (isentropic) bulk and shear modulus and Zener anisotropy factor. The values of Cijs and elastic moduli are plotted against the Fe2+ content in Figs. 4 and 5, respectively. For low Fe2+ content (≤ 0.202 apfu), the stiffness tensor components C11 and C44 are almost constant. However, for Fe2+/(Mg + Fe2+) passing from 0.202 to 0.388, both parameters visibly decrease (− 7 and − 13%, respectively). Conversely the component C12 shows a linear trend characterized by a fairly small increase (5%) along the investigated compositional range (Fig. 4).

Table 4 Density, Fe2+ content and elastic parameters of the investigated Fe–Mg samples
Full size table
Fig. 4
figure 4

Elastic stiffnesses (Cijs) as a function of Fe2+ content for the Fe–Mg aluminate spinel samples. Diamonds are for C11, squares are for C12 and circles for C44. Open symbols represent sample He3a (see text for “Discussion”), while gray symbols are from Wang and Simmons (1972). Yellow symbols are for MgAl2O4 literature data (Yoneda 1990; Askarpour et al. 1993; Suzuki et al. 2000; Fan et al. 2015; Speziale et al. 2016; Duan et al. 2018). Dashed lines are guides to the eye. Error bars are sometimes smaller than symbol size

Full size image

In cubic crystals, the bulk modulus (KS) and the shear modulus (G) are defined by Eqs. (2) and (3–5), respectively. For the studied samples, taking into account the errors associated with the measurements (in average 1–2 GPa), KS is poorly sensitive to chemical substitutions and only shows a weak negative trend with increasing Fe content (Fig. 5). On the contrary, G shows a large decrease (− 20%) along the investigated compositional range (Fig. 5). We have evaluated the elastic anisotropy quantified here by the Zener anisotropy ratio A (A = 2C44/(C11 − C12)), which shows a linear increase of 13.5% across the investigated Fe range (Table 4).

Fig. 5
figure 5

Isentropic bulk modulus (KS) and shear modulus (GVRH) as a function of Fe2+ content for the Fe–Mg aluminate spinel samples. Circles are for Ks, while diamonds are for GVRH. Gray symbols represent data from Wang and Simmons (1972), while turquoise symbol is for data from Nestola et al. (2015) corrected for the isentropic value. Open symbols represent sample He3a (see text for “Discussion”). Yellow symbols are for MgAl2O4 literature data (Yoneda 1990; Askarpour et al. 1993; Suzuki et al. 2000; Fan et al. 2015; Speziale et al. 2016; Duan et al. 2018). Dashed lines are guides to the eye. Error bars are sometimes smaller than symbol size

Full size image
Fig. 6
figure 6

Percolation threshold in the \(X_{{\text{Fe}}^{2+}(B)}\) – \(X_{{\text{Fe}}^{2+}(A)}\) plane. The arrows indicate the threshold for the A and B sublattices (Fiorani and Viticoli 1979a; Fiorani et al. 1979b; Scholl and Binder 1980). The dashed orange line is a guide to the eye

Full size image

Discussion

Our results for the elasticity of MgAl2O4 are completely consistent with literature data (Duan et al. 2018; Speziale et al. 2016; Fan et al. 2015; Suzuki et al. 2000; Askarpour et al. 1993; Yoneda 1990). However, in spite of the very simple chemistry of MgAl2O4 spinels, it is possible to observe some degree of scattering of the elastic moduli around the mean values corresponding to: C11 = 284 (2) GPa; C12 = 155 (1) GPa; C44 = 154 (1) GPa; KS = 198 (1) GPa and G = 108.4 (7) GPa (Figs. 4, 5). Given the different synthesis processes used to produce the crystals discussed in this comparison (flux growth, flame fusion, Czochralski), it is highly possible that the different samples may be characterized by a different defect structure and/or non-stoichiometry, which in turn could affect the elastic response (e.g., Verma 1960; Schreiber 1967).

The observed deviation of the crystallographic parameters for sample He3a from the trend defined by the other crystals (see Fig. 1) is due to an anomalously high inversion degree (i.e., Al at the T site, see Table 3). In normal spinels, high values of inversion degree correspond to high cation disorder induced by high temperature, as demonstrated by Andreozzi et al. (2000), Andreozzi and Princivalle (2002) and Martignago et al. (2006). The high closure temperature recorded by the He3a sample is likely ascribed to a very fast cooling path, probably experienced by this crystal because it grew close to the walls of the crucible, whereas most of the other crystals grew in the central part of the crucible. In spite of that, we decided to leave sample He3a in the present dataset, because it represents an interesting opportunity to see if and how the cation disorder affects the elastic parameters. Our results show that the elastic parameters of sample He3a agree with the trend defined by the very Fe-poor samples (Figs. 4, 5). Even though there is not a general consensus on the role of cation distribution on the elastic properties of spinels (e.g., Askarpour et al. 1993; Hazen and Yang 1999; Li et al. 2007; Nestola et al. 2007), our data suggest that in the low-Fe portion of the series, spinel–hercynite (0 ≤ Fe2+ ≤ 0.2 apfu), cation disorder has minor effects on the elastic moduli (Figs. 4, 5).

Fig. 7
figure 7

Elastic anisotropy (Zener anisotropy factor A) for spinel structure (blue symbols) and rock salt structure (red symbols) binary compounds. Circles are for solid solution between Mg and Fe2+ aluminate endmembers. Diamonds are for solid solution between Mg and Mn2+ aluminate endmembers. Triangles are for solid solution between Mg and Co2+ aluminate endmembers. When data on endmembers were only available, a linear dependency of A against composition was assumed. Dotted lines are linear weighted fit of the data. ∂A/∂M indicates the slope of the fitted line. XM denotes the mole fraction of the transition metal substituting for Mg. The value of A = 1, corresponding to elastic isotropy, is indicated by a dashed line. Data for Mg–Fe spinels: this study plus pleonaste from Wang and Simmons (1972); data for Mg–Mn spinels: Bruschini et al. (2015); data for Mg–Co spinels: Li et al. (1991); data for MgO–FeO: Jacobsen et al. 2002; data for MgO–MnO: average value from Webb et al. (1988), Uchida and Saito (1972), Sumino et al. (1980); data for MgO–CoO: average value form Uchida and Saito (1972), Sumino et al. (1980)

Full size image

The elasticity of iron aluminate spinels was studied by Wang and Simmons (1972) using ultrasounds interferometry on two samples, a natural one with composition Mg0.75Fe0.36Al1.90O4 and a synthetic one corresponding to the endmember hercynite FeAl2O4. In addition, Nestola et al. (2015) studied by high-pressure single-crystal X-ray diffraction a sample of FeAl2O4 synthesized in the same laboratory and under the same experimental conditions of the crystals investigated in this work. To obtain a consistent dataset, we converted the value of the isothermal bulk modulus (KT0) given in Nestola et al. (2015) for the hercynite endmember (193.9 ± 1.7 GPa) into the isentropic value (KS0) using the thermodynamic identity (Poirier 2000):

$${K_{{\text{S0}}}}=~{K_{{\text{T0}}}}(1+\alpha \gamma T),$$
(6)

where \(\alpha\) is the coefficient of thermal expansion (15.6 × 10−6/K; Fei 1995), \(\gamma\) is the Grüneisen parameter (1.21; Stixrude and Bertelloni 2005 and references therein) and T is the absolute temperature.

The results obtained by Wang and Simmons (1972) for the natural spinel (Fe2+ = 0.36 apfu) are in perfect agreement with our data, and the result from Nestola et al. (2015) for hercynite is consistent with the trend for KS0 defined by the available data (Figs. 4, 5). On the contrary, the results for FeAl2O4 crystal by Wang and Simmons (1972) differ significantly from the trend defined by our experimental dataset. Our results show that the components C11, C44 and GVRH after an initial plateau extending to x = 0.202 decrease as the Fe/(Fe + Mg) increases (Figs. 4, 5). There are not currently any additional published data on the elasticity of Fe2+-rich aluminate spinels, However, assuming that linear relations between C11, C44, GVRH, KS and Fe2+ content hold true in the compositional range 0.388 < Fe2+ < 1 apfu, we expect a significantly lower value of these moduli for hercynite with respect to MgAl2O4. Moreover, KS0 value for the synthetic FeAl2O4 measured by Wang and Simmons (1972) is largely different (about 7%) from KS0 obtained converting the isothermal result by Nestola et al. (2015). Only the elastic stiffness C12 determined by Wang and Simmons (1972) for FeAl2O4 agrees qualitatively with all the available experimental datasets. Considering the trend defined by our data and the data from Wang and Simmons (1972) for the natural pleonaste sample, also the value of the shear modulus for FeAl2O4 proposed by the same authors seems higher than a simple extrapolation of the other available data.

It is likely that the measurements of Wang and Simmons (1972) on FeAl2O4 may suffer from large unaccounted systematic errors which have led to an overestimation of the Cijs and hence the elastic moduli. In fact, as discussed by the same authors and later recapped by Nestola et al. (2015), the FeAl2O4 crystal used for the ultrasonic measurements was unusually small to provide accurate measurements. In more detail, if the ratio between the wavelength used in the experiment and the length of the sample is unusually large (i.e., if the crystal is too small with respect to the wavelength), the resulting velocities (and hence the Cijs) could be overestimated. Furthermore, as stated by Wang and Simmons (1972), the measurements along the <100> direction were particularly challenging due to phasing effects. In fact, any problem in the determination of the velocities in the <100> direction would directly influence the estimation of both C11 and C44 according to the following equations (Newnham 2005):

$$V_{{\text{P}}}^{{<100>}}=~\sqrt {\frac{{{C_{11}}}}{\rho }} ,$$
(7)
$$V_{{{\text{S1}}}}^{{<100>}}=V_{{{\text{S2}}}}^{{<100>}}=~\sqrt {\frac{{{C_{44}}}}{\rho }} .$$
(8)

According to Eq. (2), a high value of C11 would lead to a high value in KS0. In addition, recent literature shows that bulk modulus in oxide spinels is known be only slightly influenced by chemical substitution (e.g., Finger et al. 1986; Recio et al. 2001; Nestola et al. 2010, 2014). On this basis, the results for the synthetic FeAl2O4 by Wang and Simmons (1972) seem to be biased and inconsistent with the trend based on our results and the other available published data.

Due to the high optical absorption of the Fe-rich compositions, our study does not cover the full spinel–hercynite solid solution series, and the available data do not allow us to give a comprehensive (exhaustive) account of the compositional dependence of the elastic tensor in this system. Additional experimental and theoretical work, especially regarding the Fe-rich compositions, is definitely needed. Nevertheless, we can already provide a first consistent picture of the effect of Fe–Mg substitution on the elastic properties in the system MgAl2O4–FeAl2O4.

Magnesium and iron have a very different electronic structure, with magnesium being an alkaline earth metal, while iron is a transition metal. The different electronic structure of the two elements has profound consequences on the metal–oxygen bond strength, with direct impact on the local structure, phonon spectrum and elastic properties including anisotropy. Fe2+ in tetrahedral coordination, unlike Mg2+, gives rise to dynamic Jahn–Teller effect (Goodenough 1964; Slack et al. 1966; Taran and Langer 2001; Skogby and Hålenius 2003). While many studies discussed the effect of Jahn–Teller (JT) ions on the structural properties of spinels at both room and high pressure (e.g., Waskowska et al. 2001; Nakamura and Fuwa 2014; Kyono et al. 2015), there is much less knowledge on how the JT effect affects elasticity. Syono et al. (1971) and Ishikawa and Syono (1971) attributed the anomalously low value of the (C11–C12) and C44 modes in Fe2TiO4 ulvöspinel to the JT effect caused by Fe2+ in tetrahedral coordination (TFe2+). Wang and Simmons (1972) observed that both FeAl2O4 and Fe2TiO4 have about the same molar concentration of TFe2+, but since the elastic stiffness coefficients of hercynite are by far much larger than ulvöspinel, the anomalous elastic behavior in Fe2TiO4 must not be solely due to the JT effect. The JT effect may explain, at least in part, the general decreasing trend of the MgAl2O4–FeAl2O4 series, although more experimental data on systems characterized by JT active ions are definitely needed to address the problem.

The substantially different characters of Fe–O bonding with respect to Mg–O bonding produce a large and almost linear softening of the longitudinal and shear elastic stiffnesses in the MgO–FeO solid solution series (Jacobsen et al. 2002). An overall softening effect is also observed in the spinel–hercynite series. However, in this case the compositional dependence of the elastic coefficients C11 and C44 is non-linear. At low Fe2+ content, the values of both C11 and C44 are nearly independent of composition, while at Fe2+ contents above 20% they decrease with increasing Fe2+ content. Such non-linearity can be interpreted as due to a transition from a low concentration regime where the individual Fe atoms are isolated to one in which they show a cooperative behavior. The threshold between the two regimes can be interpreted as a critical percolation probability pc (Broadbent and Hammersley 1957; Sykes and Essam 1964; van den Marck 1997). In the spinel structure, the cations are arranged in a MgCu2-type sublattice where each tetrahedral (A) atom is surrounded by 16 close neighbors, 4 A “tetrahedral” atoms and 12 B “octahedral” atoms at very similar (less than 5% different) distances from the central A atom; in addition, the B atoms are arranged in a corner-sharing tetrahedral lattice with 6 B close neighbors at a distance almost 20% shorter than the A–A and A–B ones (e.g., Berry and Raynor 1953). In spinel–hercynite, Fe2+ is distributed almost only in the A sites (XFe2+ ≈ XFe2+(A), where XFe2+(A) is the fraction of Fe2+ in the A site) in the samples with less than 10% Fe2+–Mg substitution (He2d, He2f). In this case, the site percolation threshold corresponds to that of the tetrahedral sublattice, which is a diamond lattice with pc = 0.429 (van der Marck 1997). Samples He3a and He5a (XFe2+ = 0.202 and 0.388 respectively) have a small, but detectable fraction of Fe2+ (XFe2+(B)) in the octahedral sites (see Table 3), and this decreases the site percolation threshold because there are 12 more close neighbors available for each tetrahedral atom and there is a finite probability of close neighbors Fe2+ in the B–B sublattice (which has pc = 0.39; Scholl and Binder 1980). The percolation thresholds for interactions between cations in both A, B and AB sublattices have been treated in studies concerning the magnetic properties of spinels (Fiorani and Viticoli 1979a; Fiorani et al. 1979b; Scholl and Binder 1980). Following the results of Scholl and Binder (1980), who limited their analysis to AB interlattice interaction, and the reasoning of Hubsch et al. (1978), who also considered interactions in the A and B sublattices, we expect that site percolation threshold in spinel–hercynite is reached when the Fe2+ content is smaller than 0.429 (that is, the threshold for the A sublattice) due to the larger connectivity of the combined sublattices interactions (Fig. 6). This value is close to that determined for sample He5a (see Table 3).

The expected compositional threshold is qualitatively compatible with the results of our experimental study, which unfortunately do not include compositions between \(X_{{\text{Fe}}^{2+}}\) 0.202 and 0.388. The value of pc seems to be overestimated, especially with respect to the compositional dependence of C44, which shows a change of behavior already at values of Fe2+ close to 0.2 apfu, based on the intersection of linear fits to the values determined below \(X_{{\text{Fe}}^{2+}}\) = 0.202 and above \(X_{{\text{Fe}}^{2+}}\) = 0.388 (Fig. 4). We can speculate that the presence of a resolvable fraction of Fe3+ in the tetrahedral sites of samples He3a, He5a and He6a (Table 3) could be also partially responsible for the disagreement between our results and the value of pc. In the MgAl2O4–MnAl2O4 solid solution series investigated by Bruschini et al. (2015), which does not contain resolvable amounts of Mn3+, the strongest decrease of C11 and a visible decrease in C44 occur close to Mn2+ = 0.47 apfu. Notably, this value is quite similar to the estimated pc of 0.429 for interactions only in the A sublattice.

Our results show a strong increase of the elastic anisotropy A with increasing Fe2+. We compared our results with literature data on elastic anisotropy of other compounds containing Fe2+ and other transition metals (Mn2+ and Co2+). In addition to spinels, the comparison was extended to NaCl-type (rock salt) structure compounds (MgO, MnO and CoO; Fig. 7 and electronic supplementary information), because this is a prototype structure adopted by important minerals of the Earth mantle, such as ferropericlase (Mg,Fe)O. Moreover, the cations Mg, Fe2+, Mn2+ and Co2+ are mainly tetrahedrally coordinated in spinels, while they are octahedrally coordinated in the NaCl structure. Where data on endmember composition were only available, we assumed a linear dependency between the mole fraction of transition metal (XM) and anisotropy. From this comparison, we highlighted several interesting points (Fig. 7): (1) the substitution of Fe2+ for Mg leads to opposite effects on the elastic anisotropy in (Mg,Fe)Al2O4 and (Mg,Fe)O. In spinels, we observe a linear increase of A as iron increases, whereas in (Mg,Fe)O the anisotropy exhibits a non-linear behavior, remaining constant in the range 0 < XFe < 0.25 and then linearly decreasing for higher iron content (Jacobsen et al. 2002); (2) the values of the derivative ∂A/∂XFe2+ are identical (within uncertainties), but opposite in sign for spinel and rock salt structures (in rock salt structure, the derivative was calculated in the range 0.25 < XFe < 0.95 being null for 0 < XFe < 0.25; (3) an increase in Mn2+ and Co2+ causes a small decrease of the anisotropy in both spinel and rock salt structures; (4) the values of the derivative \(\partial A{\text{/}}\partial {X_{{\text{M}}{{\text{n}}^{{\text{2}}+}}}}\) and \(\partial A{\text{/}}\partial {X_{{\text{C}}{{\text{o}}^{{\text{2}}+}}}}\) are identical (within uncertainties) in both spinels and rock salt structure: \(\partial A{\text{/}}\partial {X_{{\text{M}}{{\text{n}}^{{\text{2}}+}}}}^{{{\text{spinel}}}}\)  = \(\partial A{\text{/}}\partial {X_{{\text{C}}{{\text{o}}^{{\text{2}}+}}}}^{{{\text{spinel}}}}\) = \(\partial A{\text{/}}\partial {X_{{\text{M}}{{\text{n}}^{{\text{2}}+}}}}^{{{\text{rock}}\;{\text{salt}}}}\) = \(\partial A{\text{/}}\partial {X_{{\text{C}}{{\text{o}}^{{\text{2}}+}}}}^{{{\text{rock}}\;{\text{salt}}}}\).

Our results highlight the role of Fe2+ in determining the anisotropy of spinels, since it has a dramatic effect on elastic anisotropy with respect to other cations. It is interesting to note that the ionic radius of Fe2+ (0.63 Å) is intermediate between those of Mn2+ (0.66 Å) and Co2+ (0.58 Å; Shannon 1976), and hence elastic anisotropy can hardly be explained in terms of geometrical/crystallographic variations. It is possible that magnetic interactions between Fe atoms may contribute to the marked variation of the elastic anisotropy, although it is not clear why the anisotropy is enhanced in spinels and reduced in (Mg,Fe)O.

Conclusions

This work is the first systematic study which describes the elastic properties in the spinel (MgAl2O4)–hercynite (FeAl2O4) series. The Brillouin scattering measurements on synthetic crystals with 0 ≤ Fe2+ ≤ 0.5 allowed us to elucidate the relationships between crystal chemistry and elastic properties. We showed that for low Fe2+ content (Fe2+ ≤ 0.202), the elastic properties remain unaltered, but for values of Fe/(Fe + Mg) equal or larger than 0.388 there is a general decrease of all parameters (with the exception of C12). This behavior is explained according to the percolation theory and the transition between the low iron content region (constant parameters) and the high iron content region (linear decrease of the elastic moduli) occurs between 0.202 and 0.388 apfu of Fe2+, which therefore corresponds to the critical percolation threshold (pc). We also showed that cation disorder has very little or no influence on the elasticity of spinels with low Fe2+ content.

These results, especially if combined with additional data about the effect of pressure and temperature, will have direct implications in crustal and mantle petrology, as Fe2+-bearing aluminate spinels are widespread accessory minerals in both the crust and the mantle, assuming also particularly high relevance as diamond inclusions (e.g., Nestola et al. 2015).