Introduction

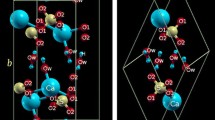
Pyrophyllite (ideally [Al2Si4O10(OH)2]) is the dioctahedral term of the phyllosilicate group consisting of simple 2:1 tetrahedral–octahedral–tetrahedral layers, namely TOT (Bruno et al. 2006; Evans and Guggenheim 1988). As shown in Fig. 1, the tetrahedral sheet is composed by individual SiO4 tetrahedra linked by sharing three oxygen atoms (basal oxygen, Ob) with SiO4 neighbours to form infinite two-dimensional sheets with a hexagonal-based patterns of linked sixfold rings; the plane formed by the basal oxygen is usually named “siloxanic basal plane”. The fourth corner (apical oxygen, Oa) does not link to other tetrahedral groups, but it is shared with the underneath Al octahedron. The octahedrally coordinated cations form a sheet, in which individual polyhedra are laterally linked by edge sharing. In pyrophyllite, only 2/3 of the octahedral sites are occupied mainly by aluminium. The 2:1 layer is composed of two opposing tetrahedral sheets with the octahedral sheet in between (see Fig. 1). Since the TOT layer is electrically neutral, no interlayer cations exist in these structures and van der Waals forces hold them together. This leads to the extreme softness of the mineral along a direction perpendicular to the TOT layers. Pyrophyllite is commonly found in nature in three polytypic forms: a two-layer monoclinic (2 M), a one-layer triclinic (1Tc) and a disordered form (Evans and Guggenheim 1988). The crystal structure of pyrophyllite-1Tc was determined by different single-crystal X-ray diffraction (XRD) refinements (Lee and Guggenheim 1981; Wardle and Brindley 1972).

Fig. 1
figure 1

Polyhedral models of the primitive cell of pyrophyllite as seen from the [010] and [001] directions. Stick and ball representation along the [100] direction was reported to clearly show the atomic arrangement

Full size image

From the geological point of view, pyrophyllite is one of the hydrous phases that in the last years has drawn a considerable interest in its high-pressure stability. Experimental studies have shown that some hydrous metamorphic minerals are stable to much greater depths in the Earth than previously evaluated (Pawley et al. 2002). Also, it seems that a range of new hydrous phases can be synthesized up to very high pressures. The attention to these minerals is mainly devoted to the processes in subduction zones, where dehydration is responsible for explosive volcanism and earthquakes (Grove et al. 2012; Sobolev and Chaussidon 1996). In this perspective, the high-pressure stability of hydrous phases determines the depth to which water can be recycled into the Earth’s mantle and the amount of recycling that can take place.

Furthermore, pyrophyllite has been studied for its utilization in whiteware body as a replacement of quartz, clay or feldspar (Alimdzhanova et al. 1999; Bhasin et al. 2003; Lintz 1938) and for its significant role in many industrial applications, such as petroleum and civil engineering, food and cosmetic industry, heterogeneous catalysis and waste storage (Mazo et al. 2008). However, its use as a ceramic raw material is not yet widely accepted, probably because pyrophyllite seldom occurs in pure state like other silicates, such as kaolinite, and the presence of associated minerals (quartz, kyanite, sericite, diaspore) in the aggregated structure can influence its properties. There is still little information regarding thermomechanical transformation of pyrophyllite, which could be of upmost importance due to depleting resources of standard alumino-silicate minerals. In this prospective, few works have been recently conducted on both pure pyrophyllite and pired-pyrophyllite for its utilization in ceramic and porcelain systems (Mukhopadhyay et al. 2010, 2011).

One of the most important thermodynamic parameters of a mineral is its equation of state (EOS), i.e. the pressure and temperature dependence of its unit-cell volume. This is essential for calculating the P–T conditions of mineral reactions. However, despite the importance of pyrophyllite in the water transport process in the Earth’s mantle or industrial applications, very few works have been proposed to fully characterize the thermodynamic properties of this mineral phase. Furthermore, the results presented in literature are quite conflicting and far from modern standards.

A set of thermomechanical data for stoichiometric pyrophyllite was reported by Holland and Powell (1998), by deriving thermodynamic properties from equilibria involving pure end-members. The bulk modulus estimated at zero pressure and at 298 K (K T0 ) by a Murnaghan equation of state fit (Murnaghan 1937) is 77 GPa, but its pressure derivative (K′) was kept fixed at four during the fitting procedure. With K T0 we indicate the bulk moduli at 0 GPa at specific temperature.

Pawley et al. (2002) measured the structural changes of pyrophyllite following a P–T path in a range of pressure from 0 to 6.8 GPa between 300 and 700 K using a X-ray powder diffractometer equipped with a multi-anvil apparatus. The authors measured a powdered sample with NaCl as internal pressure standard. The data were fitted with a Murnaghan equation to obtain K T0  = 37 GPa and K′ = 10. However, the authors did not make any high-temperature measurements at low pressure on pyrophyllite, which limited the possibility to determine the thermal expansivity (α T) of the mineral and the thermal dependence of the bulk modulus (∂K T /∂T). Very recently, Gatta et al. (2014) investigated the thermal and compressional behaviours of pyrophyllite by in situ synchrotron diffraction from 298 to 773 K (at 0.0001 GPa) and up to 6.2 GPa (at 298 K). The compressional results at room temperature were fitted with a third-order Birch–Murnaghan equation of state, with parameters K T0  = 47(4) GPa and K′ = 7.3(19). The authors calculated the volume thermal expansion coefficient between 298 and 773 K, obtaining α T = 2.2(2) × 10−5 K−1 (reference temperature T = 298 K). As also mentioned elsewhere (Ulian et al. 2014), thermomechanical data of phyllosilicates tend to be highly dependent on the chemical composition and on the physical aspects of the samples (single crystals or powders), which explains the variability of the results presented in literature.

Nowadays, the interpretation of both diffraction and thermodynamic properties of complex mineral phases, such as phyllosilicates, has been facilitated by a class of independent, first-principles (sometimes termed “ab initio”) quantum mechanical simulations. Regarding pyrophyllite, to our knowledge there is only one study aimed to obtain the elastic behaviour of this mineral (Voora et al. 2011). This work reported an interesting comparison between different density functional theory (DFT) methods, using plane-wave basis set, employed in the analysis of the mechanical behaviour of pyrophyllite. The theoretical bulk modulus and its first P derivative are in the ranges 38–41 GPa and 11–12, respectively, depending on the adopted DFT functional. The authors observed a better agreement with experimental mechanical results when using a semi-empirical correction for dispersive forces (Grimme 2006). In fact, while DFT-based approaches provide an adequate prediction of covalent bonding, they have a well-documented problem in describing long-range dispersion, which is often the driving force in weak interactions. For this reason, when dealing with weakly bound systems, such as layered minerals, it is recommendable to profit of some semi-empiric correction scheme, such as the DFT + D proposed by Grimme (2006). Recent works on talc, the trioctahedral phyllosilicate end-member, and 2M 1 muscovite, the potassium end-member of dioctahedral micas, proved the importance of this correction, which yields solid structural, chemical and physical results (Ulian et al. 2013, 2014; Ulian and Valdrè 2014a, b). However, the theoretical results of Voora et al. (2011) are related only to athermal condition, as they did not include the temperature as a variable.

To extend the investigation, in the present work we calculated the thermomechanical and thermochemical properties of pyrophyllite between 0 and 10 GPa and 10–900 K using a quantum mechanical approach based on the density functional theory (DFT) corrected for the dispersive forces, including the thermal effects by the quasi-harmonic approximation (Anderson 1995; Ulian and Valdrè 2014b). Furthermore, we have calculated and reported vibrational data of pyrophyllite, which can be useful for infrared/Raman analysis, an interpretation. Differently from the work of Voora et al. (2011), we used an all-electron localized Gaussian-type orbitals (GTO) and the B3LYP hybrid functional integrated with dispersive forces contribution. We have shown in previous works on talc mineral that this combination provides more accurate energy results than plane-wave simulations (Ulian et al. 2013, 2014). Starting from the XRD data of Lee and Guggenheim (1981), we optimized the pyrophyllite unit cell and internal geometry, and then, we investigated the vibrational and mechanical properties of the mineral. First, in order to gain information on the compressional behaviour of a pure pyrophyllite model, we analysed its structure from 0 to 10 GPa. A small range of negative pressures was also considered to explore the mineral behaviour under the effect of a hydrostatic tensile stress. These data were used to predict the equation of state, lattice and internal structural parameters of pyrophyllite at different temperatures (between 10 and 900 K) and were compared with previous theoretical and experimental results.

We reported three-dimensional plots of thermochemical results. The data can be useful to understand both the metamorphic and igneous equilibriums, and industrial applications of the mineral. Thermochemical results are compared with differential scanning calorimetry data obtained by Robie et al. (1976) and by Krupka et al. (1979).

Computational details

The calculations presented in this work have been performed with the ab initio CRYSTAL09 code (Dovesi et al. 2009), which implements the Hartree–Fock and Kohn–Sham self-consistent field method for the study of periodic systems. The graphical drawings have been carried out with the molecular graphics software VESTA (Momma and Izumi 2008).

Model structures

We modelled the pyrophyllite structure starting from XRD refinement data reported in literature (Lee and Guggenheim 1981), in the space group \(P\overline{1}\). Oxygen atoms are subdivided in three groups: apical [Oa or O(a)] shared between Si and Al; hydroxyl [Oh or O(h)]; and basal [Ob or O(b)] shared between silica tetrahedrons. Since hydrogen atoms location has not been characterized by crystallographic studies, we initially considered two models where the O–H bonds were oriented parallel and perpendicular to the [001] direction. Then, we performed a free, non-constrained geometry optimization of the two structures, and in each case, we found a reasonable minimum with the O–H bond direction canted by about 60° with respect to the [001] direction. The stick and ball model in Fig. 1 shows a graphical representation of the mineral unit cell.

Hamiltonian and other parameters

We employed for the simulations the hybrid exchange functional B3LYP, which is the combination of the Becke three-parameter functional (Becke 1993) and the gradient-corrected correlation functional of Lee et al. (1988). The exchange–correlation contribution was calculated over a grid of 75 points and 974 angular points, obtained from the Gauss–Legendre quadrature and Lebedev schemes (Prencipe et al. 2004). This represents a good compromise between accuracy and cost of calculation for geometry optimization and vibrational frequencies. The values of the tolerances that control the truncation criteria for the bielectronic Kohn–Sham integrals were set to 10−6 and the pseudo-overlap parameter to 10−14. This choice allows stabilizing the self-consistent behaviour during unit-cell deformations. The Hamiltonian matrix has been diagonalized through the Monkhorst and Pack (1976) scheme, using a 4 × 4 × 4 k mesh, which leads to 36 reciprocal lattice points (k points). We chose this sampling grid to perform a better sampling along the c axis direction, due to the dispersive forces acting in that direction.

We adopted atomic Gaussian-type orbital (GTO) basis sets to describe the multi-electron wave functions. Some of them, namely those of silicon (88-31G*), oxygen (8-411d11G) and hydrogen (3-1p1), were used by some of us in our previous works on talc (Ulian et al. 2013, 2014; Ulian and Valdrè 2014b), since it presents a similar structure compared to pyrophyllite. The chosen basis sets, in particular one of the hydrogen atoms, allow accurate calculations in both molecular and crystal structures without too high computational costs. Aluminium atoms are described by a 8-511d1G basis set, which was optimized and used by Catti et al. (1994) to investigate corundum.

Lattice constants and internal coordinates were optimized within the same run using the analytical gradient method for the atomic positions and a numerical gradient for the unit-cell parameters. The Hessian matrix was upgraded after each cycle with the Broyden–Fletcher–Goldfarb–Shanno algorithm (Broyden 1970a, b; Fletcher 1970; Goldfarb 1970; Shanno 1970). The geometry was considered converged when the tolerances for the maximum allowed gradient and the maximum atomic displacement were below 6 × 10−5 hartree bohr−1 and 1.2 × 10−5 bohr, respectively.

Generalized gradient approximation functionals and their hybrid forms, such as B3LYP, do not provide an adequate description of long-range dispersive interactions. Then, we evaluated dispersive forces according to the semi-empirical scheme (DFT + D) suggested by Grimme (2006), which adds the following contribution to the calculated DFT energy:

$$E_{\text{DISP}} = - s_{6} \sum\limits_{{\mathbf{g}}} {\sum\limits_{i \ne j} {f_{\text{dump}} \left( {R_{{ij,{\mathbf{g}}}}^{6} } \right)\frac{{C_{6}^{i} C_{6}^{j} }}{{R_{{ij,{\mathbf{g}}}}^{6} }}} }$$
(1)
$$f_{\text{dump}} = \frac{1}{{1 + e^{{ - d\left( {{{R_{{ij,{\mathbf{g}}}} } \mathord{\left/ {\vphantom {{R_{{ij,{\mathbf{g}}}} } {R_{{v{\text{d}}w}} }}} \right. \kern-0pt} {R_{{v{\text{d}}w}} }} - 1} \right)}} }}$$

The summation over all atom pairs ij and g lattice vectors exclude the self-interaction contribution (\(i = j\)) for every g. The parameters \(C_{6}^{i}\) represent the dispersion coefficient for the atom i, R ij, g is the interatomic distance between atom i in the reference cell and atom j in the neighbouring cells at distance |g| and s 6 is a functional-dependent scaling factor. We employed the \(C_{6}^{i}\) parameters reported in the work of Grimme (2006), which were obtained from atomic ionization potentials (I p ) and static dipole polarizabilities (α) according to the formula \(C_{6}^{i} = 0.05NI_{p}^{i} \alpha^{i}\), where N depends on atom row in the periodic table. The function f dump is used to dump the energy correction to avoid double counting of short-range contributions and depends on the sum of atomic van der Waals radii (R vdw ) and on a steepness parameter (d = 20). Due to the molecular nature of the E DISP correction, which tends to overestimate cohesive energy in solid crystals, the original B3LYP + D parameters were modified according to a previous study (Civalleri et al. 2008), setting s 6 to 1 and R vdw (H) to 1.30, and the heavier atom van der Waals radii were scaled by a factor 1.05 (method called B3LYP-D*). The same approach has been adopted with good results in our previous works on talc (Ulian et al. 2013, 2014; Ulian and Valdrè 2014a, b).

Vibrational features

In periodic systems and within the harmonic approximation, the phonon frequencies at Γ point are evaluated by diagonalization of the central zone (k = 0) mass-weighted Hessian matrix:

$$W_{ij} \left( {k = 0} \right) = \sum\limits_{G} {\frac{{H_{ij}^{0G} }}{{\sqrt {M_{i} M_{j} } }}}$$
(2)

\(H_{ij}^{0G}\) represents the second derivative of the electronic and nuclear repulsion energy E evaluated at equilibrium u = 0 with respect to the displacement of atom A in cell 0 (\(u_{i} = x_{i} - x_{i}^{ * }\)) and displacement of atom B in cell G (\(u_{j} = x_{j} - x_{j}^{ * }\)) from their equilibrium position \(x_{i}^{ * }\), \(x_{j}^{ * }\):

$$\sum\limits_{G} {H_{ij}^{0G} } = \sum\limits_{G} {\left[ {\frac{{\partial^{2} E}}{{\partial u_{i}^{0} \partial u_{j}^{G} }}} \right]}_{0} \quad i = 1, \ldots ,3N;j = 1, \ldots ,3N$$
(3)

The calculation of the Hessian at equilibrium is made by the analytical evaluation of the energy first derivatives, \(\varPhi_{j}\) of E with respect to the atomic displacements:

$$\varPhi_{j} = \sum\limits_{G} {\nu_{j}^{G} = \sum\limits_{G} {\frac{\partial E}{{\partial u_{j}^{G} }}\quad j = 1, \ldots ,3N} }$$
(4)

while second derivatives at u = 0 (where all first derivatives are zero) are calculated numerically using a “two-point” formula:

$$\begin{aligned} \left[ {\frac{{\partial \varPhi_{j} }}{{\partial u_{i}^{0} }}} \right]_{0} \approx \frac{{\varPhi_{j} \left( {0, \ldots ,u_{i}^{0} , \ldots ,0} \right) - \varPhi_{j} \left( {0, \ldots ,u_{i}^{0} , \ldots ,0} \right)}}{{u_{i}^{0} }}\quad i = 1, \ldots ,3N;j = 1, \ldots ,3N \hfill \\ \hfill \\ \end{aligned}$$
(5)

More details on the algorithms used by the CRYSTAL code to calculate the vibrational properties of a 3D system can be found in dedicated literature (Pascale et al. 2004; Tosoni et al. 2005). The Hessian matrix eigenvalues provide the normal harmonic frequencies ω h , and they are obtained with 3N + 1 SCF and gradient calculation. This method can be quite demanding for large unit cells, but point symmetry facilitates a remarkable time saving, because only the lines of the Hessian matrix referring to irreducible atoms need to be generated.

Results

Geometry optimization

The optimization of the pyrophyllite was made on the primitive cell (\(P\overline{1}\)) to reduce the computational costs of the procedure, and then, the results were reported in terms of the crystallographic cell. A detailed description of the data obtained by GTO/B3LYP-D* approach is presented in Table 1 alongside XRD structural refinement (Lee and Guggenheim 1981; Wardle and Brindley 1972) and very recent theoretical results (Tunega et al. 2012) reported in literature.

Table 1 Theoretical unit-cell constants and experimental lattice parameters and internal geometry of pyrophyllite
Full size table

The adoption of the modified Grimme’s dispersion parameters (B3LYP-D*) provided lattice parameters and bond lengths in very good agreement with experimental data, with only a small under-estimation of the cell volume (0.4 %). In particular, the description of the c axis is adequately accurate. Compared to the plane-waves/PBE-D approach (Tunega et al. 2012), we provide similar results in the description of the lattice axis a, b and in particular c, but there are some differences in the unit-cell angles, especially β. The volume contraction is also very similar.

The internal geometry, namely the mean bond lengths, is very similar to that obtained by previous theoretical study. Both results are slightly larger than experimental values of about 0.7 %. Pyrophyllite, as other phyllosilicates, has a distorted hexagonal tetrahedral sheet due to the non-ideal SiO4 4− tetrahedrons. The same observation can be extended to the octahedral sheet. According to literature (Bailey 1988), the tetrahedral rotation angle is defined as

$$\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\left( {\sum\limits_{i = 1}^{6} {{{\phi_{i} - 120^{^\circ } } \mathord{\left/ {\vphantom {{\phi_{i} - 120^{^\circ } } 6}} \right. \kern-0pt} 6}} } \right)$$
(6)

where ϕ i is the angle described by triples of basal oxygen atoms. We obtained α = 23.82° in our simulations, a value in good agreement with the experimental one (20.4°) (Lee and Guggenheim 1981). The octahedral rotation angle is given by

$$\cos \psi = {{\varPhi_{0} } \mathord{\left/ {\vphantom {{\varPhi_{0} } {2\left\langle {M - O,{\text{OH}}} \right\rangle }}} \right. \kern-0pt} {2\left\langle {M - O,{\text{OH}}} \right\rangle }}$$
(7)

with \(\varPhi_{0}\) the thickness of the O-layer (Å) and \(\left\langle {M - O,{\text{OH}}} \right\rangle\) the mean bond lengths in the octahedrons. The obtained ψ value is 56.0°, in good agreement with the experimental value, ψ = 57.1° (Lee and Guggenheim 1981). According to Lee and Guggenheim (1981), the tetrahedral rotation reduces the lateral dimensions of the tetrahedral sheet. Since tetrahedral faces may be approximately described as equilateral triangles, the resulting distance between apical oxygens, AO a , may be calculated as

$${\text{AO}}_{a} = {{\left[ {2e_{\text{th}} \cos \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {2e_{\text{th}} \cos \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)} \right]} {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}$$
(8)

where e th is the mean tetrahedral edge length. In the B3LYP-D* simulated structure, the AO a value is 3.01 Å, in very good agreement with the observed 3.00 Å obtained from XRD refinement (Lee and Guggenheim 1981).

Regarding the hydrogen atom position, the free relaxation of the mineral geometry led the O–H bond direction canted by about 59.87° with respect to the [001] direction, pointing versus the octahedral vacancy (see Fig. 1).

Phonon calculations

The vibrational features of pyrophyllite were simulated in the primitive cell, which has 20 atoms. The number of normal modes is given by 20 × 3 = 60, and three of them are related to translation of the whole unit cell. The remnant 57 modes are vibrational and subdivided as:

$$\varGamma_{\text{tot}} = 30A_{g} + 27A_{u}$$

Modes with A g symmetry are Raman-active, while A u ones are IR-active. None of them exhibits symmetry-related degeneracies, and thus, the IR and Raman spectra have 27 and 30 signals, respectively. We report in Table 2 the results obtained from our simulated IR/Raman analysis and the calculated IR spectrum in Fig. 2. The analysis of the vibrational modes has been conducted with the aid of the visualization software MOLDRAW (Ugliengo et al. 1993) and the potential energy distribution (PED) computed by CRYSTAL09.

Table 2 Calculated pyrophyllite harmonic phonon frequencies
Full size table
Fig. 2
figure 2

Simulated infrared spectrum of pyrophyllite. The experimental IR spectrum is from the work of Mukhopadhyay et al. (2010)

Full size image

The region between 0 and 400 cm−1, which is not completely shown in the spectrum of Fig. 2, is characterized by eight low-intensity phonon modes. The first intense peak is composed by two Al–Oa–Al modes which fall at 474 and 488 cm−1, respectively. From the PED analysis, an OH libration component in the signal at 488 cm−1 was found. The peak in the range 500–600 cm−1 is formed by three signals at 533, 549 and 556 cm−1, related to Si–Oa–Al bending modes. Again, the mode at 556 cm−1 exhibits an OH libration component. Two modes related to Oa–Si–Ob bending have been identified. The first one is at 643 cm−1, but is not visible in the spectrum because of low intensity. The second is associated with an “umbrella” bending mode at 749 cm−1, faintly visible.

In the spectral region above 800 cm−1, there are the Si–O stretching modes. There are two low-intensity signals at 819 and 842 cm−1, which have been assigned to symmetric Si–Ob stretching vibrations. Two modes have been identified as Si–Oa stretching: one is at 849 cm−1, but it is very faint and overlapped to the one at 842 cm−1; the other is at 908 cm−1, with high intensity. Finally, three signals are related to the asymmetric Si–Ob stretching modes, at 1048 (very intense), 1063 (very intense) and 1107 cm−1 at low intensity.

Regarding OH phonon modes, there is a medium-intensity signal at 1016 cm−1, related to a pure OH libration mode, and the OH stretching mode at 3886 cm−1. When anharmonicity was taken into account, the latter fell at 3709 cm−1, with an anharmonic constant of 82 cm−1. Unfortunately, the CRYSTAL09 code does not extend the anharmonic calculation to other modes but the stretching one, preventing the calculation of the anharmonicity of OH libration modes.

The simulated infrared spectrum is in reasonable agreement with the one reported in the experimental works of Mukhopadhyay et al. (2010) and of Ogorodova et al. (2011). The differences are imputable to the considered model, which is an end-member of the pyrophyllite mineral.

Equation of state of pyrophyllite

The P–T behaviour of any solid insulator can be derived from the Helmholtz energy F (Anderson 1995).

$$F = E_{\text{ST}} \left( V \right) + F_{\text{VIB}} \left( {V,T} \right)$$
(9)

where E ST is the potential of a static lattice at absolute zero (athermal limit) and F VIB is the vibrational energy related to the thermal motion of the atoms. The pressure can be obtained by the first derivative of Eq. (9).

$$P = - \left( {\frac{\partial F}{\partial V}} \right)_{T} = - \left( {\frac{{\partial E_{\text{ST}} }}{\partial V}} \right)_{T = 0} + \left( {\frac{{\partial F_{\text{VIB}} }}{\partial V}} \right)_{T}$$
(10)

In the present work, the evaluation of the pyrophyllite equation of state is subdivided into two subsections. In the first one, only the static lattice values of the mineral are obtained and an atomic description of the pressure-induced variations to the structure is provided. In the second one, the thermal contribution is included to evaluate the thermomechanical properties of the mineral at different temperatures.

Static calculations

The description of the compressional behaviour of a solid phase within the periodic boundary conditions has been conducted with the EOS algorithm present in the CRYSTAL09 code (Ottonello et al. 2009a). With this method, starting from the optimized pyrophyllite structure, a cell optimization is carried out with a symmetry-preserving relaxation procedure by exploring, at selected volumes, the minimum energy a/b and c/b ratios and internal coordinates. We considered twenty volumes between 0.90V init and 1.10V init, where V init is the volume of the original unit cell. The relaxed lattice parameters at the athermal limit are reported in Table 3. The partial derivation of a third-order polynomial fit on the computed E(V) curve (Fig. 3a) reproduced the local values of the ab initio pressure, allowing the analysis of the functional dependence of the structural details on P at T = 0:

$$P_{\text{st}} = - \left( {\frac{\partial E}{\partial V}} \right)_{T = 0} = 3p_{1} V^{2} + 2p_{2} V + p_{3}$$
(11)

with p 1  = −5.27514 × 10−7, p 2  = 3.63107 × 10−4 and p 3  = −0.0828 the fitting parameters (R = 0.99994). A graphical representation of V(P st) trend is shown in Fig. 3b.

Table 3 Simulated unit-cell constants of pyrophyllite at different volumes
Full size table
Fig. 3
figure 3

Calculated energy/volume (a) and related volume/pressure (b) diagrams for the pyrophyllite unit cell

Full size image

Pyrophyllite volume versus P st data were fitted using a third-order finite strain isothermal Birch–Murnaghan equation of state (III-BM EOS) (Birch 1947):

$$P_{{{\text{III}} - {\text{BM}}}} = \frac{3}{2}K_{\text{T0}} \left[ {\eta^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 3}} \right. \kern-0pt} 3}}} - \eta^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0pt} 3}}} } \right]\left\{ {1 - \frac{3}{4}\left( {4 - K^{{\prime }} } \right)\left( {\eta^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}} - 1} \right)} \right\} + P_{0}$$
(12)

where η = V/V 0 is a dimensionless parameter and V 0 is the volume at reference pressure P 0 . The best fitting procedure was made by least-square method, using the EOS-FIT5.2 software (Angel 2001). We obtained the refined elastic parameters at T = 0 K: V 0  = 423.26(20) Å3, K T0  = 48.63(69) GPa and K′ = 11.14(43).

In Fig. 4a, b, we report the evolution of axial and angular lattice parameters at different pressures, respectively. Regarding the compressive regime (P > 0 GPa), the calculated trend is monotonic. It is graphically clear that pyrophyllite deformation exhibits a strongly anisotropic behaviour, with smaller variations for a and b cell parameters than for the c one. It is possible to describe the observed anisotropy calculating the axial bulk moduli with a III-BM EOS fit on the lattice parameters values at different pressures. The obtained refined data for the a axis, b axis and c axis were, respectively: a 0  = 5.181(1) Å, K T0 (a) = 83.63(55) GPa and K′(a) = 3.25(41); b 0  = 8.977(1) Å, K T0 (b) = 101.94(93) GPa and K′(b) = 3.17(28); c 0  = 9.311(1) Å, K T0 (c) = 27.74(10) GPa and K′(c) = 8.16(3). The axial compressibilities, described as β = 1/3K T0 , are in ratio β(a):β(b):β(c) = 1.219:1.000:3.674. The obtained axial values are very close to those reported in a previous work on talc (Ulian et al. 2014). This is not surprising because the covalent bonds in the dioctahedral TOT layers are less compressible than the interlayer dominated by Columbian and van der Waals forces (c direction).

Fig. 4
figure 4

Compressional behaviour of pyrophyllite (a) axial and (b) angular parameters under compression and expansion

Full size image

Regarding the unit-cell angles, we observed a constant decrease of the α parameter and an increase of the γ one in the investigated pressure range. However, the β angle value decreased from 0 to 3.3 GPa and then increased up to 8 GPa.

Based on the unit-cell axial and angular values, we predict a spinodal instability in pyrophyllite upon expansion by about 4.5 % from the zero-pressure volume. According to the literature (Stixrude 2002), the spinodal consists in that point where the bulk modulus vanishes, i.e. where pressure is extremal, reaching a minimum value beyond which it decreases no more upon further expansion. At the spinodal, pyrophyllite is mechanically unstable and would be expected to fragment. Our results suggest that the spinodal coincides with the hydrostatic tensile strength of −1.6 GPa, in a defect-free, single crystal of pyrophyllite. This value is very similar to that of talc, found by the DFT simulations of Stixrude (2002). It is worth noting that this quantity is different from the usual tensile strength which is measured under uniaxial tension in minerals and materials in generals. It is expected that the uniaxial tensile strength may be less than the value calculated for hydrostatic tensile strength, because pyrophyllite is a slightly anisotropic mineral.

In the explored volume range, we observed a strong variation of the interlayer thickness (−13 % at 8 GPa), but the TOT thickness is almost unaffected (−2 % at 8 GPa). The \(\langle\)Si–O\(\rangle\) and \(\langle\)Al–O\(\rangle\) bond lengths span from 1.631 and 1.926 Å (lower limit) to 1.620 and 1.886 Å (upper limit), respectively. More in detail, in the SiO4 tetrahedrons the Si–Oa distances are slightly more influenced than the Si–Ob ones, but in AlO6 octahedrons we did not find the same trend.

Furthermore, we noticed that the expansion of the unit cell causes an increase in the distortion index both tetrahedrons and octahedrons, while the compression leads to the opposite behaviour. Similarly to talc structure (Ulian et al. 2014), the increase in pressure is followed by higher rotation angle α (34.88° at 10 GPa) than that of the uncompressed pyrophyllite structure. Expanding the unit cell, α diminishes to 20.06° at −2 GPa.

Negligible O–H bond length and Al–O–H angle variations in the pressure range investigated have been observed.

Thermal contribution and thermomechanical properties

In statistical thermodynamics, the vibrational energy is given by

$$F_{\text{VIB}} = - kT\ln Z$$
(13)

with Z the partition function calculated by taking the sum of all quantum energy levels for each independent oscillators in the solid lattice and given by:

$$Z = \sum\limits_{i} {e^{{ - \varepsilon_{i} /kT}} }$$
(14)

The ε i values are the eigenvalues of the energy operator, which can be used to define the partition function, Z i , for each vibrational mode, ϖ i ,

$$\varepsilon_{i} = \frac{1}{2}\hbar \varpi_{i} ,\frac{3}{2}\hbar \varpi_{i} ,\frac{5}{2}\hbar \varpi_{i} ,{\text{etc}} \ldots$$
(15)
$$Z_{i} = e^{{ - {{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {2kT}}} \right. \kern-0pt} {2kT}}}} \sum\limits_{i = 0}^{\infty } {e^{{ - {{3\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{3\hbar \varpi_{i} } {2kT}}} \right. \kern-0pt} {2kT}}}} } = \frac{{e^{{ - {{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {2kT}}} \right. \kern-0pt} {2kT}}}} }}{{\left( {1 - e^{{ - {{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {kT}}} \right. \kern-0pt} {kT}}}} } \right)}}$$
(16)

It is then possible to define the contribution to the Helmholtz free energy from each vibrational mode as:

$$F_{{{\text{VIB}}_{i} }} = - kT\ln Z_{i} = \frac{{\hbar \varpi_{i} }}{2kT}\ln \left( {1 - e^{{{{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {kT}}} \right. \kern-0pt} {kT}}}} } \right)$$
(17)

which can then be summed over the 3n − 3 oscillators (n the number of atoms in the unit cell) in the considered lattice to obtain the whole thermal contribution to the free energy

$$F_{\text{VIB}} = \frac{1}{2}\sum\limits_{i = 1}^{3n - 3} {\hbar \varpi_{i} } + kT\sum\limits_{i = 1}^{3n - 3} {\ln \left( {1 - e^{{ - {{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {kT}}} \right. \kern-0pt} {kT}}}} } \right)}$$
(18)

The first addendum of Eq. (18) represents the zero-point energy (E ZP ) of the solid, unaffected by the temperature, and the second term is the energy arising from excitation due to temperature (F TH). The term \({{\hbar \varpi_{i} } \mathord{\left/ {\vphantom {{\hbar \varpi_{i} } {kT}}} \right. \kern-0pt} {kT}}\) can be substituted with X i to simplify the expression

$$F_{\text{VIB}} = \frac{kT}{2}\sum\limits_{i = 1}^{3n - 3} {X_{i} } + kT\sum\limits_{i = 1}^{3n - 3} {\ln \left( {1 - e^{{ - X_{i} }} } \right)}$$
(19)

Applying Eq. (19) to Eq. (10) allows finding the pressure related to each volume transformation

$$P = - \left( {\frac{{\partial E_{\text{ST}} }}{\partial V}} \right)_{T = 0} + \frac{kT}{2V}\sum\limits_{i = 1}^{3n - 3} {\gamma_{i} X_{i} } + \frac{kT}{V}\sum\limits_{i = 1}^{3n - 3} {\gamma_{i} \frac{{X_{i} }}{{e^{{X_{i} }} - 1}}}$$
(20)

where γ i is the Grüneisen’s mode gamma of each vibrational frequency, given by

$$\gamma_{i} = \frac{{\partial \ln \varpi_{i} }}{\partial \ln V}$$
(21)

The mode gammas for pyrophyllite are summarized in Table 4.

Table 4 Pyrophyllite vibrational frequencies at 0 GPa and related mode gamma
Full size table

In the quasiharmonic treatment, the vibrational modes are dependent only on volume variations. The thermodynamic properties are dependent on temperature by the second term of Eq. (18) (Anderson 1995; Ottonello et al. 2009a, b). Rewriting Eq. (20) in terms of pressure P, we can obtain:

$$P = P_{\text{ST}} + P_{\text{ZP}} + P_{\text{TH}} = P_{{{\text{T}} = 0}} + P_{\text{TH}}$$
(22)

where the static pressure (P ST) is corrected by the zero-point energy (P ZP) and by the thermal contribution (P TH). P T = 0 , the thermal pressure, is equal to P ST + P ZP.

The above formulations were enriched by the calculation of pyrophyllite phonon dispersion for each simulated volume. Dispersion effects were simulated from vibrational frequencies in the case of super-cells (we adopted a 2 × 2 × 2 one), which allows considering eight k points. The obtained results are very close to those calculated without considering the phonon dispersion effects (ca. 1.4 kJ/mol). Then, the related thermodynamic quantities (pressure, bulk moduli, etc.) are almost unaffected by phonon dispersion. This is in good agreement with previous observations, which stated that the Grüneisen’s parameters corresponding to the vibrational modes calculated in the Γ point only are reasonably representative of the whole set of parameters, because they are numerous and depend upon the number of atoms in the unit cell. Indeed, other authors (Ottonello et al. 2009a, b; Prencipe et al. 2011; Ulian and Valdrè 2014a, b) demonstrated that it is possible to obtain reliable estimations of thermoelastic and thermodynamics quantities by neglecting dispersion effects, even with systems having relatively small unit cells. It is also worth noting that, according to the study of Kieffer (1979a), mineral thermodynamic properties, calculated as averages over the relevant quantities at the atomic level, can be obtained with high reliability even without a detailed knowledge of the phonon density of state. For completeness, we included phonon dispersion spectra at −2.2 GPa and at 8.4 GPa (athermal conditions), to show how small is the pressure influence on the pyrophyllite phonon behaviour (see Fig. 5).

Fig. 5
figure 5

Pyrophyllite phonon dispersion calculated at a −2.2 GPa and b 8.4 GPa

Full size image

In Table 5, the corrected pressure values for Eq. (20) are reported for the range of temperatures from 0 to 900 K.

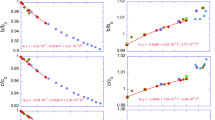
Table 5 Volume (Å3) values at different temperatures and pressures for pyrophyllite and fit parameters of the third-order Birch–Murnaghan EoS
Full size table

The thermal bulk modulus (K T) at a given cell volume (pressure) and temperature has been calculated by the third-order BM3 EOS. Using isothermal curves, at different T, we can obtain at each temperature the bulk modulus (K T), its first derivative (K′) and reference volume (V 0 ), at any fixed reference pressure. The calculated V(P, T) values for T = 300 K are in good agreement with those experimentally obtained by Pawley et al. (2002) on a powdered pyrophyllite sample, and even better comparison can be made on those reported very recently by Gatta et al. (2014) (Fig. 6). In Fig. 7, we report the V(P, T) of pyrophyllite calculated in the ranges 0–10 GPa and 0–900 K.

Fig. 6
figure 6

Comparison between theoretical pyrophyllite compression at T = 300 K (black line) and experimental results of Pawley et al. (2002), red line, and of Gatta et al. (2014), blue line, obtained at the same temperature

Full size image
Fig. 7
figure 7

Compressional behaviour of pyrophyllite between 0 and 10 GPa and 10–900 K

Full size image

Regarding the axial compressibility at room temperature, we fitted by the third-order Birch–Murnaghan equation the a axis, b axis and c axis data, obtaining, respectively: a 0  = 5.189(1) Å, K T0 (a) = 89.46(75) GPa and K′(a) = 3.00(1); b 0  = 8.990(7) Å, K T0 (b) = 109.01(1.37) GPa and K′(b) = 3.00(1); c 0  = 9.368(1) Å, K T0 (c) = 26.03(8) GPa and K′(c) = 8.12(3). The related axial compressibilities are β(a) = 3.73 × 10−3, β(b) = 3.06 × 10−3 and β(c) = 12.8 × 10−3 GPa−1, in ratio β(a):β(b):β(c) = 1.218:1.000:4.188.

From the quasi-harmonic mode gamma analysis of the 3n – 3 optic modes, we obtained the \(\alpha_{\text{T}} K_{\text{T}}\) product, by using the formula (Anderson 1995; Ottonello et al. 2010)

$$\alpha_{\text{T}} K_{\text{T}} = \frac{R}{\text{ZV}}\sum\limits_{i = 4}^{3n} {\gamma_{i} e^{{X_{i} }} \left( {\frac{{X_{i} }}{{e^{{X_{i} }} - 1}}} \right)^{2} }$$
(23)

As shown in Fig. 7a, this product asymptotically attains a constant value at high temperatures, depending on the considered pressure. For example, at 0 GPa \(\alpha_{\text{T}} K_{\text{T}}\) reaches a constant value of \(1.2 \times 10^{ - 3}\) GPa/K above the Debye temperature of the mineral (computed \(\varTheta = 927.17\) K at 0 GPa) (Fig. 8a, b).

Fig. 8
figure 8

a Isobaric αT K T product at three different pressures and b three-dimensional plot of the αTKT product at different pressures and in the temperature range 10–900 K

Full size image

We calculated the isobaric temperature derivative of bulk modulus for pyrophyllite by linear regression of the K T data as a function of temperature in the 100–900 K range. We reported the results in Table 6. It can be observed that the (∂K T /∂T) P values decrease by increasing the pressure, with a ratio (∂K T /∂T∂P) = −4.95. It is worth noting that the quasi-harmonic treatment does not consider the fact that K T would not vary linearly with T.

Table 6 Pyrophyllite bulk modulus K T (GPa) at different PT conditions
Full size table

With the knowledge of the bulk moduli at each P–T condition, obtained from the BM3 EOS fitting, we can directly calculate the thermal expansion coefficient (α T) of pyrophyllite. We calculated α T in the P range 0–10 GPa from 10 to 900 K, and the results are reported in Table 7. As it can be observed from the plot in Fig. 9a, the thermal expansion coefficient increases with T, but it is reduced by augmenting the pressure. A complete α T(P, T) plot is reported in Fig. 9b.

Table 7 Thermal expansion coefficient (α T, 10−5 K−1) in the pressure range 0–10 GPa at different temperatures
Full size table
Fig. 9
figure 9

a Isobaric thermal expansivity (α Τ ) at three different pressures and b three-dimensional plot of the α Τ at different pressures and in the temperature range 10–900 K

Full size image

The calculation of thermodynamic properties relies on the Einstein model for optic modes. Within the harmonic approximation, the isochoric heat capacity of a solid insulator can be expressed as (Anderson 1995)

$$C_{V} =\, \frac{3R}{Z}\left( {\frac{2}{\pi }} \right)^{3} \sum\limits_{i = 1}^{3} {\int_{0}^{{X_{i} }} {\frac{{\left[ {\arcsin \left( {{X \mathord{\left/ {\vphantom {X {X_{i} }}} \right. \kern-0pt} {X_{i} }}} \right)} \right]^{2} X^{2} e^{X} {\text{d}}X}}{{\left( {X_{i}^{2} - X^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {e^{X} - 1} \right)^{2} }} + } } \frac{R}{Z}\sum\limits_{i = 4}^{3n} {e^{{X_{i} }} \left( {\frac{{X_{i} }}{{e^{{X_{i} }} - 1}}} \right)^{2} }$$
(24)

The first term of Eq. (24) is the acoustic modes contribution described by Kieffer’s approach (Kieffer 1979a, b, c), while the second one is related to the optical modes.

The specific heat at constant pressure (C P) can be obtained from the relationship

$$C_{\text{P}} = C_{V} + T\alpha_{\text{T}}^{2} K_{T,P} V_{P,T}$$
(25)

where V P,T is the cell volume at pressure P and temperature T, respectively.

The complete calculation of the maximum frequency of each acoustic branch requires the knowledge of the averaged shear and longitudinal wave velocities at each volume (pressure), and these quantities can be obtained by the elastic constants at each compressional state (Perger et al. 2009; Ulian et al. 2014). Due to computational costs, we considered the acoustic mode contribution to the thermochemical properties only at 0 GPa. However, as shown in our previous work on talc (Ulian and Valdrè 2014b), the acoustic contribution to the whole property is very low (<5 %) at room temperature and above. Then, the optical part of Eq. (24) represents an adequate approximation of the heat capacity for T > 300 K.

The C V and C P values obtained at 0 GPa are plotted in Fig. 10a, alongside previous experimental isobaric heat capacity data of pyrophyllite (Krupka et al. 1979; Robie et al. 1976). There is a very good agreement between theoretical and experimental results above 400 K, but the theoretical results are slightly underestimated in the range between 10 and 400 K. The isobaric heat capacity calculated with Eq. 26 has been fitted in the range 300–900 K by the Haas–Fisher polynomial expression (Haas and Fisher 1976)

Fig. 10
figure 10

a Isochoric (dashed line) and isobaric (solid line) ab initio heat capacity at 0 GPa. Acoustic modes contribution has been reported as dotted grey line. b Three-dimensional plot of isobaric heat at different pressures and in the temperature range 10–900 K

Full size image
$$C_{\text{P}} = a + bT + cT^{ - 2} + {\text{d}}T^{2} + eT^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$
(26)

with regression coefficients a = 7.2864 × 102, b = 2.9561 × 10−2, c = −3.5316 × 10−5, d = −4.5722 × 10−5 and e = −7.7738 × 103. The polynomial regression in the chosen temperature range is very accurate, with a mean error of 0.1 J/(mol K). We reported also a three-dimensional plot of the C P data from 0 to 10 GPa (Fig. 10b) to show how the pressure affects this thermochemical property. It can be observed that, for T < 500 K, the isobaric heat capacity decreases upon increasing the pressure, while for T > 500 K C P increases.

Discussion and conclusions

The DFT/B3LYP-D* together with an all-electron GTO basis set proposed in this study proved to be adequately accurate in the description of the pyrophyllite mineral. We have shown in previous works that it is also a good modelling approach for talc and for layered silicates in general (Ulian et al. 2013, 2014; Ulian and Valdrè 2014b). The correct evaluation of the weak interaction forces is crucial for both the energy and geometry of the mineral phase, which also affects other physical–chemical properties. In particular, while a and b lattice parameters have been accurately simulated in the past by DFT, because they are dominated by strong covalent bonding, the c axis length is the most affected by dispersive forces, and prior to the semi-empirical correction for van der Waals forces in quantum mechanics codes, it was generally overestimated by 1.0–1.2 Å (Refson et al. 2003; Sainz-Diaz et al. 2001).

Regarding the vibrational spectrum, we observed that the inclusion of dispersive forces increased anharmonicity of hydroxyl group vibrations and caused a general blue shift of the other modes. These effects can be explained by the reduction of the c parameter due to the B3LYP-D* approach. The same conclusion has been drawn in a previous theoretical study on kaolinite, conducted with similar computational approach by Ugliengo et al. (2009). However, the results obtained in the present work on pyrophyllite are encouraging because the most intense signals, even the anharmonic-corrected OH stretching, are in reasonable agreement with FTIR data on the raw mineral reported in literature (Mukhopadhyay et al. 2010; Ogorodova et al. 2011). Unfortunately, the CRYSTAL09 code does not allow applying the anharmonic correction to other OH vibrational modes, such as librations, and, thus, a proper comparison with experimental data on these signals is limited.

According to our data, pyrophyllite exhibits an anisotropic behaviour, with a and b lattice parameters less compressible than the c one. This is a general observation obtained for almost all phyllosilicates, where the TOT layers are made by covalent bonds and held together by weak interactions. This is in good agreement with previous theoretical and experimental studies conducted on this mineral class (Gatta et al. 2009, 2010, 2013; Pawley et al. 2002; Ulian et al. 2014).

The bulk modulus and its pressure derivative obtained at the athermal limit (K T0  = 48.67 GPa, K′T0  = 11.14) are in quite good agreement with previous theoretical data (Voora et al. 2011), expressing a stiffer structure than the one observed by plane-wave simulations (K T0−DFT−D2  = 38 GPa, K′T0−DFT−D2  = 11; K T0−vdW−TS = 41 GPa; K′T0−vdW−TS = 12). However, it is worth noting that the reported results from the previous simulations are related to the uniaxial compression of pyrophyllite along the c axis. The authors considered a series of different c lattice vectors (in the range c ± 1.5 Å) around the equilibrium geometry and then relaxed the atomic positions at constant unit-cell volumes. Thus, the calculated bulk modulus reported by Voora et al. (2011) is an approximation, because the authors neglected the contribution of the a axis and b axis moduli to the bulk one. For this reason, we compared the results of Voora et al. (2011) only with the c axis modulus, K T0 (c) = 27.74 GPa and K′(c) = 8.16. In this sense, our results show a softer behaviour of pyrophyllite than that obtained by PBE functional corrected for dispersive forces (DFT-D2). This could be due to both the different basis sets and the k sampling along the c lattice direction (two points in the plane-wave simulation, four points in GTO). The study of Voora et al. (2011), like ours, shows the importance of the role of dispersive forces in the calculation of mechanical properties. Indeed, when using standard DFT functionals, the bulk modulus is highly underestimated (K T0−PBE = 6 GPa) and the adoption of correction improved the results, depending on both the functional and the quality of the basis set.

We made a comparison between our theoretical results with experimental ones by considering the thermal equation of state and related quantities. We included the thermal effects to the physical–chemical properties of pyrophyllite using the quasi-harmonic approximation, as also done in previous theoretical investigations of different solid phases (Ottonello et al. 2009a; Prencipe et al. 2011; Ulian and Valdrè 2014a, b; Yu and Wentzcovitch 2006).

Our results at T = 300 K [K T = 46.37(71) GPa and K ′T  = 10.51(44)] are in quite good agreement with those of Pawley et al. (2002), where the authors experimentally obtained K T = 37 GPa and K ′T  = 10. A very much better agreement was found with the recent study of Gatta et al. (2014), where the authors obtained K T = 47(4) GPa and K ′T  = 7.3(19). We have also a very good agreement of the axial compressibility data from our simulations [β(a) = 3.73 × 10−3, β(b) = 3.06 × 10−3 and β(c) = 12.8 × 10− GPa−1] with that obtained by experimental means, β(a) = 3.7 × 10−3, β(b) = 3.3 × 10−3 and β(c) = 13.6 × 10−3 GPa−1 in the work of Pawley et al. (2002) and β(a) = 3.4 × 10−3, β(b) = 3.2 × 10−3 and β(c) = 12.8 × 10−3 GPa−1 in the one of Gatta et al. (2014). More in details, the “linearized” BM3 for axial compressibilities from our simulations corroborates the results of Gatta et al. (2014): a 0  = 5.179(3) [+0.010] Å, K T0 (a) = 99(6) [+10] GPa; b 0  = 5.184 Å, K T0 (b) = 104(3) [+10] GPa; c 0  = 9.377(13) [+0.009] Å, K T0 (c) = 26(1) [+0] GPa (in square brackets, we reported the deviation between theoretical and experimental results). However, the theoretical unit-cell angles showed a slightly different behaviour upon compression. In particular, while the calculated variations of α and γ angles are similar to the experimental ones of Gatta et al. (2014), the β parameter showed a small decrease upon compression up to 3.3 GPa and then increased as experimentally observed. This discrepancy may be explained by the different chemical composition of the two structures: on the one hand, our model is a stoichiometric, defect-free pyrophyllite mineral; on the other hand, the sample investigated by Gatta et al. (2014) presented several atomic substitutions, in particular iron (Fe) atoms in the octahedral sheet and Al atoms in the tetrahedral one.

Regarding the thermal behaviour of pyrophyllite, we noted a deviation between our thermal dependency of the bulk modulus and that of Pawley et al. (2002). At 0 GPa, in the T range 100–900 K, it seems that our model softens more slowly than experimentally observed (−27.6 and −55 bar K−1, respectively). This could be derived from two reasons. First, the thermal behaviour reported by Pawley et al. (2002) is an estimation from several points on a P–T path, whereas we obtained a series of compressional isotherms, V(P) T . Second, while our model can be ascribed as a single-crystal pyrophyllite end-member, the experimental sample was a powder with some substitutional defects (mainly Fe). As previously discussed (Ulian et al. 2014), the quantum mechanical approach based on periodic boundary conditions produces results more similar to single-crystal XRD experiments than X-ray powder diffraction ones. In fact, a very good agreement was found between the theoretical thermal expansion coefficient (α T) at T = 300 K (α T = 1.8 × 105 K−1) and the one experimentally obtained by Gatta et al. (2014) (α T = 2.2(2) × 105 K−1) by single-crystal synchrotron XRD.