Introduction

Collective cell migration is an essential process during morphogenesis, wound healing, and cancer invasion (Clark and Vignjevic 2015; Clark et al. 2022; Barriga and Mayor 2019). Movement of cell collectives frequently occurs in a highly directional manner (Shellard and Mayor 2020). Directional cell movement, i.e., taxis is induced by various chemical, mechanical, and electrical stimuli. Consequently, established gradients of: (1) nutrient concentration induces chemotaxis, (2) electric field induces galvanotaxis, (3) matrix stiffness induces durotaxis, and (4) cellular adhesion sites or substrate-bound cytokines induces haptotaxis (Murray et al. 1988; Shellard and Mayor 2020, 2021). Directional cell migration has been mainly considered by monitoring free expansion of cell monolayers and movement of 2D cell clusters, as well as, 3D cell clusters (i.e., cell spheroids) on substrate matrix (Serra-Picamal et al. 2012; Nnetu et al. 2012, 2013; Beaune et al. 2018; Clark et al. 2022). Among others, collagen I gel has been widely used as a substrate matrix, because the type of network it forms represents a constituent of stroma. During early stages of epithelial cancers, cell clusters migrate along the stroma which is composed primarily of collagen I extracellular matrix (ECM) (Clark and Vignjevic 2015).

Cells generate mechanical forces on ECM in the range of ~ 10–100 nN during their movement which occurs on long timescale (i.e., a timescale of hours) (Hall et al. 2016; Steinwachs et al. 2016; Emon et al. 2021). These forces are much larger than the necessary force for breaking electrostatic and hydrophobic bonds in collagen I networks, which is equal to ~\(20 \, \mathrm{pN}\) (Nam et al. 2016). The force of a few \(\mathrm{nN}\) is enough for stretching of the collagen filament up to 20% strain (Gautieri et al. 2012). This means that cells are capable of inducing significant volumetric and surface structural rearrangements of collagen I gel which feeds back to affect the migration persistence (Clark et al. 2022). Altered volumetric rearrangement of the collagen I matrix results in matrix stiffening, while surface rearrangement influences the matrix surface tension. The volumetric and surface rearrangement of collagen I gel are interrelated based on the Young–Laplace equation (Pajic-Lijakovic and Milivojevic 2023a). Cell clusters can migrate persistently on collagen I matrix, governed by physical mechanisms, without the establishment of front-rear polarization (Clark et al. 2022). In this case, the migration persistence is caused by structural changes of matrix related to dilational and volumetric viscoelasticity (Pajic-Lijakovic et al. 2022). The dilational viscoelasticity describes the change of surface energy of collagen I gel in the form of the matrix dynamic surface tension caused by cell tractions. Volumetric structural changes of matrix induce the matrix residual stress accumulation and consequently result in matrix stiffening (Pajic-Lijakovic et al. 2022). While the directional cell movement caused by the matrix stiffness gradient (i.e., durotaxis) has been intensively studied (Sunyer et al. 2016), the influence of matrix surface tension change on the directional movement of cell clusters has been less elaborated. The main goal of this review is to discuss the influence of the physical parameters such as: matrix surface tension, tissue surface tension, cell–matrix interfacial tension accompanied by their gradients, viscoelasticity of the cell cluster and viscoelasticity of the collagen I matrix on: (1) cell rearrangement within a cell cluster, (2) cell cluster extension (wetting) or compression (de-wetting), and (3) directional movement of cells. These modes of cell migration are inter-connected (Pallarès et al. 2022). Cell clusters de-wet soft substrate and wet stiff substrate during their movement (Pallarès et al. 2022). The aim of this consideration is to clarify the inter-connection among the migration modes by discussing the role of the introduced physical parameters.

Movement of cell clusters on collagen networks causes complex in-plane and out-of-plane strains which feeds back on the movement itself in a complex way. Clark et al. (2022) revealed that cell clusters exert asymmetric inward-facing radial traction forces near the cluster edge which induce an in-plane extension of the collagen network in regions surrounding the cells and network in-plane compression in the region directly under the cell cluster. Besides in-plane strain, out-of-plane strain is generated caused by downward-facing tractions in the middle of the cluster (Pajic-Lijakovic et al. 2022). Induced in-plane strain results in surface structural changes of the matrix, while out-of-plane strain results in volumetric structural changes of the collagen I matrix which leads to the matrix stiffening. The surface structural changes of matrix include extension of collagen fibers and their radial alignment around the cell cluster, which lead to a change in the collagen concentration under the cluster and around the cluster (Clark et al. 2022). The resulting distribution of collagen concentration around the cell cluster is asymmetric such that the collagen concentration near the cluster front region is \(\sim 30\%\) times lower than the one near the cluster rear (Clark et al. 2022). Change of the collagen concentration is caused by the in-plane strain which results in an establishment of the matrix surface tension gradient. However, the impact of this gradient on the directional cell migration has not been elaborated yet. The dependence of collagen I surface tension on the collagen concentration has been considered on collagen I films in experiments without cells (Kezwon and Wojciechowski 2014). It would be interesting to compare dilational viscoelasticity of collagen I film and fibrinogen film under the same conditions in experiments without cells. Both of them are widely used as substrate matrices for cell migration assays and from these an interesting result can be extracted. While the protein concentration increase in the range of 1–4 \( \frac{\mathrm{mg}}{\mathrm{ml}}\) induces a decrease in the surface tension of collagen networks, it has no effect on the surface tension of fibrinogen networks (Gudapati et al. 2020). Consequently, it seems that the surface structural changes of the matrix, caused by cell movement, can have an impact on directional cell migration on collagen I matrix, but have no effect on cell movement on the fibrinogen matrix.

The focus of this review is to consider the rearrangement of 2D cell clusters and 3D cell clusters (i.e., cell spheroids) on collagen I matrix. Three modes of cell rearrangement via collective cell migration are distinguished: (1) the cell rearrangement within the cluster, (2) cell extension (wetting)/ compression (de-wetting) during the cluster movement, and (3) directional cell movement based on physical parameters such as: tissue and matrix surface tensions, cell–matrix interfacial tension, as well as, the corresponding gradients of surface and interfacial tensions, and the viscoelasticity of the cell cluster on the one hand and the viscoelasticity of the matrix on the other. Cell clusters are an order of magnitude larger than the size of single cells. In addition, we point out the importance of accounting for the surface characteristics of tissue and surrounding ECM in advancing cancer physics research, and discuss open problems and potential opportunities that can be addressed with these tools. We also present a new biophysical model in order to point out the role of these physical parameters in rearrangement and movement of cell collectives by considering the model system such as movement of cell clusters on a collagen I network.

Physical parameters which influence movement of cell cluster on collagen I matrix

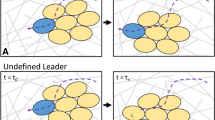
Various modes of cell cluster movement such as: (1) cell movement within the cluster, (2) cluster wetting/de-wetting, and (3) directional cell movement are shown schematically in Fig. 1.

Fig. 1
figure 1

Schematic presentation of migration modes such as: (1) the cell movement within the cluster, (2) cluster wetting/de-wetting, and (3) directional cell movement

Full size image

These migration modes depend on interplay between physical parameters such as: (1) tissue surface tension, (2) matrix surface tension, (3) cell–matrix interfacial tension, (4) gradients of surface and interfacial tensions, (5) cell residual stress, and (6) matrix residual stress influences the rearrangement and movement of cell cluster on collagen I matrix. The main characteristics of these parameters are inhomogeneous distributions near the cell–matrix biointerface and time dependence. Some physical parameters influence the movement of cells: (1) directly and (2) indirectly by influencing the cell and matrix residual stresses which have a feedback on cell packing density and velocity (Pajic-Lijakovic et al. 2023b). The interrelation among physical parameters which guide collective cell migration is shown in Fig. 2.

Fig. 2
figure 2

The interrelation among physical parameters which guide collective cell migration

Full size image

In order to discuss this complex phenomenon in the context of the formulated biophysical model, it is necessary to describe these physical parameters in more detail.

Dilational and volumetric viscoelasticity of collagen I matrix: the directional cell movement

The in-plane and out-of-plane strains, caused by movement of a cell cluster, lead to establishment of a matrix surface tension gradient and matrix stiffness gradient, respectively, which are responsible for the directional cell movement as is shown schematically in Fig. 3.

Fig. 3
figure 3

Schematic representation of the rearrangement of collagen I matrix caused by movement of cell cluster

Full size image

The altered structural changes of collagen I networks occur on various time-scales from milliseconds to hours (Pryse et al. 2003; Gautieri et al. 2012; Nam et al. 2016; Pajic-Lijakovic et al. 2022). The time-scale from nanoseconds to milliseconds corresponds to intra-filament interactions caused by single fiber conformations, while the time-scale of seconds corresponds to inter-fiber interactions and ordering of fibers within mesoscopic domains. The time-scale of minutes corresponds to sliding of network domains with respect to one another, while the time-scale of tens of minutes to hours corresponds to the rearrangement of network domains (Pryse et al. 2003; Legant et al. 2009; Gautieri et al. 2012; Nam et al. 2016). The main characteristics of the viscoelasticity of collagen I networks from milliseconds to seconds is nonlinearity (Nam et al. 2016). The cause of this non-linear behavior is related to the cumulative effects of the conformational changes of collagen filaments (Storm et al. 2005; Wen and Janmey 2013). The collagen fibers are semi-flexible and can be described by a worm-like chain model (Yamakawa 1971). The stretching of semi-flexible filaments is accompanied by entropic effects, while the larger extensional forces induce enthalpic effects which cause the non-linear rheological response of the fibers (Storm et al. 2005; Broedersz and MacKintosh 2014). In contrast to the filament stretching, the filament compression results in a more linear force–displacement relationship as a consequence of the entropic effects (Broedersz and MacKintosh 2014). The non-linear viscoelasticity of collagen I networks is related to the strain stiffening which has a feedback to cell-ECM interactions (Wen and Janmey 2013). A strain increase within a timescale from milliseconds to seconds results in a short-lived strain stiffening effect such that the stiffness returns to basal levels within about 5 min, while the collective cell migration occurs on a timescale of hours (Nam et al. 2016). However, the periodic strain of collagen networks in response to cell-mediated stresses, which occur on timescales of minutes to hours, can lead to long-lived stiffening caused by the accumulation of the residual stress during movement of cell collectives (Pajic-Lijakovic et al. 2022). Pryse et al. (2003) measured residual stress accumulation within a collagen I network during successive stretching in the experiments without cells. After the first stress relaxation cycle, the residual stress was only \(\sim 5\, \mathrm{Pa}\), while after the third stress relaxation cycle the residual stress increased up to \(\sim 35\, \mathrm{Pa}\).

In order to understand better the relationships between (1) in-plane strain and the matrix surface tension change, (2) out-of-plane strain and the matrix residual stress accumulation which results in the matrix stiffening, and (3) the matrix surface tension and matrix normal residual stress accumulation, it is necessary to point to the main characteristics of the dilational and volumetric viscoelasticity of collagen I networks obtained in various experiments without cells.

The surface tension of collagen I film relaxes on change in the surface area \(\Delta {A}_{M}\) which has been considered by Kezwon and Wojciechowski (2014) in experiments without cells. The relaxation time corresponds to a few minutes, while the necessary time for reaching the surface tension equilibrium state \({\gamma }_{Meq}\) is more than 1 h at 21 °C (Kezwon and Wojciechowski 2014). The relaxation time increases with the collagen concentration, while the collagen surface tension decreases with the collagen concentration. An increase in the collagen concentration from \(1 \) to \(4 \frac{\mathrm{mg}}{\mathrm{ml}}\) (in the experiments without cells) causes a decrease in the equilibrium collagen I surface tension \({\gamma }_{\mathrm{Meq}}\) from \(62 \)to \(57 \frac{\mathrm{mN}}{\mathrm{m}}\) at 21 °C (Kezwon and Wojciechowski 2014). It is not clear whether this surface tension difference is large or small. To clarify this issue, we would like to discuss the corresponding surface tension difference of \(5 \frac{\mathrm{mN}}{\mathrm{m}}\) for a well-known system such as water. An increase in the temperature from \(0\) to 50 °C induces a decrease in the surface tension of water of \(7 \frac{\mathrm{mN}}{\mathrm{m}}\).

The indicated range of collagen concentration also corresponds to various experiments which have been performed with cells. While the equilibrium collagen surface tension decreases with the concentration, the collagen surface tension change \(\Delta {\gamma }_{M}\) during the relaxation process, caused by changing the surface area \(\frac{\Delta {A}_{M}}{{A}_{M}}\), increases with the concentration (where \(\Delta {\gamma }_{M}={\gamma }_{M0}-{\gamma }_{\mathrm{Meq}}\) and \({\gamma }_{\mathrm{Meq}}\) is the equilibrium matrix surface tension). The phenomenon is pronounced at the higher temperature of 34.5 °C (Kezwon and Wojciechowski 2014). Consequently, the equilibrium surface tension of collagen I film satisfies the condition \({\gamma }_{\mathrm{Meq}}\sim {C}_{\mathrm{col}}^{-1}\) (where \({C}_{\mathrm{col}}\) is the collagen surface concentration). It is in accordance with fact that collagen fibers are capable of establishing inter-fiber connections in the form of physical gel-like structures at higher collagen concentrations and higher temperatures (Nam et al. 2016). The relationship between the collagen surface tension change \(\Delta {\gamma }_{M}\) and surface area \(\frac{\Delta {A}_{M}}{{A}_{M}}\) can be formulated based on some suitable constitutive model of the dilational viscoelasticity \(\Delta {\gamma }_{M}=\Delta {\gamma }_{M}(\frac{\Delta {A}_{M}}{{A}_{M}})\) (Babak et al. 2005). The Fourier transform of the constitutive model can be presented in the form of \(F\left(\Delta {\gamma }_{M}\right)={E}_{sM}^{*} F\left(\frac{\Delta {A}_{M}}{{A}_{M}}\right)\) (where \(F\left(\cdot \right)\) is the Fourier operator, \({E}_{sM}^{*}\left(\omega \right)\) is the dynamic surface modulus of the matrix equal to \({E}_{sM}^{*}\left(\omega \right)={E}_{sM}^{\prime}\left(\omega \right)+i{E}_{sM}^{{\prime}^{\prime}}\left(\omega \right)\), while \({E}_{sM}^{\prime}\) is the surface storage modulus, \({E}_{sM}^{{\prime}^{\prime}}\) is the surface loss moduli, \(\omega \) is the angular velocity, and \(i=\sqrt{-1}\)). The surface storage modulus represents a measure of the storage energy within the surface area, while the surface loss modulus represents a measure of the energy dissipation caused by the structural changes of the surface area \(\frac{\Delta {A}_{M}}{{A}_{M}}\). The main characteristic of the dilational viscoelasticity of collagen I surfaces without cells, for the concentration range 1–4 \(\frac{\mathrm{mg}}{\mathrm{ml}}\), is that \({E}_{sM}^{\prime}>{E}_{sM}^{{\prime}^{\prime}}\) which points to a viscoelastic solid-like behavior (Kezwon and Wojciechowski 2014).

The surface tension of a collagen I sample influences the residual stress accumulation under external strain conditions. The corresponding matrix normal residual stress can be expressed based on the Young–Laplace equation as: \({\widetilde{{\varvec{\sigma}}}}_{{\varvec{M}}{\varvec{r}}{\varvec{V}}}=\Delta {p}_{M}\widetilde{{\varvec{I}}}+{{\widetilde{{\varvec{\sigma}}}}_{{\varvec{M}}{\varvec{r}}{\varvec{V}}}}^{{\varvec{d}}}\) (where \(\Delta {p}_{M}\widetilde{{\varvec{I}}}\) is the isotropic part of stress equal to \(\Delta {p}_{M}=-{\gamma }_{M}\left(\overrightarrow{\nabla }\cdot \overrightarrow{{\varvec{n}}}\right)\), \(\overrightarrow{{\varvec{n}}}\) is the normal vector on the surface, \(\widetilde{{\varvec{I}}}\) is the unit tensor, and \({{\widetilde{{\varvec{\sigma}}}}_{{\varvec{M}}{\varvec{r}}{\varvec{V}}}}^{{\varvec{d}}}\) is the deviatoric part of stress caused by external strain). The residual stress within the collagen I network increases during successive stress relaxation cycles under constant uni-axial extensional strain per cycle from \(\sim 5\, {\rm Pa}\) after the first relaxation cycle to \(\sim 35\, {\rm Pa}\) after the third relaxation cycle in the experiments without cells (Pryse et al. 2003). In experiments with cells, the residual stress accumulation within the collagen network is responsible for the matrix stiffening and the establishment of the stiffness gradient, which can have a feedback on the cell movement persistence (Pajic-Lijakovic et al. 2022).

After discussing dilational and volumetric viscoelasticity of collagen I networks obtained in experiments without cells, it is necessary to point to the structural changes of the collagen I network matrix caused by movement of a cell cluster on the matrix surface. The cell movement induces the matrix in-plane extension around the cluster edge, pronounced around the cluster front, which leads to extension of collagen fibers and their radial alignment around the cluster edge (Clark et al. 2022). Consequently, the gradient of the collagen surface concentration, caused by the in-plane strain leads to an establishment of the matrix surface tension gradient such that \({\gamma }_{M }^{F}>{\gamma }_{M}^{R}\) (where the superscript \(R\) is the cluster rear region and the superscript \(F\) is the front region). The corresponding matrix surface tension gradient can contribute to the cluster migration persistence. In this context, we can provide two arguments:

  • The established gradient of the matrix surface tension \(\overrightarrow{\nabla }{\gamma }_{M}\) drives movement of partially disconnected collagen fibers from the region of lower surface tension (at the cluster rear) to the region of larger surface tension (at the cluster front). This phenomenon represents a part of the Marangoni effect recognizable in various soft matter systems (Karbalaei et al. 2016) in which the surface tension gradient is induced by a change in temperature or surface concentration of the system constituents.

  • A larger matrix surface tension corresponds to a higher cell spreading coefficient for the same tissue surface tension and cell–matrix interfacial tension (Pajic-Lijakovic and Milivojevic 2023a, b). The spreading coefficient is expressed as: \({S}^{c-M}={\gamma }_{M}-\left({\gamma }_{c }+{\gamma }_{Mc}\right)\) (where \({\gamma }_{c}\) is the surface tension of cell cluster and \({\gamma }_{Mc}\) is the cell–matrix interfacial tension). A detailed description of this complex phenomenon will be given below.

A cell cluster also induces out-of-plane compression of collagen I matrix, especially pronounced under the cluster’s central part, caused by cell tractions which contribute to the deviatoric part of the normal matrix residual stress accumulation within the matrix while the isotropic part of the matrix normal residual stress is generated by the work of the matrix surface tension based on the Young–Laplace equation (Table 1) (Pajic-Lijakovic and Milivojevic 2023a, b). The matrix residual stress distribution can thus induce the establishment of the matrix stiffness gradient (Pajic-Lijakovic et al. 2022).

Table 1 The residual stress accumulation within cell cluster and substrate matrix
Full size table

Besides matrix surface tension, the tissue surface tension accompanying the cell–matrix interfacial tensions and their gradients govern the movement of cell clusters on collagen I matrix. For a deeper understanding of the phenomenon of cell migration, it is necessary to discuss these parameters which will be incorporated within the biophysical model.

Surface tension of cell clusters: the movement of cells within the cluster

Macroscopic surface tension of cell clusters is a time dependent physical parameter which represents a measure of cluster cohesiveness. This surface tension is influenced by the state of single cells and the extension or compression of multicellular system caused by collective cell migration (Guevorkian et al. 2021; Pajic-Lijakovic and Milivojevic 2023a, b). The state of single cells includes the cell contractility and strength of cell–cell adhesion contacts. Contractile epithelial cells have larger surface tension than non-contractile ones (Devanny et al. 2021). In this context, two reasons can be provided: (1) contractile cells adsorbed contractile energy and become stiffer than non-contractile ones (Pajic-Lijakovic and Milivojevic 2022a) and (2) cell contractility enhances the strength of E-cadherin mediated adherens junctions (AJs) (Devanny et al. 2021). The surface tension of epithelial-like systems are lower than the surface tension of collagen I matrix, i.e., \({\gamma }_{c}<{\gamma }_{M}\) in the majority of cases (Pajic-Lijakovic et al. 2023a). The tissue surface tension varies significantly for various cellular systems and also depends on the applied measuring technique. Various experimental techniques have been applied for the measurement of the static tissue surface tension such as: cell spheroid uni-axial compression between parallel plates (Mombash et al. 2005; Marmottant et al. 2009), cell spheroid micropipette aspiration (Guevorkian et al. (2021), and magnetic force tensiometer (Nagle et al. 2022). The tissue surface tension measured by the cell spheroid uni-axial compression of: (1) F9 WT cell spheroids is \(4.5 \frac{\mathrm{mN}}{\mathrm{m}}\) (Stirbat et al. 2013), (2) embryonic neural retina spheroids varies from \(1.6\pm 0.6\) to \(4.0\pm 1.0 \frac{\mathrm{mN}}{\mathrm{m}}\) during the spheroid rounding within 9 days (Mombash et al. 2005), and (3) spheroids of CHO cells \(22.8\pm 3 \frac{\mathrm{mN}}{\mathrm{m}}\) (Efremov et al. 2021). Nagle et al. (2022) measured the surface tension of MCF 10-A spheroids by magnetic tensiometer and obtained a significantly larger value, i.e., \(45\pm 18 \frac{\mathrm{mN}}{\mathrm{m}}\). It has been notable that MCF-10A cells establish strong cell–cell adhesion contacts which influence the tissue surface tension (Devanny et al. 2021), but exposure of cell spheroids to the magnetic field additionally enhance the strength of cell–cell adhesion contacts as reported by Jafari et al. (2019). A systematic review of experimental values of the tissue surface tension dependence on the experimental technique does not as yet exist. The surface tension of collagen matrix obtained for the collagen concentration of \(4 \frac{\mathrm{mg}}{\mathrm{ml}}\) is significantly larger than the tissue surface tension in the majority of cases and equal to \(57 \frac{\mathrm{mN}}{\mathrm{m}}\) (Kezwon and Wojciechowski 2014).

Extension of epithelial surfaces leads to a significant increase in a tissue surface tension (Guevorkian et al. 2021). It is in accordance with fact that the extension enhances the strength of E-cadherin mediated adherens junctions (Devanny et al. 2021). Local extension of the murine sarcoma (S180) spheroid surface by applying the micropipette aspiration force in the range of 0.5–1.5 µN leads to an increase in the surface tension from \({\gamma }_{c}\sim 7 \) to \(\sim 22 \frac{\mathrm{mN}}{\mathrm{m}}\) (Guevorkian et al. 2021). Collective cell migration also induces successive extension and compression of multicellular surfaces in the form of mechanical waves (Serra-Picamal et al. 2012; Blanch-Mercader et al. 2017; Notbohm et al. 2016; Pajic-Lijakovic and Milivojevic 2020, 2022b). However, multicellular surfaces have not been considered in the context of dilational viscoelasticity as of yet. We can provide here only a qualitative analysis based on some experimental findings in the context of the relationship between the tissue surface tension change \(\Delta {\gamma }_{c}\) induced by changing the multicellular surface area \(\frac{\Delta {A}_{c}}{{A}_{c}}\) (where \(\Delta {\gamma }_{c}={\gamma }_{c}-{\gamma }_{c eq}\), \({\gamma }_{c}\) is the tissue surface tension, and \({\gamma }_{c eq}\) is the equilibrium tissue surface tension). This change in the surface tension is caused by (1) change in the number of cells per surface area which has a feedback on the strength of AJs (Pajic-Lijakovic and Milivojevic 2022a; 2023; Pajic-Lijakovic et al. 2023b), and (2) change in the surface area per single cells caused by change of the cluster surface area (Guevorkian et al. 2021). It would be interesting to extract the dynamic complex surface modulus of cells \({E}_{\rm sc}^{*}\left(\omega \right)=\frac{F\left(\Delta {\gamma }_{c}\right)}{F\left(\frac{\Delta {A}_{c}}{{A}_{c}}\right)}\) (where \(F\left(\cdot \right)\) is the Fourier operator, \({E}_{\rm sc}^{\prime}\left(\omega \right)\) is the cell surface storage modulus, and \({E}_{\rm sc}^{{\prime}^{\prime}}\left(\omega \right)\) is the cell surface loss modulus) and consider the ratio between storage and loss moduli, i.e., \(\frac{{E}_{\rm sc}^{\prime}\left(\omega \right)}{{E}_{\rm sc}^{{\prime}^{\prime}}\left(\omega \right)}\) under various experimental conditions, in order to extract more information relevant for collective cell migration.

The tissue surface tension varies along the cell cluster surface in contact with ECM. When the cell cluster is an order of magnitude larger than the size of a single cell, the multicellular surface can be considered as a continuous medium and characterized by the macroscopic tissue surface tension. Migrated epithelial-like collectives such as: larger 2D and 3D cell clusters, as well as, cell monolayers show inhomogeneous distribution of cell velocity, corresponding strain rate, cell packing density, and macroscopic tissue surface tension that change within a timescale of hours (Serra-Picamal et al. 2012; Blanch-Mercader et al. 2017; Notbohm et al. 2016; Tlili et al. 2018; Pajic-Lijakovic et al. 2023b). The local macroscopic tissue surface tension within the cell–matrix biointerface can be expressed as: \({\gamma }_{c}=\frac{\partial {E}_{ST}}{\partial A}\) (where \(A\) is the cluster surface and \({E}_{ST}\) is the mechanical energy of the cells within this region). The energy \({E}_{ST}\) includes passive and active energy contributions per single cells, \({E}_{Sp}\) and \({E}_{Sa}\), respectively. The passive energy contribution is expressed as: \({E}_{STp}=\sum_{i}\frac{K}{2}{\left({A}_{ci}-{A}_{0}\right)}^{2}+\sum_{i,j}\Lambda {l}_{ij}\) (where \({A}_{ci}\) is the effective surface area per the i-th cell, \(K\) is an effective modulus of the cell around its preferred surface area \({A}_{0}\), \({l}_{ij}\) is the interface length between the i-the and j-th cells, \(\Lambda \) is line tension per unit interface length between two cells), while the active energy contribution is equal to: \({E}_{STa}=\sum_{i}\frac{{T}_{\rm con i}}{2}{{L}_{i}}^{2}\) (where \({T}_{\rm con i}\) is the contractility coefficient, and \({L}_{i}\) is the perimeter of the i-th cell) (Koride et al. 2018). Clark et al. (2022) considered movement of the A431 cell clusters made of \(\sim 50\) cells and pointed out that the cluster peripheral region is more contractile than the cluster central region. This is in accordance with the fact that Rac1 appears to be down regulated at cell–cell junctions at the cluster interior (Hidalgo-Carcedo et al. 2011; Clark et al. 2022). Cell contractility enhances the strength of E-cadherin mediated adherens junctions (Devanny et al. 2021). Consequently, the surface tension of active, contractile epithelial-like cells is larger than the surface tension of non-contractile ones (Devanny et al. 2021). Based on these findings, we can conclude that the tissue surface tension established at the cluster peripheral region is larger than that at the cluster interior. The established cell surface tension gradient governs cell movement from the region of lower tissue surface tension (characteristic for the cluster central region) to the region of larger tissue surface tension (characteristic for the cluster peripheral region) (Pajic-Lijakovic and Milivojevic 2022c). This phenomenon represents also a part of the Marangoni effect recognizable in various soft matter systems which directs the movement of the system constituents from the region of lower surface tension to the region of higher surface tension (Karbalaei et al. 2016). This effect is also responsible for cell segregation within co-cultured cell clusters (Maître et al. 2012). Consequently, this physical mechanism accompanied by biochemical mechanisms related to cell signaling (Clark et al. 2022) influence cell self-rearrangement within the cluster.

Cell–matrix interfacial tension

The cell–matrix interfacial tension and its gradient influence the modes of cell migration directly through the spreading factor and indirectly by influencing the accumulation of cell and matrix residual stresses as is shown schematically in Fig. 2.

The cell–matrix interfacial tension has not been measured yet. The interfacial tension \({\gamma }_{\rm cm}\) can be expressed as:

$${\gamma }_{\rm cm}={\gamma }_{c}+{\gamma }_{M}-{\omega }_{a}$$
(1)

where \({\omega }_{a}\) is the adhesion energy between cells and matrix which can be expressed as: \({\omega }_{a}=\frac{1}{{A}_{int}}\sum_{i=1}^{N}\frac{1}{2}{k}_{c}{{\left|{{\overrightarrow{{\varvec{u}}}}_{{\varvec{M}}}}^{c}\right|}^{2}}_{i}\) (Murray et al. 1988), \(N\) is the number of focal adhesions (FAs) within the biointerfacial area \({A}_{int}\), \({k}_{c}\) is the elastic constant per single FA, and \({{\overrightarrow{{\varvec{u}}}}_{{\varvec{M}}}}^{c}\) is the matrix displacement field caused by cell tractions. Clark et al. (2022) revealed that cell clusters preform asymmetric tractions during their movement on collagen I matrix such that the maximum traction is induced at the cluster rear, highlighting that \({\omega }_{a}^{F}<{\omega }_{a}^{R}\). Accordingly with the previously extracted conclusion that: (1) \({\gamma }_{c}^{F}\sim {\gamma }_{c}^{R}\) caused by inhomogeneous cell extension and contractility within the cell–matrix biointerface, (2) \({\gamma }_{M}^{F}>{\gamma }_{M}^{R}\) caused by change in the collagen concentration, and (3) \({\omega }_{a}^{F}<{\omega }_{a}^{R}\) caused by asymmetric cell tractions, and based on Eq. 1, we can conclude that the interfacial tension is larger at the cluster front and decreases toward the cluster rear, i.e., \({\gamma }_{\rm cm}^{F}>{\gamma }_{cM }^{R}\). Besides, cell matrix interfacial tension, the tissue and matrix surface tensions also contribute to the cluster extension (wetting) or compression (de-wetting) expressed in the form of the cell spreading coefficient.

Physical parameters responsible for cell cluster wetting/de-wetting

Multicellular systems perform oscillatory extension (wetting) and compression (de-wetting) during collective cell migration which have been discussed in the context of mechanical waves (Serra-Picamal et al. 2012; Blanch-Mercader et al. 2017; Notbohm et al. 2016; Pajic-Lijakovic and Milivojevic 2020). The phenomenon has been recognized in various 2D and 3D model systems such as: (1) the free expansion of cell monolayers (Serra-Picamal et al. 2012; Blanch-Mercader et al. 2017), (2) rearrangement of confluent cell monolayers (Notbohm et al. 2016), (3) cell spheroid rounding after uni-axial compression (Mombash et al. 2005; Pajic-Lijakovic and Milivojevic 2022b), (4) cell spheroid wetting/de-wetting on rigid substrate (Beaune et al. 2018), and (5) fusion of two cell spheroids (Pajic-Lijakovic and Milivojevic 2023a).

We are interested in the wetting/de-wetting of 2D cell clusters and cell spheroids on a substrate matrix. Two scenarios of wetting/de-wetting can be distinguished depending on whether the clusters change their dimensionality from 2 to 3D and vice versa, or retain their dimensionality.


Scenario 1: the cluster wetting/de-wetting (i.e., the extension/compression of the cell–matrix biointerface) occurs by deforming cells and adhesion contacts, while the number of cells in direct contact with the matrix is kept constant. In this case, the cell cluster retains its dimensionality. This case corresponds to the wetting-de-wetting of cell monolayers and larger 2D cell clusters (Serra-Picamal et al. 2012; Blanch-Mercader et al. 2017; Nnetu et al. 2012; Petrolli et al. 2021).


Scenario 2: the cell–matrix biointerface extension/compression results in a change in the number of cells in direct contact with the matrix. In this case, the wetting of cell spheroids can induce a change in the dimensionality from 3 to 2D, while the de-wetting can result in 2D to 3D transition. This type of system has been considered by Beaune et al. (2018) and Pérez-González et al. (2019).

Which scenario exists during oscillatory wetting and de-wetting of cell clusters depends on the interplay between surface and volumetric physical parameters. Surface parameters in the form of the cell spreading coefficient represents interplay between tissue and matrix surface tensions accompanied by the interfacial tension between them. Volumetric parameters are the cell and matrix residual stresses (normal and shear) which represent a consequence of cell–matrix interactions at the biointerface. Consequently, an interfacial tension influences both surface and volumetric physical parameters. We will discuss this relationship in more detail in the next two sections.

Cell spreading coefficient

The cell–matrix interfacial tension accompanied by the cell and matrix surface tensions contributes to the extension (wetting) or compression (de-wetting) of the cell cluster during its movement. The corresponding spreading coefficient can be expressed as: \({S}^{c-M}={\gamma }_{M}-\left({\gamma }_{c }+{\gamma }_{Mc}\right)\) (Pajic-Lijakovic and Milivojevic 2023a). Two cases can be distinguished in the context of the spreading coefficient such as:

  1. (1)

    The case 1 for \({S}^{c-M}>0\) corresponds to the cell cluster extension which can follow one of two scenarios. Scenario 1 corresponds to the condition that \({\gamma }_{M}>{\gamma }_{c }+{\gamma }_{Mc}\), while scenario 2 corresponds to the condition that \({\gamma }_{M}\gg {\gamma }_{c }+{\gamma }_{Mc}.\)

    and

  2. (2)

    The case 2 for \({S}^{c-M}<0\) corresponds to the cell cluster compression which can follow one of two scenarios (Pajic-Lijakovic and Milivojevic 2023a). Scenario 1 corresponds to the condition that \({\gamma }_{M}<{\gamma }_{c }+{\gamma }_{Mc}\), while scenario 2 corresponds to the condition that \({\gamma }_{M}\ll {\gamma }_{c }+{\gamma }_{Mc}.\)

Consequently, the prerequisites for the appearance of scenario 2, during cell cluster wetting/de-wetting, are related to an ability of cellular systems to: (1) significantly increase the strength of cell–cell and cell–matrix adhesion contacts (as well as the tissue surface tension and cell–matrix interfacial tension) during extension in order to keep the cluster structural integrity, (2) significantly decrease the strength of cell–cell and cell–matrix adhesion contacts during compression caused by the contact inhibition of locomotion, and (3) induce the rearrangement of collagen fibers via tractions which result in oscillatory change in the matrix surface tension caused by the cluster extension/compression.

The cell–matrix interfacial tension also influences the residual stress accumulation within the migrating cell cluster and within the matrix which will be discussed based on model consideration.

The residual stress accumulation within cell cluster and within collagen I matrix

Residual stresses are defined as self-equilibrating stresses which exist in materials even in the absence of external loads. In viscoelastic materials, this stress can be dissipative or elastic depending primarily on the strength of cell–cell adhesion contacts. The corresponding shear and normal residual stresses for migrating cell cluster and collagen I matrix are shown in Table 1.

The cell normal residual stress consists of isotropic and deviatoric parts. The isotropic part of the stress is caused by the work of cell–matrix interfacial tension expressed by the Young–Laplace equation. The interfacial tension exerts work along the biointerface area between cell cluster and matrix in order to minimize the interface. Consequently, the interfacial tension is responsible for compression and extension of both cell cluster and surrounding matrix. If the cell cluster is extended during its movement (i.e., cell wetting), this extension results in the matrix compression (Pajic-Lijakovic and Milivojevic 2023a). Otherwise, the cell cluster compression caused by de-wetting leads to the matrix strain relaxation along the cell–matrix biointerfacial area (i.e., expansion). Compression of matrix or cell cluster is labeled by sign “ + ”, while the extension is labeled by sign “-”.

The deviatoric part of the cell normal residual stress accounts for: (1) the stress caused by collective cell migration and (2) stress caused by action of the gravitational force which should be included for the case of 3D cell clusters (i.e., cell spheroids) (Pajic-Lijakovic and Milivojevic 2023a, b). The gravitational force can be expressed as: \({\overrightarrow{{\varvec{f}}}}_{{\varvec{g}}}={m}_{a}\overrightarrow{{\varvec{g}}}\) (where \({m}_{a}\) is the cluster mass and \(\overrightarrow{{\varvec{g}}}\) is the gravitational acceleration). The mass of cell spheroid in liquid medium is equal to \({m}_{a}=\left({\rho }_{a}-{\rho }_{w}\right){V}_{a}\) (where \({\rho }_{a}\) is the spheroid mass density, \({\rho }_{w}\) is the density of water equal to \({\rho }_{w}=1.00 \frac{g}{{\rm cm}^{3}}\), and \({V}_{a}\) is the spheroid volume). The density of soft tissues varies from \(1.06 \frac{g}{{\rm cm}^{3}}\) for liver to \(1.09 \frac{g}{{\rm cm}^{3}}\) for skin (Schneider et al. 1999). For the preliminary calculation of the gravitation force, we used the mass density \({\rho }_{a}=1.08 \frac{g}{{\rm cm}^{3}}\) and the radius of cell spheroid equal to \({r}_{a}=100 \, \upmu {\rm m}\), the corresponding force is \({\overrightarrow{{\varvec{f}}}}_{{\varvec{g}}}=3.29\, {\rm nN}\). For the radius of the spheroid equal to \({r}_{a}=200 \, \upmu {\rm m}\), this force is \({\overrightarrow{{\varvec{f}}}}_{{\varvec{g}}}=26.24\, {\rm nN}\). This force is large enough to generate asymmetric deformation of the collagen I network depending on the structural ordering of the collagen filaments (Clark et al. 2022). This is in accordance with the fact that the force of a few pN can induce the breaking of electrostatic and hydrophobic bonds in collagen I networks, while the force of a few nN can induce stretching of the collagen filament up to 20% strain (Gautieri et al. 2012). Cell traction force is in the range from a few nN to several tens of nN (Hall et al. 2016; Emon et al. 2021). The deformation of the collagen matrix, induced by the cell spheroid weight, can cause a change in the gravitational acceleration from \(\overrightarrow{{\varvec{g}}}=\left(\mathrm{0,0},{g}_{z}\right)\) to \(\overrightarrow{{\varvec{g}}}=\left({g}_{x},{g}_{y},{g}_{z}\right)\). Appearance of the x- and y- components of the gravitational force has a feedback on the directional cell wetting which can become asymmetric (Beauene et al. 2018). Consequently, the gravitation force contributes to cell spreading, especially for the case of larger cell spheroids.

Collective cell movement induces generation of strain (volumetric and shear) which induces generation of cell stress (normal and shear), its relaxation and cell residual stress accumulation (Pajic-Lijakovic and Milivojevic 2019, 2020). Cell strain change and residual stress accumulation occur on a time-scale of hours while the stress relaxation occurs on a time-scale of minutes (Marmottant et al. 2009; Pajic-Lijakovic and Milivojevic 2019).

The cell residual stress generated by collective cell migration depends primarily on the strength of cell–cell adhesion contacts. When cells establish E-cadherin mediated adherens junctions (AJs) and migrate in the form of strongly connected cell clusters, their rheological behavior corresponds to viscoelastic solids (Pajic-Lijakovic and Milivojevic 2019, 2020). In order to formulate the cell residual stress caused by collective cell migration, it is necessary to choose a proper constitutive model. Experimental results on various epithelial-like model systems such as: (1) free expansion of cell monolayers (Serra-Picamal et al. 2012), (2) rearrangement of confluent cell monolayers (Notbohm et al. 2016), and (3) cell spheroid uni-axial compression between parallel plates (Marmottant et al. 2009) pointed to the Zener constitutive model. The main characteristics of the Zener model are: (1) stress relaxes exponentially under constant strain conditions (Marmottant et al. 2009), (2) strain relaxes exponentially under constant stress conditions (Marmottant et al. 2009), and (3) the corresponding cell residual stress is purely elastic (Serra-Picamal et al. 2012; Notbohm et al. 2016). The stress relaxation occurs on a timescale of minutes, while strain relaxation, which takes place via collective cell migration, occurs on a timescale of hours (Marmottant et al. 2009; Pajic-Lijakovic and Milivojevic 2019). The ability of strain to relax is the one of the main characteristics of viscoelastic solids (Pajic-Lijakovic 2021). The cell residual stress accumulation caused by free expansion of cell monolayers and the rearrangement of confluent cell monolayers correlates with the corresponding strain which points to the elastic nature of the cell residual stress (Serra-Picamal et al. 2012; Notbohm et al 2016). The Zener model is expressed as:

$${{\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},\boldsymbol{ }{t}_{s},\tau \right)}^{{\varvec{C}}{\varvec{C}}{\varvec{M}}}+{\tau }_{Ri}{\dot{\widetilde{{\varvec{\sigma}}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},{t}_{s},\tau \right)={E}_{ci}{\widetilde{{\varvec{\varepsilon}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},\tau \right)+{\eta }_{ci}{\dot{\widetilde{{\varvec{\varepsilon}}}}}_{{\varvec{c}}{\varvec{i}}}\boldsymbol{ }\left(\mathfrak{R},\tau \right)$$
(2)

where subscript \(i\) is shear for \(i\equiv S\) and normal (volumetric) for \(i\equiv V\), \(\mathfrak{R}=\mathfrak{R}\left(x,y,z\right)\) is the coordinate of the biointerface, \({t}_{s}\) is the short time-scale (i.e., a time scale of minutes), \(\tau \) is the long time-scale (i.e., a time-scale of hours), \({{\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},\boldsymbol{ }{t}_{s},\tau \right)}^{{\varvec{C}}{\varvec{C}}{\varvec{M}}}\) is the cell stress (shear and normal), \({\widetilde{{\varvec{\varepsilon}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},\tau \right)\) is cell strain (shear and volumetric) caused by collective cell migration, \({\tau }_{Ri}\) is the corresponding stress relaxation time, \({\dot{\widetilde{{\varvec{\sigma}}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},{t}_{s},\tau \right)\) is the rate of stress change, and \({\dot{\widetilde{{\varvec{\varepsilon}}}}}_{{\varvec{c}}{\varvec{i}}}\) is the strain rate, \({E}_{ci}\) is the module of elasticity, and \({\eta }_{ci}\) is the shear or bulk viscosity. The stress relaxation occurs via successive short time relaxation cycles under constant strain per single short time cycle, while the strain change via collective cell migration occurs on a long timescale (Pajic-Lijakovic and Milivojevic 2019, 2020). The corresponding cell stress relaxation can be expressed starting from the initial conditions at the strain \({\widetilde{{\varvec{\varepsilon}}}}_{{\varvec{c}}0{\varvec{i}}}\left(\mathfrak{R},\tau \right)\), the initial cell stress is \({\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},t=0,\tau \right)={\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}0{\varvec{i}}}\) as: \({\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},t=0,\tau \right)={\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}0{\varvec{i}}}\) as:\({\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{i}}}\left(\mathfrak{R},{t}_{s},\tau \right)={\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}0{\varvec{i}}}{e}^{-\frac{{t}_{s}}{{{\varvec{\tau}}}_{{\varvec{R}}{\varvec{i}}}}}+{\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{R}}{\varvec{i}}}\left(\mathfrak{R},\tau \right)\left(1-{e}^{-\frac{{t}_{s}}{{\tau }_{Ri}}}\right)\), while the cell residual stress is elastic and equal to \({\widetilde{{\varvec{\sigma}}}}_{{\varvec{c}}{\varvec{R}}{\varvec{i}}}\left(\mathfrak{R},\tau \right)={E}_{ci}{\widetilde{{\varvec{\varepsilon}}}}_{{\varvec{c}}0{\varvec{i}}}\).

The matrix normal residual stress consists of isotropic and deviatoric parts. The isotropic part of the stress is caused by the work of the cell–matrix interfacial tension (Pajic-Lijakovic and Milivojevic 2023a). While cell expansion leads to matrix compression, the compression of cell cluster results in the matrix extension. The deviatoric part of the matrix stress accounts for: (1) the stress caused by cell tractions and (2) stress caused by action of the gravitational force which should be included for the case of 3D cell clusters (Pajic-Lijakovic and Milivojevic 2023a).

The cell shear residual stress includes two contributions: (1) the cell stress generated by natural convection and (2) the cell stress generated by forced convection (Pajic-Lijakovic and Milivojevic 2022c; Pajic-Lijakovic et al. 2023a). Natural convection is caused by the gradient of cell–matrix interfacial tension \(\overrightarrow{\nabla }{\gamma }_{\rm cm}\) established along the interfacial area and the gradient of \(\overrightarrow{\nabla }{\gamma }_{c}\) established along the cell cluster itself. The gradient of interfacial tension can be expressed as \(\frac{\Delta {\gamma }_{\rm cm}}{\Delta L}\) (where \(\Delta {\gamma }_{\rm cm}\) is the interfacial tension difference and \(\Delta L\) is the distance in which this gradient exist). If we suppose that the interfacial tension difference corresponds to \(\Delta {\gamma }_{\rm cm}\approx 1 \frac{mN}{m}\) and the distance is \(\Delta L\approx 100 \, \upmu {\rm m}\), this gradient of the interfacial tension corresponds to a cell shear stress of \(\sim 10\, {\rm Pa}\). It is a large value when we keep in mind that the shear stress of several tens of Pa can induce inflammation of epithelial cells (Pitanes et al. 2018). The cell movement, which results in generation of the cell shear stress, occurs from the regions of lower cell surface tension and cell–matrix interfacial tension to the regions of higher cell surface tension and cell–matrix interfacial tension. It is a part of the Marangoni effect (Pajic-Lijakovic and Milivojevic 2022c). The difference in the tissue surface tension along the cell–matrix biointerface between various regions can represent an additional physical mechanism responsible for the cell rearrangement within the cluster. Accordingly with the fact that the cell–matrix interfacial tension is larger at the cluster front and decreases toward the cluster rear, i.e., \({\gamma }_{\rm cm}^{F}>{\gamma }_{cM }^{R}\), this interfacial tension gradient also stimulates cell movement from the cluster rear toward the front region. The cell shear stress caused by forced convection includes two contributions: (1) the cell shear stress caused by collective cell migration and (2) the cell shear stress caused by action of the gravitational force which should be accounted for in the case of larger 3D cell clusters (Pajic-Lijakovic and Milivojevic 2023a). The maximum cell shear stress caused by free expansion of cell monolayers is equal to \(\sim 100\, \mathrm{Pa}\) (Tambe et al. 2013).

The matrix shear stress is caused actively by cell tractions and passively by the action of the gravitational force for the case of 3D cell clusters. Both contributions are generated by forced convection.

After defining the relevant physical parameters responsible for: (1) cell self-rearrangement within the cluster, (2) cell cluster wetting and de-wetting on the substrate matrix, and (3) directional cell migration, a biophysical model in the form of cell force and mass balances can be formulated.

Biophysical model

The biophysical model for movement of a cell cluster on collagen I matrix is formulated in order to describe interplay among various model parameters such as tissue and matrix surface tensions, the interfacial tension between them, as well as the gradients of surface and interfacial tensions and cell and matrix residual stress accumulations in the form of cell force and mass balances. These parameters represent a product of dilational and volumetric viscoelasticity of both cell cluster and substrate matrix. The main goal of this modeling consideration is to elucidate the role of these physical parameters in the complex dynamics of cell migration rather than to provide exact calculations because some model parameters, such as the cell–matrix interfacial tension and the gradients of surface and interfacial tensions, have not been measured yet.

The force balance

The force balance includes the forces which drive cell movement and the forces which reduce it. Competition between driving and resistive forces leads to an oscillatory change of cell velocity and relevant rheological parameters such as cell strain and resulting cell residual stress accumulation (Pajic-Lijakovic and Milivojevic 2020). This oscillatory trend of cell spreading accounts for: successive, long-term oscillatory extension, and compression of multicellular system and oscillations of the velocity of the cluster center of mass (Serra-Picamal et al. 2012; Notbohm et al. 2016; Beaune et al. 2018). The oscillatory trend of collective cell migration has been recognized experimentally in various multicellular systems such as: (1) free expansion of cell monolayers (Serra-Picamal et al. 2012), (2) rearrangement of confluent cell monolayers (Notbohm et al. 2016), (3) cell spheroid rounding after uni-axial compression between parallel plates (Pajic-Lijakovic and Milivojevic 2022b), and (4) fusion of two cell spheroids (Pajic-Lijakovic and Milivojevic 2022b). The phenomenon has also been discussed in the context of mechanical waves (Serra-Picamal et al. 2012; Notbohm et al. 2016; Pajic-Lijakovic and Milivojevic 2020). The underlying physical mechanisms behind various types of cell movement such as: (1) the movement of cells within the cluster, (2) cell cluster wetting and de-wetting, and (3) directional cell migration are discussed in the context of various forces which were formulated based on proposed physical parameters. The roles of various forces in this complex dynamics of cell rearrangement are presented in Table 2.

Table 2 The volumetric forces which influence: (1) cell rearrangement within cluster, (2) cell cluster wetting/de-wetting, and (3) cell movement persistence
Full size table

The mixing force \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{m}}{\varvec{i}}{\varvec{x}}}}^{{\varvec{c}}-{\varvec{M}}}\) represents the product of the thermodynamic energetic effect of the mixing of two soft matter systems such as a cell cluster and collagen I matrix. This energetic effect is caused by cell–matrix interactions along the biointerface which have a feedback on cell–cell cohesion. This force drives cell cluster: (1) wetting for \({\gamma }_{c}<{\gamma }_{\rm cm}\) and (2) de-wetting for \({\gamma }_{c}>{\gamma }_{\rm cm}\) and also reduces cell self-rearrangement within the cluster (Pajic-Lijakovic and Milivojevic 2023a, b).

The Marangoni force for cells \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{M}}}}^{{\varvec{c}}}\) drives cell rearrangement within the cell cluster from a region of lower tissue surface tension within the cluster interior to a region of higher tissue surface tension within the cluster peripheral region. The phenomenon represents a part of the Marangoni effect (Pajic-Lijakovic and Milivojevic 2022c).

Interfacial tension force \({n}_{c}{{\overrightarrow{{\varvec{F}}}}_{{\varvec{i}}{\varvec{t}}}}^{{\varvec{c}}-{\varvec{M}}}\) (where \({n}_{c}\) is the cell packing density) drives cell wetting or de-wetting depending on the inter-relation between tissue and matrix surface tensions accompanied by the interfacial tension between them expressed in the form of the cell spreading factor (Pajic-Lijakovic et al. 2023a).

While the Marangoni force of cells \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{M}}}}^{{\varvec{c}}}\) and interfacial tension force \({n}_{c}{{\overrightarrow{{\varvec{F}}}}_{{\varvec{i}}{\varvec{t}}}}^{{\varvec{c}}-{\varvec{M}}}\) stimulate cell movement, the viscoelastic force of cells \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{v}}{\varvec{e}}}}^{c}\) acts to reduce cell movement through the cell residual stress accumulation (Pajic-Lijakovic and Milivojevic 2020). Induced decrease in cell velocity results in a decrease in the cell residual stress which stimulates cell movement again. This force, which depends on the viscoelasticity of the cell cluster, is responsible for oscillatory wetting and de-wetting.

Besides the interfacial tension force, the gravitational force \({\overrightarrow{{\varvec{F}}}}_{{\varvec{g}}}\), if it applies, drives wetting of the 3D cell cluster. This force can be significant in the case of larger cell spheroids (Pajic-Lijakovic and Milivojevic 2023a).

The surface and volumetric structural changes caused by cell movement induces generation of the matrix surface force \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{S}}{\varvec{T}}{\varvec{F}}}}^{{\varvec{M}}}\) and the viscoelastic force of the matrix \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{v}}{\varvec{e}}}}^{M}\), respectively which are responsible for the directional cell movement. While the matrix surface force is related to the matrix surface tension gradient, the viscoelastic force for the matrix is related to the gradient of the matrix residual stress and on that basis to the establishment of the matrix stiffness gradient. The force \({{\overrightarrow{{\varvec{F}}}}_{{\varvec{S}}{\varvec{T}}{\varvec{F}}}}^{{\varvec{M}}}\) causes movement of disconnected collagen fibers from the region of lower matrix surface tension to the region of higher matrix surface tension by natural convection. This movement of the fibers has a feedback on cell cluster movement itself. Both forces should be included in the directional movement of cell clusters on the collagen I gel (Clark et al. 2022). In the case of some other protein matrices, such as a fibrinogen matrix, directional cell movement can be induced only by the matrix stiffness gradient, while the gradient of the matrix surface tension cannot be established by cell tractions. This is in accordance with fact that the fibrinogen surface tension is not sensitive to changes in the protein concentration (Gudapati et al. 2020).

Traction force \({\rho }_{c-M}{{\overrightarrow{{\varvec{F}}}}_{{\varvec{t}}{\varvec{r}}}}^{c-M}\) restricts cell movement. The phenomenon is pronounced for higher density of FAs and higher strength of single FAs (Fuhrmann et al. 2017).

The force balance for movement of the cell cluster on collagen I gel can be expressed by the modified model proposed by Pajic-Lijakovic and Milivojevic (2023a) as:

$${{\langle m\rangle }_{c}n}_{c}\left(\boldsymbol{ }\mathfrak{R},\tau \right)\frac{D{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\left(\boldsymbol{ }\mathfrak{R},\tau \right)}{D\tau }={{\overrightarrow{{\varvec{F}}}}_{{\varvec{m}}{\varvec{i}}{\varvec{x}}}}^{{\varvec{c}}}+{{\overrightarrow{{\varvec{F}}}}_{{\varvec{M}}}}^{{\varvec{c}}-{\varvec{M}}}+{{\overrightarrow{{\varvec{F}}}}_{{\varvec{S}}{\varvec{T}}{\varvec{F}}}}^{{\varvec{M}}}+{n}_{c}{{\overrightarrow{{\varvec{F}}}}_{{\varvec{i}}{\varvec{t}}}}^{{\varvec{c}}-{\varvec{M}}}+{\overrightarrow{{\varvec{F}}}}_{{\varvec{g}}}-{{\overrightarrow{{\varvec{F}}}}_{{\varvec{T}}{\varvec{v}}{\varvec{e}}}}^{{\varvec{c}}-{\varvec{M}}}-{\rho }_{c-M}{{\overrightarrow{{\varvec{F}}}}_{{\varvec{t}}{\varvec{r}}}}^{c-M}$$
(3)

where \(\mathfrak{R}=\mathfrak{R}\left(x,y,z\right)\) represents the coordinate of cells within the cell-substrate biointerface, \({n}_{c}\) is the packing density of cells, \({\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\left(\boldsymbol{ }\mathfrak{R},\tau \right)\) is cell velocity equal to \({\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}={{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{{\varvec{C}}{\varvec{M}}}+{{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{\boldsymbol{^{\prime}}}\), \({{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{{\varvec{C}}{\varvec{M}}}\) is the velocity of the cluster center of mass, \({{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{\boldsymbol{^{\prime}}}\) is the velocity of cells within the cluster which depends on cell movement within the cluster and cell cluster wetting/de-wetting, \({\langle m\rangle }_{c}\) is the average mass of a single cell, \(\tau \) is the time scale of hours, and \(\frac{D{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}{D\tau }=\frac{\partial {\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}{\partial \tau }+({\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\cdot \overrightarrow{\nabla }){\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\) is the material derivative (Bird et al. 1960).

The mass balance

It is necessary to formulate the mass balance for cells and the mass balance for collagen matrix under the cell cluster in the form of a system of modeling equations. The mass balance of cells accounts for several contributions such as: convective or conductive flux, the Marangoni fluxes, and various taxis fluxes responsible for the directional movement of the cell cluster. When cell velocity \({\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\) is higher than diffusional cell velocity expressed as: \({{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{{\varvec{d}}}={D}_{\mathrm{eff}}\frac{1}{{L}_{\mathrm{cmax}}}\) (where \({D}_{\mathrm{eff}}\) is the effective cell diffusion coefficient and \({L}_{\mathrm{cmax}}\) is the cell persistence length), cell migration occurs via a convective mechanism (Pajic-Lijakovic and Milivojevic 2021). While the cell rearrangement near jamming corresponds to a conductive mechanism (Nnetu et al. 2013), the convective mechanism corresponds to cell movement during: (1) free expansion of cell monolayers (Nnetu et al. 2012; Serra-Picamal et al. 2012) and (2) rearrangement of confluent cell monolayers (Notbohm et al. 2016). The effective diffusion coefficients are in the range of \(\sim 0.40 \frac{{\, \upmu {\rm m}}^{2}}{\rm min}\) – \(0.10 \frac{{\, \upmu {\rm m}}^{2}}{\rm min}\) for the cell packing density of MDCK cells in the range of \(\sim 1.40 \times {10}^{5}\) to \(\sim 2.63 \times {10}^{5} \frac{\mathrm{cells}}{{\mathrm{\rm cm}}^{2}}\), respectively (Angelini et al. 2011). The maximum correlation length for 2D collective cell migration is \({L}_{\rm max}\sim 150 \, \upmu {\rm m}\) (Petrolli et al. 2021). The corresponding diffusion cell velocity is in the range of \({{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{cd}=0.005-0.010 \frac{\, \upmu {\rm m}}{\rm min}\) (Pajic-Lijakovic and Milivojevic 2021). This diffusion velocity has been measured within cellular systems near jamming (Nnetu et al. 2013). Consequently, the movement of a cell cluster on a collagen I matrix satisfies the condition that \({\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}>{{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}}^{{\varvec{d}}}\) and can be described by the convective flux expressed as: \({\overrightarrow{{\varvec{J}}}}_{conv}={n}_{c}{\overrightarrow{{\varvec{v}}}}_{{\varvec{c}}}\) (Murray et al. 1988).

While the convective cell flux describes movement of the whole cluster, the Marangoni flux induces two contributions: (1) the cell movement within the cluster guided by the cell surface tension gradient \({\overrightarrow{\nabla }}_{s}{\gamma }_{c}\) which is formulated here and (2) cell cluster wetting/de-wetting guided by the difference between cell surface tension and cell–matrix interfacial tension expressed as \({\overrightarrow{\nabla }}_{s}({\gamma }_{c}-{\gamma }_{\rm cm})\) which was formulated by Pajic-Lijakovic and Milivojevic (2023a). The tissue surface tension gradient guides cell movement within the cluster from the region of lower tissue surface tension established within the cluster interior to the region of larger cell surface tension established within the cluster peripheral region. The gradient \({\overrightarrow{\nabla }}_{s}({\gamma }_{\rm cm}-{\gamma }_{c})\) guides cell cluster: (1) wetting for the condition that \({\gamma }_{c}<{\gamma }_{\rm cm}\) and (2) de-wetting for the condition that \({\gamma }_{c}>{\gamma }_{\rm cm}\) (Pajic-Lijakovic and Milivojevic 2023a). The resulted Marangoni flux is formulated here as: \({\overrightarrow{{\varvec{J}}}}_{{\varvec{M}}}={k}_{M1}{n}_{c}\left({\overrightarrow{\nabla }}_{s}{\gamma }_{c}\right)+{k}_{M2}{n}_{c}{\overrightarrow{\nabla }}_{s}({\gamma }_{c}-{\gamma }_{\rm cm})\) (where \({k}_{M1}\) is the model parameter which quantifies the mobility of cells within the cluster caused by the gradient \({\overrightarrow{\nabla }}_{s}{\gamma }_{c}\) and \({k}_{M2}\) is the model parameter which quantifies the mobility of cells during wetting/de-wetting caused by the gradient \({\overrightarrow{\nabla }}_{s}({\gamma }_{c}-{\gamma }_{\rm cm})\)).

In the case that only surface and volumetric structural changes of matrix guide directional cell migration, without chemical and electrical stimuli, two fluxes should be included. One of them is the durotaxis flux which describe directional cell movement by following the matrix stiffness gradient. Accordingly, with the fact that the matrix stiffness gradient correlates with the gradient of the matrix residual stress, the durotaxis flux is expressed as: \({\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}={k}_{d}{n}_{c}\Delta {V}_{m}\left|\overrightarrow{\nabla }{\widetilde{{\varvec{\sigma}}}}_{{\varvec{M}}{\varvec{r}}}\right|\) (where \({k}_{d}\) is the model parameter which represents a measure of the mobility of collagen fibers within the gel induced by cell tractions and \(\Delta {V}_{m}\) is the volume of a matrix part) (Pajic-Lijakovic and Milivojevic 2023a). The stiffness gradient of the matrix can be induced by cells themselves during their movement.

The other flux (so called ‘’surfo-taxis’’ flux), formulated here, describes directional cell movement by following the gradient of matrix surface tension and can be expressed as: \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}={k}_{ST}{n}_{c}({{\overrightarrow{\nabla }}_{s}\gamma }_{M}\left({C}_{col}\right))\) (where \({k}_{ST}\) is the model parameter which represents a measure of collagen-cell surface interactions which influence cell movement and \({C}_{col}\) is the concentration of the collagen fibers under the cell cluster).

The corresponding mass balance can be expressed by a modified model proposed by Pajic-Lijakovic and Milivojevic (2023a, b) as:

$$\frac{\partial {n}_{c}(\mathfrak{R},\tau )}{\partial \tau }=-\overrightarrow{\nabla }\cdot \left({\overrightarrow{{\varvec{J}}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{v}}}+{\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}+{\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}+{\overrightarrow{{\varvec{J}}}}_{{\varvec{M}}}\right)$$
(4)

where \({\overrightarrow{{\varvec{J}}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{v}}}\) is the convective flux, \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\) is the surfo-taxis flux, \({\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\) is the durotaxis flux, and \({\overrightarrow{{\varvec{J}}}}_{{\varvec{M}}}\) is the Marangoni flux. When the directional cell movement is considered based on the proposed fluxes \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\) and \({\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\), four cases can be distinguished such as: (1) \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\ll {\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\), (2) \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\gg {\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\), (3) \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\sim {\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\) and both fluxes are oriented in the same direction, and (4) \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\sim {\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\) and fluxes are oriented in the opposite directions. Which case exists in some given experiment depends on cell type and physical properties of the matrix such as the filament rigidity and the range of inter- and intra- filament interactions. The fourth case \({\overrightarrow{{\varvec{J}}}}_{{\varvec{S}}{\varvec{T}}}\sim {\overrightarrow{{\varvec{J}}}}_{{\varvec{d}}}\) could be related to negative durotaxis. However, additional experiments are needed in order to confirm this claim.

The mass balance of the disconnected collagen fibers under the cell cluster could be expressed in the form of Marangoni flux as:

$$\frac{\partial {C}_{col}(\mathfrak{R},\tau )}{\partial \tau }=-\overrightarrow{\nabla }\cdot {\overrightarrow{{\varvec{J}}}}_{{\varvec{c}}{\varvec{o}}{\varvec{l}}\boldsymbol{ }{\varvec{M}}}$$
(5)

where \({\overrightarrow{{\varvec{J}}}}_{{\varvec{c}}{\varvec{o}}{\varvec{l}}\boldsymbol{ }{\varvec{M}}}\) is the Marangoni flux for collagen fibers equal to: \({{\overrightarrow{J}}_{col M}=k}_{col} {n}_{c}({{\overrightarrow{\nabla }}_{s}\gamma }_{M}({C}_{col}))\) and \({k}_{col}\) is the the model parameter which represents a measure of collagen-cell surface interactions capable of inducing local disintegration of the matrix and the rearrangement of collagen fibers. Model equations 3–5 should be solved simultaneously. The collagen concentration undergoes long-term changes and could reach as far as the equilibrium value when \({{\overrightarrow{\nabla }}_{s}\gamma }_{M}\to 0\) which is possible only for higher mobility of collagen fibers. Clark et al. (2022) pointed to chain mobility as the key factor for the establishment of movement persistence of a cell cluster.

Conclusion

Over the last few years it has become clear that movement of cell collectives along substrate matrix during morphogenesis, tissue regeneration and cancer invasion involves several inter-connected migration modes such as cell movement within the migrating clusters, the cluster wetting/de-wetting, and directional cell movement. The matrix stiffness gradient has been recognized as a main physical property of the matrix gel responsible for cell wetting/de-wetting and directional cell movement. Cell movement within the clusters has been discussed in the context of biochemical mechanisms related to cell signaling, while physical mechanism(s) which also could guide this cell movement have not been identified yet. The main goal of this theoretical consideration is to point out the roles of various physical parameters such as: (1) the tissue and matrix surface tensions, (2) interfacial tensions between them, (3) gradients of surface and interfacial tensions, and (4) accumulation of the cell and matrix residual stresses in the establishment of various migration modes. These parameters represent a product of dilational and volumetric viscoelasticity of both, cell cluster and the hydrogel matrix which are simultaneously changing caused by cell–matrix interactions along the biointerface. Cumulative effects of these interactions stimulate internal cellular mechanisms such as cell signaling and gene expression and also influence the physical parameters which have a feedback on single cell state. This complex cause-effect relationship has been discussed based on a biophysical model which includes cell force and mass balances formulated at a supracellular level. Th following conclusions can be extracted:

  • The cell surface tension gradient established within the migrating cell clusters guides cell movement from a region of lower cell surface tension (characteristic for the cluster central region) to a region of higher cell surface tension (characteristic for the cluster peripheral region). This phenomenon represents a part of the Marangoni effect which also exists in various soft matter systems.

  • Cell cluster wetting/de-wetting depends on interplay between physical parameters such as tissue and matrix surface tensions accompanied by the interfacial tension between them through the cell spreading factor. The gradient of the difference between cell surface tension and cell—matrix interfacial tension is included in the mixing force (the cell force balance) and in the Marangoni flux (the cell mass balance).

  • Surface and volumetric structural changes of matrix, caused by movement of cell collectives, are responsible for directional cell migration. The volumetric structural changes lead to the inhomogeneous accumulation of the matrix residual stress and on that basis result in the establishment of the matrix stiffness gradient, while the surface structural changes can induce the generation of the matrix surface tension gradient. Both gradients can appear as a product of cell movement depending on the physical properties of the matrix such as: the rigidity of filaments and the range of inter- and intra-filaments interactions.

Additional experiments are necessary to correlate: (1) the matrix surface tension gradient with the cell persistence length, (2) cell–matrix interfacial tension with the tissue surface tension, (3) cell–matrix interfacial tension with the cell normal residual stress on the one hand and with the matrix residual stress on the other.