Abstract
The synchronous model of concurrent computation (SMoCC) is well established for programming languages in the domain of safety-critical reactive and embedded systems. Translated into mainstream C/Java programming, the SMoCC corresponds to a cyclic execution model in which concurrent threads are synchronised on a logical clock that cuts system computation into a sequence of macro-steps. A causality analysis verifies the existence of a schedule on memory accesses to ensure each macro-step is deadlock-free and determinate. We introduce an abstract semantic domain \(I(\mathbb {D}, \mathbb {P})\) and an associated denotational fixed-point semantics for reasoning about concurrent and sequential variable accesses within a synchronous cycle-based model of computation. We use this domain for a new and extended behavioural definition of Berry’s causality analysis in terms of approximation intervals. The domain \(I(\mathbb {D}, \mathbb {P})\) extends the domain \(I(\mathbb {D})\) from our previous work and fixes a mistake in the treatment of initialisations. Based on this fixed-point semantics we propose the notion of Input Berry-constructiveness (IBC) for synchronous programs. This new IBC class lies properly between strong (SBC) and normal Berry-constructiveness (BC) defined in previous work. SBC and BC are two ways to interpret the standard constructive semantics of synchronous programming, as exemplified by imperative SMoCC languages such as Esterel or Quartz. SBC is often too restrictive as it requires all variables to be initialised by the program. BC can be too permissive because it initialises all variables to a fixed value, by default. Where the initialisation happens through the memory, e.g., when carrying values from one synchronous tick to the next, then IBC is more appropriate. IBC links two levels of execution, the macro-step level and the micro-step level. We prove that the denotational fixed-point analysis for IBC, and hence Berry’s causality analysis, is sound with respect to operational micro-level scheduling. The denotational model can thus be viewed as a compositional presentation of a synchronous scheduling strategy that ensures reactiveness and determinacy for imperative concurrent programming.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation
Arguably the mathematically most satisfactory way to define a compositional programming language semantics is the denotational approach, which defines the semantics of a program through a system of structurally-recursive equations involving continuous functions on abstract semantic domains. Compositionality is built into a denotational model at the outset, in the sense that the functional definition of the fixed-point semantics of a composite program entirely depends on the abstract functional denotation of its components rather than their syntax. As a consequence, algebraic axiomatisations for program verification and program transformations can be derived from the properties of these functions in the abstract domains.
Unfortunately, denotational fixed-point models for computationally rich programming languages are notoriously hard to come by. A famous case in point is the long search for a fully-abstract denotational model of the functional language PCF [1, 13, 44]. It is the tight interaction of program components, in particular for non-deterministic concurrent systems, that makes it hard to decouple a composite program into a system of continuous functions in a simple way. It is often easier to understand the interaction behaviour of a concurrent program operationally in terms of inductive relations rather than recursive functions. Hence, many concurrent programming models or process algebras, for that matter, are based on Plotkin-style structural operational semantics. Such models are then turned into an algebra through notions of behavioural congruences and pre-congruences. Thereby abstracting from behaviourally unobservable information carried by the operational rule system one achieves the desired algebraic compositionality, see, e.g., [10, 65]. However, denotational semantics generated in this fashion are essentially syntactic. Recursion is not explained by denotational fixed-points but by syntactic unfolding.
One can do better if the inductive operational rules satisfy certain structural constraints, such as the GSOS or tyft/tyxt format [33]. In these cases, general techniques are known to derive independent denotational semantics based on the approximation of a process by finite synchronization trees, see e.g. [2, 30, 45] for full-abstraction results for bisimulation-style semantics. Still, these approximation-based denotational models have their own problems. They are algebraically rather involved and depend on infinitary proof rules which fall outside the scope of normal (Horn-style) equational reasoning. One classical instance of this problem is the observation that, e.g., bisimulation equivalence for process algebras with the empty process \(0\), non-deterministic choice \(p + q\), action prefix \(a.\,p\) and recursion \(\mu x.\, p(x)\) does not admit a finitary denotational semantics based on complete partial orderings. Specifically, the Park induction principle, \(p(y) = y \Rightarrow \mu x.\, p(x) \le y\), expressing that \(\mu x.\,p(x)\) is the least fixed-point is inconsistent with monotonicity of the choice operator \(+\). It is unclear if bisimulation-style semantics can be finitely axiomatised in equational Horn logic, see e.g. [63]. Denotational fixed-point semantics with Park induction seem to exist only in special cases, such as acceptance testing, trace equivalence or simulation preorder [29, 40, 49].
While it is now clear that complex algebraic machinery is needed to reconcile genuinely independent denotational and operational semantics for general non-deterministic process calculi, attention should turn once again to more special concurrent programming models. An early and successful starting point is the data-flow semantics of Kahn networks [46], which is fully-abstract for coroutine-style operational execution [47]. Kahn process nodes are sequential and deterministic and thus fairly restricted in modelling distributed systems. Yet, as discovered by Kok [48], non-determinism can be added to the Kahn model without losing full-abstraction using (local) clocks for the synchronisation of streams. This remarkable result brings into view an important special class of concurrent programming languages where denotational and operational approaches may go well together, known as the synchronous programming paradigm [9, 35].
The Synchronous Model of Concurrent Computation (SMoCC) started in the 1980s with languages such as Statecharts [38, 69], Lustre [19, 36], Signal [34], Esterel [11, 14] and Argos [61, 62]. Developing concurrently with the emerging theory of process algebras, the SMoCC, from its beginning, has taken a practical programming perspective and targeted embedded and safety-critical systems in the automotive and avionics industries. The SMoCC languages have been very successful in these highly-demanding and complex domains. Part of this is due to their solid mathematical underpinning which inherits its robust logic from the design of digital synchronous circuits. Over the years, the quality-software assurance of the SMoCC paradigm has received attention in a wider range of applications. These include Stateflow [37], web-orchestration [15], and music accompaniment [7] to mention a few. The SMoCC approach also has spread into functional programming [60] and mainstream imperative languages like C [16, 51, 83] or Java [66].
The SMoCC paradigm is based on a globally synchronous, locally asynchronous model of concurrent computation,Footnote 1 which employs logical clocks to force asynchronous processes into a globally deterministic sequence of execution steps, called macro steps or logical instants. The SMoCC computations relate to classical automata in the sense that macro-steps correspond to automata transitions and configurations are discrete time points (automata states) on which system and environment can communicate (synchronise) with each other. At this level of modelling|under the Synchrony Hypothesis [9]—macro-steps appear as deterministic and functional input/output interactions. If this were all, synchronous programs could be analysed by the standard compositional techniques of the theory of synchronous automata, which fits both the denotational and the operational viewpoint equally well. Not much concurrency theory is needed for that.
However, there is a catch: The soundness of the automata model depends on the compiler verifying that the Synchrony Hypothesis is valid. Yet, the Synchrony Hypothesis is not compositional. The difficulty is that the SMoCC programs exhibit Mealy as opposed to Moore-style interaction. Since Mealy outputs depend instantaneously on the inputs and (in a typical SMoCC language) are also broadcast, the atomicity assumption creates a tangled causality cycle when the SMoCC automata are composed. Since each program acts as the environment of the other, the Synchrony Hypothesis expects each system to react faster than the other, and hence faster than itself! This is aggravated by the fact that in some SMoCC languages, such as Esterel or some version of Statecharts, the reaction of one component can depend on the absence of a reaction from another component. To resolve the paradoxes, i.e., to prevent deadlock and non-determinism, the synchronous interaction must satisfy stringent causality requirements. Consequently, causality analyses have been a key component in the SMoCC compilers. Typically, these analyses correspond to the derivation of clock schedules (“clock calculus”) for the activation of program statements [8, 20, 22, 78] or 3-valued circuit simulation (“ternary analysis”) [12, 27, 74]. Edwards [26] and Potop-Butucaru et al. [70] provide good overviews of compilation challenges and approaches for concurrent languages, including synchronous languages. In this article we focus on causality in control-flow oriented SMoCCs such as Esterel or Quartz rather than data-flow oriented SMoCCs such as Lustre or Signal.
The techniques for causality analysis range from checking simple static criteria on control-dependencies to full-fledged data-dependent control-flow analysis. Proving the soundness of causality analyses necessarily requires maintaining some form of refinement (“constructiveness” or “dependency”) information about a lower-level asynchronous micro-step semantics. The first to observe this were Huizing et al. [43] who showed that combining compositionality, causality and the Synchrony Hypothesis cannot be done within a single-levelled semantics (see also [24]). In other words, causality analysis establishes consistency of a synchronous macro-step with respect to an asynchronous micro-step execution model. This makes causality analyses and their soundness properties interesting from a concurrency theoretical point of view.
Different distributed execution platforms and memory models induce different degrees of uncontrollable non-determinism. They give thus rise to different notions of causality. A conservative, and thus robust, notion of causality among all the SMoCCs is the so-called constructive semantics of Esterel [11, 14] introduced by Berry in [12]. This is a pure macro-step semantics combining a structural operational semantics for macro-state transitions with a denotational fixed-point construction, also known as the “must-cannot” analysis, for computing causal reactions from every state. However, there do not seem to be soundness proofs for the causality analyses of Esterel relative to a micro-level scheduling in normal, i.e., unsynchronised memory.Footnote 2 The only available result on the lower-level operational soundness of the fixed-point construction is indirect, has never formally been proven and applies to the hardware translation given in [12]. At the hardware level it is known that constructiveness implies delay-insensitivity under non-inertial delays [58, 64, 76]. While this highlights the universal nature of the constructive semantics, it does not provide insights into the nature of constructiveness for software implementations of SMoCC languages. This question is now starting to be addressed in the literature. An interesting example is the more recent SMoCC language Quartz [72]. It has been given both macro-step operational semantics and a fixed-point semantics implementing an Esterel-style causality analysis [32, 72]. Talpin et al. [77] consider a combination of Signal and Quartz and prove that the constructive fixed-point semantics is sound for an operational micro-step semantics. In this article we proceed along similar ideas as [77] for Esterel-style imperative languages.
1.2 Contributions
In this article we prove the soundness of the denotational fixed point semantics for imperative SMoCC programs, commonly termed “constructive”, with respect to their micro-step operational behaviour when compiled into multi-threaded shared memory code. To the best of our knowledge this is the first result of its kind for Esterel-style imperative programming.
The recent constructive semantics that integrates Quartz and Signal [77] is based on a similar approach than the one proposed here in the sense that both are developed around similar mathematical structures, i.e., fixed-point on a lattice for representing signal statuses and Boolean values. The semantics framework of [77] unifies the behaviour of polychronous multi-clocked Signal networks and synchronous Quartz modules where synchronous Boolean variables are always present. In contrast, our approach significantly extends the standard 3-valued “must-cannot” semantics [12, 27, 74] with the effect that (i) it is able to handle explicit initialisation of signals, and (ii) it operates in a more structured domain of information intervals rather than flat ternary Kleene algebra. In the enriched domain we prove soundness of the fixed-point with respect to the micro-step operational execution. By “micro-step operational semantics” we mean a small-step semantics in which the reaction of a parallel composition for a single clock tick (rather than sequences of clocks) is (1) implemented by thread interleaving and (2) the execution does not use the must/cannot enriched statuses. For example, the SOS reaction rules for Quartz [32, 72] do not satisfy criterion (1). They give big-step semantics for full reaction instants. On the other hand, the operational semantics sketched by Berry [12], Chap. 4.3] or by Talpin et al. [77] do not satisfy criterion (2).
Our main Theorem 1 strengthens the results presented in [4], where a similar fixed-point semantics was introduced to prove that the sequentially constructive model of synchronous concurrent computation [85, 86] conservatively extends Berry’s notion of constructiveness for Esterel. Specifically, we extend the work of [4] in three ways: Firstly, we correct a mistake preventing the denotational semantics of [4] from detecting deadlocks that can arise from concurrent initialisations (see our Example 19). Secondly, the results presented here imply that the fixed-point analysis is not only sound for sequential constructiveness targeted in [4] but also for Esterel’s more restrictive operational model of causality, characterised by B-reactiveness (Definition 4) and SC-read-determinacy (Definition 5). The combination of these two properties is a proper strengthening of the notion of \(\varDelta _*\)-constructiveness in the sense of [4], which corresponds to the notion of sequential constructiveness introduced in [85]. Thirdly, we introduce a new definition of constructiveness, called IB-constructiveness (Definition 9), to permit implicit initialisations through memory. It is more generous than the notions of constructiveness considered in [4] where all variables must be reinitialised, by the program or the environment, at every macro step. In other words, compared to [4] our semantics guarantees a stronger form of operational robustness for a wider class of programs.
1.3 Overview
Section 2 gives an abstract account of the SMoCC principle for imperative programs based on the consolidated language model pSCL and the operational notion of free scheduling. It also offers the definitions of important terms that will be used in the following sections, particularly of B-Admissibility and SC-Admissibility, which are both scheduling protocols restricting the free scheduling with different degrees of strength. The related terms of B-Reactiveness and SC-Reactiveness are also defined as well as the notion of \(X\)-Determinacy, parametric in \(X\)-Admissibility and its special case \(X\)-read-determinacy.
Section 3 is dedicated to the definition of the abstract domains and environments on which our denotational fixed-point semantics is based. This includes the definition of the domain \(\mathbb {D} \), whose four elements represent possible signal statuses and comprise representations needed for the handling of explicit initialization of signals. The semantics operates on closed intervals over \(\mathbb {D} \) which represent predictions of variable statuses combined with a domain \(\mathbb {P} \) that is capturing initialization statuses, yielding \(I(\mathbb {D}, \mathbb {P})\) as working domain. Finally, the section introduces a domain \(I(\mathbb {C})\) of program completion statuses.
Section 4 is the core of the article, where we put the introduced technical apparatus to form our denotational fixed-point semantics for pSCL. The semantics induces three notions of constructiveness increasing in strength, Berry-constructive (BC), Input Berry-constructive (IBC) and Strong Berry constructive (SBC). This section finally contains our main Soundness Theorem 1 that states that IBC programs are B-reactive and SC-read-determinate.
Section 5 positions our work in reference to related work and Sect. 6 offers concluding remarks and mentions open problems.
2 Operational semantics of synchronous programs
2.1 Language model
For our elaborations, we employ a language that focuses on the micro-step computations of a system. This language, referred to as pSCL,Footnote 3 contains the necessary control structures for capturing multiple variable accesses as they occur inside macro-steps. pSCL abstracts syntactic and control particularities of existing synchronous languages not directly related to our analysis. This not only provides generality to the results but also avoids over-complicating our formal treatment. pSCL is pure in the sense that it manipulates Boolean variables from a finite set \( V \), which carry information over time by changing value in \({\mathbb B} = \{{0,1}\}\). A variable \(s \in V \) with value \(\gamma \in {\mathbb B} \) is denoted by \(s^\gamma \). Here, \(0,1\) are used to code, respectively, the logical statuses \( False \) (absent, initialised) and \( True \) (present, updated) of a synchronous signal. The syntax of pSCL is given by the following BNF of operators:

Since our syntax is abstract in the style of process algebras we also indicate the more concrete syntax as used in control-flow languages SCL [85] and Esterel on the right of each operator.
Intuitively, the empty statement \(\varepsilon \) indicates that a given program has been completed. That is, \(\varepsilon \) corresponds to the termination situation in which there are no further tasks to be performed in this or any subsequent macro-step. The pause control \(\pi \) forces a program to yield and wait for a global tick. This means that the execution cannot not proceed any further during the current macro-step but it will be resumed in the next. The reset (init)  and set (update) \({! \, \! s} \) constructs modify the value of \(s \in V \) to \(s^{0}\) or \(s^{1}\), respectively. The conditional control \(s \, \mathrel {?} \, P \mathrel {:} Q \) has the usual interpretation in the sense that depending on the status \(1\) or \(0\) of the guard variable \(s\) either \(P\) or \(Q\) are executed accordingly. Parallel composition \(P \!\mathrel {\mid \!\mid }\! Q \) forks \(P\) and \(Q\), so the statements of both are executed concurrently. This composition terminates (joins) when both components terminate, i.e., both are completed in the sense of \(\varepsilon \), not waiting in a pause \(\pi \). When just one of the two components in \(P \!\mathrel {\mid \!\mid }\! Q \) terminates while the other pauses, then \(P \!\mathrel {\mid \!\mid }\! Q \) pauses. Otherwise, if one component terminates and the other does not pause or terminate then the computation continues from the statements of the other component until it terminates, too, or pauses. In the sequential composition \(P\mathrel {;}Q \), the statements of \(P\) are first completely executed. Then, the control is transferred to \(Q\) which, in turn, determines the behaviour of the composition thereafter. The operator \(\mathop { rec } p.\, P\) introduces a recursion label or process name
\(p\) that can be used in its body \(P\) to reiterate the process using \(p\) as a jump label. The semantics is so that \(\mathop { rec } p.\, P\) is equivalent to its unfolding \(P\{\mathop { rec } p.\, P{\!/\!}p\}\), where \(P\{Q{\!/\!}p\}\) denotes syntactic substitution. As done in process algebras we can use \(\mathop { rec } \) to fold up recursive equation systems modelling arbitrary forward and backward jumps in control-flow graphs.
and set (update) \({! \, \! s} \) constructs modify the value of \(s \in V \) to \(s^{0}\) or \(s^{1}\), respectively. The conditional control \(s \, \mathrel {?} \, P \mathrel {:} Q \) has the usual interpretation in the sense that depending on the status \(1\) or \(0\) of the guard variable \(s\) either \(P\) or \(Q\) are executed accordingly. Parallel composition \(P \!\mathrel {\mid \!\mid }\! Q \) forks \(P\) and \(Q\), so the statements of both are executed concurrently. This composition terminates (joins) when both components terminate, i.e., both are completed in the sense of \(\varepsilon \), not waiting in a pause \(\pi \). When just one of the two components in \(P \!\mathrel {\mid \!\mid }\! Q \) terminates while the other pauses, then \(P \!\mathrel {\mid \!\mid }\! Q \) pauses. Otherwise, if one component terminates and the other does not pause or terminate then the computation continues from the statements of the other component until it terminates, too, or pauses. In the sequential composition \(P\mathrel {;}Q \), the statements of \(P\) are first completely executed. Then, the control is transferred to \(Q\) which, in turn, determines the behaviour of the composition thereafter. The operator \(\mathop { rec } p.\, P\) introduces a recursion label or process name
\(p\) that can be used in its body \(P\) to reiterate the process using \(p\) as a jump label. The semantics is so that \(\mathop { rec } p.\, P\) is equivalent to its unfolding \(P\{\mathop { rec } p.\, P{\!/\!}p\}\), where \(P\{Q{\!/\!}p\}\) denotes syntactic substitution. As done in process algebras we can use \(\mathop { rec } \) to fold up recursive equation systems modelling arbitrary forward and backward jumps in control-flow graphs.
By default, a conditional binds tighter than sequential composition, which in turn binds tighter than parallel composition; the loop prefix \(\mathop { rec } p\) has weakest binding power. As usual, brackets can be used for grouping statements to override the default associations. For instance, in the expression \(\mathop { rec } p.\, x \, \mathrel {?} \, \varepsilon \mathrel {:} p; {! \, \! y} \) the scope of the loop extends to the end of the expression as in \(\mathop { rec } p.\, ((x \, \mathrel {?} \, \varepsilon \mathrel {:} p); {! \, \! y})\) whereas \((\mathop { rec } p.\, x \, \mathrel {?} \, \varepsilon \mathrel {:} p); {! \, \! y} \) limits the scope and leave \({! \, \! y} \) outside the loop. Similarly, brackets are needed, as in \(\mathop { rec } p.\, x \, \mathrel {?} \, \varepsilon \mathrel {:} (p; {! \, \! y}) \), to include \({! \, \! y} \) into the else branch of the conditional.
Recursion without restrictions is too powerful for our purposes. We impose the following three well-formedness conditions on pSCL expressions, which suffices to model the static structure of many standard synchronous programming languages:
-
No jumps out of an enclosing parallel composition. This does not limit the power of the language, as for example aborts, traps and general gotos as proposed for/provided by Esterel or SHIM [79, 80] can still be implemented by “chaining” jumps up the thread hierarchy, but has the advantage of a simple parallel/sequential control flow structure. Formally, in every loop \(\mathop { rec } p.\, P\) the label \(p\) must not lie within the scope of a parallel operator \(\mathrel {\Vert }\). For instance, \(\mathop { rec } q.\; P \!\mathrel {\mid \!\mid }\! q \) is not permitted while \(P \!\mathrel {\mid \!\mid }\! (\mathop { rec } q.\, q) \) is accepted. This makes sure that the static control structure of a program is a series-parallel graph (see [25]) and the number of concurrently running threads is statically bounded by this graph. In particular any given static thread cannot be concurrently instantiated more than once; A fresh thread instance only runs sequentially after all previous instances of the same static thread.
-
Every loop \(\mathop { rec } p.\, P\) is clock guarded, i.e., every free occurrence of label \(p\) in \(P\) lies within the sequential scope of a pause \(\pi \). For instance, \(\mathop { rec } p.\, \pi \mathrel {;} p \) is clock guarded whereas \(\mathop { rec } p.\, p\) is not. Clock guarded processes are guaranteed to generate finite, terminating macro-steps. This corresponds to the standard requirement in Esterel to not have instantaneous loops.
-
No loop label occurs both free and bound in an expression, where the notion of a free and bound label is as usual. This a standard restriction in process calculi, see e.g., [10]. For instance, \(\mathop { rec } p.\; \mathop { rec } q.\; p \mathrel {;} q \mathrel {;} q\) is not allowed, whereas \(\mathop { rec } p.\; (\mathop { rec } r.\; p \mathrel {;} r) \mathrel {;} q\) is accepted. This restriction avoids capturing of any free variable of \(\mathop { rec } p. \, P\) by a loop recursion in \(P\) in the syntactic unfolding \(P\{ \mathop { rec } p.\, P\!{/}\!p\}\).
Henceforth, programs are assumed to be expressions satisfying these conditions. Programs without the \(\mathop { rec } \) construct will be called finite programs, or fprogs for short.
The imperative statements of a pSCL program describe discrete changes of state at the level of micro-steps. The computation of a concurrent program gets described by a collection of threads (concurrent program fragments), each one performing micro-steps independently and interacting with each other through shared memory. Generally, a computation depends on a distinction of micro-steps happening sequentially after each other or concurrently. The sequential order is instantiated from sequential composition \(P;Q\). Parallel composition \(P \mathrel {\Vert }Q\) is the construct that provides the thread topology for achieving concurrency. The resulting tree-like structure of the parallel construct determines statically which statements belong to which individual thread. At run-time, these static threads get instantiated and executed. Every one of such instantiations must have its own local control-state and, therefore, is considered a process. From this perspective, the configuration capturing the global state of a concurrent program at any given moment is determined by the local state of all its processes together with a shared global memory.
As in synchronous programming, a micro-step can take place when at least one process is active, i.e., when it is able to execute a statement other than \(\pi \). In this manner, a micro-step produces a change in the configuration resulting from a process modifying its own local state and possibly the global memory. Active processes induce micro-steps until every process either terminates or reaches a pause, thereby completing a macro-step. Then, from the resulting configuration, the environment can provide a fresh stimulus for continuing the computation with a new macro-step.
The interaction between processes at the micro-step level must be controlled according to some pre-established rules of admissible scheduling in order to enforce the Synchrony Hypothesis abstraction. For instance, suppose in \(P \mathrel {\Vert }Q\), program \(P\) performs a write to a variable \(x\) and \(Q\) concurrently reads \(x\). Then, under the Synchrony Hypothesis the producer \(P\) (system) is faster than the consumer (environment) \(Q\), or, equivalently, \(Q\) waits for \(P\). A canonical notion of admissibility that enforces such causalities is the “init;update;read” protocol [85], which is referred to as the “iur” protocol in the following. It decrees that all initialisations  must take place before any update \({! \, \! s} \) which in turn must both be scheduled before any read, i.e., any conditional test \(s \, \mathrel {?} \, P \mathrel {:} Q \) on \(s\).
must take place before any update \({! \, \! s} \) which in turn must both be scheduled before any read, i.e., any conditional test \(s \, \mathrel {?} \, P \mathrel {:} Q \) on \(s\).
In the next section we define the notion of a free unconstrained execution for pSCL programs and then in Sect. 2.3 introduce the restriction imposed by the iur protocol. This defines the operational semantics of the class of causal pSCL programs for which we shall later, in Sects. 3 and 4, provide a suitable notion of constructive macro-step responses in terms of a denotational fixed-point analysis.
2.2 Micro-step free scheduling
In our operational model, a process \(T\) is defined by its own current control-state, or state for short, which contains: \((i)\) information about the precise position of \(T\) in the tree structure of forked processes and \((ii)\) control-flow references to specific parts of the code. Formally, \(T\) is given by a triplet \({\langle id, prog, next \rangle }\) where we write \(T.id\), \(T.prog\) or \(T.next\) for referring to the individual elements of \(T\) which are called, respectively, identifier, current-program and next-control. Concretely,
-
\(T.id\) is a non-empty sequence containing an alternation of natural numbers and the symbols \(l,r\) that always starts and ends with a number. For instance, \(0 . l . 5\) and \(1 . r . 3 . l . 7\) are identifiers but \(0 . r\) and \(r . 1 . r . 2\) are not. Meta-variables to range over identifiers are \(\iota \), \(\kappa \), possibly with indices.
-
\(T.prog\) is the pSCL expression that is currently scheduled to generate \(T\)’s micro-steps. Since these are pSCL expressions we use the meta-variables \(P\), \(Q\), etc., to range over these.
-
\(T.next\) is a list of future program fragments that can be converted into micro-steps sequentially after \(T.prog\) has terminated. This list is extended when a sequential composition is executed in \(T.prog\). We use the meta-variable \( Ks \) to range over next-controls.
The identifier \(T.id\) localises process \(T\) uniquely in the sequential-parallel control flow of the program context which has generated \(T\). The intuition is that the numbers in the identifier are counting the sequential steps taken by the program context. The symbols (\(l\) for left and \(r\) for right) recall the path of previous parallel forks from which the process has emerged. Where we are only interested in the depth of a process in the thread hierarchy, we use a thread projection function \( th (\iota ) \in \{l, r\}^*\) which drops from \(\iota \) all sequencing numbers. The sequence \( th (T. id )\) can be interpreted as the static thread identifier of process \(T\).
Example 1
The serial-parallel graph in Fig. 1 gives an example of the thread identifiers generated by the fprog \(P_{\epsilon } = a_{0} \mathrel {;} (P_{l} \mathrel {\Vert }P_{r}) \mathrel {;} a_{2}\) with
where all \(a_{\iota }\) are primitive statements  . The subscripts \(\iota \) indicate the thread identifier associated with the statement \(a_{\iota }\) when it is executed. In Fig. 1 these primitive statements are shown as rectangular boxes with their identifier written inside it. Notice how the letters \(l\) and \(r\) (displayed in red colour) identify the static thread in which the statement is executed. For instance the statement \(a_{0.r.2.l.1}\) is executed in the static thread \(r.l\), which is the left child of the right child of the main thread. This is the projection \( th (0 . r . 2 . l . 1) = r . l\). The first top level statement \(a_0\) is in the root thread \(\varepsilon \), i.e., \( th (0) = \varepsilon \), where \(\varepsilon \) denotes the empty sequence. The hierarchical thread structure is visualised by the dotted gray background boxes. \(\square \)
. The subscripts \(\iota \) indicate the thread identifier associated with the statement \(a_{\iota }\) when it is executed. In Fig. 1 these primitive statements are shown as rectangular boxes with their identifier written inside it. Notice how the letters \(l\) and \(r\) (displayed in red colour) identify the static thread in which the statement is executed. For instance the statement \(a_{0.r.2.l.1}\) is executed in the static thread \(r.l\), which is the left child of the right child of the main thread. This is the projection \( th (0 . r . 2 . l . 1) = r . l\). The first top level statement \(a_0\) is in the root thread \(\varepsilon \), i.e., \( th (0) = \varepsilon \), where \(\varepsilon \) denotes the empty sequence. The hierarchical thread structure is visualised by the dotted gray background boxes. \(\square \)
Definition 1
To compare the sequential depth of processes, we use the (partial) lexicographic order \(\prec \) on path identifiers. The natural numbers are ordered in the usual way, i.e., \(0 < 1 < 2 \dots \) while the symbols \(l,r\) are considered incomparable. Thus, for identifiers \(\iota = d_1 \dots d_n\) and \(\iota ' = d'_1 \dots d'_m\) we have that \(\iota \;\prec \; \iota '\) iff \(\iota \) is a proper prefix of \(\iota '\) or \(\iota \) is lexically below \(\iota '\). Formally, \(\iota \;\prec \; \iota '\) iff
-
\(n < m\) and \(\forall 1 \le j \le n. \ d_j = d'_j\), or
-
there is \(0 \le i < n\) such that \(d_{i+1} \;<\; d'_{i+1}\) and \(\forall 1 \le j \le i\) we have \(d_j = d_j'\).
We write \(\preceq \) for the reflexive closure of \(\prec \), i.e., \(\iota \preceq \iota '\) iff \(\iota \prec \iota '\) or \(\iota = \iota '\). \(\square \)
The order \(\preceq \) contains both the thread hierarchy and sequencing. If \(\iota \preceq \iota '\) then \(\iota '\) is a sequential successor of \(\iota \) in program order. If \(\iota \not \preceq \iota '\) and also \(\iota ' \not \preceq \iota \) then both \(\iota \) and \(\iota '\) are concurrent. Note that there is no relationship between \(\iota \prec \iota '\) and the prefix order on \( th (\iota )\) and \( th (\iota ')\). The sequential successor \(\iota '\), in general, can be both a descendant or an ancestor of \(\iota \) in the thread hierarchy.
Example 2
For instance, in our example of Fig. 1, we have \(1 . r . 2 \prec 1 . r . 2 . l . 1 \prec 1 . r . 3\) following the sequential program order but \(1 . l . 0 \not \prec 1 . r . 2. l .1\) and \(1 . r . 2. l .1 \not \prec 1 . l . 0\), because the labels \(l\) and \(r\) are incomparable. The micro-steps with thread identifiers \(1 . l . 0\) and \(1 . r . 2. l .1\) are not sequentially ordered. They are executed in the concurrent threads \( th (1 . r . 2 . l . 1) = r . l\) and \( th (1 . l . 0) = l\). Observe that \(1 . r . 2 . l . 1 \preceq 1 . r . 3\) but \( th (1 . r . 2 . l . 1) = r . l\) is not a prefix of \(r = th (1 . r . 3)\). In the other direction, the fork node \(1 . r . 2\) is a sequential predecessor of \(1 . r . 2 . l . 1\) and \(r = th (1 . r . 2)\) is an ancestor of \(r . l = th (1 . r . 2 . l . 1)\). \(\square \)
Formally, the global memory is a Boolean valuation function \(\rho : V \rightarrow {\mathbb B} \) which indicates the current value for each variable \(s \in V \). Any micro-step of a process \(T\) (relative to a given memory \(\rho \)) produces a new memory \(\rho '\) and a set of successor processes \(T'\). Thus, any micro-step is completely specified by the memory function \(\rho ' := mem (T, \rho )\) and the succession function \(T' := nxt (T, \rho )\). For any \(s \in V \), the memory function is defined by:

This says that for a given variable \(s \in V \), if \(T\) performs a reset  then \(s\) is changed to \(0\), if \(T\) performs a set \({! \, \! s}\) then \(s\) is changed to \(1\), otherwise, \(s\) keeps its value from the previous memory. We define the succession \( nxt (T, \rho )\) by case analysis on \(T. prog \), where the sequential enumeration for identifier \(\iota \) is computed by an increment function \( inc (\iota )\) which increases by \(1\) the last number of the identifier \(\iota \), e.g., \( inc (1 . r . 6) = 1 . r . 7\):
then \(s\) is changed to \(0\), if \(T\) performs a set \({! \, \! s}\) then \(s\) is changed to \(1\), otherwise, \(s\) keeps its value from the previous memory. We define the succession \( nxt (T, \rho )\) by case analysis on \(T. prog \), where the sequential enumeration for identifier \(\iota \) is computed by an increment function \( inc (\iota )\) which increases by \(1\) the last number of the identifier \(\iota \), e.g., \( inc (1 . r . 6) = 1 . r . 7\):



Let us explain the different cases one by one:
-
(1)
If the program \(T. prog \) is one of the basic statements (i.e., empty \(\varepsilon \), set \({! \, \! s} \) or reset
 ) and the list of continuation processes in the next-control \(T. next \) is empty \([\,]\), then the process (after execution) is terminated and disappears from the configuration. This is achieved by setting the succession to be the empty set.
) and the list of continuation processes in the next-control \(T. next \) is empty \([\,]\), then the process (after execution) is terminated and disappears from the configuration. This is achieved by setting the succession to be the empty set. -
(2)
If \(T. prog \) is one of the basic statements and the list of continuation processes in \(T. next \) is a non-empty list \(Q{::} Ks \), then we start \(Q\) in a new process with next-control \( Ks \) and a sequentially incremented index \( inc (\iota )\).
-
(3)
If \(T. prog \) is a sequential composition \(P \mathrel {;} Q\) then we start \(P\) in a new process with the same identifier and add \(Q\) to the front of the next-control list. The identifier does not increment since we do not consider the new process \({\langle \iota , P, Q{::} Ks \rangle } \) a sequential successor but only a structural replacement.
-
(4)
A loop \(T. prog = \mathop { rec } p.\, P\) behaves like its unfolding \(P\{\mathop { rec } p.\, P\!{/}\!p\}\), without modification to the identifier and next-controls.
-
(5)
Next consider a process with conditional program \(T. prog = s \, \mathrel {?} \, P \mathrel {:} Q \) in memory \(\rho \). Depending on whether the memory value for the variable \(s\) is \(1\) or \(0\) we install the \(P\) or the \(Q\) branch, respectively, with an incremented identifier and the same next-control. The identifier is incremented because the branches are considered as being executed strictly after the conditional test, in sequential program order.
-
(6)
Finally, executing a parallel program \(T. prog = P \mathrel {\Vert }Q\) instantiates the two sub-threads \(P\) and \(Q\) in their own process \({\langle \iota . l . 0, P, [\,] \rangle } \) and \({\langle \iota . r . 0, Q, [\,] \rangle } \), respectively, with a fresh and empty next-control but extended identifiers. The process \(P\) is the initial sequential statement of the left child of the parent process \({\langle \iota , P \!\mathrel {\mid \!\mid }\! Q, Ks \rangle } \). Therefore, we add the suffix \(l . 0\) to the parent’s identifier, and analogously \(r . 0\) for the right child \(Q\). At the same time that the parent process forks its two children, it transforms itself into a join process \({\langle \iota , \varepsilon , Ks \rangle } \). Since \(\iota \prec \iota . l . 0\) and \(\iota \prec \iota . r . 0\) both children have strictly larger identifiers. Since only processes with maximal identifiers are executable (details below), the join process must wait for the children to terminate before it can release the next-controls \( Ks \), or terminate itself in case \( Ks = [\,]\).
Note that there is no clause for the succession of a pausing process or a process label, i.e., \( nxt ({\langle \iota , \pi , Ks \rangle },\rho )\) and \( nxt ({\langle \iota , p, Ks \rangle }, \rho )\) are undefined. This is no problem since (i) program \(\pi \) is never executed in a micro-step but only by the next global clock tick (see below), and (ii) we are only interested in the behaviour of closed pSCL expressions which do not have any free process labels.
Example 3
Consider the process  . This process resets variable \(x\) and then either pauses or sets variable \(x\) depending on the value of variable \(y\). Let us derive its behaviour in the formal semantics.
. This process resets variable \(x\) and then either pauses or sets variable \(x\) depending on the value of variable \(y\). Let us derive its behaviour in the formal semantics.
Starting from some initial memory \(\rho _0\), executing \(T_0\) yields a new memory \(\rho _1 = mem (T_0, \rho _0)\) and a set of successors \(S_1 = nxt (T_0,\rho _0)\). This first micro-step breaks up the sequential composition operator \(;\) according to rule (3). This results in \(S_1 = \{{T_1}\}\) where  . The micro-step does not modify the memory, i.e., \(\rho _1 = \rho _0\). Proceeding with \(T_1\) from \(\rho _1\), we come to execute the reset
. The micro-step does not modify the memory, i.e., \(\rho _1 = \rho _0\). Proceeding with \(T_1\) from \(\rho _1\), we come to execute the reset  following rule (2), obtaining \(\rho _2 = mem (T_1, \rho _1)\) and successors \(S_2 = nxt (T_1, \rho _1)\). Memory \(\rho _2\) now assigns \(0\) to variable \(x\), while \(y\) retains its initial value from \(\rho _0\). The succession is \(S_2 = \{{T_2}\}\) with \(T_2 = {\langle 1, y \, \mathrel {?} \, \pi \mathrel {:} {! \, \! x} , [\,] \rangle } \). Notice the increment of the identifier \(T_2.id = 1 = inc (0) = inc (T_1.id)\) which reflects the fact that execution has passed a sequential composition operator. The conditional \(T_2\) now reads the value of \(y\) in memory \(\rho _2\) and passes control to the ‘then’ or ‘else’ branch:
following rule (2), obtaining \(\rho _2 = mem (T_1, \rho _1)\) and successors \(S_2 = nxt (T_1, \rho _1)\). Memory \(\rho _2\) now assigns \(0\) to variable \(x\), while \(y\) retains its initial value from \(\rho _0\). The succession is \(S_2 = \{{T_2}\}\) with \(T_2 = {\langle 1, y \, \mathrel {?} \, \pi \mathrel {:} {! \, \! x} , [\,] \rangle } \). Notice the increment of the identifier \(T_2.id = 1 = inc (0) = inc (T_1.id)\) which reflects the fact that execution has passed a sequential composition operator. The conditional \(T_2\) now reads the value of \(y\) in memory \(\rho _2\) and passes control to the ‘then’ or ‘else’ branch:
-
If \(\rho _2(y) = \rho _0(y) = 1\) then the conditional executes the ‘then’ branch. We get \(\rho _3 = mem (T_2, \rho _2) = \rho _2\) and \(S_3 = nxt (T_2, \rho _2) = \{{T_3}\}\) with \(T_3 = {\langle 2, \pi , [\,] \rangle } \) by rule (5). There are no micro-step rules for \(\pi \) which is forced to pause during the current macro-step. \(T_3\) makes progress only at the next global clock tick where it transforms into \(T_3' = {\langle 0, \varepsilon , [\,] \rangle } \) as described later.
-
If \(\rho _2(y) = \rho _0(y) = 0\) then \(\rho _3 = mem (T_2, \rho _2) = \rho _2\) and \(S_3 = nxt (T_2, \rho _2) = \{{T_3}\}\) with \(T_3 = {\langle 2, {! \, \! x}, [\,] \rangle } \) by rule (5). From here, the execution of \({! \, \! x} \) sets variable \(x\) and yields the new memory \(\rho _4 = mem (T_3,\rho _3)\) with \(\rho _4(x) = 1\) and \(\rho _4(y) = \rho _2(y)\). Since \(S_4 = nxt (T_3, \rho _3) = \emptyset \) by rule (1), there are no more processes from which we can continue. The execution of \(T_0\) has terminated instantaneously in the current macro-step. \(\square \)
Let us combine the memory and succession functions for a single process to define the micro-steps of an arbitrary set of processes running concurrently. This requires the notion of a configuration, defined next:
Definition 2
A configuration is given by a pair \(({\varSigma }, \rho )\), where \(\rho \) is the global memory and \({\varSigma } \), called the process pool, is a finite set of (closed) processes such that
-
all identifiers are distinct, i.e., for all \(T_1, T_2 \in {\varSigma } \), if \(T_1.id = T_2.id\) then \(T_1 = T_2\);
-
the sequential ordering of identifiers coincides with the thread hierarchy, i.e., for all \(T_1, T_2 \in {\varSigma } \), we have \(T_1.id \preceq T_2.id\) iff \( th (T_1.id)\) is a (not necessarily proper) prefix of \( th (T_2.id)\);
-
the identifiers form a full thread tree, i.e., for each \(T \in {\varSigma } \) and every proper prefix (ancestor) \(t \in \{ r, l \}^*\) of \( th (T.id)\), there is a process \(T' \in {\varSigma } \) of \(T\) with \( th (T'.id) = t\).
A configuration \(({\varSigma }, \rho )\) is empty if \({\varSigma } = \emptyset \). We call a process \(T \in {\varSigma } \)
-
pausing when \(T.prog = \pi \);
-
active if it is not pausing and \(T.id\) is \(\preceq \)-maximal (identifier order) in \({\varSigma } \);
-
waiting if it is neither pausing nor active.
A configuration with memory \(\rho \) in which all the processes in \({\varSigma } \) are waiting or pausing, is called quiescent. \(\square \)
Micro-sequences. From a given configuration \(({\varSigma }, \rho )\) and a selection \(T \in {\varSigma } \) of an active process, we can let \(T\) execute a micro-step to produce a micro-step
where in the free scheduling there is no constraint on the selection of \(T\) other than it being active. The resulting memory \(\rho ' = mem (T, \rho )\) is computed directly from the \( mem \) function. The new process pool \({\varSigma } '\) is obtained by removing \(T\) from \({\varSigma } \) and replacing it by the set of successors generated by \( nxt \), i.e., \({\varSigma } ' = {\varSigma } {\setminus }\{{T}\} \ \cup \ nxt (T, \rho )\). Note that in the free schedule both the next process pool \({\varSigma } '\) and the new memory \(\rho '\) only depend on the active process \(T\) that is executed and the current memory \(\rho \). They do not depend on the other processes in \({\varSigma } \). Since the successor configuration is uniquely determined by \(({\varSigma }, \rho )\) and \(T\), we may write \(({\varSigma } ', \rho ') = T({\varSigma }, \rho )\). In a micro-sequence the scheduler runs through a succession
of micro-steps obtained from the interleaving of process executions. We let \(\mathop {\twoheadrightarrow }\limits ^{} \) be the reflexive and transitive closure of \(\mathop {\rightarrow }\limits ^{} \). That is, we write
to express that there exists a micro-sequence \(R\), not necessarily maximal, from configuration \(({\varSigma } _0, \rho _0)\) to \(({\varSigma } _{k}, \rho _{k})\). The sequence \(R\) is a function mapping each index \(1 \le j \le k\) to the process \(R(j) = T_j\) executed at micro-step \(j\) and \( len (R) = k\) is the length of the micro-sequence executed so far. We call any pair \((i, R(i))\) consisting of a micro-step index \(1 \le i \le len (R)\) together with the process \(R(i)\) executed at position \(i\), a process instance of \(R\). Further, it will be necessary to restrict a micro-sequence \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) to its prefixes \(R{\tiny @}i :({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _i, \rho _i)\) for \(i \le n = len (R)\).
Macro-steps. A macro-step, also called a synchronous instant, or instant for short, abbreviated
is a maximal micro-sequence R that reaches a final quiescent configuration. Note that for any memory \(\rho \), a configuration \((\emptyset , \rho )\) is trivially quiescent. For the sake of simplicity, sometimes we drop the mapping \(M\) from our relations \(\mathop {\twoheadrightarrow }\limits ^{} \) and \(\mathop {\Longrightarrow }\limits ^{} \). When \(({\varSigma } _{k}, \rho _{k})\) is quiescent but non-empty then no further micro-step is possible (which explains the term ‘quiescent’) since all processes are waiting for the clock to tick. Such a clock tick
consists of eliminating every pausing process with empty continuation \({\langle \iota \,d, \pi , [\,] \rangle } \in {\varSigma } _k\) and replacing every pausing process \({\langle \iota \,d, \pi , Q{::} Ks \rangle } \in {\varSigma } _k\) with a non-empty continuation by a new process \({\langle \iota \,0, Q, Ks \rangle } \in {\varSigma } '\) preserving the sequential identifier of all ancestors but restarting the current thread at sequence number \(0\). The new memory \(\rho '\) preserves all internal and output variables but permits the environment to change any input variables for the next macro-step. For the investigations in this article, however, we are only interested in single macro-steps generated by the behaviour of pSCL expressions. Therefore, we will not be concerned with the modelling of successions of clock ticks.
Example 4
Let \(({\varSigma } _1,\rho _0)\) be a configuration where \(\rho _0\) gives value \(0\) to every variable and the process pool \({\varSigma } _1 = \{ T_1 \}\) consists of the root process:  . The complete computation graph for the free scheduling from \(({\varSigma } _1,\rho _0)\) is depicted in Fig. 2. The processes are abbreviated as follows:
. The complete computation graph for the free scheduling from \(({\varSigma } _1,\rho _0)\) is depicted in Fig. 2. The processes are abbreviated as follows:

Each edge in Fig. 2 is a single micro-step. For ease of explanation we do not use the selected process \(T_i\) as the label like in (7) but instead the primitive operator executed in the micro-step, i.e., a sequential composition \(\mathrel {;} \) (rule (3)), atomic set, reset or the empty statements \({! \, \! s} \), \({! \, \! t} \),  , \(\varepsilon \) (rules (1) and (2)) or a parallel composition \(\mathrel {\Vert }\) (rule (6)). The shaded regions named \(A\) and \(B\) will be explained later.
, \(\varepsilon \) (rules (1) and (2)) or a parallel composition \(\mathrel {\Vert }\) (rule (6)). The shaded regions named \(A\) and \(B\) will be explained later.
The free scheduling graph of process \(T_1\) of Example 4
Since \(T_1\) is active it can induce the micro-step \(({\varSigma } _1, \rho _0) \mathop {\rightarrow }\limits ^{} ({\varSigma } _2, \rho _0)\) with the a succession \({\varSigma } _2 = \{{T_{20},T_{21},T_{22}}\}\) of three processes as a result of executing the parallel fork, the parent \(T_{20}\) and its two children \(T_{21}\) and \(T_{22}\). Observe that in \({\varSigma } _2\) the two children are active but the parent with identifier \(0\) is waiting, because \(0 \prec 0 . l . 0\) and \(0 \prec 0 . r . 0\). The parent \(T_{20}\) now plays the role of a ‘join’ in the sense that it cannot execute any micro-step until the two children terminate and its own identifier becomes maximal again. Let us suppose that \(T_{21}\) and \(T_{22}\) are scheduled in that order to get \(({\varSigma } _2, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _4, \rho _0)\) with \({\varSigma } _4 = \{{T_{20}, T_{31}, T_{32}}\}\), where \(T_{31}\) and \(T_{32}\) are both active. The configuration \(({\varSigma } _4, \rho _0)\) is underlined in Fig. 2. Notice that we reach exactly the same configuration if we first schedule \(T_{22}\) and then \(T_{21}\). The concurrent execution of the sequential compositions in \(T_{21}\) and \(T_{22}\) is confluent, because there are no read or write accesses to variables. However, in \(({\varSigma } _4, \rho _0)\) things become interesting since the chosen scheduling order will result in different configurations. For if \(({\varSigma } _4, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _6, \rho _{11})\), with \({\varSigma } _6 = \{ T_{20}, T_{41}, T_{42} \}\), results from scheduling \(T_{32}\) followed by \(T_{31}\), then first the reset  is performed and thereafter the set \({! \, \! s} \), so that \(\rho _{11}(s) = 1\). On the other hand, if first \(T_{31}\) is picked and then \(T_{32}\) does its initial micro-step, then \(({\varSigma } _4, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _6, \rho _{12})\) with \(\rho _{12}(s) = 0\). Although the resulting process pool \({\varSigma } _6\) is the same in both configurations, the global memory is not.
is performed and thereafter the set \({! \, \! s} \), so that \(\rho _{11}(s) = 1\). On the other hand, if first \(T_{31}\) is picked and then \(T_{32}\) does its initial micro-step, then \(({\varSigma } _4, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _6, \rho _{12})\) with \(\rho _{12}(s) = 0\). Although the resulting process pool \({\varSigma } _6\) is the same in both configurations, the global memory is not.
Continuing the schedule from configuration \(({\varSigma } _6, \rho _{11})\), also underlined in Fig. 2, we see that there is a race between the reading of variable \(t\) by \(T_{42}\) and the writing to \(t\) by \(T_{41}\). If we first execute \(T_{41}\), then the conditional \(T_{42}\) will activate its ‘then’-branch \(\varepsilon \). Therefore, we eventually reach the configuration \(({\varSigma } _{9}, \rho _{21})\) with \({\varSigma } _{9} = \{ T_{20} \}\) where the memory satisfies \(\rho _{21}(s) = \rho _{21}(t) = 1\). Now ‘join’ process \(T_{20}\) becomes active, which instantaneously terminates reaching the quiescent configuration \((\{ \}, \rho _{21})\). On the other hand, if in \(({\varSigma } _6, \rho _{11})\) the process \(T_{42}\) first gets to test the value of \(t\), which is \(0\), before \(T_{41}\) sets it to \(1\), then the ‘else’-branch is selected and we end up in the configuration \(({\varSigma } _{8}, \rho _{21})\) where \({\varSigma } _8 = \{ T_{20}, T_{522} \}\). This configuration is also quiescent as it contains no active processes. Here, the ‘join’ process \(T_{20}\) is still waiting since it has a strictly smaller sequence number than process \(T_{522}\) which is pausing. No progress can be made until the next clock tick makes \(T_{522}\) disappear from the configuration, thereby activating \(T_{20}\) which then terminates instantaneously. Note that the conflict between \(T_{41}\) and \(T_{42}\) in \(({\varSigma } _6, \rho _{11})\) results in a non-determinism of control, viz. between terminating in the same instant or the next. \(\square \)
Clearly, as demonstrated in Example 4 the selection strategy applied in the free scheduling of a program determines the final memory content and termination behaviour of a program in a macro-step. If we would consider pSCL as a just another clocked process algebra such as [21, 41, 55] or a model of general statecharts, e.g., [39, 69, 82] (or in fact Java threads, for that matter) the non-determinism would not worry us. It is a natural consequence of the asynchrony of parallel execution. We can leave it in the responsibility of the versed programmer to harness her or his programs by explicit synchronisation through shared memory mutual exclusion algorithms (see [57]) in order to get rid of non-determinacy. Yet, this is not the right approach for synchronous programming where every program, by compilation, is required to code a deterministic Mealy machine. In synchronous programming it is the compiler which has to achieve determinate tick responses under pessimistic assumption on the varying degree of perturbations arising from the non-determinism of target run-time system.
In synchronous programming the programmer is supported by static schedulability and causality analyses. Often non-determinism can be eliminated by restricting the free scheduling to so-called admissible schedules that are natural for, or intended by, the programmer and at the same time reliably implemented on the chosen run-time platform by a trusted compiler.
Example 5
Consider Example 4 in which the non-determinacy of the tick response is due to races between the setting and resetting of variable \(s\) and the reading and writing of variable \(t\). Suppose we compile the root process \(T_0\) as a data-flow network in which the non-determinism maps to the concurrent execution of function blocks. Then it is easy to ensure that the data-flow always executes reset of a variable (value initialisation) before any set (value update) and all write accesses before the reads. This natural ordering prohibits the execution of the transitions shown in Fig. 2 as dashed arrows. It eliminates the paths in region \(A\) with the resets  occurring after the sets
occurring after the sets  and the path in region \(B\) in which the set \({! \, \! t} \) happens after the reads \(t ?\). The remaining admissible scheduling paths then all lead, deterministically, to instantaneous termination in configuration \((\{ \}, \rho _{21})\). \(\square \)
and the path in region \(B\) in which the set \({! \, \! t} \) happens after the reads \(t ?\). The remaining admissible scheduling paths then all lead, deterministically, to instantaneous termination in configuration \((\{ \}, \rho _{21})\). \(\square \)
A canonical notion of admissibility to avoid causality locks is the “init;update;read” (iur) protocol, which forces the accesses of every variable to undergo strict cycles of first initialisations ( ), then updates (
), then updates ( ) and finally reads (\(s ?\)). Moreover, the iur protocol can be refined by limiting the number of initialisations that are permitted during a single macro-step on any variable. Liberal notions of sequential constructiveness permitting more than one init;update;read cycle have recently been proposed [85, 86]. In the traditional model of synchronous programming|paradigmatically represented by Esterel|only one iur cycle is permitted. This leads to a more conservative notion of constructiveness which is the subject of this article and formalised in the next section.
) and finally reads (\(s ?\)). Moreover, the iur protocol can be refined by limiting the number of initialisations that are permitted during a single macro-step on any variable. Liberal notions of sequential constructiveness permitting more than one init;update;read cycle have recently been proposed [85, 86]. In the traditional model of synchronous programming|paradigmatically represented by Esterel|only one iur cycle is permitted. This leads to a more conservative notion of constructiveness which is the subject of this article and formalised in the next section.
Since well-formed pSCL programs are clock-guarded, we can unfold all loops and extract finite \(\mathop { rec } \)-free expressions that fully describe the program’s macro step reactions. Therefore, as the main results in this article concern the scheduling of micro-steps inside a single finite macro-step, it suffices to consider only finite, recursion-free pSCL programs, i.e., fprogs.
2.3 Reactiveness and determinacy
All non-determinism of concurrent execution arises from two types of data races: write-write conflicts and write-read conflicts. To remove these races, the iur scheduling protocol enforces precedence of resets over sets and of writes over reads. The strict ordering can be broken only if the variable accesses are confluent. A suitable notion of confluence has been introduced in [85, 86].
Definition 3
(Confluence of processes) Let \(T_1\) and \(T_2\) be two arbitrary processes and \(({\varSigma }, \rho )\) a configuration. Then,
-
1.
\(T_1, T_2\) are called conflicting in \(({\varSigma }, \rho )\) if both \(T_1\) and \(T_2\) are active in \({\varSigma } \) and \(T_1(T_2({\varSigma }, \rho )) \ne T_2(T_1({\varSigma }, \rho ))\);
-
2.
\(T_1, T_2\) are confluent in \(({\varSigma }, \rho )\), written \(T_1 \thicksim _{({\varSigma }, \rho )} T_2\), if there is no micro-sequence \(({\varSigma }, \rho ) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } ', \rho ')\) such that \(T_1\) and \(T_2\) are conflicting in \(({\varSigma } ', \rho ')\). \(\square \)
Example 6
As an illustration consider once more Example 4. Processes \(T_{31}\) and \(T_{32}\) are conflicting in configuration \(({\varSigma } _4,\rho _0) = (\{ T_{20}, T_{31}, T_{32} \}, \rho _0)\) because, as we have seen, both are active in this configuration and, moreover, different execution orders lead to different results. Since the first micro-step of \(T_{31}\) is \({! \, \! s} \) (update) and the first micro-step of \(T_{32}\) is the reset  (init), the scheduling protocol gives precedence to \(T_{32}\). Similarly, \(T_{41}\) and \(T_{42}\) are in conflict in configuration \(({\varSigma } _6, \rho _{12})\) with \({\varSigma } _6 = \{ T_{20}, T_{41}, T_{42} \}\) as can be seen from Fig. 2. For their part, processes \(T_{21}\) and \(T_{22}\) are independent or confluent in \(({\varSigma } _2,\rho _0)\) with \({\varSigma } _2 = \{ T_{20}, T_{21}, T_{22} \}\). This is so because in every micro-sequence \(({\varSigma } _2, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } ', \rho ')\) the only configuration in which both \(T_{21}\) and \(T_{22}\) are active is precisely \(({\varSigma } _2, \rho _0)\). Furthermore, as can be seen from Fig. 2, the order of execution is unimportant in this case, namely \(T_{21}(T_{22}({\varSigma } _2,\rho _0)) = T_{21}(T_{22}({\varSigma } _2,\rho _0)) = ({\varSigma } _4,\rho _0)\), where \({\varSigma } _4 = \{ T_{20}, T_{31}, T_{32} \}\). Note that since the initial micro-step of both \(T_{21}\) and \(T_{22}\) is the breaking up of the sequential composition, and thus not variable accesses, their ordering is unconstrained by the “init;update;read” scheduling protocol. \(\square \)
(init), the scheduling protocol gives precedence to \(T_{32}\). Similarly, \(T_{41}\) and \(T_{42}\) are in conflict in configuration \(({\varSigma } _6, \rho _{12})\) with \({\varSigma } _6 = \{ T_{20}, T_{41}, T_{42} \}\) as can be seen from Fig. 2. For their part, processes \(T_{21}\) and \(T_{22}\) are independent or confluent in \(({\varSigma } _2,\rho _0)\) with \({\varSigma } _2 = \{ T_{20}, T_{21}, T_{22} \}\). This is so because in every micro-sequence \(({\varSigma } _2, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } ', \rho ')\) the only configuration in which both \(T_{21}\) and \(T_{22}\) are active is precisely \(({\varSigma } _2, \rho _0)\). Furthermore, as can be seen from Fig. 2, the order of execution is unimportant in this case, namely \(T_{21}(T_{22}({\varSigma } _2,\rho _0)) = T_{21}(T_{22}({\varSigma } _2,\rho _0)) = ({\varSigma } _4,\rho _0)\), where \({\varSigma } _4 = \{ T_{20}, T_{31}, T_{32} \}\). Note that since the initial micro-step of both \(T_{21}\) and \(T_{22}\) is the breaking up of the sequential composition, and thus not variable accesses, their ordering is unconstrained by the “init;update;read” scheduling protocol. \(\square \)
In this article we introduce a fairly stringent interpretation of the iur protocol derived from conservative SMoCCs such as Esterel or Quartz, which we term Berry admissibility (Definition 4 below). It uses confluence to permit “ineffective” sets after reads but is stronger than SC-admissibility [85], as it enforces the iur protocol on all accesses not just concurrent ones as in [85]. Whatever synchronisation protocol \(X\) we use—there may be many other interesting ones still to be discovered—the restriction to X-admissible executions not only reduces non-determinacy. Such synchronisation constraints may lead to deadlock, i.e., configurations in which no micro-step is possible without violating X-admissiblity. Thus we must care about X-reactiveness, i.e., the property that a program does not get stuck when executed in an X-admissible fashion.
2.3.1 B-admissibility and B-reactiveness
The tighter the underlying notion of X-admissibility the more information we have from knowing that a program is X-reactive. If all X-admissible schedules are also Y-admissible then a program without deadlocks under X is also deadlock-free under Y. Here we introduce a suitable notion of admissibility that captures the essence of Esterel which is tighter than SC-admissibility introduced in [85, 86].
Definition 4
(Berry admissibility and reactiveness) A micro-sequence \(R: ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _{n}, \rho _{n})\) is Berry admissible (B-admissible) iff
-
(1)
\(R\) does not reset any variable that has been set before.
Formally, if \(R(i)\) for \(0 < i \le n\) executes a set \({! \, \! s} \) for some \(s \in V \), then no \(R(j)\) for \(i < j \le n\) executes a reset
 .
. -
(2)
\(R\) does not write any variable which has been read before, unless this late write is ineffective in the sense that the write is confluent with the read and the very same value has been written already before the read.
Formally, if \(R(j)\) for \(0 < j \le n\) executes a conditional test \(s \, \mathrel {?} \, P \mathrel {:} Q \) for some \(P, Q\), and \(R(k)\) for \(j < k \le n\) performs a set \({! \, \! s} \) (reset
 ), then there exists an index \(i < j\) before the read where \(R(i)\) already executed a set \({! \, \! s} \) (reset
), then there exists an index \(i < j\) before the read where \(R(i)\) already executed a set \({! \, \! s} \) (reset  ) and \(R(j) \thicksim _{({\varSigma } _j, \rho _j)} R(k)\).
) and \(R(j) \thicksim _{({\varSigma } _j, \rho _j)} R(k)\).
An fprog \(P\) is called Berry reactive (B-reactive) if from every initial configuration \((\{ {\langle 0, P, [\,] \rangle } \}, \rho _0)\) there is at least one B-admissible instant. \(\square \)
Example 7
If a reset happens sequentially after a set (violating Definition 4(1)), as in  , then this violates the monotonicity of signal stabilisation. In the conservative delay-insensitive model of Esterel this is a hazard, since a concurrent environment could read either the first output value \(s = 1\) (which is interpreted as an emit) or the second \(s = 0\) (which is an initialization). This creates a write-write race, thus jeopardising determinism. \(P_1\) does not have a B-admissible execution. The opposite ordering
, then this violates the monotonicity of signal stabilisation. In the conservative delay-insensitive model of Esterel this is a hazard, since a concurrent environment could read either the first output value \(s = 1\) (which is interpreted as an emit) or the second \(s = 0\) (which is an initialization). This creates a write-write race, thus jeopardising determinism. \(P_1\) does not have a B-admissible execution. The opposite ordering  of a reset followed by a set is B-admissible, since it adheres to the monotonic stabilisation protocol.
of a reset followed by a set is B-admissible, since it adheres to the monotonic stabilisation protocol.
A read-write race (violating Definition 4(2)) occurs in the sequential programs \(P_3 :=s \, \mathrel {?} \, {! \, \! s} \mathrel {:} \varepsilon \) and  . The write accesses \({! \, \! s} \) and
. The write accesses \({! \, \! s} \) and  , respectively, may effectively overwrite the externally controlled value of \(s\) which is tested in the conditionals. If we consider \(P_3\) and \(P_4\) to be environments of themselves then we run into a causality loop: the test \(s?\) must wait until the program has set or reset its value, which however can only happen after the test has been executed. If \(R\) is the micro-sequence generated from \(P_3\) with initial memory \(\rho _0(s) = 1\) then it executes the set \({! \, \! s} \) after the read \(s?\) without any set having happened before the read. Similarly, we get a reset
, respectively, may effectively overwrite the externally controlled value of \(s\) which is tested in the conditionals. If we consider \(P_3\) and \(P_4\) to be environments of themselves then we run into a causality loop: the test \(s?\) must wait until the program has set or reset its value, which however can only happen after the test has been executed. If \(R\) is the micro-sequence generated from \(P_3\) with initial memory \(\rho _0(s) = 1\) then it executes the set \({! \, \! s} \) after the read \(s?\) without any set having happened before the read. Similarly, we get a reset  after the read \(s?\) in \(P_4\) but this reset value has not been established before the read. Therefore, neither \(P_3\) nor \(P_4\) are B-reactive. In the hardware translation of Esterel, \(P_3\) would be a delay loop \(s = s\) which has two stable solutions \(s = 0\) and \(s = 1\), while \(P_4\) generates essentially the feed-back system \(s = \overline{s} \cdot s\) which may produces glitches before it settles at \(s =0\), if it stabilises at all.
after the read \(s?\) in \(P_4\) but this reset value has not been established before the read. Therefore, neither \(P_3\) nor \(P_4\) are B-reactive. In the hardware translation of Esterel, \(P_3\) would be a delay loop \(s = s\) which has two stable solutions \(s = 0\) and \(s = 1\), while \(P_4\) generates essentially the feed-back system \(s = \overline{s} \cdot s\) which may produces glitches before it settles at \(s =0\), if it stabilises at all.
\(P_3\) and \(P_4\) were acceptable if the status of \(s\) was already decided before the test \(s ?\). For instance, in \({! \, \! s} \mathrel {;} P_3\) the second \({! \, \! s} \) in \(P_3\) is ineffective from the point of view of the read access because the status \(1\) on \(s\) is determined by the first \({! \, \! s} \) which occurs sequentially before the read. Thus, executing \({! \, \! s} \mathrel {;} P_3\) is B-admissible. \(P_4\) can be executed admissibly in the form  which then bypasses the reset
which then bypasses the reset  in \(P_4\). On the other hand, \({! \, \! s} \mathrel {;} P_4\) would not be B-reactive because it generates a reset
in \(P_4\). On the other hand, \({! \, \! s} \mathrel {;} P_4\) would not be B-reactive because it generates a reset  after a set \({! \, \! s} \). We note that all programs \(P_1\)–\(P_4\) are sequentially admissible [85] (called \(\varDelta _*\)-admissibility in [4]) because under sequential admissibility glitches can only be generated from concurrent accesses, not sequential ones as in \(P_1\) and \(P_2\). \(\square \)
after a set \({! \, \! s} \). We note that all programs \(P_1\)–\(P_4\) are sequentially admissible [85] (called \(\varDelta _*\)-admissibility in [4]) because under sequential admissibility glitches can only be generated from concurrent accesses, not sequential ones as in \(P_1\) and \(P_2\). \(\square \)
Example 8
Although each fprog \(P :=x \, \mathrel {?} \, {! \, \! y} \mathrel {:} \varepsilon \) and \(Q :=y \, \mathrel {?} \, {! \, \! x} \mathrel {:} \varepsilon \) is B-reactive, their concurrent composition fprog \(P \!\mathrel {\mid \!\mid }\! Q \) is not. There is only one initial memory \(\rho _0\) from which this has any B-admissible instants, viz. \(\rho _0(x) = \rho _0(y) = 0\).
Suppose initially \(\rho _0(x) = 1\) or \(\rho _0(y) = 1\). Then either the write statement \({! \, \! y} \) in \(P\) is executed after \(y\) has been read by \(Q\), or \({! \, \! x} \) in \(Q\) is executed after \(x\) is read by \(P\). Both violates Definition 4(2) because there are no other writes before the read which would make the “late” write ineffective. \(\square \)
Example 9
All the scheduling sequences \(R : (\{T_1\}, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} (\{\,\}, \rho _{21})\) of Example 4, following the transitions colored green in Fig. 2 are B-admissible. None of the scheduling sequences going through a red transition, entering region \(A\) or \(B\), is B-admissible. The sequences entering region \(A\) are violating Definition 4(1) by resetting variable \(s\) (dashed red arrows labelled  ) after \(s\) has been set (solid red arrows labelled \({! \, \! s} \)). The sequences entering region \(B\) are breaking the constraint Definition 4(2) because variable \(t\) is set (solid red arrow labelled \(!t\)) after it has been read (dashed red arrows labelled \(t?\)), without any setting of variable \(t\) before the read. However, since at least one B-admissible scheduling sequence leads to completion, the program
) after \(s\) has been set (solid red arrows labelled \({! \, \! s} \)). The sequences entering region \(B\) are breaking the constraint Definition 4(2) because variable \(t\) is set (solid red arrow labelled \(!t\)) after it has been read (dashed red arrows labelled \(t?\)), without any setting of variable \(t\) before the read. However, since at least one B-admissible scheduling sequence leads to completion, the program  of Example 4 is \(B\)-reactive. \(\square \)
of Example 4 is \(B\)-reactive. \(\square \)
2.3.2 SC-admissibility and SC-read-determinacy
When it comes to the question of determinacy then we want the underlying notion of X-admissibility to be as weak as possible. If a program analysis detects determinacy under all X-admissible executions, then the implied level of robustness depends on how much non-determinism is still permitted by X-admissible executions. For instance, if X-admissibility limits execution to a single micro-sequence, e.g. through a global linear priority ordering on all statements, then determinacy is trivial. On the other hand, knowing that a program is determinate under all free schedules, is a very strong (and rare) property for a program to have. To get more headroom for our main result we use SC-admissibility. In contrast to B-admissibility this admits writes-after-reads and resets-after-sets, if these are sequential successors in program order or confluent. The following definition is rephrased from [85, 86].
Definition 5
(SC-admissibility and reactiveness) A micro-sequence \(R: ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _{k}, \rho _{k})\) is SC-admissible if for every two processes \(R(i)\), \(R(j)\) such that \(0 < i < j \le n\) and either
-
(i)
\(R(i)\) reads (tests) a variable \(s\), on which \(R(j)\) subsequently performs a reset
 or set \({! \, \! s} \), or
or set \({! \, \! s} \), or -
(ii)
\(R(i)\) performs a set \({! \, \! s} \) on a variable \(s\), on which \(R(j)\) subsequently performs a reset
 ,
,
then
-
(i)
\(R(i)\) is sequentially before \(R(j)\) in program order, i.e., \(R(i).id \preceq R(j).id\) or
-
(ii)
\(R(i)\) and \(R(j)\) are confluent, i.e., \(R(i) \thicksim _{({\varSigma } _{i},\rho _{i})} R(j)\).
An fprog \(P\) is SC-reactive, if from every initial configuration \((\{ {\langle 0, P, [\,] \rangle } \}, \rho _0)\) there is at least one SC-admissible instant for \(P\). \(\square \)
One can show that B-admissibility is more restrictive than SC-admissibility.
Proposition 1
Every B-admissible micro-sequence is also SC-admissible.
Proof
Let \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _{n}, \rho _{n})\) be a B-admissible micro-sequence, with processes instances \(R(i)\) and \(R(j)\) such that \(0 < i < j \le n\). First note that by condition (1) of B-admissibility Definition 4, the situation (ii) of Definition 5 cannot occur. We only need to care about the situation (i), where \(R(i)\) is a read and \(R(j)\) a write of the same variable \(s\). But then condition (2) of B-admissibility implies both are confluent, i.e., \(R(i) \thicksim _{({\varSigma } _{i},\rho _{i})} R(j)\). This was to be shown. \(\square \)
Example 10
The Example 4 is B-reactive and thus also SC-reactive. However, it does not have any SC-admissible scheduling sequences which are not B-admissible at the same time. None of the scheduling sequences entering regions \(A\) or \(B\) in Fig. 2 are SC-admissible. Let us look at what happens in region \(A\). For instance, take the scheduling
in which \(R(3) = T_{31}\) performs a set \({! \, \! s} \) and later \(R(6) = T_{32}\) performs a reset  . This violation of resets-before-sets is permitted under SC-admissibility only if the micro-steps are sequentially ordered or confluent. The former is not the case, \(T_{31}.id = 0.l.0 \not \preceq 0.r.0 = T_{32}.id\), because both processes are from concurrent threads. The latter is not the case either, because
. This violation of resets-before-sets is permitted under SC-admissibility only if the micro-steps are sequentially ordered or confluent. The former is not the case, \(T_{31}.id = 0.l.0 \not \preceq 0.r.0 = T_{32}.id\), because both processes are from concurrent threads. The latter is not the case either, because  . In fact, there is the (free) schedule \(T_{22} : (\{ T_{20}, T_{31}, T_{22} \}, \rho _0) \mathop {\rightarrow }\limits ^{} (\{ T_{20}, T_{31}, T_{32} \}, \rho _0)\) (underlined in Fig. 2) which reaches the configuration \((\{ T_{20}, T_{31}, T_{32} \}, \rho _0)\) in which both \(T_{31}\) and \(T_{32}\) are active and conflicting (see Definition 3). Executing \(T_{31}, T_{32}\) from here leads to \((\{ T_{20}, T_{41}, T_{42} \}, \rho _{12})\) while the swapped ordering \(T_{32}, T_{31}\) ends up in \((\{ T_{20}, T_{41}, T_{42} \}, \rho _{11})\) which have different memories.
. In fact, there is the (free) schedule \(T_{22} : (\{ T_{20}, T_{31}, T_{22} \}, \rho _0) \mathop {\rightarrow }\limits ^{} (\{ T_{20}, T_{31}, T_{32} \}, \rho _0)\) (underlined in Fig. 2) which reaches the configuration \((\{ T_{20}, T_{31}, T_{32} \}, \rho _0)\) in which both \(T_{31}\) and \(T_{32}\) are active and conflicting (see Definition 3). Executing \(T_{31}, T_{32}\) from here leads to \((\{ T_{20}, T_{41}, T_{42} \}, \rho _{12})\) while the swapped ordering \(T_{32}, T_{31}\) ends up in \((\{ T_{20}, T_{41}, T_{42} \}, \rho _{11})\) which have different memories.
Similarly, one can show that the two concurrent processes \(T_{42}\) and \(T_{41}\) which read and set variable \(t\) are in conflict on every schedule that runs through region \(B\). The critical configuration for region \(B\) is \((\{ T_{20}, T_{41}, T_{42} \}, \rho _{11})\) (underlined in Fig. 2) in which processes \(T_{42}\) and \(T_{41}\) are in conflict with each other. \(\square \)
Clearly, by Proposition 1, every B-reactive program is also SC-reactive. An X-reactive program is guaranteed not to deadlock under X-admissible execution. However, it may be non-determinate, i.e., generate different final memory states. In defining determinacy precisely we meet another degree of freedom, depending on whether or not we permit the outcome at the end of an instant to be functionally dependent on the memory configuration at the beginning of the instant. For instance, we might distinguish, as done in Esterel V7, between temporary and registered variables. The value of a temporary variable is ephemeral and must be recomputed by the program at every instant. The value of a registered variable is provided by the environment in memory at the beginning of each instant. Hence, the final response may depend on the initial value of registered variables but not on the initial value of the temporary variables. This gives rise to the following definition, parametric in X-admissibility, where the notations \(\twoheadrightarrow _{ X } \) and \(\Longrightarrow _{ X } \) are used to indicate that the corresponding micro-sequence complies with a particular notion X of admissibility. For example, \(\twoheadrightarrow _{ B } \) refers to a B-admissible micro-sequence and \(\Longrightarrow _{ SC } \) indicates a SC-admissible instant.
Definition 6
(X-determinacy) For a given set of temporary variables \( W \subseteq V \), an fprog \(P\) is X-determinate for \( W \) (\(\text {X}_ W \)-determinate) iff the following two conditions hold:
-
1.
For every fixed initial memory, \(P\) computes the same final memory in all X-admissible instants.
Formally, if \(({\langle \iota , P \rangle }, \rho _0) \Longrightarrow _{ X } ({\varSigma } _0, \gamma _0)\) and \(({\langle \iota , P \rangle }, \rho _0) \Longrightarrow _{ X } ({\varSigma } _1, \gamma _1)\) then \(\gamma _0 = \gamma _1\).
-
2.
For every temporary variable in \( W \), \(P\) either \((i)\) computes the very same final value in all X-admissible instants, or \((ii)\) it does not modify the initial memory value of this variable in any X-admissible instant. In other words, if \(P\) changes the value of a variable \(x \in W \) in any X-admissible instant then this must be the final value for \(x\) in all X-admissible instants.
Formally, for all \(x \in W \) and \(\gamma _0\), \(\rho _0\), \({\varSigma } _0\): if \(({\langle \iota , P \rangle }, \rho _0) \Longrightarrow _{ X } ({\varSigma } _0, \gamma _0)\) and \(\gamma _0(x) \ne \rho _0(x)\), then for all \(\gamma _1\), \(\rho _1\), \({\varSigma } _1\) such that \(({\langle \iota , P \rangle }, \rho _1) \Longrightarrow _{ X } ({\varSigma } _1, \gamma _1)\), we have \(\gamma _1(x) = \gamma _0(x)\). \(\square \)
In this article we will treat two special cases: When \( W \) is the empty set, \( W = \emptyset \), then \(\text {X}_{W}\)-determinacy is simply called X-determinacy. When \( W = rd (P) \) is the set of read variables of \(P\), defined by
then \(\text {X}_{W}\)-determinacy is referred to as X-read-determinacy. The following proposition is obvious, with Proposition 1:
Proposition 2
Every X-read-determinate fprog is also X-determinate and every SC-determinate program is B-determinate.
Note that purely sequential programs, i.e., those without the concurrency operator \(\mathrel {\Vert }\), are trivially deterministic and hence SC-read-determinate. Sequential programs are also always SC-reactive. They can however fail B-reactiveness, i.e., if their execution is not B-admissible because it generates a causal hazard in the access to a variable (see Example 7). This models the stronger interpretation of reactiveness in the more conservative SMoCCs like Esterel and Quartz which we deal with, here. Also, SC-read-determinacy is trivial for pure input variables which are never written by a program because their final value will always be the same as the initial value. Hence, all programs, including those containing the \(\mathrel {\Vert }\) operator, with disjoint input and output variables, are SC-read-determinate but possibly not B-reactive.
The following Example 11 brings home the problems causality poses for compositionality.
Example 11
All \(P_1\), \(P_3\), \(P_4\) from Example 7 are purely sequential programs which are not B-reactive but SC-read-determinate. An fprog which is B-reactive but not SC-determinate is the parallel composition \(P \!\mathrel {\mid \!\mid }\! Q \), where \(P :=x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \) and \(Q :=y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \). The left component \(P\) sets \(y\) to \(1\) if \(x\) is \(0\) and the right sub-expression \(Q\) sets \(x\) to \(1\) if \(y\) is \(0\). Indeed, if both variables \(x, y \in rd (P \mathrel {\Vert }Q) \) are initially \(\rho _0(x) = \rho _0(y) = 0\), the response of \(P \!\mathrel {\mid \!\mid }\! Q \) is non-determinate (under B-admissible scheduling). If \(P\) is first executed to termination and then \(Q\), we get the final memory \(\gamma _0(x)=0, \gamma _0(y)=1\); otherwise, if we first execute \(Q\) and then \(P\), the result will be \(\gamma _0(x)=1, \gamma _0(y)=0\). This is an internal non-determinism observable from a single fixed initial memory. \(P \!\mathrel {\mid \!\mid }\! Q \) is B-reactive but not B-determinate and thus neither SC-determinate.
That a program is non-determinate does not mean all its sub-programs must be non-determinate, too. For example, both fprogs \(P\) and \(Q\) in this example are SC-read-determinate. The only read variable \(x \in rd (P) \) is not touched by \(P\) and thus left to be controlled by the environment. This satisfies condition (2) of Definition 6. Note that the value of \(y\) is changed in the SC-admissible execution of \(P\) starting from \(\rho _0(x) = 0\) and \(\rho _0(y) = 0\) and its final value \(\gamma _0(y) = 1\) is not the final value for all SC-admissible instants, e.g., if \(\rho _0(x) = 1\) and \(\rho _0(y) = 0\) then we get \(\gamma _0(y) = 0\). However, this is not a violation of Definition 6(2) because \(y \not \in rd (P) \).
Finally note that non-determinate programs can become determinate in context. For example, the SC-admissibility rules make sure that in \(P \!\mathrel {\mid \!\mid }\! Q \!\mathrel {\mid \!\mid }\! {! \, \! x} \) the set \({! \, \! x} \) is executed before the test \(x?\) in \(P\), which means that \(P\) does not write \({! \, \! y} \) which prevents \(Q\) from writing \({! \, \! x} \), thereby avoiding an admissibility hazard with any earlier read of \(y\) by \(Q\). Moreover, since the set \({! \, \! x} \) is executed before the read \(x?\) by \(P\), the set \({! \, \! x} \) by \(Q\) is confluent with the read. As a consequence, for any given initial memory \(\rho _0\), all SC-admissible executions of \(P \!\mathrel {\mid \!\mid }\! Q \!\mathrel {\mid \!\mid }\! {! \, \! x} \) produce the same determinate response \(\gamma _0\) with \(\gamma _0(x)=1\) and \(\gamma _0(y) = \rho _0(y)\) is the initial value. Thus, the fprog \(P \!\mathrel {\mid \!\mid }\! Q \!\mathrel {\mid \!\mid }\! {! \, \! x} \) is SC-read-determinate. \(\square \)
In Sect. 4 below we shall give a sound denotational fixed-point analysis to check whether a program is B-reactive and SC-read-determinate. Our fixed-point characterisation defines the class of input Berry constructive (IBC) programs which includes more programs than the strong Berry constructive (SBC) programs introduced in [4]. The result established in [4], that every SBC program is SC-reactive and SC-determinate, is a corollary of the main Theorem 1 in this article which says that every IBC program is B-reactive and SC-read-determinate.
We first need to introduce the appropriate abstract semantical domains. This is done in the following Sect. 3.
3 Abstract domains and environments
The constructiveness analysis on finite pSCL programs (fprogs) takes place in an abstract domain of information values which describe the sequential and concurrent interaction of signals. It accounts for data dependencies and can deal with the difference of a variable retaining its original initial value from the initial memory (pristine), being initialised to 0 and then either remaining 0 (signal absence) or being set to 1 (signal presence). This includes monotonic value changes from 0 to 1 and, essentially, corresponds to Berry’s notion of constructiveness in Esterel [12], yet is able to deal with explicit initialisations which requires the ability to cope with prescriptive sequencing. This section introduces this abstract domain and its natural extension to environments, namely discrete structures able to maintain the information of a number of signal variables.
3.1 Semantic domain \(I(\mathbb {D})\) of value status
Instead of distinguishing just two signal statuses “absent” and “present” as in traditional SMoCC, we consider the sequential behaviour of a variable (during each instant) as taking place in a linearly ordered 4-valued domain \(\mathbb {D} = \{{\bot \le 0 \le 1 \le \top }\}\). This requires to consider two additional logical memory values, namely \(\bot \) and \(\top \). The former indicates that the corresponding variable contains its initial memory value, i.e., a pristine \(0\) or \(1\). The latter tells us that the variable value has passed from \(1\) to \(0\) at some point, independently of what the final memory result is. The linear ordering \(\le \) captures a trajectory through a single instance of the iur protocol. Observe the difference between the variable values \({\mathbb B} = \{0,1\}\), which appear at “run-time” as defined in the operational semantics, and the signal statuses \(\mathbb {D} \), which are the basis of constructiveness analysis. The latter lifts our description to a higher level in which the semantics of variables is enriched to reflect the fact that they are controlled by an implicit synchronisation protocol. Observe that the ordering \(\le \) in \(\mathbb {D} \) is transitive which permits monotonic status changes from \(\bot \) directly to \(1\), without first passing through \(0\). This means a program can set a variable (emit a signal in Esterel) which has not been explicitly reset. This matches the iur protocol, from which the notions of B/SC-admissibility are derived, which does not require an update to be preceded by an init operation. However, our fixed-point semantics can be easily modified, without changing the domain \(\mathbb {D} \), for the stronger requirement if needed.
We now go one step further in the abstraction. In the analysis we operate on predictions of variable statuses. Possible statuses of variables are approximated by closed intervals \(I(\mathbb {D}) = \{ [a, b] \mid a,b \in \mathbb {D}, a \le b \}\) over \(\mathbb {D} \). An interval \([a,b] \in I(\mathbb {D})\) in this 10-valued domain corresponds to the set of statuses \( set ([a, b]) = \{{x \mid a \le x \le b}\} \subseteq \mathbb {D} \). Intervals \([a, b]\) such that \(a < b\) denote uncertain information, i.e., a potential non-deterministic response. Such a general interval represents an approximation to the final (stable) state of a variable from its two ends, the lower bound \(a\) and the upper bound \(b\). An interval \([a,b]\) associated with a variable \(x \in V \) can thus be read as follows: “the executions of the statements so far ensure that \(x\) has currently status \(a\), yet it cannot be excluded that some statements might be executed which could change (increase) the status of \(x\) up to \(b\)”. In this vein, the intervals \([a,a]\) correspond to decided, or crisp, statuses which are naturally identified with the values \(\bot = [\bot ,\bot ]\), \(0 = [0,0]\), \(1 = [1,1]\) and \(\top = [\top ,\top ]\) of \(\mathbb {D} \), respectively, i.e., \(\mathbb {D} \subset I(\mathbb {D})\). A variable \(s \in V \) with status \(\gamma \in I(\mathbb {D})\) is denoted by \(s^\gamma \).
Example 12
When computing the reaction of fprog  , the interval for \(s\) will be \([0,1]\), assuming the status of \(x\) is not decided yet, say, \(x^{[\bot , \top ]}\). The status \(s^{[0,1]}\) for variable \(s\) indicates that a reset
, the interval for \(s\) will be \([0,1]\), assuming the status of \(x\) is not decided yet, say, \(x^{[\bot , \top ]}\). The status \(s^{[0,1]}\) for variable \(s\) indicates that a reset  must definitively be executed, but there is at least one set \({! \, \! s}\) that can potentially be executed, which is why the status of \(s\) ranges between \(0\) and \(1\). \(\square \)
must definitively be executed, but there is at least one set \({! \, \! s}\) that can potentially be executed, which is why the status of \(s\) ranges between \(0\) and \(1\). \(\square \)
On the domain \(I(\mathbb {D})\) we can define two natural orderings:
-
The point-wise ordering \([a_1,b_1] \preceq [a_2,b_2]\) iff \(a_1 \le a_2\) and \(b_1 \le b_2\), and
-
the (inverse) inclusion ordering \([a_1, b_1] \sqsubseteq [a_2, b_2]\) iff \( set ([a_2, b_2]) \subseteq set ([a_1, b_1])\),
which endow \(I(\mathbb {D})\) with a full lattice structure for \(\preceq \) and a lower semi-lattice structure for \(\sqsubseteq \). The point-wise lattice \({\langle I(\mathbb {D}), \preceq \rangle } \) has minimum element \([\bot ,\bot ]\) and the minimum for the inclusion semi-lattice \({\langle I(\mathbb {D}), \sqsubseteq \rangle } \) is \([\bot ,\top ]\). The element \([\top , \top ]\) is a maximal element for both orderings but it is the maximum only for \(\preceq \). For \(\sqsubseteq \) all singleton intervals \([a,a]\) are maximal. Join \(\vee \) and meet \(\wedge \) for the \(\preceq \)-lattice are obtained in the point-wise manner:
In the inclusion \(\sqsubseteq \)-lattice the meet \(\sqcap \) is
The semi-lattice \({\langle I(\mathbb {D}), \sqsubseteq \rangle } \) does not possess joins, but it is consistent complete, i.e., whenever in a non-empty subset \(\emptyset \ne X \subseteq \mathbb {D} \) any two elements \(x_1, x_2 \in X\) have an upper bound \(y \in \mathbb {D} \), i.e., \(x_1 \sqsubseteq y\) and \(x_2 \sqsubseteq y\), then there exists the least upper bound \(\sqcup X = \sqcap \{ y \mid \forall x \in X.\; x \sqsubseteq y \}\). This will give us least fixed-points.
Figure 3 illustrates the two-dimensional lattice structure of \(I(\mathbb {D})\). The vertical direction (upwards, green arrows) corresponds to \(\preceq \) and captures the sequential dimension of the statuses. The horizontal direction (left-to-right, blue arrows) is the inclusion ordering \(\sqsubseteq \) and expresses the degree of precision of the approximation. The most precise status description is given by the crisp values on the right side, which are \(\sqsubseteq \)-maximal and are order-isomorphic to the embedded domain \(\mathbb {D} \). The least precise information value is the interval \([\bot , \top ]\) on the left. The following Example 13 illustrates how we can use the domain \(I(\mathbb {D})\) in the fixed-point analysis to navigate in both dimensions \(\preceq \) and \(\sqsubseteq \) for determining the instantaneous response of a program.
Example 13
Consider the fprog \(P :=(x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z})) \mathrel {\Vert }(y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} )\). Suppose that we execute \(P\) in a sequential thread in which all three variables are initially pristine, i.e., with status \(x^{\bot }\), \(y^{\bot }\) and \(z^{\bot }\). What are the final values of of the variables when \(P\) is completed? Since we do not know what the memory values of \(x\) and \(y\) are, we do not know how the branches are decided, i.e., whether the first concurrent thread \(x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z}) \) will execute \(\varepsilon \) or set both variables \(y\) and \(z\) in \({! \, \! y} \mathrel {\Vert }{! \, \! z} \). Similarly, we cannot decide if the second thread \(y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \) sets \(x\) or not. Yet, what we do know is that the variables \(x\), \(y\) or \(z\) may be set but cannot crash because there is no reset on any of them. So, the best approximation for the response of \(P\), in terms of intervals \(I(\mathbb {D})\), is the final status \(x^{[\bot ,1]}\), \(y^{[\bot ,1]}\), and \(z^{[\bot ,1]}\).
Now put \(P\) in parallel with the program  . Since \(Q\) certainly executes the reset
. Since \(Q\) certainly executes the reset  and no other write accesses to \(x\), this produces the response \(x^{0}\). Combining this with the status obtained from \(P\) gives the joint response \(x^{0 \vee [\bot ,1]} = x^{[0,1]}\). This tells us that \(x\) must certainly be reset (viz. by \(Q\)) and then might be set (viz. by \(P\)). Notice how the interval \([\bot ,1]\) has shrunk to \([0,1]\), which provides tighter information. What about variable \(y\)? It is set by \(Q\) and never reset, which means its status, after executing \(Q\), is at least \(1\). By the iur protocol the set \({! \, \! y} \) must wait for any potential reset on \(y\) to have happened in the environment. In this case, \(P\) does not have a reset on \(y\), so the set \({! \, \! y} \) of \(Q\) must go ahead, giving \(y^{1}\) for the response of \(Q\). This merges with the information from \(P\) to the joint response \(y^{1 \vee [\bot ,1]} = y^{1}\).
and no other write accesses to \(x\), this produces the response \(x^{0}\). Combining this with the status obtained from \(P\) gives the joint response \(x^{0 \vee [\bot ,1]} = x^{[0,1]}\). This tells us that \(x\) must certainly be reset (viz. by \(Q\)) and then might be set (viz. by \(P\)). Notice how the interval \([\bot ,1]\) has shrunk to \([0,1]\), which provides tighter information. What about variable \(y\)? It is set by \(Q\) and never reset, which means its status, after executing \(Q\), is at least \(1\). By the iur protocol the set \({! \, \! y} \) must wait for any potential reset on \(y\) to have happened in the environment. In this case, \(P\) does not have a reset on \(y\), so the set \({! \, \! y} \) of \(Q\) must go ahead, giving \(y^{1}\) for the response of \(Q\). This merges with the information from \(P\) to the joint response \(y^{1 \vee [\bot ,1]} = y^{1}\).
But now we have narrowed down the status of \(y\) to a crisp \(1\), which implies that the conditional test \(y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \) in the second thread of \(P\) is decided. So we conclude that the set \({! \, \! x} \) must definitely be executed. Therefore, the status of \(x\) from \(P\) in our first approximation can now be tightened from \(x^{[\bot ,\top ]}\) to \(x^1\). Once we have that, the conditional \(x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z}) \) in the first thread of \(P\) is decided, too, implying that the set \({! \, \! z} \) must be executed by \(P\) implying \(1\) as a lower bound for the status of \(z\) and an increase of information from \(z^{[\bot ,1]}\) to \(z^1\). Since all three variables are now fixed to have crisp statuses \(x^1\), \(y^1\), \(z^1\), the program \(P \mathrel {\Vert }Q\) is called strongly Berry constructive. From [4] this implies that \(P \mathrel {\Vert }Q\) is sequentially constructive, i.e., SC-reactive and SC-determinate. From the results in this article it will follow that it is also B-reactive and SC-read-determinate. \(\square \)
Observe that the well-known ternary domain (Kleene) for the fixed-point analysis of Pure Esterel [12] or constructive Boolean circuits [64] is captured, as indicated in Fig. 3, by the inner part with values \([0,0]\) (“absent”), \([1,1]\) (“present”) and \([0,1]\) (“undefined”). In ternary analysis all signal variables are implicitly assumed initialised, hence no need for \(\bot \). Moreover, since there is no reset operator and thus programs cannot fail the monotonic single-change requirement, there is no need for \(\top \) either, in languages such as Esterel, as long as initialisation of signals is implemented by the run-time rather than the program. This ternary fragment of \(I(\mathbb {D})\) corresponds to three-valued Kleene logic with \(\vee \) disjunction and \(\wedge \) logical conjunction. Figure 3 visualises clearly how the 10-valued domain \(I(\mathbb {D})\) offers an extended playground to represent the logic of explicit initialisation.
Interestingly, another recent approach to enrich the standard ternary domain is the constructive semantics by Talpin et al. [77] for a multi-clocked synchronous (polysynchronous) data-flow language which integrates Quartz and Signal. This extension is based on a lattice \(\mathcal {D}\) which extends \(\{ [0,0], [1,1], [0,1] \}\) by elements \(?\) for representing unknown and  for inconsistent signal statuses similar to our \(\bot \) and \(\top \). It also contains Boolean values for “true” and “false” (embedded as refinements of the present status) which our domain \(I(\mathbb {D})\) does not model. On the other hand, the partial order \(\mathcal {D}\) of [77] does not have an interval structure like \(I(\mathbb {D})\), which is the key to modelling Esterel-style reaction to absence. This is not needed in the data-flow semantics of [77].
for inconsistent signal statuses similar to our \(\bot \) and \(\top \). It also contains Boolean values for “true” and “false” (embedded as refinements of the present status) which our domain \(I(\mathbb {D})\) does not model. On the other hand, the partial order \(\mathcal {D}\) of [77] does not have an interval structure like \(I(\mathbb {D})\), which is the key to modelling Esterel-style reaction to absence. This is not needed in the data-flow semantics of [77].
3.2 Semantic domain \(I(\mathbb {D},\mathbb {P})\) of signal status
There is one logical refinement to the domain \(I(\mathbb {D})\) that we need to make in order to keep properly track of the completion of the initialisation phase on each variable. According to the synchronous protocol a set \({! \, \! s} \) contained in a program can only go ahead if it is guaranteed that no reset  on this variable is possibly outstanding. There is no information in the intervals of \(I(\mathbb {D})\) to express that no reset is outstanding. For instance, the status \(s^{[0,1]}\) specifies that the initialisation of \(s\) has been started and that there is a waiting update access on \(s\), but it does not tell if there are any other resets
on this variable is possibly outstanding. There is no information in the intervals of \(I(\mathbb {D})\) to express that no reset is outstanding. For instance, the status \(s^{[0,1]}\) specifies that the initialisation of \(s\) has been started and that there is a waiting update access on \(s\), but it does not tell if there are any other resets  still pending. However, this is important in the constructive scheduling, because only if the initialisation phase has been completed, the waiting update \({! \, \! s} \) is permitted to proceed changing the status to \(s^{[1,1]}\).
still pending. However, this is important in the constructive scheduling, because only if the initialisation phase has been completed, the waiting update \({! \, \! s} \) is permitted to proceed changing the status to \(s^{[1,1]}\).
To capture the termination of the initialisation phase of the “init;update;read” protocol, we enrich the interval domain by an additional token \(r \in \mathbb {P} = \{ \mathsf{0 }, \mathsf{1 }, \mathsf{2 } \}\), called the init status. The status \(\mathsf{2 } \) expresses that the “init” phase is ongoing and a reset is still predicted. The status \(\mathsf{1 } \) means that no more resets are outstanding, i.e., the init phase is completed, but the protocol is still running. Finally, if the “init;update” is finished, and thus the value of the variable determined, the init status \(\mathsf{0 } \) is obtained.
As for \(I(\mathbb {D})\) there are natural sequential and information-theoretic orderings on \(\mathbb {P} \) as seen in Fig. 4. The sequential ordering \(\preceq \) is given by \(\mathsf{0 } \preceq \mathsf{1 } \preceq \mathsf{2 } \) which reflects the fact that in sequential order a finished computation (\(\mathsf{0 } \)) must first become blocked at a set or a conditional test (\(\mathsf{1 } \)) to start a running protocol, before it reaches a predicted reset  which witnesses an incomplete initialisation (\(\mathsf{2 } \)) for the reset variable \(s\). In contrast, the information ordering on \(\mathbb {P} \) is the opposite, \(\mathsf{2 } \sqsubseteq \mathsf{1 } \sqsubseteq \mathsf{0 } \), which models the narrowing of behaviour that occurs when the status of variables becomes more and more decided. The init status \(\mathsf{2 } \) is least informative. It says that the protocol is contingent and that there may still be potential resets outstanding. With the value \(\mathsf{1 } \) the protocol is still contingent but the init phase is finished, i.e., no resets are possible any more. Finally, \(\mathsf{0 } \) is the tightest status for it says that the protocol is finished and that no resets are possible.
which witnesses an incomplete initialisation (\(\mathsf{2 } \)) for the reset variable \(s\). In contrast, the information ordering on \(\mathbb {P} \) is the opposite, \(\mathsf{2 } \sqsubseteq \mathsf{1 } \sqsubseteq \mathsf{0 } \), which models the narrowing of behaviour that occurs when the status of variables becomes more and more decided. The init status \(\mathsf{2 } \) is least informative. It says that the protocol is contingent and that there may still be potential resets outstanding. With the value \(\mathsf{1 } \) the protocol is still contingent but the init phase is finished, i.e., no resets are possible any more. Finally, \(\mathsf{0 } \) is the tightest status for it says that the protocol is finished and that no resets are possible.
The domain \((\mathbb {P}, \preceq , \sqsubseteq )\) is a lattice for both \(\preceq \) and \(\sqsubseteq \) in which only the semi-lattice structure will be relevant induced by the join operations \(r_1 \vee r_2 = r_1 \sqcap r_2 = \textit{max} (r_1, r_2)\). Our definition of constructive behaviours will be based on a fixed-point analysis in the product domain
We will write a typical element \(([l,u], r) \in I(\mathbb {D},\mathbb {P})\) more compactly as \([l,u]{:}r\) and refer to the interval \([l, u]\) as the value status to separate it from the init status \(r\). If \(r = \mathsf{0 } \) we simply write \([l, u]\) instead of \([l, u]{:}\mathsf{0 } \) or even \(a\) instead of \([a,a]{:}\mathsf{0 } \). In this fashion we naturally consider \(\mathbb {D} \) as a subset of \(I(\mathbb {D},\mathbb {P})\). Generally, as before, when an interval is a singleton we write it as an element in \(\mathbb {D} \), even if its init status is not \(\mathsf{0 } \). For instance, \(0{:}\mathsf{1 } \) is the same as \([0,0]{:}\mathsf{1 } \) or \(\bot {:}\mathsf{2 } \) stands for \([\bot ,\bot ]{:}\mathsf{2 } \). These singleton intervals are contained within the dotted regions in Fig. 5.
The orderings \(\sqsubseteq \) and \(\preceq \) on \(I(\mathbb {D},\mathbb {P})\) are inherited component-wise from the corresponding orderings in the domains \(I(\mathbb {D})\) and \(\mathbb {P} \), respectively. The init status is logically part of the upper bound and so we define the upper projection on \(I(\mathbb {D},\mathbb {P})\) by stipulating \(\mathop { upp } ([l,u]{:}r) = [\bot ,u]{:}r\), and for the lower projection we set \(\mathop { low } ([l,u]{:}r) = [l,\top ]{:}\mathsf{2 } \). The same is obtained if we define the upper projection separately on \(\mathbb {P} \) as the identity, i.e., \(\mathop { upp } (r) = r\) for all \(r \in \mathbb {P} \) and the lower projection as the constant function \(\mathop { low } (r) = \mathsf{2 } \) for all \(r \in \mathbb {P} \). Then, \(\mathop { upp } \) and \(\mathop { low } \) on \(I(\mathbb {D},\mathbb {P})\) are obtained component-wise from \(\mathop { upp } \) and \(\mathop { low } \) on \(I(\mathbb {D})\) and \(\mathbb {P} \), respectively.
Note that \(I(\mathbb {D},\mathbb {P})\) is essentially a tripling of \(I(\mathbb {D})\), extending the domain \(I(\mathbb {D})\) by the information contained in \(\mathbb {P} \).Footnote 4 This is illustrated Fig. 5.
Example 14
Consider the fprog  . Suppose we do not know anything about the status of \(x\) in the current environment. This is captured by the status \(x^{[\bot ,\top ]{:}\mathsf{2 }}\) which is the \(\sqsubseteq \)-minimal element in \(I(\mathbb {D},\mathbb {P})\). It not only leaves open the full range \([\bot ,\top ]\) for the value status of \(x\). The init status \(\mathsf{2 } \) models an unfinished “init” and a possible outstanding reset on \(x\). Now, if the status of \(x\) is so maximally undetermined, the conditional
. Suppose we do not know anything about the status of \(x\) in the current environment. This is captured by the status \(x^{[\bot ,\top ]{:}\mathsf{2 }}\) which is the \(\sqsubseteq \)-minimal element in \(I(\mathbb {D},\mathbb {P})\). It not only leaves open the full range \([\bot ,\top ]\) for the value status of \(x\). The init status \(\mathsf{2 } \) models an unfinished “init” and a possible outstanding reset on \(x\). Now, if the status of \(x\) is so maximally undetermined, the conditional  is undecided. We cannot say if the initial reset
is undecided. We cannot say if the initial reset  in \(P\) is followed by the set \({! \, \! s} \) or the reset
in \(P\) is followed by the set \({! \, \! s} \) or the reset  . Consequently, the response of \(P\) for \(s\) will be \([0,1]{:}\mathsf{2 } \). The init status \(\mathsf{2 } \) indicates that the protocol execution of \(P\) on \(s\) is speculative and that there is a possible reset on \(s\) which may become active. The response of \(P\) on variable \(x\), on the other hand, yields \(x^{\bot {:}\mathsf{1 }}\) because the value status is guaranteed to remain pristine but that the computation is nevertheless speculative (because of the blocked conditional test on \(x\)).
. Consequently, the response of \(P\) for \(s\) will be \([0,1]{:}\mathsf{2 } \). The init status \(\mathsf{2 } \) indicates that the protocol execution of \(P\) on \(s\) is speculative and that there is a possible reset on \(s\) which may become active. The response of \(P\) on variable \(x\), on the other hand, yields \(x^{\bot {:}\mathsf{1 }}\) because the value status is guaranteed to remain pristine but that the computation is nevertheless speculative (because of the blocked conditional test on \(x\)).
When the state of \(x\) becomes decided with a crisp \(x^{0} = x^{[0,0]{:}\mathsf{0 }}\), then the conditional is switched through into the left branch containing the reset  and the response of \(P\) for \(s\) refines into \(0= [0,0]{:}\mathsf{0 } \), too. When \(x\) is decided present \(x^1\) then the conditional is unblocked and the set \({! \, \! s} \) is executed. Hence, the response for \(s\) becomes \(1 = [1,1]{:}\mathsf{0 } \). Both responses for \(s\) have init status \(\mathsf{0 } \) stating that the “init;update;read” protocol on \(s\) is completed. \(\square \)
and the response of \(P\) for \(s\) refines into \(0= [0,0]{:}\mathsf{0 } \), too. When \(x\) is decided present \(x^1\) then the conditional is unblocked and the set \({! \, \! s} \) is executed. Hence, the response for \(s\) becomes \(1 = [1,1]{:}\mathsf{0 } \). Both responses for \(s\) have init status \(\mathsf{0 } \) stating that the “init;update;read” protocol on \(s\) is completed. \(\square \)
Example 15
Consider a reset followed by a set, i.e., the cprog  . Let us schedule the micro-steps of \(P\) starting from the sequential status \(S_0 = x^{\bot }\), or equivalently, \(S_0 = x^{[\bot ,\bot ]{:}\mathsf{0 }}\). This represents a fully determined initial memory of unknown value. The reset
. Let us schedule the micro-steps of \(P\) starting from the sequential status \(S_0 = x^{\bot }\), or equivalently, \(S_0 = x^{[\bot ,\bot ]{:}\mathsf{0 }}\). This represents a fully determined initial memory of unknown value. The reset  is the first micro-step of \(P\) to be scheduled, raising the status of \(x\) to \(S_1 = x^0\). The init status is still \(\mathsf{0 } \) because the reset terminates instantaneously. Thus, we reach the set \(P' :={! \, \! x} \) as the continuation program. To be scheduled the set must wait for the completion of the init phase which depends on the concurrent environment. In the environment \(C_0 :=x^{[\bot ,\top ]{:}\mathsf{2 }}\) our sequential thread is blocked at the set. However, what we can conclude about the sequential response of \(P\) is that \(x\) undergoes a reset and then possibly a set, yielding the final status \(S_2 :=x^{[0,1]{:}\mathsf{1 }}\). We cannot put the lower bound to \(1\) because we have no guarantee that the set is actually executed. Also, the init status \(\mathsf{1 } \) informs the environment that the “init;update” in \(P\) is blocked but \(P\) does not produce any further resets, if it ever were to be continued. Assuming that \(P\) is running alone by itself we can strengthen the initial approximation \(C_0\) of the environment by \(C_1 :=S_2\) and reanalyse \(P\), again from the sequential status \(S_0\). Now as we reach the set \({! \, \! x} \), the refined environment \(C_1\) with init status \(\mathsf{1 } \) unblocks the set \({! \, \! x} \) and we obtain the final sequential status \(S_3 :=x^{1}\). \(\square \)
is the first micro-step of \(P\) to be scheduled, raising the status of \(x\) to \(S_1 = x^0\). The init status is still \(\mathsf{0 } \) because the reset terminates instantaneously. Thus, we reach the set \(P' :={! \, \! x} \) as the continuation program. To be scheduled the set must wait for the completion of the init phase which depends on the concurrent environment. In the environment \(C_0 :=x^{[\bot ,\top ]{:}\mathsf{2 }}\) our sequential thread is blocked at the set. However, what we can conclude about the sequential response of \(P\) is that \(x\) undergoes a reset and then possibly a set, yielding the final status \(S_2 :=x^{[0,1]{:}\mathsf{1 }}\). We cannot put the lower bound to \(1\) because we have no guarantee that the set is actually executed. Also, the init status \(\mathsf{1 } \) informs the environment that the “init;update” in \(P\) is blocked but \(P\) does not produce any further resets, if it ever were to be continued. Assuming that \(P\) is running alone by itself we can strengthen the initial approximation \(C_0\) of the environment by \(C_1 :=S_2\) and reanalyse \(P\), again from the sequential status \(S_0\). Now as we reach the set \({! \, \! x} \), the refined environment \(C_1\) with init status \(\mathsf{1 } \) unblocks the set \({! \, \! x} \) and we obtain the final sequential status \(S_3 :=x^{1}\). \(\square \)
The status of variables and their evolutions over time are kept in discrete structures, called environments \(E: V \rightarrow I(\mathbb {D}, \mathbb {P})\) mapping each variable \(x \in V \) to a status \(E(x) \in I(\mathbb {D}, \mathbb {P})\). The orderings and (semi-)lattice operations are lifted to environments by stipulating
If \(E(x) = [a, b]{{:}r}\) then we will also write \(x^{[a,b]{{:}r}} \in E\) and further \(x^{a} \in E\) when \(E(x) = [a, a]{{:}\mathsf{0 }}\). Using this notation we can view environments as sets of variable statuses \(E = \{ x^{[a,b]{{:}r}} \mid E(x) = [a,b]{{:}r} \}\) with the property that if \(x^{[a,b]{{:}r}} \in E\) and \(x^{[a',b']{{:}r'}} \in E\), then \(a = a'\) and \(b = b'\) and \(r = r'\).
It is natural to identify the values \([a,b]{{:}r} \in I(\mathbb {D})\) with constant environments such that \(([a,b]{{:}r})(x) = [a,b]{{:}r}\) for all \(x \in V \). An environment \(E\) is called decided if for all variables \(x \in V \) there exists \(b \in \mathbb {D} \) with \(b{:}\mathsf{1 } \sqsubseteq E(x)\); crisp if for all variables \(x \in V \) there exists \(b \in \mathbb {D} \) such that \(b \sqsubseteq E(x)\); ternary if \(E(x) \in \{0, 1, [0,1] \}\) for all variables \(x \in V \); crash-free if \(E(x) \preceq 1{{:}\mathsf{2 }}\) for all \(x \in V \). An environment \(E\) in which all entries are one-sided lower (upper) intervals, i.e., in which \(x^{[a,b]{{:}r}} \in E\) implies \(b = \top \) and \(r = \mathsf{2 } \) (\(a = \bot \)) is called a lower (upper) environment. Every environment can be separated into its lower and upper projections
so that
where the join exists since \(\mathop { low } (E) \sqsubseteq E\) and \(\mathop { upp } (E) \sqsubseteq E\), i.e., \(\mathop { low } (E)\) and \(\mathop { upp } (E)\) are always consistent. Observe further that \(\mathop { low } (E) = E \vee [\bot ,\top ]{:}\mathsf{2 } = E \sqcap \top {:}\mathsf{2 } \) and \(\mathop { upp } (E) = E \sqcap \bot {:}\mathsf{0 } \).
We use the set-like notation \(\{\!\langle {x_1^{\gamma _1}, x_2^{\gamma _2}, \ldots , x_n^{\gamma _n}}\rangle \!\} \) to specify a finite environment that explicitly sets the status for the listed variables \(x_i\) and implicitly defines the status \(\bot \) for all other variables \(z \in V {\setminus }\{ x_1, x_2, \ldots , x_n \}\). Then, the empty environment \(\{\!\langle {\,}\rangle \!\} = \bot \ = [\bot ,\bot ]{:}\mathsf{0 } \) is the neutral element for \(\vee \) which acts as the operator for set union.
Example 16
Let \(S_1 = \{\!\langle {x^0, y^{[0,\top ]{{:}\mathsf{2 }}}}\rangle \!\} \) and \(S_2 = \{\!\langle {x^{[\bot ,1]{{:}\mathsf{1 }}}, z^{[0,1]}}\rangle \!\} \). Then, \(S_1 = \{\!\langle {x^0}\rangle \!\} \vee \{\!\langle {y^{[0,\top ]{{:}\mathsf{2 }}}}\rangle \!\} \), \(S_2 = \{\!\langle {x^{[\bot ,1]{{:}\mathsf{1 }}}}\rangle \!\} \vee \{\!\langle {z^{[0,1]}}\rangle \!\} \) and
\(\square \)
3.3 Domain \(I(\mathbb {C})\) of completion status
The completion status for an fprog \(P\) in concurrent environment \(C\) is given by a set of completion codes \( cmpl ^{}\langle P, C \rangle \subseteq \mathbb {C} :=\{ \bot , 0, 1 \}\) which model the uncertainty about the termination behaviour of \(P\), analogous to the status intervals for signal variables. The code \(0 \) stands for instantaneous (normal) termination, \(1 \) for pausing and \(\bot \) for blocking to model a situation when a program’s control flow is stuck at a conditional test which cannot be decided. These completion codes \(\mathbb {C} \) must not to be confused with the signal statuses in \(\mathbb {D} \).
What is the information content of a subset \( cmpl ^{}\langle P, C \rangle \subseteq \mathbb {C} \) of completion codes? When \(c \in cmpl ^{}\langle P, C \rangle \) then \(c\) is a possible completion of \(P\), but it is not guaranteed unless \( cmpl ^{}\langle P, C \rangle = \{c \}\) is a singleton, in which case \(c\) must be the completion type of \(P\). Otherwise, if \(c' \ne c\) with \(c' \in cmpl ^{}\langle P, C \rangle \), then \(c'\) is another type of completion that can happen for \(P\) in environment \(C\). Complementarily, if \(c \not \in cmpl ^{}\langle P, C \rangle \) then \(c\) cannot occur. The “must” and “cannot” information |which is the basis for defining the completion semantics of programs in Esterel| is completely captured by the five subsets
The sets \(\{ \}\), \(\{0, 1\}\) and \(\{ \bot \}\) are missing because every program must at least possibly terminate instantaneously or possibly pause, and if a program possesses both possible codes \(0\) and \(1\) then this is so because some conditional test cannot be decided, which means it is blocked. So, \(\bot \) must be a possible code for this program, too.Footnote 5
The precise relation between \(I(\mathbb {C})\) to the completion codes of Esterel [12] is given by defining the sets
of codes that must and cannot/can be obtained by program \(P\) in environment \(C\), respectively. We observe that \( must _k(P, C) \cap cannot _k(P, C) = \emptyset \) and that both \( must _k(P, C) \ne \{0, 1\}\) and \( cannot _k(P, C) \ne \{0, 1\}\). This makes sense since must and cannot completions are contradictory and there is no program which must terminate and must pause at the same time, or cannot terminate and cannot pause at the same time. Since we do not consider completion codes for traps, every program can at least potentially terminate or pause. More specifically, \( must _k(P,C)\) and \( cannot _k(P,C)\) are either empty \(\emptyset \) or a singleton set \(\{ 0 \}\) or \(\{ 1 \}\). Also, directly from the definition we find that if \( must _k(P,C)\) is a singleton, then \( cannot _k(P,C)\) is the complementary singleton set, i.e., \( must _k(P,C) = \{0\}\) implies \( cannot _k(P,C) = \{1\}\) and \( must _k(P,C) = \{1\}\) implies \( cannot _k(P,C) = \{0\}\). Finally, \( must _k(P,C) = \emptyset \) iff \(\bot \in cmpl ^{}\langle P, C \rangle \) and \( cannot _k(P,C) = \emptyset \) iff \( cmpl ^{}\langle P, C \rangle = \{ \bot , 0, 1 \}\).
Note that (i) every \(P\) has at least one possible completion status, i.e., \(0 \in cmpl ^{}\langle P, C \rangle \) or \(1 \in cmpl ^{}\langle P, C \rangle \) and (ii) if we cannot decide whether \(P\) terminates instantaneously or pauses then this is because we cannot decide if \(P\) completes at all, i.e., if \(\{ 0, 1 \} \subseteq cmpl ^{}\langle P, C \rangle \) then \(\bot \in cmpl ^{}\langle P, C \rangle \). This explains why not all of the eight possible subsets of \(\mathbb {C} \) can occur as the completion status of a program.
4 Denotational semantics of synchronous programs
Now that the technical apparatus of status intervals and environments is in place it is time to put it to use. What we will do in this section is to introduce an extended version of the causality analysis for Esterel, which includes initialisation. This analysis defines the class of constructive programs. This analysis performs an abstract program simulation using the interval environments \(I(\mathbb {D}, \mathbb {P})\) introduced above. To keep matters simple we consider only finite pSCL programs (fprogs), i.e., programs without \(\mathop { rec } \). This is without loss of generality. Since well-formed pSCL programs are clock-guarded, we can unfold all loops and extract finite \(\mathop { rec } \)-free expressions that fully describe the program’s macro step reactions. We first describe the computation of completion codes in Sect. 4.1 and then the computation of program responses in Sect. 4.2.
4.1 Computing completion codes
How are completion codes computed for a program \(P\) and environment \(C\)? As for the response semantics \(\langle \!\langle P \rangle \!\rangle ^{{}}_{{}}\) this is done by structural recursion on \(P\). However, while the computation of the sets \( must _k(P,C)\) and \( cannot _k(P,C)\) in [12] is performed separately through a combinatorial construction, we here give a uniform and algebraic definition of the same information for \( cmpl ^{}\langle P, C \rangle \). Specifically, we exploit that \(I(\mathbb {C})\), like \(I(\mathbb {D})\), forms a meet semi-lattice under the (inverse) inclusion ordering \(\sqsubseteq \), i.e., \(\gamma _1 \sqsubseteq \gamma _2\) iff \(\gamma _2 \subseteq \gamma _1\). The completion set \(\{\bot , 0, 1 \}\) is the minimal element in \(I(\mathbb {C})\) and the meet \(\sqcap \) is \(\gamma _1 \sqcap \gamma _2 = \gamma _2 \sqcap \gamma _1 = \gamma _1\) if \(\gamma _1 \sqsubseteq \gamma _2\) and \(\gamma _1 \sqcap \gamma _2 = \{\bot , 0, 1 \}\) if \(\gamma _1\) and \(\gamma _2\) are \(\sqsubseteq \)-incomparable. Let \(\oplus \) be the strict lifting of Boolean summation to \(\mathbb {C} \), i.e., \(0 \oplus 1 = 1 = 1 \oplus 0 = 1 \oplus 1 \) and \(0 \oplus 0 = 0 \), while \(x \oplus y = \bot \) iff \(x = \bot \) or \(y = \bot \). This can then further be lifted to completion sets, \(\gamma _1 \oplus \gamma _2 :=\{ x \oplus y \mid x \in \gamma _1, y \in \gamma _2\}\). Notice that if we consider the completion codes \(0 \) and \(1 \) as numbers, then \(\oplus \) is the same as \(\textit{max} \). Indeed, \(\oplus \) on \(I(\mathbb {C})\) is analogous to \(\vee \) on \(I(\mathbb {D})\). The upper projection is given by \(\mathop { upp } (\gamma ) :=\gamma \cup \{ \bot \}\). One shows that \(\oplus \) and \(\mathop { upp } \) are well-defined on \(I(\mathbb {C})\) and monotonic with respect to \(\sqsubseteq \).
The function \( cmpl ^{}\langle P, C \rangle \in I(\mathbb {C})\) is as described in Fig. 6. One shows by induction on \(P\) that if \(P\) is purely combinational, i.e., it does not contain the \(\pi \) operator, then \( cmpl ^{}\langle P, C \rangle = \{ 0\}\) or \( cmpl ^{}\langle P, C \rangle = \{ \bot , 0 \}\). Furthermore, it is easy to see that the only way in which the status \(\bot \) can enter the completion set is through the ‘otherwise’ case of a set or a conditional. More strictly, we have \(\bot \in cmpl ^{}\langle P, C \rangle \) iff (i) the control flow reaches some set \({! \, \! s} \) in \(P\) which is blocked on the condition \([\bot , \top ]{:}\mathsf{1 } \not \sqsubseteq C(s)\), or (ii) there is some conditional \(s \, \mathrel {?} \, P' \mathrel {:} Q' \) executed in \(P\) for which the guard variable \(s\) is undecided, i.e., \(1{:}\mathsf{1 } \not \sqsubseteq C(s)\) and \(0{:}\mathsf{1 } \not \sqsubseteq C(s)\). The condition \([\bot , \top ]{:}\mathsf{1 } \sqsubseteq C(s)\) in the definition of \( cmpl ^{}\langle {! \, \! s}, C \rangle \) requires that the init status of \(C(s)\) is at most \(\mathsf{1 } \), i.e., that initialisations  are no longer possible. However, this does not constrain the value status. If we wanted to make a set \({! \, \! s} \) wait for at least one initialisation
are no longer possible. However, this does not constrain the value status. If we wanted to make a set \({! \, \! s} \) wait for at least one initialisation  to take place, we could strengthen the condition \([\bot , \top ]{:}\mathsf{1 } \sqsubseteq C(s)\) to \([0, \top ]{:}\mathsf{1 } \sqsubseteq C(s)\).
to take place, we could strengthen the condition \([\bot , \top ]{:}\mathsf{1 } \sqsubseteq C(s)\) to \([0, \top ]{:}\mathsf{1 } \sqsubseteq C(s)\).
Example 17
The completion intervals \(\{ 0 \}\) and \(\{ 1 \}\) are obtained from the pSCL expressions \(\varepsilon \) and \(\pi \), respectively. The intervals \(\{\bot , 0 \}\) and \(\{\bot , 1 \}\) are the completion codes for expressions \(x \, \mathrel {?} \, \varepsilon \mathrel {:} \varepsilon \) and \(x \, \mathrel {?} \, \pi \mathrel {:} \pi \) in every concurrent environment \(C\) with \(0{:}\mathsf{1 } \not \sqsubseteq C\) and \(1{:}\mathsf{1 } \not \sqsubseteq C\). Finally, if \(x\) is undecided, we get \( cmpl ^{}\langle x \, \mathrel {?} \, \varepsilon \mathrel {:} \pi , C \rangle = \{ \bot , 0, 1 \}\). The completion statuses \(\{\bot , 0 \}\) and \(\{\bot , 1 \}\) may also be obtained from programs \({! \, \! x} \mathrel {;} \varepsilon \) and \({! \, \! x} \mathrel {;} \pi \), respectively, in an environment \(C\) where \(\bot {:}\mathsf{2 } \preceq C(x)\). \(\square \)
4.2 Computing program responses
The denotational semantics of a fprog \(P\) is given by a function \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) that determines constructive information on the instantaneous response of \(P\) to an external stimulus consisting of a sequential environment \(S\) and a concurrent environment \(C\). The sequential context \(S\) can be thought of as an initialisation under which \(P\) is activated. It represents knowledge about the status of variables sequentially before \(P\) is started. In contrast, the parallel environment \(C\) contains the external stimulus which is concurrent with \(P\). The lower bound \(\mathop { low } \,\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) of the response tells us what \(P\) must write to the variables and the upper bound \(\mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) is the level that the variables may reach upon execution of \(P\).
The function \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) is defined by recursion on the structure of the fprog \(P\) as seen in Fig. 7.
-
The empty fprog \(\langle \!\langle \varepsilon \rangle \!\rangle ^{{S}}_{{C}}\) passes out its sequential stimulus \(S\) and does not add anything to it. The same applies to the pausing program \(\pi \).
Fig. 7 Denotational response analysis for fprogs (the function \( cmpl ^{}\langle P, C \rangle \) is explained in Fig. 6
-
The result of resetting a variable
 depends on whether the sequential stimulus \(S\) already contains a status \(1\) for \(s\) or not and on the init status for \(s\):
depends on whether the sequential stimulus \(S\) already contains a status \(1\) for \(s\) or not and on the init status for \(s\):-
If \(1 \preceq S(s) \preceq \top \), then the sequential status is \(S(s) = [l,u]{:}r\) where the value status \([l,u]\) is one of \(\{ 1, [1,\top ], \top \}\) and the init status is \(r = \mathsf{0 } \). This indicates that \(s\) must have been set sequentially before the execution of the reset
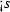 . Hence, we must crash \(s\) since a change from \(1\) to \(0\) falls outside of the model. Also, \(r = \mathsf{0 } \) means that the scheduling control flow has reached the reset
. Hence, we must crash \(s\) since a change from \(1\) to \(0\) falls outside of the model. Also, \(r = \mathsf{0 } \) means that the scheduling control flow has reached the reset  and since it terminates instantaneously the down-stream computation continues with the init status \(\mathsf{0 } \). All other variables \(x \ne s\) retain their status from \(S\). This is what \(S \vee \{\!\langle {s^\top }\rangle \!\} \) achieves, viz. \((S \vee \{\!\langle {s^\top }\rangle \!\})(s) = S(s) \vee \{\!\langle {s^\top }\rangle \!\} (s) = S(s) \vee \top = \top \) and \((S \vee \{\!\langle {s^\top }\rangle \!\})(x) = S(x) \vee \{\!\langle {s^\top }\rangle \!\} (x) = S(x) \vee \bot = S(x)\).
and since it terminates instantaneously the down-stream computation continues with the init status \(\mathsf{0 } \). All other variables \(x \ne s\) retain their status from \(S\). This is what \(S \vee \{\!\langle {s^\top }\rangle \!\} \) achieves, viz. \((S \vee \{\!\langle {s^\top }\rangle \!\})(s) = S(s) \vee \{\!\langle {s^\top }\rangle \!\} (s) = S(s) \vee \top = \top \) and \((S \vee \{\!\langle {s^\top }\rangle \!\})(x) = S(x) \vee \{\!\langle {s^\top }\rangle \!\} (x) = S(x) \vee \bot = S(x)\). -
If \(1{:}\mathsf{1 } \preceq S(s)\) then \(S(s) = [l, u]{:}r\) with a value status \([l, u]\) in the set \(\{ 1, [1,\top ], \top \}\) as above, but now the init status is \(r \succeq \mathsf{1 } \). Hence the up-stream computation must have set the variable but is still contingent, so that the
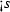 is speculative. In this case we crash the value status and raise the init status to \(\mathsf{2 } \) since the reset is executed only speculatively. We must consider it as a possibly outstanding reset. The response, therefore is \(S \vee \{\!\langle {s^{\top {:}\mathsf{2 }}}\rangle \!\} \).
is speculative. In this case we crash the value status and raise the init status to \(\mathsf{2 } \) since the reset is executed only speculatively. We must consider it as a possibly outstanding reset. The response, therefore is \(S \vee \{\!\langle {s^{\top {:}\mathsf{2 }}}\rangle \!\} \). -
If \(S(s) \preceq 0\) then the sequential status of \(s\) is one of \(S(s) \in \{ \bot , [0, \bot ], 0 \}\) again with init status \(\mathsf{0 } \). This says that the upstream computation has finished and \(s\) cannot have been set before. So we can execute the reset by returning \((S \vee \{\!\langle {s^0}\rangle \!\})(s) = 0\). The init status stays \(\mathsf{0 } \) because the schedule passes the reset
 which terminates instantaneously.
which terminates instantaneously. -
If \(\bot {:}\mathsf{1 } \preceq S(s) \preceq 0{:}\mathsf{2 } \) then \(S(s) = [l, u]{:}r\) with \(u \le 0\) and \(\mathsf{1 } \preceq r\). The constraint \(u \le 0\) again guarantees that \(s\) is not set before while \(\mathsf{1 } \preceq r\) tells us that the up-stream schedule is contingent. Consequently, we must put the init status to \(\mathsf{2 } \) to record that the
 is only speculative. This gives the response \((S \vee \{\!\langle {s^{0{:}\mathsf{2 }}}\rangle \!\})(s) = 0{:}\mathsf{2 } \).
is only speculative. This gives the response \((S \vee \{\!\langle {s^{0{:}\mathsf{2 }}}\rangle \!\})(s) = 0{:}\mathsf{2 } \). -
Finally, the remaining cases are \(S(s) = [l,u]:r\), where \(l < 1\), \(u \ge 1\) and \(\mathsf{1 } \preceq r\). These cases are subsumed by the constraint \([\bot ,1]{:}\mathsf{1 } \preceq S(s) \preceq [0,\top ]{:}\mathsf{2 } \). These statuses say that \(s\) may have been set before. We can neither be sure that a set on \(s\) must have happened earlier, nor that it cannot have happened. So, the execution of
 may crash the model, whence the result \(S \vee \{\!\langle {s^{[0,\top ]:\mathsf{2 }}}\rangle \!\} \) forces the value status of \(s\) to be \([0,\top ]\). The init status must be \(\mathsf{2 } \) because the speculative control flow passes a reset.
may crash the model, whence the result \(S \vee \{\!\langle {s^{[0,\top ]:\mathsf{2 }}}\rangle \!\} \) forces the value status of \(s\) to be \([0,\top ]\). The init status must be \(\mathsf{2 } \) because the speculative control flow passes a reset.
-
-
Setting a variable \(\langle \!\langle {! \, \! s} \rangle \!\rangle ^{{S}}_{{C}}\) updates the sequential environment \(S\) with the status \(s^1\) for variable \(s\). However, the “init;update;read” protocol permits a set \({! \, \! s} \) to be executed only if and when the init phase on \(s\) has been completed. This is checked by the condition \([\bot , \top ]{:}\mathsf{1 } \sqsubseteq C(s)\) on the environment which is the same as \(C(s) \preceq \top {:}\mathsf{1 } \). If \(C(s) \preceq \top {:}\mathsf{1 } \) then \(C(s) = [l, u]{:}r\) with \(r \preceq \mathsf{1 } \). Thus, there cannot be any contingent reset still outstanding and we can execute the set \({! \, \! s} \) which terminates instantaneously. This gives the response \((S \vee \{\!\langle {s^1}\rangle \!\})(s) = S(s) \vee 1\). On the other hand, if \(C(s) \not \preceq \top {:}\mathsf{1 } \), then the update \({! \, \! s} \) is blocked and only executed speculatively. In this case, the set \({! \, \! s} \) only forces the status of \(s\) to be in the interval \([\bot ,1]\). This leaves open if the set is actually executed or not. Also, the init status for all variables must be set to \(\mathsf{1 } \) in order to inform any sequential successor that its execution is only speculative rather than factual. Hence our definition of the response as \(S \vee \{\!\langle {s^{[\bot ,1]}}\rangle \!\} \vee \bot {:}\mathsf{1 } \).
-
The response of a parallel \(\langle \!\langle P \!\mathrel {\mid \!\mid }\! Q \rangle \!\rangle ^{{S}}_{{C}}\) is obtained by letting each of the children \(P\), \(Q\) react to the \(S\) and \(C\) environments, independently, and then combine their responses using \(\vee \). This implements a logical disjunction on Boolean values and implements the idea that in B-admissible executions resets happen before any concurrent sets of a variable. If one of \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) or \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C}}\) generates a crash, then the composition \(\langle \!\langle P \!\mathrel {\mid \!\mid }\! Q \rangle \!\rangle ^{{S}}_{{C}}\) does so, too. Also the init status of combined with the join \(\vee \) operator: the schedule of the “init;update” phases on a variable \(s\) in the parallel composition is completed, \(\langle \!\langle P \!\mathrel {\mid \!\mid }\! Q \rangle \!\rangle ^{{S}}_{{C}}(s) \preceq \top {:}\mathsf{0 } \) if and only if the scheduling of both threads is completed, i.e., if both \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} (s) \preceq \top {:}\mathsf{0 } \) and \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C}} (s) \preceq \top {:}\mathsf{0 } \) Further, the schedule of \(P \!\mathrel {\mid \!\mid }\! Q \) is blocked and has a speculative reset, \(\langle \!\langle P \!\mathrel {\mid \!\mid }\! Q \rangle \!\rangle ^{{S}}_{{C}}(s) \succeq \bot {:}\mathsf{2 } \) iff in one of the threads a reset is pending, i.e., if \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} (s) \succeq \bot {:}\mathsf{2 } \) or \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C}} (s) \succeq \bot {:}\mathsf{2 } \).
-
In order to derive information about the variables’ status under arbitrary SC-admissible scheduling, conditionals need to be evaluated cautiously. The result of a branching test \(s \, \mathrel {?} \, P \mathrel {:} Q \) can only be predicted if and when the value of \(s\) has been firmly established as a decided \(0\) or \(1\) under all possible SC-admissible schedules. The decision value for \(s\) is taken from the concurrent environment \(C\). Accordingly, if \(1{:}\mathsf{1 } \sqsubseteq C(s)\) then \(\langle \!\langle s \, \mathrel {?} \, P \mathrel {:} Q \rangle \!\rangle ^{{S}}_{{C}}\) behaves like \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) and if \(0{:}\mathsf{1 } \sqsubseteq C(s)\) the result of the evaluation is \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C}}\). As long as the value of \(s\) is still undecided, i.e., if \(1{:}\mathsf{1 } \not \sqsubseteq C(s)\) and \(0{:}\mathsf{1 } \not \sqsubseteq C(s)\), we cannot know if branch \(P\) or \(Q\) will be executed. However, at least the write accesses already recorded in the sequential environment \(S\) must become effective. This gives the condition \(\mathop { low } \,\langle \!\langle s \, \mathrel {?} \, P \mathrel {:} Q \rangle \!\rangle ^{{S}}_{{C}} = \mathop { low } (S)\) for the lower bound. A write access may be produced by \(s \, \mathrel {?} \, P \mathrel {:} Q \) if it may be generated by \(S\) or by one of the branches \(P\) or \(Q\). So, we speculatively compute the response of \(P\) and \(Q\) in the sequential environment \(S \vee \bot {:}\mathsf{1 } \). This sets the init status of all variables to \(\mathsf{1 } \) (at least) in order to mark all write accesses in \(P\) and \(Q\) as speculative. This implies \(\mathop { upp } \,\langle \!\langle s \, \mathrel {?} \, P \mathrel {:} Q \rangle \!\rangle ^{{S}}_{{C}} = \mathop { upp } (S) \vee \mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}\) for the upper bound. Both can be expressed by the single equation \(\langle \!\langle s \, \mathrel {?} \, P \mathrel {:} Q \rangle \!\rangle ^{{S}}_{{C}} = S \vee \mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S\,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S\,\vee \bot {:}\mathsf{1 }}}_{{C}}\) which is seen as follows:
$$\begin{aligned}&\mathop { low } (S \vee \mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S\,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}) \\&\quad = \mathop { low } (S) \vee \mathop { low } \,(\mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}) \vee \mathop { low } \,\mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \\&\quad = \mathop { low } (S) \vee [\bot ,\top ]:\mathsf{2 } \vee [\bot ,\top ]:\mathsf{2 } \\&\quad = \mathop { low } (S) \vee [\bot ,\top ]:\mathsf{2 } \\&\quad = S \vee [\bot ,\top ]:\mathsf{2 } \vee [\bot ,\top ]:\mathsf{2 } \;=\; S \vee [\bot ,\top ]:\mathsf{2 } \;=\; \mathop { low } (S) \end{aligned}$$by the properties of \(\vee \) and the projections and similarly
$$\begin{aligned}&\mathop { upp } (S \vee \mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}) \\&\quad = \mathop { upp } (S) \vee \mathop { upp } \,\mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}) \vee \mathop { upp } \,\mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \\&\quad = \mathop { upp } (S) \vee \mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}. \end{aligned}$$Notice that \(\mathop { upp } \, \langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}\) is the same as \(\mathop { upp } (\langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}} \sqcap \langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}})\), the upper projection of the best over-approximation of both \(\langle \!\langle P \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}\) and \(\langle \!\langle Q \rangle \!\rangle ^{{S \,\vee \bot {:}\mathsf{1 }}}_{{C}}\). It is here that the meet operator \(\sqcap \) is hidden in the semantics.
-
The response of a sequential composition \(P\mathrel {;}Q \) depends on a set of possible completion codes \( cmpl ^{}\langle P, C \rangle \subseteq \{ \bot , 0 , 1\}\) from which we can tell whether \(P\) is known to terminate or pause or neither. The code \(0 \) stands for instantaneous termination, \(1 \) for pausing and \(\bot \) for “unknown” or “blocked”, to model the situation when \(P\)’s control flow is stuck at a conditional test which cannot be decided. If \(0 \not \in cmpl ^{}\langle P, C \rangle \) then \(P\) cannot terminate instantaneously. In this case, \(Q\) will never be executed in the current instant, so that \(\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\). However, if \( cmpl ^{}\langle P, C \rangle = \{ 0 \}\), then \(P\) is guaranteed to terminate instantaneously. Thus, the overall response \(\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}}\) is that of \(Q\) reacting to the concurrent stimulus \(C\) and using the response \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) as the sequential stimulus. Otherwise if \(0 \in cmpl ^{}\langle P, C \rangle \) and \( cmpl ^{}\langle P, C \rangle \ne \{ 0 \}\), then this means that some conditional test on the execution path in \(P\) cannot be decided in \(C\). Thus, it is not known yet how \(P\) will complete and, as a consequence, if \(Q\) will be executed. Therefore, we can only say a variable must be written by \(P\mathrel {;}Q \) if it must be written by \(P\) in the present environments \(S\) and \(C\). This leads to \(\mathop { low } \,\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}} = \mathop { low } \,\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\). As regards upper bounds, a variable may be written if it may be written by \(Q\) with the response of \(P\) as its sequential stimulus: \(\mathop { upp } \,\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}} = \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}}}_{{C}}\). One can show, as above in the case of conditionals, that both lower and upper bound equations can be combined into \(\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \vee \mathop { upp } \, \langle \!\langle Q \rangle \!\rangle ^{{\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}}}_{{C}}\), or equivalently \(\langle \!\langle P\mathrel {;}Q \rangle \!\rangle ^{{S}}_{{C}} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \sqcap \langle \!\langle Q \rangle \!\rangle ^{{\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}}}_{{C}}\).
Example 18
Consider the fprog \(P :=(x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z})) \mathrel {\Vert }(y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} )\) with the environments \(S = \{\!\langle {\;}\rangle \!\} = \bot \) and \(C_0 = \{\![{\;}]\!\} = [\bot ,\top ]{:}\mathsf{2 } \). The response \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_0}}\) is the information to be got from a single pass through \(P\) without letting \(P\) communicate with itself. In doing that the sequential environment \(S\) sums up the variable status that has been established by the upstream control flow as the execution reaches \(P\). The environment \(C_0\) accumulates our information about the global status of all variables, including the concurrent environment in which \(P\) is running. Considering that neither \(x\) nor \(y\) is decided in \(C_0\), both the conditionals block. Since the updates \({! \, \! x} \), \({! \, \! y} \), \({! \, \! z} \) may possibly be executed and there is no later reset, the variables’ expected status is at least \(\bot \) and at most \(1\), i.e., \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \, \{\!\langle {x^{[\bot ,1]}, y^{[\bot ,1]}, z^{[\bot ,1]}}\rangle \!\} \). The init status \(\bot {:}\mathsf{1 } \) is imposed to record that the computation for all variables is incomplete, yet there is no contingent reset for any of them. Indeed, this is what the calculation using Fig. 7 obtains: The response of the first thread is
Similarly, we obtain \(\langle \!\langle y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \, \{\!\langle {x^{[\bot ,1]}}\rangle \!\} \) for the second thread. Joined together, the parallel composition then is
as claimed.
Without further assumptions on the environment this is the end of the story, none of the variables’ value status can be decided beyond \([\bot ,1]\). One shows that \( cmpl ^{}\langle P, C_0 \rangle = \{\bot , 0\}\), i.e., \(P\) does not terminate. Now put \(P\) in parallel with fprog  , to continue the discussion begun in Example 11. Running \(Q\) from \(S\) and \(C_0\) gives \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {x^0, y^{[\bot ,1]}}\rangle \!\} \). The response is contingent because the set \({! \, \! y} \) cannot proceed in \(C_0\) which does not exclude further resets on \(y\). Therefore,
, to continue the discussion begun in Example 11. Running \(Q\) from \(S\) and \(C_0\) gives \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {x^0, y^{[\bot ,1]}}\rangle \!\} \). The response is contingent because the set \({! \, \! y} \) cannot proceed in \(C_0\) which does not exclude further resets on \(y\). Therefore,
This says that \(x\) must be reset but may be set later (stabilising without crash), \(y\) and \(z\) may remain pristine or stabilise at \(1\). In addition, the init status of all variables is \(\mathsf{1 } \), excluding any further possible resets arising from \(P \mathrel {\Vert }Q\). Notice that \(C_1\) is a more precise description of the response compared to \(C_0\), i.e., \(C_0 \sqsubset C_1\).
The remaining uncertainty arises because the single application of \(\langle \!\langle P \mathrel {\Vert }Q \rangle \!\rangle ^{{S}}_{{C_0}}\) blocks the setting of \(y\) in the write access in \(Q\). For this, \(P \mathrel {\Vert }Q\) needs to communicate with itself to find out that the set \({! \, \! y} \) can proceed. This is achieved by running a second pass, now feeding the concurrent environment \(C_1\) instead of \(C_0\). Since \(C_1\) indicates a completed “init” phase for \(y\) the set \({! \, \! y} \) in \(Q\) is unblocked. We find \(\langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C_1}} = \{\!\langle {x^0, y^{1}}\rangle \!\} \). Since variable \(y\) is now a decided \(1\) the conditional in the second thread of \(P\) is turned off which makes the set \({! \, \! x} \) non-executable, so variable \(x\) cannot be set. The calculation for the second thread now is \(\langle \!\langle y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \rangle \!\rangle ^{{S}}_{{C_1}} = \langle \!\langle \varepsilon \rangle \!\rangle ^{{S}}_{{C_1}} = S = \bot \). It terminates, i.e., \( cmpl ^{}\langle y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} , C_1 \rangle = \{ 0 \}\), as one shows without difficulty from the definition in Fig. 6. The first thread still does not terminate because \(x\) is still undecided in \(C_1\) and we have \(\langle \!\langle x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z}) \rangle \!\rangle ^{{S}}_{{C_1}} = \bot {:}\mathsf{1 } \vee \, \{\!\langle {y^{[\bot ,1]}, z^{[\bot ,1]}}\rangle \!\} \) as before. This means \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_1}} = \bot {:}\mathsf{1 } \vee \, \{\!\langle {y^{[\bot ,1]}, z^{[\bot ,1]}}\rangle \!\} \vee \bot = \{\!\langle {y^{[\bot ,1]}, z^{[\bot ,1]}}\rangle \!\} \).
Thus, overall, this gives the refined response
which is a more precise status description, i.e., \(C_1 \sqsubset C_2\), since \(C_2\) now also endows variable \(x\) with a decided value \(0\). As a result, the conditional in the first thread of \(P\) must execute \({! \, \! z} \) which finally resolves the status of \(z\): \(\langle \!\langle x \, \mathrel {?} \, \varepsilon \mathrel {:} ({! \, \! y} \mathrel {\Vert }{! \, \! z}) \rangle \!\rangle ^{{S}}_{{C_2}} = \langle \!\langle {! \, \! y} \mathrel {\Vert }{! \, \! z} \rangle \!\rangle ^{{S}}_{{C_2}} = \{\!\langle {y^{1}, z^{1}}\rangle \!\} \) which means
The environment \(C_3\), which satisfies \(C_2 \sqsubset C_3\), is a crisp fixed-point, \(\langle \!\langle P \mathrel {\Vert }Q \rangle \!\rangle ^{{S}}_{{C_3}} = C_3\), in which the parallel composition \(P \mathrel {\Vert }Q\) terminates, i.e., \( cmpl ^{}\langle P \mathrel {\Vert }Q, C_3 \rangle = \{ 0 \}\). \(\square \)
Example 18 is what we shall call a strongly Berry-constructive program (cf. Definition 7) which generates a crisp fixed-point response. This implies (cf. Theorem 1) that the program is B-reactive and SC-read-determinate. There are however programs which cannot be scheduled because they contain a causal cycle which makes the schedule lock up. These deadlocks arise from the “init;update;read” protocol constraint that makes read accesses wait for the prior completion of all possible write accesses and sets wait for the completion of any possible resets. The following examples illustrates the two typical cases of deadlocks.
Example 19
The program  is not constructive. Indeed it does not admit any SC-admissible (and hence neither any B-admissible) schedule because in all its free schedules a reset happens after a concurrent set to the same variable, yet they are not confluent with each other. Hence, each schedule violates SC-admissibility. Also, the final memory is non-deterministic depending on the schedule. If we chose the sequence
is not constructive. Indeed it does not admit any SC-admissible (and hence neither any B-admissible) schedule because in all its free schedules a reset happens after a concurrent set to the same variable, yet they are not confluent with each other. Hence, each schedule violates SC-admissibility. Also, the final memory is non-deterministic depending on the schedule. If we chose the sequence  the final memory has \(y = 0\), whereas if we schedule
the final memory has \(y = 0\), whereas if we schedule  the we get \(y = 1\). If we run the fixed-point analysis the problem becomes visible as a deadlock: From \(S :=\bot \) and \(C_0 :=[\bot ,\top ]{:}\mathsf{2 } \) the two concurrent sets \({! \, \! x} \) and \({! \, \! y} \) both block so that \(\langle \!\langle {! \, \! x} \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {x^{[\bot ,1]}}\rangle \!\} \) and \(\langle \!\langle {! \, \! y} \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {y^{[\bot ,1]}}\rangle \!\} \). Then, because the sets guard the resets
the we get \(y = 1\). If we run the fixed-point analysis the problem becomes visible as a deadlock: From \(S :=\bot \) and \(C_0 :=[\bot ,\top ]{:}\mathsf{2 } \) the two concurrent sets \({! \, \! x} \) and \({! \, \! y} \) both block so that \(\langle \!\langle {! \, \! x} \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {x^{[\bot ,1]}}\rangle \!\} \) and \(\langle \!\langle {! \, \! y} \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {y^{[\bot ,1]}}\rangle \!\} \). Then, because the sets guard the resets  and
and  , respectively, their init status is set to \(\mathsf{2 } \):
, respectively, their init status is set to \(\mathsf{2 } \):

In this updated environment \(C_1 :=\langle \!\langle P_1 \rangle \!\rangle ^{{S}}_{{C_0}}\) both variables still indicate contingent resets. As a consequence, in the next iteration the sets \({! \, \! x} \) and \({! \, \! y} \) again block, whence \(\langle \!\langle P_1 \rangle \!\rangle ^{{S}}_{{C_1}} = C_1\). This fixed-point \(C_1\) is not crisp (not even decided) and constitutes a scheduling deadlock. Observe that the deadlock is detected with the help of the init status not reducing from \(\mathsf{2 } \) to \(\mathsf{1 } \). In the fixed-point semantics of [4] where the init status is missing \(P_1\) would wrongly be classified as SC-constructive. This is a mistake that our extended semantics now fixes. \(\square \)
Example 20
Another unschedulable program is the “arbiter” \(P_2 :=x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \mathrel {\Vert }y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \). It is not constructive because it fails to have any admissible schedules. Every execution order forces a set to happen concurrently after a read and both are not guaranteed to be confluent (depends on the initial memory). As one can verify, our domain-theoretic analysis of \(P_2\) obtains \(C_1 :=\langle \!\langle P_1 \rangle \!\rangle ^{{S}}_{{C_0}} = \bot {:}\mathsf{1 } \vee \{\!\langle {x^{[\bot ,1]}, y^{[\bot ,1]}}\rangle \!\} \) and then \(\langle \!\langle P_1 \rangle \!\rangle ^{{S}}_{{C_1}} = C_1\), again choosing \(S :=\bot \) and \(C_0 :=[\bot ,\top ]{:}\mathsf{2 } \). The fixed-point \(C_1\) is undecided and therefore \(P_1\) not (strongly) Berry-constructive (Definition 7). \(\square \)
The completion codes \( cmpl ^{}\langle P, C \rangle \) control the analysis of sequential composition. As long as \(P\) does not terminate or pause, a sequential successor \(Q\) only enters the calculation for \(P\mathrel {;}Q \) to reduce the “may” (upper bound) information on signal statuses, never the “must” (lower bound) information. This is similar to the treatment of conditionals \(s \, \mathrel {?} \, P \mathrel {:} Q \) in which we block the “must” reaction of \(P\) and \(Q\) until variable \(s\) becomes decided. Until this happens the conditional does not terminate. One can show that termination and crisp reaction environments are closely related. For this we call an environment \(E\) synchronized when (i) \(E(x) = [l, u]{:}\mathsf{0 } \) implies \(l = u\), and (ii) \(\bot {:}\mathsf{1 } \preceq E(x)\) implies \(\forall y.\, \bot {:}\mathsf{1 } \preceq E(y)\), for all variables \(x \in V \). As we shall see, all our environments will be synchronized. Hence the difference between a completed schedule marked by \(\mathsf{0 } \) and a contingent schedule marked by one of \(\{\mathsf{1 }, \mathsf{2 } \}\) is a feature of the whole environment rather than an individual variable.
Proposition 3
Let \(S\) be synchronized then
-
1.
\(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) is synchronized.
-
2.
If \(S\) is a crisp sequential environment, i.e., \(S(x) \in \mathbb {D} \) for all \(x \in V \), then the response of a terminating or pausing fprog starting from \(S\) is crisp, too: If \( cmpl ^{}\langle P, C \rangle = \{ 0 \}\) or \( cmpl ^{}\langle P, C \rangle = \{ 1 \}\) then \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} (x) \in \mathbb {D} \) for all \(x \in V \). The converse also holds, i.e., if \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) is crisp, then \(\bot \not \in cmpl ^{}\langle P, C \rangle \).
Although a program does not terminate it may be possible to constructively prove that its response is decided. For example, the fprog \(s \, \mathrel {?} \, \varepsilon \mathrel {:} \varepsilon \) does not complete in the concurrent environment \(C(s) = [\bot , \top ]{{:}\mathsf{2 }}\) but still has the decided response \(\langle \!\langle s \, \mathrel {?} \, \varepsilon \mathrel {:} \varepsilon \rangle \!\rangle ^{{\bot }}_{{C}}(s) = \bot {:}\mathsf{1 } \), implying that the \(s\) remains pristine and environment-controlled.
Proposition 4
For every reset-free fprog \(P\), the sets \( must _k(P, C)\) and \( cannot _k(P, C)\) extracted from \( cmpl ^{}\langle P, C \rangle \) as defined in Sect. 3.3 are identical to the completion semantics of Esterel [12].
4.3 The fixed-point semantics and constructivity
While \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) describes the instantaneous behaviour of \(P\) in a compositional fashion, the constructive response of \(P\) running by itself is obtained by the least fixed-point
where \(C_0 :=[\bot ,\top ]{{:}\mathsf{2 }}\) and \(C_{i+1} :=\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_i}}\). Note that the sequential environment \(S\) is not updated in the iteration. This reflects the fact that the fixed point approximates the reaction always from the beginning of and concurrent with \(P\). In contrast, the environment \(S\) is an initialisation which captures the sequential history of the thread \(P\) which remains fixed each time the iteration takes place. The fixed-point \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) closes \(P\) off against its concurrent environment \(C\). It lets \(P\) communicate with itself by treating \(P\) as its own concurrent context.
For the fixed-point to exist the termination function \( cmpl ^{}\langle P, C \rangle \) and functional \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) must be well-behaved. This is the content of the following Proposition 5. We do not use more than elementary fixed-point theory over finite domains, here. For a detailed exposition of the technical background the reader is referred to [23].
Proposition 5
Let \(P\) be an arbitrary fprog, \(S\), \(E\) environments. Then,
-
1.
The functional \( cmpl ^{}\langle P, E \rangle \) is monotonic with respect to \(\sqsubseteq \) in \(E\).
-
2.
The functional \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) is inflationary in the sequential environment \(S\) with respect to \(\preceq \).
-
3.
The functional \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{E}}\) is monotonic with respect to \(\sqsubseteq \) in both the concurrent environment \(E\) and the sequential environment \(S\) and monotonic for \(\preceq \) in \(S\).
Monotonicity (Proposition 5) together with finiteness of \(I(\mathbb {D}, \mathbb {P})\) implies that the least fixed point \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) given by (11) is well-defined, for any sequential environment \(S\), if we start from an initial concurrent environment \(C_0\) that is a post-fixed-point of \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{\_}}\), i.e., if \(C_0 \sqsubseteq \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_0}}\). The trivial concurrent environment satisfying this is \(C_0= [\bot ,\top ]{{:}\mathsf{2 }}\) for all \(x \in V \). This is the least element wrt \(\sqsubseteq \) which codes null-information about the concurrent environment. With this choice of \(C_0\), the sequential environment \(S\) is in fact completely arbitrary. We then have \(C_i \sqsubseteq C_{i+1}\) and (11) is the stationary limit of this monotonically increasing sequence, which must exist because of the finiteness of \(I(\mathbb {D}, \mathbb {P})\).
On the modelling side, the fixed-point semantics, discussed so far, is able to accommodate different levels of synchronous constructiveness within it, as we will see next. Different notions of constructiveness are specified by means of certain properties in the fixed-point response. First, the connection with Esterel can be made through the two versions of constructiveness introduced in [4]. Then, the denotational companion for the operational notion of IB-causality, namely IB-constructiveness (IBC), is identified and a soundness result is presented. The relationship between the various notions of constructiveness is also discussed.
The class of strongly Berry-constructive programs corresponds to the notion of constructiveness in Esterel, yet is able to manage explicit initialisations. This, as expected, can deal with a variable being reset to \(0\) and then either remaining \(0\) (signal absence) or being set to \(1\) (signal presence). Besides, it verifies proper initialisations as part of the constructiveness analysis. It holds the programmer responsible for proper initialisation, not the compiler or the run-time system. Thus, it is important to distinguish whether a variable retains its original value \(\bot \) from the initial memory or not.
Definition 7
(Strong Berry-Constructiveness [4] SBC) An fprog \(P\) is strongly Berry-constructive, or SBC, iff for all variables \(x \in V \) we have \((\mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}})(x) \in \{{\bot , 0 ,1}\}\). \(\square \)
It is worth observing that in a SBC program the status \(\bot \) for a variable corresponds to a witness for checking initialisations. It indicates that the variable is neither set nor reset by the program. If such a variable is read and thus used in a branching decision the program would be rejected, except for trivial cases. In other words, the resulting status \(\bot \) from the fixed-point indicates that the variable is indeed never accessed (set, reset or read) by the program.
Example 21
Fprog \(P :=x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \) is not SBC since variable \(x\) (with status \(\bot \)) is not properly initialised in the code and thus it cannot be decided if variable \(y\) is set or not. The fixed-point satisfies \(\mu C.\, \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}} (y) = [\bot , 1]{:}\mathsf{1 } \). In contrast, for the properly initialised fprog \({! \, \! x} \mathrel {;} P\) the fixed-point will give us \(\mu C.\, \langle \!\langle {! \, \! x} \mathrel {;} P \rangle \!\rangle ^{{\bot }}_{{C}} = \{\!\langle {x^1, y^\bot }\rangle \!\} \) which is SBC. \(\square \)
On the other hand, the actual Esterel’s semantics resets all signals to \(0\) by default, at the beginning of every instant. Thus, in this case, we need to look at ternary behaviours, i.e., those which remain inside environments with \(E(x) \in \{ 0, 1, [0,1] \}\) for all \(x \in V \). In order to keep the status of variables in the ternary domain, we could initialise with the reset construct and avoid sequentially forced resets from happening after sets. However, in the semantics \(\langle \!\langle \_ \rangle \!\rangle ^{{S}}_{{}}\) one can emulate initialisation directly by running the fixed-point in the sequential environment \(S = 0\) instead of \(S = \bot \). This give us the class of Berry-constructive programs:
Definition 8
(Berry-Constructiveness [4] BC) An fprog \(P\) is Berry-constructive, or BC, iff for all variables \(x \in V \) we have \((\mu C. \langle \!\langle P \rangle \!\rangle ^{{0}}_{{C}})(x) \in \{{0 ,1}\}\). \(\square \)
Example 22
The fprog \(P\) from Example 21 is BC because now \(\mu C.\, \langle \!\langle P \rangle \!\rangle ^{{0}}_{{C}} (y) = \{\!\langle {x^0,y^1}\rangle \!\} \). In Esterel’s hardware translation [12], the corresponding Boolean equations are \(x = 0\) and \(y = \overline{x} + 0\) which stabilise to \(x = 0\) and \(y = 1\). This depends on the initialisation of \(x\) to \(0\), however. On the other hand, \(Q :=x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! x} \), which emits signal \(x\) if \(x\) is absent and does not emit it if \(x\) is present, is not BC: \(\mu C.\, \langle \!\langle Q \rangle \!\rangle ^{{0}}_{{C}} (x) = [0,1]{:}\mathsf{1 } \). Its hardware translation would be an inverter loop, or combinational equation \(x := \overline{x} + 0\), which may exhibit oscillations. \(Q\) is not SBC either since \(\mu C.\, \langle \!\langle Q \rangle \!\rangle ^{{\bot }}_{{C}} (x) = [\bot ,1]{:}\mathsf{1 } \). \(\square \)
Examples 21 and 22 show that SBC is properly more restrictive than BC. The difference between the two forms of Berry-constructiveness is whether we run the simulation with the sequential stimulus \(\bot \) or \(0\), respectively.
The above are not sufficient for capturing SC-read-determinacy as given in Definition 6 which induces an open-world version of constructiveness that takes into consideration external inputs to the program. SC-read-determinacy is constructed from any arbitrary initial memory state that is not controlled by the code such as registered variables. The conditions imposed by this notion can, therefore, be read as follows. For all external inputs, there is always a schedule that does not lead to \(\top \) (reset safe) and for all read variables and all such schedules either: the final memory value for the variable (temporary variable) is controlled by the program and always the same (\(0\) or \(1\)) or by the environment (registered variable) in which case it is not changed at all during the computation (read safe). In short, this specifies that every variable used for branching of control is either causally justified or never modified in the code, independently of the initial external input. This leads us to the following definition:
Definition 9
(IB-constructiveness IBC) Fprog \(P\) is Input Berry-constructive (IB-constructive or IBC), iff its fixed-point \(C_* = \mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}}\) is safe for \(P\), that is:
-
reset-safe: \(\forall x \in V . \ C_*(x) \preceq 1{:}\mathsf{1 } \), and
-
read-safe: \(\forall x \in rd (P). \ C_*(x) \in \{{\bot , 0, 1}\}\). \(\square \)
One can show that the class of IBC programs lies between the SBC and the BC programs and that these inclusions are proper.
Example 23
The BC fprog \(x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \) from Example 21, which is not SBC, is also IBC. The fixed-point result is \(\mu C.\, \langle \!\langle x \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \rangle \!\rangle ^{{\bot }}_{{C}} = \{\!\langle {x^\bot ,y^{[\bot ,1]{:}\mathsf{1 }}}\rangle \!\} \). Since \(x\) is not properly initialised the status of \(y\) cannot be decided. This does not matter for IBC as \(y\) is not a read variable. Now take the program \(Q :=x \, \mathrel {?} \, (y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} ) \mathrel {:} \varepsilon \). If we initialise with \(0\), we get \(\mu C.\langle \!\langle Q \rangle \!\rangle ^{{0}}_{{C}} = \{\!\langle {x^0,y^0}\rangle \!\} \), so \(Q\) is BC. Yet, it is not IBC because \(\mu C.\langle \!\langle Q \rangle \!\rangle ^{{\bot }}_{{C}} (y) = [\bot ,1]{:}\mathsf{1 } \) and \(y \in rd (Q) \) is a read variable. The problem is that not every initial memory for \(Q\) admits of an IB-causal micro-step execution. Specifically, if \(\rho _0(x) = 1\), then the sub-program \(y \, \mathrel {?} \, \varepsilon \mathrel {:} {! \, \! y} \) is scheduled which creates a read-write hazard. It reads the initial (environment-controlled) value of \(y\) and then, sequentially afterwards, may change it itself. \(\square \)
The result in [4] establishes that for every fprog \(P\), if \(P\) is SBC then \(P\) is SC-reactive and SC-determinate. Here, we show the following stronger result:
Theorem 1
For every fprog \(P\), if \(P\) is IBC then it is B-reactive and SC-read-determinate.
Theorem 1 gives a stronger soundness result for the application of the theory compared to Theorem 1 of [4] because it permits us to prove strictly stronger forms of reactiveness and determinacy for a strictly wider class of programs, considering that there are more IBC programs than SBC programs.
4.4 Soundness of the denotational fixed-point semantics
In the following we summarise the main elements of the proof for Theorem 1 stating that every IB-constructive fprog is B-reactive and SC-read-determinate, and a fortiori also sequentially constructive as introduced in [85, 86]. More details can be found in a technical report [5].
The key element in the soundness proof is to relate the abstract values in \(\mathbb {D} \) and \(\mathbb {P} \) used in the fixed-point analysis with the operational behavior of process executions. These status values are interpreted as abstractions of the write accesses in a finite sequence of micro steps generating what we call the sequential yield of each thread. More precisely, a sequential yield is a function \(\mu \) which assigns each possible thread identifier \(\iota \in TI \) to a sequential environment \(\mu (\iota ) : V \rightarrow \mathbb {D} \times \mathbb {P} \) subject to the condition that \(\iota \preceq \iota '\) implies \(\mu (\iota ') \preceq \mu (\iota )\). The idea is that \(\mu (\iota )\) codes the local view of a thread instance \(\iota \) about the sequential status of the variable values. So, if \(\iota \prec \iota '\) then \(\iota '\) is a (sequential) descendant of thread \(\iota \) all of whose memory write accesses are visible to the waiting ancestor thread \(\iota \). The fact that the view of the ancestor \(\iota \) is wider, also encompassing other threads (e.g., siblings of \(\iota \) and their descendants) running concurrently with \(\iota \), is captured by the constraint \(\mu (\iota ') \preceq \mu (\iota )\). The descendant \(\iota '\) is behind the parent since the parent \(\iota \) sees all variable accesses of all its active children while \(\iota '\) only knows about its own.
With the following definition of the sequential yield we are interpreting the steps of a micro-sequence as an incremental update of a sequential state. The pairs in \(\mathbb {D} \times \mathbb {P} \) are treated naturally as elements of \(I(\mathbb {D}, \mathbb {P})\), viz. \((a,r) \in \mathbb {D} \times \mathbb {P} \) is the same as \([a,a]{:}r \in I(\mathbb {D},\mathbb {P})\) and therefore written \(a{:}r\). In this way, all operations on environments over \(I(\mathbb {D},\mathbb {P})\) can be used for the sequential environments, too.
Definition 10
(Sequential yield) Let \(R\) be a finite sequence of micro-steps \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) and \(C\) an environment. We define the sequential yield \(|R| _{C} : TI \rightarrow V \rightarrow \mathbb {D} \times \mathbb {P} \) of \(R\) by iteration through \(R\), as follows: If \(R = \varepsilon \), then \(|R| _{C} (\iota )(x) :=\bot = \bot {:}\mathsf{0 } \) for all \(\iota \in TI \) and \(x \in V \). Otherwise, suppose \(R = R',T_n\) consists of a sequence \(R' : ({\varSigma } _1, \rho _1) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _{n-1}, \rho _{n-1})\) followed by a final micro-step \(T_{n} : ({\varSigma } _{n-1}, \rho _{n-1}) \mathop {\rightarrow }\limits ^{} ({\varSigma } _{n}, \rho _{n})\). Then, \(|R| _{C} \) is computed from \(|R'| _{C} \) by case analysis on the micro-step \(T_{n}\).
Generally, the yield does not change for all threads concurrent to \(T_n. id \), i.e., for all \(\kappa \in TI \) such that \(\kappa \not \preceq T_n. id \) and \(T_n. id \not \preceq \kappa \) we have \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa )\). Also, if the next control is a non-empty list \(T_n. next = Q{::} Ks '\) and the program  instantaneously terminates, then the execution of \(T_n\) installs the process \({\langle inc (\iota ), Q, Ks ' \rangle } \). This incremented thread inherits the sequential state from \(\iota \). In this case we put \(|R| _{C} ( inc (\iota )) :=|R| _{C} (\iota )\). Otherwise, if
instantaneously terminates, then the execution of \(T_n\) installs the process \({\langle inc (\iota ), Q, Ks ' \rangle } \). This incremented thread inherits the sequential state from \(\iota \). In this case we put \(|R| _{C} ( inc (\iota )) :=|R| _{C} (\iota )\). Otherwise, if  and \( Ks = [\,]\) is empty, then \(|R| _{C} ( inc (\iota )) :=|R'| _{C} (\iota )\).
and \( Ks = [\,]\) is empty, then \(|R| _{C} ( inc (\iota )) :=|R'| _{C} (\iota )\).
In all other cases, for ancestor and descendant threads \(\kappa \), the new yield \(|R| _{C} (\kappa )\) is determined according to the following clauses:
-
1.
Executing a sequential composition or the empty statement does not change the yield. Formally, if \(T_{n}.prog \in \{ P\mathrel {;}Q, \varepsilon \}\), then \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa )\);
-
2.
Executing a conditional test which is undecided in environment \(C\) raises the init status of the thread and its ancestors to \(\mathsf{1 } \); otherwise, if the test is decided in \(C\) the yield is preserved. Formally, if \(T_{n} = {\langle \iota , s \, \mathrel {?} \, P \mathrel {:} Q, Ks \rangle } \) and for all \(b \in \{\bot , 0, 1\}\), \(b{:}\mathsf{1 } \not \sqsubseteq C(s)\), then we put \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa ) \vee \bot {:}\mathsf{1 } \) for all \(\kappa \preceq inc (\iota )\); Otherwise, for \(\kappa \not \preceq inc (\iota )\) or if \(b{:}\mathsf{1 } \sqsubseteq C(s)\) for some \(b \in \{\bot , 0, 1\}\), then we define \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa )\);
-
3.
Upon forking a parallel process we copy the sequential status of the parent thread to its two children. Formally, if \(T_{n} = {\langle \iota , P \!\mathrel {\mid \!\mid }\! Q, Ks \rangle } \), then \(|R| _{C} (\iota .l.0) = |R| _{C} (\iota .r.0) :=|R'| _{C} (\iota )\) and for all \(\kappa \ne \iota .r.0\) and \(\kappa \ne \iota .l.0\) we have \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa )\);
-
4.
A set \({! \, \! s} \) increases the sequential yield of \(s\) in the executing thread and its ancestors and also the speculation status (for all variables) if the set is blocked by \(C\) due to a potentially pending reset. Formally, suppose \(T_{n} = {\langle \iota , {! \, \! s}, Ks \rangle } \). Then, for all \( inc (\iota ) \prec \kappa \), \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa )\) and for all \(\kappa \preceq \iota \),
-
if \([\bot ,\top ]{:}\mathsf{1 } \sqsubseteq C(s)\) then \(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee 1\) and \(|R| _{C} (\kappa )(x) :=|R'| _{C} (\kappa )(x)\) for all variables \(x \ne s\). More compactly, \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa ) \vee \{\!\langle {s^1}\rangle \!\} \);
-
if \([\bot ,\top ]{:}\mathsf{1 } \not \sqsubseteq C(s)\) then \(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee 1{:}\mathsf{1 } \) and \(|R| _{C} (\kappa )(x) :=|R'| _{C} (\kappa )(x) \vee \bot {:}\mathsf{1 } \) for \(x \ne s\). More compactly, \(|R| _{C} (\kappa ) :=|R'| _{C} (\kappa ) \vee \{\!\langle {s^1}\rangle \!\} \vee \bot {:}\mathsf{1 } \).
-
-
5.
A reset
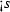 increases the sequential yield for \(s\) to \(0\) if the status is still smaller than \(0\), or to \(\top \) if the status of \(s\) in the thread is already at or above \(1\). At the same time, if the thread has entered the speculative mode, then the reset
increases the sequential yield for \(s\) to \(0\) if the status is still smaller than \(0\), or to \(\top \) if the status of \(s\) in the thread is already at or above \(1\). At the same time, if the thread has entered the speculative mode, then the reset  raises the speculation status to \(\mathsf{2 } \). Formally, if
raises the speculation status to \(\mathsf{2 } \). Formally, if  , then \(|R| _{C} (\kappa )(x) :=|R'| _{C} (\kappa )(x)\) for all \( inc (\iota ) \prec \kappa \) or \(x \ne s\); Otherwise, for all \(\kappa \preceq \iota \) we put
, then \(|R| _{C} (\kappa )(x) :=|R'| _{C} (\kappa )(x)\) for all \( inc (\iota ) \prec \kappa \) or \(x \ne s\); Otherwise, for all \(\kappa \preceq \iota \) we put-
\(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee \top \) if \(1 \preceq |R'| _{C} (\iota )(s) \preceq \top \);
-
\(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee \top {:}\mathsf{2 } \) if \(1{:}\mathsf{1 } \preceq |R'| _{C} (\iota )(s)\);
-
\(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee 0\) if \(|R'| _{C} (\iota )(s) \preceq 0\);
-
\(|R| _{C} (\kappa )(s) :=|R'| _{C} (\kappa )(s) \vee 0{:}\mathsf{2 } \) if \(\bot {:}\mathsf{1 } \preceq |R'| _{C} (\iota )(s) \preceq 0{:}\mathsf{2 } \); \(\square \)
-
A special case is the totally pristine sequential yield \(\mu _\bot \) with \(\mu _\bot (\iota ) = \bot \) for all \(\iota \in TI \). This is the yield \(|\varepsilon | _{C} \) of the empty micro sequence. Moreover, the yield operation is monotonic, i.e., if \(R\) is a prefix of \(R'\) then \(|R| _{C} (\iota ) \preceq |R'| _{C} (\iota )\). Observe that if \(R\) does not have any write accesses to a variable \(x\) then the value status of \(x\) in the sequential yield remains \(\bot \), the init status may raise to \(\mathsf{1 } \) but not to \(\mathsf{2 } \), i.e., \(|R| _{C} (\iota )(x) \preceq \bot {:}\mathsf{1 } \). For SC-admissible micro-sequences the yield gives a sound approximation of the final memory state:
Lemma 1
Let \(R : (\varSigma _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} (\varSigma _n, \rho _n)\) be an SC-admissible micro-step sequence and \(C\) an environment. Then, \(|R| _{C} \) is consistent for the final memory \(\rho _n\) in the following sense:
-
(i)
If \(|R| _{C} ({\mathsf{\textit{Root} }}.id)(x) \preceq \bot {:}\mathsf{2 } \) then \(\rho _0(x) = \rho _n(x)\);
-
(ii)
If \(|R| _{C} ({\mathsf{\textit{Root} }}.id)(x) = b{:}r\) with \(b \in \{0, 1\} \subset \mathbb {D} \) then \(\rho _n(x) = b\);
-
(iii)
If \(|R| _{C} ({\mathsf{\textit{Root} }}.id)(x) \succeq 1\) then there exists a micro step \(1 \le i \le n\) such that \(T_i.prog = {! \, \! x} \) and for all \(T \in \varSigma _n\) with \(T_i.id \preceq T.id\) we have \(1 \preceq |R| _{C} (T.id)(x)\).
-
(iv)
Whenever in \(R\) a thread \(\iota \) reads a variable \(x\), the value status of \(x\) in any other concurrent thread remains constant from this point onwards. In other words, no thread changes the value status of \(x\) after it is has been read by another thread concurrent to it. Formally, suppose \(R(i) = {\langle \iota , x \, \mathrel {?} \, P \mathrel {:} Q, Ks \rangle } \) and for some \(i \le j \le n\) and \(\iota ' \in TI \) we have \(|R{\tiny @}i | _{C} (\iota ') (x) \wedge \top \ne |R{\tiny @}j | _{C} (\iota ') (x) \wedge \top \). Then, \(\iota ' \preceq \iota \) or \(\iota \preceq \iota '\). \(\square \)
The strategy for proving Theorem 1, stating that every IB-constructive program is B-reactive and SC-determinate, is to show that the fixed-point \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}} \in I(\mathbb {D}, \mathbb {P})\) computes sound information about the sequential yield of every SC-admissible micro-step sequence \(R\) of \(P\). More specifically, we show that \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}}\) is an abstract predictor for the SC-admissible behavior of \(P\) in the sense that (i) the yield of every SC-admissible micro-sequence lies within the window specified by \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}}\) and (ii) there exists a B-admissible instant. This is done by induction on the structure of \(P\). However, since the fixed-point of a composite expression cannot be obtained from the fixed-points of its sub-expressions, induction on \(P\) for the full fixed-point \(\mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}}\) does not work. Instead, we need to break up the fixed-point and do an outer induction along the iteration that obtains the fixed-point in the limit. The idea is to extract the logical meaning of a single iteration step \(C_{i+1} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_i}}\) as a conditional specification of the SC-admissible behavior of \(P\) assuming a sequential environment \(S\) and concurrent environment \(C_i\). This can then be proven by induction on \(P\).
The main observation is that a single application of the response functional \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_i}}\) covers the behavior of an initial slice of any micro-sequence \(R\) generated from \(P\), consisting of an atomic “read;update” burst of \(P\). This burst consists of all those statements of \(R\) that can be executed solely based on the concurrent environment \(C_i\) to decide which branch to take in a conditional and whether a set can go ahead or is blocked because of a pending reset. At such a point, or if a conditional is undecided the slice stops. We have reached the stopping index of the slice in \(R\). In the slice, control branching is decided entirely in terms of the variables whose values are decided in \(C_i\) and not on variables whose value may be changing as a result of executing \(P\). In particular, the execution in \(R\) covered by a slice decided from \(C_i\) does not involve any communication between concurrent processes inside \(P\). Since the effect of executing the slice is described by the response environment \(C_{i+1} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_i}}\), the communication between threads is then handled by feeding back the result \(C_{i+1}\) as the new concurrent environment in the next iteration \(C_{i+2} = \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C_{i+1}}}\) of the response functional.
Definition 11
(Stopping index) Let \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) be a micro-sequence and \(C\) an environment. A process \(T_i \in {\varSigma } _i\) for \(0 \le i < n\) is called \(C\)-blocked if \(T_i\) is active in \({\varSigma } _i\) and either
-
\(T_i.prog\) is a branching \(x \, \mathrel {?} \, Q \mathrel {:} R \) and \(\bot {:}\mathsf{1 } \not \sqsubseteq C(x)\), \(0{:}\mathsf{1 } \not \sqsubseteq C(x)\) and \(1{:}\mathsf{1 } \not \sqsubseteq C(x)\), or
-
\(T_i.prog\) is a set \({! \, \! x} \) and \([\bot ,\top ]{:}\mathsf{1 } \not \sqsubseteq C(x)\).
In all other cases, \(T_i\) is called \(C\)-enabled. Let \({\langle \iota _P, P, Ks \rangle } \in {\varSigma } _i\) be active in \({\varSigma } _i\). The \(C\)-stopping index of \(P\) in \(R\) is the earliest step index \(i \le t \le n\) such that one of the following holds:
-
\(P\) pauses
-
\(P\) has terminated instantaneously and handed over to \(Q\) in the next control \( Ks = Q:: Ks '\)
-
all remaining active descendants \({\langle \iota ', P', Ks \rangle } \in {\varSigma } _t\) with \(\iota \preceq \iota '\) are \(C\)-blocked. \(\square \)
Note that the \(C\)-stopping index of a program in a micro-sequence \(R\) may not exist if \(R\) is not long enough so that \(R\) still has an active process from \(P\) in its last configuration and this process is not \(C\)-blocked. Also, if \(C\) is safe, i.e., reset-safe and read-safe, then at its \(C\)-stop in \(R\) the program \(P\) must either pause or terminate instantaneously.
The \(C\)-stopping index of \(P\) in a micro-sequence \(R\) marks the maximal horizon until which we will follow the execution of \(P\) when using \(C\) as a predictor environment. However, this does not mean that the memory is actually consistent with the prediction \(C\). The notion of \(C\)-consistency in the following Definition 12 fills this gap. A micro-sequence \(R\) is \(C\)-consistent if every read of every variable \(x\) for which \(C\) predicts a decided value, i.e., for which \(b{:}\mathsf{1 } \sqsubseteq C(x)\), for \(b \in \{ \bot ,0,1 \}\), the actual value of \(x\) in the memory coincides with this prediction \(b\). So, if \(R\) happens to be \(C\)-consistent then the prediction will be sound up to the \(C\)-stopping index.
Definition 12
(\(C\)-consistency) Let \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) be a micro sequence and \(C\) an environment. For any \(0 \le i < n\), abbreviate by \(\rho _i(x) \doteq b\) the condition that \(\rho _{i}(x) = b\) if \(b \in \{0, 1\}\) and \(\rho _{i}(x) = \rho _0(x)\) if \(b = \bot \). We say a read \(R(i). prog = x \, \mathrel {?} \, P \mathrel {:} Q \) with \(0 < i \le n\) is \(C\)-consistent in \(R\) if \(b{:}\mathsf{1 } \sqsubseteq C(x)\) for \(b \in \{ \bot ,0,1 \}\) implies \(\rho _{i-1}(x) \doteq b\). \(R\) is called \(C\)-consistent for a thread \(\iota \) if all reads performed by all descendants of \(\iota \) in \(R\) are \(C\)-consistent. \(\square \)
The following two Proportions 6 and 7 are instrumental. They relate the environment obtained from a single computation of the denotational function \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) as upper and lower bounds of the sequential yield of a \(C\)-consistent execution of \(P\). Also, the completion information \( cmpl ^{}\langle P, C \rangle \) is related to the completion behaviour of \(P\).
Proposition 6
(Soundness of the lower/must prediction) Let \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) be a micro sequence with an active process \({\langle \iota _P, P, Ks \rangle } \) in \(\varSigma _{s}\), \(0 < s \le n\), and \(C\) an environment such that \(R\) is \(C\)-consistent for \(\iota _P\) and \(n\) the \(C\)-stopping index of \(P\) in \(R\).
-
(i)
If \( cmpl ^{}\langle P, C \rangle = \{ 0 \}\) then \(P\) instantaneously terminates at step \(n\) by executing a statement of the form \(\varepsilon \),
 , \({! \, \! s} \); If \( cmpl ^{}\langle P, C \rangle = \{ 1 \}\) then \(P\) pauses at step \(n\) where the last of its descendants has reached the statement \(\pi \).
, \({! \, \! s} \); If \( cmpl ^{}\langle P, C \rangle = \{ 1 \}\) then \(P\) pauses at step \(n\) where the last of its descendants has reached the statement \(\pi \). -
(ii)
Suppose \(S \preceq |R{\tiny @}s | _{C} (\iota _P) \preceq \top \) for some sequential environment \(S\). Then, for each variable \(x \in V \) there exists an index \(s \le i \le n\) and a descendant thread \(\iota \succeq \iota _P\) such that \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} (x) \wedge \top \preceq |R{\tiny @}i | _{C} (\iota )(x) \vee [\bot ,\top ] \preceq \top \). Moreover, if \(\bot \not \in cmpl ^{}\langle P, C \rangle \) then \(i = n\) and \(\iota = \iota _P\).
-
(iii)
If \(S \preceq \mathop { low } \,|R{\tiny @}s | _{C} (\iota _P)\) then \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \preceq \mathop { low } \,|R{\tiny @}n | _{C} (\iota _P)\).
Proof
Both parts (i) and (ii) are shown by induction on \(P\). Regarding part (iii) we observe that under the assumptions of (ii) it follows that \(\mathop { low } (\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} (x) \wedge \top ) \preceq \mathop { low } (|R{\tiny @}i | _{C} (\iota )(x) \vee [\bot ,\top ]) = \mathop { low } \,|R{\tiny @}i | _{C} (\iota )(x) \preceq \mathop { low } \,|R{\tiny @}n | _{C} (\iota _P)(x)\) and therefore \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \preceq (\mathop { low } \, \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}) \wedge \top {:}\mathsf{2 } \;=\; \mathop { low } \, \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \wedge \mathop { low } (\top ) \;=\; \mathop { low } \,(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} \wedge \top ) \;\preceq \; \mathop { low } \,|R{\tiny @}n | _{C} (\iota _P)\). \(\square \)
Proposition 7
(Soundness of upper/cannot prediction) Let \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\) be a finite micro sequence with an active process \({\langle \iota _P, P, Ks \rangle } \in \varSigma _s\), \(0 \le s \le n\), and \(C\) an environment such that \(R\) is \(C\)-consistent for \(\iota _P\). Suppose that all micro-steps executed between \(s\) and \(n\) are from processes concurrent to \(\iota _P\) or from descendants of \(P\). In particular, there are no micro-steps from the continuation list \( Ks \). Then,
-
(i)
If \(0 \not \in cmpl ^{}\langle P, C \rangle \) then at least one descendant of \(P\) is active or pausing in \(\varSigma _n\) and if \(1 \not \in cmpl ^{}\langle P, C \rangle \) then not all descendants of \(P\) in \({\varSigma } _n\), if there are any, are pausing.
-
(ii)
\(\mathop { upp } \,|R{\tiny @}s | _{C} (\iota _P) \preceq S\) implies \(\mathop { upp } \,|R{\tiny @}n | _{C} (\iota _P) \preceq \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\).
Proof
We proceed by induction on the structure of the program and the length of the continuation list \( Ks \). Note that the statements (i) and (ii) of the Proposition 7 hold trivially, if program \(P\) does not perform any micro-steps between \(s\) and \(n\). In this case, \(\mathop { upp } \,|R{\tiny @}n | _{C} (\iota _P) = \mathop { upp } \,|R{\tiny @}s | _{C} (\iota _P) \preceq S \preceq \langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}}\) by the inflationary nature of the prediction (Proposition 5(2)). \(\square \)
Proposition 8
For every fprog \(P\), if \(P\) is IBC then \(P\) is B-reactive.
Proof
Let \(P\) be an IBC program, i.e., \(C_* = \mu C. \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}}\) is safe: for all \(x \in V \), \(C_*(x) \preceq 1{:}\mathsf{1 } \) and for all \(x \in rd (P) \), \(C_*(x) \in \{{\bot , 0, 1}\}\). Further, let \(({\varSigma } _0, \rho _0)\) be an initial configuration in which program \(P\) appears as the sole active process in the pool, i.e., \({\varSigma } _0 = \{ \mathsf Root \}\), where \(\mathsf Root = {\langle \iota _P, P, [\,] \rangle } \) and \(\iota _P = \mathsf Root . id = 0\).
We show that there must exist at least one B-admissible execution for \(P\) from any memory state. This proof demonstrates how the fixed point iteration can be used as a predictive B-admissible scheduler. We are going to build iteratively a contiguous sequence of B-admissible micro-sequences
with \(n_0 = 0\) and \(n_{i-1} \le n_{i}\), where in each scheduling round \(R_{i-1}\) we are pushing the execution as far as possible while staying \(C_{i-1}\)-enabled, where \(C_{i-1}\) is the sequence of concurrent environments generated by the fixed-point iteration. Since the initial pool is \({\varSigma } _0 = \{ {\langle \iota _P, P, [\,] \rangle } \}\), all threads in any of the process pools \({\varSigma } _k\) reached during \(R_0, R_1, \ldots , R_{i-1}\) are descendants of \(P\). By construction, each descendant thread remaining active in round \(R_{i-1}\) is \(C_{i-1}\)-stopped in the final configuration \({\varSigma } _{n_{i}}\). For the fixed-point \(C_{*}\), which is safe, this means that in the corresponding end configuration \(({\varSigma } _{n_*}, \rho _{n_*})\) all threads descending from \(\iota _P\) are either instantaneously terminated or pausing. Recall that in the final configuration \(({\varSigma } _{n_*}, \rho _{n_*})\) no set \({! \, \! x} \) can be \(C_*\)-blocked since \(C_*\) is reset-safe and no read \(x \, \mathrel {?} \, P' \mathrel {:} Q' \) can be blocked because \(C_*\) is read-safe. Hence, at the fixed-point, we have constructed a maximal micro sequence and thus reached the end of the macro step (instant). Here are the key invariants:
-
(I1)
The yield of each partial schedule is in the range predicted by the fixed-point approximation, i.e., \(C_i \sqsubseteq |R_0, R_1, \ldots , R_{i-1}| _{C_{i-1}} (\iota _P)\).
-
(I2)
Each partial schedule \(R_0, R_1, \ldots , R_{i-1}\) is B-admissible.
-
(I3)
For every free schedule \(R'\) from \(({\varSigma } _{n_{i}}, \rho _{n_{i}})\), the extended schedule \(R_{0}, R_{1}, \ldots , R_{i-1}, R'\) is \(C_{i}\)-consistent. Further, if \(C_i(x) \preceq \top {:}\mathsf{1 } \) then \(R'\) does not contain a reset
 .
.
The invariants (I1–I3) tell us that the full sequence \(R = R_0, R_1, \ldots , R_{*}\) up to the fixed-point, obtained as the result of our scheduling strategy, is \(C_{*}\)-consistent and that every conditional test performed in the full schedule \(R\) reads exactly the memory value predicted by the read-safe fixed-point environment.
Base case. Observe that the empty schedule \(\varepsilon \) is trivially B-admissible and its sequential yield \(|\varepsilon | (\iota _P) = \bot \) lies in the environment \(C_0 = [\bot ,\top ]{:}\mathsf{2 } \), i.e., \(C_0 \sqsubseteq \bot \). So, both (I1) and (I2) hold for the empty sequences. Regarding (I3) note that every free schedule \(R'\) starting in the configuration \(({\varSigma } _{n_0}, \rho _{n_0})\) is trivially \(C_0\)-consistent since no variable is decided in \(C_0\). Since \(C_0 \not \preceq \top {:}\mathsf{1 } \) the schedule \(R'\) is not constrained regarding resets.
Step case. By way of induction hypothesis (I1)–(I3), suppose we have constructed a B-admissible schedule \(R_0, R_1, \ldots , R_{i-1}\) (I2) such that for every \(j \le i\) (using course-of-values induction) the yield of \(R_0, R_1, \ldots , R_{j-1}\) with respect to \(C_{j-1}\) lies in the range predicted by \(C_{j}\) (I1) and for every free schedule \(R'\) from \(({\varSigma } _{n_j}, \rho _{n_j})\) the extension \(R_0, R_1, \ldots , R_{j-1}, R'\) is \(C_j\)-consistent (I3). Moreover, from (I3) we may assume that if \(C_j(x) \preceq \top {:}\mathsf{1 } \) then \(R'\) is reset-free for \(x\). From \(({\varSigma } _{n_i}, \rho _{n_i})\) we now continue to schedule all and only those processes that are active and \(C_i\)-enabled. We do this until \(\iota _P\) stops under \(C_i\), i.e., until it completes or all remaining active threads are \(C_i\)-blocked. This procedure builds a round schedule \(R_{i}\) and leads to a configuration \(({\varSigma } _{n_{i+1}}, \rho _{n_{i+1}})\). Then, \(n_{i+1}\) is the \(C_i\)-stopping index of \(P\) in \(R_0, R_1, \ldots , R_{i-1}, R_{i}\). If it happens that there is no active process in \({\varSigma } _{n_i}\) which is \(C_{i}\)-enabled, then \({\varSigma } _{n_{i+1}} = {\varSigma } _{n_i}\) and \(\rho _{n_{i+1}} = \rho _{n_{i}}\). In this case, we just move on to the next iteration round \(C_{i+1}\) of the fixed-point without progressing the schedule. \(\square \)
Proposition 9
For every fprog \(P\), if \(P\) is IBC then \(P\) is SC-read-determinate.
Proof
Again let \(({\varSigma } _0, \rho _0)\) be an initial configuration with \({\varSigma } _0 = \{ {\langle \iota _P, P, [\,] \rangle } \}\) and \(\iota _P = \mathsf Root . id = 0\). Fix an SC-admissible instant \(R : ({\varSigma } _0, \rho _0) \mathop {\twoheadrightarrow }\limits ^{} ({\varSigma } _n, \rho _n)\), where \(n = len (R)\). Observe that all processes in every pool \({\varSigma } _i\) are descendants of \(\iota _P\). We cover the micro-sequence \(R\) incrementally with the results from the fixed point iteration, showing that \(R\) can only ever execute variable read accesses within the corridor predicted by the fixed-point responses \(C_i\), where \(C_0 = [\bot , \top ]{:}\mathsf{2 } \) and \(C_{i+1} = \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C_i}}\). This exploits the soundness of lower and upper predictions, Proportions 6 and 7. More precisely, let \(i_{k+1}\) be the \(C_k\)-stopping index of \(P\) in \(R\) for \(k \ge 0\). These must exist because \(R\) is an instant and thus a maximal micro-sequence. One shows by induction on \(k\) that \(R\) is \(C_k\)-consistent and
which says that the environment \(C_{k+1}\) is a sound approximation of the yield from \(i_{k+1}\) onwards. At the fixed-point \(C_* = \mu C.\, \langle \!\langle P \rangle \!\rangle ^{{\bot }}_{{C}} \in \{ \bot , 0, 1 \}\), this implies that that \(R\) is \(C_*\)-consistent for \(\iota _P\) and \(C_* \sqsubseteq |R{\tiny @}n | _{C_* } (\iota _P)\). In view of Lemma 1 this shows that all SC-admissible instants \(R\) of \(P\) have the same deterministic final memory value and this memory value is the one computed by the IBC fixed-point analysis. \(\square \)
5 Related work
The usefulness of synchronisation primitives is well-established in main-stream concurrent programming. For example, C++ and Java are based on a multi-threaded shared-memory execution model which provides synchronisation of methods to isolate threads and to ensure safety properties such as mutual exclusion. The clock synchronisation (pause) and associated scheduling constraints of our SMoCC approach may also be seen as a synchronisation pattern to ensure memory safety. It provides global snapshot barriers and pruning of thread interleaving with the aim of ensuring reactiveness and memory determinacy. The programmer must decide which synchronisation model is the right one for a given application context. In reactive and embedded systems the SMoCC has turned out to be a natural choice.
In terms of programming languages, the work presented here is at the interface between synchronous concurrent languages and C-like sequential languages, and is strongly influenced by both worlds. Edwards [26] and Potop-Butucaru et al. [70] provide good overviews of compilation challenges and approaches for concurrent languages, including synchronous languages. They discuss efficient mappings from Esterel to C, thus their work is related to ours in the sense that we present a means to express Esterel-style signal behavior and deterministic concurrency directly with variables in a C-like language. However, a key difference is that we do not “compile away” the concurrency as part of our signal-to-variable mapping, but fully preserve the original, concurrent semantics with shared variables.
Introducing the constructive causality classes SBC, IBC, BC we redress the synchronous model of computation, well-known in the embedded systems domain, for main-stream programming. There are already many proposals that extend C or Java with synchronous concurrency constructs. Reactive C [16] is an extension of C that employs the concepts of ticks and preemptions, but does not provide concurrency. FairThreads [17] are an extension introducing concurrency via native threads. PRET-C [6] and Synchronous C, a.k.a. SyncCharts in C [83], provide macros for defining synchronous concurrent threads. SC also permits dynamic thread scheduling, and thus would be a suitable implementation target for the pSCL language discussed here. SHIM [79], another C-like language, provides concurrent Kahn process networks with rendezvous communication [42] and exception handling. SHIM has also been inspired by synchronous languages, but it does not use the synchronous programming model, instead relying on communication channels for synchronisation. None of these language proposals claims and proves to embed the concept of Esterel-style constructiveness into shared variables as we do here. As far as these language proposals include signals, they come as “closed packages” that do not, for example, allow to separate initialisations from updates.
As traditional sequential, single-core execution platforms are being replaced by multi-core/processing architectures, determinism is no longer a trade secret of synchronous programming but has become an important issue in shared memory concurrent programming. Powerful techniques have recently been developed to verify program determinism statically. For Java with structured parallelism, the tool DICE by Vechev et al. [81] performs static analysis to check that concurrent tasks do not interfere on shared array accesses. Leung et al. [53] present a test amplification technique based on a combination of instrumented test execution and static data-flow analysis to verify that the memory accesses of cyclic, barrier-synchronised, CUDA C++ threads do not overlap during a clock cycle (barrier interval). For polyhedral X10 programs with finish/async parallelism and affine loops over array-based data structures, Yuki et al. [87] describe an exact algorithm for static race detection that ensures deterministic execution.
These recently published analyses [53, 81, 87] are targeted at data-intensive, array/pointer/based code building on powerful arithmetical models and decision procedures for memory separation. Yet, they address determinism in more limited models of communication. SMoCC constructiveness concerns the determinism and reactivity of “control-parallel” rather than “data-parallel” synchronous programs and permits instantaneous communication between threads during a single tick. The challenge is to deal with feedbacks and reaction to absence, as in circuit design, which is difficult. The causality of the SMoCC memory accesses cannot necessarily be captured in terms of regular affine arithmetics as done in the polyhedral model of [81, 87] or reduced to a “small core of configuration inputs” as in [53]. Further, analyses such as [53, 81, 87] verify race-freedom for maximally strong data conflicts: Within the barrier no write must ever compete with a concurrent read or another conflicting write. Soundness of the analysis is straightforward under such full isolation. Full thread isolation is fine for Moore-style communication but does not hold in the SMoCCs whose hallmark is the Mealy model. Threads do in fact share variables during a clock phase and multi-emissions are permitted. Analysing SMoCC determinism, therefore, is tricky and arguing soundness of the constructivity analysis in the SMoCCs (our Theorem 1) is non-trivial. This is particularly true if reaction to absence is permitted, as in our work, which introduces non-monotonic system behaviour on which the standard (naive) fixed-point techniques fail.
For functional programming languages, traditionally abstracting from the impurity of low-level scheduling, determinism on concurrent platforms also has become an issue. For instance, Kuper et al. [50] extend the IVar/LVar approach in Haskell to provide deterministic shared data-structures permitting multiple concurrent reads and writes. This extension, dubbed LVish, adds asynchronous event handlers and explicit value freezing to implement negative data queries. Since the negative information is transient, run-time exceptions are possible due to the race between freezing and writing. However, all error-free executions produce the same result which is called quasi-determinism. Because of the instantaneous communication and the negative information carried by the value status of shared data, the quasi-deterministic model of [50] is similar in spirit to our approach. However, there are at least two differences: First, our programming model deals with first-order imperative programs on Boolean data, while [50] considers higher-order \(\lambda \)-functions on more general “atomistic” data structures. Second, our \(\langle \!\langle \_ \rangle \!\rangle ^{{}}_{{}}\) constructivity includes reactivity, which is a liveness property, whereas [50] only address the safety property of non-interference.
Our two-dimensional lattice \(I(\mathbb {D})\) seems richer than the lifted domain \( Freeze (\mathbb {D})\) of [50] which only distinguishes between the “unfrozen” statuses \([\bot ,\top ]\), \([0,\top ]\), \([1,\top ]\), \([\top ,\top ]\) (lower information) and the “frozen” statuses \([\bot , \bot ]\), \([0,0]\), \([1,1]\) (crisp information). There do not seem to be genuine upper bound approximations expressible in \( Freeze (\mathbb {D})\). It will be interesting to study the exact relationship between the two models on a common language fragment.
There is also a large body of related work investigating different notions of constructiveness. Causal Esterel programs on pure signals satisfy a strong scheduling invariant: they can be translated into constructive circuits which are delay-insensitive [18] under the non-inertial delay model, which can be fully decided using ternary Kleene algebra [64]. This makes Malik’s work [58] on causality analysis of cyclic circuits applicable to constructiveness analysis of (instantaneous) Esterel program. This has been extended by Shiple et al. [76] to state-based systems, as induced by Esterel’s pause operator, thus handling non-instantaneous programs as well. The algebraic transformations proposed by Schneider et al. [75] increase the class of programs considered constructive by permitting different levels of partial evaluation. Pnueli and Shalev’s non-deterministic model of Statecharts [69] has been studied using an axiomatic semantics in intuitionistic logic [54], which subsequently has been extended to Esterel [56]. In [3] a game-theoretic approach is used to define a hierarchy of levels constructiveness using maximal post fixed-points. However, none of these approaches considers imperative programming, separates initialisations and updates, or permits sequential writes within a tick as we do here.
Recently, Mandel et.al.’s clock domains [59] and Gemünde et.al.’s clock refinement [32] provide sequences of micro-level computations within an outer clock tick. This also increases sequential expressiveness albeit in an upside-down fashion compared to our approach. Our work on SC aims to reconstruct the scope of a synchronous instant on top of the primitive notion of sequential composition. Different classes of constructiveness are distinguished by how generous they are in bundling sequences of variable accesses from concurrent threads within a single clock tick. In the clock domains and clock refinement approach, clocks are the only sequencing mechanism, so micro-level sequencing is implemented in terms of lower-level clocks. It should be possible to combine our approach with that of [32, 59] by considering the sequential composition operator as a local micro-level clock nested inside an outer, and global, macro-level clock. This might generate a useful theory of causal clock abstractions.
Our work focuses on imperative, i.e., control-dominated synchronous programs rather than data flow semantics. Recently, Talpin et.al. within the “Polycore” project have started important work on semantically integrating the control-flow synchronous language Quartz with the data flow language Signal. In [77] they present the first micro-step (or “small-step”) operational fixed-point semantics that is capable of executing both Signal code and the guarded actions of Quartz. The operational semantics models the behaviour of each variable in a 6-valued lattice domain \(\mathcal {D}\) coding the signal statuses unknown (\(?\)), absent (\(\bot \)), present (\(\top \)), present-and-false (\(0\)), present-and-true (\(1\)) as well as inconsistency ( ). Based on the operational execution model they define the notion of constructive programs and prove a soundness theorem stating that each constructive program is deterministic.
). Based on the operational execution model they define the notion of constructive programs and prove a soundness theorem stating that each constructive program is deterministic.
One difference compared to our work is that the domain \(I(\mathbb {D}, \mathbb {P})\) supports reaction to absenceFootnote 6 which is a hall-mark of Esterel-style SMoCCs and motivates its richer interval structure. On the other hand, the polychronous language of [77] is richer than pSCL in that is has preemption and boolean data values which we do not consider here. However, these concepts can be easily mapped to pSCL, as demonstrated in SCCharts [84]. Finally, note that our definition of constructive programs (e.g., Definition 9) is based on a genuine denotational semantics \(\langle \!\langle \_ \rangle \!\rangle ^{{}}_{{}}\), not an operational one as in [77]. For example, it follows from our results that if two program \(P\) and \(Q\) generate the same response function \(\langle \!\langle P \rangle \!\rangle ^{{S}}_{{C}} = \langle \!\langle Q \rangle \!\rangle ^{{S}}_{{C}}\) in \(S\) and \(C\), then \(P\) and \(Q\) are behaviourally equivalent in all program contexts. Also, our operational semantics (e.g., Sect. 2) uses free multi-threaded scheduling in a memory that is ignorant of the signal statuses. In particular, it does not perform any implicit enabledness, synchronisation or deadlock checks like the operational semantics of [77] does, in which execution maintains scheduling information through variable values in \(\mathcal D\). Hence, our Soundness Theorem 1 which guarantees B-reactiveness and SC-determinacy makes a stronger soundness statement which is considerably more difficult to prove. Our result can be applied directly to standard imperative C/Java code which is not normally executed under a \(\mathcal D\)-instrumented run-time scheduler. Yet, given the limited language constructs of pSCL compared to [77], it would be very interesting to combine both approaches.
An acknowledged strength of synchronous languages is their formal foundation [9], which facilitates formal verification, timing analyses, and inclusion results of the type presented in this work. This formal foundation has been developed in several ways in the past; e.g., Berry [12] presents several Plotkin-style structural operational semantics [68], as well as a definition in terms of circuits for Esterel. Our functional/algebraic approach based on \(I(\mathbb {D},\mathbb {P})\) generalizes the “must-cannot” analysis for constructiveness [12] and the ternary analysis for synchronous control flow [73] and circuits [58, 76]. The extension lies in the ability to deal with non-initialization (\(\bot \)) and re-initialization (\(\top \)) in sequential control flow, which the analyses [12, 58, 73, 76, 77] cannot handle. Due to the two-sided nature of intervals our semantics permits the modeling of instantaneous reaction to absence, a definitive feature of Esterel-style synchrony for control-flow languages. In contrast, the balance equations (see, e.g., [52]) or the clock calculus (see, e.g., [19, 31, 67, 77]) of synchronous reactive data flow do not handle reaction to absence. These analyses are concerned with inter-tick causality (i.e., in which ticks a signal is present) rather than intra-tick causality (i.e., presence or absence in a given tick) which we focus on here. Reflected into \(I(\mathbb {D})\), Lustre clocks collapse the signal status (within a tick) to either \(\bot \) (value not initialized or computed) or \([0,\top ]\) (value computed). However, since each program abstracts to a continuous function on \(I(\mathbb {D},\mathbb {P})\)-valued environments our model fits naturally into the Kahn-style fixed-points semantics and scheduling analysis for synchronous block diagrams [28, 71].
6 Conclusions
In this article we study constructiveness analysis, the center-piece of the synchronous model of concurrent computations, from a scheduling perspective. We advocate the view that constructiveness is the property of a synchronous program being deadlock-free and determinate with respect to a given scheduling protocol defining admissible executions. This permits us (i) to apply the concept to (clocked) multi-threaded shared memory programs and (ii) to obtain different interpretations of constructiveness by varying the notion of admissibility. The two notions addressed are Berry-admissibility (Definition 4) introduced here and SC-admissibility (Definition 5) defined in [86]. Both are instances of the “init-update-read” protocol, which schedules initialising writes before updating writes, and writes before reads.
For a small imperative synchronous language pSCL we extend the causality analysis from [4] by initialisation information \(\mathbb {P}\) and define the class of IBC programs as those (recursion-free) pSCL programs for which abstract simulation in the extended domain \(I(\mathbb {D}, \mathbb {P})\) returns a reset- and read-safe fixed-point (Definition 9). We then prove that this implies deadlock-freeness under Berry-admissible scheduling (Berry-reactiveness) and determinacy under SC-admissible scheduling (SC-read-determinacy). This shows that the denotational fixed-point semantics which associates with every program \(P\) a response behaviour \(\langle \!\langle P \rangle \!\rangle ^{{}}_{{}}\) in the domain \(I(\mathbb {D}, \mathbb {P})\) is sound and compositional for the operational semantics defined in terms of micro-step scheduling. This strengthens the results of [4] showing that IBC programs are guaranteed to be deadlock-free and determinate under scheduling principles more robust than those in [4]: B-reactiveness does not permit reinitialisations as SC-reactiveness does in [4]. SC-read-determinacy forces read variables to be stable (any change of a read variable must be constant across all initial memories), which is not precluded by soundness in [4].
We leave as an open problem the question if the \(I(\mathbb {D}, \mathbb {P})\) fixed-point semantics is also complete for the notions of admissible scheduling discussed here, or, if there are natural variations of the scheduling principles for which our semantics is complete. The ideal is a situation like in [64] where it is shown that Berry’s must-cannot analysis [12] when applied to circuits is (sound and) complete for scheduling under non-inertial delays. In another direction, it will be interesting to search for suitable, more expressive, extensions of the domain \(I(\mathbb {D}, \mathbb {P})\) in which the fixed-point analysis of pSCL is complete for SC-constructiveness as defined in [86]. Our fixed-point analysis is sound but rejects programs with more than one init-update-read cycle. This, however, is permitted by SC-constructiveness.
Notes
This is sometimes referred to as the ‘LAGS’ model and not to be confused with the well-known but orthogonal ‘GALS’ model which features globally asynchronous and locally synchronous computations.
There is an informal sketch of a micro-step semantics in [12], Sect. 4.3] which is not developed further or formally related with the fixed-point semantics for macro-steps.
This stands here for “pure Synchronous Constructive Language” indicating not only that signal variables in pSCL carry Boolean status but also that pSCL is a minimalistic version of control-flow synchronous languages in an abstract algebraic syntax.
This extra bit for indicating predicted resets has been missing in our publication [4] where this fixed-point analysis was introduced for the first time.
In other words, the free set-theoretic “collection semantics”, which defines the completion code of a program as the set of all it possible completions (under a given choice of environments), would produce exactly the sets in \(I(\mathbb {C})\). We could have defined \(I(\mathbb {C})\) more generously as the set of subsets of completion codes \(\mathcal{P}\{ \bot , 0, 1 \}\). However, our explicit description reveals more of the algebraic properties of \(I(\mathbb {C})\) than \(\mathcal{P}\{ \bot , 0, 1 \}\). For instance, it makes clear that the internal logic of \(I(\mathbb {C})\) is not a Boolean algebra.
The oversampling feature of Signal may be seen as an implicit form of reaction to absence in the asynchronous data-flow part of [77]. Synchronous reaction to absence would map \(\bot \) to \(\top \) and \(\top \) to \(\bot \) in the domain \(\mathcal {D}\) which does not seem to be expressible by the control-flow operators considered in [77].
References
Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163(2), 409–470 (2000)
Aceto, L., Ingolfsdottir, A.: CPO models for compact GSOS languages. Inf. Comput. 129(2), 107–141 (1996)
Aguado, J., Mendler, M.: Constructive semantics for instantaneous reactions. Theor. Comput. Sci. 241, 931–961 (2011)
Aguado, J., Mendler, M., von Hanxleden, R., Fuhrmann, I.: Grounding synchronous deterministic concurrency in sequential programming. In: Proceedings of the 23rd European Symposium on Programming (ESOP’14). LNCS 8410, pp. 229–248. Springer, Grenoble, France (2014)
Aguado, J., Mendler, M., von Hanxleden, R., Fuhrmann, I.: Denotational fixed-point semantics for constructive scheduling of synchronous concurrency. Technical report 96, University of Bamberg, Faculty of Information Systems and Applied Computer Sciences (2015). ISSN 0937–3349
Andalam, S., Roop, P.S., Girault, A.: Deterministic, predictable and light-weight multithreading using PRET-C. In: Proceedings of the Conference on Design. Automation and Test in Europe (DATE’10), pp. 1653–1656. Dresden, Germany (2010)
Baudart, G., Mandel, L., Pouzet, M.: Programming mixed music in ReactiveML. In: Proceedings of the First ACM SIGPLAN Workshop on Functional Art. Music, Modeling & #38; Design, FARM ’13, pp. 11–22. ACM, New York, NY, USA (2013)
Benveniste, A., Caillaud, B., Guernic, P.L.: Compositionality in dataflow synchronous languages: specification and distributed code generation 1,2,3. Inf. Comput. 163(1), 125–171 (2000)
Benveniste, A., Caspi, P., Edwards, S.A., Halbwachs, N., Guernic, P.L., de Simone, R.: The Synchronous Languages Twelve Years Later. In: Proceedings of IEEE, Special Issue on Embedded Systems, vol. 91, pp. 64–83. IEEE, Piscataway, NJ, USA (2003)
Bergstra, J., Ponse, A., Smolka, S. (eds.): Handbook of Process Algebra. Elsevier (2001)
Berry, G.: The foundations of Esterel. In: Plotkin, G., Stirling, C., Tofte, M. (eds.) Proof, Language, and Interaction: Essays in Honour of Robin Milner, pp. 425–454. MIT Press, Cambridge (2000)
Berry, G.: The Constructive Semantics of Pure Esterel. Draft Book, Version 3.0, Centre de Mathématiques Appliqées, Ecole des Mines de Paris and INRIA, 2004 route des Lucioles, 06902 Sophia-Antipolis CDX, France (2002)
Berry, G., Curien, P.L., Lévy, J.J.: Full abstraction for sequential languages: the state of the art. In: Nivat, M., Reynolds, J.C. (eds.) Algebraic Semantics, pp. 89–132. Cambridge University Press, Cambridge (1985)
Berry, G., Gonthier, G.: The Esterel synchronous programming language: design, semantics, implementation. Sci. Comput. Program. 19(2), 87–152 (1992)
Berry, G., Nicolas, C., Serrano, M.: Hiphop: A synchronous reactive extension for Hop. In: Proceedings of the 1st ACM SIGPLAN International Workshop on Programming Language and Systems Technologies for Internet Clients. PLASTIC ’11, pp. 49–56. ACM, New York, NY, USA (2011)
Boussinot, F.: Reactive C: an extension of C to program reactive systems. Softw. Pract. Exp. 21(4), 401–428 (1991)
Boussinot, F.: Fairthreads: mixing cooperative and preemptive threads in C. Concurr. Comput. Pract. Exp. 18(5), 445–469 (2006)
Brzozowski, J.A., Seger, C.J.H.: Asynchronous Circuits. Springer, New York (1995)
Caspi, P., Pilaud, D., Halbwachs, N., Plaice, J.A.: Lustre: a declarative language for programming synchronous systems. In: Proceedings of the 14th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages (POPL’87), pp. 178–188. ACM, Munich, Germany (1987)
Caspi, P., Pouzet, M.: A co-iterative characterization of synchronous stream functions. Electron. Notes Theor. Comput. Sci. 11(0), 1–21 (1998). CMCS’98, First Workshop on Coalgebraic Methods in Computer Science
Cleaveland, R., Lüttgen, G., Mendler, M.: An algebraic theory of multiple clocks. In: CONCUR ’97, LNCS, vol. 1243, pp. 166–180. Springer (1997)
Cohen, A., Duranton, M., Eisenbeis, C., Pagetti, C., Plateau, F., Pouzet, M.: N-synchronous Kahn networks: a relaxed model of synchrony for real-time systems. Symposium on Principles of Programming Languages. POPL’06, pp. 180–193. ACM, New York, NY, USA (2006)
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order. Cambridge University Press, Cambridge (2002)
de Roever, W.P., Lüttgen, G., Mendler, M.: What is in a step: new perspectives on a classical question. In: Manna, Z., Peled, D.A. (eds.) Time for Verification, pp. 370–399. Springer LNCS 6200 (2010)
Duffin, R.J.: Topology of series-parallel networks. J. Math. Anal. Appl. 10(2), 303–318 (1965)
Edwards, S.A.: Tutorial: compiling concurrent languages for sequential processors. ACM Trans. Design Autom. Electron. Syst. 8(2), 141–187 (2003)
Edwards, S.A., Lee, E.A.: The semantics and execution of a synchronous block-diagram language. Sci. Comput. Program. 48(1), 21–42 (2003)
Edwards, S.A., Lee, E.A.: The semantics and execution of a synchronous block-diagram language. In: Science of Computer Programming, vol. 48. Elsevier (2003)
Ésik, Z.: Axiomatizing the least fixed point operation and binary supremum. In: Clote, P., Schwichtenberg, H. (eds.) Computer Science Logic (CSL’00), LNCS 1862, pp. 302–316. Springer (2000)
Fiore, M., Moggi, E., Sangiorgi, D.: A fully abstract model for the \(\pi \)-calculus. Inf. Comput. 179(1), 76–117 (2002)
Gamatié, A., Gonnord, L.: Static analysis of synchronous programs in Signal for efficient design of multi-clocked embedded systems. ACM Sigplan Notices 46(5), 71–80 (2011)
Gemünde, M., Brandt, J., Schneider, K.: Clock refinement in imperative synchronous languages. EURASIP J. Embed. Syst. 2013, 3 (2013)
Groote, J.F., Vaandrager, F.: Structured operational semantics and bisimulation as a congruence. Inf. Comput. 100, 202–260 (1992)
Guernic, P.L., Goutier, T., Borgne, M.L., Maire, C.L.: Programming real time applications with SIGNAL. Proc. IEEE 79(9), 1321–1336 (1991)
Halbswachs, N.: Synchronous Programming of Reactive Systems. Kluwer Academic Publishers, Dordrecht (1993)
Halbwachs, N., Caspi, P., Raymond, P., Pilaud, D.: The synchronous data-flow programming language LUSTRE. Proc. IEEE 79(9), 1305–1320 (1991)
Hamon, G.: A denotational semantics for Stateflow. In: EMSOFT’05: Proceedings of the 5th ACM International Conference on Embedded Software, pp. 164–172. ACM Press, New York, NY, USA (2005)
Harel, D.: Statecharts: a visual formalism for complex systems. Sci. Comput. Program. 8(3), 231–274 (1987)
Harel, D., Naamad, A.: The STATEMATE semantics of statecharts. ACM Trans. Softw. Eng. 5(4), 293–333 (1996)
Hennessy, M.: Acceptance trees. J. ACM 32(4), 896–928 (1985)
Hennessy, M., Regan, T.: A process algebra for timed systems. Inf. Comput. 117, 221–239 (1995)
Hoare, C.A.R.: Communicating Sequential Processes. Prentice Hall, Upper Saddle River, NJ (1985)
Huizing, C., Gerth, R., de Roever, W.: Modeling Statecharts behavior in a fully abstract way. In: Dauchet, M., Nivat, M. (eds.) 13th CAAP (CAAP ’88). Lecture Notes in Computer Science, vol. 299, pp. 271–294. Springer, Nancy, France (1988)
Hyland, M., Ong, L.: On full abstraction for PCF: I. II and III. Inf. Comput. 163(2), 285–408 (2000)
Ingólfsdóttir, A., Schalk, A.: A fully abstract denotational model for observational precongruence. Theor. Comput. Sci. 254(1–2), 35–61 (2001)
Kahn, G.: The semantics of a simple language for parallel programming. In: Rosenfeld, J.L. (ed.) Information Processing 74: In: Proceedings of the IFIP Congress 74, pp. 471–475. North-Holland Publishing Co., IFIP (1974)
Kahn, G., MacQueen, D.B.: Coroutines and networks of parallel processes. In: IFIP Congress, pp. 993–998 (1977)
Kok, J.N.: Denotational semantics of nets with nondeterminism. In: Robinet, B., Wilhelm, R. (eds.) European Symposium on Programming (ESOP’86), LNCS 213, pp. 237–249. Springer (1986)
Kozen, D.: A completeness theorem for Kleene algebras and the algebra of regular events. Inf. Comput. 110(2), 366–390 (1994)
Kuper, L., Turon, A., Krishnaswami, N.R., Newton, R.R.: Freeze after writing: Quasi-deterministic parallel programming with LVars. In: Principles of Programming Languages (POPL’14), pp. 257–270. ACM, New York, USA (2014)
Lavagno, L., Sentovich, E.: ECL: a specification environment for system-level design. In: Proceedings of 36th ACM/IEEE Conference on Design Automation (DAC’99), pp. 511–516. ACM (1999)
Lee, E.A., Messerschmitt, D.G.: Synchronous data flow. In: Proceedings of the IEEE, vol. 75, pp. 1235–1245. IEEE Computer Society Press (1987)
Leung, A., Gupta, M., Agarwal, Y., Gupta, R., Jhala, R., Lerner, S.: Verifying GPU kernels by test amplification. In: Programming Language Design and Implementation PLDI 2012, pp. 383–394. ACM, New York, USA (2012)
Luettgen, G., Mendler, M.: The intuitionism behind statecharts steps. ACM Trans. Comput. Log. 3(1), 1–41 (2002)
Lüttgen, G., von der Beeck, M., Cleaveland, R.: Statecharts via process algebra. In: Proceedings of 10th International Conference on Concurrency Theory CONCUR’99, pp. 399–414 (1999)
Lüttgen, G., Mendler, M.: Towards a model-theory for Esterel. In: Maraninchi, F., Girault, A., Rutten, E. (eds.) SLAP 2002, ENTCS, vol. 65,5. Elsevier Science (2002)
Lynch, N.: Distributed Algorithms. Morgan Kaufmann Publishers, Los Altos (1996)
Malik, S.: Analysis of cyclic combinational circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 13(7), 950–956 (1994)
Mandel, L., Pasteur, C., Pouzet, M.: Time refinement in a functional synchronous language. In: Principles and Practice of Declarative Programming (PPDP’13), pp. 169–180. ACM (2013)
Mandel, L., Pouzet, M.: ReactiveML: a reactive extension to ML. In: Proceedings of 7th ACM SIGPLAN Int’l Conference on Principles and Practice of Declarative Programming, pp. 82–93 (2005)
Maraninchi, F.: The Argos language: graphical representation of automata and description of reactive systems. In: IEEE Workshop on Visual Languages (1991)
Maraninchi, F., Rémond, Y.: Argos: an automaton-based synchronous language. Comput. Lang. 27(27), 61–92 (2001)
Mendler, M., Lüttgen, G.: Is observational congruence axiomatisable in equational Horn logic? Inf. Comput. 208(6), 634–651 (2010)
Mendler, M., Shiple, T.R., Berry, G.: Constructive boolean circuits and the exactness of timed ternary simulation. Form. Methods Syst. Des. 40(3), 283–329 (2012)
Milner, R.: Communication and Concurrency. Prentice Hall, Englewood Cliffs (1989)
Motika, C., von Hanxleden, R., Heinold, M.: Programming deterministice reactive systems with Synchronous Java (invited paper). In: Proceedings of the 9th Workshop on Software Technologies for Future Embedded and Ubiquitous Systems (SEUS 2013), IEEE Proceedings. Paderborn, Germany (2013)
Ngo, V.C., Talpin, J.P., Gautier, T.: Precise deadlock detection for polychronous data-flow specifications. In: Proceedings of the Electronic System Level Synthesis Conference (ESLsyn), pp. 1–6. IEEE (2014)
Plotkin, G.D.: A Structural Approach to Operational Semantics. Technical report DAIMI FN-19, University of Aarhus, Denmark (1981)
Pnueli, A., Shalev, M.: What is in a step: on the semantics of Statecharts. In: Proceedings of International Conference on Theoretical Aspects of Computer Software (TACS’91), pp. 244–264. Springer, London, UK (1991)
Potop-Butucaru, D., Edwards, S.A., Berry, G.: Compiling Esterel. Springer, Berlin (2007)
Pouzet, M., Raymond, P.: Modular static scheduling of synchronous data-flow networks—an efficient symbolic representation. Des. Autom. Embed. Syst. 14(3), 165–192 (2010)
Schneider, K.: The synchronous programming language Quartz. Internal Report 375, Department of Computer Science, University of Kaiserslautern, Kaiserslautern, Germany (2009)
Schneider, K., Brandt, J., Schuele, T.: Causality analysis of synchronous programs with delayed actions. In: Conference on Compilers, Architecture, and Synthesis for Embedded Systems (CASES’04), pp. 179–189. ACM, Washington DC, USA (2004)
Schneider, K., Brandt, J., Schuele, T., Tuerk, T.: Maximal causality analysis. In: Conference on Application of Concurrency to System Design (ACSD’05), pp. 106–115. IEEE Computer Society (2005)
Schneider, K., Brandt, J., Schüle, T., Türk, T.: Improving constructiveness in code generators. In: Maraninchi, F., Pouzet, M., Roy, V. (eds.) International Workshop on Synchronous Languages, Applications, and Programming (SLAP’05), pp. 1–19. ENTCS, Edinburgh, Scotland, UK (2005)
Shiple, T.R., Berry, G., Touati, H.: Constructive Analysis of Cyclic Circuits. In: Proceedings of European Design and Test Conference (ED&TC’96), Paris, France, pp. 328–333. IEEE Computer Society Press (1996)
Talpin, J.P., Brandt, J., Gemünde, M., Schneider, K., Shukla, S.: Constructive polychronous systems. Sci. Comput. Program. 96(3), 377–394 (2014)
Talpin, J.P., Ouy, J., Gautier, T., Besnard, L., Guernic, P.L.: Compositional design of isochronous systems. Sci. Comput. Program. 77(2), 113–128 (2012)
Tardieu, O., Edwards, S.A.: Scheduling-independent threads and exceptions in SHIM. In: Proceedings of the International Conference on Embedded Software (EMSOFT’06), pp. 142–151. ACM (2006)
Tardieu, O., Edwards, S.A.: Instanteneous transitions in Esterel. In: Proceedings of Model Driven High-Level Programming of Embedded Systems (SLA++P’07). Braga, Portugal (2007)
Vechev, M., Yahav, E., Raman, R., Sarkar, V.: Automatic verification of determinism for structured parallel programs. In: Cousot, R., Martel, M. (eds.) Static Analysis (SAS 2010), LNCS, vol. 6337, pp. 455–471. Springer (2010)
von der Beeck, M.: A comparison of Statecharts variants. In: Langmaack, H., de Roever, W., Vytopil, J. (eds.) 3rd International School and Symposium on Formal Techniques in Real-Time and Fault-Tolerant Systems (FTRTFT ’94), Lecture Notes in Computer Science, vol. 863, pp. 128–148. Springer (1994)
von Hanxleden, R.: SyncCharts in C-A Proposal for Light-Weight, Deterministic Concurrency. In: Proceedingsof International Conference on Embedded Software (EMSOFT’09), pp. 225–234. ACM, Grenoble, France (2009)
von Hanxleden, R., Duderstadt, B., Motika, C., Smyth, S., Mendler, M., Aguado, J., Mercer, S., O’Brien, O.: SCCharts: sequentially constructive statecharts for safety-critical applications. In: Proceedings of ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI’14). ACM (2014)
von Hanxleden, R., Mendler, M., Aguado, J., Duderstadt, B., Fuhrmann, I., Motika, C., Mercer, S., O’Brien, O.: Sequentially constructive concurrency—a conservative extension of the synchronous model of computation. In: Design, Automation and Test in Europe (DATE’13), pp. 581–586. IEEE (2013)
von Hanxleden, R., Mendler, M., Aguado, J., Duderstadt, B., Fuhrmann, I., Motika, C., Mercer, S., O’Brien, O., Roop, P.: Sequentially constructive concurrency—a conservative extension of the synchronous model of computation. ACM Trans. Embed. Comput. Syst.,Special Issue on Applications of Concurrency to System Design 13(4s), 144:1–144:26 (2014)
Yuki, T., Feautrier, P., Rajopadye, S., Saraswat, V.: Array dataflow analysis for polyhedral X10 programs. In: Principles and Practice of Parallel Programming (PPoPP 2013), pp. 23–34. ACM (2013)
Acknowledgments
This work has been supported by the German National Research Council DFG as part of the PRETSY Project (HA 4407/6-1, ME 1427/6-1). The authors would also like to thank the anonymous reviewers for their trenchant yet constructive criticisms and their useful suggestions regarding related work and expository improvements of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Aguado, J., Mendler, M., von Hanxleden, R. et al. Denotational fixed-point semantics for constructive scheduling of synchronous concurrency. Acta Informatica 52, 393–442 (2015). https://doi.org/10.1007/s00236-015-0238-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-015-0238-x






 ) and the list of continuation processes in the next-control
) and the list of continuation processes in the next-control 
 .
. ), then there exists an index
), then there exists an index  ) and
) and  or set
or set  ,
,




 depends on whether the sequential stimulus
depends on whether the sequential stimulus 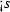 . Hence, we must crash
. Hence, we must crash  and since it terminates instantaneously the down-stream computation continues with the init status
and since it terminates instantaneously the down-stream computation continues with the init status  is speculative. In this case we crash the value status and raise the init status to
is speculative. In this case we crash the value status and raise the init status to  which terminates instantaneously.
which terminates instantaneously. is only speculative. This gives the response
is only speculative. This gives the response  may crash the model, whence the result
may crash the model, whence the result  increases the sequential yield for
increases the sequential yield for  raises the speculation status to
raises the speculation status to  , then
, then  ,
,  .
.