1 Introduction

Ginger (Zingiber officinale Rosc.) is one of the most important and extensively used spices worldwide. In ancient times, ginger was used for its flavoring but more valued for its medicinal properties and was therefore a constituent of many pharmaceutical preparations [1]. Ginger rhizomes contain about 82.6 % moisture content [2]. Most ginger rhizomes are sold commercially as fresh vegetable without processing. Besides consumption at the natural stage, there are various products that can be obtained from ginger rhizomes, such as juice, concentrated ginger powders, and dried products. Drying is an ancient method to preserve food. Dried food is also more concentrated in its chemical composition than any other pre-served form of food stuff. The process is therefore effective because it lowers the cost of packaging, storing and transportation by reducing both weight and volume of the final product [2].

Drying is a complex thermal process in which unsteady heat and moisture transfer occur simultaneously [3, 4]. From an engineering point of view, it is important to develop a better understanding of the controlling parameters of this complex process. Mathematical models of the drying processes are used for designing new or improving existing drying systems or even for the control of the drying process. Many mathematical models have proposed to describe the drying process, of them, thin-layer drying models have been widely in use. These models can be categorized as theoretical, semi-theoretical, and empirical [4, 5].

The convective heat transfer coefficient is an important parameter in drying rate simulation since the temperature difference between the air and product varies with this coefficient. Usually, two methods are available to determine the convective heat transfer coefficient of grains like barley, malt, etc. These are dimensional analysis and direct measurement of heat transfer on a grain bed by comparing the temperature curves with Shumann’s exact solution [6]. The dimensional analysis is mathematically simple and has a wide range of applications. This method is incomplete without sufficient experimental data, although it facilitates the interpretation and extends the range of application of experimental data by correlating them in terms of dimensional groups [7].

Accurate determination of moisture diffusivity as important mass transfer parameter is crucial to precise mass transfer analysis and modelling of the drying process. Despite of numerous complex models to predict heat and mass transfer for various food products, simple models verified by experimental data are more applicable to provide optimum solutions for the operating drying process [5].

Recently, some studies have been conducted on the investigation of drying behavior of ginger using different drying methods and systems [2, 8–16]. Phoungchandang et al. [2, 11] determined drying constants and effective moisture diffusivity in the drying models over a range of temperatures and humidity for ginger dried by tray, heat pump–dehumidified and mixed-mode solar drying. Eze and Agbo [8] compared open sun and solar drying process of peeled and unpeeled ginger. Prasad et al. [9] dried ginger to evaluate the performance of an integral type natural convection solar drier with the provision of biomass heating. Thorat et al. [10] experimentally studied the thin-layer vacuum drying characteristics of ginger slices. Alakalı et al. [12] determined the effect of storage conditions on moisture adsorption characteristics of ginger slices. Parlak [13] investigated drying kinetics of ginger in a fluidized bed dryer. Ganesapillai et al. [14] used microwave drying technique to investigate drying characteristics of ginger. Jayashree and Visvanthan [15] used a mechanical tray drier to evaluate the thin layer drying characteristics of ginger. Afolabi et al. [16] investigated the effect of the air temperature and slice thickness on the effective moisture diffusivity, energy of activation and energy consumption for thin-layer drying of ginger. However, study on convective heat transfer coefficients and drying kinetics of ginger in thin-layer drying has not been reported yet. The objectives of this study were: (a) to study drying kinetics, (b) to fit the experimental data to twelve mathematical models, (c) to determine convective heat transfer coefficient of ginger slices.

2 Materials and methods

2.1 Experimental set up

The cyclone type dryer, the system developed for experimental work was introduced in the literature [17, 18]. Briefly, it consists of fan, resistance and heating control systems, air-duct, drying chamber in cyclone type, and measurement instruments. The heating system consisted of an electric 4000 W heater placed inside the duct. The rectangular duct included air fan and resistance was constructed from sheet iron in 1000 mm length, 200 mm width and 250 mm height. The drying chamber was constructed from sheet iron in 600 mm diameter and 800 mm height cylinder.

In the measurements of the temperatures in drying chamber and the product temperature, J type iron-constantan thermocouples were used with a manually controlled 20-channel automatic digital thermometer (Elimko 6400, Ankara, Turkey), with reading accuracy of ±0.1 °C. A thermo hygrometer (Extech 444731, Shenzhen, China) was used to measure humidity levels of air at various locations in drying chamber and relative humidity measurement just above the product surface. Moisture loss was recorded at 20-min intervals during drying by means of a digital balance (Bel, Mark 3100, Monza, Italy) an accuracy of ±0.01 g.

2.2 Experimental procedure

Fresh ginger slices were used in the experiments. Before the drying process, the gingers were cut into slices of 4 mm thickness and 30 mm in diameter with a mechanical cutter, approximately. After the dryer had reached steady state temperature conditions for operation, 150 g ginger slices are put on the tray of dryer and dried there. The initial and final moisture contents of the ginger slices were determined at 80 °C using an infrared moisture analyzer (Mettler LJ16, Greifensee, Switzerland).

Drying experiments were carried out at 40, 50, 60, and 70 °C drying air temperatures and 0.8, 1.5 and 3 m/s air velocities. Drying was continued until the final moisture content of the samples reached approximately 0.06 g water/g dry matter. During the experiments, ambient temperature and relative humidity, and the inlet and outlet temperatures of the drying air in the dryer chamber were recorded.

2.3 Mathematical modelling of drying curves

The moisture ratio (MR) of the ginger slices during the thin layer drying experiments was calculated using the following equation:

$$ MR = \frac{{M_{t} - M_{e} }}{{M_{o} - M_{e} }} $$
(1)

where M t , M o and M e are the anytime, the initial and equilibrium moisture contents (% dry basis) respectively [4].

The drying rate (DR) is expressed as the amount of the evaporated moisture over time. The drying rates calculated by using Eq. (2):

$$ DR = \frac{{M_{t1} - M_{t2} }}{{t_{2} - t_{t} }} $$
(2)

where M t1 and M t2 are the moisture content of samples (g water/g dry matter) at time t 1 and t 2 (s), respectively [4].

The experimental moisture ratio data of ginger obtained were fitted to the 12 commonly used thin-layer drying models in Table 1 [19–29]. Non-linear least square regression analysis was performed using Levenberg–Marquardt procedure in Statistica 6.0 computer program. The determination coefficient (R 2) was primary criterion for selecting the best equation to describe the drying curve equation. In addition to R 2, reduced χ 2 as the mean square of the deviations between the experimental and calculated values for the models and root mean square error analysis (RMSE) were used to determine the goodness of the fit. For quality fit, R 2 value should be higher and χ 2 and RMSE values should be lower. These can be calculated as:

$$ R^{2} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {MR_{i} - MR_{pre,i} } \right)} \cdot \sum\nolimits_{i = 1}^{n} {\left( {MR_{i} - MR_{\exp ,i} } \right)} }}{{\sqrt {\left[ {\sum\nolimits_{i = 1}^{n} {\left( {MR_{i} - MR_{pre,i} } \right)^{2} } } \right] \cdot \left[ {\sum\nolimits_{i = 1}^{n} {\left( {MR_{i} - MR_{\exp ,i} } \right)^{2} } } \right]} }} $$
(3)
$$ \chi^{2} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {MR_{\exp ,i} - MR_{pre,i} } \right)^{2} } }}{N - n} $$
(4)
$$ RMSE = \left[ {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {MR_{pre,i} - MR_{\exp ,i} } \right)^{2} } } \right]^{1/2} $$
(5)

where, MR exp,i is the ith experimentally observed moisture ratio, MR pre,i the ith predicted moisture ratio, N the number of observations and n is the number constants [30, 31].

Table 1 Thin layer drying curve models for the variation of moisture ratio (MR) with time (t)
Full size table

2.4 Determination of the effective moisture diffusivity and activation energy

Fick’s second law of diffusion equation, symbolized as a mass-diffusion equation for drying of agricultural products drying in a falling rate period, is shown in the following equation:

$$ \frac{dM}{dt} = D_{eff} \frac{{d^{2} M}}{{dr^{2} }} $$
(6)

where, where M is the moisture content (g water/g dry matter), r is the diffusion path (m), t is the time (s) and D eff is the effective moisture diffusivity in (m2/s).

D eff varies considerably with moisture and can be estimated by an analysis of the drying data (moisture M vs. time t)

With the appropriate initial and boundary conditions;

$$ t = 0\quad 0 < r < L\quad M = M_{o} $$
$$ t > 0\quad r = 0\quad \frac{dM}{dt} = 0 $$
$$ t > 0\quad r = L\quad M = M_{e} $$

For slices shapes, the first boundary condition states that moisture is initially uniformly distributed throughout the ginger slices. The second implies that the mass transfer is symmetric with respect to the centre of the slab. The third conditions states that the surface moisture content of the samples instantaneously reaches equilibrium with the conditions of surroundings air. The analytical solutions of Fick’s second law [Eq. (6)] for infinite slab can be given as Eq. (7) with the assumption that neglecting shrinkage, constant temperature and diffusion coefficients and uniform initial moisture distribution [32].

$$ MR = \frac{8}{{\pi^{2} }}\sum\limits_{n = 0}^{\infty } {\frac{1}{{(2n + 1)^{2} }}\exp } \left( { - \frac{{(2n + 1)^{2} \pi^{2} D_{eff} t}}{{4L^{2} }}} \right) $$
(7)

where, n is a positive integer, L is the half-thickness of samples (m).

For long drying periods, the Eq. (7) can be further simplified to only the first term of the series. Equation (8) is written in a logarithmic form as follows [4, 33]:

$$ \ln (MR) = \ln \left( {\frac{8}{{\pi^{2} }}} \right) - \left( {\frac{{\pi^{2} D_{eff} t}}{{4L^{2} }}} \right) $$
(8)

The effective moisture diffusivity was calculated from a slope of a straight line by plotting data in terms of ln(MR) versus drying time, which gives a straight line with a slope of (K), in which:

$$ K = \frac{{\pi^{2} D_{eff} }}{{4L^{2} }} $$
(9)

The dependence of the effective diffusivity on temperature is generally described by the Arrhenius equation [4, 33, 34]:

$$ D_{eff} = D_{0} \exp \left( { - \frac{{E_{a} }}{R(T + 273.15)}} \right) $$
(10)

here D 0 is the pre-exponential factor of Arrhenius equation in (m2/s), E a is the activation energy in kJ/mol, R is the universal gas constant in (kJ/mol K), and T is temperature in (°C).

2.5 Determination of the convective heat transfer coefficient

The convective heat transfer coefficient (h c ) can be determined using the expression for Nusselt number as [7, 35–37]:

$$ h_{c} = \frac{{N_{u} K_{v} }}{X} $$

or, for forced convection:

$$ h_{c} = \frac{{K_{v} }}{X}C(RePr)^{n} $$
(11)

The rate of heat utilized for moisture evaporation is given as [7, 35–37],

$$ \dot{Q}_{e} = 0.016h_{c} [P(T_{c} ) - \gamma P(T_{e} )] $$
(12)

On substituting h c from Eq. (11), Eq. (12) becomes

$$ \dot{Q}_{e} = 0.016\frac{{K_{v} }}{X}C(RePr)^{n} [P(T_{c} ) - \gamma P(T_{e} )] $$
(13)

The moisture evaporated is determined by dividing Eq. (13) by the latent heat of vaporization (λ) and multiplying with the area of tray (At) and time interval (t)

$$ \dot{m}_{ev} = \frac{{\dot{Q}_{e} }}{\lambda }A_{t} t = 0.016\frac{{K_{v} }}{X\lambda }C(RePr)^{n} [P(T_{c} ) - \gamma P(T_{e} )]A_{t} t $$
(14)

Putting

$$ 0.016\frac{{K_{v} }}{X\lambda }[P(T_{c} ) - \gamma P(T_{e} )]A_{t} t = Z $$

Eq. (15) becomes

$$ \frac{{\dot{m}_{ev} }}{Z} = C(RePr)^{n} $$
(15)

Taking the logarithm of both sides,

$$ \ln \left[ {\frac{{\dot{m}_{ev} }}{Z}} \right] = \ln C + n\ln (RePr) $$
(16)

Eq. (16) is the analogy of an equation of a straight line,

$$ Y = b_{1} X + b_{0} $$

where

$$ Y = \ln \left[ {\frac{{\dot{m}_{ev} }}{Z}} \right],\quad b_{1} = n,\quad X = \ln (RePr),\quad b_{0} = \ln C $$

Thus \( C = e^{{b_{0} }} \)

The different physical properties of humid air, i.e. density (ρ v ), thermal conductivity (K v ), specific heat (C v ) and viscosity (μ v ), used in the computation of Reynolds number (Re), Grashof number (Gr) and Prandtl number (Pr) have been determined using the following polynomial expressions. For obtaining physical properties of humid air, T i is taken as mean of temperature of ginger (T c ) and temperature above ginger (T e ) [7, 35–37]:

$$ \rho_{v} = \frac{353.44}{{(T_{i} + 273.15)}} $$
(17)
$$ K_{v} = 0.0244 + 0.6773 \times 10^{ - 4} T_{i} $$
(18)
$$ C_{v} = 999.2 + 0.1434T_{i} + 1.101 \times 10^{ - 4} T_{i}^{2} - 6.7581 \times 10^{ - 8} T_{i}^{3} $$
(19)
$$ \mu_{v} = 1.718 \times 10^{ - 5} + 4.620 \times 10^{ - 8} T_{i} $$
(20)
$$ P(T) = \exp \left[ {25.317 - \frac{5144}{{(T_{i} + 273.15)}}} \right] $$
(21)

The values of the constants C and n have been determined by linear regression analysis by using measured data of the product and exit air temperatures, exit air relative humidity and moisture evaporated during a certain time period.

3 Results and discussion

Ginger slices (4.8 g water/g dry matter average initial moisture content) were dried to 0.06 g water/g dry matter in the cyclone dryer. The final moisture contents represent moisture equilibrium between the sample and drying air under dryer conditions, beyond which any changes in the mass of sample could not occur. The final moisture content was taken as the equilibrium moisture content (M e ) in the later computations.

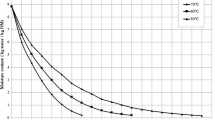
Figures 1 and 2 presents the variations of moisture content with drying time based on drying air temperatures and at drying air velocities, respectively. The times to reach 0.06 g water/g dry matter moisture content from the initial moisture content at the various drying air temperature and velocity of the ginger samples were found to be between 8700 and 24900 s. As a result, it was found out that; the temperature is the major effect on the drying process, and, air velocity has less important effect on the drying of ginger slices. According to our experimental results, the temperature of drying seems to be the most important parameter influencing drying kinetics of ginger slices. This result is confirmed by Van Arsdel et al. [38]. Drying kinetics depends greatly on temperature, especially for biological products presenting a big internal resistance to water migration. Variation of temperature within the product modifies water activity in it, but exerts an influence on other factors such as evaporation heat of liquid water, which varies as a function of temperature. In this case, the measurement of the product temperature during drying enables us to understand the modifications of drying kinetics or to take into account changes in product quality [39]. The drying rate does not vary a lot as a function of drying air velocity. This fact corroborates our experimental results. Drying air velocity is a parameter, which intervenes essentially in heat and mass transfers taking place between the product and the air. It has a remarkable influence on the rate of drying when drying kinetics presents a constant rate period. In return, when the product does not present a constant rate period, drying air velocity has a weak influence. This fact shows that heat and mass transfers by convection are not limitable factors in the drying process. They are internal factors, which control water transfer velocity from the interior towards the surface of product [39].

Fig. 1
figure 1

Variation of moisture content with drying time at constant air velocities and different air temperatures

Full size image
Fig. 2
figure 2

Variation of moisture content with drying time at constant air temperatures and different air velocities

Full size image

Drying rate decreases continuously with moisture content or drying time (Figs. 3, 4). This shows that the drying rate is a strong function of temperature, air velocity and time. It is highest at the first 1 h of continuous drying for all temperatures and decreases with time. This is a result of low internal resistance of moisture at the beginning of drying; therefore when energy is impacted moisture can easily move to surface, where evaporated. As the drying progressed, more energy was required to break the molecular bond of the moisture and since constant energy was supplied, it took longer time to break, therefore drying rate decreased [40]. There is not any constant-rate drying period in these curves and all the drying operations are seen to occur in the falling rate period. In the falling rate period the material surface is no longer saturated with water and drying rate is controlled by diffusion of moisture from the interior of solid to the surface [20]. These results are in agreement with the observations of earlier researchers [2, 8–16].

Fig. 3
figure 3

Variation of drying rate with moisture content at different air temperatures and constant air velocities

Full size image
Fig. 4
figure 4

Variation of drying rate with drying time at different air temperatures and constant air velocities

Full size image

In order to normalize the drying curves, the data involving dry basis moisture content versus time were transformed to a dimensionless parameter called as moisture ratio versus time (Fig. 5). The moisture content data at the different experimental mode were converted to the most useful moisture ratio expression and then curve fitting computations with the drying time were carried on twelve drying models evaluated by the different researches (Table 1). The results of statistical analyses undertaken on these models for the thin layer drying of ginger slices (Table 2) were evaluated based on R 2, χ 2 and RMSE. For the thin layer drying of ginger slices, The Midilli and Kucuk model gave a higher R 2 and lower χ 2, RMSE (bold values in Table 2), thus, was selected to represent the thin layer drying behaviour of the ginger slices. From the Midilli and Kucuk model for ginger slices, it was determined that R 2 = 0.91073, χ 2 = 0.008339581, RMSE = 0.090408072.

Fig. 5
figure 5

Variation of moisture ratio with drying time at different air temperatures and constant air velocities

Full size image
Table 2 Modelling of moisture ratio according to the drying time
Full size table

Validation of the established model was made by comparing the computed moisture contents with the measured moisture contents in any particular drying run under certain conditions. The performance of the model for the thin layer drying of ginger slices was illustrated in Fig. 6. The experimental data are generally banded around the straight line representing data found by computation, which indicates the suitability of the mathematical model in describing drying behavior of ginger slices.

Fig. 6
figure 6

Comparison of experimental moisture ratios with those predicted from the Midilli and Kucuk model

Full size image

The effective moisture diffusivity was calculated by Eq. (10), using slopes derived from the linear regression of ln[(π 2/8)MR] versus time data. This analysis was introduced in the literature [33]. The determined values of the effective moisture diffusivity values of ginger slices were found to range between 2.807 × 10−10 to 6.977 × 10−10 m2/s. The moisture diffusivity was affected by air temperature and air velocity. The activation energy was calculated by plotting lnD eff versus the reciprocal of the temperature (1/(T + 273.15)). The activation energy values were found to be 19.313, 20.153 and 22.722 kJ/mol for air velocity of 3, 1.5 and 0.8 m/s, respectively (Table 3). The effective moisture diffusivity and activation energy values are increased with increasing of air temperature and velocity, which is in accordance with the previous studies (Table 3).

Table 3 The variation with drying air temperature and velocity of effective diffusion coefficients and activation energy values of ginger slices
Full size table

The average product temperature, air temperature and air relative humidity have been used for determining the physical properties of humid air which, in turn, where used for calculating the values of Reynolds number and Prandtl number. The constants, C and n, were determined by linear regression analysis and have been considered further for obtaining the values of the convective heat transfer coefficients by Eq. (11). Convective heat transfer coefficient of ginger slices showed changes in ranges 0.33–2.11 W/m2 °C (Table 4). The values of the convective heat transfer coefficient were found to increase with the increase of air velocity and temperature of drying. The convective heat transfer coefficient of ginger is not available in the open literature. Anwar and Tiwari [37] studied the drying of six crops (green chilies, green peas, white gram, onion flakes, potato slices and cauliflower) under forced convection drying mode. The values of convective heat transfer coefficients were found to vary between 1.31 and 12.80 W/m2 °C and between 1.25 and 10.94 W/m2 °C in indoor open and closed conditions under forced mode, respectively. Akpinar [7] determined the convective heat transfer coefficient of various agricultural products, namely, mulberry, strawberry, apple, garlic, potato, pumpkin, eggplant, and onion under indoor forced convection drying mode. The convective heat transfer coefficient of these crops was found to vary from crop to crop between 0.644 and 7.121 W/m2 °C. It was shown in this work that the range of the convective heat transfer coefficient values fit with the range in the literature for forced convection. The convective heat transfer coefficient can significantly vary due to differences in porosity, moisture content, and shape and size of the crop, drying conditions, the climatic conditions and experimental set-up.

Table 4 The variation with drying air temperature and velocity of convective heat transfer coefficients of ginger slices
Full size table

4 Conclusions

In the present study, the influence of drying air temperature and velocity on drying kinetics and convective heat transfer coefficients of ginger slices was investigated. Drying of ginger slices occurred in falling rate period; no constant rate period of drying was observed for the present study, which implies that moisture removal from the material was governed by diffusion phenomenon. The drying rates of ginger slices were higher when drying was performed at higher drying temperatures and velocities. The drying time was found to be drying rate and moisture content dependent. The experimental drying data was fitted to twelve different mathematical models and compared using statistical criteria. Midilli and Kucuk model was found to be best suitable to describe the drying kinetics of ginger slices among the tested models. The moisture ratio obtained experimentally and predicted by Midilli and Kucuk shows good agreement and fitted smoothly to straight line. The model attained the highest value of R 2, lowest value of χ 2, and RMSE (R 2 = 0.91073, χ 2 = 0.008339581, RMSE = 0.090408072).

The effective moisture diffusivities were determined to be between 2.807 × 10−10 and 6.977 × 10−10 m2/s for ginger slices in the temperature range of 40–70 °C. The activation energies for samples were varied to be 19.313–22.722 kJ/mol. Convective heat transfer coefficient of ginger slices showed changes in ranges 0.33–2.11 W/m2 °C. Moisture diffusivity and convective heat transfer coefficients increased as air temperature and velocity increased. It was found out that; the temperature is the major effect on the drying process, and, air velocity has less important effect on the drying of ginger slices.