1 Introduction

We consider the problem of maximum online perfect bipartite matching. Suppose that we have a set of jobs and a set of workers. At every time step, a single job arrives to be served by one of the workers. Upon a job’s arrival, we observe the utility of assigning the job to each of the workers. We must immediately decide which worker will serve the job. Once a worker is assigned a job, the worker is busy and cannot be assigned to another job. Jobs continue to arrive until all workers are busy.

It is natural to model this problem setup as a bipartite graph, where there is an edge between each worker and job. The weight of the edge equals the non-negative utility of assigning that worker to that job. The assignment of workers to jobs will form a perfect matching in this bipartite graph. Our goal is to design a dispatching algorithm that maximizes the expected sum of utilities of the perfect matching.

In this work, we consider the maximum online perfect bipartite matching problem with independent and identically distributed (i.i.d.) arrivals. This means that, at each time step, a job is drawn i.i.d. from a known distribution over job types.

We introduce the randomized algorithm Dispatch for the problem of online weighted perfect bipartite matching with i.i.d. arrivals. Dispatch is 0.5-competitive algorithm: the total expected utility of the perfect matching produced by Dispatch is at least half of the total expected utility of an optimal algorithm that knows the job arrival sequence in advance. We also describe a family of problem instances for which 0.5 is the best-possible competitive ratio. The Dispatch algorithm, thus, achieves the best-possible competitive ratio. In contrast, the same problem with adversarial job arrivals cannot be bounded, as observed by Feldman et al. [8].

To assign workers to jobs, Dispatch first selects a preferred worker. This preferred worker is determined based on an optimal solution to a fractional transportation problem. If the preferred worker is available, then the job is assigned to this worker. Otherwise, Dispatch randomly selects a worker from the available workers.

1.1 Related Work

Our work resides in the space of online matching problems. We review several variants of online matching, including the maximum (imperfect) bipartite matching problem and the minimum (perfect) bipartite matching problem. We also review the closely-related k-Server problem. For each of these problems, several arrival models are considered. Arrival models including adversarial, where the adversary chooses jobs and their arrival order; random order, where the adversary chooses jobs but not their arrival order; and i.i.d., where the adversary specifies a probability distribution over job types and each arrival is sampled independently from the distribution. We briefly describe each of these problems and present best-known results, contrasting it to the setting considered here. A summary is in Table 1.

Table 1 Best-known competitive ratios and impossibility bounds for online bipartite matching problems
Full size table

1.1.1 Maximum Online (Imperfect) Bipartite Matching

The maximum online (imperfect) bipartite matching problem is defined on a bipartite graph with n known workers and n jobs that arrive one at a time. Jobs either get assigned to a worker or are discarded. The goal is to maximize the cardinality (or sum of weights) of the resulting matching. In contrast to our problem, jobs may be the discarded and the resulting matching may be imperfect.

For the unweighted problem with adversarial arrivals, Karp, Vazirani, and Vazirani [12] showed a best-possible algorithm that achieves a competitive ratio of \(1-\frac {1}{e} \approx 0.632\). Variations of the problem have been proposed: addition of edge or vertex weights, the use of budgets, different arrival models, etc. Mehta [19] provides an excellent overview of this literature. When the arrivals are in a random order, it is possible to do better than \(1-\frac {1}{e}\). Mahdian and Yan [16], in 2011, achieved a competitive ratio of 0.696. Manshadi et al. [18] showed that you cannot do better than 0.823. If the problem also has weights, then the best-possible competitive ratio is 0.368 by a reduction from the secretary problem as shown by Kesselheim et al. [13]. They also give an algorithm that attains this competitive ratio.

The problem has also been studied when the jobs are drawn i.i.d. from a known distribution. This problem is also referred to as Online Stochastic Matching. The first result to break the \(1 - \frac {1}{e}\) barrier for the unweighted case was the 0.67-competitive algorithm of Feldman et al. [9] in 2009. To date, the best-known competitive ratio of 0.730 is due to Brubach et al [4]. This is close the best-known bound of 0.745 by Correa et al. [6].

1.1.2 Online Minimum (Perfect) Bipartite Matching

The online minimum (perfect) bipartite matching addresses the question of finding a minimum cost perfect matching on a bipartite graph with n workers and n jobs. Given any arbitrary sequence of jobs arriving one by one, each job needs to be irrevocably assigned to worker on arrival. This problem is the minimization version of the problem considered in this work. However, the obtained competitive ratios do not transfer.

The problem was first considered by Khuller, Mitchell, and Vazirani [14] and independently by Kalyanasundaram and Pruhs [11]. If the weights are arbitrary, then the competitive ratio cannot be bounded. To address this, both papers considered the restriction where the edge weights are distances in some metric on the set of vertices. They give a 2n − 1 competitive algorithm, which is the best-possible for deterministic algorithms. When randomized algorithms are allowed, the best-known competitive ratio is \(O(\log ^{2}(n))\) by Bansal et al. [3]. If the arrival order is also randomized, then Raghvendra [21] shows that \(2\log {(n)}\) is attainable. He also shows that this is the best possible.

1.1.3 k-Server Problem

In the k-server problem, k workers are distributed at initial positions in a metric space. Jobs are elements of the same metric space and arrive one at a time. When a job arrives, it must be assigned to a worker which moves to the job’s location. The goal in the k-server problem is to minimize the total distance traveled by all workers to serve the sequence of jobs. After an assignment, the worker remains available for assignment to new jobs. This reassignment distinguishes the k-server problem from ours, where workers are fixed to a job once assigned.

The k-server problem was introduced by Manasse, McGeoch, and Sleater [17]. A review of the k-server problem literature was written by Koutsoupias [15]. For randomized algorithms in discrete metrics, the competitive ratio \(O(\log ^{2}{(k)} \log {(n)})\) was attained by Bubeck et al. [5], where n is the number of points in the discrete metric space. On the other hand, \({\varOmega }(\log {(k)})\) is a known lower bound. In the i.i.d. setting, Dehghani et al. [7] consider a different kind of competitive ratio: they give an online algorithm with a cost no worse than \(O(\log {(n)})\) times the cost of the optimal online algorithm.

1.2 Applications

We offer four examples of settings where the model of maximum online perfect bipartite matching with i.i.d. arrivals may be suitable. These examples are not intended to be exhaustive, only to illustrate how the model can be applied in diverse settings.

In the first setting, consider the problem of assigning medical practitioners to patients arriving in an emergency room [23]. Here, workers represent medical practitioners, the jobs are the patients that arrive, and the job type is determined by the patient’s symptoms. Most patients arrive unannounced, forming a stochastic arrival sequence. Since not every practitioner is equally suitable to treat a given patient, the goal is to assign practitioners to arriving patients such that practitioners and patients are well-matched in the resulting assignment.

In the second setting, consider customers calling a call center [2]. The customer calls arrive stochastically and needs to be assigned to an operator, the worker. The callers are typically asked to categorize their problem and are routed accordingly. The utility is a measure of the operator’s expertise in handling the particular call type.

In the third setting, consider the problem of matching ad impressions to customers in an online marketplace for e.g. travel, lodgings, or insurance [19]. In this case, the customers are the jobs, arriving one at a time. Customers are characterized into types based on their demographic information and any other factors that may affect the bids of advertisers, such as previous activity on the site. Unlike general search engine advertising, the business needs of an online marketplace dictate that an advertisement must be shown. The utility of displaying an advertisement is the increase in revenue from the customer.

In the fourth setting, consider the problem of matching drivers to riders in a ride-sharing system [1]. Trips are bucketed geographically according to the regions in which the ride starts and ends. More granular regions result in more job types. The utility of a pairing between driver and rider depends on many aspects, but is not limited to the distance and duration of the trip, the current location of the driver, and the driver’s desire to go to the trip’s destination.

The arrival sequence of jobs in many of these applications can be cast as a Poisson process. When jobs are split into sub-processes according to their type, the resulting process is a Poisson splitting process. It is well-known that the sub-processes are independent Poisson processes and that the distribution of waiting times in a Poisson process is memoryless [22]. As a result, the arrival type of the jobs is i.i.d. when the the distribution over types is (approximately) independent of time. The i.i.d arrival model, as used here, is thus well-suited when an arrival sequence is a Poisson process.

1.3 Structure of this Work

This paper is organized as follows. Section 2 formally introduces the problem of online perfect bipartite matching with i.i.d. arrivals and defines the concept of competitive ratio. Section 3 describes Dispatch, presents an example to demonstrate the algorithm, and provides the proof that Dispatch is 0.5-competitive. Section 4 introduces a family of instances of the online perfect bipartite matching problem for which no online algorithm performs better than \(\frac {1}{2}\) in terms of competitive ratio. Finally, Section 5 summarizes the results and suggests directions for future research.

2 Preliminaries

The set of workers is denoted by W with size n = |W|. The set J denotes the set of job types with size k = |J|. For every worker w ∈ W and job type j ∈ J there is a utility of uwj ≥ 0 for assigning a job of type j to worker w. Let \(\mathcal {D}(J)\) be a known probability distribution over the job types.

At every time step \(t=1, \dots , n\), a single job is drawn i.i.d. from J according to \(\mathcal {D}\). The job must be irrevocably assigned to a worker before the next job arrives. Workers are no longer available after they have been assigned a job. Let rj denote the expected number of jobs of type j that arrive. After n steps, each worker is assigned to one job and the resulting assignment forms a perfect matching. Our goal is to design a procedure such that the expected sum of the utilities of the resulting perfect matching is as high as possible.

Throughout this work, we will repeatedly use two bipartite graphs; the expectation graphG and the realization graph\(\widehat {G}\). The expectation graph G = (W,J,E) is a complete bipartite graph defined over the set of workers W and the set of job types J. An edge [w,j] ∈ E has associated utility uwj ≥ 0, for w ∈ W and j ∈ J. The realization graph \(\widehat {G} = (W, \widehat {J}, \widehat {E})\) is the random bipartite graph obtained after all n jobs have arrived. \(\widehat {J}\) denotes the set of n jobs that arrived. We use \(\hat {j}_{t} \in \widehat {J}\) to denote the job that arrives at time t and jt ∈ J to denote its job type. The edge set \(\widehat {E}\) consists of all worker-job pairs, such that \(\widehat {G}\) is a complete bipartite graph defined over W and \(\widehat {J}\). Every edge \([w, \hat {j}] \in \widehat {E}\) has utility uwj, where j is the job type of job \(\hat {j}\). It is important to remember that the expectation graph G is deterministic and known in advance whereas the realization graph \(\widehat {G}\) is a random graph representing a realization of the job arrival process and is revealed over time.

An instance of the online perfect bipartite matching problem with i.i.d. arrivals is defined by the set of workers W, the job types J, non-negative utilities uwj, and a distribution over the job types \(\mathcal {D}(J)\). Equivalently, the expectation graph G and the distribution \(\mathcal {D}(J)\) defines an instance of this problem. Here we analyze the family of potentially randomized algorithms that return a perfect matching \(\hat {M}\) on \(\widehat {G}\). The performance of an algorithm ALG for a single realization \(\widehat {G}\) is given by:

$$ ALG(\widehat{G}) = \mathbb{E}\left[\sum\limits_{[w,j] \in E} u_{wj} I_{wj}\right], $$

where Iwj is a random indicator variable that equals 1 if ALG assigned a job of type j to worker w and equals 0 otherwise. For a given problem instance defined by expectation graph G and distribution \(\mathcal {D}(J)\), \(\mathbb {E}\left [ ALG(\widehat {G})\right ]\) measures the algorithm’s expected performance over samples of \(\widehat {G}\) from G according to \(\mathcal {D}(J)\).

The worst-case performance across instances is measured by the competitive ratio. Let \(OPT(\widehat {G})\) be the maximum weight perfect matching in the realization graph \(\widehat {G}\) and let \(\mathbb {E}\left [ OPT(\widehat {G}) \right ]\) be its expectation across different realizations for a given expectation graph G and distribution \(\mathcal {D}(J)\). \(\mathbb {E}\left [ OPT(\widehat {G}) \right ]\) measures the performance of an optimal algorithm that has full information about the arrival sequence. This is known as an adaptive online adversary. The ratio \(\frac {\mathbb {E}\left [ ALG(\widehat {G}) \right ]}{\mathbb {E}\left [ OPT(\widehat {G}) \right ]}\) measures the performance of ALG relative to the optimal algorithm for a given instance of the problem. The competitive ratio is the worst-case, i.e. lowest, ratio among all possible instances of the expectation graph G and distributions \(\mathcal {D}(J)\):

Definition 1 (Competitive Ratio)

An algorithm ALG is said to have a competitive ratio of α when α is the largest value such that, for all instances of the expectation graph G and distribution \(\mathcal {D}(J)\),

$$ \alpha \le \frac{\mathbb{E}\left[ ALG(\widehat{G}) \right]}{\mathbb{E}\left[ OPT(\widehat{G}) \right]}. $$

2.1 Bounding the Performance of OPT

It is difficult to compute \(\mathbb {E}\left [ OPT(\widehat {G}) \right ]\) directly. We show that the randomness in \(\widehat {G}\) reduces the expected value of the optimal perfect matching compared to the value of the optimal transportation problem where the number of jobs of each type is equal to its expectation. This offline transportation problem is then used to guide the online assignment.

A similar approach was used in the context of unweighted online imperfect bipartite matching by Feldman et al. [9] and Haepler et al. [10]. Here, we use a transportation problem instead of a maximum weight matching. We also bound the performance of OPT differently.

Recall that, in expectation, rj jobs of job type j ∈ J will arrive in \(\hat {G}\). An optimal fractional matching of these jobs is obtained by solving a fractional transportation problem on the expectation graph G, where each job type has a demand of rj and each worker has a supply of 1 and the sum of utilities is maximized.

Formally, let fwj ≥ 0 be the flow from worker w ∈ W to job type j ∈ J. This can be interpreted as a fractional assignment of worker w to jobs of job type j. We define the transportation problem TPP:

$$ \begin{array}{@{}rcl@{}} TPP(G) &=& \max_{f_{wj} \ge 0} \quad \sum\limits_{w \in W} \sum\limits_{j \in J} u_{wj} f_{wj},\\ \sum\limits_{w \in W} f_{wj} & =& r_{j} \quad \forall j \in J, \\ \sum\limits_{j \in J} f_{wj} & =& 1 \quad \forall w \in W. \end{array} $$

Let \(f^{*}_{wj}\) be an optimal flow on edge [w,j] ∈ E.

We claim that \(\mathbb {E}\left [ OPT(\widehat {G}) \right ] \le TPP(G)\). The reason is that the weighted average of perfect matchings \(OPT(\widehat {G})\) forms a feasible solution to the transportation problem above.

Lemma 1

Given any expectation graph G and distribution over jobtypes\(\mathcal {D}(J)\),

$$ \mathbb{E}\left[ OPT(\widehat{G}) \right] \le TPP(G).\enlargethispage{-25.5pt} $$

Proof

Assign each edge in G an indicator variable Iwj, which takes on the value 1 if OPT assigns worker w to a job of type j in \(\widehat {G}\) and 0 otherwise. We claim that \(f_{wj} = \mathbb {E}\left [ I_{wj}\right ]\) forms a feasible solution to the transportation problem in G. Indeed,

$$ \sum\limits_{w \in W}\mathbb{E}\left[ I_{wj}\right] = \mathbb{E}\left[ \sum\limits_{w \in J} I_{wj} \right] = r_{j}, \qquad \sum\limits_{j \in J}\mathbb{E}\left[ I_{wj}\right] = \mathbb{E}\left[ \sum\limits_{j \in J} I_{wj} \right] = 1. $$

Since \(\mathbb {E}\left [I_{wj}\right ]\) is feasible for the transportation problem, it must have objective smaller than TPP(G):

$$ \mathbb{E}\left[OPT(\widehat{G})\right] = \mathbb{E}\left[ \sum\limits_{[w, j] \in E} u_{wj} I_{wj} \right] = \sum\limits_{[w,j] \in E} u_{ij} \mathbb{E}\left[I_{wj}\right] \leq TPP(G). $$

□

This implies that we can bound the performance of an algorithm with respect to TPP(G). We apply this technique in Section 3.3.

3 A 1/2-Competitive Algorithm

3.1 The Dispatch Algorithm

Before any jobs arrive, Dispatch solves the offline transportation problem TPP on the expectation graph G. We find an optimal flow \(f^{*}_{wj}\) from workers to jobs. Throughout the online stage, the algorithm reconstructs this flow between job types and workers as much as possible. For each arriving job, a preferred workerwP is randomly selected with a probability proportional to the optimal flow f∗ between the corresponding job type and the worker in the transportation problem. If the preferred worker is no longer available, then the job is assigned to a worker selected uniformly at random from the set of available workers AW. We refer to this worker as the assigned workerwA. The resulting assignment forms a perfect matching on \(\widehat {G}\) since each worker is assigned at most once and each job is assigned to a worker.

In the context of online bipartite matching, the idea of using an offline solution to guide the online algorithm was used in the “Suggested Matching” algorithm [9] and subsequent work, e.g. [10]. Our algorithm differs in two ways. First, the offline solution is a transportation problem instead of a maximum weight matching problem. Second, the job is randomly assigned instead of discarded when the preferred worker is no longer available. This random selection ensures that we obtain a perfect matching and is crucial for Lemma 3. The analysis of the competitive performance of Dispatch is also novel except for Lemma 2.

The algorithm is formally defined in Algorithm 1. We prove the following result:

Theorem 1

Dispatch achieves a competitive ratio of at least \(\frac {1}{2}\) for the online perfect bipartite matching problem with i.i.d. arrivals.

figure a

3.2 Example

To illustrate Dispatch, we consider the example shown in Fig. 1. The example has five workers (n = 5) and three job types (k = 3). The expectation graph is shown in Fig. 1a. Note that the distribution over job types, \(\mathcal {D}(J)\), is fully specified by rj. An instance of the realization graph is shown in Fig. 1c.

Fig. 1
figure 1

An example of the Dispatch algorithm on the realization graph shown in Fig. 1c. The underlying expectation graph G with n = 5 and k = 3 is shown in Fig. 1a. In Fig. 1d up to h, the numbers in parenthesis denote the probability of selecting that worker as the preferred worker. Red edges represent the assignment made by the algorithm, thick black edges are previous assignments, and blue edges mark unavailable preferred workers. Figure 1h shows an instance where the preferred worker is busy

Full size image

Figure 1b shows f∗, the solution to the transportation problem on G that is used by Dispatch. The corresponding objective value is TPP(G) = 8. Figure 1d to h show the arrival of the jobs and the corresponding assignment made by Dispatch. Figure 1h illustrates an instance where the preferred worker selected by Dispatch is not available, and a different worker is assigned. For this particular realization \(\widehat {G}\), the perfect matching constructed by Dispatch has a total utility 6, while the optimal perfect matching on \(\widehat {G}\) has a total utility 8. Note that these values are for this particular realization of \(\widehat {G}\). The performance guarantee is with respect to the expectation over all realizations of \(\widehat {G}\).

3.3 Proof of \(\frac {1}{2}\)-Competitiveness

To prove that the perfect matching produced by Dispatch has a competitive ratio of a \(\frac {1}{2}\), we rely on a key feature of Dispatch: It maintains the invariant, Lemma 4, that workers are equally likely to be available even though the distribution over job types may not be uniform. To prove this invariant, we first show that both the preferred and the assigned worker are selected uniformly across workers. Recall that the preferred worker may be different than the assigned worker. In fact, the preferred worker does not have to be available and could have been assigned to another job already. Lemma 2 states this formally for the selection of the preferred worker. The observation underlying this lemma is that each worker is selected with a probability proportional to the total flow f∗ originating at the worker, which is equal to one for each worker.

Throughout this section we use additional notation. Let the random variable \({W_{t}^{P}}\) represent the preferred worker for the job arriving at time t, and let the random variable \({W_{t}^{A}}\) be the assigned worker. Furthermore, let the random set AWt consist of the available workers when the job at time t arrives. We make no further assumptions on the expectation graph G and/or distribution \(\mathcal {D}(J)\) other than those outlined in Section 2. Lemmas and theorems in this section are therefore applicable to all problem instances.

Lemma 2

At each time t, thepreferredworker\({W^{P}_{t}}\)isdrawn uniformly from all workers:

$$ \mathbb{P}\left( {W^{P}_{t}} = w\right) = \frac{1}{n} \quad \text{for all } w \in W \text{ and } t = 1,\dots, n. $$

Proof

By conditioning on the job type jt at stage t and using the law of total probability, we can rewrite the probability of selecting worker w as:

$$ \mathbb{P}\left( {W^{P}_{t}} = w\right) = \sum\limits_{j \in J} \mathbb{P}\left( {W^{P}_{t}} = w | j_{t} = j\right) \mathbb{P}\left( j_{t} = j\right). $$

Since the jobs are drawn i.i.d., a job of type j is selected with probability \(\mathbb {P}\left (j_{t} = j\right ) = \frac {r_{j}}{n}\), by definition of rj. Given a job of type j, the algorithm selects a worker w as the preferred worker with probability \(\mathbb {P}\left ({W^{P}_{t}} = w | j_{t} = j\right ) = \frac {f^{*}_{wj}}{r_{j}}\). Thus,

$$ \mathbb{P}\left( {W^{P}_{t}} = w\right) = \sum\limits_{j \in J} \frac{f^{*}_{wj}}{r_{j}} \frac{r_{j}}{n} = \sum\limits_{j \in J} \frac{f^{*}_{wj}}{n}. $$

Finally, recall that every worker supplies a unit of flow in the offline transportation problem, equivalent to the expected number of jobs it serves. The edges adjacent to worker w must thus transport a unit of flow, so \({\sum }_{j} f^{*}_{wj} = 1\). Thus, \(\mathbb {P}\left ({W^{P}_{t}} = w\right )\)\(= \frac {1}{n}\). □

Next we show that the assigned worker is selected uniformly at random from the set of available workers. For this lemma to hold, it is crucial that the draw of the assigned worker is done uniformly at random when the preferred worker is not available. Recall that \({W_{t}^{A}}\) is the assigned worker for the job arriving at time t and that AWt are the available workers before the job arrives.

Lemma 3

At each time step t, theassignedworker\({W^{P}_{t}}\)isdrawn uniformly from the available workers:

$$ \mathbb{P}\left( {W^{A}_{t}} = w |w \in AW_{t}\right) = \frac{1}{n-(t-1)}. $$

Proof

Assume that w is fixed and that w ∈ AWt. There are two ways for w to be the assigned worker. Either w is the preferred worker or the preferred worker is not available and w is randomly selected. We express this as:

$$ \begin{array}{@{}rcl@{}} \mathbb{P}\left( {W^{A}_{t}} = w | w \in AW_{t}\right) &=& \mathbb{P}\left( {W^{P}_{t}} = w | w \in AW_{t}\right)\\ &&+ \mathbb{P}\left( {W^{A}_{t}} = w | {W^{P}_{t}} \notin AW_{t}, w \in AW_{t}\right) \\ && \times \mathbb{P}\left( {W^{P}_{t}} \notin AW_{t} | w \in AW_{t}\right) \end{array} $$

The selection of \({W^{P}_{t}}\) is independent of whether w ∈ AWt. Therefore,

$$ \begin{array}{@{}rcl@{}} \mathbb{P}\left( {W^{A}_{t}} = w | w \in AW_{t}\right) &=& \mathbb{P}\left( {W^{P}_{t}} = w \right) \\ &&+ \mathbb{P}\left( {W^{A}_{t}} = w | {W^{P}_{t}} \notin AW_{t}, w \in AW_{t}\right) \mathbb{P}\left( {W^{P}_{t}} \notin AW_{t}\right) \end{array} $$

Now we use three observations to complete the proof. First, Lemma 2 implies that \(\mathbb {P}\left ({W^{P}_{t}} = w\right ) = \frac {1}{n}\). Second, since there are t − 1 busy workers, Lemma 2 implies that \(\mathbb {P}\left ({W^{P}_{t}} \notin AW_{t}\right ) = \frac {(t-1)}{n}\). Third, the fact that the assigned worker is drawn uniformly at random when the preferred worker is not available implies that \(\P {{W^{A}_{t}} = w | {W^{P}_{t}} \notin AW_{t}, w \in AW_{t}} = \frac {1}{n-(t-1)}\). Thus,

$$ \mathbb{P}\left( {W^{A}_{t}} = w | w \in AW_{t}\right) = \frac{1}{n} + \frac{1}{n-(t-1)} \frac{(t-1)}{n} = \frac{1}{n-(t-1)}. $$

□

Lemma 3 specifies each available worker is equally likely to be assigned to the next job. As a consequence, we can derive the probability that a worker is still available after t − 1 jobs have arrived:

Lemma 4

Dispatch maintains the following invariant throughout the online stage:

$$ \mathbb{P}\left( w \in AW_{t}\right) = \frac{n-(t-1)}{n} \quad \text{for all } w \in W \text{ and } t = 1,\dots, n. $$

Proof

At every time step, a worker is chosen randomly from the remaining available workers, as shown in Lemma 3. The probability that an available worker in time step t is still available in time step t + 1 is:

$$ \begin{array}{@{}rcl@{}} \mathbb{P}\left( w \in AW_{t+1} | w \in AW_{t}\right) &=& 1 - \mathbb{P}\left( {W^{A}_{t}} = w | w \in AW_{t}\right)\\ &=& 1 - \frac{1}{n-(t-1)} = \frac{n-t}{n-(t-1)}. \end{array} $$

Thus, the probability of being available for the tth job is equal to:

$$ \begin{array}{@{}rcl@{}} \mathbb{P}\left( w \in AW_{t}\right) &=& {\prod}_{i=1}^{t}{\P{w \in AW_{t} | w \in AW_{t-1}}}\\ &=& \frac{n- (t-1)}{n - (t-2)} \frac{n- (t-2)}{n - (t-3)} {\dots} \frac{n-1}{n} = \frac{n-(t-1)}{n}. \end{array} $$

□

From Lemma 4, we know the probability that a worker is available at each time step. We use this to bound the probability that a worker w is assigned to a job with job type j by Dispatch. We use the indicator random variable Iwj. Iwj = 1 when the Dispatch assigns worker w to a job with job type j, and Iwj = 0 otherwise. We bound the probability with respect to \(f^{*}_{wj}\) in TPP(G). By bounding the algorithm’s performance with respect to TPP(G) we can bound the competitive ratio of Dispatch. See Section 2.1 for more details.

Lemma 5

Given a perfect matching\(\hat {M}\)constructedbyDispatch, the probability that worker w is assigned to a job of type j is bounded by:

$$ \mathbb{P}\left( I_{wj} = 1\right) \ge \frac{1}{2} f^{*}_{wj}. $$

Proof

If Iwj = 1, then worker w must have been assigned to a job of type j in one of the time steps. Thus, \(I_{wj} = {\sum }_{t=1}^{n} I^{t}_{wj}\) where \(I^{t}_{wj}\) is indicator for whether worker w is assigned to a job of type j at time step t:

$$ \mathbb{P}\left( I_{wj} = 1\right) = \sum\limits_{t=1}^{n} \mathbb{P}\left( I^{t}_{wj} = 1\right). $$

Let us bound the probability \(\mathbb {P}\left (I^{t}_{wj} = 1\right )\) for all \(t=1, \dots , n\). First, we condition on the job type arriving at time t. Note that jt must equal j:

$$ \mathbb{P}\left( I^{t}_{wj} = 1\right) = \mathbb{P}\left( I^{t}_{wj} = 1 | j_{t} = j\right) \mathbb{P}\left( j_{t} = j\right). $$

Recall that there are two ways for worker w to be assigned after a job of type j arrives. Either w is the preferred worker and is assigned the job, or another worker \(w^{\prime }\) is selected as the preferred worker but is not available. w is then selected as the assigned worker. We lower bound the probability that worker w is assigned for the job of type j by considering only the case where w is the preferred worker.

$$ \begin{array}{@{}rcl@{}} \mathbb{P}\left( I^{t}_{wj} = 1\right) &\ge& \mathbb{P}\left( w \in AW_{t}, {W^{P}_{t}} = w | j_{t} = j\right) \mathbb{P}\left( j_{t} = j\right)\\ &=& \mathbb{P}\left( w \in AW_{t}\right) \mathbb{P}\left( {W^{P}_{t}} = w| j_{t} = j\right) \mathbb{P}\left( j_{t} = j\right)\\ &=& \frac{n-(t-1)}{n} \frac{f^{*}_{wj}}{r_{j}} \frac{r_{j}}{n}\\ &=& \frac{1}{n}\frac{n-(t-1)}{n} f^{*}_{wj}. \end{array} $$

For the first equality, we use that the job type at time t and the selection of the preferred worker are independent from whether w is available at time t. The second equality follows from Lemma 4, the weighted random selection of the preferred worker, and the job arrival process.

We use \(\mathbb {P}\left (I^{t}_{wj} = 1\right ) = \frac {1}{n}\frac {n-(t-1)}{n} f^{*}_{wj}\) to bound the total probability of assigning worker w for a job of type j:

$$ \mathbb{P}\left( I_{wj} = 1\right) = \sum\limits_{t=1}^{n} \mathbb{P}\left( I^{t}_{wj} = 1\right) \ge \sum\limits_{t=1}^{n} \frac{1}{n}\frac{n-(t-1)}{n} f^{*}_{wj} = \frac{1}{2} \frac{n+1}{n}f^{*}_{wj} \ge \frac{1}{2}f^{*}_{wj}. $$

□

Lemma 5 bounds the probability that worker w is matched to a job of type j. By linearity of expectation, Theorem 1 and the \(\frac {1}{2}\) competitive ratio follow almost immediately from Lemma 5.

Proof Proof of Theorem 1

The expected utility returned by the algorithm is a weighted sum of indicators Iwj, where Iwj = 1 when worker w is assigned to a job of type j and 0 otherwise. Note that each worker is assigned to at most one job (type). We can then apply Lemma 5 to bound the probability P(Iwj = 1) and the expected utility of the algorithm:

$$ \begin{array}{@{}rcl@{}} \mathbb{E}\left[\textsc{Dispatch}{}(\widehat{G})\right] &=& \mathbb{E}\left[ \sum\limits_{w \in W, j \in J} u_{wj} I_{wj} \right] \\ &=& \sum\limits_{w \in W, j \in J} u_{wj} \mathbb{E}\left[I_{wj}\right] \\ &=& \sum\limits_{w \in W, j \in J} u_{wj} \P{I_{wj} = 1} \\ &\ge& \frac{1}{2} \sum\limits_{w \in W, j \in J} u_{wj} f^{*}_{wj}= \frac{1}{2} TPP(G). \end{array} $$

Note that the inequality requires that the utility weights are non-negative.

Finally, we apply Lemma 1 to obtain a bound on the competitive ratio attained by Dispatch for any expectation graph G and distribution \(\mathcal {D}(J)\):

$$ \mathbb{E}\left[\textsc{Dispatch}{}(\widehat{G})\right] \ge \frac{1}{2} TPP(G) \ge \frac{1}{2} \mathbb{E}\left[OPT(\widehat{G})\right] $$

□

4 Best-Possible Competitive Ratio

We present here a family of instances for which any online algorithm attains a competitive ratio of at most \(\frac {1}{2}\). The Dispatch algorithm guarantees a competitive ratio of \(\frac {1}{2}\) and is thus optimal with respect to competitive ratio.

Theorem 2

For the online perfect bipartite matching problem with an i.i.d. arrival process, no online algorithm can achieve a competitive ratio better than \(\frac {1}{2}\) .

Proof

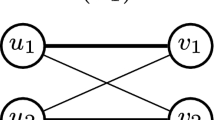
Consider an instance G with the number of job types k = n + 1. Let the job types be indexed from 0 to n and the workers from 1 to n. Job types 1 to n each arrive with probability p/n and job type 0 arrives with probability 1 − p. For this graph, we set uwj = 1 if w = j and to 0 otherwise. This implies uw,0 = 0 for all w ∈ W. See Fig. 2 for an illustration.

Fig. 2
figure 2

Expectation graph G = (W,J,E) used in the proof of Theorem 2. Edges in black have a utility of 1 and edges in gray have a utility of 0

Full size image

Note that OPT gains a utility of one per unique job type in {1,…,n} that arrives. The expected number of unique job types is computed by considering each job type as a geometric random variable with a success probability of \(\frac {p}{n}\). Thus, \(\mathbb {E}\left [OPT(\widehat {G})\right ] = n \left (1 - \left (1 - \frac {p}{n}\right )^{n}\right )\).

For any online algorithm ALG∗, t − 1 workers are no longer available at time step t regardless of the strategy. Thus, with probability \((1-p) + p \frac {t-1}{n}\) the increase in utility is zero. Thus, the total expected utility increases by at most \(p \frac {n - (t-1)}{n}\) in time step t. The total expected utility obtained by ALG∗ is then:

$$ \mathbb{E}\left[ALG^{*}(\widehat{G})\right] \le p \frac{n}{n} + p \frac{n-1}{n} + p \frac{n-2}{n} + {\dots} + p \frac{1}{n} = \frac{1}{2} p (n+1) $$

We compute the relevant ratio and then take the limit as n goes to infinity:

$$ \lim_{n \rightarrow \infty} \frac{\mathbb{E}\left[ALG^{*}(\widehat{G})\right]}{\mathbb{E}\left[OPT(\widehat{G})\right]} = \lim_{n \rightarrow \infty} \frac{\frac{1}{2} p (n+1)}{n \left( 1 - \left( 1 - \frac{p}{n}\right)^{n}\right)} = \frac{1/2 \cdot p}{1 - e^{-p}} $$

Since p can take on any value in the interval (0,1), we consider the limit as p goes to zero:

$$ \lim_{p \rightarrow 0^{+}} \frac{1/2 \cdot p}{1 - e^{-p}} = \frac{1}{2}. $$

□

Corollary 1

Dispatch achieves the best-possible competitive ratio of \(\frac {1}{2}\) for the Online Perfect Bipartite Matching problem.

5 Conclusion

In this paper, we examine the problem of online perfect bipartite matching with i.i.d. arrivals from a known distribution. We present the Dispatch algorithm. It attains a competitive ratio of \(\frac {1}{2}\). We show that this is the best possible. Thus, the algorithm Dispatch is optimal in terms of competitive ratio.

There is an intriguing difference between online perfect bipartite matching algorithms for minimization and the Dispatch algorithm for maximization. Whereas the competitive ratio for minimization is bounded logarithmically, a constant bound was obtained for maximization with i.i.d. arrivals. This raises the question of whether a constant competitive ratio is possible for minimization with i.i.d. arrivals.

It may be possible to translate the analysis in this work to other contexts. Our analysis relied on two key ideas; the use of the expectation graph and proving that, regardless of how the jobs arrive, the Dispatch algorithm effectively translates the non-uniform sampling over jobs to a uniform sampling over workers.