The Strong Price of Anarchy of Linear Bottleneck Congestion Games

Abstract

We study the inefficiency of equilibrium outcomes in Bottleneck Congestion games. These games model situations in which strategic players compete for a limited number of facilities. Each player allocates his weight to a (feasible) subset of the facilities with the goal to minimize the maximum (weight-dependent) latency that he experiences on any of these facilities. We analyze the (strong) Price of Anarchy of these games for a natural load balancing social cost objective, i.e., minimize the maximum latency of a facility. In our studies, we focus on Bottleneck Congestion games with linear latency functions. These games still constitute a rich class of games and generalize, for example, Load Balancing games with identical or uniformly related machines (with or without restricted assignments). We derive upper and (asymptotically) matching lower bounds on the (strong) Price of Anarchy of these games. We also derive more refined bounds for several special cases of these games, including the cases of identical player weights, identical latency functions and symmetric strategy sets. Further, we provide lower bounds on the Price of Anarchy for k-strong equilibria.

1 Introduction

Load Balancing games constitute an important class of strategic games that capture many applications of practical relevance. These games model situations in which a set of strategically acting players (or jobs) compete for a limited number of resources (or machines). Every player chooses one of the resources available to him and assigns his weight (or load) to this resource. The latency of a resource depends on the total weight of the players using it. The goal of each player is to select a resource such that the latency that he experiences on this resource is minimized.

The study of Load Balancing games is motivated by the need for quantifying the inefficiency caused by the selfish behavior of a set of autonomous players that utilize distributed processors upon which a system is built. The social cost objective of an assignment of loads to processors is measured by the makespan, i.e., the completion time of the most loaded machine, which reflects the distance from equi-distribution (balancing) of the load to the machines. Load Balancing games have recently been studied extensively for a variety of different machine environments, including identical [20], uniformly related [11, 15, 19, 20], restricted assignment [5, 15], and unrelated machines [2].

A natural generalization of Load Balancing games are Bottleneck Congestion games (BCGs) [6, 17]. Here, every player chooses a subset of the resources (also referred to as facilities in this context) from a set of feasible facility allocations and assigns his weight to each of these facilities. The goal of each player is to select a subset of the facilities such that the maximum latency that he experiences over the chosen facilities is minimized. Load Balancing games constitute a special case of BCGs in that the strategy space of each player contains only singleton subsets of facilities (machines), i.e., the strategy of each player is always a single facility. Another interesting special case of BCGs are Bottleneck Network Routing games [6]. In these games, the facilities are identified with the links of an underlying network and the players’ strategies correspond to paths in the network. Despite their importance, BCGs have received relatively little attention in the literature and are far from being well-understood. In this paper we study the inefficiency of stable outcomes in these games.

Bottleneck Congestion games essentially generalize the context of Load Balancing games by modeling the activity of each selfish player upon complexes of interrelated resources. This generalization brings the model closer to reality because in most large scale computing systems, the workload of a player occupies different components of the system simultaneously. For example, instantiations of such games emerge if the components form paths in networks, or if they correspond to interconnected parallel processors, etc. It is natural to assume that each player wants to balance his load across the different components available to him and, hence, attempts to minimize the maximum latency of a facility that he uses.

One of the most prominent solution concepts for the prediction of outcomes of rational behavior in strategic games is the Nash equilibrium concept. It describes outcomes that are resilient to unilateral player deviations. Throughout this paper we will focus exclusively on pure strategy deviations. A more general solution concept is the strong equilibrium concept introduced by Aumann [3]. It describes outcomes of strategic games that are stable with respect to coordinated pure deviations of player subsets (also referred to as coalitions). More precisely, an outcome of a strategic game is a strong equilibrium if no coalition of the players can deviate such that every member of the coalition strictly benefits. An outcome is said to be a k-strong equilibrium if this property holds for all coalitions of size at most k. Strong equilibria thus generalize the pure Nash equilibrium concept (k = 1). Harks, Klimm and Möhring [17] showed that (under quite loose assumptions) BCGs always admit strong equilibria.

It is well known that equilibrium outcomes might be inefficient in the sense that they are suboptimal with respect to some socially desirable objective function. A natural social cost objective function that has been studied intensively in the context of Load Balancing games is to minimize the maximum latency of a facility. We will use it also here for our investigations of the inefficiency of equilibria for BCGs.

The Price of Anarchy (PoA) [20, 21, 23] has become the standard measure to assess the inefficiency of equilibrium outcomes. It is defined as the worst-case ratio (over all instances) of the maximum cost of a Nash equilibrium outcome and the cost of a socially optimal outcome. The strong Price of Anarchy (SPoA) and the k-strong Price of Anarchy (k-SPoA) [2] refer to the natural adaptations of this measure to strong and k-strong equilibrium outcomes, respectively.

1.1 Our Contributions

We study the inefficiency of both pure Nash equilibria and strong equilibria of BCGs. In our studies, we focus on BCGs with linear latency functions, where the latency of each facility is a linear function of the total weight assigned to it. These games still constitute a rich class of games and generalize, for example, Load Balancing games with identical or uniformly related machines (with or without restricted assignments). We provide upper and lower bounds on the (strong) Price of Anarchy for symmetric and asymmetric linear BCGs (definitions will be given below). An overview of the main results obtained in this paper is given in Table 1. Here, n and m refer to the number of players and facilities, respectively.

Table 1 Summary of the bounds obtained for the SPoA and the k − SPoA of linear BCGs

Our main contributions are as follows:

• 1. We show that both the PoA and the SPoA of linear BCGs is Θ(m). More precisely, we show that m ≤ PoA ≤ 2m−1 and m−1 ≤ SPoA ≤ m. These results hold for linear BCGs in general.

  For comparison, Gairing et al. [15] proved that m−1 ≤ PoA ≤ m for the case of Load Balancing games with uniformly related machines and restricted assignments (which is a special case of the linear BCGs considered here). Further, Banner and Orda in [6] showed that PoA = Θ(m) for network BCGs with identical latency functions of the form x ^p (where p is a constant).

• 2. We also derive bounds for linear BCGs with identical players, i.e., when all players have the same weight. In general, for asymmetric BCGs, we establish an upper bound of $\text {SPoA} =O\left (\sqrt {n}\right )$. For symmetric BCGs, i.e., when all players have the same strategy space, we derive an (exact) bound of SPoA = 2.

  Previously, Gairing et al. [15] proved an upper bound $\text {PoA} = O(\log n/\log \log n)$ for Load Balancing games with uniformly related machines and restricted assignments (which is a special case of asymmetric linear BCGs).

• 3. We also consider linear BCGs with identical facilities, i.e., when the latency functions of all facilities are the same. For asymmetric BCGs, we show that $\text {SPoA} = \Theta \left (\sqrt {m}\right )$. Further, for symmetric BCGs, we show that SPoA = 2. In fact, the lower bound of 2 on the SPoA for symmetric BCGs with identical players mentioned above also holds for identical facilities. We also give elaborate lower bounds on the k-SPoA for symmetric and asymmetric BCGs (see Table 1 for details).

  We note that Load Balancing games with identical machines constitute a special case of symmetric linear BCGs with identical facilities. For these games, Andelman, Feldman and Mansour [2] showed a lower bound of 2m/(m + 1) on the SPoA, which approaches 2 as the number m of machines (which correspond to the facilities) goes to infinity. Our bound is exact and we show that the worst-case occurs even for a constant number of facilities and players. In [2] an exact bound of 2 was shown for the SPoA of Load Balancing games with unrelated machines; in this setting, the weights of the players may vary, depending on the machine they choose. Thus, the lower bound of 2 in this case is incomparable to our lower bound.

• 4. Finally, we also provide asymptotically tight worst-case examples for (directed) network linear BCGs (definitions will be given below).

1.2 Related Work

One of the earliest works concerning Network BCGs is by Caragiannis et al. [9]. The authors devised polynomial time algorithms for computing pure Nash equilibria, on single sink and/or single source networks, with linear latency functions. They also provided bounds on the PoA of equilibria for such networks. Network BCGs were also considered by Banner and Orda [6]. The authors showed existence of pure Nash equilibria and provided an Θ(m) bound on the PoA for identical network links with latency functions of the form x ^p, where p is some constant. Busch and Magdon-Ismail [8] studied the PoA of network BCGs with identical players. Harks et al. [17] introduced general BCGs and showed that strong equilibria are guaranteed to exist in these games. In [16], the problem of computing pure Nash equilibria and strong equilibria is addressed. The paper shows several hardness results and proposes polynomial time algorithms for special cases. In a very recent work, Busch and Kannan [7] study the PoA of BCGs under the assumption that the players have strategy spaces with bounded stretch; here the stretch constitutes a measure of variation in resource utilization.

As mentioned above, BCGs generalize Load Balancing games, which have been studied intensively in recent years. Load Balancing games were first studied by Koutsoupias and Papadimitriou in their seminal work [20], where they introduce the Price of Anarchy notion. Among other results, they prove for Load Balacing games with m identical machines a lower bound of $\Omega (\log m/\log \log m)$ on the PoA for mixed Nash equilibria. Czumaj and Vöcking [11] and Koutsoupias, Mavronicolas and Spirakis [19] proved a matching upper bound. For Load Balancing games with uniformly related machines, Czumaj and Vöcking [11] show that $\text {PoA}=\Theta (\log m/\log \log \log m)$ for mixed Nash equilibria.

Concerning the PoA of pure Nash equilibria, an upper bound of $\frac {2m}{m+1}$ for m identical machines follows from an early approximation analysis of a local search heuristic for scheduling by Finn and Horowitz [14]. Schuurman and Vredeveld [25] gave a matching lower bound example. Czumaj and Vöcking [11] proved that the pure PoA for Load Balancing games on uniformly related machines is $\Theta (\log m/\log \log m)$. Awerbuch et al. [5] showed that the pure PoA of Load Balancing games with m identical machines and restricted assignments is also $\Theta (\log m/\log \log m)$. Independently, Gairing et al. [15] obtained the same bounds. Further, the authors prove that for m uniformly related machines with restricted assignments, m−1 ≤ PoA ≤ m. For a detailed coverage of these results we refer the reader to [26].

Andelman, Feldman and Mansour [2] were the first to study strong equilibria and k-strong equilibria in the context of Load Balancing games. For the case of munrelated machines, they proved that m ≤ SPoA ≤ 2m−1. Later, Fiat et al. [13] improved these bounds and showed that SPoA = m for these games. The authors also proved that for uniformly related machines the SPoA is $\Theta \left (\log m/(\log \log m)^{2}\right )$. For results in the context of more general scheduling games and associated scheduling policies (called coordination mechanisms), the interested reader is referred to [18] and the references therein.

Bottleneck Congestion games owe their name to their similarity to congestion games, which were introduced by Rosenthal [24]. In these games, the latency on each facility depends on the number of players using it (i.e., players have unit weights). The goal of each player is to minimize his cost which is defined as the sum (as opposed to the maximum for BCGs) of the latencies over the facilities used by the player. Rosenthal [24] proved the existence of pure Nash equilibria in congestion games, by usage of potential function arguments. Monderer and Shapley proved in [22] that the class of congestion games coincides isomorphically with the class of finite potential games. The Price of Anarchy of pure Nash equilibria for congestion games was resolved by Christodoulou and Koutsoupias [10] and, independently, by Awerbuch, Azar and Epstein [4]. It is shown in [10] that $\text {PoA}=\Theta \left (\sqrt {n}\right )$ for asymmetric linear congestion games and the social cost being the maximum over the players’ costs, and $\text {PoA}=\frac {5}{2}$ for (symmetric and asymmetric) linear congestion games and the social cost being the sum of the players’ costs. Bounds for polynomial latency functions were also derived in [10]. Exact bounds for polynomial latencies and also for weighted players were developed in [1].

2 Preliminaries

In a Bottleneck Congestion game, we are given a set N = [n] of n players that want to utilize non-cooperatively a set E = [m] of m resources, which we also refer to as facilities.¹ Every player i ∈ N has a positive weight (or load) w _i > 0 and a strategy set $\Sigma _{i}\subseteq 2^{E}$ of feasible facility subsets which he can choose from. If player i chooses facility subset S _i ∈Σ _i , he allocates his entire weight w _i to each facility e ∈ S _i . Let $\Sigma = \Sigma _{1} \times {\dots } \times \Sigma _{n}$ be the set of all possible strategy choices of the players. A strategy profile $S = (S_{1}, \dots , S_{n}) \in \Sigma$ specifies for each player i ∈ N a strategy S _i ∈Σ _i that he has chosen. We define N _e (S) to be the set of players that have chosen facility e ∈ E under S, i.e., N _e (S) = {i ∈ N | e ∈ S _i }. The total weight of facility e ∈ E with respect to S is defined as $w_{e}(S) = {\sum }_{i \in N_{e}(S)} w_{i}$.

Every facility e ∈ E is associated with a latency function $l_{e}: \Sigma \rightarrow \mathbb {R}^{+}$, which satisfies the following three properties (see also [17]):

• 1. Non-negativity: l _e (S) ≥ 0 for all S∈Σ.

• 2. Independence of irrelevant alternatives: $l_{e}(S) = l_{e}(S^{\prime })$ for all $S, S^{\prime } \in \Sigma$ with $N_{e}(S) = N_{e}(S^{\prime })$.

• 3. Monotonicity: $l_{e}(S) \geq l_{e}(S^{\prime })$ for all $S, S^{\prime } \in \Sigma$ with $N_{e}(S) \supseteq N_{e}(S^{\prime })$.

In this paper, we focus on linear latency (thus, also cost) functions; we motivate our choice in Example 1 below. We call a game symmetric if all players have the same strategy set, i.e., Σ _i = Σ _j for all i, j ∈ N; we call a game asymmetric otherwise. Under a given a strategy profile S∈Σ, every player i ∈ N experiences an individual cost c _i (S) equal to the latency of the facility in S _i with the highest latency, i.e., $c_{i}(S)=\max _{e\in S_{i}}l_{e}(S)$. We assume that every player i ∈ N acts strategically and chooses his strategy S _i ∈Σ _i in order to minimize his own individual cost c _i (S).

Aumann [3] introduced the notion of a strong equilibrium. Here we consider the refined notion of k-strong equilibrium. We use the standard notation S _−i for $(S_{1},\dots , S_{i-1}, S_{i+1},\dots , S_{n})$. Similarly, for a subset of players $I\subseteq N$ we use S _I and S _−I to refer to the strategy profiles induced by the strategies of players in I and N∖I, respectively. For every facility e ∈ E and every subset of players $I \subseteq N$, we use the notation l _e (S _I ) to denote the latency of e under the strategy profile S _I , induced only by the players in I (i.e., as if all players in N∖I are absent).

Definition 1

A strategy profile S∈Σ is a k-strong equilibrium if for every non-empty player subset $I\subseteq N$ with |I| ≤ k and for every possible joint deviation $S_{I}^{\prime }$ of I there is at least one player i ∈ I, whose cost with respect to $S^{\prime } = \left (S_{-I}, S_{I}^{\prime }\right )$ is not stroctly better than with respect to S, i.e., $c_{i}\left (S_{-I},S_{I}^{\prime }\right ) \ge c_{i}(S)$.

With this definition, a strong equilibrium is a k-strong equilibrium with k = n, and a pure Nash equilibrium is a k-strong equilibrium with k = 1. Very recently, Harks, Klimm and Möhring [17] showed that strong equilibria always exist in BCGs satisfying Properties 1–3 above.

We are interested in characterizing the inefficiency of k-strong equilibria for (linear latency) BCGs. We assess the efficiency of a strategy profile S by the maximum load of a facility under S. That is, the social cost C(S) of a strategy profile S∈Σ is defined as the maximum latency over all facilities, which is equivalent to the maximum cost over all players, i.e., $C(S)=\max _{e \in E} l_{e}(S)=\max _{i \in N} c_{i}(S)$. We will use S ^∗ to refer to an optimal strategy profile that minimizes C(S) and denote its cost by γ ^∗=C(S ^∗).

The k-strong Price of Anarchy (k-SPoA) [2, 20] refers to the worst-case ratio over all possible input instances of the maximum cost of a k-strong equilibrium and the cost γ ^∗ of the social optimum. We will simply refer to the Price of Anarchy (PoA) and strong Price of Anarchy (SPoA) for the 1-SPoA and the n-SPoA, respectively.

We next give an example showing that the SPoA is unbounded, even for symmetric BCGs with arbitrary latency functions on the facilities satisfying Properties 1–3 above.

Example 1

We construct a BCG with n = 2 players and m = 3 facilities, denoted e ₁, e ₂ and e ₃. Let Σ₁ = {{e ₁},{e ₂}} and Σ₂ = {{e ₂},{e ₃}}. The latency functions are defined as follows. Let M≫𝜖 > 0.

$$l_{e_{1}}(S) = \epsilon, {\kern15pt} l_{e_{3}}(S) = M, {\kern15pt} \text{and}{\kern15pt} l_{e_{2}}(S)= \left\{\begin{array}{ll} M & \text{if} \,\,N_{e_{2}}(S) = \{1,2\} \\ \epsilon & \text{otherwise.} \end{array}\right. $$

The socially optimal strategy profile is $S^{\ast }=\left (S_{1}^{\ast },S_{2}^{\ast }\right )$ with $S_{1}^{\ast }=\{e_{1}\}$ and $S_{2}^{\ast }=\{e_{2}\}$. We have C(S ^∗) = 𝜖. Consider the strategy profile $S=\left (S_{1},S_{2}\right )$, where S ₁ = {e ₂} and S ₂ = {e ₃}. Clearly, C(S) = M. We claim that S is a strong equilibrium. Indeed, the only alternative strategy for player 1 is {e ₁}, which will incur him an individual cost of 𝜖 = c ₁(S). This rules out a unilateral deviation of player 1, but also a joint deviation along with player 2. The only alternative strategy for player 2 is {e ₂}, which will incur him a cost of M = c ₂(S), if he deviated unilaterally. The SPoA in this example is at least M/𝜖.

We can easily modify the above instance to make it a symmetric BCG: we include strategy {e ₁} in Σ₂ and define $l_{e_{1}}(S)=\infty$ if $2\in N_{e_{1}}(S)$ (thus, e ₁∈S ₂). Similarly, we include strategy {e ₃} in Σ₁ and define $l_{e_{3}}(S)=\infty$ if $1\in N_{e_{3}}(S)$ (thus, e ₃∈S ₁). Note that the latency functions of the resulting symmetric BCG satisfy Properties 1–3 above.

A final comment is in order. Structurally, the BCG defined in Example 1 appears to be identical to a Load Balancing game (such as the ones studied in [2]) with 2 players and 3 machines. The difference, however, is in the definition of the latency functions. In Load Balancing games the latency of each machine (facility) is additive in the players’ loads (weights), whereas in our example the latencies are super-additive; this is especially visible in the definition of $l_{e_{2}}$ above.

This example motivates our study of linear BCGs. We assume that the latency function l _e of each facility e ∈ E is a linear function of the total weight assigned to it, i.e., l _e (S) = a _e w _e (S) for some a _e ≥ 0. Linear BCGs constitute an important class of BCGs because they generalize, for example, various Load Balancing games as outlined in the Introduction. In particular, Load Balancing games with uniformly related [11] or identical machines, also involving restricted assignments (see [15]), constitute important special cases of linear BCGs.

A BCG is called a network BCG if there exists a directed graph G = (V, E) such that every player i ∈ N is associated with a source s _i ∈V and a sink t _i ∈V and i’s strategy set Σ _i refers to the set of all directed paths from s _i to t _i in G. Observe that the above example corresponds to a network BCG, with parallel links connecting a single source node to a single sink (each facility corresponds to a distinct link).

Unless stated otherwise, we assume subsequently that all player weights are at least one, i.e., w _i ≥ 1 for every i ∈ N; this assumption is without loss of generality as we can always enforce it, by scaling the weights appropriately. Moreover, when studying identical facilities, we assume that the latency functions are identities, i.e., l _e (S) = w _e (S) for every e ∈ E.

3 Facilities with Arbitrary Linear Latencies

In this section, we derive bounds on the PoA and SPoA of linear BCGs. We consider both the general and the identical player case.

3.1 Arbitrarily Weighted Players

We first consider the most general case of arbitrary linear latency functions and arbitrary player weights. We show that the PoA is at most 2m−1 in this case. We obtain a better bound of m on the SPoA and present an almost tight lower bound.

Theorem 1

The Price of Anarchy of linear Bottleneck Congestion games is at most 2m−1 and at least m.

Proof

Let S be a pure Nash equilibrium with cost C(S) = αγ ^∗ for some α ≥ 1. We prove by induction that for every integer k, $1 \le k < \frac {\alpha +1}{2}+1$, there is a set E _k of k distinct facilities such that for every e ∈ E _k , l _e (S) ≥ (α−k + 1)γ ^∗.

The claim holds true for k = 1 because there must exist a facility e ∈ E with latency l _e (S) = αγ ^∗. Suppose that the induction hypothesis holds true for $k < \frac {\alpha +1}{2}$. We will prove that there exists a set E _{k + 1} of k + 1 distinct facilities such that l _e (S) ≥ (α−k)γ ^∗ for every e ∈ E _{k + 1}. Choose from E _k a facility $\hat e$ with the smallest a _e , i.e., $\hat e = \arg \min _{e \in E_{k}} a_{e}$. By the induction hypothesis, we have $l_{\hat e}(S) \geq (\alpha -k+1)\gamma ^{\ast } > k\gamma ^{\ast }$. Let $I_{\hat e} = N_{\hat e}(S)$ be the set of players choosing $\hat e$ under S. Note that $w_{\hat {e}}(S) = l_{\hat {e}}(S)/a_{\hat {e}} > k\gamma ^{\ast }/a_{\hat {e}}$. Consider the strategies that the players in $I_{\hat e}$ choose under S ^∗ and suppose for the sake of deriving a contradiction that for every $i \in I_{\hat {e}}$, $S^{\ast }_{i} \cap E_{k} \neq {\O }$. Then, by the pigeongole principle, there is a facility e ∈ E _k with $w_{e}(S^{\ast }) \ge w_{\hat e}(S)/k > \gamma ^{\ast }/a_{\hat e}$. By the choice of $\hat e$, we have l _e (S ^∗) = a _e w _e (S ^∗)> γ ^∗, which is a contradiction to the definition of γ ^∗. Thus there is a player $j \in I_{\hat e}$ that chooses a strategy $S_{j}^{\ast }$ that is disjoint from E _k . Note that for every $e \in S_{j}^{\ast }$ we have a _e w _j ≤ γ ^∗. Since S is a pure Nash equilibrium, player j cannot decrease his cost by deviating to $S_{j}^{\ast }$ and, thus, there is some facility $e^{\prime } \in S_{j}^{\ast }\setminus S_{j}$ such that:

$$\begin{array}{@{}rcl@{}} l_{e^{\prime}}(S) &=& \left(a_{e^{\prime}} w_{e^{\prime}}(S) + a_{e^{\prime}} w_{j}\right) - a_{e^{\prime}} w_{j}\\ &\ge& c_{i}(S) - a_{e^{\prime}} w_{j} \ge l_{\hat{e}}(S) - \gamma^{\ast} \ge (\alpha-k)\gamma^{\ast} \end{array} $$

The inductive step follows by setting $E_{k+1} = E_{k} \cup \{ e^{\prime }\}$. By choosing $k = \lceil \frac {\alpha +1}{2} \rceil < \frac {\alpha +1}{2} + 1$, we obtain that there is a set $E_{k} \subseteq E$ with |E _k | ≥ k and thus $m \ge |E_{k}| \ge k \ge \frac {\alpha +1}{2}$. We conclude that PoA = α ≤ 2m−1.

The following instance shows that PoA ≥ m, even for symmetric BCGs with identical facilities and identical players. Consider a BCG with player set N = [n] and facility set E = [m] with m = n. Every player i ∈ N has unit weight w _i = 1 and the latency function l _e (S) of every e ∈ E is the identity function, i.e., l _e (S) = w _e (S). Suppose that each player i ∈ N has strategy set Σ _i = 2^E. If every player chooses a distinct facility we obtain an optimal strategy profile S ^∗ with γ ^∗ = 1. On the other hand, consider the strategy profile S in which every player utilizes all the facilities in E. This is a pure Nash equilibrium of cost C(S) = m. □

We derive a better upper bound on the SPoA for linear BCGs. The following key lemma will be used several times in the paper.

Lemma 1

Let S be a strong equilibrium and let $I_{\lambda } \subseteq I$ be a non-empty subset of players such that for every i∈I _λ we have c _i (S) ≥ λγ ^∗ , for some λ ≥ 1.

• 1. Then, there is a player i∈I _λ and a facility $e \in S_{i}^{\ast }$ such that l _e (S _{−I λ}) ≥ (λ−1)γ ^∗.

• 2. Suppose that I _λ is maximal. Then, there is a subset of players $T_{\lambda } \subseteq N \setminus I_{\lambda }$ with w(T _λ ) ≥ λ−1 and for every i∈T _λ we have (λ−1)γ ^∗ ≤ c _i (S)<λγ ^∗.

Proof

We first prove the first part of the lemma. Note that for every player i ∈ I _λ and every $e \in S_{i}^{\ast }$ we have

$$ l_{e}\left(S_{I_{\lambda}}^{\ast}\right) \le l_{e}\left(S^{\ast}\right) \le \gamma^{\ast}. $$

(1)

Suppose for the sake of a contradiction that for every player i ∈ I _λ and for every $e \in S_{i}^{\ast }$ it holds that l _e (S _{−I λ})<(λ−1)γ ^∗. Consider the strategy profile $S^{\prime } = \left (S_{-I_{\lambda }}, S_{I_{\lambda }}^{\ast }\right )$ in which the players in I _λ deviate to their optimal strategies in S ^∗. Using (1), we obtain for every i ∈ I _λ and for every $e \in S_{i}^{\ast }$:

$$ l_{e}\left(S^{\prime}\right) = l_{e}\left(S_{I_{\lambda}}^{\ast}\right) + l_{e}\left(S_{-I_{\lambda}}\right) < \gamma^{\ast} + (\lambda-1)\gamma^{\ast} = \lambda \gamma^{\ast}. $$

(2)

Thus, for every i ∈ I _λ, $c_{i}\left (S^{\prime }\right ) = \max _{e \in S_{i}^{\ast }} l_{e}\left (S^{\prime }\right ) < \lambda \gamma ^{\ast }$, which is a contradiction to S being a strong equilibrium.

We next prove the second part of the lemma. Let i ∈ I _λ be a player and $e \in S_{i}^{\ast }$ be a facility satisfying $l_{e}\left (S_{-I_{\lambda }}\right ) \ge (\lambda -1) \gamma ^{\ast }$. Define T _λ as the set of players that choose e under S but are not contained in I _λ, i.e., $T_{\lambda } = N_{e}(S) \setminus I_{\lambda } \subseteq N \setminus I_{\lambda }$. We have

$$ a_{e} w(T_{\lambda}) = l_{e}(S_{T_{\lambda}}) = l_{e}(S_{-I_{\lambda}}) \ge (\lambda-1) \gamma^{\ast}. $$

(3)

Since $e \in S_{i}^{\ast }$ and w _i ≥ 1 for every i ∈ N, we have a _e ≤ γ ^∗. Thus, w(T _λ) ≥ λ−1. Consider an arbitrary player i ∈ T _λ. By the above we have, c _i (S) ≥ l _e (S) ≥ l _e (S _{T λ}) ≥ (λ−1)γ ^∗. Moreover, by the maximality of I _λ and since i∉I _λ, we have c _i (S)< λγ ^∗. □

Remark 1

Observe that in the above proof we exploit the linearity of the latency functions only in (2). In fact, we can draw exactly the same conclusion if all latency functions are sub-additive, i.e., for every e ∈ E, l _e (x + y) ≤ l _e (x) + l _e (y) for every $x, y \in \mathbb {R}^{+}$. As a consequence, all our upper bounds on the SPoA that exploit the first part of Lemma 1 hold for sub-additive latency functions.

Theorem 2

The strong Price of Anarchy of linear Bottleneck Congestion games is at most m.

Proof

Let S be a strong equilibrium with cost C(S) = αγ ^∗ for some α > 1. For an arbitrary real value 1 < λ ≤ α, let I _λ be the maximal non-empty set of players I _λ = {i ∈ N | c _i (S) ≥ λγ ^∗}. Applying Lemma 1, we obtain a player set T _λ such that for every i ∈ T _λ we have (λ−1)γ ^∗ ≤ c _i (S)< λγ ^∗. Moreover, w(T _λ) ≥ λ−1 > 0 because λ > 1 and, thus, T _λ is non-empty. We can thus identify a family $F = \{T_{\alpha }, T_{\alpha -1}, \dots , T_{\alpha -k}\}$ of k + 1 player sets that are non-empty and pairwise disjoint, where k is the largest integer satisfying α−k > 1. Every set T _λ∈F identifies at least one distinct facility e ∈ E with (λ−1)γ ^∗ ≤ l _e (S)< λγ ^∗. Moreover, there is one facility e ∈ E with l _e (S) = αγ ^∗. We conclude that m ≥ |F|+1=k + 2 ≥ α and, thus, SPoA = α ≤ m. □

Theorem 3

The strong Price of Anarchy is at least m−1 in general linear Bottleneck Congestion games and at least $\frac {m+1}{3}$ in single-sink linear network Bottleneck Congestion games.

Proof

We describe a directed network BCG; the general case will follow directly. Define 0!=1 and let player i∈[n] have weight w _i = 1/(i−1)! and a source vertex s _i . There is a single sink t for all players and n−1 auxiliary vertices v _i , $i=2,\dots , n$. The set of arcs is $E=E_{1}\cup E_{2}\cup \{\,(s_{1},t),\,(s_{n},t)\,\}$, where:

$$\begin{array}{@{}rcl@{}} E_{1} &=&\left\{\,(s_{i}, v_{i+1})\,\big | \,i=1,\dots,n-1\,\right\} \cup \left\{\,(s_{i},v_{i})\,\big | \,\ i=2,\dots,n\,\right\} \\ E_{2} &=&\left\{\,(v_{i},t)\,\big | \,i=2,\dots,n\,\right\} \end{array} $$

Then, m = |E| = |E ₁| + |E ₂| + 2 = 2(n−1) + (n−1) + 2 = 3n−1. For each arc e ∈ E ₁ set a _e = 1. For $i=2,\dots , n-1$ let $a_{(v_{i},t)}=(i-1)!$. Also, set $a_{(s_{1},t)}=1$ and $a_{(s_{n},t)}=n!$. An example for the case n = 4 appears in Fig. 1. Each player has two strategies, an upper path { (s _i , v _{i + 1}), (v _{i + 1}, t) }, $i=1,\dots , n-1$, and a lower path { (s _i , v _i ), (v _i , t) }, $i=2,\dots , n$. The upper path of player n is {(s _n , t)} and the lower path of player 1 is { (s ₁, t) }.

Fig. 1

An example of a single-sink linear network BCG used to prove the lower bound of Theorem 3. There are n = 4 players and m = 11 links. Player i has weight w _i and source node s _i . Each link is labeled with its latency factor. If every player plays the “lower” path available to him, the maximum latency on any facility is 1. If every player plays the “upper” path available to him, the maximum latency on any facility is 4=(m + 1)/3

Under configuration S, wherein all players play their upper paths we have c _i (S) = i!/(i−1)! = i, thus $C(S)=n=\frac {m+1}{3}$. We claim S is a strong equilibrium. Consider deviation of any coalition $I\subseteq N$ and call $S^{\prime }$ the resulting profile. Let i be a player of minimum index in I and assume first i ≥ 2. Then, under S and $S^{\prime }$, i−1 plays his upper path, { (s _i−1, v _i ), (v _i , t) }. The only deviation available to i is { (s _i , v _i ), (v _i , t) }. Then:

$$\begin{array}{@{}rcl@{}} c_{i}(S^{\prime}) & = & \max\left\{\,l_{(s_{i}, v_{i})}(S^{\prime}),\,l_{(v_{i},t)}(S^{\prime})\,\right\}\\ & = & \max\left\{\,\frac{1}{(i-1)!},\,(i-1)! \cdot \left(\frac{1}{(i-1)!}+\frac{1}{(i-2)!}\right)\,\right\}\\ & = & \max\left\{\,\frac{1}{(i-1)!},\,1+(i-1)\,\right\}=i=c_{i}(S) \end{array} $$

Player 1 will not participate in any coalition, because a cost of 1 is incurred to him under S and when playing his lower path. Then S is a strong equilibrium. In the socially optimum configuration every player plays his lower path alone and has cost c _i (S ^∗)=(i−1)!/(i−1)! = 1. Thus $\text {SpoA}\geq \frac {m+1}{3}$. For the general case we simply regard links in $\{\,(s_{1},t)\,\}\cup E_{2}\cup \{\,(s_{n},t)\,\}$ as m = n + 1 facilities e _j , j∈[n + 1] and restrict every player’s i strategy space to { e _i , e _{i + 1} }. If every player plays e _{i + 1} we obtain a strong equilibrium similar to S described above. The social optimum occurs when player i plays e _i . We omit a detailed analysis because a similar construction appeared in [15]. □

3.2 Identically Weighted Players

We next derive an upper bound on the SPoA for linear BCGs if the weights of all players are identical. In this subsection, we assume, without loss of generality, that the weight of each player i ∈ N is w _i = 1.

Theorem 4

The strong Price of Anarchy of linear Bottleneck Congestion games with identically weighted players is, in general, at most $\frac {1}{2}+\sqrt {2n-\frac {3}{2}}$ ; it is exactly 2 for symmetric such games.

Proof

We prove the first part of the theorem. Let S be a strong equilibrium with cost C(S) = αγ ^∗ for some α > 1. As in the proof of Theorem 2, we can apply Lemma 1 to identify a family $F = \{ T_{\alpha }, T_{\alpha -1}, \dots , T_{\alpha -k}\}$ of k + 1 player sets that are non-empty and pairwise disjoint, where k is the largest integer satisfying α−k > 1. Each such set T _λ∈F contains at least λ−1 players, i.e., |T _λ| ≥ ⌈λ−1⌉ for every α−k ≤ λ ≤ α. Moreover, there is at least one player that experiences a congestion of αγ ^∗. Thus:

$$n \geq 1 + \sum\limits_{\lambda = 1}^{\lceil \alpha-1 \rceil} \lambda \ge 1 + \frac{\alpha(\alpha-1)}{2}. $$

Solving for α, we obtain $\alpha \leq 1/2 + \sqrt {2n - 3/2}$.

We next prove the second part of the theorem. In a strong equilibrium S, at least one player i ∈ N must have cost c _i (S) ≤ γ ^∗ since otherwise the grand coalition could deviate to the socially optimal strategy profile. Suppose there is a player j ∈ N whose cost is more than two times larger than the cost of i. Consider the deviation $S^{\prime } = (S_{-j}, S_{i})$ where player j deviates to the strategy of player i. Then $c_{j}(S^{\prime }) \le \max _{e \in S_{i}} a_{e} (w_{e}(S) + 1) \le \max _{e \in S_{i}} 2a_{e} w_{e}(S) \le 2 c_{i}(S),$ which is a contradiction to S being a strong equilibrium.

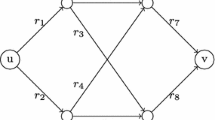
The following example establishes the tightness of this bound. Let N = [3] and E = [6]. Every player i ∈ N has weight w _i = 1 and every facility e ∈ E incurs latency a _e = 1 per unit of load. The strategy set of every player is:

$$\left\{\, \sigma_{1} = \{e_{1}\},\, \sigma_{2} = \{e_{2},e_{3}\},\, \sigma_{3} = \{e_{4},e_{5}\},\, \sigma_{4} =\{e_{2},e_{5},e_{6}\}\, \right\}. $$

The social optimum is $S_{i}^{\ast } = \sigma _{i}$ for every player i∈[3] with γ ^∗ = 1. A strong equilibirum is given by S ₁ = σ ₄ and S ₂ = S ₃ = σ ₁. The cost of S is C(S) = 2. It is easy to see that this example is a (symmetric) network BCG, as depicted in Fig. 2; define the directed arcs e ₁ = (s, t), e ₂ = (s, u), e ₃ = (u, t), e ₄ = (s, v), e ₅ = (v, t), and e ₆ = (u, v). Then each strategy corresponds to an (directed) s – t path. □

Fig. 2

A symmetric network linear BCG instance with identical links as used in the proof of Theorem 4. The strong Price of Anarchy is at least 2 on this instance

4 Facilities with Identical Linear Latencies

In this section, we study the SPoA for the case of linear BCGs with identical facilities, i.e., the latency function of every facility e ∈ E is l _e (S) = w _e (S).

Theorem 5

The strong Price of Anarchy of linear Bottleneck Congestion games with identical facilities is at most $-\frac {1}{2} + \sqrt {2m+\frac {1}{4}}$ , in general, and exactly 2 in the case of symmetric games.

Proof

For the symmetric case we claim that in any strong equilibrium configuration S, there is at least one player i ₀ with $c_{i_{0}}(S)\leq \gamma ^{\ast }$. Indeed, if c _i (S) > γ ^∗ for all players i, then the grand coalition would deviate to S ^∗. Now for any player i we have γ ^∗≥w _i . Let i be any player with e ∈ S _i such that c _i (S) = l _e (S) = C(S). Consider unilateral deviation $S_{i}^{\prime }=S_{i_{0}}$ of i. Then, because S is also a pure Nash equilibrium, C(S) = c _i (S) ≤ c _{i 0}(S) + w _i ≤ 2γ ^∗. A tight lower bound has already been presented in Theorem 4 (with a directly corresponding network example in Fig. 2).

For the asymmetric case let the cost of a strong equilibrium S be C(S) = αγ ^∗, for some α > 1. Similar to the proof of Theorem 2, let I _λ be the maximal non-empty set of players $I_{\lambda } = \left \{i \in N | c_{i}(S) \ge \lambda \gamma ^{\ast } \right \}$ for some 1 < λ ≤ α. By Lemma 1, we obtain a player set T _λ such that for every i ∈ T _λ we have (λ−1)γ ^∗ ≤ c _i (S)< λγ ^∗. We can refine the argument given in the proof of Lemma 1 to bound the weight of T _λ for identical facilities as follows: By inequality (3), we have w(T _λ) ≥ (λ−1)γ ^∗/a _e = (λ−1)γ ^∗, where the last equality holds because for identical facilities a _e = 1 for every e ∈ E. Moreover, w(T _λ) ≥ (λ−1)γ ^∗ > 0 because λ > 1 and thus T _λ is non-empty. That is, we can identify a family $F = \{T_{\alpha }, T_{\alpha -1}, \dots , T_{\alpha -k}\}$ of k + 1 player sets that are non-empty and pairwise disjoint, where k is the largest integer satisfying α−k > 1. Moreover, by construction we have $I_{\alpha } \cap {T}_{\lambda } = {\O }$ for every T _λ∈F and w(I _α )≥αγ ^∗ since facilities are identical. The total weight w(N) is then:

$$\begin{array}{@{}rcl@{}} w(N) &\geq& \alpha \gamma^{\ast} + \sum\limits_{\lambda = \alpha-k}^{\alpha} w(T_{\lambda}) \geq \alpha \gamma^{\ast} + \sum\limits_{\lambda = \alpha-k}^{\alpha} (\lambda - 1) \gamma^{\ast}\\ &\geq & \alpha \gamma^{\ast} + \sum\limits_{\lambda = 0}^{\alpha-1} \lambda \gamma^{\ast}= \alpha \gamma^{\ast} + \sum\limits_{\lambda = 1}^{\alpha-1}\lambda \gamma^{\ast}= \sum\limits_{\lambda = 1}^{\alpha}\lambda \gamma^{\ast} \end{array} $$

The latter equals $\frac {1}{2}\alpha \gamma ^{\ast } (1 + \alpha )$. Observe that γ ^∗ ≥ w(N)/m because facilities are identical. We obtain 2m ≥ α(1+α) or, equivalently, $\alpha \le -1/2 + \sqrt {2m+1/4}$. Since SPoA ≤ α the claim follows. □

Theorem 6

The strong Price of Anarchy of linear Bottleneck Congestion games with identical players and identical facilities is at least $\left \lfloor -\frac {1}{2}+\sqrt {2m+\frac {1}{4}}\right \rfloor$ . For single-sink linear network Bottleneck Congestion games, it is at least $\left \lfloor -\frac {1}{4}+\frac {1}{2}\sqrt {2+2m}\right \rfloor$.

Proof

We give a family of instances with m facilities and n = Θ(m) unweighted players, which we turn into a family of network instances subsequently. Consider a partition of the set of players N into q subsets, $N=\bigcup _{j=1}^{q}P_{j}$, where |P _j |=j, j∈[q]. Denote players in P _j by p _ji , i∈[j]. For each subset P _j make a new set of j distinct facilities $E_{j}=\left \{{e_{1}^{j}},\dots ,{e_{j}^{j}}\right \}$. Define E _{q + 1} = E ₁. For every player p _ji ∈P _j , i∈[j], set the strategy space of p _ji to:

$$\Sigma_{p_{ji}}=\left\{\{e\}\,\big|\,e\in E_{j}\right\}\cup \left\{E_{j+1}\right\} $$

For the socially optimal configuration set $S_{p_{ji}}^{\ast }=\left \{{e_{i}^{j}}\right \}$. Then C(s ^∗)=1. Now consider the configuration S where $S_{p_{ji}}=E_{j+1}$ for i∈[j], j∈[q]. The cost of S is defined by the latency of the unique facility $e = {e_{1}^{1}}\in E_{1}$ and is C(S) = l _e (S) = |P _q |=q. For every player p ∈ P _j , we have c _p (S) = j. We claim that S is a strong equilibrium. Consider any deviation of any coalition $I\subseteq N$. Denote by $S_{p}^{\prime }$ the novel strategy that any player p ∈ I adopts and let $S^{\prime }$ denote the resulting configuration. Notice that for the unique player p ∈ P ₁ we have c _p (S) = 1, hence no deviation may lessen his cost and $P_{1}\cap I={\O }$.

Let $j=\min \left \{j^{\prime }\ |\ P_{j^{\prime }} \cap I \neq {\O }\right \}$; then j ≥ 2, and $S_{j}^{\prime } \cap E_{j} \not = {\O }$. For all j−1 players p _{j−1, i} ∈P _j−1 it holds that $S_{p_{j-1,i}}=E_{j}$, because $I \cap P_{j-1} = {\O }$. Hence, $c_{j}(S^{\prime }) = j - 1 + 1 = j = c_{j}(S)$. In any deviation of any coalition I, at least one player does not have an incentive to deviate jointly with I and, hence, SpoA ≥ q. Now q is the largest integer satisfying $m=|\cup _{j} E_{j}|\geq {\sum }_{j=1}^{q}j=q(q+1)/2$, which yields $q = \lfloor -1/2+\sqrt {2m+1/4} \rfloor$.

We convert the example into a network BCG. To grant access to players in P _j−1 to facilities in E _j , we make a path of length 3, $\left \{(s_{j},u_{ji}),(u_{ji},v_{ji}), (v_{ji},t)\right \}$, for every facility ${e_{i}^{j}}\in E_{j},i\leq j-1$ and a length-2 path $\left \{(s_{j},u_{jj}),(u_{jj},t)\right \}$ for ${e_{j}^{j}}$. Let A _j be the set of arcs in these paths. Node s _j is the source of all players in P _j and t is a common sink for all players. Now we add auxiliary arcs $A_{j}^{\prime }=\left \{(v_{ji},u_{j,i+1})\ |\ i \in [j-1]\right \}$. And, finally, an arc $(s_{j-1}, u_{j1}),j \in \{2,\dots , q\}$, by which players P _j−1 gain access to A _j . For the last group of players we add an arc $\left (s_{q},t\right )$. Let us illustrate the analog of configuration S on the constructed network. All players in p _ji ∈P _j , i∈[j], play the same path strategy:

$$\begin{array}{@{}rcl@{}} S_{ji} & = & \left\{\,\left(s_{j},u_{j+1,1}\right)\,\right\}\\ && \cup \left\{\left(u_{j+1,r},v_{j+1,r}\right),\left(v_{j+1,r}, u_{j+1,r+1}\right)\,\left |\,\right.\ r \in [j]\,\right\}\\ &&\cup \left\{\,\left(u_{j+1,j+1},t\right)\,\right\} \end{array} $$

and $S_{iq}=\left (s_{q},t\right )$ for i∈[q]. See Fig. 3 for an example with q = 4. The proof that S is strong is analogous to the proof given for the non-network example. For the optimal configuration we set $S_{ji}^{\ast }=\left \{(s_{j},u_{ji}),(u_{ji},v_{ji}), (v_{ji},t)\right \}$, for each player p _ij ∈P _j , i< j, and $S_{jj} = \left \{(s_{j}, u_{jj}), (u_{jj}, t)\right \}$. We identify q as the largest integer satisfying for the total number of links m:

$$m\geq\sum\limits_{j=1}^{q}\left(|A_{j}|+|A_{j}^{\prime}|\right)+q=\sum\limits_{j=1}^{q}(3j-1+(j-1))+q-1= 2q^{2}+q-1 $$

which yields $q = \left \lfloor -\frac {1}{4}+\frac {1}{2}\sqrt {2+2m}\right \rfloor$. □

Fig. 3

An example for the SpoA on a single-sink network BCG with 35 identical links and 10 identical players. The strong equilibrium configuration consists of the dotted paths for all players with the same source node and incurs a maximum latency of 4 on the uppermost link in the figure. The social optimum has a cost of 1 and occurs if each player utilizes a distinct (lowermost possible) path from his source node to t. Then, $\text {SpoA}=4\geq -\frac {1}{4}+\frac {1}{2}\sqrt {2+2m}$ (Theorem 6)

4.1 k-Strong Equilibria

In this subsection, we derive more refined lower bounds for the k-SPoA for asymmetric and symmetric BCGs with identical facilities. Particularly, in the symmetric case, we exhibit a lower bound for the k-SpoA of symmetric network linear BCGs which is of the same order as for general symmetric linear BCGs (Theorem 8 below).

Theorem 7

For any k ≥ 2, the k-strong Price of Anarchy of linear Bottleneck Congestion games is at least $\max \left \{\,\left \lfloor \frac {m}{k-1}\right \rfloor -1,\, \left \lfloor -\frac 12 +\sqrt {2m+\frac 14}\right \rfloor \right \}$.

Proof

Take an instance with a set E of m identical facilities and a set N of n = |N|=m identical players (of unit weights). For $k\leq \lfloor \sqrt {m}+1\rfloor$, we divide the facilities and the players into p = k − 1 groups $\left \langle E_{0},N_{0}\right \rangle , \left \langle E_{1},N_{1}\right \rangle ,\dots ,\left \langle E_{p-1},N_{p-1}\right \rangle$. For each group 〈E _r , N _r 〉, we place $\left \lfloor \frac {m}{k-1}\right \rfloor$ facilities in E _r and $\left \lfloor \frac {m}{k-1}\right \rfloor$ players in N _r . The remaining at most k − 2 players and k − 2 facilities are distributed into the existent groups (one player and facility per group). These players and facilities we call residual. We shall not be concerned with residual players and facilities in our construction; for a residual player i ∈ N _r , we will have the corresponding residual facility, e ∈ E _r , to be the player’s only available strategy. Moreover, the residual facility e will not be part of any other player’s strategy. Thus, we may ignore existence of residual players and facilities, as they will not affect the strategic choices of other players, or be affected by them. Then, define $q=\left \lfloor \frac {m}{k-1}\right \rfloor$ and, without loss of generality, we assume q = |E _r | = |N _r |, for $r=0,\dots ,p-1$; we name the facilities in E _r by ${e_{0}^{r}},\dots ,e_{q-1}^{r}$. Let [⋅] _q denote (⋅) mod q. For $r=0,\dots ,p-1$, we define over E _r two kinds of strategies, called ${s_{j}^{r}}$ and ${\sigma _{j}^{r}}$, for every $j\in \{0,\dots ,q-1\}$:

$${s_{j}^{r}} =\left\{\,e^{r}_{j+1},\,\dots,\,e^{r}_{[j+q-1]_{q}}\,\right\},\quad {\sigma_{j}^{r}} =\left\{\,{e_{j}^{r}}\,\right\} $$

Now any specific subset N _r contains q players. Assume w.l.o.g. that they are indexed by $i\in \{0,\dots ,q-1\}$. For a socially optimal configuration, S ^∗, we set $S_{i}^{\ast }=\sigma _{i}^{[r+1]_{p}}$ for $i=0,\dots ,q-1$. Then, each player uses exactly one facility under S ^∗ and C(S ^∗)=1.

Now consider the configuration S, where for each i ∈ N _r , $S_{i}={s_{i}^{r}}$. We make this strategy, along with $\sigma _{i}^{[r+1]_{p}}$, to be the only two available strategies for i. Under S, every player from N _r plays |E _r |−1 = q−1 distinct facilities from E _r and each different player has a different facility of E _r left out of his strategy, S _i . Thus, $C(S) = q-1=\left \lfloor \frac {m}{k-1}\right \rfloor -1$. An example of a 3-strong such configuration S with m = 10 facilities and n = m = 10 players is described in Fig. 4, along with the previously described socially optimal configuration.

Fig. 4

An example for the 3-SPoA of asymmetric linear BCGs with identical facilities (Theorem 7), involving m = 10 facilities (depicted as boxes) and n = m = 10 identical players. Each facility is labeled (inside the box) with the index of a single player using it in the socially optimal configuration. Player indices on the top denote players using each facility at 3-strong equilibrium

We argue that S is a k-strong equilibrium. Consider any coalition, $I\subseteq N$, of players that attempt to switch to their socially optimal strategies. We will show that |I| ≥ k + 1. First, we show that I must contain at least one player from every group. Indeed, let $i_{r}\in I\subseteq N_{r}$ for any $r=0,\dots ,p-1$. Then, i _r has an optimum singleton strategy in $E_{[r+1]_{p}}$. Thus, at least two players from $N_{[r+1]_{p}}$ (using under S the single optimum facility, ${e_{i}^{r}}$, of i _r ) must belong to I, so that it is beneficial for i _r to deviate to his (only alternative) optimum strategy. Then, we deduce inductively that I must contain players from each of the p = k − 1 distinct groups. Secondly, we observe that, from each group, there must exist in I at least 2 players from each group, so that a beneficial (socially optimal) strategy is created for some other player of I (outside the group), to switch to. Otherwise, some player will not be able to strictly improve his cost by deviating jointly within I. Thus, we obtain |I| ≥ k + 1.

For an illustration of the argument, consider the example of Fig. 4 which depicts a 3-strong equilibrium. Only a joint deviation of 4 (or more) players is possible: each player in I = {0,1,7,8} can switch jointly to their optimal strategies and improve their cost by 1.

Combination of the lower bound C(S)/C(S ^∗) obtained above, with the one shown earlier in Theorem 6 for strong equilibria (that are also k-strong for any value of k), yields the result. □

For the social inefficiency of k-strong equilibria in symmetric linear BCGs we obtain the following result.

Theorem 8

The k-strong Price of Anarchy of symmetric linear Bottleneck Congestion games is at least $\max \{\,2,\,\left \lceil m/(2k)\right \rceil \,\}$ . It is at least $\max \{\,2,\,\lceil (m+2)/(6k)\rceil \,\}$ for symmetric network linear Bottleneck Congestion games.

Proof

Take n identical players (of unit weight) and a set of m = 2n identical facilities $E\cup F$, where $E=\{e_{j}\ |\ j=0,\dots ,n-1\}$, $F=\{f_{j}\ |\ j=0,\dots ,n-1\}$. Without loss of generality, we index the players by $i=0,\dots ,n-1$. Let us first define the strategy space of player i. A strategy of player i consists of any contiguous ordered sequence of facilities $e_{j},\dots ,e_{t}$, followed by any contiguous ordered sequence of facilities $f_{t},\dots ,f_{l}$. We allow sequences of facilities in E or F, that “wrap around” modulo n. In the socially optimal configuration player i plays {e _i , f _i } and the social cost is 1.

Now we demonstrate a k-strong equilibrium configuration. Let $q=\left \lceil \frac {n}{k}\right \rceil - 1$. Set the strategy of player i, to $S_{i}=\left \{\{e_{i},\dots ,e_{[i+q]_{n}}\}, \{f_{[i+q]_{n}},\dots ,f_{[i+2q]_{n}}\}\right \}$, where for any $i=0,\dots ,n-1$, we define [i + q] _n = (i + q) mod n. This way each player uses 2(q + 1) facilities, q + 1 from set E and q + 1 from set F. Now we note that every facility in E or F is the first for some player, the second for another and, continuing in the same manner, the (q + 1)-th for some player (distinct from the previous ones). Hence every facility is used by exactly q + 1 players, which yields $C(S)=\left \lceil \frac {n}{k}\right \rceil =\left \lceil \frac {m}{2k}\right \rceil$.

We claim that S is a k-strong equilibrium. Consider deviation of any coalition $I\subseteq N$, |I| ≤ k. We examine the number of valid beneficial strategies that emerge under S _−I , for members of I to adopt in the new configuration. First we notice that removal of any pair of players i ₁, i ₂ from the configuration does not incur a strictly more beneficial valid strategy for any of them. In particular, the most beneficial strategy will include either $\left \{e_{[i_{1}+q]_{n}}, f_{[i_{1}+q]_{n}}\right \}$ or $\left \{e_{[i_{2}+q]_{n}}, f_{[i_{2}+q]_{n}}\right \}$. However $S_{i_{1}}$ and $S_{i_{2}}$ may intersect in at most one facility from each of these sets. Hence there is a facility with cost C(S)−1 in both sets. Now we consider successive removal of players i _r , $r=3,\dots , k$. Strategy $S_{i_{r}}$ can intersect at best with the strategy of one of i ₁, i ₂ at $\left \{e_{[i_{r}+q]_{n}}\right \}$ and with the strategy of the other at $\left \{f_{[i_{r}+q]_{n}}\right \}$. Thus, removal of i ₃ creates a beneficial strategy $\left \{e_{[i_{r}+q]_{n}}, f_{[i_{r}+q]_{n}}\right \}$ of cost C(S)−2, for one player (out of i ₁, i ₂, i ₃). At most q such strategies may be created by removal of q players whose strategies intersect “in their middle” with $S_{i_{1}}$, $S_{i_{2}}$ appropriately. In any case, we may not create more than k − 2 beneficial strategies, by removal of k players. Thus S is k-strong.

By combining the derived lower bound C(S)/C(S ^∗) with the lower bound from Theorem 4, we conclude the proof of the first statement of the result.

For the second statement, we present a network version of the example discussed above. A link is made for each facility e _j , which is followed by a link for facility f _j . Arc e _j leads by an additional link to arc $e_{[j+1]_{n}}$. Similarly for each arc f _j and $f_{[j+1]_{n}}$. Finally, we use n−1 additional arcs for making all players emanate from a single source and n−1 arcs to guide them to a single sink. The source is the tail vertex of some arc in E and the sink is the head vertex of some arc in F. In total we use m = 6n−2 arcs, which yields a k-SpoA lower bound of $\left \lceil \frac {n}{k}\right \rceil =\left \lceil \frac {m+2}{6k}\right \rceil$. By combining this bound with the lower bound of Theorem 4 (which is a network example, as depicted in Fig. 2), we conclude the proof of the second statement.

For an illustration of this construction, Fig. 5 presents a 2-strong equilibrium for 6 identical players and 34 identical links. The maximum latency over all links under this configuration is 3. The social optimum has cost 1 and emerges when all players use link-disjoint paths to reach t from s.

Fig. 5

A lower bounding example for the 2-SPoA of symmetric network linear BCGs with identical links (Theorem 8), involving 6 identical players. Player indices mark the links used by each player at 2-strong equilibrium. In the socially optimal configuration each of the players uses a distinct path from s to t, that is disjoint from the paths used by other players. 6 such paths are visibly existent in the figure

□

5 Summary and Open Problems

In this work, we derived inefficiency bounds for equilibria of linear Bottleneck Congestion games. These games generalize Load Balancing games, which have been investigated extensively in the literature [11, 15, 21]. In particular, we proved upper and lower bounds on the Price of Anarchy of pure Nash equilibria and strong equilibria of linear BCGs. We considered several special cases of these games, including identical players, identical facilities and symmetric strategy spaces. For most of our lower bounds we were able to provide asymptotically equivalent network worst-case examples, wherein the players’ strategies constitute paths over directed networks.

There are still several problems that remain to be resolved, towards completing our understanding of the social inefficiency of equilibria in linear BCGs. In particular, we miss tight upper and lower bounds for symmetric linear BCGs (with arbitrarily weighted players). Additionally, it would be interesting to derive tight upper bounds for the k-strong Price of Anarchy for BCGs with identical facilities to obtain a complete picture of the model’s performance in dependence on the size of the coalitions that can deviate. Finally, it would be also very interesting to derive tight bounds for networks BCGs.